Estimation of the Optimal Surrogate Based on a Randomized Trial

Summary:

A common scientific problem is to determine a surrogate outcome for a long-term outcome so that future randomized studies can restrict themselves to only collecting the surrogate outcome. We consider the setting that we observe n independent and identically distributed observations of a random variable consisting of baseline covariates, a treatment, a vector of candidate surrogate outcomes at an intermediate time point, and the final outcome of interest at a final time point. We assume the treatment is randomized, conditional on the baseline covariates. The goal is to use these data to learn a most-promising surrogate for use in future trials for inference about a mean contrast treatment effect on the final outcome. We define an optimal surrogate for the current study as the function of the data generating distribution collected by the intermediate time point that satisfies the Prentice definition of a valid surrogate endpoint and that optimally predicts the final outcome: this optimal surrogate is an unknown parameter. We show that this optimal surrogate is a conditional mean and present super-learner and targeted super-learner based estimators, whose predicted outcomes are used as the surrogate in applications. We demonstrate a number of desirable properties of this optimal surrogate and its estimators, and study the methodology in simulations and an application to dengue vaccine efficacy trials.

1. Introduction

A common scientific problem is to determine a surrogate outcome for a long-term outcome so that future randomized studies can restrict themselves to only collecting the surrogate outcome. We consider a study where we observe n independent and identically distributed observations of a random variable consisting of baseline covariates, a treatment, a vector of candidate surrogate outcomes measured at or before an intermediate time point, and the outcome of interest at a final time point. We assume that the treatment is randomized, conditional on the baseline covariates. The goal is to use these data to produce a candidate surrogate that is maximally promising for use in future trials for estimation and testing of a mean contrast treatment effect on the final outcome. We define an optimal surrogate for the current study as the function of the true data generating distribution collected by the intermediate time point that satisfies the Prentice definition of a valid surrogate endpoint and that optimally predicts the final outcome: this optimal surrogate is an unknown parameter. In Section 2 we show the highly desirable property that the optimal predictor automatically satisfies the Prentice definition, with one appealing consequence that this optimal surrogate guarantees avoidance of the disastrous ‘surrogate paradox’ [defined as (i) the effect of the treatment on the surrogate is positive, (ii) the surrogate and outcome are strongly positively correlated, but (iii) the effect on the treatment on the outcome is negative] (VanderWeele, 2013) cannot occur. In addition, the average causal effect on the optimal surrogate has the same interpretation as the average causal effect on the clinical endpoint, such that, appealingly, the surrogate effect has the same interpretation as the clinical effect.

In Section 3 we give conditions under which the optimality of the surrogate (and thus its Prentice-validity) is invariant to changes in the joint distribution of the covariates, treatment, and intermediate outcomes. This describes “transportability assumptions” under which the average treatment effect on the optimal surrogate in the new trial (optimized in the current trial and applied in the new trial) equals the average treatment effect on the final outcome in the new trial. Consequently, in a thought experiment where the current trial has infinite sample size such that the optimal surrogate itself is measurable and is used as the surrogate in the new trial, a (1 − α)% confidence interval for the optimal surrogate treatment effect parameter is also a (1 − α)% confidence interval for the clinical treatment effect parameter.

In practice, an estimate of the optimal surrogate must be used as the actual surrogate endpoint. In Section 4 we present a super-learner estimator of the optimal surrogate, thereby incorporating the state of the art in machine learning and nonparametric estimation in an asymptotically optimal way. The cross-validated mean squared error can be used as an objective measure of performance of the surrogate in predicting the final outcome, and the literature provides a confidence interval for the true mean squared error of the super-learner estimator when applied to the training samples in the cross-validation scheme (e.g., van der Laan, Hubbard, and Pajouh, 2013), and is implemented in the SuperLearner R package. In Section 5 we further propose to update the super-learner fit of the optimal surrogate to solve an estimating equation [via targeted minimum loss-based estimation (TMLE)] that ensures that the estimator of the effect of treatment on this targeted estimated optimal surrogate is an asymptotically linear and efficient estimator of the average causal effect of treatment on the outcome of interest in the current trial. Whereas the TMLE update is advantageous compared to the untargeted super-learner estimator of the optimal surrogate given its asymptotic efficiency for the clinical parameter of interest θ₀, it does not improve the ability to generalize inferences to new settings, such that the super-learner alone is a sound strategy for generating promising candidate surrogate endpoints.

Our objective is to develop a most-promising surrogate outcome based on a clinical outcome study with possibly high-dimensional candidate surrogates; in future work we plan to address the related important objective of using the developed surrogate outcome as an endpoint in a future study to make inference (i.e., construct confidence intervals) on the causal effect of treatment in that setting without measuring the clinical outcome (future work is needed because inference based on nonparametric super-learning is a hard problem). However, in Web Appendix A we discuss approaches to inference for the future study based on the previously developed estimated optimal surrogate, accounting for the estimation error. We stress that because the assumptions needed for bridging clinical efficacy based on a surrogate endpoint to a new setting (stated in Theorem 2) are generally difficult to verify, it is recommended that wherever possible (e.g., not prohibited by ethics) future efficacy trials assess efficacy directly based on the true clinical endpoint; moreover this manuscript is about searching for a promising surrogate and does not address surrogate validation that is also of critical importance. In Section 6 we apply the proposed approach to two dengue vaccine efficacy trials. Web Appendix G studies the proposed approach in two simulations and Section 7 concludes with remarks.

1.1. Connection of the optimal surrogate framework to other surrogate frameworks

The newly proposed framework does not fit squarely into any of five existing frameworks for surrogate endpoints– the Prentice (1989) replacement endpoint framework, the controlled direct and indirect causal effects framework (Robins and Greenland, 1992; Joffe and Greene, 2009), the principal stratification framework (Frangakis and Rubin, 2002), the meta-analysis framework (Daniels and Hughes, 1997; Buyse et al., 2000), and the causal selection diagram framework (Pearl and Bareinboim, 2011). It is more similar to the Prentice, meta-analysis, and causal selection diagram frameworks, in being based purely on statistical parameters that are estimable under the basic assumptions typically made in randomized clinical trials. In particular, it aligns most closely with the Prentice framework by taking as its starting point the excellent Prentice definition of a valid surrogate endpoint. In fact, the optimal surrogate is constructed to guarantee satisfaction of the Prentice definition, a unique advantage compared to previous approaches. Under standard assumptions of randomized trials, if the estimated optimal surrogate is consistent for the optimal surrogate as attained via nonparametric learning, then for large sample size trials it must approximately satisfy the Prentice definition. Web Appendix B elaborates the connections of the optimal surrogate framework with the other surrogate frameworks.

The optimal surrogate approach also breaks new ground by searching for promising surrogates based on supervised nonparametric statistical learning. While historically pre-selected univariable or low-dimensional vector candidate surrogates are considered, the proposed approach allows all collected baseline and intermediate response data to potentially contribute to the optimal surrogate, selected and combined through unbiased machine learning, and not requiring parametric modeling assumptions.

2. Statistical Formulation of Estimation of an Optimal Surrogate

Let O_i = (W_i, A_i, S_i, Y_i) ~ P₀ for i = 1,…, n be the i.i.d. data, where W is a vector of baseline covariates, A is a binary treatment assigned at baseline, and S is a vector of intermediate outcomes measured at (or before) some time point τ, and Y is the final univariate outcome of interest measured at a final time point after τ. We assume A is randomized conditional on W.

With S_a and Y_a potential outcomes under each treatment a, let X = (W, S₀, S₁, Y₀, Y₁) denote the full-data structure, with probability distribution P_X,0. The observed data distribution P₀ of O is determined by the full-data distribution P_X,0 and the conditional distribution g₀ of A, given X, where g₀(a | X) = g₀(a | W). The statistical model for P₀ makes at most some assumptions about the conditional distribution g₀ of A given W. For example, if it is a randomized trial, then g₀ is known. Thus the statistical model M for P₀ only (possibly) constrains g₀, but puts no assumptions on the marginal distribution of W nor on the conditional distribution of (S, Y), given A, W.

In future studies one hopes to replace the final outcome Y by a so-called surrogate outcome measured by the intermediate time point τ. At first we consider candidate surrogates as true unknown parameters, where we refer to any real-valued function $(W,A,S)\to \psi (W,A,S)\in ℝ$ as a candidate surrogate, representing a function of the true observed data generating distribution P₀ and of the random variables (W, A, S) collected by time τ. If one wants to consider surrogates that depend on S only through a subset/summary of the S, then the setting is simply applied to S defined by this subset. The key question is now how are we going to define a good surrogate, defined in terms of P₀? To start with we want the surrogate S^ψ ≡ ψ(W, A, S) to be a valid surrogate in the actual study, according to the Prentice definition: that is, E₀(Y₁ − Y₀) = 0 if and only if $E_0\left(S_1^{\psi }-S_0^{\psi }\right)=0$, where the counterfactual $S_a^{\psi }=\psi \left(W,a,S_a\right),a\in \{0,1\}$. This guarantees that in this particular study involving sampling from P₀, a test for $H_0^{\psi }:E_0\left(S_1^{\psi }-S_0^{\psi }\right)=0$, which controls the type-I error at level α, yields a test for H₀ : E₀(Y₁ − Y₀) = 0 with type-I error control at level α, where the latter test is simply defined by rejecting H₀ if and only if $H_0^{\psi }$ is rejected. Importantly, by estimating E₀(Y₁) and E₀(Y₀) separately, our approach applies for a general treatment effect contrast.

We also need a criterion depending on P₀ that can be used to rank valid surrogates based on the data O₁,…, O_n, and to define a P₀- optimal surrogate with respect to that criterion. In this manner, we not only select a P₀-valid surrogate but a P₀-optimal one in the class of P₀-valid surrogates. We would like to select the criterion such that the P₀-optimal surrogate is not only optimal under P₀ with respect to this criterion, but that being P₀-optimal implies that the validity of the optimal surrogate is invariant to a variety of possible changes in the data generating experiment. Or, even better, we would like that the P₀-optimal surrogate is also a P-optimal surrogate (and thus valid) under a variety of P’s different from P₀. For these purposes, our proposed criterion is the following full-data mean squared error:

$$\psi \to MS{E}_{P_{X,0}}(\psi )\equiv \sum _a{E}_{P_{X,0}}\left\{g_0(a|W){\left(Y_a-\psi \left(W,a,S_a\right)\right)}^2\right\}.$$ (1)

That is, our goal is to minimize the weighted mean square prediction error for predicting the actual counterfactual outcome of interest, across the different treatment values, with constraint that the solution must satisfy the Prentice definition as stated above. The idea is that if a participant is assigned treatment A = a and one uses as surrogate outcome $S_a^{\psi }=\psi \left(W,a,S_a\right)$, then one wants that surrogate outcome to be a good approximation of the future outcome Y_a. Depending on the future use of the surrogate, this particular weighting scheme g₀(a | W) could be replaced by another weighting scheme. Given a class Ψ of possible surrogate functions ψ(), the P₀-optimal surrogate in this class is defined as

$${\psi }_0^F=\text{arg}\underset{\psi \in \Psi }{\text{min}}MS{E}_{P_{X,0}}(\psi ).$$

We focus on the nonparametric class Ψ consisting of all functions of (W, A, S). In this case, the choice of weight in $MS{E}_{P_{X,0}}\left(\text{i}.\text{e}.,g_0(a|W)\right)$ does not affect the optimal solution: i.e., the optimal surrogate will be optimal for each choice of weight. The P₀-optimal surrogate ${\psi }_0^F$ is given by

$${\psi }_0^F(w,a,s)=E_0\left(Y_a|W=w,S_a=s\right),$$

which is a standard solution to a minimization problem that is the same under and not under the Prentice definition constraint. The conditional randomization assumption implies that the full-data MSE equals the observed data MSE:

$$MS{E}_{P_{X,0}}(\psi )=MS{E}_{P_0}(\psi )\equiv E_{P_0}{(Y-\psi (W,A,S))}^2.$$

As a consequence, ${\psi }_0^F$ is identifiable from P₀ and can also be defined as:

$${\psi }_0^F(W,A,S)={\psi }_0(W,A,S)\equiv E_0(Y|W,A,S).$$

In other words, due to the randomization of A, we have E₀(Y_a | W = w, S_a = s) = E₀(Y | W = w, S = s, A = a). It also follows that E_P0(ψ₀(W, a, S_a) | W) = E_P0(Y_a | W), which demonstrates that the treatment-specific counterfactual mean of the P₀-optimal surrogate equals the treatment-specific counterfactual mean of the outcome. This shows that an average causal effect of treatment on the P₀-optimal surrogate equals the desired average causal effect of treatment on the outcome. We state this as a theorem.

THEOREM 1: Assume positivity: P₀(A = a|W) > 0 a.e. for a ∈ {0, 1}. Then the minimizer of the counterfactual mean squared error $\psi \to MS{E}_{P_{X,0}}(\psi )$ over all functions (W, A, S) → ψ(W, A, S) satisfying the Prentice definition of a valid surrogate endpoint is given by:

$${\overline{S}}_0={\psi }_0(W,A,S)\equiv E_0(Y|W,A,S).$$

We call this the P₀-optimal surrogate. We also note that the counterfactuals of this P₀-optimal surrogate are given by: ${\overline{S}}_{0,a}=E_0\left(Y_a|W,S_a\right),a\in \{0,1\}$, and $E_{P_0}\left({\overline{S}}_{0,a}|W\right)=E_{P_0}\left(Y_a|W\right)$.

This shows that the P₀-optimal surrogate has the perfect properties of a valid surrogate in the actual P₀-study. Moreover, if each treatment is considered separately, then the minimizer of ${\psi }_a\to MS{E}_{P_{X,a,0}}\left({\psi }_a\right)$ over all functions (W, a, S) → (ψ_a(W, a, S)) is E₀(Y|W, A = a, S), where $MS{E}_{P_{X,a,0}}$ is the a^th term in the sum $MS{E}_{P_{X,0}}(\psi )$ in (1). Therefore the P₀-optimal surrogate is the same whether one minimizes the overall MSE in (1) or minimizes the treatment-specific MSEs separately (as we do in the application and simulations).

In practice, of course, the optimal surrogate cannot be used as a study endpoint, rather it must be estimated and the fitted values used. The statistical estimation problem for the original trial is now defined: we observe n i.i.d. O ~ P₀ ∈ M, the target parameter mapping is defined by Ψ : M → Ψ with Ψ(P) = E_P(Y | W, A, S), and ψ₀ = E_P0(Y | W, A, S) is the true value we aim to learn from the data.

3. Conditions on the New Study P Under Which the P₀-Optimal Surrogate is Also the P-Optimal Surrogate

3.1. Invariance of the P₀-optimal surrogate to changes in the distribution of (W, A, S)

The following theorem is a trivial consequence of the fact that E_P0(Y | W, A, S) does not depend on the choice of joint distribution of (W, A, S), and E_P(Y | W, A = a, S = s) = E_P(Y_a | W, S_a = s) if A is randomized in the P-world. Nonetheless, it demonstrates that the P₀-optimal surrogate is also the P-optimal surrogate in any study P that only differs in the joint distribution of (W, A, S), and preserves the conditional randomization of treatment. We assume both the current and future studies are randomized studies for data structures (W, A, S, Y) and (W*, A*, S*, Y*) with probability distribution P₀ and P, respectively.

THEOREM 2: Assume the current and future randomized studies defined above satisfy (1) Equal Conditional Means: $E_P\left(Y^{*}|W^{*}=w,A^{*}=a,S^{*}=s\right)=E_{P_0}(Y|W=w,A=a,S=s)$ for all (w, a, s) in a support of (W*, A*, S*), (2) a support of (W*, A*, S*) is contained in a support of (W, A, S), and (3) positivity: P₀(A = a|W) > 0 a.e. and P(A* = a|W*) > 0 a.e. for a ∈ {0, 1}. Then, the P₀-optimal surrogate equals the P-optimal surrogate.

Theorem 2 gives sufficient conditions to make the P₀-optimal surrogate still a valid surrogate in a new randomized study that differs in the marginal distribution of W, in the conditional distribution of A given W, and in the conditional distribution of S given A, W.

3.2. Generalizability when the surrogate completely blocks the effects of both treatments

If the new study considers a whole different treatment than in the current study, then its effect on the outcome will be different and one would thus expect that the conditional mean of Y, given W, A, S, will be modified as well. Therefore, the conditions on the new study P in the previous theorem essentially exclude studies that evaluate a new treatment. However, there is an important exception where Equal Conditional Means may more easily hold. The following theorem is merely a special case of the previous theorem, but its implication is that if the outcome Y only depends on the treatment through its effect on the surrogate vector S (i.e., Prentice’s ‘full mediation’ criterion), then the new study can even consider a different treatment as long as it also only affects Y through S again. That is, if S is rich enough that it blocks the effect of the future treatment on the outcome, then the P₀-optimal surrogate can also be used in future studies evaluating different treatments, under a simpler Equal Conditional Means assumption that conditions on (W, S) but not on A.

THEOREM 3: In addition to the conditions of Theorem 2, assume E₀(Y|W, A, S) = E₀(Y|W, S) [and thus also assume E_P(Y*|W*, A*, S*) = E_P(Y*|W*, S*)]. Then, the P-optimal surrogate equals the P₀-optimal surrogate and $E_P\left(Y^{*}|W^{*}=w,A^{*}=a,S^{*}=s\right)=E_P\left(Y_a^{*}|W^{*}=w,S_a^{*}=s\right)$. In addition, $a\to E_{P_0}\left(Y_a|W=w,S_a=s\right)$and$a\to E_P\left(Y_a^{*}|W^{*}=w,S_a^{*}=s\right)$ are constant in a.

3.3. How to define the surrogate in a future study when the transportability assumptions fail?

Typically it is not reasonable to assume that the intermediate variable S completely blocks the effect of treatment (current and new) on the outcome, and even if it did, Equal Conditional Means may not hold. Web Appendix A discusses how E_P0(Y | W, A, S) may still often be a good candidate surrogate for such a future study, and discusses implications about differences between E_P(Y* | W* = w, A* = a, S*= s) and $E_{P_0}(Y|W=w,A=a,S=s)$.

4. Super-learning of the P₀-Optimal Surrogate

Estimation of the P₀-optimal surrogate is a standard prediction problem. That is, we estimate E₀(Y | W, A, S) with a minimizer of the risk of a loss: ψ₀ = argmin_ψ P₀L(ψ), with Pf ≡ ʃ f(o)dP(o). For example, one could use squared error loss L(ψ)(O) = (Y − ψ(W, A, S))². To construct an optimal estimator among any given class of candidate estimators, we use loss-based super-learning. The oracle inequality for the cross-validation selector guarantees that the estimator is asymptotically at least as good as any candidate in the set of candidate estimators (van der Laan, Polley, and Hubbard, 2007; van der Laan and Rose, 2011). We summarize how super-learner is used, with details provided in Web Appendix D. Super-learner operates by specifying a library of candidate estimators, and for each one computing the cross-validated risk (CV-RISK) [formula (1) in Web Appendix D] using squared error loss L(·) to be consistent with our proposed criterion (1) for the optimal surrogate. The discrete super-learner estimator is the candidate estimator with smallest CV-RISK and the super-learner is the convex combination of candidate estimators with smallest CV-RISK. Estimation of CV-RISK involves re-running the whole super-learner on learning samples and averaging estimates of the conditional risk on test samples.

One can also define a cross-validated R² (CV-R²) taking values between 0 and 1 based on CV-RISK [formula (2) in Web Appendix D] that provides a universal measure of the strength of a given estimated surrogate $\widehat{\text{Ψ}}$, allowing us to compare different candidate surrogate estimators within and across studies. For example, one might construct a super-learner ${\widehat{\text{Ψ}}}_{\delta }$ based on δ-specific subsets (W_δ, A, S_δ) of the complete (W, A, S), where δ is a measure of the complexity of the resulting surrogate as a function of (W, A, S). One could now plot CV-R² of ${\widehat{\text{Ψ}}}_{\delta }$ against δ for a sequence of δ-values, and the user can decide on a choice of δ taking into account both complexity and strength of the surrogate. This analysis is practically important given that all of the variables (W_δ, S_δ) used in the estimated optimal surrogate need to be collected in a future trial to use this surrogate in that trial; in practice some variable sets may be selected based on their high likelihood of being collected.

5. The Targeted Estimated Optimal Surrogate Captures All Information About Outcome for the Sake of Estimation of the Average Treatment Effect

One could estimate the optimal surrogate E₀(Y | W, A, S) based on any model for the conditional mean. If (W, S) is moderate-to-high dimensional, then it is typically infeasible to attain a consistent estimator of E₀(Y | W, A, S) based on a particular parametric model, because of insufficient knowledge. Accordingly the super-learner estimator is advantageous for maximizing the chance of achieving consistent estimation and providing the most accurate finite-sample estimation. In this section, we provide a result that updating the initial super-learner estimator through TMLE yields a targeted estimate of the P₀-optimal surrogate that captures all information about the clinical outcome in the following sense. If one would use this targeted estimate as the actual outcome of interest in the current study, and one estimates the average treatment effect on this surrogate with an efficient TMLE based on the reduced data in the current study that ignores the clinical outcome, then this TMLE estimate is an efficient estimator of the average treatment effect on the actual clinical outcome.

5.1. The targeted estimate of the P₀-optimal surrogate using TMLE

Suppose Y is binary or continuous in (0, 1). Let ψ_n be the super-learner estimator of ψ₀(W, A, S) = E₀(Y | W, A, S). Consider the submodel $\text{Logit\hspace{0.17em}}{\psi }_n^{\#}(ϵ)=\hspace{0.17em}\text{Logit\hspace{0.17em}}{\psi }_n^{\#}+ϵH_{g_n}$, where $H_{g_n}\left(W,A,S\right)=\left(2A-1\right)/g_n\left(A|W\right)$, and g_n is an estimator of g₀(A | W). In a randomized clinical trial (RCT), we might set g_n = g₀. Let ${ϵ}_n=\text{arg }{\text{min}}_{ϵ}{P}_{n}L\left({\psi }_n^{\#}(ϵ)\right)$ be the MLE, where P_n is the empirical distribution of the n observations and

$$L(\psi )(O)=-\{Y\text{log}\psi (W,A,S)+(1-Y)\text{log}(1-\psi (W,A,S))\}$$ (2)

is the log-likelihood loss function. This ∊_n is easily calculated with a standard univariate logistic regression of Y on $H_{g_n}$, incorporating an o set. Let ${\psi }_n^{\#}={\psi }_n^{\#}\left({ϵ}_n\right)$ be the corresponding estimator of ψ₀, which is a TMLE (indicated by the superscript #) for reasons that we summarize below. This estimator ${\psi }_n^{\#}$ does not have a closed-form solution unless the super-learner library is very simple, but this does not matter for the purpose of achieving a most predictive surrogate given its values are easily calculated.

TMLE is a general approach that allows one to target an initial estimator of a data distribution or parameter thereof in such a way that this targeted version will solve a user-supplied estimating equation (van der Laan and Rose, 2011). In a typical application of TMLE one targets the initial estimator to solve the efficient influence curve equation for the target parameter of interest so that the resulting substitution estimator is an asymptotically efficient estimator. In the above case, we depart from this objective, instead using the TMLE solely as a technical procedure to make the estimator solve the equation

$$0=\frac{1}{n}\sum _{i=1}^n{H}_{g_n}\left(W_i,A_i\right)\left(Y_i-{\psi }_n^{\#}\left(W_i,A_i,S_i\right)\right),$$ (3)

which is the crucial equation that we will need later for a main result (Theorem 4) that a TMLE of the average treatment effect (ATE) on the estimated optimal surrogate ${\psi }_n^{\#}$ is also a TMLE of the ATE on Y and is thus asymptotically linear and efficient for the ATE on Y.

5.2. The targeted estimate of the P₀-optimal surrogate is optimal in the current study.

Suppose we use this ${\psi }_n^{\#}(W,A,S)$ in place of the final outcome Y, and, based on the reduced data $\left(W_i,A_i,{\psi }_n^{\#}\left(W_i,A_i,S_i\right)\right),i=1,\dots ,n$, in our current study, compute the TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ of the ATE ${\theta }_{{\psi }_n^{\#}}={\theta }_{{\psi }_n^{\#}}^1-{\theta }_{{\psi }_n^{\#}}^0=E_0\left({\psi }_n^{\#}\left(W,1,S_1\right)\right)-E_0\left({\psi }_n^{\#}\left(W,0,S_0\right)\right)$. Under conditions, this TMLE is an efficient estimator of this data adaptive target parameter ${\theta }_{{\psi }_n^{\#}}$, but we are really interested in estimating the ATE θ₀ = E₀(Y₁ − Y₀) on the clinical outcome Y. Therefore, we wonder if this TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ is also efficient for θ₀ based on observing O = (W, A, S, Y)? In other words, how much information did we lose by replacing the outcome Y by this estimated surrogate outcome ${\psi }_n^{\#}(W,A,S)$ for the sake of estimation of the desired parameter θ₀?

To answer this question, we first define both the reduced data TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ of ${\theta }_{{\psi }_n^{\#}}$ and the TMLE ${\tilde{\theta }}_n^{TMLE}$ of θ₀ based on the full data (W, A, S, Y) including Y. From this it will be clear that ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ is an actual TMLE of θ₀ based on O = (W, A, S, Y) so that its asymptotic properties follow from the well-known theory for TMLE.

TMLE ${\tilde{\theta }}_n^{TMLE}$ of E₀(Y₁−Y₀) based on O = (W, A, S, Y): First, we note that an efficient estimator of EY₁ − EY₀ can ignore S so that it suffices to work with (W, A, Y) (in our setup with complete data on Y the efficient influence curve is the same with or without S). Let ${\overline{Q}}_n^0$ be an initial estimator of ${\overline{Q}}_0=E_0(Y|W,A)$ based on (W, A, Y). Let $L(\overline{Q})$ be the log-likelihood loss (2), $\text{Logit\hspace{0.17em}}{\overline{Q}}_n^0(ϵ)=\hspace{0.17em}\text{Logit\hspace{0.17em}}{\overline{Q}}_n^0+ϵH_{g_n}$ be the least favorable submodel, and ${\widetilde{ϵ}}_n=\text{arg }{\text{min}}_{ϵ}{P}_{n}L\left({\overline{Q}}_n^0(ϵ)\right)$ be the MLE of the fluctuation parameter ∊. The TMLE of ${\overline{Q}}_0$ is defined as ${\overline{Q}}_n^1={\overline{Q}}_n^0\left({\widetilde{ϵ}}_n\right)$ and the TMLE of the average treatment effect E₀(Y₁ − Y₀) is given by ${\tilde{\theta }}_n^{TMLE}=\frac{1}{n}\sum _{i=1}^n\left\{{\overline{Q}}_n^1\left(W_i,1\right)-{\overline{Q}}_n^1\left(W_i,0\right)\right\}$. Due to the TMLE-update step we have that ${\overline{Q}}_n^1$ solves the score equation

$$0=\frac{1}{n}\sum _{i=1}^n{H}_{g_n}\left(W_i,A_i\right)\left(Y_i-{\overline{Q}}_n^1\left(W_i,A_i\right)\right),$$ (4)

and, as a result, the TMLE ${\tilde{Q}}_n^1=\left(Q_{W,n},{\overline{Q}}_n^1\right)$ (with Q_W,n the empirical distribution of W) solves the efficient influence curve equation for E₀(Y₁ − Y₀):

$$0=\frac{1}{n}\sum _{i=1}^n{D}^{eff}\left({\tilde{Q}}_n^1,g_n\right)\left(W_i,A_i,Y_i\right)=0$$ (5)

with $D^{eff}\left({\tilde{Q}}_n^1,g_n\right)\left(W_i,A_i,Y_i\right)=D^{eff,1}\left({\tilde{Q}}_n^1,g_n\right)\left(W_i,A_i,Y_i\right)-D^{eff,0}\left({\tilde{Q}}_n^1,g_n\right)\left(W_i,A_i,Y_i\right)$, where $D^{eff,a}\left({\tilde{Q}}_n^1,g_n\right)\left(W_i,A_i,Y_i\right)=\left(I\left(A_i=a\right)/g_n(a|W_i)\right)\left(Y_i-{\overline{Q}}_n^1\left(W_i,a\right)\right)+{\overline{Q}}_n^1\left(W_i,a\right)-{\tilde{\theta }}_n^{TMLE,a}$, and ${\tilde{\theta }}_n^{TMLE,a}=\frac{1}{n}\sum _{i=1}^n{\overline{Q}}_n^1\left(W_i,a\right)$ depends on both ${\overline{Q}}_n^1$ and Q_W,n. If we replace H_gn by a two dimensional ${\overline{Q}}_n^1$ with $H_{g_n}^a=I(A=a)/g_n(a|W)$, then the updated ${\overline{Q}}_n^1={\overline{Q}}_n^0\left({\widetilde{ϵ}}_n\right)$ (where ${\widetilde{ϵ}}_n$ is now a two dimensional parameter) also yields a TMLE for the bivariate parameter (EY₀, EY₁) (the above TMLE targets the difference), which solves $0=P_n{D}^{eff,a}\left({\tilde{Q}}_n^1,g_n\right)$ for each a = 0, 1. We use such treatment-specific TMLEs because in the application we estimate non-additive difference treatment effects (i.e., relative risk EY₁/EY₀). These equations are standard TMLE equations (e.g., defined in van der Laan and Rose, 2011, p. 527–529), and are the basis for the double robustness and asymptotic efficiency of the TMLEs.

TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ of the ATE ${\theta }_{{\psi }_n^{\#}}$ on the estimated optimal surrogate ${\psi }_n^{\#}$ based on $O^r=\left(W,A,{\psi }_n^{\#}(W,A,S)\right)$: This TMLE is the same as the TMLE above but with Y replaced by ${\psi }_n^{\#}(W,A,S)$. Thus, one first regresses ${\psi }_n^{\#}\left(W_i,A_i,S_i\right)$ on (W_i, A_i) to obtain an initial estimator of ${\overline{Q}}_0(W,A)=E_0\left({\psi }_0(W,A,S)|W,A\right)=E_0(Y|W,A)$, where one might again use super-learning. Let us denote this estimator with ${\overline{Q}}_n^{\#0}$. This is nothing else than an estimator of ${\overline{Q}}_0(W,A)=E_0\left(E_0(Y|W,A,S)|W,A\right)$, which estimates the inner expectation E₀(Y | W, A, S) with ${\psi }_n^{\#}$ and then estimates the outer expectation with a regression of ${\psi }_n^{\#}$ on (W, A). One now defines the submodel $\text{Logit\hspace{0.17em}}{\overline{Q}}_n^{\#0}(ϵ)=\hspace{0.17em}\text{Logit\hspace{0.17em}}{\overline{Q}}_n^{\#0}+ϵH_{g_n}$, and defines ${ϵ}_{n1}=\text{arg }{\text{min}}_{ϵ}{\sum }_{i=1}^n{L}_1\left({\overline{Q}}_n^{\#0}(ϵ)\right)\left(O_i^r\right)$ solves the following score equation (analog to (4)):

$$0=\frac{1}{n}\sum _{i=1}^n{H}_{g_n}\left(W_i,A_i\right)\left({\psi }_n^{\#}\left(W_i,A_i,S_i\right)-{\overline{Q}}_n^{\#1}\left(W_i,A_i\right)\right).$$ (6)

The TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ of ${\theta }_{{\psi }_n^{\#}}$ is now the substitution estimator

$${\theta }_{{\psi }_n^{\#}}^{TMLE}=\frac{1}{n}\sum _{i=1}^n\left\{{\overline{Q}}_n^{\#1}\left(W_i,1\right)-{\overline{Q}}_n^{\#1}\left(W_i,0\right)\right\}.$$

Now we utilize the fact that ${\psi }_n^{\#}$ was targeted so that it solves the equation (3). Equation (3) combined with the score equation (6) implies that ${\overline{Q}}_n^{\#1}$ solves

$$0=\frac{1}{n}\sum _{i=1}^n{H}_{g_n}\left(W_i,A_i\right)\left(Y_i-{\overline{Q}}_n^{\#1}\left(W_i,A_i\right)\right).$$ (7)

Thus, this TMLE $Q_n^1=\left(Q_{W,n},{\overline{Q}}_n^{\#1}\right)$ also solves the efficient influence curve equation for θ₀:

$$0=\frac{1}{n}\sum _{i=1}^n{D}^{eff}\left(Q_n^1,g_n\right)\left(W_i,A_i,{\psi }_n^{\#}\left(W_i,A_i,S_i\right)\right)=0.$$ (8)

(And parallel to the above, the TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE,a}$ of ${\theta }_{{\psi }_n^{\#}}^a$ solves $0=P_n{D}^{eff,a}\left(Q_n^1,g_n\right)$ with $D^{eff,a}\left(Q_n^1,g_n\right)\left(W_i,A_i,{\psi }_n^{\#}\left(W_i,A_i,S_i\right)\right)=\left(I\left(A_i=a\right)/g_n(a|W_i)\right)\left(Y_i-{\overline{Q}}_n^{\#1}\left(W_i,a\right)\right)+{\overline{Q}}_n^{\#1}\left(W_i,a\right)-{\theta }_{{\psi }_n^{\#}}^{TMLE,a}.)$ Thus, ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ is an actual TMLE of E₀(Y₁ − Y₀) based on the original data (W, A, S, Y), with the only twist that it uses a special initial estimator ${\overline{Q}}_n^{\#0}$ of ${\overline{Q}}_0$ (as discussed above, involving first regressing Y on W, A, S and then regressing that fit on W, A). This proves that ${\theta }_{{\psi }_n^{\#}}^{TMLE}$– which we defined as a TMLE of the treatment effect on the estimated optimal surrogate – is also a double robust efficient substitution estimator of the clinical treatment effect of interest E₀(Y₁ −Y₀) based on the full data O = (W, A, S, Y) in model M.

THEOREM 4: Consider the estimator ${\psi }_n^{\#}$ of the optimal surrogate ψ₀ = E₀(Y | W, A, S) and the TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}=\frac{1}{n}{\sum }_{i=1}^n\left\{{\overline{Q}}_n^{\#1}\left(W_i,1\right)-{\overline{Q}}_n^{\#1}\left(W_i,0\right)\right\}$of ${\theta }_{{\psi }_n^{\#}}=E_0({\psi }_n^{\#}\left(W,1,S_1\right)-{\psi }_n^{\#}\left(W,0,S_0\right))$ based on $\left(W_i,A_i,{\psi }_n^{\#}\left(W_i,A_i,S_i\right)\right),i=1,\dots ,n$. Let θ₀ = E₀(Y₁ − Y₀). Let $Q_0=\left({\overline{Q}}_0=E_0(Y|W,A),Q_{W,0}\right)$, where Q_W,0 is the probability distribution of W under P₀. Let $D^{eff}\left(Q_0,g_0\right)(O)=H_{g_0}(W,A)\left(Y-{\overline{Q}}_0(W,A)\right)+{\overline{Q}}_0(W,1)-{\overline{Q}}_0(W,0)-\theta \left(Q_0\right)$ be the efficient influence curve of E₀(Y₁ − Y₀) based on O = (W, A, S, Y) ~ P₀ ∈ M. Let $Q_n^1=\left(Q_{W,n},{\overline{Q}}_n^{\#1}\right)$ and let $\Vert f{\Vert }_{P_0}=\sqrt{\int f{(o)}^{2}d{P}_0(o)}$. Assume 1) $D^{eff}\left(Q_n^1,g_n\right)$ falls in a P₀-Donsker class with probability tending to 1; 2) ${\Vert {\overline{Q}}_n^{\#1}-{\overline{Q}}_0\Vert }_{P_0}{\Vert g_n-g_0\Vert }_{P_0}=o_P(1/\sqrt{n})$ (so in an RCT, this only requires ${\Vert {\overline{Q}}_n^{\#1}-{\overline{Q}}_0\Vert }_{P_0}\to 0$ in probability); 3) for some δ > 0 min_a∊{0,1}g₀(a | W) > δ > 0 with probability 1. Then ${\theta }_{{\psi }_n^{\#}}^{TMLE}-{\theta }_0=\left(P_n-P_0\right)D^{eff}\left(Q_0,g_0\right)+o_P(1/\sqrt{n})$_. Thus, ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ an efficient estimator of θ₀ based on O = (W, A, S, Y) in model M.

Thus, even though ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ is based on a reduced data structure, it is asymptotically linear with influence curve equal to that of the TMLE ${\tilde{\theta }}_n^{TMLE}$ of θ₀ = E₀(Y₁ − Y₀) based on the observed data (W, A, S, Y). This is an important result since it establishes that in our original study the estimated optimal surrogate carries as much information as the outcome itself for the sake of estimation of the average clinical treatment effect (and for other contrasts of EY₀ and EY₁). This means that a Wald (1 − α)% confidence interval for ${\theta }_{{\psi }_n^{\#}}$ based on ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ is also a (1 − α)% confidence interval for θ₀ = E₀(Y₁ − Y₀) and is as narrow as a (1 − α)% confidence interval based on an efficient estimator of θ₀ using (W, A, S, Y).

This result may be surprising given that the estimated optimal surrogate is based on the reduced data. In fact, if a super-learner estimator were used as the estimated optimal surrogate, without targeting the estimator, then the TMLE ${\theta }_{{\psi }_n^{\#}}^{TMLE}$ would not be efficient for E₀(Y₁−Y₀). Specifically, the bias of a super-learner fit is larger than the inverse of root-n and this bias translates into the same order of bias for the ATE on Y. The key to achieve efficiency is therefore to use a targeted super-learner fit of the optimal surrogate designed so that the TMLE of the ATE on this targeted estimate is in fact an asymptotically linear estimator of the ATE on Y. However, this targeting is only possible if we use the actual observed outcomes Y, and the targeting is specific for the current data generating experiment and thus the TMLE of the ATE on our targeted surrogate based in a new study would not result in an asymptotically efficient estimator of the ATE on Y*. Nevertheless, it is an appealing property of the estimated optimal surrogate that in the current study it yields an asymptotically efficient estimator of the average clinical treatment effect.

6. Application to Two Dengue Vaccine Efficacy Trials

Two randomized, double-blinded, placebo-controlled, multicenter, Phase 3 trials of the identical recombinant, live, attenuated, tetravalent dengue vaccine (CYD-TDV) versus placebo were conducted in Asia (Capeding et al., 2014) and Latin America (Villar et al., 2015), respectively. These trials– referred to as CYD14 and CYD15– randomized 10,275 2–14 year-old children and 20,869 9–16 year-old children, respectively, in 2:1 allocation to vaccine:placebo, with immunizations administered at months 0, 6, and 12. The primary analyses assessed vaccine efficacy (V E) against symptomatic, virologically confirmed dengue (VCD) occurring at least 28 days after the third immunization through to the Month 25 visit. Based on a proportional hazards model, estimated V E was 56.5% (95% CI 43.8–66.4) for CYD14 and 64.7% (95% CI 58.7–69.8) for CYD15.

The trials measured, from Month 13 blood samples, neutralizing antibody titers to each of the four dengue serotypes contained in the CYD-TDV vaccine using two different assays [PRNT₅₀ and Microneutralization Version 2 (MNv2)]. Our analysis restricts to participants with Month 13 titer data, which were measured in a random sample of study participants and in all participants with the study endpoint. We use simple inverse probability weighted complete-case analysis to account for this sampling design. Each trial data set consists of baseline covariates W (age, sex, estimated frequencies of the 4 serotypes causing dengue disease in placebo recipients in the participant’s country of residence), treatment A (1=vaccine, 0=placebo), S (several variables based on the eight Month 13 titer measurements), and Y, the indicator of occurrence of the VCD endpoint between Month 13 and Month 25. The analyzed cohorts are participants observed to be free of the VCD endpoint through to the Month 13 visit with (W, A, S) measured. We treat CYD14 as the current trial and CYD15 as the future trial, where in CYD15 we only include data from 9–14 year-olds to increase the credibility of the contained support assumption of Theorem 2.

We first calculate the targeted estimated optimal surrogate ${\psi }_n^{\#}(W,A,S)$ for the CYD14 trial, thus obtaining TMLEs ${\theta }_{{\psi }_n^{\#}}^{TMLE,a}$ of each mean ${\theta }_{{\psi }_n^{\#}}^a=E_0\left({\psi }_n^{\#}\left(W,a,S_a\right)\right)$ and of a vaccine efficacy contrast version of ${\theta }_{{\psi }_n^{\#}}^{TMLE},V{E}_{{\psi }_n^{\#}}^{TMLE}=1-{\theta }_{{\psi }_n^{\#}}^{TMLE,1}/{\theta }_{{\psi }_n^{\#}}^{TMLE,0}$ of, $V{E}_{{\psi }_n^{\#}}=1-{\theta }_{{\psi }_n^{\#}}^1/{\theta }_{{\psi }_n^{\#}}^0$. Wald 95% confidence intervals for each ${\theta }_{{\psi }_n^{\#}}^a$ are calculated by estimating the variance of each ${\theta }_{{\psi }_n^{\#}}^{TMLE,a}$ by the sample variance of the efficient influence curve values $D^{eff,a}\left(Q_n^1,g_n\right)\left(W_i,A_i,{\psi }_n^{\#}\left(W_i,A_i,S_i\right)\right)$ defined above. The delta method is then applied to obtain the variance of $\text{log}\left({\theta }_{{\psi }_n^{\#}}^{TMLE,1}/{\theta }_{{\psi }_n^{\#}}^{TMLE,0}\right)$ and the resulting symmetric Wald 95% confidence limits are transformed to obtain the CI for $V{E}_{{\psi }_n^{\#}}$. The same approach to obtain Wald CIs is used for E₀(Y₀), E₀(Y₁), and θ₀ = 1 − E₀(Y₁)/E₀(Y₀) based on (W_i, A_i, Y_i), with values $D^{eff,a}\left(Q_n^1,g_n\right)\left(W_i,A_i,{\psi }_n^{\#}\left(W_i^{*},A_i^{*},S_i^{*}\right)\right)$ replaced with $D^{eff,a}\left({\tilde{Q}}_n^1,g_n\right)\left(W_i,A_i,Y_i\right)$.

Second, we calculate the ${\psi }_n^{\#}\left(W_i^{*},A_i^{*},S_i^{*}\right)$ surrogate outcome values for the n* CYD15 participants (with ${\psi }_n^{\#}(\cdot )$ calculated from CYD14), and, based on the CYD15 data $(W_i^{*},A_i^{*},S_i^{*}{\psi }_n^{\#}\left(W_i^{*},A_i^{*},S_i^{*}\right))$, estimate the treatment-specific surrogate means in CYD15: ${\theta }_{{\psi }_n}^a(P)=E_P\left(E_P\left({\psi }_n^{\#}\left(W^{*},a,S^{*}\right)|W^{*},A^{*}=a\right)\right)$ for a = 0,1 and $V{E}_{{\psi }_n^{\#}}(P)=1-{\theta }_{{\psi }_n^{\#}}^1(P)/{\theta }_{{\psi }_n^{\#}}^0(P)$. Here the TMLE ${\theta }_{{\psi }_n}^{TMLE,a}(P)$ of ${\theta }_{{\psi }_n^{\#}}^a(P)$ is the solution to $0=P_{n*}{D}^{eff,a}\left(Q_n^1,g_n\right)$. Lastly, to check how well the estimated optimal surrogate performs in its use to estimate the clinical parameters in the new trial, we compare the TMLEs of the surrogate parameters to the TMLEs of $E_P\left(Y_0^{*}\right),E_P\left(Y_1^{*}\right)$, and ${\theta }_P^{*}=V{E}_P^{*}=1-E_P\left(Y_1^{*}\right)/E_P\left(Y_0^{*}\right)$, calculated based on the CYD15 data $\left(W_i^{*},A_i^{*},Y_i^{*}\right)$, where ${\tilde{\theta }}_{n*}^{TMLE,a}(P)$ is the TMLE of $E_P\left(Y_a^{*}\right)$. Wald 95% confidence intervals for the $E_P\left(Y_a^{*}\right)$ and V E*(P) parameters based on $\left(W_i^{*},A_i^{*},Y_i^{*}\right)$ are computed in the identical way as done for CYD14. The CIs for the surrogate parameters in CYD15 are computed similarly, where the variance of each ${\theta }_{{\psi }_n^{\#}}^{TMLE,a}(P)$ for a ∈ {0, 1} is estimated by the sample variance of the n* values $D^{eff,a}\left(Q_n^1,g_n\right)\left(W_i^{*},A_i^{*},{\psi }_n^{\#}\left(W_i^{*},A_i^{*},S_i^{*}\right)\right)$.

6.1. Targeted super-learner estimate of ψ₀ = E₀(Y|W, A, S) in the CYD14 trial

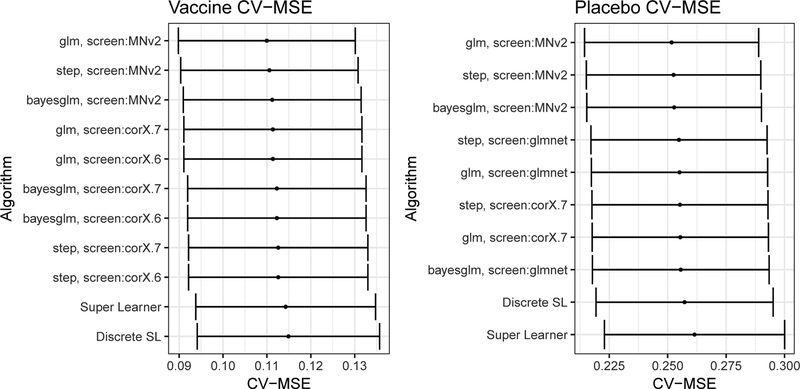
We applied super-learner with 7-fold cross-validation, separately for the vaccine and placebo groups. Table 1 displays the input variables, learner types, and pre-screening approaches applied to each learner type for estimating ψ₀ = E₀(Y |W, A = a, S). Figure 1 shows point and 95% CI estimates of the cross-validated MSEs (van der Laan, Hubbard, and Pajouh, 2013) for each individual statistical algorithm as well as for discrete super-learner and super-learner. A logistic regression model (glm) after variable screening that disallows PRNT₅₀ titers performs best (with the lowest CV-MSE) for each treatment group (Table 2). For both treatment groups the super-learner performs with similar, but slightly higher, CV-MSE. Classification accuracy is better for the vaccine than placebo group with CV-MSE of the super-learner 0.11 (95% CI 0.09–0.13) and 0.26 (95% CI 0.22–0.30), respectively.

Table 1.

Input variables, screens, and learner types used in the super-learner for the CYD14 dengue vaccine efficacy trial (35 total statistical algorithms for estimating ψ₀ = E₀(Y|W, A, S) defined by screens crossed with learner types).

Input Variables
W	Baseline demographics age (range 2–14 years), sex, empirical frequencies of the 4 serotypes in placebo group failure events by country of the participant
S	Month 13 seropositivity to each of the 4 serotypes in the CYD-TDV vaccine, and average, minimum, and maximum of the 4 titers for both PRNT50 and Microneutralization Version 2 (V2) assays
Screens	Boldfaced courier-font screens (e.g., screen.glmnet) available in the SuperLearner R package available at CRAN
screen.glmnet	Include variables with non-zero coefficients in a standard implementation of SL.glmnet (i.e., lasso)
screen.univar.logistic.x	Univariate logistic regression p-value < 0.10 using “x” most univariatly significant terms.
screen.corX.x	Disallow pairs of quantitative variables with R2 > “0.x”
screen.PRNT	Disallow Microneutralization V2 titer variables
screen.MNv2	Disallow PRNT50 titer variables
Learner Types	Boldfaced courier-font learning algorithms (e.g., SL.mean) are available in the SuperLearner R package available at CRAN
SL.mean	E0(Y|W, A = a, S)a = βa for a ∈ {0,1}
SL.glm	Logistic regression with all input variables
SL.step	Best logistic regression model by AIC from a step-wise search
SL.bayesglm	Logistic regression utilizing Cauchy Bayesian priors on model parameters
SL.polymars	Multivariate adaptive polynomial spline regression
Discrete SL	van der Laan, Polley, and Hubbard (2007)
Super Learner (SL)	van der Laan, Polley, and Hubbard (2007)

^aAll learners were fit separately for each treatment group A = a for a ∈ {0, 1} as described in Section 6.1. This is explicitly stated here for SL.mean.

Figure 1.

Point and 95% confidence interval estimates of cross-validated mean squared error (CV-MSE) for the vaccine and placebo groups of the CYD14 trial, for the top performing individual learners, the discrete super-learner, and the super-learner.

Table 2.

Best performing models for estimating ψ₀ = E₀(Y |W, A, S) for the vaccine and placebo groups of the CYD14 trial. For both the vaccine and placebo groups the model with the lowest CV-MSE was a logistic regression (glm) using variables selected from the screen screen.MNv2 in Table 1.

Model Term	Coefficient	Odds Ratio	2-Sided P-value
Vaccine Model
(Intercept)	1.09	2.96	0.26
AGE.9.11	−0.09	0.91	0.74
AGE.12.14	−2.46	0.09	<0.01
MALE	−0.36	0.70	0.09
M13.MNv2.S1b	−3.62	0.03	<0.01
M13.MNv2.S2	0.77	2.16	0.02
M13.MNv2.S3	1.41	4.09	0.04
M13.MNv2.S4	−0.12	0.89	0.81
M13.MNv2.Avec	3.45	31.53	<0.01
M13.MNv2.Min	−3.53	0.03	<0.01
M13.MNv2.Max	−0.59	0.55	0.28
Sero2.frequencyd	−0.91	<0.01	<0.01
Sero3.frequency	−0.57	<0.01	<0.01
Sero4.frequency	−0.38	0.02	<0.01
Placebo Model
(Intercept)	1.97	7.16	0.01
AGE.9.11	0.84	2.32	<0.01
AGE.12.14	−0.17	0.85	0.55
MALE	0.04	1.04	0.82
M13.MNv2.S1b	−1.10	0.33	<0.01
M13.MNv2.S2	0.25	1.29	0.34
M13.MNv2.S3	0.56	1.76	0.10
M13.MNv2.S4	0.06	1.06	0.84
M13.MNv2.Avec	1.01	2.75	0.43
M13.MNv2.Min	−2.62	0.07	<0.01
M13.MNv2.Max	−0.25	0.78	0.51
Sero2.frequencyd	−0.72	<0.01	<0.01
Sero3.frequency	−0.54	<0.01	<0.01
Sero4.frequency	−0.46	<0.01	<0.01

^aThe reference age category is 2–8 year olds.

^bM13.MNv2.S1 is the binary indicator of a Month 13 positive response to serotype 1 using the MNv2 assay, with positive response defined by MNv2 serotype neutralization titer ⩾ 10. M13.MNv2.S2–M13.MNv2.S4 are defined similarly.

^cM13.MNv2.Ave, M13.MNv2.Min, and M13.MNv2.Max coefficients are per one log₁₀ increase in neutralization titer value.

^dSerotype frequency variable coefficients are per 0.10 increase in the estimated serotype frequency of a participant’s country.

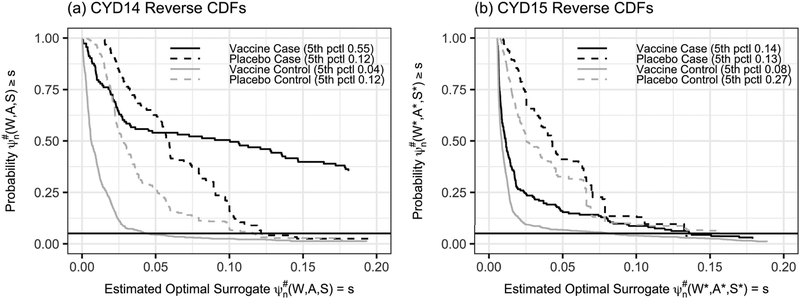
Next, the TMLE ${\psi }_n^{\#}(W,A,S)$ was obtained from CYD14 data as described in Section 5. Figure 2(a) shows empirical reverse cdf plots of ${\psi }_n^{\#}\left(W_i,A_i=a,S_i\right)$ by treatment group a ∈ {0, 1} and VCD case-control outcome y ∈ {0, 1} for CYD14 data, again showing better classification in the vaccine group. Based on ${\psi }_n^{\#}(W,A,S)$, ${\widehat{E}}_0\left(Y_1\right)={\theta }_{{\psi }_n^{\#}}^{TMLE,1}=0.017(95\%\text{\hspace{0.17em}CI 0.016 - 0.019)}$, ${\widehat{E}}_0\left(Y_0\right)={\theta }_{{\psi }_n^{\#}}^{TMLE,0}=0.039(95\%\text{\hspace{0.17em}CI\hspace{0.17em}}0.036-0.042)$, and ${\widehat{VE}}_0={\theta }_{{\psi }_n^{\#}}^{TMLE}=55\%(95\%\text{ CI }49-61)$. These estimates are close to those obtained based on (W_i, A_i, Y_i), with ${\tilde{\theta }}_n^{TMLE,1}=0.017(95\%\text{\hspace{0.17em}CI }0.014-0.021)$, ${\tilde{\theta }}_n^{TMLE,0}=0.039(95\%\text{\hspace{0.17em}CI\hspace{0.17em}}0.031-0.047)$, and ${\widehat{VE}}_0={\tilde{\theta }}_n^{TMLE}=55\%(95\%\text{\hspace{0.17em}CI\hspace{0.17em}}40-66)$ as they should be based on the results in Section 5.

Figure 2.

(a) Empirical reverse cumulative distribution functions (cdfs) of the estimated optimal surrogate ${\psi }_n^{\#}\left(W_i,A_i=a,S_i\right)$ for the CYD14 trial by vaccine/placebo assignment A = a ∈ {0, 1} and dengue outcome case/control status Y = y ∊, {0, 1}. (b) Empirical reverse cdfs of ${\psi }_n^{\#}\left(W_i,A_i=a,S_i^{*}\right)$ for CYD15 participants by vaccine/placebo assignment A* = a ∈ {0, 1} and dengue outcome case/control status Y* = y ∈ {0, 1}, where ${\psi }_n^{\#}(\cdot )$ was estimated from the CYD14 trial data. The results show that the surrogate better classifies dengue outcomes of participants in the original trial than in the new trial (not surprisingly).

6.2. Applying the estimated optimal surrogate from the original trial to the new trial

Figure 2(b) shows empirical reverse cdf plots of ${\psi }_n^{\#}\left(W_i^{*},A_i^{*}=a,S_i^{*}\right)$ for each treatment a ∈ {0, 1} by case-control status y ∈ {0, 1} in CYD15, showing diminution of classification accuracy of the estimated optimal surrogate built on CYD14 for the new study CYD15 (as expected). Table 3 compares estimates of ${\theta }_{{\psi }_n^{\#}}^a(P)$ and of ${\theta }_{{\psi }_n^{\#}}(P)=V{E}_{{\psi }_n^{\#}}(P)$ to the estimates of $E_P\left(Y_0^{*}\right),E_P\left(Y_1^{*}\right)$, and ${\theta }_P^{*}=V{E}_P^{*}=1-E_P\left(Y_1^{*}\right)/E_P\left(Y_0^{*}\right)$. The results show similar vaccine efficacy estimates, with $V{E}_{{\psi }_n^{\#}}^{TMLE}(P)=66\%(95\%\text{\hspace{0.17em}CI\hspace{0.17em}}58-72)$ and ${\widehat{VE}}_P^{*}={\tilde{\theta }}_{n*}^{TMLE}(P)=61\%(95\%\text{\hspace{0.17em}CI\hspace{0.17em}}51-69)$. However, the estimates of the treatment-specific surrogate means overestimate the VCD disease rates in CYD15, especially for the placebo group. The discrepancy stems from imperfect adherence to the Theorem 2 assumptions. The diagnostic analysis in Web Appendices E–F supports that the assumptions were approximately satisfied, with only minor violations, which was made possible by the fact that CYD14 and CYD15 were essentially the same protocol implemented in two geographic regions.

Table 3.

Comparison of inferences on the surrogate parameters ${\theta }_{{\psi }_n^{\#}}^a(P)\equiv E_P\left(E_P\left({\psi }_n^{\#}\left(W^{*},a,S^{*}\right)|W^{*},A^{*}=a\right)\right)$ for each a ∈ {0,1} and $V{E}_{{\psi }_n^{\#}}(P)=1-{\theta }_{{\psi }_n^{\#}}^1(P)/{\theta }_{{\psi }_n^{\#}}^0(P)$ based on $\left(W^{*},A^{*},{\psi }_n^{\#}\left(W^{*},A^{*},S^{*}\right)\right)$ versus direct inferences on the clinical dengue endpoint parameters $E_P\left(Y_a^{*}\right)$ and ${\theta }_P^{*}=V{E}_P^{*}=1-E_P\left(Y_1^{*}\right)/E_P\left(Y_0^{*}\right)$ in CYD15. Included is a summary of enrollment numbers, incidence of VCD, and number of participants with measured titers for each study.

Surrogate Parameters Estimated by TMLEsa		Clinical Parameters Estimated by TMLEsb
${\theta }_{{\psi }_n^{\#}}^1(P)$	0.020 (95% CI 0.017–0.022)	$E_P\left(Y_1^{*}\right)$	0.014 (95% CI 0.012–0.017)
${\theta }_{{\psi }_n^{\#}}^0(P)$	0.057 (95% CI 0.049–0.065)	$E_P\left(Y_0^{*}\right)$	0.037 (95% CI 0.031–0.043)
$V{E}_{{\psi }_n^{\#}}(P)$	66% (95% CI 58–72)	$V{E}_P^{*}$	61% (95% CI 51–69)
	No. Enrolled	No. VCD cases (Y = 1 or Y* = 1)	No. with (W, A, S) or (W*,A*,S*) measuredc
Study	Vaccine, Placebo	Vaccine, Placebo	Vaccine, Placebo
CYD14	6851, 3424	117, 133	736, 415
CYD15	13920, 6949	184, 232	944, 587

^aTMLEs ${\theta }_{{\psi }_n^{\#}}^{TMLE,1}(P)$, ${\theta }_{{\psi }_n^{\#}}^{TMLE,0}(P)$, and $V{E}_{{\psi }_n^{\#}}^{TMLE}(P)=1-{\theta }_{{\psi }_n^{\#}}^{TMLE,1}(P)/{\theta }_{{\psi }_n^{\#}}^{TMLE,0}(P)$.

^bTMLEs ${\tilde{\theta }}_{n*}^{TMLE,1}(P)$, ${\tilde{\theta }}_{n*}^{TMLE,0}(P)$, and ${\widetilde{VE}}_{n*}(P)=1-{\tilde{\theta }}_{n*}^{TMLE,1}(P)/{\tilde{\theta }}_{n*}^{TMLE,0}(P)$.

^cMeasured in 98.3% and 99.8% of endpoint cases with Y = 1 or Y* = 1 for CYD14 and CYD15, respectively.

7. Discussion

VanderWeele (2013) and discussants Joffe (2013) and Pearl (2013) suggest that a minimal requirement for an intermediate endpoint to be a useful surrogate endpoint is that it avoids the surrogate paradox, which can have disastrous consequences. Yet, VanderWeele (2013) shows that commonly used methods for surrogate endpoint evaluation generally do not guarantee avoiding this paradox. The first useful feature of the newly proposed approach is that it starts at this minimal requirement, defining the optimal surrogate in a way guaranteed to satisfy the Prentice definition of a valid surrogate within the original trial and thus avoid the paradox (and then the estimated optimal surrogate (EOS), which can be used as a surrogate endpoint in practice, satisfies the Prentice definition in large samples). As such the proposed approach responds to Pearl’s (2013) question: “If we take the negation of the “surrogate paradox” as a criterion for “good” surrogate, why cannot we create a new, formal definition of “surrogacy” that (1) will automatically avoid the paradox?…” A second useful feature of the approach is that the treatment effect on the EOS has the same interpretation as the treatment effect on the clinical endpoint of interest.

A third useful feature of the proposed approach is that the EOS– in being built by super-learner followed by a TMLE update– contains all information about the average clinical treatment effect in the original trial. A fourth useful feature is the approach’s use of super-learner with its principled cross-validation approach to build and compare best models for estimating the optimal surrogate. Super-learner is useful for applications where multiple baseline covariates and/or intermediate response endpoints are measured, yet there is considerable uncertainty about how to best predict the study outcome from these collected data. Moreover, while we have focused on randomized studies, this framework also applies for generating promising candidate surrogates based on observational studies, with all of the results holding under the additional (challenging) assumption that all confounders W of treatment assignment are measured and included in the super-learner.

A challenge posed to the framework is that through super-learner the EOS may be based on a complicated combination of models that is hard to interpret. This underscores the importance of building multiple EOSs from different input variable sets ranging from single-variable to all-variable models, where cross-validation criteria allow principled selection of a most parsimonious EOS with near-optimal predictive performance. A related challenge is that researchers in future trials may not have access to the code used by the previous researchers to calculate the EOS. This may require use of an open research paradigm where web calculators are made available that input (W, A, S) values and output EOS values.

This article considers an ideal setting with no missing data and where the clinical outcome is never observed before the intermediate response endpoints are measured. Moreover, we used a particular loss function for defining optimal prediction. Future work is of interest to accommodate these issues. Theorems 2 and 3 provide conditions for using the EOS from an original trial to confer correct estimation of the clinical treatment effect in a new setting/trial based on this surrogate endpoint without measuring the clinical endpoint. The inference part of these results hold for an infinite original trial, such that additional research is needed to provide confidence intervals about the clinical treatment effect in a new setting accounting for the error in estimating the optimal surrogate; valid inference is straightforward if the EOS is modeled parametrically but not if modeled nonparametrically. Importantly, because in many practical applications the critical assumption of our Theorems 2 and 3 for making valid inferences for a new setting– Equal Conditional Means– is implausible or dubious, a utility of the theorems is in clarifying why direct clinical endpoint studies are generally needed. Additional research is of interest to allow deviations from the theorem assumptions. Moreover, additional research may consider applications where a set of randomized clinical efficacy trials are available that provide direct clinical endpoint data for estimating how the conditional means vary over settings, which could allow new transportability results under weaker assumptions. Dummy versions of the dengue application data sets and R code producing all of the (dummy) data results is provided in Web Appendix H.