Abstract
Using fluorescence correlation spectroscopy (FCS) to distinguish between different types of diffusion processes is often a perilous undertaking because the analysis of the resulting autocorrelation data is model dependant. Two recently introduced strategies, however, can help move toward a model-independent interpretation of FCS experiments: 1) the obtention of correlation data at different length scales and 2) their inversion to retrieve the mean-squared displacement associated with the process under study. We use computer simulations to examine the signature of several biologically relevant diffusion processes (simple diffusion, continuous-time random walk, caged diffusion, obstructed diffusion, two-state diffusion, and diffusing diffusivity) in variable-length-scale FCS. We show that, when used in concert, length-scale variation and data inversion permit us to identify non-Gaussian processes and, regardless of Gaussianity, to retrieve their mean-squared displacement over several orders of magnitude in time. This makes unbiased discrimination between different classes of diffusion models possible.
Introduction
Many intra- or extracellular processes, in particular those involving molecular signaling or concentration-gradient formation, heavily rely on protein or nucleic acid diffusion. Quantifying the motions of macromolecules in cells and tissues is thus an important task; however, it turns out to be quite complicated. The cellular environment is crowded and heterogenous, and many biomolecules transiently interact with others. Because of this, macromolecular diffusion in cells can take many forms and is seldom simply Brownian. Whereas simple Brownian diffusion is characterized by a mean-squared displacement (MSD) that is linear in time and a distribution of displacements that is always Gaussian, macromolecular diffusion in cells often exhibits a nonlinear MSD, a non-Gaussian distribution of displacements, or both (1). Langowski’s study of the diffusion of the green fluorescent protein in cells, using fluorescence correlation spectroscopy (FCS), was one of the first to put this anomalous behavior in the spotlight (2). The consequences of a nonstandard diffusive behavior can be profound, affecting processes such as the kinetics of target search and molecular reactions (3, 4, 5, 6, 7) or the robustness of pattern formation (8, 9).
Among the techniques used to measure biomolecular diffusion, FCS is the best suited to the range of concentrations (1–100 nM) and diffusion coefficients (1–100 μm2/s) typical of soluble proteins in cells (10, 11). FCS is based on the statistical analysis, via inspection of its autocorrelation function (ACF), of the fluorescence signal recorded from a small observation volume, usually an ellipsoidal confocal volume with diffraction-limited radius 0.3 μm. The ability to systematically vary w has made FCS especially useful for the study of anomalous diffusion processes, which are often length-scale dependent (e.g., in cells, protein diffusion may slow down at large scales because of transient interactions with immobile structures or partial confinement caused by obstacles). This scheme, known as spot-variation FCS, or more generally variable-length-scale FCS (VLS-FCS), allows the construction of the so-called “diffusion law” (12). By this, one means the relationship between the average time taken for particles to explore the observation volume (i.e., the characteristic decay time of the ACF, τ1/2) and the projected area of this volume (w2). The diffusion law provides a proxy for the particles’ MSD. Initially, VLS-FCS was achieved by enlarging the usually diffraction-limited point-spread function that sets the value of w (12, 13, 14). With the introduction of super-resolution imaging techniques, it is also now possible to extend the range of available w below the diffraction limit (15, 16, 17). Another exciting development, made possible by increase in camera speed, has been the generation of VLS-FCS data from imaging modalities (total internal reflection, single-plane illumination), in which case the observation volume size is varied by binning pixels (18, 19).
The ultimate limit on FCS spatial resolution, however, is not set by the size of the observation volume but by the temporal resolution of the fluorescence signal (20, 21, 22). The displacements of fluorophores over distances smaller than w result in changes in fluorescence intensity—with low contrast—and they are therefore captured in the short-time regime of its ACF. Thus, even with a fixed-size observation volume, FCS can resolve motions over a range of length scales on either side of w. This capacity was demonstrated in a cluster of studies exploring DNA segment dynamics, in which the ACF was inverted to directly recover the MSD of the segments (23, 24, 25). The same ACF inversion procedure was used to study the effect of crowding in membranes and polymer solutions (26, 27). A similar idea was later implemented for image correlation spectroscopy, using a different mathematical scheme to extract the MSD from spatiotemporal ACFs, and used to characterize the anomalous behavior of green fluorescent protein diffusion in cells (22, 28). Of note, both these MSD recovery schemes work under the assumption of a process with a Gaussian propagator.
Following analytical work by Höfling and Franosch (1, 29), we recently showed that variation of the FCS observation volume size can be combined with ACF inversion to obtain the MSD of tracer particles for over five orders of magnitude in time in good conditions (27). The two model systems we studied (crowded dextran solutions and agarose gels) behaved very differently in regard to the superimposition of the apparent MSDs extracted from ACFs obtained at different length scales (27). This dissimilarity reflects a qualitative difference in the nature of the propagator (a.k.a. distribution of displacements) of the underlying process. Because only processes with Gaussian propagators are expected to lead to a perfect superimposition of the apparent MSDs, the combination of VLS-FCS with ACF inversion provides a test of the Gaussianity of the diffusive process (27, 30).
Here, we examine the signatures of several biologically relevant diffusive processes (continuous-time random walk, two-component diffusion, diffusing diffusivity, obstructed diffusion, and caged diffusion) in VLS-FCS experiments. Because analytical solutions are only available in a small number of limiting cases, we performed three-dimensional (3D) single-agent simulations to obtain, for each process, an apparent MSD from the inversion of the ACFs calculated for different w. By highlighting the different signature of each process, we provide a benchmark for model-independent interpretation of inverted VLS-FCS experiments. We also explore the relationship between the MSD obtained using the inversion procedure and the real MSD and show in particular that they are equal at short lag times regardless of the nature of the propagator. This leads us to suggest possible experimental directions to explore in future VLS-FCS experiments.
Theory
General form of the ACF
The fluorescence signal I(t) obtained in an FCS experiment is correlated in time to give the ACF, , where . For a transport process with propagator , and a 3D Gaussian observation volume (radius w, aspect ratio S) with normalized profile , the ACF becomes
| (1) |
where is the average fluorophore concentration.
ACF for an isotropic Gaussian diffusive process
If the propagator is both Gaussian and isotropic, it can be expressed as a function of the MSD, :
| (2) |
which leads to
| (3) |
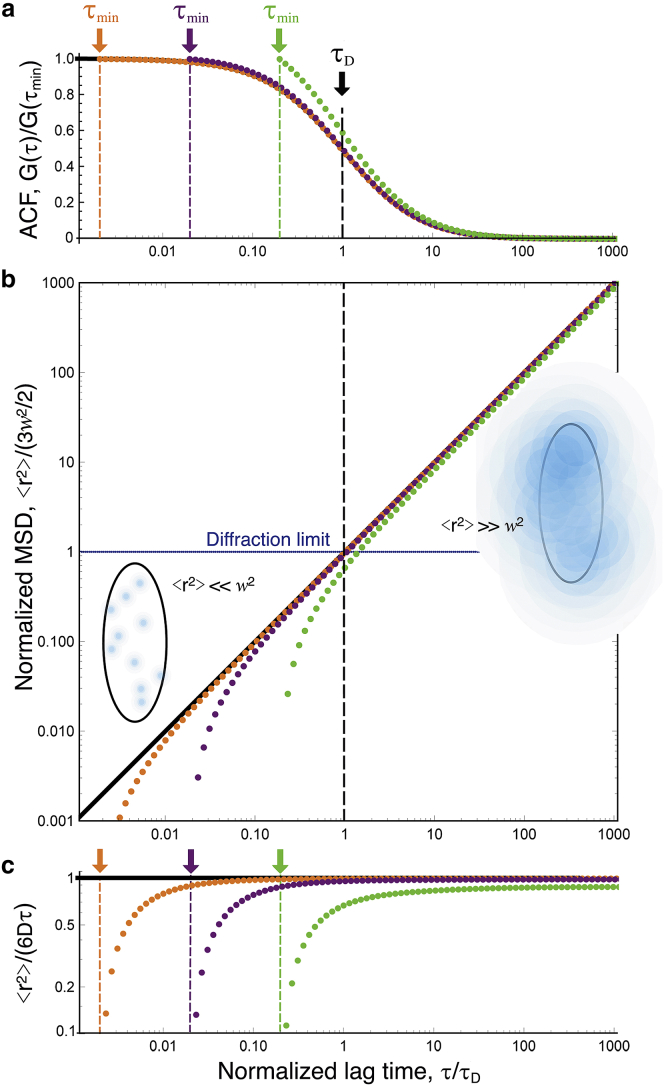
The above equation is valid for any lag time τ at which the propagator is Gaussian. It is the basis for the inversion procedure used in this work and illustrated in Fig. 1, where is obtained from G(τ, w)/G(0, w) by inverting Eq. 3 (the tilde is used as a reminder that the apparent MSD extracted from the ACF might differ from the actual MSD when the propagator is not Gaussian).
Figure 1.
(a) Simple diffusion ACFs (analytical form), normalized by amplitude at shortest lag time (black line: τmin = 0, orange symbols: τmin = τD/500, purple symbols: τmin = τD/50, green symbols: τmin = τD/5). (b) Apparent MSDs obtained by inversion of the ACFs shown in (a) are shown, displaying a departure from the real MSD at lag times close to τmin. Schematic representations of the detection volume illustrate particle displacements shorter and larger than the diffraction limit for lag times below and above τD, respectively. (c) Apparent and actual MSDs after normalization by 6Dτ are shown. To see this figure in color, go online.
Relationship between ACF and MSD at short lag times
We show in this section that for short τ, there is a simple linear relationship between G(τ, w)/G(0, w) − 1 and , whether the propagator is Gaussian or not. The only necessary assumption is that the propagator is isotropic, in which case it can be written p(r, τ). At lag times much smaller than the ACF characteristic decay time (), particles have not yet diffused over distances comparable to the observation volume radius; in other words, . This means that for r > w, in which case can be replaced in Eq. 1 by the first two even terms of its Taylor series expansion in ρ/w (the odd terms are left out because they disappear when integrating over ). Performing the integration over in Eq. 1 then yields
| (4) |
Again, ignoring higher order terms in (ρ/w)2 and using the equality valid for an isotropic propagator, we get (for , or )
| (5) |
For a Gaussian process, this linear relationship between ACF and MSD can be recovered directly from Eq. 3, by performing a first-order Taylor expansion in . A more general form of this equation has been derived in (31).
Normalization of the ACF
When inverting an experimentally obtained ACF to obtain the apparent MSD, the first step is to normalize its amplitude to obtain G(τ, w)/G(0, w). When the actual value of G(0, w) is unknown, the most straightforward solution is to perform the inversion on G(τ, w)/ G(τmin, w), where τmin is the shortest lag time at which a reliable value of the ACF can be obtained (Fig. 1). Obviously, for the inversion to work properly, one needs . If this condition is fulfilled, then at short τ (when Eq. 5 is valid), the apparent MSD is
| (6) |
This highlights an additional necessary condition for the inversion procedure to work properly, which is that τ needs to be large enough for . This is illustrated in Fig. 1 for a simple diffusive process: deviates from the actual by less than 5% as long as τ > 20τmin.
ACF for a truncated detection volume
In the simulations presented below, the observation volume profile was truncated in all three space directions to reduce computational times. Truncated observation volumes have been considered before for either reflective or absorbing boundary conditions (32, 33). Here, we consider the case that corresponds to our simulations, in which particles become invisible when leaving the rectangular volume with dimensions 2bw × 2bw × 2bSw centered on the observation volume but are allowed to diffuse in and out. For a Gaussian propagator and Gaussian detection profile, the ACF is then given by
| (7) |
where
| (8) |
and
| (9) |
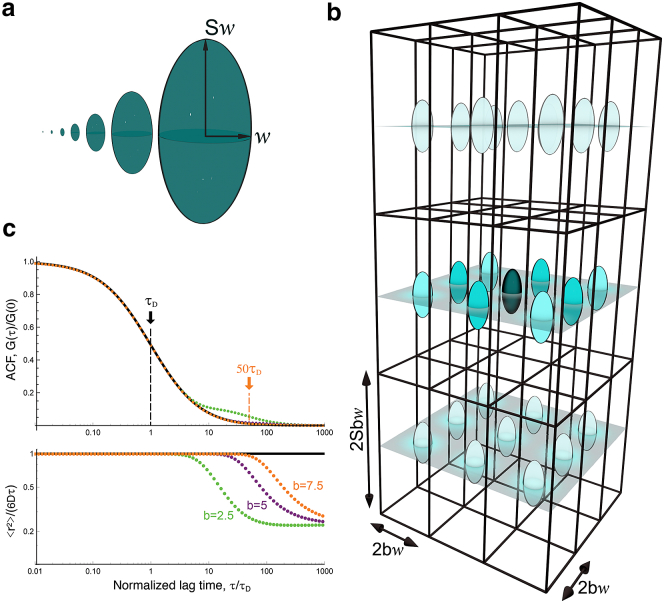
Although there is no simple analytical expression for GT(τ, w, b), Eq. 8 can be integrated numerically. The truncated ACF (Eq. 7) becomes indistinguishable from the ACF obtained in the absence of truncation (Eq. 1) for b ≥ 1 (Fig. 2). Because in our simulations b = 7.5, we consider in the following that .
Figure 2.
(a) Respective sizes of the seven different 3D Gaussian ellipsoidal observation volumes used in our simulations. (b) An array of observation volumes is shown. (c) ACFs expected for simple diffusion in a single observation volume (black line, Eq. 3) or for a regular array of detection volumes (green symbols: b = 2.5, purple symbols: b = 5, orange symbols: b = 7.5, Eq. 11) are shown. The lower panel shows the corresponding MSD (, as obtained by inversion of the ACFs shown in the upper panel). To see this figure in color, go online.
ACF for a regular array of detection volumes
To make our VLS-FCS simulations more efficient, we calculated the signal from an array of observation volumes spaced by 2bw in the focal plane and 2bSw along the optical axis (Fig. 2). In this case, the ACF takes the form
| (10) |
where is the intensity profile of the detection volume centered at {2bwi, 2bwj, 2bSwk}. Eq. 10 can be simplified by recognizing that only adjacent detection volumes are likely to record correlated events. Thus, for an n × n × n array,
| (11) |
where Gopq denotes the correlation between two detection volumes spaced by :
| (12) |
where a2(τ, w) is given by Eq. 9. This expression can be derived in the same way as the ACF for two-focus FCS experiments (34). For an elongated observation volume (S = 5), the first three terms in Eq. 11 dominate, where the maxima for G100(τ, w, b) and G110(τ, w, b) are much higher and occur at shorter lag times than for the other terms. As can be expected, for τ < (bw)2/(4D) (Fig. 2 c). Thus, in practice, simulations done for an array of detection volumes can be used for ACF inversion up to τ = b2τ1/2 (in our case, ).
Methods
Generation of particle trajectories
We used a generic 3D single-agent continuum simulation procedure, written in C++, to generate particle trajectories and simulate VLS-FCS experiments with observation volumes varying in size between w = 0.3 and 30 μm. Particles (usually 32) were placed at random positions within a 3D rectangular simulation box with periodic boundary conditions. The box dimensions, a × a × 5a with a = 450 μm, were chosen to be 15 times larger than those of the largest observation volume considered. The particle concentration was thus c = 5.8 × 10−16 M. A time step Δt = 100 ns was selected to ensure particle trajectories with sufficient resolution, even in the smallest observation volume considered. Simulations were typically run for 1011 time steps, i.e., a total experimental time T = 104 s. For simple diffusion, displacements at each step and in each spatial direction were drawn from a continuous normal distribution with variance (2DΔt)1/2 (diffusion coefficient D = 500 μm2/s).
Anomalous and obstructed trajectories
The algorithm used to simulate simple Brownian diffusion was modified to simulate five different diffusive processes, illustrated in Fig. 3. 1) Simulations of continuous-time random walks (CTRWs) were carried out following (35, 36, 37). Step lengths were drawn from the same continuous Gaussian distribution as for simple diffusion, but after each step, a wait time τw was added, with duration drawn from a Pareto distribution, (τmin = 10−9 s, α = 0.8). To allow for a range of wait times, the time step was changed for this diffusion process to 10−9 s, although intensities were saved only every Δt = 10−7 s. Also, for the CTRW, intensity traces were much shorter (106 points in total), but the simulation was repeated 105 times to allow for ensemble averaging of the data. 2) Two-component diffusion was simulated by allowing tracer particles to switch between a fast (D = 500 μm2/s) and a slow diffusive state (D′ = 50 μm2/s). Transitions between states were assumed to be Poisson processes with constant rates kon = koff = 0 or kon = koff = 500 s−1. 3) Diffusing diffusivity was simulated following Chubynsky and Slater (38). The diffusion coefficient of each particle was allowed to undergo a one-dimensional random walk between Dmin = 0 μm2/s and Dmax = 500 μm2/s (with a random initial value within that range), with a “diffusion coefficient” d = 5.5 × 10−17 m4/s3, chosen such that the full range of possible diffusion coefficients was explored by a given particle over a time comparable to its characteristic diffusion time through one of the smaller observation volumes. 4) The obstructed diffusion of particles hindered by the presence of fixed obstacles was simulated as previously done in 2D by Saxton (35). Fixed reflective cubic obstacles with dimensions 0.75 μm were placed randomly on a cubic lattice at a volume fraction ϕ = 0.310 just below the percolation limit (ϕ∗ = 0.3116). 5) Caged diffusion in cubic 1 μm corrals separated by semipermeable barriers was simulated as done in 2D in (12, 39). Particles could cross barriers only with probability p = 0.005 and were reflected otherwise. For the obstructed and caged diffusion models, the value of b was changed very slightly for the smallest observation volumes to avoid always placing their center in the same position within the cubic cells used to generate the obstacles.
Figure 3.
Illustration of the different models considered, showing short two-dimensional trajectories. Successive positions are marked by black dots, whereas pink dots signal a wait time before taking the next step. The halos around each position represent the Gaussian distribution from which the next step is drawn. The color of the halos represents either the value of the diffusion coefficient (a–e) or in which cage the particle is at that time (f). To see this figure in color, go online.
MSD and non-Gaussian parameter
Both the second moment (, MSD) and fourth moment () of the particle displacement were calculated from particle trajectories using two separate sampling times. For the first 107 steps, particle positions were saved at each step (every 100 ns), and from these and were calculated up to τ = 1 s. After 107 steps, positions were saved only every 1 ms, and and were calculated from this parsed data for τ > 1 ms. The moments calculated with different sampling times were stitched together to give data sets spanning the full explored time range, τ = 100 ns to 104 s. The non-Gaussian parameter, β, was then calculated according to its definition:
| (13) |
where d = 3 is the number of spatial dimensions (1).
Computation of the ACFs
A set of seven ACFs was calculated from the same particle trajectories for 3D Gaussian detection volumes with 1/e2 radii, wi (i = 1–7), ranging from 300 nm to 30 μm and equally spaced on a log scale. The aspect ratio was kept the same for all detection volumes: S = 5, a typical value for confocal observation volumes. For the ACF to converge, the fluorescence trace must contain a sufficient number of “events,” that is, a sufficient number of particles must have diffused through the observation volume. The number of events is ni ≈ cVeffT/τD,i, where the effective observation volume is and the average residence time of the particles in this volume is . Thus, ni ≈ 4π3/2SDcTwi. Although ni is acceptable in the case of the largest observation volume (n7 = 58), this is no longer true for smaller observation volumes (n1 < 1). To circumvent this issue, the simulation box was split into smaller boxes of size 2bwi × 2bwi × 2bSwi, with b = 7.5, and a detection volume placed at the center of each of these smaller boxes (Fig. 2 b). This effectively increased the number of events by a factor a/(2bwi)3 and insured that particle noise was low for all detection volume sizes. For each wi, the fluorescence intensity collected for a particle placed at (x, y, z) was thus calculated as
| (14) |
where Mod(x, bwi) is the remainder of the division of x by bwi. We used a finite value of B = 1 for the molecular brightness of the particles (defined as the average number of photons per seconds registered for a molecule placed at the center of the observation volume—this constant parameter drops from the expression of the ACF because of the normalization). However, it is important to note that using Eq. 14, i.e., equating the measured intensity to its average value, , means that we neglected photon noise. Thus, in effect, the ACFs we obtained have the same quality as those expected for molecules with infinite molecular brightness (the effect of photon noise, i.e., the consequence of having a finite molecular brightness, is discussed in the Supporting Materials and Methods and illustrated in Fig. S3). At each simulation step, s, and for each detection volume size, wi, the fluorescence intensity emitted by each particle was calculated using Eq. 14, and individual particle intensities were summed to give the total intensity, Fi(sΔτ). At the end of the simulation, both the original and binned data were correlated using a discrete fast Fourier transform to obtain the ACF between 10−7 and s and 1 ms and 103 s, respectively. A symmetric normalization procedure was used to correct for the discrete nature of the correlation, imposing that the numerator and denominator of the ACF are calculated from the same number of points (40, 41). See the Supporting Materials and Methods for more details on the computation of the ACFs.
ACF inversion
An apparent MSD, , was calculated from each ACF using an inversion procedure justified in the case of Gaussian diffusion (23, 26). Specifically, the amplitude of the ACFs was first normalized to 1 using G(Δτ, w), after which Eq. 3 was solved for at each lag time, τ, to obtain .
ACFs were also fitted to the general expression derived for a Gaussian anomalous process with (1, 42):
| (15) |
Results
We performed 3D single-agent simulations for different diffusive processes and characterized the obtained particle trajectories in two different ways. First, we calculated the MSD of the particles, , the non-Gaussian parameter, β(τ), and the distribution of displacements, P(x, τ), directly from the trajectories (represented by black lines or symbols in Figs. 4, 5, 6, 7, 8, 9, 10, and 11). Second, we simulated the result of VLS-FCS experiments, generating ACFs for observation volumes ranging in size from w = 0.3 to 30 μm (ACFs and derived parameters are represented by colored symbols in Figs. 4, 5, 6, 7, 8, 9, 10, and 11). Each ACF was inverted according to the procedure suggested by Shusterman et al. (23, 24) to yield an apparent MSD, , to be compared to the actual MSD. ACFs were also fitted to the general expression often used to assess anomalous diffusion processes, Eq. 15, to construct the diffusion law and recover an apparent anomalous exponent, α.
Figure 4.
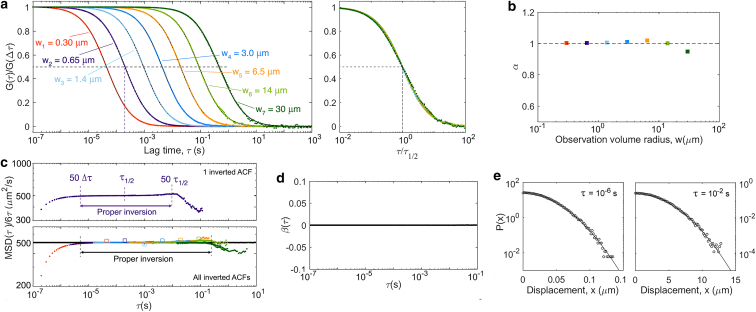
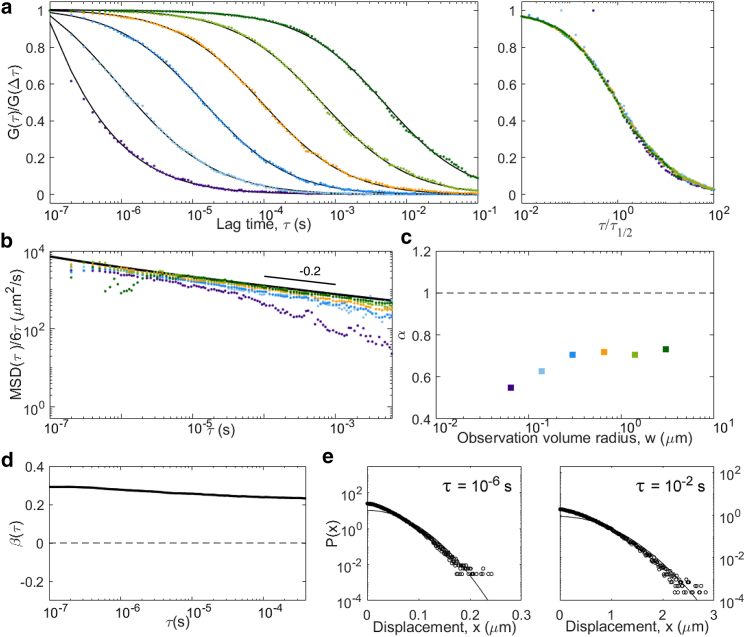
Results of the VLS-FCS simulations for simple diffusion (D = 500 μm/s2). (a) ACFs obtained for different observation volume sizes are shown (colored symbols: simulations; black lines: fit of Eq. 15 to the simulated data—the fit is behind the data and difficult to see except for the largest detection volumes). The same ACFs, with lag time normalized by τ1/2, are shown in the right panel. Their perfect superposition is a reflection of the self-similarity of the process. (b) The apparent anomalous exponent obtained from the fit of the ACFs in (a) is shown. The dashed line is a guide for the eye showing the expected α = 1 value for simple diffusion. (c) Upper panel: apparent diffusion coefficient, , calculated from the inversion of a single ACF (w2 = 0.65 μm), which has the expected constant value for several decades in time around τ1/2. Lower panel: apparent diffusion coefficient calculated from the inversion of all the ACFs shown in (a) and compared to the actual diffusion coefficient, , obtained directly from the particle trajectories (black line). Empty symbols show the diffusion law (i.e., the value of w2/(4τ1/2) as a function of τ1/2 for each ACF). (d) The non-Gaussian parameter calculated from the trajectories (black line) and expected β = 0 value for simple diffusion (dashed line) is shown. (e) Distributions of displacements for τ = 10−6s (left) and τ = 10−2s (right) are shown. Lines are fitted to a Gaussian distribution. To see this figure in color, go online.
Figure 5.
Results obtained for particles undergoing a CTRW (wait time drawn from a Pareto distribution with α = 0.8) in which all quantities (ACFs, MSD, non-Gaussian parameter, distribution of displacements) have been calculated in the same way as for all the other models, that is, taking both a time and an ensemble average over particles. In this particular case, the simulation was repeated 105 times but for only 106 steps (note the smaller lag-time range in (a) compared to other models), and the ACFs shown here are average of the ACF calculated for each measurement. (a) ACFs (color code is the same as in Fig. 4)); (b) inverted ACFs, normalized to provide a visualization of the apparent diffusion coefficient and compared to the diffusion coefficient obtained from particle trajectories; (c) apparent anomalous exponent α obtained from the fit of the ACFs in (a); (d) non-Gaussian parameter; and (e) representative distribution of displacements are shown. To see this figure in color, go online.
Figure 6.
Results for the same CTRW simulation as in Fig. 5 but in which the ACFs (a) and derived apparent anomalous exponents (c), MSD (b), non-Gaussian parameter (d), and distribution of displacements (e) have all been calculated using only an ensemble average over particles. To achieve this, the simulation was repeated 105 times but only for 106 steps (the same particle trajectories were used as those used to generate the ACFs in Fig. 5), and each point in the MSD or ACFs was calculated by averaging over different repeats of the simulation rather than for different times for a single simulation. To see this figure in color, go online.
Figure 7.
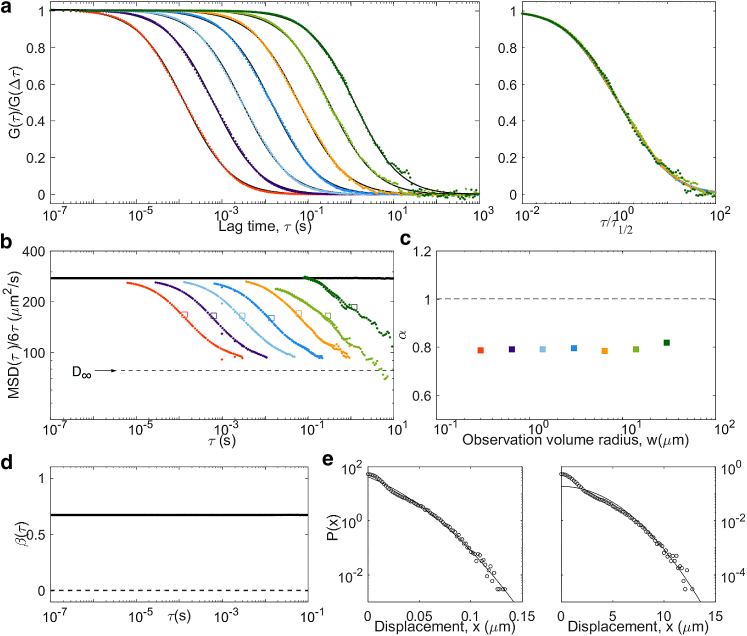
Two-component diffusion for populations of tracers with different diffusion coefficients (D = 500 μm2/s, D′ = 50 μm2/s, f = 0.5) not allowed to interchange (kon = koff = 0). In these conditions, we expect and observe a linear MSD with Davg = 275 μm2/s and a linear apparent MSD at large lag times with apparent diffusion coefficient D∞ = 78 μm2/s, and a constant non-Gaussian parameter is β = 0.67. Panels are the same as in Fig. 5: (a) ACFs, (b) inverted ACFs, (c) apparent anomalous exponent, (d) non-Gaussian parameter, and (e) representative distributions of displacements. To see this figure in color, go online.
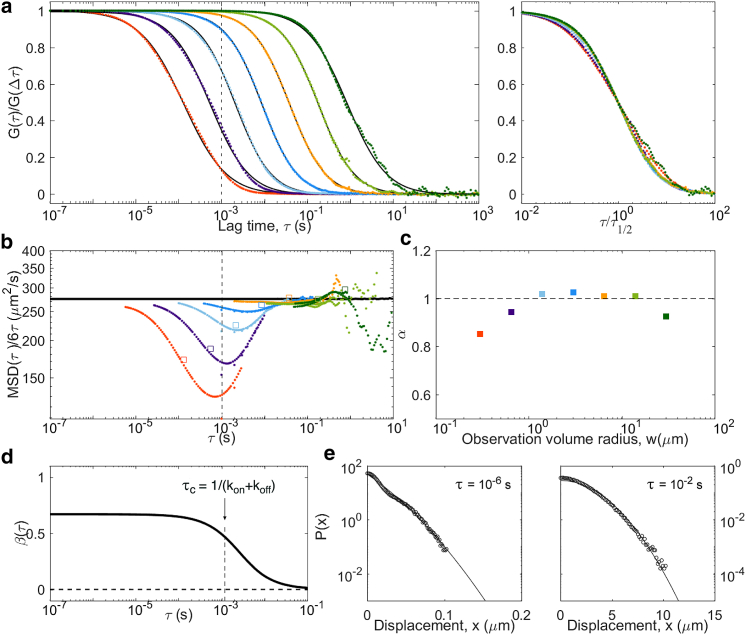
Figure 8.
Two-component diffusion (D = 500 μm2/s, D′ = 50 μm2/s) for particles allowed to interchange (kon = koff = 550 s−1). As in the non-interchanging case, the actual MSD is linear in time with Davg = 275 μm2/s, but for interchanging particles, a crossover between non-Gaussian and Gaussian diffusion is expected (and observed) around τc = 1 ms and . Panels are the same as in Fig. 5: (a) ACFs, (b) inverted ACFs, (c) apparent anomalous exponent, (d) non-Gaussian parameter, and (e) representative distributions of displacements. To see this figure in color, go online.
Figure 9.
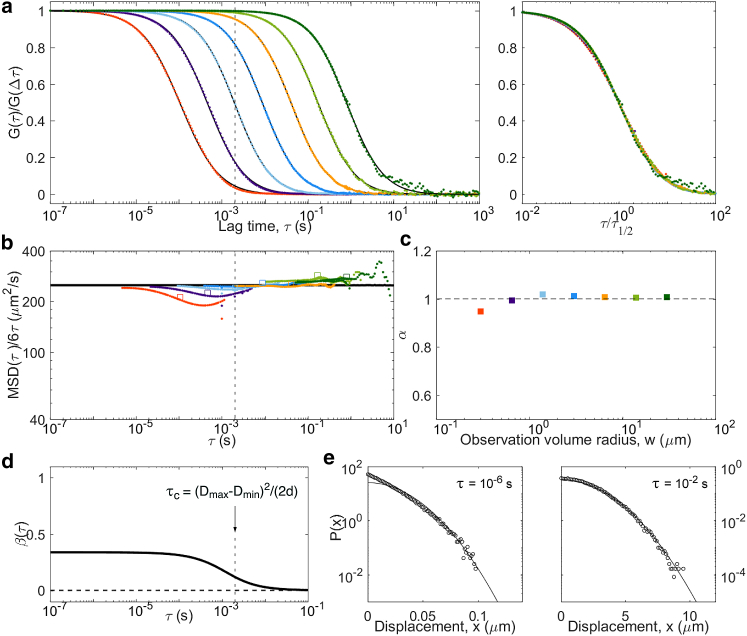
Results from simulations of particles undergoing diffusing diffusivity, with a diffusion coefficient diffusing between Dmin = 0 μm2/s and Dmax = 500 μm2/s with a diffusion coefficient d = 5.5 × 107μm4/s3. Defining features of this model are a linear MSD (with Dapp = 250 μm2/s) and a distribution of displacements that is near exponential at short lag times (below τc = 2 ms). Panels are the same as in Fig. 5: (a) ACFs, (b) inverted ACFs, (c) apparent anomalous exponent, (d) non-Gaussian parameter, and (e) representative distributions of displacements. To see this figure in color, go online.
Figure 10.
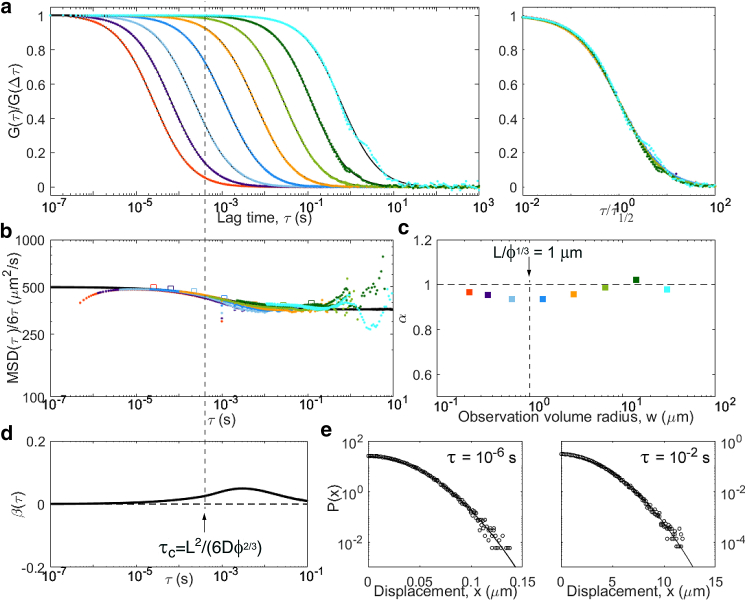
Results from simulations of particles undergoing obstructed diffusion, with d = 500 μm2/s, and cubic obstacles of size L = 0.75 μm at a volume fraction ϕ = 0.31. Although the diffusive process is close to Gaussian, with the apparent MSD obtained from ACF inversion close to the actual MSD, a clear crossover is observed around τc = 0.4 ms. Panels are the same as in Fig. 5: (a) ACFs, (b) inverted ACFs, (c) apparent anomalous exponent, (d) non-Gaussian parameter, and (e) representative distributions of displacements. For this model, an additional simulation was run with a finer time step in order to add another ACF for a smaller observation volume. To see this figure in color, go online.
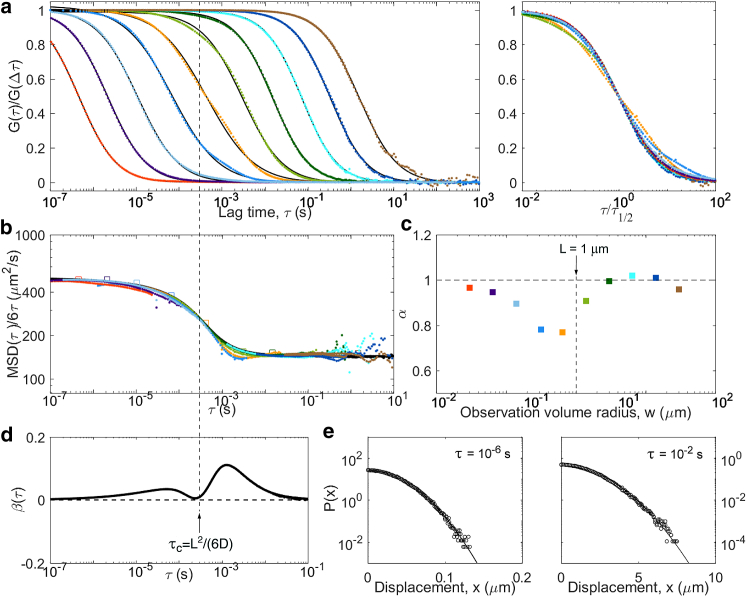
Figure 11.
Results from simulations undergoing caged diffusion (D = 500 μm2/s, cubic cages L = 1 μm) with a small escape probability (p = 0.005). As for obstructed diffusion, the process is near Gaussian, with a crossover around τc = 0.3 ms. Panels are the same as in Fig. 5: (a) ACFs, (b) inverted ACFs, (c) apparent anomalous exponent, (d) non-Gaussian parameter, and (e) representative distributions of displacements. For this model, an additional simulation was run with a finer time step in order to add three ACFs for small observation volumes (red, purple and light blue curves in (a)). To see this figure in color, go online.
Simple Brownian diffusion
We first considered simple Brownian diffusion to check how faithfully our simulations could reproduce analytical results (Fig. 4). As calculated from particle trajectories, the expected and β = 0 (black lines in Fig. 4, c and d) are obtained with good precision up to τ = 10 s. The ACFs obtained from the simulated VLS-FCS data have the expected self-similar form, with an anomalous exponent (Fig. 4 b) and a normal diffusion law (w2 ∝ τ1/2, Fig. 4 c). For the larger observation volumes, the effect of having fewer detection events (fewer particles crossing the observation volume during the simulation) and the value of the ACF around τ1/2 averaged over a smaller number of time intervals than for smaller volumes is manifest in the larger noise present in the corresponding ACF, especially at larger lag times. As a result, the values of α and the diffusion law have a visibly larger associated error for the three largest observation volumes, and we expect this to remain true for all the simulations presented here, which were performed in the same conditions (same concentration of particles and same total simulation time). Performing the ACF inversion in this simple Gaussian case, in which we should have at all τ, shows that three separate factors affect the quality of . 1) Because of the finite simulation time, for τ > 1 s, the ACFs (and therefore ) become noisy. 2) Because simulations were done for regular arrays of detection volumes spaced by 15w, a small positive correlation (∼0.1% of the ACF amplitude), resulting in a dip in , is observed around (15w)2/4D = 225τD (see ACF for a Regular Array of Detection Volumes; Fig. 2). 3) The apparent MSD differs from at short lag times (τ < 50Δτ) because of the imperfect normalization of the ACFs, which were just divided by their value at Δτ = 10−7 s (see Normalization of the ACF; Fig. 1). Despite these limitations, considering only the inverted ACFs between 50Δτ and 10τD for each ACF results in an apparent MSD that is equal to the actual MSD for five decades in time, from below 10−5 s to beyond 10−1 s.
Continuous-time random walk
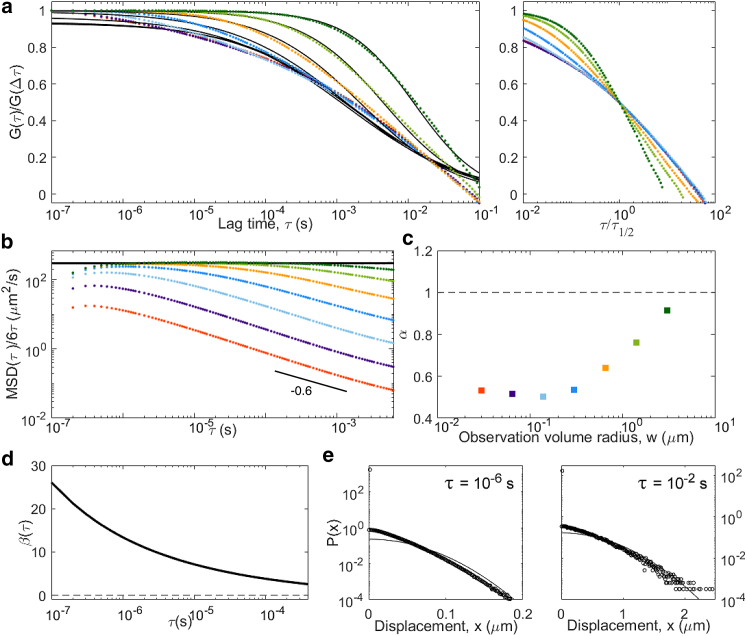
We next simulated an anomalous diffusion model, a CTRW, in which a wait time τw drawn from a power-law distribution (α = 0.8) was introduced between each step. CTRW processes are nonergodic (36, 43). As a consequence, the MSD obtained by performing both a time and ensemble average is linear in time (Fig. 5). However, when performing only an ensemble average, the MSD is anomalous (; Fig. 6). Our simulation shows that the non-Gaussian parameter also depends on how averages are performed: it is high (because of a large number of immobilized particles) and decays as a power law when performing a time average (Fig. 5 d) but has a low and almost constant value when performing only an ensemble average (Fig. 6 d). To check whether ergodicity can also be detected from FCS experiments, we calculated ACFs in two ways (see the Methods; Supporting Materials and Methods for details). First, we performed the averaging necessary to calculate the ACFs in the usual way by performing a time average on the signal (Eq. S2), which itself already represents an ensemble average over the different particles present in the observation volume. The results of this combined time and ensemble-average integration for particles undergoing a CTRW are shown in Fig. 5. Second, we generated ACFs by avoiding any time of time average, averaging over many different repeats of the experiment instead of over time (Eq. S4), as also done in (43). The results of this purely ensemble-average integration are shown in Fig. 6. Whereas ACFs calculated in these two different ways are similar for ergodic processes, we see a clear difference for the CTRW process. The time-averaged ACFs never stabilize (their shape depends on the length of the measurement), a reflection of the aging of the sample (44). Their shape also depends on the size of the observation volume (with α increasing from 0.5 to 1 as w increases). The apparent MSD extracted by inversion of these ACFs differs from the actual linear MSD and from one another (consistent with the fact that the process is strongly non-Gaussian), with over a large range of lag times. Of note, however, apparent and actual MSD coincide when (a regime that can be observed only for the larger detection volumes), as expected from the calculations presented in Relationship between ACF and MSD at Short Lag Times. In contrast, the ensemble-average ACFs (Fig. 6) are well behaved and self-similar, with an apparent anomalous exponent close to the actual α = 0.8. Accordingly, the inversion of the ensemble-averaged ACFs gives apparent MSDs that largely capture the power-law dependence of the actual MSD (except for those curves with very short τ1/2, for which the normalization does not work well).
Our simulations confirm the result from previous 2D simulations, which had shown that for a CTRW, the anomalous exponent recovered from FCS experiments using Eq. 15 can be significantly different from the real anomalous exponent (36, 45). In addition, our simulations emphasize that the apparent α depends strongly on the size of the observation volume (Fig. 5 c), a phenomenon directly linked to the scale dependence of the non-Gaussian parameter (Fig. 5 d). Calculating the ACF as an ensemble average only (as first done in (43)) leads to much better-behaved results, with stable self-similar ACFs and an apparent anomalous exponent approaching the actual one.
Two-component diffusion
We next examined three cases in which tracer particles could switch (with constant rates kon and koff) between two modes with diffusion coefficients D and D′.
The simplest case is that of two separate populations of tracers (fractions f and f′ = 1 − f) that are not allowed to interchange (kon = koff = 0). Although a simple analytical solution exists in this case, we still performed a simulation, whose results are shown in Fig. 7. For such a process, the MSD is linear in time, with at all lag times with Davg = fD + (1 − f)D′. Yet, the propagator associated with the process is non-Gaussian (it is the sum of two Gaussians). The non-Gaussian parameter has a constant value, . The ACFs (a weighted sum of the ACFs that would be obtained from either population of tracers) are self-similar, with an apparent in the conditions of our simulation. Because of the non-Gaussian nature of the process, coincides with only for . For , all the instead approach a simple diffusion MSD with diffusion coefficient . The diffusion law is linear in time, with an apparent diffusion coefficient comprised between Davg and D∞.
We then considered the general case, in which particles can switch back and forth between two simple diffusion modes with Poisson statistics (kon = koff = 500 s−1). In this scenario (one of the few considered before in the context of VLS-FCS (46, 47)), we expect a crossover around the relaxation time, τc = 1/(kon + koff). In the “fast diffusion” regime (), tracers remain in the same state while crossing the observation volume and behave as two separate populations. In the “fast reaction” regime (), tracers switch state many times while crossing the observation volume and appear to be undergoing simple diffusion with diffusion coefficient Davg. Meanwhile, β passes from to 0 around τc, and α becomes subdiffusive below (Fig. 8). As in the previous case, the actual MSD is linear in time at all lag times. However, this time the propagator is Gaussian for τ > τc; thus, coincides with both below τ1/2 and above τc and tends toward D∞ in between. Notably, for large w > wc (i.e., τ1/2 > τc), at all lag times.
Finally, we considered the limiting case in which tracers transiently experience immobilization (D′ = 0). The signature of this “stick-and-diffuse” model has been considered in the case of single-scale FCS experiments (48). It differs significantly from a CTRW because the distribution of immobilization times is exponential. Its VLS-FCS signature is no different from that of the general case, with a crossover from anomalous and non-Gaussian to Gaussian around the crossover time τc = 1 ms (Fig. S1) but with higher non-Gaussianity (β = (1 − f)/f at small τ), lower Davg = fD, and D∞ = 0.
Diffusing diffusivity
As another example of a diffusive process with linear MSD but non-Gaussian propagator, we considered the diffusive diffusivity model (38). Particles were given a diffusion coefficient that varied in time according to a one-dimensional random walk between Dmax = 500 μm2/s and Dmin = 0 μm2/s. We then expect—and observe—a crossover around τc = (Dmax − Dmin)2/(2d) = 2 ms. The MSD is linear at all lag times, with apparent diffusion coefficient Dapp = (Dmax − Dmin)/2 and a switch from non-Gaussian () to Gaussian (β = 0) behavior around τc (Fig. 9). Below τc, the distribution of displacements approaches an exponential distribution, as previously noted by Chubynsky and Slater (38). Accordingly, the ACFs display an anomalous shape for , with α approaching 0.9 at the smallest detection volumes. As for the two-component models, coincide with both for and . Overall, the signature of diffusing diffusivity (which should be a more realistic model of diffusion for proteins in cells than the pure two-component models) resembles that of a two-component model but with fewer marked anomalous features.
Obstructed diffusion
Another model often invoked to account for anomalous diffusion in complex media is obstructed diffusion, in which the motion of the tracers is restricted by the presence of immobile obstacles. If the obstacle concentration is below the percolation limit, anomalous diffusion occurs as a transient regime between unhindered short-scale diffusion and large-scale effective diffusion. We simulated obstructed diffusion using randomly placed cubic obstacles of size L at a volume fraction ϕ slightly below the percolation limit (ϕ∗ = 0.3116 in this geometry). As seen before in 2D simulations (29, 49), the apparent diffusion coefficient of the tracers switches from their actual diffusion coefficient (D = 500 μm2/s) to an effective value (D∞ = 360 μm2/s in our conditions) around ms (Fig. 10). This transient anomalous regime is visible in the ACFs around , where α has a minimum. Just above τc, a small peak is observed for the non-Gaussianity factor (a similarly weak non-Gaussianity was shown for 2D simulation of obstructed diffusion at large lag time (50)). Accordingly, deviates very slightly from in that region for curves for which τ1/2 is around or below τc. We expect the same signature to be visible in more realistic cases in which obstacles would have a range of shapes and sizes, i.e., a near-Gaussian process with a crossover from faster to slower diffusion, only with a larger crossover range.
Caged diffusion
The last considered model was caged diffusion, in which tracer particles diffuse through an array of semipermeable cages. As for obstructed diffusion, a transitory anomalous regime visible in the ACFs is expected (51, 52, 53). We simulated caged diffusion for regularly arranged cubic cages of size L = 1 μm and a probability p = 0.005 to cross the barriers between cages when encountering them (Fig. 11). We observe the expected crossover between short-term and long-term diffusion coefficients, with an MSD that more or less follows the approximate 2D analytical expression derived by Destainville et al. (i.e., a switch from microscopic to effective diffusion coefficient around the relaxation time of the particles in the cages) (39, 52, 54). Interestingly, the non-Gaussian parameter displays two small amplitude peaks. The first, found below τc = (L)2/6D = 0.3 ms, corresponds to the particles equilibrating in a cage. The second corresponds to the particles leaving the cage. Yet as β remains small, at all lag times (the strongest deviation is observed just above τc). ACFs with reflect the imperfect confinement of the particles in the cage by displaying two separate timescales, and therefore α < 1. As in the obstructed diffusion case, we expect the same signature to be visible in more realistic cases with cages with a range of shapes and sizes, only with a larger crossover region.
An interesting particular case is that of impermeable cages (p = 0). In practice, FCS experiments would be difficult to perform for such a system because confined particles photobleach rapidly, yet it is interesting to think about the signature of such processes. In this case, the apparent diffusion coefficient falls all the way to 0 above τc, and instead of a second peak, β goes to negative values (Fig. S2). The distribution of displacements has a hard limit at x = L, eventually assuming a triangular shape at large τ. As w increases, the ACFs rapidly assume a shape reflecting confinement, with α > 1 and with a characteristic decay time τ1/2 that no longer depends on w.
Discussion
Each of the models considered in this work is representative of a class of diffusion processes relevant to biological systems. CTRW and two-component diffusion are plausible models of molecules interacting with slow or immobile binding partners, whereas diffusing diffusivity, obstructed diffusion, and caged diffusion reflect different crowding scenarios. In cells, crowding and molecular interactions both play a part in protein mobility. Our simulations highlight the signature of these different processes in VLS-FCS experiments.
Until recently, the information contained in VLS-FCS experiments has been exploited via the dependence of τ1/2 on w2 (diffusion law), initially introduced to distinguish simple diffusive processes (τ1/2 ∝ w2) from photophysical processes (τ1/2 independent of w) (55). This model-independent approach has also proved useful to help distinguish between different types of diffusion (12, 14, 20, 56). For example, in 2D, caged diffusion and dynamic partitioning into domains result in negative and positive τ = 0 intercepts of the diffusion law, respectively (20, 51). However, an important limitation of the diffusion law, which our simulations illustrate, is that it coincides with the MSD only for Gaussian or near-Gaussian processes. In more complex cases (CTRW, two-component diffusion), the diffusion law relates to the MSD in a nontrivial and ill-defined way, and thus one must make assumptions about the underlying diffusion process to extract information from it (a problem already pointed out in the context of imaging FCS (57)).
Ultimately, the issue with the diffusion law is that it collapses the rich information contained in the shape of the ACF into a single value, τ1/2. In contrast, analysis of the detailed shape of the ACFs obtained at different w can give a lot of information about the underlying process (as shown for obstructed diffusion (29), two-component diffusion (46, 47), and diffusion in phase-separated membranes (58)). However, shape analysis via fitting is model dependent. This is why the inversion procedure introduced by Krichevsky et al. to obtain the MSD from the ACF (see ACF Inversion ), and its combination with length-scale variation as first considered by Höfling et al. (29), is so powerful. It uses the full range of information contained in the ACFs to allow a precise characterization of the diffusion process over many decades in time in a model-independent manner.
By using the same framework to study different classes of diffusion models and simulate VLS-FCS experiments, we provide here a library of inverted ACFs and thus an unbiased way to interpret the results of such experiments. Although comparisons of different anomalous diffusion models using simulations are available (notably a comparison of fractional Brownian motion and CTRW (36)), they have not yet been examined from the point of view of inverted VLS-FCS. All the considered models (except for simple diffusion) resulted in ACFs with “anomalous” behavior, i.e., with α < 1 for at least some of the observation volume sizes considered. However, they varied greatly with respect to several essential features that can be accessed through a VLS-FCS experiment (see Table 1 for a summary), namely 1) self-similarity versus presence of a characteristic timescale (visible as a crossover in the inverted ACFs), 2) linearity of the MSD, and 3) Gaussianity of the distribution of displacement. All these models are non-Gaussian, an important characteristic observed in many biological systems (59), e.g., RNA-protein particle diffusion in cells (60). Of particular interest, the models involving interchange between different diffusion modes with Poisson statistics (two-component models) or via a continuous diffusive process (diffusing diffusivity) exhibit an “anomalous, yet Brownian” behavior (non-Gaussian propagators associated with a “normal” linear MSD), a feature observed in many biologically relevant contexts (for example, diffusion in crowded polymer solutions (27) or actin networks (61)). This linear behavior of the MSD can be observed in inverted VLS-FCS, whereas the diffusion law has an apparent power-law dependence on time (Figs. 8 and 9).
Table 1.
Characteristics of the Different Classes of Models Considered in This Work plus Fractional Brownian Motion
| Model Class | Characteristic Timescale(s) | MSD | Propagator |
|---|---|---|---|
| Simple diffusion | no (self-similar) | linear | Gaussian |
| Fractional Brownian motion | no (self-similar) | power law | Gaussian (nonlinear time dependance of the variance) |
| CTRW | no (ensemble-averaged ACF self-similar), but aging produces non-self-similar time-averaged ACF | linear (time average), power law (ensemble average) | non-Gaussian |
| Two-component diffusion | Relaxation time, τc = 1/(k01 + k10) | linear | sum of two Gaussians well below τc, Gaussian well above |
| Diffusing diffusivity | Time required to explore diffusion space, τc = (DM − Dm)2/2d | linear | quasiexponential well below τc, Gaussian well above |
| Caged diffusion | Cage relaxation time, τc = L2/(6D), escape time τ′c = τc/p | linear well below τc and well above τ′c | Gaussian well below τc and well above τ′c |
| Obstructed diffusion | Average time before obstacle encounter, τc = L2/(6Dϕ2/3)) | linear well below and well above τc | Gaussian well below and well above τc |
In addition to the features mentioned above that can be retrieved by inversion of the VLS-FCS data, our study also highlights the possibility of investigating the ergodicity of the process by calculating purely ensemble-averaged ACFs, meaning that each point G(τ) in the correlation function is obtained as an average of the correlation between pair of intensities (I(0) and I(τ)), each of which is recorded for the same times (t = 0 and t = τ) but for different simultaneous repeats of the experiment, for example, at different positions in the same sample. This is not currently easy to achieve experimentally because it would require acquiring many fluorescence traces simultaneously. However, the recent advances in camera performance that have permitted the development of imaging FCS modalities (e.g., spinning-disk confocal FCS, total internal reflection FCS, single-plane illumination FCS) suggests that it might one day become possible. Collecting imaging FCS data for a 200 × 200 pixel field of view in a homogeneous sample (4 × 104 repeats of a single FCS measurement) would result in a quality of the ensemble-averaged ACF around τ = 1 ms (i.e., for time bins of 0.1 ms) equivalent to that obtained for an ACF time-averaged over 4 s. This should be enough to detect clear violation of ergodicity such as those expected for the CTRW model.
It has been pointed out that a limitation of the inversion procedure (the fact that it faithfully returns the MSD only for Gaussian processes) could be turned to an advantage in the case of VLS-FCS because it can be used as a test for Gaussianity (27, 30). Indeed, for all the models considered here, at those lag times for which the process is not Gaussian (i.e., where ), we observe a spread in the value of the inverted ACFs obtained for different w (i.e., depends on w). Moreover, the further β(τ) is from 0, the further the family of inverted ACFs deviate from one another. More than a simple test for Gaussianity, an inverted VLS-FCS can thus inform on the range of lag times over which the process is non-Gaussian and on how far from Gaussian the process is.
Maybe the most interesting result from our study is that, regardless of Gaussianity, the inversion procedure based on Eq. 3 returns the actual MSD if . This can be proven by performing a Taylor expansion of the ACF in (as shown in Relationship between ACF and MSD at Short Lag Times) and can be seen in for all the models simulated here. The linear relationship existing between the ACF and the MSD at short lag time has been noted before (31, 62). However, we show here that this linear regime can be greatly extended by increasing w. Performing a single-point FCS experiment for a large detection volume will allow recovering the actual MSD from ≈20Δτ (where Δτ is the experiment’s time resolution) up to , whether the underlying process is Gaussian or not. The MSD can then be retrieved for all kinds of diffusive processes over several orders of magnitude in time (something which we have previously observed for fluorescent beads diffusing in gels (27)). Remarkably, the MSD can then extend below the diffraction limit (a point that has been made before eloquently (21, 63)): correlations at timescales shorter than τD come from fluctuations in the signal due to displacements of the fluorophore within the detection volume at length scales smaller than w. Thus, in FCS experiments, the best strategy to retrieve information on processes at a short timescale may not be to physically achieve subdiffraction-limited detection volume but instead to work on achieving high-quality point-spread function for larger detection volumes with a shape as close as possible to a 3D Gaussian profile (ensuring the inversion procedure faithfully returns the MSD at short lag time).
In practice, fully exploiting the rich information present in VLS-FCS experiments will only be possible if the noise levels in the ACFs are low. Two sources of noise are particularly relevant for FCS experiments: the shot noise due to the Poissonian nature of photon detection and the particle noise due to the limited number of detected events during a single measurement (64). The effect of particle noise is visible in the simulated ACFs at long lag times (as it would be in experimental ACFs). It therefore greatly limits the precision with which the MSD can be retrieved at these timescales (see, e.g., Fig. 4 a; Fig. S3). On the other hand, to clearly show the characteristic features of the different models studied, the photon noise was not taken into account in the simulations presented here (a simulation taking into account photon noise is shown in Fig. S3). Photon noise is large when the number of photons collected per time bin is small, i.e., it becomes predominant at short lag times. It will be a problem particularly when trying to invert ACFs obtained for rapidly diffusing molecules and small observation volumes. Photon noise can be reduced by increasing the molecular brightness of the fluorophores. Meanwhile, the issues with both photon and particle noise can be alleviated by taking long measurements. This, however, requires the system to be sufficiently stable, a condition rarely met in living systems. A better solution, if one needs to access the short lag-time region of the MSD, could be to average many different measurements acquired, ideally simultaneously, in the same sample. Another practical limitation is the photophysics of the dye (its effect on the inversion is illustrated in Fig. S4) because it can prevent a proper normalization of the amplitude of the ACFs, an essential first step in the inversion procedure. Unless this process can be accounted for with confidence, it will be difficult to invert the ACF and recover the MSD at the timescales at which photophysics occur. A better solution in this case will be to use dyes—and conditions—in which photophysics is absent or negligible. There is no doubt that it is an experimental challenge to produce data of high enough quality for the inversion procedure to work, although we have demonstrated it to be possible for in vitro systems (27). However, should those challenges be overcome, this work shows that a lot of information about the nature of diffusive processes will become available.
Author Contributions
M.S. designed and performed simulations, helped write the manuscript, and prepared figures. C.F. helped design simulations and wrote the manuscript.
Acknowledgments
This article is dedicated to Jörg Langowski, whose encouragements have been an inspiration for our work, and who was very passionate about the capacity of FCS to resolve subdiffraction motions. We also thank Felix Höfling for many helpful discussions.
This work was funded by the Natural Sciences and Engineering Research Council of Canada and enabled by the use of computing resources provided by SHARCNET and Compute Canada.
Editor: Jochen Mueller.
Footnotes
Supporting Materials and Methods and five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(19)30060-8.
Supporting Material
References
- 1.Höfling F., Franosch T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013;76:046602. doi: 10.1088/0034-4885/76/4/046602. [DOI] [PubMed] [Google Scholar]
- 2.Wachsmuth M., Waldeck W., Langowski J. Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially-resolved fluorescence correlation spectroscopy. J. Mol. Biol. 2000;298:677–689. doi: 10.1006/jmbi.2000.3692. [DOI] [PubMed] [Google Scholar]
- 3.Guigas G., Weiss M. Sampling the cell with anomalous diffusion - the discovery of slowness. Biophys. J. 2008;94:90–94. doi: 10.1529/biophysj.107.117044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mirny L., Slutsky M., Kosmrlj A. How a protein searches for its site on DNA: the mechanism of facilitated diffusion. J. Phys. A Math. Theor. 2009;42:434013. [Google Scholar]
- 5.Bénichou O., Loverdo C., Voituriez R. Intermittent search strategies. Rev. Mod. Phys. 2011;83:81–129. doi: 10.1103/PhysRevE.80.031146. [DOI] [PubMed] [Google Scholar]
- 6.Weiss M. Crowding, diffusion, and biochemical reactions. In: Hancock R., Jeon K.W., editors. New Models of the Cell Nucleus: Crowding, Entropic Forces, Phase Separation, and Fractals. Volume 307. Academic Press; 2014. pp. 383–417. [DOI] [PubMed] [Google Scholar]
- 7.Liu L., Cherstvy A.G., Metzler R. Facilitated diffusion of transcription factor proteins with anomalous bulk diffusion. J. Phys. Chem. B. 2017;121:1284–1289. doi: 10.1021/acs.jpcb.6b12413. [DOI] [PubMed] [Google Scholar]
- 8.Henry B.I., Wearne S.L. Existence of Turing instabilities in a two-species fractional reaction-diffusion system. SIAM J. Appl. Math. 2002;62:870–887. [Google Scholar]
- 9.Hornung G., Berkowitz B., Barkai N. Morphogen gradient formation in a complex environment: an anomalous diffusion model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:041916. doi: 10.1103/PhysRevE.72.041916. [DOI] [PubMed] [Google Scholar]
- 10.Hess S.T., Huang S., Webb W.W. Biological and chemical applications of fluorescence correlation spectroscopy: a review. Biochemistry. 2002;41:697–705. doi: 10.1021/bi0118512. [DOI] [PubMed] [Google Scholar]
- 11.Rigler R., Elson E.S. Volume 65. Springer Science & Business Media; Berlin, Germany: 2012. Fluorescence Correlation Spectroscopy: Theory and Applications. [Google Scholar]
- 12.Wawrezinieck L., Rigneault H., Lenne P.-F. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys. J. 2005;89:4029–4042. doi: 10.1529/biophysj.105.067959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Masuda A., Ushida K., Okamoto T. New fluorescence correlation spectroscopy enabling direct observation of spatiotemporal dependence of diffusion constants as an evidence of anomalous transport in extracellular matrices. Biophys. J. 2005;88:3584–3591. doi: 10.1529/biophysj.104.048009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Humpolícková J., Gielen E., Engelborghs Y. Probing diffusion laws within cellular membranes by Z-scan fluorescence correlation spectroscopy. Biophys. J. 2006;91:L23–L25. doi: 10.1529/biophysj.106.089474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kastrup L., Blom H., Hell S.W. Fluorescence fluctuation spectroscopy in subdiffraction focal volumes. Phys. Rev. Lett. 2005;94:178104. doi: 10.1103/PhysRevLett.94.178104. [DOI] [PubMed] [Google Scholar]
- 16.Samiee K.T., Moran-Mirabal J.M., Craighead H.G. Zero mode waveguides for single-molecule spectroscopy on lipid membranes. Biophys. J. 2006;90:3288–3299. doi: 10.1529/biophysj.105.072819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vobornik D., Banks D.S., Johnston L.J. Fluorescence correlation spectroscopy with sub-diffraction-limited resolution using near-field optical probes. Appl. Phys. Lett. 2008;93:163904. [Google Scholar]
- 18.Bag N., Yap D.H., Wohland T. Temperature dependence of diffusion in model and live cell membranes characterized by imaging fluorescence correlation spectroscopy. Biochim. Biophys. Acta. 2014;1838:802–813. [PubMed] [Google Scholar]
- 19.Krieger J.W., Singh A.P., Wohland T. Imaging fluorescence (cross-) correlation spectroscopy in live cells and organisms. Nat. Protoc. 2015;10:1948–1974. doi: 10.1038/nprot.2015.100. [DOI] [PubMed] [Google Scholar]
- 20.Ruprecht V., Wieser S., Schütz G.J. Spot variation fluorescence correlation spectroscopy allows for superresolution chronoscopy of confinement times in membranes. Biophys. J. 2011;100:2839–2845. doi: 10.1016/j.bpj.2011.04.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Krichevsky O. Comment on “Polymer dynamics, fluorescence correlation spectroscopy, and the limits of optical resolution”. Phys. Rev. Lett. 2013;110:159801. doi: 10.1103/PhysRevLett.110.159801. [DOI] [PubMed] [Google Scholar]
- 22.Di Rienzo C., Gratton E., Cardarelli F. Fast spatiotemporal correlation spectroscopy to determine protein lateral diffusion laws in live cell membranes. Proc. Natl. Acad. Sci. USA. 2013;110:12307–12312. doi: 10.1073/pnas.1222097110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shusterman R., Alon S., Krichevsky O. Monomer dynamics in double- and single-stranded DNA polymers. Phys. Rev. Lett. 2004;92:048303. doi: 10.1103/PhysRevLett.92.048303. [DOI] [PubMed] [Google Scholar]
- 24.Shusterman R., Gavrinyov T., Krichevsky O. Internal dynamics of superhelical DNA. Phys. Rev. Lett. 2008;100:098102. doi: 10.1103/PhysRevLett.100.098102. [DOI] [PubMed] [Google Scholar]
- 25.Wocjan T., Krieger J., Langowski J. Dynamics of a fluorophore attached to superhelical DNA: FCS experiments simulated by Brownian dynamics. Phys. Chem. Chem. Phys. 2009;11:10671–10681. doi: 10.1039/b911857h. [DOI] [PubMed] [Google Scholar]
- 26.Horton M.R., Höfling F., Franosch T. Development of anomalous diffusion among crowding proteins. Soft Matter. 2010;6:2648–2656. [Google Scholar]
- 27.Banks D.S., Tressler C., Fradin C. Characterizing anomalous diffusion in crowded polymer solutions and gels over five decades in time with variable-lengthscale fluorescence correlation spectroscopy. Soft Matter. 2016;12:4190–4203. doi: 10.1039/c5sm01213a. [DOI] [PubMed] [Google Scholar]
- 28.Di Rienzo C., Piazza V., Cardarelli F. Probing short-range protein Brownian motion in the cytoplasm of living cells. Nat. Commun. 2014;5:5891. doi: 10.1038/ncomms6891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Höfling F., Bamberg K.-U., Franosch T. Anomalous transport resolved in space and time by fluorescence correlation spectroscopy. Soft Matter. 2011;7:1358–1363. [Google Scholar]
- 30.Kubečka J., Uhlík F., Košovan P. Mean squared displacement from fluorescence correlation spectroscopy. Soft Matter. 2016;12:3760–3769. doi: 10.1039/c6sm00296j. [DOI] [PubMed] [Google Scholar]
- 31.Khadem S.M., Hille C., Sokolov I.M. What information is contained in the fluorescence correlation spectroscopy curves, and where. Phys. Rev. E. 2016;94:022407. doi: 10.1103/PhysRevE.94.022407. [DOI] [PubMed] [Google Scholar]
- 32.Gennerich A., Schild D. Fluorescence correlation spectroscopy in small cytosolic compartments depends critically on the diffusion model used. Biophys. J. 2000;79:3294–3306. doi: 10.1016/S0006-3495(00)76561-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fradin C., Abu-Arish A., Elbaum M. Fluorescence correlation spectroscopy close to a fluctuating membrane. Biophys. J. 2003;84:2005–2020. doi: 10.1016/S0006-3495(03)75009-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dertinger T., Pacheco V., Enderlein J. Two-focus fluorescence correlation spectroscopy: a new tool for accurate and absolute diffusion measurements. Chemphyschem. 2007;8:433–443. doi: 10.1002/cphc.200600638. [DOI] [PubMed] [Google Scholar]
- 35.Saxton M.J. Anomalous diffusion due to binding: a Monte Carlo study. Biophys. J. 1996;70:1250–1262. doi: 10.1016/S0006-3495(96)79682-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Szymanski J., Weiss M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys. Rev. Lett. 2009;103:038102. doi: 10.1103/PhysRevLett.103.038102. [DOI] [PubMed] [Google Scholar]
- 37.Klafter J., Sokolov I.M. Oxford University Press; Oxford, UK: 2011. First Steps in Random Walks: From Tools to Applications. [Google Scholar]
- 38.Chubynsky M.V., Slater G.W. Diffusing diffusivity: a model for anomalous, yet Brownian, diffusion. Phys. Rev. Lett. 2014;113:098302. doi: 10.1103/PhysRevLett.113.098302. [DOI] [PubMed] [Google Scholar]
- 39.Meilhac N., Le Guyader L., Destainville N. Detection of confinement and jumps in single-molecule membrane trajectories. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:011915. doi: 10.1103/PhysRevE.73.011915. [DOI] [PubMed] [Google Scholar]
- 40.Schätzel K., Drewel M., Stimac S. Photon correlation measurements at large lag times: improving statistical accuracy. J. Mod. Opt. 1988;35:711–718. [Google Scholar]
- 41.Shi X., Wohland T. Fluorescence correlation spectroscopy. In: Diaspro A., editor. Nanoscopy and Multidimensional Optical Fluorescence Microscopy. CRC Press; 2010. [Google Scholar]
- 42.Schwille P., Korlach J., Webb W.W. Fluorescence correlation spectroscopy with single-molecule sensitivity on cell and model membranes. Cytometry. 1999;36:176–182. doi: 10.1002/(sici)1097-0320(19990701)36:3<176::aid-cyto5>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 43.Lubelski A., Klafter J. Fluorescence correlation spectroscopy: the case of subdiffusion. Biophys. J. 2009;96:2055–2063. doi: 10.1016/j.bpj.2008.10.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Metzler R., Jeon J.H., Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014;16:24128–24164. doi: 10.1039/c4cp03465a. [DOI] [PubMed] [Google Scholar]
- 45.Weiss M., Elsner M., Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004;87:3518–3524. doi: 10.1529/biophysj.104.044263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Vagias A., Raccis R., Holm C. Complex tracer diffusion dynamics in polymer solutions. Phys. Rev. Lett. 2013;111:088301. doi: 10.1103/PhysRevLett.111.088301. [DOI] [PubMed] [Google Scholar]
- 47.Ipiña E.P., Dawson S.P. From free to effective diffusion coefficients in fluorescence correlation spectroscopy experiments. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;87:022706. doi: 10.1103/PhysRevE.87.022706. [DOI] [PubMed] [Google Scholar]
- 48.Yeung C., Shtrahman M., Wu X.L. Stick-and-diffuse and caged diffusion: a comparison of two models of synaptic vesicle dynamics. Biophys. J. 2007;92:2271–2280. doi: 10.1529/biophysj.106.081794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Saxton M.J. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys. J. 1994;66:394–401. doi: 10.1016/s0006-3495(94)80789-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ernst D., Köhler J., Weiss M. Probing the type of anomalous diffusion with single-particle tracking. Phys. Chem. Chem. Phys. 2014;16:7686–7691. doi: 10.1039/c4cp00292j. [DOI] [PubMed] [Google Scholar]
- 51.Lenne P.F., Wawrezinieck L., Marguet D. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J. 2006;25:3245–3256. doi: 10.1038/sj.emboj.7601214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Destainville N. Theory of fluorescence correlation spectroscopy at variable observation area for two-dimensional diffusion on a meshgrid. Soft Matter. 2008;4:1288–1301. doi: 10.1039/b718583a. [DOI] [PubMed] [Google Scholar]
- 53.Enderlein J. Polymer dynamics, fluorescence correlation spectroscopy, and the limits of optical resolution. Phys. Rev. Lett. 2012;108:108101. doi: 10.1103/PhysRevLett.108.108101. [DOI] [PubMed] [Google Scholar]
- 54.Destainville N., Saulière A., Salomé L. Comment to the article by Michael J. Saxton: a biological interpretation of transient anomalous subdiffusion. I. qualitative model. Biophys. J. 2008;95:3117–3119. doi: 10.1529/biophysj.108.136739. author reply 3120–3122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Haupts U., Maiti S., Webb W.W. Dynamics of fluorescence fluctuations in green fluorescent protein observed by fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. USA. 1998;95:13573–13578. doi: 10.1073/pnas.95.23.13573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Eggeling C., Ringemann C., Hell S.W. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. 2009;457:1159–1162. doi: 10.1038/nature07596. [DOI] [PubMed] [Google Scholar]
- 57.Veerapathiran S., Wohland T. The imaging FCS diffusion law in the presence of multiple diffusive modes. Methods. 2018;140–141:140–150. doi: 10.1016/j.ymeth.2017.11.016. [DOI] [PubMed] [Google Scholar]
- 58.Burns M.C., Nouri M., Veatch S.L. Spot size variation FCS in simulations of the 2D Ising model. J. Phys. D Appl. Phys. 2016;49:214001. doi: 10.1088/0022-3727/49/21/214001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Metzler R. Gaussianity fair: the riddle of anomalous yet non-Gaussian diffusion. Biophys. J. 2017;112:413–415. doi: 10.1016/j.bpj.2016.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lampo T.J., Stylianidou S., Spakowitz A.J. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys. J. 2017;112:532–542. doi: 10.1016/j.bpj.2016.11.3208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wang B., Anthony S.M., Granick S. Anomalous yet Brownian. Proc. Natl. Acad. Sci. USA. 2009;106:15160–15164. doi: 10.1073/pnas.0903554106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Winkler R.G., Keller S., Rädler J.O. Intramolecular dynamics of linear macromolecules by fluorescence correlation spectroscopy. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:041919. doi: 10.1103/PhysRevE.73.041919. [DOI] [PubMed] [Google Scholar]
- 63.Di Rienzo C., Gratton E., Cardarelli F. Spatiotemporal fluctuation analysis: a powerful tool for the future nanoscopy of molecular processes. Biophys. J. 2016;111:679–685. doi: 10.1016/j.bpj.2016.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Saffarian S., Elson E.L. Statistical analysis of fluorescence correlation spectroscopy: the standard deviation and bias. Biophys. J. 2003;84:2030–2042. doi: 10.1016/S0006-3495(03)75011-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.