Forecasting future Humphrey Visual Fields using deep learning

Joanne C Wen; Cecilia S Lee; Pearse A Keane; Sa Xiao; Ariel S Rokem; Philip P Chen; Yue Wu; Aaron Y Lee

doi:10.1371/journal.pone.0214875

. 2019 Apr 5;14(4):e0214875. doi: 10.1371/journal.pone.0214875

Forecasting future Humphrey Visual Fields using deep learning

Joanne C Wen ^1,^‡, Cecilia S Lee ^1,^‡, Pearse A Keane ², Sa Xiao ¹, Ariel S Rokem ³, Philip P Chen ¹, Yue Wu ^1,^‡, Aaron Y Lee ^1,^3,^‡,^*

Editor: Demetrios G Vavvas⁴

PMCID: PMC6450620 PMID: 30951547

Abstract

Purpose

To determine if deep learning networks could be trained to forecast future 24–2 Humphrey Visual Fields (HVFs).

Methods

All data points from consecutive 24–2 HVFs from 1998 to 2018 were extracted from a university database. Ten-fold cross validation with a held out test set was used to develop the three main phases of model development: model architecture selection, dataset combination selection, and time-interval model training with transfer learning, to train a deep learning artificial neural network capable of generating a point-wise visual field prediction. The point-wise mean absolute error (PMAE) and difference in Mean Deviation (MD) between predicted and actual future HVF were calculated.

Results

More than 1.7 million perimetry points were extracted to the hundredth decibel from 32,443 24–2 HVFs. The best performing model with 20 million trainable parameters, CascadeNet-5, was selected. The overall point-wise PMAE for the test set was 2.47 dB (95% CI: 2.45 dB to 2.48 dB), and deep learning showed a statistically significant improvement over linear models. The 100 fully trained models successfully predicted future HVFs in glaucomatous eyes up to 5.5 years in the future with a correlation of 0.92 between the MD of predicted and actual future HVF and an average difference of 0.41 dB.

Conclusions

Using unfiltered real-world datasets, deep learning networks show the ability to not only learn spatio-temporal HVF changes but also to generate predictions for future HVFs up to 5.5 years, given only a single HVF.

Introduction

Glaucoma is a leading cause of blindness worldwide.[1] Of the 32.4 million blind people globally in 2010, an estimated 4.0 to 15.5% were from glaucoma.[2] Visual field (VF) testing using standard automated perimetry remains a clinical standard for monitoring glaucomatous damage, and estimating future VF loss is integral to glaucoma management. With Humphrey standard automated perimetry, linear regression of global indices such as mean deviation (MD) and visual field index (VFI) are commonly used to assess glaucoma progression and risk of future progression.[3] However, as glaucomatous visual field changes are frequently focal, these global indices may fail to detect more subtle changes. Point-wise linear regression analyses were developed to evaluate changes at each test point and have been shown to identify glaucomatous progression earlier than global indices.[4] A number of linear and non-linear regression models have been described,[5–7] yet these models often assume a constant amount or rate of progression and typically evaluate progression rates of single visual field test points independent of adjacent test points. Furthermore, a relatively large number of VF tests are frequently required in these models to achieve reasonably accurate predictions.[7]

Recently, predictive machine learning methods have been developed with the advent of deep neural networks. Specifically the integration of "spatially aware" convolutional filters [8] paired with non-linear activation functions [9] has allowed computer vision researchers to achieve unprecedented accuracy in classification of real-world objects. These data-driven methods are able to directly ingest pixel intensities of a photograph and learn spatial features important for a given task. Ophthalmologic applications of deep learning include optical coherence tomography (OCT) image classification[10] and segmentation,[11–13] fundus photo analysis,[14] and the diagnosis and classification of glaucoma based on disc photos, OCTs and VFs.[15–20] While most studies using deep learning have focused on classification, there has been limited application of deep learning in forecasting future findings. In addition to classification, deep learning algorithms can include segmentation, regression, localization, and generative models. The purpose of this study is to apply a deep learning generative model to predict future VFs with preserved spatial information using minimal baseline VF test input.

Materials and methods

This study was approved by the Institutional Review Board at the University of Washington. A waiver of consent and waiver of HIPAA authorization were granted by the IRB. All patients obtaining a Humphrey Visual Field (HVF) (Humphrey Visual Field Analyzer II-i, Carl Zeiss Meditec, Inc. Dublin, CA) using program 24–2 and the Swedish Interactive Thresholding Algorithm (SITA) Standard between the years of 1998 and 2018 at the University of Washington were included in the study. Using an in-house created, fully automated extraction algorithm that yields 54 perimetry point values to the hundredth decibel, consecutive extraction of HVF 24–2 data was performed. Additional clinical variables such as age, gender, date of HVF, and eye tested were extracted and fully de-identified prior to subsequent analysis.

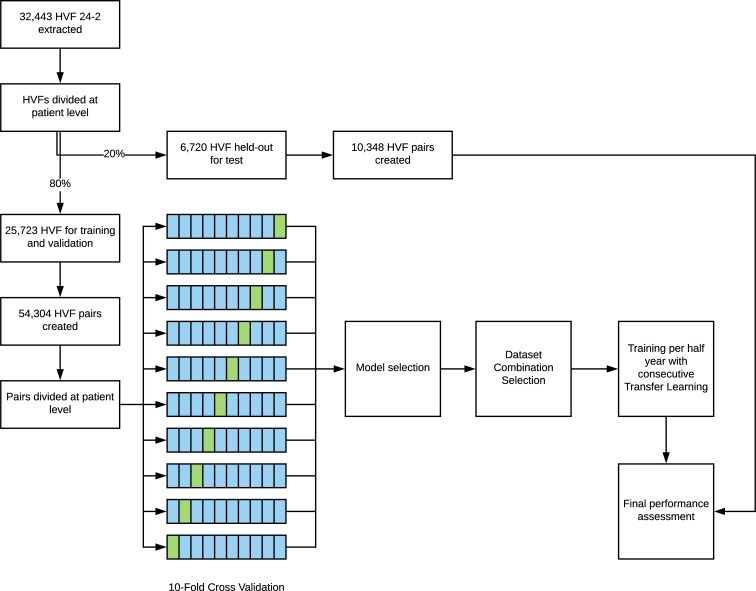
The resulting HVFs were then divided at the patient level into two parts: 80% for training and validation and 20% as a held-out test set. With the training and validation test, a total of 10 disjoint sets, divided again at the patient level, were created for 10-fold cross validation. For each set in the training, validation, and test sets, the HVFs were paired into every possible temporal combination, binned into 0.5 year intervals. Patients with only one visual field were excluded from the study. Any combinations greater than 5.5 years and less than 0.75 years in interval were excluded. For example, if there were three HVFs done: A, B, and C and the time interval between A and B was 3 months and the time interval between B and C was 1.5 years, we excluded the combination of A and B since this was less than 0.75 years. However, we included the combinations of A and C as well as B and C since each of these combinations were greater than 0.75 years. Three main phases of model development were then performed: model architecture selection, dataset combination selection, and time-interval model training with transfer learning. The final model's weights were then frozen at each time-interval and were used to assess the performance on the final held-out test set. The study design is depicted and summarized in Fig 1, and the evaluation strategy is shown in S1 Fig.

Fig 1 — A combination of cross validation and held-out test set was used for the development and evaluation of the models.

Model selection was performed by testing 9 different network architectures (Table 1). Deep learning models were created such that they could take an input tensor with the HVF as a single 8x9 tensor and output as a single 8x9 tensor representing the target HVF. The final layer activation was set to linear, and the loss function for each model was defined as masked point-wise mean absolute error (PMAE). The models were randomly initialized with parameters using the Xaiver algorithm[21] and optimized using Adam, a stochastic gradient descent optimization algorithm,[22] with an initial learning rate of 1 x 10⁻³. Each model was trained for 1000 epochs 10 times, and validation accuracy was assessed at the end of each epoch using the interval data at one year (0.75 year to 1.25 years). The highest validation accuracy was recorded for each model and 10-fold cross-validation. The best performing model was then carried forward to all the subsequent training.

Table 1. Different model architectures trained for 1,000 epochs.

	Layers (n)	Batch Size	Optimizer with learning rate	Space Complexity (MB)	Parameters
Fully Connected	2	32	Adam 1x10^-3	4	336,968
FullBN-3	10	32	Adam 1x10^-3	23	1,921,795
FullBN-5	16	32	Adam 1x10^-3	40	3,472,771
FullBN-7	22	32	Adam 1x10^-3	58	5,023,747
Residual-3	12	32	Adam 1x10^-3	27	2,332,163
Residual-5	18	32	Adam 1x10^-3	45	3,883,139
Residual-7	24	32	Adam 1x10^-3	63	5,434,115
Cascade-3	10	32	Adam 1x10^-3	81	6,992,086
Cascade-5	16	32	Adam 1x10^-3	238	20,694,754

Open in a new tab

Clinical dataset combination selection was done by taking the best performing model in the previous step and testing every possible combination of clinical predictor variables. Categorical variables such as eye and gender were appended in a one-hot vector format to the input tensor and continuous variables were encoded as a single additional tensor face with every cell encoded as the continuous value. For example, the input tensor without any additional data is shaped 1x8x9 encoding the spatial information of the perimetry sensitivities. If age were added to the input, the tensor would become 2x8x9 with the first 8x9 encoding the perimetry sensitivities and the second 8x9 array with every cell value set to the age. If eye laterality were added to the input, the tensor would become 3x8x9 with the first 8x9 encoding perimetry values and the 2x8x9 encoding the eye laterality as a one-hot vector representation. Each data combination was again trained for 1000 epochs 10 times and validation accuracy was assessed at the end of each epoch using the interval data at one year (0.75 year to 1.25 years). The highest validation accuracy was recorded for each data combination and 10-fold cross-validation. The best performing data combination was then carried forwarded to the all the subsequent training.

After the best performing model and data combination was determined in the prior two phases, time intervals from 0.75 years to 5.5 years in 0.5 year intervals were trained. Transfer learning was performed with weights carried from the first temporal interval, and consecutive transfer learning was performed with weights carried from the immediately preceding time interval. Final accuracy and performance were assessed by predicting the final held-out test set. The mean predictions from the 10-fold cross validation were used to generate each prediction.

All deep learning was performed with Keras (version 2.1.2, https://keras.io/)[23] and Tensorflow (version 1.4.1, https://www.tensorflow.org/).[24] Custom code was written in Python (version 2.7.12, https://www.python.org/) to scale and automate the training, and all training was performed using a single server equipped with 8 x Nvidia Tesla P100 graphics processing units with NVIDIA cuda (v8.0) and cu-dnn (v6.0) libraries (http://www.nvidia.com). Statistical analyses were performed using R (version 3.4.3, https://www.r-project.org/). The code has been open sourced and is available on Github (https://github.com/uw-biomedical-ml/hvfProgression).

We compared the deep learning model against three baseline models in ascending order of complexity. The first model (simulated model) is based on the mean and standard deviation for the rate of progression (ROP) from the literature. Specifically, we used data from the Early Manifest Glaucoma Trial and used -0.36 dB / year and 0.60 dB / year for the mean and standard deviation for the rate of progression.[25] Mathematically, the rate of progression can be considered a Gaussian distribution model with a mean rate of progression of -0.36*t and standard deviation 0.60*t, where t is the time in years. For each point in an input HVF, we sampled from this normal distribution and calculated a point-wise prediction of the future HVF. In the second model (empirical ROP model), we measured the empirical ROP distribution from the training set and applied it in the same manner as the first model in the held-out test set. In the third model (regressed point-wise model), the training set was used to regress 54 different linear models, one for each perimetry point. This model was then applied to the test set to measure the performance. Further details are provided in the supplementary materials.

Results

A total of 32,443 24–2 HVFs were extracted from 1998 to 2018 contiguously resulting in 1,751,922 perimetry points with hundredth decimal precision. All available HVFs were used, and no filtering or data cleaning was performed prior to the training of the models. The HVFs were split into training, validation, and held-out test sets as described in Fig 1. Table 2 shows the baseline demographic factors of the study population.

Table 2. Baseline demographic factors at patient eye level.

	Training / Validation Set	Held-out Test Set	Total
Patients (n)	3,972	903	4,875
Eyes (n)	6,536	1,727	8,263
HVFs (n)	25,723	6,720	32,443
Mean age at first HVF (SD)	62.0 (14.8)	61.8 (15.1)	61.9 (14.8)
Gender
Male, n (%)	3,026 (46.3%)	768 (44.2%)	3,789 (45.8%)
Female, n (%)	3,510 (53.7%)	969 (55.8%)	4,484 (54.2%)
Eye
Right, n (%)	3,281 (50.2%)	869 (50.0%)	4,153 (50.2%)
Left, n (%)	3,255 (49.8%)	868 (50.0%)	4,120 (49.8%)
Mean number of HVFs (SD)	3.7 (1.9)	3.6 (1.8)	3.6 (1.9)
Mean follow-up between first and last HVFs in years (SD)	3.5 (2.8)	3.4 (2.8)	3.5 (2.8)
Average mean deviation (SD)	-6.73 (6.26)	-6.70 (6.10)	-6.73 (6.23)

Open in a new tab

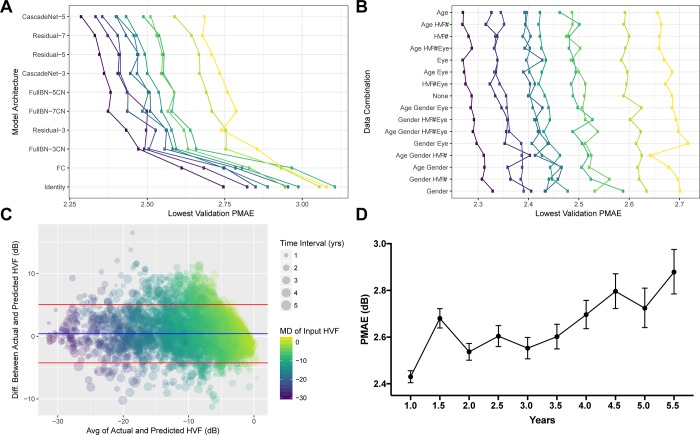
Model development occurred in two distinct phases using HVF pairs from 0.75 months to 1.25 months. First, many different model architectures were explored (Table 1). For every model, 10-fold cross validation training was performed and the lowest validation PMAE was recorded. CascadeNet-5 (S2 Fig) resulted in the best network performance compared to the other network tested (Fig 2A).

The second phase of model development was to repeat the test giving the neural networks more clinical context. With the available predictors including age, gender, eye, and the HVF test number (ie the first, second or third, etc. VF test a patient has taken), all 16 possible combinations were trained and the lowest validation PMAE was recorded. Consistently including age as an input into the deep learning model yielded statistically significant superior performance with an improvement of 0.02 dB to the PMAE (p = 0.0003, paired Wilcoxon rank sum test) (Fig 2B). Using CascadeNet-5 and age as an additional input parameter to the first HVF, continuous forward transfer learning was performed to train a separate model for each 0.5 year intervals. The average predictions from final trained models were then used the evaluate the held-out test set.

Bland-Altman plot of the difference in mean deviations (Fig 2C) revealed a mean difference of +0.41 dB. A temporal dependence was noted in the prediction accuracy with the model predicting more accurately in shorter time intervals than longer time intervals (Fig 2D). The overall PMAE (Fig 2D) and root mean squared error (RMSE) for the test set were 2.47 dB (95% CI: 2.45 dB to 2.48 dB) and 3.47 dB (95% CI: 3.45 dB to 3.49 dB), using the evaluation strategy shown in S2 Fig. Fig 3 shows representative predictions at different time points against the real HVFs for glaucoma of varying severity, as well as an example of a non-progressing non-glaucomatous hemifield VF defect. Fig 4 shows two examples of serial history in the test set where the same input HVF is used to predict multiple time points in the future.

Fig 3 — The input HVF is used for predicting HVF at the respective designated time points. A variety of different starting HVFs are shown ranging from a hemifield defect to very severe glaucoma with the corresponding Point-wise Mean Absolute Error (PMAE).

Fig 4 — The single input HVF is used for multiple predictions at different time points. Point-wise mean absolute errors for the left panel from top to bottom were 3.8, 3.8, 5.1, and 4.0 dB respectively, and for the right panel from top to bottom were 2.3, 2.5, 3.2, and 3.2 dB, respectively.

In comparison to three different linear models, deep learning showed a statistically significant improvement in the PMAE (Table 3). In addition, by relating Jensen’s inequality to the pointwise prediction error, we show that the expected theoretical lower limit of the PMAE for the held-out test set is 2.32 dB (S1 File).

Table 3. Held-out test-set performance with deep learning compared to linear models using pointwise mean absolute error (PMAE).

Model	Average PMAE	95% Lower CI	95% Upper CI
Deep learning model	2.47	2.45	2.48
Simulated ROP linear model^*	3.77	3.72	3.81
Empirical ROP linear model	3.96	3.91	4.00
Pointwise regressed linear model	3.29	3.24	3.34

Open in a new tab

Rate of Progression (ROP), Confidence Intervals (CI).

* Based on Early Manifest Glaucoma Trial[25]

Discussion

Using more than 1.7 million perimetry points from 32,443 consecutive 24–2 HVFs performed during 20 years of routine clinical practice, deep learning was able to predict future VF defects seen in HVFs. The algorithm was able to generate predictions on HVFs at a point-wise level occurring between 0.5 to 5 years. Unsurprisingly, the only clinical factor that modestly improved the AI’s prediction was the patient’s age. The overall PMAE for the test set was 2.47 dB (95% CI: 2.45 dB to 2.48 dB) and the RMSE was 3.47 dB (95% CI: 3.45 dB to 3.49 dB) which represents a statistically significant improvement over linear models (Table 3) and approaches the theoretical lower limit of 2.32 dB.

Prior algorithms for generating predictions of HVFs have centered around fitting regression models for consecutive HVFs and extrapolating the next HVF. Although easy to interpret, simple linear regression analyses such as mean deviation, pattern standard deviation or visual field index do not take into account the spatial nature of visual field loss in glaucoma.[26] Pointwise, exponential regression models have been developed to characterize fast or slow progression rate in VF loss better than linear models.[27] However, these models assume a constant rate of VF deterioration and fail to address varying rates of glaucomatous decay over time.[5] Multiple model approaches that include exponential and logistic function appear to predict future progressions better.[6] Chen et al. reported average RMSEs of 2.925 and 3.056 for logistic and exponential functions, respectively.[6] More recently, a pointwise sigmoid regression model with a mean RMSE of 4.1 has been described to capture the varying rates of glaucomatous deterioration over time and characterize both early and late stages of glaucoma.[5]. Another approach has been in the Bayesian setting to incorporate the spatial data in the VF. Long-term variability in HVF has been one of the major limitations in assessing progression in HVF, and several models have been described to take into account of spatio-temporal correlations in the perimetry data.[28–31] However, the majority of studies were limited by small sample sizes (in the hundreds), data cleaning of the training sets, and evaluation/validation sets with stringent criteria.

A number of recent studies have reported various methods for determining progression among VF series.[32–36] However, few studies attempt to forecast future VFs, and current models that predict future VFs require many VF tests obtained over relatively long periods of time. Using a point-wise ordinary least squares linear regression with series of 15 VFs, Taketani et al. achieved the minimum absolute prediction error of 2.4 ± 0.9 dB using the maximally available number of 14 VFs.[7] As these VFs are acquired approximately every 6 months, many years of testing would be needed to accurately predict future VFs. In another study, Zhu et al. reported the superior performance of analysis with non-stationary Weibull error regression and spatial enhancement (ANSWERS) to permutation of pointwise linear regression for predicting future VF tests.[35] However, even at the shortest prediction interval of 10 months after baseline testing, 6 VFs were used to make the VF prediction.[35] Furthermore, to make a VF prediction for 24 months after baseline, 14 VFs were used.[35] To decrease the number of necessary VFs, Fujino et al. applied a least absolute shrinkage and selection operator regression and reported a prediction error of 2.0 ± 2.2 dB using only 3 VFs.[37] However, even with this model, over a year would need to pass before an accurate prediction could be made. A notable aspect of our approach is that by using deep learning models trained on the temporal history for a large group of patients, we are able to take single HVFs and predict point-wise HVFs at half-year time intervals, up to five years later, with an overall PMAE of 2.57 dB. Prior studies have shown that automated perimetric threshold test variability ranges between 2 and 3 dB for normal subjects[38,39] but can be much more variable in patients with glaucoma.[40] To our knowledge, no prior algorithm has been shown to reliably predict the VF changes based on a single HVF such as ours, to a comparable level of accuracy.

One possible reason for the improved accuracy over prior published models is that our model received an extra 2 digits of precision for each perimetry point. In general, the predicted HVFs tended to be slightly less progressed than the actual HVFs, as seen in the Bland-Altman plot (Fig 2C), whereby the mean difference in MD between predicted and actual HVFs was 0.41 dB. This may be because the dataset we used to train our algorithm was unfiltered. Our dataset included non-glaucomatous VFs and VFs after ocular surgeries that may increase perimetry sensitivity, such as cataract extraction. The majority of studies on forecasting VFs and estimating VF progression utilize highly filtered datasets with strict inclusion and exclusion criteria. Most require a certain number of VF tests per study subject that meet certain reliability criteria, and/or a known diagnosis of glaucoma before inclusion. Our model was developed using unfiltered data and included every single VF test performed at our institution regardless of diagnosis or test reliability, and yet the algorithm was still able to make reasonably accurate predictions. Even in cases of non-glaucomatous VF changes, such as a hemifield defect from a cerebrovascular accident (Fig 3), the program forecasts an appropriate future VF, which in this example is a stable VF defect, likely based on the predicted stability of both unaffected and severely affected points. Conversely, the VF for a moderate glaucoma example in Fig 3 has the appearance of a quadrantanopia on cursory visual inspection, yet the program was able to accurately predict that it would progress in a glaucomatous manner. The algorithm would likely perform even better were the program trained and evaluated on a rigorously filtered dataset.

Previous applications of deep learning in glaucoma have been limited to classification rather than forecasting and included analysis of disc photos,[17,19,41] OCT images,[18,42] and VFs.[15] Recently, Li et al. used a deep learning system to classify over 48,000 optic disc photos for referable glaucomatous optic neuropathy and reported an area under the receiver operating characteristic curve (AUROC) of 0.986 with a 95.6% sensitivity and 92.0% specificity.[19] Using a hybrid deep learning method to analyze 102 single wide-field OCT scans, Muhammad et al. found that their protocol outperformed standard OCT and VF clinical metrics in differentiating suspects from early glaucomatous eyes.[18] Asaoka et al. used a multilayer, feed-forward neural network to detect preperimetric glaucoma VFs (AUC 92.6%, 95% CI 89.8–95.4) using 171 preperimetric VFs and 108 control VFs.[15] The deep learning classifier performed significantly better than other machine learning algorithms in distinguishing preperimetric glaucoma from healthy VFs. Unlike these previous classification studies, our study demonstrates a novel application of deep learning to build generative models in glaucoma.

Ideally, forecasted VFs would guide clinical decision-making and disease management. Kalman Filter models have been recently developed to determine the best VF testing frequency to detect glaucoma progression most efficiently and also to forecast glaucoma progression trajectories at different target intraocular pressures.[43,44] Our current model incorporates very little clinical data, although the predictive accuracy was already improved after including subject age. Future research will focus on developing models that incorporate additional clinical parameters, such as IOP, medication and surgical intervention, to assess their effects on forecasted VFs and progression, which may aid in clinical decision making. Additionally, our model could be used to determine how HVFs would change depending on the intervention selected for each individual patient. This type of AI application may help enable precision medicine for glaucoma management in the future.

Our study has several limitations. First, this study included data from a single academic center and only included 24–2 HVF tests, thus our AI-algorithm may not be widely applicable. Furthermore, because the patients included in this study were actively being treated for their respective diseases, predictions may vary with management. However, we included all available 24–2 HVFs over a twenty year period, including numerous providers of different subspecialties, with no filtering, to improve the generalizability of the algorithm. Future work may include training with datasets from multiple centers and testing in a geographically separated cohort. Second, our test set did not include any pairs of HVFs that were beyond 5.5 years of duration. With this current AI-algorithm, predictions beyond 5.5 years of duration became less accurate. Future algorithms that incorporate more clinical parameters will hopefully produce accurate predictions for greater future durations. It is also possible that longitudinal data of longer duration (i.e. >5.5 years) may have included more HVFs with progression to advanced glaucomatous loss resulting in substantial change in the decay rate. Under such circumstances, e.g. for the rapidly progressing glaucoma patient, the AI-algorithm may be less accurate in its predictions given the unusual and less common progression pattern. Third, given the variability of VF testing, it is possible for the AI-algorithm to be misled by a poor baseline VF test due to learning effects. In the Ocular Hypertension Treatment Study, 85.9% of VF abnormalities in reliable tests were not confirmed on retesting.[45] Indeed, upon review of our top outliers, a number of them resulted from a baseline VF demonstrating various defects that led the AI-algorithm to forecast a severely depressed future field, while the actual VF paradoxically improved considerably. Finally, the AI-algorithm was not trained as a classification tool; rather, it was constructed to generate prediction maps for future HVFs that incorporate both spatial and temporal data, a more challenging task for AI than the classification of a subject as progressed or stable.

In conclusion, we have developed a novel deep learning algorithm that is able to forecast, with reasonable accuracy, HVFs up to 5 years from a single HVF as input. The ability to quickly anticipate future glaucomatous progression may prevent unnecessary functional loss that can occur with the current practice of multiple confirmatory tests. With further incorporation of clinical data such as IOP, medication and surgical history, our AI-model may assist in clinical decision-making in the future and allow development of a personalized treatment regimen for each patient.

Supporting information

S1 Fig. Evaluation strategy for test set after models training.

For each of the ten time intervals, there are 10 trained models, one for each cross validation set. Each HVF prediction is then averaged together and the final prediction is compared with the actual HVF.

(PDF)

Click here for additional data file.^{(31.3KB, pdf)}

S2 Fig. Simplified schematic of the CascadeNet architecture.

CascadeNet-1 has 1 copy of convolutional (CN) layers of 64, 128, and 256 filters. CascadeNet-2 has 2 copies of CN layers of 64, 128, and 256 filters. Each black arrow represents a copy-concatenation of the output tensors “cascaded” forward to every possible neural network block. The final model, CascadeNet-5 has 5 copies of CN layers with 64, 128, and 256 filters.

(PDF)

Click here for additional data file.^{(25KB, pdf)}

S1 File. Mathematical modeling description for HVF progression.

Baseline models are described in depth as well as a derivation of the theoretical limit of point-wise prediction models.

(PDF)

Click here for additional data file.^{(131.5KB, pdf)}

Data Availability

Data cannot be shared publicly due to violation of patient privacy and lack of informed consent for data sharing. Data are available from the University of Washington, Department of Ophthalmology (contact Ian Luttrell, research coordinator staff for UW Ophthalmology, luttri@uw.edu) for researchers who meet the criteria for access to confidential data. In order to reconstruct the data set underlying the present study, researchers would need to list the name of the study, the title of the manuscript, the age range of interest, the gender, HVF sequence number, and interval time between HVFs.

Funding Statement

JCW, CSL, SX, PPC, YW, AYL received an unrestricted department grants from Research to Prevent Blindness, New York, NY (https://www.rpbusa.org/rpb/?). CSL received grant K23EY024921 from the National Institutes of Health (https://grants.nih.gov/grants/funding/ac_search_results.htm?text_curr=k23&Search_Type=Activity). AYL received grant K23EY029246 from the NIH. ASR received funding from The Gordon & Betty Moore Foundation, Palo Alto, CA and The Alfred P. Sloan Foundation, New York, NY (https://www.moore.org; https://sloan.org/grants/apply). AYL has received research grant funding from Novartis Pharmaceutical, NVIDIA Corporation, and Microsoft Corporation (https://www.pharma.us.novartis.com/; https://www.nvidia.com/; https://www.microsoft.com/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1.Kapetanakis VV, Chan MPY, Foster PJ, Cook DG, Owen CG, Rudnicka AR. Global variations and time trends in the prevalence of primary open angle glaucoma (POAG): a systematic review and meta-analysis. Br J Ophthalmol. 2016. January;100(1):86–93. 10.1136/bjophthalmol-2015-307223 [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Bourne RRA, Stevens GA, White RA, Smith JL, Flaxman SR, Price H, et al. Causes of vision loss worldwide, 1990–2010: a systematic analysis. The Lancet Global Health. 2013;1(6):e339–49. 10.1016/S2214-109X(13)70113-X [DOI] [PubMed] [Google Scholar]
3.Bengtsson B, Patella VM, Heijl A. Prediction of glaucomatous visual field loss by extrapolation of linear trends. Arch Ophthalmol. 2009. December;127(12):1610–5. 10.1001/archophthalmol.2009.297 [DOI] [PubMed] [Google Scholar]
4.Smith SD, Katz J, Quigley HA. Analysis of progressive change in automated visual fields in glaucoma. Invest Ophthalmol Vis Sci. 1996. June;37(7):1419–28. [PubMed] [Google Scholar]
5.Otarola F, Chen A, Morales E, Yu F, Afifi A, Caprioli J. Course of Glaucomatous Visual Field Loss Across the Entire Perimetric Range. JAMA Ophthalmol [Internet]. 2016. March 10; Available from: 10.1001/jamaophthalmol.2016.0118 [DOI] [PubMed] [Google Scholar]
6.Chen A, Nouri-Mahdavi K, Otarola FJ, Yu F, Afifi AA, Caprioli J. Models of glaucomatous visual field loss. Invest Ophthalmol Vis Sci. 2014. November 6;55(12):7881–7. 10.1167/iovs.14-15435 [DOI] [PubMed] [Google Scholar]
7.Taketani Y, Murata H, Fujino Y, Mayama C, Asaoka R. How Many Visual Fields Are Required to Precisely Predict Future Test Results in Glaucoma Patients When Using Different Trend Analyses? Invest Ophthalmol Vis Sci. 2015. June;56(6):4076–82. 10.1167/iovs.14-16341 [DOI] [PubMed] [Google Scholar]
8.Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems 25. Curran Associates, Inc; 2012. p. 1097–105. [Google Scholar]
9.Hahnloser RH, Sarpeshkar R, Mahowald MA, Douglas RJ, Seung HS. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature. 2000. June 22;405(6789):947–51. 10.1038/35016072 [DOI] [PubMed] [Google Scholar]
10.Lee CS, Baughman DM, Lee AY. Deep Learning Is Effective for Classifying Normal versus Age-Related Macular Degeneration OCT Images. Ophthalmology Retina. 2017;1(4):322–7. 10.1016/j.oret.2016.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Schlegl T, Waldstein SM, Bogunovic H, Endstraßer F, Sadeghipour A, Philip A-M, et al. Fully Automated Detection and Quantification of Macular Fluid in OCT Using Deep Learning. Ophthalmology [Internet]. 2017. December 8; Available from: 10.1016/j.ophtha.2017.10.031 [DOI] [PubMed] [Google Scholar]
12.Lee CS, Tyring AJ, Deruyter NP, Wu Y, Rokem A, Lee AY. Deep-learning based, automated segmentation of macular edema in optical coherence tomography. Biomed Opt Express. 2017. July 1;8(7):3440–8. 10.1364/BOE.8.003440 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Xiao S, Bucher F, Wu Y, Rokem A, Lee CS, Marra KV, et al. Fully automated, deep learning segmentation of oxygen-induced retinopathy images. JCI Insight [Internet]. 2017. December 21;2(24). Available from: 10.1172/jci.insight.97585 [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Ting DSW, Cheung CY-L, Lim G, Tan GSW, Quang ND, Gan A, et al. Development and Validation of a Deep Learning System for Diabetic Retinopathy and Related Eye Diseases Using Retinal Images From Multiethnic Populations With Diabetes. JAMA. 2017. December 12;318(22):2211–23. 10.1001/jama.2017.18152 [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Asaoka R, Murata H, Iwase A, Araie M. Detecting Preperimetric Glaucoma with Standard Automated Perimetry Using a Deep Learning Classifier. Ophthalmology. 2016. September;123(9):1974–80. 10.1016/j.ophtha.2016.05.029 [DOI] [PubMed] [Google Scholar]
16.Chen Xiangyu, Xu Yanwu, Damon Wing Kee Wong, Tien Yin Wong, Jiang Liu. Glaucoma detection based on deep convolutional neural network. Conf Proc IEEE Eng Med Biol Soc. 2015. August;2015:715–8. 10.1109/EMBC.2015.7318462 [DOI] [PubMed] [Google Scholar]
17.Cerentini A, Welfer D, Cordeiro d’Ornellas M, Pereira Haygert CJ, Dotto GN. Automatic Identification of Glaucoma Using Deep Learning Methods. Stud Health Technol Inform. 2017;245:318–21. [PubMed] [Google Scholar]
18.Muhammad H, Fuchs TJ, De Cuir N, De Moraes CG, Blumberg DM, Liebmann JM, et al. Hybrid Deep Learning on Single Wide-field Optical Coherence tomography Scans Accurately Classifies Glaucoma Suspects. J Glaucoma. 2017. December;26(12):1086–94. 10.1097/IJG.0000000000000765 [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Li Z, He Y, Keel S, Meng W, Chang RT, He M. Efficacy of a Deep Learning System for Detecting Glaucomatous Optic Neuropathy Based on Color Fundus Photographs. Ophthalmology [Internet]. 2018. March 2; Available from: 10.1016/j.ophtha.2018.01.023 [DOI] [PubMed] [Google Scholar]
20.Lee A, Taylor P, Kalpathy-Cramer J, Tufail A. Machine Learning Has Arrived! Ophthalmology. 2017. December;124(12):1726–8. 10.1016/j.ophtha.2017.08.046 [DOI] [PubMed] [Google Scholar]
21.Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. Aistats. 2010;9. [Google Scholar]
22.Kingma D, Ba J. Adam: A Method for Stochastic Optimization [Internet]. arXiv [cs.LG]. 2014. Available from: http://arxiv.org/abs/1412.6980 [Google Scholar]
23.Chollet F. Keras [Internet]. 2015. Available from: https://keras.io/ [Google Scholar]
24.Abadi Martín, Agarwal Ashish, Barham Paul, Brevdo Eugene, Chen Zhifeng, Citro Craig, et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems [Internet]. 2015. Available from: http://tensorflow.org/ [Google Scholar]
25.Heijl A, Leske MC, Bengtsson B, Hyman L, Bengtsson B, Hussein M, et al. Reduction of intraocular pressure and glaucoma progression: results from the Early Manifest Glaucoma Trial. Arch Ophthalmol. 2002. October;120(10):1268–79. [DOI] [PubMed] [Google Scholar]
26.Chauhan BC, Drance SM, Douglas GR. The use of visual field indices in detecting changes in the visual field in glaucoma. Invest Ophthalmol Vis Sci. 1990. March 1;31(3):512–20. [PubMed] [Google Scholar]
27.Caprioli J, Mock D, Bitrian E, Afifi AA, Yu F, Nouri-Mahdavi K, et al. A method to measure and predict rates of regional visual field decay in glaucoma. Invest Ophthalmol Vis Sci. 2011. July 1;52(7):4765–73. 10.1167/iovs.10-6414 [DOI] [PubMed] [Google Scholar]
28.Warren JL, Mwanza J-C, Tanna AP, Budenz DL. A Statistical Model to Analyze Clinician Expert Consensus on Glaucoma Progression using Spatially Correlated Visual Field Data. Transl Vis Sci Technol. 2016. August;5(4):14 10.1167/tvst.5.4.14 [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Betz-Stablein BD, Morgan WH, House PH, Hazelton ML. Spatial modeling of visual field data for assessing glaucoma progression. Invest Ophthalmol Vis Sci. 2013. February 28;54(2):1544–53. 10.1167/iovs.12-11226 [DOI] [PubMed] [Google Scholar]
30.Anderson AJ. Comparison of Three Parametric Models for Glaucomatous Visual Field Progression Rate Distributions. Transl Vis Sci Technol. 2015. July;4(4):2 10.1167/tvst.4.4.2 [DOI] [PMC free article] [PubMed] [Google Scholar]
31.VanBuren J, Oleson JJ, Zamba GKD, Wall M. Integrating independent spatio-temporal replications to assess population trends in disease spread. Stat Med. 2016. December 10;35(28):5210–21. 10.1002/sim.7056 [DOI] [PubMed] [Google Scholar]
32.O’Leary N, Chauhan BC, Artes PH. Visual field progression in glaucoma: estimating the overall significance of deterioration with permutation analyses of pointwise linear regression (PoPLR). Invest Ophthalmol Vis Sci. 2012. October 1;53(11):6776–84. 10.1167/iovs.12-10049 [DOI] [PubMed] [Google Scholar]
33.Garway-Heath DF, Quartilho A, Prah P, Crabb DP, Cheng Q, Zhu H. Evaluation of Visual Field and Imaging Outcomes for Glaucoma Clinical Trials (An American Ophthalomological Society Thesis). Trans Am Ophthalmol Soc. 2017. August;115:T4 [PMC free article] [PubMed] [Google Scholar]
34.Karakawa A, Murata H, Hirasawa H, Mayama C, Asaoka R. Detection of progression of glaucomatous visual field damage using the point-wise method with the binomial test. PLoS One. 2013. October 25;8(10):e78630 10.1371/journal.pone.0078630 [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Zhu H, Crabb DP, Ho T, Garway-Heath DF. More Accurate Modeling of Visual Field Progression in Glaucoma: ANSWERS. Invest Ophthalmol Vis Sci. 2015. September;56(10):6077–83. 10.1167/iovs.15-16957 [DOI] [PubMed] [Google Scholar]
36.Zhu H, Russell RA, Saunders LJ, Ceccon S, Garway-Heath DF, Crabb DP. Detecting changes in retinal function: Analysis with Non-Stationary Weibull Error Regression and Spatial enhancement (ANSWERS). PLoS One. 2014. January 17;9(1):e85654 10.1371/journal.pone.0085654 [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Fujino Y, Murata H, Mayama C, Asaoka R. Applying “Lasso” Regression to Predict Future Visual Field Progression in Glaucoma Patients. Invest Ophthalmol Vis Sci. 2015. April;56(4):2334–9. 10.1167/iovs.15-16445 [DOI] [PubMed] [Google Scholar]
38.Lewis RA, Johnson CA, Keltner JL, Labermeier PK. Variability of quantitative automated perimetry in normal observers. Ophthalmology. 1986. July;93(7):878–81. [DOI] [PubMed] [Google Scholar]
39.Heijl A, Lindgren G, Olsson J. Normal variability of static perimetric threshold values across the central visual field. Arch Ophthalmol. 1987. November;105(11):1544–9. [DOI] [PubMed] [Google Scholar]
40.Heijl A, Lindgren A, Lindgren G. Test-retest variability in glaucomatous visual fields. Am J Ophthalmol. 1989. August 15;108(2):130–5. [DOI] [PubMed] [Google Scholar]
41.Xiangyu Chen, Chen X, Xu Y, Wong DWK, Wong TY, Liu J. Glaucoma detection based on deep convolutional neural network. In: 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) [Internet]. 2015. Available from: 10.1109/embc.2015.7318462 [DOI] [PubMed]
42.Devalla SK, Chin KS, Mari J-M, Tun TA, Strouthidis NG, Aung T, et al. A Deep Learning Approach to Digitally Stain Optical Coherence Tomography Images of the Optic Nerve Head. Invest Ophthalmol Vis Sci. 2018. January 1;59(1):63–74. 10.1167/iovs.17-22617 [DOI] [PubMed] [Google Scholar]
43.Schell GJ, Lavieri MS, Helm JE, Liu X, Musch DC, Van Oyen MP, et al. Using filtered forecasting techniques to determine personalized monitoring schedules for patients with open-angle glaucoma. Ophthalmology. 2014. August;121(8):1539–46. 10.1016/j.ophtha.2014.02.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Kazemian P, Lavieri MS, Van Oyen MP, Andrews C, Stein JD. Personalized Prediction of Glaucoma Progression Under Different Target Intraocular Pressure Levels Using Filtered Forecasting Methods. Ophthalmology [Internet]. 2017. December 1; Available from: 10.1016/j.ophtha.2017.10.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Keltner JL, Johnson CA, Quigg JM, Cello KE, Kass MA, Gordon MO. Confirmation of visual field abnormalities in the Ocular Hypertension Treatment Study. Ocular Hypertension Treatment Study Group. Arch Ophthalmol. 2000. September;118(9):1187–94. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Fig. Evaluation strategy for test set after models training.

(PDF)

Click here for additional data file.^{(31.3KB, pdf)}

S2 Fig. Simplified schematic of the CascadeNet architecture.

(PDF)

Click here for additional data file.^{(25KB, pdf)}

S1 File. Mathematical modeling description for HVF progression.

Baseline models are described in depth as well as a derivation of the theoretical limit of point-wise prediction models.

(PDF)

Click here for additional data file.^{(131.5KB, pdf)}

Data Availability Statement

[pone.0214875.ref001] 1.Kapetanakis VV, Chan MPY, Foster PJ, Cook DG, Owen CG, Rudnicka AR. Global variations and time trends in the prevalence of primary open angle glaucoma (POAG): a systematic review and meta-analysis. Br J Ophthalmol. 2016. January;100(1):86–93. 10.1136/bjophthalmol-2015-307223 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref002] 2.Bourne RRA, Stevens GA, White RA, Smith JL, Flaxman SR, Price H, et al. Causes of vision loss worldwide, 1990–2010: a systematic analysis. The Lancet Global Health. 2013;1(6):e339–49. 10.1016/S2214-109X(13)70113-X [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref003] 3.Bengtsson B, Patella VM, Heijl A. Prediction of glaucomatous visual field loss by extrapolation of linear trends. Arch Ophthalmol. 2009. December;127(12):1610–5. 10.1001/archophthalmol.2009.297 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref004] 4.Smith SD, Katz J, Quigley HA. Analysis of progressive change in automated visual fields in glaucoma. Invest Ophthalmol Vis Sci. 1996. June;37(7):1419–28. [PubMed] [Google Scholar]

[pone.0214875.ref005] 5.Otarola F, Chen A, Morales E, Yu F, Afifi A, Caprioli J. Course of Glaucomatous Visual Field Loss Across the Entire Perimetric Range. JAMA Ophthalmol [Internet]. 2016. March 10; Available from: 10.1001/jamaophthalmol.2016.0118 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref006] 6.Chen A, Nouri-Mahdavi K, Otarola FJ, Yu F, Afifi AA, Caprioli J. Models of glaucomatous visual field loss. Invest Ophthalmol Vis Sci. 2014. November 6;55(12):7881–7. 10.1167/iovs.14-15435 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref007] 7.Taketani Y, Murata H, Fujino Y, Mayama C, Asaoka R. How Many Visual Fields Are Required to Precisely Predict Future Test Results in Glaucoma Patients When Using Different Trend Analyses? Invest Ophthalmol Vis Sci. 2015. June;56(6):4076–82. 10.1167/iovs.14-16341 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref008] 8.Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems 25. Curran Associates, Inc; 2012. p. 1097–105. [Google Scholar]

[pone.0214875.ref009] 9.Hahnloser RH, Sarpeshkar R, Mahowald MA, Douglas RJ, Seung HS. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature. 2000. June 22;405(6789):947–51. 10.1038/35016072 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref010] 10.Lee CS, Baughman DM, Lee AY. Deep Learning Is Effective for Classifying Normal versus Age-Related Macular Degeneration OCT Images. Ophthalmology Retina. 2017;1(4):322–7. 10.1016/j.oret.2016.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref011] 11.Schlegl T, Waldstein SM, Bogunovic H, Endstraßer F, Sadeghipour A, Philip A-M, et al. Fully Automated Detection and Quantification of Macular Fluid in OCT Using Deep Learning. Ophthalmology [Internet]. 2017. December 8; Available from: 10.1016/j.ophtha.2017.10.031 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref012] 12.Lee CS, Tyring AJ, Deruyter NP, Wu Y, Rokem A, Lee AY. Deep-learning based, automated segmentation of macular edema in optical coherence tomography. Biomed Opt Express. 2017. July 1;8(7):3440–8. 10.1364/BOE.8.003440 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref013] 13.Xiao S, Bucher F, Wu Y, Rokem A, Lee CS, Marra KV, et al. Fully automated, deep learning segmentation of oxygen-induced retinopathy images. JCI Insight [Internet]. 2017. December 21;2(24). Available from: 10.1172/jci.insight.97585 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref014] 14.Ting DSW, Cheung CY-L, Lim G, Tan GSW, Quang ND, Gan A, et al. Development and Validation of a Deep Learning System for Diabetic Retinopathy and Related Eye Diseases Using Retinal Images From Multiethnic Populations With Diabetes. JAMA. 2017. December 12;318(22):2211–23. 10.1001/jama.2017.18152 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref015] 15.Asaoka R, Murata H, Iwase A, Araie M. Detecting Preperimetric Glaucoma with Standard Automated Perimetry Using a Deep Learning Classifier. Ophthalmology. 2016. September;123(9):1974–80. 10.1016/j.ophtha.2016.05.029 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref016] 16.Chen Xiangyu, Xu Yanwu, Damon Wing Kee Wong, Tien Yin Wong, Jiang Liu. Glaucoma detection based on deep convolutional neural network. Conf Proc IEEE Eng Med Biol Soc. 2015. August;2015:715–8. 10.1109/EMBC.2015.7318462 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref017] 17.Cerentini A, Welfer D, Cordeiro d’Ornellas M, Pereira Haygert CJ, Dotto GN. Automatic Identification of Glaucoma Using Deep Learning Methods. Stud Health Technol Inform. 2017;245:318–21. [PubMed] [Google Scholar]

[pone.0214875.ref018] 18.Muhammad H, Fuchs TJ, De Cuir N, De Moraes CG, Blumberg DM, Liebmann JM, et al. Hybrid Deep Learning on Single Wide-field Optical Coherence tomography Scans Accurately Classifies Glaucoma Suspects. J Glaucoma. 2017. December;26(12):1086–94. 10.1097/IJG.0000000000000765 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref019] 19.Li Z, He Y, Keel S, Meng W, Chang RT, He M. Efficacy of a Deep Learning System for Detecting Glaucomatous Optic Neuropathy Based on Color Fundus Photographs. Ophthalmology [Internet]. 2018. March 2; Available from: 10.1016/j.ophtha.2018.01.023 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref020] 20.Lee A, Taylor P, Kalpathy-Cramer J, Tufail A. Machine Learning Has Arrived! Ophthalmology. 2017. December;124(12):1726–8. 10.1016/j.ophtha.2017.08.046 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref021] 21.Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. Aistats. 2010;9. [Google Scholar]

[pone.0214875.ref022] 22.Kingma D, Ba J. Adam: A Method for Stochastic Optimization [Internet]. arXiv [cs.LG]. 2014. Available from: http://arxiv.org/abs/1412.6980 [Google Scholar]

[pone.0214875.ref023] 23.Chollet F. Keras [Internet]. 2015. Available from: https://keras.io/ [Google Scholar]

[pone.0214875.ref024] 24.Abadi Martín, Agarwal Ashish, Barham Paul, Brevdo Eugene, Chen Zhifeng, Citro Craig, et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems [Internet]. 2015. Available from: http://tensorflow.org/ [Google Scholar]

[pone.0214875.ref025] 25.Heijl A, Leske MC, Bengtsson B, Hyman L, Bengtsson B, Hussein M, et al. Reduction of intraocular pressure and glaucoma progression: results from the Early Manifest Glaucoma Trial. Arch Ophthalmol. 2002. October;120(10):1268–79. [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref026] 26.Chauhan BC, Drance SM, Douglas GR. The use of visual field indices in detecting changes in the visual field in glaucoma. Invest Ophthalmol Vis Sci. 1990. March 1;31(3):512–20. [PubMed] [Google Scholar]

[pone.0214875.ref027] 27.Caprioli J, Mock D, Bitrian E, Afifi AA, Yu F, Nouri-Mahdavi K, et al. A method to measure and predict rates of regional visual field decay in glaucoma. Invest Ophthalmol Vis Sci. 2011. July 1;52(7):4765–73. 10.1167/iovs.10-6414 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref028] 28.Warren JL, Mwanza J-C, Tanna AP, Budenz DL. A Statistical Model to Analyze Clinician Expert Consensus on Glaucoma Progression using Spatially Correlated Visual Field Data. Transl Vis Sci Technol. 2016. August;5(4):14 10.1167/tvst.5.4.14 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref029] 29.Betz-Stablein BD, Morgan WH, House PH, Hazelton ML. Spatial modeling of visual field data for assessing glaucoma progression. Invest Ophthalmol Vis Sci. 2013. February 28;54(2):1544–53. 10.1167/iovs.12-11226 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref030] 30.Anderson AJ. Comparison of Three Parametric Models for Glaucomatous Visual Field Progression Rate Distributions. Transl Vis Sci Technol. 2015. July;4(4):2 10.1167/tvst.4.4.2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref031] 31.VanBuren J, Oleson JJ, Zamba GKD, Wall M. Integrating independent spatio-temporal replications to assess population trends in disease spread. Stat Med. 2016. December 10;35(28):5210–21. 10.1002/sim.7056 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref032] 32.O’Leary N, Chauhan BC, Artes PH. Visual field progression in glaucoma: estimating the overall significance of deterioration with permutation analyses of pointwise linear regression (PoPLR). Invest Ophthalmol Vis Sci. 2012. October 1;53(11):6776–84. 10.1167/iovs.12-10049 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref033] 33.Garway-Heath DF, Quartilho A, Prah P, Crabb DP, Cheng Q, Zhu H. Evaluation of Visual Field and Imaging Outcomes for Glaucoma Clinical Trials (An American Ophthalomological Society Thesis). Trans Am Ophthalmol Soc. 2017. August;115:T4 [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref034] 34.Karakawa A, Murata H, Hirasawa H, Mayama C, Asaoka R. Detection of progression of glaucomatous visual field damage using the point-wise method with the binomial test. PLoS One. 2013. October 25;8(10):e78630 10.1371/journal.pone.0078630 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref035] 35.Zhu H, Crabb DP, Ho T, Garway-Heath DF. More Accurate Modeling of Visual Field Progression in Glaucoma: ANSWERS. Invest Ophthalmol Vis Sci. 2015. September;56(10):6077–83. 10.1167/iovs.15-16957 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref036] 36.Zhu H, Russell RA, Saunders LJ, Ceccon S, Garway-Heath DF, Crabb DP. Detecting changes in retinal function: Analysis with Non-Stationary Weibull Error Regression and Spatial enhancement (ANSWERS). PLoS One. 2014. January 17;9(1):e85654 10.1371/journal.pone.0085654 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref037] 37.Fujino Y, Murata H, Mayama C, Asaoka R. Applying “Lasso” Regression to Predict Future Visual Field Progression in Glaucoma Patients. Invest Ophthalmol Vis Sci. 2015. April;56(4):2334–9. 10.1167/iovs.15-16445 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref038] 38.Lewis RA, Johnson CA, Keltner JL, Labermeier PK. Variability of quantitative automated perimetry in normal observers. Ophthalmology. 1986. July;93(7):878–81. [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref039] 39.Heijl A, Lindgren G, Olsson J. Normal variability of static perimetric threshold values across the central visual field. Arch Ophthalmol. 1987. November;105(11):1544–9. [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref040] 40.Heijl A, Lindgren A, Lindgren G. Test-retest variability in glaucomatous visual fields. Am J Ophthalmol. 1989. August 15;108(2):130–5. [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref041] 41.Xiangyu Chen, Chen X, Xu Y, Wong DWK, Wong TY, Liu J. Glaucoma detection based on deep convolutional neural network. In: 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) [Internet]. 2015. Available from: 10.1109/embc.2015.7318462 [DOI] [PubMed]

[pone.0214875.ref042] 42.Devalla SK, Chin KS, Mari J-M, Tun TA, Strouthidis NG, Aung T, et al. A Deep Learning Approach to Digitally Stain Optical Coherence Tomography Images of the Optic Nerve Head. Invest Ophthalmol Vis Sci. 2018. January 1;59(1):63–74. 10.1167/iovs.17-22617 [DOI] [PubMed] [Google Scholar]

[pone.0214875.ref043] 43.Schell GJ, Lavieri MS, Helm JE, Liu X, Musch DC, Van Oyen MP, et al. Using filtered forecasting techniques to determine personalized monitoring schedules for patients with open-angle glaucoma. Ophthalmology. 2014. August;121(8):1539–46. 10.1016/j.ophtha.2014.02.021 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref044] 44.Kazemian P, Lavieri MS, Van Oyen MP, Andrews C, Stein JD. Personalized Prediction of Glaucoma Progression Under Different Target Intraocular Pressure Levels Using Filtered Forecasting Methods. Ophthalmology [Internet]. 2017. December 1; Available from: 10.1016/j.ophtha.2017.10.033 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0214875.ref045] 45.Keltner JL, Johnson CA, Quigg JM, Cello KE, Kass MA, Gordon MO. Confirmation of visual field abnormalities in the Ocular Hypertension Treatment Study. Ocular Hypertension Treatment Study Group. Arch Ophthalmol. 2000. September;118(9):1187–94. [DOI] [PubMed] [Google Scholar]

PERMALINK

Forecasting future Humphrey Visual Fields using deep learning

Joanne C Wen

Cecilia S Lee

Pearse A Keane

Sa Xiao

Ariel S Rokem

Philip P Chen

Yue Wu

Aaron Y Lee

Roles