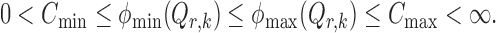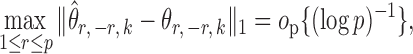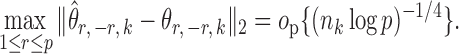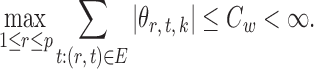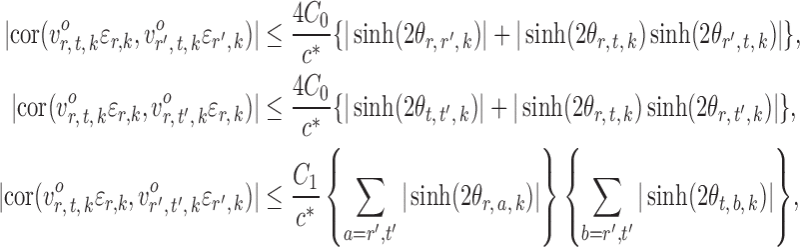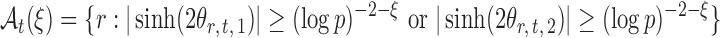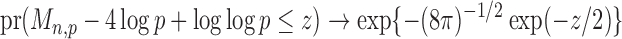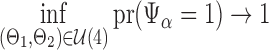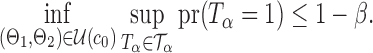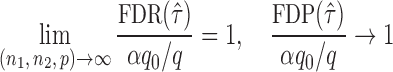Summary
Micro-organisms such as bacteria form complex ecological community networks that can be greatly influenced by diet and other environmental factors. Differential analysis of microbial community structures aims to elucidate systematic changes during an adaptive response to changes in environment. In this paper, we propose a flexible Markov random field model for microbial network structure and introduce a hypothesis testing framework for detecting differences between networks, also known as differential network analysis. Our global test for differential networks is particularly powerful against sparse alternatives. In addition, we develop a multiple testing procedure with false discovery rate control to identify the structure of the differential network. The proposed method is applied to data from a gut microbiome study on U.K. twins to evaluate how age affects the microbial community network.
Keywords: Differential network, High-dimensional logistic regression, Microbiome, Multiple testing
1. Introduction
1.1. Markov random field model for microbial networks
High-throughout sequencing technologies provide comprehensive surveys of the human microbiome using either 16S rRNA or shotgun metagenomics sequencing (Kuczynski et al., 2012). An important objective in microbiome studies is to infer the interactions among various microorganisms (Faust & Raes, 2012). There is growing interest in studying microbial community structures, because the underlying ecological structures are highly dynamic and undergo differential changes in response to changes in their environment. An example that motivates this paper is to understand how age-related physiological changes in the gut and modifications in lifestyle influence gut microbial interaction structures (Biagi et al., 2010; Claesson et al., 2011). Motivated by this goal of uncovering changes in microbial interactions associated with age, we develop a method for detecting differential microbial community networks.
Microbiome data present at least two challenges. First, the observations in sequencing-based microbiome studies are often relative abundances of different bacteria, and the absolute microbial abundances are unavailable. The observation from each sample can be represented by a compositional vector 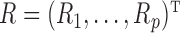 with
with  taxa and the unit-sum constraint
taxa and the unit-sum constraint 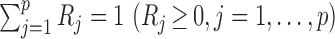 . Because typical microbial communities consist of both rare and common taxa, the second obstacle is the sparsity of the compositional vector
. Because typical microbial communities consist of both rare and common taxa, the second obstacle is the sparsity of the compositional vector 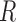 ; many taxa are absent from the sample or their abundances are below the detection level. There is a lack of flexible statistical models that can capture the complex dependency structures among the taxa in a given community. For instance, methods based on Gaussian graphical models cannot be directly applied to study the conditional dependence relationships, due to the unit-sum constraint, and naive application of such models can lead to spurious associations (Aitchison, 1982).
; many taxa are absent from the sample or their abundances are below the detection level. There is a lack of flexible statistical models that can capture the complex dependency structures among the taxa in a given community. For instance, methods based on Gaussian graphical models cannot be directly applied to study the conditional dependence relationships, due to the unit-sum constraint, and naive application of such models can lead to spurious associations (Aitchison, 1982).
Gaussian graphical models have been applied to centred log-ratio transformed data to study conditional dependence relationships among microbes (Kurtz et al., 2015), but this transformation has difficulty in dealing with zeros and the resulting transformed data are not even close to being Gaussian or sub-Gaussian. Furthermore, graphical models based on the centred log-ratio transformation are difficult to interpret. Biswas et al. (2016) proposed studying conditional microbial interactions by modelling the residuals from a Poisson regression, but their approach does not account for the compositional nature of the data. Fang et al. (2017) modelled the conditional dependence among the latent absolute abundances that generate the compositional data using a logistic normal distribution, but this method does not address the sparsity issue. Finally, existing works based on graphical models do not assign uncertainties or statistical significance to the conditional associations, and are not developed with a focus on differential network analysis.
To address the above challenges, we propose to discretize the compositional vector 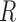 into a vector
into a vector 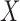 of binary measurements
of binary measurements 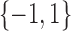 based on a prespecified abundance threshold such as the median relative abundance. In particular,
based on a prespecified abundance threshold such as the median relative abundance. In particular, 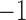 represents absence or a relative abundance below the given threshold, whereas
represents absence or a relative abundance below the given threshold, whereas 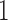 represents presence or a relative abundance above the threshold. After discretizing the data, one can use a binary Markov random field to model conditional dependencies between the components of the discretized vector
represents presence or a relative abundance above the threshold. After discretizing the data, one can use a binary Markov random field to model conditional dependencies between the components of the discretized vector 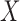 . The pairwise relationships can be captured by an undirected graph
. The pairwise relationships can be captured by an undirected graph 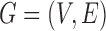 whose vertex set is
whose vertex set is 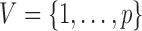 and whose edge set
and whose edge set 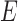 corresponds to conditional dependencies. The binary Markov random field associated with graph
corresponds to conditional dependencies. The binary Markov random field associated with graph 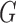 has the joint distribution
has the joint distribution
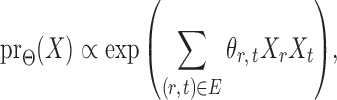 |
(1) |
subject to a normalizing constant, where 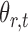 quantifies the conditional dependence between taxa
quantifies the conditional dependence between taxa 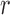 and
and 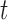 . With binary
. With binary 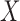 , this model has a clear biological interpretation: positive
, this model has a clear biological interpretation: positive 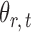 implies co-existence and negative
implies co-existence and negative 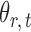 implies co-exclusiveness.
implies co-exclusiveness.
1.2. Differential network analysis
Let 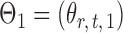 and
and 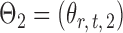 be the matrices that represent the microbial network among discretized taxa abundances for two age groups. In this paper, we are interested in the global test
be the matrices that represent the microbial network among discretized taxa abundances for two age groups. In this paper, we are interested in the global test
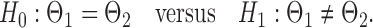 |
(2) |
If the global null in (2) is rejected, it becomes of interest to test for entrywise changes in the differential network 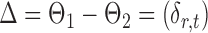 ,
,
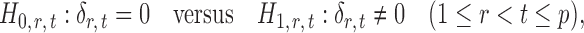 |
(3) |
while controlling the false discovery rate at a prespecified level.
The gut microbial networks of young adults and the elderly often differ only in a small number of links (Goodrich et al., 2016). Our proposed global test uses the maximum of the standardized entrywise differences as the test statistic, and is thus particularly powerful against such sparse alternatives, compared to tests based on the Frobenius norm (Schott, 2007; Li & Chen, 2012). Our multiple testing procedure for differential network analysis accounts for the multiplicity in testing the 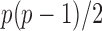 hypotheses, with both the false discovery proportion and the false discovery rate controlled asymptotically. The proposed global and multiple testing procedures are implemented in the R package TestBMN (R Development Core Team, 2019), which is available on GitHub. The merits of the proposed tests are further demonstrated through extensive simulations and a gut microbiome study of U.K. twins.
hypotheses, with both the false discovery proportion and the false discovery rate controlled asymptotically. The proposed global and multiple testing procedures are implemented in the R package TestBMN (R Development Core Team, 2019), which is available on GitHub. The merits of the proposed tests are further demonstrated through extensive simulations and a gut microbiome study of U.K. twins.
1.3. Our contribution
In an unpublished 2016 technical report from the University of Pittsburgh, Z. Ren developed a method for estimation of individual entries in 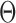 for a single binary Markov random field model. In contrast, this paper studies global and multiple testing of two Markov random field models with multiple testing error control. Nodewise logistic regressions are used to develop the entrywise test statistics, whose dependence structure is much more complicated than in the Gaussian case (Xia et al., 2015; Cai & Liu, 2016; Xia et al., 2018). The debiased entrywise estimators for testing Gaussian graphical models are based on the residuals from nodewise linear regressions whose correlations are straightforward to characterize. However, the estimators in the current paper depend not only on the residual from each nodewise logistic regression but on carefully defined projection directions needed for bias correction. By overcoming these challenges, we establish theoretical properties of the proposed testing procedures.
for a single binary Markov random field model. In contrast, this paper studies global and multiple testing of two Markov random field models with multiple testing error control. Nodewise logistic regressions are used to develop the entrywise test statistics, whose dependence structure is much more complicated than in the Gaussian case (Xia et al., 2015; Cai & Liu, 2016; Xia et al., 2018). The debiased entrywise estimators for testing Gaussian graphical models are based on the residuals from nodewise linear regressions whose correlations are straightforward to characterize. However, the estimators in the current paper depend not only on the residual from each nodewise logistic regression but on carefully defined projection directions needed for bias correction. By overcoming these challenges, we establish theoretical properties of the proposed testing procedures.
2. Global and multiple testing of Markov networks
2.1. Notation and problem set-up
Let 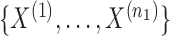 be the
be the 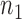 independent binary observations from the first population and
independent binary observations from the first population and 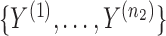 the
the 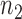 independent binary observations from the second population, often conveniently written as matrices
independent binary observations from the second population, often conveniently written as matrices 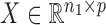 and
and 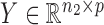 . For a matrix
. For a matrix 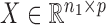 ,
, 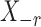 denotes the
denotes the 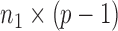 submatrix with the
submatrix with the 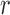 th column removed. For a matrix
th column removed. For a matrix 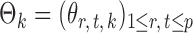 and
and 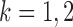 , let
, let 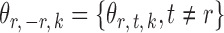 denote the
denote the 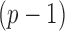 -dimensional subvector of parameters. For a symmetric matrix
-dimensional subvector of parameters. For a symmetric matrix 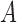 ,
, 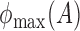 and
and 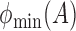 denote the largest and smallest eigenvalues of
denote the largest and smallest eigenvalues of 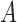 . For a vector
. For a vector 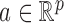 , the usual vector
, the usual vector 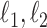 and
and 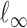 norms are denoted, respectively, by
norms are denoted, respectively, by 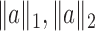 and
and 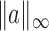 . The indicator function is denoted by
. The indicator function is denoted by 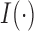 .
.
To leverage the sparsity in the differential network 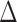 , we propose a test based on the maximum of the standardized entrywise differences between the two matrices (Xia et al., 2015). Our motivation is that the global null hypothesis in (2) is equivalent to
, we propose a test based on the maximum of the standardized entrywise differences between the two matrices (Xia et al., 2015). Our motivation is that the global null hypothesis in (2) is equivalent to
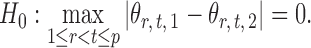 |
Therefore one can construct the test statistic 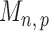 by first obtaining nearly unbiased estimators of
by first obtaining nearly unbiased estimators of 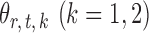 and then deriving the standardized entrywise difference
and then deriving the standardized entrywise difference 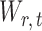 , such that
, such that 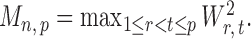
If the global null 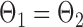 is rejected, simultaneous testing of entrywise differences is often of interest to identify where the two networks differ. To this end, we also consider multiple testing of all entries in
is rejected, simultaneous testing of entrywise differences is often of interest to identify where the two networks differ. To this end, we also consider multiple testing of all entries in 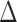 , as formally defined in (3). A natural test statistic for each individual test in (3) is the standardized entrywise difference
, as formally defined in (3). A natural test statistic for each individual test in (3) is the standardized entrywise difference 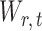 . For any given threshold level
. For any given threshold level 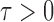 , the null hypothesis
, the null hypothesis 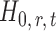 is rejected if
is rejected if 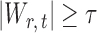 . Our goal is to choose an optimal threshold
. Our goal is to choose an optimal threshold 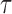 such that the proposed multiple testing procedure rejects as many true positives as possible while controlling the false discovery rate at a prespecified level.
such that the proposed multiple testing procedure rejects as many true positives as possible while controlling the false discovery rate at a prespecified level.
2.2. Derivation of the standardized entrywise statistics
To obtain 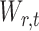 , we first derive nearly unbiased estimators of
, we first derive nearly unbiased estimators of 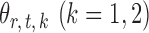 and evaluate their variances. Without loss of generality, it suffices to focus on estimation of
and evaluate their variances. Without loss of generality, it suffices to focus on estimation of 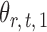 from
from 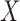 .
.
Given 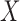 , one can recover the association parameters in a binary Markov random field using
, one can recover the association parameters in a binary Markov random field using 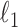 -penalized nodewise logistic regression (Ravikumar et al., 2010), because the conditional distribution of
-penalized nodewise logistic regression (Ravikumar et al., 2010), because the conditional distribution of 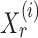 given
given 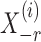 is
is
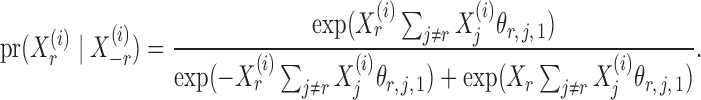 |
(4) |
Thus the variable 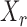 can be viewed as the response in a logistic regression where all remaining variables
can be viewed as the response in a logistic regression where all remaining variables 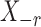 act as covariates. However,
act as covariates. However, 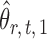 obtained via
obtained via 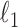 -penalized estimation (Ravikumar et al., 2010) is biased.
-penalized estimation (Ravikumar et al., 2010) is biased.
To correct for the bias in 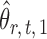 , it is instructive to write the
, it is instructive to write the 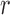 th variable as a nonlinear function of all remaining variables, i.e., for every node
th variable as a nonlinear function of all remaining variables, i.e., for every node 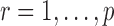 ,
,
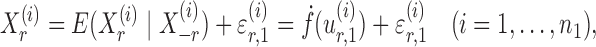 |
(5) |
where 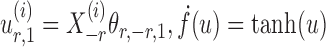 and
and 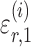 are random variables satisfying
are random variables satisfying 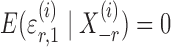 . We adopt the projection-based debiasing approach of Zhang & Zhang (2014). Specifically, for a suitably chosen score vector
. We adopt the projection-based debiasing approach of Zhang & Zhang (2014). Specifically, for a suitably chosen score vector 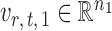 and
and 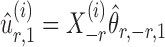 , one can show that the estimator
, one can show that the estimator
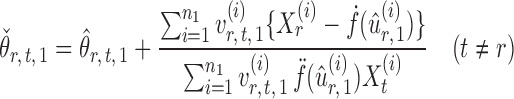 |
(6) |
is nearly unbiased under mild conditions on the initial estimate 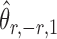 . The second term on the right-hand side of (6) projects the residual
. The second term on the right-hand side of (6) projects the residual 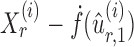 onto the direction of
onto the direction of 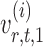 , thereby reducing the bias in
, thereby reducing the bias in 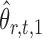 to an acceptable level. As shown in the unpublished 2016 technical report by Z. Ren, the desired score vector
to an acceptable level. As shown in the unpublished 2016 technical report by Z. Ren, the desired score vector 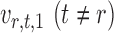 can be defined as
can be defined as
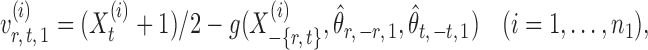 |
(7) |
where for 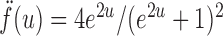 ,
,
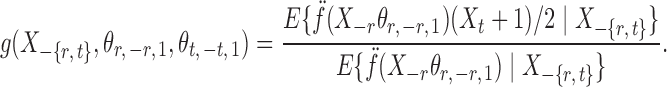 |
Intuitively, the score vector 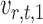 resembles the residual for regressing
resembles the residual for regressing 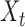 on
on 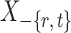 . The choice in (7) ensures that
. The choice in (7) ensures that 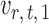 is uncorrelated with
is uncorrelated with 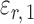 and that
and that 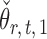 achieves asymptotic efficiency. Given
achieves asymptotic efficiency. Given 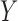 and the initial estimate
and the initial estimate 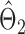 , the nearly unbiased
, the nearly unbiased 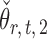 can be derived similarly.
can be derived similarly.
Remark 1.
Inference for high-dimensional models via the
penalty typically requires bias correction, because the
regularization achieves variable selection by shrinking every component of the regression coefficients towards zero (Zhang & Zhang, 2014; van de Geer et al., 2014). Existing work on bias correction focuses primarily on linear models, with the exception of van de Geer et al. (2014), which is based on inverting the Karush–Kuhn–Tucker conditions and is applicable to generalized linear models. In contrast, our debiasing approach is based on a local Taylor expansion of
about
in (5), which yields an approximately linear surrogate to the nonlinear conditional mean and facilitates the construction of entrywise statistics.
The estimators 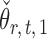 and
and 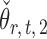 have unequal variances, so we must adjust for their variances before constructing the test statistic for the global null hypothesis. Denote by
have unequal variances, so we must adjust for their variances before constructing the test statistic for the global null hypothesis. Denote by 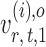 the oracle score vector calculated based on
the oracle score vector calculated based on 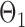 ,
,
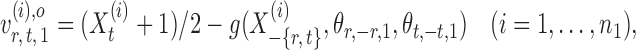 |
and let
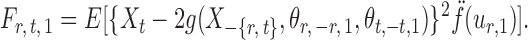 |
By definition, 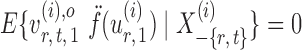 , so
, so 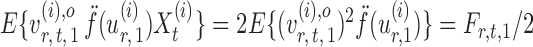 . Hence, for a reasonably good initial estimate
. Hence, for a reasonably good initial estimate 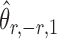 , one expects
, one expects 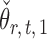 to be close to
to be close to
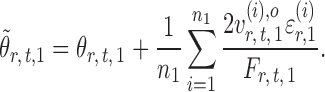 |
Indeed, it can be shown that 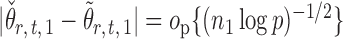 for
for 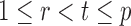 , under certain conditions. With
, under certain conditions. With 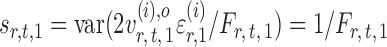 , one can use
, one can use 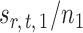 as an approximation to
as an approximation to 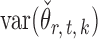 .
.
Finally, let the empirical variance estimates be defined as
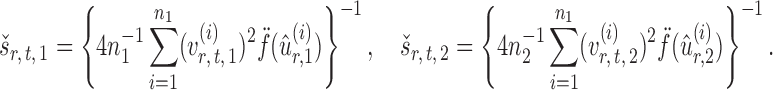 |
The standardized entrywise difference is thus
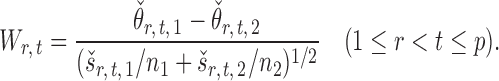 |
2.3. Implementation of the testing procedure
Once we have the standardized entrywise statistic 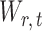 , we can construct the test statistic for the global null in (2):
, we can construct the test statistic for the global null in (2):
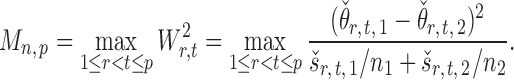 |
(8) |
Section 3.2 shows that under certain mild conditions, 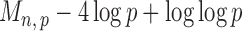 converges to a Type I extreme value distribution under the null. Indeed, the
converges to a Type I extreme value distribution under the null. Indeed, the 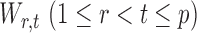 are asymptotically standard normal under the null and are only weakly dependent. Hence the maximum of
are asymptotically standard normal under the null and are only weakly dependent. Hence the maximum of 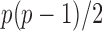 such variables squared, that is,
such variables squared, that is, 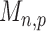 , should be close to
, should be close to 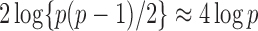 . Let
. Let
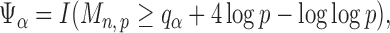 |
(9) |
where 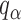 is the
is the 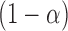 quantile of the Type I extreme value distribution with the cumulative distribution function
quantile of the Type I extreme value distribution with the cumulative distribution function 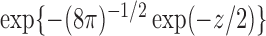 . We reject the hypothesis
. We reject the hypothesis 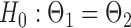 whenever
whenever 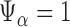 .
.
In the multiple testing problem (3), for any given threshold level 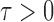 and
and 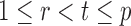 , each individual hypothesis
, each individual hypothesis 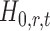 is rejected if
is rejected if 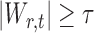 . Let
. Let 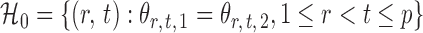 denote the set of true nulls. Let
denote the set of true nulls. Let 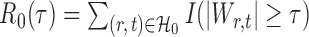 be the total number of false positives and
be the total number of false positives and 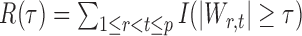 the total number of rejections. The false discovery proportion and false discovery rate are defined, respectively, as
the total number of rejections. The false discovery proportion and false discovery rate are defined, respectively, as
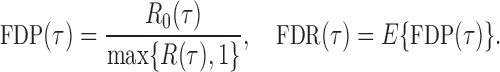 |
For a prespecified level 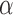 , an ideal choice of
, an ideal choice of 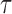 that is able to control the false discovery proportion and false discovery rate is
that is able to control the false discovery proportion and false discovery rate is
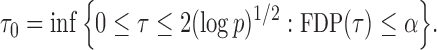 |
Here the choice of 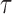 is restricted to
is restricted to 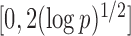 because the asymptotic null distribution of
because the asymptotic null distribution of 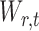 is standard normal so that
is standard normal so that 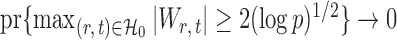 as
as 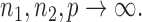
However, the ideal 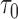 is unavailable because
is unavailable because 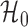 is unknown. To estimate
is unknown. To estimate 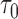 , it is helpful to understand the properties of
, it is helpful to understand the properties of 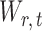 . Let
. Let 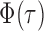 be the standard normal cumulative distribution function and let
be the standard normal cumulative distribution function and let 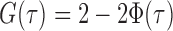 . Under the null hypothesis in (3) and some regularity conditions, one can show that as
. Under the null hypothesis in (3) and some regularity conditions, one can show that as 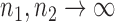 ,
,
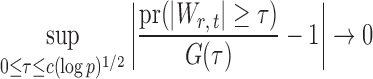 |
(10) |
uniformly for all 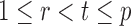 , where
, where 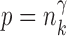 , for any
, for any 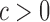 and any
and any 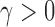 . Therefore one can estimate
. Therefore one can estimate 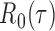 by
by 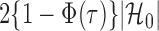 as in Cai & Liu (2016), where
as in Cai & Liu (2016), where 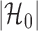 can be estimated by
can be estimated by 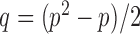 due to the sparsity of
due to the sparsity of 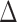 . In fact, for weakly dependent
. In fact, for weakly dependent 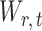 , it can be shown that
, it can be shown that
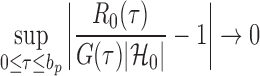 |
(11) |
in probability for 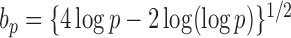 as
as 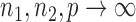 . So, we estimate
. So, we estimate  by
by
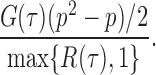 |
This leads to the following estimate of 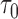 :
:
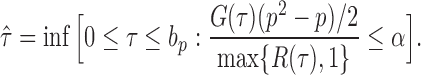 |
(12) |
If the solution to (12) does not exist, we set 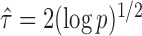 . For
. For 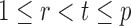 , the null hypothesis
, the null hypothesis 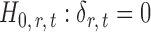 is rejected if and only if
is rejected if and only if 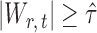 .
.
Remark 2.
It is important to restrict
in (12) for false discovery proportion control, because the convergence in (11) may not hold for
. In such cases, direct thresholding on
with
is used to control the false discovery rate. Without the constraint
, our multiple testing procedure reduces to the Benjamini–Hochberg procedure, which may not control the false discovery proportion with some positive probability if the number of true alternatives
is fixed as
. An alternative approach to approximating
is to bootstrap, as in Cai & Liu (2016).
3. Theoretical properties
3.1. Assumptions
We make assumptions to establish the theoretical properties of the proposed testing procedures. For 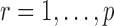 , let
, let
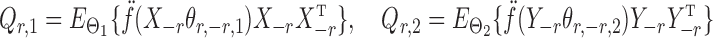 |
denote the Hessians of the likelihood functions associated with the 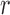 th logistic regression in the first and second populations, respectively. For
th logistic regression in the first and second populations, respectively. For 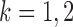 , the matrix
, the matrix 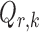 is the Fisher information matrix associated with the local conditional probability distribution, and is analogous to the
is the Fisher information matrix associated with the local conditional probability distribution, and is analogous to the 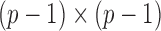 submatrix of the precision matrix in Gaussian graphical models.
submatrix of the precision matrix in Gaussian graphical models.
Assumption 1.
Assume that
and
. For each
, there exist constants
such that
Further, assume that the initial estimators
satisfy
(13)
(14)
The bounded eigenvalue assumption on 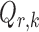 is standard in inference for high-dimensional Ising models (Ravikumar et al., 2010), and ensures that the
is standard in inference for high-dimensional Ising models (Ravikumar et al., 2010), and ensures that the 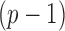 variables do not become overly dependent. It is also crucial for establishing the asymptotic normality of
variables do not become overly dependent. It is also crucial for establishing the asymptotic normality of 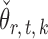 . Initial estimators satisfying (13) and (14) can be obtained via
. Initial estimators satisfying (13) and (14) can be obtained via 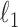 -penalized nodewise logistic regression if the maximum node degree is
-penalized nodewise logistic regression if the maximum node degree is 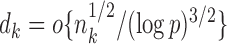 . The conditions in (13) and (14) are slightly stronger than those required for entrywise normality in the unpublished 2016 technical report by Z. Ren, because smaller biases are required for testing procedures in order to provide significance quantification for each pair of edges.
. The conditions in (13) and (14) are slightly stronger than those required for entrywise normality in the unpublished 2016 technical report by Z. Ren, because smaller biases are required for testing procedures in order to provide significance quantification for each pair of edges.
Assumption 2.
For each
, there exists a constant
such that the maximum neighbourhood weight satisfies
Assumption 2 implies that 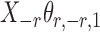 and
and 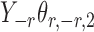 are sub-exponential random variables, and therefore
are sub-exponential random variables, and therefore 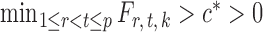 for
for 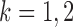 and some
and some 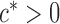 . In view of the conditional distribution (4), violation of Assumption 2 may lead to degenerate marginal distributions. This assumption is crucial for controlling the dependence in Lemma 1, and is also used in Santhanam & Wainwright (2012).
. In view of the conditional distribution (4), violation of Assumption 2 may lead to degenerate marginal distributions. This assumption is crucial for controlling the dependence in Lemma 1, and is also used in Santhanam & Wainwright (2012).
To ensure good performance of the proposed testing procedures, it is important to characterize the dependence between the standardized entrywise statistics 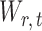 and
and 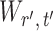 for
for 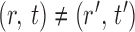 , and to understand when such dependences are weak. The reason for
, and to understand when such dependences are weak. The reason for 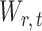 and
and 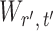 being dependent is the correlation among
being dependent is the correlation among 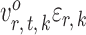 for
for 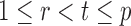 and
and 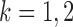 . In contrast to the Gaussian case (Xia et al., 2015), it is difficult to evaluate these correlations analytically in the current setting due to the unknown normalizing constant in (1). However, the following lemma says that these correlations are bounded under mild conditions.
. In contrast to the Gaussian case (Xia et al., 2015), it is difficult to evaluate these correlations analytically in the current setting due to the unknown normalizing constant in (1). However, the following lemma says that these correlations are bounded under mild conditions.
Lemma 1.
Under Assumption 2, for
and
,
where
and
are absolute constants that depend only on
.
Lemma 1 implies that the correlation among the nearly unbiased estimators 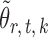 , or equivalently the correlation among the
, or equivalently the correlation among the 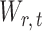 , is bounded above by a function of
, is bounded above by a function of 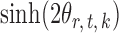 for
for 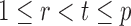 and
and 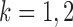 . However, establishing such results for high-dimensional binary Markov random fields is challenging. The proof of Lemma 1 requires careful analysis based on the conditional distributions
. However, establishing such results for high-dimensional binary Markov random fields is challenging. The proof of Lemma 1 requires careful analysis based on the conditional distributions 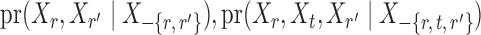 and
and 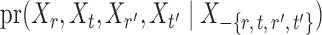 .
.
The next assumption requires that the entrywise conditional associations not be too large and ensures that 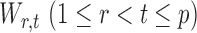 only weakly dependent.
only weakly dependent.
Assumption 3.
For a constant
, let
be small enough that
for
.
Variants of Assumption 3 are commonly used (Cai et al., 2013; Cai & Liu, 2016; Xia et al., 2015, 2018). This assumption is also mild for microbial networks because evolutionary stability and robustness often result in only a small number of strong microbial interactions (Leclerc, 2008).
3.2. Limiting null distribution and optimality of the global test
For 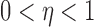 , let
, let
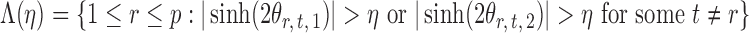 |
denote the set of indices 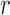 such that either
such that either 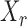 is highly correlated with some
is highly correlated with some 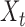 or
or 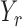 is highly correlated with some
is highly correlated with some 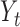 , given all remaining variables. Let
, given all remaining variables. Let 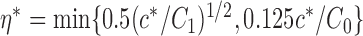 .
.
Theorem 1.
Suppose that Assumptions 1–3 hold. If there exist
and a sequence of numbers
such that
, then under the null hypothesis in (2), for any
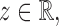
(15) as
, where
is defined in (8). Under the null hypothesis, the convergence in (15) is uniform for all
and
satisfying Assumptions 1–3.
Remark 3.
The bounded cardinality condition on
is similar to that in Cai et al. (2013), and is mild because the magnitude of
reflects the conditional association between each pair of microbial taxa. Most of the entries in
should be bounded from above, or the rare taxa might go extinct, which is undesirable for maintaining a robust ecological system. This condition together with Assumptions 2 and 3 guarantee weak dependence among the
, and allows us to apply strategies for extreme values in the Gaussian case.
In addition to the limiting null distribution, our global testing procedure also maintains rate-optimal power. Consider the matrices
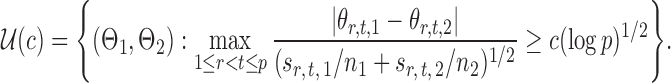 |
(16) |
Let 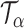 be the set of all
be the set of all 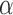 -level tests, that is,
-level tests, that is, 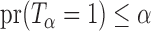 for any
for any 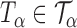 .
.
Theorem 2.
for
and
with
. Then there exists a constant
such that for all sufficiently large
and
,
Remark 4.
Statement (i) in Theorem 2 says that
rejects the null hypothesis in (2) with high probability when
, and statement (ii) says that the lower bound of order
in (16) cannot be further improved.
3.3. False discovery rate control in multiple testing
Let 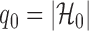 , let
, let 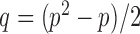 , and let
, and let
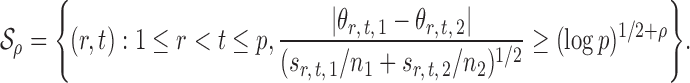 |
The following theorem shows that our multiple testing procedure ensures asymptotic control of the false discovery proportion and false discovery rate at the prespecified level 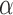 .
.
Theorem 3.
Suppose
for some
and
. Assume further that
for some
and that
for some
and
. Then under the assumptions of Theorem 1,
in probability as
.
Remark 5.
The condition on the size of
is mild in that it only requires a few standardized entrywise differences to be at least of order
, which is necessary to ensure that (11) holds. The proof of Theorem 3 again relies heavily on knowledge of the dependence among the
as characterized in Lemma 1.
4. Simulations
4.1. Data and model selection
We consider (a) the Erdős–Rényi random graph 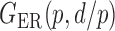 (Erdős & Rényi, 1960) with average degree
(Erdős & Rényi, 1960) with average degree 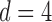 , (b) the Watts–Strogatz model
, (b) the Watts–Strogatz model 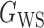 (Watts & Strogatz, 1998), which forms networks with small-world properties, and (c) the Barabasi–Albert scale-free network model
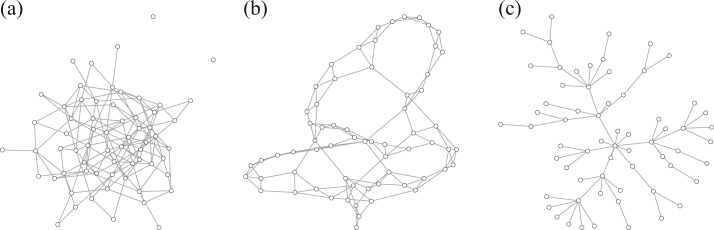
(Watts & Strogatz, 1998), which forms networks with small-world properties, and (c) the Barabasi–Albert scale-free network model 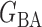 (Barabási & Albert, 1999), as illustrated in Fig. 1. In all comparisons, the graph sizes and the sample sizes are taken as
(Barabási & Albert, 1999), as illustrated in Fig. 1. In all comparisons, the graph sizes and the sample sizes are taken as 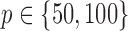 and
and 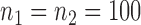 . For a given graph, the nonzero entries
. For a given graph, the nonzero entries 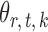 were drawn uniformly from
were drawn uniformly from 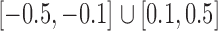 . Given the two matrices
. Given the two matrices 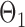 and
and 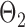 , binary data
, binary data 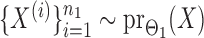 and
and  were generated by Gibbs sampling.
were generated by Gibbs sampling.
Fig. 1.
Illustrations of different graphs used in our simulations: (a) random graph 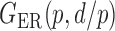 , (b) small-world network
, (b) small-world network 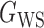 , and (c) scale-free network
, and (c) scale-free network 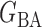 .
.
To get an initial estimator of 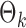 , we run nodewise
, we run nodewise 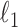 -regularized logistic regression with penalty parameter
-regularized logistic regression with penalty parameter 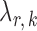 , using the R package glmnet (Friedman et al., 2010). Symmetric estimates were obtained by averaging the nodewise estimates. The optimal tuning parameters
, using the R package glmnet (Friedman et al., 2010). Symmetric estimates were obtained by averaging the nodewise estimates. The optimal tuning parameters 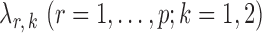 were chosen to maximize the performance of the global and the multiple testing procedures. For the global test, the tuning parameter
were chosen to maximize the performance of the global and the multiple testing procedures. For the global test, the tuning parameter 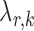 in each logistic regression was selected based on the extended Bayesian information criterion (Barber & Drton, 2015). As the multiple testing procedure relies on the approximation of
in each logistic regression was selected based on the extended Bayesian information criterion (Barber & Drton, 2015). As the multiple testing procedure relies on the approximation of 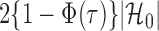 to
to 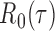 , the tuning parameters needed in multiple testing were chosen by ensuring
, the tuning parameters needed in multiple testing were chosen by ensuring 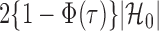 was as close to
was as close to 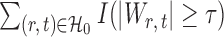 as possible.
as possible.
4.2. Results
We compare our approach with two-sample testing based on Gaussian graphical models (Xia et al., 2015) and two other permutation-based methods for global testing. The first permutation method uses the same 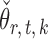 and
and 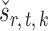 as in our approach and takes the minimum
as in our approach and takes the minimum 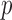 -value of the entrywise test
-value of the entrywise test 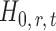 in (3) as the test statistic. The significance of the global test is then calibrated using a permutation approach. The second permutation method differs from the first only in the way the parameters
in (3) as the test statistic. The significance of the global test is then calibrated using a permutation approach. The second permutation method differs from the first only in the way the parameters 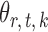 and
and 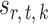 are estimated. Specifically, it estimates
are estimated. Specifically, it estimates 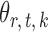 and its variance using maximum likelihood with specified support of
and its variance using maximum likelihood with specified support of 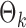 and finite-sample bias correction (Firth, 1993). In our comparisons, the per replication
and finite-sample bias correction (Firth, 1993). In our comparisons, the per replication 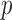 -values for both permutation methods were evaluated over 1000 permutations.
-values for both permutation methods were evaluated over 1000 permutations.
Table 1 presents the empirical Type I errors of the global test, and confirms that our method and the two permutation tests control the Type I errors well in all settings. In comparison, the Type I errors of the method of Xia et al. (2015) are slightly inflated, which is not surprising because the data are not multivariate normal.
Table 1.
Empirical Type I errors and powers 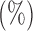 of the global test with
of the global test with 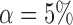 and
and 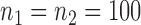 . The Type I errors were evaluated over
. The Type I errors were evaluated over 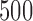 replications, and the powers were calculated over
replications, and the powers were calculated over 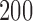 replications
replications
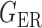
|
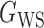
|
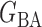
|
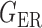
|
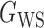
|
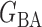
|
||
|---|---|---|---|---|---|---|---|
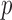
|
Method | Type I error | Power | ||||
| 50 | Proposed method | 3.0 | 1.6 | 3.6 | 94.5 | 88.0 | 91.5 |
| Xia et al. (2015) | 8.4 | 9.4 | 7.2 | 69.5 | 70.0 | 91.0 | |
| PermBMN | 5.8 | 5.8 | 5.0 | 97.0 | 93.5 | 96.5 | |
| PermMLE | 4.6 | 5.2 | 3.8 | 98.5 | 97.0 | 99.5 | |
| 100 | Proposed method | 2.0 | 3.0 | 2.4 | 95.5 | 94.0 | 97.5 |
| Xia et al. (2015) | 6.2 | 7.8 | 7.4 | 80.0 | 87.0 | 94.5 | |
| PermBMN | 5.4 | 5.0 | 4.2 | 98.0 | 97.0 | 99.0 | |
| PermMLE | 4.6 | 4.8 | 4.6 | 97.0 | 99.0 | 100.0 | |
PermBMN, permutation-based test using 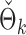 ; PermMLE, permutation-based test using the modified maximum likelihood estimator of
; PermMLE, permutation-based test using the modified maximum likelihood estimator of 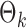 assuming that the true graph structures are known.
assuming that the true graph structures are known.
To evaluate the power of the global test, we constructed the differential network 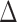 such that five entries in the upper triangular part of
such that five entries in the upper triangular part of 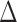 were uniformly drawn from
were uniformly drawn from 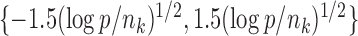 . Let
. Let  be generated from one of the three models
be generated from one of the three models  or
or  , and let
, and let 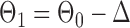 and
and 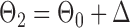 . The empirical powers, which are proportions of null hypothesis rejections, are shown in Table 1. Our method yields very high powers for all settings and uniformly outperforms the method of Xia et al. (2015). The two permutation-based methods, especially the second one based on the modified maximum likelihood estimator of
. The empirical powers, which are proportions of null hypothesis rejections, are shown in Table 1. Our method yields very high powers for all settings and uniformly outperforms the method of Xia et al. (2015). The two permutation-based methods, especially the second one based on the modified maximum likelihood estimator of 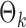 , demonstrate superior performance in terms of power. The downside is that both permutation methods require heavy computation.
, demonstrate superior performance in terms of power. The downside is that both permutation methods require heavy computation.
Finally, using the same design 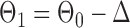 and
and 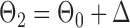 , we examined multiple testing of individual entries in the differential network
, we examined multiple testing of individual entries in the differential network 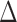 while controlling the false discovery rate at
while controlling the false discovery rate at 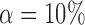 . The true differential network
. The true differential network 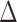 was constructed to be sparse such that the number of edges is approximately
was constructed to be sparse such that the number of edges is approximately  , with nonzero entries drawn uniformly from
, with nonzero entries drawn uniformly from 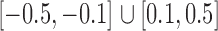 . The empirical false discovery and true positive rates of our method and that of Xia et al. (2015) were estimated by
. The empirical false discovery and true positive rates of our method and that of Xia et al. (2015) were estimated by
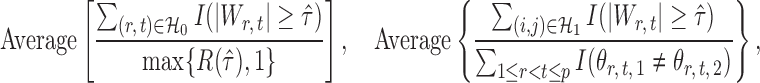 |
where  denotes the set of nonzero locations. Permutation-based methods are inapplicable to multiple testing. Table 2 shows that our multiple testing procedure controls the false discovery rate well in all scenarios, and returns reasonably high true positive rates. In contrast, the multiple testing method of Xia et al. (2015) yields slightly higher false positive and lower true positive rates. The difference in true positive rates between the methods increases with
denotes the set of nonzero locations. Permutation-based methods are inapplicable to multiple testing. Table 2 shows that our multiple testing procedure controls the false discovery rate well in all scenarios, and returns reasonably high true positive rates. In contrast, the multiple testing method of Xia et al. (2015) yields slightly higher false positive and lower true positive rates. The difference in true positive rates between the methods increases with  .
.
Table 2.
Empirical false discovery rates and true positive rates 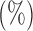 for multiple testing with false discovery rate
for multiple testing with false discovery rate 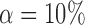 and
and 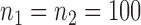 over
over 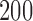 replications
replications
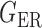
|
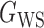
|
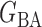
|
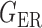
|
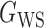
|
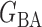
|
||
|---|---|---|---|---|---|---|---|
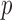
|
Method | False discovery rate | True positive rate | ||||
| 50 | Proposed method | 10.0 | 9.1 | 10.6 | 52.9 | 59.9 | 61.0 |
| Xia et al. (2015) | 13.8 | 13.7 | 13.5 | 51.7 | 54.9 | 59.9 | |
| 100 | Proposed method | 8.3 | 9.4 | 9.2 | 56.1 | 57.7 | 62.9 |
| Xia et al. (2015) | 12.2 | 12.3 | 11.7 | 50.5 | 49.6 | 57.2 | |
5. Application to gut microbiome data in U.K. twins
We applied the proposed testing procedures to data from a gut microbiome study of U.K. twins. The original study (Goodrich et al., 2016) investigated whether host genotype shapes the gut microbiome composition, using 16S rRNA sequencing data collected from faecal samples of 2731 individuals. The data are available at http://www.ebi.ac.uk/ena/data/view/PRJEB13747. We are interested in whether the microbial community structures summarized as conditional dependence relationships among the microbial taxa are associated with the age of the host.
To ensure robust detection of microbial interactions, samples with total read counts less than 20 were first removed. For each of the remaining 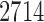 samples, the relative abundance of each genus was calculated by dividing the read count for each genus by the total number of reads in the sample. Of the 294 genera, only those with at least 0.001% of relative abundance in at least 75% of the 2714 samples were used, which reduces the total number of genera to
samples, the relative abundance of each genus was calculated by dividing the read count for each genus by the total number of reads in the sample. Of the 294 genera, only those with at least 0.001% of relative abundance in at least 75% of the 2714 samples were used, which reduces the total number of genera to 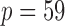 . To examine the association of microbial interactions with host age, we selected 286 young adults who were at most 43 years and 284 elderly subjects aged at least 74 years. Since these samples included twins, we randomly chose one individual from each pair of twins, which gave
. To examine the association of microbial interactions with host age, we selected 286 young adults who were at most 43 years and 284 elderly subjects aged at least 74 years. Since these samples included twins, we randomly chose one individual from each pair of twins, which gave 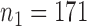 independent young adults and
independent young adults and 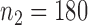 elderly subjects in our analysis.
elderly subjects in our analysis.
Because of possible errors in sequencing reads, genera with relative abundance lower than 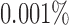 are expected to be due to noise or sequencing errors. We therefore first discretized the relative abundances using a cut-off of 0.001%, where for a given genus,
are expected to be due to noise or sequencing errors. We therefore first discretized the relative abundances using a cut-off of 0.001%, where for a given genus, 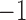 represents absence or extremely low abundance of the genus and
represents absence or extremely low abundance of the genus and 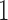 represents presence. However, some more abundant genera are present in over 75% of the samples. For these genera, we used the 25th percentile as the cut-off to discretize the data, so
represents presence. However, some more abundant genera are present in over 75% of the samples. For these genera, we used the 25th percentile as the cut-off to discretize the data, so 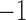 represents low abundance of the genus and
represents low abundance of the genus and 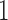 represents high abundance. One should keep the definitions in mind when interpreting the
represents high abundance. One should keep the definitions in mind when interpreting the 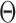 parameters.
parameters.
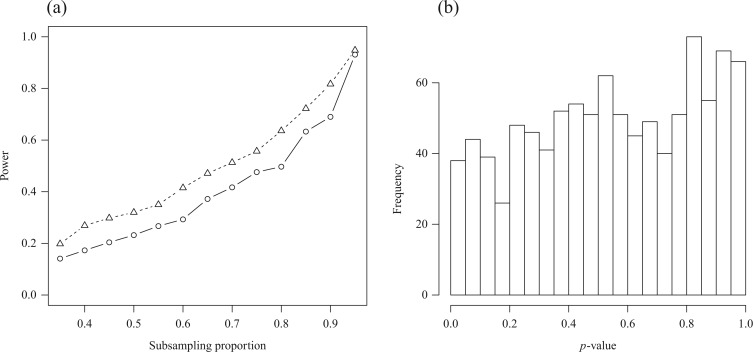
We applied the global testing procedure to the two groups of subjects and obtained a 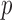 -value of 0.009, indicating that the microbial networks for the two age groups are significantly different. To assess the stability of our method and perform power comparisons, we generated 1000 subsamples within each age group, with sampling proportions ranging from
-value of 0.009, indicating that the microbial networks for the two age groups are significantly different. To assess the stability of our method and perform power comparisons, we generated 1000 subsamples within each age group, with sampling proportions ranging from 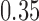 to
to 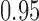 . The empirical powers of our method and the permutation method using
. The empirical powers of our method and the permutation method using 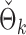 are presented in Fig. 2(a). Our method performs slightly worse than the permutation method, but we believe that the gap reduces with larger samples. Another advantage of our method is that it runs much faster than the permutation method. We also performed back-testing for the global null hypothesis by randomly splitting the pooled data into two groups with
are presented in Fig. 2(a). Our method performs slightly worse than the permutation method, but we believe that the gap reduces with larger samples. Another advantage of our method is that it runs much faster than the permutation method. We also performed back-testing for the global null hypothesis by randomly splitting the pooled data into two groups with 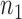 and
and 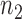 subjects over 1000 replications. Figure 2(b) shows the resulting
subjects over 1000 replications. Figure 2(b) shows the resulting 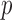 -values, which are slightly skewed towards the right, indicating that the proposed test is conservative.
-values, which are slightly skewed towards the right, indicating that the proposed test is conservative.
Fig. 2.
(a) Empirical power curves of the proposed method (circles) and the permutation method using 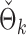 (triangles) by subsampling the two datasets at different proportions. (b) A histogram of the
(triangles) by subsampling the two datasets at different proportions. (b) A histogram of the 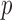 -values from our method in back-testing by randomly generating two datasets 1000 times.
-values from our method in back-testing by randomly generating two datasets 1000 times.
To recover the differential microbial network, we applied the proposed multiple testing procedure with 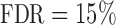 and show the results in Fig. 3. The same differential links were selected by fdr between 14% to 16%. For fdr between 12% to 14%, all edges in Fig. 3 except that between Bacteroides and Blautia were selected. Here the two values associated with each differential edge represent the estimated odds ratios between the two genera for the two age groups. For example, the odds ratio between Faecalibacterium and Campylobacter among young adults is
and show the results in Fig. 3. The same differential links were selected by fdr between 14% to 16%. For fdr between 12% to 14%, all edges in Fig. 3 except that between Bacteroides and Blautia were selected. Here the two values associated with each differential edge represent the estimated odds ratios between the two genera for the two age groups. For example, the odds ratio between Faecalibacterium and Campylobacter among young adults is 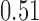 , indicating that high abundance in Faecalibacterium is associated with lower odds of high abundance in Campylobacter. In other words, Faecalibacterium and Campylobacter have a competitive relationship within the microbial community, which could be due to their competition for space, nutrients, and so on. In contrast, the relationship between Faecalibacterium and Campylobacter is collaborative for the elderly group, since the odds ratio is
, indicating that high abundance in Faecalibacterium is associated with lower odds of high abundance in Campylobacter. In other words, Faecalibacterium and Campylobacter have a competitive relationship within the microbial community, which could be due to their competition for space, nutrients, and so on. In contrast, the relationship between Faecalibacterium and Campylobacter is collaborative for the elderly group, since the odds ratio is 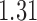 . A collaborative relationship between two microbes can be due to cross-feeding, co-colonization or other reasons (Faust & Raes, 2012). Each pair of values associated with each edge shows a significant difference, suggesting changes in the microbial community structure as people age. Indeed, the abundance of Faecalibacterium has been found to be negatively associated with age (Franceschi et al., 2017). Further, Ruminococcus was significantly enriched in immune-mediated inflammatory diseases (Forbes et al., 2016), and Oscillospira was enriched in inflammatory diseases (Konikoff & Gophna, 2016). Thus Ruminococcus and Oscillospira may also play an important role in the ageing process, because age is characterized by chronic low-grade inflammation. Figure 3 provides additional evidence on how these genera are implicated in the ageing process. More importantly, genera involved in the differential network may be potential microbial targets that can be manipulated through dietary or medical interventions for healthy ageing. As the true differential network is unknown, further experimental validation is needed to confirm these results.
. A collaborative relationship between two microbes can be due to cross-feeding, co-colonization or other reasons (Faust & Raes, 2012). Each pair of values associated with each edge shows a significant difference, suggesting changes in the microbial community structure as people age. Indeed, the abundance of Faecalibacterium has been found to be negatively associated with age (Franceschi et al., 2017). Further, Ruminococcus was significantly enriched in immune-mediated inflammatory diseases (Forbes et al., 2016), and Oscillospira was enriched in inflammatory diseases (Konikoff & Gophna, 2016). Thus Ruminococcus and Oscillospira may also play an important role in the ageing process, because age is characterized by chronic low-grade inflammation. Figure 3 provides additional evidence on how these genera are implicated in the ageing process. More importantly, genera involved in the differential network may be potential microbial targets that can be manipulated through dietary or medical interventions for healthy ageing. As the true differential network is unknown, further experimental validation is needed to confirm these results.
Fig. 3.
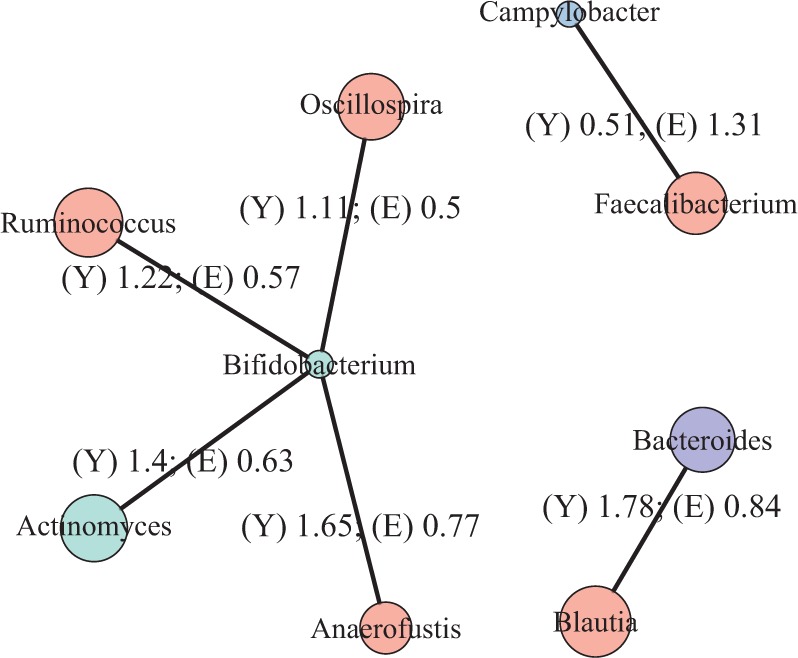
Estimated differential microbial network between young and elderly individuals using our multiple testing procedure with fdr = 15%, where isolated genera are not shown. Each node represents a genus coloured by phylum, and node size is proportional to the prevalence of 1s among all samples for the corresponding genus. Edge width is proportional to the magnitude of the entrywise test statistic. Turquoise circles, Actinobacteria; purple circles, Bacteroidetes; red circles, Firmicutes; blue circles, Proteobacteria.
Since the method of Xia et al. (2015) does not perform well for discrete data, we applied their method to the centred log-ratio transformed relative abundance data and obtained a 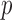 -value of 0.007 for the global test, which is consistent with the conclusion from the proposed global test. At 15% false discovery rate, application of the multiple testing procedure of Xia et al. (2015) only gave one differential edge between Holdemania from the phylum Firmicutes and Butyricimonas from Bacteroidetes. The difference is largely due to the fact that the centred log-ratio transformed data are far from being normally distributed.
-value of 0.007 for the global test, which is consistent with the conclusion from the proposed global test. At 15% false discovery rate, application of the multiple testing procedure of Xia et al. (2015) only gave one differential edge between Holdemania from the phylum Firmicutes and Butyricimonas from Bacteroidetes. The difference is largely due to the fact that the centred log-ratio transformed data are far from being normally distributed.
6. Discussion
To deal with excessive zeros and the unit sum constraint, in this paper we proposed using a binary Markov random field to study microbial interactions characterized by their conditional dependence relationships. Such models are robust and largely free of distributional assumptions on the data and have a natural interpretation in terms of co-existence or co-exclusiveness of the microbial communities. For very rare taxa, we suggest using a very small cut-off to discretize the data. For more common taxa, sample median or quartiles can be used. Using different cut-offs may lead to different results and thus to models with different interpretations. One may explore different ways of dichotomizing the data to see whether consistent results can be obtained.
The proposed method for testing binary Markov random fields can be applied to other data with binary observations, such as cancer somatic mutation data in cancer genomics or characterization of neural firing patterns and the reconstruction of neural connections in neuroscience. Our methods can be extended to study more general Markov random fields with each node taking more than two discrete values.
Supplementary Material
Acknowledgement
This research was supported by the U.S. National Institutes of Health and National Science Foundation and by the National Natural Science Foundation of China.
Supplementary material
Supplementary material available at Biometrika online includes technical lemmas and proofs.
References
- Aitchison, J. (1982). The statistical analysis of compositional data (with discussion). J. R. Statist. Soc. B 44, 139–77. [Google Scholar]
- Barabási, A.-L. & Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–12. [DOI] [PubMed] [Google Scholar]
- Barber, R. F. & Drton, M. (2015). High-dimensional Ising model selection with Bayesian information criteria. Electron. J. Statist. 9, 567–607. [Google Scholar]
- Biagi, E., Nylund, L., Candela, M., Ostan, R., Bucci, L., Pini, E., Nikkïla, J., Monti, D., Satokari, R., Franceschi, C.. et al. (2010). Through ageing, and beyond: Gut microbiota and inflammatory status in seniors and centenarians. PLoS One 5, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswas, S., McDonald, M., Lundberg, D. S., Dangl, J. L. & Jojic, V. (2016). Learning microbial interaction networks from metagenomic count data. J. Comp. Biol. 23, 526–35. [DOI] [PubMed] [Google Scholar]
- Cai, T. T. & Liu, W. (2016). Large-scale multiple testing of correlations. J. Am. Statist. Assoc. 111, 229–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai, T. T., Liu, W. & Xia, Y. (2013). Two-sample covariance matrix testing and support recovery in high-dimensional and sparse settings. J. Am. Statist. Assoc. 108, 265–77. [Google Scholar]
- Claesson, M. J., Cusack, S., O’Sullivan, O., Greene-Diniz, R., de Weerd, H., Flannery, E., Marchesi, J. R., Falush, D., Dinan, T., Fitzgerald, G.. et al. (2011). Composition, variability, and temporal stability of the intestinal microbiota of the elderly. Proc. Nat. Acad. Sci. 108, 4586–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdős, P. & Rényi, A. (1960). On the evolution of random graphs. Pub. Math. Inst. Hungar. Acad. Sci. 5, 17–61. [Google Scholar]
- Fang, H., Huang, C., Zhao, H. & Deng, M. (2017). gCoda: Conditional dependence network inference for compositional data. J. Comp. Biol. 24, 699–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust, K. & Raes, J. (2012). Microbial interactions: From networks to models. Nat. Rev. Microbiol. 10, 538–50. [DOI] [PubMed] [Google Scholar]
- Firth, D. (1993). Bias reduction of maximum likelihood estimates. Biometrika 80, 27–38. [Google Scholar]
- Forbes, J. D., Van Domselaar, G. & Bernstein, C. N. (2016). The gut microbiota in immune-mediated inflammatory diseases. Front. Microbiol. 7, 1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschi, C., Garagnani, P., Vitale, G., Capri, M. & Salvioli, S. (2017). Inflammaging and ‘garb-aging’. Trends Endocrinol. Metab. 28, 199–212. [DOI] [PubMed] [Google Scholar]
- Friedman, J. H., Hastie, T. J. & Tibshirani, R. J. (2010). Regularization paths for generalized linear models via coordinate descent. J. Statist. Software 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Goodrich, J. K., Davenport, E. R., Beaumont, M., Jackson, M. A., Knight, R., Ober, C., Spector, T. D., Bell, J. T., Clark, A. G. & Ley, R. E. (2016). Genetic determinants of the gut microbiome in UK twins. Cell Host & Microbe 19, 731–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konikoff, T. & Gophna, U. (2016). Oscillospira: A central, enigmatic component of the human gut microbiota. Trends Microbiol. 24, 523–4. [DOI] [PubMed] [Google Scholar]
- Kuczynski, J., Lauber, C. L., Walters, W. A., Parfrey, L. W., Clemente, J. C., Gevers, D. & Knight, R. (2012). Experimental and analytical tools for studying the human microbiome. Nat. Rev. Genet. 13, 47–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtz, Z. D., Müller, C. L., Miraldi, E. R., Littman, D. R., Blaser, M. J. & Bonneau, R. A. (2015). Sparse and compositionally robust inference of microbial ecological networks. PLoS Comp. Biol. 11, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leclerc, R. D. (2008). Survival of the sparsest: Robust gene networks are parsimonious. Molec. Syst. Biol. 4, 213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J. & Chen, S. X. (2012). Two sample tests for high-dimensional covariance matrices. Ann. Statist. 40, 908–40. [Google Scholar]
- R Development Core Team (2019). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; ISBN 3-900051-07-0, http://www.R-project.org. [Google Scholar]
-
Ravikumar, P., Wainwright, M. J. & Lafferty, J. D. (2010). High-dimensional Ising model selection using
 -regularized logistic regression. Ann. Statist. 38, 1287–319. [Google Scholar]
-regularized logistic regression. Ann. Statist. 38, 1287–319. [Google Scholar] - Santhanam, N. P. & Wainwright, M. J. (2012). Information-theoretic limits of selecting binary graphical models in high dimensions. IEEE Trans. Info. Theory 58, 4117–34. [Google Scholar]
- Schott, J. R. (2007). A test for the equality of covariance matrices when the dimension is large relative to the sample sizes. Comp. Statist. Data Anal. 51, 6535–42. [Google Scholar]
- van de Geer, S., Bühlmann, P., Ritov, Y. & Dezeure, R. (2014). On asymptotically optimal confidence regions and tests for high-dimensional models. Ann. Statist. 42, 1166–202. [Google Scholar]
- Watts, D. J. & Strogatz, S. H. (1998). Collective dynamics of small-world networks. Nature 393, 440–2. [DOI] [PubMed] [Google Scholar]
- Xia, Y., Cai, T. & Cai, T. T. (2015). Testing differential networks with applications to the detection of gene-gene interactions. Biometrika 102, 247–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia, Y., Cai, T. & Cai, T. T. (2018). Multiple testing of submatrices of a precision matrix with applications to identification of between pathway interactions. J. Am. Statist. Assoc. 113, 328–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, C.-H. & Zhang, S. S. (2014). Confidence intervals for low dimensional parameters in high dimensional linear models. J. R. Statist. Soc. B 76, 217–42. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.