Abstract
Despite ongoing large-scale population-based whole-genome sequencing (WGS) projects such as the NIH NHLBI TOPMed program and the NHGRI Genome Sequencing Program, WGS-based association analysis of complex traits remains a tremendous challenge due to the large number of rare variants, many of which are non-trait-associated neutral variants. External biological knowledge, such as functional annotations based on the ENCODE, Epigenomics Roadmap and GTEx projects, may be helpful in distinguishing causal rare variants from neutral ones; however, each functional annotation can only provide certain aspects of the biological functions. Our knowledge for selecting informative annotations a priori is limited, and incorporating non-informative annotations will introduce noise and lose power. We propose FunSPU, a versatile and adaptive test that incorporates multiple biological annotations and is adaptive at both the annotation and variant levels and thus maintains high power even in the presence of noninformative annotations. In addition to extensive simulations, we illustrate our proposed test using the TWINSUK cohort (n = 1,752) of UK10K WGS data based on six functional annotations: CADD, RegulomeDB, FunSeq, Funseq2, GERP++, and GenoSkyline. We identified genome-wide significant genetic loci on chromosome 19 near gene TOMM40 and APOC4-APOC2 associated with low-density lipoprotein (LDL), which are replicated in the UK10K ALSPAC cohort (n = 1,497). These replicated LDL-associated loci were missed by existing rare variant association tests that either ignore external biological information or rely on a single source of biological knowledge. We have implemented the proposed test in an R package “FunSPU”.
Author summary
In recent years, large-scale whole-genome sequencing (WGS) data have been generated, such as those in the UK10K project and the ongoing NIH Trans-Omics for Precision Medicine (TOPMed) WGS program, providing unprecedented opportunities to investigate low-frequency variants and rare variants in association with complex diseases and traits. However, WGS-based association analysis of complex traits remains a tremendous challenge due to the large number of rare variants, many of which are non-trait-associated neutral variants. External biological knowledge, such as functional annotations based on the ENCODE, Epigenomics Roadmap and GTEx projects, can be helpful in distinguishing causal rare variants from neutral ones; however, each functional annotation can only provide certain aspects of the biological functions. To this end, we have proposed a versatile and adaptive association test, FunSPU, to exploit multiple sources of biological knowledge in the analysis of WGS data. We illustrate our proposed test using the TWINSUK cohort of UK10K WGS data based on six functional annotations. We identified genome-wide significant genetic loci associated with low-density lipoprotein, which are replicated in the UK10K ALSPAC cohort. These replicated loci were missed by existing rare variant association tests that either ignore external biological information or rely on a single source of biological knowledge.
Introduction
In recent years, large-scale whole-exome sequencing and whole-genome sequencing (WGS) data have been generated, such as those in the Exome Sequencing Project [1], the UK10K project [2] and the ongoing NIH NHLBI Trans-Omics for Precision Medicine (TOPMed) WGS program [3], providing unprecedented opportunities to investigate low-frequency variants (minor allele frequency [MAF] between 1% and 5%) and rare variants (RVs; MAF < 1%) in association with complex diseases and traits. However, WGS-based association analysis of complex traits remains a tremendous challenge due to the large number of RVs, many of which are non-trait-associated neutral variants. External biological knowledge, such as functional annotations, might be informative to distinguish causal RVs from neutral ones. Some recent large-scale functional genomic studies, such as ENCODE [4], NIH Roadmap Epigenomics [5] and GTEx [6] projects, provide rich resources to use in characterizing the functional consequences of single nucleotide variants (SNVs), especially those in non-coding regions. Many approaches have been developed for functional annotations by integrating these data, e.g., CADD [7], GenoSkyline [8] and Eigen [9]; see Liu et al for a recent comparative review [10]. In WGS analysis, investigators may filter a subset of SNVs by annotations [2, 11], or use a single source of functional scores as weights in association tests to boost the statistical power [12–14]; however, each functional annotation can only provide a certain aspect of the biological functions, e.g., sequence conservation across species or biochemical activity of non-coding regions in a tissue. Our a priori knowledge to select the informative annotation(s) regarding a phenotype and genomic regions of interest is limited, and incorporating noninformative annotations will introduce noise and lose power.
To address this analytical challenge, we propose a family of versatile and powerful tests called “FunSPU” that allow for incorporating multiple functional annotations simultaneously in the adaptive sum of powered score (aSPU) test framework [15]. The fundamental idea of aSPU is to construct a general class of association tests, each of which is the most powerful under varying, yet unknown, local genetic architecture, then data-adaptively select the most significant test. Since each functional annotation system contains limited biological knowledge, multiple sources of functional annotations may provide complementary information. Therefore, a test that integrates multiple functional annotations simultaneously is potentially powerful. The proposed test is adaptive at both the annotation and variant levels and thus maintains high power even in the presence of noninformative annotations and a large number of neutral RVs. We also propose minimum p-value (minP) and Fisher’s meta-analysis-like approaches to combine the p-values with respect to multiple annotations. Moreover, to further increase the statistical power, we propose to incorporate a trait-specific global weight for each annotation based on partitioning the heritability.
Using extensive simulations and application to the UK10K WGS data [2], we compared our proposed FunSPU tests with the corresponding annotation-ignorant aSPU test as well as some existing RV association tests, such as the T5 burden test and SKAT [16]. We also compared our method with a recently published multiple functional annotation-based association test called functional score test (FST) [17]. Using the UK10K TWINSUK WGS cohort as the discovery sample (n = 1,752), we considered six functional annotations, CADD [7], RegulomeDB [18], FunSeq [19], Funseq2 [20], GERP++ [21] and GenoSkyline [8], and four quantitative traits, low-density lipoprotein (LDL), high-density lipoprotein (HDL), body mass index (BMI) and systolic blood pressure (SBP). We identified genome-wide significant genetic loci on chromosome 19 near gene TOMM40 and APOC4-APOC2 that are associated with LDL, which are replicated in the UK10K ALSPAC WGS cohort (n = 1,497). These replicated LDL-associated loci were missed by existing RV association tests that either ignore external biological information or rely on a single source of biological knowledge. We have implemented the proposed test in an R package “FunSPU”.
Materials and methods
Notations
Suppose that for subject i = 1, …, n, Y = (Y1, …, Yn) is the vector of a trait, and Xi = (Xi1, …, Xik)’ is the vector of the genotype scores of k RVs, for example, from a gene or some genomic region. Here, we use additive coding for each RV; that is, Xij is the count of the minor allele at RV j for subject i. For simplicity, we ignore other covariates in our model. We consider a generalized linear model (GLM):
where g is a link function; for continuous Yi, g is the identity link g(μ) = μ and the GLM is reduced to a linear model, whereas g is the logit link for binary Yi. For the purpose of exposition, we introduce our proposed tests in the linear model framework with a quantitative trait and no covariates, though the methods can be similarly extended to binary traits, and adjusted for covariates in the GLM and score function framework [15, 22, 23].
We test the null hypothesis H0: β = (β1, …, βk)’ = 0, that is, there is no association between any of the RVs and the trait under H0. Our proposed tests are based on the score vector U = (U1, …, Uk)’ for β and its covariance matrix V,
where and are the sample means of the Yi’s and Xi’s, respectively.
Review of the data-adaptive aSPU test
Pan et al. [15] proposed a new adaptive test that retains high power across a wide range of varying, yet unknown, genetic architecture for the analysis of RVs. This test is based on a class of the SPU test:
where γ≥1 is a positive integer. Suppose that we have a set of candidate values of γ in Γ, e.g., Γ = {1, 2, …, 8, ∞}, as used in our later experiments. It is known that SPU(1) is equivalent to the burden test, while SPU(2) is a variance-component score test equivalent to SKAT with a linear kernel. Importantly, as γ increases (as an even integer), the SPU(γ) test puts more weights on the larger component of U while gradually ignoring the remaining component. In particular, we have , as γ→∞. The SPU(∞) is closely related to the minP test (but ignores possibly varying variances of Uj’s); the two tests often perform similarly [24]. Since the power of an SPU(γ) test depends on the choice of γ while the optimal choice of γ depends on the unknown true association pattern of the RVs to be tested, it would be desirable to data-adaptively choose the value of γ. To this end, the aSPU test takes the minimum p-value of the SPU(γ) tests as its test statistic: TaSPU = minγ∈ΓpSPU(γ. In this case, TaSPU is no longer a genuine p-value; we use resampling approaches such as residual permutation or parametric bootstrap to obtain its p-value.
New test: FunSPU—A data-adaptive test incorporating multiple annotations
Our proposed test is in the data-adaptive aSPU test framework. Importantly, the proposed test is adaptive at both the annotation and SNV levels. Suppose that we have the score vector U = (U1, …, Uk)’ for k RVs from a gene region or sliding window based on a linear regression model. Let 0≤wlj≤1 denote the functional score from the lth of m properly scaled annotations for the jth of k RVs. The proposed functional annotation-based SPU test is
where two positive integers γ≥1 and γa≥1 respectively control the individual variants’ and annotations’ relative contributions to the overall test statistic; e.g., γa = 1 treats all annotations equally, while γa = ∞ only considers the most significant annotation. The inner sum of weighted Uj with power γ is the weighted SPU, and they are normalized to the power of 1/γ before being subjected to the outer sum with power γa. Since the number of the RVs in this test statistic is identical across all m annotations, it is not necessary to further normalize the weighted SPU test by the number of RVs.
The intuition to use γa as the powers of the weighted SPU is similar to that for γ. In general, a smaller γa, e.g., γa = 1, is more effective when there are more informative annotations, each of which is roughly equally discriminative regarding the deleteriousness of the RVs for the trait of interest. In contrast, a larger γa is preferred if there is only one or fewer informative annotations that can well distinguish causal variants from neutral ones for the trait. As γa→∞, only the most significant weighted SPU is considered.
We aim to perform powerful tests when there are unknown association patterns of RVs and unknown informativeness of functional annotations. In practice, since we have no a priori knowledge about choosing γ and γa, we need to conduct a grid search over a set of possible values of both γ and γa. However, searching too many values will introduce extra variability and lead to reduced power. This effect was later confirmed when we used γa∈{1,2,3,…,8,∞} and γ∈{1,2,3,…,8,∞} in some preliminary simulations. Based on the results of aSPU tests [15] and the feature of annotations, we decided to use γa∈Γa = {1,2,4,8,∞} and γ∈Γ = {1,2,3,…,6} for the rest of the study. We retained γa = ∞ as an approximation to the minP test and ignored some higher values of γ since the results tend to be similar to γ = 6.
Given a set of γ and γa, e.g., γ∈Γ = {1,2,3,…,6} and γa∈Γa = {1,2,4,8,∞}, the proposed data-adaptive FunSPU test statistic is defined as
where is calculated by the resampling methods detailed below. Although the score vector U has an asymptotic normal distribution N(0, V), it is not easy to derive the asymptotic distribution of TFunSPU. Therefore, we propose using a single layer of permutations (without covariates) or residual permutations (with covariates) to obtain p-values as done in aSPU [15, 22]. Specifically, we first permute the original set of trait Y to obtain a new set of Y(b) for b = 1, …, B. Then, we calculate the null score vector U(b) and the corresponding test statistic as well as their p-values . Therefore, we have , and the final p-value of the FunSPU test .
In the FunSPU test above, we ignored the possibly different variances of the score function component Uj, for example, due to varying MAF of the RVs. On the other hand, previous research has shown that it may be beneficial to account for the heterogeneity of variances in the SPU framework [24]. Therefore, we further propose an inverse-variance weighted version of FunSPU:
where Vjj is the jth diagonal element of V = Cov(U|H0) as given before.
Alternative approaches to incorporating multiple functional annotations: aSPU_minP and aSPU_Fisher
We considered alternative approaches to incorporate multiple functional annotations into the aSPU test. In contrast to the two-level FunSPU approach, we can obtain modified aSPU tests via the score vector U weighted by each functional annotation, i.e., , for l = 1, …, m. We can obtain the genuine p-value by resampling methods. To combine multiple functional annotations, we can further employ some general approaches to combine multiple p-values, . For example, we can simply use as the test statistic of m modified aSPU tests. This aSPU_minP test is similar, but not exactly equivalent to the case of FunSPU with γa = ∞: the latter chooses the maximum and then uses resampling methods to obtain a genuine p-value directly, while the aSPU_minP test calculates the empirical p-value first, and then uses the minimum p-value TaSPU_minP as the new test statistic and resampling to calculate the final p-value.
Another common method for combining p-values is Fisher’s meta-analysis approach, i.e., . If the m p-values were independent, TaSPU_Fisher would follow a chi-squared distribution with 2m degrees of freedom. However, our tests are correlated via the score vector U. Hence, we also use resampling approaches to calculate the final p-value. We can similarly apply the inverse-variance weighted method to aSPU_minP and aSPU_Fisher tests, respectively denoted as aSPUw_minP and aSPUw_Fisher.
Of note, aSPU_minP is closely related to the FST test [17]. Specifically when we restrict 𝛾 = 1,2, aSPU_minP is equivalent to FST_minP except for the up-weight of rarer variants and weighted sum approach to combine burden and dispersion test statistics in the latter, as compared to the minP approach in the former. Similarly, aSPU_Fisher is closely related to FST_Fisher.
wtFunSPU: Extension of FunSPU to allow for global weighting of multiple annotations
In our proposed FunSPU test, we treated all m functional annotations equally a priori and completely relied on the data to adaptively combine multiple annotations in each test unit, for example, a sliding window. This may be less efficient in the presence of overall inferior or superior annotations for a trait of interest, in which case it would be desirable to globally down-weight inferior annotations (and up-weight superior annotations). To this end, we propose to modify the FunSPU test by introducing an annotation-level weight ρ = (ρ1,…,ρm)′ and denote the modified test as wtFunSPU:
Since we assume no a priori knowledge regarding the informativeness of a functional annotation for a given trait, we propose to estimate ρl based on some global correlation measure between the annotation weights, genotypes and phenotype. A promising approach is based on partitioning the heritability h2 by functional annotations [25]: a functional annotation is more informative for the trait of interest if SNVs with higher functional scores contribute to more heritability on average. Specifically, given an annotation, we first partition the genome-wide RVs based on Q discrete functional categories or percentiles of continuous functional scores; we then estimate the heritability for all SNVs in functional category q = 1,…, Q, using the GCTA tool [26]. We next compute the average per-SNV heritability for each annotation category q and regress on q to estimate the slope: , where β is used as the global weight ρ for the corresponding functional annotation in the wtFunSPU test. Prior to this calculation, we transform the functional annotation to positive integers q = 1,…, Q such that larger q corresponds to a more likely functional category. If a functional category has a very small number of SNVs or close to zero, this category is combined with a nearby category; see S1 to S4 Figs and S2 Table for details.
Results
Simulation setups
We conducted extensive simulations to evaluate and compare the performance of our proposed functional annotation-based tests with existing association tests for RVs. To make the simulation study representative of real RV data, we randomly selected 200 RVs from chr16:56.8M~57.1M of the UK10K TWINSUK genotype data of 1,718 unrelated individuals. MAFs of the selected RVs were no larger than 1%.
To evaluate power, we generated the simulated phenotypes as follows. First, we simulated 3 sets of informative annotations (w1j,w2j,w3j) and 3 sets of random annotations (w4j,w5j,w6j) independently (j = 1, 2, …, 200 ordered by genomic positions). We designated the first 100 RVs as causal variants (j = 1, 2, …, 100) and the remaining 100 RVs as neutral variants (j = 101, 102, …, 200). The informative annotations were generated from a uniform distribution U(0.4, 1) corresponding to causal variants and from U(0, 0.6) corresponding to neutral variants. All of the random annotations were generated from U(0, 1). Second, we randomly selected k = k1+ k2 RVs: k1 causal RVs from j = 1, 2, …, 100 and k2 neutral RVs from j = 101, 102, …, 200. Third, we used only informative annotations to calculate the effect size βj = cβ(w1j,w2j,w3j) for each causal RV. Fourth, the simulated phenotype was obtained from , where εi followed N(0,3) and i = 1,2,…,1718. Furthermore, to evaluate the globally weighted wtFunSPU test, we calculated the correlations between the sum of the genotypes weighted by each annotation and simulated phenotypes for each of the 1,000 simulation replications, and used the mean of the 1,000 correlations as the global weight of each annotation, i.e., (l = 1, 2, …,6), where and are the vectors of Yi and Xij in each replication correspondingly.
We considered two simulation scenarios. In scenario A, we used all three informative annotations, three random annotations and one dummy annotation (1’s for all RVs) in functional annotation-based tests (FunSPU, aSPU_minP, and others). To test the effect of more “noisy” annotations, we implemented scenario B, which used only one informative annotation, all three random annotations and one dummy annotation in the tests. In both scenarios A and B, we used identical procedure as above to generate simulated phenotypes Yi, and fixed k1 = 8 and k2 = {8, 16, 32, 64, 128}, respectively. We set cβ = 0.5 for tests that incorporated global weights and cβ = 1 for other tests.
To evaluate the type I error rate, we simulated Yi~N(0,3) (i = 1,2,…,1718), independent of k neutral RVs and 6 random annotations all from U(0,0.6) in each replication. We set increasing numbers of neutral RVs with k = {8, 16, 32, 64, 128}.
The empirical type I error rate was calculated based on 50,000 replications with the significance level α = 0.005, while the empirical power was calculated based on 1,000 replications for each scenario with α = 0.05. For permutation-based tests, 10,000 and 1,000 resamplings were conducted for each replication to evaluate type I error and power, respectively.
Simulation results
As shown in Table 1, all the tests under comparison could control the type I error rate satisfactorily around 0.005, except for aSPU(w)_minP and aSPU(w)_Fisher tests, which were slightly inflated (between 0.006 and 0.007) with fewer number (e.g., 8) of neural variants. Besides Monte Carlo error, one possible reason for the slight inflation was that combining multiple annotations at the level of p-values might be sometimes numerically unstable in the presence of extreme p-values.
Table 1. Empirical type I error rates of various tests at significance level α = 0.005 for increasing number of neutral RVs with 50,000 simulation replications (B = 10,000 for resampling-based tests).
Annotation-based tests were based on six random annotations. aSPU: adaptive sum of powered score test; aSPU_minP: combining multiple p-values of aSPU tests by minimum p approach; aSPU_Fisher: to combining multiple p-values of aSPU tests by Fisher’s meta-analysis approach; FunSPU: multiple functional annotation-based SPU test; wtFunSPU: global weighted FunSPU; T1: burden test of variants with MAF smaller than 1%; SKAT: the sequence kernel association test; (w): inverse-variance weighted score function in the SPU framework.
| Test | No. of neutral RVs | ||||
|---|---|---|---|---|---|
| 8 | 16 | 32 | 64 | 128 | |
| aSPU | 0.0059 | 0.0057 | 0.0050 | 0.0046 | 0.0043 |
| aSPU_minP | 0.0067 | 0.0058 | 0.0054 | 0.0062 | 0.0043 |
| aSPUw_minP | 0.0060 | 0.0053 | 0.0044 | 0.0056 | 0.0056 |
| aSPU_Fisher | 0.0061 | 0.0054 | 0.0059 | 0.0054 | 0.0047 |
| aSPUw_Fisher | 0.0062 | 0.0062 | 0.0051 | 0.0050 | 0.0047 |
| FunSPU | 0.0053 | 0.0047 | 0.0043 | 0.0045 | 0.0037 |
| FunSPUw | 0.0057 | 0.0062 | 0.0041 | 0.0050 | 0.0037 |
| wtFunSPU | 0.0045 | 0.0046 | 0.0046 | 0.0037 | 0.0042 |
| wtFunSPUw | 0.0047 | 0.0056 | 0.0039 | 0.0034 | 0.0050 |
| T1 | 0.0052 | 0.0053 | 0.0049 | 0.0053 | 0.0055 |
| SKAT | 0.0051 | 0.0050 | 0.0053 | 0.0045 | 0.0038 |
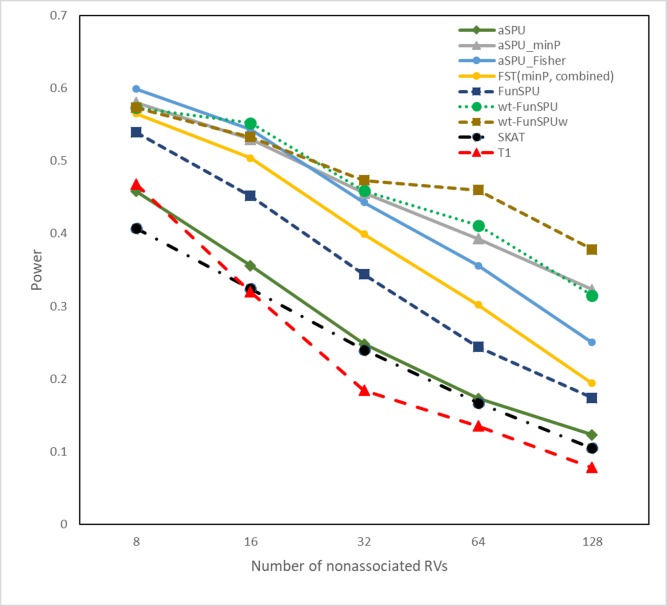
Regarding power, we first considered scenario A (Fig 1), which was an advantageous scenario for our proposed tests since all three informative annotations together with three random annotations and one dummy annotation were used in the tests. The dummy annotation (constant 1) was supposed to retain the unweighted SPU in the adaptive tests, as in aSPU. Although the simulated annotations for causal and neutral RVs had modest differences, i.e., from U(0.4, 1) and U(0,0.6), respectively, the tests incorporating functional annotations, such as FunSPU, wtFunSPU, aSPU_minP and FST, always had higher power than tests that ignored functional annotations, such as aSPU, SKAT and T1. The FunSPU test appeared to be less powerful than aSPU_minP, suggesting a lack of efficiency in the former’s complete data-adaptive strategy to combine multiple annotations. On the other hand, wtFunSPU and wtFunSPUw outperformed aSPU_minP and FST, supporting the effectiveness of the global weighting scheme. Between the latter two, aSPU_minP had an increasing edge over FST in the presence of larger number of neural variants, due to its going beyond burden (SPU(γ = 1)) and variance-component (SPU(γ = 2)) tests with additional γ parameters. We also observed that the inverse-variance weighted tests always outperformed the original tests, e.g., wtFunSPUw versus wtFunSPU, and this advantage became more obvious with a higher proportion of neutral RVs. Lastly, the power of the aSPU_Fisher test was similar to that of the aSPU_minP test until the number of neural variants increased to 64 and 128, when the former became less powerful than the latter.
Fig 1. Empirical power of various tests for eight causal RVs and increasing number of nonassociated RVs at significance level α = 0.05.
The incorporated annotations for association tests include all three informative annotations and three noninformative annotations (Scenario A). All the results were based on 1000 simulation replications.
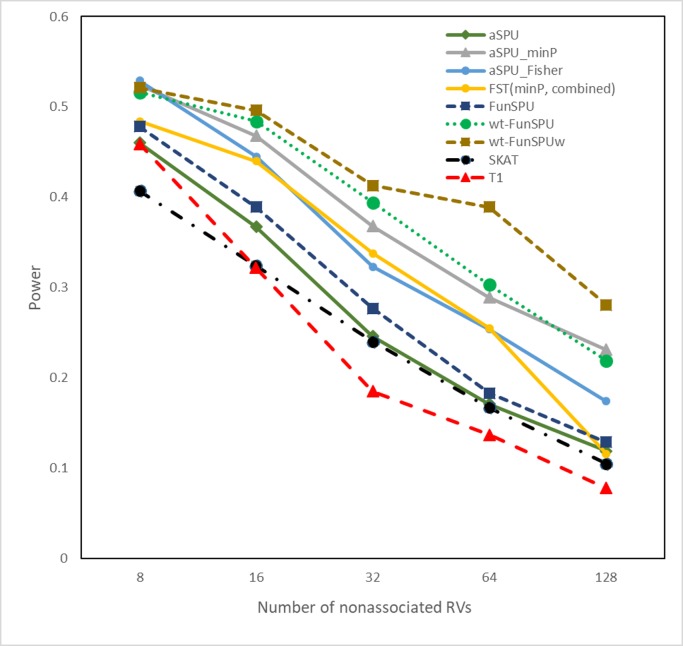
Next, we considered a weaker scenario for our proposed tests. In scenario B (Fig 2), we used only one informative annotation, but all three random annotations and one dummy annotation in the tests. In this case, we had a higher proportion of “noisy” annotations in our tests. We observed that the FunSPU test was marginally more powerful than aSPU, SKAT and T1, but was less powerful than the aSPU_minP test by a large margin. In fact, scenario B was an advantageous scenario for the latter test, which only considered the most informative annotation. Similarly, aSPU_minP was more powerful than aSPU_Fisher when the number of neutral variants exceeded 16, due to the latter treating the one informative and three non-informative annotations equally. Finally, the globally weighted wtFunSPU and wtFunSPUw, especially the latter, were more powerful than the aSPU_minP and FST tests, again suggesting the benefit of globally down-weighting noninformative annotations.
Fig 2. Empirical power of various tests for eight causal RVs and increasing number of nonassociated RVs at significance level α = 0.05.
The incorporated annotations for association tests include one out of three informative annotations and three noninformative annotations (Scenario B). All the results were based on 1000 simulation replications.
We also compared the computational time needed for different methods. As shown in S1 Table, FunSPU and aSPU_minP were on par with aSPU, but were more computationally intensive than the asymptotic-based burden and SKAT tests. As shown in the real data analysis later on, by employing a step-up permutation strategy, we were able to perform genome-wide scan of WGS data with FunSPU and related tests.
Application to the UK10K WGS data
To further evaluate the performance of our proposed tests on real data, we applied FunSPU and other state-of-the-art tests, including SKAT, T5 burden test and FST (combined test)[17], to association analysis of the UK10K WGS data with four complex quantitative traits: LDL, HDL, BMI and SBP. We used the TWINSUK samples as the discovery cohort and the ALSPAC samples as the replication cohort with n = 1706/1497 (TWINSUK/ ALSPAC), 1718/1497, 1752/1792 and 1740/1796, respectively, for LDL, HDL, BMI and SBP, after merging WGS genotype and phenotype data. After removing SNVs that did not pass quality control (QC) as done in the original UK10K analysis[2], as well as singletons and INDELs, we had a total of 10,979,027 RVs and low-frequency variants with MAF< 5% in the discovery cohort. Briefly, the UK10K WGS data QC included various low-level variant calling and filtering QC measures, variant-level QC to exclude variants with Hardy-Weinberg equilibrium (HWE) test p-value < 10−6, and sample-level QC to exclude samples in poor concordance with their corresponding GWAS data[2]. Since the discovery cohort TWINSUK only included women, we adjusted for age at baseline, but not gender, as a covariate in association testing in both discovery and replication cohorts.
We considered six types of functional annotations for RVs. CADD[7], FunSeq[19], FunSeq2[20], RegulomeDB[18] and GERP++[21] were extracted from the precomputed WGSA [27] library, and GenoSkyline (blood) annotation was generated from the region-based GenoSkyline library [8]. We re-scaled all annotations to numerical weights within the interval (0, 1), with larger weights corresponding to a greater likelihood of being functional (S5 Fig). Among the above annotations, rank scores for CADD, Funseq2, GenoSkyline and GERP++ were provided in the WGSA library [27], and the re-scaled score was defined as w = (raw rank score–min)/(max-min), where min and max were, respectively, the minimum and maximum raw rank scores for a given functional annotation. The RegulomeDB categories s = (1,2, …, 6) were transformed into (0, 1) by f(s) = (7-s)/6, whereas the Funseq categories s = (0,1,2, …, 6) were transformed by f(s) = (1+s)/7. We substituted the missing values or zero values with 0.01 (FunSeq, FunSeq2, RegulomeDB) or 0.0001 (GERP++). There was no missing value in CADD and GenoSkyline for the RVs considered here. S6 Fig shows the pairwise correlation coefficients among the 6 annotations: while some annotations were moderately correlated (r > 0.3), for example, GERP++ with CADD, and Funseq2 with RegulomeDB/Genoskyline, others were much less correlated. This suggests that multiple annotations may provide complementary information regarding the functional consequence of genetic variants, and it may be beneficial to incorporate them simultaneously in association analysis as proposed in the FunSPU framework here. Following the procedure proposed in Section 2.5, we calculated the phenotype-specific weight for each of the six annotations and used them as global weights in the wtFunSPU test. As shown in S1 to S4 Figs and S2 Table, RegulomeDB, Funseq and GenoSkyline tended to have consistently higher weights than GERP++, Funseq2 and CADD, while the numerical values and the relative magnitudes of the weights could vary across phenotypes.
We employed a sliding window approach to group RVs with a window length of 10k base pairs (bp) and a step size of 8.75k bp, resulting in 319,306 windows in total. Using the conservative Bonferroni procedure, we set the family-wise error rate at 0.05 with a significance level = 0.05/319306 = 1.56e-07, which equals 6.81 on the -log10 scale. To achieve this genome-wide significance level, we used a step-up permutation strategy [22, 28]. We first performed B = 10,000 permutations for all sliding windows and gradually increased B; if those sliding windows with estimated p-values <10/B, we increased B to 10 times the current value and re-estimated the p-values for these sliding windows. The number of permutations in the final stage was B = 108. Of note, the variant-specific score functions in aSPU, aSPU_minP, FunSPU and wtFunSPU were not weighted by MAF, while those in aSPUw, aSPUw_minP, FunSPUw, and wtFunSPUw were inverse-variance weighted, where variants with lower MAF were up-weighted. By default, SKAT and FST used Beta(1,25) weights to up-weight variants with lower MAF [16, 17].
As shown in S7 to S10 Figs, the quantile-quantile plots for the proposed FunSPU tests were well behaved, with no discernible indication of global p-value inflation, suggesting that the FunSPU tests could control the type I error rate well in genome-wide scans. Table 2 shows all sliding windows with at least one genome-wide significant p-value in the TWINSUK discovery cohort by any of the association tests under consideration. To confirm our findings in the TWINSUK cohort, we performed replication analysis of the genome-wide significant sliding windows in the ALSPAC cohort. As shown in Table 2, four sliding windows were replicated for the corresponding phenotypes and association tests with a replication p-value < 0.05/24 = 2.1e-3 based on the Bonferroni correction for 24 sliding windows: 3 by at least one of the functional annotation-based tests (1 by wtFunSPU, 1 by FunSPU and aSPU_minP and 1 by aSPUw_minP) and one by the aSPU test. In contrast, none of the 6 sliding windows identified by the FST test in the discovery cohort was replicated; neither did SKAT nor T5 replicate any sliding window.
Table 2. Genome-wide significant sliding windows identified by various tests in the UK10K TWINSUK cohort and replication in the ALSPAC cohort of UK10K.
Significant p-values are in boldface; only significant p-values in the ALSPAC cohort were reported (TWINSUK p-value/ALSPAC p-value shaded when both are significant). cMAF: cumulative minor allele frequency. Base pair (bp) position based on reference genome hg19.
| Trait | Chr | Start position- Stop position (bp) | Gene(s) | cMAF | # SNVs | p-Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Globally weighted | Not globally weighted | aSPU _minP |
aSPUw _minP |
aSPU | FST (combined) |
SKAT | T5 | ||||||||
| wtFun-SPU | wtFun -SPUw | Fun-SPU | Fun-SPUw | ||||||||||||
| HDL | 1 | 39,070,016–39,080,016 | Intergenic | 0.14/0.33 | 39/38 | 4.3e-2 | 2.3e-3 | 3.3e-2 | <1e-8 | 2.0e-2 | 3.2e-6 | 3.6e-2 | 1.2e-3 | 5.2e-2 | 2.0e-4 |
| HDL | 2 | 173,903,159–173,913,159 | RAPGEF4 | 0.084/0.21 | 33/31 | <1e-8 | <1e-8 | 2.4e-6 | <1e-8 | 4.9e-6 | 8.9e-6 | 2.4e-5 | 2.5e-6 | 1.1e-6 | 1.2e-4 |
| HDL | 3 | 63,804,000–63,814,000 | C3orf49 | 0.02/0.17 | 37/36 | 2.9e-3 | <1e-8 | 4.0e-2 | 1.8e-5 | 3.1e-2 | 4.5e-5 | 0.12 | 3.2e-3 | 1.6e-2 | 5.2e-2 |
| HDL | 5 | 6,548,648–6,558,648 | Intergenic | 0.001/0.32 | 59/59 | 0.13 | <1e-8 | 0.18 | <1e-8 | 6.2e-2/ <1e-4 | 0.15 | 2.0e-5 | 2.1e-3 | 0.19 | |
| HDL | 5 | 6,557,398–6,567,398 | Intergenic | 0.34/0.26 | 48/43 | 4.3e-2 | 1.5e-2 | 0.13 | <1e-8 | 9.5e-3 | <1e-8/ | 0.24 | 1.2e-8 | 1.8e-2 | 0.81 |
| LDL | 3 | 102,287,400–102,297,400 | Intergenic | 0.25/0.19 | 56/39 | 4.4e-5 | 9.9e-3 | <1e-8 | 3.6e-2 | 9.0e-6 | 1.3e-2 | 8.1e-6 | 1.3e-4 | 2.5e-5 | 4.5e-3 |
| LDL | 3 | 102,427,400–102,437,400 | Intergenic | 0.16/0.27 | 32/40 | <1e-8 | 5e-8 | <1e-8 | 1.3e-3 | 1.2e-6/ <1e-4 | 5.1e-5 | 2.5e-4 | 3.3e-7 | 1.3e-4 | 0.68 |
| LDL | 5 | 43,259,958–43,269,958 | NIM1K | 0.43/0.29 | 41/46 | 9e-8 | <1e-8 | 6.5e-7 | 3.0e-7 | 1.7e-5/ <1e-4 | 8.2e-6 | 2.5e-5 | 1.5e-5 | 2.4e-3 | 4.4e-6 |
| LDL | 12 | 13,771,517–13,781,517 | GRIN2B | 0.18/0.23 | 43/48 | 3.5e-3 | 5.8e-4 | 0.80 | 3.5e-5 | 5.9e-6 | 1.7e-6 | 0.60 | 2.4e-11 | 0.23 | 0.96 |
| LDL | 12 | 13,780,267–13,790,267 | GRIN2B | 0.26/0.27 | 45/43 | 6.0e-2 | 8.0e-4 | 0.47 | 1.3e-4 | 1.0e-6 | 1.7e-6 | 0.33 | 2.0e-11 | 4.9e-2 | 0.53 |
| LDL | 19 | 45,387,096–45,397,096 | PVRL2/ TOMM40 | 0.21/ 0.22 | 33/ 37 | 5.4e-2/ 1.8e-3 | 0.10 | 3.5e-7/ <1e-4 | 5.0e-3/ 1.6e-3 | 2.1e-7/ <1e-4 | 4.5e-3 | 2.4e-4 | 2.4e-4/ 7.9e-6 | 0.25 | |
| LDL | 19 | 45,395,846–45,405,846 | TOMM40 | 0.42/0.59 | 65/62 | 8.6e-3/ <1e-4 | 8.6e-2 | 1.4e-4/ 1.9e-3 | 5.8e-5/ <1e-4 | 5.0e-7 | 1.2e-4/ 1.0e-10 | 4.7e-4/ 1.1e-6 | 0.28 | ||
| LDL | 19 | 45,439,596–45,449,596 | APOC4-APOC2 | 0.37/0.18 | 25/25 | 1.1e-4 | 1.2e-6/ <1e-4 | 6.9e-4 | 2.1e-5/ <1e-4 | 1.4e-4 | 2.3e-4 | 4.7e-5/ 2.4e-7 | 1.1e-3/ 9.0e-4 | 0.15 | |
| BMI | 3 | 35,619,294–35,629,294 | Intergenic | 0.24/0.24 | 39/40 | <1e-8 | 4.2e-5 | 5.0e-5 | 1.1e-4 | 3.9e-5 | 3.6e-5 | 8.0e-5 | 2.9e-6 | 4.4e-5 | 1.5e-5 |
| BMI | 4 | 22,825,237–22,835,237 | Intergenic | 0.18/0.24 | 47/48 | 1.3e-3 | 5.2e-5 | 1.8e-3 | 6.0e-5 | 1.6e-4 | 3.4e-4/ <1e-4 | 2.8e-3 | 2.6e-8 | 1.4e-6 | 3.0e-5 |
| BMI | 10 | 13,937,041–13,947,041 | FRMD4A | 0.28/0.30 | 49/53 | 8.5e-2 | 2.4e-3 | 0.16 | 1.4e-4 | 5.9e-4 | 2.4e-4 | 0.18 | 1.9e-8 | 0.12 | 7.2e-2 |
| BMI | 12 | 26,179,017–26,189,017 | RASSF8 | 0.38/0.40 | 37/37 | 7.5e-2 | 1.2e-4 | 0.12 | 4.4e-4 | 2.1e-4 | 3.5e-4/ <1e-4 | 0.12 | 7.5e-8 | 6.6e-2 | 2.1e-4 |
| BMI | 15 | 42,935,528–42,945,528 | STARD9 | 0.28/0.23 | 43/56 | <1e-8 | 2.7e-6 | <1e-8 | 1.2e-5 | 2.1e-6 | 4.5e-5 | 1.2e-6 | 4.8e-7 | 8.4e-8 | 1.1e-7 |
| BMI | 16 | 60,159,304–60,169,304 | Intergenic | 0.27/0.12 | 29/28 | 4.3e-4 | <1e-8 | 2.5e-2 | 2.1e-4 | 6.1e-4/ <1e-4 | 6.4e-6/ <1e-4 | 5.1e-3 | 1.4e-5 | 0.15 | 3.0e-4 |
| BMI | 21 | 40,851,354–40,861,354 | SH3BGR | 0.26/0.17 | 32/26 | 4.4e-4 | <1e-8 | 2.5e-3 | 1.1e-4 | 1.3e-3 | 6.7e-5 /2.6e-3 | 1.2e-3 | 3.9e-4 | 1.5e-2 | 3.4e-4 |
| SBP | 4 | 118,855,917–118,865,917 | Intergenic | 0.36/0.16 | 32/27 | 5.5e-2 | <1e-8 | 0.68 | 8.1e-5 | 5.2e-2 | 4.2e-5/ <1e-4 | 0.75 | 2.5e-2 | 0.39 | 0.34 |
| SBP | 6 | 42,558,580–42,568,580 | UBR2 | 0.96/0.095 | 28/22 | <1e-8 | 1.3e-4 | 3.4e-4 | 5.6e-4 | 1.1e-6 | 1.6e-4 | 3.9e-4 | 1.7e-6 | 2.7e-3 | 7.8e-5 |
| SBP | 6 | 121,241,282–121,251,282 | Intergenic | 0.50/0.23 | 53/46 | <1e-8 | 1.8e-4 | 1.2e-4 | 1.4e-3 | 1.6e-4 | 2.1e-3/ <1e-4 | 5.5e-4 | 3.0e-4 | 1.1e-4 | 7.0e-4 |
| SBP | 11 | 38,236,659–38,246,659 | Intergenic | 0.60/0.48 | 61/61 | <1e-8 | 1.4e-4 | 8.6e-5 | 6.4e-6 | 2.1e-5 | 1.9e-4 | 3.8e-3 | 4.4e-6 | 8.5e-3 | 0.36 |
Significance threshold: p<1.56×10−7 for TWINSUK and p<2×10−3 for ALSPAC
Three of the four replicated sliding windows were close to each other on chromosome 19 around TOMM40, APOE and APOC4-APOC2 genes. These loci have been previously identified and replicated to be associated with LDL by large-scale meta-analysis of GWAS common variants [29–31]. Numerous functional and genetic association studies have shown that APOE plays a central role in lipoprotein metabolism and neurodegeneration [32–34]. Specifically, APOE has three isoforms, 2, 3, and 4: APOE2 is associated with elevated plasma LDL level and increased cardiovascular disease risk, whereas APOE4 is associated with increased risk of Alzheimer’s disease[34]. While previous large-scale whole-exome sequencing and ExomeChip-based association studies did not identify exonic RVs in APOE associated with LDL[35, 36], a recent association analysis of 16,324 deep-coverage WGS samples from the TOPMed project identified LDL-associated rare non-coding variants upstream of APOE[37]. Here we were able to identify the TOMM40/APOE locus and additionally APOC4-APOC2 locus that harbor LDL-associated RVs with fewer than a couple of thousand samples, suggesting that the power of the FunSPU test was boosted by incorporating external biological knowledge.
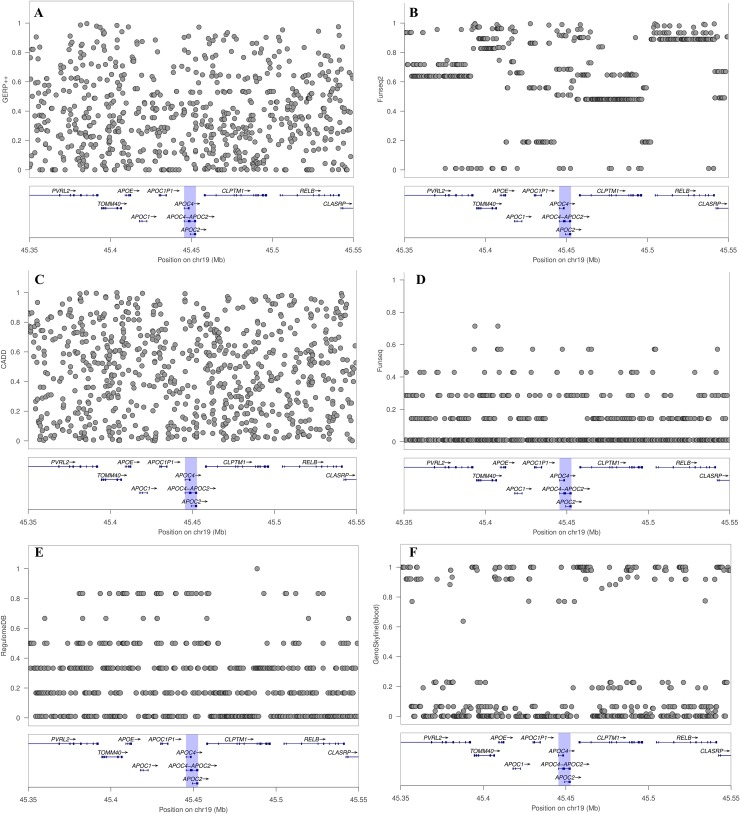
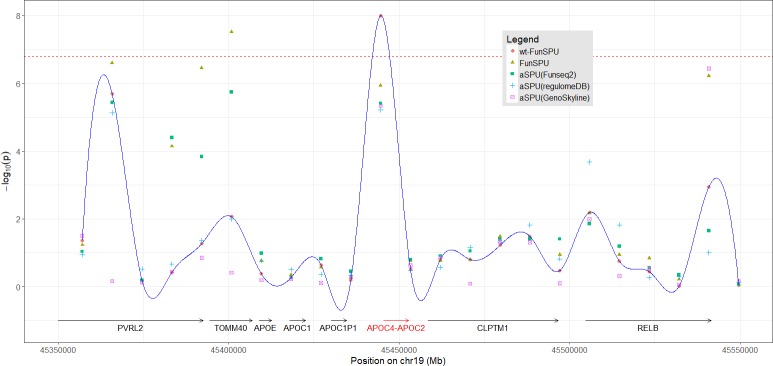
We also looked into the effects of multiple annotations on the FunSPU tests. Although some high scores were observed around the TOMM40 and APOC4-APOC2 gene regions for Funseq2, Funseq, RegulomeDB and GenoSkyline (Fig 3), they did not appear to be obviously different from those scores outside these two loci. Fig 4 shows the association signals of selected tests in this genomic region, whereas S11 Fig shows all individual annotation-based aSPU tests. As for APOC4-APOC2, three of the six annotations, namely, Funseq2, RegulomeDB and GenoSkyline (S11E, S11H and S11I Fig), positively contributed to the highly significant p-values of wtFunSPU and FunSPU (S11A and S11B Fig), although none of these individual annotation-based aSPU tests would reach the genome-wide significance threshold, demonstrating the benefit of integrating multiple functional annotations in the FunSPU framework. RegulomeDB and GenoSkyline also had higher global weights for LDL (S2B Table), which further boosted the p-value of the wtFunSPU test to the genome-wide significance level. As for TOMM40, Funseq2, CADD and GERP++ (S11E, S11F and S11D Fig) positively contributed to the genome-wide significance of FunSPU and aSPU_minP (S11A Fig and Table 2); whereas wtFunSPU missed this locus due to its low global weighting of these three annotations (S2B Table). This suggests that wtFunSPU, FunSPU and aSPU_minP may complement each other and may be used together in association analysis of WGS data.
Fig 3.
Rescaled scores of functional annotations: (A) GERP++, (B) Funseq2, (C) CADD, (D) Funseq, (E) RegulomeDB, and (F) GenoSkyline (blood) at the locus around gene APOC4-APOC2. The scores were rescaled to the interval [0, 1].
Fig 4. Association test results for LDL at the locus around gene APOC4-APOC2.
The round points and the trace show the results from the globally weighted wtFunSPU test. Other points correspond to the results of FunSPU and single annotation-based aSPU (GERP++, Funseq2, RegulomeDB, GenoSkyline), respectively. Dashed line indicates the threshold of genome-wide significance level (p < 1.56e-7).
To further investigate whether the TOMM40 and APOC4-APOC2 loci identified for LDL cholesterol were driven by coding RVs, we only retained nonsynonymous RVs in the original sliding windows in this region (13 nonsynonymous RVs out of total 784 RVs) and applied the aSPU test to each sliding window which had at least two RVs. For a sliding window with a single RV, we merged it with its neighboring sliding window. As shown in S12 Fig, none of the sliding windows had a p-value < 0.01, far less significant than the original association testing results (Fig 4). We therefore conclude that it is very unlikely the identified associations were driven by coding RVs.
Discussion
We have proposed a versatile and adaptive association test, FunSPU, to exploit multiple sources of biological knowledge in the analysis of WGS data. It is adaptive at both the annotation and variant levels, and thus maintains high statistical power, even in the presence of noninformative annotations and a larger number of neutral variants. We have further proposed a globally weighted wtFunSPU test to more effectively down-weight less informative functional annotations in a trait-specific manner. Using the UK10K WGS data, we demonstrated that our proposed FunSPU test and its extensions, including the wtFunSPU and aSPU_minP tests, are more powerful tools to identify genome-wide significant loci than existing RV association tests that either ignore external biological information or rely on a single source of biological knowledge. The FunSPU family of tests would thus serve as a powerful and complementary tool for ongoing and future large-scale WGS studies, such as the NHLBI TOPMed project [3] of over 100,000 individuals and the UK Biobank [38] WGS project of 50,000 individuals. We have also summarized and compared the FunSPU family of tests in S3 Table.
The six functional annotations we considered here are diverse in terms of resources and features. For example, GERP++[21] is a sequence conservation score, whereas other annotations are ensemble scores based on integrating multiple sources of features, such as various functional genomic assays in the ENCODE project[4] and eQTL evidence. As demonstrated in S6 Fig, a majority of the annotations were only moderately correlated with each other, supporting our proposal to incorporate multiple annotations’ approximately orthogonal yet complementary information regarding the functional consequence of RVs in the framework of the FunSPU association test. The FunSPU test can easily incorporate additional functional annotations, including some newly developed ones [10], such as fathmm-MKL[39], Eigen/Eigen-PC[9] and DeepSEA[40].
To further de-noise noninformative annotations, we proposed a novel trait-specific measure based on partitioning the heritability and used it as a global weight for each annotation in the wtFunSPU test. Interestingly, our proposal is along the line of estimating group-specific weights in the context of weighted hypothesis testing [41, 42], though the latter is based on the mixture model, in contrast to the mixed model-based heritability partition here. Although it may look counterintuitive at first glance, our proposed data-dependent global weights actually did not inflate the type I error rates in both simulations (Table 1) and the real data analysis, as evidenced by the QQ plots of wtFunSPU (S7 to S10 Figs). The reason is that we used a much larger number of observations, i.e., RVs across the whole genome, to estimate a few annotation category-specific heritability parameters h2, based on which we derived a single global weight. This is in line with the “sieve principle”, which justifies using aggregated data to estimate a much smaller number of weights and then using them in subsequent hypothesis testing of small units of data (e.g., genes or sliding windows) with controlled family-wise error rate [42, 43]. Our proposed measure also has the potential to be used to compare the discriminative performance of whole-genome annotations for a complex trait of interest, for which known deleterious and neutral variants are rarely available (see S2 Table). This warrants further investigation. We have also applied the LD score regression method [44] to calculate the weights for common variants (MAF>5%) using the UK10K TWINSUK WGS data. As shown in S4 Table, the weights were largely qualitatively similar to those derived from RVs, suggesting that our proposed strategy to infer the global weighting of annotations is quite robust.
We have some practical considerations for our proposed tests. First, some functional annotations are not well-defined across the whole genome, resulting in relatively high missing data rates, for example, 68% for Funseq; the missing scores may reduce the reliability of annotation-based association tests. On the other hand, considering multiple complementary functional annotations simultaneously may at least partially remedy the problem of missing information. Second, by employing parallel computing and a step-up residual permutation strategy for the FunSPU family of tests, we are able to perform computationally feasible genome-wide scans for WGS data. For example, in the UK10K TWINSUK WGS data application, it took 24 hours for 500 computing cores to complete the sliding window-based FunSPU scan in R, including 108 residual permutations for the top sliding windows to reach the genome-wide significance threshold. We expect that further implementation of the core functions in the C language should reduce the computational burden to a more affordable level. In addition, it would be desirable to develop some asymptotic theory and test to save the computational time. Of note, some asymptotic theory has been developed for the aSPU test in the context of testing two high-dimensional means for common variants [45]; however, extension to rare variants and the FunSPU test proposed here is not trivial and warrants future research.
We have implemented the proposed FunSPU test and its extensions in an R package “FunSPU”, available at https://github.com/sputnik1985/FunSPU, and to be posted to R/CRAN.
Supporting information
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Global quantile-quantile (QQ) plots for association analysis of rare variants with HDL in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 1.004), (B) FunSPUw (λ = 1.076), (C) wtFunSPU with global weights (λ = 1.004), and (D) wtFunSPUw with global weights (λ = 1.047).
(PDF)
Global QQ plots for association analysis of rare variants with LDL in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 0.611), (B) FunSPUw (λ = 0.805), (C) wtFunSPU with global weights (λ = 0.642), and (D) wtFunSPUw with global weights (λ = 0.789).
(PDF)
Global QQ plots for association analysis of rare variants with BMI in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 0.604), (B) FunSPUw (λ = 0.825), (C) wtFunSPU with global weights (λ = 0.635), and (D) wtFunSPUw with global weights (λ = 0.825).
(PDF)
Global QQ plots for association analysis of rare variants with SBP in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 0.601), (B) FunSPUw (λ = 0.821), (C) wtFunSPU with global weights (λ = 0.631), and (D) wt-FunSPUw with global weights (λ = 0.793).
(PDF)
LocusZoom plots of association test results for LDL at the locus around TOMM40 and APOC4-APOC2 in the UK10K TWINSUK cohort: (A) FunSPU, (B) wtFunSPU incorporating global weights, (C) aSPU, and (D)-(I) aSPU incorporating a single functional annotation: (D) GERP++, (E) Funseq2, (F) CADD, (G) Funseq, (H) RegulomeDB, and (I) GenoSkyline (blood).
(PDF)
(PDF)
(PDF)
The corresponding phenotypes: (A) HDL, (B) LDL, (C) BMI, and (D) SBP.
(PDF)
(PDF)
(PDF)
Acknowledgments
We thank Drs. Wei Pan and Xiaoming Liu for helpful discussions and Ms. Lee Ann Chastain for editorial assistance. We are grateful to three anonymous reviewers for their many helpful and constructive comments that improved the presentation of the paper. The authors acknowledge the Texas Advanced Computing Center at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper.
Data Availability
This study makes use of data generated by the UK10K Consortium, derived from samples from the TwinsUK and ALSPAC cohorts. A full list of the investigators who contributed to the generation of the data is available from www.UK10K.org. Data are available from UK10K Data Access Committee for researchers who meet the criteria for access to confidential data.
Funding Statement
This research was supported by National Institutes of Health grants R01HL116720 (to PW), R01CA169122 (to PW) and R21HL126032 (to PW). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Funding for UK10K was provided by the Wellcome Trust under award WT091310.
References
- 1.Crosby J, Peloso GM, Auer PL, Crosslin DR, Stitziel NO, Lange LA, et al. Loss-of-function mutations in APOC3, triglycerides, and coronary disease. N Engl J Med. 2014;371(1):22–31. 10.1056/NEJMoa1307095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.The UK10K Project Consortium, Walter K, Min JL, Huang J, Crooks L, Memari Y, et al. The UK10K project identifies rare variants in health and disease. Nature. 2015;526(7571):82–90. 10.1038/nature14962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brody JA, Morrison AC, Bis JC, O'Connell JR, Brown MR, Huffman JE, et al. Analysis commons, a team approach to discovery in a big-data environment for genetic epidemiology. Nature genetics. 2017;49(11):1560–3. 10.1038/ng.3968 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Consortium EP. An integrated encyclopedia of DNA elements in the human genome. Nature. 2012;489(7414):57–74. 10.1038/nature11247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roadmap Epigenomics C, Kundaje A, Meuleman W, Ernst J, Bilenky M, Yen A, et al. Integrative analysis of 111 reference human epigenomes. Nature. 2015;518(7539):317–30. 10.1038/nature14248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.GTEx Consortium, Laboratory DA, Coordinating Center -Analysis Working G, Statistical Methods groups-Analysis Working G, Enhancing Gg, Fund NIHC, et al. Genetic effects on gene expression across human tissues. Nature. 2017;550(7675):204–13. 10.1038/nature24277 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kircher M, Witten DM, Jain P, O'Roak BJ, Cooper GM, Shendure J. A general framework for estimating the relative pathogenicity of human genetic variants. Nature genetics. 2014;46(3):310–5. 10.1038/ng.2892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lu Q, Powles RL, Wang Q, He BJ, Zhao H. Integrative Tissue-Specific Functional Annotations in the Human Genome Provide Novel Insights on Many Complex Traits and Improve Signal Prioritization in Genome Wide Association Studies. PLoS Genet. 2016;12(4):e1005947 10.1371/journal.pgen.1005947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ionita-Laza I, McCallum K, Xu B, Buxbaum JD. A spectral approach integrating functional genomic annotations for coding and noncoding variants. Nature genetics. 2016;48(2):214–20. 10.1038/ng.3477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu X, Li C, Boerwinkle E. The performance of deleteriousness prediction scores for rare non-protein-changing single nucleotide variants in human genes. J Med Genet. 2017;54(2):134–44. 10.1136/jmedgenet-2016-104369 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Werling DM, Brand H, An JY, Stone MR, Zhu L, Glessner JT, et al. An analytical framework for whole-genome sequence association studies and its implications for autism spectrum disorder. Nature genetics. 2018;50(5):727–36. 10.1038/s41588-018-0107-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim T, Wei P. Incorporating ENCODE information into association analysis of whole genome sequencing data. BMC Proc. 2016;10(Suppl 7):257–61. 10.1186/s12919-016-0040-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Morrison AC, Huang Z, Yu B, Metcalf G, Liu X, Ballantyne C, et al. Practical Approaches for Whole-Genome Sequence Analysis of Heart- and Blood-Related Traits. American journal of human genetics. 2017;100(2):205–15. 10.1016/j.ajhg.2016.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Su YR, Di CZ, Hsu L, C GEC. A unified powerful set-based test for sequencing data analysis of GxE interactions. Biostatistics. 2017;18(1):119–31. 10.1093/biostatistics/kxw034 WOS:000397063700009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pan W, Kim J, Zhang Y, Shen X, Wei P. A powerful and adaptive association test for rare variants. Genetics. 2014;197(4):1081–95. 10.1534/genetics.114.165035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. American journal of human genetics. 2011;89(1):82–93. 10.1016/j.ajhg.2011.05.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.He Z, Xu B, Lee S, Ionita-Laza I. Unified Sequence-Based Association Tests Allowing for Multiple Functional Annotations and Meta-analysis of Noncoding Variation in Metabochip Data. American journal of human genetics. 2017;101(3):340–52. 10.1016/j.ajhg.2017.07.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Boyle AP, Hong EL, Hariharan M, Cheng Y, Schaub MA, Kasowski M, et al. Annotation of functional variation in personal genomes using RegulomeDB. Genome research. 2012;22(9):1790–7. 10.1101/gr.137323.112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Khurana E, Fu Y, Colonna V, Mu XJ, Kang HM, Lappalainen T, et al. Integrative annotation of variants from 1092 humans: application to cancer genomics. Science. 2013;342(6154):1235587 10.1126/science.1235587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fu Y, Liu Z, Lou S, Bedford J, Mu XJ, Yip KY, et al. FunSeq2: a framework for prioritizing noncoding regulatory variants in cancer. Genome biology. 2014;15(10):480 10.1186/s13059-014-0480-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Davydov EV, Goode DL, Sirota M, Cooper GM, Sidow A, Batzoglou S. Identifying a high fraction of the human genome to be under selective constraint using GERP++. PLoS computational biology. 2010;6(12):e1001025 10.1371/journal.pcbi.1001025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pan W, Kwak IY, Wei P. A Powerful Pathway-Based Adaptive Test for Genetic Association with Common or Rare Variants. American journal of human genetics. 2015;97(1):86–98. 10.1016/j.ajhg.2015.05.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yang T, Chen H, Tang H, Li D, Wei P. A powerful and data-adaptive test for rare-variant-based gene-environment interaction analysis. Stat Med. 2018. Epub 2018/11/22. 10.1002/sim.8037 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pan W. Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genet Epidemiol. 2009;33(6):497–507. 10.1002/gepi.20402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gusev A, Lee SH, Trynka G, Finucane H, Vilhjalmsson BJ, Xu H, et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. American journal of human genetics. 2014;95(5):535–52. 10.1016/j.ajhg.2014.10.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. American journal of human genetics. 2011;88(1):76–82. 10.1016/j.ajhg.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu X, White S, Peng B, Johnson AD, Brody JA, Li AH, et al. WGSA: an annotation pipeline for human genome sequencing studies. J Med Genet. 2016;53(2):111–2. 10.1136/jmedgenet-2015-103423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wei P, Cao Y, Zhang Y, Xu Z, Kwak IY, Boerwinkle E, et al. On Robust Association Testing for Quantitative Traits and Rare Variants. G3 (Bethesda). 2016;6(12):3941–50. 10.1534/g3.116.035485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kathiresan S, Willer CJ, Peloso GM, Demissie S, Musunuru K, Schadt EE, et al. Common variants at 30 loci contribute to polygenic dyslipidemia. Nature genetics. 2009;41(1):56–65. 10.1038/ng.291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Waterworth DM, Ricketts SL, Song K, Chen L, Zhao JH, Ripatti S, et al. Genetic variants influencing circulating lipid levels and risk of coronary artery disease. Arteriosclerosis, thrombosis, and vascular biology. 2010;30(11):2264–76. 10.1161/ATVBAHA.109.201020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Willer CJ, Sanna S, Jackson AU, Scuteri A, Bonnycastle LL, Clarke R, et al. Newly identified loci that influence lipid concentrations and risk of coronary artery disease. Nature genetics. 2008;40(2):161–9. 10.1038/ng.76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lin YT, Seo J, Gao F, Feldman HM, Wen HL, Penney J, et al. APOE4 Causes Widespread Molecular and Cellular Alterations Associated with Alzheimer's Disease Phenotypes in Human iPSC-Derived Brain Cell Types (vol 98, pg 1141, 2018). Neuron. 2018;98(6):1294–. 10.1016/j.neuron.2018.06.011 WOS:000436587600025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kawashiri MA, Tsukamoto K, Secreto A, Usher DC, Pure E, Rader DJ. Apoe2 and apoE4 are less effective than ApoE3 in inhibiting atherosclerosis in LDL receptor deficient mice. Circulation. 2000;102(18):145–. WOS:000090072300703. [Google Scholar]
- 34.Huang YWA, Zhou B, Wernig M, Sudhof TC. ApoE2, ApoE3, and ApoE4 Differentially Stimulate APP Transcription and A beta Secretion. Cell. 2017;168(3):427–+. 10.1016/j.cell.2016.12.044 WOS:000396249600012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liu DJ, Peloso GM, Yu H, Butterworth AS, Wang X, Mahajan A, et al. Exome-wide association study of plasma lipids in > 300,000 individuals. Nature genetics. 2017;49(12):1758–+. 10.1038/ng.3977 WOS:000416480600016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lange LA, Hu YN, Zhang H, Xue CY, Schmidt EM, Tang ZZ, et al. Whole-Exome Sequencing Identifies Rare and Low-Frequency Coding Variants Associated with LDL Cholesterol. American journal of human genetics. 2014;94(2):233–45. 10.1016/j.ajhg.2014.01.010 WOS:000331419500007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Natarajan P, Peloso GM, Zekavat SM, Montasser M, Ganna A, Chaffin M, et al. Deep-coverage whole genome sequences and blood lipids among 16,324 individuals. Nat Commun. 2018;9 ARTN 3391 10.1038/s41467-018-05747-8 WOS:000442521500016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J, et al. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015;12(3):e1001779 10.1371/journal.pmed.1001779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Shihab HA, Rogers MF, Gough J, Mort M, Cooper DN, Day IN, et al. An integrative approach to predicting the functional effects of non-coding and coding sequence variation. Bioinformatics. 2015;31(10):1536–43. 10.1093/bioinformatics/btv009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhou J, Troyanskaya OG. Predicting effects of noncoding variants with deep learning-based sequence model. Nat Methods. 2015;12(10):931–4. 10.1038/nmeth.3547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Roeder K, Devlin B, Wasserman L. Improving power in genome-wide association studies: Weights tip the scale. Genetic Epidemiology. 2007;31(7):741–7. 10.1002/gepi.20237 WOS:000250904800007. [DOI] [PubMed] [Google Scholar]
- 42.Roeder K, Wasserman L. Genome-Wide Significance Levels and Weighted Hypothesis Testing. Stat Sci. 2009;24(4):398–413. 10.1214/09-STS289 WOS:000277257000003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bickel PJ. Efficient and adaptive estimation for semiparametric models. Baltimore: Johns Hopkins University Press; 1993. xix, 560 p. p. [Google Scholar]
- 44.Finucane HK, Bulik-Sullivan B, Gusev A, Trynka G, Reshef Y, Loh PR, et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nature genetics. 2015;47(11):1228–+. 10.1038/ng.3404 WOS:000363988200005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Xu GJ, Lin LF, Wei P, Pan W. An adaptive two-sample test for high-dimensional means. Biometrika. 2016;103(3):609–24. 10.1093/biomet/asw029 WOS:000384599800008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Global quantile-quantile (QQ) plots for association analysis of rare variants with HDL in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 1.004), (B) FunSPUw (λ = 1.076), (C) wtFunSPU with global weights (λ = 1.004), and (D) wtFunSPUw with global weights (λ = 1.047).
(PDF)
Global QQ plots for association analysis of rare variants with LDL in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 0.611), (B) FunSPUw (λ = 0.805), (C) wtFunSPU with global weights (λ = 0.642), and (D) wtFunSPUw with global weights (λ = 0.789).
(PDF)
Global QQ plots for association analysis of rare variants with BMI in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 0.604), (B) FunSPUw (λ = 0.825), (C) wtFunSPU with global weights (λ = 0.635), and (D) wtFunSPUw with global weights (λ = 0.825).
(PDF)
Global QQ plots for association analysis of rare variants with SBP in the UK10K TWINSUK cohort: (A) FunSPU (genomic control λ = 0.601), (B) FunSPUw (λ = 0.821), (C) wtFunSPU with global weights (λ = 0.631), and (D) wt-FunSPUw with global weights (λ = 0.793).
(PDF)
LocusZoom plots of association test results for LDL at the locus around TOMM40 and APOC4-APOC2 in the UK10K TWINSUK cohort: (A) FunSPU, (B) wtFunSPU incorporating global weights, (C) aSPU, and (D)-(I) aSPU incorporating a single functional annotation: (D) GERP++, (E) Funseq2, (F) CADD, (G) Funseq, (H) RegulomeDB, and (I) GenoSkyline (blood).
(PDF)
(PDF)
(PDF)
The corresponding phenotypes: (A) HDL, (B) LDL, (C) BMI, and (D) SBP.
(PDF)
(PDF)
(PDF)
Data Availability Statement
This study makes use of data generated by the UK10K Consortium, derived from samples from the TwinsUK and ALSPAC cohorts. A full list of the investigators who contributed to the generation of the data is available from www.UK10K.org. Data are available from UK10K Data Access Committee for researchers who meet the criteria for access to confidential data.