Transcriptional Bursts in a Nonequilibrium Model for Gene Regulation by Supercoiling

Abstract

We analyze transcriptional bursting within a stochastic nonequilibrium model, which accounts for the coupling between the dynamics of DNA supercoiling and gene transcription. We find a clear signature of bursty transcription when there is a separation between the timescales of transcription initiation and supercoiling dissipation (the latter may either be diffusive or mediated by topological enzymes, such as type I or type II topoisomerases). In multigenic DNA domains, we observe either bursty transcription or transcription waves; the type of behavior can be selected for by controlling gene activity and orientation. In the bursty phase, the statistics of supercoiling fluctuations at the promoter are markedly non-Gaussian.

Introduction

Transcription, the mechanism through which DNA is read by a polymerase to create a messenger RNA, is a crucial process in living cells, and its regulation is an important determinant of cell function (1). The dynamics of transcription are inherently stochastic because its initiation requires an RNA polymerase (RNAP) and associated cofactors to bind at the promoter of a gene (2). Not only can the copy numbers of RNAPs and transcription factors be low, but the mechanism through which they find their specific binding sites (a combination of three-dimensional diffusion through the nucleoplasm or cytoplasm and one-dimensional diffusion along the genome (3, 4)) leads to a broad distribution of search times. As a consequence, transcription initiation is a rare event with rates of the order of inverse hours in mammals (5), whereas in bacteria, tens of minutes may elapse between successive initiation events at the same promoter (6).

An intriguing feature of transcription as a stochastic process is that it is often “bursty.” This means that when recording transcription events for a given gene in a given cell, one observes clusters of closely spaced events separated by longer dormant periods in which the gene is silent, and the distribution of interval times is non-Poissonian. Transcription bursts are common to both bacterial and eukaryotic cells; this phenomenon is thought to provide a potential basis for the variability in behavior, which is observed in genetically identical cells within the same environment (2). Bursting may therefore play a key role in the pathway through which a cell can spontaneously break symmetry, for instance to choose its fate early in development in higher eukaryotes (7).

From a general point of view, a dynamical system yields bursty behavior when there is intermittent switching between states with high and low activity (8, 9). But what is the biophysical mechanism underlying such intermittency? Several possibilities have been proposed in the literature, and they may differ in different organisms. In mammals, proposed mechanisms for bursting are typically gene specific (10); cycles of higher transcription activity may be due to chromatin remodeling (11) or to the action of cis-regulatory DNA elements (10). In both cases, refractory periods during which genes are silent last for hours. In bacteria, refractory timescales only span tens of minutes, and other scenarios may be more relevant. For instance, pausing of an RNAP along a gene may lead to the formation of a queue of multiple RNAPs behind it, producing bursts of transcripts (12, 13). This mechanism requires that the gene in question is highly expressed so that multiple polymerases can be recruited to its promoter within minutes. Recently, a set of experiments (14) has demonstrated that transcriptional bursts in DNA plasmids in vitro are associated with DNA supercoiling (15), which is the extent of over- or underwinding of the two strands in a DNA double helix. Specifically, it was shown that the buildup of positive supercoiling (DNA overtwisting) stalls transcription, and the addition of gyrase (which relaxes this supercoiling) leads to transcriptional bursts (14). The conclusions of this work are consistent with the hypothesis in the earlier rate-based theoretical model in (9), which suggested that the timescales observed in bacterial bursts are compatible with supercoiling-dependent initiation.

Here, we consider a stochastic model, which couples the dynamics of supercoiling and transcription in DNA (first introduced in (16)) and ask whether, and under which conditions, supercoiling may lead to transcriptional bursts. Our main result is that supercoiling can induce bursts in a wide range of parameter space. Perhaps surprisingly, bursts occur only when the overall transcriptional rate is low and are absent when it is high. When gene density is low (e.g., if we model a single gene), significant bursting is primarily found in the presence of topological enzymes, which relax supercoiling at a fixed rate. For higher gene density, highly significant bursts can also arise in the absence of topoisomerases through the action of a self-organized nonequilibrium regulatory network mediated by supercoiling. Intriguingly, this same pathway can also generate transcription waves and upregulate divergent transcription, both of which eventually disrupt the bursty behavior. A final key finding is that bursting leaves a detectable signature in the distribution of supercoiling at the promoter; it leads to a nonnormal distribution and the appearance of a singularity or small peak in the tails of the distribution. Observation of such signatures may be an aim of future experiments, along the lines of existing ones, performed either in vitro (14) or in vivo (17, 18).

Materials and Methods

Model

The key dynamical variable in our model is a one-dimensional scalar field σ(x,t), which denotes the local supercoiling density at a point x on the DNA. This is the local analog of the global supercoiling density, defined as (Lk−Lk₀)/Lk₀, where Lk is the linking number of a DNA molecule (which can be decomposed into twist and writhe (15)) and Lk₀ is the linking number of a torsionally relaxed B-DNA (i.e., 1 for every 10.5 base pairs [bps]). Because both Lk and Lk₀ can be defined for a segment of the DNA molecule, an analogous formula can be used to define σ locally; doing this is analogous to approximating writhe with a local field (19). The dynamics are then described in continuous space by

$$\frac{\partial \sigma \left(x,t\right)}{\partial t}=\frac{\partial }{\partial x}\left[D\frac{\partial }{\partial x}\sigma \left(x,t\right)-J_{\text{tr}}\left(x,t\right)\right]-k_{\text{topo}}\sigma \left(x,t\right),$$ (1)

where the three terms on the right-hand side represent diffusion of supercoiling, supercoiling flux generated by transcription, and supercoiling dissipation due to topological enzymes. Below, we will discuss each term in turn. Although we have written Eq. 1 as continuous in space, we solve it on a lattice of length L = 15 kbp with spacing Δx = 15 bp (which is approximately the footprint size of an RNAP).

If we consider a closed DNA loop, then in the absence of topological enzymes, the total level of supercoiling is conserved (it is a topological invariant of the system). Therefore, we require that supercoiling obeys “model B” (conserved) dynamics (20). Further, the free-energy density of supercoiling (twist and writhe) f is, to a good approximation, quadratic in the supercoiling density (15, 16); so the chemical potential $\left(\partial f/\partial \sigma \right)$ is linear in σ. Because the flux in model B dynamics is proportional to the gradient of the chemical potential, this results in a diffusion equation (when the mobility is constant) (16), giving the first term on the right of Eq. 1. Single-molecule measurements of the dynamics of plectonemic supercoils in vitro (21) and studies of transcription in vivo (22) are also consistent with a diffusive dynamics for supercoiling.

The second term in Eq. 1 represents supercoiling fluxes due to transcription. Through this term, we couple the supercoiling dynamics to stochastic transcriptional kinetics, where each of N RNAPs can bind at the promoters of n genes (each of size $\mathit{\lambda }=$ 66Δx ≈ 1000 bp) located at lattice positions y_j, j = 1, …, n. Transcription initiates stochastically when an inactive RNAP binds at gene j with rate k_{in, j}. The RNAP then elongates with velocity v (positive or negative depending on the direction of transcription) such that at a time t_i after initiating it is located at position $x_i\left(t_i\right)=y_j+v{t}_i$ (where the index i labels the RNAP). Transcription terminates (and the promoter becomes again available for initiation) once the RNAP reaches the end of a gene. The total flux is then given by

$$J_{\text{tr}}\left(x,t\right)=\sum _{i=1}^N{J}_i\left(t_i\right)\delta \left(x-x_i\left(t_i\right)\right){\eta }_i\left(t\right),$$ (2)

where the sum is over all RNAPs, $J_i\left(t_i\right)$ is the flux generated by RNAP i, and the function ${\eta }_i\left(t\right)$ represents its state, taking a value of zero if it is unbound and one if it is actively transcribing. The initiation dynamics is coupled back to the supercoiling by making k_{in, j} a function of the supercoiling at the promoter,

$$k_{\text{in},j}\left(t\right)=k_0\text{max}\left\{1-\alpha \sigma \left(x_j,t\right),0\right\},$$ (3)

where α is a coupling parameter (it represents the sensitivity of RNAP-DNA binding to the level of supercoiling).

According to the twin supercoiling domains model (23), a moving RNAP generates a supercoiling flux if its rotation is hindered because as the enzyme progresses, the DNA has to locally unwind. (The rotational drag on the RNAP in vivo is likely to be large in view of its size and of its interactions with other macromolecules). As a result, positive supercoiling is generated in front of the RNAP and negative supercoiling behind. More specifically, as the RNAP moves, all the DNA twist in front of it (minus any rotation of the RNAP if present) is pushed forward. This reasoning suggests that the flux generated will depend on the level of twist ahead of the RNAP, which might in principle vary (12). However, to obtain a tractable model, we assume the flux to be constant. In practice, this approximation is likely good because DNA can only support small levels of twist before writhing (24).

A final complication is that the diffusion of supercoils through the RNAP also requires its rotation; hence, we expect this effect to be small. We could prohibit flux through the RNAPs by introducing no-flux boundary conditions at the points x_i, but an alternative, which yields a more tractable model, is to instead ramp up the flux as transcription progresses; to do this we set

$$J_i\left(t_i\right)=J_0\left(1+\frac{\left|v\right|t_i}{\mathit{\Delta }x}\right).$$ (4)

The sign of J₀ depends on the direction of transcription. Any residual net diffusive leak only plays a minor role because it is small compared to J₀. (Additionally, a small leak of supercoiling may not be unrealistic even for a polymerase acting as a topological barrier for twist, if the region of DNA containing it writhes in three dimensions). In what follows, we define $\overline{J}=J_0\left[1+\lambda /\left(2\mathit{\Delta }x\right)\right]$; this is a useful quantity because it is the average value of the supercoiling flux generated during a transcription event.

The third term on the right of Eq. 1 represents the loss of supercoiling due to the action of topoisomerases (such as, e.g., topoI, topoII, gyrase). This is introduced in the model in a minimal way as a first-order reaction where both positive and negative supercoiling relax at the same rate $k_{\text{topo}}$. In general, this term does not conserve the total supercoiling; however, here, we start with a uniform initial condition $\sigma \left(x,t=0\right)\equiv {\sigma }_0$, where σ₀ = 0, so in this case, the total supercoiling is conserved.

This model was first described in (16). In that work, it was found that by increasing the ratio $\overline{J}/D$, there is a crossover from a relaxed regime in which transcription is virtually Poissonian to a supercoiling-regulated regime in which transcription of neighboring genes is highly correlated. In this work, we examine under what conditions the coupling between supercoiling and transcription can lead to bursty dynamics.

Key model quantities and parameter values

Key quantities that control the model behavior are the ratios $\overline{J}/D$ and k_topo/k₀. In the results section below, we will explore the ability of the model to exhibit bursty behavior at different points within the $\overline{J}/D$–k_topo/k₀ parameter space for different gene arrangement cases. Although the values that these quantities have in vivo have not yet been well characterized experimentally, here, we discuss what ranges of values might be relevant based on available evidence. For our simulations, we vary several parameters to get an understanding of how such a system might behave under different conditions.

The diffusion constant for supercoiling is difficult to measure, not least because one would expect very different values for twist and writhe. Intuitively, one would expect twist to diffuse very quickly (12), whereas writhe diffusion would be much slower because it requires more global DNA rearrangements. Also, it has been shown that DNA is unable to support much deviation of twist from its relaxed state: the theory in (24) (and the references therein) indicate that it will writhe if the supercoiling density exceeds 0.01. This suggests that the slower diffusion of writhe will dominate the dynamics. Single-molecule experiments presented in (21), which measured the motion of plectonemes in a stretched DNA molecule, indeed obtained a relatively small diffusion coefficient, with a value significantly less than 1 kbp²/s (see Fig. 3 F in (21)). Specifically, when a DNA molecule is subjected to tensions of less than 1–2 pN, plectoneme diffusivity is at most ∼0.1 kbp²/s. Taking this value and a typical size for a bacterial gene of λ ≈ 1 kbp, the time it takes for supercoiling to diffuse away from the promoter after transcription terminates is λ²/2D ≈ 5 s. In vivo, macromolecular crowding is likely to further slow down writhe/supercoiling diffusion, so for our simulations, we consider values for D that are between ∼4 and ∼40 times smaller than the value quoted above. Specifically, we consider D ≈ 2.25 × 10⁻² kbp²/s in Fig. 1 and D ≈ 2.25 × 10⁻³ kbp²/s in other figures. Both values allow the supercoiling generated during transcription of a gene to dissipate in at most minutes after transcription termination (the smaller value was used for the more systematic analyses because it enables more efficient simulations using a larger value for the time step).

Figure 3.

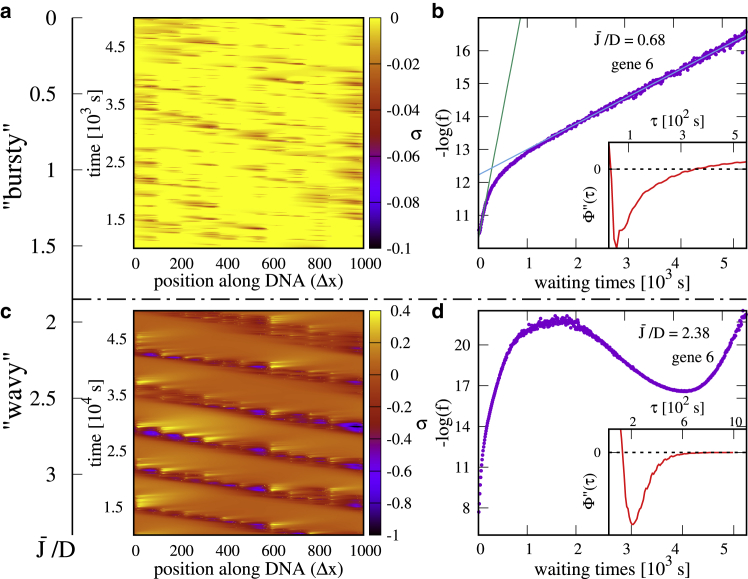
Bursty and wavy regimes for an array of 10 tandem genes. (a) A kymograph in the bursty regime $\left(\overline{J}/D=0.68\right)$ is shown. For clarity, we only show the negative supercoiling range. There are correlations between neighboring genes but no clear periodic pattern. Note that genes 1 and 10 turn red more often (compare to genomic map in Fig. 5a) because they are slightly upregulated. (b) A plot of the pdf of waiting times in the bursty regime, showing the emergence of two timescales is shown. The inset shows the second derivative of the ssf, which displays two zeros. (c) A kymograph in the supercoiling-regulated regime $\left(\overline{J}/D=2.38\right)$ is shown. For high values of the flux, the bursty dynamics are replaced by transcription waves. (d) The pdf of waiting times in the supercoiling-regulated regime is shown. The new timescale associated with the wave modifies the shape of the distribution, giving rise to a “bump” at ∼4 × 10³ s (local minimum in linear-log plot). The inset shows the second derivative of ssf. In the physically relevant range of waiting times ($\tau \mathrm{\lesssim }{10}^3$ s), the function asymptomatically approaches zero without crossing the axis $\left({\tau }_2\to +\infty \right)$.To see this figure in color, go online.

Figure 1.

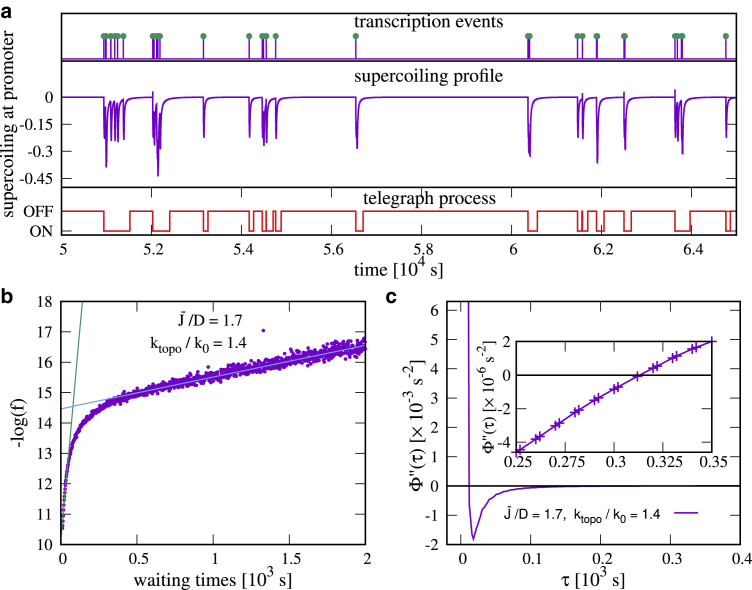
Transcriptional bursts and the sequence-size function (ssf). (a) A time series for a simulation with $\overline{J}/D=1.7$, k_topo/k₀ = 1.4., is shown. Transcription events (top) are often grouped in bursts. Transcription initiation depends on the level of supercoiling at the gene promoter (middle). The state of the system (bottom) is defined as OFF if ${\sigma }_p\ge \left(1-{\left(k_0{\tau }_2\right)}^{-1}\right)/\alpha$ and ON otherwise. (b) The negative logarithm of the pdf of waiting times is shown. The existence of two linear regions characterizes the dynamics as bursty. (c) The second derivative of the ssf is shown: the existence of roots at ${\tau }_1$ and ${\tau }_2$ demonstrates the presence of two timescales. The inset shows the zoom of the intersection of this second derivative with the x axis close to ${\tau }_2$. To see this figure in color, go online.

The typical RNAP velocity in bacteria is 100 bp/s (1), so that the time taken to transcribe a λ = 1 kbp gene is τ ∼ λ / ν ∼ 10 s. Then, through dimensional analysis, we expect an order-of-magnitude estimate for the $\overline{J}$ to be ∼ λ² / τ or νλ ∼ 0.1 kbp²/s; notably, this is the same order of magnitude as D. Thus, in our simulations, we explore a range of values for $\overline{J}/D$, which is typically between 0.34 and 3.4.

Turning now to the dynamics of transcription initiation, measured RNAP initiation rates can vary widely, and typical values are in the range 1 s⁻¹ to 1 h⁻¹ are observed (see (16, 25, 26, 27)). Likewise, the number of RNAPs has a large variability. For example, in the bacteria Escherichia coli, there are an estimated 1000–10,000 RNAPs per cell (28) and ∼5000 genes. To reflect this ratio, we take one RNAP per gene in our simulations unless otherwise stated (see Fig. S4). The rate of topoisomerase action in vivo is equally difficult to estimate. Reference (29) counts ∼500 topoisomerase I per cell in E. coli. Assuming that approximately half the enzymes are bound and that there are two genomes per cell on average, we arrive at ∼100 topoisomerase proteins bound per genome or 0.02 per gene. Assuming additionally that each enzyme can on average relax 1–10 supercoils per second (30) and that the baseline bacterial supercoiling is equal to $-0.05$, we get $k_{\text{topo}}\approx 0.005$–0.05 s⁻¹. We note this rough estimate is within the physiological value of the baseline transcriptional rate (in our simulations, $k_0$). Because of this and because the values of k_topo and k₀ are not known accurately, in our simulations, we have systematically varied their ratio k_topo/k₀ between 0 and 1.4. (Specifically we set $k_0=0.001$ s⁻¹ and varied k_topo.) In this way, we can examine all possible scenarios concerning the balance between initiation and topoisomerase relaxation rates.

To determine whether supercoiling can affect RNAP initiation at a promoter, we need to consider the time it takes for supercoiling generated by a previous transcription event to diffuse away and the typical initiation rate (k_{in, j} in our model). In (16), a mean field model was used to estimate the extent of residual supercoiling at the promoter, and this was given by

$$\left|{\sigma }_p\right|\simeq \frac{\overline{J}}{2D}{k}_0\tau .$$ (5)

If this quantity is larger than α⁻¹ (see Eq. 3 for the definition of α), then supercoiling can indeed increase the rate at which RNAP binds the promoter, leading to a positive feedback. Experiments in bacterial genes suggest that a supercoiling density of ${\sigma }_p\le -0.01$ is sufficient to enhance RNAP binding (see (16, 31, 32)), so in our simulations, we have set α = 100. These considerations explain why $\overline{J}/D$ and $k_{0}n\tau$ are key dimensionless quantities in our model.

In what follows, we give parameter values either in physical units or in terms of dimensionless ratios. When required, the physical values of all parameters can be reconstructed by referring back to this section. As noted above, to solve Eq. 1 numerically, we discretize space into a lattice with 15-bp spacing; we discretize time into steps of between 0.1 and 1 s, chosen to balance efficiency and numerical stability (which depends on the other parameters).

The sequence-size function

A classic model to describe transcriptional bursting is the interrupted Poisson process (33) (see Supporting Materials and Methods, Section SII), which describes transitions between an active (ON) and an inactive (OFF) state with Poissonian rates k_ON and k_OFF, as in a random telegraph process (8), together with transcription at a constant rate k_i while the system is in the ON state. The process can be characterized by the probability distribution function (pdf) f(t) of waiting times, the time intervals between two consecutive transcriptional events, which is given by a double exponential (33), where the two characteristic times are related to the interval between transcriptions in a single burst and the interval between two consecutive bursts (see Eqs. S10–S13).

To determine whether our system is bursty for a given set of parameters ($\overline{J}/D$ and k_topo/k₀), we measure the distribution f(t). We then analyze the so-called sequence-size function (ssf) (33, 34), which is defined in terms of f(t) as

$$\mathit{\Phi }\left(\tau \right)=\frac{1}{1-{\int }_0^{\tau }f\left(t\right)dt}.$$ (6)

This is the inverse of the probability of observing a waiting time larger than τ or, equivalently, the proportion of transcriptional event intervals that are longer than τ. If the dynamics are bursty, we expect two well-separated timescales for the decay of f(t); correspondingly, Φ will display a plateau and two inflection points. These points, ${\tau }_1$ and ${\tau }_2>{\tau }_1$, can be found as the zeros in the second derivative of Φ; these values also approximate the two timescales for f(t) (this is not a strict equality but rather an order-of-magnitude estimate). The value of Φ in the middle of the plateau, ($\mathit{\Phi }\left({\tau }_x\right)=\left(\mathit{\Phi }\left({\tau }_1\right)+\mathit{\Phi }\left({\tau }_2\right)\right)/2$), then yields the average number of transcriptional events in a burst or burst size, β (33). If the dynamics are not bursty, Φ will have no more than one inflection point. An analysis of f(t) and Φ(t) shows that these criteria work qualitatively well for our model. For sufficiently large values of k_topo, we find that the dynamics are indeed bursty (Fig. 1): f(t) has two characteristic timescales (Fig. 1 b), and $\mathit{\Phi }\left(\tau \right)$ has two well-defined inflection points (Fig. 1 c). For small k_topo and high values of the flux, there are no well-defined timescales in f(t) or inflection points in $\mathit{\Phi }\left(\tau \right)$; inspection of the transcriptional dynamics show this is not bursty (see Fig. S3 c).

To quantify the burstiness of a transcriptional time series, we define the following parameter,

$$\mathit{\xi }=\frac{{\mathit{\Phi }}^{\prime }\left({\tau }_1\right)-{\mathit{\Phi }}^{\prime }\left({\tau }_2\right)}{{\mathit{\Phi }}^{\prime }\left({\tau }_1\right)},$$ (7)

which measures the area under ${\mathit{\Phi }}^{″}\left(\tau \right)$ between the two inflection points (when they exist), normalized by ${\mathit{\Phi }}^{\prime }\left({\tau }_1\right)$ so that the result remains between 0 and 1 (prime and double prime denote the first and second derivatives, respectively). ξ is zero when the dynamics are not bursty and increases as the separation between the two characteristic timescales ${\tau }_1$ and ${\tau }_2$ becomes clearer: we refer to this parameter as the burst significance.

Results and Discussion

A single gene

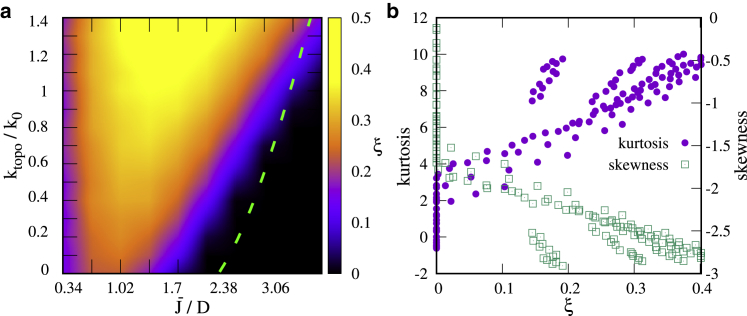
We first consider the case of a single gene. By computing ξ from simulations with different values of $\overline{J}/D$ and k_topo/k₀, we find two distinct regimes (Fig. 2 a): the nonbursty regime, identified by ξ = 0, and the bursty regime, for ξ > 0 (a mean field theory gives a good prediction of the boundary between the two). In the most significant region ($k_{\text{topo}}/k_0\sim 1.4$, $\overline{J}/D\sim 1.5$), the burst size is between 2 and 3, close to that measured in E. coli in vivo (6). Estimates of the other bursts parameters (i.e., burst duration and OFF-state duration) are given in Supporting Materials and Methods (Section SIII) and are also in good agreement with experimental results (6, 14). However, we note that the burst size depends on the model parameters: the system can produce bursts of significantly more than two to three events (at most ∼10 on average in our simulations). However, this only occurs in the transition region between the nonbursty and bursty regimes (see Fig. S2 a). In this transition region, burst significance is smaller, which means that the separation between timescales is less marked.

Figure 2.

Burstiness for a single gene. (a) A phase diagram shows the burst significance as a function of model parameters. A nonbursty regime is indicated by ξ = 0 (black), whereas ξ > 0 indicates a bursty regime (yellow-red). The dashed green line is the boundary predicted via mean field (see Supporting Materials and Methods, Section SI). (b) Non-Gaussian parameters of the distribution of the supercoiling at the promoter ${\sigma }_p$ as a function of ξ, for different values of $\overline{J}/D$ and k_topo/k₀ are shown. The kurtosis (skewness) is correlated (anticorrelated) with ξ. To see this figure in color, go online.

The results in Fig. 2 a also show that when the positive feedback between supercoil generation and transcription initiation is strong (for large $\overline{J}/D$ and k_topo = 0, identified as the supercoiling-regulated regime of (16)), the dynamics are never bursty; bursts are most significant when this feedback is much weaker (but nonzero). The reason for this seemingly surprising result is that if supercoiling upregulates transcription too much, the gene is essentially always on and the transcriptionally silent state is absent (see Fig. S3 c).

Our results show that topoisomerase action favors burstiness. In other words, although the dynamics can be bursty for k_topo = 0, burst significance is larger when k_topo $\ne$ 0.

Since bursting is generally due to switching back and forth between two transiently stable states, it is natural to ask whether there are any signatures of bistability in the stochastic transcriptional process we simulate. As we show in Fig. 2 b, one such signature can be obtained from moments of the distribution of supercoiling at the promoter σ_p. For nonbursty behavior, σ_p exhibits close-to-Gaussian fluctuations about an average value (see Fig. S3 b). For bursty transcription, this distribution is more markedly non-Gaussian and bistable (see Fig. S3 a). Quantitatively, burst significance correlates with the magnitude of non-Gaussianity parameters such as kurtosis and skewness (Fig. 2 b; Fig. S3).

Multiple genes

The single-gene case considered above is an important starting point for our model and could be relevant to the experimental investigation in (6), where the transcription of a gene on a bacterial plasmid was monitored. However, it is also of interest to consider the case of multiple genes. This is because gene density is variable both across organisms and within genomes: for instance, in both yeast and bacteria, gene density is high so that transcription is likely to affect neighboring genes. This is also relevant for understanding synthetic DNA constructs containing multiple genes, which can be used in biotechnology applications. In this section, we study the burstiness in arrays of multiple genes without topoisomerases (i.e., k_topo = 0).

In Fig. 3, we consider the supercoiling-coupled transcriptional dynamics within an array of genes, which have the same orientation (we refer to these as “tandem” genes). We find that bursts are typically more significant than in the single-gene case. For instance, for $\overline{J}/D=1$ and $k_{topo}=0$, the single-gene case was only weakly bursty (ξ ≈ 0.23, burst size β ≈ 1.53, and duration T ≈100 s (see Fig. S2)), whereas for an array of 10 tandem genes, the same parameters give rise to bursting, which is approximately twice as significant (ξ ≈ 0.4−0.5 for the most bursty genes, burst size β ≈ 2, and duration T ≈ 3–4 min (see Fig. S7)). This is because transcription generates positive supercoils ahead of a gene, which act to downregulate its downstream (right) neighbor (while upregulating the upstream [left] neighbor). As a result, some genes may be transiently “switched off”; this can be appreciated, for instance, by inspecting the time series of supercoiling at the promoter, which at times can take sufficiently positive values such that $k_{\text{in}}\left(t\right)=0$, see Fig. S5 a. Just as in the case of a single gene with $k_{\text{topo}}\ne 0$, the activity of each gene is effectively described by a two-state dynamics (ON$\leftrightarrow$OFF), and bursts can occur (Fig. 3 a). As expected, the pdf of waiting times is well described by a double exponential (see Fig. 3 b) and ${\mathit{\Phi }}^{″}\left(\tau \right)$ displays two zeros (Fig. 3 b, inset).

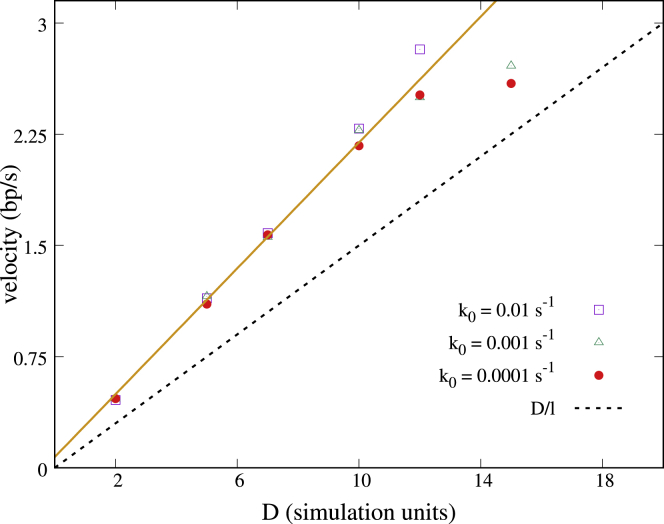
As for the single-gene case, in the multigene system, bursting does not occur for large values of $\overline{J}/D$. In this regime, the supercoiling-mediated intergenic interactions instead give rise to transcription waves, which travel in the opposite direction to transcription (Fig. 3, c and d). Transcription waves arise because transcription of a gene upregulates its upstream (left) neighbor (16): as a consequence, transcription of gene i is followed by that of gene i−1, then i−2, and so on. We find that the wave velocity is v ∼ D/l, independent of $k_0$ (Fig. 4, inset; l = 100Δx is the mean separation between promoters in our simulations). Given our parameter choice, the wave speed is between 0.5 and 3.0 bp/s, and the time needed to trigger activity of the neighboring upstream gene is between 6 and 12 min. The scaling of v can be understood by assuming that supercoiling propagates diffusively over the distance l between a gene, and its upstream-neighbor; simulation show that the prefactor in this relationship is slightly larger than one. When in the “wavy” regime, the system can no longer be mapped onto a telegraph-like process, and bursts are no longer observed (accordingly, $\xi =0$ because $\mathit{\Phi }\left(t\right)$ does not have two inflection points; see Fig. 3 d).

Figure 4.

Wave velocity and scaling relation. Wave velocity for different values of D$\left(\overline{J}=25.5\right)$ and k₀ so that we span a large range of $\overline{J}/D$ values between 1.7 and 12.7. Values of D are given in simulation units (i.e., in units of $\mathit{\Delta }{x}^2/\mathit{\Delta }t$). Simulation data are well fitted by a straight line (orange), whereas the simple scaling theory discussed in the text underestimates the data slightly (dashed black line). To see this figure in color, go online.

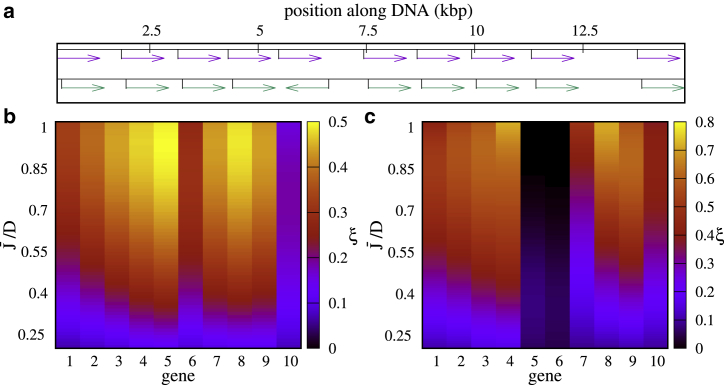
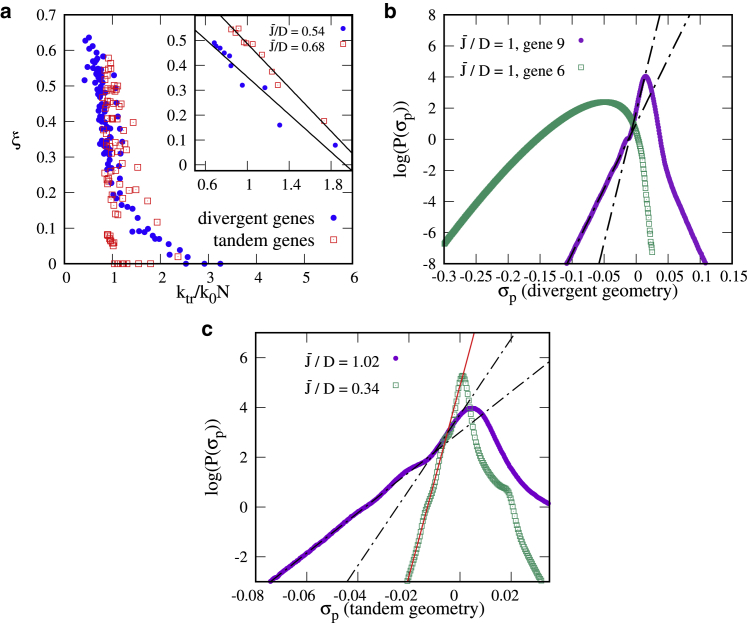
Transcription waves only arise for arrays of tandem genes and do not occur (or do so only transiently) for genes of differing orientation. In that case, transcription-generated supercoiling upregulates pairs of divergent genes at the expense of other (convergent or tandem) genes, which are downregulated (16): this renders the situation qualitatively closer to that of a single gene (see Supporting Materials and Methods, Section SIV). For either kind of gene orientation, burstiness is gene dependent, and the values of ξ for different genes are substantially different from each other (Fig. 5). Note that even for small $\overline{J}/D$, some genes are slightly upregulated than others (as shown in the kymograph in Fig. 3 a) because of the particular position in the array. We find that ξ is anticorrelated with the overall transcription rate so that the genes that are expressed more (e.g., genes 1, 6, and 10 in the tandem setup or genes 5 and 6 in the divergent setup; see Figs. 5 a, S6, and S9 a) are less bursty (Fig. 6 a). Burst size is also different in the tandem and bidirectional setups, being substantially smaller in the latter case ($\beta \mathrm{\lesssim }$ 2; see Fig. S7 a). Burst sizes measured experimentally in E. Coli (6) are closer to the value for single or tandem genes $\left(\beta \simeq 2.2\right)$; this is reasonable because they refer to the transcription of operons, which are normally made up from tandem genes controlled by a single promoter.

Figure 5.

Burstiness for a multiple-gene array. (a) A map of gene positions for tandem (top) and divergent geometry (bottom) is shown. (b and c) A plot of ξ for tandem geometry (b) and divergent geometry (c) (geometries used are in a) is shown. The range of $\overline{J}/D$ (0.06–1.02) is chosen so that the system is in the bursty regime. To see this figure in color, go online.

Figure 6.

Bursty and wavy regimes for an array of 10 tandem genes. (a) The burstiness, ξ, is plotted for a different value of the overall time-averaged transcription rate k_tr for tandem (red squares) and bidirectional (blue circles) genes (each point represents a gene; points are shown for different values of $\overline{J}/D$ between 0.06 and 1.02). The inset shows that for a given value of $\overline{J}/D$, ξ depends linearly on k_tr (each point represents a gene). (b) A log-linear plot of the distribution of σ_p is shown. For bursty genes (gene 9, which is not part of the divergent pair), this distribution shows a singularity or bump. Such a singularity does not appear for highly transcribed genes (gene 6, in the divergent pair). (c) For a given gene (gene 4, tandem geometry), the slope of the negative tail of the distribution depends on $\overline{J}/D$. For small ξ (small $\overline{J}/D$), the bump disappears. To see this figure in color, go online.

An analysis of the distribution of supercoiling values at the promoter shows that these differ qualitatively for the cases of multiple genes and a single gene (e.g., compare Fig. 6 with Fig. S3). Unlike in the single-gene case, the non-Gaussian parameters for the distribution of supercoiling at the promoter now only weakly correlate with the burst significance (see Fig. S8). This is because the supercoiling-mediated interaction between genes give rise to non-Gaussian fluctuations even for nonbursty genes. Nevertheless, for both the tandem and divergent gene cases, bursting leaves a detectable signature in the tails of the distribution.

For the bursty transcription case, there is a singularity or a bump, whereas for nonbursty transcription, the curve is smooth, as shown in Fig. 6 b for a divergent geometry and in Fig. 6 c for a tandem array. The singular point is located at ${\sigma }_p\approx \left(1-{\left(k_0{\tau }_x\right)}^{-1}\right)/\alpha$, where ${\tau }_x=\left({\tau }_1+{\tau }_2\right)/2$. We note that similar changes in the behavior of large fluctuations were linked to phase transitions in other systems (35, 36).

Conclusions

In summary, we have studied the occurrence of transcriptional bursts in a nonequilibrium model for supercoiling-regulated transcription, first introduced in (16). For an isolated gene, we found that significant bursting occurs primarily in the presence of topological enzymes, which relax positive and negative supercoiling. This is qualitatively consistent with experimental evidence that bursts in E. coli arise because of the action of the DNA gyrase enzyme, which can relax positive supercoiling (14). It is interesting to note that in the region of parameter space where bursts are most significant, the properties of the bursts generated in the model (size, duration, and interburst time) match well with those found in bacteria in vivo (6). Notably, topoisomerase action is not required for highly significant bursting in gene clusters because there, supercoiling can mediate transient inhibition of the neighbors of highly active genes. We considered both tandem and bidirectional gene geometries, which could be recreated synthetically using plasmids of selected sequence in the presence of the transcriptional machinery. We found that the existence of bursting is intimately linked to the nature of fluctuations of supercoiling at gene promoters: bursting becomes most significant when these are strongly non-Gaussian. It would be of interest to look for such effects in experiments with populations of synthetic DNA loops for which psoralen binding (17, 18) might, in principle, be used to monitor averages and distributions of supercoiling along the DNA.

Although additional ingredients may be required to understand transcriptional bursts in eukaryotes, in which stochastic promoter-enhancer interactions or other regulatory processes are known to play a key role (2, 13, 37), our current results uncover a possible mechanism for transcriptional bursts in bacteria based on the interplay between transcription initiation, supercoiling, and topological enzymes. Our results are consistent with the work in (9), which identified supercoiling as one potential mechanism for bursting based on the comparison between experimental data and a simplified kinetic model; in our case, we consider a full stochastic dynamics for supercoiling and elucidate the role of topoisomerases. As discussed in the Introduction, a related study (12) instead analyzed the interplay between supercoiling and transcriptional elongation, providing a complementary mechanism to the one identified here; that model may be particularly relevant for the case of ribosomal genes for which expression is extremely high, whereas our work concerns more moderate expression for which there is not significantly more than one polymerase transcribing the same gene at once.

Author Contributions

M.A., A.B., C.A.B., G.G., and D.M. designed research. M.A. and A.B. performed simulations. M.A. analyzed data. M.A., A.B., C.A.B., G.G., and D.M. wrote the article.

Editor: Andrew Spakowitz.