Applications of Molecular Dynamics Simulation in Structure Prediction of Peptides and Proteins

Abstract

Compared with rapid accumulation of protein sequences from high-throughput DNA sequencing, obtaining experimental 3D structures of proteins is still much more difficult, making protein structure prediction (PSP) potentially very useful. Currently, a vast majority of PSP efforts are based on data mining of known sequences, structures and their relationships (informatics-based). However, if closely related template is not available, these methods are usually much less reliable than experiments. They may also be problematic in predicting the structures of naturally occurring or designed peptides. On the other hand, physics-based methods including molecular dynamics (MD) can utilize our understanding of detailed atomic interactions determining biomolecular structures. In this mini-review, we show that all-atom MD can predict structures of cyclic peptides and other peptide foldamers with accuracy similar to experiments. Then, some notable successes in reproducing experimental 3D structures of small proteins through MD simulations (some with replica-exchange) of the folding were summarized. We also describe advancements of MD-based refinement of structure models, and the integration of limited experimental or bioinformatics data into MD-based structure modeling.

1. Introduction

Three-dimensional (3D) structures of proteins and their complexes provide invaluable information, not only for understanding the molecular basis of the machinery of life, but also for screening and designing of new drugs for medical applications [1]. Since the first protein 3D structure (of myoglobin) was solved by X-ray crystallography sixty years ago [2,3], enormous efforts have been paid for protein structure determinations [[4], [5], [6], [7], [8], [9]]. However, to obtain high-resolution structure of a protein experimentally is still quite expensive and time-consuming. On the other hand, the cost of obtaining new protein sequences has dramatically decreased due to significant progresses in high-throughput DNA sequencing technology [10,11]. Therefore, there is a huge and increasing gap between the numbers of known structures and sequences. Thus, protein structure prediction (PSP) has become a cost-effective and high-throughput way to provide structure information for biological and pharmaceutical researches.

Various methods for PSP have been developed, which can generally be classified into two types: template-based modeling (TBM) and de novo structure prediction. TBM predicts the native structure of a protein target by identifying known protein structure(s) as template(s) [12], based on sequence-sequence (homology modeling) or sequence-structure (threading) alignments. Without suitable template, de novo PSP (template-free modeling) can be used to predict novel protein fold. The most popular and successful ones are usually based on assembly of known structure fragments with potential energy (scoring) functions from mining know protein structures (such as Rosetta [13,14] and QUARK [15]). Also, inter-residue contacts inferred from co-evolutionary signals in sequence homologs can significantly facilitate the de novo PSP [16,17]. The predicted protein models can span a broad range of accuracies and are potentially suitable for different applications [18].

All above popular PSP methods require certain database(s) of sequences and structures, which are thus called knowledge-based. However, the fundamental theory supporting PSP is that the 3D structure of a native-state protein in physiological condition is encoded in its amino acid sequence, as its lowest-free-energy conformation [19,20]. Thus, in theory, PSP can be achieved with only an accurate energy function with a proper conformational search method. Most popular conformational search methods include Monte Carlo (MC) and molecular dynamics (MD). MC approach has been successfully used to study the folding of peptides and proteins, using either atomistic models [[21], [22], [23]] or more coarse-grained models [[24], [25], [26], [27], [28]]. It has also been used to predict protein loop structures [29]. In theory, MC methods can be as accurate as MD methods, but MC may suffer from lower efficiency when using fine-grained representation of the system, especially with large number of explicit solvent molecules. There is also a danger of biasing the sampling when using MC.

MD simulation methods have a long history. The method was originally developed about sixty years ago, for theoretical physicists to study systems of many interacting particles (such as atoms or atom groups) under classical mechanics [30,31]. The now-dominant version of MD was also soon established [32], which numerically solves classical equations of motion according to physical force on each particle. Because small integration time steps of femtoseconds (10^-15 s) are usually necessary for all-atom simulations, to simulate biologically-relevant event (such as protein folding on > microseconds, 10^-6 s) by MD requires a huge number of numeric calculations. Over the past 40 years, the timescales that can be reached by atomistic MD simulation are increasing rapidly, even faster than the Moore's law [33,34]. Now, MD simulations have become an important and pervasive physics-based method to explore the conformational space of peptides and proteins, which can even fold small proteins (<80 amino acids) to their native structures [35].

Here we review applications of MD simulation in ab initio structure prediction of peptides and small proteins, refinement of protein structure models, as well as structure modeling assisted by experimental or bioinformatics data. However, we will not review following research areas traditionally not regarded as a PSP problem, although they are somehow related to structure prediction and heavily relying on MD simulations:

• 1.MD simulation has been extensively used in studying the conformational dynamics of proteins, for a long time [36]. This can be regarded as the prediction of an ensemble of structures for a protein in the native state [37]. However, this type of MD studies rely on known (representative or average) structure of a protein.
• 2.Some proteins or protein segments do not fold to ordered structures in the native condition [38]. The prediction of structure ensembles of intrinsically disordered proteins is very important, and MD simulation also plays a very important role [39].

Of course, we cannot cover all related works in this mini-review, but intended to give some representative examples about the topic of MD-based structure prediction of peptides and proteins.

2. Methodology Developments for MD Simulation

Since the first protein MD simulation in 1977 [36], with rapidly developing computing hardware and software, significantly longer simulation times and larger simulated systems can be achieved. Supercomputers have been built for biomolecular MD simulations such as protein folding [40]. Software packages for highly efficient MD simulations on parallel computing architectures have also been developed [41,42]. Using special-purpose supercomputer Anton [43], all-atom MD simulation reaching millisecond time-scale has been reported in 2010 [44]. Recently, the most exciting progress is the development of software for routine use of graphic processing unit (GPU) for MD simulations [[45], [46], [47]]. Now, MD simulation is becoming a powerful tool extensively used in studying biomolecular systems. Currently, a few hundred nanoseconds (ns) per day can be routinely achieved on a small protein system in explicit solvent.

In an MD simulation, forces are often calculated using a potential energy function (force field) of the system, which is crucial to the reliability of the MD simulation. A protein force field contains terms for both bonded (for bond lengths, bond angles, and dihedral angles) and non-bonded interactions (van der Waals and electrostatics). It has relatively simple mathematical formula, but usually contain many empirical parameters that determine its accuracy. With increasing computational performance and development of enhanced sampling methods (will be described below), more and more inaccuracies in protein force fields have been revealed [48,49].

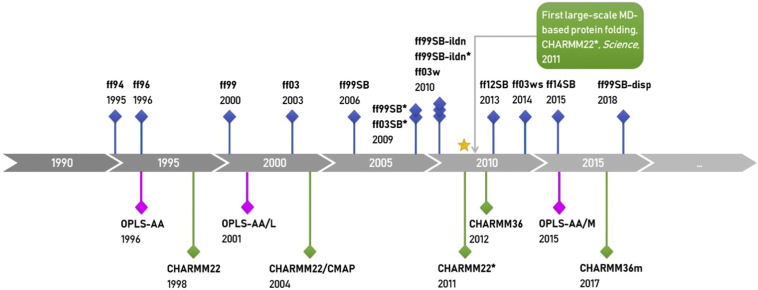
These findings have been continuously spurring improvements of classical protein force fields, including AMBER [[50], [51], [52], [53]], CHARMM [[54], [55], [56], [57]], and OPLS-AA [[58], [59], [60]]. Most of the recent updates have been focused on the parameters of backbone and/or side-chain dihedral-angle (torsion) terms to fit ab initio quantum mechanics calculations or experimental (especially NMR) observables, because these parameters are closely related to the conformational behavior of simulated peptide or protein.

Water molecules plays a crucial role in driving protein folding [61], and determining the structure and dynamics of protein molecules [62]. Water models like TIP3P [63] and TIP4P [63] developed in the early 1980s have been able to accurately describe the various physicochemical properties of water at room temperature, and are still widely used in MD. In these explicit-solvent simulations, a vast majority of the computational resources are consumed in calculating forces on water molecules. To increase efficiency, methods to treat water solvent implicitly have been developed, mostly based on the Generalized Born (GB) solvation model [[64], [65], [66]]. Sometimes, an energy term related to solvent-accessible surface areas (SA) was used for approximating the non-polar contributions to solvation [64].

Besides the accuracy and reliability of force field (including solvent model), another important factor severely limits the applications of MD: the time scale that can be easily achieved by a conventional MD simulation is usually much shorter than those related to real problems. Thus, enhanced sampling methods have been developed. Some use biased potential to force barrier crossing on pre-defined reaction coordinates (collective variables), such as umbrella sampling [67] and metadynamics [68]. However, these methods can hardly be used in actual structure prediction because the end point of folding should be unknown. Thus, enhanced sampling methods using energy as a reaction coordinate were developed, including biased potential methods such as accelerated molecular dynamics [69], generalized ensemble methods such as replica-exchange molecular dynamics (REMD) [70], and methods combining the two aspects [71]. Currently, the REMD method becomes the most popular one for ab initio folding, partly because it can utilize current main-stream multi-node parallel computing architectures very efficiently. In addition, replica-exchange method can also be used with MC simulation, which has been used in I-TASSER [72] structure prediction pipeline by Zhang’s group to facilitate the fragment assembly and conformational search.

3. Peptide Structure Prediction

Peptides fill the gap between small-molecule drugs and proteins, and potentially can have both their advantages [73]. Numerous peptides have been found in natural products, and some of them have become drugs with great biological functional diversity. Still, millions of peptide sequences are estimated occurring in prokaryotic genomes [74], plants [75], venom in eukaryotes [76,77] and there are even larger sequence space for designed peptides as chemical tools and drug leads [[78], [79], [80], [81]]. Because the function of a peptides is always related to its unique conformational behavior [82,83], accurate peptide structure prediction (PepSP) would contribute significantly to the peptide-based drug design.

Many attempts have been made for developing PepSP, including evaluations of some common PSP methods (Rosetta, I-TASSER) and specific development of PepSP methods (PepLook, Pep-Fold). However, these methods often cannot consistently predict the experimental structures of peptides. For example, Rosetta cannot reproduce the experimental structure of an α-conotoxin [84]. Peplook, Pep-Fold and I-Tasser predicted a set of 38 cyclic peptides consisting of 5-30 residues with average backbone RMSD (root-mean-square deviation from corresponding experimental structure) values of 3.8 Å, 4.1Å and 2.5 Å, respectively [85]. At the same time, solvent effect has been found very important for conformations of peptides [83,86], which can be treated explicitly in MD simulation, and the configuration entropy can be considered. In addition, a peptide in solution can have distinct conformations [87,88] with small free energy difference, bringing high demand on the accuracy of the energy function and solvent model.

For many naturally occurring or designed peptides, MD-based methods can be very suitable for predicting their 3D structures. Firstly, alignment of short sequences may be less reliable, hindering the use of comparative modeling techniques for PepSP [89]. Secondly, structures of short peptides are usually highly sensitive to their exact sequences, small variations may cause massive conformational alterations [90]. Third, compared with proteins, converged conformational sampling of small peptides can be much more easily achieved by MD simulations, especially with enhanced sampling methods.

Dill and coworkers studied the structure prediction of peptide fragments using REMD simulations with implicit solvent [91,92]. For 133 8-residue fragments from six different proteins, 85 of them have no preferred structure, while the structures of 41 out of 48 structured peptides bear some resemblance to their native structures [91]. Most linear peptides do not have a stable structure that can be determined by experiments, making it very difficult to benchmark PepSP methods on them. Still, there are some designed foldable linear peptides, including β-peptides [93,94], that can be folded by MD simulations two decades ago.

Cyclization of linear peptides, either by backbone or side-chain linkages, can achieve much lower conformational flexibility [95,96] and better drug-like properties, which are attracting more and more attentions. Because availability of their experimental structures (especially X-ray crystal structures) and resemblance to protein loops, we think that cyclic peptides (CPs) are much better candidate for benchmarking structure prediction methods, compared with linear peptides.

REMD simulations using AMBER ff96 with GBSA implicit solvent were performed to 18 cyclic RGD peptides [97], showing agreements between the simulated and experimental inter-proton distances. Among them, the predicted structure of cilengitide (5 residues) have 0.25 Å backbone-RMSD to its crystal structure bound to integrin. A structure prediction study of peptoid [98] shows, REMD simulation using generalized AMBER force field (GAFF) [99] with implicit solvation, combing a quantum mechanical refinement, correctly predicted the X-ray crystallographic structures of a N-aryl peptoid trimer and a cyclic peptoid nonamer to the accuracy of 0.2 Å and 1.0 Å RMSDs, respectively.

Recently, MD simulations using explicit solvent models have become more and more widely used. REMD simulation of Vasopressin and Oxytocin (peptide hormones cyclized by disulfide bond) and their mutants were performed [100], and the resulted structural ensembles were validated against experimental NMR chemical shifts and ³J_HαHN scalar couplings. In 2016, Lin and coworkers investigated the ability of MD with bias-exchange metadynamics (BE-META) to predict the structure of a cyclic octapeptide [101]. Representative structures of five most commonly populated states from simulations with four different force fields gave RMSD ranging from 1.11 Å to 1.88 Å to the NMR structure.

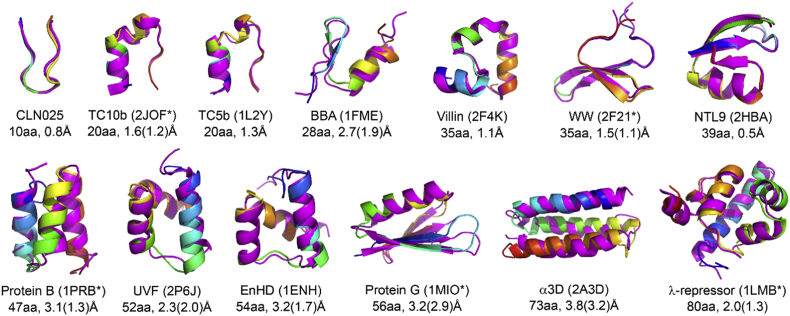
Recently, we simulated 20 all-trans CPs of 5-12 residues using explicit-water REMD with four different force fields: AMBER ff99SB –ILDN, OPLS-AA/L, RSFF1, and RSFF2 [102,103]. Our recently developed RSFF2 [104] force field performs the best (Fig. 3), which can predict the crystal structures of 17 out of these 20 CPs with backbone RMSD < 1.1 Å, and 8 CPs with backbone RMSD < 0.5Å. Metadynamics with RSFF2 was used recently by Lin and coworkers to study sequence–structure relationships of some simple cyclic hexapeptides [90], and design well-structured cyclic pentapeptides [105]. REMD with RSFF2 has also been used to study α-helical stapled peptides, together with GAFF to describe the non-standard amino acids, giving prediction in excellent agreements with experimental observations [[106], [107], [108]]. In one case with X-ray crystal structure solved, the predicted structure is almost identical to experimental one (RMSD of 0.3Å). (See Fig. 1, Fig. 2).

Fig. 3.

Large-scale folding simulations reported in 2014 [137], using REMD with explicit solvent model. Experimental and predicted (center of the most populated cluster) structures are shown in magenta and rainbow color, respectively. PDB ID for each protein is given in parentheses with a star indicating a close variant was used. The number of amino acid (aa) residues and the Cα-RMSD (value in parenthesis is without a few terminal residues) of each predicted structure are also given.

Fig. 1.

Developments of the variants of the three most popular all-atom protein force fields: AMBER, CHARMM, and OPLS-AA.

Fig. 2.

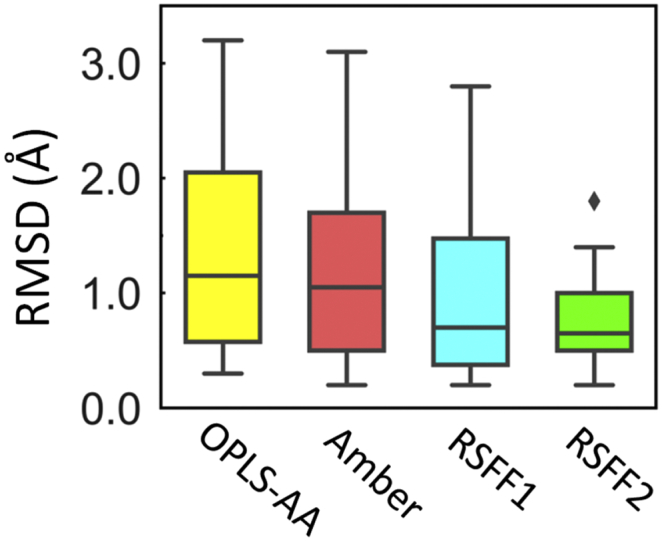
Statistics (box plots) of the backbone RMSD values between predicted structures from REMD simulations with various force fields and their X-ray crystal structures of 20 all-trans CPs of 5-12 residues.

However, in spite of good conformational sampling and advanced force fields, MD simulation still cannot accurately predict peptide structures in all cases. Very recently, it was shown that the cis/trans isomerization of N-methylated cyclic hexapeptides cannot be reliably predicted [109]. Recently, simulation of guanylin (a 15-residue peptide with four cysteines) showed that the distribution of three disulfide-bond isomers is in qualitative agreement with experiment, but the most stable conformation of the isomer 2 is significantly different from the poorly ordered structure of the truncated peptide [110]. In another study, BE-META simulations were performed on five cyclic isoDGR-containing α/β-peptides using eight widely used force fields with explicit water to reproduce 79 NMR observables [111]. Most of the force fields display good agreement with experimental ³J_(HN,Hα), but poor agreement was observed for NMR observables directly related to β-amino acids. In addition, accelerated MD simulations of three CPs were performed to predict their conformations [112], and benchmarked against inter-proton distances from NMR experiments and X-ray structures, revealing discrepancy between calculations and experimental observations. These studies are showing that MD-based PepSP can be a very good approach to evaluate force fields.

4. Ab Initio Protein Folding

As early as in 1975, Levitt & Warshel reported the folding simulation of a small protein (bovine pancreatic trypsin inhibitor) from fully extended conformation to RMSD of 5.3 Å, using a very simple model (two particles per residue) [113]. Limited by computational resource, energy minimization and normal-mode thermalisation were used instead of MD. Since then, there were numerous computational studies of folding and tertiary structure prediction of peptides and proteins, mostly using simplified protein models with Monte Carlo methods [114]. At early time, the direct atomistic MD simulation of folding has been impractical.

With increasing time resolution of experiments, people began to realize that some ultrafast folding proteins (with 20 ~ 106 residues) can fold on the time scale of a few μs [115]. This encourage the use MD simulation to study protein folding. In 1998, using a massively parallel supercomputer, a simulation of the folding of 36-residue villin headpiece subdomain (villin HP-36) in explicit water was performed for 1 μs [116]. Collapsed structures with native-like secondary structures were observed, and the RMSD of the representative structure is 5.7 Å. In 1999, Takada et al. reported successful folding of an artificial three-helix-bundle protein (54 residues) using overdamped Langevin dynamics (an MD version usually for implicit-solvent coarse-gained simulations) [117]. A simplified model of 3~4 particles per residue allowed trajectories up to 1 microsecond (μs). Soon later, a naturally occurring three-helix-bundle protein was folded from random-coil structures to RMSD of ~ 3 Å within 1 μs, by similar method [118].

Since 2000, successful atomistic folding simulations of some miniproteins in implicit solvent were reported, including: 20-residue three-stranded β-sheet Beta3s [119], 16-residue C-terminal β-hairpin from protein G [120], 23-residue BBA5 with ββα structure [121,122], 20-residue α-helical Trp-cage [123]. Besides, 35-residue villin HP [124], 10-residue chignolin [125], and 46-residue α-helical fragment B of protein A [126] were successfully folded using explicit solvent. Plain MD or REMD were used in these works, but other enhanced sampling methods can also be used. For example, accelerated MD has been used to fold four fast-folding proteins (chignolin, Trp-cage, villin HP, and WW domain) [127].

Besides, more efficient discrete molecular dynamics (DMD) simulation can be performed based on stepwise potentials with implicit solvation [128]. Using replica-exchange DMD, six small proteins (20–60 residues) with diverse native structures have been successfully folded [129]. For the smallest three (Trp-cage, villin HP, WW domain), predictions of RMSDs between 2~3 Å can be achieved. However, we do not see wide spread use of DMD in folding studies, possibly due to using less realistic physics model.

One approach to surmount the time scale barrier is to construct Markov state models (MSMs) using many different MD trajectories. It has been successfully used for all-atom ab initio folding of small systems such as the villin HP-35, for which the most populated state has an average RMSD of 2.3Å [130]. Combining thousands of MD simulations with explicit solvent (each trajectory up to 1 μs, totally 1.3 ms), an atomistic model of the folding of an 80-residue fragment of the λ repressor was obtained to capture dynamics on a 10 milliseconds time scale [131]. Using Folding@Home distributed computing platform [132], ∼3000 unfolded-initiated trajectories of implicit-solvent MD were generated for 39-residue protein NTL-9 with an experimental folding time of ∼1.5 ms, two trajectories reached RMSD < 3.5 Å [133]. An alternative method is Milestoning [134,135], developed by Elber and coworkers. Milestoning samples slow processes by coarse graining conformational space and performing large numbers of short simulations, yielding kinetics and pathways. However, these methods are too expensive to be applied in practical ab initio structure prediction, although very useful for folding mechanism studies.

With increasing computing power and force field improvements, simultaneously folding simulations of more proteins have been reported. Using special purpose computer Anton, Lindorff-Larsen et al. reported the first successful large-scale folding simulation [35]. Eleven proteins of 10~80 residues were reversibly folded to RMSD < 3.6 Å using the CHARMM22* force field in explicit water. Using REMD with our RSFF1 [136] force field, we also folded all these 11 proteins to RMSD < 3.8 Å, along with the Trp-cage TC5b and wild-type engrailed homeodomain (EnHD) [137] (Fig. 3). By analyzing continuous trajectories tracking every replica exchange, we also found that REMD can increase the folding rate by about 6 times, through significantly (> 10² times in most cases) increases the diffusion rate on rough energy landscape. Using inexpensive GPUs and implicit solvent model (~1 μs/day can be achieved), Simmerling and coworkers reported successful folding for 16 of 17 proteins (10–92 residues) with a variety of secondary structures and topologies, although the native conformations may not be thermodynamically preferred [138].

Although ultrafast folding proteins are relatively rare, a considerable fraction of protein domains can fold within time scale of milliseconds [139,140]. Using Anton machine, Piana et al. performed eight one-millisecond (1 ms) MD simulations of ubiquitin (a very common 76-residue protein) in explicit water [141]. Starting from the folded structure, spontaneously unfolding to RMSDs of > 20Å and refolding to Cα RMSDs of 0.5 Å was observed. However, no folding events were observed in the two simulations initiated in the unfolded state, which is understandable since the estimated folding time is about 3 ms.

From above, it is clear that atomistic MD simulation of folding can be used for ab initio PSP, but it is still quite expensive and do not have significant advantage compared with fragment-assembly and MC-based methods in real PSP application. Instead, it is often used to study the folding mechanism, which is also scientifically very important. However, when using coarse-gained force field (such as UNRES [142]), much more efficient conformational sampling can be achieved and larger protein can be folded, even in real ab initio PSP, rather than reproducing known structures. Especially, UNRES model with REMD simulation outperformed bioinformatics methods on predicting the correct topology of target T0663 (about 200 residues) in the CASP10 without any input from template or experiment [143,144].

5. Protein Structure Refinement

Currently, various informatics-based PSP methods have been developed. Usually, MD-based methods are not necessary, even when a detectable template is not available. However, currently predicted protein models are often much less accurate compared with experiments, limiting their usage in some important applications including structure-based drug design [18,145]. Thus, structure refinement from low-accuracy models to high-accurate ones is very important, although it is also a very difficult challenge [146]. A crucial motivation for developing physics-based refinement methods is that if the limits of informatics-based methods were being reached, utilizing physics was essential to finally have modeling methods that rival experiment.

In 2000, refinement using explicit-solvent MD simulations that employ the locally enhanced sampling (LES) was applied to low-resolution model of a small disulfide-rich 29-residue protein CMTI-1, and improvement from 3.7 Å to 2.5 Å was reported [147]. Explicit-solvent MD simulation of Rosetta models (of 36-mer HP-36 and 65-mer S15) was also used to generate structures for subsequent ranking using the MM-PBSA free energy function [148], and structures with RMSD < 1.5 Å can be sampled. However, a systematic study (in 2001) on 12 small, single-domain proteins failed to observe successful refinement [149]. On a set of 20 proteins, explicit-solvent MD simulations of most proteins moved initial model structures further away from their native conformations, with performances worse than energy minimization using implicit-solvent potentials [150]. Several studies reveal the importance of proper scoring functions to select more native-like ones among structures sampled during MD [[151], [152], [153]], because the percentage of more native-like (improved) structures is usually <50% and may decrease as refinement progress.

Restraints can be applied to focus the conformational sampling on the vicinity of the initial model. In 2007, Chen & Brooks performed implicit-solvent REMD simulations with distance restraints between Cα atoms on five protein models, and significantly refinements were observed on three of them [154]. Later, Feig & coworkers [155,156] made significant progress, using restrained explicit-solvent MD and special structure selection and averaging protocol assisted by a statistical potential (DFIRE [157]). Their method ranked the first in the model refinement category of CASP10 [146]. Lee’s group also developed a refinement protocol based on a series of short (5 ns in total) explicit-solvent MD simulations with weak positional and distance restraints [158]. Recently, the combination of restrained MD simulations with accurate force fields is clearly useful and has been adopted by most top-ranking groups in the CASP12 refinement challenge [159]. However, the top-ranking groups are relatively conservative, yielding structures that are quite close to the initial ones.

Shaw and colleagues found that their CHARMM22* force field, which can fold a diverse set of small proteins, may not stabilize the experimental structure of a protein in long-time MD simulations, and good refinement can hardly be achieved [160]. Thus, the success of structure refinement highly relies on the force field accuracy. We recently evaluated the applicability of RSFF1 in protein structure refinement [161]. For 30 single-domain proteins from CASP8-10 refinement targets with diverse structures and a large C_α RMSD coverage of 1-9 Å, MD simulations (380 K) with weak C_α position restraints gave best structures with RMSD reduced by -0.85 Å on average. Using long-time REMD simulations with RSFF1, two homology models (TR614 and TR624) with initial RMSD > 5 Å, can be improved to RMSD < 3 Å. Results from CASP12 indicate that our approach is adventurous, and can provide significantly refined models for some targets (such as TR866, TR894 and TR944) but performs modestly overall.

6. Data-assisted Modeling

As described above, applications of MD in both ab initio structure prediction and model refinement [162] suffer from two interrelated challenges: insufficient conformational sampling and inaccurate force field. However, limited amounts of structural information can accelerate MD-based structure determination and may also improve simulation accuracy [163]. Meanwhile, experimental techniques have been developed to provide limited (low-resolution, sparse, ambiguous, or uncertain) structure information in a relatively short time and low cost, and bioinformatics techniques have also been developed to predict structure information including secondary structures and residue-residue contacts. Data-assisted modeling has become a sub-category of the CASP experiments since CASP11 (2014) [164].

It has been a long history to use data from known protein structures to guide MD folding simulation and structure prediction. In 1989, Friedrichs and Wolynes proposed the “associative memory Hamiltonians” (AMH) [165], which can learn structure features from a set of memory proteins. With the incorporation of homologous protein(s) in the memory set and certain information based on secondary structure prediction, near-native structures of a 111-residue protein (rice cytochrome c) can be obtained starting from random structures using simulated annealing MD with a simplified model [166]. With AMH constructed from a database of non-homologous proteins, several α-helical proteins [167] and α/β proteins [168] can be folded to near-native structures (4–8 Å) using MD-based simulated annealing. Further improvements were made by the same group, especially the incorporation of water-mediated interactions [169]. After years of developments, a coarse-grained protein force field called AWSEM (associative memory, water mediated, structure and energy model) was established, which incorporates local structure biasing from fragments with known structures and similar sequences [170]. However, it seems not to be superior to popular fragment-assembly-based de novo PSP methods. Recently, a new scheme called AAWSEM (atomistic associative memory, water mediated, structure and energy model) has been developed [171]. It is an ab initio PSP method that starts from the ground up without using bioinformatics input.

MD-based methods have also been developed to incorporate distance distribution derived from the SAXS experiment as restraints, including the use of coarse-grained force field [172]. Restraints from various paramagnetic NMR experiments (including pseudo-contact shifts, residual dipolar couplings, paramagnetic relaxation enhancement, and cross-correlated relaxation) can be incorporated in computer modeling of protein 3D atomic structures, but substantial challenges remain before wide spread use [173].

Chemical crosslinking mass spectrometry (XL-MS) can provide information about residue-pairs in close proximity that can be incorporated into modeling, although the data may be spares and of low-resolution. Replica-exchange DMD simulations using the Medusa potential with distance restraints from XL-MS experiments gave lowest-energy models of 2.7 Å and 5.4 Å for FK506-binding protein and myoglobin, respectively [174]. MD simulations of a large number of proteins can also be used to find appropriate distance constraint from investigating Lys side-chain motions [175].

Dill and coworkers developed a method called Modeling Employing Limited Data (MELD) that can harness problematic experimental or theoretical data in a Bayesian framework to assist physics-based structure modeling [176,177], which can use a variety of sampling methods obeying detailed balance but implicit-solvent REMD is a good choice. Using loose physical insights (such as proteins have hydrophobic cores and secondary structures), MD simulations of protein folding can be speed up by two ~ five orders of magnitude [178]. Therefore, the MELD method can also be used for ab initio PSP, and structures of three proteins (with 97, 67, 68 residues, respectively) from CASP targets can be predicted blindly with RMSD of 2.8 Å , 1.4 Å, 1.5 Å from native structures, respectively [179].

Besides altering the potential energy function in MD, an iterative screening-after-sampling strategy can be used [180]. By selecting conformations that better fit with the low-resolution data from each cycle of MD simulations, high-quality atomic model can be achieved.

7. Summary

With rapid increasing of computer performance, as well as continuous software and force field developments, MD simulation has been increasingly used in studying biomolecular systems. In principle, it can describe the underline physics of detailed atomic interactions determining a protein structure, and potentially be more accurate than knowledge-based PSP methods. In this mini-review, we showed that all-atom MD simulations can predict structures of cyclic peptides and other peptide-based foldamers with accuracy similar to experiments. Then, we summarized some notable successes in reproducing experimental 3D structures of small proteins through ab initio folding simulations. We also described recent advancements of using MD simulations with state-of-the-art force fields in improving structure models from bioinformatics-based PSP, which is one of the most useful for real-word applications. Finally, some methodology developments and applications of using limited experimental or theoretical data to guide MD-based structure modeling were also introduced. We feel that, in the future, more sophisticated and integrative methods will be developed, including those combining different levels of structure representation (multi-scale MD simulations) and those utilizing the power of machine learning (to take advantage of large amount of data generated by MD) [181].

Declaration of Competing Interest

The authors claim no conflict of interest.