Dopaminergic medication reduces striatal sensitivity to negative outcomes in Parkinson’s disease

McCoy et al. show that dopaminergic medication in Parkinson’s disease leads to changes in striatal signalling and in behaviour during learning, but that changes are specific to the processing of negative reinforcements. These within-patient changes are predictive of changes in future value-based choice behaviour and striatal responses.

Abstract

Reduced levels of dopamine in Parkinson’s disease contribute to changes in learning, resulting from the loss of midbrain neurons that transmit a dopaminergic teaching signal to the striatum. Dopamine medication used by patients with Parkinson’s disease has previously been linked to behavioural changes during learning as well as to adjustments in value-based decision-making after learning. To date, however, little is known about the specific relationship between dopaminergic medication-driven differences during learning and subsequent changes in approach/avoidance tendencies in individual patients. Twenty-four Parkinson’s disease patients ON and OFF dopaminergic medication and 24 healthy controls subjects underwent functional MRI while performing a probabilistic reinforcement learning experiment. During learning, dopaminergic medication reduced an overemphasis on negative outcomes. Medication reduced negative (but not positive) outcome learning rates, while concurrent striatal blood oxygen level-dependent responses showed reduced prediction error sensitivity. Medication-induced shifts in negative learning rates were predictive of changes in approach/avoidance choice patterns after learning, and these changes were accompanied by systematic striatal blood oxygen level-dependent response alterations. These findings elucidate the role of dopamine-driven learning differences in Parkinson’s disease, and show how these changes during learning impact subsequent value-based decision-making.

Introduction

Learning from trial and error is a core adaptive mechanism in behaviour (Packard et al., 1989; Glimcher, 2002). This learning process is driven by reward prediction errors (RPEs) that signal the difference between expected and actual outcomes (Houk, 1995; Montague et al., 1996; Schultz et al., 1997). Substantia nigra and ventral tegmental area (VTA) midbrain neurons use bursts and dips in dopaminergic signalling to relay positive and negative RPEs to prefrontal cortex (Deniau et al., 1980; Swanson, 1982) and the striatum, activating the so-called Go and NoGo pathways (Beckstead et al., 1979; Surmeier et al., 2007).

Parkinson’s disease is caused by a substantial loss of dopaminergic neurons in the substantia nigra (Edwards et al., 2008), leading to the depletion of dopamine in the striatum (Koller and Melamed, 2007). Dopaminergic medication has been shown to alter how Parkinson’s disease patients learn from feedback (Cools et al., 2001; Bódi et al., 2009) and how they use past learning to make value-based choices in novel situations (Frank et al., 2004; Frank, 2007; Shiner et al., 2012). A common finding is that, when required to make value-based decisions after learning, patients ON compared to OFF medication are better at choosing the option associated with the highest value (approach), whereas when OFF medication, they are better at avoiding the option with the lowest value (avoidance) (Frank et al., 2004; Frank, 2007). However, it is currently unknown how dopamine-induced changes during the learning process relate to these subsequent dopamine-induced changes in approach/avoidance choice behaviour.

An influential framework of dopamine function in the basal ganglia proposes that the dynamic range of phasic dopamine modulation in the striatum, in combination with tonic baseline dopamine levels, gives rise to the medication differences observed in Parkinson’s disease (Frank, 2005). This theory suggests that lower baseline dopamine levels in unmedicated Parkinson’s disease are favourable for the upregulation of the NoGo pathway, leading to an emphasis on learning from negative outcomes. In contrast, higher tonic dopamine levels in medicated Parkinson’s disease lead to continued suppression of the NoGo pathway, resulting in (erroneous) response perseveration even after negative feedback. Extremes in these medication-induced changes in brain signalling are thought to manifest behaviourally in dopamine dysregulation syndrome, in which patients exhibit compulsive tendencies, such as pathological gambling or shopping (Voon et al., 2010). In support of the theory on Go/NoGo signalling, impairments in learning performance associated with higher dopamine levels have been found mainly in negative-outcome contexts; during probabilistic selection (Frank et al., 2004), reversal learning (Cools et al., 2006), and probabilistic classification (Bódi et al., 2009).

In addition to these behavioural adaptations, increased striatal activations have been reported in medicated Parkinson’s disease patients during the processing of negative RPEs (Voon et al., 2010). Similarly, a recent study on rats performing a reversal learning task revealed a distinct impairment in the processing of negative RPE with increased dopamine level (Verharen et al., 2018). However, little is known about how these medication-related changes in striatal responsivity to RPE relate to (i) later behavioural choice patterns; and (ii) changes in brain activity during subsequent value-based choices.

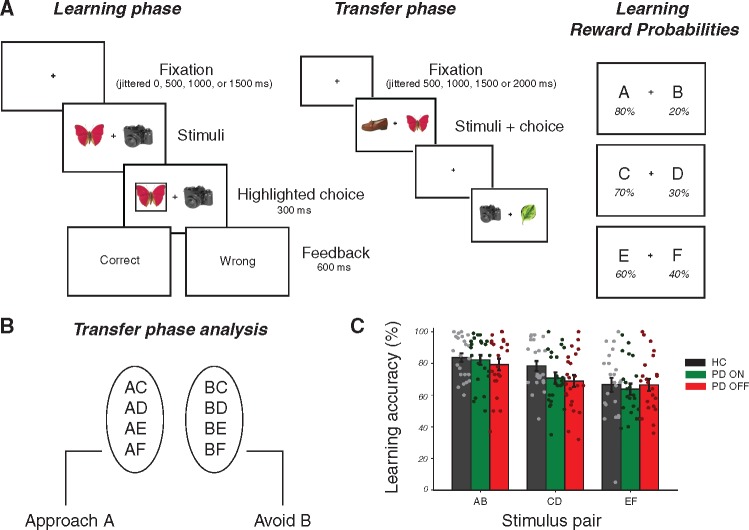
We examined the role of dopaminergic medication in choice behaviour and associated brain mechanisms. Twenty-four Parkinson’s disease patients ON and OFF medication and a reference group of 24 age-matched control subjects performed a two-stage probabilistic selection task (Frank et al., 2004) (Fig. 1A) while undergoing functional MRI. The experiment’s first stage was a learning phase, during which participants gradually learned to make better choices for three fixed pairs of stimulus options, based on reward feedback. In the second, transfer stage, participants used their learning phase experience to guide choices when presented with novel combinations of options, without receiving any further feedback (Fig. 1A). Value-based decisions during the transfer phase were examined using an approach/avoidance framework (Fig. 1B). To better describe the underlying processes that contribute to learning, behavioural responses were fit using a hierarchical Bayesian reinforcement learning model (Jahfari et al., 2018; Van Slooten et al., 2018), adapted to estimate both within-patient effects of medication and across-subject effects of disease (Sharp et al., 2016). This quantification of behaviour then informed our model-based functional MRI analysis, in which we examined medication-related changes in blood oxygen level-dependent (BOLD) brain signals in response to RPEs during learning, as well as medication-related changes in approach/avoidance behaviour and brain responses during subsequent value-based choices.

Figure 1.

Experimental design and learning performance. (A) Learning phase: in each trial participants chose between two everyday objects and observed a probabilistic outcome ‘correct’ or ‘wrong’, corresponding to winning 10 cents or nothing. Each participant viewed three fixed pairs of stimuli (AB, CD, and EF) and tried to learn which was the best option of each pair, based on the feedback received. Reward probability contingency per stimulus during learning is shown on the right. Transfer phase: participants were presented with all possible combinations of stimuli from the learning phase and had to choose what they thought was the better option, based on what they had learned. No feedback was provided in this phase. (B) The transfer phase analysis was performed on correctly choosing A on trials in which A was paired with another stimulus (approach accuracy) or correctly avoiding B on trials where B was paired with another stimulus (avoidance accuracy). (C) Accuracy in choosing the better option of each pair across each group during learning (mean ±1 SEM). Parameter estimates of these medication and disease effects are presented in Supplementary Fig. 1. HC = healthy controls; PD = Parkinson’s disease.

Materials and methods

Participants

Twenty-four patients with Parkinson’s disease (seven females, mean age = 63 ± 8.2 years old) were recruited via the VU medical center, Zaans medical center, and OLVG hospital in Amsterdam. All patients were diagnosed by a neurologist as having idiopathic Parkinson’s disease according to the UK Parkinson’s Disease Society Brain Bank criteria. This study was approved by the Medical Ethical Review committee (METc) of the VU Medical Center, Amsterdam. Twenty-four age-matched control subjects (nine females, mean age = 60.3 ± 8.5 years old) were also recruited from the local community or via the Parkinson’s disease patients (e.g. spouses, relatives). In total, five spouses of Parkinson’s disease patients were included in the control sample. At each session of the study, the severity of clinical symptoms was assessed according to the Hoehn and Yahr rating scale (Hoehn and Yahr, 1967) and the motor part of the Unified Parkinson’s Disease Rating Scale (UPDRS III; Fahn et al., 1987). Demographic and clinical data of the included participants can be seen in Supplementary Table 1. Information on Parkinson-related medication per patient is available in Supplementary Table 2. We excluded one patient with Parkinson’s disease (excessive falling asleep in scanner) and one control subject (could not learn the task) from both learning and transfer phase behavioural and functional MRI analyses. Functional MRI data of one control subject could not be analysed (T₁ scan was not collected; session was terminated early because of claustrophobia). Transfer phase functional MRI and behavioural data were not collected for one other control subject because of early termination of scanning session (technical malfunction). Overall, we included 23 Parkinson’s disease patients ON and OFF dopaminergic medication in all behavioural and functional MRI analyses. Twenty-three control subjects were included in the learning phase behavioural analysis, 22 in the learning phase functional MRI analysis, and 21 in the transfer phase behavioural and functional MRI analyses. Additional participant information is provided in the Supplementary material.

Procedure

The study was set up as a dopaminergic manipulation, within-subject design in Parkinson’s disease patients, to reduce the variance associated with interindividual differences. All Parkinson’s disease patients and control subjects took part in at least two sessions, the first of which was always a neuropsychological examination (lasting 2 h; 30 min of which were spent practicing the reinforcement learning task with basic-shape stimuli). Parkinson’s disease patients subsequently participated in two separate functional MRI scanning sessions (once in a dopamine-medicated ‘ON’ state and once in a lower dopamine ‘OFF’ state), and control subjects underwent one functional MRI session. The patient functional MRI sessions were carried out over the same weekend in all but one patient (2 weeks apart) and were counterbalanced for ON/OFF medication order. All OFF sessions had to be carried out in the morning for ethical reasons. Patients were instructed to withhold from taking their usual dopamine medication dosage on the evening prior to and the morning of the OFF session, thereby allowing >12 h withdrawal at the time of scanning. Patients on dopamine-agonists (pramipexole, ropinerol) took their final dopamine-agonist dose on the morning prior to the day of scanning (∼24-h withdrawal). One Parkinson’s disease patient took his medication 8.5 h before OFF day scanning to relieve symptoms but was nevertheless included in the analysis.

Neuropsychological assessment

Participants completed a battery of neuropsychological tests on their first visit. A description of these tests and self-report questionnaires, along with group results, is included in Supplementary Table 1. All patients used their dopaminergic medication as usual during this session. These assessments were not examined in the current study, but are discussed in greater detail elsewhere (Engels et al., 2018a, b).

Reinforcement learning task

Participants completed a probabilistic selection reinforcement learning task consisting of two stages; a learning phase and transfer phase. This task has been used in several previous studies, in both Parkinson’s disease patients (Frank et al., 2004; Shiner et al., 2012; Grogan et al., 2017) and healthy participants (Jocham et al., 2011; Jahfari et al., 2018; Van Slooten et al., 2018). We used pictures of everyday objects from different object categories, such as hats, cameras, and leaves (stimulus set extracted from Konkle et al., 2010).

Learning phase

In the learning phase, three different pairs of object stimuli (denoted as AB, CD and EF) were repeatedly presented in random order. Each pair had specific reward probabilities associated with each stimulus, and participants had to learn to choose the best option of each pair based on the feedback provided (Fig. 1A). Participants were instructed to try to find the better option of a pair in order to maximize reward. Feedback was either ‘Goed’ or ‘Fout’ text (meaning ‘correct’ or ‘wrong’ in Dutch), indicating a payout of 10 cents for correct trials and nothing for incorrect trials. Different objects were used across each functional MRI session of patients, so as not to induce any familiarity or reward associations with particular stimuli. In the ‘easiest’ AB pair, the probability of receiving reward was 80% for the A stimulus and 20% for the B stimulus, with ratios of 70:30 for CD and 60:40 for EF. The EF pair was therefore the hardest to learn because of more similar reward probabilities between the two options. All object stimuli were counterbalanced for reward probability pair and for better versus worse option of a pair across subjects (for instance, a leaf and hat as the A and B stimuli for one participant were the D and C stimuli for another participant). In total, there were 12 object stimuli and each participant viewed six of these objects in a given functional MRI session, with Parkinson’s disease patients viewing the remaining six stimuli in their second functional MRI session. The learning phase consisted of two runs of 150 trials each (totalling 100 trials per stimulus pair). Each run was interspersed with 15 null trials to improve model fitting of this rapid event-related functional MRI design. Null trials, during which only the fixation cross was presented, lasted at least 4 s plus an additional interval generated randomly from an exponential distribution with a mean of 2 s. Each task trial had a fixed duration of 5000 ms, and began with a jittered interval of 0, 500, 1000, or 1500 ms to obtain an interpolated temporal resolution of 500 ms. During the interval, a black fixation cross was presented and participants were asked to hold fixation. Two objects were then presented simultaneously left and right of the fixation cross (counterbalanced across left/right locations per pair) and remained on the screen until a response was made. If a response was given on time, a black frame surrounding the chosen object was shown (300 ms) and followed by feedback (600 ms). Omissions were followed by the text ‘te langzaam’ (‘too slow’ in Dutch). The fixation cross was displayed alone after feedback was presented, until the full trial duration was reached.

Transfer phase

In the transfer phase, novel pairings of all possible combinations of the six stimuli were presented in addition to the original three stimulus pairs, thereby making up 15 possible pairings. This phase consisted of two runs of 120 trials each (eight trials per pair), and each run randomly interspersed with 12 null trials. The duration of these null trials was generated in the same way as in the learning phase. Participants were instructed to choose what they thought was the better option, given what they had learned. There was no feedback in this phase and no frame surrounded the chosen response. Each trial began with a jittered interval of 500, 1000, 1500 or 2000 ms, with a new trial starting whenever a response was made.

Learning and transfer

Each object stimulus was presented equally often on the left or right side in both learning and transfer phases. Responses were made with the right hand, using the index or middle finger to choose the left or right stimulus, respectively. One patient was uncomfortable using two fingers of the right hand and so responded with the left and right index finger on separate button boxes (in both ON and OFF sessions). The feedback text was made larger for one patient in both ON and OFF sessions to make it easier to read.

Computational model

The Q-learning reinforcement learning algorithm (Sutton and Barto, 1998) captures trial-by-trial updates in the expected value of options and has been used extensively to model behaviour during learning (Daw et al., 2011; Jocham et al., 2011; Schmidt et al., 2014; Grogan et al., 2017; Jahfari et al., 2018). We used a variant of this model with three free parameters, allowing us to determine how subjects learned separately from positive and negative feedback (α_gain and α_loss) and how much they exploited differences in value between stimulus pair options (β). In hierarchical models, group and individual parameter distributions are fit simultaneously and constrain each other, leading to greater statistical power over standard non-hierarchical methods (Ahn et al., 2011; Steingroever et al., 2013; Wiecki et al., 2013; Kruschke, 2015; Jahfari et al., 2018). We also fit two additional models, one model with only one learning rate for any outcome event, and another model with an additional free parameter, relating to persistence of choices irrespective of feedback. We then performed model comparison, allowing us to verify that the chosen model better represented the data (Supplementary Table 3). These models were performed using R (R Development Core and Team, 2017) and RStan.

Subject-level Q-learning model

The Q-learning algorithm assumes that after receiving feedback on a given trial, subjects update their expected value of the chosen stimulus (Q_chosen) based on the difference between the reward received for choosing that stimulus (r = 1 or 0 for reward or no reward, respectively) and their prior expected value of that stimulus, according to the following equation:

$$Q_{\mathit{chosen}}\left(t+1\right)=\mathrm{\hspace{0.5em}}{Q}_{\mathit{chosen}}\left(t\right)+\{\begin{array}{c}{\alpha }_{\mathit{gain}}[r\left(t\right)-Q_{\mathit{chosen}}\left(t\right)],\hspace{1em}\mathit{if}\mathrm{\hspace{0.5em}}r=1\\ {\alpha }_{\mathit{loss}}[r\left(t\right)-Q_{\mathit{chosen}}t)],\hspace{1em}\mathit{if}\hspace{0.5em}r=0\end{array}$$ (1)

The term $\mathit{r}\left(t\right)-Q_{\mathit{chosen}}\left(t\right)$ is the reward prediction error (RPE). Accordingly, choices followed by positive feedback (r = 1) were weighted by the α_gain learning rate parameter and choices followed by negative feedback (r = 0) were weighted by the α_loss learning rate parameter (0 < α_gain, α_loss<1). All Q-values were initialized at 0.5 (no initial bias in value). The probability of choosing one stimulus over another is described by the softmax rule:

$$P_{\mathit{chosen}}\left(t\right)=\frac{\hspace{0.5em}\text{exp}\hspace{0.5em}\left(\beta \times Q_{\mathit{chosen}}\left(t\right)\right)}{\hspace{0.5em}\text{exp}\hspace{0.5em}\left(\beta \times Q_{\mathit{unchosen}}\left(t\right)\right)+\hspace{0.5em}\text{exp}\hspace{0.5em}\left(\beta \times Q_{\mathit{chosen}}\left(t\right)\right)}$$ (2)

where β is known as the inverse temperature or ‘explore-exploit’ parameter (0 < β < 100). Effectively, β is used as a weighting on the difference in value between the two options. The free parameters α_gain, α_loss and β were fit for each individual subject, in a combination that maximizes the probability of the actual choices made by the subject.

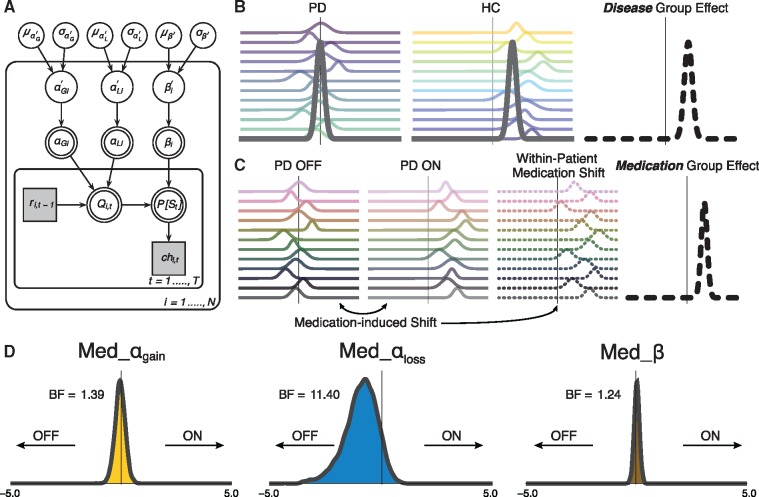
Figure 2A shows a graphical representation of the model. The free parameters α_gain and α_loss are labelled as α_G and α_L for viewing purposes, respectively. The quantities r_{i, t−1}–(reward for participant i on trial t–1) and ch_i,t (choice for participant i on trial t) are obtained directly from the data. The subject-level quantities α_Gi, α_Li and β_i are deterministic, and were transformed during estimation using the inverse probit (phi) transformation Z′_i (α′_Gi, α′_Li, β^′_i), which is the cumulative distribution function of a unit normal distribution. An prime symbol attached to parameters indicates that a phi transformation was applied to these parameters. The transformed parameters have no prime symbol. The parameters Z′_i (i.e. α′_Gi, α′_Li, β^′_i) lie on the probit scale covering the entire real line. In this way, transformed parameters were obtained by applying an inverse probit transformation to normally-distributed priors centred on zero, with a standard deviation (SD) of 1, e.g. ${\mu }_{\alpha \text{'}G}\hspace{0.5em}$∼ N (0,1). Weakly informative priors such as these are recommended in small sample sizes to reduce the influence of the priors on posterior distributions (Gelman et al., 2013; Ahn et al., 2017). This guarantees that the converted priors will be uniformly distributed between 0 and 1 (Wetzels et al., 2010; Ahn et al., 2014, 2017). The calculation for the transformed β parameter included a multiplicative factor of 100 in the same step as the transformation to allow for a range between 0 and 100. Following recommendations from the Stan development team (2016) we used non-centred reparameterization to reduce the dependency between μ_z′, δ_z′ and Z′_i when for example, moving from α′_Gi to α_Gi with the phi transformation [see below for elaboration, or Ahn et al. (2017) for more examples with non-centred reparameterization]. Stan provides a fast approximation of the inverse probit transformation with the Phi_approx function.

Figure 2.

Modelling approach and medication-driven parameter shifts in Parkinson’s disease. (A) Graphical outline of the Bayesian hierarchical Q-learning model with three free parameters, i.e. α_gain (denoted here as α_G), α_loss (denoted here as α_L) and β. The prime symbol attached to these parameters indicates that an inverse probit (phi) transformation was applied to the parameters (refer to the ‘Materials and methods’ section for description). The model consists of an outer subject (i = 1, …, N, including P = 1, …, N_PD, and h = 1, …, N_HC), and an inner trial plane (t = 1, …, T). Nodes represent variables of interest. Arrows are used to indicate dependencies between variables. Double borders indicate deterministic variables. Continuous variables are denoted with circular nodes, and discrete variables with square nodes. Observed variables are shaded in grey. Per subject and session, r_i,t−1 is the reward received on the previous trial of a particular option pair, Q_i,t is the current expected value of a particular stimulus, and P[S_t] is the probability of choosing a particular stimulus in the current trial. On top of the three-parameter Q-learning model, dummy variables were defined in accordance with Sharp et al. (2016) to capture group-level disease-related differences in learning (denoted as: Dis_α_gain, Dis_α_loss, Dis_β), and within-subject medication differences (Med_α_gain, Med_α_loss, Med_β). (B) Graphical cartoon for the comparison of Parkinson’s disease to control subjects in an illustrative Dis parameter. (C) Demonstration of the within-subject comparison of Parkinson’s disease OFF to Parkinson’s disease ON, resulting in both a subject-level and group-level posterior medication shift in an illustrative Med parameter. Refer to the ‘Materials and methods’ section for a detailed description of the model with these subject/group difference parameters and definition of priors and transformations. (D) Group-level posteriors for medication shift in Parkinson’s disease during the learning phase, for all parameters. A leftward shift in the Med_α_loss distribution indicates greater learning from negative outcomes in Parkinson’s disease OFF compared to ON. HC = healthy controls; PD = Parkinson’s disease.

Group-level Q-learning model

The subject-level model described above was nested inside a group-level model in a hierarchical manner (Ahn et al., 2017). Parameters Z′_i were drawn from group-level normal distributions with mean μ_z′ and standard deviation δ_z′. A normal prior was assigned to group-level means μ_z′∼N(0,1), and a half-Cauchy prior to the group-level standard deviations δ_z′∼Cauchy(0,5). The model was extended in two ways in accordance with Sharp et al. (2016). To capture medication-related shifts (Parkinson’s disease ON versus OFF) in each of the three parameters, we included three additional parameters on both the subject level and on the group level (Fig. 2C and D). Similarly, we incorporated three additional parameters to capture disease-related differences (control subjects versus Parkinson’s disease) on the group level.

For the α_gain parameters, these were: Med_α_G′p (for the effect of medication on α_gain in Parkinson’s disease patient p) and Dis_α_G′h (for the effect of no disease on α_gain in control participant h), with the analogous terms for α_loss (Med_α_L′p and Dis_α_L′h) and β (Med_β′p and Dis_β′h). Symmetric boundaries for all phi transformed Med and Dis parameter distributions were used to constrain the model and assist with convergence (−5 < Med, Dis < 5). These boundaries were adopted from recent work with a similar hierarchical Bayesian parameter approach (Pedersen et al., 2016). Prior to committing to these bounds we evaluated two alternative bounds for these parameters, with either −1 < Med, Dis < 1 or −10 < Med, Dis < 10. The [−1,1] bounds were found to be too conservative, as posterior distributions were cut off at boundary values. In contrast, the [−10,10] bounds were overly liberal, as the distributions were well-contained within the [−5,5] interval. Group-level priors were the same as those on the subject-level, i.e. a normal prior was assigned to the group-level means of all the Med and Dis free parameters, e.g. Med_${\mu }_{\alpha \text{'}\mathrm{G}}$ ∼ N (0,1), and a half-Cauchy prior was applied to all group-level standard deviations, e.g. Med_${\mathrm{\sigma }}_{\alpha \text{'}G}$ ∼ Cauchy (0,5).

We took Parkinson’s disease OFF as ‘baseline’ by using two binary indicators: $I\left(\text{'}o{n}^{\text{'}}\right)$ = 0, and $I\left(\text{'}\mathit{health}{y}^{\text{'}}\right)$ = 0. Parkinson’s disease ON was coded as $I\left(\text{'}o{n}^{\text{'}}\right)$ = 1, $I\left(\text{'}\mathit{health}{y}^{\text{'}}\right)$ = 0, and control subjects was coded as $I\left(\text{'}o{n}^{\text{'}}\right)$ = 0, $I\left(\text{'}\mathit{health}{y}^{\text{'}}\right)$ = 1. For subject s and medication condition m, the phi transformed α_gain parameter (denoted as $\alpha G$ below) of an individual subject was formulated as follows:

$${\alpha G}_{s,m}={\mathit{Phi}}_{\mathit{approx}}\left({\mu }_{\alpha G}+\left({\sigma }_{\alpha G}\times {\alpha \mathrm{\text{'}}G}_{s,m}\right)+[\mathit{Me}{d}_{\alpha G}\times Im,\mathrm{\prime }on\mathrm{\prime }]+[\mathit{Di}{s}_{\alpha G}\times I\left(s{,}^{\mathrm{\text{'}}}h\mathit{ealth}{y}^{\mathrm{\text{'}}}\right)]\right)$$ (3)

As mentioned, $\mathit{Ph}{i}_{\mathit{approx}}\hspace{0.5em}$is an approximation of the inverse probit transformation, a function provided by Stan for efficient computation. We used a non-centred reparameterization technique to move from ${\alpha \text{'}G}_{s,m}$to $\alpha G_{s,m};$ a normal (μ, σ) distribution can be reparameterized and sampled from a unit normal distribution that is multiplied by the scale parameter σ and then shifted by the location parameter μ (Stan Development Team, 2015; Ahn et al., 2017). Using the binary indicators described above, Parkinson’s disease OFF did not contain either of the Med_$\alpha G\hspace{0.5em}$or Dis_$\alpha G\hspace{0.5em}$terms, Parkinson’s disease ON included the Med_$\alpha G\hspace{0.5em}$term to indicate the within-subject effect of medication, and control subjects included the Dis_$\alpha G\hspace{0.5em}$term to denote the between-subject effect of disease. α_loss and β parameters were distributed in the same way with their corresponding terms. As the medication effect was within-subject, it was itself a subject-specific random variable with its own population-level mean and variance. Once again using non-centred reparameterization, the medication effect was formulated as follows:

$${\mathit{Med}\_\alpha G}_s={\mathit{Phi}}_{\mathit{approx}}\left(\mathit{Med}\_\alpha G+\left({\sigma }_{\mathit{Med}\_\alpha G}\times {\mathit{Med}\_\alpha \mathrm{\text{'}}G}_s\right)\right)$$ (4)

Refer to the Supplementary material for the model estimation procedure and Supplementary Fig. 2 for an evaluation of the model fit. Bayes factors (BFs) of group level posterior distributions for medication and disease differences were calculated as the ratio of the posterior density above zero relative to the posterior density below zero (Pedersen et al., 2016). This method is possible as the priors for the distributions of these parameters were symmetric (unbiased) around zero (Marsman and Wagenmakers, 2017). Categories of evidential strength of an effect are based on Jeffreys (1998), with BFs >10 considered as strong evidence that the shift in the posterior distribution is different from zero. We provide all fitting code online at: https://github.com/mccoyb4/Parkinson_RL.

Statistical evaluations of behaviour

General

As Parkinson’s disease patients were tested twice and control participants only once, we confirmed that session order effects did not affect performance during either the learning phase or transfer phase (Supplementary material and Supplementary Fig. 3).

Learning phase

Bayesian mixed-effects logistic regression modelling was carried out on trial-by-trial behaviour (Wunderlich et al., 2012; Doll et al., 2016; Sharp et al., 2016). These analyses were performed in R (R Development Core and Team, 2017), using the Bayesian Linear Mixed-Effects Models (blme) package (Chung et al., 2013), built on top of lme4 (Bates et al., 2014). In our mixed-effects models, we coded for both fixed and random trial-by-trial effects and allowed for a varying intercept on a per subject basis. For the model on learning behaviour, the dependent variable was accuracy in choosing the better stimulus of a pair (correct = 1, incorrect = 0). Stimulus pair (‘Pair’) was taken as a within-subject (random-effect) explanatory variable (EV), from easiest to most difficult (AB pair = 1, CD pair = 0, EF pair = −1). We also included two binary covariates (as in Sharp et al., 2016); the between-subject effect of disease (Dis, where Parkinson’s disease = 0, control subjects = 1) and the within-subject effect of dopaminergic medication state (Med, where OFF = 0, ON = 1), as well as their interactions with the stimulus pair variable. The medication variable for control subjects was coded as 0 as we wanted this to capture only the within-subject effect of medication. As disease and medication status were both included in the same model, Parkinson’s disease OFF was considered to act as a baseline (Dis = 0, Med = 0). Within-subject effects of medication for Parkinson’s disease ON (Dis = 0, Med = 1) were therefore captured by the medication variable only and between-subject effects of disease for control subjects (Dis = 1, Med = 0) were captured by the disease variable only (with Dis = 1 meaning ‘healthy’). This is summarized in the following regression equation:

$$\text{Correct}=\text{Pair}+\text{Med}+\text{Dis}+\text{Pair}\times \text{Med}+\text{Pair}\times \text{Dis}+\text{Subject Intercept}$$ (5)

Positive beta estimates obtained from the model therefore indicate higher accuracy for either Parkinson’s disease ON or control subjects compared to Parkinson’s disease OFF in the Med and Dis variables, respectively, with negative estimates for those variables reflecting greater accuracy for Parkinson’s disease OFF.

Transfer phase

The mixed-effects regression on transfer phase behaviour was carried out on trials in which either the A or B stimulus appeared, excluding those in which both appeared together (Fig. 1B). The expectation was that participants should opt to choose A (Approach A) and avoid choosing B (Avoid B) whenever they were presented, since they were associated with the highest and lowest reward probabilities during learning, respectively. The regression was performed similarly to that in the learning phase, except that the stimulus pair variable was replaced with an Approach A / Avoid B trial variable (A = 1, B = −1). The dependent variable (accuracy) was then coded as 1 for correctly choosing A in Approach A or correctly not choosing B in Avoid B trials, and as 0 for incorrectly choosing the other option for each trial type. Medication and disease status were included as covariates, with a varying intercept per subject. To assess the role of medication and disease status on Approach A and Avoid B performance separately, we carried out a regression analysis on each subset, with the same covariates as described previously.

Learning and transfer

The relationship between medication-induced shifts during learning and transfer was evaluated in two steps. First, we compared three multiple regression models, as shown in Supplementary Table 4, to evaluate how the learning rate medication shifts (i.e. Med_αG, Med_αL, or both) relate to the transfer phase approach/avoid shifts on an individual level. In these (multiple) regression models, the approach/avoid shift (defined for each subject as the OFF > ON medication difference in Avoid B > Approach A accuracies) was set as the dependent variable. Next, Bayesian information criterion (BIC) scores were computed for each regression (with explanatory variables being either only Med_αG, Med_αL, or both), to select the optimal model for the evaluation of medication relationships between the learning and transfer phase. Individual learning-rate medication differences were quantified as the modes of the within-subject medication difference parameter distributions, to capture peak probability densities (Supplementary Fig. 4).

Functional MRI image acquisition

Functional MRI scanning was carried out using a 3 T GE Signa HDxT MRI scanner (General Electric) with 8-channel head coil at the VU University Medical Center (Amsterdam, The Netherlands). Functional data for the learning and transfer phase runs were acquired using T₂*-weighted echo-planar images with BOLD contrasts, containing ∼410 and 240 volumes for learning and transfer runs, respectively. The first two repetition time volumes were removed to allow for T₁ equilibration. Each volume contained 42 axial slices, with 3.3 mm in-plane resolution, repetition time = 2150 ms, echo time = 35 ms, flip angle = 80°, field of view = 240 mm, 64 × 64 matrix. Structural images were acquired with a 3D T₁-weighted magnetization prepared rapid gradient echo (MPRAGE) sequence with the following acquisition parameters: 1 mm isotropic resolution, 176 slices, repetition time = 8.2 ms, echo time = 3.2 ms, flip angle = 12°, inversion time = 450 ms, 256 × 256 matrix. The subject’s head was stabilized using foam pads to reduce motion artefacts.

Functional MRI analysis

Preprocessing was performed using FMRIPREP version 1.0.0-rc2 (Esteban et al., 2018a, b), a Nipype-based tool (Gorgolewski et al., 2011, 2017). On the learning phase data, we carried out a single-trial whole-brain analysis and deconvolution analyses on targeted striatal regions of interest. For the transfer phase data, BOLD per cent signal change was extracted for the relevant approach/avoidance conditions. See Supplementary material for full details on each of these steps.

Data availability

Related analysis code is available at https://github.com/mccoyb4/Parkinson_RL.

For ethical reasons, we are unable to share the patient data. The raw data underpinning the findings of this study are available upon reasonable request from the corresponding author. These are in BIDS format and preprocessed with fMRIPrep to ease and encourage sharing upon request. Functional MRI statistics maps and associated tables of activated regions per group and per group comparison are available to view on figshare, at: https://doi.org/10.6084/m9.figshare.6989024.v2.

Results

During the learning phase, participants successfully learned to choose the best option out of three fixed pairs of stimuli (Fig. 1C). Each pair was associated with its own relative reward probability among the two options, labelled as AB (with 80:20 reward probability for A:B stimuli), CD (70:30) and EF (60:40). Choice accuracy analysis showed that learning took place in Parkinson’s disease ON, Parkinson’s disease OFF and control subjects (n = 23 in each group), with the probability with which participants chose the better option of each stimulus pair largely reflecting the underlying reward probabilities (Parkinson’s disease ON: 82.3% ± 3.1, 70.8% ± 3.5, and 63.7% ± 3.5; Parkinson’s disease OFF: 76.6% ± 3.4, 70.7% ± 3.7, and 64.4% ± 3.6; and control subjects: 83.7% ± 2.7, 78.4% ± 3.1, and 66.5% ± 4.4 for AB, CD, and EF stimulus pairs, respectively).

We examined within- and between-subject differences in choice accuracy using a Bayesian mixed-effects logistic regression on the observed trial-by-trial behaviour (Supplementary Fig. 1). This analysis assessed how choice accuracy was affected by stimulus pair, medication, disease status, and their interactions. When patients were ON medication, overall performance was more accurate in comparison to OFF, with the biggest difference for the easier AB choices and a smaller difference for the more uncertain EF pair. This was evidenced by a main effect of stimulus pair [β (standard error, SE) = 0.35 (0.03), z = 10.19, P << 0.001], medication [β (SE) = 0.11 (0.04), z = 2.80, P = 0.005], and, specifically, an interaction between medication and stimulus pair [β (SE) = 0.17 (0.05), z = 3.47, P < 0.001]. Importantly, this specific effect of medication was reflected in an analogous effect of disease when comparing Parkinson’s disease OFF to control subjects, with a significant interaction between disease status and stimulus pair [β (SE) = 0.20 (0.05), z = 3.81, P < 0.001]. As learning of the AB pair plays a particularly important role in subsequent transfer phase choices during Approach A and Avoid B trials, we also carried out mixed-effects logistic regression analyses to assess how positive and negative feedback affect choice behaviour for the AB pair during learning. We found that in trials following negative, but not positive, feedback, Parkinson’s disease ON chose the better A stimulus more often than Parkinson’s disease OFF [β (SE) = 0.52 (0.13), z = 3.96, P < 0.001], indicating that Parkinson’s disease ON are less likely to use negative outcomes to guide subsequent choices (Supplementary material).

Overall, these first analyses show an improvement in choice accuracy when patients are ON compared to OFF medication, with performance on the easiest option pair restored to the level of control subjects. However, although choice accuracy provides us with a general assessment of medication effects on performance, it does not relate these effects to a mechanistic explanation of how underlying indices of learning might be affected by medication. These underlying mechanisms can be studied and defined both at the group level (control subjects versus Parkinson’s disease), and within-subject level (Parkinson’s disease ON versus OFF) by adopting a formal learning model of behaviour, to which we turn next.

Medication reduces learning rate for negative outcomes

Reinforcement learning theories describe how an agent learns to select the highest-value action for a given decision, based on the incorporation of received rewards (Rescorla and Wagner, 1972; Sutton and Barto, 1998). We implemented a Q-learning model, graphically represented in Fig. 2A–C, to describe both value-based decision-making and the integration of reward feedback in our experiment (Daw et al., 2011; Jocham et al., 2011; Schmidt et al., 2014). Our model used separate parameters to describe, for a given agent, how strongly current value estimates are updated by positive (α_gain) and negative (α_loss) feedback, i.e. positive and negative learning rates (Grogan et al., 2017; Jahfari et al., 2018; Van Slooten et al., 2018; Verharen et al., 2018), as well as a parameter that determines the extent to which differences in value between stimuli are exploited (β). To understand how medication affects learning in Parkinson’s disease we examined the posterior distributions of group-level parameters representing the within-subject medication shift in α_gain, α_loss and β (Fig. 2D). The large leftward shift of the α_loss posterior distribution indicates higher learning rates after negative outcomes in Parkinson’s disease OFF compared to ON (BF = 11.40). This is consistent with the theory that Parkinson’s disease increases the sensitivity to negative outcomes, and that dopaminergic medication remediates specifically this disease symptom. Conversely, shifts in the distributions of the α_gain and β parameters were merely anecdotal (1 < BFs < 2, see Supplementary Table 5 and Supplementary Fig. 4 for individual within-subject effects of medication). For parameter comparisons between Parkinson’s disease and control subjects based on disease status, we found strong evidence for a higher β, i.e. greater exploitation, in control subjects compared to Parkinson’s disease (BF = 16.89) in addition to a moderate effect on α_loss (Supplementary Figs 5 and 6).

Medication in Parkinson’s disease reduces the sensitivity of dorsal striatum to reward prediction error

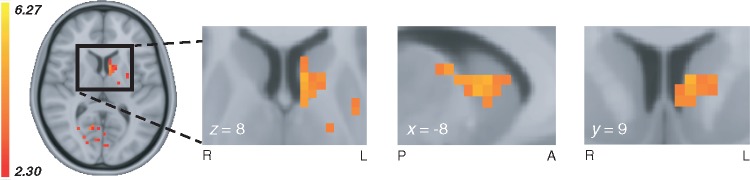
In the Q-learning model, the learning rate weighs the extent to which value beliefs are updated based on trial-by-trial RPE. The processing of choice outcomes is known to influence BOLD signals in the striatum, where the sensitivity to RPE is changed when dopamine levels are manipulated (Pessiglione et al., 2006; Jocham et al., 2011; Schmidt et al., 2014). To establish whether RPE processing in the current study was influenced by dopaminergic state, we first examined within-subject medication-related differences in whole-brain responses to all positive and negative RPEs in the learning phase using a single-trial general linear model (Supplementary material). This analysis provides an unbiased overview of any RPE-related (positive and/or negative) differences caused by dopaminergic medication across the entire brain. We found a significant Parkinson’s disease OFF > ON medication difference in RPE modulation of the caudate nucleus and putamen (Fig. 3), and in several other regions including the globus pallidus interna and externa, thalamus, cerebellum, lingual gyrus and precuneus. Comparisons of control subjects with Parkinson’s disease (ON and OFF) showed no RPE-related differences in the striatum, with significant RPE differences in frontal medial cortex, subcallosal cortex, and precuneus (control subjects > Parkinson’s disease OFF) and in the occipital pole (control subjects > Parkinson’s disease ON). The opposing contrasts, i.e. Parkinson’s disease ON/OFF > control subjects, showed more extended activations, with RPE-related group differences in the paracingulate gyrus, superior frontal gyrus, frontal pole, supramarginal gyrus, cerebellum, occipital pole and lateral occipital cortex (Parkinson’s disease OFF > control subjects) and in the cerebellum, brainstem, and lateral occipital cortex (Parkinson’s disease ON > control subjects). Because our model-based behavioural analysis revealed a medication-related difference specific to learning from negative outcomes (Fig. 2D), we proceeded by analysing BOLD response time series to positive and negative outcomes separately.

Figure 3.

Whole-brain medication-related difference in RPE modulation. Whole-brain medication effects for the comparison Parkinson’s disease OFF > ON in RPE-related modulations during the learning phase (z = 2.3, P < 0.01, cluster-corrected), showing a dopamine-driven difference in the left dorsal striatum (see Supplementary Table 5 for a full list of brain region differences and contrast statistics). Whole-brain group-level contrasts of RPE and feedback valence are available to view on figshare, at https://doi.org/10.6084/m9.figshare.6989024.v2. A = anterior; L = left; P = posterior; R = right.

Medication effects in dorsal striatum are specific to the processing of negative reward prediction errors

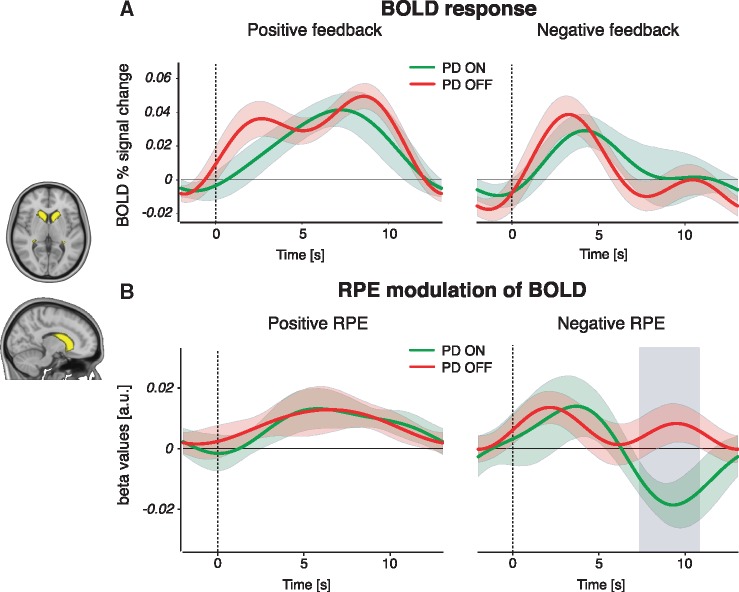
To disentangle the separate effects of positive and negative RPE signalling, we examined feedback-triggered BOLD time courses from three independent striatal masks; the caudate nucleus, putamen, and nucleus accumbens (Supplementary material and Supplementary Figs 7 and 8). We found a significant medication difference only in the caudate nucleus, in BOLD activity associated only with negative RPE (Fig. 4). RPE modulation of the BOLD response was greater in Parkinson’s disease OFF compared to ON, during the interval 7.51–10.67 s after the onset of negative feedback. Medication status did not alter the BOLD responses to positive RPE, indicating that changes due to dopaminergic medication are specific to negative RPE signalling in the caudate nucleus, the most dorsal part of the striatum. As well as tracking RPEs at the time of feedback, the striatum has been shown to represent the Q-value of the (to-be) chosen stimulus during the choice period (Kim et al., 2009; Horga et al., 2015; Jahfari et al., 2019). We therefore also performed a separate time-course analysis on the effect of Q-values on the BOLD signal in striatal regions of interest during stimulus presentation (Supplementary material). This showed a medication-related increase in the modulation of BOLD by Q-values in the putamen (Supplementary Fig. 9).

Figure 4.

BOLD response and RPE modulation of the BOLD signal during feedback events. (A) BOLD per cent signal change in response to positive (left) and negative (right) feedback events, in Parkinson’s disease (PD) patients ON and OFF medication. There were no significant medication-driven differences for either event type. (B) BOLD RPE covariation time courses for positive (left) and negative (right) feedback events. We found a significant difference between Parkinson’s disease OFF and ON in negative RPE responses, but not in positive RPE responses. The grey shaded area reflects a significant Parkinson’s disease OFF > ON difference passing cluster-correction for multiple comparisons across time points (P < 0.05). Coloured bands represent 68% confidence intervals (±1 SEM). A similar comparison between control subjects and each Parkinson’s disease ON or OFF state showed no significant differences in the caudate nucleus (Supplementary Fig. 7). The same analyses of putamen and nucleus accumbens regions of interest revealed no medication-related RPE differences in these regions (Supplementary Fig. 8).

Behavioural analysis of transfer phase

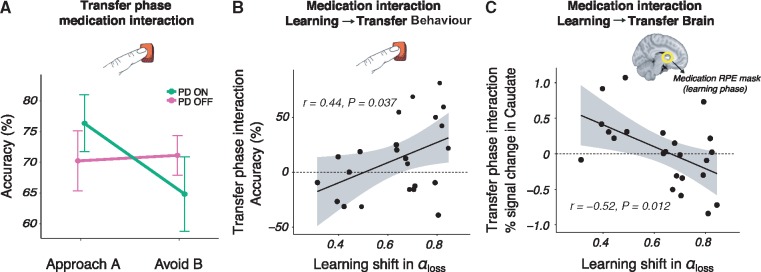
The previous sections reveal how medication remediates the way patients learn from negative outcomes by detailing medication-related changes in brain and behaviour. Much of the previous literature, however, has focused on how subsequent decision-making in the transfer phase is affected by dopaminergic medication (Frank et al., 2004; Frank, 2007; Shiner et al., 2012; Grogan et al., 2017). We next set out to explore the relation between medication-induced changes in learning and subsequent behaviour. In the transfer phase of the experiment, participants were presented with novel pairings of the learning phase stimuli and were asked to choose the best option based on their previous experience with the options (Fig. 1A). We examined accuracy in correctly choosing the stimulus associated with the highest value from the learning phase (‘Approach A’ trials) and correctly avoiding the stimulus associated with the lowest value (‘Avoid B’ trials) (Frank et al., 2004; Jocham et al., 2011), as in Fig. 1B (also refer to the ‘Materials and methods’ section). Replicating several previous reports (Frank et al., 2004; Frank, 2007), results showed a strong interaction between medication (Parkinson’s disease ON or OFF) and trial type (Approach A or Avoid B) [β (SE) = 0.34 (0.06), z = 5.75, P < 0.001]. That is, medication in Parkinson’s disease improved accuracy scores for Approach trials, but decreased accuracy for Avoid trials (Fig. 5A). Notably, there were no main effects of trial type, medication or disease status in addition to this pivotal approach/avoidance medication interaction. Thus, medication only influenced Approach A versus Avoid B choice patterns, with no further differences in the overall accuracy across groups or trials. An independent analysis of Approach A and Avoid B trials separately revealed a main effect of medication on performance for both approach trials [a positive effect of medication on accuracy; β (SE) = 0.39 (0.08), z = 4.28, P < 0.001] and avoid trials [a negative effect of medication on accuracy; β (SE) = −0.35 (0.09), z = 4.03, P < 0.001]. Finally, an evaluation of control subjects’ performance showed an interaction between disease status (control subjects versus Parkinson’s disease OFF) and Approach A/Avoid B trial type [β (SE) = 0.29 (0.06), z = 4.56, P < 0.001], with control subjects showing an approach/avoid asymmetry similar to Parkinson’s disease ON (Supplementary Fig. 10). There were no main effects of disease, i.e. there was no significant difference between control subjects and Parkinson’s disease OFF for either trial type. Approach/avoidance asymmetries are therefore particularly evident when assessing within-patient effects of dopaminergic medication.

Figure 5.

Medication-induced changes in learning from negative outcomes in Parkinson’s disease predicts the magnitude of medication difference in subsequent approach/avoidance behavioural choices and striatal response. (A) Transfer phase behavioural accuracy in Approach A and Avoid B responses, showing a significant within-subject medication interaction in approach/avoidance behaviour (P < 0.001). Parkinson’s disease (PD) ON had a higher accuracy in approach trials but a lower accuracy in avoid trials than Parkinson’s disease OFF. Control subjects’ performance is shown in Supplementary Fig. 10. (B) A positive relationship between the medication difference, i.e. the parameter shift for OFF > ON, in negative learning rate and the transfer phase medication accuracy difference (OFF > ON) in avoiding the lowest-value stimulus versus approaching the highest-valued stimulus, i.e. the interaction observed in A. (C) A negative relationship between the medication difference (OFF > ON) in negative learning rate and the same transfer phase medication difference (OFF > ON) in avoid compared to approach trials, here in terms of BOLD per cent signal change in the caudate nucleus.

Medication shifts in learning rate for negative outcomes relate to behavioural and striatal changes during transfer

We have described how medication affects the updating of individual patients’ beliefs after encounters with negative feedback, and replicate previous work by showing medication-induced changes in approach/avoidance choices during a follow-up transfer phase with no feedback. In this final section we explore how the shift in learning rates caused by medication during learning relates to the subsequent approach/avoidance interaction in (i) choice outcomes; and (ii) the BOLD response of the dorsal striatum.

Consistent with the observation that medication only affects learning rates after negative outcomes, we found that only the medication-related shift in α_loss (and not α_gain) was predictive of the magnitude of change in approach/avoidance behaviour, as indicated by the lowest BIC in a formal model comparison analysis (Supplementary Table 4). In other words, the more α_loss was lowered by medication, the bigger the medication-induced interaction effect in future approach/avoidance choice patterns [β (SE) = 91.97 (41.26), t(22) = 2.23, P = 0.037] (Fig. 5B). Because the dorsal striatum was differentially responsive to RPE during learning, we additionally examined how learning rate shifts relate to the striatal BOLD response in approach/avoidance trials, while patients were ON or OFF medication. To this end, we masked the caudate and putamen using the whole-brain RPE z-statistics map shown in Fig. 3. From these masks BOLD responses were extracted for Approach A and Avoid B trials, for each of the Parkinson’s disease ON and OFF sessions. Again, only the medication-induced shift in α_loss predicted the magnitude of change in the BOLD response of the caudate nucleus, but not the putamen, for approach/avoidance trials of OFF compared to ON (Supplementary Table 4) [β (SE) = 1.54, (0.56), t(22) = 2.77, P = 0.012] (Fig. 5C). In summary, these findings show that within-subject medication-related shifts in learning from negative outcomes are predictive of subsequent approach/avoidance medication-related changes, both in terms of behavioural accuracy and BOLD signalling in the caudate nucleus.

Discussion

Our findings provide a bridge between a previously disparate set of findings relating to reinforcement learning in Parkinson’s disease. First, using a formalized learning theory, we show how dopaminergic medication remediates learning behaviour by reducing the patient’s emphasis on negative outcomes. These behavioural adaptations were tied to BOLD changes in the dorsal striatum, with medication reducing the sensitivity to RPEs, specifically during the processing of negative outcomes. Second, we show a relationship between how the medication-induced change in learning and subsequent approach/avoidance choices that differ in Parkinson’s disease when patients are ON or OFF medication. We found that the greater the degree of restoration by medication in the learning rate for negative outcomes, the greater the medication-related impact on both subsequent behaviour and associated BOLD responses of the dorsal striatum during value-based decision-making.

Our finding that medication reduces negative learning rate directly replicates studies showing a medication-driven impairment in behavioural responses relating to negative feedback, in a variety of probabilistic learning tasks (Frank et al., 2004; Cools et al., 2006; Bódi et al., 2009; Palminteri et al., 2009). Furthermore, this finding corroborates a dopamine-driven reduction in model-based negative learning rate in Parkinson’s disease patients (Voon et al., 2010) and rats (Verharen et al., 2018). The shift towards lower sensitivity to negative outcomes in Parkinson’s disease ON reflects a partially restorative effect. While sensitivity to negative outcomes became more similar to that observed in healthy controls, decision-making volatility, i.e. the exploitation of higher-valued options, did not (Supplementary Fig. 6). Although theory on dopaminergic signalling has suggested a dual influence of medication on learning from both positive and negative outcomes (Frank, 2005), conclusions in the literature have been mixed. While this dual effect has been shown in several studies (Bódi et al., 2009; Palminteri et al., 2009; Voon et al., 2010; Maril et al., 2013), much literature has indicated an effect of medication only on negative feedback learning (Frank et al., 2004; Cools et al., 2006; Frank, 2007; Mathar et al., 2017) or only on positive feedback learning (Rutledge et al., 2009; Shiner et al., 2012; Smittenaar et al., 2012). The notion of a dual influence of medication on both positive and negative RPEs is therefore not always, and in fact frequently is not, seen in the literature.

The medication interaction in subsequent approach/avoidance behaviour we find in the transfer phase supports previous research on the transfer of learned value to new contexts (Frank et al., 2004; Frank, 2007; Cox et al., 2015). A similar interaction effect for control subjects compared to Parkinson’s disease OFF suggests that medication may play a role in normalizing the balance in approach/avoidance behaviour towards healthy levels (Supplementary Fig. 10). This reinforces the notion that dopaminergic medication shifts the balance in activation of the Go and NoGo pathways of the striatum (Frank, 2005). It has been an open question whether these Go and NoGo pathways are in competition with each other or function independently. A recent review suggests that the Go and NoGo pathways should not be viewed as separate, parallel systems (Calabresi et al., 2014). The two pathways are instead described to be structurally and functionally intertwined, with ‘cross-talk’ occurring between Go and NoGo neuronal subtypes. It is therefore possible that differences in the processing of negative feedback during learning not only affect the NoGo pathway, but also the Go pathway (in a push-pull manner). This account represents a potential means by which the dopamine-dependent alterations in learning from negative outcomes observed in the current study can lead to an integrated (interactive) effect on subsequent approach and avoidance behaviour and associated BOLD activation in the striatum.

We observed greater RPE modulation of BOLD signalling in Parkinson’s disease OFF compared to ON, indicating a medication-related role in the modulation of caudate nucleus activity during learning. Striatal BOLD activations have previously been demonstrated to track RPE, with numerous studies implicating the caudate nucleus in RPE signalling during goal-directed behaviour (Davidson et al., 2004; O’Doherty et al., 2004; Delgado et al., 2005; Haruno and Kawato, 2006). The whole-brain analysis used in the current study reveals greater within-subject RPE modulation in patients OFF compared to ON medication in the dorsal striatum, a region well established to suffer substantial depletion of dopamine availability in Parkinson’s disease (Bernheimer et al., 1973; Dauer and Przedborski, 2003). Patients in our study do not exhibit clear medication-related differences that signify an excessive level of dopamine in the ventral striatum, as postulated by the dopamine overdose hypothesis (Cools et al., 2001, 2006) and presented in studies focusing on the nucleus accumbens (Cools, 2006; Schmidt et al., 2014). In our data, there does appear to be a quantitative medication-induced increase in the modulation of nucleus accumbens activity by positive RPE, however, this effect is not significant (Supplementary Fig. 8). One recent study describing the mechanisms underlying ‘optimism bias’ (a higher rate of learning from positive than negative outcomes) revealed greater RPE signalling in the ventral striatum for individuals who had a higher optimism bias (Lefebvre et al., 2017). Given that we found reduced sensitivity to negative outcomes in Parkinson’s disease ON than OFF, with no difference in learning from positive outcomes, we deem it likely that there is a relationship between optimism bias and (quantitative) medication-related differences in the ventral striatum in Parkinson’s disease.

Activation of the dorsal striatum has been reported for instrumental but not Pavlovian learning, suggesting its role in establishing stimulus-response-outcome associations (O’Doherty et al., 2004). A prominent theory of dopamine functioning, the actor-critic model, highlights distinct roles for reward prediction and action-planning in reinforcement learning (Houk, 1995; Suri and Schultz, 1999; Joel et al., 2002), with the ventral striatum (critic) implicated in the prediction of future rewards (Cardinal et al., 2002), and the dorsal striatum (actor) proposed to maintain information about rewarding outcomes of current actions to help inform future actions (Packard and Knowlton, 2002; Atallah et al., 2007). Connectivity between the midbrain substantia nigra and dorsal striatum has also been found to predict the impact of differing reinforcements on future behaviour (Kahnt et al., 2009). Overall, the caudate nucleus has been put forward as a hub that integrates information from reward and cognitive cortical areas in the development of strategic action planning (Haber and Knutson, 2010). The dopamine-dependent differences in RPE modulation of BOLD activity in the caudate nucleus presented here therefore suggest that Parkinson’s disease’s dopamine-related effects are specific to the processing of feedback to guide future actions. The dopamine-related interaction in approach/avoidance behaviour found in the transfer phase, in which actions were guided by previously learned values, provides further support for this interpretation.

A separate evaluation of medication-related differences during the choice period revealed that modulation of BOLD activation by Q-values was higher in the putamen when patients were ON compared to OFF medication (Supplementary Fig. 9). Interestingly, the putamen has been demonstrated to track action-specific (Q-) value signals (Jahfari et al., 2019) and the covariation of this tracking was found to be higher in good compared to bad learners (Horga et al., 2015). Our behavioural analysis on choice accuracy during learning demonstrated greater overall learning in Parkinson’s disease ON compared to OFF, which fits well with this Parkinson’s disease ON > OFF group level difference of Q-value signalling in the putamen. Medication-related differences in the putamen for choice valuation during learning is thus an interesting avenue for future Parkinson’s disease research.

We established a link between medication-dependent changes in learning from negative outcomes to subsequent changes in approach/avoidance striatal activity by specifically focusing on the region that showed a robust medication-dependent difference in phasic RPE modulation during learning. This suggests that the caudate nucleus’ processing of negative RPE in Parkinson’s disease ON plays an important role in the subsequent medication-induced shift in balance between approach and avoidance behaviour. Although focusing on the ventral striatum, a recent study on rats showed that increased activation in the VTA-NAc (nucleus accumbens) pathway associated with a higher dopaminergic state was reflected in behaviour by a reduced sensitivity to negative outcomes (Verharen et al., 2018). Our findings suggest that the caudate nucleus may play a similar role in the processing of negative outcomes in Parkinson’s disease. Future research could address whether this is modulated by substantia nigra-caudate nucleus connectivity and/or the interplay between instrumental and Pavlovian learning.

In several previous studies, dopamine level was manipulated pharmacologically in healthy adults, via levodopa medication (Pessiglione et al., 2006) or NoGo (D2) receptor antagonists (Jocham et al., 2011; Van Der Schaaf et al., 2014). Here, we examined separable disease-related and dopaminergic medication-related effects in Parkinson’s disease. Patients in the current study used a combination of dopaminergic medications, including those acting on both Go and NoGo receptors (levodopa), inhibitors that slow the effect of levodopa to give a more stable release, and dopamine agonists, which have a particular affinity for NoGo receptors. Accordingly, a limitation of our study is that we cannot pin down the relationship between specific dopaminergic medications and changes in learning. Dissociation between the different types of dopaminergic medication could therefore be a potential avenue for future research.

Although there is moderate evidence for a higher sensitivity to negative feedback in Parkinson’s disease OFF compared to control subjects, we found that the greatest disease-related difference lies in the explore/exploit parameter of the model (Supplementary Fig. 5). Higher choice accuracy during easier decisions in control subjects is likely strongly influenced by greater exploitation of value differences between options; indeed, a positive correlation has recently been shown between choice accuracy and exploitation in a similar reinforcement learning task (Jahfari et al., 2018). In the current study, this difference in exploitation was observed regardless of Parkinson’s disease medication state (Supplementary Fig. 6), showing that dopamine medication in Parkinson’s disease does not reinstate healthy exploitative behaviour. This selectivity of dopaminergic medication’s effects on learning may indicate certain mechanisms underlying Parkinson’s disease-related psychiatric disorders (Voon et al., 2010). Recent evidence from a perceptual decision-making study in Parkinson’s disease showed an impaired use of prior information in patients in making perceptual decisions (Perugini et al., 2016), a deficiency that also was not alleviated by dopaminergic medication (Perugini et al., 2018). Thus, regardless of medication status, Parkinson’s disease patients show impairment in the integration of memory with the current sensory input. As the explore/exploit parameter of the task used in our experiments is dependent upon the retrieval of the expected value of chosen options, a similar memory-guided decision-making impairment may have also played a role in the current reinforcement learning task.

We included several spouses of Parkinson’s disease patients in our control sample. Spouses of patients may be under more stress or anxiety than usual, which may impact how they learn from reinforcements. Since control subjects as a group performed significantly better than Parkinson’s disease patients during the learning phase and similar to control subjects during the transfer phase in a similar previous study (Frank et al., 2004), it seems likely that our control sample was sufficiently representative of healthy older adults to allow us to examine disease-related differences in learning.

Computational psychiatry is a burgeoning field of research with the aim of translating advances in computational methods to practical benefits for patient diagnosis and intervention (Huys et al., 2016; Maia and Conceição, 2017). The surge in the application of reinforcement learning models to patient data warrants extensive examination of the model fitting procedures, parameter recovery, and model identifiability, i.e. if parameters are highly correlated, then one parameter may falsely absorb an effect that is not actually true (Maia and Conceição, 2017). With this in mind, we used a hierarchical Bayesian modelling approach where individual and group parameters are estimated simultaneously in a mutually constraining manner (Wetzels et al., 2010; Steingroever et al., 2013; Wiecki et al., 2013; Ahn et al., 2017). The performance of this model was subsequently extensively evaluated with a focus on reliability. Overall, we show: (i) that our model’s parameters are only weakly related (Supplementary Fig. 11); (ii) accurate parameter recovery for each participant in our study; and (iii) accurate data recovery (Supplementary Fig. 2), which indicates that the model can suitably reproduce the observed data for both patients and healthy controls. Moreover, we note that the parameter estimates in this study are comparable to our other work using this task and a similar Q-learning model (Jahfari and Theeuwes, 2017; Jahfari et al., 2018; Van Slooten et al., 2018, 2019).

In conclusion, we comprehensively illustrate how dopaminergic medication used in Parkinson’s disease can help remediate sensitivity to negative outcomes, indicated by both changes in negative learning rate and the dorsal striatum’s response to negative RPE. Furthermore, we show how, when using experience garnered during learning to guide subsequent value-based decisions, these effects shift the balance of approach/avoidance behaviour and associated striatal activation. Aside from explicating dopamine’s role in reinforcement learning and value-based decision-making, our findings open new avenues of treatment in Parkinson’s disease and its associated psychiatric symptoms.

Glossary

Abbreviations

BOLD =

blood oxygen level-dependent

RPE =

reward prediction error