Integrative Multi-View Regression: Bridging Group-Sparse and Low-Rank Models

Summary:

Multi-view data have been routinely collected in various fields of science and engineering. A general problem is to study the predictive association between multivariate responses and multi-view predictor sets, all of which can be of high dimensionality. It is likely that only a few views are relevant to prediction, and the predictors within each relevant view contribute to the prediction collectively rather than sparsely. We cast this new problem under the familiar multivariate regression framework and propose an integrative reduced-rank regression (iRRR), where each view has its own low-rank coefficient matrix. As such, latent features are extracted from each view in a supervised fashion. For model estimation, we develop a convex composite nuclear norm penalization approach, which admits an efficient algorithm via alternating direction method of multipliers. Extensions to non-Gaussian and incomplete data are discussed. Theoretically, we derive non-asymptotic oracle bounds of iRRR under a restricted eigenvalue condition. Our results recover oracle bounds of several special cases of iRRR including Lasso, group Lasso and nuclear norm penalized regression. Therefore, iRRR seamlessly bridges group-sparse and low-rank methods and can achieve substantially faster convergence rate under realistic settings of multi-view learning. Simulation studies and an application in the Longitudinal Studies of Aging further showcase the efficacy of the proposed methods.

1. Introduction

Multi-view data, or measurements of several distinct yet interrelated sets of characteristics pertaining to the same set of subjects, have become increasingly common in various fields. In a human lung study, for example, segmental airway tree measurements from CT-scanned images, patient behavioral data from questionnaires, gene expressions data, together with multiple pulmonary function test results from spirometry, were all collected. Unveiling lung disease mechanisms then amounts to linking the microscopic lung airway structures, the genetic information, and the patient behaviors to the global measurements of lung functions (Chen et al., 2016). In an Internet network analysis, the popularity and influence of a web page are related to its layouts, images, texts, and hyperlinks as well as by the content of other web pages that link back to it. In Longitudinal Study of Aging (LSOA) (Stanziano et al., 2010), the interest is to predict current health conditions of patients using historical information of their living conditions, household structures, habits, activities, medical conditions, among others. The availability of such multi-view data has made tackling many fundamental problems possible through an integrative statistical learning paradigm, whose success owes to the utilization of information from various lenses and angles simultaneously.

The aforementioned problems can all be cast under a multivariate regression framework, in which both the responses and the predictors can be high dimensional, and in addition, the predictors admit some natural grouping structure. In this paper we investigate this simple yet general framework for achieving integrative learning. To formulate, suppose we observe $X_k\in {ℝ}^{n\times p_k}$ for k = 1, … , K, each consisting of n copies of independent observations from a set of predictor/feature variables of dimension p_k, and also we observe data on q response variables $Y\in {ℝ}^{n\times q}$. Let $X=\left(X_1,\dots ,X_K\right)\in {ℝ}^{n\times p}$ be the design matrix collecting all the predictor sets/groups, with $p={\sum }_{k=1}^K{p}_k$. Both p and q can be much larger than the sample size n. Consider the multivariate linear regression model,

$$Y=X{B}_0+E=\sum _{k=1}^K{X}_k{B}_{0k}+E\text{,}$$ (1)

where $B_0={\left(B_{01}^{\text{T}},\dots ,B_{0K}^{\text{T}}\right)}^{\text{T}}\in {ℝ}^{p\times q}$ is the unknown regression coefficient matrix partitioned corresponding to the predictor groups, and E contains independent random errors with zero mean. For simplicity, we assume both the responses and the predictors are centered so there is no intercept term. The naive least squares estimation fails miserably in high dimensions as it leverages neither the response associations nor the grouping of the predictors.

In recent years, we have witnessed an exciting development in regularized estimation, which aims to recover certain parsimonious low dimensional signal from noisy high dimensional data. In the context of multivariate regression or multi-task learning (Caruana, 1997), many exploit the idea of sparse estimation (Rothman et al., 2010; Peng et al., 2010; Lee and Liu, 2012; Li et al., 2015), in which information sharing can be achieved by assuming that all the responses are impacted by the same small subset of predictors. When the predictors themselves exhibit a group structure as in model (1), a group penalization approach, for example, the convex group Lasso (grLasso) method (Yuan and Lin, 2006), can be readily applied to promote groupwise predictor selection. Such methods have shown to be effective in integrative analysis of high-throughput genomic studies (Ma et al., 2011; Liu et al., 2014); a comprehensive review of these methods is provided by Huang et al. (2012).

For multivariate learning, another class of methods, i.e., the reduced-rank methods (Anderson, 1951; Reinsel and Velu, 1998), has also been attractive, where a low-rank constraint on the parameter matrix directly translates to an interpretable latent factor formulation, and conveniently induces information sharing among the regression tasks. Bunea et al. (2011) cast the high-dimensional reduced-rank regression (RRR) as a non-convex penalized regression problem with a rank penalty. Its convex counterpart is the nuclear norm penalized regression (NNP) (Yuan et al., 2007; Negahban and Wainwright, 2011; Koltchinskii et al., 2011),

$$\underset{\mathbf{\text{B}}\in {ℝ}^{p\times q}}{\text{min}}\frac{1}{2n}\Vert Y-XB{\Vert }_{\mathbb{F}}^2+\mathrm{\lambda }\Vert B{\Vert }_{\star },$$ (2)

where $\Vert \cdot {\Vert }_{\mathbb{F}}$ denotes the Frobenius norm, and the nuclear norm is defined as $\Vert \mathbf{\text{B}}{\Vert }_{\star }={\sum }_{j=1}^{p\wedge q}\sigma (B,j)$, with σ(·,j) denoting the jth largest singular value of the enclosed matrix. Other forms of singular value penalization were considered in, e.g., Mukherjee and Zhu (2011), Chen et al. (2013) and Zhou and Li (2014). In addition, some recent efforts further improve low-rank methods by incorporating error covariance modeling, such as envelope models (Cook et al., 2015), or by utilizing variable selection (Chen et al., 2012; Bunea et al., 2012; Chen and Huang, 2012; Su et al., 2016).

In essence, to best predict the multivariate response, sparse methods search for the most relevant subset or groups of predictors, while reduced-rank methods search for the most relevant subspace of the predictors. However, neither class of existing methods can fulfill the needs in the aforementioned multi-view problems. The predictors within each group/view may be strongly correlated, each individual variable may only have weak predictive power, and it is likely that only a few of the views are useful for prediction. Indeed, in the lung study, it is largely the collective effort of the sets of local airway features that drives the global lung functions (Chen et al., 2016). In the LSOA study, the predictor groups have distinct interpretations and thus warrant distinct dependence structures with the health outcomes.

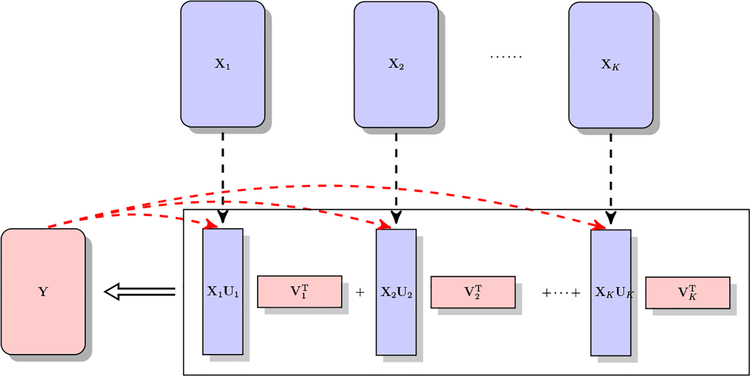
In this paper, we propose an integrative multi-view reduced-rank regression (iRRR) model, where the integration is in terms of multi-view predictors. To be specific, under model (1), we assume each set of predictors has its own low-rank coefficient matrix. Figure 1 shows a conceptual diagram of our proposed method. Latent features or relevant subspaces are extracted from each predictor set X_k under the supervision of the multivariate response Y, and the sets of latent variables/subspaces in turn jointly predict Y. The model setting strikes a balance between flexibility and parsimony, as it nicely bridges two seemingly quite different model classes: reduced-rank and group-sparse models. On the one hand, iRRR generalizes the two-set regressor model studied in Velu (1991) by allowing multiple sets of predictors, each of which can correspond to a low-rank coefficient matrix. On the other hand, iRRR subsumes group-sparse model setup by allowing the rank of B_0k being 0, for any k = 1, … , K, i.e., the coefficient matrix of a predictor group could be entirely zero.

Figure 1:

A diagram of integrative multi-view reduced-rank regression (iRRR). Latent features, i.e., X_kU_k, are learned from each view/predictor set under the supervision of Y.

In Section 2, we develop a new convex optimization approach via composite nuclear norm penalization (cNNP) to conduct model estimation for iRRR, which ensures the scalability to large-scale applications. We devise an Alternating Direction Method of Multipliers (ADMM) algorithm to solve the optimization problem with convergence guarantee; extensions to non-Gaussian response, incomplete data, among others, are also considered, and all the details are reported in the Web Appendix A. In Section 3, we derive non-asymptotic oracle bounds for the iRRR estimator, which subsume the results for several existing regularized estimation methods, and show that our proposed approach can achieve superior performance under realistic settings of multi-view learning. Comprehensive simulation studies are contained in Section 4, and a real data analysis of the LSOA example is contained in Section 5. In Section 6, we conclude with some discussions.

2. Integrative Multi-View Reduced-Rank Regression

2.1. Proposed Model

We consider the multivariate regression model in (1) to pursue integrative learning. Recall that in model (1), there are K views or groups of predictors denoted by X = (X₁, … , X_K), where $X_k\in {ℝ}^{n\times p_k}$ and ${\sum }_{k=1}^K{p}_k=p$. Correspondingly, the coefficient matrix B₀ is partitioned into K parts as $B_0={\left(B_{01}^{\text{T}},\dots ,B_{0K}^{\text{T}}\right)}^{\text{T}}$, where $B_{0k}\in {ℝ}^{p_k\times q}$. Denote r(·) as the rank of the enclosed matrix. By assuming each B_0k is possibly of low rank or even a zero matrix, i.e., 0 ⩽ r_0k ≪ p_k ∧ q where r_0k = r(B_0k), for k = 1, … , K, we reach our proposed integrative multi-view reduced-rank regression (iRRR) model.

The groupwise low-rank structure in iRRR is distinct from a globally low-rank structure for B₀ in standard RRR models. The low-rankness of B_0ks does not necessarily imply that B₀ is of low rank. Conversely, if B₀ is of low rank, i.e., r₀ = r(B₀) ≪ p ∧ q, all we know is that the rank of each B_0k is upper bounded by r₀.

Nevertheless, we can first attempt an intuitive understanding of the potential parsimony of iRRR in multi-view settings. The numbers of free parameters in B₀ (the naive degrees of freedom) for an iRRR model, a globally reduced-rank model and a group-sparse model are ${\text{df}}_1={\sum }_{k=1}^K{p}_k+q-r_{0k}$, df₂ = (p+q−r₀) and ${\text{df}}_3={\sum }_{k=1}^K{p}_{k}qI\left(r_{0k}\ne 0\right)$, respectively, where I(·) is an indicator function. For high-dimensional multi-view data, consider the scenario that only a few views/predictor groups impact the prediction in a collective way, i.e., r_0ks are mostly zero, and each nonzero r_0k could be much smaller than (p_k ∧ q). Then df₁ could be substantially smaller than both df₂ and df₃. For example, if r₀₁ > 0 while r_0k = 0 for any k > 1 (i.e., r₀ = r₀₁), we have df₁ = (p₁+q−r₀₁)r₀₁, df₂ = (p+q−r₀₁)r₀₁ and df₃ = p₁q, respectively. Another example is when $r_0={\sum }_{k=1}^K{r}_{0k}$, e.g., B_0ks in model (1) have distinct row spaces. Since ${\sum }_{k=1}^K\left(p_k+q-r_{0k}\right)r_{0k}⩽\left\{q+{\sum }_{k=1}^K\left(p_k-r_{0k}\right)\right\}\left\{{\sum }_{k=1}^K{r}_{0k}\right\}=\left(p+q-r_0\right)r_0$, iRRR is more parsimonious than the globally reduced-rank model. The above observations will be rigorously justified in Section 3 through a non-asymptotic analysis.

2.2. Composite Nuclear Norm Penalization

To recover the desired view-specific low-rank structure in the iRRR model, we propose a convex optimization approach with composite nuclear norm penalization (cNNP),

$$\widehat{B}\in \text{arg}\underset{B\in {ℝ}^{p\times q}}{\text{min}}\frac{1}{2n}\Vert Y-XB{\Vert }_{\text{F}}^2+\mathrm{\text{λ}}\sum _{k=1}^K{w}_k{\Vert B_k\Vert }_{\star },$$ (3)

where $\Vert B_k{\Vert }_{\star }={\sum }_{j=1}^{p_k\wedge q}\sigma (B_k,j)$ is the nuclear norm of B_k, w_ks are some prespecified weights, and λ is a tuning parameter controlling the amount of regularization. The use of the weights is to adjust for the dimension and scale differences of X_ks. We choose

$$w_k=\sigma \left({\mathbf{\text{X}}}_k,1\right)\left\{\sqrt{q}+\sqrt{r\left({\mathbf{\text{X}}}_k\right)}\right\}/n,$$ (4)

based on a concentration inequality of the largest singular value of a Gaussian matrix. This choice balances the penalization of different views and allows us to use only a single tuning parameter to achieve desired statistical performance; see Section 3 for details.

Through cNNP, the proposed approach can achieve view selection and view-specific subspace selection simultaneously, which shares the same spirit as the bi-level selection methods for univariate regression (Breheny and Huang, 2009; Huang et al., 2012; Chen et al., 2016). Moreover, iRRR seamlessly bridges group-sparse and low-rank methods as its special cases.

Case 1: nuclear norm penalized regression (NNP). When p₁ = p and K = 1, (3) reduces to the NNP method as in (2), which learns a globally low-rank association structure.

Case 2: multi-task learning (MTL). When p_k = 1 and p = K, (3) becomes a special case of MTL (Caruana, 1997), in which all the tasks are with the same set of features and the same set of samples. MTL achieves integrative learning by exploiting potential information sharing across the tasks, i.e., all the task models share the same sparsity pattern of the features.

Case 3: Lasso and grLasso. When q = 1, (3) becomes a grLasso method, as ‖B_k‖_⋆ = ‖B_k‖₂ when $B_k\in {ℝ}^{p_k}$. Further, when p_k = 1 and p = K, (3) reduces to a Lasso regression.

Different loss functions can be adopted in (3) to handle various statistical learning problems. In particular, multivariate dichotomous outcomes are frequently encountered in practice. For example, in the LSOA example, the health outcomes are responses to a collection of dichotomous questions. More generally, we extend iRRR to non-Gaussian responses by exploiting the generalized linear model (GLM) setup. Let $Y=\left(y_{ij}\right)\in {ℝ}^{n\times q}$ be the response matrix consisting of n independent samples from q response variables. We assume each y_ij follows a distribution in the exponential family with probability density f(y_ij; θ_ij, ϕ_j) = exp{(y_ijθ_ij − b(θ_ij))/(a(ϕ_j)) + c(y_ij; ϕ_j)}, where θ_ijs are the natural parameters which collectively form $\mathbf{\Theta }=\left({\theta }_{ij}\right)\in {ℝ}^{n\times q}$, ϕ_j is the dispersion parameter of the jth response, and a(·), b(·), c(·) are known functions determined by the response distribution. To streamline the idea, we focus on the natural exponential family distributions for which the dispersion parameter ϕ_j is known. For example, ϕ_j = 1 for Bernoulli or Poisson distributions. Without loss of generality, the canonical link g = (b′)⁻¹ is applied, so that $\mathbb{E}\left(y_{ij}\right)=b^{\prime }\left({\theta }_{ij}\right)=g^{-1}\left({\theta }_{ij}\right)$, where b′ is the derivative of b. The iRRR model can then be expressed as $\mathbf{\Theta }=\mathbf{1}{\mathit{\mu }}_0^{\text{T}}+{\sum }_{k=1}^K{X}_k{B}_{0k}$, where μ₀ is an intercept vector, B_0ks are possibly of low rank, and the remaining terms are the same as in model (1). An estimation criterion can then be formed by replacing the first term in (3) by the negative log-likelihood function.

The convex optimization of (3) has no closed-form solution in general, for which we propose an ADMM algorithm (Boyd et al., 2011). Due to space limit, all the details are presented in Web Appendix A; there we also provide details on handling incomplete data and binary responses as an example of the GLM setup, and on further extensions including the incorporation of ℓ₂ regularization and adaptive estimation.

3. Theoretical Analysis

We investigate the theoretical properties of the proposed iRRR estimator from solving the convex cNNP problem. In particular, we derive its non-asymptotic performance bounds for estimation and prediction. Our general results recover performance bounds of several related methods, including Lasso, grLasso and NNP. We further show that iRRR is capable of substantially outperforming those methods under realistic settings of multi-view learning. All the proofs are provided in Web Appendix D.

We mainly consider the multi-view regression model in (1), i.e., $Y={\sum }_{k=1}^K{X}_k{B}_{0k}+E$, and the iRRR estimator in (3) with the weights defined in (4), i.e.,

$$\widehat{B}\in \text{arg}\underset{B\in {ℝ}^{p\times q}}{\text{min}}\frac{1}{2n}\Vert Y-XB{\Vert }_{\text{F}}^2+\mathrm{\lambda }\sum _{k=1}^K\sigma \left({\mathbf{\text{X}}}_k,1\right)\{\sqrt{q}+\sqrt{r\left(X_k\right)}\}{\Vert B_k\Vert }_{\star }/n.$$

Define Z = X^TX/n, and $Z_k=X_k^{\text{T}}{X}_k/n$, for k = 1, … , K. We scale the columns of X such that the diagonal elements of Z all equal to 1. Denote Λ(Z, l) as the lth largest eigenvalue of Z, so that Λ(Z, l) = σ(X, l)²/n.

Theorem 1: Assume E has independent and identically distributed (i.i.d.) N(0, τ²) entries. Let λ = (1+θ)τ, with θ > 0 arbitrary. Then with probability at least $1-{\sum }_{k=1}^K\text{exp}[-{\theta }^2\left\{q+r\left({\text{X}}_k\right)\right\}/2]$, we have

$${\Vert X\widehat{B}-X{B}_0\Vert }_{\text{F}}^2⩽{\Vert XC-X{B}_0\Vert }_{\text{F}}^2+4\mathrm{\text{λ}}\sum _{k=1}^K\sigma \left(X_k,1\right)\{\sqrt{q}+\sqrt{r\left(X_k\right)}\}{\Vert C_k\Vert }_{\star },$$

for any $C_k\in {ℝ}^{p_k\times q}$, k = 1, … , K and $C={\left(C_1^{\text{T}},\dots ,C_K^{\text{T}}\right)}^{\text{T}}$.

Theorem 1 shows that $\widehat{\mathbf{\text{B}}}$ balances the bias term $\Vert XC-X{B}_0{\Vert }_{\text{F}}^2$ and the variance term $4\mathrm{\lambda }{\sum }_{k=1}^K\sigma \left({\mathbf{\text{X}}}_k,1\right)\{\sqrt{q}+\sqrt{r\left({\mathbf{\text{X}}}_k\right)}\}{\Vert {\mathbf{\text{C}}}_k\Vert }_{\star }$. An oracle inequality for $\widehat{\mathbf{\text{B}}}$ is then readily obtained for the low-dimensional scenario σ(X, p) > 0; see the corollary in Web Appendix D.

We now investigate the general high-dimensional scenario. Motivated by Lounici et al. (2011), Negahban and Wainwright (2011), Koltchinskii et al. (2011), among others, we impose a restricted eigenvalue condition (RE). We say that X satisfies RE condition over a restricted set $\mathcal{C}\left(r_1,\dots ,r_K;\delta \right)\subset {ℝ}^{p\times q}$ if there exists some constant κ(X) > 0 such that

$$\frac{1}{2n}\Vert \mathbf{\text{X}}\mathrm{\Delta }{\Vert }_{\text{F}}^2⩾\kappa (\mathbf{\text{X}})\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2,\text{ for all }\mathrm{\Delta }\in \mathcal{C}\left(r_1,\dots ,r_K;\delta \right).$$

Here each r_k is an integer satisfying 1 ⩽ r_k ⩽ min(p_k, q) and δ is a tolerance parameter. The technical details on the construction of the restricted set is provided in Web Appendix B.

Theorem 2: Assume that E has i.i.d. N(0, τ²) entries. Suppose X satisfies the RE condition with parameter κ(X) > 0 over the set $\mathcal{C}\left(r_1,\dots ,r_K;\delta \right)$. Let λ = 2(1 + θ)τ with θ > 0 arbitrary. Then with probability at least $1-{\sum }_{k=1}^K\text{exp}[-{\theta }^2\left\{q+r\left({\mathbf{\text{X}}}_k\right)\right\}/2]$,

$$\begin{gathered} \begin{array}{l}{\Vert \widehat{B}-B_0\Vert }_{\mathbb{F}}^2\preccurlyeq \text{max}\{{\delta }^2,{\tau }^2{(1+\theta )}^2\sum _{k=1}^K\frac{\mathrm{\Lambda }\left(Z_k,1\right)}{\kappa {(X)}^2}\frac{{\{\sqrt{q}+\sqrt{r\left(X_k\right)}\}}^2{r}_k}{n},\\ \tau \\ (1+\theta )\sum _{k=1}^K\frac{\sqrt{\mathrm{\Lambda }\left(Z_k,1\right)}}{\kappa (X)}\frac{\left\{\sqrt{q}+\sqrt{r\left(X_k\right)}\right\}\left\{{\sum }_{j=r_k+1}^{m_k}\sigma \left(B_{0k},j\right)\right\}}{\sqrt{n}}\}.\end{array} \end{gathered}$$

On the right hand side of the above upper bound, the first term is from the tolerance parameter in the RE condition, which ensures that the condition can possibly hold when the true model is not exactly low-rank (Negahban and Wainwright, 2011), i.e., when ${\sum }_{j=r_k+1}^{m_k}\sigma \left(B_{0k},j\right)\ne 0$. The second term gives the estimation error of recovering the desired view-specific low-rank structure, and the third term gives the approximation error incurred due to approximating the true model with the view-specific low-rank structure. When the true model is exactly of low rank, i.e., r(B_0k) = r_0k, it suffices to take δ = 0 and the upper bound then yields the estimation error, i.e. ${\tau }^2{\sum }_{k=1}^K\left\{q+r\left(X_k\right)\right\}{r}_{0k}/n$,. This rate holds with high probability in the high-dimensional setting that q + r(X_k) → ∞. In the classical setting of n → ∞ with fixed q and r(X_k), by choosing $\theta \propto \sqrt{\text{log}n}$, the rate becomes ${\tau }^2\text{log}(n){\sum }_{k=1}^K{r}_{0k}/n$ with probability approaching 1.

Intriguingly, the results in Theorem 2 can specialize into oracle inequalities of several existing regularized estimation methods, such as NNP, MTL and Lasso. This is because these models can all be viewed as special cases of iRRR. As such, iRRR seamlessly bridges group-sparse and low-rank methods and provides a unified theory of the two types of regularization. Several examples are provided in Web Appendix C.

To see the potential advantage of iRRR over NNP or MTL, we make some comparisons of their error rates based on Theorem 2. To convey the main message, consider the case where p_k = p₁, $r\left({\text{X}}_k\right)=r_{X_1}$ for k = 1, … , K, r_0k = r₀₁ for k = 1, … , s, and r_0k = 0 for k = s + 1, … , K. The error rate is ${\tau }^{2}s{r}_{01}\left(q+r_{X_1}\right)/n$, τ²r₀(q + r_X)/n, for iRRR and NNP, respectively, with high probability. As long as sr₀₁ = O(r₀), iRRR achieves a faster rate since $r_{X_1}⩽r_X$ always holds. For comparing iRRR and MTL, we get that with probability 1−p⁻¹, iRRR achieves an error rate ${\tau }^2\left(\log p+q+r_{X_1}\right)s{r}_{01}/n$ (by choosing $\theta =\sqrt{4\log p/\left(q+r_{X_1}\right)}$) while MTL achieves τ²(log p + q + 1)sp₁/n. The two rates agree with each other in the MTL setting when $r_{X_1}=r_{01}=p_1=1$, and the former rate can be much faster in the iRRR setting when, for example, r₀₁ ≪ p₁ and $r_{X_1}=O\left(\log \left(p\right)+q\right)$.

4. Simulation

4.1. Settings and Evaluation Metrics

We conduct simulation studies to demonstrate the efficacy of the proposed iRRR method. We consider two response types: Gaussian and binary. In Gaussian settings, we compare iRRR with the ordinary least squares (OLS), the ridge RRR (RRRR) (Mukherjee and Zhu, 2011) (which contains RRR as a special case), and the adaptive NNP (aNNP) (which has been shown to be computationally efficient and can outperform NNP in Chen et al., 2013). For the settings in which the true coefficient matrix is sparse, we also include MTL (Caruana, 1997) (by treating each predictor as a group in iRRR), as well as Lasso (Tibshirani, 1996) and grLasso (Yuan and Lin, 2006) for each response variable separately (grLasso accounts for the grouping information in the multi-view predictors). In binary settings, we compare iRRR with the generalized RRR (gRRR) (She, 2013; Luo et al., 2018) and the univariate penalized logistic regression (glmnet) with the elastic net penalty (Zou and Hastie, 2005).

For the Gaussian models, we consider a range of simulation settings. Setting 1 is the basic setting, where n = 500, K = 2, p₁ = p₂ = 50 (p = 100), and q = 100. We generate the rows of the design matrix X independently from a p-variate Gaussian distribution N(0, Σ_x) with Σ_x = I_p, followed by column centering. The error matrix E is filled with i.i.d. standard Gaussian random numbers. (We also consider correlated errors. The results are similar and contained in Web Appendix E.) Each coefficient matrix B_0k has rank r_0k = 10, which is generated as $B_{0k}=L_k{R}_k^{\text{T}}$ with the entries of $L_k\in {ℝ}^{p_k\times r_{0k}}$ and $R_k\in {ℝ}^{q\times r_{0k}}$ both generated from N(0, 1). Consequently, $B_0={\left(B_{01}^{\text{T}},B_{02}^{\text{T}}\right)}^{\text{T}}$ has rank r₀ = r₀₁ + r₀₂ = 20. The response matrix Y is then generated based on the model in (1). As such, there are more than 10,000 unknown parameters in this model, posing a challenging large-scale problem. Furthermore, we also consider incomplete responses, with 10%, 20%, 30% entries missing completely at random.

The other settings are variants of Setting 1:

• Setting 2 (multi-collinear): The predictors in the two views X₁ and X₂ are highly correlated. All the p = p₁ + p₂ predictors are generated jointly from a p-variate Gaussian distribution N_p(0, Σ_x), where Σ_x has diagonal elements 1 and off-diagonal 0.9.

• Setting 3 (globally low-rank): We set R₁ = R₂ when generating B₀₁ and B₀₂, so that the low rank structures in separate coefficient matrices also imply a globally low-rank structure. We consider three scenarios: r₀ = r₀₁ = r₀₂ = 20, r₀ = r₀₁ = r₀₂ = 40, and r₀ = 60, r₀₁ = r₀₂ = 50.

• Setting 4 (multi-set): We consider multiple views, K ∈ {3, 4, 5}. The additional design matrices and coefficient matrices are generated in the same way as in Setting 1.

• Setting 5 (sparse-view): We consider K = 3, where the last predictor set X₃ is generated in the same way as in Setting 1 but is irrelevant to prediction, i.e., B₀₃ = 0.

For the binary models, we consider two settings: the basic setting (Setting 6) and the sparse-view setting (Setting 7), which are similar to Setting 1 and Setting 5, respectively. The differences are that the sample size is set to n = 200, the intercept μ₀ is set as a vector of random numbers from the uniform distribution on [−1, 1], and the entries of Y are drawn from Bernoulli distributions with their natural parameters given by $\mathbf{\Theta }=\mathbf{1}{\mathit{\mu }}_0^{\text{T}}+{\sum }_{k=1}^K{X}_k{B}_{0k}$.

In Settings 1–5, we use the MSPE to evaluate the performance of different methods,

$$\text{MSPE}\left(B_0,\widehat{B}\right)=\text{tr}\left\{{\left(B_0-\widehat{B}\right)}^{\text{T}}{\mathrm{\Sigma }}_x\left(B_0-\widehat{B}\right)\right\},$$

where tr(·) represents the trace of a matrix, $\widehat{\mathbf{\text{B}}}$ is the estimate of B₀, and Σ_x is the covariance matrix of X. In Settings 6–7, we evaluate the average cross entropy between the true and estimated probabilities on an independently generated validation data set of size n = 500,

$$\text{En}\left({\mu }_0,B_0,\widehat{\mu },\widehat{B}\right)=-\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^q\left\{p_{ij}\text{log}{\widehat{p}}_{ij}+\left(1-p_{ij}\right)\text{log}\left(1-{\widehat{p}}_{ij}\right)\right\},$$

where p_ij = exp(θ_ij)/{1 + exp(θ_ij)}, and ${\widehat{p}}_{ij}$ is its corresponding estimate.

For each simulation setting, we first generate an independent testing data set to select tuning parameters for different methods. Once selected, the tuning parameters are fixed in subsequent analyses. This unified approach alleviates inaccuracy in the empirical tuning parameter selection to ensure a fair comparison of different regularization methods. We have also tried 5-fold CV. The results are similar to those from the validation data tuning and thus omitted for brevity. In each setting, the experiment is replicated 100 times.

4.2. Results

Table 1 reports the results for Settings 1–4. In all the settings, the three regularized estimation methods always substantially outperform OLS, indicating the strength and necessity of dimension reduction. In Setting 1 (basic), iRRR provides the best prediction performance, followed by aNNP and RRRR. When the outcomes are incomplete, only iRRR is applicable. The mean and standard deviation of MSPE over 100 repetitions are 7.87 (0.20), 8.64 (0.20), and 9.96 (0.24), when 10%, 20%, and 30% of the responses are missing, respectively. In Setting 2 (multi-collinear), iRRR is still the best. It is worth noting that owing to shrinkage estimation, RRRR slightly outperforms aNNP. In Setting 3 (globally low-rank), aNNP and RRRR can slightly outperform iRRR when r₀ is much smaller than ${\sum }_{k=1}^K{r}_{0k}$. This can be explained by the fact that under this setting iRRR may be less parsimonious than the globally reduced-rank methods. To see this, when r₀ is small and r₀ = r₀₁ = r₀₂, we have that ${\sum }_{k=1}^K\left(p_k+q-r_{0k}\right)r_{0k}=\left\{p+K\left(q-r_0\right)\right\}{r}_0>\left(p+q-r_0\right)r_0$, i.e., iRRR yields a larger number of free parameters than RRR. Nevertheless, iRRR regains its superiority over the globally low-rank methods when r₀ becomes large. We remark that in multi-view problems the scenario of r₀ ≪ ∑_k r_0k rarely happens unless the relevant subspace from each view largely overlaps with each other. In Setting 4 (multi-set), we confirm that the advantage of iRRR becomes more obvious as the number of distinct view sets increases.

Table 1:

Simulation results for Settings 1–4. The mean and standard deviation (in parenthesis) of MSPE over 100 simulation runs are presented. In each setting, the best results are highlighted in boldface.

		iRRR	aNNP	RRRR	OLS
Setting 1		7.22 (0.17)	7.76 (0.22)	8.38 (0.24)	25.15 (0.36)
Setting 2		4.21 (0.10)	4.69 (0.11)	4.52 (0.11)	25.15 (0.36)
Setting 3	(r0 = 20)	10.13 (0.22)	7.81 (0.25)	8.25 (0.26)	25.16 (0.39)
	(r0 = 40)	12.48 (0.19)	12.39 (0.22)	13.76 (0.26)	25.04 (0.37)
	(r0 = 60)	13.62 (0.21)	14.66 (0.26)	15.66 (0.17)	25.11 (0.39)
Setting 4	(K = 3)	10.19 (0.21)	13.99 (0.32)	15.44 (0.31)	43.76 (0.59)
	(K = 4)	13.04 (0.22)	19.99 (0.35)	19.68 (0.19)	68.00 (0.89)
	(K = 5)	14.84 (0.25)	24.90 (0.32)	21.43 (0.21)	101.87 (1.38)

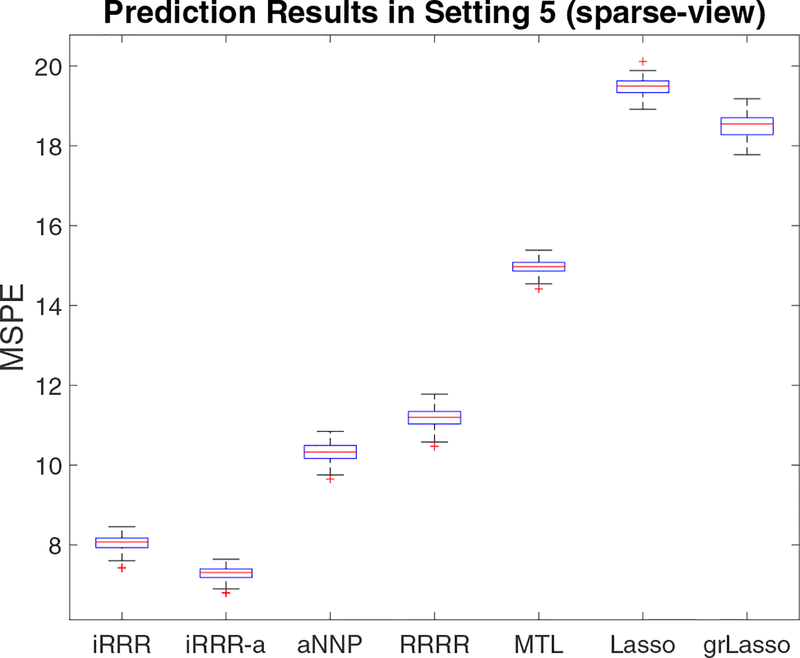
Figure 2 displays the results for Setting 5 (sparse-view). We find that the iRRR solution tuned based on predictive accuracy usually estimates the third coefficient matrix (which is a zero matrix in truth) as a nearly zero matrix and occasionally an exact zero matrix; in view of the construction of the cNNN penalty in iRRR, this “over-selection” property is analogous to that of Lasso or grLasso. Motivated by Zou (2006), we also experiment with an adaptive iRRR (denoted by iRRR-a) approach, where we first fit iRRR and then adjust the predefined weights by the inverse of the Frobenius norms of the estimated coefficient matrices. As a result, the iRRR-a approach achieves much improved view selection performance and even better prediction accuracy than iRRR. In contrast, MTL, Lasso and grLasso have worse performance than the low-rank methods, because they fail to leverage information from the multivariate response and/or multi-view predictor structures.

Figure 2:

Simulation results for Setting 5 (sparse-view). OLS is omitted as its performance is much worse than the reported methods.

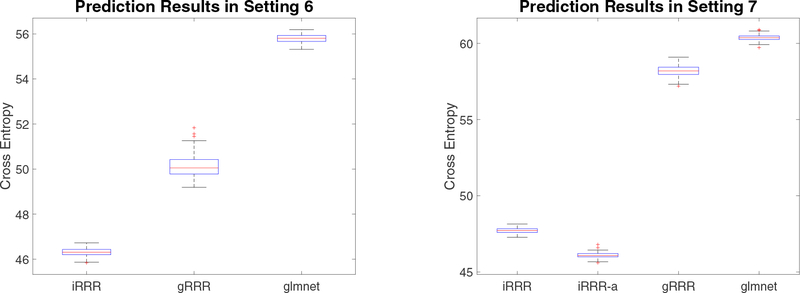
The simulation results of Settings 6–7 for binary models are displayed in Figure 3. The results are similar as in the Gaussian models, i.e., the iRRR methods substantially outperform the competing sparse or low-rank methods in prediction.

Figure 3:

Simulation results for Settings 6–7 with binary response variables.

We have also compared the computational time of different methods (on a standard desktop with Intel i5 3.3GHz CPU). For example, the average time (in seconds) under Setting 1 is 0.68 (0.06), 0.07 (0.01) and 0.02 (0.00) for iRRR, aNNP and RRRR, respectively; under Setting 4 with K = 5 the average time becomes 0.96 (0.12), 0.09 (0.01) and 0.05 (0.01); under Setting 6 with binary responses, the average time is 1.71 (0.03), 0.98 (0.08) and 0.70 (0.08) for iRRR, gRRR and glmnet. As expected, iRRR is more computationally expensive than the globally low-rank or sparse methods. However, in view of the scale of the problem, the computational cost for iRRR is still low and acceptable.

5. An Application in the Longitudinal Studies of Aging

The LSOA (Stanziano et al., 2010) was a collaborative effort of the National Center for Health Statistics and the National Institute on Aging. The study interviewed a large cohort of senior people (70 years of age and over) in 1997–1998 (WAVE II) and 1999–2000 (WAVE III), respectively, and measured their health conditions, living conditions, family situations, health service utilizations, among others. Here our objective is to examine the predictive relationship between health-related events in earlier years and health outcomes in later years, which can be formulated as a multivariate regression problem.

There are n = 3988 common subjects who participated in both WAVE II and WAVE III interviews. After data pre-processing (Luo et al., 2018), p = 294 health risk and behavior measurements in WAVE II are treated as predictors, and q = 41 health outcomes in WAVE III are treated as multivariate responses. The response variables are binary indicators, characterizing various cognitive, sensational, social, and life quality outcomes, among others. Over 20% of the response data entries are missing. The predictors are multi-view, including housing condition (X₁ with p₁ = 38), family structure/status (X₂ with p₂ = 60), daily activity (X₃ with p₃ = 40), prior medical condition (X₄ with p₄ = 114), and medical procedure since last interview (X₅ with p₅ = 40). We thus apply the proposed iRRR method to perform the regression analysis. As a comparison, we also implement gRRR (Luo et al., 2018), and both classical and sparse logistic regression methods using the R package glmnet, denoted as glm and glmnet, respectively.

We use a random-splitting procedure to evaluate the performance of different methods. More specifically, each time we randomly select n_tr = 3000 subjects as training samples and the remaining n_te = 988 subjects as testing samples. For each method, we use 5-fold CV on the training samples to select tuning parameters, and apply the method to all the training data with the selected tuning parameters to yield its coefficient estimate. The performance of each method is measured by the average deviance between the observed true response values and the estimated probabilities, defined as

$$\text{ Average Deviance }=\frac{-2{\sum }_{i=1}^{n_{te}}{\sum }_{j=1}^q\left\{y_{ij}\text{log}{\widehat{p}}_{ij}+\left(1-y_{ij}\right)\text{log}\left(1-{\widehat{p}}_{ij}\right)\right\}{\delta }_{ij}}{{\sum }_{i=1}^{n_{te}}{\sum }_{j=1}^q{\delta }_{ij}},$$

where δ_ij is an indicator of whether y_ij is observed. We also calculate the Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC) curve for each outcome variable. This procedure is repeated 100 times and the results are averaged.

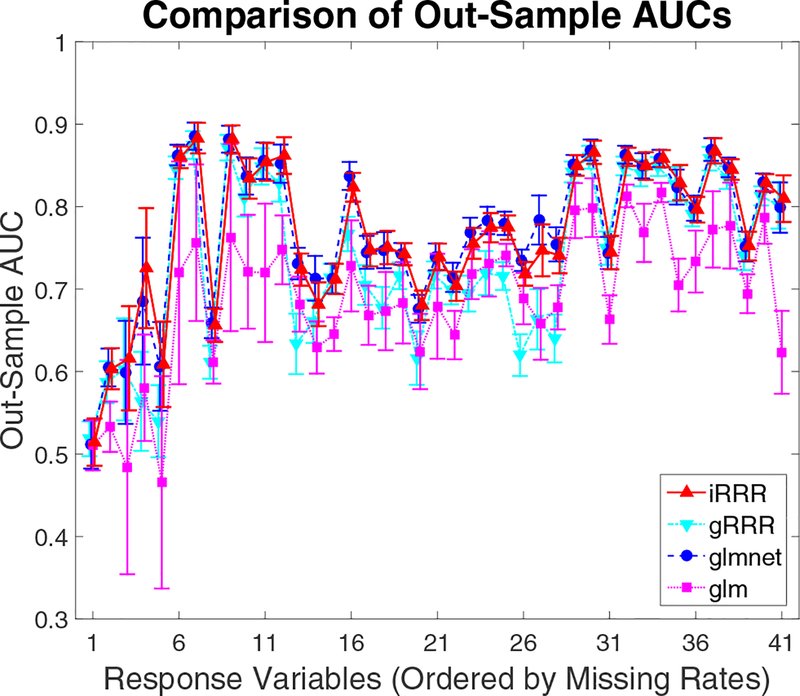
In terms of the average deviance, iRRR and glmnet yield very similar results (with mean 0.77 and standard deviation 0.01), and both substantially outperform gRRR (with mean 0.83 and standard deviation 0.01) and glm (fails due to a few singular outcomes). The outsample AUCs for different response variables are shown in Figure 4. The response variables are sorted based on their missing rates from large (over 70%) to small (about 13%). Again, the performance of iRRR is comparable to that of glmnet. The iRRR tends to have a slight advantage over glmnet for responses with high missing rates. This could be due to the fact that iRRR can borrow information from other responses while the univariate glmnet cannot.

Figure 4:

LSOA data analysis. The mean and standard deviation (error bar) of AUC for each response variable over 100 random-splitting procedures. The responses, from left to right, are ordered by missing rates from large to small.

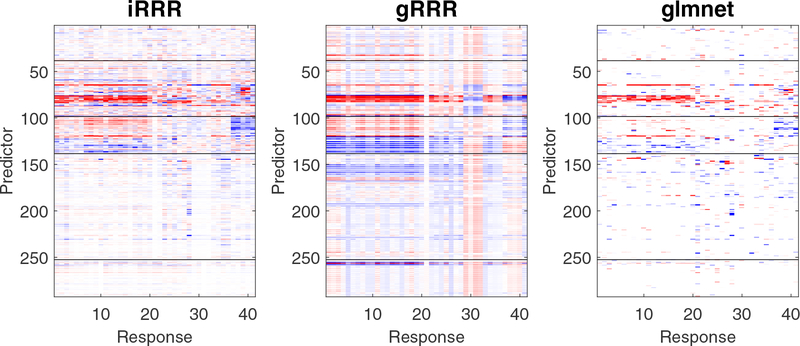
To understand the impact of different views on prediction, we produce heatmaps of the estimated coefficient matrices in Figure 5 (glm is omitted due to its poor performance). The estimates from iRRR and glmnet show quite similar patterns: it appears that the family structure/status group and the daily activity group have the most predictive power, and the variables within these two groups contribute to the prediction in a collective way. As for the other three views, iRRR yields heavily shrunk coefficient estimates, while glmnet yields very sparse estimates. These agreements partly explain the similarity of the two methods in their prediction performance. In contrast, the gRRR method tries to learn a globally low-rank structure rather than a view-specific structure; consequently, it yields a less parsimonious solution with less competitive prediction performance. Therefore, our results indicate that generally knowing the family structure/status and daily activity measurements, the information on housing condition, prior medical conditions, and medical procedures do not provide much new contribution to the prediction of health outcomes on cognition, sensation, social behavior, life quality, among others.

Figure 5:

LSOA data analysis. The heat maps of the coefficient matrices estimated from different methods. The predictors fall into 5 groups, namely, housing condition, family status, daily activity, prior medical condition, and change in medical procedure since last interview, from top to bottom separated by horizontal black lines. For visualization purpose, we also sort the responses based on their grouping structure (e.g., cognition, sensation, social behavior, and life quality).

6. Discussion

With multi-view predictor/feature sets, it is likely that some of the views are irrelevant to the prediction of the outcomes, and the features within a relevant view may be highly correlated and hence contribute to the prediction collectively rather than sparsely. When dealing with such problem, the two commonly used methodologies, i.e., sparse methods and low-rank methods, both have shortcomings. The joint extraction of latent features from each view in a supervised fashion offers a better solution; indeed, this is what iRRR strives to achieve.

There are many directions for future research. For conducting simultaneous view selection and within-view subspace selection, the proposed cNNP scheme can be extended to a general composite singular value penalization scheme, $\mathrm{\lambda }{\sum }_{k=1}^K{w}_k{\rho }_{\mathcal{O}}\left({\sum }_{j=1}^{p_k\wedge q}{\rho }_{\mathcal{I}}\left(\sigma \left(B_k,j\right)\right)\right)$,where ${\rho }_{\mathcal{I}}$ is an inner penalty function for inducing sparsity among the singular values of each B_k, and ${\rho }_{\mathcal{O}}$ is an outer penalty function for enforcing sparsity among the B_k matrices. For example, the family of bridge penalties (Huang et al., 2008) can be used in both inner and outer penalization. Incorporating sparse within-view variable selection to iRRR could also be fruitful; one way to achieve this is to use an additive penalty form of cNNP and grLasso. Moreover, it is possible to combine iRRR with a covariate-adjusted (inverse) covariance estimation method (Rothman et al., 2010), to jointly estimate the mean and covariance structures. Another pressing problem is to generalize iRRR to handle heterogeneous data, as in practice data may be count-valued, interval-valued, or mixed of several types with substantial missing values (Luo et al., 2018). Computationally, the ADMM algorithm can be coupled with a Majorization-Minimization algorithm to handle these cases.