Topography in the Bursting Dynamics of Entorhinal Neurons

SUMMARY

Medial entorhinal cortex contains neural substrates for representing space. These substrates include grid cells that fire in repeating locations and increase in scale progressively along the dorsal-to-ventral entorhinal axis, with the physical distance between grid firing nodes increasing from tens of centimeters to several meters in rodents. Whether the temporal scale of grid cell spiking dynamics shows a similar dorsal-to-ventral organization remains unknown. Here, we report the presence of a dorsal-to-ventral gradient in the temporal spiking dynamics of grid cells in behaving mice. This gradient in bursting supports the emergence of a dorsal grid cell population with a high signal-to-noise ratio. In vitro recordings combined with a computational model point to a role for gradients in non-inactivating sodium conductances in supporting the bursting gradient in vivo. Taken together, these results reveal a complementary organization in the temporal and intrinsic properties of entorhinal cells.

Graphical Abstract

In Brief

Bant et al. report that temporal spiking statistics of grid cells progressively change along the dorsal-to-ventral axis of the entorhinal cortex in behaving animals. These spiking dynamics are associated with improved spatial coding in vivo and correspond to a complementary dorsal-ventral organization in ion channel conductances in vitro.

INTRODUCTION

Neurons in the medial entorhinal cortex (MEC) provide signals for building an internal map of space that supports navigation (Gil et al., 2018; Hafting et al., 2005; Mallory et al., 2018; Sargolini et al., 2006; Solstad et al., 2008). These neurons include functionally defined grid cells that fire in multiple place-specific locations, border cells that fire maximally near boundaries, cells with stable but non-geometric spatial firing patterns, and cells that encode the head direction and running speed of the animal (Diehl et al., 2017; Hafting et al., 2005; Kropff et al., 2015; Solstad et al., 2008). Although these classifications reflect changes in firing rates (FRs) as a function of position, head direction, or speed, MEC cells can also be classified along the lines of their spike patterns at a millisecond timescale, with cells that fire bursts of action potentials (125–500 Hz) more often expressing grid cell firing patterns (Latuske et al., 2015). What these bursting dynamics contribute to MEC computation and the potential mechanisms contributing to such bursting dynamics, however, remain incompletely understood.

Previous work in other brain regions has indicated that bursting can provide unique computational benefits (Lisman, 1997). First, bursting may facilitate the reliability of information transfer (Kepecs et al., 2002; Lisman, 1997). Bursts of spikes, as well as the duration of the burst, increase the chance of a response in postsynaptic neurons in striate cortex and the hippocampus (Csicsvari et al., 1998; Snider et al., 1998). Second, bursting has been proposed to improve the signal-to-noise ratio. This feature of bursting has been observed in cortical regions, including visual and auditory cortex (Cattaneo et al., 1981; Eggermont and Smith, 1996; Livingstone et al., 1996), and in regions associated with navigation. In the hippocampus, bursts provide a more accurate estimate regarding the animal’s position compared with single spikes, and cells that burst are more likely to exhibit spatially tuned firing patterns (Epsztein et al., 2011; Mizuseki et al., 2011; Muller et al., 1987; Otto et al., 1991). Correspondence between bursting and spatial coding is also observed in the subiculum, the primary output structure of the hippocampus, where bursts encode position significantly better than isolated spikes and the propensity to burst can be used to classify cells (Simonnet and Brecht, 2019). The presence of neural populations in the subiculum classifiable by their bursting dynamics may support the formation of parallel streams of information, as the propensity to burst is highly associated with a cells efferent target area (Cembrowski et al., 2018; Graves et al., 2012; Kim and Spruston, 2012). Subiculum neurons that project to the amygdala, lateral entorhinal cortex, nucleus accumbens, and orbitofrontal cortex consist primarily of non-bursting neurons, while those that project to the MEC, retrosplenial cortex and presubiculum primarily consist of bursting neurons (Kim and Spruston, 2012). Finally, bursts have been proposed to form a parallel code, in which they code for different stimulus features in the same spike train (Oswald et al., 2004).

Although burst dynamics could arise from large transient inputs, several lines of evidence in the hippocampus point to the possibility that bursts reflect an interaction between two factors: synaptic inputs and intrinsic conductances (Bittner et al., 2015; Carette et al., 1992; Wong et al., 1979). In MEC, both of these factors progressively change along the dorsal-to-ventral (DV) MEC axis. For example, multiple ion channel expression patterns change and the number of synaptic contacts from GABAergic inhibitory neurons to layer II excitatory MEC cells decreases along the DV MEC axis (Beed et al., 2013; Garden et al., 2008; Giocomo and Hasselmo, 2008; Hafting et al., 2005; Ramsden et al., 2012). These changes correlate with DV gradients in the tuning features of functionally defined MEC neurons, such as the spatial distance between grid cell firing fields and the width of head direction tuning curves (Giocomo et al., 2014; Hafting et al., 2005; Stensola et al., 2012). Whether bursting shows DV topography, as well as the impact of such topography on MEC coding in behaving animals, is not known.

Here, we examined the relationship between bursting, functionally defined coding and intrinsic conductances along the DV axis of MEC. We first considered whether a graded organization in the spike patterns of MEC cells in behaving animals exists. We report that the propensity for neurons to burst decreased along the DV axis and that bursting occurred predominately in grid cells. Moreover, both the propensity to burst and fidelity of grid coding increased at fast running speeds, raising the possibility that spiking dynamics in dorsal MEC are ideally suited to support spatial navigation. We then used whole-cell in vitro recordings and computational modeling to demonstrate that the organization in bursting relies, at least in part, on non-inactivating Na conductances. Together, these results reveal a DV organization in the temporal spiking dynamics of MEC cells that could complement the DV organization in the scale of spatial tuning of MEC cells.

RESULTS

Dorsal-Ventral Gradient in Bursting In Vivo

We first considered the spiking activity of 821 superficial putative principal MEC cells recorded as mice foraged in open arenas (STAR Methods; Figure S1). We labeled spikes that occurred within 10 ms of each other “burst spikes” and used this to define a bursting score (BS; number of burst spikes/total number of spikes) (STAR Methods). Bursts typically occurred as doublets (mean spikes per burst ± SD = 2.22 ± 0.59), with spikes per burst and a neuron’s average FR positively correlating with the BS (Pearson’s correlation: spikes per burst × BS, R² = 0.87, p < 0.001; FR × BS, R² = 0.021, p < 0.001) (Figures 1A and 1B; Figures S2 and S3). BSs were stable across recording sessions, and jittering the bursting threshold of 10 ms resulted in similar BSs across the population (Figures S3 and S4). Interestingly, the propensity for cells to burst was organized along the dorsal-ventral MEC axis, and the BS of cells progressively decreased from dorsal to ventral MEC (R² = −0.017, p < 0.001, n = 821) (Figure 1C). This effect was preserved even when normalizing the BS to bursting expected via Poisson firing (Figure S4). However, bursting also varied across the MEC population (BS range 0–0.65, mean BS ± SD = 0.093 ± 0.11), and many cells in dorsal MEC had low BSs (Figure 1C). Thus, the DV gradient in the BS of cells represented a progressive decrease in the proportion of cells with a high BS, as indicated by a significant DV decrease in the top 25th percentile of BS (R² = −0.97, p < 0.02, for four bins; Figure 1C).

Figure 1. In Vivo Bursting Dynamics Are Graded along the MEC DV Axis.

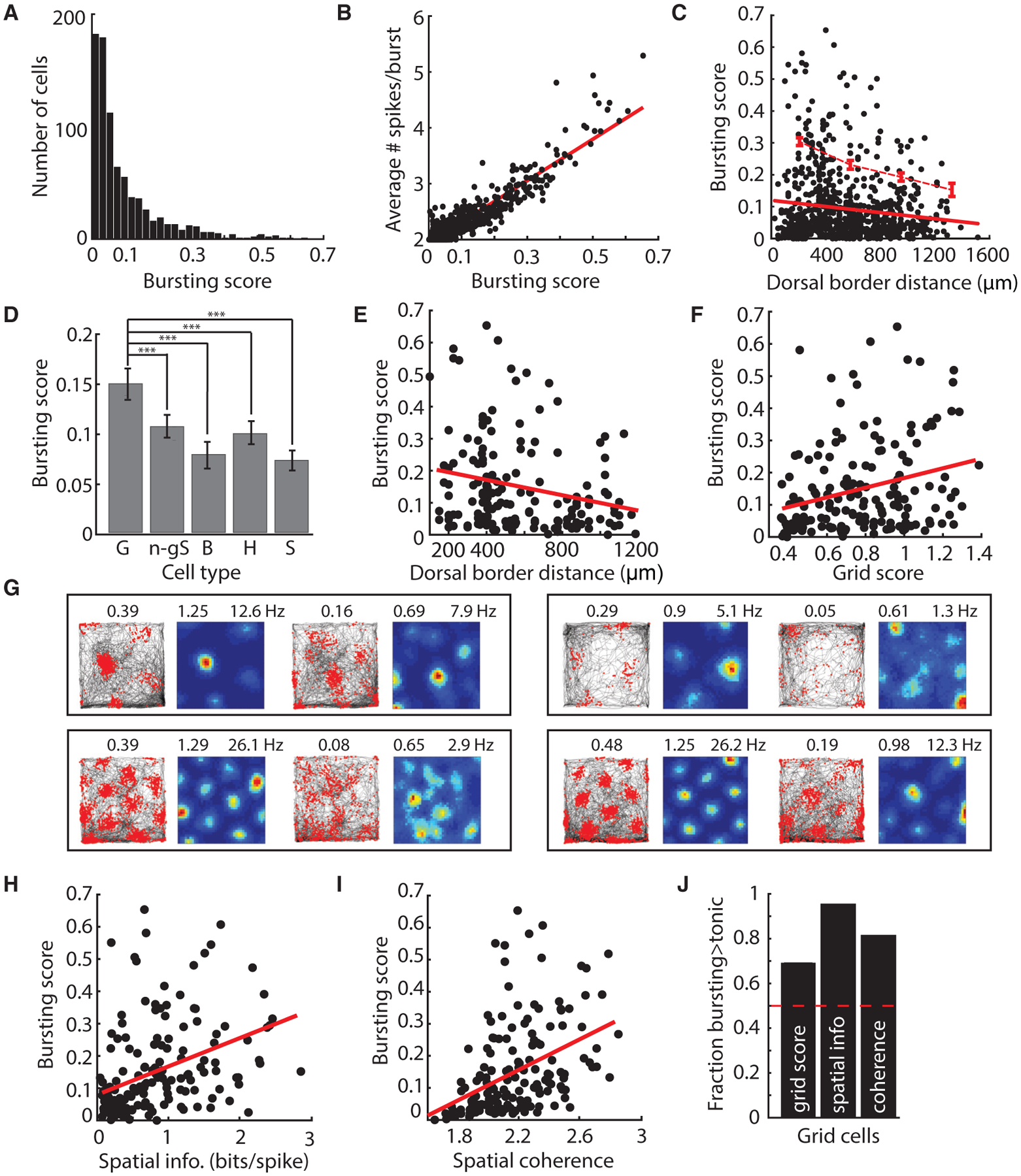
(A) Histogram of BS for 821 MEC cells.

(B) Average spikes per burst increased with BS.

(C) BS decreases in a DV fashion among the top 25% of bursting scores (top dotted red line). Bottom red line indicates the linear fit for all cells.

(D) Average BS ± SEM for grid (G), non-grid spatial (n-gS), border (B), head direction (H), and speed (S) cells. Grid cells showed higher BSs compared with other cell types (BS ± SEM: G = 0.15 ± 0.01, n-gS = 0.11 ± 0.01, B = 0.08 ± 0.01, H = 0.10 ± 0.01, S = 0.07 ± 0.01; one-way ANOVA: F[4, 856] = 10.9, p < 0.001; G versus n-gS, t[417] = 3.5, p < 0.001; B, t[251] = 4.3, p < 0.001; H, t[377] = 3.8, p < 0.001; S, t[309] = 5.7, p < 0.001). ***p < 0.001.

(E and F) For grid cells, BS decreased with DV location (E) (BS × depth: R² = 0.056, p < 0.01), and grid score increased with BS (F) (BS × grid score: R² = 0.075, p < 0.01). Best-fit lines to data are in red. BS was significantly predicted by grid score even when depth and average firing rate were taken into account (significant coefficient in linear model predicting BS from grid score, depth, average FR: t[163] = 3.55, p < 0.001). BS was not significantly predicted by grid score in a model for which BS was predicted from grid score, spatial information, spatial coherence, depth, and average firing rate (“full model”: grid score, t[163] = 1.08, p = 0.28). However, grid score correlated strongly with spatial information (p < 0.001) and spatial coherence (p < 0.001), which were significant in this same model.

(G) Each box shows trajectory (left) and rate maps (right) for two co-recorded grid cells. Cells on the left exhibited higher BSs than cells on the right. BSs denoted above plots showing the animal’s trajectory (black) overlaid with spikes (red dots). The grid score (left) and maximum firing rate (right) are denoted above the rate map, color-coded for minimum (blue) and maximum (red) values.

(H and I) For grid cells, spatial information (H) and spatial coherence (I) increased with BS (BS × spatial information, R² = 0.15, p < 0.001; BS × spatial coherence, R² = 0.19, p < 0.001). Best-fit lines to data are in red. BS was significantly predicted by spatial information and spatial coherence, when depth and average firing rate were taken into account (spatial information, t[163] = 10.5, p < 0.001; spatial coherence, t[163] = 6.1, p < 0.001). BS was significantly predicted by spatial information, but not spatial coherence, in the full joint model (“full model”: spatial information, t[163] = 5.61, p < 0.001; spatial coherence, t[163] = −1.08, p = 0.28), although spatial information and spatial coherence were strongly correlated (p < 0.001).

(J) Grid score, spatial information, and coherence computed from burst spikes are larger than those computed from the same number of tonic spikes. See also Figures S1–S4.

Bursting in Functionally Defined Entorhinal Cells

Given the variation in bursting across the MEC population (Figure 1C), we next examined whether the gradient in the BS of cells was associated with specific functionally defined MEC cell classes (cell numbers: grid, n = 167; non-grid/border spatial, n = 252; border, n = 86; head direction, n = 212; speed, n = 144) (STAR Methods). Grid cells had significantly higher bursting values compared with all other MEC cell classes, consistent with previous work (Figure 1D; Figures S3 and S4; Latuske et al., 2015). Moreover, the DV gradient was evident in only two classes of functionally defined MEC cells: grid cells and non-grid, non-border spatially tuned cells (Figures 1E–1G; Figure S3; STAR Methods). Because grid cells showed the highest bursting values compared with other MEC cell classes, as well as a significant dorsal-ventral gradient in BS, we focused our analyses on this cell population. We found that the BSs of grid cells positively correlated with spatial information, spatial coherence, and grid score, a measure of the 60° symmetry present in the grid firing pattern (Figures 1F–1I; Figure S3; all correlations performed separately). However, BSs did not appear to correlate with theta modulation or theta locking (Figure S2).

Why did the propensity to burst correlate with grid coding features? One possibility is that burst spikes convey high spatial symmetry and coherence and thus, cells with bursts will be more informative. To test this idea, we enforced a refractory period in each cell by deleting the spikes that followed the first spike in the burst, in essence converting burst spikes to tonic spikes. We then re-computed the grid score for each cell. Enforcing a refractory period decreased the correlation between the newly computed grid score and the original BS (Figure 2A). Increasing the enforced refractory period further decreased the correlation between newly computed grid scores and the original BS (slope < 0: F statistic versus constant model = 49.6, p < 0.01, F test). However, one possibility is that any decrease in the number of spikes will reduce the correlation between grid score and BS. To rule out this possibility, we performed a control analysis in which we randomly rejected the number of spikes to match the number of spikes deleted in the enforced refractory period analysis. We then re-computed the grid score for each cell. This analysis revealed a decrease in the correlation between the newly computed grid scores and the original BS, but importantly, this decrease was significantly less than what was observed when burst spikes were preferentially deleted (slope < 0: F statistic versus constant model = 55.6, p < 0.01, F-test; analysis of covariance [ANCOVA] slopes different with F = 8.88, p < 0.05) (Figure 2A). This demonstrates that burst spikes are more accurate than tonic spikes and raises the possibility that bursts could act as an error correction code to improve downstream decoding of position signals (Hsu et al., 2018).

Figure 2. Bursting In Vivo Likely Reflects Large or High-Frequency Inputs.

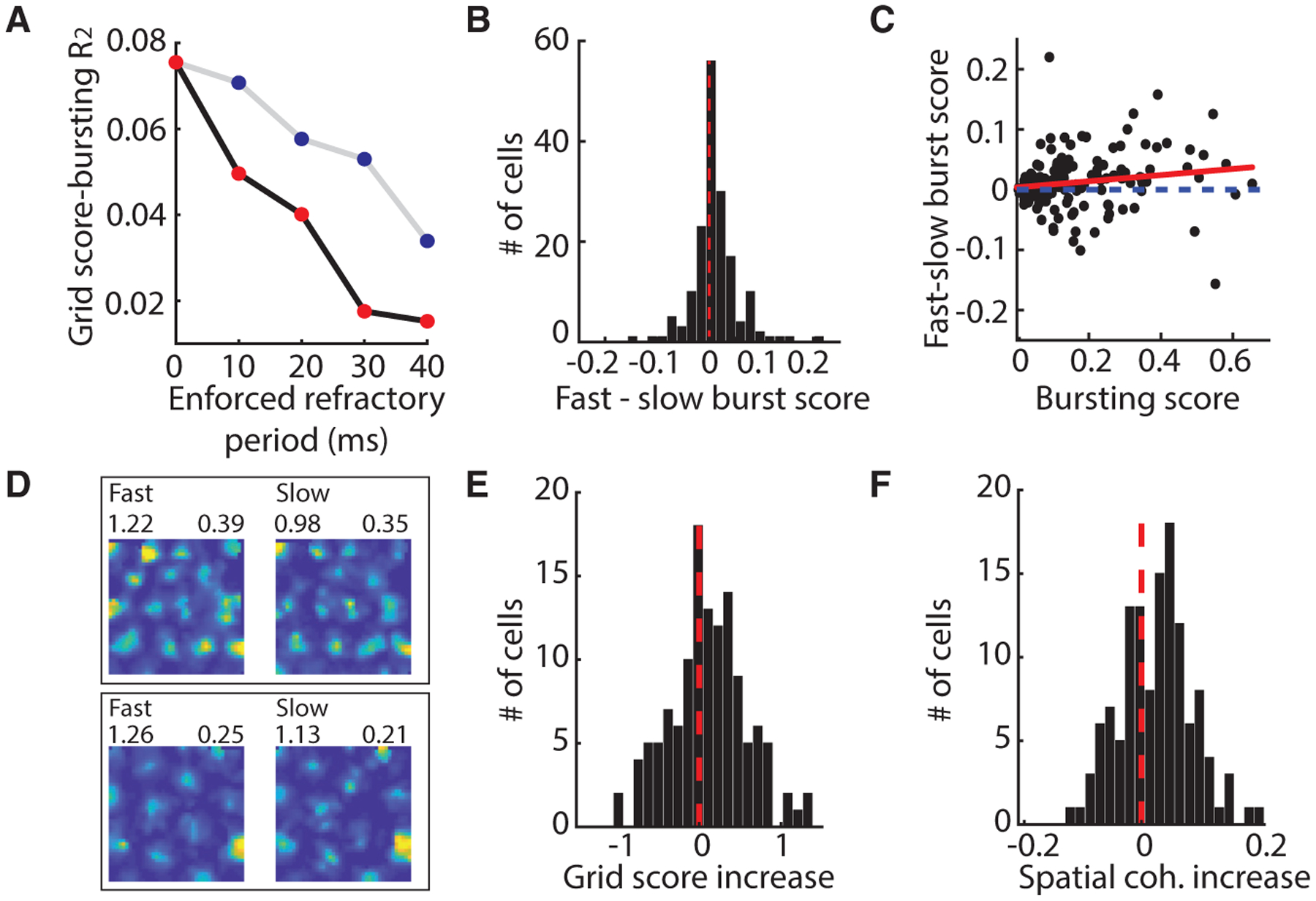
(A) The correlation between grid score and BS decreases when bursts are replaced by single tonic spikes and continues to decrease as the minimum refractory period used to define a burst is increased (black line, red dots). Transparent dots correspond to values for which the correlation is not significant. Random rejection of spikes does not decrease the correlation (gray line, blue dots).

(B) The BS increased during fast speeds.

(C) The increase in BS during fast-compared with slow-speed epochs increases with the BS of a cell. Best-fit line to data is in red.

(D) Firing rate maps of grid cell firing during fast (left) and slow (right) epochs color-coded for minimum (blue) and maximum (red) values. Grid score (top left) and BS (top right).

(E and F) Grid score (E) and spatial coherence (F) increase during fast epochs.

See also Figures S1–S4.

We next considered why burst spikes might be more accurate than tonic spikes. As suggested by previous work (Lisman, 1997), bursts can result from large or high-frequency excitatory inputs. If this is the case, we could expect that an increase in the magnitude or frequency of excitatory inputs would increase the amount of bursting. One condition under which the magnitude or frequency of inputs to grid cells likely increases is at high running speeds (Burak and Fiete, 2009; Burgess et al., 2007; Kropff et al., 2015). To investigate whether running speed is associated with the propensity to burst, we re-computed the grid cell BS after splitting each session into slow and fast running speed epochs, on the basis of the average running speed across sessions (slow, 2.5–10 cm/s; fast, 10–50 cm/s; Figure S4). We found that the propensity to burst increased during fast speeds (sign test z = 3.58, p < 0.001) and that this increase in bursting correlated with the BS of a cell (R² = 0.03, p < 0.05) (Figures 2B and 2C). Consistent with the idea that the spatial coding of grid cells improves as the propensity to burst increases, the score and spatial coherence of grid cells also increased during fast running speeds (n = 126, down-sampled to match position coverage and time points; grid score, p < 0.05; spatial coherence, p < 0.01; sign test) (STAR Methods) (Figures 2D–2F). These results point to a framework in which bursts occur more often when large or high-frequency inputs are received, driving higher coherence and symmetry in the grid code.

Dorsal-Ventral Gradient in Temporally Specific Input Integration

Bursting can reflect both the temporal dynamics of inputs and intrinsic conductances (Bittner et al., 2015; Carette et al., 1992; Wong et al., 1979). To next examine how these two factors influence bursting in MEC, we conducted a series of whole-cell patch-clamp recordings of MEC layer II/III cells. We began by considering how the integration of temporally precise inputs by single cells varied along the DV axis. We leveraged a current-clamp protocol that takes into consideration how the timing of inputs influences the propensity of cells to burst. In this protocol, the threshold for evoking an action potential was first assayed with a 1 ms current injection. Consistent with the known DV gradient in input resistance, the threshold for evoking an action potential varied along the DV axis (threshold range 800–3,400 pA; mean ± SEM = 1,820 ± 102 pA; DV position × pA, R² = 0.38, p < 0.0001; n = 42) (Garden et al., 2008). We then examined the ease with which we could evoke a second action potential (Metz et al., 2005). We injected a second 1 ms step current at varying latencies (2–64 ms after the first spike), increasing the amplitude of the second current until it produced a second spike (Figures 3A and 3B). This second spike threshold (SST) was then normalized to the first spike threshold. The SST will be smaller in cells that require less current to produce a second spike and represents the amount of input required to generate a spike in a temporally precise manner.

Figure 3. In Vitro Bursting Dynamics Vary along the DV Axis of MEC.

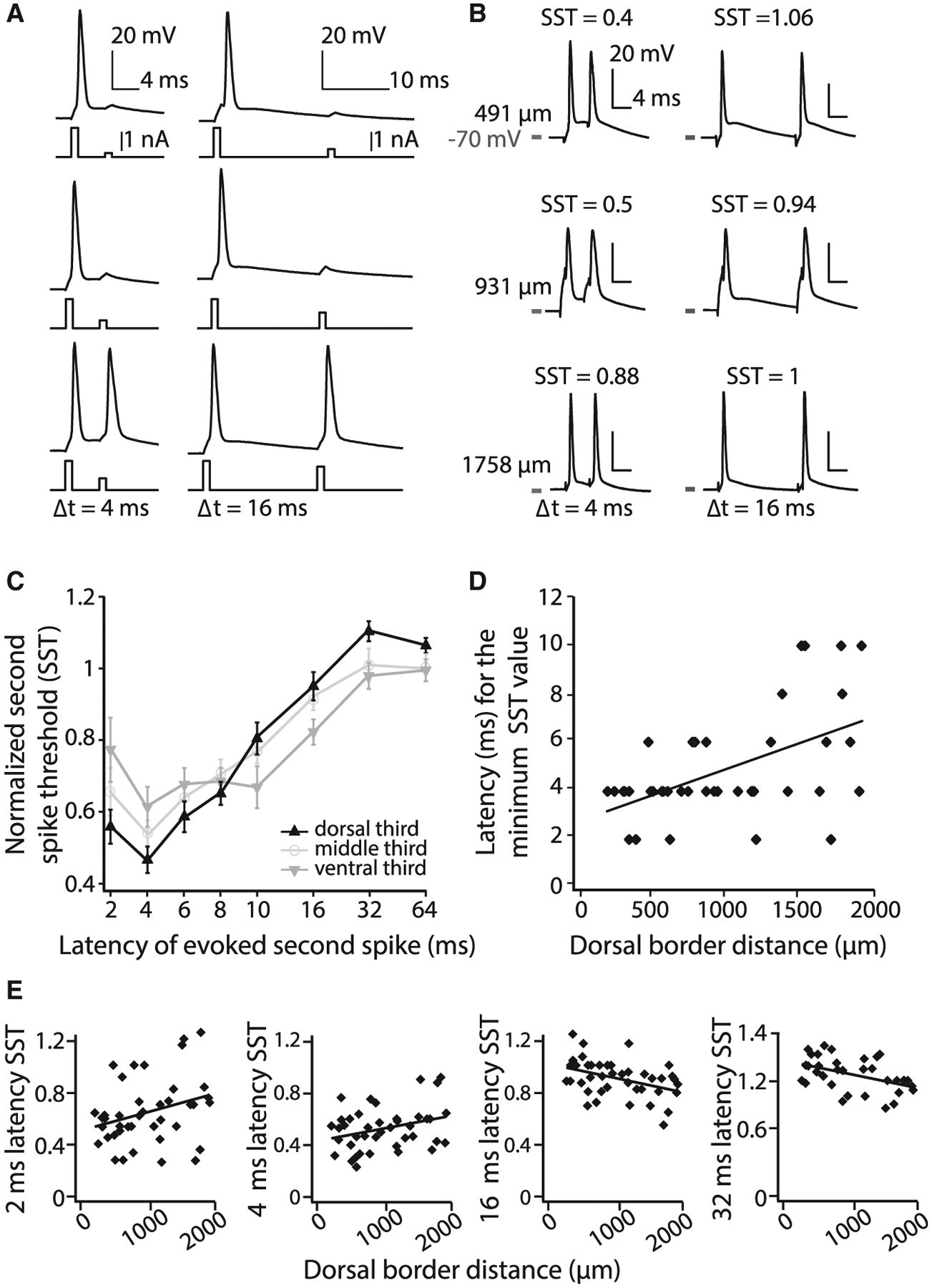
(A) Illustration of the current-clamp assay used to quantify the propensity to burst. The current required to evoke a spike is empirically determined and used as the first stimulus. The second 1 ms pulse (shown for two of eight latencies) is then increased in 100 pA increments until the cell reliably fires a second action potential.

(B) Examples of the dual-pulse protocol at three latencies in three cells located along the DV axis (DV depth noted to the left and SST values at the top of each trace).

(C) SST values for different latencies (log axis). Mean ± SEM plotted. The DV axis is binned into thirds (range 254–1,885 μm). Only cells in which all eight latencies were tested were included in this analysis.

(D) For each cell, the latency at which the lowest SST value was measured is plotted relative to the cell’s position along the DV axis. Best-fit line to data is shown.

(E) SST values for individual cells at different DV depths at four latencies. Best-fit lines to data are shown.

See also Figure S5.

Using the SST assay, we found a significant effect of DV position and interval duration, with cells showing smaller SST values at short latencies and larger SST values at longer latencies (repeated-measures ANOVA, Huynh-Feldt correction: latency effect, F[7, 189] = 69.53, p < 0.001; DV × latency interaction, F[14, 189] = 4.40, p < 0.001; n = 30; no between-subjects effect of DV position, F[1, 27] = 0.10, p = 0.91) (Figure 3C). Moreover, the latency at which the minimum SST value occurred progressively increased along the DV axis (R² = 0.28, p < 0.001, n = 41) (Figure 3D). Consistent with this, dorsal cells had smaller SST values for short latencies and larger SST values for longer latencies compared with ventral cells (2 ms, R² = 0.09, p = 0.05, n = 41; 4 ms, R² = 0.10, p < 0.05, n = 41; 16 ms, R² = 0.16, p < 0.01, n = 41; 32 ms, R² = 0.20, p < 0.01, n = 35) (Figure 3E). Together, these data demonstrate that a spike in dorsal cells opens a narrow temporal window (4–10 ms) in which the input required to elicit a second spike is lower than in ventral cells, after which the input required to elicit a spike is higher in dorsal compared with ventral cells. These temporal dynamics (Figure 3C) indicate that dorsal cells are more likely to burst in response to high-frequency (>~166 Hz) compared with low-frequency (~62 Hz) inputs.

A Mathematical Model of Bursting Derived from Experimentally Measured Dynamics

Next, to consider whether the observed in vitro differences in temporal dynamics across the DV axis could influence the in vivo dorsal-ventral differences in bursting, we implemented a “spike-response model,” an integrate-and-fire model incorporating intrinsic after-spike dynamics (Brette and Gerstner, 2005; Figure 4). This model simulates spike trains by modeling a neuron’s membrane voltage over time, according to external inputs and intrinsic dynamics, recording the times at which this voltage surpasses a spiking threshold, and then immediately re-setting the voltage to the resting potential. Single-cell voltage dynamics over time are governed by a fixed external input I, a leak term, and a noise term, while after-spike dynamics are captured by a spiking threshold that varies with the time since the last spike (see Data S1). Critically, this threshold is defined to be precisely what is measured by the normalized SST in our in vitro experiments and thus allows us to simulate spike trains with a firing threshold rule that is taken directly from the experimentally measured SSTs.

Figure 4. Model Captures In Vivo Bursting Using Measured In Vitro Temporal Dynamics.

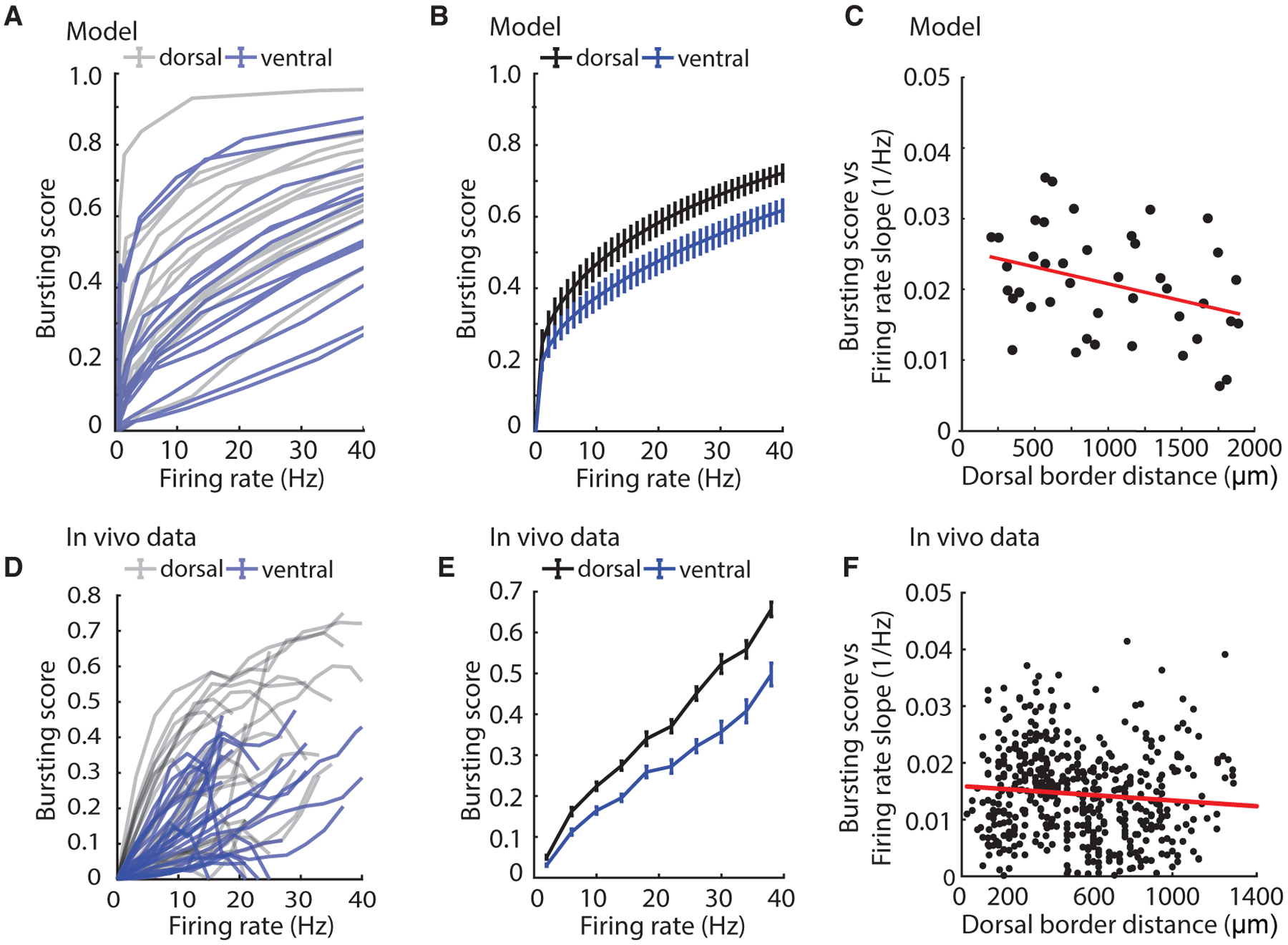
(A) Bursting score versus firing for modeled cells on the basis of in vitro SST recordings and slow exponential decay times (simulations based on values from most dorsal third of axis in gray and most ventral third of axis in blue).

(B) Summary data for dorsal and ventral thirds of modeled cells.

(C) Slope of linear fit to all modeled single-cell curves in (A) as a function of dorsal border distance.

(D) Bursting score versus firing rate for a random sample of in vivo cells (gray, most dorsal third; blue, most ventral third of axis).

(E) Summary bursting score versus firing rate tuning curves for dorsal and ventral thirds of all in vivo cells (dorsal, n = 122; ventral, n = 90). Mean ± SEM plotted.

(F) Slope of linear fit to all single-cell curves in (D) as a function of dorsal border distance.

See also Figure S5.

Using this framework, we simulated spike trains on the basis of dorsal and ventral neurons recorded in vitro by inserting their experimentally measured normalized SSTs into the spike response model. By sweeping over different values of the external input I, we then computed the BS for different mean FRs for each neuron. The model reveals that dorsal neurons will have a higher BS for a given FR than ventral neurons, which agrees with our experimental observations in vivo (model: R² = 0.12, p < 0.05, n = 42; data: R² = 0.01, p < 0.05, n = 509) (Figures 4A–4C). Importantly, the variability in the SST responses we observed in individual neurons in vitro creates a distribution of BSs similar to what we observe in vivo (Figures 4C and 4F) and points to the presence of heterogeneity in the temporal coding features of MEC neurons.

Whole-Cell Recordings Reveal a DV Gradient in Na Currents

We then considered how intrinsic conductances might influence the DV MEC gradient in bursting. We focused on Na conductances, as in the hippocampus, cerebellum, and neocortex, sub- or peri-threshold Na conductances play a critical role in driving bursts (Azouz et al., 1996; Brumberg et al., 2000; Traub et al., 2003; Khaliq et al., 2003). In a subset of whole-cell patch-clamp recordings, we washed in 10 μM riluzole (2- amino-6-triffluoromethoxy benzothiazole) after the baseline SST assay (Urbani and Belluzzi, 2000; Figure 5A). Riluzole is a pharmacological compound that blocks sodium currents (Hebert et al., 1994; Song et al., 1997) and preferentially targets the persistent sodium current in cortical neurons (Sheroziya et al., 2009; Urbani and Belluzzi, 2000). After washing in riluzole, we repeated the SST assay in the same neuron. We then post hoc quantified the amount of additional current needed to rescue the SST observed in the control condition. The larger the amount of additional current needed, the more the SST observed in the control condition depends on persistent sodium currents. We found that riluzole had a significantly larger effect in dorsal cells, with the current required to evoke a second spike decreasing as a function of DV position (R² = 0.33, p < 0.05, n = 17) (Figure 5B). This effect was most pronounced for shorter SST latencies (repeated-measures ANOVA: between-subjects dorsal versus ventral, F[1, 13] = 7.01, p < 0.05; dorsal, n = 8; ventral, n = 9; post hoc comparisons, p < 0.05 at 2, 4, and 8 ms). The threshold for a second spike then returned after washout of the drug (F[1, 18] = 0.045, p = 0.835, n = 10) (Figure 5C). This suggests that the DV gradient in SST responses could be indicative of a DV gradient in Na currents.

Figure 5. Na Current Components Are Graded along the MEC DV Axis.

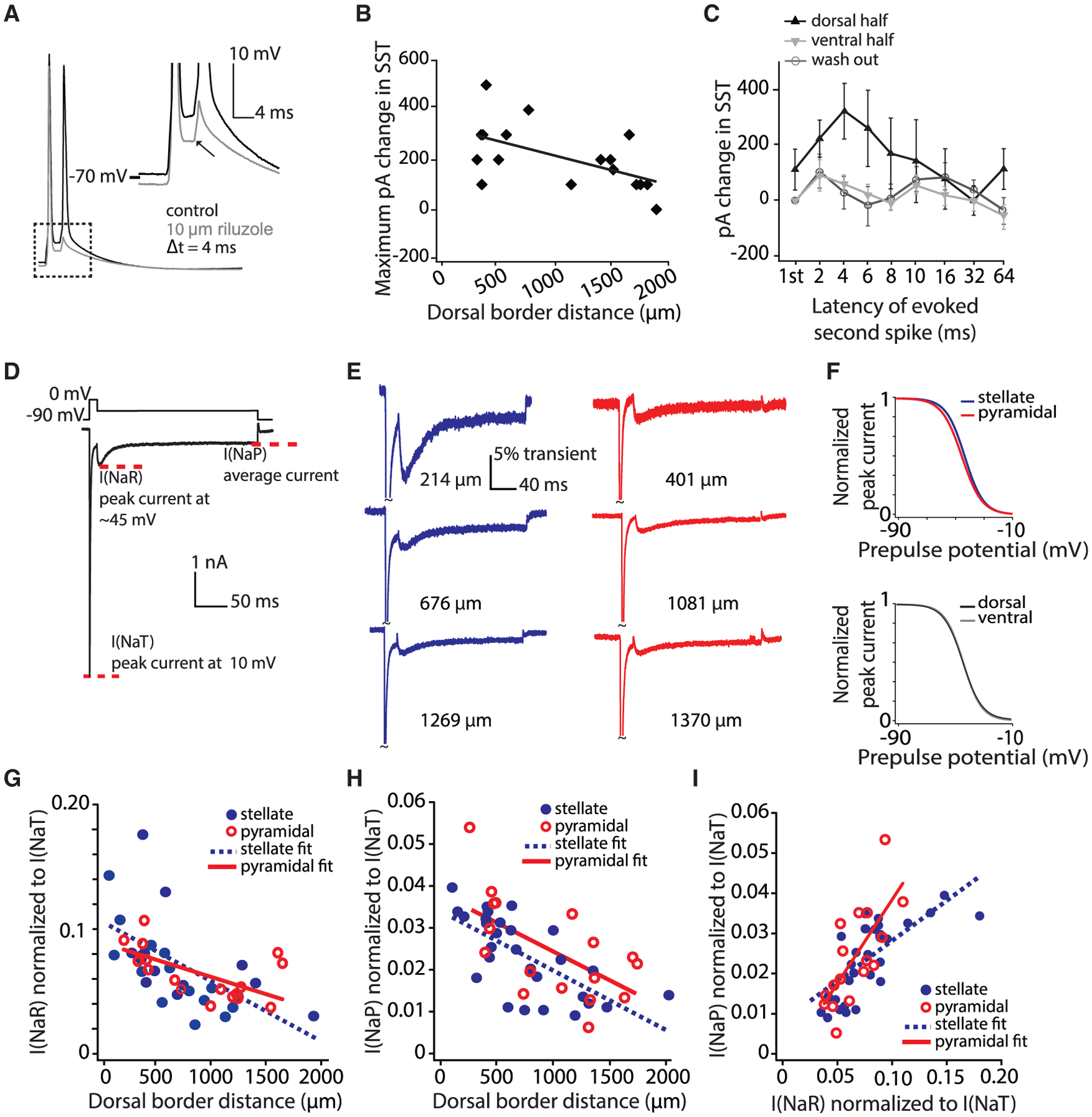
(A) A representative SST protocol recording in control (black) and riluzole (gray). Inset depicts the decrease in depolarization following a spike in the presence of riluzole.

(B) Largest change (across all latencies) in the SST value in riluzole as a function of the cell’s position along the DV axis. Current plotted (pA) indicates the additional current required to rescue a second spike at a given latency. Best-fit line to data is shown.

(C) Increase in picoamperes required to rescue control SST values at various latencies (log axis). Mean ± SEM plotted. The DV axis is binned into halves (dorsal, 315–1,139 μm; ventral, 1,140–1,885 μm). Only cells for which data on all eight latencies were obtained were included in this analysis.

(D) Voltage-clamp protocol used to assay Na current components. The transient current is measured as the peak current elicited at 10 mV. I(NaR) is measured as the peak current elicited by any voltage repolarization. I(NaP) is measured as the average of the last 10 ms of the step.

(E) Representative voltage-clamp recordings of stellate (blue) and pyramidal (red) neurons (DV location listed to the right of each trace).

(F) Normalized Boltzman equation-derived steady-state inactivation curves plotted for average values from individual fits. Top shows stellate (blue) versus pyramidal (red) neurons and bottom shows dorsal (black) and ventral (gray) neurons. Four cells with insufficient traces were not included in this analysis. Na gradients did not show significant differences in inactivation parameters between stellate and pyramidal cells (mean ± SEM; V1/2, stellate = −42.7 ± 1.1 mV, pyramidal = −44.7 ± 1.2 mV, t[39] = 1.17, p = 0.25; slope factor (k), stellate = 6.41 ± 0.17 mV, pyramidal = 6.87 ± 0.15 mV, t[39] = −1.46, p = 0.15; Imax, stellate = −5.84 ± 0.33 nA, pyramidal = −4.67 ± 0.33 nA, t[39] = −0.99, p = 0.33). Inactivation parameters also did not differ between dorsal (0–1,000 μm) and ventral (>1,000 μm) cells (mean ± SEM; V1/2, dorsal = −43.4 ± 1.1 mV, ventral = −43.7 ± 1.2 mV, t[39] = 0.13, p = 0.90; slope factor (k), dorsal = 6.45 ± 0.16 mV, ventral = 6.80 ± 0.29 mV, t[39] = −1.14, p = 0.26; Imax, dorsal = −4.92 ± 0.40 nA, ventral = −5.30 ± 0.48 nA, t[39] = 0.61, p = 0.54).

(G) Normalized I(NaP) density in stellate (blue) and pyramidal (red) neurons decreases along the DV axis. Best-fit lines to data are shown.

(H) Same as (F) but for normalized I(NaP). The gradients of Na current component amplitudes did not differ between cell types (ANCOVA, comparison of slopes: I[NaP], F[1, 41] = 0.017, p = 0.90, η² = 0; I[NaR], F[1, 41] = 1.98, p = 0.17, η² = 0.05).

(I) Correlation of I(NaR) and I(NaP) within individual neurons. Best-fit lines to data are shown.

See also Figure S5.

Superficial MEC neurons show high expression levels of two components of the Na current active at sub- or peri-threshold membrane potentials: persistent Na current (I[NaP]) and resurgent Na(+) current (I[NaR]) (Alonso and Llinás, 1989; Azouz et al., 1996; Castelli et al., 2007; Magistretti et al., 1999). Because the current-clamp data pointed to a potential role for Na currents in bursting, we examined whether I(NaP) and I(NaR) were graded along the DV MEC axis. We performed whole-cell voltage-clamp recordings of MEC cells and assayed I(NaP) and I(NaR) as features of the whole-cell Na current (Aman et al., 2009; Bant and Raman, 2010). Cells were held in voltage clamp at −90 mV, stepped to 10 mV for 20 ms to inactivate or block the transient Na current, and then repolarized to membrane potentials ranging from −25 to −60 mV for 200 ms (Raman and Bean, 1997; Figure 5D). Currents were then normalized to the transient current. We found DV gradients in the amplitude of peak I(NaR) and I(NaP) in layer II/III stellate and pyramidal cells, with both cell types also showing similar inactivation parameters (Pearson’s correlation, DV position versus I[NaR]: stellate, R² = 0.35, p < 0.001, n = 28; pyramidal, R² = 0.31, p = 0.02, n = 17; I[NaP]: stellate, R² = 0.47, p < 0.001, n = 28; pyramidal, R² = 0.39, p = 0.007, n = 17) (Figures 5E–5H; Figure S5). The amplitudes of these currents correlated to a degree larger than predicted by the cell’s DV position (residuals of currents with position regressed out: R² = 0.266, p < 0.05, n = 45) (Figure 5I). Moreover, although current amplitudes at repolarized membrane potentials showed DV gradients, inactivation parameters did not vary between dorsal and ventral cells (Figure 5F), suggesting that the observed gradients do not simply reflect differences in steady-state channel availability (Magistretti and Alonso, 1999).

Consistent with the DV gradient in I(NaR) and I(NaP) observed, unnormalized I(NaR) and I(NaP) amplitudes exhibited DV gradients. Transient amplitudes did not exhibit a DV gradient, suggesting that there were no DV differences in axonal compartments due to differences in slicing (Figure S5). However, although outside-out macropatch recordings were consistent with the presence of a DV gradient in somatic I(NaP), they lacked I(NaR), suggesting that I(NaR) may be preferentially expressed in the axon initial segment (Castelli et al., 2007; Hamada et al., 2016; Khaliq and Raman, 2006; Kole, 2011; Royeck et al., 2008; Figure S5). Taken together, these data point to gradients in non-inactivating Na currents as a key contributor to bursting in MEC cells.

DISCUSSION

Here, we revealed a DV gradient in the bursting dynamics of spatially modulated MEC cells in behaving animals. Moreover, we found that high-frequency FRs are associated with robust spatial signals, particularly in response to high-frequency inputs, such as those that likely occur at fast running speeds. A corresponding DV gradient in bursting dynamics and peri-threshold Na channels was observed in vitro, pointing to intrinsic conductances as potential single-cell mechanisms for in vivo bursting dynamics. Together, these results reveal topographic organization in spiking dynamics that could complement the organization in the spatial scale of MEC grid cells. Moreover, future work could consider whether the gradient in bursting we observe could play a role in supporting a differential function of dorsal versus ventral MEC in behavior. In the hippocampus, it has been proposed that dorsal versus ventral neural populations support different behaviors, such as spatial memory, anxiety, or fear (Fanselow and Dong, 2010; Moser and Moser, 1998; Strange et al., 2014). Although the anatomical range over which we considered bursting did not extend across the entire DV MEC axis, the findings that dorsal cells show a higher propensity to burst and that bursts carry higher spatial information and coherence raise the possibility that the dorsal MEC pole contains coding features that may play a role specifically in spatial learning.

Our findings have implications for network-level models capable of generating grid cell firing patterns. Many of these models rely on translation-invariant attractor networks, in which the animal’s movement drives the translation of an activity pattern across a neural population (Burak and Fiete, 2009; Couey et al., 2013; Fuhs and Touretzky, 2006). Such models often rely on network homogeneity, with only a few attractor states surviving heterogeneity in cellular excitability or synaptic inputs (Renart et al., 2003). Here, we report heterogeneity in the bursting propensity of grid cells of the same spatial scale. However, the effects this variability in spiking features may have in attractor-based grid cell network models remains unknown. Even so, the presence of heterogeneity in grid cell spiking dynamics, and the challenge this may present to attractor models, are complementary to reports of heterogeneity in the spatial tuning features of MEC cells (Hardcastle et al., 2017a, 2017b), suggesting future computational work needs to account for heterogeneity in the intrinsic and synaptic features of grid cells.

A remaining question is what underlying mechanism gives rise to the larger range in bursting we observe in dorsal MEC in vivo and in vitro (Figures 1C and 4C), compared with the less variable range in dorsal Na current amplitudes we observed in vitro (Figures 5G and 5H). First, our computational model as well as previous work indicates that the lower variability observed in vitro could give rise to higher variability in vivo, when considering the variability in the timing of inputs, changes in noise or conductance (Dorval and White, 2005; Fernandez and White, 2008), or the increase in population-wide rhythmic activity (Mitchell and Ranck, 1980) that occur under in vivo conditions. Second, it is important to also consider that multiple ion channels are graded in a cell type-specific manner along the DV MEC axis (Garden et al., 2008; Giocomo and Hasselmo, 2008; Pastoll et al., 2012a). Moreover, grid cell firing properties have been observed in both stellate and pyramidal cell-types in MEC (Sun et al., 2015; Tang et al., 2014). Thus, the degree of variability in bursting we observed in vivo could reflect the interaction of Na kinetics with the dynamics of other ion channels, which vary in a cell type-specific manner (Alonso and Klink, 1993; Eder and Heinemann, 1994; Pastoll et al., 2012a; Yoshida and Alonso, 2007). For example, given that putative excitatory speed cells increase their FR with running speed, it is reasonable to hypothesize that grid cells receive high-frequency inputs from these cells at high running speeds. In MEC, the accurate integration of high-frequency inputs is supported by the presence of the hyperpolarization activated cation current I(h) and leak K+ current, which are both graded along the DV axis in stellate cells (Garden et al., 2008; Giocomo and Hasselmo, 2008, 2009). In dorsal MEC, these integrated inputs may thus more effectively translate into high-frequency bursts of action potentials because of larger amplitude sodium currents, resulting in more a more accurate grid code. In this framework, the larger heterogeneity we observe in bursting dynamics, compared with Na current amplitudes in vitro, could reflect the fact that stellate and pyramidal cells contain significantly different densities of multiple ion channel currents (Alonso and Klink, 1993; Eder and Heinemann, 1994; Pastoll et al., 2012a; Yoshida and Alonso, 2007). Thus, although pyramidal cells have the capacity to burst because of their Na conductances, they may lack the ion channel kinetics to drive integration in way that results in a robust position code in vivo.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Lisa M. Giocomo (giocomo@stanford.edu). This study did not generate new reagents or mouse lines.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

In vivo experimental model and subject details

The dataset consisted of MEC neurons from previously published datasets (male mouse n = 18) (Eggink et al., 2014; Giocomo et al., 2011; Hardcastle et al., 2017b). For in vivo experiments from Eggink et al. (2014) and Giocomo et al. (2011), all experiments were performed in accordance with the Norwegian Animal Welfare Act and the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes and approved by the National Animal Research Authority of Norway. For in vivo experiments from Hardcastle et al. (2017b), all techniques were approved by the Institutional Animal Care and Use Committee at Stanford University School of Medicine. Mice were housed together with their littermates (50:50 C57B6/129SvEv and C57B6) until surgery. At implantation, mice ranged in age from 3 to 12 months.

In vitro experimental model and subject details

All techniques were approved by the Institutional Animal Care and Use Committee at Stanford University School of Medicine. In vitro recordings were performed in male and female C57BL/6 mice. Mice were house together with their littermates. At the time of the recordings, mice were aged P18 – P30, providing developmental conditions under which Na currents have fully expressed (Nigro et al., 2012).

METHOD DETAILS

Surgical implantation of chronic recording devices and in vivo single-unit data acquisition

For chronic implantation of recording electrodes, mice were first deeply anesthetized with isoflurane (induction chamber 3.0% with air flow at 1200 ml/min, reduced to 1% once the animal was secured in the stereotaxic apparatus) and then given a subcutaneous injection of buprenorphrine (0.3 mg/ml). A tetrode bundle composed of two polyimide-coated platinum iridium 90%–10% wire tetrodes, cut flat with impedances reduced to 200 kΩ at 1 kHz, was implanted in the left or right hemisphere, angled at 0 – 8 degrees in the posterior direction in the sagittal plane, at 0.3 – 0.5 mm anterior to the transverse sinus, 3.1 – 3.3 mm from the midline and 0.5 to 1.1 mm below the dura. The microdrive was secured to the skull using dental cement adhered to jeweler’s screws, with one screw serving as a ground electrode. Mice were then housed individually in transparent plexiglass cages.

For all data collection, mice were allowed to recover for at least one week after surgery, after which data acquisition began. Mice were connected to the recording equipment via AC coupled unity-gain operation amplifiers and placed in a recording box (70 × 70 cm, 90 × 90 cm or 1 × 1 m) with a single white polarizing cue, surrounded by black curtains. Mice foraged for randomly sprinkled food over a 20 – 60 minute long recording session. After each finished set of experiments, the floor of the test box was washed with soapy water, tetrodes were moved by ≥ 25 μm until new well-separated cells were encountered, after which mice rested in their home cage until the next recording session. Mice did not experience the open field more than twice per day (sessions separated by ≥ 3 hours). After the completion of recordings, offline cluster cutting software was used to sort spikes (TINT software, Axona Ltd.) and video tracking data was analyzed for the location and head direction of the animal. Manual cluster cutting was performed using two-dimensional projections of the multidimensional parameter space (waveform amplitude), with additional separation utilizing autocorrelation functions.

Cell layers and the location of all recorded cells relative the border between MEC and other cortical regions were determined from post hoc Nissl-stained sagittal brain sections. After the final recording session, electrodes were not moved. Mice were then killed with an overdose of pentobarbital and transcardially perfused with 0.9% saline (wt/vol) followed by formaldehyde. Brains were extracted and stored in 4% formaldehyde and later (> 24 hours) were frozen, cut in sagittal sections (30 μm) and stained with cresyl violet. The positions of the tips of the recording electrodes and measurements were determined from digital pictures of the brain sections made using AxioVision (LE Rel. 2.4). The position of the tip of the tetrode was identified and a measurement between this position and the dorsal border of medial entorhinal cortex was made. The dorsal-ventral location of recorded cells was then back calculated from the position of the tip of the tetrode and the noted tetrode depth on the day of the recording. The laminar location of recording electrodes was determined on the basis of cytoarchitectonic criteria (Giocomo et al., 2011) (Figure S1).

Shuffling procedures for cell classification

Any cells with < 100 spikes or that came from sessions with < 75% coverage of the environment were removed from the analysis. Shuffling for grid, border and head direction cells was then performed as in Giocomo et al. (2011). One hundred random perturbations of all cells in the sample determined the chance levels. For each permutation trial, the entire sequence of spikes fired by a given cell was time shifted along the animal’s path by a random interval between 20 s and the total trial length minus 20 s, with the end of the trial wrapping to the beginning. For grid cells, an autocorrelation map was constructed and a grid score calculated for each permutation. Border scores and mean vector lengths were calculated for each permutation as described above. The 95^th percentile was then determined from the overall distribution of grid, border or head direction scores in the shuffled dataset.

Shuffling for speed scores followed the same shuffling procedures as that used for grid, border and head direction cells but two scores were calculated and used to define the speed cell population. First, the correlation between running speed and firing rate was determined (speed score) and second, the recording session was divided into four equal sections and the correlation between the running speed × firing rate relationship calculated (speed score stability). Both positive and negative tails of the speed score distribution were considered so that cells with significant relationships with running speed – whether they be positive or negative – would be included (97.5^th percentile for positive speed scores = 0.071 and 97.5^th percentile for negative speed score = −0.053). For speed score stability, the 95^th percentile was determined from the overall distribution (P95 for speed score stability = 0.43). Cells were defined as speed cells only when they crossed the threshold for both speed score and speed score stability. After shuffling, neurons were identified as putative interneurons based on their firing rate and the width of their waveform (mean firing rate > 10 Hz or trough to peak duration < 0.25 ms). Interneurons were removed from further analysis, leaving a total of 821 putative excitatory neurons.

Definition of spatially and directionally-responsive neurons

Spatially-responsive neurons were classified based on previously published methods (Langston et al., 2010). Position data was binned (2.5 cm × 2.5 cm bins) and smoothed with a 21-sample boxcar window filter (400 ms, ten samples on each side). The peak firing rate was defined as the rate in the bin with the highest firing rate. The structure of grid cell rate maps was quantified for cells with more than 100 spikes by calculating the spatial autocorrelation for each smoothed rate map. To classify grid cells, a grid score was calculated by taking the circular sample of the autocorrelation and comparing it to rotated version of the same sample (60° and 120° versus 30° , 90° and 150°). The minimum distance between elements in the first group (60° and 120°) and elements in the second group (30°, 90° and 150°) was defined as the cell’s grid score. Neurons with a grid score higher than P95 = 0.36 were defined as grid cells. For each grid cell, we also computed the spatial information and the spatial coherence of the rate map. Spatial information was reported in bits/spike, and computed as spatial information: $\sum _i{p}_i\left({\lambda }_i/\lambda \right){\mathit{\text{log}}}_2\left({\lambda }_i/\lambda \right)$, where i is the bin number, λ_i is the mean firing rate of the cell in the i-th bin, λ is the mean firing rate, and p_i is the probability of the animal being in the i-th bin. Spatial coherence was computed as the arc-tangent, or the Fisher z-transformation, of the correlation between a given pixel and the average value of the neighboring 3–8 pixels in the spatial map, and roughly corresponds to the similarity of neighboring pixel values.

Border cells were identified by computing a previously published border score (Solstad et al., 2008). The difference between the proportion of high firing rate-bins along one of the environmental walls and the normalized mean product of the firing rate and distance of a high firing-rate bin to the nearest wall was divided by the sum of those two values. Border cells were classified as neurons with a higher border score than P95 = 0.52.

Non-grid, non-border spatial cells were identified through the application of a linear-nonlinear Poisson model (Butler et al., 2019; Hardcastle et al., 2017b). In this model, cells were identified as encoding position (P), head direction (H), or speed (S). However, here we only considered if the cell encoded P. In this framework, the model estimates the spiking rate of each cell, $\widehat{r}$, as a function of position, head direction, or running speed as:

$$\widehat{r}=\frac{\exp \left(b+{\sum }_i{X}_i^T{w}_i\right)}{d_t}$$

where r denotes a vector of firing rates over T time bins,b denotes the baseline input (a learned parameter), $X_i^T$ denotes the input matrix for variable i (i∈[P, H, S], $X_i^T$ is a T x (length of w_i) matrix), w_i denotes the learned parameters for variable i, and dt is the time bin width (fixed to be 20 ms; all navigational variables are linearly interpolated to this sampling rate). Each row in the matrix $X_i^T$ indicates the feature related to variable i at time point t, and is computed using cardinal spline interpolation (Butler et al., 2019). The model was fit assuming that spikes followed a Poisson noise distribution. Learned parameters were computed by maximizing the log-likelihood of observing the data given the model:

$$\widehat{w}={\text{argmax}}_{w_i,b}\sum _t\log P(n_t|exp\left(b+\sum _i{X}_i^T{w}_i\right)-\frac{1}{2}{\beta }_i\sum _i\sum _j{w}_{i,j}^2$$

where n_t is the number of spikes for in time bin t, and β_i is the weight of the L2 penalty. This was set to 1 for all variables. This maximization problem was carried out using fminunc in MATLAB. Models were fit and performance was assessed using 10-fold cross-validation. Model performance was computed as the log-likelihood increase from a mean-firing rate model, divided by the number of spikes observed in that testing data fold. Determination of which variables were encoded was accomplished via a forward search method (Hardcastle et al., 2017b).

Directional analyses were only performed for experiments with two LEDs (cell number n = 819). The direction of the mouse’s head was calculated for each sample by determining the relative position of the two head-mounted LEDs onto the horizontal plane. Directional tuning curves were plotted by calculating the firing rate as a function of the mouse’s directional heading, divided into bins of 2 degrees and smoothed with a 15 degree mean window filter. The length of the mean vector (MVL) for the circular distribution of the firing rate was then used to quantify the strength of directional tuning. Neurons with a mean vector length larger than P95 = 0.14 were classified as head direction cells.

Speed cells were identified by computing a speed score, defined as the correlation between firing rate (smoothed with a Gaussian filter with σ = 20, following Kropff et al., 2015) and running speed (smoothed with a Gaussian filter with σ = 5), and speed stability. Tuning curves were computed by first binning along speed values (0–50 cm/s in 20 equally sized bins) and computing the average firing rate in each bin.

Quantification of theta-locking and theta-modulation

To quantify the degree of theta-locking, we first filtered the LFP for theta frequency (6–10 Hz) using a Butterworth filter. We then computed the Hilbert transform (using the Hilbert function in MATLAB), and computed the ‘theta-phase’ as the arctangent of the imaginary and real part of the Hilbert transform. Phase values were shifted to run between 0 and 2*pi. We then computed a theta-locking score by first computing the histogram of theta-phases at the time of each spike, with bin size = 2 degrees and smoothing over 15 degrees. Next, we computed the mean vector length of this histogram as the theta-locking score.

To quantify the degree of theta modulation, we implemented the procedure outlined in Climer et al. (2015). This method allows for robust calculation of theta rhythmicity under conditions of low firing rates, which is typically the case with entorhinal neurons (Climer et al., 2015). Briefly, this method fits a parametric function to the marginal distribution of all spikes given that another spike occurred within 600 ms. The parametric model is fit by maximizing the following likelihood function:

$$L(x;\tau ,b,c,f,r,s)=D((1-b)\exp \left(-\frac{x}{{10}^{\tau }}\right)\left(r\exp -\frac{x}{{10}^c}\right)F(t,s)+1)+b)$$

where x is the lag, and τ; b; c; f; r; s are all parameters that control the specific shape of this function and are found through the maximization process. The function F(t, s) is a combination of two sinusoids, and allows this function to model potential theta-skipping. As in Climer et al. (2015), we computed the magnitude of rhythmicity, termed a, based on the value of these parameters: a = (1−b)r, where b is a baseline likelihood and r is a rhythmicity factor. This measure varied between 0 and 1, where 1 is maximally rhythmic, and served as our theta modulation index. We could also compute a p value that reported whether fitting a rhythmic model (r > 0) fit the data significantly better than a non-rhythmic model (r = 0. Following Climer et al. (2015), we computed the p value from the log-likelihood ratio test between the rhythmic and non-rhythmic models.

Generation of simulated spike trains

Simulated spike trains were generated based on the parameters fit by a generalized linear model (GLM). Specifically, for each cell, we fit a GLM which modeled the cell’s spiketrain (n) as a set of observations from a non-stationary Poisson process with mean r(t). This mean was computed as a nonlinear function of the animal’s position, head direction, running speed, and the phase of the theta-filtered LFP: r(t) = exp(w_p*p(t) + w_h*h(t) + w_s*s(t) + w_th*th(t)), where p(t), h(t), s(t), and th(t) are features corresponding to the animal’s position, head direction, running speed, and LFP-theta phase respectively. We chose these specific variables due to their prominence in the literature for driving entorhinal spiking. Features were all splines, as described above, and thus all parameters corresponded to the value of control points. Further, this model was exactly the same as the one described above, except it included LFP data, spike history, used dt = 2 ms, and did not include any cross-validation or feature selection. We learned parameters w_i that maximized our model fit to the full set of data collected during a recording session. With w_i in hand, we were then able to use the equation $\widehat{r}=(\exp (b+{\sum }_i{X}_i^T{w}_i)/dt)$ to compute $\widehat{r}$ for every time bin. Using the poissrnd function in MATLAB, we then generated an estimated spike count for each time bin (using poissrnd$({\widehat{r}}_t*dt)$). This generated a simulated spike train from which we could compute a simulated bursting score. We then computed a “normalized bursting score,” using the simulated bursting score as the normalization:

$$\mathit{\text{Normalized\hspace{0.17em}BS}}=\frac{\mathit{\text{True\hspace{0.17em}BS}}-\mathit{\text{simulated\hspace{0.17em}BS}}}{\mathit{\text{simulated\hspace{0.17em}BS}}+\mathit{\text{true\hspace{0.17em}BS}}}$$

PCA on the ISI histograms

To further validate our definition of bursting score, we compared our approach to that taken by Latuske et al. (2015). In this approach, we first computed the ISI histograms, using 1 ms bins and only considering intervals less than 12 ms, for each cell. Each histogram could be described using a single vector of numbers (the value of each histogram bin), and these vectors could be stacked for all cells to form a matrix (size = # of cells × 12). Plotting values in this matrix corresponded to plotting N cells in a 12-dimensional space. Since we could not visualize this space, we then performed PCA on this matrix, and re-embedded the N data points in a 2–3 dimensional space. This allowed for an unsupervised method to visualize how cells varied in their in vivo spiking dynamics. We followed this procedure, which was identical to that taken in Latuske et al. (2015), but also colored each data point according to its bursting score, or rank in the sorted list of bursting scores. In addition, we correlated the bursting score with the projection of the data onto the first, second, and third principal component.

In Vitro data collection and analysis

In vitro slice physiology

For slice preparation, mice were first continuously anesthetized with isoflurane and perfused with cold artificial cerebrospinal fluid (ACSF) oxygenated by bubbling 95% O₂/5% CO₂ through the ACSF. After perfusion, the mouse was rapidly decapitated and the brain removed under cold (4° C), oxygenated ACSF (ACSF concentrations in mM: 126 NaCl, 26 NaHCO₃, 3 KCl, 1.25 NaH₂PO4, 2 MgCl₂, 2 CaCl₂, 10 Glucose). The brain was then cut in halves through the corpus callosum and each half of the brain glued with the cut side down to allow slicing of sagittal medial entorhinal cortex (MEC) sections (300 μm thick). For slicing, we used the same ACSF solution listed above (sucrose-free). Slices were then held in a chamber stored at 31 – 33°C for 30 minutes, followed by room temperature for a minimum of 30 minutes and up to six hours. For whole cell patch clamp recordings, slices were placed in a chamber continuously perfused with oxygenated (95% O₂/5% CO₂) ACSF under an upright microscope (Zeiss A1). Cells were clearly visible with a 40X water-immersion objective lens, which allowed easy identification of the laminar and dorsal-ventral location of MEC cells. Putative layer II/III neurons were identified by their superficial location and their morphology, with stellate cells showing several thick branching dendrites (Klink and Alonso, 1997). All recordings were amplified by a Multiclamp 700B (Molecular Devices; sampling 50 kHz for voltage clamp, 20 kHz for current clamp, filtered at 10 kHz) and digitzed by a Digidata1440. The liquid junction potential was not corrected (voltage clamp = ~6 mV (versus ACSF), current clamp = ~12 mV, nucleated patches = ~8 mV). Capacitative artifacts were reduced for visualization purposes in all voltage clamp recordings except those shown in Figure S5I, which displays raw records.

The dorsal-ventral location of each recorded neuron was calculated from a 10x photograph of the slice with the cell either still patched (n = 43 cells included in voltage clamp experiments, all cells included in current clamp experiments), or identified after the experiment by being filled with fluorescent dye or biocytin (n = 3 cells included in voltage clamp experiments). The borders between MEC and other cortical layers and the ventral MEC end were identified based on DIC images and referenced to the Allen Brain Mouse Atlas (Pastoll et al., 2012b). Pixel measurements in Photoshop were used to quantify the distance to the dorsal border of MEC for each recorded neuron. These pixel measurements were then converted into actual dorsal-ventral micron distances using a calibration scale (conversion rate = 1.6).

Whole-cell voltage clamp recordings

Patch pipettes for voltage clamp recordings (2.9–5.8 MΩ) were pulled from 10 cm borosilicate glass capillary tubes (0.86 inside diameter, 1.5 outside diameter) using a P-1000 puller (Sutter Instrument Company). Pipettes were filled with an intracellular solution containing (in mM): 115 CsMethanesulfonate, 15 NaCl, 5 TEA, 2 MgCl₂, 0.5 EGTA, 10 HEPES, 1 sucrose, 14 Tris-creatine PO₄, 4 NaATP, 0.3 Tris-GTP, 0.1%–0.3% biocytin and 20–70 μM Alexa488 hydrazide (Invitrogen). The voltage-clamp extracellular contained (in mM): 60 NaCl, 26 NaHCO₃, 60 TEACl, 3 KCl, 2 MgCl₂, 0.5 CdCl₂, 2 BaCl₂, 4 4-AP, 1–5 glucose and 10 μM ZD7288. To improve voltage control during clamp of whole-cell currents, we employed three strategies. First, ten minutes before recording, sub-saturating TTX (15 nM, ~IC₅₀) was added to the ACSF. Sub-saturating TTX has been shown to reduce Na⁺ current amplitudes and improve space clamp (Carter and Bean, 2009; Milescu et al., 2010). When the voltage-clamp extracellular was washed in (after the cell was patched) it contained the same concentration of TTX. Second, solutions resulting in a reduced sodium gradient of [Na]_out = 86 mM / [Na]_in = 19 mM were used to reduce the amplitudes of Na currents. Finally, cells were patched at room temperature to slow currents. For recordings, tight seals (> 1 GΩ) were formed between the recording pipette and cell membrane, then ruptured with negative mouth pressure.

We started wash-in of the reduced Na extracellular solution five minutes before voltage-clamp recordings. To examine membrane properties before Cs perfused the cell (and thus blocked I(h)), input resistance was measured, and the cell was tested for sag (a slow depolarizing shift in the membrane potential) immediately after break-in using current clamp (Dickson et al., 2000). Current was applied to hold the cell at −70 mV and applied 1 s long hyperpolarizing current steps. Traces which had a minimum trough value in their sag at a membrane potential between −90 and −100 mV were analyzed. Sag ratio was quantified by dividing the minimum trough value of the membrane potential by the membrane potential achieved at steady state. After current clamp measurements were made and transient current amplitudes stabilized (~5–10 minutes), we applied a standard protocol used for assaying non-inactivating Na currents. We found that slow ramps, usually used to record persistent current, allowed adequate clamp but slowly drove channels into long-lived slow-inactivated states (Magistretti and Alonso, 1999) making assay of recovery difficult. On the other hand, short ramps were plagued by escaping spikes or unusual hysteresis between upward and downward ramps, indicating non-equilibrium gating or space clamp artifacts. In order to better separate equilibrium and non-equilibrium components, we used a standard resurgent step protocol assaying persistent current as the steady-state level of current at the end of a 200 ms step, allowing for extended settling time of the clamp (see Figure 5D, step to +10 mV for 20 ms, then back to various hyperpolarized potentials from −25 to −60, in 5 mV increments for 200 ms; Raman and Bean, 1997).

Series resistance and capacitance compensation were monitored throughout the recording and cancelled using a seal test. After the extracellular solution had fully washed in, a change of greater than 10% in either series resistance or capacitance was grounds for discarding a cell. Series resistances ranged from 6.2 −18 MΩ, (mean series resistance ± SEM = 13.5 ± 2.0 MΩ) and were compensated 48 ± 4%, as much as possible without ringing. Pipette capacitance was zeroed and retouched if it drifted during a recording, as it had fast kinetics and was separable by eye. Cell capacitance was cancelled manually so as to cause the least current deflection possible in a seal test during a 10 mV test pulse (mean cancelled capacitance ± SEM; stellate cells = 38.6 pF ± 2.2; pyramidal cells = 35.1 ± 3.1 pF). After recording whole-cell currents evoked by our resurgent step protocol in sub-saturating TTX solution, a trace of whole-cell currents in a saturating TTX solution was obtained after full wash-on (TTX = 900 nM, time for full wash-on > 6 min). Reported TTX-sensitive currents were generated by subtracting these conditions (sub-saturating to saturating.)

Whole-cell current clamp recordings

For current clamp recordings, slices were placed in a recording chamber continuously perfused with carboxygenated ACSF (kept at 36.0 ± 0.5°C). Electrodes were pulled from 10 cm borosilicate glass capillary tubes (3.8–5.9 MΩ, 0.86 mm inside diameter (ID), 1.5 mm outside diameter (OD)) and were filled with a K-gluconate-based intracellular solution containing (in mM): 120 K Gluconate, 10 HEPES, 0.2 EGTA, 20 KCl, 2 MgCl₂, 7 Phosphocreatine Di-tris, 4 Na-ATP, 0.3 Tris-GTP, 0.1% biocytin and/or 40 μM Alexa488 hydrazide. For recordings, tight seals (> 1 GΩ) were formed between the recording pipette and cell membrane, then ruptured with negative mouth pressure. After break-in, cells were only included if their resting potential ≤ −60 mV and had an action potential peak of ≥ +10 mV. Bridge and electrode capacitance compensations were applied. Input resistance was monitored by frequency-intensity (FI) curves obtained by holding the cell at −70 mV and applying 1 s long depolarizing current injections. For the dual-pulse protocol, 1 ms long depolarizing current steps were given in 100 pA increments to determine the action potential threshold. For all dual-pulse protocols, cells were held at −70 ± 2 mV and bridge balance and holding current were adjusted after each latency tested. Any change of > 200 pA in holding current or 20% of the bridge balance was grounds for discarding a recording. Occasional failures for the first spike (for example, a positive drift or increase in the current required to evoke an action potential) were observed. If more than one in ten action potentials failed for this first spike and it was not due to a small change in holding (< 200 pA), the cell was discarded. After establishing the first-spike threshold stimulus, the second-spike threshold (SST) was measured as the first injection to elicit a spike (with 50–100 pA resolution) in one of two ways: manually (n = 21) or using a pre-programmed stimulus file (n = 21), in which a set first injection was followed by a series of 10–20 s-spike injections at any of 8 latencies, with each injection pair separated by 1 s and tiling 20%–120% of the first spike threshold in 100-pA steps. Not all latencies were tested in all cells and cells that had measurements for < 4 latency values were not included. In addition, one cell was not included when computing the latency at which the minimum SST value occurred, as all SST values were monotonic and thus a trough was not present (Figure 2C).

In a subset of experiments, 10 μM Riluzole (in DMSO, diluted 1:1000) was washed in after the completion of the initial dual-pulse protocol and a second, identical, dual-pulse protocol was performed. Riluzole recordings did not begin for > 10 minutes after wash-in, to allow the drug to equilibrate. A small subset of recordings remained stable long enough to wash out the effect of Riluzole (> 45 minutes total, 15 minute wash-on and 15 minute wash-off of drug, after ~10–15 minutes of initial measures).

Nucleated patch recordings

Outside-out macropatches (nucleated patches, Sather et al., 1992) were pulled to isolate a small population of somatic channels. Thick-walled borosilicate glass electrodes (1.5 mm OD 0.75 mm ID, Sutter) were pulled to 3.2 – 4.8 MΩ after fire polishing. Electrodes were wrapped in parafilm to within ~300 μm of the tip to reduce pipette capacitance. Cells were held at 36 ± 0.5°C to measure realistic kinetics for cells in vivo. Layer II cells with a shadow of a nucleus near a smooth surface (to increase the chance of a macropatch) were patched. Bath ACSF was the same as that in voltage-clamp recordings, with a low Na intracellular used to boost current amplitudes containing (in mM): 120 CsMethanesulfonate, 1.8 NaCl, 5 TEA, 0.5 EGTA, 10 HEPES, 1 sucrose, 14 Tris-creatine PO₄, 4 Mg-ATP, 0.3 Tris-GTP. Upon sealing, the resting membrane potential was measured using current clamp and cells with a resting membrane potential > −60 mV were discarded. Nucleated patch recordings were then made by slowly withdrawing the electrode (0.1 – 0.2 μm a second) while applying 1–1.2 psi of negative pressure. TTX (2 μM, to increase wash-on speed 2x) was then washed in, with recordings running repeatedly until the patch died. A single resurgent step (+10 mV for 20 ms, followed by repolarization to −45 mV for 200 ms) was used to assay Na currents as the patch was formed and through the process of pulling as well as in the isolated patch. The greatest number of quality traces immediately before and after TTX perfusion were averaged and subtracted (4–40 traces for each).

After a patch detached fully from the soma we readjusted pipette and cell capacitance, as well as series resistance, to cancel out these currents in the recordings. However, due to the small size of the patch and slow but constant shearing of membrane in fluid flow, patch capacitances drifted downward. Drift on a long (5–10 minutes) timescale was not grounds for discarding a recording, as subtractions could be obtained ± 30 s after wash-on, over which period the cell capacitance was stable. The whole-cell compensations immediately before wash-in were not readjusted, resulting in the subtraction of any artifacts shared by both the control and TTX traces (see raw recordings in Figure S5I). Due to the overlap (at 37°C) in the temporal components of the patch capacitance and the extended inactivation kinetics of the Na currents, it is possible that some subtractions contained artifactual changes in patch capacitance between control and TTX and thus appeared to extend the inactivation kinetics of the “Na” currents. While this was a possibility we could not fully rule out, we could not detect this scenario based on changes in subthreshold leak subtraction pulses or online cancellation (n = 11). Series resistance was cancelled to measure and watch for drift (traces in which this was stable to within 20% were used for subtraction), but compensation was not used as current amplitudes were small enough to make the series resistance error insignificant, as reported previously (Martina and Jonas, 1997).

QUANTIFICATION AND STATISTICAL ANALYSIS

Quantification and statistical analysis in vivo dataset

Custom-written MATLAB scripts were used to analyze all data. Unless stated otherwise, all error bars and data quantifications are expressed as mean ± standard error of the mean (SEM). Statistical tests are listed following the relevant result in the results, figure legend or Materials and Methods detail. Unless otherwise stated, p < 0.05 was taken as the criterion for significance. Unless otherwise specified, data was speed filtered and data from times in which speed was less than 2 cm/s were not used for analysis.

The bursting score was computed as the number of burst spikes (spikes that preceded or followed another spike within 10 ms) divided by the number of total spikes. This threshold is consistent with previous studies characterizing bursts in the hippocampus (Harris et al., 2000; Hussaini et al., 2011; Mizuseki et al., 2009), MEC (Constantinou et al., 2016; Mizuseki et al., 2009), septum (Ranck, 1973), Bursting score versus firing rate curves were generated by first computing the average firing and bursting score in 500 ms time bins, and then computing the average bursting score per 3-Hz wide firing rate bins. For further analysis, only curves with more than 5 bins were considered. The slope of the linear fit of bursting score as a function of mean firing rate was computed assuming the intercept = 0.

To compare coding properties of burst spikes and tonic spikes, the spike train for each cell was first divided into ‘bursting’ and ‘tonic’ spikes. We then identified the first spike in each burst (FB spikes) and randomly downsampled the tonic spikes to match the number of FB spikes. We then re-computed the grid score, spatial information, spatial coherence, and speed slope using FB spikes only, or tonic spikes only.

To determine whether burst spikes were driving correlations between bursting score and grid score (and speed slope), we first identified burst spikes for a given cell. We then identified the first spike in each burst and deleted the remaining spikes in each burst (deleting n_i spikes total for cell i). We then recomputed the grid score (for grid cells) or speed slope (for speed cells) using the remaining spikes. We compared this analysis to one in which spikes were randomly rejected; i.e., for cell i, n_i spikes were deleted at random, and then the grid score or speed slope was re-computed.

To compare bursting and spatial coding during fast or slow running speeds, we first split each recording session into times of slow (2 – 10 cm/s) or fast (10 – 50 cm/s) running speed. To compare bursting in each speed epoch, we re-computed the bursting score for each epoch, for each session. To compare the grid score, spatial information, and spatial coherence for each speed epoch, we down-sampled speed epochs such that the fast and slow speed epochs for a given session matched in coverage (using 2.5 × 2.5 cm² bins), number of time points (which follows from matching coverage), and number of spikes. Epochs were randomly down-sampled. Due to variations in output due to random down-sampling, this analysis was repeated 20 times, and averages across iterations are reported. Grid score and spatial coherence increases were computed as the difference between each metric for each epoch, divided by the maximum of each metric for each epoch. Values were only computed for cells that exhibited coherent grid patterns in either the fast or slow speed epochs for 10/15 iterations of the down-sampling procedure, which were then averaged across these iterations.

Quantification and statistical analysis in vitro dataset

MATLAB or SPSS were used to analyze the data. Unless stated otherwise, all error bars and data quantifications are expressed as mean ± standard error of the mean (SEM). Statistical tests are listed following the relevant result. Unless otherwise stated, p < 0.05 was taken as the criterion for significance. For all correlations, Pearson’s correlation coefficients are reported. For the comparison of I(NaR) and I(NaP) gradients in stellate and pyramidal neurons along the DV axis, slope and Y intercept measures were based on a univariate analysis of covariance (ANCOVA) in SPSS. We first tested for an interaction between the main factors to determine whether the regression lines showed significantly different slopes. Next, to test for a significant difference in the Y intercept, we used the presence or absence of a significant slope difference to set up the ANCOVA model. As no significant difference in slope was detected, the ANCOVA was run without an interaction term, making the assumption of equal slopes between the two groups. Effect size is reported as ɳ². For second spike threshold analyses, ANOVA with repeated-measures were performed in SPSS.

DATA AND CODE AVAILABILITY

This study did not generate any unique in vivo datasets. The in vitro datasets are available from the corresponding author on request. The code used in the linear-nonlinear Poisson model can be accessed at: https://github.com/GiocomoLab/ln-model-of-mec-neurons. The code used for the leaky integrate-and-fire model can be accessed at: https://github.com/GiocomoLab.

ADDITIONAL RESOURCES

No reagents were generated for this study.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Riluzole hydrochloride	Tocris	0768
Deposited Data
Raw and analyzed data	This paper	N/A
Experimental Models: Organisms/Strains
Mouse: C57BL/6	The Jackson Laboratories	000664
Mouse: 50:50 C57B6/129SvEv	Steven Siegelbaum, Columbia University	N/A
Software and Algorithms
Linear-nonlinear Poisson model	Hardcastle et al., 2017b	https://github.com/GiocomoLab/lnmodel-of-mec-neurons
Integrate and fire model	This paper	https://github.com/GiocomoLab

Highlights.

• Interspike interval of grid cells increases along the dorsal-to-ventral entorhinal axis

• Bursting is associated with a high signal-to-noise ratio in grid cells

• Sodium current kinetics differ along the dorsal-to-ventral entorhinal axis