INTRODUCTION
The number of approved antibody-drug conjugates (ADCs) has grown in recent years with five ADCs approved by the Food and Drug Administration (FDA) and several more in late stage clinical trials. However, developing effective ADC candidates for cancer therapy with a sufficient therapeutic index has been difficult, and several clinical failures of ADCs could have been avoided by minor improvements in the therapeutic window (1). This is due to the highly complex ADC pharmacokinetics and pharmacodynamics in the tumor environment, especially for solid tumors. To date, ado-trastuzumab emtansine (T-DM1), commercially known as Kadcyla, is the only FDA-approved ADC for solid tumors.
ADCs are composed of three main parts - a targeting antibody (Ab), a cytotoxic payload, and a linker connecting the two. These agents must be optimized to specifically deliver the payload to cancer cells while minimizing healthy tissue uptake as they traverse multiple drug delivery barriers. After intravenous administration, ADCs flow through the blood to the tumor, extravasate from blood vessel, diffuse through the interstitial tumor tissue, bind antigens, are internalized by cancer cells, and, upon linker cleavage or digestion, release the cytotoxic payload that diffuses across membranes to their site of action (often DNA or microtubules) inside the cells. Tumors may vary in blood vessel density, receptor expression, and receptor internalization, all affecting ADC delivery.
ADC distribution in solid tumors is typically heterogeneous, which can impact efficacy (2). Because of the large size of ADCs, uptake into the tumor is limited by extravasation from the blood to the tumor tissue (i.e., they are permeability-limited) (3), resulting in reduced amounts of drug in the tissue. Once in the tissue, tumor penetration is slow as a result of elevated interstitial pressure, making them reliant on diffusion through the interstitial space. ADCs rapidly bind to antigens surrounding tumor blood vessels and are typically internalized before they can dissociate and diffuse deeper into the tissue. For example, at clinical doses of 3.6 mg/kg, T-DM1 localizes perivascularly, as seen in multiple mouse models (4), due to its large size and high affinity to HER2 receptors.
We and others have demonstrated that some ADC regimens can improve ADC distribution, efficacy, and tolerability. As previously established in our lab, the co-administration of T-DM1 with its unconjugated antibody, trastuzumab, improves drug penetration and efficacy (5). Other work from Hinrichs et al. and Jumbe et al. show that fractionating a single dose into 3 weekly doses can lead to similar efficacy, but better tolerability (6, 7).
Despite these findings, the design principles underlying the best choice of regimen and drug combinations are not well-understood. For example, it is not clear if/when a ‘carrier dose’ will increase drug penetration and improve efficacy. The impact of HER2 expression level and payload potency on the increase or reduction in efficacy from a carrier dose are also not well defined. Finally, the interplay of dose fractionation with carrier doses on overall efficacy is currently unknown.
Testing all combinations of receptor expression, payload potencies, carrier doses, dose fractionation regimes, etc. in vivo would be a daunting and expensive process. For this reason, computational models that guide experiments and predict best drug regimens are becoming more widely used. Computational models to capture the pharmacokinetics of ADCs are already established in the field (8) (9) (10) (11), but to our knowledge, there is not a pharmacokinetic/pharmacodynamic (PKPD) model of ADC distribution that captures the heterogeneous distribution of ADCs on individual cells to connect experimental single cell PK data to overall efficacy.
Here we took a systems pharmacology approach to study and predict the best ADC regimens. We developed a hybrid agent-based model (ABM) to capture ADC and/or antibody delivery and predict individual cell killing and tumor growth kinetics. This multiscale model enables detailed depictions of heterogeneous ADC delivery, cancer cell death, and tumor growth. Partial and ordinary differential equation models of ADC extravasation from multiple vessels, diffusion, binding, and processing are overlaid on a grid of individual cancer cells (agents). These cells undergo growth (cell division) and respond to the drug by cell death as a probability function of their intracellular payload concentration. Tumor growth rate is a function of the total number of cancer cells at a given time. The model was validated by comparison to experimental measurements in a HER2 positive NCI-N87 mouse xenograft model (5).With this model, the role of the carrier dose was analyzed, and predictions for the best regimen for different types of tumors overexpressing HER2 are presented.
MATERIALS AND METHODS
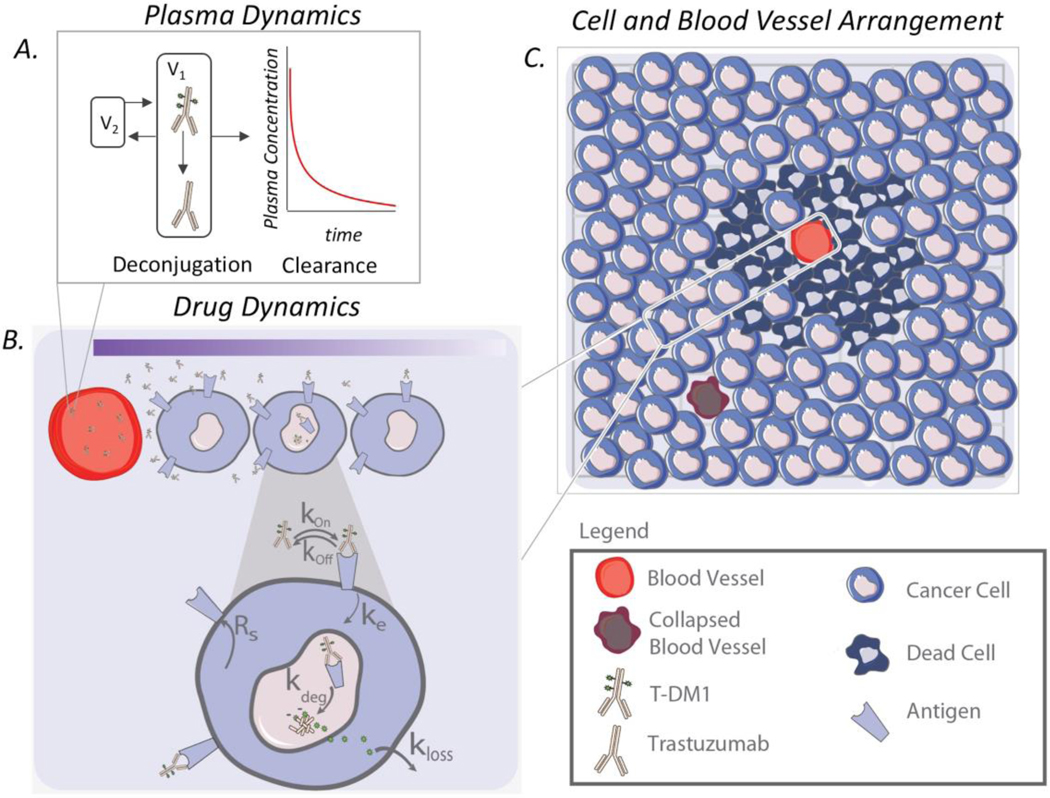
We built a computational model to predict the efficacy of particular ADC regimens, accounting for ADC distribution in a heterogeneous tumor microenvironment. Our model is a hybrid ABM comprised of cancer cells and blood vessels that compose the tumor microenvironment and behave based on predefined rules and changes in their local microenvironment. The multi-scale model has portions that describe the tumor environment and PKPD: plasma dynamics, drug dynamics for T-DM1 and trastuzumab, and individual cancer cell dynamics (e.g., cell division, death) (Figure 1).
Fig. 1.
Model schematic. a Plasma dynamics describe the intact ADC concentration in the blood as a result of local and systemic clearance, including deconjugation. b ADCs in the blood extravasate from the blood vessel, diffuse through the interstitial tissue, bind to HER2 antigens, and are internalized. After ADC degradation in lysosomes, cytotoxins are released to kill the cell. c Individual cells and blood vessels are placed on a 2D lattice, forming the tumor environment
Simulation Environment
We simulate a subsection of a tumor and assume that i) the dynamics are representative of the entire tumor and ii) the tumor volume is proportional to the number of cells in the simulation. The model was simplified to a 2D representation because ADC concentration along the blood vessel is approximately constant (permeability limited) (3). The representative subsection of the tumor includes a zero net-flux boundary condition on its border. At low doses, few drug molecules reach the boundaries of the subsection, so the effects of the boundary conditions are minimal. At higher doses, a zero net-flux boundary condition is convenient to represent the equal diffusion of drug into and out of the subsection from adjacent regions of the tumor. Because antibodies are permeability limited, this changes the location of the cells that are targeted but has a negligible impact on the total tumor uptake or fraction of cells targeted by the ADC. Each simulation starts with approximately 2500 cells, which is used to represent an initial tumor size of 250mm3. Cancer cells and blood vessels each have different states, i.e., alive or dead for cells and functional and non-functional for vessels, and they occupy a position on the simulation grid. Their state changes during the simulation depending on their microenvironment. For example, a sufficient number of released payloads can kill a cancer cell or sufficient time allows the cells to proliferate. Blood vessel density and placement within tumors is highly variable (both between tumors and within the same tumor). The range in vessel density in the simulations was determined by image analysis of xenograft tumors from mice using the MATLAB algorithm described in (5). A range from 18 to 36 blood vessels per simulation best matched histology data and doses showing tumor saturation. To capture the heterogeneity in vessel distribution, each simulation has blood vessels randomly placed in the tumor space at its initialization, creating a different microenvironment for each cancer cell in the simulation. This variability can change the drug spatial distribution across cancer cells and consequently impact efficacy.
Trastuzumab and T-DM1 Plasma Dynamics
The concentrations of trastuzumab and T-DM1 in the blood are a function of dosing, total antibody clearance rate, and payload deconjugation rate (rate at which the cytotoxin detaches from the antibody). A simplified ordinary differential equation (ODE) model from (12) to describe DM1 deconjugation was implemented here:
| (1) |
| (2) |
| (3) |
| (4) |
where [TDM1] is the T-DM1 concentration in the central or plasma compartment (nM), [TDM1p2] is the T-DM1 concentration in the compartment 2 (peripheral tissue) (nM), [Tras] is the unconjugated antibody concentration in the central compartment (nM), [TDM1p2] is the unconjugated antibody concentration in the peripheral compartment (nM), CLTT is the total antibody clearance (L/s), CL2 is the antibody clearance for the peripheral compartment (L/s), CLDEC is the deconjugation rate (L/s), V1 is the volume of the central compartment (L), and V2 is the volume of the peripheral compartment (L) as seen on Figure 1A at clinical doses. CLTT and CL2 were calibrated to experimental data (13) as seen in Supplemental data S1, and CLDEC was set to be the same as CLTT, making T-DM1 clearance twice as fast as trastuzumab clearance (12).
Trastuzumab and T-DM1 Extravasation and Diffusion
Trastuzumab and T-DM1 extravasate from the blood vessels into the tumor, and this is described by a Robin boundary condition at the vessel boundary:
| (5) |
| (6) |
where x is distance from the blood vessel (μm), P is permeability (μm/s), ε is fraction of free interstitial tissue, and Deff is the effective diffusivity (μm2/s), which describes the diffusion within the tissue (14, 15). Because ADCs are large molecules that cannot traverse cell membranes, the use of ε here accounts for the accessible interstitial volume that ADCs diffuse through. This parameter also adjusts for the relative higher concentration of these molecules in the interstitium compared to an average tumor volume concentration (16).
Diffusion of trastuzumab and T-DM1 on the 2D grid occurs according to Fick’s law:
| (7) |
where C is trastuzumab or T-DM1 concentration in (nM), t is time (s), D is the effective diffusivity (μm2/s), x and y are the Cartesian coordinates. A zero net-flux boundary condition at the edges of the tissue was used since this is a subsection of a large tumor where edge effects are minimal (17).
Trastuzumab and T-DM1 Binding, Internalization, and Degradation
Within the tumor, ADCs bind target molecules, are internalized, and after degradation in the lysosomes, payloads are released to kill the cancer cells through apoptosis as seen in Figure 1B. These drug dynamics are described by the following reactions:
This results in the following equations:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
All variables are listed on Table I and model parameters on Table II. Both free and bound HER2 receptors are assumed to be internalized with the same rate constant. We also assume that the total number of receptors on the cell surface remains constant due to new receptor synthesis and unbound receptor recycling. Thus, Rs= kin [HER2]o. Because the binding and dissociation reactions between the trastuzumab backbone and HER2 receptors are fast in comparison to internalization, we assumed a pseudo-steady state for binding in each compartment to reduce computational time.
Table I:
Drug Dynamics Variables
| Variables | Unit | Description |
|---|---|---|
| TDM1 | nM | Free T-DM1 |
| HER2 | nM | Free HER2 |
| HER2e | nM | HER2 in endosome |
| B | nM | T-DM1 bound to HER2 |
| Be | nM | T-DM1 bound to HER2 in endosome |
| DM1 | nM | DM1 |
| Tras | nM | Trastuzumab |
Table II:
Model Parameters
| Parameter | Value | Unit | Description | Reference |
|---|---|---|---|---|
| CLTT | 1.74 × 10−9 | L/s | Total antibody clearance | Estimated (13) |
| CL2 | 2.31 × 10−8 | L/s | Antibody clearance for compartment 2 | Estimated (13) |
| CLDEC | 1.74 × 10−9 | L/s | Deconjugation rate | Estimated (12) |
| V1 | 1.2 × 10−3 | L | Volume central compartment | Estimated (13) |
| V2 | 1.5 × 10−3 | L | Volume peripheral compartment | Estimated (13) |
| kon | 7.1 × 105 | M−1s−1 | T-DM1 binding rate constant | (18) |
| Kd | 0.5 | nM | T-DM1 dissociation constant | (18) |
| koff | 3.5 × 10−4 | s−1 | T-DM1 dissociation rate constant | (18) |
| ke | 3.3 × 10−5 | s−1 | Internalization rate constant | (19) |
| kdeg | 8 × 10−6 | s−1 | T-DM1 lysosomal degradation rate constant | (20) |
| kloss | 3.94 × 10−5 | s−1 | Cytotoxin loss rate constant | Estimated (21) |
| DAR | 3.5 | - | DM1 to antibody ratio | (22) |
| Rs | 2.75 × 10−11 | M/s | Target synthesis | (14) |
| HER2o* | 5 × 104-2 × 106 | receptors/cell | Total targets per cell | Varied |
| ε | 0.24 | - | Intracellular void fraction | (23) |
| D | 1 × 10−11 | m2/s | Diffusivity | (14) |
| P | 3 × 10−9 | m /s | Vascular permeability | (24) |
| Pmax | 0.014 | - | Maximum probability for cell killing | Calibrated |
| Km | 800 | nM | Michaelis-Menten constant | Calibrated |
| td (in vivo) | 5–17 | days | In vivo doubling time | Calibrated |
| td (in vitro) | 1–2.5 | days | In vitro doubling time | Estimated |
1 million receptors per cell corresponds to 833nM receptors where each cell occupies about 2× 10−12 L.
Cell Division and Death
Tumor volume is proportional to the number of cancer cells in the simulation. Cancer cells proliferate depending on the tumor doubling time (td) assigned at the beginning of the simulation, and td is assumed to account for natural cell death. All cells in the same simulation are given the same doubling time but a different (random) birthtime to avoid synchronization. At cell division, two identical cells are created, and their bound drug and internalized drug are evenly divided between them. One of the daughter cells is placed in the original grid compartment, and the other daughter cells is placed on a neighboring grid compartment. If there is no space in the neighboring compartment, cells shuffle to make space for the new cell (see algorithm in supplemental methods 2).
Cancer cells die only depending on the payload concentration inside the cells, and they are then removed from the simulation grid. The probability for cell killing (Pkill) during each agent time step (i.e., the integral of the cell killing rate over the time step) is given by the Michaelis-Menten equation:
| (15) |
where Pmax is the maximum probability for cell killing, [DM1] is the concentration of cytotoxin inside the cells in nM, and Km is the Michalis-Menten constant. Pmax and Km were calibrated to experimental data (5). The overall probability for cell killing becomes the integration of all the probabilities for cell killing over the simulation time. While Eqn. 15 always has a probability of death > 0 for a non-zero payload concentration, in practice, low concentrations of drug typically exhibit a threshold effect below which no discernable difference between treated and untreated cells is seen. Therefore, we estimated the minimum concentration for cell killing (a cell killing threshold) to be 120 nM based on experimental data (5) (supplemental methods 3). If the payload concentration inside the cell is below this threshold, the probability for cell killing is set to zero. Trastuzumab was assumed to have no effect on cell killing, although very high doses of trastuzumab might have an impact on efficacy in an NCI-N87 xenograft model system. Dead cells were estimated to stay on the grid for 2.5 days (supplemental methods 2) before they are removed from the grid. Neighboring cells shuffle from the outer border to fill the empty grid space caused by the removal of the dead cell (supplemental methods 2).
In Vitro Simulations
To model in vitro toxicity experiments, we assumed that all cells are exposed to the same external concentration of trastuzumab and T-DM1 present in the media. For this reason, ε is set equal to 1 in Eqns. 8, 9, 10, 13, and 14, as ADC diffusion is not hindered by the tumor tissue. For the toxicity assays, cells in each simulation are exposed to a constant T-DM1 concentration, and cell viability was calculated at 6 days. For the coincubation of trastuzumab and T-DM1, cells were exposed to a total concentration of 10nM and various ratios of the concentrations of trastuzumab to T-DM1. For all in vitro simulations, cell doubling time was varied from 1 to 2.5 days.
Computational environment and Numerical Methods
The model was constructed in C++ with Boost (distributed under the Boost software license – available at www.boost.org). The graphical user interface (GUI) was built using the Qt framework (open-source, distributed under GPL – available at qt.digia.com). Efficient linking and solution of our hybrid multiscale ABM followed the principles described in (25). We used a molecular time step of 2 seconds, a diffusion time step of 4 seconds, and an agent time step of 10 minutes. The diffusion equation was solved using the alternating-direction explicit (ADE) method and ODEs were solved using the 4th order Runge-Kutta method.
Fluorescence Histology
Methods for fluorescence histology have been published previously by our lab (5). Briefly, for mouse tumor xenografts, 5×106 NCI- N87 cells, purchased from ATCC, were injected in the rear flanks of 4–8 week-old female nude (Foxn1nu/nu) mice from Jackson Laboratories. Kadcyla was conjugated with AlexaFluor 680 NHS Ester (AF680, Thermo Fisher Scientific, A37567) with antibody to dye ratio of 0.3 or less and given intravenously. The mice were then sacrificed 24 hours after injection and histology slices were labeled ex-vivo with anti-mouse CD31 conjugated with AlexaFluor 555 (Thermo FisherScientific, A37571) and mouse antihuman IgG Fc antibody conjugated with AlexaFluor 488 (Thermo Fisher Scientific, A20000). All animal studies were conducted according to University of Michigan Institutional Animal Care and Use Committee.
RESULTS
Simulating Heterogeneous Distribution of Antibodies in Tumor Slices
Our model captures the heterogeneous distribution of ADCs and antibodies seen in NCI-N87 tumor xenografts (2). Here, vessel density varies between simulations following a normal distribution with an average blood vessel density of 28 functional vessels per simulation. At clinical doses (3.6 mg/kg), T-DM1 localizes perivascularly, but coadministration with trastuzumab competes for the perivascular binding sites, allowing more T-DM1 to penetrate farther in the tissue. Therefore, a constant dose of T-DM1 is ‘diluted’ in the tumor tissue to reach more cells as seen in images of mouse tumors (Figure 2A). With the same image contrast for the same drug regimens, our model also captures this dilution and spreading of ADCs in the simulation with T-DM1 reaching all cells at regimens of 8:1 ratio, Figure 2B.
Fig. 2.
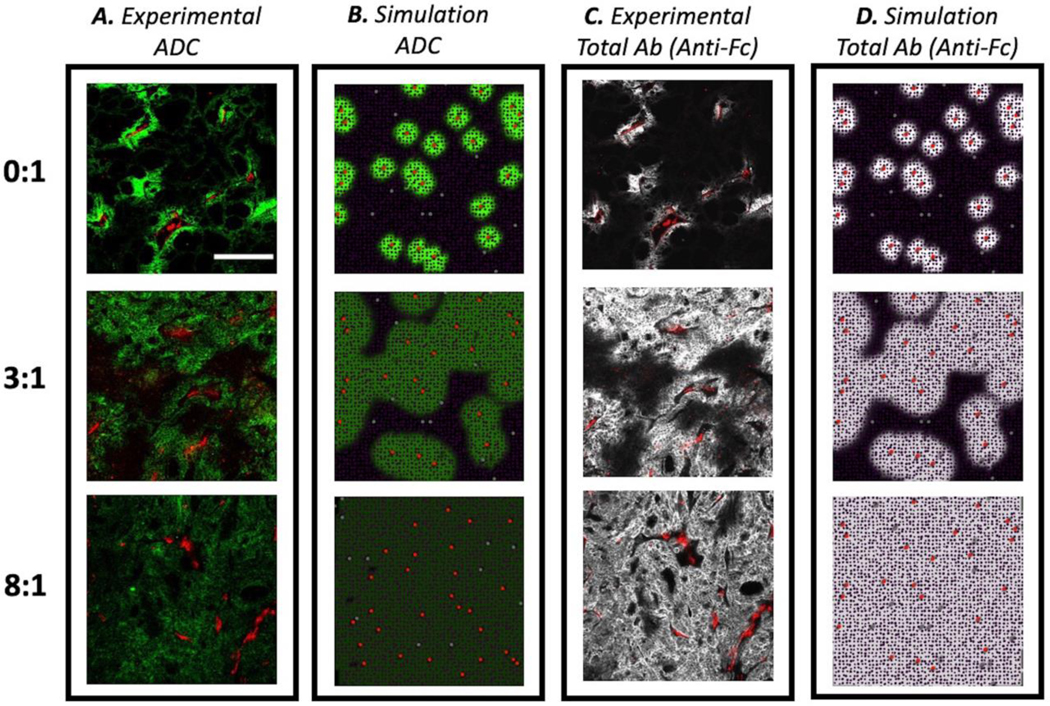
Comparison between experimental and simulated drug distributions in tumor tissue. a Tumor sections from mice bearing NCI-N87 xenograft tumors dosed with 3.6 mg/kg of AlexaFluor680 labeled T-DM1 and different ratios of trastuzumab:T-DM1 were imaged after 24 hours using the same settings and then set to the same window level for different carrier dose (trastuzumab) concentrations. T-DM1 intensity decreases as it is “diluted” with trastuzumab at higher ratios and spreads out to reach more cells. b Simulation results showing bound T-DM1. c The same tumor sections were stained with anti-Fc labeled antibody and window-leveled the same to show total drug penetration in tumor. d Simulation results show total antibody (T-DM1 + trastuzumab) penetration into the tumor. For all figure portions, scale bar = 200 μm
Likewise, our model captures the total antibody uptake as seen in mouse tumor slices stained with antihuman-Fc labeling that targets all antibody backbones (T-DM1 and trastuzumab), methods found in previous work (5). Here, although the concentration of T-DM1 is diluted through the tumor tissue, higher antibody concentrations are achieved with coadministration of trastuzumab along with T-DM1 to improve tumor penetration. As seen on Figure 2C and 2D, our model also captures this total antibody uptake by the tumor reaching receptor saturation at the 8:1 ratio.
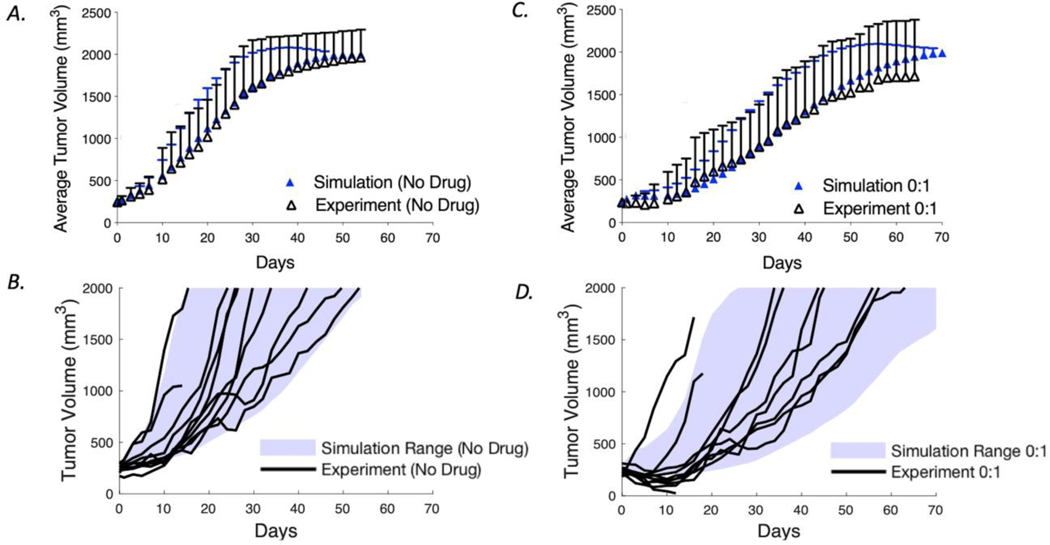
Calibrating Tumor Growth Kinetics and In Vivo Cell Killing
After demonstrating that the ABM can capture the heterogeneous distribution of antibodies and ADCs around vessels, we moved to capture the pharmacodynamics within the tumor. To understand how the drug microenvironment impacts efficacy, our model was calibrated to in vivo data (5) on cell proliferation and cell killing due to drug action to capture the tumor growth dynamics. The tumor growth rate for the simulations was calibrated by fitting the average tumor cell doubling time and range to capture tumor volume growth curves from experimental control (untreated) mice as seen in Figure 3A and 3B. The calibrated tumor volumes have a doubling time range from 5 to 17 days. In this model, the doubling time for each tumor is defined at the initialization based on a normal distribution in which tumors with higher vessel density have a higher probability to grow faster (i.e., a smaller doubling time, supplemental data Figure S2). This was implemented to account for the blood vessels as the source for nutrients and oxygen that enables cell proliferation (26). The proliferation rate constitutes the net cell division above the level needed to replace intrinsic cell death within the tumor.
Fig. 3.
Model calibration of tumor growth rate and cell killing using average and variability of NCI-N87 xenograft tumors from Cilliers et al. (5). a The average experimental data and SD are plotted with the average and SD of simulated tumor sizes from 100 computational runs for the control group. b The range of growth rates for the simulations (shaded area) is shown together with individual tumor curves in the absence of drug treatment. c The average experimental data and SD are plotted with the average and SD of calibrated tumor sizes for a single dose. To calibrate cell killing in vivo, the growth curves for tumors treated with 3.6 mg/kg of T-DM1 were used to calibrate the probability of individual cell death as a function of intracellular payload concentration (Eq. 15). d The range of growth rates for the simulation (shaded area) is shown together with individual experiment curves for a treatment with a single dose
The probability of cancer cell killing due to drug action was also calibrated to the in vivo experimental data for T-DM1 treatment at the clinical 3.6 mg/kg dosing. Using the Michaelis-Menten equation for the killing probability, the average efficacy in 10 experimental mouse tumors was matched to the average efficacy of 100 simulations. Pmax and Km are highly correlated and are mostly in the linear range of Eqn. 15 for these simulations, so we set Km to 800nM based on the likely range of payload concentration inside of the cell and calibrated Pmax to 0.014. Using these two parameters, cell killing results matched the range and average as seen of Figure 3C and 3D.
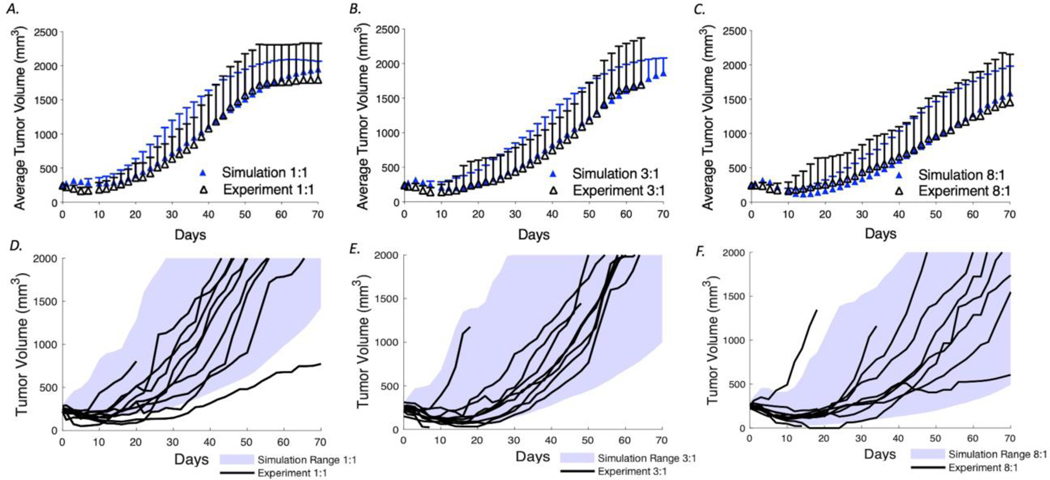
Simulation Accurately Predicts the Effect of Coadministration of Trastuzumab with T-DM1 on Tumor Growth
Previously, our lab demonstrated that coadministration of trastuzumab and T-DM1 improved efficacy. Using the model that was calibrated to data from a single dose of T-DM1, we next simulated regimens for 1:1, 3:1, and 8:1 ratio and compared the results to the experimental curves for model validation (Figure 4A-C). The mean tumor volumes and SD of the simulations (n=100) agree closely with the experimental data (n=10). Figure 4D-F shows the simulation range achieved with the 100 simulations (blue shading) and the experimental tumor curves (black lines). These results demonstrate the ability of our model to capture the variability in tumor growth and impact of carrier doses on efficacy.
Fig. 4.
Coadministration of T-DM1 with trastuzumab. Using the calibrated tumor growth and cell killing probabilities determined in Fig. 3, the model was used to predict the tumor growth curves for mice treated with 3.6 mg/kg T-DM1 with trastuzumab to T-DM1 ratios of 1:1, 3:1, and 8:1. These independently generated simulations were then compared with the experimental data from Cilliers et al. (5). a–c Mean and SD of the experimental and simulation data. d–f Simulation ranges (shaded area) and the experimental tumor volume curves (black lines)
Reaching Maximum Number of Cells with Lower but Lethal Concentrations of Payload Results in the Greatest Tumor Efficacy
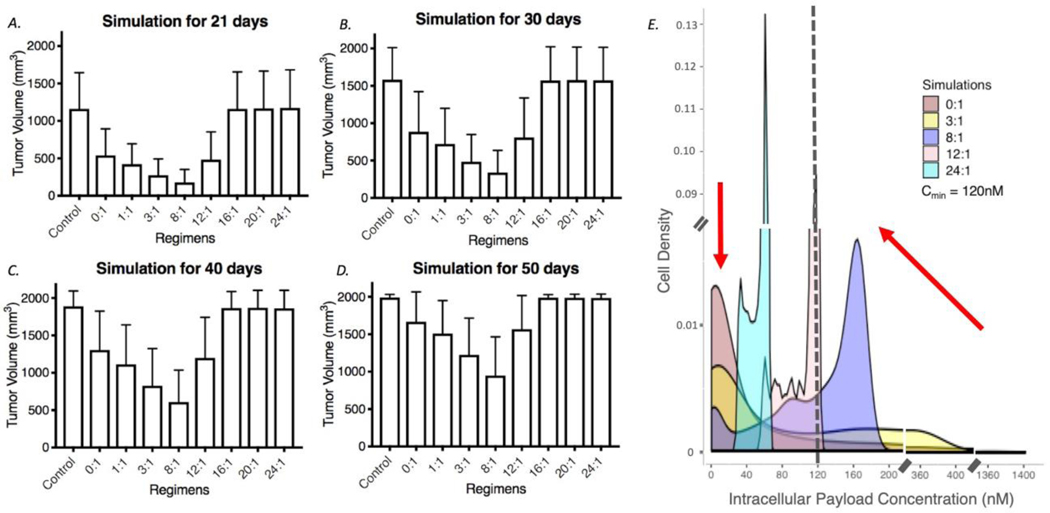
We next simulated drug regimens with different ratios of trastuzumab to a fixed clinical dose (3.6 mg/kg) of T-DM1 to identify which dose regimen gives the best treatment outcome. Figure 5A shows the efficacy of regimens with trastuzumab to T-DM1 ratios ranging from 0:1 to 24:1 and over the course of 21, 30, 40, and 50 days. Increasing the ratio results in greater competition of the unconjugated antibody to ADC. At a regimen of 8:1, the tumor approaches saturation by the antibody, and the maximum tumor uptake of T-DM1 reaches all of the cells within the tumor. At higher than saturating (super-saturating) doses, the unconjugated antibody competes with T-DM1, decreasing the uptake of payload into individual cells, while not reaching any more regions of the tumor. Both total tumor uptake of ADC and individual cell uptake decrease beyond this point. When graphing the fraction of cells receiving a given intracellular payload concentration for increasing carrier doses at 48 hrs, both the number of cells with very high levels of payload and those with no payload are reduced (Figure 5E) while more cells receive a moderate dose of payload (i.e., reducing the heterogeneity of drug distribution). Importantly, even at the 8:1 carrier dose, ~60% of the targeted cells have greater than the 120 nM intracellular concentration needed for cell death. However, as the carrier dose increases, the concentration of the payload decreases below 120 nM, resulting in reduced efficacy. In summary, despite competition of T-DM1 uptake by the large antibody dose, the model predicts a better prognosis when more cells are reached at a lower (but still lethal) number of T-DM1 payloads per cell than when fewer cells receive high doses (‘overkill’).
Fig. 5.
Influence of carrier dose on tumor efficacy. a-d The simulated efficacy of coadministration of trastuzumab with T-DM1 at 21, 30, 40, and 50 days, respectively, is shown for 3.6 mg/kg T-DM1 and trastuzumab to T-DM1 ratios from 0:1 to 24:1. Efficacy drops at higher concentrations of trastuzumab due to tumor saturation and/or reducing the number of payloads per cell below the threshold needed for cell death. N = 100 simulations for each bar. e Density plot for cells in the simulation (live or dead) receiving particular intracellular payload concentrations was calculated at 48 hours. Here, the area under the curve of the density function represents the probability of getting an intracellular payload concentration value between a range of payload concentration values. The number of cells that receive no drug decreases (arrow on the left) with an increasing carrier dose increase evidencing an improvement in distribution. However, the payload concentration per cell decreases with an increasing carrier dose (arrow on the right)
The Potency of the Payload Affects the Influence of a Carrier Dose
The simulations indicated that a carrier dose improves efficacy when the increased number of cells reached by T-DM1 outweighs the reduced killing due to fewer payloads per cell. Implicit in this statement is that adding a carrier dose beyond the level needed for tumor saturation will lower efficacy since no new cells are reached. In the system studied here (T-DM1 with NCI-N87 xenografts), the payload is very potent relative to the number of payloads delivered per cell, and the doses are below tumor saturation. However, for moderately potent payloads, there are examples where concentrating the payload on fewer cells results in greater efficacy (2) such as seen with sacituzumab govitecan (27). If the concentration of the payload delivered by pure ADC is just enough to kill these cells (i.e., there is no ‘overkill’), decreasing the concentration of the payload per cell with a carrier dose would lead to lower treatment efficacy because no cells would receive a toxic dose even though the new regimen is reaching more cells. To determine when a carrier dose might decrease efficacy even prior to tumor saturation, we used the simulations to examine the role of the minimum concentration needed for cell death (Cmin).
The presence of a minimum threshold payload concentration for cell death has a significant impact on efficacy, particularly when the dose range is high enough to saturate the first cell layer but lower than required for tumor saturation. In this range, such as simulated in this work, the dose has a major impact on tissue penetration. We simulated tumor efficacy with a Cmin of 500 nM, 10 nM, and no minimum threshold in toxicity needed for cell death (Figure S3). The latter scenario assumes a pure Michaelis-Menten relationship where any drug concentration, no matter how small, has some impact on cell viability. If this were the case, the carrier dose is virtually always beneficial prior to saturation of the tumor. This can be explained in terms of the number of cells reached and probability of cell death. If efficacy is the product of the number of cells targeted by the ADC multiplied by the fractional cell killing, the number of cells reached increases linearly with the total antibody dose. The fractional cell killing for payload concentrations well below the Km results in close to, but always slightly less than, a linear decrease. Therefore, a carrier dose would always improve the overall product under these assumptions. However, most drugs exhibit some threshold below which there is no detectable response, so it was important to explicitly define a minimum concentration needed for cell death regardless of the pharmacodynamic model used (including the Michaelis Menten model in this work). If a carrier dose reduces the payload uptake below this amount, a dramatic loss in efficacy is seen.
To simulate cells that are more resistant to the payload (i.e. the potency is decreased), Cmin was set to a 500 nM intracellular concentration needed to induce some cell death. In this case, even a 1:1 carrier dose starts to decrease overall efficacy (Figure S3). This highlights how diluting the ADC to achieve better drug penetration depends on the potency of the payload to reach a minimum threshold while reaching the largest number of cells.
The Impact of the Carrier Dose is Dependent on the Average Tumor Expression of HER2
ADC distribution within a tumor also depends on the number of receptors per cell (10) (5) (21). As seen in previous work, a higher number of receptors decreases drug penetration into the tumor, and for those tumors, higher doses of coadministrated trastuzumab are needed to improve efficacy compared to tumors with lower receptor density. For this reason, the optimal drug regimen is dependent on the average number of receptors per cell in the tumor.
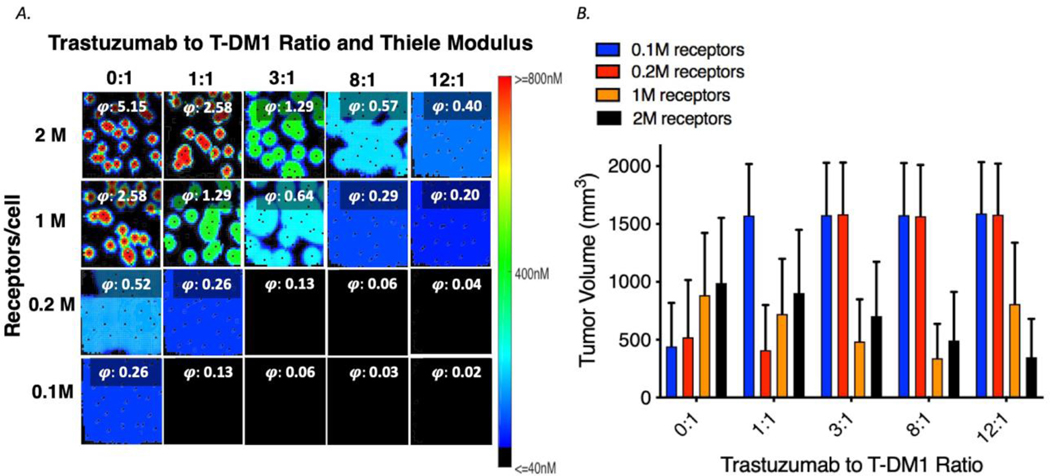
Tumors with different HER2 receptor expression levels were simulated with various drug regimens, and the results are shown in Figure 1A. Regimens with doses of trastuzumab and T-DM1 at 0:1, 1:1, 3:1, 8:1, and 12:1 were simulated for tumors with average of 0.1, 0.2, 1, and 2 million receptors per cell. The Thiele modulus, a dimensionless number that predicts the antibody saturation level in tumors (19) is listed in each box. For levels below ~0.2 the tumor is saturated (28). For tumors with lower HER2 expression, e.g. an average of 0.1 million receptors per cell, the best efficacy occurs at lower total antibody concentrations. However, at very low receptor expression levels, such as < 50,000 HER2 per cell, no response was observed as the minimum accumulation of payloads inside the cell to lead to efficacy is not reached (Figure S4). For tumors with higher expression density (e.g., 2M receptors per cell), the best treatment with coadministration occurs at higher doses of total antibody. However, at lower receptor expression, increasing the total antibody coadministered can actually decrease efficacy (Figure 6B).
Fig.6.
Interplay of dose and receptor density. A Bound concentration of T-DM1with coadministration with trastuzumab (ratios trastuzumab to T-DM1 from 0:1 to 12:1) for tumors with different receptor densities. The Thiele modulus (calculated using total antibody dose) shows saturation when the value is less than ~ 0.2. b Average tumor volume at 30 days for different treatment regimens and tumors with different average receptor densities. The optimal carrier dose is dependent on receptor expression with higher trastuzumab doses needed for higher receptor expression. With the potency of this ADC, no efficacy is seen below 50,000 HER2/cell (Fig S4)
Single Dosing with Coadministration is Better than Coadministration with Fractionated Dosing
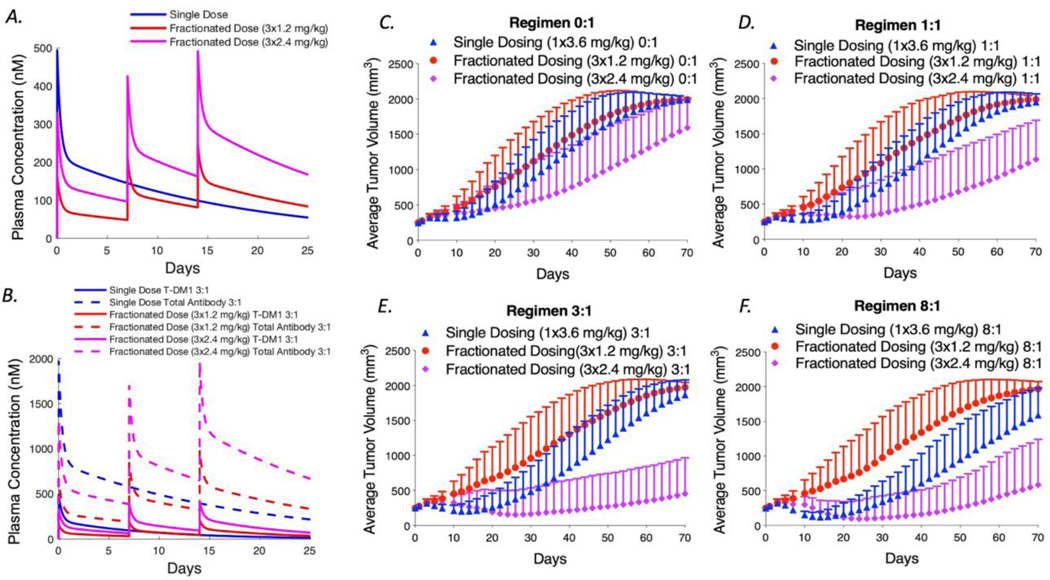
Previous work has demonstrated that fractionated doses can lead to similar efficacy, but better tolerability compared to single dosing. We simulated fractionated dosing treatment with 3 weekly doses of 1.2 mg/kg of T-DM1 and compared it with a single dosing (3.6 mg/kg). The maximum concentration (Cmax) of single dose antibody in the plasma (3.6 mg/kg) is much higher than the Cmax of fractionated dosing as shown in Figure 7A. However, the area under the curve (AUC) for these two regimens is the same. With the same total administered dose at the end of 3 weeks, the efficacy of fractionated dosing is reduced but not significantly different than a single dose as shown on Figure 7C. This is in agreement with reports by Hinrich et al. and Jumbe et al. showing lower efficacy when fractionating an ADC dose (6, 7), but not significant differences in the case of Hinrich et al.
Fig. 7.
Simulations of fractionated dosing with and without a carrier dose for NCI-N87 tumor xenografts. a Plasma concentration of T-DM1 for a single 3.6 mg/kg dose or 3 fractionated doses at 1.2 and 2.4 mg/kg. b Single T-DM1 versus total antibody concentration clearance for single and fractionated dosing at 3:1. c–f Simulated tumor volumes for the coadministration of trastuzumab to T-DM1 at 0:1, 1:1, 3:1, and 8:1 ratios are shown, respectively. Each plot compares a single bolus dose of 3.6 mg/kg to 3 weekly fractionated doses at 1.2 and 2.4 mg/kg T- DM1. In general, fractionation lowers efficacy due to reduced tissue penetration. This is exacerbated with high carrier doses (e.g., 8:1) because the lower payload delivery is significantly diluted below a threshold needed for cell death. This can be compensated, however, by increased tolerability if a reduction in toxicity allows larger ADC doses to be administered (e.g., 2.4 mg/kg weekly versus 3.6 mg/kg every 3 weeks)
We also simulated single dosing and fractionated dosing for different carrier dose regimens of 1:1, 3:1, and 8:1 as shown in Figure 7B-F. Here, for example, an 8:1 fractionated dose is equal to 3 weekly doses of 1.2 mg/kg T-DM1 coadministered with 9.6 mg/kg of trastuzumab. Our results predict that at higher carrier doses (e.g. 8:1), dose fractionation results in much lower efficacy than for single dosing regimens with the same carrier dose. Although more cells are reached by the higher total antibody dose, e.g. 8:1 regimen, the lower T-DM1 concentration in each dose plus the dilution that occurs by adding a carrier decreases payload concentration per cell below the minimum needed for efficacy.
One benefit of dose fractionation is greater tolerability. In the clinic it has been shown that the maximum tolerable dosing for T-DM1 is 3.6 mg/kg every 3 weeks or 2.4 mg/kg every week (29). We therefore simulated weekly doses of 2.4 mg/kg T-DM1 with different carrier levels, which led to better predicted efficacy. With regimens of 2.4 mg/kg every week for 3 weeks, the total T-DM1 concentration is increased. Therefore, fractionated dosing with a carrier dose can be beneficial if this allows an increase in the total ADC dose reaching more cells with a lethal concentration of payload.
Model Calibration in Vivo Matches Drug Efficacy in Vitro
The pharmacodynamic model, calibrated to the in vivo data, also captures the toxicity of in vitro experiments (Figure S5). Originally, the pharmacodynamic model parameters were fit to in vivo data (Fig. 3) because it was not clear if the sensitivity of the cells in the tumor microenvironment would be different than in cell culture. Using the same parameters for in vivo calibration to simulate toxicity curves in vitro (either single-agent or coincubation of trastuzumab and T-DM1), the curves were similar to previously published results in our lab. Therefore, in this system, there did not appear to be a major shift in potency in vitro versus in vivo.
DISCUSSION
The complexity of ADC development, encompassing the antibody design, target selection, linker development, payload potency, dosing regimen, along with delivery barriers, tumor heterogeneity, patient variability, and potential for drug combinations, requires tools beyond cellular and animal efficacy-based screening to efficiently identify compounds and drug regimens for clinical success. Agent-based modeling is a powerful tool to capture both the multiscale and heterogeneous distribution of ADCs within tumors and also single cell responses and overall tumor efficacy (Fig. 1). A significant advantage of the current ABM model compared to previous ADC models is the ability to look at individual cellular responses for simulating pharmacodynamics, unlike our previous Krogh cylinder model which mainly captures pharmacokinetics. Here, we simulate the tumor environment in the context of many irregularly placed blood vessels, with some functional while others are not, capturing the irregularity seen in experimental data (Fig. 2).
Another advantage of the ABM is the ability to capture the cellular level pharmacodynamic behavior of ADCs. Recent advances in pharmacodynamic modeling of ADCs have started incorporating tissue gradients (10) or cellular heterogeneity (e.g., antigen positive and negative cells (8) (30)). In the current model, by simulating individual cells within tissue-scale drug gradients, we capture both these effects across thousands of cells. An ABM enables direct comparisons between single cell PK/PD data gathered in the lab and the computational model.
Treating a solid tumor as a homogeneous unit could overlook important effects of drug treatment regimens such as adding a carrier dose. Here, our model captures the correct drug distribution and efficacy of different regimens as compared with in vivo data from our lab (Fig. 2, 3, and 4), demonstrating that our model is a powerful tool to capture ADC and antibodies administration in the tumor environment.
The simulations also provide a series of predictions (Fig. 5, 1, and 7) that can aid in the development of drugs and design of new experiments. Although achieving greater tissue penetration (up to tumor saturation) has been shown to improve efficacy for tumors with high antigen expression treated with T-DM1, increasing the total antibody dose too much can also diminish cellular cytotoxin uptake and therefore lower efficacy (Fig. 5A-D). These results are dependent on the delivery (antigen expression, internalization rate, tumor vascularization, etc.) and payload efficacy (linker cleavage, payload potency, etc.) necessitating a quantitative analysis for each individual ADC case rather than extrapolating the model results to all systems.
In addition to the payload potency, another important consideration in adding a carrier dose to the regimen is the average tumor target expression. For tumors with lower antigen expression, adding a carrier dose results in no improvement, and potentially lowers the efficacy. This is seen for regimens in tumors with lower antigen expression such as ≤ 100,000 receptors per cell. In these tumors, single-agent ADC dosing at 3.6 mg/kg already saturates the tumor, delivering the maximum cytotoxin potency to the tumor cells (Fig. 1). Adding a carrier dose to those tumors can only reduce the concentration of payload per cell. However, for even lower antigen expression such as 50,000 receptors per cell, even with ADC alone, there is not enough payload per cell to cause a tumor response (Fig S4). For this reason, administering a carrier dose must be considered in the context of the target’s average tumor expression and payload potency.
A major consideration in the development of ADCs is the drug to antibody ratio (DAR). T-DM1 has an average DAR of 3.5, but adding a carrier dose reduces the average DAR in circulation (e.g., DAR 3.5 at 3.6 mg/kg compared to DAR 1.75 at 7.2 mg/kg dose – or 1:1 regimen). Lowering the DAR allows higher antibody doses because toxicity is typically driven by the payload dose. In the absence of DAR-dependent effects (such as DAR-dependent clearance and DAR-dependent deconjugation (31)), lowering the average DAR by adding unconjugated (DAR 0) antibody is equivalent to lower the DAR of the ADC alone. However, DAR-dependent effects could lead to higher ADC exposure (AUC) for a lower DAR on the ADC compared to adding a carrier dose. The lower ADC DAR could improve efficacy by increasing tumor exposure from a higher AUC, but it also has the potential to change the toxicity profile (e.g., less deconjugation resulting in higher exposure to tissues such as the eye). Conversely, increasing the DAR of an ADC is expected to increase the toxicity (at a constant antibody dose), lowering the maximum tolerated dose (MTD). The lower antibody dose can result in challenges such as target-mediated drug disposition and increased intratumor heterogeneity, which can reduce efficacy. Interestingly, some site-specific conjugation strategies result in lower DAR (32), and lower potency payloads (e.g., topoisomerase inhibitors) also allow higher antibody doses to be administered, which can result in improved tissue distribution at the MTD.
Reaching the maximum number of cells with the minimum payload needed for efficacy is also a subject of attention in fractionated dosing. With single-agent ADC dosing, fractionating the dose only results in slightly lower efficacy, likely because single dosing was probably overkilling perivascular cells. However, fractionated doses with coadministration of the carrier dose significantly decreased efficacy compared to a single bolus dose with a carrier at the same ratio (e.g., 8:1, Fig. 7). The lower T-DM1 concentration per dose and dilution of the payload from the carrier dose pushes too many cells below a lethal number of payloads per cell. However, fractionated dosing can increase tolerability, which leads to the possibility of increasing ADC dosing and tumor drug exposure. The coadministration of ADC with carrier and fractionated dosing can provide not only better tumor penetration but also greater AUC and total payload tumor uptake. Therefore, our results show that fractionated dosing can be beneficial if it improves tolerability enough to increase the dose and overcome the decreased tissue penetration caused by a lower Cmax, consistent with previous publications on fractionating dosing (Fig S6) (7). This is the approach taken with the clinical dosing for enfortumab vedotin, currently in phase III clinical trials with a 1.25 mg/kg weekly dose (33).
The current model has several limitations. Although this model is helpful in capturing the tumor growth efficacy of ADCs, it currently does not capture the development of resistance that could occur when cancer cells are exposed to diluted drug concentrations (34). All the cells in this model are sensitive to the drug, and results here have indicated that the best regimens are found with increased drug distribution even at lower payloads per cell. The trade-off in increased efficacy versus increased risk of resistance is complicated by other factors such as tissue-level secondary drug effects (e.g., collapse of vessels in heavily treated areas) and additional mechanisms of action (e.g., immune cell interactions) described below. For this reason, regimens that select resistant cells and stimulate cell mutation should be studied in the future with this model.
We calibrated our model to in vivo toxicity, and our probabilities could have overestimated cell killing due to secondary effects from the drug treatment. Cancer cells in vivo can die through direct and indirect mechanisms. For example, as cancer cells around a blood vessel die, blood vessels can also collapse, limiting the oxygen and nutrient delivery to other cells nearby. This may alter cell death or proliferation rates locally and could be considered in future work. Further work might also consider other sources of heterogeneity, such as heterogeneous antigen receptor expression, and the simultaneous actions of the immune system toward killing tumor cells. Despite these caveats, our model results reasonably match the toxicity from in vitro experimental data (after accounting for a faster doubling time and lack of transport limitations, which are important considerations for in vitro/in vivo correlations (30)). In addition, our model results agree with IC50 values found in previously publications (35).
Finally, our current model does not take into consideration the immune system in combating cancer, including multiple mechanisms of action through the antibody Fc domain (36). In fact, ADCs have been shown to be more effective in immunocompetent animal models (37). Fortunately, our computational model has the potential to study and incorporate the probabilistic behavior of the immune system in response to these therapies, as already established in our lab for the study of an infectious disease (38, 39). Once appropriately calibrated to a particular ADC, the model also has the potential to be used to set preclinical benchmarks for targets with expression levels quantified by immunohistochemistry or even personalizing treatment with individualized dosing(40). Therefore, this ABM has the capability of addressing the complexities in ADC therapy including the impact of carrier doses and dosing regiments on the heterogeneous tissue delivery and single-cell responses demonstrated here.
CONCLUSION
We developed a hybrid ABM to capture heterogenous drug delivery of ADCs and individual cellular responses and to predict tumor growth curves and overall efficacy. The ABM enables detailed depictions of heterogeneous vascularization and ADC delivery, cancer cell death, tumor growth, and treatment efficacy following different drug regimens. The model results demonstrate that a carrier dose of unconjugated antibody can improve efficacy if the number of cells reached by the ADC outweighs the reduction in targeted cell killing, which depends on expression, payload potency, and dosing. This will result in the largest number of cells receiving a lethal dose. Likewise, fractionated dosing can improve efficacy if increased tolerability allows higher ADC dosing to overcome the loss in tissue penetration from a lower Cmax. By incorporating multiple competing effects within the tumor microenvironment, the simulations can aid in the development of new drugs and targeted therapies.
Supplementary Material
ACKNOWLEDGMENTS
The authors acknowledge funding from NIH R01 CA196018 (JJL) and R35 GM128819 (GMT). The authors also thank Paul Wolberg for technical assistance.
REFERENCES
- 1.Coats S, Williams M, Kebble B, Dixit R, Tseng L, Yao NS, et al. Antibody-drug conjugates: future directions in clinical and translational strategies to improve the therapeutic Index. Clinical cancer research : an official journal of the American Association for Cancer Research. 2019. [DOI] [PubMed] [Google Scholar]
- 2.Cilliers C, Guo H, Liao J, Christodolu N, Thurber GM. Multiscale modeling of antibody-drug conjugates: connecting tissue and cellular distribution to whole animal pharmacokinetics and potential implications for efficacy. AAPS J. 2016;18(5):1117–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bhatnagar S, Deschenes E, Liao J, Cilliers C, Thurber GM. Multichannel Imaging to Quantify Four Classes of Pharmacokinetic Distribution in Tumors. J Pharm Sci. 2014;103(10):3276–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baker JHE, Kyle AH, Reinsberg SA, Moosvi F, Patrick HM, Cran J, et al. Heterogeneous distribution of trastuzumab in HER2-positive xenografts and metastases: role of the tumor microenvironment. Clin Exp Metastasis. 2018;35(7):691–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cilliers C, Menezes B, Nessler I, Linderman J, Thurber GM. Improved tumor penetration and single-cell targeting of antibody–drug conjugates increases anticancer efficacy and host survival. Cancer Research. 2018;78(3):758–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hinrichs MJM, Ryan PM, Zheng B, Afif-Rider S, Yu XQ, Gunsior M, et al. Fractionated Dosing Improves Preclinical Therapeutic Index of Pyrrolobenzodiazepine-Containing Antibody Drug Conjugates. Clinical cancer research : an official journal of the American Association for Cancer Research. 2017;23(19):5858–68. [DOI] [PubMed] [Google Scholar]
- 7.Jumbe NL, Xin Y, Leipold DD, Crocker L, Dugger D, Mai E, et al. Modeling the efficacy of trastuzumab-DM1, an antibody drug conjugate, in mice. J Pharmacokinet Pharmacodyn. 2010;37(3):221–42. [DOI] [PubMed] [Google Scholar]
- 8.Shah DK, Haddish-Berhane N, Betts A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: a case study with brentuximab-vedotin. J Pharmacokinet Pharmacodyn. 2012;39(6):643–59. [DOI] [PubMed] [Google Scholar]
- 9.Thurber GM, Dane Wittrup K. A mechanistic compartmental model for total antibody uptake in tumors. J Theor Biol. 2012;314:57–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vasalou C, Helmlinger G, Gomes B. A mechanistic tumor penetration model to guide antibody drug conjugate design. PLoS One. 2015;10(3):e0118977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Singh AP, Shah DK. A “dual” cell-level systems PK-PD model to characterize the bystander effect of ADC. J Pharm Sci. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bender B, Leipold DD, Xu K, Shen BQ, Tibbitts J, Friberg LE. A mechanistic pharmacokinetic model elucidating the disposition of trastuzumab emtansine (T-DM1), an antibody-drug conjugate (ADC) for treatment of metastatic breast cancer. The AAPS journal. 2014;16(5):994–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cilliers C, Nessler I, Christodolu N, Thurber GM. Tracking Antibody Distribution with Near-Infrared Fluorescent Dyes: Impact of Dye Structure and Degree of Labeling on Plasma Clearance. Mol Pharm. 2017;14(5):1623–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thurber GM, Weissleder R. A systems approach for tumor pharmacokinetics. PLoS One. 2011;6(9):e24696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nugent L, Jain RK. Extravascular diffusion in normal and neoplastic tissues. Cancer Res. 1984;44:238–44. [PubMed] [Google Scholar]
- 16.Thurber GM, Schmidt MM, Wittrup KD. Antibody tumor penetration: transport opposed by systemic and antigen-mediated clearance. Adv Drug Deliv Rev. 2008;60(12):1421–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thurber GM, Weissleder R. Quantitating antibody uptake in vivo: conditional dependence on antigen expression levels. Molecular imaging and biology : MIB : the official publication of the Academy of Molecular Imaging. 2011;13(4):623–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bostrom J, Haber L, Koenig P, Kelley RF, Fuh G. High affinity antigen recognition of the dual specific variants of herceptin is entropy-driven in spite of structural plasticity. PLoS One. 2011;6(4):e17887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Thurber GM, Zajic SC, Wittrup KD. Theoretic criteria for antibody penetration into solid tumors and micrometastases. Journal of nuclear medicine : official publication, Society of Nuclear Medicine. 2007;48(6):995–9. [DOI] [PubMed] [Google Scholar]
- 20.Maass KF, Kulkarni C, Betts AM, Wittrup KD. Determination of cellular processing rates for a trastuzumab-maytansinoid antibody-drug conjugate (ADC) highlights key parameters for ADC design. AAPS J. 2016;18(3):635–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Khera E, Cilliers C, Bhatnagar S, Thurber GM. Computational transport analysis of antibody-drug conjugate bystander effects and payload tumoral distribution: implications for therapy. Molecular Systems Design & Engineering. 2018;3(1):73–88. [Google Scholar]
- 22.Poon KA, Flagella K, Beyer J, Tibbitts J, Kaur S, Saad O, et al. Preclinical safety profile of trastuzumab emtansine (T-DM1): mechanism of action of its cytotoxic component retained with improved tolerability. Toxicol Appl Pharmacol. 2013;273(2):298–313. [DOI] [PubMed] [Google Scholar]
- 23.Schmidt MM, Wittrup KD. A modeling analysis of the effects of molecular size and binding affinity on tumor targeting. Mol Cancer Ther. 2009;8(10):2861–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yuan FD M. Fukumura D. Leunig M. Berk D. Torchilin V. Jain RK. Vascular permeability in a human tumor xenograft: molecular size dependence and cutoff size. Cancer Research. 1995;55:3752–6. [PubMed] [Google Scholar]
- 25.Cilfone NA, Kirschner DE, Linderman JJ. Strategies for efficient numerical implementation of hybrid multi-scale agent-based models to describe biological systems. Cellular and molecular bioengineering. 2015;8(1):119–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Forster JC, Harriss-Phillips WM, Douglass MJ, Bezak E. A review of the development of tumor vasculature and its effects on the tumor microenvironment. Hypoxia (Auckl). 2017;5:21–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cardillo TM, Govindan SV, Sharkey RM, Trisal P, Arrojo R, Liu D, et al. Sacituzumab Govitecan (IMMU-132), an Anti-Trop-2/SN-38 Antibody-Drug Conjugate: Characterization and Efficacy in Pancreatic, Gastric, and Other Cancers. Bioconjug Chem. 2015;26(5):919–31. [DOI] [PubMed] [Google Scholar]
- 28.Ahmed S, Ellis M, Li H, Pallucchini L, Stein AM. Guiding dose selection of monoclonal antibodies using a new parameter (AFTIR) for characterizing ligand binding systems. J Pharmacokinet Pharmacodyn. 2019;46(3):287–304. [DOI] [PubMed] [Google Scholar]
- 29.Prabhu SB A. Leipold D. Khawli L. Li D. Lu D. Theil F. Joshi A. Lum B. . Antiboy delivery of drugs and radionuclides factors influencing clinical phamacology. Therapeutic Delivery. 2011;6(2):769–91. [DOI] [PubMed] [Google Scholar]
- 30.Shah DK, Loganzo F, Haddish-Berhane N, Musto S, Wald HS, Barletta F, et al. Establishing in vitro-in vivo correlation for antibody drug conjugate efficacy: a PK/PD modeling approach. J Pharmacokinet Pharmacodyn. 2018;45(2):339–49. [DOI] [PubMed] [Google Scholar]
- 31.Hamblett K, Senter P, Chace D, Sun M, Lenox J, Cerveny C, et al. Effects of drug loading on the antitumor activity of a monoclonal antibody drug conjugate. Clinical Cancer Research. 2004;10:7063–70. [DOI] [PubMed] [Google Scholar]
- 32.Sukumaran S, Gadkar K, Zhang C, Bhakta S, Liu L, Xu K, et al. Mechanism-Based Pharmacokinetic/Pharmacodynamic Model for THIOMAB Drug Conjugates. Pharm Res. 2015;32(6):1884–93. [DOI] [PubMed] [Google Scholar]
- 33.Rosenberg JE, O’Donnell PH, Balar AV, McGregor BA, Heath EI, Yu EY, et al. Pivotal trial of enfortumab vedotin in urothelial carcinoma after platinum and anti-programmed death 1:programmed death ligand 1 therapy. Journal of Clinical Oncology. 2019:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang J, Seebacher N, Shi H, Kan Q, Zhenfeng D. Novel strategies to prevent the development of multidrug resistance (MDR) in cancer. Oncotarget. 2017;8 (No 48):84559–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Erickson HK, Lewis Phillips GD, Leipold DD, Provenzano CA, Mai E, Johnson HA, et al. The effect of different linkers on target cell catabolism and pharmacokinetics/pharmacodynamics of trastuzumab maytansinoid conjugates. Mol Cancer Ther. 2012;11(5):1133–42. [DOI] [PubMed] [Google Scholar]
- 36.Wittrup KD. Antitumor Antibodies Can Drive Therapeutic T Cell Responses Trends in cancer. 2017;3(9):615–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rios-Doria J, Harper J, Rothstein R, Wetzel L, Chesebrough J, Marrero A, et al. Antibody-Drug Conjugates Bearing Pyrrolobenzodiazepine or Tubulysin Payloads Are Immunomodulatory and Synergize with Multiple Immunotherapies. Cancer Res. 2017;77(10):2686–98. [DOI] [PubMed] [Google Scholar]
- 38.Pienaar E, Sarathy J, Prideaux B, Dietzold J, Dartois V, Kirschner DE, et al. Comparing efficacies of moxifloxacin, levofloxacin and gatifloxacin in tuberculosis granulomas using a multi-scale systems pharmacology approach. PLoS Comput Biol. 2017;13(8):e1005650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cilfone NA, Ford CB, Marino S, Mattila JT, Gideon HP, Flynn JL, et al. Computational modeling predicts IL-10 control of lesion sterilization by balancing early host immunity-mediated antimicrobial responses with caseation during mycobacterium tuberculosis infection. J Immunol. 2015;194(2):664–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bartelink IH, Jones EF, Shahidi-Latham SK, Lee PRE, Zheng Y, Vicini P, et al. Tumor drug penetration measurements could be the neglected piece of the personalized cancer treatment puzzle. Clin Pharmacol Ther. 2019;106(1):148–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.