Deep Learning in Protein Structural Modeling and Design

Summary

Deep learning is catalyzing a scientific revolution fueled by big data, accessible toolkits, and powerful computational resources, impacting many fields, including protein structural modeling. Protein structural modeling, such as predicting structure from amino acid sequence and evolutionary information, designing proteins toward desirable functionality, or predicting properties or behavior of a protein, is critical to understand and engineer biological systems at the molecular level. In this review, we summarize the recent advances in applying deep learning techniques to tackle problems in protein structural modeling and design. We dissect the emerging approaches using deep learning techniques for protein structural modeling and discuss advances and challenges that must be addressed. We argue for the central importance of structure, following the “sequence $\to$ structure $\to$ function” paradigm. This review is directed to help both computational biologists to gain familiarity with the deep learning methods applied in protein modeling, and computer scientists to gain perspective on the biologically meaningful problems that may benefit from deep learning techniques.

The Bigger Picture

Proteins are linear polymers that fold into an incredible variety of three-dimensional structures that enable sophisticated functionality for biology. Computational modeling allows scientists to predict the three-dimensional structure of proteins from genomes, predict properties or behavior of a protein, and even modify or design new proteins for a desired function. Advances in machine learning, especially deep learning, are catalyzing a revolution in the paradigm of scientific research. In this review, we summarize recent work in applying deep learning techniques to tackle problems in protein structural modeling and design. Some deep learning-based approaches, especially in structure prediction, now outperform conventional methods, often in combination with higher-resolution physical modeling. Challenges remain in experimental validation, benchmarking, leveraging known physics and interpreting models, and extending to other biomolecules and contexts.

Proteins fold into an incredible variety of three-dimensional structures to enable sophisticated functionality in biology. Advances in machine learning, especially in deep learning-related techniques, have opened up new avenues in many areas of protein modeling and design. This review dissects the emerging approaches and discusses advances and challenges that must be addressed.

Introduction

Proteins are linear polymers that fold into various specific conformations to function. The incredible variety of three-dimensional (3D) structures determined by the combination and order in which 20 amino acids thread the protein polymer chain (sequence of the protein) enables the sophisticated functionality of proteins responsible for most biological activities. Hence, obtaining the structures of proteins is of paramount importance in both understanding the fundamental biology of health and disease and developing therapeutic molecules. While protein structure is primarily determined by sophisticated experimental techniques, such as X-ray crystallography,¹ NMR spectroscopy² and, increasingly, cryoelectron microscopy,³ computational structure prediction from the genetically encoded amino acid sequence of a protein has been used as an alternative when experimental approaches are limited. Computational methods have been used to predict the structure of proteins,⁴ illustrate the mechanism of biological processes,⁵ and determine the properties of proteins.⁶ Furthermore, all naturally occurring proteins are a result of an evolutionary process of random variants arising under various selective pressures. Through this process, nature has explored only a small subset of theoretically possible protein sequence space. To explore a broader sequence and structural space that potentially contains proteins with enhanced or novel properties, techniques, such as de novo design can be used to generate new biological molecules that have the potential to tackle many outstanding challenges in biomedicine and biotechnology.^7,8

While the application of machine learning and more general statistical methods in protein modeling can be traced back decades,9, 10, 11, 12, 13 recent advances in machine learning, especially in deep learning (DL)-related techniques,¹⁴ have opened up new avenues in many areas of protein modeling.15, 16, 17, 18 DL is a set of machine learning techniques based on stacked neural network layers that parameterize functions in terms of compositions of affine transformations and non-linear activation functions. Their ability to extract domain-specific features that are adaptively learned from data for a particular task often enables them to surpass the performance of more traditional methods. DL has made dramatic impacts on digital applications like image classification,¹⁹ speech recognition,²⁰ and game playing.²¹ Success in these areas has inspired an increasing interest in more complex data types, including protein structures.²² In the most recent Critical Assessment of Structure Prediction (CASP13 held in 2018),⁴ a biennial community experiment to determine the state-of-the-art in protein structure prediction, DL-based methods accomplished a striking improvement in model accuracy (see Figure 1), especially in the “difficult” target category where comparative modeling (starting with a known, related structure) is ineffective. The CASP13 results show that the complex mapping from amino acid sequence to 3D protein structure can be successfully learned by a neural network and generalized to unseen cases. Concurrently, for the protein design problem, progress in the field of deep generative models has spawned a range of promising approaches.23, 24, 25

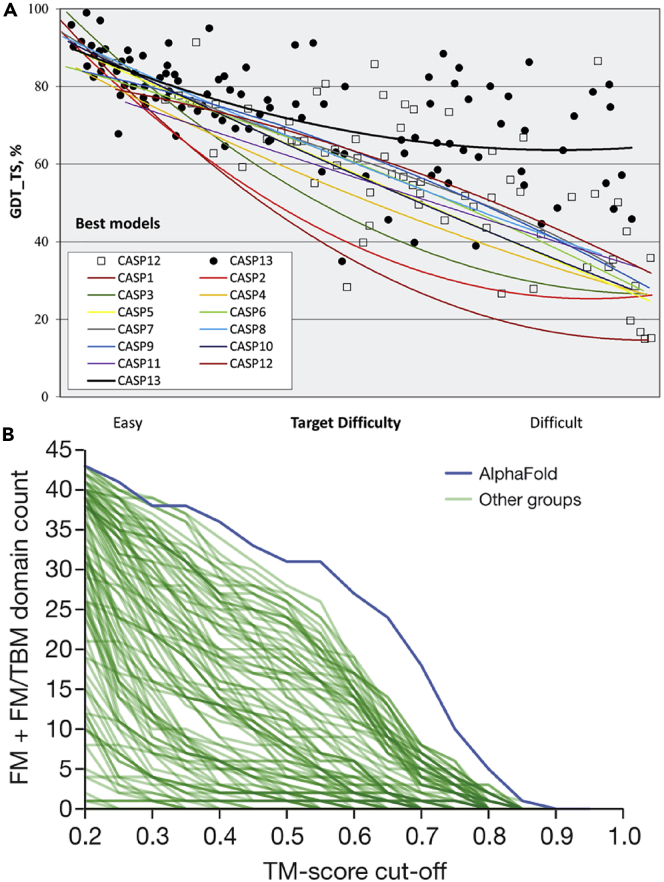
Figure 1.

Striking Improvement in Model Accuracy in CASP13 Due to the Deployment of Deep Learning Methods

(A) Trend lines of backbone accuracy for the best models in each of the 13 CASP experiments. Individual target points are shown for the two most recent experiments. The accuracy metric, GDT_TS, is a multiscale indicator of the closeness of the Cα atoms in a model to those in the corresponding experimental structure (higher numbers are more accurate). Target difficulty is based on sequence and structure similarity to other proteins with known experimental structures (see Kryshtafovych et al.⁴ for details). Figure from Kryshtafovych et al. (2019).⁴

(B) Number of FM + FM/TBM (FM, free modeling; TBM, template-based modeling) domains (out of 43) solved to a TM score threshold for all groups in CASP.¹³ AlphaFold ranked first among them, showing that the progress is mainly due to the development of DL-based methods. Figure from Senior et al. (2020).²⁶

In this review, we summarize the recent progress in applying DL techniques to the problem of protein modeling and discuss the potential pros and cons. We limit our scope to protein structure and function prediction, protein design with DL (see Figure 2), and a wide array of popular frameworks used in these applications. We discuss the importance of protein representation, and summarize the approaches to protein design based on DL for the first time. We also emphasize the central importance of protein structure, following the sequence $\to$ structure $\to$ function paradigm and argue that approaches based on structures may be most fruitful. We refer the reader to other review papers for more information on applications of DL in biology and medicine,^16,15 bioinformatics,²⁷ structural biology,¹⁷ folding and dynamics,^18,28 antibody modeling,²⁹ and structural annotation and prediction of proteins.^30,31 Because DL is a fast-moving, interdisciplinary field, we chose to include preprints in this review. We caution the reader that these contributions have not been peer-reviewed, yet are still worthy of attention now for their ideas. In fact, in communities such as computer science, it is not uncommon for manuscripts to remain in this stage indefinitely, and some seminal contributions, such as Kingma and Welling's definitive paper on autoencoders (AEs),³² are only available as preprints. In addition, we urge caution with any protein design studies that are purely in silico, and we highlight those that include experimental validation as a sign of their trustworthiness.

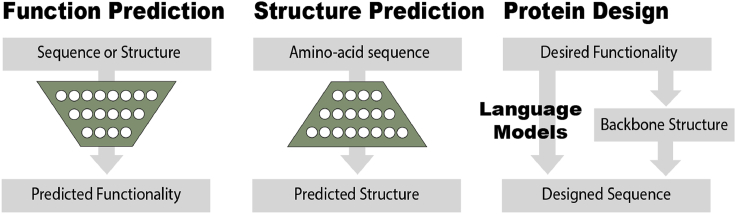
Figure 2.

Schematic Comparison of Three Major Tasks in Protein Modeling: Function Prediction, Structure Prediction, and Protein Design

In function prediction, the sequence and/or the structure is known and the functionality is needed as output of a neural net. In structure prediction, sequence is known input and structure is unknown output. Protein design starts from desired functionality, or a step further, structure that can perform this functionality. The desired output is a sequence that can fold into the structure or has such functionality.

Protein Structure Prediction and Design

Problem Definition

The prediction of protein 3D structure from amino acid sequence has been a grand challenge in computational biophysics for decades.^33,34 Folding of peptide chains is a fundamental concept in biophysics, and atomic-level structures of proteins and complexes are often the starting point to understand their function and to modulate or engineer them. Thanks to the recent advances in next-generation sequencing technology, there are now over 180 million protein sequences recorded in the UniProt dataset.³⁵ In contrast, only 158,000 experimentally determined structures are available in the Protein Data Bank. Thus, computational structure prediction is a critical problem of both practical and theoretical interest.

More recently, the advances in structure prediction have led to an increasing interest in the protein design problem. In design, the objective is to obtain a novel protein sequence that will fold into a desired structure or perform a specific function, such as catalysis. Naturally occurring proteins represent only an infinitesimal subset of all possible amino acid sequences selected by the evolutionary process to perform a specific biological function.⁷ Proteins with more robustness (higher thermal stability, resistance to degradation) or enhanced properties (faster catalysis, tighter binding) might lie in the space that has not been explored by nature, but is potentially accessible by de novo design. The current approach for computational de novo design is based on physical and evolutionary principles and requires significant domain expertise. Some successful examples include novel folds,³⁶ enzymes,³⁷ vaccines,³⁸ novel protein assemblies,³⁹ ligand-binding protein,⁴⁰ and membrane proteins.⁴¹ While some papers occasionally refer to redesign of naturally occurring proteins or interfaces as “de novo”, in this review we restrict that term only to works where completely new folds or interfaces are created.

Conventional Computational Approaches

The current methodology for computational protein structure prediction is largely based on Anfinsen's⁴² thermodynamic hypothesis, which states that the native structure of a protein must be the one with the lowest free energy, governed by the energy landscape of all possible conformations associated with its sequence. Finding the lowest-energy state is challenging because of the immense space of possible conformations available to a protein, also known as the “sampling problem” or Levinthal's⁴³ paradox. Furthermore, the approach requires accurate free energy functions to describe the protein energy landscape and rank different conformations based on their energy, referred to as the “scoring problem.” In light of these challenges, current computational techniques rely heavily on multiscale approaches. Low-resolution, coarse-grained energy functions are used to capture large-scale conformational sampling, such as the hydrophobic burial and formation of local secondary structural elements. Higher-resolution energy functions are used to explicitly model finer details, such as amino acid side-chain packing, hydrogen bonding, and salt bridges.⁴⁴

Protein design problems, sometimes known as the inverse of structure prediction problems, require a similar toolbox. Instead of sampling the conformational space, a protein design protocol samples the sequence space that folds into the desired topology. Past efforts can be broadly divided into two broad classes: modifying an existing protein with known sequence and properties, or generating novel proteins with sequences and/or folds unrelated to those found in nature. The former class evolves an existing protein's amino acid sequence (and as a result, structure and properties) and can be loosely referred to as protein engineering or protein redesign. The latter class of methods is called de novo protein design, a term originally coined in 1997 when Dahiyat and Mayo⁴⁵ designed the FSD-1 protein, a soluble protein with a completely new sequence that folded into the previously known structure of a zinc finger. Korendovych and DeGrado's⁴⁶ recent retrospective chronicles the development of de novo design. Originally de novo design meant creation of entirely new proteins from scratch exploiting a target structure but, especially in the DL era, many authors now use the term to include methods that ignore structure in creating new sequences, often using extensive training data from known proteins in a particular functional class. In this review, we split our discussion of methods according to whether they trained directly between sequence and function (as certain natural language processing [NLP]-based DL paradigms allow), or whether they directly include protein structural data (like historical methods in rational protein design; see below in the section on “Protein Design”).

Despite significant progress in the last several decades in the field of computational protein structure prediction and design,^7,34 accurate structure prediction and reliable design both remain challenging. Conventional approaches rely heavily on the accuracy of the energy functions to describe protein physics and the efficiency of sampling algorithms to explore the immense protein sequence and structure space. Both protein engineering and de novo approaches are often combined with experimental directed evolution^8,47 to achieve the optimal final molecules.⁷

DL Architectures

In conventional computational approaches, predictions from data are made by means of physical equations and modeling. Machine learning puts forward a different paradigm in which algorithms automatically infer—or learn—a relationship between inputs and outputs from a set of hypotheses. Consider a collection of N training samples comprising features $\mathit{x}$ in an input space $\mathcal{X}$ (e.g., amino acid sequences), and corresponding labels y in some output space $\mathcal{Y}$ (e.g., residue pairwise distances), where ${\left\{{\mathit{x}}_{\mathit{i}},y_i\right\}}_{i=1}^N$ are sampled independently and identically distributed from some joint distribution $\mathcal{P}$. In addition, consider a function $f:\mathcal{X}\to \mathcal{Y}$ in some function class $\mathcal{H}$, and a loss function $\ell :\mathcal{Y}\times \mathcal{Y}\to \mathbb{R}$ that measures how much $f\left(\mathit{x}\right)$ deviates from the corresponding label y. The goal of supervised learning is to find a function $f\in \mathcal{H}$ that minimizes the expected loss, $\mathbb{E}\left[\ell \left(f\left(\mathit{x}\right),y\right)\right]$, for $\left(\mathit{x},y\right)$ sampled from $\mathcal{P}$. Since one does not have access to the true distribution but rather N samples from it, the popular empirical risk minimization (ERM) approach seeks to minimize the loss over the training samples instead. In neural network models, in particular, the function class is parameterized by a collection of weights. Denoting these parameters collectively by $\mathit{\theta }$, ERM boils down to an optimization problem of the form

$$\underset{\mathit{\theta }}{\text{min}}\frac{1}{N}\sum _{i=1}^N\ell \left(f_{\mathit{\theta }}\left({\mathit{x}}_{\mathit{i}}\right),y_i\right)\text{.}$$ (Equation 1)

The choice of the network determines how the hypothesis class is parameterized. Deep neural networks typically implement a non-linear function as the composition of affine maps, ${\mathcal{W}}_l:{\mathbb{R}}^{n_l}\to {\mathbb{R}}^{n_{l+1}}$, where ${\mathcal{W}}_l\mathit{x}=W_l\mathit{x}+{\mathit{b}}_l$, and other non-linear activation functions, $\sigma (\cdot )$. Rectifying linear units and max-pooling are some of the most popular non-linear transformations applied in practice. The architecture of the model determines how these functions are composed, the most popular option being their sequential composition $f\left(\mathit{x}\right)={\mathcal{W}}_L\sigma \left({\mathcal{W}}_{L-1}\sigma \left({\mathcal{W}}_{L-2}\sigma \left(\dots {\mathcal{W}}_2\sigma \left({\mathcal{W}}_1\mathit{x}\right)\right)\right)\right)$ for a network with L layers. Computing $f\left(\mathit{x}\right)$ is typically referred to as the forward pass.

We will not dwell on the details of the optimization problem in Equation (1), which is typically carried out via stochastic gradient descent algorithms or variations thereof, efficiently implemented via back-propagation (see instead, e.g., LeCun et al.,¹⁴ Sun,⁴⁸ and Schmidhuber).⁴⁹ Rather, in this section we summarize some of the most popular models widely used in protein structural modeling, including how different approaches are best suited for particular data types or applications. High-level diagrams of the major architectures are shown in Figures 3.

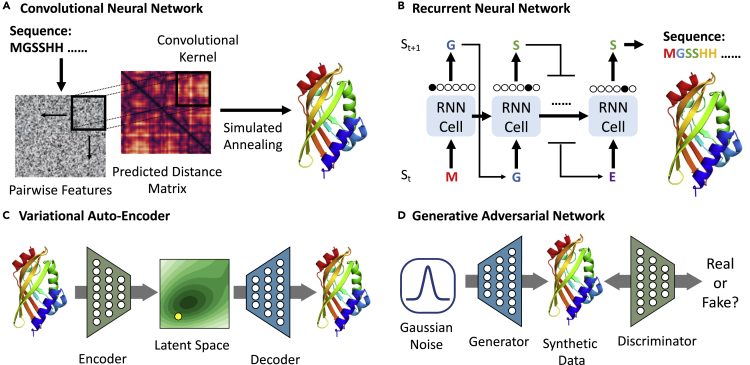
Figure 3.

Schematic Representation of Several Architectures Used in Protein Modeling and Design

(A) CNNs are widely used in structure prediction.

(B) RNNs learn in an auto-regressive way and can be used for sequence generation.

(C) The VAE can be jointly trained by protein and properties to construct a latent space correlated with properties.

(D) In the GAN setting, a mapping from a priori distribution to the design space can be obtained via the adversarial training.

Convolutional Neural Networks

Convolutional networks architectures⁵⁰ are most commonly applied to image analysis or other problems where shift-invariance or covariance is needed. Inspired by the fact that an object on an image can be shifted in the image and still be the same object, convolutional neural networks (CNNs) adopt convolutional kernels for the layer-wise affine transformation to capture this translational invariance. A 2D convolutional kernel $\mathbf{w}$ applied to a 2D image data $\mathit{x}$ can be defined as

$$\mathit{S}\left(i,j\right)=\left(\mathit{x}\text{∗}\mathbf{w}\right)\left(i,j\right)=\sum _m\sum _n\mathit{x}\left(m,n\right)\mathbf{w}\left(i-m,j-n\right)\text{,}$$ (Equation 2)

where $\mathit{S}\left(i,j\right)$ represents the output at position $\left(i,j\right)$, $\mathit{x}\left(m,n\right)$ is the value of the input $\mathit{x}$ at position $\left(m,n\right)$, $\mathbf{w}\left(i-m,j-n\right)$ is the parameter of kernel $\mathbf{w}$ at position $\left(i-m,j-n\right)$, and the summation is over all possible positions. An important variant of CNN is the residual network (ResNet),⁵¹ which incorporates skip-connections between layers. These modification have shown great advantages in practice, aiding the optimization of these typically huge models. CNNs, especially ResNets, have been widely used in protein structure prediction. An example is AlphaFold,²² which used ResNets to predict protein inter-residue distance maps from amino acid sequences (Figure 3A).

Recurrent Neural Networks

Recurrent architectures are based on applying several iterations of the same function along a sequential input.⁵² This can be seen as an unfolded architecture, and it has been widely used to process sequential data, such as time series data and written text (i.e., NLP). With an initial hidden state ${\mathit{h}}^{\left(0\right)}$ and sequential data [${\mathit{x}}^{\left(1\right)},{\mathit{x}}^{\left(2\right)},\dots ,{\mathit{x}}^{\left(n\right)}$], we can obtain hidden states recursively:

$${\mathit{h}}^{\left(t\right)}=g^{\left(t\right)}\left({\mathit{x}}^{\left(t\right)},{\mathit{x}}^{\left(t-1\right)},{\mathit{x}}^{\left(t-2\right)},\dots ,{\mathit{x}}^{\left(1\right)}\right)=f\left({\mathit{h}}^{\left(t-1\right)},{\mathit{x}}^{\left(t\right)};\mathit{\theta }\right)\text{,}$$ (Equation 3)

where f represents a function or transformation from one position to the next, and $g^{\left(t\right)}$ represents the accumulative transformation up to position t. The hidden state vector at position i, ${\mathit{h}}^{\left(i\right)}$, contains all the information that has been seen before. As the same set of parameters (usually called a cell) can be applied recurrently along the sequential data, an input of variable length can be fed to a recurrent neural network (RNN). Due to the gradient vanishing and explosion problem (the error signal decreases or increases exponentially during training), more recent variants of standard RNNs, namely long short-term memory (LSTM)⁵³ and gated recurrent unit⁵⁴ are more widely used. An example of an RNN approach in the context of protein structure prediction is using an N-terminal subsequence of a protein to predict the next amino acid in the protein sequence (Figure 3B; e.g., Müller et al.⁵⁵).

In conjunction with recurrent networks, attention mechanisms were first proposed (in an encoder-decoder framework) to learn which parts of a source sentence are most relevant to predicting a target word.⁵⁶ Compared with RNN models, attention-based models are more parallelizable and better at capturing long-range dependencies, and they are driving big advances in NLP.^57,58 Recently, the transformer model, which solely adopted attention layers without any recurrent or convolutional layers, was able to surpass state-of-the-art methods on language translation tasks.⁵⁷ For proteins, these methods could learn which parts of an amino acid sequence are critical to predicting a target residue or the properties of a target residue. For example, transformer-based models have been used to generate protein sequences conditioned on target structure,²³ learn protein sequence data to predict secondary structure and fitness landscapes,⁵⁹ and to encode the context of the binding partner in antibody-antigen binding surface prediction.⁶⁰

Variational Autoencoder

AEs,⁶¹ unlike the networks discussed so far, provide a model for unsupervised learning. Within this unsupervised framework, an AE does not learn labeled outputs but instead attempts to learn some representation of the original input. This is typically accomplished by training two parametric maps: an encoder function $g:\mathcal{X}\to {\mathbb{R}}^m$ that maps an input $\mathit{x}$ to an m-dimensional representation or latent space, and a decoder intended to implement the inverse map so that $f\left(g\left(\mathit{x}\right)\right)\approx \mathit{x}$. Typically, the latent representation is of small dimension (m is smaller than the ambient dimension of $\mathcal{X}$) or constrained in some other way (e.g., through sparsity).

Variational autoencoders (VAEs),^32,62 in particular, provide a stochastic map between the input space and the latent space. This map is beneficial because, while the input space may have a highly complex distribution, the distribution of the representation $\mathit{z}$ can be much simpler; e.g., Gaussian. These methods derive from variational inference, a method from machine learning that approximates probability densities through optimization.⁶³ The stochastic encoder, given by the inference model $q_{\phi }\left(\mathit{z}|\mathit{x}\right)$ and parametrized by weights $\phi$, is trained to approximate the true posterior distribution of the representation given the data, $p_{\mathit{\theta }}\left(\mathit{z}|\mathit{x}\right)$. The decoder, on the other hand, provides an estimate for the data given the representation, $p_{\mathit{\theta }}\left(\mathit{x}|\mathit{z}\right)$. Direct optimization of the resulting objective is intractable, however. Thus, training is done by maximizing the “evidence lower bound,” ${\mathcal{L}}_{\mathit{\theta },\phi }\left(\mathit{x}\right)$, instead, which provides a lower bound on the log-likehood of the data:

$${\mathcal{L}}_{\mathit{\theta },\phi }\left(\mathit{x}\right)={\mathrm{E}}_{\mathit{z}\sim q_{\phi }\left(\mathit{z}|\mathit{x}\right)}\text{log}{p}_{\mathit{\theta }}\left(\mathit{x}|\mathit{z}\right)-D_{KL}\left(q_{\phi }\left(\mathit{z}|\mathit{x}\right)\left|\right|p_{\mathit{\theta }}\left(\mathit{z}|\mathit{x}\right)\right)\text{.}$$ (Equation 4)

Here, $D_{KL}\left(q_{\phi }\left|\right|p_{\mathit{\theta }}\right)$ is the Kullback-Leibler divergence, which quantifies the distance between distributions $q_{\phi }$ and $p_{\mathit{\theta }}$. Employing Gaussians for the factorized variational and likelihood distributions, as well as using a change of variables via differentiable maps, allows for the efficient optimization of these architectures.

An example of applying VAE in the protein modeling field is learning a representation of antimicrobial protein sequences (Figure 3C; e.g., Das et al.⁶⁴). The resulting continuous real-valued representation can then be used to generate new sequences likely to have antimicrobial properties.

Generative Adversarial Network

Generative adversarial networks (GANs)⁶⁵ are another class of unsupervised (generative) models. Unlike VAEs, GANs are trained by an adversarial game between two models, or networks: a generator, G, which given a sample, $\mathit{z}$, from some simple distribution $p_{\mathit{z}}\left(\mathit{z}\right)$ (e.g., Gaussian), seeks to map it to the distribution of some data class (e.g., naturally looking images); and a discriminator, D, whose task is to detect whether the images are real (i.e., belonging to the true distribution of the data, $p_{\text{data}}\left(\mathit{x}\right)$), or fake (produced by the generator). With this game-based setup, the generator model is trained by maximizing the error rate of the discriminator, thereby training it to “fool” the discriminator. The discriminator, on the other hand, is trained to foil such fooling. The original objective function as formulated by Goodfellow et al.⁶⁵ is:

$$\underset{G}{\text{min}}\underset{D}{\text{max}}V\left(D,G\right)={\mathrm{E}}_{\mathit{x}\sim p_{\text{data}}\left(\mathit{x}\right)}\left[\text{log}D\left(\mathit{x}\right)\right]+{\mathrm{E}}_{\mathit{z}\sim p_{\mathit{z}}\left(\mathit{z}\right)}\left[\text{log}\left(1-D\left(G\left(\mathit{z}\right)\right)\right)\right]\text{.}$$ (Equation 5)

Training is performed by stochastic optimization of this differentiable loss function. While intuitive, this original GAN objective can suffer from issues, such as mode collapse and instabilities during training. The Wasserstein GAN (WGAN)⁶⁶ is a popular extension of GAN which introduces a Wasserstein-1 distance measure between distributions, leading to easier and more robust training.⁶⁷

An example of a GAN, in the context of protein modeling is learning the distribution of protein backbone distances to generate novel protein-like folds (Figure 3D).⁶⁸ During training, one network G generates folds, and a second network D aims to distinguish between generated folds and fake folds.

Protein Representation and Function Prediction

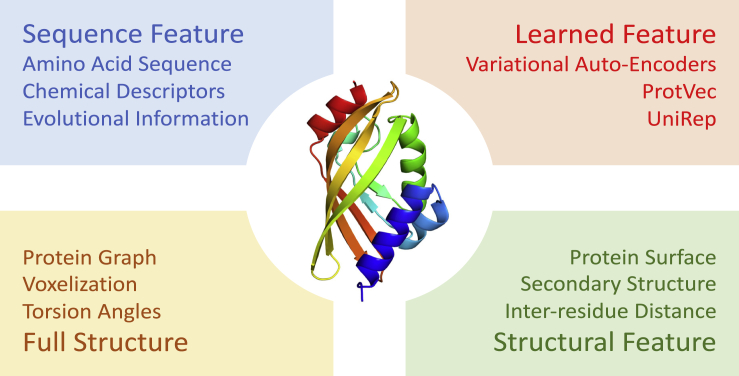
One of the most fundamental challenges in protein modeling is the prediction of functionality from sequence or structure. Function prediction is typically formulated as a supervised learning problem. The property to predict can either be a protein-level property, such as a classification as an enzyme or non-enzyme,⁶⁹ or a residue-level property, such as the sites or motifs of phosphorylation (DeepPho)⁷⁰ and cleavage by proteases.⁷¹ The challenging part here and in the following models is how to represent the protein. Representation refers to the encoding of a protein that serves as an input for prediction tasks or the output for generation tasks. Although a deep neural network is in principle capable of extracting complex features, a well-chosen representation can make learning more effective and efficient.⁷² In this section, we will introduce the commonly used representations of proteins in DL models (Figure 4): sequence-based, structure-based, and one special form of representation relevant to computational modeling of proteins: coarse-grained models.

Figure 4.

Different Types of Representation Schemes Applied to a Protein

Amino Acid Sequence as Representation

As the amino acid sequence contains the information essential to reach the folded structure for most proteins,⁴² it is widely used as an input in functional prediction and structure prediction tasks. The amino acid sequence, like other sequential data, is typically converted into one-hot encoding-based representation (each residue is represented with one high bit to identify the amino acid type and all the others low) that can be directly used in many sequence-based DL techniques.^73,74 However, this representation is inherently sparse and, thus, sample-inefficient. There are many easily accessible additional features that can be concatenated with amino acid sequences providing structural, evolutionary, and biophysical information. Some widely used features include predicted secondary structure, high-level biological features, such as sub-cellular localization and unique functions,⁷⁵ and physical descriptors, such as AAIndex,⁷⁶ hydrophobicity, ability to form hydrogen bonds, charge, solvent-accessible surface area, etc. A sequence can be augmented with additional data from sequence databases, such as multiple sequence alignments (MSA) or position-specific scoring matrices (PSSMs),⁷⁷ or pairwise residue co-evolution features. Table 1 lists typical features as used in CUProtein.⁷⁸

Table 1.

Features Contained by CUProtein Dataset

Feature Name	Description	Dimensions	Type	IO
AA Sequence	sequence of amino acid	n $\times$ 1	21 chars	input
PSSM	position-specific scoring matrix, a residue-wise score for motifs appearance	n $\times$ 21	real [0, 1]	input
MSA covariance	covariance matrix across homologous NA sequences	n $\times$ n	real [0, 1]	input
SS	a coarse categorized secondary structure (Q3 or Q8)	n $\times$ 1	3 or 8 chars	input
Distance matrices	pairwise distance between residues (Cα or Cβ)	n $\times$ n	positive real (Å)	output
Torsion angles	variable dihedral angles for each residues (φ, ψ)	n $\times$ 2	real [−π, +π] (radians)	output

n, number of residues in one protein. Data from Drori et al.⁷⁸

Learned Representation from Amino Acid Sequence

Because the performance of machine learning algorithms highly depends on the features we choose, labor-intensive and domain-based feature engineering was vital for traditional machine learning projects. Now, the exceptional feature extraction ability of neural networks makes it possible to “learn” the representation, with or without giving the model any labels.⁷² As publicly available sequence data are abundant (see Table 2), a well-learned representation that utilizes these data to capture more information is of particular interest. The class of algorithms that address the label-less learning problem fall under the umbrella of unsupervised or semi-supervised learning, which extracts information from unlabeled data to reduce the number of labeled samples needed.

Table 2.

A Summary of Publicly Available Molecular Biology Databases

Dataset	Description	N	Website
European Bioinformatics Institute (EMBL-EBI)	a collections of wide range of datasets	–	https://www.ebi.ac.uk
National Center for Biotechnology Information (NCBI)	a collections of biomedical and genomic databases	–	https://www.ncbi.nlm.nih.gov
Protein Data Bank (PDB)	3D structural data of biomolecules, such as proteins and nucleic acids	$\sim$160,000	https://www.rcsb.org
Nucleic Acid Database (NDB)	structure of nucleic acids and complex assemblies	$\sim$10,560	http://ndbserver.rutgers.edu
Universal Protein Resource (UniProt)	protein sequence and function infromations	$\sim \mathrm{562,000}$	http://www.uniprot.org/
Sequence Read Archive (SRA)	raw sequence data from “next-generation” sequencing technologies	$\sim 3\times {10}^{16}$	NCBI database

The most straightforward way to learn from amino acid sequence is to directly apply NLP algorithms. Word2Vec⁷⁹ and Doc2Vec⁸⁰ are groups of algorithms widely used for learning word or paragraph embeddings. These models are trained by either predicting a word from its context or predicting its context from one central word. To apply these algorithm, Asgari and Mofrad⁸¹ first proposed a Word2Vec-based model called BioVec, which interprets the non-overlapping 3-mer sequence of amino acids (e.g., alanine-glutamine-lysine or AQL) as “words” and lists of shifted “words” as “sentences.” They then represent a protein as the summation of all overlapping sequence fragments of length k, or k-mers (called ProtVec). Predictions based on the ProtVec representation outperformed state-of-the-art machine learning methods in the Pfam protein family⁸² classification (93% accuracy for ~7,000 proteins, versus 69.1%–99.6%⁸³ and 75%⁸⁴ for previous methods). Many Doc2Vec-type extensions were developed based on the 3-mer protocol. Yu et al.⁸⁵ showed that non-overlapping k-mers perform better than the overlapping ones, and Yang et al.⁸⁶ compared the performance of all Doc2Vec frameworks for thermostability and enantioselectivity prediction.

In these approaches, the three-residue segmentation of a protein sequence is arbitrary and does not embody any biophysical meaning. Alternatively, Alley et al.⁸⁷ directly used an RNN (unidirectional multiplicative long-short-term-memory or mLSTM)⁸⁸ model, called UniRep, to summarize arbitrary length protein sequences into a fixed-length real representation by averaging over the representation of each residue.⁸⁷ Their representation achieved lower mean squared errors on 15 property prediction tasks (e.g., absorbance, activity, stability) compared with former models, including Yang et al.’s⁸⁶ Doc2Vec. Heinzinger et al.⁸⁹ adopted the bidirectional LSTM in a manner similar to Peters et al.’s90, 90 ELMo (Embeddings from Language Models) model and surpassed Asgari and Mofrad's⁸¹ Word2Vec model at predicting secondary structure and regions with intrinsic disorder at the per-residue level.⁸⁹ The success of the transformer model in language processing, especially those trained on large number of parameters, such as BERT⁵⁸ and GPT3,⁹¹ has inspired its application in biological sequence modeling. Rives et al.⁵⁹ trained a transformer model with 670 million parameters on 86 billion amino acids across 250 million protein sequences spanning evolutionary diversity. Their transformer model was superior to traditional LSTM-based models on tasks, such as the prediction of secondary structure and long-range contacts, as well as the effect of mutations on activity on deep mutational scanning benchmarks.

AEs can also provide representations for subsequent supervised tasks.³² Ding et al.⁹² showed that a VAE model is able to capture evolutionary relationships between sequences and stability of proteins, while Sinai et al.⁹³ and Riesselman et al.⁹⁴ showed that the latent vectors learned from VAEs are able to predict the effects of mutations on fitness and activity for a range of proteins, such as poly(A)-binding protein, DNA methyltransferase, and β-lactamase. Recently, a lower-dimensional embedding of the sequence was learned for the more complex task of structure prediction.⁷⁸ Alley et al.’s⁸⁷ UniRep surpassed former models, but since UniRep is trained on 24 million sequences and previous models (e.g., Prot2Vec) were trained on much smaller datasets (0.5 million), it is not clear if the improvement was due to better methods or the larger training dataset. Rao et al.⁹⁵ introduced multiple biological-relevant semi-supervised learning tasks, TAPE, and benchmarked the performance against various protein representations. Their results show conventional alignment-based inputs still outperform current self-supervised models on multiple tasks, and the performance on a single task cannot evaluate the capacity of models. A comprehensive and persuasive comparison of representations is required.

Structure as Representation

Since the most important functions of a protein (e.g., binding, signaling, catalysis) can be traced back to the 3D structure of the protein, direct use of 3D structural information, and analogously, learning a good representation based on 3D structure, are highly desired. The direct use of raw 3D representations (such as coordinates of atoms) is hindered by considerable challenges, including the processing of unnecessary information due to translation, rotation, and permutation of atomic indexing. Townshend et al.96, 97^,97 and Simonovsky and Meyers^96,97 obtained a translationally invariant, 3D representation of each residue by voxelizing its atomic neighborhood for a grid-based 3D CNN model. The work of Kolodny et al.,⁹⁸ Taylor,⁹⁹ and Li and Koehl¹⁰⁰ representing the 3D structure of a protein as 1D strings of geometric fragments for structure comparison and fold recognition may also prove useful in DL approaches. Alternatively, the torsion angles of the protein backbone, which are invariant to translation and rotation, can fully recapitulate protein backbone structure under the common assumption that variation in bond lengths and angles is negligible. AlQuraishi¹⁰¹ used backbone torsion angles to represent the 3D structure of the protein as a 1D data vector. However, because a change in a backbone torsion angle at a residue affects the inter-residue distances between all preceding and subsequent residues, these 1D variables are highly interdependent, which can frustrate learning. To circumvent these limitations, many approaches use 2D projections of 3D protein structure data, such as residue-residue distance and contact maps,^24,102 and pseudo-torsion angles and bond angles that capture the relative orientations between pairs of residues.¹⁰³ While these representations guarantee translational and rotational invariance, they do not guarantee invertibility back to the 3D structure. The structure must be reconstructed by applying constraints on distance or contact parameters using algorithms, such as gradient descent minimization, multidimensional scaling, a program like the Crystallography and NMR system (CNS),¹⁰⁴ or in conjunction with an energy-function-based protein structure prediction program.²²

An alternative to the above approaches for representing protein structures is the use of a graph, i.e., a collection of nodes or vertices connected by edges. Such a representation is highly amenable to the graph neural network (GNN) paradigm,¹⁰⁵ which has recently emerged as a powerful framework for non-Euclidean data¹⁰⁶ in which the data are represented with relationships and inter-dependencies, or edges between objects or nodes.¹⁰⁷ While the representation of proteins as graphs and the application of graph theory to study their structure and properties has a long history,¹⁰⁸ the efforts to apply GNNs to protein modeling and design is quite recent. As a benchmark, many GNNs^69,109 have been applied to classify enzymes from non-enzymes in the PROTEINS¹¹⁰ and D&D¹¹¹ datasets. Fout et al.¹¹² utilized a GNN in developing a model for protein-protein interface prediction. In their model, the node feature comprised residue composition and conservation, accessible surface area, residue depth, and protrusion index; and the edge feature comprised a distance and an angle between the normal vectors of the amide plane of each node/residue. A similar framework was used to predict antibody-antigen binding interfaces.⁶⁰ Zamora-Resendiz and Crivelli¹¹³ and Gligorijevic et al.¹¹⁴ further generalized and validated the use of graph-based representations and the graph convolutional network (GCN) framework in protein function prediction tasks, using a class activation map to interpret the structural determinants of the functionalities. Torng and Altman¹¹⁵ applied GCNs to model pocket-like cavities in proteins to predict the interaction of proteins with small molecules, and Ingraham et al.²³ adopted a graph-based transformer model to perform a protein sequence design task. These examples demonstrate the generality and potential of the graph-based representation and GNNs to encode structural information for protein modeling.

The surface of the protein or a cavity is an information-rich region that encodes how a protein may interact with other molecules and its environment. Recently, Gainza et al.¹¹⁶ used a geometric DL framework¹¹⁷ to learn a surface-based representation of the protein, called MaSIF. They calculated “fingerprints” for patches on the protein surface using geodesic convolutional layers, which were further used to perform tasks, such as binding site prediction or ultra-fast protein-protein interaction (PPI) search. The performance of MaSIF approached the baseline of current methods in docking and function prediction, providing a proof-of-concept to inspire more applications of geometry-based representation learning.

Score Function and Force Field

A high-quality force field (or, more generally, score function) for sampling and/or ranking models (decoys) is one of the most vital requirements for protein structural modeling.¹¹⁸ A force field describes the potential energy surface of a protein. A score function may contain knowledge-based terms that do not necessarily have a valid physical meaning, and they are designed to distinguish near-native conformations from non-native ones (for example, learning the GDT_TS).¹¹⁹ A molecular dynamics (MD) or Monte Carlo (MC) simulation with a state-of-the-art force field or score function can reproduce reasonable statistical behaviors of biomolecules.120, 121, 122

Current DL-based efforts to learn the force field can be divided into two classes: “fingerprint” based and graph based. Behler and Parrinello¹²³ developed roto-translationally invariant features, i.e., the Behler-Parrinello fingerprint, to encode the atomic environment for neural networks to learn potential surfaces from density functional theory (DFT) calculations. Smith et al. extended this framework and tested its accuracy by simulating systems up to 312 atoms (Trp-cage) for 1 ns.^124,125 Another family that includes deep tensor neural networks¹²⁶ and SchNet¹²⁷ uses graph convolutions to learn a representation for each atom within its chemical environment. Although the prediction quality and the ability to learn a representation with novel chemical insight make the graph-based approach increasingly popular,²⁸ the application scales poorly to larger systems and thus has mainly focused on small organic molecules.

We anticipate a shift toward DL-based score functions because of the enormous gains in speed and efficiency. For example, Zhang et al.¹²⁸ showed that MD simulation on a neural potential was able to reproduce energies, forces, and time-averaged properties comparable with ab initio MD (AIMD) at a cost that scales linearly with system size, compared with cubic scaling typical for AIMD with DFT. Although these force fields are, in principle, generalizable to larger systems, direct applications of learned potentials to model full proteins are still rare. PhysNet, trained on a set of small peptide fragments (at most eight heavy atoms), was able to generalize to deca-alanine (Ala10),¹²⁹ and ANI-1x and AIMNet have been tested on chignolin (10 residues) and Trp-cage (20 residues) within the ANI-MD benchmark dataset.^125,130 Lahey and Rowley¹³¹ and Wang et al.¹³² combined the quantum mechanics/molecular mechanics (QM/MM) strategy¹³³ and the neural potential to model docking with small ligands and larger proteins.^131,132 Recently, Wang et al.¹³⁴ proposed an end-to-end differential MM force field by training a GNN on energies and forces to learn atom-typing and force field parameters.

Coarse-Grained Models

Coarse-grained models are higher-level abstractions of biomolecules, such as using a single pseudo-atom or a bead to represent multiple atoms, grouped based on local connectivity and/or chemical properties. Coarse graining smoothens out the energy landscape, and thereby helps avoid trapping in local minima and speeds up conformational sampling.¹³⁵ One can learn the atomic-level properties to construct a fast and accurate neural coarse-grained model once the coarse-grained mapping is given. Early attempts to apply DL-based methods to coarse-graining focus on water molecules with the roto-translationally invariant features.^136,137 Wang et al.¹³⁸ developed CGNet and learned the coarse-grained model of the mini protein, chignolin, in which the atoms of a residue are mapped to the corresponding C_α atom. The free energy surface learned with CGNet is quantitatively correct and MD simulations performed with CGNet potentially predict the same set of metastable states (folded, unfolded, and misfolded). Another critical question for coarse graining is determining which sets of atoms to map into a united atom. For example, one choice is to use a single coarse-grained atom to represent a whole residue, and a different choice is to use two coarse-grained atoms, one to represent the backbone and the other to represent the side chain. To determine the optimal choice, Wang and Gómez-Bombarelli¹³⁹ applied an encoder-decoder-based model to explicitly learn the lower-dimensional representation of proteins by minimizing the information loss at different levels of coarse graining. Li et al.¹⁴⁰ treated this problem as a graph segmentation problem and presented a GNN-based coarse-graining mapping predictor called Deep Supervised Graph Partitioning Model.

Structure Determination

The most successful application of DL in the field of protein modeling so far has been the prediction of protein structure. Protein structure prediction is formulated as a well-defined problem with clear inputs and outputs: predict the 3D structure (output) given amino acid sequences (input), with the experimental structures as the ground truth (labels). This problem perfectly fits the classical supervised learning approach, and once the problem is defined in these terms, the remaining challenge is to choose a framework to handle the complex relationship between input and output. The CASP experiment for structure prediction is held every 2 years and served as a platform for DL to compete with state-of-the-art methods and, impressively, outshine them in certain categories. We will first discuss the application of DL to the protein folding problem, and then comment on some problems related to structure determination. Table 3 summarizes major DL efforts in structure prediction.

Table 3.

A Summary of Structure Prediction Models

Model	Architecture	Dataset	N_train	Performance	Testset	Citation
/	MLP(2-layer)	proteases	13	3.0 Å RMSD (1TRM),1.2 Å RMSD (6PTI)	1TRM, 6PTI	Bohr et al.9
PSICOV	graphical Lasso	–	–	precision: Top-L 0.4, Top-L/2 0.53,Top-L/5 0.67, Top-L/10 0.73	150 Pfam	Jones et al.141
CMAPpro	2D biRNN + MLP	ASTRAL	2,352	precision: Top-L/5 0.31, Top-L/10 0.4	ASTRAL 1.75 CASP8, 9	Di Lena et al.142
DNCON	RBM	PDB SVMcon	1,230	precision: Top-L 0.46, Top-L/2 0.55, Top-L/5 0.65	SVMCON_TEST, D329, CASP9	Eickholt et al.143
CCMpred	LM	–	–	precision: Top-L 0.5, Top-L/2 0.6, Top-L/5 0.75, Top-L/10 0.8	150 Pfam	Seemayer et al.144
PconsC2	Stacked RF	PSICOV set	150	positive predictive value (PPV) 0.44	set of 383 CASP10(114)	Skwark et al.145
MetaPSICOV	MLP	PDB	624	precision: Top-L 0.54, Top-L/2 0.70, Top-L/5 0.83, Top-L/10 0.88	150 Pfam	Jones et al.146
RaptorX-Contact	ResNet	subset of PDB25	6,767	TM score: 0.518 (CCMpred: 0.333, MetaPSICOV: 0.377)	Pfam, CASP11, CAMEO, MP	Wang et al, 2017102
RaptorX-Distance	ResNet	subset of PDB25	6,767	TM score: 0.466 (CASP12), 0.551 (CAMEO), 0.474 (CASP13)	CASP12 + 13, CAMEO	Xu, 2018147
DeepCov	2D CNN	PDB	6,729	precision: Top-L 0.406, Top-L/2 0.523, Top-L/5 0.611, Top-L/10 0.642	CASP12	Jones et al, 2018148
SPOT	ResNet, Res-bi-LSTM	PDB	11,200	AUC: 0.958 (RaptorX-contact ranked 2nd: 0.909)	1,250 chains after June 2015	Hanson et al.149
DeepMetaPSICOV	ResNet	PDB	6,729	precision: Top-L/5 0.6618	CASP13	Kandathil et al, 2019150
MULTICOM	2D CNN	CASP 8-11	425	TM score: 0.69, GDT_TS: 63.54, SUM Z score (− 2.0): 99.47	CASP13	Hou et al.151
C-I-TASSER∗	2D CNN	–	–	TM score: 0.67, GDT_HA: 0.44, RMSD: 6.19, SUM Z score($-2.0$): 107.59	CASP13	Zheng et al.152
AlphaFold	ResNet	PDB	31,247	TM score: 0.70, GDT_TS: 61.4,SUM Z score (− 2.0): 120.43	CASP13	Senior et al.22
MapPred	ResNet	PISCES	7,277	precision: 78.94% in SPOT, 77.06% in CAMEO, 77.05 in CASP12	SPOT, CAMEO, CASP12	Wu et al, 2019153
trRosetta	ResNet	PDB	15,051	TM_score: 0.625 (AlphaFold: 0.587)	CASP13, CAMEO	Yang et al, 2020103
RGN	bi-LSTM	ProteinNet 12 (before 2016)∗∗	104,059	10.7 Å dRMSD on FM, 6.9 Å on TBM	CASP12	AlQuraishi, 2019101
/	biGRU, Res LSTM	CUProtein	75,000	preceded CASP12 winning team, comparable with AlphaFold in RMSD	CASP12 + 13	Drori et al.78

FM, free modeling; GRU, gated recurrent unit; LM, pseudo-likelihood maximization; MLP, multi-layer perceptron; MP, membrane protein; RBM, restricted Boltzmann machine; RF, random forest; RMSD, root-mean square deviation; TBM, template-based modeling.

∗C-I-TASSER and C-QUARK were reported, we only report one here.

∗∗RGN was trained on different ProteinNet for each CASP, we report the latest one here.

Protein Structure Prediction

Before the notable success of DL at CASP12 (2016) and CASP13 (2018), the state-of-the-art methodology used complex workflows based on a combination of fragment insertion and structure optimization methods, such as simulated annealing with a score function or energy potential. Over the last decade, the introduction of co-evolution information in the form of evolutionary coupling analysis (ECA)¹⁵⁴ improved predictions. ECA relies on the rationale that residue pairs in contact in 3D space tend to evolve or mutate together; otherwise, they would disrupt the structure to destabilize the fold or render a large conformational change. Thus, evolutionary couplings from sequencing data suggest distance relationships between residue pairs and aid structure construction from sequence through contact or distance constraints. Because co-evolution information relies on statistical averaging of sequence information from a large number of MSAs,^145,155,156 this approach is not effective when the protein target has only a few sequence homologs. Neural networks were, at first, introduced to deduce evolutionary couplings between distant homologs, thereby improving ECA-type contact predictions for contact-assisted protein folding.¹⁵⁴ While the application of neural networks to learn inter-residue protein contacts dates back to the early 2000s,^157,158 more recently this approach was adopted by MetaPSICOV (two-layer NN),¹⁴⁶ PConsC2 (two-layer NN),¹⁴⁵ and CoinDCA-NN (five-layer NN),¹⁵⁵ which combined neural networks with ECAs. However, there was no significant advantage to neural networks compared with other machine learning methods at that time.¹⁵⁹

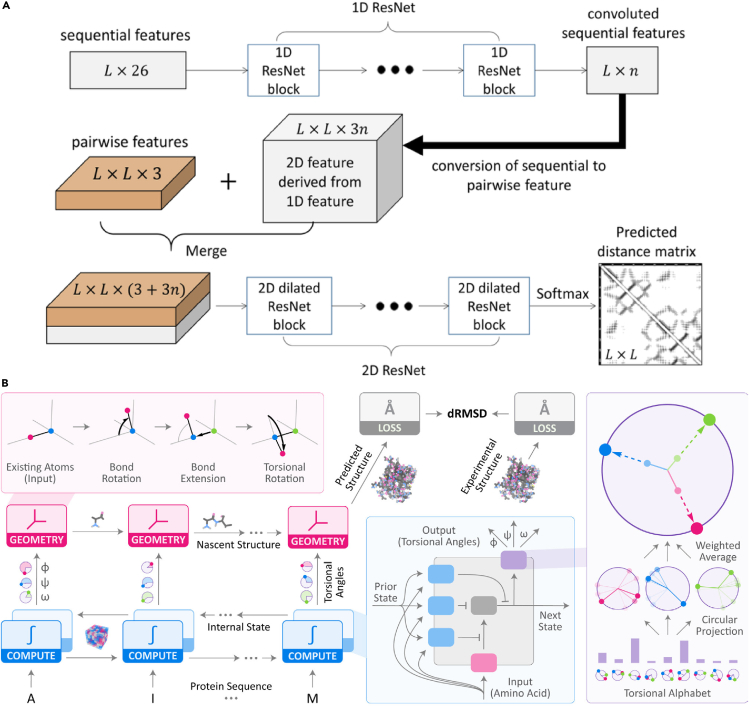
In 2017, Wang et al.¹⁰² proposed RaptorX-Contact, a residual neural network (ResNet)-based model,⁵¹ which, for the first time used a deep neural network for protein contact prediction, significantly improving the accuracy on blind, challenging targets with novel folds. RaptorX-Contact ranked first in free modeling targets at CASP12.¹⁶¹ Its architecture (Figure 5(a)) entails (1) a 1D ResNet that inputs MSAs, predicted secondary structure and solvent accessibility (from DL-based prediction tool RaptorX-Property)¹⁶² and (2) a 2D ResNet with dilations that inputs the 1D ResNet output and inter-residue co-evolution information from CCMpred.¹⁴⁴ In its original formulation, RaptorX-Contact outputs a binary classification of contacting versus non-contacting residue pairs.¹⁰² Later versions were trained to learn multi-class classification for distance distributions between C_β atoms.¹⁴⁷ The primary contributors to the accuracy of predictions was the co-evolution information from CCMpred and the depth of the 2D ResNet, suggesting that the deep neural network learned co-evolution information better than previous methods. Later, the method was extended to predict $C_{\mathrm{\alpha }}$−C_α, $C_{\mathrm{\alpha }}$−C_γ, $C_{\mathrm{\gamma }}$−C_γ, N-O distances and torsion angles (DL-based RaptorX-Angle),¹⁶³ giving constraints to locate side chains and additionally constrain the backbone; all five distances, torsions, and secondary structure predictions were converted to constraints for folding by CNS.¹⁴⁷ At CASP12, however, RaptorX-Contact (original contact-based formulation) and DL drew limited attention because the difference between top-ranked predictions from DL-based methods and hybrid DCA-based methods was small.

Figure 5.

Two Representative DL Approaches to Protein Structure Prediction

(A) Residue distance prediction by RaptorX: the overall network architecture of the deep dilated ResNet used in CASP13. Inputs of the first-stage, 1D convolutional layers are a sequence profile, predicted secondary structure, and solvent accessibility. The output of the first stage is then converted into a 2D matrix by concatenation and fed into a deep ResNet along with pairwise features (co-evolution information, pairwise contact, and distance potential). A discretized inter-residue distance is the output. Additional network layers can be attached to predict torsion angles and secondary structures. Figure from Xu and Wang (2019).¹⁶⁰

(B) Direct structure prediction: overview of recurrent geometric networks (RGN) approach. The raw amino acid sequence along with a PSSM are fed as input features, one residue at a time, to a bidirectional LSTM net. Three torsion angles for each residue are predicted to directly construct the 3D structure. Figure from AlQuraishi (2019).¹⁰¹

This situation changed at CASP13 4 when one DL-based model, AlphaFold, developed by team A7D, or DeepMind,^26,22,164 ranked first and significantly improved the accuracy of “free modeling” (no templates available) targets (Figure 1). The A7D team modified the traditional simulated annealing protocol with DL-based predictions and tested three protocols based on deep neural networks. Two protocols used memory-augmented simulated annealing (with domain segmentation and fragment assembly) with potentials generated from predicted inter-residue distance distributions and predicted GDT_TS,¹⁶⁵ respectively, whereas the third protocol directly applies gradient descent optimization on a hybrid potential combining predicted distance and Rosetta score. For the distance prediction network, a deep ResNet, similar to that of RaptorX,¹⁰² inputs MSA data and predicts the probability of distances between $\beta -$ carbons. A second network was trained to predict GDT_TS of the candidate structure with respect to the true or native structure. The simulated annealing process was improved with a conditional variational autoencoder (CVAE)¹⁶⁶ model that constructs a mapping between the backbone torsions and a latent space conditioned by sequence. With this network, the team generated a database of nine-residue fragments for the memory-augmented simulated annealing system. Gradient-based optimization performed slightly better than the simulated annealing, suggesting that traditional simulated annealing is no longer necessary and state-of-the-art performance can be reached with simply optimizing a network predicted potential. AlphaFold's authors, like the RaptorX-Contact group, emphasized that the accuracy of predictions relied heavily on learned distance distributions and co-evolutionary data.

Yang et al.¹⁰³ further improved the accuracy of predictions on CASP13 targets using a shallower network than former models (61 versus 220 ResNet blocks in AlphaFold) by also training their neural network model (named trRosetta) to learn inter-residue orientations along with $\beta -$ carbon distances. The geometric features—C_α-C_β torsions, pseudo-bond angles, and azimuthal rotations—directly describe the relevant coordinates for the physical interaction of two amino acid side chains. These additional outputs created significant improvement on a relatively fixed DL framework, suggesting that there is room for additional improvement.

An alternative and intuitive approach to structure prediction is directly learning the mapping from sequence to structure with a neural network. AlQuraishi¹⁰¹ developed such an end-to-end differentiable protein structure predictor, called RGN, that allows direct prediction of torsion angles to construct the protein backbone (Figure 5B). RGN is a bidirectional LSTM that inputs a sequence, PSSM, and positional information and outputs predicted backbone torsions. Overall 3D structure predictions are within 1–2 Å of those made by top-ranked groups at CASP13, and this approach boasts a considerable advantage in prediction time compared with strategies that learn potentials. Moreover, the method does not use MSA-based information and could potentially be improved with the inclusion of evolutionary information. The RGN strategy is generalizable and well suited for protein structure prediction. Several generative methods (see below) also entail end-to-end structure prediction models, such as the CVAE framework used by AlphaFold, albeit with more limited success.²²

Related Applications

Side-chain prediction is required for homology modeling and various protein engineering tasks, such as fixed-backbone design. Side-chain prediction is often embedded in high-resolution structure prediction methods, traditionally with dead-end elimination¹⁶⁷ or preferential sampling from backbone-dependent side-chain rotamer libraries.¹⁶⁸ Liu et al.¹⁶⁹ specifically trained a 3D CNN to evaluate the probability score for different potential rotamers. Du et al.¹⁷⁰ adopted an energy-based model (EBM)¹⁷¹ to recover rotamers for backbone structures. Recent protein structure prediction models, such as Gao et al.’s¹⁶³ RaptorX-angle and Yang et al.’s¹⁰³ trRosetta, predict the structural features that help locate the position of side-chain atoms as well.

PPI prediction identifies residues at the interface of the two proteins forming a complex. Once the interface residues are determined, a local search and scoring protocol can be used to determine the structure of a complex. Similar to protein folding, efforts have focused on learning to classify contact or not. For example, Townshend et al.⁹⁶ developed a 3D CNN model (SASNet) that voxelizes the 3D environment around the target residue, and Fout et al.¹¹² developed a GCN-based model with each interacting partner represented as a graph. Unlike those starting from the unbound structures, Zeng et al.¹⁷² reuse the model trained on single-chain proteins (i.e., RaptorX-Contact) to predict PPI with sequence information alone, which resulted in the RaptorX-Complex that outperforms ECA-based methods at contact prediction. Another interesting approach directly compares the geometry of two protein patches. Gainza et al.¹¹⁶ trained their MaSIF model by minimizing the Euclidean distances between the complementary surface patches on the two proteins while maximizing the distances between non-interacting surface patches. This step is followed by a quick nearest-neighbor scanning to predict binding partners. The accuracy of MaSIF was comparable with traditional docking methods. However, MaSIF, similar to existing methods, showed low prediction accuracy for targets that involve conformational changes during binding.

Membrane proteins (MPs) are partially or fully embedded in a hydrophobic environment composed of a lipid bilayer and, consequently, they exhibit hydrophobic motifs on the surface unlike the majority of the proteins that are water soluble. Wang et al.¹⁷³ used a DL transfer learning framework comprising one-shot learning from non-MPs to MPs. They showed that transfer learning works surprisingly well here because the most frequently occurring contact patterns in soluble proteins and MPs are similar. Other efforts include classification of the trans-membrane topology.¹⁷⁴ Since experimental biophysical data are sparse for MPs, Alford and Gray¹⁷⁵ compiled a collection of 12 diverse benchmark sets for membrane protein prediction and design for testing and learning of implicit membrane energy models.

Loop modeling is a special case of structure prediction, where most of the 3D protein structure is given, but coordinates of segments of the polypeptide are missing and need to be completed. Loops are irregular and sometimes flexible segments, and thus their structures have been difficult to capture experimentally or computationally.^176,177 So far, DL frameworks based on inter-residue distance prediction (similar to protein structure prediction),¹⁷⁸ and those based on treating the loop residue distances with the remaining residues as an image inpainting problem¹⁷⁹ have been applied to loop modeling. Recently, Ruffolo et al.¹⁷⁷ used a RaptorX-like network setup and a trRosetta geometric representation to predict the structure of antibody hypervariable complementarity-determining region (CDR) H3 loops, which is critical for antigen binding.

Protein Design

We divide the current DL approaches to protein design into two broad categories. The first uses knowledge of other sequences (either “all” sequenced proteins or a certain class of proteins) to design sequences directly (Table 4). These approaches are well suited to create new proteins with functionality matching existing proteins based on sequence information alone, in a manner similar to consensus design.¹⁸⁰ The second class follows the “fold-before-function” scheme and seeks to stabilize specific 3D structures, perhaps but not necessarily with the intent to perform a desired function (Tables 5 and 6). The first approach can be described as function$\to$sequence (structure agnostic), and the second approach fits the traditional stepwise inverse design: function $\to$structure $\to$ sequence.

Table 4.

Generative Models to Identify Sequence from Function (Design for Function)

Model	Architecture	Output	Dataset	N_train	Performance	Citation
–	WGAN + AM	DNA	chromosome 1 of human hg 38	4.6M	~4 times stronger than training data in predicted TF binding	Killoran et al.181
–	VAE	AA	5 protein families	–	natural mutation probability prediction rho = 0.58	Sinai et al.93
–	LSTM	AA	ADAM, APD, DADP	1,554	predicted antimicrobial property 0.79 ± 0.25 (random: 0.63 ± 0.26)	Müller et al, 201855
PepCVAE	CVAE	AA	–	15K labeled,1.7M unlabeled	generate predicted AMP with 83% (random, 28%; length, 30)	Das et al.64
FBGAN	WGAN	DNA	UniProt (res., 50)	3,655	predicted antimicrobial property over 0.9 after 60 epochs	Gupta et al.182
DeepSequence	VAE	AA	mutational scan data	41 scans	aimed for mutation effect prediction, outperformed previous models	Riesselman et al.94
DbAS-VAE	VAE+AS	DNA	simulated data	–	predicted protein expression surpassed FB-GAN/VAE	Brookes et al.183
–	LSTM	musical scores	–	56 betas + 38 alphas	generated proteins capture the secondary structure feature	Yu et al.184
BioSeqVAE	VAE	AA	UniProt	200,000	83.7% reconstruction accuracy,70.6% EC accuracy	Costello et al.185
–	WGAN	AA	antibiotic resistance determinants	6,023	29% similar to training sequence (BLASTp)	Chhibbar et al.186
PEVAE	VAE	AA	3 protein families	31,062	latent space captures phylogenetic, ancestral relationship, and stability	Ding et al.92
–	ResNet	AA	mutation data + Ilama immune repertoire	1.2M (nano)	predicted mutation effect reached state-of-the-art, built a library of CDR3 seq	Riesselman et al.187
Vampire	VAE	AA	immuneACCESS	–	generated sequences predicted to be similar to real CDR3 sequences	Davidson et al, 2019188
ProGAN	CGAN	AA	eSol	2,833	solubility prediction $R^2$ improved from 0.41 to 0.45	Han et al, 2019189
ProteinGAN	GAN	AA	MDH from UniProt	16,706	60 sequences were tested in vitro, 19 soluble, 13 with catalytic activity	Repecka et al.190
CbAS-VAE	VAE+AS	AA	protein fluorescence dataset	5,000	predicted protein fluorescence surpassed FB-VAE/DbAS	Brookes et al.183

AA, amino acid sequence; AM, activation maximization; AS, adaptive sampling; CGAN, conditional generative adversarial network; CVAE, conditional variational autoencoder; DNA, DNA sequence; EC, enzyme commission.

Table 5.

Generative Models for Protein Structure Design

Model	Architecture	Representation	Dataset	N_train	Performance	Citation
–	DCGAN	Cα-Cα distances	PDB (16-, 64-, 128-residue fragments)	115,850	meaningful secondary structure, reasonable Ramachandran plot	Anand et al.24
RamaNet	GAN	torsion angles	ideal helical structures from PDB	607	generated torsions are concentrated around helical region	Sabban et al.191
–	DCGAN	backbone distance	PDB (64-residue fragment)	800,000	smooth interpolations; recover from sequence design and folding	Anand et al.68
Ig-VAE	VAE	coordinates and backbone distance	AbDb (antibody structure)	10,768	sampled 5,000 Igs screened for SARS-CoV2 Binder	Eguchi et al.192
–	CNN (input design)	same as trRosetta	–	–	27 out of 129 sequence-structure pairs experimentally validated	Anishchenko et al.193

CNN, convolutional neural network; DCGAN, deep convolutional generative adversarial network; GAN, generative adversarial network; VAE, variational autoencoder.

Table 6.

Generative Models to Identify Sequence from Structure (Protein Design)

Model	Architecture	Input	Dataset	N_train	Performance	Citation
SPIN	MLP	sliding window with 136 features	PISCES	1,532	sequence recovery of 30.7% on 1,532 proteins (CV)	Li et al.100
SPIN2	MLP	sliding window with 190 features	PISCES	1,532	sequence recovery of 34.4% on 1,532 proteins (CV)	O’Connell et al.25
–	MLP	target residue and its neighbor as pairs	PDB	10,173	sequence recovery of 34% on 10,173 proteins	Wang et al.194
–	CVAE	string encoded structure or metal	PDB, MetalPDB	3,785	verified with structure prediction and dynamic simulation	Greener et al.195
SPROF	Bi-LSTM + 2D ResNet	112 1-D features + Cα distance map	PDB	11,200	sequence recovery of 39.8% on protein	Chen et al.196
ProDCoNN	3D CNN	gridded atomic coordinates	PDB	17,044	sequence recovery of 42.2% on 5,041 proteins	Zhang et al.197
–	3D CNN	gridded atomic coordinates	PDB-REDO	19,436	sequence recovery 70%, experimental validation of mutation	Shroff et al.198
ProteinSolver	Graph NN	partial sequence, adjacency matrix	UniParc	$72\times {10}^6$ residues	sequence recovery of 35%, folding and MD test with 4 proteins	Strokach et al, 2019199
gcWGAN	CGAN	random noise + structure	SCOPe	20,125	diversity and TM score of prediction from designed sequence $\ge$cVAE	Karimi et al.200
–	Graph Transformer	backbone structure in graph	CATH based	18,025	perplexity: 6.56 (rigid), 11.13 (flexible) (random: 20.00)	Ingraham et al.23
DenseCPD	ResNet	gridded backbone atomic density	PISCES	$2.6\times {10}^6$ residues	sequence recovery of 54.45% on 500 proteins	Qi et al.201
–	3D CNN	gridded atomic coordinates	PDB	21,147	sequence recovery from 33% to 87%, test with folding of TIM barrel	Anand et al.202
–	CNN (input design)	Same as trRosetta	–	–		Norn et al.203

Bi-LSTM, bidirectional long short-term memory; CV, cross-validation; MLP, multi-layer perceptron.

Many of the recent studies describe novel algorithms that output putative designed protein sequences, but only a few studies also present experimental validation. In traditional protein design studies, it is not uncommon for most designs to fail, and some of the early reports of protein designs were later withdrawn when the experimental evidence was not confirmed by others. As a result, it is usually expected that design studies offer rigorous experimental evidence. In this review, because we are interested in creative, emerging DL methods for design, we include papers that lack experimental validation, and many of these have in silico tests that help gauge validity. In addition, we make a special note of recent studies that present experimental validation of designs.

Direct Design of Sequence

Approaches that attempt to design for sequences parallel work in the field of NLP, where an auto-regressive framework is common, most notably, the RNN. In language processing, an RNN model is able to take the beginning of a sentence and predict the next word in that sentence. Likewise, given a starting amino acid residue or a sequence of residues, a protein design model can output a categorical distribution for each of the 20 amino acid residues for the next position in the sequence. The next residue in the sequence is sampled from this categorical distribution, which in turn is used as the input to predict the following one. Following this approach, new sequences, sampled from the distribution of the training data, are generated, with the goal of having properties similar to those in the training set. Müller et al.⁵⁵ first applied an LSTM RNN framework to learn sequence patterns of antimicrobial peptides (AMPs),²⁰⁴ a highly specialized sequence space of cationic, amphipathic helices. The same group then applied this framework to design membranolytic anticancer peptides.²⁰⁵ Twelve of the generated peptides were synthesized and six of them killed MCF7 human breast adenocarcinoma cells with at least 3-fold selectivity against human erythrocytes. In another application, instead of traditional RNNs, Riesselman et al.¹⁸⁷ used a residual causal dilated CNN²⁰⁶ in an auto-regressive way and generated a functional single-domain antibody library conditioned on the naive immune repertoires from llamas; although experimental validation was not presented. Such applications could potentially speed up and simplify the task of generating sequence libraries in the lab.

Another approach to sequence generation is mapping the latent space to the sequence space, and common strategies to train such a mapping include AEs and GANs. As mentioned earlier, AEs are trained to learn a bidirectional mapping between a discrete design space (sequence) and a continuous real-valued space (latent space). Thus, many applications of AEs use the learnt latent representation to capture the sequence distribution of a specific class of proteins, and subsequently, to predict the effect of variations in sequence (or mutations) on protein function.92, 93, 94 The utility of this learned latent space, however, is more than that. A well trained real-valued latent space can be used to interpolate between two training samples, or even extrapolate beyond the training data to yield novel sequences. One such example is the PepCVAE model.⁶⁴ Following a semi-supervised learning approach, Das et al.⁶⁴ trained a VAE model on an unlabeled dataset of $1.7\times {10}^6$ sequences and then refined the model for the AMP subspace using a 15,000 sequence-labeled dataset. By concatenating a conditional code indicating if a peptide is antimicrobial, the CVAE framework allows efficient sampling of AMPs selectively from the broader peptide space. More than 82% of the generated peptides were predicted to exhibit antimicrobial properties according to a state-of-the-art AMP classifier.

Unlike AEs, GANs focus on learning the unidirectional mapping from a continuous real-valued space to the design space. In an early example, Killoran et al.’s¹⁸¹ developed a model that combines a standard GAN and activation maximization to design DNA sequences that bind to a specific protein. Repecka et al.¹⁹⁰ trained ProteinGAN on the bacterial enzyme malate dehydrogenase (MDH) to generate new enzyme sequences that were active and soluble in vitro, some with over 100 mutations, with a 24% success rate. Another interesting GAN-based framework is Gupta and Zou's²⁰⁷ FeedBack GAN (FBGAN) that learns to generate cDNA sequences for peptides. They add a feedback-loop architecture to optimize the synthetic gene sequences for desired properties using an oracle (an external function analyzer). At every epoch, they update the positive training data for the discriminator with high-scoring sequences from the generator so that the score of generated sequences increases gradually. They demonstrated the efficacy of their model by successfully biasing generated sequences toward antimicrobial activity and a desired secondary structure.

Design with Structure as Intermediate

Within the fold-before-function scheme, for design one first picks a protein fold or topology according to certain desirable properties, then determines the amino acid sequence that could fold into that structure (function $\to$ structure $\to$sequence). Under the supervised learning setting, most efforts use the native sequences as the ground truth and recovery rate of native sequences (i.e., the percentage of sequence that matches the native one) as a success metric. To compare, Kuhlman and Baker²⁰⁸ reported sequence recovery rates of 51% for core residues and 27% for all amino acid residues using traditional de novo design approaches. Because the mapping from sequence to structure is not unique (within a neighborhood of each structure), it is not clear that higher sequence recovery rates would be meaningful.

A class of efforts, pioneered by the SPIN model,²⁰⁹ inputs a five-residue sliding window to predict the amino acid probabilities for the center position to generate sequences compatible with a desired structure. The features in such models include φ and ψ dihedrals, a sequence profile of a five-residue fragment derived from similar structures, and a rotamer-based energy profile of the target residue using the DFIRE potential. SPIN²⁰⁹ reached a 30.7% sequence recovery rate and Wang et al.¹⁹⁴ and O'Connell et al.’s²⁵ SPIN2 further improved it to 34%. Another class of efforts inputs the voxelized local environment of an amino acid residue. In Zhang et al.’s197, 198^,198 and Shroff et al.’s197, 198^,198 models, voxelized local environment was fed into a 3D CNN framework to predict the most stable residue type at the center of a region. Shroff et al.¹⁹⁸ reported a 70% recovery rate and the mutation sites were validated experimentally. Anand et al.²⁰² trained a similar model to design sequences for a given backbone. Their protocol involves iteratively sampling from predicted conditional distributions, and it recovered from 33% to 87% of native sequence identities. They tested their model by designing sequences for five proteins, including a de novo TIM barrel. The designed sequences were 30%–40% identical to native sequences and predicted structures were 2–5 Å root-mean-square deviation from the native conformation.

Other approaches generate full sequences conditioned by a target structure. Greener et al.¹⁹⁵ trained a CVAE model to generate sequences conditioned on protein topology represented in a string.⁹⁹ The resulting sequence was verified to be stable with molecular simulation. Karimi et al.²¹⁰ developed gcWGAN that combined a CGAN and a guidance strategy to bias the generated sequences toward a desired structure. They used a fast structure prediction algorithm²¹¹ as an “oracle” to assess the output sequence and provide feedback to refine the model. They examined the model for six folds using Rosetta-based structure prediction, and gcWGAN had higher TM score distributions and more diverse sequence profiles than CVAE.¹⁹⁵ Another notable experiment is Ingraham et al.’s²³ graph transformer model that inputs a structure, represented as a graph, and outputs the sequence profile. They treat the sequence design problem similar to a machine translation problem, i.e., a translation from structure to sequence. Like the original transformer model,⁵⁷ they adopted an encoder-decoder framework with self-attention mechanisms to dynamically learn the relationship between information in two neighbor layers. They measured their results by perplexity, a widely used metric in speech recognition,²¹² and the per-residue perplexity (lower is better) for single chains was 9.15, lower than the perplexity for SPIN2 (12.86). Norn et al. treated the protein design problem as that of maximizing the probability of a sequence given a structure. They back-propagate through the trRosetta structure prediction network¹⁰³ to find a sequence that minimizes the distance between predicted structure and a desired structure.²⁰³ Norn et al. validate their designs computationally by showing the generated sequences have deep wells in their modeled energy landscapes. Strokach et al. treated the design of protein sequence given a target structure as a constraint satisfaction problem. They optimized their GNN architecture on the related problem of filling in a Sudoku puzzle followed by training on millions of protein sequences corresponding to thousands of structural folds. They were able to validate designed sequences in silico and demonstrate that some designs folded to their target structures in vitro.²¹³

An ambitious design goal is to generate new structures without specifying the target structure. Anand and Huang were the first to generate new structures using DL. They tested various representations (e.g., full atom, torsion-only) with a deep convolutional GAN (DCGAN) framework that generates sequence-agnostic, fixed-length short protein structural fragments.²⁴ They found that the distance map of C_α atoms gives the most meaningful protein structures, although the asymmetry of ψ and φ torsion angles²¹⁴ was only recovered with torsion-based representations. Later they extended this work to all atoms in the backbone and combined with a recovery network to avoid the time-consuming structure reconstruction process.⁶⁸ They showed that some of the designed folds are stable in molecular simulation. In a more narrowly focused study, Eguchi et al.¹⁹² trained a VAE model with the structures of immunoglobulin (Ig) proteins, called Ig-VAE. By sampling the latent space, they generated 5,000 new Ig structures (sequence-agnostic) and then screened them with computational docking to identify putative binders to SARS-CoV2-RBD.

Another approach exploits a DL structure prediction algorithm and a Markov Chain MC (MCMC) search to find sequences that fold into novel compact structures. Anishchenko et al.¹⁹³ iterated sequences through the DL network, trRosetta,¹⁰³ to “hallucinate”²¹⁵ mutually compatible sequence-structure pairs in a manner similar to “input design”.¹⁸³ By maximizing the contrast between the distance distributions predicted by trRosetta and a background network trained on noise, they obtained new sequences with geometric maps with sharp geometric features. Impressively, 27 of the¹²⁷ hallucinated sequences were experimentally validated to fold into monomeric, highly stable, proteins with circular dichroism spectra compatible with the predicted structure.

Outlook and Conclusion

In this review, we have summarized the current state-of-the-art DL techniques applied to the problem of protein structure prediction and design. As in many other areas, DL shows the potential to revolutionize the field of protein modeling. While DL originated from computer vision, NLP and machine learning, its fast development combined with knowledge from operations research,²¹⁶ game theory,⁶⁵ and variational inference³² among other fields, has resulted in many new and powerful frameworks to solve increasingly complex problems. The application of DL for biomolecular structure has just begun, and we expect to see more efforts on methodology development and applications in protein modeling and design.

We observed several trends.

Experimental Validation

An important gap in current DL work in protein modeling, especially protein design (with few notable exceptions),^{205,190,198,193} is the lack of experimental validation. Past blind challenges, e.g., CASP and CAPRI, and design claims have shown that experimental validation in this field is of paramount importance, where computational models are still prone to error. A key next stage for this field is to engage collaborations between machine learning experts and experimental protein engineers to test and validate these emerging approaches.

Importance of Benchmarking

In other fields of machine learning, standardized benchmarks have triggered rapid progress.217, 218, 219 CASP is a great example that provides a standardized platform for benchmarking diverse algorithms, including emerging DL-based approaches. A well-defined question and proper evaluation (especially experimental) would lead to more open competition among a broader range of groups and, eventually, the innovation of more diverse and powerful algorithms.

Imposing a Physics-Based Prior

One common topic among the machine learning community is how to utilize existing domain knowledge to reduce the effort during training. Unlike certain classical ML problems, such as image classification, in protein modeling, a wide range of biophysical principles restrict the range of plausible solutions. Some examples in related fields include imposing a physics-based model prior,^220,221 adding a regularization term with physical meaning,²²² and adopting a specific formula to conserve physical symmetry.^223,224 Similarly, in protein modeling, well-established empirical observations can help restrict the solution space, such as the Ramanchandran distribution of backbone torsion angles²¹⁴ and the Dunbrack or Richardsons library of side-chain conformations.^225,226

Closed-Loop Design

The performance of DL methodologies relies heavily on the quality of data, but the publicly available datasets may not cover important sample space because of experimental accessibility at the time of experiments. Furthermore, the dataset may contain harmful noise from non-uniform experimental protocols and conditions. A possible solution may be to combine model training with experimental data generation. For instance, one may devise a closed-loop strategy to generate experimental data, on-the-fly, for queries (or model inputs) that are most likely to improve the model, and update the training dataset with the newly generated data.227, 228, 229, 230 For such a strategy to be feasible, automated synthesis and characterization is necessary. As high-throughput synthesis and testing of protein (or DNA and RNA) can be carried out in parallel, automation is possible. While such a strategy may seem far-fetched, automated platforms such as those from Ginkgo Bioworks or Transcriptic are already on the market.

Reinforcement Learning

Another approach to overcome the limitation of data availability is reinforcement learning (RL). Biologically meaningful data may be generated on-the-fly in simulated environments, such as the Foldit game. In the most famous application of RL, AlphaGo Zero,²¹ an RL agent (network) was able to learn and master the game by learning from the game environment alone. There are already some examples of RL in the field of chemistry and electric engineering to optimize organic molecules or computational chips.231, 232, 233 One suitable protein modeling problem for an RL algorithm would be training an artificial intelligence (AI) agent to make a series of “moves” to fold a protein, similar to the Foldit game.^234,235 Such studies are still rare and previous attempts have focused on folding the 2D hydrophobic-polar model of proteins.^236,237 Although the results did not yet beat conventional methods, Gao²³⁸ recently explored using policy and reward networks in an RL scheme to fold 3D protein structures de novo by guiding the selection of MC moves in Rosetta. Angermueller et al.²³⁹ applied a model-based RL framework to designing sequences of AMPs and transcription factor binding sites.

Model Interpretability

One should keep in mind that a neural network represents nothing more (and nothing less) than a powerful and flexible regression model. In addition, due to their highly recursive nature, neural networks tend to be regarded as “black-boxes”, i.e., too complicated for practitioners to understand the resulting parameters and functions. Although model interpretability in ML is a rapidly developing field, many popular approaches, such as saliency analysis240, 241, 242 for image classification models, are far from satisfactory.²⁴³ Although other approaches^244,245 offer more reliable interpretations, their application to DL model interpretation has been largely missing in protein modeling. As a result, current DL models offer limited understanding of the complex patterns they learn.

Beyond Proteins

DL-based methods are general and so, with appropriate representation and sufficient training data, they can be applied to other molecules. Like proteins, nucleic acids, carbohydrates, and lipids are also polymers, composed of nucleotides, monosaccharides, and aliphatic subunits and head groups, respectively. Many approaches developed for learning protein sequence and structural information can be extended to these other classes of biomolecules.^246,247 Finally, biology often conjugates these molecules, e.g., for glycoproteins. DL approaches that build up from basic chemistry, such as those being developed for small molecule drugs,248, 249, 250, 251 may inspire methods to treat these biomolecules that do not fall into a strict polymer type.

The “Sequence $\to$ Structure $\to$ Function” Paradigm

We know from molecular biophysics that a sequence translates into function through the physical intermediary of a 3D molecular structure. Allosteric proteins,²⁵² for instance, may exhibit different structural conformations under different physiological conditions (e.g., pH) or environmental stimuli (e.g., small molecules, inhibitors), reminding us that context is as important as protein sequence. That is, despite Anfinsen's⁴² hypothesis, sequence alone does not always fully determine the structure. Some proteins require chaperones to fold to their native structure, meaning that a sequence could result in non-native conformations when the kinetics of folding to the native structure may be unfavorable in the absence of a chaperone. Because many powerful DL algorithms in NLP operate on sequential data, it may seem reasonable to use protein sequences alone for training DL models. In principle, with a suitable framework and training, DL could disentangle the underlying relationships between sequence and structural elements. However, a careful selection of DL frameworks that are structure or mechanism-aware will accelerate learning and improve predictive power. Indeed, many successful DL frameworks applied so far (e.g., CNNs or graph CNNs) factor in the importance of learning on structural information.

Finally, with the hope of gaining insight into the fundamental science of biomolecules, there is a desire to link AI approaches to the underlying biochemical and biophysical principles that drive biomolecular function. For more practical purposes, a deeper understanding of underlying principles and hidden patterns that lead to pathology is important in the development of therapeutics. Thus, while efforts strictly limited to sequences are abundant, we believe that models with structural insights will play a more critical role in the future.