Consistent Force Field Captures Homolog Resolved HP1 Phase Separation

Abstract

Many proteins have been shown to function via liquid-liquid phase separation. Computational modeling could offer much needed structural details of protein condensates and reveal the set of molecular interactions that dictate their stability. However, the presence of both ordered and disordered domains in these proteins places a high demand on the model accuracy. Here, we present an algorithm to derive a coarse-grained force field, MOFF, that can model both ordered and disordered proteins with consistent accuracy. It combines maximum entropy biasing, least-squares fitting, and basic principles of energy landscape theory to ensure that MOFF recreates experimental radii of gyration while predicting the folded structures for globular proteins with lower energy. The theta temperature determined from MOFF separates ordered and disordered proteins at 300 K and exhibits a strikingly linear relationship with amino acid sequence composition. We further applied MOFF to study the phase behavior of HP1, an essential protein for posttranslational modification and spatial organization of chromatin. The force field successfully resolved the structural difference of two HP1 homologs, despite their high sequence similarity. We carried out large scale simulations with hundreds of proteins to determine the critical temperature of phase separation and uncover multivalent interactions that stabilize higher-order assemblies. In all, our work makes significant methodological strides to connect theories of ordered and disordered proteins and provides a powerful tool for studying liquid-liquid phase separation with near-atomistic details.

Graphical Abstract

INTRODUCTION

Many proteins encoded by eukaryotic genomes contain disordered regions that do not adopt well-defined tertiary structures.^1–6 Disordered domains could facilitate the target search process while retaining protein-binding specificity via the folding-upon-binding mechanism.^7,8 It has recently become widely appreciated that another important property of these intrinsically disordered proteins (IDPs) lies in their collective behavior.^9,10 The multivalent interactions that are intrinsic to them can drive the formation of membraneless organelles, including stress granules,¹¹ P granules,¹² superenchancers,¹³ and heterochromatin^14,15 through the liquid-liquid phase separation mechanism. The increased protein concentration in these organelles could lead to more efficient biochemical reactions.^16,17 Characterizing the structural details of these condensates could provide crucial insight into the function of the cellular processes. While progress is being made, connecting the atomistic properties of IDPs to the global structure, composition, and dynamics of the organelles remains challenging.^18,19

One prominent example of IDPs is heterochromatin protein 1 (HP1), a key component of constitutive heterochromatin.^20–22 HP1 consists of ordered, conserved chromo (CD) and chromoshadow (CSD) domains connected via a variable disordered hinge region. The CD helps to recruit the protein to chromatin segments marked with histone H3 trimethylation (H3K9me3), while the CSD domain enables dimerization and also serves as a docking site for other nuclear proteins.²³ In contrast to the canonical view that HP1 proteins are merely accessory players with no active role in chromatin organization, several studies recently found them spontaneously form phase-separated liquid droplets.^14,15,24,25 These droplets could support new forms of chromatin structures that differ dramatically from the regular fibril conformations.^26,27 One noteworthy feature of HP1, which is shared by many of the proteins involved in forming membraneless compartments,^28,29 is the presence of both ordered and disordered domains. This feature has made a high-resolution structural characterization of the full-length protein and the functional state with many proteins challenging.

Computational modeling could offer much needed structural details of IDPs and their aggregates and reveal the set of molecular interactions that dictate the stability of liquid droplets.³⁰ However, the presence of both ordered and disordered domains in these proteins places a strong demand on the model’s accuracy. All-atom force fields, with their ever-improving accuracy,^31–36 can in principle, accurately model protein conformations. They are computational expensive though, and long-timescale simulations needed to study slow conformational rearrangement and aggregation kinetics remain inaccessible for most proteins of interest. While many coarse-grained force fields have been introduced and proven effective at predicting the structures of globular proteins,^37,38 they cannot be directly generalized to study IDPs. Separate efforts have been carried out to parameterize force fields specialized for disordered proteins.^39–42 These force fields, while succeeding in modeling the phase separation and IDP structural heterogeneity,^42,43 are not advised for applications of globular proteins. Since the two classes of proteins share the same set of amino acids for their composition, it is hopeful that a unified force field can be derived to model both of them with consistent accuracy. Such a consistent force field would greatly facilitate the investigation of IDPs’ collective behaviors in large scale condensates.

In this paper, we introduce a new algorithm to parameterize coarse-grained protein force fields with implicit solvation. We generalize the maximum entropy optimization algorithm by ensuring that for globular proteins, the force field predicts an energy gap between the native conformation and the unfolded or partially folded structures. The maximum entropy optimization algorithm was developed for parameterizing transferable IDP force fields using biasing energies derived from experimental constraints.^44,45 Energy gap maximization, on the other hand, has been a successful strategy for deriving force fields of folded proteins.^46–49 The resulting force field, MOFF, indeed provides a more balanced set of interactions that can predict the radii of gyration of both ordered and disordered proteins. The theta temperatures determined using MOFF classify the two types of proteins by the biological temperature at 300 K. They exhibit a striking linear relationship on the protein sequence composition. We applied MOFF to characterize the three homologs of human HP1, α, β, and γ. Simulations succeeded at predicting the relative size of the homologs despite their high sequence similarity, and revealed multivalent, charged interactions that stabilize the more collapsed HP1α conformations. The computational efficiency of the force field enabled direct simulations of the phase separation process. These large scale simulations helped quantify the critical temperature of the proteins and uncovered higher-order protein clusters mediated via the same interactions that cause the collapse of dimers. We anticipate MOFF to be a useful tool for studying IDPs and provide its implementation in GROMACS (https://github.com/ZhangGroup-MITChemistry/MOFF).

METHODS

Coarse-grained Protein Force Field

We modeled proteins with a coarse-grained representation for efficient conformational sampling and large scale simulations of phase separation. Each amino acid is represented with one bead at the α-carbon position. The chemical properties of each bead are provided in Table S1. The potential energy for quantifying the stability of a protein structure r is defined as

$$U_{\text{MOFF }}(r)=U_{\text{backbone}}+U_{\text{memory}}+U_{\text{electrostatics}}+U_{\text{contact}}.$$ (1)

U_backbone is responsible for maintaining the backbone geometry of the protein and consists of the bond, angle, and dihedral potentials. U_memory helps stabilize protein secondary structures. These two terms are dependent on input protein conformations. U_{electrostatics} describes electrostatic interactions between charged residues with the Debye-Hückle theory. We used a distance-dependent dielectric constant to more accurately capture the change in the solvation environment upon protein folding^50,51 (Figure S1). The last term U_contact is the amino acid type dependent pairwise contact potential. Parameters that quantify the strength of such interactions will be derived using the algorithm introduced in the next section to ensure consistency for both ordered and disordered proteins. The full functional form of the potential energy is given in the Supporting Information (SI).

Amino Acid Contact Potential from Maximum Entropy Optimization

Efficient modeling of protein molecules is a problem of long-standing interest in computational biophysics. Numerous algorithms have been introduced to parameterize coarse-grained force fields with implicit solvation for globular proteins.^37,52–57 One class of algorithms that is of relevance to this study is inspired by the energy landscape theory,^58–61 which states that an energy gap between the folded native structure and unfolded conformations is necessary and sufficient for ensuring reliable protein folding on a reasonable timescale. Several force fields have been introduced via maximization of the energy gap and successfully applied to predict protein structures and study folding kinetics.^46–49

The force fields designed for globular proteins often need to be adjusted when applied for IDPs.^40–42 Maximum entropy optimization has become widely popular in recent years^62–69 as an efficient means to improve the agreement between modeling and experiment. While optimization can be used during post-processing to reweight the simulated structure ensemble,^62,70,71 correction terms can also be directly introduced to the force field to alter simulation outcomes.⁷² As shown in Refs.,^64,73,74 linear corrections are optimal and incur the least amount of the bias to the model. We further designed an iterative algorithm (see SI for details) to create a transferable force field by reparameterizing the protein-specific correction terms into pair-wise contact potentials between amino acids,⁴⁴

$$\Delta \mathit{ϵ}C\equiv \alpha R_g.$$ (2)

C is the contact matrix that indicates the number of contacts for each pair of amino acids in a given structure. Δϵ is the list of changes to the pairwise amino acid specific contact energy. αR_g is the biasing energy based on the radius of gyration (R_g) derived from maximum entropy optimization. When solved over an ensemble of structures collected for a large set of proteins in the training set, the changes to the contact energy matrix (Δϵ) can be determined. The resulting force field (MOFF-IDP) is transferable and reproduces the radius of gyration for various IDPs.

It is worth noting that IDP force fields, either modified from existing ones designed for globular proteins or parameterized from scratch, often cannot be applied to predict the size and structure of folded proteins. Therefore, there appears to be a disconnect between folded and unfolded proteins. Force fields often only work on one of them, but not the other. This paper introduces a new algorithm to parameterize force fields that can be applied to model both ordered and disordered proteins with consistent accuracy.

The starting point of the algorithm is still the iterative maximum entropy optimization (see Figure 1). While our previous study focused on IDPs, here we added globular proteins as well in the training set to build a consistent force field. In addition, we borrowed ideas from the energy landscape theory to enforce that the total contact energy of the PDB structure is lower than that of any structure sampled in computer simulations, up to some tolerance. Mathematically, this constraint can be expressed as

$${\mathit{ϵ}}^{\mathit{\prime }}{C}_{\text{PDB}}\le {\mathit{ϵ}}^{\mathit{\prime }}{C}_{\text{sim}},$$ (3)

where ϵ′ = Δϵ + ϵ is the new pair-wise contact energy updated with the correction term from Eq. 2. Thus, using the interior-point algorithm,⁷⁵ we simultaneously solved Eq. 2 for all proteins in our training set under the constraint of Eq. 3 for the ordered proteins (Figure 1). In practice, we added an additional term, γσ_sim to the right hand side of Eq. 3. γ is a flexible tolerance parameter used to tune the strength of the constraint, and σ_sim is the standard deviation of the contact energy estimated for each protein using simulations performed in the previous iteration. To aid the convergence of the algorithm, we used single value decomposition (SVD) to reduce noise and placed an additional constraint on the change in amino acid contact energies from one iteration to the next. As seen previously,⁴⁴ the relationship between energy and contact formation is not perfectly linear, requiring this entire algorithm to be done iteratively.

Figure 1:

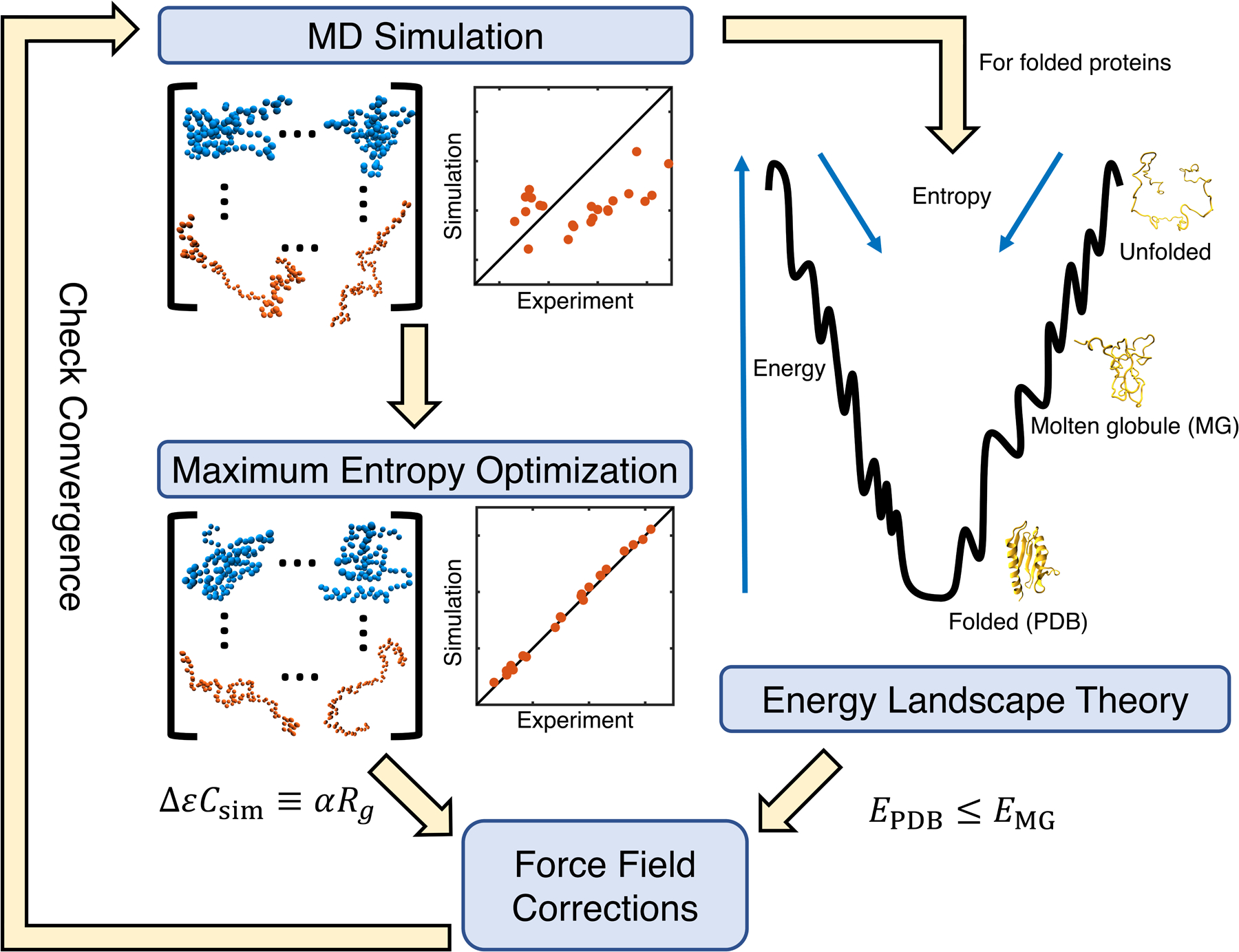
Illustration of the algorithm that combines maximum entropy optimization and energy gap constraint for force field parameterization.

Details on Molecular Dynamics Simulations

We implemented MOFF in GROMACS⁷⁶ to perform molecular dynamics simulations with a time step of 10 fs. Replica exchange simulations were performed with temperatures at 300, 320, 340, 360, 380, and 400K to enhance conformational sampling. Exchanges between neighboring replicas were attempted at every 100 steps, with all odd pairs on odd attempts and all even pairs on even attempts. Langevin dynamics was used to control the temperature with a coupling constant of 1 ps.

The simulations used for force field optimization were initialized from PDB structures for ordered sequences, or I-TASSER predictions for disordered sequences.⁷⁷ Proteins were placed in cubic boxes with side lengths of 50 nm to prevent them from contacting the periodic images. Simulations lasted for 4×10⁷ steps, and protein configurations were sampled at every 20000 steps. We excluded the first 10⁷ steps for equilibration. More simulation details can be found in the SI Section: Simulation Details on Force Field Optimization.

To stabilize tertiary contacts of globular domains in HP1, we augmented MOFF with additional biases derived from the initial structures. These biases were limited to individual ordered domains and dimer interfaces. They do not impact our prediction of the radius of gyration and inter-dimer interactions. More details on these biases are provided in SI Section: Folding potential for HP1 tertiary structure stabilization. We built initial structures for HP1 dimers using RaptorX,⁷⁸ with the crystal structure of the HP1α CSD domain as a template (PDB: 3I3C). These structures were placed in cubic boxes with side lengths of 50 nm. Five independent simulations that lasted for 5 × 10⁸ steps were performed, and samples were taken every 5 × 10⁴ steps. The first 10⁸ steps were excluded for equilibration. Clustering was done following the gromos clustering algorithm.⁷⁹

Slab simulations performed to study HP1 phase separation are explained in the SI Section: HP1 Slab Simulation Details.

RESULTS AND DISCUSSION

Parameterization of the Consistent Force Field

We applied an iterative optimization algorithm to parameterize the tertiary contact potentials of a coarse-grained force field (Eq. 1) and ensure consistent accuracy for both IDPs and ordered proteins. Details of the algorithm can be found in the Methods Section. As illustrated in Figure 1, it matches the simulated radius of gyration of protein molecules with experimental values via maximum entropy optimization.⁷² In addition, we enforce the constraint that, for folded proteins, the energy of the native structure is lowest, i.e., there is a gap between folded and unfolded configurations. This gap is necessary to ensure reliable protein folding into the native state. A total of 23 proteins, including seven ordered and 16 disordered (Table S2), were included in the training set. We ensured that ordered proteins cover a variety of secondary structures, and that monomeric Small Angle X-ray Scattering (SAXS) measurements are available for all proteins to determine R_g. We tracked the percent error given by

$$\frac{1}{N}\sum _{i=1}^N\frac{\left|R_{g,i}^{\text{sim}}-R_{g,i}^{\text{exp}}\right|}{100\times R_{g,i}^{\text{exp}}}$$ (4)

to measure the improvement caused by our optimization. The sum is taken over all N = 23 proteins in our training set. $R_{g,i}^{\text{exp}}$ is the experimental radius of gyration for the i-th protein, and $R_{g,i}^{\text{sim}}$ is the corresponding simulated value estimated from the average of 1500 structures sampled with the latest force field parameters. In addition to tracking the percent error on our training set, we monitored the performance of the force field on an independent validation set as well (Table S3). The validation set includes four ordered and four disordered proteins. We terminated the optimization when the percent error on the validation set fails to decrease upon two consecutive iterations. Starting values of the amino acid contact energies were set as the Miyazawa-Jernigan (MJ) potential⁸⁰ scaled by a factor of 0.4. The scale factor was determined as the value with the least percent error for proteins in the training set (Figure S2). We gradually relaxed the constraint defined in Eq. 3 by increasing the tolerance term along the iterations (Figure S3).

As shown in Figure S3, the iterative algorithm succeeds in gradually improving the force field accuracy. The percent error begins at 33.6, but reaches 9.6 by the final iteration. Importantly, the resulting force field (MOFF) outperforms the initial one built from the MJ potential for every protein in the training set (Figure 2A). When examining the validation set, we again noticed that (MOFF) improves relative to both MJ and MOFF-IDP, where MOFF-IDP is a force field parameterized specifically for IDPs using the maximum entropy optimization algorithm.⁴⁴ The percent error for proteins in the validation set is 17.9, compared to 51.2 and 41.2 for MOFF-IDP and MJ respectively (Figure 2B). In particular, we note that the new force field significantly improves on the ordered proteins (low R_g) relative to MOFF-IDP. This improvement likely stems from the newly added ordered proteins in the training set for force field parameterization. MOFF performs better than the other two force fields on all but one protein, 4cpv.

Figure 2:

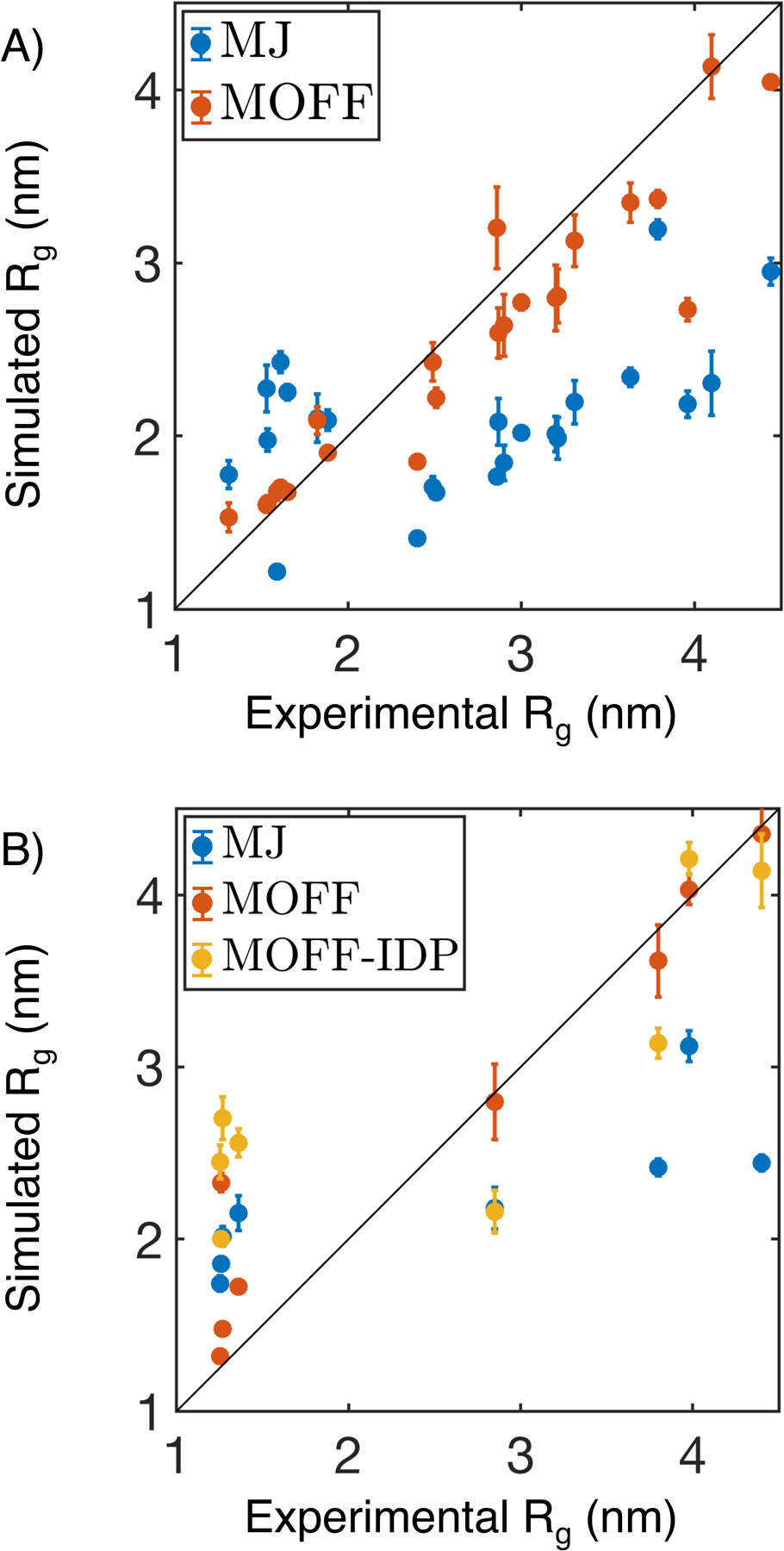
Comparison between experimental and simulated radius of gyration (R_g) for protein molecules in the training (A) and validation (B) set. In addition to the force field introduced in this paper (MOFF, orange), we included simulation results using the Miyazawa-Jernigan potential (MJ, blue) and a previous version of MOFF optimized for IDPs (MOFF-IDP, yellow) as well. Error bars represent standard deviation after block averaging.

The optimization also succeeded at ensuring that the folded structure is lower in energy than the unfolded configurations. The energy gap, defined as the difference between the mean contact energy of the simulated structures and the contact energy of the folded structure (Figure 3A), is indeed positive for all the globular proteins in the training set (Figure 3B). Upon a close inspection of the protein configurations simulated with the converged force field at 300 K, we observed deviations from the native conformations. As shown in Figure S4, the probability distributions of the root mean squared displacement (RMSD) from the PDB structure peak around 1.5 nm for most proteins. It is worth noting that several proteins do sample configurations close to the native state with RMSD less than 0.5 nm. In particular, 1wla shows a bimodal distribution with one of the peaks located at 0.5 nm (Figure 3C). Furthermore, simulated annealing simulations were able to predict structures with small RMSD values for three of the seven proteins (Figure S5). These improvements seem to be related to secondary structure content. For example, MOFF performs best on 1wla, which is an α-helical protein, while it performs worst on 5tvz, which is a β-sheet protein.

Figure 3:

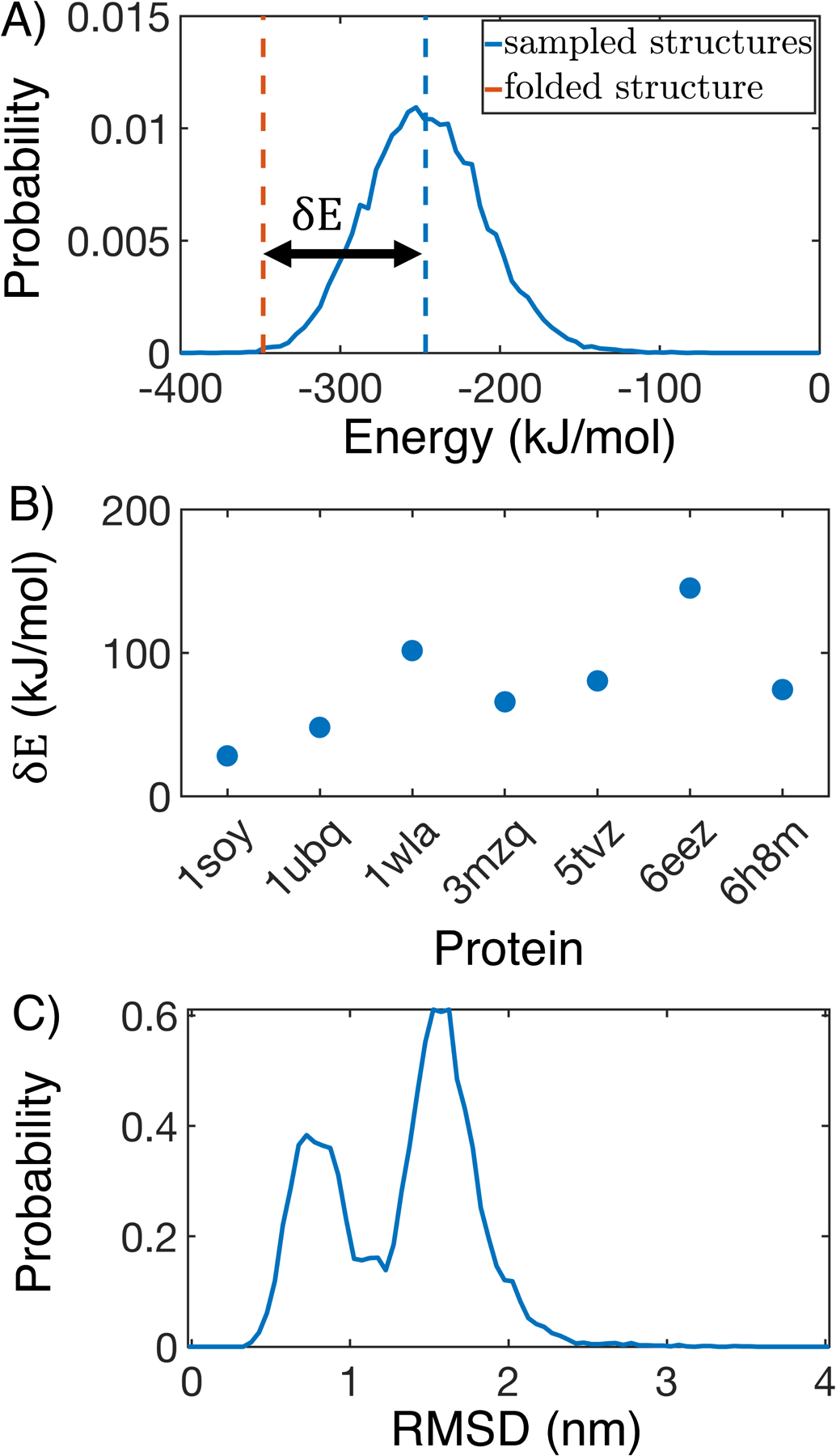
MOFF succeeds in creating energy gaps for folded proteins. (A) Contact energy of the folded structure (orange) relative to those sampled in simulation (blue) for 1wla. The energy gap δE is defined as the difference between the folded energy and the average simulated energy. (B) δE for all folded proteins in the training set. (C) Probability distribution of the root mean squared displacement (RMSD) relative to the folded structure for 1wla at 300 K.

MOFF Identifies Sequence Features to Differentiate Ordered and Disordered Proteins

To gain insight into the molecular interactions that dictate MOFF’s success in predicting protein sizes, we performed a hierarchical clustering on the contact energy matrix based on euclidean distances between column vectors. The resulting clusters generally sort the amino acids into groups with increasing hydrophobicity (Figure 4A and Table 1). We note that because electrostatic interactions were modeled separately, the clustering based on the contact potential alone may not strictly follow a typical hydrophobicity ordering. When evaluating the frequency of encountering the various amino acid clusters in the ordered and disordered proteins from our training set, we found that cluster 3 consists of mainly hydrophilic amino acids and is significantly enriched in disordered proteins. On the other hand, the hydrophobic cluster 6 is more often seen in folded proteins. Similar trends have been seen in more expansive studies, which compared the frequency of amino acids in the DisProt database with the frequency in the PDB.^81,82 The example configurations shown in Figure 4C further highlights the spatial distribution of the various clusters in an ordered and a disordered protein.

Figure 4:

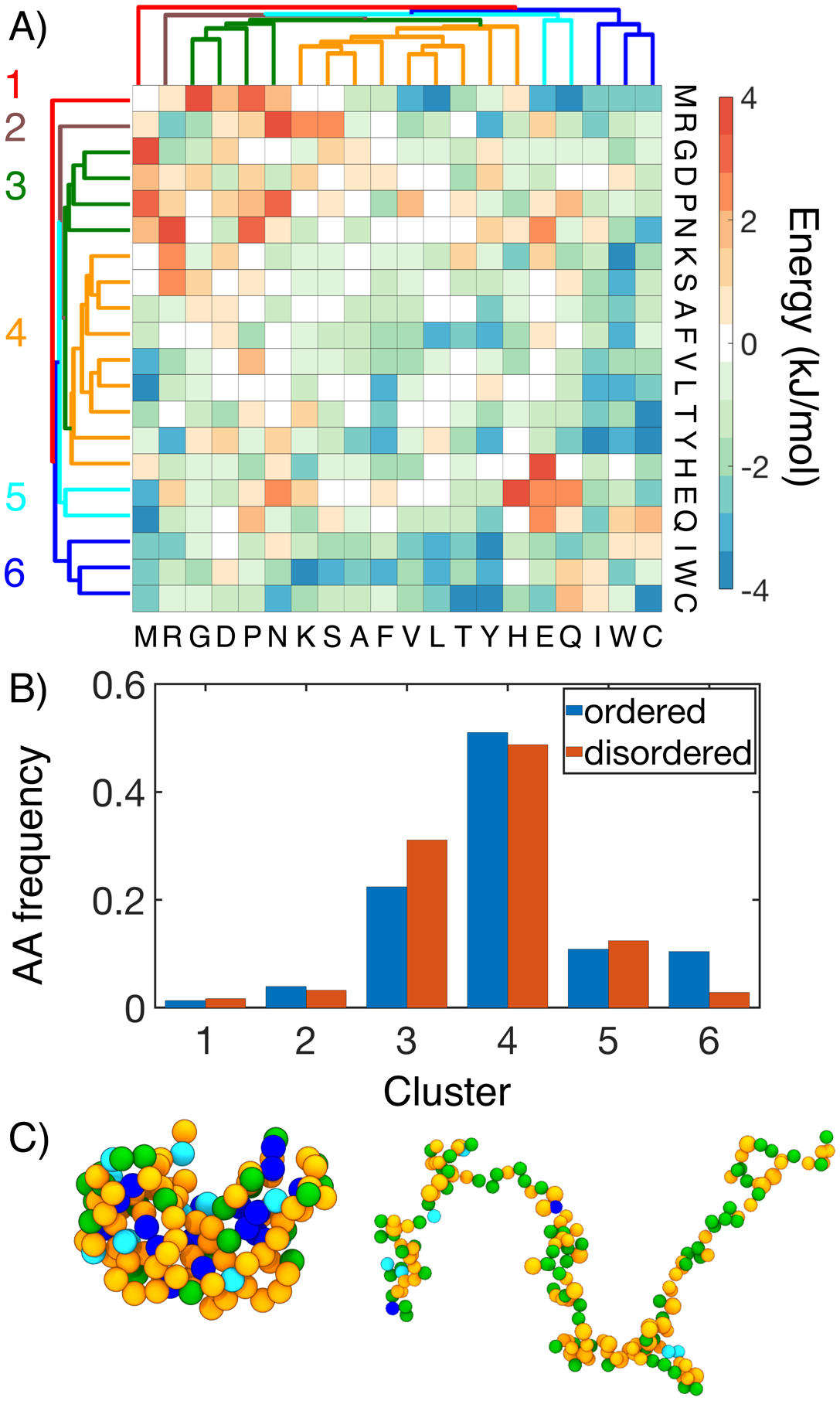
MOFF differentiates “ordered” and “disordered” amino acids with distinct contact energy patterns. (A) Hierarchical clustering of MOFF contact energy between amino acid pairs (ϵ_IJ in Eq. S16). (B) Comparison of the amino acid frequency by cluster in the ordered (blue) and disordered (orange) portions of our training set. (C) Spatial distribution of amino acid clusters in example structures of an ordered (3mzq, left) disordered protein (NSP, right). Amino acids are shown in the same coloring scheme for clusters as in part A.

Table 1:

Amino acid clusters determined from hierarchical clustering of MOFF contact energy.

Cluster	Amino Acids
Cluster 1 (red)	MET
Cluster 2 (brown)	ARG
Cluster 3 (green)	PRO ASN ASP GLY
Cluster 4 (orange)	HIS PHE LYS SER ALA VAL LEU THR TYR
Cluster 5 (cyan)	GLN GLU
Cluster 6 (blue)	ILE TRP CYS

The presence of well-defined amino acid clusters that sets apart ordered proteins from disordered ones provides an intuitive explanation of the distinct size distribution of the two protein types. The “disordered” amino acids from cluster 3 are mainly repulsive and will lead to the more expanded structure seen in IDPs; the “ordered” amino acids from cluster 6, on the other hand, are attracted to most of the other residues and tend to localize in the interior of collapsed proteins. The interaction energy among amino acids also explains the performance of the three force fields shown in Figure 2. Compared to the MJ potential (Figure S6), interactions between hydrophilic residues are more repulsive in MOFF. Similar results were seen with MOFF-IDP, where repulsive interactions rescue IDPs from over collapse. However, when ordered proteins are also included in the training set, we see these repulsive interactions grow stronger, as well as the development of stronger contact energy among hydrophobic residues. These changes are likely necessary to balance the collapse of ordered sequences and the swelling of disordered sequences.

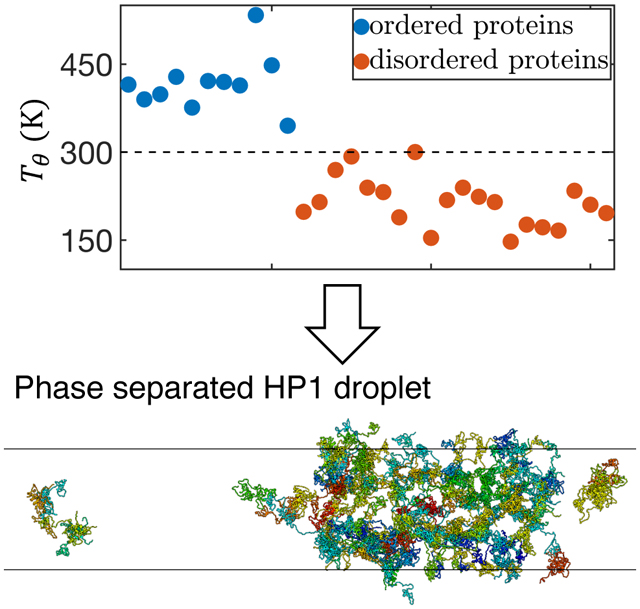
We next attempted to establish a more quantitative relationship between protein size, interaction energy, and the sequence. Towards that end, we first computed the theta temperature, T_θ, by monitoring the change of scaling exponent ν as a function of temperature. ν measures the variation of spatial distance between two residues i and j versus their linear distance in sequence, R α |i − j|^ν. At T_θ, proteins behave like an ideal Gaussian chain and ν = 1/2. As the temperature decreases from above to below T_θ, one expects the proteins to become more compact and transition from swollen polymers to collapsed globules, as can be seen in Figure 5A–B. T_θ, therefore, provides a direct measure of the interaction strength within a protein. Strikingly, MOFF predicts that the biological temperature provides a clear cut between ordered and disordered proteins, with the corresponding T_θ above and below 300 K, respectively. Such a partition indicates that MOFF treats the two types of proteins as polymers in a poor or good solvent and is consistent with the results shown in Figure 2.

Figure 5:

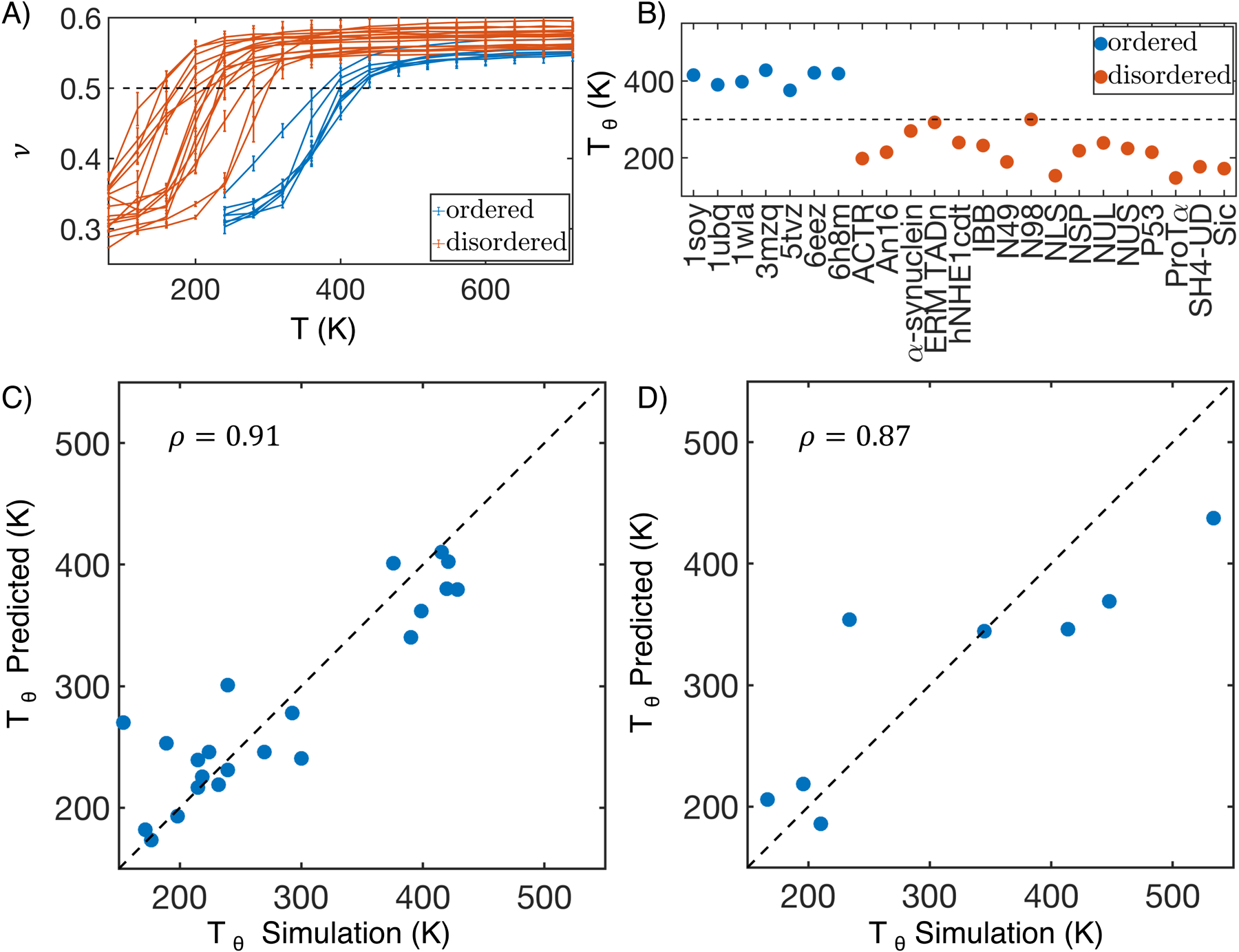
MOFF uncovers a linear relationship between protein theta temperature and sequence composition. (A) Polymer scaling exponent (ν) as a function of T for ordered (blue) and disordered (orange) protein sequences in our training set. Error bars represent standard deviation after block averaging. (B) Theta temperature (T_θ) for proteins in the training set. The 300K mark is highlighted as a guide for the eye. (C, D) Comparison between values of T_θ predicted using a linear equation of sequence composition (Eq. 5) and determined from molecular dynamics simulations for proteins in the training (C) and validation (D) set. ρ is the Pearson correlation coefficient between the two data sets, and the dashed black line represents perfect agreement.

The interaction potential of a protein and T_θ is ultimately dictated by the underlying sequence. Given the similarity among amino acids in their contact energy, we wondered whether a simple relationship between T_θ and the sequence composition can be found. Using the least absolute shrinkage and selection operator (LASSO),⁸³ we determined a linear regression model to fit T_θ with a minimal set of amino acid clusters identified in Figure 4.

The model that minimizes the mean squared error adopts the following expression

$$T_{\theta }=-528c_2-47c_3+337c_4+1921c_6+41,$$ (5)

where c_i is the percent of the sequence that is from cluster i (Figure S7). The fitted values are strongly correlated with the simulated ones despite our neglect of clusters 1 and 5 in the expression (Figure 5C). This expression supports the notion of hydrophobic effect^84,85 since amino acids from clusters 4 and 6 are mostly hydrophobic, and they contribute positively to the theta temperature by promoting protein collapse. It is also consistent with our conclusion that IDPs are more expanded because of their enrichment in residues from cluster 3. Arg, which is the sole residue in cluster 2, appears to be effective at reducing T_θ as well, potentially resulting from electrostatic repulsion.

We further computed T_θ for proteins in the test set and observed separation between ordered and disordered proteins at 300 K again (Figure S8). Notably, T_θ computed from replica exchange simulations are in good agreement with the values predicted using Eq. 5, with a Pearson correlation coefficient of 0.87 between the two (Figure 5D). Therefore, the linear relationship between T_θ and the sequence composition is general and transferable.

Multivalent Interactions Differentiate HP1 Homologs

After validating its accuracy in modeling the size of both ordered and disordered proteins, we applied MOFF to characterize the structure and phase behavior of human HP1. We first investigated the difference between the two isoforms, HP1α and HP1β. Previous experimental studies on the HP1 dimers showed that HP1β takes an open conformation, while HP1α is more collapsed.^14,86 The size difference is particularly striking considering the sequence similarity between the two proteins. As shown in Figure 6A, the ordered regions that include chromodomain and chromoshadow domain share a sequence identity over 80%. Even the disordered N-terminal extension, hinge region, and C-terminal extension have a sequence similarity of over 30%.⁸⁷

Figure 6:

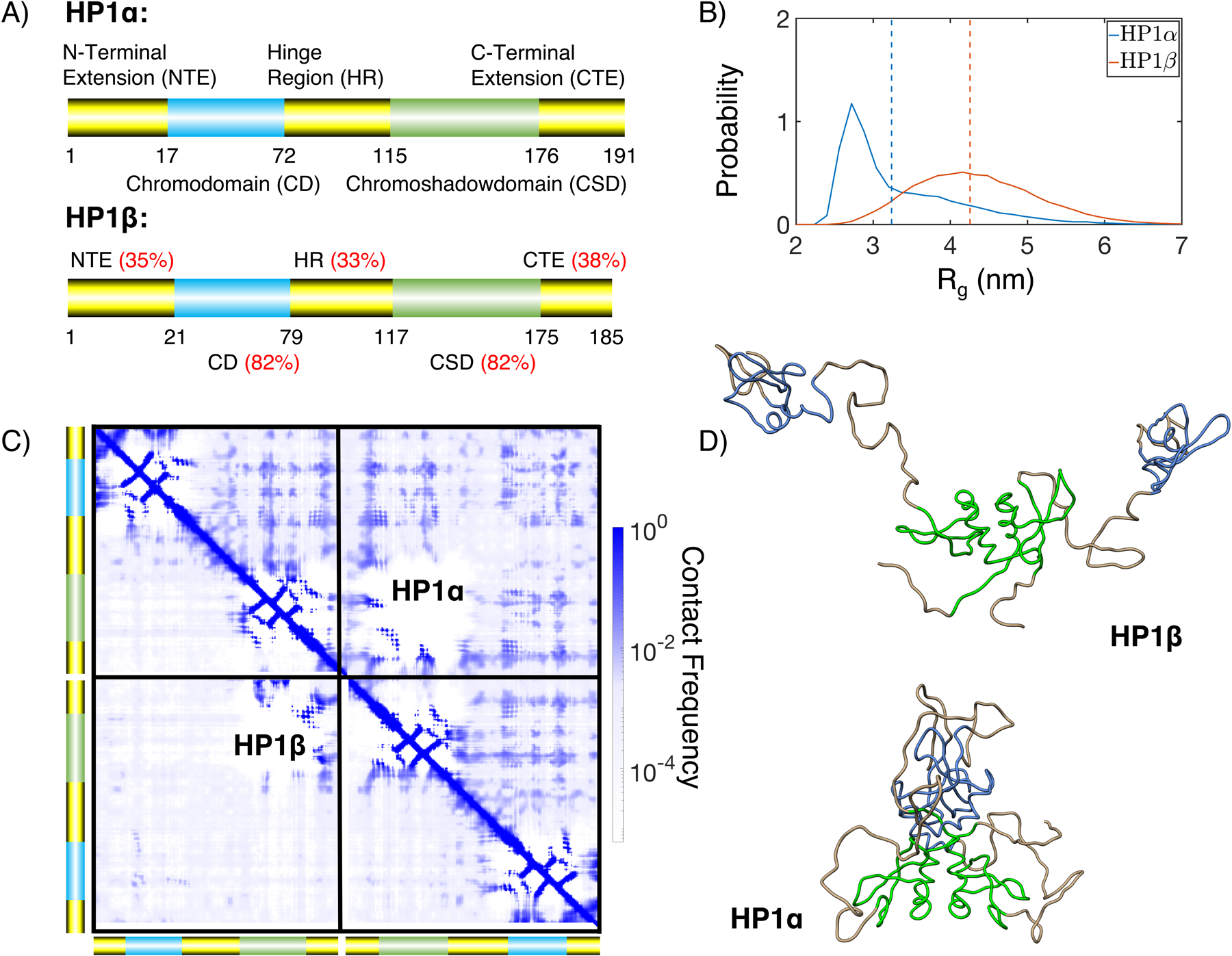
MOFF resolves the structural difference between HP1α and HP1β. (A) Cartoon diagrams for the two HP1 homologs, with the disordered regions shown in yellow and ordered regions in blue and green. The red numbers indicate sequence identity between the two proteins for various regions.⁸⁷ (B) Probability distributions of the radius of gyration (R_g) for HP1α (blue) and HP1β (orange). Dashed lines show mean values of each distribution. (C) Contact maps of HP1α (top right) and HP1β (bottom left), with cross-dimer interactions shown in the diagonal quadrants. (D) Representative structures of HP1β and HP1α determined from the most populated cluster. The coloring scheme is the same as in part A.

We performed replica exchange simulations of the HP1 dimers. Similar to experimental studies, we find that HP1α takes a more collapsed configuration at 300 K, with R_g = 3.24 ± 0.08 nm, compared to R_g = 4.26 ± 0.08 nm for HP1β (Figure 6B). These results compare more favorably to experimental values of 3.59 nm and 4.7 nm than those from MJ and MOFF-IDP (Table S4).^14,86

We found that multivalent interactions between charged residues cause the more compact configurations of HP1α. These interactions are evident in the contact maps shown in Figure 6C for HP1α (upper triangle) and HP1β (lower triangle). The off-diagonal quadrants correspond to interactions between the two monomers. For HP1β, these interactions are mostly limited to the dimerization of the chromoshadow domain. The contacts are more widespread in HP1α and arise from charged interactions between positive residues from the chromodomain or hinge regions and the negative counterparts of the chromoshadow or C-terminal extension domains. Such contacts can be readily seen in the central structure of the most populated cluster shown in Figure 6D. The clustering was performed over the simulated structural ensemble based on RMSD (Figure S9). On the contrary, we see that in HP1β, the hinges are completely extended, and there are minimal interactions between the two monomers.

We also simulated a third homolog, HP1γ, and found an intermediate size in between HP1α and HP1β (Figure S10). We were unable to find SAXS data for this protein, and future experiments could help validate the prediction.

Homolog Specific HP1 Phase Separation

The multivalent interactions found in HP1α are weak and can come undone to form more extended structures. These structures give rise to the long tail of the probability distribution of R_g (Figure 6B) and become more stable at higher temperatures (Figure S11). The extended configurations could facilitate contacts between different dimers to promote liquid-liquid phase separation.

We performed slab simulations^40,43 with 100 dimers of HP1α, HP1β, or HP1γ to directly probe their phase behavior. Starting from configurations with a high concentration of protein molecules in a cubic box, we extended the simulation box along the z direction by ~ 20 times. The system was then relaxed under constant volume simulations with periodic boundary conditions to reach desired temperatures. After equilibration, protein molecules will either disperse throughout the simulation box (Figure 7A), or stabilize into two phases with different concentrations (Figure 7B). A total of ten simulations with temperatures ranging from 150 K to 400 K were performed for each protein. We monitored the dynamics of these simulations by tracking the size of the largest cluster of HP1 dimers as a function of time. As shown in Figure S12, while low-temperature simulations preserve the initial dense phase, proteins begin to shake off as the temperature increases, leading to a drop in the cluster size.

Figure 7:

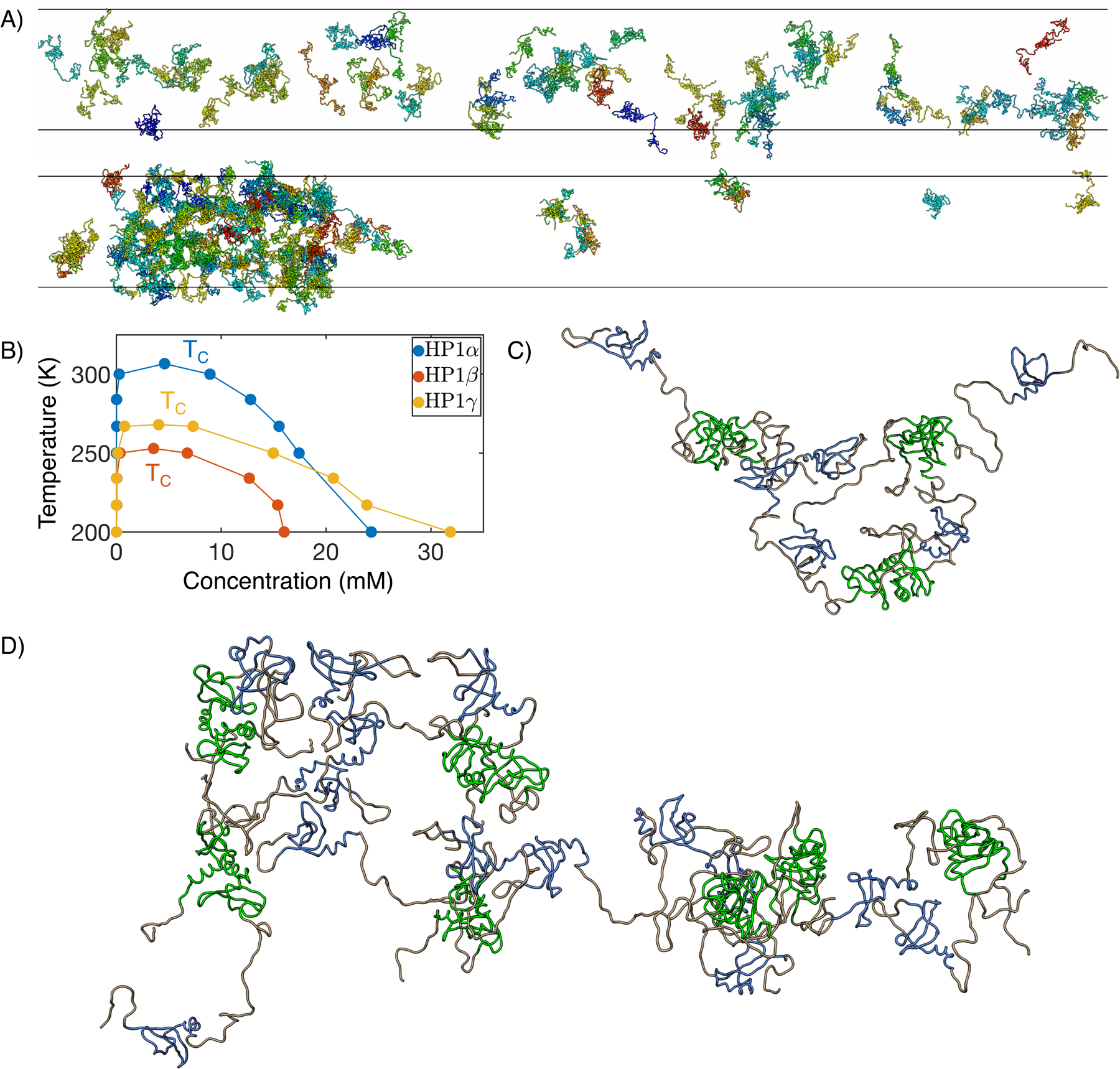
MOFF enables quantitative simulations of HP1 phase separation. (A) Example configurations from slab simulations of HP1α at 350 (top) and 300 (bottom) K. (B) Phase diagram and critical temperature for HP1α (blue), HP1β (orange), and HP1γ (yellow). (C, D) Representative cluster structures formed with three (C) and seven (D) HP1α dimers. The coloring scheme is the same as in Figure 6A.

Using the identified HP1 clusters, we further partitioned the system into two phase regimes and computed the corresponding protein concentration in each phase at high temperatures (Figure 7C). We then determined the critical temperature, T_C, by fitting the concentrations as a function of temperature using the following expression

$${\rho }_H-{\rho }_L=A{\left(T_C-T\right)}^{\beta },$$ (6)

with β = 0.325.⁴³ The resulting values for the three homologs are 306.7, 252.9, and 268.0 K respectively (Figure S13). The higher T_C of HP1α indicates that its dense phase is more stable than other homologs. This conclusion is in agreement with experimental observations that only HP1α can phase separate in vitro at room temperature, while HP1β and HP1γ cannot.^14,25 On the other hand, similar results obtained using MJ or MOFF-IDP suggest that those two force fields struggle to capture the complexity of HP1 phase behavior (Table S5).

We found that the multivalent interactions that drive the collapse of HP1α dimer indeed mediate inter-dimer interactions. For example, contacts between the N terminal extension (NTE) and the NTE, Chromodomain (CD), and hinge region of other dimers can be readily seen in the example clusters shown in Figure 7D,E. The interactions are also evident in the contact map between dimers (Figure S14 red box). Our results agree with previous experimental studies, which proposed that NTE bridges dimers through charged interactions.¹⁴ In addition, we also observed inter-dimer interactions mediated by C-terminal extension (CTE) (Figure S14 green box). The inter-dimeric contacts are largely preserved in clusters of HP1β and HP1γ, though at a weaker strength (Figure S15, S16). These highly patterned, multivalent interactions are, therefore, consistent across homologs.

CONCLUSIONS

In this work, we introduced an algorithm to parameterize force fields that can be used to study both ordered and disordered proteins with consistent accuracy. We combined principles of the energy landscape theory with the maximum entropy optimization to recreate experimental radii of gyration for ordered and disordered proteins while simultaneously ensuring that the folded structures are lower in energy than the unfolded ones. The resulting force field, which we term as MOFF, indeed outperforms two existing force fields that work well for globular proteins or IDPs to recreate protein size. The force field further helped identify two clusters of amino acids critical for determining protein size and the theta temperature.

When applied to the human HP1, MOFF successfully resolves the structural difference between three homologs with high sequence similarity. It identified non-specific, charged interactions that stabilize a more collapsed configuration in HP1α than HP1β. In addition, the force field was shown to be computationally efficient for studying phase separation. We determined the critical temperature for the three homologs. The values agree with qualitative experimental observations that only HP1α can phase seperate. Our simulations also provided structural insight into the condensates. The multivalent interactions found in dimers can now bridge contacts across dimers to mediate cluster formation.

We note that while MOFF can reliably predict the size of globular proteins, it has not yet achieved consistent accuracy for de novo structure prediction. When studying large proteins with both ordered and disordered regions, it is beneficial to include biases that stabilize the tertiary structure and prevent partial unfolding. Notably, these biases can be limited to individual globular domains so that they do not impact the overall protein size. Their strength can be tuned to reproduce the root mean squared fluctuation determined using short atomistic simulations. With the ordered regions restricted to the PDB conformations, MOFF should provide an accurate description of interactions between domains within the same protein and interactions between proteins as demonstrated for HP1. We provided scripts in the GitHub to facilitate simulation setup.

Despite the progress made in this work, there is room for improving MOFF further. As detailed in the SI Section: Mathematical Expressions of Energy Function, the secondary structure potential of the force field is protein-specific and non-transferable. A more predictive secondary structure model may improve the force field’s accuracy in simulating globular structures and in capturing the conformational flexibility of IDPs.⁸⁸ Furthermore, we grouped all nonbonded interactions between amino acids into a single contact potential. A more refined functional form that differentiates short-range direct contacts from long-range interactions mediated by water molecules may prove beneficial.^49,89 Additionally, generalized maximum entropy algorithms⁶⁵ and Bayesian approaches^90–92 can be incorporated into the force field optimization procedure to better account for error and uncertainty in experimental data. More advanced algorithms that maximize the ratio of the folding temperature versus the glass transition temperature can also be adopted to better sculpt the funneled energy landscape for globular proteins.⁴⁶