Thermodynamics and folding landscapes of large proteins from a statistical mechanical model

Abstract

Statistical mechanical models that afford an intermediate resolution between macroscopic chemical models and all-atom simulations have been successful in capturing folding behaviors of many small single-domain proteins. However, the applicability of one such successful approach, the Wako-Saitô-Muñoz-Eaton (WSME) model, is limited by the size of the protein as the number of conformations grows exponentially with protein length. In this work, we surmount this size limitation by introducing a novel approximation that treats stretches of 3 or 4 residues as blocks, thus reducing the phase space by nearly three orders of magnitude. The performance of the ‘bWSME’ model is validated by comparing the predictions for a globular enzyme (RNase H) and a repeat protein (IκBα), against experimental observables and the model without block approximation. Finally, as a proof of concept, we predict the free-energy surface of the 370-residue, multi-domain maltose binding protein and identify an intermediate in good agreement with single-molecule force-spectroscopy measurements. The bWSME model can thus be employed as a quantitative predictive tool to explore the conformational landscapes of large proteins, extract the structural features of putative intermediates, identify parallel folding paths, and thus aid in the interpretation of both ensemble and single-molecule experiments.

Graphical abstract

Highlights

• •A novel statistical mechanical bWSME model, applicable to large proteins, is developed.
• •The number of allowed conformations is lower than earlier model approximations.
• •Multiple conformational features, folding paths and intermediates can be predicted.
• •The model quantitatively reproduces the folding behavior of IκBα, RNase H and MBP.

1. Introduction

Structure-based models of protein folding have revealed rich insights into the conformational behavior of numerous proteins, enzymes, protein–protein and protein-DNA complexes (Mirny and Shakhnovich, 2001, Papoian and Wolynes, 2003, Clementi et al., 2003, Levy et al., 2005, Hyeon and Thirumalai, 2011, Chan et al., 2011, Li et al., 2011, Orozco et al., 2011, Naganathan, 2013a, Truong et al., 2015, Kmiecik et al., 2016). These models work on the general principle that only those interactions present in the native structure define the folding mechanism, as originally proposed by Gō (Taketomi et al., 1975), a phenomenology that is enshrined in the energy landscape theory of protein folding (Bryngelson et al., 1995), and validated via extensive analysis of long time-scale all-atom MD simulations (Best et al., 2013). The successes of these models have spawned an array of coarse-grained treatments of protein folding to enable efficient sampling and thus minimizing the time taken to generate well-equilibrated folding paths and ensembles. While many of the treatments are customized to the problem that is being addressed, it is common to study protein folding via models that consider only the C_α-atoms or a combination of C_α and minimal side-chain and backbone representations. The latter allows for introducing energetic flavors via either specific residue–residue interaction energy matrices (for example, the Miyazawa-Jernigan potential (Miyazawa and Jernigan, 1985)) or electrostatics through monopole–monopole interactions.

One class of structure-based models are statistical mechanical models that treat residues as independent units of folding (Wako and Saito, 1978a, Wako and Saito, 1978b, Ikegami, 1981, Go and Abe, 1981, Abe and Go, 1981, Zwanzig, 1995, Hilser and Freire, 1996, Hilser et al., 1998, Hilser et al., 2006, Muñoz and Eaton, 1999, Alm and Baker, 1999, Muñoz, 2002, Bruscolini and Pelizzola, 2002, Bruscolini and Naganathan, 2011, Naganathan, 2012) (Fig. 1A). Unlike all-atom or coarse-grained simulations that accumulate conformations as a function of time, statistical models pre-assume an ensemble from physical considerations. Following this, the statistical weight of every microstate and hence the overall canonical partition function is calculated from structure-based expectations enabling predictions of numerous thermodynamic features including heat capacity, residue folding probabilities, free-energy profiles and surfaces (Muñoz, 2001, Naganathan, 2016). The Wako-Saitô-Muñoz-Eaton (WSME) model is one such statistical mechanical model that was first developed by Wako and Saitô (Wako and Saito, 1978a, Wako and Saito, 1978b), discussed in detail by Gō and Abe (Go and Abe, 1981, Abe and Go, 1981), and then later independently developed by Muñoz and Eaton (1999). Originally seen as a physical tool to predict the folding rates of proteins from three-dimensional structures (Muñoz and Eaton, 1999, Henry and Eaton, 2004), the model has expanded its scope to quantitatively analyze folding behaviors of folded globular domains (Bruscolini and Naganathan, 2011, Garcia-Mira et al., 2002, Narayan and Naganathan, 2014, Narayan and Naganathan, 2017, Narayan and Naganathan, 2018, Naganathan and Muñoz, 2014, Naganathan et al., 2015, Munshi and Naganathan, 2015, Rajasekaran et al., 2016, Narayan et al., 2017, Itoh and Sasai, 2006), repeat proteins (Faccin et al., 2011, Sivanandan and Naganathan, 2013, Hutton et al., 2015), disordered proteins (with appropriate controls) (Naganathan and Orozco, 2013, Gopi et al., 2015, Munshi et al., 2018a), predict and engineer thermodynamic stabilities of proteins via mutations (Naganathan, 2012, Naganathan, 2013b, Rajasekaran et al., 2017) and entropic effects (Rajasekaran et al., 2016), model allosteric transitions (Itoh and Sasai, 2011, Sasai et al., 2016), protein-DNA binding (Munshi et al., 2018b), quantifying folding pathways at different levels of resolution (Henry et al., 2013, Kubelka et al., 2008, Gopi et al., 2017), force-spectroscopic measurements (Imparato et al., 2007) and even crowding effects (Caraglio and Pelizzola, 2012).

Fig. 1.

The bWSME model. (A, B) Conformational units as residues (panel A) or blocks (panel B) for a three-stranded beta-hairpin. The eleven blocks are alternatively colored in red and blue in panel B. (C) Number of microstates as a function of number of residues in a protein for block size = 1 (i.e. residues as conformational units; black), block size = 3 (blue) and block size = 4 (red). Note that the ordinate is in logarithmic scale.

In the classic WSME model, each residue is allowed to sample two sets of conformations – folded (represented as 1 in binary notation) and unfolded (0) – thus allowing for a maximum of 2^N conformations or microstates for an N-residue polypeptide. The exact solution, or the total partition function with contributions from all the 2^N microstates, can be calculated via different methods (Wako and Saito, 1978b, Go and Abe, 1981, Bruscolini and Pelizzola, 2002, Henry and Eaton, 2004). The underlying assumption in these methods is that while there can be numerous independent nucleating events or folded islands (stretches of 1s), two different islands can interact if they are interacting in the native structure (Gō-model) and importantly only when all the intervening residues connecting the two islands are also folded. In other words, the model assumes a specific folding mechanism wherein local interactions form first while non-local interactions form later. It is of course possible that two structured regions can interact despite an intervening unfolded region and constitute a valid microstate as long as the entropic destabilization is sufficiently offset by a gain in energy from the interacting regions. Sasai and co-workers developed the extended WSME model to address this via virtual loop closures (Inanami et al., 2014).

In parallel, Eaton and co-workers came up with a more realistic ensemble description by considering only single stretches of folded residues (single-sequence approximation or SSA), two stretches of folded residues (double-sequence approximation or DSA) and DSA allowing for interactions across structured islands even if the intervening residues are unfolded (DSAw/L) (Henry and Eaton, 2004, Kubelka et al., 2008). The number of model microstates for an N residue protein under this ensemble definition, which we call rWSME as residues (r) are the folding units and for easy reference, can be calculated using the combinatorial expression ${}_{N+1}{}^{2}C+2{}_{N+1}{}^{4}C$. This gives an upper limit on the number of microstates, since microstates defined by DSAw/L depend on the interaction across the structured islands if and only if they are present in the folded structure. While this approach reduces the number of microstates drastically (compared to the 2^N states), it has been successful in predicting the folding mechanism of the Villin head-piece domain in quantitative agreement with experiments and all-atom MD simulations (Henry et al., 2013). A similar model but with more detailed energetics (van der Waals interactions, electrostatics, implicit solvation and excess conformational entropy) has been instrumental in providing a detailed description of folding pathway heterogeneity in five different proteins in quantitative agreement with ensemble and single-molecule data (Gopi et al., 2017).

Despite these obvious advantages, one downside is the size limitation of this method. For example, the maximum number of microstates for a 300 or 400 residue protein (as in multi-domain proteins) from the ensemble description involving rWSME is >670.5 million and >2.1 billion, respectively, making it computationally intensive (Fig. 1C). In this work, we circumvent the apparent size-limitation by introducing an approximation to reduce the accessible phase space – called the bWSME model with ‘b’ for block – by grouping residues into blocks (for example, see Fig. 1B and Supporting Figure S1). We show that this approximation works as well as the original approach providing a detailed view of conformational landscapes of large proteins in quantitative agreement with experiments.

2. Methods

2.1. The bWSME model

The bWSME model considers short stretches of 2, 3, 4 or 5 residues folding together and acting as a single unit. The blocks are constructed in such a way to ensure that they do not span two different secondary-structure descriptions as identified by STRIDE (Heinig and Frishman, 2004). When we say a block size consideration for a given protein is, say 3, it means that the majority of the blocks in the protein will have a length of 3. There will be exceptions specifically when the length of a specific secondary structural region is not a multiple of 3 or if there is only one residue identified as a coil but bridging two secondary structure elements. In such cases, the block will span just 2 residues or even 1 residue. The effective free energy of the microstate with a folded structure between and involving blocks p and q (p, q) can be calculated as follows,

$$\Delta G_{p,q}=\Delta G_{p,q}^{stab}-T\sum _{i=p}^q\Delta S_i^{conf}$$

To retain the residue-level information and provide a physically reasonable energetic description in the bWSME model variant, the stabilization free energy for the microstate (p, q) is written as,

$$\Delta G_{p,q}^{stab}=\sum _{i=p}^q\sum _{j\ge i}^q\sum _{k=L\left(i\right)}\sum _{\left[l=L\left(j\right)\right]>k}\Delta G_{k,l}^{stab}$$

where L is the set of residues comprising the protein, L(i) and L(j) represents the set of constituent residues of block i and j, respectively. Note that the above expression accounts for the stabilization free energy due to the interaction between residues within the same block. The stabilization free energy includes contributions from mean-field van der Waals interaction term (E_vdW; a uniform interaction energy $\xi$ for the vdW contacts identified using a Gō-like approach), all-to-all electrostatics without a distance cut-off modeled using the Debye-Hückel formalism (E_Elec) and an implicit solvation term (ΔG_Solv, calculated as the heat capacity change per native contact $\text{Δ}{C}_p^{cont}$) (Naganathan, 2012, Naganathan, 2013b).

The entropic cost associated with the microstate (p, q) is given as,

$$\Delta S_{p,q}^{conf}=\sum _{i=p}^q\sum _{j=L\left(i\right)}\Delta S_j^{conf}$$

here, $\text{Δ}{S}_j^{conf}$ is the entropic cost associated with fixing residue j in the native conformation, L(i) represents the set of residues within block i. An excess entropic penalty (ΔΔS = −6.1 J mol⁻¹ K⁻¹ per residue) is additionally assigned to residues identified as coil by STRIDE and glycine residues. Proline, which exhibits limited flexibility, is assigned an entropic cost of 0 J mol⁻¹ K⁻¹ per residue (Daquino et al., 1996).

2.2. Partition function and predicting experimental observables

The total partition function (Z) is calculated as the sum of statistical weights associated with the microstates defined within the model framework,

$$Z=\sum _{i=1}^{\mu }\text{exp}\left(-{\text{ΔG}}_{\text{i}}/RT\right)$$

here, μ is the total number of microstates, ΔG_i is the effective free energy of the microstate i, R is the gas constant and T is temperature. Heat capacity profiles can be directly calculated through derivatives of total partition function as a function of temperature:

$$C_P\cong C_V=2RT\left(\frac{d\ln Z}{dT}\right)+R{T}^2\left(\frac{d^2\ln Z}{d{T}^2}\right)$$

The folding probability of residue i (${\chi }_i$) is calculated by algorithmically accumulating the statistical weights of microstates in which residue i is folded,

$${\chi }_i=Z^{-1}\sum _k\text{exp}\left(-\text{Δ}{G}_k/RT\right)$$

Here, ΔG_k is the effective free energy of microstate k, and k runs over all the microstates with residue i folded. The mean residue folding probability (${\langle {\chi }_i\rangle }_T$) as a function of temperature can serve as a proxy for global unfolding curve, say as monitored by far-UV CD or fluorescence experiments. One-dimensional free energy profiles and two-dimensional free energy surfaces are constructed by appropriately summing up the statistical weights of the microstates as a function of the number of structured blocks, either globally or in a specific part of the structure.

In the current work, heavy-atom contacts are identified using a 6 Å distance cut-off excluding the nearest neighbors, and charges are assigned based on the protonation state at pH 7. The value of dielectric constant in the Debye-Hückel formalism is fixed to 29 derived from our previous works involving comparison of unfolding curves of homologous proteins and mutations involving charged residues (Naganathan, 2012, Naganathan, 2013b). The model is independently parameterized for RNase H (1F21), IκBα (1NFI; with contact map correction similar to a previous work (Sivanandan and Naganathan, 2013)) and Maltose-Binding protein (MBP; 1OMP) to reproduce the experimental thermal unfolding profiles (Table S1). 1D free-energy profiles and 2D free-energy surfaces are constructed at 298 K, unless otherwise mentioned.

3. Results and discussion

3.1. Free-energy profiles and intermediates are insensitive to block definition

We validate the bWSME predictions using the 213-residue repeat protein IκBα as a model system (Fig. 2A), the folding and dynamics of which is driven by a combination of order and disorder (Lamboy et al., 2011, Lamboy et al., 2013). For this protein, the number of possible microstates is >169 million from the rWSME while it reduces to just >900,000 by the bWSME treatment and on considering a block-size of 4 (Figure S1). As a first step, we adjust the model parameters to simultaneously reproduce the excess heat capacity curve and the unfolding pre-transition seen in experiments (Ferreiro et al., 2007) (Fig. 2B, C) by eliminating the non-local contacts (but maintaining local contacts) involving the 5^th and 6^th repeats as described before (Sivanandan and Naganathan, 2013). The effective entropic penalty is estimated to be −14.5 J mol⁻¹ K⁻¹ per residue, which is of the same order expected from size-scaling arguments on large proteins (−16.5 J mol⁻¹ K⁻¹ per residue). Moreover, the van der Waals interaction energy is estimated to be −58.6 J mol⁻¹ per atom-level contact within 6 Å, which is very similar to the expectation from atomic-level force–field parameters (−46.1 J mol⁻¹ interaction energy for two carbon atoms separated by 6 Å; Table S1).

Fig. 2.

Conformational landscape of IκBα. (A) The holo-structure of the six-repeat α-helical protein IκBα. (B) The experimental excess heat capacity (blue) used for calibrating the model parameters together with the fit (red). (C) The average probability of finding a helical residue folded as a function of temperature with a 16% ‘pre-transition’ amplitude as observed in far-UV CD experiments. (D) Fraction of amide exchanged correlates well with the folded fraction within individual repeats. The numbers within the figure represent the repeat identity. (E) One-dimensional free energy profiles for various block definitions. Two slightly different block definitions of length 4 (green and red) were also studied. (F) The folded probability as a function of residue index for different states as observed from the free-energy profile in panel E. Solid lines represent the residue probabilities while the bWSME model predicted block probabilities are shown in the shaded regions.

The bWSME is able to capture the fraction of amide exchanged (averaged over all residues in a specific repeat) employing the mean residue unfolding probability per repeat as a proxy (Fig. 2D). The predicted 1D free energy profiles are characterized by multiple intermediates and partially structured states with the fully folded native state never populated. This can be seen from the fact that the minimum of the free energy profile occurs at a reaction coordinate value of 0.6 that corresponds to just ~128 folded residues (213*0.6, Fig. 2E). Importantly, the basic features of the free energy profiles and the nature of the intermediates are relatively insensitive to the block definition (Fig. 2E, F). On comparison, it is clear that the native ensemble is defined by structure only in the first four repeats with a state N' representing a conformation in which the 5th repeat is also folded. The free energy profiles however appear slightly smoother in the block definitions, which is in agreement with the expectation from block averaging that further coarse-grains the landscape. The overall picture suggests a complex native ensemble that is intimately determined by disorder in the 5^th and 6^th repeats. Our results are therefore consistent not only with experiments (Lamboy et al., 2011) but also with the previous attempts at reproducing the conformational landscape using the WSME model with 2²¹³ microstates (Sivanandan and Naganathan, 2013).

Similarly, the basic energetics of the model was parameterized by using the thermal unfolding curve of RNase H, a globular enzyme of 152 residues (Fig. 3A, B, Figure S1). The number of microstates as per the rWSME model is >43 million that reduces to just >200,000 for the bWSME variant (block size = 4; Table S1). The predicted free energy profile with and without block definition are in agreement with each other (Fig. 3C) and with the WMSE model that accounts for 2¹⁵² microstates (Narayan and Naganathan, 2014). The identity of the predicted intermediates is also in agreement between the two block definitions (Fig. 3D). HX-MS experiments point to a likely folding mechanism wherein the helices A/D form first, followed by helix BC and strand 4, and then finally the strands 1/2/3/5 and helix E (Hu et al., 2013). The bWSME model predicts a mechanism with the helices BC and D forming first (residues 70–110, intermediate I₁), followed by helix A (residues 42–56, I₂) and strands 4/5 (residues 61–67, 112–118, I₂), strands 1/2/3 (residues 1–40, I₃) and finally helix E (residues 126–140) (Fig. 3D, Figure S2). The differences in the nature of the initial nucleating event between the two approaches (experiments and bWSME model) likely originates from the intrinsic secondary structure propensity of helix A (Narayan and Naganathan, 2014), which is not captured in the current model. The late intermediate I₃ is identical to the high free-energy excited state observed in independent HX experiments (Chamberlain et al., 1996). Effectively, the agreement of the block model predictions with experiments and the internal consistency with both the rWSME and the WSME model with 2^N states strongly support our reduced approach that maximizes the information with a fewer number of microstates but without losing the strong underlying physical basis.

Fig. 3.

Predicted folding mechanism of RNase H. (A) Structure of the 152-residue RNase H. (B) Experimental fraction folded (blue) used to calibrate the model parameters and the resulting fit (red). (C) Predicted one-dimensional free-energy profile as a function of reaction coordinate, the fraction of structured residues or blocks. (D) The identity of intermediates extracted from the rWSME (lines) and bWSME (shaded regions).

3.2. Conformational landscape of maltose binding protein

To further explore the applicability of the model, we study the folding of Maltose Binding Protein (MBP), a mixed α/β protein with a complex topology comprising 370 residues (Fig. 4A, S1). Single-molecule force spectroscopy experiments indicate that MBP unfolds via an intermediate but through two parallel paths (Aggarwal et al., 2011). It is challenging to employ the rWSME model for this protein given that this would involve algorithmically accumulating the statistical weights of >1.5 billion microstates. However, the block approximation (block size = 4, 104 sequential blocks) makes this problem more amenable by reducing the number of microstates to just over 9.5 million (Table S1). We reproduce the excess heat capacity profile of MBP to calibrate the model parameters that determine the unfolding sharpness (entropic penalty per residue), melting temperature (van der Waals interaction energy per contact) and the higher unfolding heat capacity (heat capacity change on forming a native contact) (Fig. 4B).

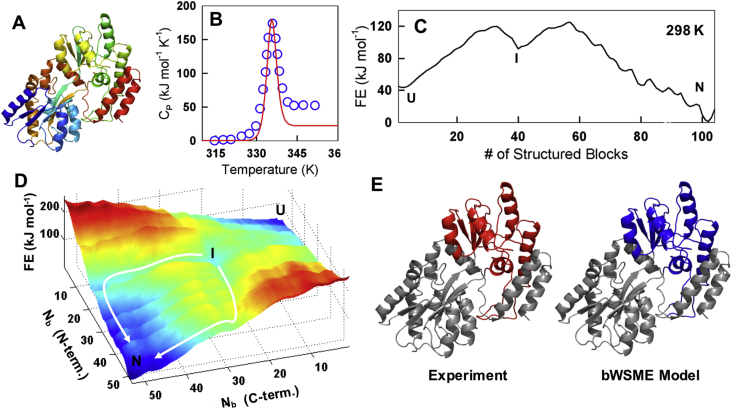
Fig. 4.

Intermediates and parallel folding paths in MBP conformational landscape. (A) Structure of the 370-residue multi-domain MBP. (B) The experimental excess heat capacity curve (blue) and the bWSME model fit (red). The fit was primarily employed to estimate the thermodynamic cooperativity in the system. (C) The one-dimensional free-energy profile as a function of the number of structured blocks highlighting an intermediate-like state (I). (D) A free-energy surface generated by partitioning the structure into two equal halves involving 52 blocks in the N- and C-termini, respectively. The arrows highlight the two likely folding paths from the intermediate. (E) The identity of the folded regions in the intermediate as obtained from the bWSME model prediction (blue) compared against the experiments (red). The gray regions represent unfolded regions.

The resulting one-dimensional free-energy profile highlights a single intermediate at ~40 structured blocks following which a downhill gradient is seen towards the native state (Fig. 4C). A structural view of the intermediate can be obtained from a three-dimensional free energy surface with the number of structured blocks at the N- and C-termini as the x- and y-coordinates (52 blocks each) - it represents to a structure with 23 and 19 structured blocks at the C- and N-terminus, respectively (Fig. 4D). In terms of the residue level information, this corresponds to a fully folded C-terminal domain (residues 114–257 or blocks 34–74 based on the MBP domain definition) in exact agreement with single-molecule experiments (Fig. 4E) (Aggarwal et al., 2011). In other words, the bWSME model predicts a folding mechanism in which C-terminal domain of MBP forms first (Figure S3), following which two parallel paths can be populated. In one macroscopic high free-energy path, the entire N-terminal region of the protein forms (including the residues constituting the N-terminal domain, residues 1–113 or blocks 1–33), following which the terminal helices (residues 286–370 or blocks 82–104) fold. In a second but low free-energy path, the terminal helices form first and then mechanically weak N-terminal domain folds in a gradual manner contributing to the shallow gradient towards the folded state in the 1D free energy profile. The exact reverse sequence of events is observed in the single-molecule force spectroscopy unfolding experiments (Aggarwal et al., 2011) highlighting the advantages of bWSME method for large proteins. We would like to emphasize that the surface representations and free-energy profiles provide only the most probable macroscopic folding paths and not the microscopic residue- or block-level routes that could be more complex, as previously shown for several small single-domain proteins (Gopi et al., 2017).

4. Conclusions

We develop and validate a simplified version of the WSME model by switching the fundamental conformational units from residues to blocks that can be 2 to 5 residues in length. This re-formatting reduces the combinations drastically and therefore the number of conformational states by nearly three orders of magnitude. The model, termed the block WSME method or bWSME, can be employed as a predictive tool in the same vein as the original version developed by Wako and Saitô or in the sequence approximations of Muñoz and Eaton. The fewer number of microstates enables the generation of conformational landscapes of large proteins (~300–400 residues in length) without compromising on the predictive ability or the physical underpinnings. The bWSME model does not assume any folding mechanism and allows for stabilization of conformations via both local and non-local interactions. Therefore, it can be employed as a first step to probe regions of protein that are thermodynamically less (more) stable contributing to unfolding (folding) and in identifying the number and nature of macroscopic folding paths.

One of the limitations of block approximation is that the populations of the partially structured states (for example, Fig. 2, Fig. 3C) can vary slightly depending on the block approximation employed. Second, many large proteins unfold irreversibly on temperature changes that cannot be captured by the current model. Therefore, it is challenging to obtain a perfect agreement between experimental and predicted unfolding curve (for example, see Fig. 2, Fig. 3, Fig. 4B). The fitting procedures should therefore be seen as avenues to capture the overall sharpness or cooperativity of the unfolding transition. Third, while the model currently incorporates contributions from van der Waals interactions, electrostatics, and implicit solvation, it does not include intrinsic conformational preferences of amino acids to be in specific secondary structure elements, a feature that can be incorporated in future versions. Despite these, we expect the bWSME model to be successful in not only exploring conformational landscapes but also to quantify the effect of mutations in large multi-domain proteins that frequently underlie many diseases. It should also be possible to capture the effect of DNA, RNA or even ligand binding on the conformational landscapes of larger proteins by extending a recently developed protocol that maps the protein-ligand interactions on to the protein (Munshi et al., 2018b). Similarly, post-translational modifications, particularly those that introduce or remove charges can be introduced in a straightforward manner as before (Gopi et al., 2015). The bWSME model thus stands on the cusp of addressing and exploring numerous questions on the conformational behavior of large proteins.

Funding

This work was supported by the grant BT/PR26099/BID/7/811/2017 to A. N. N. from the Department of Biotechnology, Ministry of Science and Technology, India.

Appendix A. Supplementary data

The following is the Supplementary data to this article: