A Bayesian multivariate mixture model for skewed longitudinal data with intermittent missing observations: An application to infant motor development

Abstract

In studies of infant growth, an important research goal is to identify latent clusters of infants with delayed motor development—a risk factor for adverse outcomes later in life. However, there are numerous statistical challenges in modeling motor development: the data are typically skewed, exhibit intermittent missingness, and are correlated across repeated measurements over time. Using data from the Nurture study, a cohort of approximately 600 mother-infant pairs, we develop a flexible Bayesian mixture model for the analysis of infant motor development. First, we model developmental trajectories using matrix skew-normal distributions with cluster-specific parameters to accommodate dependence and skewness in the data. Second, we model the cluster-membership probabilities using a Pólya-Gamma data-augmentation scheme, which improves predictions of the cluster-membership allocations. Lastly, we impute missing responses from conditional multivariate skew-normal distributions. Bayesian inference is achieved through straightforward Gibbs sampling. Through simulation studies, we show that the proposed model yields improved inferences over models that ignore skewness or adopt conventional imputation methods. We applied the model to the Nurture data and identified two distinct developmental clusters, as well as detrimental effects of food insecurity on motor development. These findings can aid investigators in targeting interventions during this critical early-life developmental window.

1 ∣. INTRODUCTION

Infant motor development is an important predictor of health later in life. Early motor development is associated with improved physical activity, cognitive function, and educational attainment (Taanila et al., 2005; Aaltonen et al., 2015), while delayed development is associated with increased sedentary time (Sánchez et al., 2017) and has been linked to adult cognitive disorders such as schizophrenia (Filatova et al., 2017). Thus, there is growing interest in identifying developmental patterns that may place infants at risk for long-term adverse health outcomes. One approach to tackling this problem is to identify underlying subgroups of infants with delayed motor development, and to isolate important predictors of subgroup membership. Our goal, therefore, is to introduce a flexible latent growth mixture model to detect high-risk developmental patterns and associated risk factors.

Our work is motivated by the Nurture study, a birth cohort of predominately black women and their infants residing in the southeast United States (Benjamin Neelon et al., 2017). The aim of the study was to examine how infant feeding, physical activity, motor development, sleep, and stress contribute to infant weight gain. The second aim was to identify infant subpopulations that exhibit unique motor development trajectories, and to examine cluster-specific associations between household food security and motor development.

The Nurture data pose several statistical challenges. First, the repeated outcomes are correlated across measurement occasions, and the pairwise correlations vary across timepoints, suggesting the need for a flexible error term covariance structure. Second, the development outcomes are skewed, with the direction of skewness varying over time. The Nurture data also feature intermittent missingness. Thus, we require a framework capable of addressing potentially nonignorable missing data. Finally, we seek to develop a model that incorporates covariate information into both the multivariate regression model of infant development trajectories and the clustering model.

To address these challenges, we propose a Bayesian multivariate mixture model for the analysis of longitudinal skewed infant motor development data with intermittent missing observations. Our approach builds on recent work on mixture models for skewed cross-sectional data. Frühwirth-Schnatter and Pyne (2010) proposed a multivariate skew-normal (MSN) model for high-dimensional flow cytometric data. However, their focus was on marginal inference (ie, density estimation) rather than cluster-specific inferences, as is our focus here. More recently, Lin et al. (2018) proposed a mixture of skew-t factor analyzers for settings in which cluster-specific inference is of primary interest (Lin et al., 2018). However, like Frühwirth-Schnatter and Pyne (2010), their approach excluded covariates in the cluster-membership model, a focal point in our study as we expect demographics to not only play a key role in predicting cluster membership, but also help characterize developmental trajectories within clusters. Additionally, their approach, while quite flexible, relied on a computationally elaborate expectation-conditional maximization algorithm that does not enjoy the inferential benefits of a Bayesian approach. Finally, the authors adopted a single-imputation scheme for ignorable missing data that does not readily account for the uncertainty in the imputation process without additional multiple imputation steps.

Our proposed model extends these prior studies in a number of ways. First, our model enables cluster-specific inferences for longitudinal growth trajectories, while accommodating skewness patterns that may vary over time and across clusters. Second, our model accommodates both time-dependent and time-invariant covariate designs. Third, we estimate parameters in a Bayesian framework that introduces covariates into the cluster-membership model using a novel application of Pólya-Gamma data augmentation (Polson et al., 2013). Fourth, we accommodate intermittent missingness of longitudinal responses under a “conditional ignorability” assumption, whereby the missing data mechanism is assumed to be ignorable conditional on cluster assignment. Marginally, we allow for dependence between the missing data mechanism and the missing responses, thus relaxing standard missing at random (MAR) assumptions. We develop a Markov chain Monte Carlo (MCMC) embedded imputation procedure in which missing observations are updated at each MCMC iteration conditional on cluster allocation. Finally, we propose a Bayesian modeling approach that makes use of convenient matrix skew-normal and skew-t representations. Our model is appropriate for settings where interest lies in identifying clusters in longitudinal data with complex features, such as skewness, heavy tails, and intermittent missing responses that are potentially missing not at random.

2 ∣. NURTURE STUDY

The Nurture study is a birth cohort of predominately black women and their infants residing in the southeastern United States from 2013 and 2017 (Benjamin Neelon et al., 2017). The study followed mothers and infants for 12 months after birth and collected data on infant gross motor development and household food security, among other measures. Infant development was assessed quarterly at 3, 6, 9, and 12 months of age using the Bayley composite scale of motor development (Bayley, 2006), a standard measure of infant development ranging from 40 to 160, with higher scores indicating more advanced development compared to normally developing infants. Household food security was assessed using the 18-item US Household Food Security Survey Module restricted to the 10 items related to household food security measured during pregnancy (USDA, 2019). Following standard protocol, a final dichotomous food security exposure was defined as “food insecure” households and “food secure” households. The Institutional Review Board of Duke University Medical Center approved this study and protocol.

Of the 666 infants who were consented into the study, 106 were missing Bayley score measurements at all timepoints, 68 infants were missing Bayley scores at three timepoints, 72 infants were missing Bayley scores at two timepoints, 123 were missing Bayley scores at one time-point, and 297 were not missing any Bayley scores. We restricted our analytic sample to the 560 remaining infants who had at least one nonmissing Bayley score over the study period. Of the 560 × 4 = 2240 possible observations, 471 (21%) were missing, leaving an available-case sample size of 1769. Sample characteristics for the 560 participants are given in Web Table 1. In the sample, 68% of infants were black and 39% of households identified as food insecure during pregnancy. The Bayley motor development scores ranged from 49.0 to 145.0 across visits, with a mean of 102.4 and standard deviation (SD) of 13.5.

Figure 1 presents trajectory plots of the motor development scores for each infant in the available-case sample, with an overlay of the mean score at each visit. The plot indicates substantial heterogeneity in the trajectories. To quantify the mean trend, we fit a repeated-measures model of the form: Y_i = X_iβ + e_i, where X_i includes an intercept, a linear time trend and effects for gender, race, and baseline food security status; and e_i is a multivariate normal error term with unstructured covariance pattern. The restricted maximum likelihood estimate of the linear trend coefficient was −1.16 (CI = [−1.29, −1.03]), suggesting an average decline in motor development over time in the Nurture cohort relative to normally developing infants. However, because most of the literature on infant motor development has focused on the average effect over time (Shoaibi et al., 2019), little is known about trends for specific subgroups of interest—for example, among infants who may be at high risk for delayed motor milestone achievement. Importantly, these subgroups may not be obvious from marginal trajectory plots such as Figure 1 and may only become evident through appropriate modeling of germane features of the data such as skewness, missingness, and explanatory covariates, among other factors. In this paper, we present methods for uncovering latent subgroups by modeling these important features of the data.

FIGURE 1.

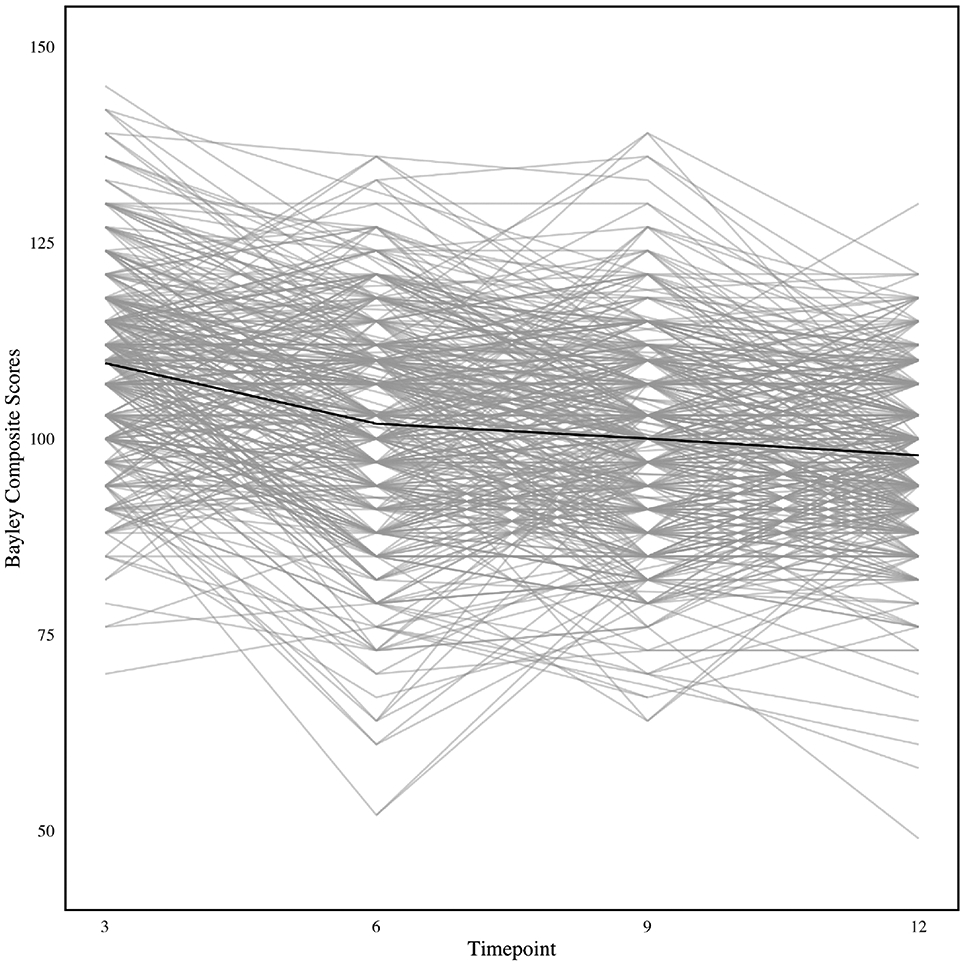
Longitudinal profile plot of infant development trajectories, with mean Bayley motor development score shown in black Note. Plot is based on the N = 1769 available measurements for n = 560 infants

Figure 2 presents centered and scaled residual densities from the repeated-measures model used in Figure 1. The residuals were subset by visit to yield visit-specific residual density plots. As shown in Figure 2, the residuals are skewed at each visit, particularly at 3 and 6 months, with the direction of skewness varying over time. Shapiro-Wilk tests accounting for multiple testing rejected the null hypothesis of normality at 6 months, contravening standard assumptions. While there is a modest indication of skewness in the available-case sample, it is not clear how skewness patterns vary across latent subgroups of infants, or how missing observations impact skewness. We seek to answer these questions in subsequent analyses.

FIGURE 2.

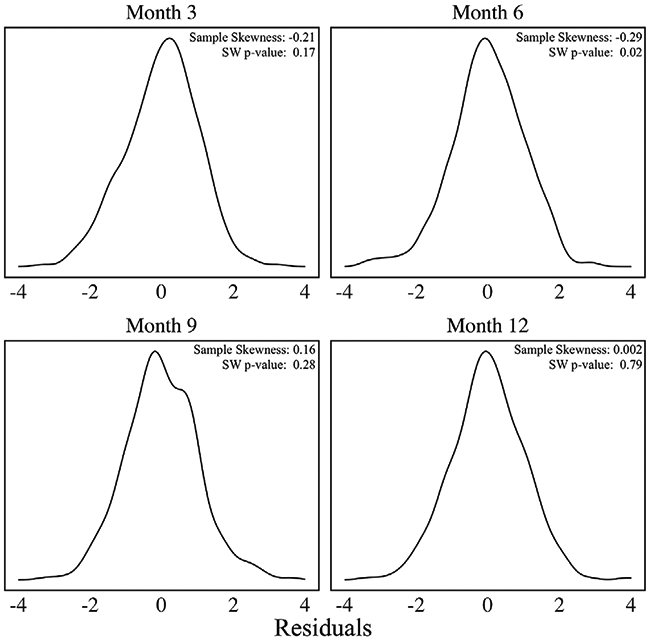
Scaled residual plots at each visit based on a repeated-measures linear regression model with Bayley score as the outcome Note. Sample skewness statistics and P-values from Shapiro-Wilk (SW) tests are provided in the legends. Plots are based on the N = 1769 available measurements for n = 560 infants

Additionally, the motor development scores are correlated over time, with pairwise correlations ranging in an unstructured pattern. As an illustration, we fit three repeated-measures models of the form used in Figure 1, but with varying correlation structures for the errors: AR1, compound symmetric and unstructured. The AIC values for these models were 27 599, 27 517, and 27 478, respectively, indicating best fit under the unstructured pattern among the patterns considered. We present the estimated correlation matrix from this model in Web Table 2. Finally, the Nurture data feature intermittent missing data, with approximately one third of the sample missing observations at any given visit (Web Table 1). While it may be reasonable to assume that the missing data are MAR, as we have no a priori reason to believe that the occurrence of missing observations is directly related to missing Bayley scores, we relax this assumption below by assuming ignorable missingness conditional on latent motor development cluster assignment.

3 ∣. MODEL

In Section 3, we develop a model that accounts for the important features of the Nurture data described in Section 2. Section 3.1 begins with developing a finite mixture model and proposes a MSN regression framework for within-cluster inference. Section 3.2 proposes a multinomial regression model for cluster probabilities that utilizes Pólya-Gamma data augmentation for efficient Gibbs sampling. Section 3.3 discusses extensions to the multivariate skew-t (MST) setting, and Section 3.4 proposes a missing data imputation scheme under the assumption of conditional ignorability.

3.1 ∣. Multivariate skew-normal mixture model

We propose a finite mixture model that accommodates relevant features of the data, namely skewness, missing values, and dependence among the responses. While alternative mixture models (eg, Dirichlet process mixtures) provide flexibility for marginal inferences and density estimation, finite mixtures are appealing when the focus is on practical within-cluster inferences. In such cases, the primary goal is to identify a small number of clinically relevant clusters to help design targeted interventions to improve health outcomes. However, to avoid misspecifying the number of finite mixtures, it is imperative to properly model the within-cluster distributions by accounting for important features, such as skewness or heavy tails. With this goal in mind, we present a repeated-measures regression model based on a MSN distribution—and by extension, a MST distribution—in which the Bayley scores across the J measurement occasions represent correlated responses. Specifically, let y_i = (y_i1, … , y_iJ)^T be a J × 1 vector of standardized Bayley scores for subject i (i = 1, … , n). We propose a mixture model of the form

$$f({\mathbf{y}}_i)=\sum _{k=1}^K{\pi }_{ki}f({\mathbf{y}}_i\mid {\theta }_k),$$ (1)

where θ_k is the set of parameters specific to cluster k (k = 1, … , K) and π_ki is a subject-specific mixing weight representing the probability that subject i belongs to cluster k. For now we assume that K is fixed; we discuss model-selection strategies for choosing the optimal value of K in Section 3.5.2.

For posterior inference, we introduce a latent cluster indicator variable z_i taking the value k ∈ {1, … , K} with probability π_ki. Given z_i = k, we assume y_i is distributed according to a J-dimensional MSN density (Azzalini and Valle, 1996)

$$\begin{gathered} {\mathbf{y}}_i\mid (z_i=k)\sim {\text{MSN}}_J({\zeta }_{ki},{\alpha }_k,{\Omega }_k),\text{with density} \\ f({\mathbf{y}}_i\mid z_i=k)=2{\varphi }_J({\mathbf{y}}_i;{\zeta }_{ki},{\Omega }_k)\Phi \{{\alpha }_k^T({\mathbf{y}}_i-{\zeta }_{ki})\}, \end{gathered}$$ (2)

where ϕ_J(y_i; ζ_ki, Ω_k) denotes a J-dimensional normal density with mean ζ_ki and covariance matrix Ω_k; Φ(·) is the CDF of a scalar standard normal random variable; ζ_ki is a J × 1 vector of subject- and cluster-specific location parameters; α_k is a J × 1 vector of cluster-specific parameters that control the skewness of each outcome in cluster k; and Ω_k is a J × J cluster-specific scale matrix that captures dependence among the J responses for subject i. When α_k = 0, the MSN distribution reduces to the multivariate normal (MVN) distribution N_J(ζ_ki, Ω_k), where ζ_ki represents a J × 1 mean vector and Ω_k is a J × J unstructured covariance matrix.

We complete model (2) by incorporating covariates into ζ_ki. We first discuss the general case in which the model includes both time-varying and time-invariant predictors; later, we present simplifications when only time-invariant covariates are included in the model. Here, we adopt a convenient conditional representation of the MSN density (Azzalini and Valle, 1996; Frühwirth-Schnatter and Pyne, 2010):

$${\mathbf{y}}_i\mid (z_i=k,t_i)={\mathbf{X}}_i{\beta }_k+t_i{\psi }_k+{ϵ}_i,$$ (3)

where X_i is a J × Jp design matrix that includes potential time-dependent covariates; β_k = (β_k11, … , β_k1p, … , β_kJ1, … , β_kJp)^T is a Jp × 1 vector of cluster- and outcome-specific regression coefficients; t_i ~ N_[0,∞)(0,1) is a subject-specific standard normal random variable truncated below by zero; ψ_k = (ψ_k1, … , ψ_kJ)^T is a J × 1 vector of cluster-specific parameters that control skewness; and ϵ_i∣(z_i = k) ~ N_J(0, ∑_k) is a J × 1 vector of correlated error terms. Thus, conditional on t_i and z_i = k, y_i is distributed as N_J(X_iβ_k + t_iψ_k, ∑_k). Marginally (integrated over t_i), y_i∣(z_i = k) is distributed MSN_J(ζ_ki, α_k, Ω_k), where through back-transformation the parameters ζ_ki, Ω_k, and α_k can be obtained as described in Web Appendix B.

As detailed in Web Appendix B, conjugate full conditionals are available for all parameters in model (3), leading to straightforward Gibbs sampling when both time-varying and time-invariant covariates are included in the model. However, the Nurture analysis described in Section 5 involves no time-varying covariates, only time-varying covariate effects. In such cases, we can express the MSN density more compactly using a matrix skew-normal (MatSN) representation. Structuring the data in this way greatly facilitates posterior computation by permitting low-dimensional matrix updates for the regression coefficients. For cluster k, let Y_k be an n_k × J matrix with rows ${\mathbf{y}}_i^T$ for i = 1, … , n_k, where n_k is the number of subjects in cluster k. From Equation (2), it follows that Y_k is distributed as

$${\mathbf{Y}}_k\mid {\mathbf{B}}_k,{\alpha }_k,{\Omega }_k\sim {\text{MatSN}}_{n_k\times J}({\mathbf{X}}_k{\mathbf{B}}_k,{\alpha }_k,{\mathbf{I}}_{n_k},{\Omega }_k),$$ (4)

where I_nk is the n_k × n_k identity matrix, and X_k and B_k are, respectively, n_k × p and p × J matrices described in Web Appendix B.

If we set x_i1 = 1 for all i, then the first row of B_k, (β_k11, … , β_k1J), represents time-specific intercepts that capture the time trend for the reference covariate group in cluster k. Adapting Equation (7) from Chen and Gupta (2005), the density function for Y_k is

$$\begin{gathered} f({\mathbf{Y}}_k\mid {\mathbf{B}}_k,{\alpha }_k,{\Omega }_k) \\ =2^{n_k}{\varphi }_{n_k\times J}({\mathbf{Y}}_k;{\mathbf{X}}_k{\mathbf{B}}_k,{\mathbf{I}}_{n_k},{\Omega }_k){\Phi }_{n_k}\{({\mathbf{Y}}_k-{\mathbf{X}}_k{\mathbf{B}}_k){\alpha }_k\}, \end{gathered}$$ (5)

where ϕ_nk×J(Y_k; X_kB_k, I_nk, Ω_k) is the density function for a matrix normal (MatNorm) random variable of dimension n_k × J with mean X_kB_k and scale matrices I_nk and Ω_k, and Φ_nk (·) denotes the CDF of an n_k-dimensional standard MVN random variable.

Further, let t_k = (t₁, … , t_nk)^T denote the n_k × 1 vector of latent variables for cluster k. By extending Equation (3), it follows that the conditional distribution of Y_k given t_k is

$${\mathbf{Y}}_k\mid {\mathbf{t}}_k\sim {\text{MatNorm}}_{n_k\times J}({\mathbf{X}}_k^{\ast }{\mathbf{B}}_k^{\ast },{\mathbf{I}}_{n_k},{\Sigma }_k),$$ (6)

where ${\mathbf{X}}_k^{\ast }$ is an n_k × (p + 1) augmented design matrix formed by right column-binding t_k to X_k, ${\mathbf{B}}_k^{\ast }$ is a (p + 1) × J matrix of regression coefficients formed by lower row-binding ψ_k = (ψ₁, … , ψ_J)^T to B_k, and ∑_k is the J × J covariance of ϵ_i in Equation (3). Updating both ψ_k and B_k simultaneously using the augmented matrix ${\mathbf{B}}_k^{\ast }$ simplifies the MCMC sampler and is equivalent to separate updates of ψ_k and B_k when ψ_k and B_k are uncorrelated. This matrix normal representation admits conditionally conjugate prior distributions, which in turn leads to efficient Gibbs sampling for posterior inference. We formalize this in the following proposition, which establishes the conditional conjugacy of ${\mathbf{B}}_k^{\ast }$ and ∑_k.

Proposition 1. Let ${\mathbf{B}}_k^{\ast }$ and ∑_k in Equation (6) have a joint matrix normal-inverse Wishart (IW) prior, denoted $MatNorm\text{-}I{W}_{(p+1)\times J}({\mathbf{B}}_{0k}^{\ast },{\mathbf{L}}_{0k},v_{0k},{\mathbf{V}}_{0k})$, of the form

$$\begin{gathered} \pi ({\mathbf{B}}_k^{\ast },{\Sigma }_k)=\pi ({\mathbf{B}}_k^{\ast }\mid {\Sigma }_k)\pi ({\Sigma }_k)\Rightarrow ({\mathbf{B}}_k^{\ast },{\Sigma }_k)\mid ({\mathbf{B}}_{0k}^{\ast },{\mathbf{L}}_{0k},v_{0k},{\mathbf{V}}_{0k}) \\ \sim MatNor{m}_{(p+1)\times J}({\mathbf{B}}_{0k}^{\ast },{\mathbf{L}}_{0k},{\Sigma }_k)IW(v_{0k},{\mathbf{V}}_{0k}), \end{gathered}$$

where ${\mathbf{B}}_{0k}^{\ast }$ is a (p + 1) × J prior location matrix, L_0k and V_0k are, respectively, (p + 1) × (p + 1) and J × J prior scale matrices, and v_0k denotes the prior degrees of freedom. Then, the full conditional distribution of ${\mathbf{B}}_k^{\ast }$ is $MatNor{m}_{(p+1)\times J}({\mathbb{B}}_k^{\ast },{\mathbf{L}}_k,{\Sigma }_k)$, where

$$\begin{gathered} {\mathbb{B}}_k^{\ast }={\mathbf{L}}_k({\mathbf{L}}_{0k}^{-1}{\mathbf{B}}_{0k}^{\ast }+{\mathbf{X}}_k^{\ast T}{\mathbf{Y}}_k) \\ {\mathbf{L}}_k=({\mathbf{L}}_{0k}^{-1}+{\mathbf{X}}_k^{\ast T}{\mathbf{X}}_k^{\ast }{)}^{-1}, \end{gathered}$$

and ${\mathbf{X}}_k^{\ast }$ is the augmented covariate matrix defined in Equation (6). Likewise, the full conditional distribution of ∑_k is IW(v_k, V_k), where

$$\begin{gathered} v_k=v_0+n_k+p+1and \\ {\mathbf{V}}_k={\mathbf{V}}_{0k}+({\mathbf{B}}_k^{\ast }-{\mathbf{B}}_{0k}^{\ast }{)}^T{\mathbf{L}}_{0k}^{-1}({\mathbf{B}}_k^{\ast }-{\mathbf{B}}_{0k}^{\ast }) \\ +({\mathbf{Y}}_k-{\mathbf{X}}_k^{\ast }{\mathbf{B}}_k^{\ast }{)}^T({\mathbf{Y}}_k-{\mathbf{X}}_k^{\ast }{\mathbf{B}}_k^{\ast }). \end{gathered}$$

The proof is provided in Web Appendix A.

3.2 ∣. Pólya-Gamma multinomial regression for cluster probabilities

To accommodate heterogeneity in the cluster-membership probabilities, we model π_ki as a function of covariates using a multinomial logit model

$${\pi }_{ki}=\text{Pr}(z_i=k\mid {\mathbf{w}}_i)=\frac{{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_k}}{{\sum }_{h=1}^K{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_h}},k=1,\dots ,K,$$ (7)

where w_i is an r × 1 vector of subject-level covariates, δ_k is an r × 1 vector of cluster-specific regression parameters. For identifiability, we choose category K as reference and set δ_K = 0. To facilitate sampling, we adopt the efficient data-augmentation approach introduced by Polson et al. (2013), which expresses the inverse-logit function as a scale-normal mixture of Pólya-Gamma densities. A random variable w is said to follow a Pólya-Gamma distribution with parameters b > 0 and $c\in \mathbb{R}$ if

$$f(w\mid b,c)=\frac{1}{2{\pi }^2}\sum _{s=1}^{\infty }\frac{g_s}{(s-1∕2{)}^2+c^2∕(4{\pi }^2)},$$ (8)

where $g_s\stackrel{\text{iid}}{\sim }\text{Ga}(b,1)$ for s = 1, … , ∞. Polson et al. (2013) establish that, for a logistic regression model, the likelihood can be written as a scale-mixture of normal densities with Pólya-Gamma precision terms w, resulting in closed-form MVN full conditional distributions for logistic regression parameters. To extend the augmentation approach to the multinomial setting, we first introduce the binary indicators $U_{ki}=1_{(z_i=k)}$, where $1_{(z_i=k)}$ is the indicator function equal to 1 if (z_i = k) and 0 otherwise. The conditional distribution of δ_k, given U_k = (U_k1, … , U_kn)^T and the remaining regression coefficients δ_h≠k, is

$$\begin{gathered} p({\delta }_k\mid \mathbf{z},{\delta }_{h\ne k}) \\ =p({\delta }_k\mid {\mathbf{U}}_k,{\delta }_{h\ne k})\propto p({\delta }_k)\prod _{i=1}^n{\pi }_{ki}^{U_{ki}}(1-{\pi }_{ki}{)}^{1-U_{ki}}, \end{gathered}$$ (9)

where p(δ_k) is the prior distribution of δ_k. We rewrite π_ki as

$${\pi }_{ki}=\text{Pr}(U_{ki}=1)=\frac{{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_k}}{{\sum }_{h=1}^K{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_h}}=\frac{{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_k}}{{\sum }_{h\ne k}^K{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_h}+{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_k}},$$

where dividing throughout by ${\sum }_{h\ne k}^K{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_h}$ yields

$${\pi }_{ki}=\frac{{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_k-c_{ki}}}{1+{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_k-c_{ki}}}=\frac{{\mathrm{e}}^{{\eta }_{ki}}}{1+{\mathrm{e}}^{{\eta }_{ki}}},$$

with $c_{ki}=\log {\sum }_{h\ne k}{\mathrm{e}}^{{\mathbf{w}}_i^T{\delta }_h}$ and ${\eta }_{ki}={\mathbf{w}}_i^T{\delta }_k-c_{ki}$. We use c_ki and η_ki to reexpress Equation (9) as

$$\begin{gathered} p({\delta }_k\mid \mathbf{z},{\delta }_{h\ne k})\propto p({\delta }_k)\prod _{i=1}^n{\left(\frac{{\mathrm{e}}^{{\eta }_{ki}}}{1+{\mathrm{e}}^{{\eta }_{ki}}}\right)}^{U_{ki}}{\left(\frac{1}{1+{\mathrm{e}}^{{\eta }_{ki}}}\right)}^{1-U_{ki}} \\ =p({\delta }_k)\prod _{i=1}^n\frac{({\mathrm{e}}^{{\eta }_{ki}}{)}^{U_{ki}}}{1+{\mathrm{e}}^{{\eta }_{ki}}}, \end{gathered}$$ (10)

where the product term denotes the likelihood from a logistic regression model. We can therefore apply the Pólya-Gamma sampler for logistic regression to update each δ_k one at a time based on the binary indicators U_ki. First, we define for k = 1, … , K, the n × 1 vector ${\mathbf{U}}_k^{\ast }={\left(\frac{U_{k1}-1∕2}{w_{k1}}+c_{k1},\dots ,\frac{U_{kn}-1∕2}{w_{kn}}+c_{kn}\right)}^T$. As shown in Web Appendix B, the conditional distribution of ${\mathbf{U}}_k^{\ast }$ given w = (w_k1, … , w_kn)^T is ${\mathrm{N}}_n(\mathbf{W}{\delta }_k,{\mathbf{O}}_k^{-1})$, where O_k = Diag(w_k1, … , w_kn) and W is an n × r design matrix with rows ${\mathbf{w}}_i^T$ for i = 1, … , n. Thus, the full conditional distribution of δ_k is given by

$$\begin{gathered} p({\delta }_k\mid \mathbf{z},{\mathbf{O}}_k,{\delta }_{h\ne k}) \\ \propto p({\delta }_k)\text{exp}\left\{-\frac{1}{2}({\mathbf{U}}_k^{\ast }-\mathbf{W}{\delta }_k{)}^T{\mathbf{O}}_k({\mathbf{U}}_k^{\ast }-\mathbf{W}{\delta }_k)\right\}. \end{gathered}$$ (11)

Assuming a N_r(d_0k, S_0k) prior for δ_k allows for Gibbs sampling for the clustering model as detailed in Web Appendix B.

3.3 ∣. Extensions to multivariate skew-t distributions

To accommodate outliers and heavy tails, we extend Equation (1) by assuming, conditional on z_i = k, that y_i follows a MST distribution (Gupta, 2003):

$$\begin{gathered} {\mathbf{y}}_i\mid (z_i=k)\stackrel{ind}{\sim }{\text{MST}}_J({\zeta }_{ki},{\alpha }_k,{\Omega }_k,v_k),\text{with density} \\ f({\mathbf{y}}_i\mid z_i=k)=2f_{t_J}({\mathbf{y}}_i;{\zeta }_{ki},{\Omega }_k,v_k)T_{v_k+J} \\ \times \left\{{\alpha }_k^T({\mathbf{y}}_i-{\zeta }_{ki})\sqrt{\frac{v_k+J}{v_k+Q_{y_i}}}\right\}, \end{gathered}$$ (12)

where f_tJ(y_i; ζ_ki, Ω_k, v_k) denotes the CDF of a J-dimensional t distribution with location ζ_ki, covariance Ω_k, and fixed degrees of freedom v_k that may vary across clusters; T_vk+J denotes the distribution function of the scalar standard t distribution with v_k + J degrees of freedom; and $Q_{y_i}=({\mathbf{y}}_i-{\zeta }_{ki}{)}^T{\Omega }_k^{-1}({\mathbf{y}}_i-{\zeta }_{ki})$. As before, we adopt a conditional representation for y_i to facilitate Gibbs sampling (Frühwirth-Schnatter and Pyne, 2010). Specifically, we augment the MSN conditional representation in Equation (3) by introducing subject-specific scale terms, d_i, yielding an MST regression conditional on z_i, t_i, and d_i of the form:

$${\mathbf{y}}_i={\mathbf{X}}_i{\beta }_k+\frac{t_i}{\sqrt{d_i}}{\psi }_k+\frac{1}{\sqrt{d_i}}{ϵ}_i,$$ (13)

where d_i ~ Gamma $\left(\frac{\xi }{2},\frac{\xi }{2}\right)$, with ξ being a prespecified known degrees of freedom parameter common to all clusters, and t_i and ϵ_i are defined as in Equation (3). In principle, ξ may be prespecified but vary across clusters (becoming ξ_k), though here we a constant value across clusters for simplicity. For details on posterior inference, see Web Appendix B.

3.4 ∣. Cluster-specific imputation under conditional ignorability

To accommodate intermittent missing data, we propose a convenient MCMC-embedded imputation algorithm in which we assume that the missingness mechanism is conditionally ignorable given the cluster indicators z_i, extending recent work on latent class pattern mixture models for informative dropout (Roy, 2007). We use the term “MCMC-embedded” to denote the fact that each missing value is imputed once per MCMC iteration using current cluster-specific parameter values, allowing for convenient multiple imputation as part of the MCMC algorithm. Ensuring subjects have complete response vectors also enables us to update the regression parameters in a compact manner, as described in Web Appendix B. Here, z_i functions as a discrete shared parameter that induces unobserved association between the missingness process and the missing data. Suppose y_i has q_i ∈ (1, … , J) observed values, denoted ${\mathbf{y}}_i^{obs}$, and J − q_i intermittent missing values, denoted ${\mathbf{y}}_i^{miss}$. Let R_i = (R_i1, … , R_iJ)^T be a J × 1 vector of binary response indicators, such that R_ij = 1 if infant i has a Bayley measurement at visit j. Under conditional ignorability, the conditional distribution of R_i given (z_i, ${\mathbf{y}}_i^{obs}$, ${\mathbf{y}}_i^{miss}$) is

$$\begin{gathered} f({\mathbf{R}}_i\mid z_i=k,{\mathbf{y}}_i^{obs},{\mathbf{y}}_i^{miss},{\mathbf{X}}_i,{\gamma }_k) \\ =f({\mathbf{R}}_i\mid z_i=k,{\mathbf{y}}_i^{obs},{\mathbf{X}}_i,{\gamma }_k), \end{gathered}$$ (14)

where, in this context, X_i is a J × m design matrix and γ_k is an m × 1 vector of cluster-specific parameters related to the missing data mechanism. As detailed in Step 4 of Web Appendix B, z_i serves as a latent shared parameter that induces marginal correlation between $Y_i^{miss}$ and R_i.

Under conditional ignorability, conditioning on z_i ensures that R_i does not depend on the missing observations ${\mathbf{y}}_i^{miss}$. We can therefore impute ${\mathbf{y}}_i^{miss}$ from its conditional MVN distribution given (z_i, t_i, ${\mathbf{y}}_i^{obs}$) as described in Web Appendix B. While the complete data vector ${\mathbf{y}}_i=\{{\mathbf{y}}_i^{obs},{\mathbf{y}}_i^{miss}\}$ follows a MVN distribution conditional on t_i, after marginalizing over t_i, y_i follows a joint MSN distribution. Thus, the proposed conditional imputation procedure provides a convenient way of imputing missing MSN responses using samples from more standard densities.

Finally, given z_i = k, we independently model the J response indicators for infant i as

$$\begin{gathered} R_{ij}\mid (z_i=k,{\gamma }_k,b_{ki})\sim \text{Bern}({\varphi }_{ijk}),j=1,\dots ,J \\ \mathrm{logit}({\varphi }_{ijk})={\mathbf{x}}_{ij}^T{\gamma }_k+b_{ki}, \end{gathered}$$ (15)

where x_ij is an m × 1 vector of covariates, and γ_k is the m × 1 vector of cluster-specific regression parameters from Equation (14). We note that while the missing data regression parameters may in principle be shared across clusters, cluster-specific parameters allow investigators to identify different missing data patterns across clusters. Further, correctly modeling cluster-specific missingness mechanisms is necessary to obtain appropriate inference for cluster-specific parameters. Because the response indicators may be correlated over time, we also include a subject-level random intercept b_ki conditionally distributed as N(0, ${\sigma }_k^2$) given z_i = k. Although we assume conditional ignorability of R_i and ${\mathbf{y}}_i^{miss}$ given z_i, because the ϕ_ijk terms from model (15) appear in the full conditional update for z_i (Web Appendix B), R_i and ${\mathbf{y}}_i^{miss}$ are marginally correlated, resulting in a marginal missing not at random (MNAR) mechanism.

3.5 ∣. Bayesian inference

3.5.1 ∣. Prior specification

We adopt a Bayesian approach and assign prior distributions to all model parameters. For designs not involving time-dependent covariates, we assign a joint ${\text{MatNorm-IW}}_{(p+1)\times J}({\mathbf{B}}_{0k}^{\ast },{\mathbf{L}}_{0k},v_{0k},{\mathbf{V}}_{0k})$ to (${\mathbf{B}}_k^{\ast }$, ∑_k) as described in Proposition 1. For time-varying designs, we assign independent MVN priors to β_k and ψ_k from Equation (3); details are provided in Step 5(b) of Web Appendix B. For the multinomial logit model, the regression parameters δ_k = (δ_k1, … , δ_kr)^T are assigned a N_r(d_0k, S_0k) prior for k = 1, … , K − 1, which is conditionally conjugate under the Pólya-Gamma sampling scheme described in Section 3.2. Finally, from Equation (15), we assume a N_m(g_0k, G_0k) prior for γ_k and an inverse-gamma IG(λ_1k, λ_2k) prior for ${\sigma }_k^2$, where λ_2k is a scale parameter. In general, hyperparameters can vary across clusters, though they may be shared across clusters in practice. For the skew-t model, we assume d_i ~ Gamma ($\frac{\xi }{2}$, $\frac{\xi }{2}$), where ξ is a prespecified value.

3.5.2 ∣. Posterior computation, assessment of MCMC convergence, label switching, and model selection

The above prior specification induces closed-form full conditionals for all model parameters, which can be efficiently updated as part of the Gibbs sampler detailed in Web Appendix B. We monitor MCMC convergence through standard diagnostics, such as trace plots and effective sample sizes. To address label switching, a common issue for Bayesian mixture models, we implemented the iterative Equivalence Classes Representatives (ECR) relabeling algorithm included in the label.switching package in R (Papastamoulis, 2016). In our simulation studies and application, we observed immediate convergence of the ECR algorithm, indicating no evidence of label switching in our analyses. Because our primary objective is to identify a small number of clinically meaningful motor development clusters, we adopt the widely applicable information criterion (WAIC) to select the number of clusters K (Watanabe, 2010). In Section 4.3, we demonstrate that this measure accurately recovers the true number of clusters under realistic parameter settings.

4 ∣. SIMULATION STUDIES

4.1 ∣. Simulation to compare the MSN model to the MVN model

Our first simulation compared MSN and MVN mixture models to investigate whether ignoring skewness leads to poor inferences in a setting resembling the Nurture study. To emulate the Nurture study, we simulated n = 1000 subjects from the following model:

$$f({\mathbf{y}}_i)=\sum _{k=1}^3{\pi }_{ki}f({\mathbf{y}}_i\mid {\theta }_k),$$ (16)

where y_i = (y_i1, … , y_i4)^T to conform to the J = 4 measurement occasions in the Nurture study; θ_k is the set of parameters specific to cluster k (k = 1, 2, 3), and y_i∣θ_k ~ MSN₄(ζ_ki, α_k, Ω_k); ζ_ki = (ζ_ki1, … , ζ_ki4)^T, ζ_ki1 = β_kj1 + β_kj2x_i, and x_i is a N(0,1) covariate whose effect varies across the J measurement occasions. We modeled the cluster probabilities in Equation (7) as a function of an intercept and one baseline covariate, w_i1, implying that r = 2. We did not introduce missing data into this simulation, as we address missing data in the second simulation study. As a result, the total number of complete measurements was N = n × J = 4000. The generated data included n₁ = 318 infants in cluster 1, n₂ = 288 in cluster 2, and n₃ = 394 in cluster 3.

Because the model included no time-varying covariates—only time-varying effects—we used the matrix normal formulation given in Proposition 1, yielding a (p + 1) × J = 3 × 4 matrix ${\mathbf{B}}_k^{\ast }$. We chose the matrix normal hyperparameters described in Section 3.5.1 to be homogeneous across the three clusters by setting, for k = 1, 2, 3, ${\mathbf{B}}_{0k}^{\ast }=0_{3\times 4}$, L_0k = I₃, V_0k = I₄, and v_0k = J + 2 = 6, which gives E(∑_k) = I₄. Similarly, for the clustering model, we set d₀₁ = d₀₂ = (0, 0)^T and S₀₁ = S₀₂ = I₂, noting that k = 3 is the reference cluster. To investigate the effect of ignoring skewness, we allowed the vector of skewness parameters, α_k, to vary across clusters; for cluster 3, we assumed no skewness (α₃ = 0), implying MVN data for this cluster. We then fit both MSN and MVN mixture models to data generated from model (16). We ran the MCMC for 10 000 iterations with a burn-in of 1000. MCMC diagnostics indicated rapid convergence and excellent mixing (Web Figure 1).

The WAIC values for the MSN and MVN mixture models were 12 112 and 17 499, respectively, indicating better fit for the MSN model, as expected. Table 1 presents posterior mean estimates and 95% credible intervals (CrIs) for cluster 1 from the MSN and MVN models. Web Table 3 presents the results for the other two clusters. As expected, the MSN model provided accurate estimates throughout, whereas the MVN model consistently produced incorrect estimates with poor coverage when data were skewed, as in clusters 1 and 2. In particular, ignoring skewness inflated the variance estimates under the MVN model as a way to compensate for the skewness in the data. However, when data were not skewed, as in cluster 3, both models performed similarly (Web Table 3). Thus, the MSN model can be reliably used in place of the MVN model even when data are not overtly skewed.

TABLE 1.

Results for cluster 1 from Simulation 1 with n = 1000, J = 4, p = 2, K = 3, r = 2

Model component (k = 1)	Parameter	True value	MSN Est. (95% CrI)	MVN Est. (95% CrI)
MSN regression	β111	110.00	110.20 (109.97, 110.41)	106.36 (105.97, 108.71)
	β121	115.00	115.13 (114.91, 115.33)	104.17 (103.93, 104.44)
	β131	120.00	120.08 (119.83, 120.49)	128.02 (128.57, 129.08)
	β141	125.00	125.15 (124.86, 125.49)	126.67 (126.31, 127.05)
	β112	1.00	0.97 (0.84, 1.11)	0.90 (0.74, 1.08)
	β122	1.50	1.51 (1.40, 1.62)	1.53 (1.41, 1.66)
	β132	2.00	2.01 (1.89, 2.14)	2.20 (2.08, 2.33)
	β142	2.50	2.50 (2.35, 2.66)	2.46 (2.28, 2.64)
	Σ111	1.00	0.96 (0.77, 1.14)	2.42 (2.06, 2.84)
	Σ112	0.50	0.47 (0.34, 0.61)	1.20 (0.99, 1.48)
	Σ113	0.25	0.25 (0.04, 0.40)	−0.54 (−0.75, −0.34)
	Σ114	0.12	0.11 (−0.02, 0.30)	−1.35 (−1.67, −1.06)
	Σ122	1.00	0.99 (0.74, 1.19)	1.20 (0.99, 1.48)
	Σ123	0.50	0.49 (0.26, 0.66)	1.24 (1.06, 1.46)
	Σ124	0.25	0.24 (0.10, 0.43)	0.08 (−0.06, 0.21)
	Σ133	1.00	0.99 (0.77, 1.09)	1.24 (1.06, 1.46)
	Σ134	0.50	0.47 (0.22, 0.65)	1.15 (0.93, 1.40)
	Σ144	1.00	1.01 (0.63, 1.23)	2.48 (2.15, 2.91)
	α11	−2.00	−2.05 (−2.28, −1.66)	/
	α12	−1.00	−1.01 (−1.30, −0.75)	/
	α13	1.00	0.97 (0.65, 1.28)	/
	α14	2.00	1.97 (1.67, 2.28)	/
Multinomial logita	δ11	−0.27	−0.23 (−0.47, −0.09)	−0.14 (−0.35, 0.08)
	δ12	0.07	0.07 (−0.24, 0.37)	0.08 (−0.24, 0.38)
Missing Data	γ11	−0.82	−0.84 (−0.96, −0.73)	−1.08 (−1.19, −0.99)
	γ12	−1.08	−1.01 (−1.20, −0.91)	−1.80 (−1.96, −1.64)
	γ13	−1.12	−1.08 (−1.20, −1.00)	−0.90 (−1.00, −0.80)
	${\sigma }_1^2$	1.00	1.07 (0.92, 1.28)	0.89 (0.76, 1.07)
Estimated proportionb	π1	0.32	0.32 (0.31, 0.33)	0.32 (0.30, 0.34)

Note. 10 000 iterations were run with a burn-in of 1000. Posterior means (95% CrIs) are presented for the multivariate skew-normal (MSN) and multivariate normal (MVN) mixtures. No missing data were introduced.

^aMultinomial logit parameters comparing cluster 1 to cluster 3 (reference cluster).

^bEstimated proportion of infants in cluster 1.

Slashes (/) indicate that estimates are not applicable.

4.2 ∣. Simulation to compare imputation methods

Next, we evaluated the effect of failing to account for the missing data model in Equation (15). To do so, we generated n = 1000 observations from a 3-cluster (K = 3) MSN mixture model similar in design to Simulation 1. We then removed observations intermittently across the four measurement occasions according to model (15), which included two continuous covariates and an intercept, implying m = 3 from Equation (15). The model also included a random intercept with a common variance of ${\sigma }_k^2=1$ across clusters. After removing missing data, the number of available measurements in each cluster was N₁ = 1463, N₂ = 819, and N₃ = 1209. We ran each model for 10 000 iterations with a burn-in of 1000. MCMC diagnostics showed rapid convergence as shown in Web Figure 2.

We then fit two MSN mixture models to the simulated data, each with different missing data assumptions. The first method assumed conditional ignorability, as described in Section 3.4, where the missing responses and missing data pattern were assumed to be independent conditional on z_i, and a model of the missing data pattern was fit as in Equation (15). The second method assumed marginal ignorability, where the missing responses and missing data pattern were assumed to be independent marginally (ie, not conditional on z_i). Thus, the marginal ignorability approach did not adopt a model of the missing data mechanism as in Equation (15). Both imputation methods utilized MCMC-embedded imputation, where missing values were updated from cluster-specific multivariate normal conditional distributions at each MCMC iteration using the current values of parameters in the sampler.

As shown in Table 2, the conditional ignorability imputation method more accurately recovered true parameter values when compared to marginal ignorability. This result suggests that even when all other components of the model are correctly specified, making the strict marginal ignorability assumption (and thus ignoring model (15) altogether) can lead to biased estimates.

TABLE 2.

Results for cluster 1 from Simulation 2

Model component (k = 1)	Parameter	True value	Conditional ignorability	Marginal ignorability
MSN regression	β111	−2.90	−3.03 (−3.70, −2.60)	−3.72 (−3.99, −3.45)
	β121	−2.70	−2.82 (−2.96, −2.69)	−2.87 (−2.92, −2.64)
	β131	−2.92	−2.79 (−3.69, −2.43)	−3.76 (−4.04, −3.48)
	β141	−3.68	−3.87 (−4.01, −3.73)	−3.83 (−3.96, −3.69)
	β112	−2.78	−2.67 (−3.42, −2.24)	−3.57 (−3.86, −3.29)
	β122	−2.59	−2.81 (−2.94, −2.67)	−2.87 (−2.91, −2.73)
	β132	−2.71	−2.43 (−3.11, −2.15)	−3.44 (−3.70, −3.17)
	β142	−2.79	−2.98 (−3.11, −2.84)	−2.97 (−3.10, −2.83)
	Σ111	1.00	1.25 (0.84, 1.82)	1.54 (1.31, 1.85)
	Σ112	0.50	0.59 (0.19, 1.15)	1.12 (0.91, 1.39)
	Σ113	0.25	0.24 (0.11, 0.38)	0.93 (0.73, 1.19)
	Σ114	0.12	0.17 (0.08, 0.21)	0.85 (0.65, 1.10)
	Σ122	1.00	0.95 (0.49, 1.51)	1.12 (0.91, 1.39)
	Σ123	0.50	0.52 (0.14, 1.04)	1.66 (1.40, 1.97)
	Σ124	0.25	0.31 (0.12, 0.41)	1.15 (0.92, 1.41)
	Σ133	1.00	1.12 (0.81, 1.19)	0.93 (0.73, 1.18)
	Σ134	0.50	0.53 (0.24, 0.89)	0.85 (0.65, 1.10)
	Σ144	1.00	1.08 (0.61, 1.75)	0.93 (0.73, 1.18)
	α11	−1.00	−0.81 (−1.36, −0.05)	−1.91 (−2.17, −1.74)
	α12	−1.00	−1.18 (−1.63, −0.03)	−1.22 (−0.75, −1.66)
	α13	−1.00	−1.10 (−1.66, −0.14)	−1.50 (−2.25, −0.64)
	α14	−1.00	−1.29 (−1.62, −0.37)	−1.43 (−1.88, −1.01)
Multinomial logita	δ11	−0.54	−0.53 (−0.75, −0.31)	−0.64 (−0.85, −0.43)
	δ12	−0.01	−0.02 (−0.33, 0.38)	−0.08 (−0.33, 0.28)
Missing data	γ11	−1.10	−1.06 (−1.40, −0.75)	/
	γ12	−1.27	−1.13 (−1.42, −0.86)	/
	γ13	−1.07	−1.17 (−1.49, −0.87)	/
	${\sigma }_1^2$	1.00	1.01 (0.86, 1.15)	/

Note. Posterior means (95% CrIs) are presented for conditional ignorability and marginal ignorability. 10 000 iterations were run with a burn-in of 1000.

^aMultinomial logit parameters comparing cluster 1 to cluster 3 (reference cluster).

Slashes (/) indicate that estimates are not applicable.

4.3 ∣. Simulation to validate choice of K

We conducted a final simulation to validate the use of WAIC for determining the number of clusters, K. We generated four MSN data sets; one data set for each value of K = {2, 3, 4, 5}. For each simulated data set, we fit the proposed Bayesian MSN model with K = {2, 3, 4, 5} and computed WAIC in each case. For each scenario, we ran the MCMC algorithms for 10 000 iterations with a burn-in of 1000. MCMC diagnostics indicated rapid convergence for all models (Web Figure 3). As shown in Web Table 5, the WAIC measure recovered the true value of K in all cases. For some simulations (eg, true K = 2), we were unable to fit the MSN model when the fitted K was large due to the occurrence of vacant clusters during MCMC sampling. We have found that this generally occurs when the data do not support large values of K.

5 ∣. APPLICATION TO NURTURE STUDY

We applied our proposed model to the Nurture data by fitting an MSN mixture model that included Bayley scores centered and scaled by timepoint as the response, indicators for the four study visits corresponding to timepoint-specific intercepts, and binary food security status as the exposure of interest. The model also included time-invariant birth weight for gestational age z-score, number of children in the household, and an indicator for breastfeeding, as these likely impact infant development within each cluster. We allowed the covariate effects to vary over time, resulting in a parameter dimension of p = 20 for this component of the model (Table 3). For the multinomial logit cluster-membership model, we included an intercept, birth weight for gestational age z-score, infant race, and infant gender as covariates, as these variables are believed to affect the placement of infants into latent development clusters. The 471 missing measurements were imputed using the MCMC-embedded MNAR imputation method described in Section 3.4. The missing data model (15) included a fixed intercept, birth weight for gestational age z-score, infant gender, infant race, and a random intercept. To select the number of clusters, we fit several MSN models with varying specifications for K and used WAIC to choose the best fitting model. The WAIC values were 9141, 10 088, 11 203, and 11 410 for K = 2, 3, 4, 5, respectively. We also fit 3-df MST models with two to five clusters; these yielded WAIC values of 13 228, 13 934, 14 002, and 14 356 respectively, suggesting that the 2-cluster MSN model provided best fit among all models considered. We ran each model for 10 000 MCMC iterations, with a burn-in of 1000. We observed fast MCMC convergence in all cases with no evidence of label switching. MCMC diagnostics for the 2-cluster MSN model are presented in Web Figure 4.

TABLE 3.

Results from the 2-cluster model applied to the Nurture data

Model component	Parameter	Variable	Cluster 1 (37.0%)a Est. (95% CrI)	Cluster 2 (63.0%)a Est. (95% CrI)
MSN regression	βk11	3 mo	−0.33 (−0.48, −0.18)	0.26 (−0.04, 0.53)
	βk21	6 mo	−0.22 (−0.37, −0.05)	0.54 (0.17, 0.86)
	βk31	9 mo	−0.20 (−0.52, 0.11)	0.10 (−0.47, 0.56)
	βk41	12 mo	−0.35 (−0.45, −0.27)	0.80 (0.37, 1.11)
	βk12	FS (3 mo)	−0.55 (−0.68, −0.40)	−0.10 (−0.28, 0.12)
	βk22	FS (6 mo)	−0.40 (−0.56, −0.23)	0.08 (−0.08, 0.32)
	βk32	FS (9 mo)	−0.22 (−0.41, −0.03)	−0.15 (−0.27, −0.02)
	βk42	FS (12 mo)	−0.33 (−0.50, −0.12)	−0.13 (−0.26, −0.06)
	βk13	BW (3 mo)	−0.02 (−0.09, 0.06)	0.07 (−0.05, 0.16)
	βk23	BW (6 mo)	−0.03 (−0.11, 0.04)	0.03 (−0.09, 0.11)
	βk33	BW (9 mo)	−0.03 (−0.13, 0.06)	0.11 (−0.07, 0.29)
	βk43	BW (12 mo)	−0.03 (−0.11, 0.04)	0.06 (−0.05, 0.14)
	βk14	BF (3 mo)	0.41 (0.29, 0.51)	0.07 (−0.15, 0.22)
	βk24	BF (6 mo)	0.46 (0.36, 0.55)	0.04 (−0.14, 0.20)
	βk34	BF (9 mo)	0.62 (0.30, 0.91)	0.03 (−0.05, 0.12)
	βk44	BF (12 mo)	0.17 (−0.21, 0.55)	0.04 (−0.12, 0.24)
	βk15	TC (3 mo)	0.01 (−0.03, 0.06)	−0.02 (−0.09, 0.05)
	βk25	TC (6 mo)	0.02 (−0.02, 0.06)	−0.07 (−0.13, −0.02)
	βk35	TC (9 mo)	0.02 (−0.03, 0.07)	0.00 (−0.06, 0.06)
	βk45	TC (12 mo)	0.01 (−0.03, 0.06)	0.17 (−0.01, 0.35)
	αk1	Skewness (3 mo)	0.00 (−0.12, 0.11)	0.16 (−0.23, 0.41)
	αk2	Skewness (6 mo)	−0.02 (−0.15, 0.1)	−0.53 (−0.80, −0.17)
	αk3	Skewness (9 mo)	−0.02 (−0.16, 0.13)	0.05 (−0.32, 0.44)
	βk4	Skewness (12 mo)	−0.03 (−0.16, 0.10)	−0.07 (−0.41, 0.28)
Multinomial logitb	δk1	Intercept	1.03 (0.79, 1.25)	Reference
	δk2	BW	0.03 (−0.09, 0.15)	Reference
	δk3	Race (black)	−0.02 (−0.29, 0.27)	Reference
	δk4	Gender (female)	0.90 (0.65, 1.27)	Reference
Missing data	γk1	Intercept	0.37 (0.32, 0.41)	−0.16 (−0.19, −0.14)
	γk2	BW	0.05 (−0.51, 0.59)	0.03 (−0.14, 0.19)
	γk3	Gender (female)	0.80 (0.25, 1.57)	−0.04 (−0.41, 0.30)
	γk4	Race (black)	0.35 (−0.56, 1.37)	−0.60 (−1.02, −0.20)
	${\sigma }_k^2$	Random intercept variance	1.34 (0.86, 1.74)	1.11 (0.79, 1.43)

Note. Posterior means (95% CrI) are presented in each cluster for the effects of time, food security during pregnancy (FS), birth weight for gestational age z-score (BW), an indicator for any breastfeeding throughout the study period (BF), and total number of children in the household (TC). The effects of time, FS, BW, BF, and TC were allowed to vary over time, yielding separate estimates for each 3-month visit. Posterior means (95% CrI) are also given for effects of birth weight for gestational age z-score, race, and gender in the multinomial logit clustering and missing data models.

^aPosterior mean percent in each cluster.

^bWith only two clusters, this reduces to a conventional logistic model.

Table 3 presents posterior means and 95% CrIs for the 2-cluster model. In cluster 1, we observed a significant detrimental effect of food insecurity at each timepoint. However, in cluster 2, we only observed a significant detrimental effect of food insecurity at months 9 and 12, though the effect sizes were more modest than in cluster 1. These trends are also displayed in Figure 3. We observed a significant positive effect of breastfeeding in cluster 1, but not in cluster 2, suggesting that breastfeeding may especially benefit infants exhibiting delayed motor development. We did not observe a significant effect of either birth weight for gestational age z-score or number of children in the household. From the Pólya-Gamma multinomial logit component, we found that female infants were more likely to belong to cluster 1. From the missing data model, the intercepts suggest that more missing observations occur for infants in cluster 1 compared to those in cluster 2 for the reference covariate group. Moreover, female infants in cluster 1 had significantly higher log-odds of missing a measurement compared to male infants in cluster 1, while black infants in cluster 2 had significantly lower log-odds of missing a measurement compared to other infants.

FIGURE 3.

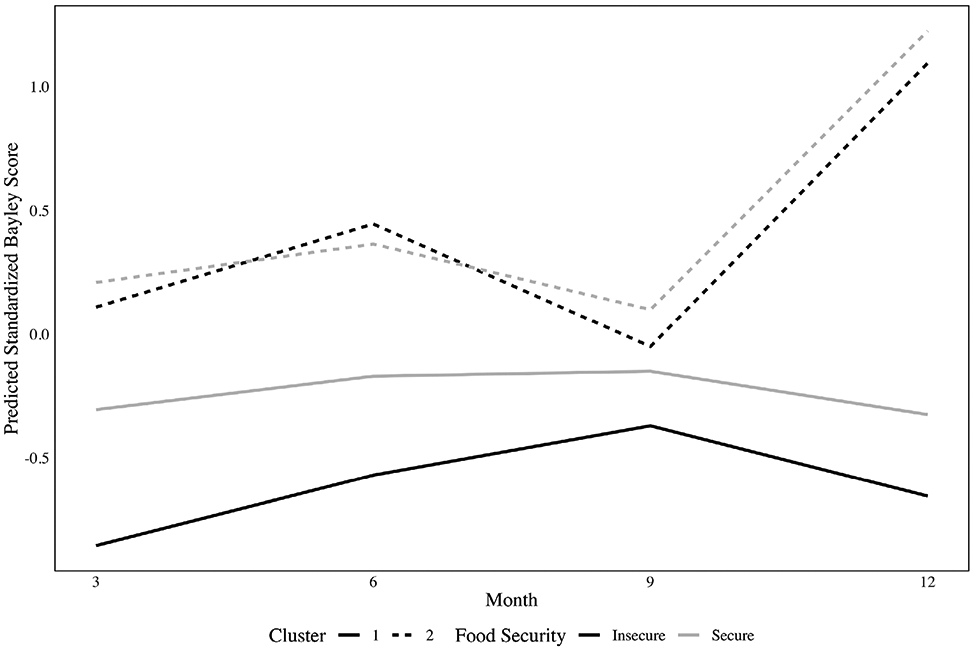
Predicted motor development trajectories for each cluster and food security group in the application to the Nurture data Note. The model included timepoint-specific intercepts, time-invariant birth weight for gestational age z-score, the number of children in the household, and an indicator for breastfeeding. Estimated trajectories are given for a typical infant with a birth weight for gestational age z-score of 0, who was not breastfed, and who had 2.5 other children in the household. Solid lines indicate cluster 1 and dashed lines indicate cluster 2. Light shading represents food-secure infants, while dark shading represents food-insecure infants

As shown in Table 3, the skewness estimates for cluster 1 indicate little evidence of skewness, as all associated 95% CrIs contained zero. However, in cluster 2, the predicted Bayley scores were negatively skewed at 6 months, in agreement with the preliminary analysis presented in Section 2. This suggests that the skewness observed in the data was driven primarily by the healthy-developing class, highlighting the model’s ability to discern different skewness patterns across clusters. Further, the clusters identified by the model were distinct from one another, as 510 (91%) of infants remained in the same cluster across the postburn-in MCMC iterations. Finally, the estimated covariance and correlation matrices (Web Table 6 and 7, respectively), indicated an unstructured pattern for both clusters, with greater variability in cluster 2.

6 ∣. DISCUSSION

We have developed Bayesian MSN and MST for skewed longitudinal data that feature intermittent missingness. The model has many appealing features: it accounts for skewness in the infant development scores, associations among repeated measures, and allows for efficient inference of the cluster assignment probabilities. The model can be applied to skewed as well as symmetric data, since the symmetric version is contained as a special case. Additionally, the model handles missing data under a conditional ignorability assumption that relaxes standard MAR assumptions.

Through simulations, we showed that ignoring skewness in even moderately skewed data results in incorrect inference, whereas the MSN mixture model recovers the true parameter values when the data are skewed. Furthermore, we showed that failing to account for conditional ignorability results in biased estimates when the response mechanism depends on cluster assignment. Finally, we conducted simulations to validate the use of WAIC, supporting the use of this measure in practice.

We applied our method to the Nurture data to assess the effect of household food security during pregnancy on motor development scores and to investigate possible clustering of infant development trajectories. We identified two distinct clusters of infants: one with delayed motor development and significantly impaired by food insecurity, and a second that exhibited healthy motor development and was only modestly affected by food insecurity toward the end of infancy. This suggests that household food insecurity may compound the negative impacts of delayed motor development. On the other hand, we found that breastfeeding improved motor development among infants with delayed development. These results add to the growing body of literature on the effect of household food security on infant outcomes.

To extend this work, the model could accommodate dropout in addition to intermittent missingness using a cluster-specific discrete time-to-event model. Additionally, cluster-specific shared parameters could link the outcome and missing data models, relaxing the conditional ignorability assumption. More broadly, the method should prove useful in a range of settings involving multivariate skew data with informative missing responses. From a practical perspective, investigators looking to model clustered repeated-measures data can use the diagnostics described in Section 2 to determine whether the MSN model is appropriate. Given that the computational demand of the MSN and MST models is negligible compared to the MVN model, we recommend fitting the MSN or MST model first and using the estimated skewness parameters to determine whether simplifications to the MVN model can be made.

DATA AVAILABILITY STATEMENT

The Nurture data were collected as part of grant R01DK094841 from the National Institutes of Health and are housed at Duke University Medical Center. The Nurture data are available upon request with appropriate permissions, agreements between institutions, and documentation of ethical approval.