A graph neural network model to estimate cell-wise metabolic flux using single-cell RNA-seq data

Abstract

The metabolic heterogeneity and metabolic interplay between cells are known as significant contributors to disease treatment resistance. However, with the lack of a mature high-throughput single-cell metabolomics technology, we are yet to establish systematic understanding of the intra-tissue metabolic heterogeneity and cooperative mechanisms. To mitigate this knowledge gap, we developed a novel computational method, namely, single-cell flux estimation analysis (scFEA), to infer the cell-wise fluxome from single-cell RNA-sequencing (scRNA-seq) data. scFEA is empowered by a systematically reconstructed human metabolic map as a factor graph, a novel probabilistic model to leverage the flux balance constraints on scRNA-seq data, and a novel graph neural network–based optimization solver. The intricate information cascade from transcriptome to metabolome was captured using multilayer neural networks to capitulate the nonlinear dependency between enzymatic gene expressions and reaction rates. We experimentally validated scFEA by generating an scRNA-seq data set with matched metabolomics data on cells of perturbed oxygen and genetic conditions. Application of scFEA on this data set showed the consistency between predicted flux and the observed variation of metabolite abundance in the matched metabolomics data. We also applied scFEA on five publicly available scRNA-seq and spatial transcriptomics data sets and identified context- and cell group–specific metabolic variations. The cell-wise fluxome predicted by scFEA empowers a series of downstream analyses including identification of metabolic modules or cell groups that share common metabolic variations, sensitivity evaluation of enzymes with regards to their impact on the whole metabolic flux, and inference of cell–tissue and cell–cell metabolic communications.

Metabolic dysregulation is a hallmark of many disease types including cancer, diabetes, cardiovascular disease, and Alzheimer's disease (Mattson and Chan 2001; Rask et al. 2001; Matsuzawa 2006; Dunn et al. 2014; Hirschey et al. 2015; Kochanek et al. 2019; Sun et al. 2020). In cancer, the diseased cells are well understood to rewire their metabolism and energy production to support rapid proliferation, sustain viability, and promote acquired drug resistance (Thompson et al. 2005; DeBerardinis et al. 2008; Hanahan and Weinberg 2011; Ward and Thompson 2012). Here, the diseased cells often react differently to the microenvironmental stress. Such heterogeneity often results in an increased repertoire of possible cellular responses to compromise the efficacy of drug therapies, leading to the enhanced survival of the entire diseased cell population (Bishop et al. 2007; Lidstrom and Konopka 2010). The metabolome is an excellent indicator of phenotypic heterogeneity owing to its high dynamics and plasticity (Zenobi 2013). Current high-throughput metabolic profiling has been largely applied to bulk cell or tissue samples from which we could only observe an averaged metabolic signal over a large number of cells, whereas single-cell metabolomics is still in its infancy because of its relatively low throughput and low sensitivity (Zenobi 2013; Fessenden 2016; Emara et al. 2017; Zampieri et al. 2017; Ali et al. 2019, 2020; Duncan et al. 2019). Overall, our understanding of metabolic dysregulation of human disease has been immensely limited by our technology to study the metabolic landscape at the single-cell level and in the context of their tissue microenvironment (Jaenisch and Bird 2003; Feinberg 2007; Heintzman et al. 2007; Harris et al. 2010; The ENCODE Project Consortium 2012; Roadmap Epigenomics Consortium et al. 2015; Robertson-Tessi et al. 2015; Kim and DeBerardinis 2019).

Single-cell RNA-seq (scRNA-seq) data has been widely used to characterize cell type–specific transcriptional states and its underlying phenotypic switches in a complex tissue (Vasdekis and Stephanopoulos 2015; Damiani et al. 2019; Evers et al. 2019; Honkoop et al. 2019; Saurty-Seerunghen et al. 2019; Xiao et al. 2019, 2020; Rohlenova et al. 2020; Zhang et al. 2020; Levine et al. 2021). Realizing the strong connections between transcriptomic and metabolomic profiles (Hirayama et al. 2009; Lee et al. 2012; Mehrmohamadi et al. 2014; Damiani et al. 2019; Xiao et al. 2019b; Wagner et al. 2021), scRNA-seq data has found its application in portraying metabolic variations. Using scRNA-seq data, the existing research studied metabolic changes of predefined cell groups relying on differential expression and enrichment analysis of key metabolic enzymes and pathways (Vasdekis and Stephanopoulos 2015; Evers et al. 2019; Honkoop et al. 2019; Saurty-Seerunghen et al. 2019; Xiao et al. 2019, 2020; Rohlenova et al. 2020; Levine et al. 2021). However, for this type of analysis, the node/edge structures in a metabolic pathway graph or the mass balance constraints of metabolic network is not considered. Studies coupling single-cell transcriptomics data and the flux balance analysis (FBA) at steady-state framework have only recently emerged (Damiani et al. 2019; Zhang et al. 2020). The FBA describes the potential flux over the topological structure of a metabolic network, with a set of equations governing the mass balance at steady state. The advantage of incorporating FBA into the model is twofold: considering the chemical stoichiometry in FBA could lead to more accurate estimation of the metabolite abundance; and flux estimation for each individual metabolite can be solved, leading to high-resolution characterization of the metabolic profiling. Damiani et al. (2019) developed scFBA that uses the cell group–specific gene expression status derived from scRNA-seq data to regularize the network topology for FBA. Wagner et al. (2021) proposed a method, namely, Compass, that maximizes the coherence between scRNA-seq expression profile and predicted flux in solution space of FBA. However, as stated in the original works (Wagner et al. 2021), the stringent flux balance and steady-state assumption in scFBA and Compass may not be rational for certain disease types with constantly severe “imbalance” of many metabolites, namely, cancer. Another limitation of the FBA-based methods is that the single cells’ gene expression is not used directly to model metabolic flux. Both scFBA and Compass used single-cell gene expression as certain constraints to guide the search in the solution space of flux balance condition. In addition, both models are intended for modeling the fluxes for cells of predefined groups instead of at a single-cell resolution, and they are restricted to a small portion of the whole metabolic map. Therefore, it remains an urgent task to design advanced computational tools for reliable estimation of cell-wise metabolic flux and states by translating single-cell transcriptomes to single-cell fluxomes. Such a tool is vital to unravel the principles of how the disease microenvironment may affect the metabolic phenotypes for the heterogeneous cell types (Damiani et al. 2019; Evers et al. 2019).

Computational challenges to estimate cell-wise metabolic flux arise from the following aspects: (1) multiple key factors determine cells’ metabolic states, including exogeneous nutrient availability, leading to the discrepancy of cell type–specific markers and metabolic phenotypes and states; (2) the whole metabolic network is of high complexity, hence, a proper computational reduction and reconstruction of the network is needed to reach a balance between resolution of metabolic state characterization and computational feasibility; (3) the intricate nonlinear dependency between transcriptomic expressions and metabolic reaction rates calls for a more sophisticated model to fully capitulate the relationships; and (4) alternative enzymes with similar functions may result in common metabolic phenotypes, however, exactly which enzymes share such common effect to the metabolic flux change remains largely unknown.

In this study, we developed a novel computational method, namely, single-cell flux estimation analysis (scFEA), to estimate the relative rate of metabolic flux at single-cell resolution from scRNA-seq data. Specifically, scFEA can effectively solve the aforementioned challenges with the following computational innovations: (1) an optimization function derived based on a probabilistic model to consider the flux balance constraints among a large number of single cells with varied metabolic fluxomes, (2) a metabolic map reduction approach based on network topology and gene expression status, (3) a multilayer neural network model to capture the nonlinear dependency of metabolic flux on the enzymatic gene expressions, and (4) a novel graph neural network architecture and solution to maximize the overall flux balance of intermediate substrates throughout all cells. The central hypotheses of scFEA are (1) the flux variations of a metabolic module can be modeled as a nonlinear function of the transcriptomic-level changes of the catalyzing enzymes; and (2) the total flux imbalance of all intermediate substrates should be minimized throughout all single cells. The cell-wise fluxome estimated by scFEA enables a series of downstream analyses, including identification of cell- or tissue-level metabolic stress, sensitivity evaluation of individual enzymes to the whole metabolic network, and inference of cell–tissue and cell–cell metabolic exchanges. To validate scFEA, we generated an scRNA-seq data set with matched tissue-level metabolomic profiles under different biochemical perturbations. Applications of scFEA on synthetic data sets, the newly generated data set with matched scRNA-seq and metabolomic profiles, and six other independent real-world data sets, validated the prediction accuracy, robustness, and biological interpretability of scFEA.

Results

Systems biology considerations, hypotheses, and analysis pipeline of scFEA

The reaction rate of a simple enzyme catalyzed metabolic reaction follows the Michaelis–Menten kinetic model: V = K_cat ([E][S]/K_m + [S]), which is a nonlinear function of enzyme concentration [E], substrate concentration [S], and kinetic parameters K_cat and K_m. On one hand, the reaction rate is approximately a linear function of the enzyme concentration when the substrate concentration is much larger than K_m, that is, when [S]/(K_m + [S]) is ∼1; on the other hand, the enzyme concentrations could often serve as a surrogate for the substrate concentration considering the regulatory effect of substrate availability on the enzyme transcription. Overall, we consider the reaction rate to be a (non)linear function of the enzyme concentration. Obviously, the flux of a reaction chain is mostly determined by the rate-limiting steps, which depend on the flux distribution, substrate concentration, and kinetic parameters. Hence, the rate-limiting steps are often context specific and unknown because of the dynamics of the physiological and biochemical conditions of the cells. Based on these considerations, we developed scFEA to estimate cell-wise metabolic flux from scRNA-seq data. scFEA consists of three major computational components: (1) network reduction and reconstruction, (2) estimation of cell-wise metabolic flux, and (3) downstream analyses including estimation of metabolic stress, perturbation of metabolic genes, and clustering of cells with different metabolic states (Fig. 1). The required input of scFEA is an scRNA-seq data set, whereas optional inputs, including cell group labels or the subset of metabolic reactions of interest, can be specified for additional analysis.

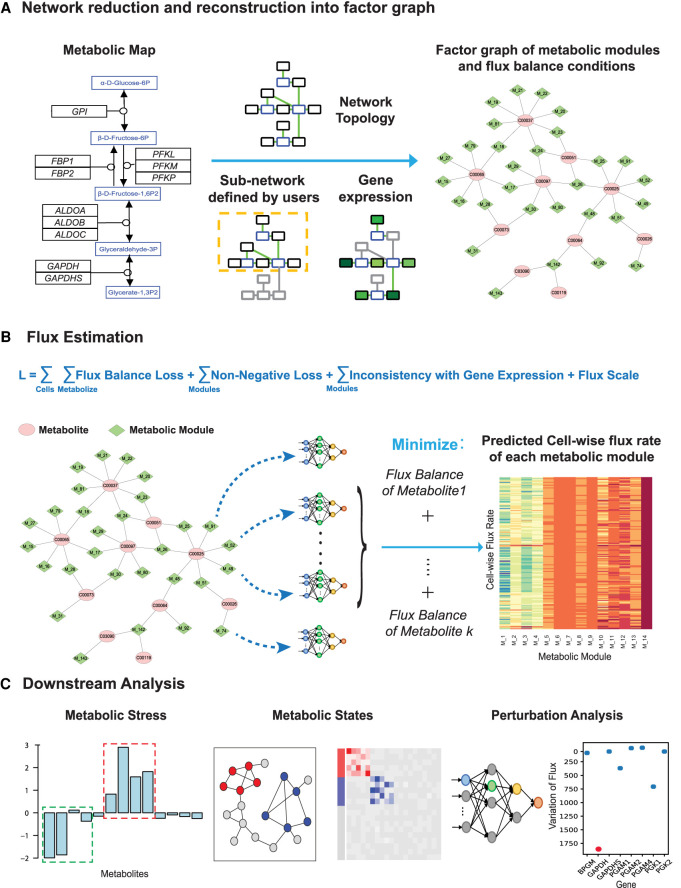
Figure 1.

The computational framework of scFEA. (A) Metabolic reduction and reconstruction. A metabolic map was reduced and reconstructed into a factor graph based on network topology, significantly non-zero gene expressions, and users’ input. (B) A novel graph neural network architecture–based prediction of the cell-wise fluxome. A loss function (L) composed by loss terms of flux balance, non-negative flux, coherence between predicted flux and gene expression, and constraint of flux scale, were used to estimate cell-wise metabolic flux from scRNA-seq data. See detailed models and formulations in Results and Methods. (C) Downstream analysis of scFEA is provided, including inference of metabolic stress, cell and module clusters of distinct metabolic states, and the genes of the top impact to the whole metabolic flux.

To reduce the complexity of the metabolic map, we reconstructed it into a factor graph composed by connected metabolic modules as variables and intermediate metabolites as factors (Fig. 1A). Specifically, connected reactions are merged into one module, if changes in the reaction rates within the module do not affect the rates of the rest of the reactions, given a fixed flux rate of the module. In other words, the estimated flux of a module stays the same, with or without merging the reactions, under the flux balance condition. This approach increases the robustness of flux estimation and reduces the computational complexity.

The central computational component of scFEA is a novel graph neural network architecture, which models the cell-wise metabolic flux of each metabolic module using gene expression levels of the catalyzing enzymes (Fig. 1B). We hypothesize that the metabolic flux throughout all the single cells in a tissue sample should minimize the overall imbalance of the influx/outflux of intermediate substrates. The rationality of this assumption is that cells within the same tissue exchange metabolites with each other, hence the total flux balance constraint on all the single cells from one tissue sample is more robust than in individual cells. In scFEA, we use the gene expression variations to reflect the protein level change of enzymes and transporters. Note that this assumption is supported by many existing studies that reveal the high explainability of the transcriptome for the proteome (Schnell 2014; Roadmap Epigenomics Consortium et al. 2015; Liu et al. 2016). We assume the flux variations of a module generally impact its neighboring modules, which can be reflected by aggregating the expression variations of the genes in its neighborhood over the metabolic network. The nonlinear dependency between gene expression and metabolic flux is modeled as a fully connected neural network of 2–4 layers, which could be considered as a nonlinear approximation of the Michaelis–Menten model. To solve the neural network parameters, scFEA minimizes a loss function that mimics the overall flux imbalance of all modules in all cells, with further non-negativity and other prior assumptions on the module fluxome. The large number of single cells in scRNA-seq data grants sufficient statistical power to detect the flux variations and avoids the overfitting of the neural network training (for details, see Methods). It is noteworthy that the parameters of the neural network could serve as sensitivity measures of the metabolic flux balance to the variations of the genes. In other words, genes with higher impact are likely to be associated with rate-limiting reactions under the particular context.

The estimated cell-wise metabolic flux enables the prediction of (1) the metabolites or pathways with high imbalance in certain cell groups, (2) groups of metabolic modules or cells with varied metabolic states, and (3) the metabolic genes whose perturbation highly impacts the overall metabolic flux (Fig. 1C). In this study, we mainly focus on solving cell-wise metabolic flux and states and method validations in human cells. A capability for mouse data analysis is also provided in the software package of “scFEA.”

Metabolic map reduction and reconstruction

The whole metabolic network in human and mouse have been well studied. However, although databases including the Kyoto Encyclopedia of Genes and Genomes (KEGG) provide well categorized metabolic pathways and the comprehensive set of metabolic genes (Kanehisa and Goto 2000), the network topological structure needs to be further optimized for fluxome estimation because of the following reasons: (1) the flux balance constraints depend on the optimization goal or computational assumption, such as the balance of carbon, redox, or pH; (2) the network complexity needs to be reduced to enable computational feasibility; and (3) a manual correction and annotation of the directions of reactions and transporters is needed. In addition, cells of different types or physiological states naturally have varied metabolic states. In scFEA, we first manually curated and annotated the metabolic map of human and mouse retrieved from the KEGG database. The global metabolic map is further reduced and reconstructed into a factor graph based on its topological property. scFEA also allows the selection of a connected subnetwork in the global metabolic network for flux estimation.

Collection of human and mouse metabolic map

The metabolic map consists of pathways and reactions that fall under four major types, namely, import, metabolism, biosynthesis, and export. To ensure a comprehensive coverage of the global metabolic map, we collected reactions of metabolism and biosynthesis as well as transporters for import and export from different data sources. Specifically, metabolic reactions were directly retrieved from the KEGG database (Kanehisa and Goto 2000); the transporters and annotations of import and export reactions were accessed from the transporter classification database (Saier et al. 2006); biosynthesis reactions were collected from the biosynthesis pathways encoded in KEGG and curated by using additional literature (for details, see Supplemental Methods). The final metabolic map covers the metabolism, transport, and biosynthesis of carbohydrate, amino acids, fatty acids and lipids, glycan, and nucleic acids in human and mouse, including 862 genes of 390 enzymes, 1880 reactions, 1219 metabolites, and 116 transporter genes of 35 metabolites in human. Complete lists of genes and reactions of the collected human metabolic map is given in Supplemental Table S1.

Reconstruction of the metabolic map into a factor graph

The metabolic reaction map naturally forms a directed factor graph when considering each reaction as a variable and each metabolite as a factor. A directed factor graph was first reconstructed by the stoichiometric matrix of all reactions in the global metabolic map. In the factor graph, variable, factor, and directed edge are reactions, metabolites, and whether or not a reaction involves a metabolite as the substrate or product, respectively. In this study, we use a flux balance assumption of carbon-based metabolites. Therefore, 273 compounds that do not affect the flux balance of carbon-based molecules were excluded from the stoichiometric matrix, such as H₂O, ATP, NADH, or other cofactors (for a complete list, see Supplemental Table S1). We further reduced the complexity of the factor graph based on its topological structure. In this step, connected reactions were merged into a module if (1) none of the merged intermediate metabolites had more than one influx or outflux reaction that corresponded to more than one module's inputs or outputs; and (2) none of the merged intermediate metabolites had an influx or outflux other than the merged reactions or the module input and output. We have proved that under these two conditions and the flux balance condition, changes of the reactions inside the module will not affect the reactions outside the module conditional on a fixed flux rate of the module. In other words, solving the flux of each individual reaction in a merged module is equivalent to solving the flux of the module (for details, see Supplemental Methods). The merged reactions will form a variable node containing multiple reactions in the factor graph, while the factor nodes are still individual metabolites. In addition, we identified certain classes of metabolites, including different types of fatty acids, pyrimidines, purines, and steroid hormones, that form highly connected web-like metabolic pathways. Instead of solving the flux for each individual metabolite, we consider the metabolites of the same class as one factor. The network reduction approach enables a more robust flux estimation of reaction modules instead of individual reactions and a more efficient computation over the simplified network topological structure.

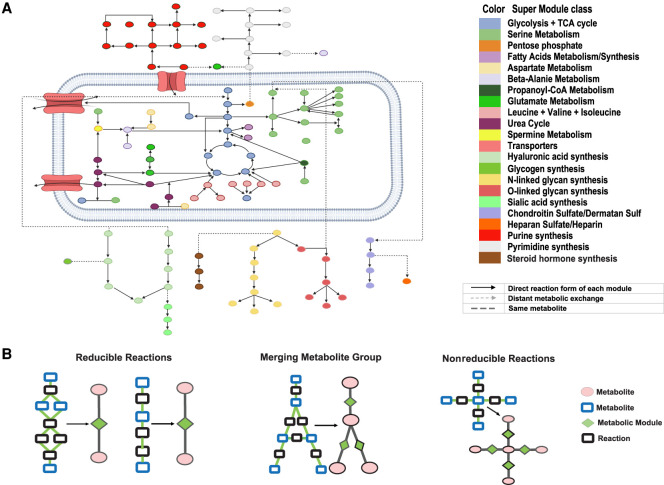
We reconstructed the human metabolic map into a factor graph consisting of 169 modules of 22 supermodule classes, 862 genes, and 128 metabolites, of which 66 are intermediate substrates. Here, each supermodule is a manually curated group of modules with similar functions (Table 1). More details on the factor graphs can be found in Supplemental Table S1 and Supplemental Figure S1. Figure 2A illustrates the functional group and complete topological structure of the collected metabolic modules and supermodules in human. Figure 2B illustrates several examples of how network motifs in the input metabolic network are merged into one metabolic module.

Table 1.

Supermetabolic module information

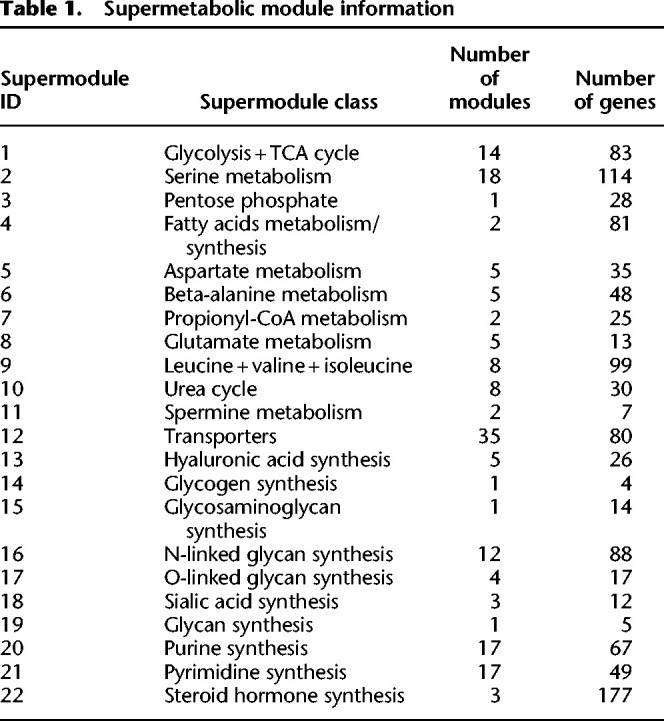
Figure 2.

Reduced and reconstructed human metabolic map. (A) Collected human metabolic modules and supermodule classes. (B) Examples of how the network motifs in the metabolic map are simplified into metabolic modules, where the reactions and metabolites are represented by black and blue rectangles, and modules and metabolites are colored by green and pink. Chainlike reactions can be directly simplified; a complicated module connected by multiple branches can be shrunk into one point linked with the multiple in/out branches; and complicated intersections cannot be simplified.

For a given scRNA-seq data and a user defined task, scFEA further refines the task-specific metabolic factor graph by (1) limiting the analysis to user-selected metabolic networks, and (2) excluding the modules without significantly expressed genes. For (2), scFEA will first determine for all the genes whether they have a significant non-zero expression state, using our in-house left-truncated mixture Gaussian model (Methods; Wan et al. 2019). By default, scFEA considers a module as blocked if it becomes disconnected with other modules after removing the reactions whose associated genes do not have a non-zero expression state. The blocked modules will be excluded from further analysis. On account of the common dropout events in scRNA-seq data, scFEA allows keeping a module as long as at least one of the genes involved in this module has significantly non-zero expressions.

The topological structure of metabolic modules including input, output, and intermediate metabolites and genes associated with each module, serve as the input to our graph neural network model.

Mathematical formulation of metabolic flux estimation in individual cells

For a clear model setup, we first formulate the metabolic network as a directed factor graph. Here, each metabolic module is represented as a variable, and each compound is represented as a factor node carrying a loss function that evaluates the level of flux imbalance among modules, and the direction represents whether a metabolite is the input or output of a metabolic module (Supplemental Fig. S1). We denote FG(C^1×K, RM^1×M, E = {E_C→R, E_R→C}) as the factor graph, where C^1×K = {C_k, k = 1, …, K} is the set of K compounds; RM^1×M = {R_m, m = 1, …, M} is the set of M metabolic modules; and E_R→C and E_C→R represent direct edges from module to compound and from compound to module, respectively. For the kth compound C_k, we define the set of reactions producing and consuming C_k as $F_{\mathrm{in}}^{C_k}=\{R_m|(R_m\to C_k)\in E_{R\to C}\}$ and $F_{\mathrm{out}}^{C_k}=\{R_m|(C_k\to R_m)\in E_{C\to R}\}$, which is derived from the stoichiometric matrix of the whole metabolic map. For an scRNA-seq data set with N cells, we denote Flux_m,j as the flux of the mth module in the cell j, j = 1…N, and let F_j = {Flux_1,j, …, Flux_M,j}. Our computational hypothesis is that the total flux imbalance of the intermediate metabolites throughout all the collected cells should be minimized, based on which we developed the likelihood function of the flux of all modules throughout all cells as

$$\varphi (C,F)=\prod _{j=1}^N\prod _{k=1}^K\varphi (C_{k,j}|F_j)\phi (F_j),$$

where

$$\varphi (C_{k,j}|F_j)=\varphi (C_{k,j}|F_{\mathrm{in}}^{C_k},F_{\mathrm{out}}^{C_k})\propto e^{-{\displaystyle \frac{\lambda {\left({\sum }_{m\in F_{in}^{C_k}}{\mathrm{Flux}}_{m,j}-{\sum }_{m^{\mathrm{\prime }}\in F_{\mathrm{out}}^{C_k}}{\mathrm{Flux}}_{m^{\mathrm{\prime }},j}\right)}^2}{2}}}$$

and φ(F_j) represents the prior distribution of the fluxome in cell j, and λ is a tuning hyperparameter. scFEA models the flux of reach reaction, Flux_m,j, as a nonlinear function of the expression changes of the genes associated with the module. Denote ${\mathit{G}}^{\mathit{m}}=\{G_1^m,\dots ,G_{i_m}^m\}$ as the genes associated with the reactions in R_m, and ${\mathit{G}}_{\mathit{j}}^{\mathit{m}}=\{G_{i_1,j}^m,\dots ,G_{i_m,j}^m\}$ as their expressions in sample j, where i_m stands for the number of genes in R_m. We model ${\mathrm{Flux}}_{m,j}=f_{nn}^m({\mathit{G}}_{\mathit{j}}^{\mathit{m}}|{\mathit{\theta }}_{\mathit{m}})$ as a multilayer fully connected neural network with the input ${\mathit{G}}_{\mathit{j}}^{\mathit{m}}$, where θ_m denotes the parameters of the neural network (Fig. 3). It is noteworthy that the cell group and tissue context–specific distribution of the flux φ(F_j) and the reaction parameters θ_m are always unknown. Apparently, without further constraints, Flux_m,j ≡ 0 is a trivial solution. To provide a robust and rational solution, we introduced two additional constraints to Flux_m,j, namely, (1) the predicted flux, Flux_m,j, should be non-negative; and (2) within a supermodule (Fig. 2A), the total predicted flux should be correlated with gene expression variation. The second assumption assumes that the metabolic flux variation within large metabolic modules should be coherent to their gene expression change, which is supported by recent studies (Damiani et al. 2019; Wagner et al. 2021). This assumption effectively avoids the trivial solution. Hence, instead of directly maximizing ϕ(C, F), we solve the θ_m and cell-wise flux Flux_m,j by minimizing the following loss function L:

$$\begin{array}{rl}L& =\sum _{j=1}^N\sum _{k=1}^K{\left(\sum _{m\in F_{in}^{C_k}}{\mathrm{Flux}}_{m,j}-\sum _{m^{\mathrm{\prime }}\in F_{\mathrm{out}}^{C_k}}{\mathrm{Flux}}_{m^{\mathrm{\prime }},j}\right)}^2+\alpha \sum _{j=1}^N\sum _{m=1}^M(\left|{\mathrm{Flux}}_{m,j}\right|-{\mathrm{Flux}}_{m,j})\\ & +\text{β}\sum _{j=1}^N\left[1-\left|\mathrm{cor}({\mathrm{Flux}}_{:,j}^{SM},{\mathrm{GE}}_{:,j}^{SM})\right|\right]+\gamma \sum _{j=1}^N{\left(\sum _{m=1}^M\left|{\mathrm{Flux}}_{m,j}\right|-T{A}_j\right)}^2,\end{array}$$

where α, β, and γ are hyperparameters; cor represents Pearson correlation coefficient; Flux^SM and GE^SM are two NSM × N matrices, here NSM is number of supermodules; ${\mathrm{Flux}}_{m,j}^{SM}$ represents the sum of the flux of the modules in the supermodule m; ${\mathrm{GE}}_{m,j}^{SM}$ represents the sum of expression of the genes in the supermodule m, in cell j; and TA_j is a surrogate for total metabolic activity level of cell j, which is assigned as the total expression of metabolic genes in cell j. The first, second, third, and fourth terms of L are related to constraints on flux balance, non-negative flux, the coherence between predicted flux and total gene expression level of each supermodule, and the relative scale of flux, respectively. Here Pearson's correlation, which is scale-free, is used to model the coherence between gene expression and predicted flux, as genes may have varied intrinsic expression range. Our empirical and robustness analyses suggested that α = 1, β = 0, γ = 1, and α = 1, β = 1, γ = 1 result in a good leverage of the flux balance loss and other constraints for Smart-seq2 and 10x Genomics data, respectively (for details, see robustness analysis and Supplemental Methods).

Figure 3.

A toy model of the factor graph of metabolic modules, flux balance conditions, and the flux model for the module R₂ (top right). In the factor graph, each C (metabolites) corresponds to one flux balance condition and serves as a factor, and each R (can be a reaction or a module) is a variable. For example, $C^0(R_0,R_1,R_2|L_{c^0})$ simply represents that the metabolite C⁰ is determined by the flux balance loss of R₀, R₁, R₂, where $L_{c^0}$ is the flux balance term of C⁰. Import and export/degradation reactions are considered as having no input or output substrates.

The preceding formulation defines a new graph neural network architecture for flux estimation over a factor graph: on one hand, each variable is defined as a neural network of biologically meaningful attributes, that is, the genes participating in each metabolic module; on the other hand, the information aggregation between adjacent variables is constrained by the balance of the influx and outflux of each intermediate metabolite. The number of intermediate constraints (K) and large number of cells (N) of scRNA-seq data ensures the identifiability of θ_m for the multilayer $f_{nn}^m$ at a certain complexity level. Detailed analysis of the computational feasibility, scalability, tuning of hyperparameters, and options of additional loss terms are provided in Methods and Supplemental Methods.

The challenges to minimize the loss function L include the following: (1) the balance of one intermediate substrate is influenced by multiple modules, hence updating the module flux one at a time may not be computationally efficient; and (2) the updating strategy for a large group of fluxes cannot be theoretically derived. The two challenges prohibit a direct usage of back propagation or gradient descending methods. We developed an effective optimization strategy for L by adopting the idea of information transfer in belief propagation, which has been commonly used in analyzing cyclic networks such as Markov random field (Lan et al. 2006). Specifically, L is minimized by iteratively minimizing the flux imbalance of C_k and the weighted sum of the flux imbalance of the Hop-2 neighbors of C_k in the factor graph, as the $L_k^{\ast }$ defined below:

$$\begin{array}{rl}{L}_k^{\ast }& =\sum _{j=1}^N{(\sum _{m\in F_{in}^{C_k}}{\mathrm{Flux}}_{m,j}-\sum _{m^{\mathrm{\prime }}\in F_{\mathrm{out}}^{C_k}}{\mathrm{Flux}}_{m^{\mathrm{\prime }},j})}^2\\ & +\sum _{k^{\mathrm{\prime }}}{W}_{k^{\mathrm{\prime }}}\sum _{j=1}^N{(\sum _{m\in F_{in}^{C_{k^{\mathrm{\prime }}}}}{\mathrm{Flux}}_{m,j}-\sum _{m^{\mathrm{\prime }}\in F_{\mathrm{out}}^{C_{k^{\mathrm{\prime }}}}}{\mathrm{Flux}}_{m^{\mathrm{\prime }},j})}^2,\end{array}$$

where $C_{k^{\mathrm{\prime }}}$are the Hop-2 neighbors of C_k, and $W_{k^{\mathrm{\prime }}}$ is proportional to the current total imbalance of all the Hop-2 neighbors of $C_{k^{\mathrm{\prime }}}$ except for C_k itself (for more details, see Methods). Here the Hop-2 neighbors of a compound (or module) on the factor graph is defined as all other compounds (or modules) having a connection with the modules (or compounds) who connect to the compound (or module). Such a regional perturbation strategy over the whole graph can effectively leverage the search of global minimum and computational feasibility.

The output of scFEA includes $f_{nn}^m$, θ_m for each module and predicted cell-wise metabolic flux Flux_m,j. The predicted flux Flux_m,j is a relative measure of unfixed scale. However, Flux_m,j is comparable among cells (Flux_m,) or metabolic modules (Flux_,j).

Method validation on an scRNA-seq data with perturbed metabolic conditions and matched metabolomics data

To validate the cell-wise flux estimated by scFEA, we generated an scRNA-seq data set consisting of 162 patient-derived pancreatic cancer cells (Pa03c cell) under two crossed experimental conditions: APEX1 knockdown (APEX1 KD) or control, and under hypoxia or normoxia conditions (for detailed experimental procedure and data processing, see Methods). Metabolomics profiling of 14 metabolites were collected on bulk wild-type Pa03c cells and APEX1 inhibition cells under the normoxia conditions, each with three replicates (Supplemental Table S2). The 14 metabolites include glucose, glucose-1 phosphate, glucose-6 phosphate, pyruvate, and lactate in the glycolysis pathway, citrate, 2-oxoglutarate, succinate, fumarate, malate in the TCA cycle, and amino acids glutamate, glutamine, serine, and ornithine. We used the Smart-seq2-fluidigm protocol for single-cell RNA sequencing. It allows for saturated gene detection of each single cell, to enable a more accurate modeling of metabolic flux. APEX1 is a multifunctional protein that interacts with multiple transcriptional factors (TFs) to regulate cellular responses to hypoxia and oxidative stress (Kelley et al. 2012). Our previous studies identified significant roles of APEX1 in the regulation of Pa03c cells’ response to metabolic environment changes (Shah et al. 2017; Wan et al. 2019).

To the best of our knowledge, scFEA is the first computational tool to estimate metabolic flux at single-cell level. Without baseline methods for comparisons, we validate scFEA by examining the consistency between the metabolic flux variation predicted by scFEA and experimental observations. We identified 126 up-regulated and 443 down-regulated genes in APEX1 KD versus control under the normoxia condition, and 260 up-regulated and 1496 down-regulated genes under hypoxia condition. Pathway enrichment analysis showed that the TCA cycle (normoxia: P = 0.003, hypoxia: P = 1.12 × 10⁻⁷) and oxidative phosphorylation (normoxia: P = 3.17 × 10⁻⁴, hypoxia: P = 1.77 × 10⁻⁸) pathways are significantly enriched by down-regulated genes, under both normoxia and hypoxia conditions. This suggests that the knockdown of APEX1 may lead to inhibited cellular aerobic respiration. In addition, genes regulated by hypoxia-inducible factor 1-alpha (HIF1A), including glycolysis and TCA cycle genes, were observed to be up-regulated in hypoxia conditions compared with normoxia conditions in the control Pa03c cells. This is consistent with the common knowledge of hypoxia response. Of the 14 metabolites, we have seen an increase of abundance in glucose, glucose-1 phosphate, glucose-6 phosphate, and lactate, and decrease in 2-oxoglutarate, succinate, fumarate, and malate in APEX1-KD versus control cells under the normoxia condition. In summary, analysis of the single-cell gene expression and bulk cell metabolomic data revealed that knockdown of APEX1 affects the cells’ glucose metabolism and inhibits the cells’ TCA cycle pathway under both normoxia and hypoxia condition. Figure 4A illustrates the variation of genes and metabolites involved in glycolysis, pentose phosphorylation, TCA cycle, glutaminolysis, and aspartate metabolism pathways in APEX1-KD versus control under the normoxia condition. We conducted a qRT-PCR experiment to confirm the down-regulated genes in glycolysis, TCA cycle, and oxidative phosphorylation pathways (Supplemental Fig. S2). A complete list of differentially expressed genes and pathway enrichment results are provided in Supplemental Table S3.

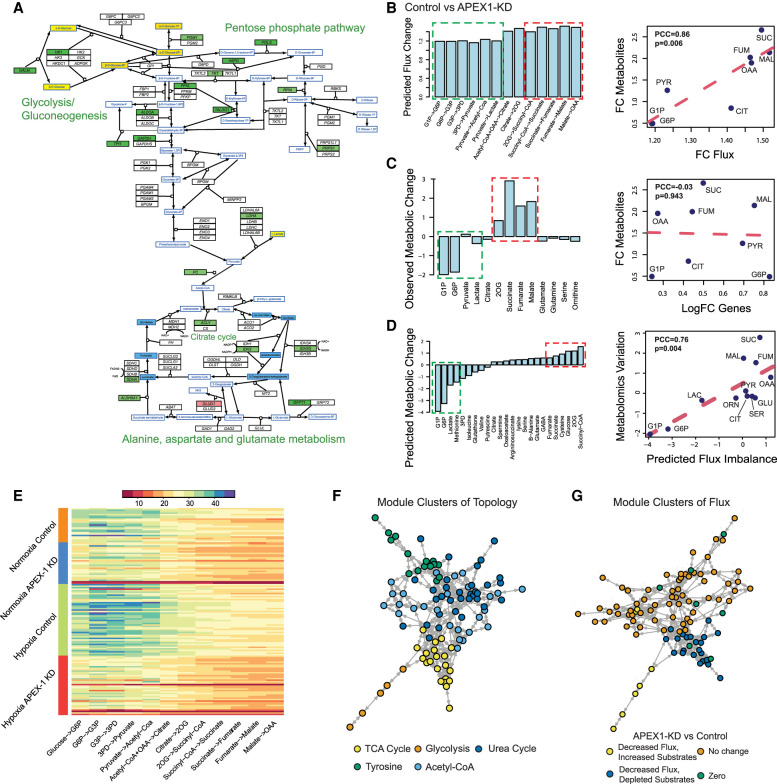
Figure 4.

Application of scFEA on matched scRNA-seq and metabolomics data of Pa03C cells. (A) Gene expression and metabolomic variations of the glycolysis, pentose phosphate, TCA cycle, glutamine, and aspartate metabolic pathways in APEX1-KD versus control under normoxia condition. Genes/metabolites are shown in rectangular boxes with black/blue borders, up-regulated/down-regulated genes are colored in red/green, increased and decreased metabolites are colored in yellow/blue, respectively. The darker color suggests a higher variation. (B) Predicted flux fold change (left, x-axis: metabolic module, y-axis: predicted flux change) in control versus APEX1-KD, and correlation between fold change of predicted flux and observed metabolite change (right, x-axis: fold change of predicted flux, y-axis: fold change of observed metabolite abundance, each data point is one metabolite). (PYR) pyruvate; (CIT) citrate; (FUM) fumarate; (SUC) succinate; (MAL) malate. (C) Observed metabolomic change (left, x-axis: metabolites, y-axis: abundance difference observed in the metabolomics data) in control versus APEX1-KD, and correlation between log fold change of gene expressions involved in each reaction and observed metabolomics change (right, x-axis: log fold change of the averaged expression of the genes involved in each reaction, y-axis: fold change of observed metabolites abundance observed in the metabolomics data, each data point is one metabolite). (D) Predicted metabolic stress (left, x-axis: metabolites, y-axis: predicted abundance difference) in control versus APEX1-KD and correlation between predicted metabolic stress and observed difference in metabolite abundance (right, x-axis: top scFEA-predicted imbalance of the influx/outflux of intermediate metabolites, y-axis: difference of observed metabolomic abundance, in control versus APEX1-KD, each data point is one metabolite: (LAC) lactate; (SER) serine; (GLU) glutamine; (ORN) ornithine. In B–D, all comparisons were made by comparing control versus APEX1-KD under normoxia. The fold change of metabolomic abundance is used in calculating the correlation in B–C and difference of metabolomic abundance is used in D. The green and red dashed blocks represents the accumulated (green) and depleted (red) metabolites in Control versus APEX1-KD. (E) Profile of the predicted fluxome of 13 glycolytic and TCA cycle modules. Here, each column represents the flux between two metabolites (shown on the x-axis) for all the cells of the four experimental conditions (shown on the y-axis). For two neighboring fluxes, the product of the reaction on the left is the substrate of the reaction on the right, and in a perfectly balanced flux condition, the two neighboring fluxes should be equal. (F) Clusters of metabolic modules inferred by using the network connectivity structure only. (G) Clusters of metabolic modules inferred by using the network topological structure (weight of 0.3) combined with the predicted fluxome (weight of 0.7).

Consistency between the scFEA-predicted flux variation and the metabolomics data

We applied scFEA to the aforementioned scRNA-seq data of the four conditions, with hyperparameters α = 1, β = 0, and γ = 1. We first focus on the normoxia conditions in which matched single-cell expression and metabolomics data are available. scFEA-predicted decreased metabolic flux for the modules in glycolysis and TCA cycle in APEX1-KD versus control, that is, glucose → D-Glucose 1-phosphate (G1P) → alpha-D-Glucose 6-phosphate (G6P) → glyceraldhyde-3P (G3P) → 3-Phospho-D-glyceroyl phosphate (3PD) → pyruvate → acetyl-CoA → citrate → 2-Oxoglutarate (2OG) → succinate-CoA →succinate → fumarate → malate → oxaloacetate (OAA) and pyruvate → lactate. Particularly, the reactions toward the downstream from this reaction chain has even lower flux in APEX1-KD versus control (Fig. 4B). We then examined the Pearson's correlation between the averaged predicted flux change with the observed metabolomic change of intermediate metabolites in glycolysis and TCA cycle pathways. In APEX1-KD versus control cells under normoxia condition, we observed a Pearson correlation coefficient (PCC) of 0.86 (P = 0.006) (Fig. 4B), suggesting the high consistency between predicted flux variation with the observed metabolic changes. Using metabolomics data, we observed an increase of production for glucose, G1P, G3P, and lactate, and a decrease of production for 2OG, succinate, fumarate, and malate in APEX1-KD versus control (Fig. 4C). By the Michaelis–Menten model, the substrates of largely varied concentration determine the reaction rate in a nonlinear manner (close to linear when the reaction is less saturated). Hence, variations in the concentration of the metabolites with one dominating outflux could partially reflect the changes of the outflux rate. We also correlated the metabolomic change with the averaged expression change of the enzymes catalyzing the reactions. However, no significant correlation was observed (PCC = −0.03, P = 0.943) (Fig. 4C), suggesting that single-cell gene expression alone does not produce a good estimate of single-cell metabolomic landscape. In addition, single sample gene set enrichment analysis (ssGSEA) has been used to model cell-wise pathway activity in scRNA-seq data (Chen et al. 2020). Again, the correlation between the metabolomic changes and the differences in averaged ssGSEA score in APEX1-KD versus control cells is not significantly large (PCC = 0.42, P = 0.299) (Supplemental Fig. S3). Here, we showed that scFEA-predicted metabolic flux is much more consistent to the true metabolomics changes, as it leveraged the nonlinear relationships between gene expression and enzymatic reaction rate and the flux balance constraints of the metabolites.

High consistency of the predicted metabolic stress with experimentally observed metabolomic changes

scFEA allows us to investigate the cell-wise metabolic stress, which was defined as the imbalance of the influxes/outfluxes of each intermediate metabolite in each cell. Figure 4D shows that the G1P, G6P, and lactate were accumulated while 2OG, succinate, succinyl-CoA, and fumarate were depleted in APEX1-KD versus control. A PCC of 0.75 (P = 0.004) was observed between the predicted metabolic stress and the true metabolic change on 12 metabolites with both measured metabolomic profile and predicted metabolic stress. This shows the high accuracy of the predicted and observed metabolic stress level. Details on the predicted and observed metabolic imbalance were provided in Supplemental Table S3. Figure 4E shows the predicted cell-wise fluxome of the glycolysis and TCA cycle modules for cells of the four conditions. We observed, in general, higher flux of the glycolytic modules than the TCA cycle modules, with the largest average flux gap seen on pyruvate → acetyl-CoA and acetyl-CoA → citrate. In addition, the flux of the downstream reactions (citrate → 2OG → succinyl-CoA → succinate) of the TCA cycle is lower than the upstream reactions (succinate → fumarate → malate → OAA). A possible explanation for the leaky metabolic flux is that some of the intermediate substrates flow to other branches, primarily for biosynthesis of amino acids. Among the four conditions, we identified that the hypoxia control group has the highest flux rate of glycolysis and TCA cycle modules. Clearly, the inhibition of APEX1 significantly decreased the metabolism rate of glucose. Seeing the accumulations of glycolytic substrates and depletions of TCA cycle substrates, we speculate that the knockdown of APEX1 may directly impact the downstream part of glycolysis, the whole TCA cycle and further oxidative phosphorylation, leading to accumulation of G1P and G6P as a result of the blockage. Up-regulation of glucose transporters was also observed in APEX1 KD versus control, further suggesting the accumulation of glycolytic substrates.

Perturbation analysis to detect key flux determining genes

We also conducted a perturbation analysis to detect the key genes with high impact on each metabolic module (for details, see Methods). The following genes were identified to have the highest impact on metabolic flux: HK1 and HK2 (Glucose→G6P, EC: 2.7.1.1); ALDOA, PFKL, and GPI (G6P→G3P, EC: 5.3.1.9); GAPDH and PGK1 (G3P→3PD, EC: 1.2.1.12, 2.7.2.3); ENO1, PGAM1, and PKM (3PD→Pyruvate, EC: 5.4.2.11, 4.2.1.11); PDHA2 (Pyruvate→acetyl-CoA, EC: 1.2.4.1); LDHA (Pyruvate→Lactate, EC: 1.1.1.27); ACLY (acetyl-CoA + OAA→Citrate, EC: 2.3.3.8); IDH2 (Citrate→2OG, EC: 1.1.1.42); DLD and OGDH (2OG→Succinyl-CoA, EC: 1.2.4.2); SUCLG1 (Succinyl-CoA→Succinate, EC: 6.2.1.4); SDHA (Succinate→Fumarate, EC: 1.3.5.1); FH (Fumarate→Malate, EC: 4.2.1.2); and MDH1 (Malate→OAA, EC: 1.1.1.37). Detailed results of the perturbation analysis were illustrated in Supplemental Figure S4. A qRT-PCR experiment was conducted to confirm the down-regulation of the aforementioned key metabolic genes, including HK1, PFKL, ACLY, SDHA, and IDH2 (Supplemental Fig. S2). We also compared the predicted high impact enzymes in the modules containing multiple enzymes (seven in total) with the rate-limiting enzymes reported in the rate-limiting enzymes database (RLEdb) (Zhao et al. 2009). We observed that six of the seven predicted high impact enzymes, namely, 2.7.1.1, 1.2.1.12, 2.7.2.3, 5.4.2.11, 1.2.4.1, and 1.2.4.2, have been reported in RLEdb, suggesting a significant enrichment (P = 0.0005 by Fisher's exact test) of our predictions to RLEdb. We further conducted a module level perturbation analysis by increasing or decreasing the expression of genes in a certain module (Methods). Consistent to our experimental observations, a decrease of expression on genes of the downstream part of glycolysis pathway in the control cells will lower the flux of the TCA cycle, causing the accumulation of glycolytic intermediate substrates and depletion of TCA cycle metabolites.

Detecting groups of metabolic modules with similar variations and cells with distinct metabolic states

We also applied scFEA to a larger metabolic map, with the 11 metabolic supermodules and transporters. Figure 4F illustrated five distinct groups of metabolic modules derived using a spectral clustering method purely based on their network topology (see Methods), namely, (1) glycolysis, (2) TCA cycle and glutamine metabolism–related modules, (3) tyrosine and serine metabolism, (4) urea cycle–related modules, and (5) acetyl-CoA-related metabolisms such as fatty acids and propanoyl-CoA metabolisms. To examine the high-level structure based on the flow of flux, we conducted a clustering analysis of the metabolic modules by considering both the network connectivity and flux similarity. The distance between two modules R_i and R_j is defined as αd(R_i, R_j) + (1 − α)d^F (R_i, R_j), where d(R_i, R_j) is the normalized spectral distance based on the metabolic network connectivity, and d^F (R_i, R_j) is the normalized similarity based on the estimated flux of all the normoxia cells (Methods). Here, α = 0.3 is used in the analysis. Figure 4G shows the metabolic module clusters by integrating topological structure and flux similarity. Four distinct clusters were identified, including (1) glycolysis and fatty acids metabolism of decreased flux and accumulated substrates in APEX1-KD versus control, (2) TCA cycle and pyruvate metabolism with decreased flux and depleted substrates, (3) metabolism of amino acids and other metabolites with unchanged flux and metabolites, and (4) a few other modules of 0 flux rates, respectively. This observation further validated the rationality of the scFEA-predicted fluxome.

We also conducted cell clustering based on the estimated single-cell flux (Methods). It is no surprise that the cell clusters coincide with experimental conditions, forming five groups of cells of high, intermediate, and low metabolic rates, high lactate production, and low TCA cycle rate (Supplemental Fig. S5).

Method validation and robustness analysis on synthetic and independent real-world data sets

Method validation on independent real-world data

We also validated scFEA on an independent scRNA-seq data of perivascular adipose tissue derived mesenchymal stem cells (PV-ADSC) (NCBI Gene Expression Omnibus [GEO; https://www.ncbi.nlm.nih.gov/geo/] accession number GSE132581) (Gu et al. 2019) by using hyperparameters α = 1, β = 0, and γ = 1. To the best of our knowledge, this data set, in addition to our newly generated data set, are the only two scRNA-seq data with matched tissue-level targeted metabolomics profiling available in the public domain. We first reconducted cell clustering analysis and identified two distinct PV-ADSC cell clusters corresponding to different levels of differentiation, as reported in the original work (Fig. 5A; Gu et al. 2019). Here, the clusters were visualized using UMAP (McInnes et al. 2018). Owing to the small sample size (85 cells), scFEA was applied to estimate only the fluxome of glycolysis and TCA cycle pathways. We observed an increased flux of glycolytic reactions (P < 1.56 × 10⁻⁶), lactate production (P = 0.002), and the reactions from cis-aconitate to oxaloacetate in the TCA cycle (P < 0.02) in the more differentiated (MD) versus the high stemness (HS) PV-ADSC cells. The reactions from acetyl-CoA to citrate were not significantly changed (P = 0.887) (Fig. 5B). This is consistent with the observations made on the metabolomics data in the original work; that is, the glycolytic intermediate metabolites, lactate production, and metabolites in the later part of TCA cycle were elevated in the MD cells, but citrate was not significantly changed. We also analyzed the metabolic modules of two amino acid supermodules with metabolomics profile reported in the original study, namely, valine and isoleucine metabolism and glutamate and glutathione metabolism (Supplemental Fig. S6). Elevated valine and isoleucine metabolic flux in MD versus HS cells has been predicted by scFEA, which is consistent to the original report. scFEA also predicted an increased flux of the modules from glutathione → glutamate → glutamine → TCA cycle; this could explain the increased flux rate of TCA cycle but less increase in citrate production. The original study only reported a depletion of glutathione and glutamate; our metabolic stress analysis also predicted more decreased glutathione and glutamate in MD versus HS cells. Our analysis suggested that the elevated glutamate and glutathione metabolism is to fuel the substrate source for TCA cycle in MD cells, which depleted the concentration of glutathione and glutamate.

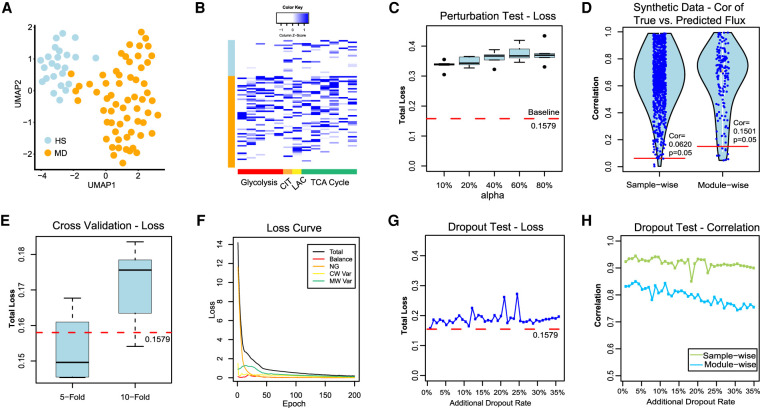
Figure 5.

Method validations on real-world and synthetic data sets. (A) UMAP-based clustering visualization of the GSE132581 PV-ADSC data, in which HS and MD stand for PV-ADSC of HS and more differentiation, respectively. (B) Distribution of predicted cell-wise flux of glycolytic and TCA cycle modules. Each row is one cell, and row side color bar represents HS and MD PV-ADSC by blue and orange, respectively. Each column is one module. The left five columns (red) are glycolytic modules from glucose to acetyl-CoA, the CIT column (orange) is the reaction from acetyl-CoA to Citrate, the LAC column (yellow) is the reaction from pyruvate to lactate, and the right six columns (green) are TCA cycle modules from citrate to oxaloacetic acid. (C) The total loss (y-axis) for cases in which different proportion (x-axis) of cell samples have randomly shuffled gene expressions of the pancreatic cancer cell line data. The baseline loss 0.1579 was computed using the original expression profile of all 166 cells. (D) The sample-wise and module-wise correlation (y-axis) between the true and predicted module flux in synthetic data-based method validation with multiple repetitions, in which Cor = 0.5775 (P = 0.05) and 0.5778 (P = 0.05) correspond to the sample-wise and module-wise correlation, respectively. (E) Total loss (y-axis) computed under 5-fold/10-fold cross-validation (x-axis) versus baseline loss. (F) Convergency of the total loss and four loss terms during the training of neural networks on the pancreatic cancer cell line data. (G) Total loss (y-axis) computed from the robustness test by adding 0%–35% artificial dropouts to the original data (50.22% zero rate) versus baseline loss. (H) Sample-wise and module-wise correlation (y-axis) of the module flux predicted from the data with 0%–35% additional artificial dropouts with the module flux predicted from the original data.

Method validation on randomly shuffled gene expression profile

In scFEA, we assume that the flux distribution in each single cell should be constrained by the flux balance condition, whereas the reaction rate of each module could be modeled as a nonlinear function of the gene expressions involved in this module. These two assumptions suggested that the distribution of the gene expressions involved in the metabolic modules was constrained by a set of equations governed by the metabolic flux distribution and the flux balance condition. One existing evidence that directly supports our assumptions is that the expression of closely related metabolic genes tend to be co-up-regulated or co-down-regulated (van der Knaap and Verrijzer 2016; Li et al. 2018). To further validate our assumption, we randomly shuffled the expression profile of each gene in a certain proportion (10%, 20%, 40%, 60%, and 80%) of cells in our pancreatic cancer cell line data and applied scFEA to each shuffled data (for details, see Supplemental Methods). We observed that the minimized total loss is positively associated with the level of perturbations (Fig. 5C) and the original scRNA-seq data achieved the smallest total loss, which partially supports our underlying assumption.

Method validation on synthetic data

We simulated matched metabolic flux and gene expression data on 1000 single cells. For the 1000 cells, we first randomly generated a different flux distribution of 169 connected modules from the solution space satisfying flux balance condition of these modules. The expression profile of the genes involved in each module was reversely simulated by assuming that its flux follows a fixed nonlinear function of the gene expressions. A detailed data simulation approach was provided in Supplemental Methods. We applied scFEA on the simulated single-cell gene expression profile and compared the fluxome predicted by scFEA and the known fluxome. We observed that scFEA-predicted fluxes are highly consistent to the true flux distribution, on both directions of the cells and metabolic modules (Fig. 5D). Specifically, >99.6% single cells achieved at least 0.0620 (P = 0.05) sample-wise correlation and >84.79% modules achieved at least 0.1501 (P = 0.05) module-wise correlation. Our analysis showed that under the assumption of scFEA, that is, if the flux balance constraint and nonlinear dependency between gene expression and metabolic hold, the formulation and solution strategy of scFEA could accurately estimate the cell-wise fluxome from single-cell gene expression data.

Robustness analysis based on perturbed sample inputs, cross-validation, and analysis of hyperparameters

We also tested the robustness of scFEA by 5-fold/10-fold cross validations on the pancreatic cancer cell line data. Compared with the baseline total loss achieved by using all cells, the total loss of the testing data does not change significantly when using different training cells to train the model (Fig. 5E). In training the neural networks, scFEA used Adam as the optimizer (Kingma and Ba 2015), which can adaptively adjust the learning rate. To choose the most suitable hyperparameters of the four terms in the loss function, we conducted experiments by changing the relative scale of any two terms and fixing the remaining two on the pancreatic cancer cell line data. We changed the relative ratio of two hyperparameters from 10 to 1000. Our experiments suggested a similar optimal solution can always be achieved under our hyperparameter perturbation range (Supplemental Fig. S7). Figure 5F showcases the convergence of the four loss terms and total loss in the model fitting of the pancreatic cancer cell line data. In addition, the applications on six real-world data (see further results) and simulated data suggested that the default hyperparameters always generate results of good convergence of the total loss and high biological implications. The default hyperparameters of the current version and details in hyperparameter running codes were provided via GitHub (https://github.com/changwn/scFEA).

Robustness analysis with respect to a different level of dropout

To further examine the method's robustness, we simulated different levels of additional dropout events to our pancreatic cancer cell line data. Our data was collected by using the Smart-seq2-fluidigm protocol, whose original ratio of zero expressions of the metabolic genes is 50.22%. We simulated additional dropout rate ranging from 4.34% to 34.78%, to reach a typical dropout level of a droplet-based scRNA-seq data (∼85%), and applied scFEA on the tampered data (for details, see Supplemental Methods). We observed that the total loss slightly increases from 0.1649 to 0.2722 when the zero ratio increased from 50% to 85% (Fig. 5G). The module-wise and cell-wise correlation between the flux estimated from the original data and the tampered data are consistently higher than 0.7437 and 0.8505 (Fig. 5H), suggesting the high robustness of scFEA with respect to different levels of dropout events.

Application of scFEA on scRNA-seq data of tumor and brain microenvironment revealed distinct metabolic stress, exchange, and varied metabolic states in different types of cells

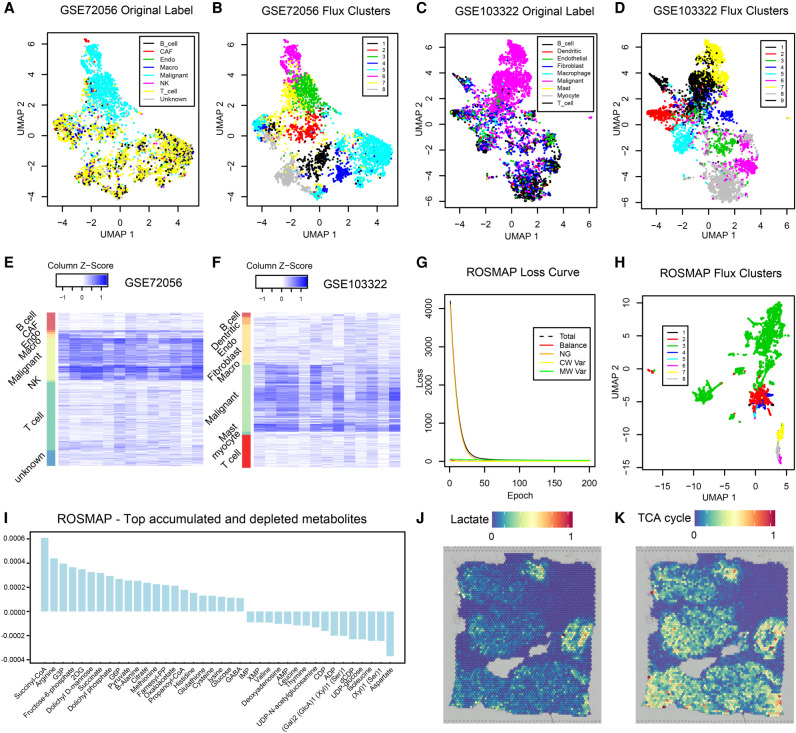
In this section, we primarily focused on validating the computational concept and applicability of scFEA on five real-world data sets, including two scRNA-seq data of cancer microenvironment, one single nuclei RNA-seq data of brain tissue, and one spatial transcriptomics data of breast cancer tissue. The data information is detailed in Supplemental Methods. All 169 metabolic modules across the whole metabolomic network were used in the analysis. Owing to the lack of matched metabolomics information, we focused on demonstrating the capability of scFEA in inferring metabolic flux, metabolic stress, and subgroups of cells and metabolic modules having distinct variations on these data sets.

Application on scRNA-seq data of cancer microenvironment

We applied scFEA on two publicly available scRNA-seq data sets collected from the microenvironment of melanoma (GEO GSE72056) and head and neck cancer (GEO GSE103322) by using hyperparameters α = 1, β = 0, and γ = 1. In both data sets, we generated UMP-based cell and cell group visualization by using predicted fluxomes of the 169 modules (Fig. 6A–D). We identified that the metabolic flux distributions are quite homogeneous within cancer cells while being distinct from immune and stromal cells in both data sets (Fig. 6A,C). Distinct cell clusters of immune and stromal cells corresponding to varied metabolic fluxomes were also identified (Fig. 6B,D). A possible explanation is that cancer cells having a reprogrammed metabolism are more robust to the biochemical variations than immune and stromal cells in the tumor microenvironment.

Figure 6.

Application on two tumor scRNA-seq data sets, ROSMAP, and one breast cancer spatial transcriptomics data set. (A) UMAP-based clustering visualization using predicted metabolic fluxes of the GSE72056 melanoma data; the cell label was provided in the original work (Tirosh et al. 2016). (B) UMAP-based clustering visualization using predicted metabolic fluxes of the GSE72056; k-means clustering was used for cell clustering. (C) UMAP-based clustering visualization using predicted metabolic fluxes of the GSE103322 head and neck cancer data; the cell label was provided in the original work (Puram et al. 2017). (D) UMAP-based clustering visualization using predicted metabolic fluxes of the GSE103322; k-means clustering was used for cell clustering. (E) Distribution of predicted cell-wise flux of glycolytic and TCA cycle modules of GSE72056 melanoma data. Each row is one cell, and row side color bar represents eight cell types. Each column is one module. The left five columns are glycolytic modules from glucose to acetyl-CoA, the sixth column is the reaction from acetyl-CoA to Citrate, the seventh column is the reaction from pyruvate to lactate, and the right-most six columns (columns 8–13) are TCA cycle modules from citrate to oxaloacetic acid. (F) Distribution of predicted cell-wise flux of glycolytic and TCA cycle modules of GSE103322 head and neck cancer data. Each row is one cell, and row side color bar represents nine cell types, respectively. The columns are the same as E. (G) UMAP-based clustering visualization using predicted metabolic fluxes of the ROSMAP data; k-means clustering was used for cell clustering. (H) Convergency curve of the total loss and four loss terms during the training of neural networks on the ROSMAP data. (I) Top accumulated and depleted metabolites predicted in the AD neuron cells in the ROSMAP data. The y-axis is metabolism stress level (or level of accumulation and depletion), where a positive value represents accumulation and a negative value represents depletion. The x-axis are metabolites in a decreasing order of the accumulation level. (J) scFEA-predicted flux rate of lactate product on the spatial breast cancer data. The color of each point represents the spatial-wise predicted lactate product rate. The spatial plot is overlaid on the tissue slice image. (K) scFEA-predicted flux rate of TCA cycle (citrate to 2OG) on the spatial breast cancer data.

We observed that the malignant cells have the highest metabolic rates in most metabolic reactions compared to other cell types in both melanoma and head and neck cancer, especially for the glucose and amino acids metabolic modules (Fig. 6E,F). On average, the TCA cycle and lactate production account for 43.4% and 52.5% of the total glycolysis flux in head and neck cancer, and 65.3% and 46.1% of the total glycolysis flux (with additional carbon flow from other metabolites such as glutaminolysis) in melanoma, respectively. In the nonmalignant cells, the ratio of lactate production is much lower. Our observation clearly suggested the existence of Warburg effect and metabolic shift in cancer cells, which is consistent to our previous findings of high lactate production in melanoma (Xu et al. 2012).

We identified that the malignant cells have the highest metabolic stress, which is defined as the total imbalance of intermediate substrates, followed by fibroblast and endothelial cells and then immune cells. Similar to the pancreatic cancer cell line data, we identified that both cancer and stromal cells in both cancer types tend to have depleted glucose, G1P, and G6P. In addition, cancer cells tend to suffer from a high depletion level of acetyl-CoA. On the other hand, TCA cycle intermediates and amino acids tend to be accumulated in cancer cells. These observations are consistent with the findings derived from quantitative metabolomics data collected on solid cancer (Hirayama et al. 2009).

We noticed that the direction of imbalance for most intermediate metabolites seem to be the same throughout different cell types, although the imbalance level is much lower in stromal cells compared to cancer cells. A possible explanation is that these cells were collected in a small region of the same microenvironment, and the similar stresses, such as hypoxia and altered pH level, cause a similar impact on the metabolic landscape of cells of different types. The predicted cell type–specific fluxome and imbalance level of metabolites were given in Supplemental Table S4.

Application on droplet-based snRNA-seq data of Alzheimer's disease

We also applied scFEA on the ROSMAP single nuclei RNA-sequencing (snRNA-seq) data collected from cells in the central nervous systems of Alzheimer's disease (AD) patients and healthy donors (Mathys et al. 2019) by using hyperparameters α = 1, β = 1, and γ = 1. Specifically, the ROSMAP snRNA-seq data was collected using the 10x Genomics Chromium droplet-based protocol. Comparing to the Smart-seq based scRNA-seq data, droplet-based data often have lower total expression signals and a higher dropout rate. scFEA has been successfully applied on this data set. Changes of the total loss over the running epochs suggested the total loss converge to a small value during the training of the scFEA model (Fig. 6G). Specifically, the flux imbalance loss forms the major loss term in the beginning of the training and quickly converges to a small value, suggesting a solution with good flux balance condition has been identified in this data set. Based on the scFEA-predicted flux, we identified that metabolic activity is higher in neuron cells than in other brain cell types. Cell clusters of different metabolic states were computed (Fig. 6H), in which a large cluster consisting of cells with more active metabolism has been identified (in green). We further studied the metabolic stress of this cell cluster, which is enriched by neuron cells from AD patients (Fig. 6I). We found that glucose, glycolytic and TCA cycle substrates, and glutathione are among the top accumulated metabolites. Suppressed glycolysis and dysfunctional TCA cycle that may lead to increased glucose and other intermediate metabolites, and elevated glutathione in response to reactive oxygen species, have been reported in AD (Atamna and Frey 2007; Mandal et al. 2019; Le Douce et al. 2020). On the other hand, molecules involved in DNA synthesis and valine/leucine/isoleucine metabolism are most depleted in the AD neuron cells, which are consistent to the recently reported observations of suppressed DNA synthesis and valine metabolism in AD (Yurov et al. 2011; Polis and Samson 2020). We predicted aspartate and metabolites involved in glycosaminoglycan synthesis are largely depleted in the AD neuron cells. Previous studies reported the association of these metabolites to AD (Doraiswamy 2003; Huynh et al. 2019), however their abundance change has been less studied. We anticipate that the cell-wise metabolic stress prediction enabled by scFEA could offer novel and systematic insight for biomarker prioritization.

Application on spatial transcriptomics data

As discussed above, distinct cell clusters of different metabolic states were identified in two cancer microenvironment data (GSE72056 and GSE103322) by using hyperparameters α = 1, β = 0, and γ = 1. We speculate that the different metabolic states are caused by varied biochemical conditions, such as hypoxia or oxidative stress level, in the tumor microenvironment. To further validate this hypothesis and the method, we applied scFEA on a spatial transcriptomics data of human breast cancer collected from 10x Genomics visium protocol by using hyperparameters α = 1, β = 0, and γ = 1. Clearly, cells that are spatially near each other should be exposed to similar biochemical stress conditions. We predicted spatial spot-specific metabolic flux by first applying scFEA on the spatial gene expression profile and then conducting associations of the predicted flux with spatial positions. scFEA identified two distinct spatial regions of high lactate production flux (Fig. 6J) and six spatial regions of high TCA cycle flux (Fig. 6K). Ratio of pyruvate → lactate flux and pyruvate → TCA cycle flux were computed, and the two high lactate production regions were predicted as of high hypoxia level, which were further validated by the high expression level of HIF1A-regulated genes in cells of these regions.

Discussion

Despite the ample knowledge we have gained on metabolic dysregulation for many disease types, there are still major gaps in our understanding of the integrated behavior and metabolic heterogeneity of cells in the context of tissue microenvironment. Essentially, the metabolic behavior can vary dramatically from cell to cell driven by the need to cope with various dynamic metabolic stress. A large amount of scRNA-seq has proven its potential in delivering information on a cell functioning state and its underlying phenotypic switches. Designing advanced computational tools to harness the power of large-scale scRNA-seq data for reliable prediction of cell-wise metabolic flux and states is crucial to bridge the technological gap of single-cell metabolomics. Knowledge derived therefrom will substantially benefit our understanding of the metabolic regulation intrinsic to diseased cells and on microenvironmental factors imposed upon the diseased cells and shed light on potential therapeutic vulnerabilities.

scFEA is developed to predict metabolic flux at single-cell resolution from scRNA-seq data, to construct a compendium of metabolic states for different cell types and tissue contexts, and understand their relevance to various disease phenotypes. To experimentally validate scFEA, we generated an scRNA-seq data of a patient-derived pancreatic cancer cells under four conditions of perturbed oxygen level and metabolic regulators and matched tissue-level metabolomics data and qRT-PCR profiles of key metabolic genes. We validated that the variations of metabolic flux predicted by scFEA are highly consistent with the observed metabolomic changes under different conditions. We also applied scFEA on in-drop or droplet-based scRNA-seq data and spatial transcriptomics data. Our analysis suggested that scFEA could robustly predict cell and cell group–specific metabolic shift for the data generated from different protocols. The fluxome estimated by scFEA enables a series of downstream analysis including identification of cell or tissue-level metabolic stress, sensitivity evaluation of enzymes to the whole metabolic flux, and inference of cell–tissue and cell–cell metabolic exchanges.

The scFEA model has the following advantages: (1) the model characterizes true biological flux by leveraging the metabolic network structure, and it is generally applicable as it requires only the input of scRNA-seq data; (2) the number of constraints, that is, the number of flux balance conditions multiplied by the single-cell number, is larger than the number of parameters, avoiding possible overfitting; and (3) the neural network–based flux estimation can well handle the nonlinear dependency between enzymatic gene expression and reaction rates. In the network reduction and reconstruction of scFEA, connected reactions were merged to form one metabolic module. The neural network model allows for a nonlinear dependency between gene expression and module flux. Theoretically, the flux rate could be determined by an “OR” operation of the high expression of any gene involved in the module. scFEA uses neighboring genes on the metabolic map to infer the metabolic flux of connected metabolic reactions, which increases robustness to dropout events and prediction accuracy. Our analysis suggested that scFEA is capable of identifying the interactive effect of multiple rate-limiting enzymes in one module.

scFEA seeks for a constrained optimization of flux balance, and each flux was modeled as a nonlinear function of the relevant enzymatic gene expression levels. The flux of each module is constrained by three additional loss terms, namely, (1) non-negativity, (2) consistency between predicted metabolic flux and gene expression level, and (3) the cell-wise total metabolic activity, TA_j. Although our current setting has been validated using matched scRNA-seq and metabolomics data, applications to publicly available cancer data suggested a similar trend metabolic “imbalance” for both cancer and stromal cells. Our analysis suggested that setting A_mj for each supermodule m in cell j may increase the flexibility of cell-specific metabolic imbalance, but at the price of possible overfitting. A more sensitive approach is to train a specific model for each predefined cell group. The biological rationale is that the neural network parameters contain the information of “kinetic parameters” that link gene expression with metabolic rate, which may differ among distant cell types, or cells under different conditions. Hence it is rational to assume cell type–specific parameters.

In this study, we did not provide a theoretical proof of the correctness of the scFEA model. Future efforts on generating high quality validating data or more comprehensive systems biological derivations could improve the understanding of the dependency between gene expression and metabolic state in individual cells. Compared with the existing FBA-based solutions, which tend to ignore kinetics and assume stringent flux balance condition, our new model treating flux balance as a loss function and seeking for modeling the nonlinear dependency between transcriptome and fluxome is more flexible, robust, and scientifically reasonable. Unlike other FBA-based approaches, scFEA does not require a prior knowledge of the imports and exports of the whole system. The flux distribution, including the influxes/outfluxes of the system, is estimated by minimizing the loss terms through a large number of cells. We consider such a consideration is more suitable for cell-wise flux estimation because the influxes and outfluxes are always cell and context specific and unknown. Although the flux balance in the scFEA model is robust to the stoichiometric coefficients, the predicted fluxome is represented by relative reaction rates scaled by total metabolic activity.

The neural network–based optimization framework of scFEA could enable a potential integration of metabolomics data, kinetic parameters, spatial information, or other prior knowledge of metabolic imbalance, to better characterize cell and tissue-level metabolic shifts of the target system. One future direction is to use metabolomics data, kinetic parameters, or other prior knowledge to better design the first layer of the neural network in modeling the flux of each module. Spatial information can be used to preselect a group of cells for training a spatially dependent model. Another future direction is to implement the current flux estimation analysis in spatial transcriptomics to infer (1) metabolic shifts specific to spatial patterns and (2) metabolic exchange between adjacent cells. This application to spatial transcriptomics data will be particularly interesting for cancer studies, to reveal how the metabolism and macromolecule biosynthesis in stromal cells such as cancer-associated fibroblasts, affect the adjacent cancer cells.

Overall, scFEA can efficiently delineate the sophisticated metabolic flux and imbalance specific to certain cell groups. We anticipate that it has the potential to decipher metabolic heterogeneity, tease out the metabolomic susceptibility to certain drugs, and ultimately warrant novel mechanistic and therapeutic insights of a diseased biological system at an unprecedented resolution.

Methods

Collection of the human metabolic map

We consider the human metabolic network as composed of different reaction types including metabolism, transport (including uptake and export), and biosynthesis. As detailed in Results, the reconstructed network consists of 22 supermodule classes of 169 modules. All reactions related to metabolism were collected from the Kyoto Encyclopedia of Genes and Genomes database (KEGG) (Kanehisa and Goto 2000). In total, 11 metabolism-related supermodules were manually summarized and are made up of glycolysis, the TCA cycle, pentose phosphate, fatty acids metabolism and synthesis; metabolism of amino acids, namely, serine, aspartate, beta-alanine, glutamate, leucine/valine/isoleucine; and the urea cycle, propionyl-CoA, and spermidine metabolism (Cao et al. 2017). The 11 metabolism supermodules contain 1388 reactions, 317 enzymes, which corresponds to 563 genes.

Transporters enable the trafficking of molecules in and out of cell membranes. We collected the human transporter proteins, their corresponding genes, and metabolite substrates from the Transporter Classification Database (Lin et al. 2015; Bhutia et al. 2016). In total, 80 transporter genes and 35 related metabolites were collected.

An essential part of the metabolic map are the biosynthesis pathways. The KEGG database and literature (Moffatt and Ashihara 2002; DeAngelis et al. 2013; Zhang et al. 2015a,b; Krasnova and Wong 2016; Zulueta et al. 2016; Lv et al. 2017; Sun et al. 2018, 2020; Gao and Edgar 2019) are the main information sources used for building biosynthesis modules. We collected 69 biosynthesis modules forming 10 supermodules, namely, biosynthesis of hyaluronic acid, glycogen, glycosaminoglycan, N-linked glycan, O-linked glycan, sialic acid, glycan, purine, pyrimidine, and steroid hormones. Overall, the biosynthesis modules include 459 genes of 269 enzymes catalyzing 869 reactions.

More details of the collection of the human metabolic map and the statistics of the mouse metabolic map are provided in Supplemental Methods.

Selecting genes of significant expression

We applied our in-house method, Left Truncated Mixture Gaussian model (LTMG), to determine the expression status of each gene in each single cell. LTMG considers the multimodality of the expression profile of each gene throughout all the single cells, by assuming that the gene's expression follows a mixture of suppressed state and activated states as represented by the following likelihood function (Wan et al. 2019):

$$\prod _{j=1}^N\left(\sum _{i=1}^S{a}_i{p}_i(x_j|u_i,{\sigma }_i)+a_{S+1}{p}_{S+1}(x_j|u_{S+1},{\sigma }_{S+1})\right),$$

where x_j, j = 1…N is the expression profile of gene x in N cells; the index 1…S are the S active expression states and S + 1 is the suppressed expression state; a_i is the proportion of each state with a₁ + · · · + a_S+1 = 1; a_1…S > 0 and a_S+1 ≥ 0; and p_i, u_i, and σ_i are the pdf, mean, and standard deviation of each expression state. Specifically, LTMG considers the distribution of each mixing component, p_i, as a left-truncated Gaussian distribution to account for the noise of dropout events. In this work, LTMG was used to fit to each gene's expression and a gene was determined to have significant expression if ${\sum }_{i=1}^S{a}_i\ge 0.1$; that is, the gene has active expression states in at least 10% cells.

Prefiltering of active modules based on gene expression

Each metabolic module contains an input, an output, and a number of enzymes catalyzing the reactions. A reaction is considered as disconnected if none of the genes encoding its catalyzing enzymes is significantly expressed. A metabolic module is considered as blocked if there is no connected path from the input to the output. Considering the common dropout events in scRNA-seq data, especially for the drop-seq data, we adopted a conservative approach to pretrim the metabolic modules: essentially, a module will be removed from further analysis if none of the genes involved in all reactions of this module has significantly active expressions.

scFEA model setup and a belief propagation–based solution of the flux model

Model setup

We developed a novel optimization strategy to minimize L similar to the idea of belief propagation (Yedidia et al. 2001). Specifically, the flux balance of each metabolite C_k, $L_K\triangleq {\sum }_{j=1}^N{\left({\sum }_{m\in F_{in}^{C_k}}{\mathrm{Flux}}_{m,j}-{\sum }_{m^{\mathrm{\prime }}\in F_{\mathrm{out}}^{C_k}}{\mathrm{Flux}}_{m^{\mathrm{\prime }},j}\right)}^2$, will be iteratively optimized, by taking into account all the Hop-2 neighbors in the factor graph (metabolites), denoted as Ne(C_k), and Hop-4 neighbors (metabolites), that is, $N{e}^2(C_k):=\left\{C_{k^{\mathrm{\prime }}}\right|C_{k^{\mathrm{\prime }}}\in Ne(Ne(C_k))\mathrm{\setminus }{C}_k\}$. Specifically, for a more efficient optimization, we adopt the idea of belief propagation by minimizing a reweighted flux imbalance: $L_K^{\ast }\triangleq L_K+{\sum }_{C_{k^{\mathrm{\prime }}}\in N{e}^2(C_k)}{W}_{k^{\mathrm{\prime }}}{L}_{k^{\mathrm{\prime }}}$at each iteration, where $W_{k^{\mathrm{\prime }}}$ is a weight value in (0, 1] representing the reliability of the current flux balance of $C_{k^{\mathrm{\prime }}}$. We set $W_{k^{\mathrm{\prime }}}=\exp \left(-{\sum }_{C_{k^{\mathrm{\prime \prime }}}\in Ne(Ne(C_{k^{\mathrm{\prime }}}))\mathrm{\setminus }\left\{C_{k^{\mathrm{\prime }}},C_k\right\}}{L}_{k^{\mathrm{\prime \prime }}}/\left|N{e}^2(C_{k^{\mathrm{\prime }}})\mathrm{\setminus }\left\{C_{k^{\mathrm{\prime }}},C_k\right\}\right|\right)$ as an exponential function of the negative averaged imbalance level of 2-hop neighbors (metabolite) of $C_{k^{\mathrm{\prime }}}$ excluding C_k, with higher $W_{k^{\mathrm{\prime }}}$ denoting lower imbalance level of the metabolites. The intuition is that the more reliable the current flux is estimated for the modules involving $C_{k^{\mathrm{\prime }}}$, which is reflected by the averaged imbalance level of its 2-hop neighbors, a higher weight $W_{k^{\mathrm{\prime }}}$ should be given to $C_{k^{\mathrm{\prime }}}.$ Therefore, that when minimizing L_K, a disruption of the flux balance of $C_{k^{\mathrm{\prime }}}$ of higher weight will be more heavily penalized and less desirable.

Neural network model setup

For each module, a neural network is used to represent the nonlinear dependency between gene expressions and reaction rates. Each neural network has a₁ hidden layers, each with a₂ hidden nodes, and one output node. In this study, we took a₁ = 3 and a₂ = 8. A Hyperbolic Tangent activation function, Tanhshrink(x) = x − tanh(x), is used. The number of nodes and the number of hidden layers determines the complexity of network structure, which impacts the convergence time of optimization. A too simple structure may not fully capture the nonlinear relationship, but a too complex structure may make it difficult to train all parameters and reach convergence. Our organized metabolic modules have an average gene number of eight, which determines the input nodes of scFEA. Because scFEA has 169 parallel subnetworks for each metabolic module, we decide that three hidden layers can leverage the level of nonlinearity and overfitting and ensure a feasible computational cost (for details, see Supplemental Methods).

Clustering analysis of cells with distinct metabolic states

scFEA adopts an attributed graph clustering approach to identify the groups of cells and metabolic modules forming a distinct metabolic state. Two clustering approaches were provided to the results of scFEA for different purposes, namely, clustering of (1) metabolic modules based on the metabolic map and the predicted flux, and (2) cells sharing a common state on the overall metabolic map based on the predicted flux.

Clustering of metabolic modules

Denote the adjacency matrix of the context-specific metabolic map as A^M×M and predicted metabolic flux as Flux^M×N, where Flux_m,j represents the predicted flux rate of the module m in cell j, and a two-stage spectral clustering was applied to cluster the metabolic modules based on A^M×M and Flux^M×N. Specifically, denote A^{F, M×M} as the Euclidean distance of the M modules calculated using Flux^M×N, and D^M×M and D^{F, M×M} as two diagonal matrices, in which $D_{ii}={\sum }_{j=1}^M{A}_{ij}$ and $D_{ii}^F={\sum }_{j=1}^M{A}_{ij}^F$. The normalized graph Laplacian matrices for the network topology and attributes similarity were defined as $L=I-D^{-1/2}A{D}^{-1/2}$ and L^F = I − D^F−1/2 A^F D^F−1/2. The normalized graph Laplacian matrices scale the topological similarity and attributes similarly into the same scale. Denote d(R_i, R_j) and d^F (R_i, R_j) as the Euclidean distance between the metabolic modules R_i and R_j calculated using the smallest P₁ eigenvectors of L and the smallest P₂ eigenvectors of L^F, respectively, the modules were clusters by the k-means method with the following distance measure:

$$\alpha d(R_i,R_j)+(1-a)d^F(R_i,R_j),$$

where α, P₁, and P₂, and the number of clusters are hyperparameters. Our empirical analysis suggested a default setting as α = 0.3, which assigns a higher weight to the similarity of the predict flux; $P_1=\max \left\{3,\mathrm{floor}(\mathrm{\#}SM/2)\right\}$, where $\mathrm{\#}SM$ is the number of supermodules in the current metabolic map; and $P_2=\max \left\{3,\mathrm{floor}(\mathrm{\#}M/17)\right\}$, where $\mathrm{\#}M$ is the number of non-zero modules in the current metabolic map. The number of clusters should be predetermined by users and depends on the number of cells, cell types, and metabolic modules.

Analysis of cell group–specific metabolic stress and metabolic exchanges among cell groups

The cell-wise metabolic flux estimated by scFEA enables the analysis of metabolic stress. For a predefined cell group such as cells of the same type, the total imbalance of each compound will be computed and ranked. A one-way t-test was applied to test if the imbalance is significantly different from 0. The metabolic exchange among different cell groups from one tissue sample was identified as the metabolites with different signs of metabolic imbalance in different cell groups, such as accumulation and depletion, or exporting or importing. Tissue-level metabolic stress is computed as the total imbalance throughout multiple cells.

Perturbation analysis

In scFEA, to evaluate the impact of the change in gene expression on the whole metabolic map, a perturbation analysis is conducted that includes three components: (1) the direct impact of each gene $G_i^m$to the flux module m can be directly computed by its derivative $d{f}_{nn}^m/d{G}_i^m$ for all the modules containing $G_i^m$; (2) the impact of the flux change of one module A on a target module B could be estimated as the variations of flux in B calculated under different values of flux in A, while keeping the other parameters/input fixed, that is, a Monte Carlo–based method; (3) the impact of each gene's expression to the flux of distant modules can be evaluated by integrating (1) and (2) using a chain rule, that is, by first computing the flux change of the modules containing the gene and then evaluating the change of other modules.

Patient-derived cell line models of pancreatic cancer

Pa03C cells were obtained from Dr. Anirban Maitra's laboratory at The Johns Hopkins University (Jones et al. 2008). All cells were maintained at 37°C in 5% CO₂ and grown in DMEM (Invitrogen) with 10% serum (Hyclone). Cell line identity was confirmed by DNA fingerprint analysis (IDEXX BioResearch) for species and baseline short tandem repeat analysis testing in February 2017. All cell lines were 100% human, and a nine-marker short tandem repeat analysis is on file. They were also confirmed to be mycoplasma free.

scRNA-seq experiment

Cells were transfected with either Scrambled (SCR) (5′-CCAUGAGGUCAGCAUGGUCUG-3′, 5′-GACCAUGCUGACCUCAUGGAA-3′) or siAPEX1 (5′-GUCUGGUACGACUGGAGUACC-3′, 5′-UACUCCAGUCGUACCAGACCU-3′ siRNA). Briefly, 1 × 10⁵ cells are plated per well of a six-well plate and allowed to attach overnight. The next day, Lipofectamine RNAiMAX reagent (Invitrogen) was used to transfect in the APEX1 and SCR siRNA at 20 nM following the manufacturer's indicated protocol. Opti-MEM, siRNA, and Lipofectamine was left on the cells for 16 h and then regular DMEM media with 10% serum was added.

Three days posttransfection, SCR/siAPEX1 cells were collected and loaded into 96-well microfluidic C1 Fluidigm array (Fluidigm). All chambers were visually assessed, and any chamber containing dead or multiple cells was excluded. The SMARTer system (Clontech) was used to generate cDNA from captured single cells. The dscDNA quantity and quality was assessed using an Agilent Bioanalyzer (Agilent Technologies) with the High Sensitivity DNA Chip. The Purdue Genomics Facility prepared libraries using a Nextera kit (Illumina). Unstrained 2 × 100 bp reads were sequenced using the HiSeq 2500 on rapid run mode in one lane.

scRNA-seq data processing and analysis

FastQC was applied to evaluate the quality of the single-cell RNA sequencing data. Counts were called for each cell sample by using STAR alignment pipeline (Dobin et al. 2013) against human GRCh38 reference genome. Cells with fewer 250 or more than 10,000 non-zero expressed genes were excluded from the analysis. Cells with >15% counts mapped to the mitochondrial genome were excluded as low-quality cells, resulting in 40 APEX1 KD and 48 Control cells under hypoxia condition and 27 APEX1 KD and 46 Control cells under normoxia condition for further analysis.

We used our in-house left truncated mixture Gaussian model to identify differentially expressed genes (Wan et al. 2019). Pathway enrichment analysis of the genes in the identified biclusters are computed using a hypergeometric test against the 1329 canonical pathways in the MSigDB database (Liberzon et al. 2011), with P < 0.001 as a significance cutoff.

Metabolomic profiling and data analysis

To address the function of the mitochondria, S-1 MitoPlates (Biolog) Mitochondrial Function Assays were performed following the manufacturer's protocol. The assay covers 14 metabolites in central metabolic pathways, namely, glucose, glucose-1 phosphate, glucose-6 phosphate, pyruvate, and lactate in the glycolysis pathway; citrate, 2-oxoglutarate, succinate, fumarate, malate in the TCA cycle; and amino acids glutamate, glutamine, serine, and ornithine. Specifically, assay mix (60 min at 37°C) was added to the plates to dissolve the substrates. We collected, counted, resuspended PDAC cells in provided buffer and plated them at 5 × 104 cells/well after treatment. Readings at 590 nm were taken every 5 min for 4 h at 37°C. Experiments were performed in triplicate with three biological replicates for the siAPEX1 and control PDAC cells under the normoxia condition. Raw data was analyzed using GraphPad Prism 8, and statistical significance was determined using the two-way ANOVA, and P-values < 0.05 were considered statistically significant.

qRT-PCR

qRT-PCR was used to measure the mRNA expression levels of the various genes identified from the scRNA-seq analysis. Following transfection, total RNA was extracted from cells using the Qiagen RNeasy Mini kit (Qiagen) according to the manufacturer's instructions. First-strand cDNA was obtained from RNA using random hexamers and MultiScribe reverse transcriptase (Applied Biosystems). Quantitative PCR was performed using SYBR Green Real Time PCR master mix (Applied Biosystems) in a CFX96 Real Time detection system (Bio-Rad). The relative quantitative mRNA level was determined using the comparative Ct method using ribosomal protein L6 (RPL6) as the reference gene. Experiments were performed in triplicate for each sample. Statistical analysis performed using the 2−ΔΔCT method and analysis of covariance (ANCOVA) models, as previously published (Fishel et al. 2015).

Data access

The raw and processed scRNA-seq data generated in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession numbers GSE99305 (normoxia) and GSE173433 (hypoxia). The scFEA package, full set of process scRNA-seq data, metabolomic profile, and analysis codes used in this work are available at GitHub (https://github.com/changwn/scFEA) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.