Abstract
Mixed models are commonly used to analyze stepped wedge trials (SWTs) to account for clustering and repeated measures on clusters. One critical issue researchers face is whether to include a random time effect or a random treatment effect. When the wrong model is chosen, inference on the treatment effect may be invalid. We explore asymptotic and finite-sample convergence of variance component estimates when the model is misspecified and how misspecification affects the estimated variance of the treatment effect. For asymptotic results, we rely on analytical solutions rather than simulation studies, which allows us to succinctly describe the convergence of misspecified estimates, even though there are multiple roots for each misspecified model. We found that both direction and magnitude of the bias associated with model-based standard errors depends on the study design and magnitude of the true variance components. We identify some scenarios in which choosing the wrong random effect has a large impact on model-based inference. However, many trends depend on trial design and assumptions about the true correlation structure, so we provide tools for researchers to investigate specific scenarios of interest. We use data from a SWT on disinvesting from weekend services in hospital wards to demonstrate how these results can be applied as a sensitivity analysis, which quantifies the impact of misspecification under a variety of settings and directly compares the potential consequences of different modeling choices. Our results will provide guidance for pre-specified model choices and supplement sensitivity analyses to inform confidence in the validity of results.
Keywords: stepped wedge, model misspecification, random effects, variance estimation, model selection
1. Introduction
Stepped wedge trials (SWTs) are a type of cluster randomized trial that have been growing in application.1 In a typical SWT, all clusters begin in the control state at baseline, and at every subsequent time point some of the clusters cross over until all clusters have received treatment. A group of clusters that adhere to the same unique pattern of crossing over is called a sequence or wave. Cross-over times are pre-specified for each sequence and clusters are typically randomized into sequences. See Hughes, Granston, and Heagerty2 for a more thorough introduction to SWTs.
One of the most common tools used for the analysis of SWTs is a mixed model.1 The overall treatment impact is represented by a fixed effect, and because time and treatment are confounded in SWTs it is critical to also include a fixed effect for time.3 The unique SWT structure gives rise to three natural choices for random effects: random intercept effects (sometimes called random cluster effects since each cluster is allowed a unique intercept), random time effects, and random treatment effects. Random intercept effects have been recommended as the most fundamental random effect by Hussey and Hughes.3 Other authors have also recommended adding random time effects4 and/or random treatment effects5 in addition to the random intercept effects. Most researchers using a mixed model for a SWT choose a model somewhere between the “full model” (random intercept, time, and treatment effects) and the random intercepts only model. SWTs that follow cohorts of individuals or that have more than two levels (e.g. subjects are grouped into schools, schools are grouped into school districts) may have additional random effects, but we do not address these designs here. Misspecification of the mean model via fixed effects is also an important topic, but in this manuscript we focus on potential misspecification of the covariance structure via the choice of random effects.
There has been ample research on the impacts of over-fitting and under-fitting random effects in mixed models. Choosing the full model may be inefficient but this strategy ensures that inference on the treatment effect is valid.6 Researchers who choose a random intercepts only model when there are actually additional random effects risk invalid inference on the treatment effect.6 As a result, some scientists advise erring in the direction of including potentially unnecessary random effects.6
Unfortunately, it is not always possible or practical to fit the full model. If a SWT has a limited number of clusters, a researcher might be hesitant to specify such a complex model given limited replication across clusters. Even when a SWT has a large number of clusters, sometimes mixed model software will fit variance components as exactly zero, effectively simplifying the model’s covariance structure; in this case, it may be unclear whether fitted values are actually the maximum likelihood estimators (MLEs) or are the result of algorithm convergence issues that may be associated with multiple roots. Alternatively, software might fit non-zero variance components but encounter other convergence issues, and the researcher might decide to remove a random effect to improve convergence. This decision to reduce the model is equivalent to a partially data-driven model selection procedure, which may not be desirable or appropriate. Some of these issues with model fit can be mitigated without removing components from the model, e.g. using strategies presented by Cheng et al.7 However, if the full model is an over-parameterization, this can cause convergence issues which cannot be mitigated without removing terms from the model. Therefore, choice of a primary pre-specified model is often challenging and driven by both desire for insurance of broad potential validity (favoring more complex models) and desire for stable estimation properties (favoring more simple models).
A researcher selecting a reduced random effects model must decide which component is the least important. In a SWT, the random intercept effects are the highest level of correlation, so we do not want to remove those from the model; instead, we may choose to remove either time or treatment random effects. Unfortunately, practical guidance on model choice and robustness is not readily available in the current literature. Other papers have examined the impact of excluding nested random effects,8 but time and treatment random effects are not nested in SWTs, so it is not immediately apparent which one might be less detrimental to exclude. Thompson et al.4 used simulation studies to examine misspecification of random effects in a specific SWT design. They found that including a random time effect can account for some variation coming from a random treatment effect (and vice versa), although a model with random time effects was more robust than a model with random treatment effects. However, these simulations only covered binary outcomes in a cohort SWT with an unusual design: three sequences observed over only two time points, where one sequence remains exclusively on control, one crosses over, and the last receives treatment at both time points. It is unknown whether the observations from these simulations hold for more general SWT designs.
Although researchers who are interested in a very specific and simple case may find it feasible to explore model misspecification via simulations, there are some issues which make simulation studies unattractive. First, they are very time-consuming, particularly if a study has many clusters or complex random effects. Second, issues with model fit make it difficult to reflect real-life research decisions in automated simulations. For example, Thompson et al.4 excluded simulations where the model failed to converge. Depending on the settings, this resulted in up to 33% of simulations being excluded from the results, potentially biasing conclusions. Last, reliance on simulations may conceal crucial details. For example, if there are multiple asymptotic solutions it may be very difficult to detect that with simulations. For these reasons, we avoid simulations and rely instead on closed-form solutions whenever possible. This enables one to quickly and accurately examine a vast range of settings and reveals some complexities which would be difficult to discern through simulations.
As a motivating example, we consider a study reported by Haines et al.9 that investigated the impact of removing weekend health services (or ‘disinvesting’) from 12 hospital wards in Australia. The original investigators did not report the use of any random time or treatment effects, yet we know that using an over-simplified covariance structure could impact the validity of their conclusions. A complex random effects model would be an ambitious choice given the limited number of clusters. Therefore, we use this concrete example to illustrate the practical issues around selection of alternative covariance models and in this case study we evaluate how that choice may affect inference.
The layout of the paper is as follows: in Section 2, we describe the models and notation. In Section 3, we examine the convergence of the misspecified parameters. In Section 4, we calculate and visualize the asymptotic impact of misspecification on the treatment effect variance. To demonstrate how our results might be used in practice, we apply this research to the disinvestment example in Section 5. Finally, a brief discussion is given in Section 6.
2. Notation and models
2.1. The SWT design
In this paper, we consider SWT designs with M unique treatment sequences, each observed over J time points. We assume that each sequence contains N clusters, and each cluster contains K individuals at each point in time. We assume that each individual is observed only once; that is, a cross-sectional design as opposed to a cohort design. For each sequence, we denote Tm as the number of time points during which sequence m is receiving treatment. Throughout, m = 1 corresponds to the sequence that crosses over first, and m = M corresponds to the last sequence to cross over. Figure 1 shows an example of a ‘classic’ SWT design; that is, every cluster starts on control and ends on treatment, and one sequence crosses over at each time point. In this example, there are M=4 sequences, J=5 time points, N=6 clusters per sequence, and T1=4, T2=3, T3=2, and T4=1. In non-classic designs, modifications might include: extra time on treatment or control; some sequences never receiving treatment or control; or extra time points between transitions. Another common modification to the classic design is to vary the number of clusters per sequence or individuals per cluster; however, these generalizations of N and K are not addressed in this paper. Note that classic designs can be fully described by just M, N, and K, since J=M+1 and T1,…, TM = M,…, 1.
Figure 1:
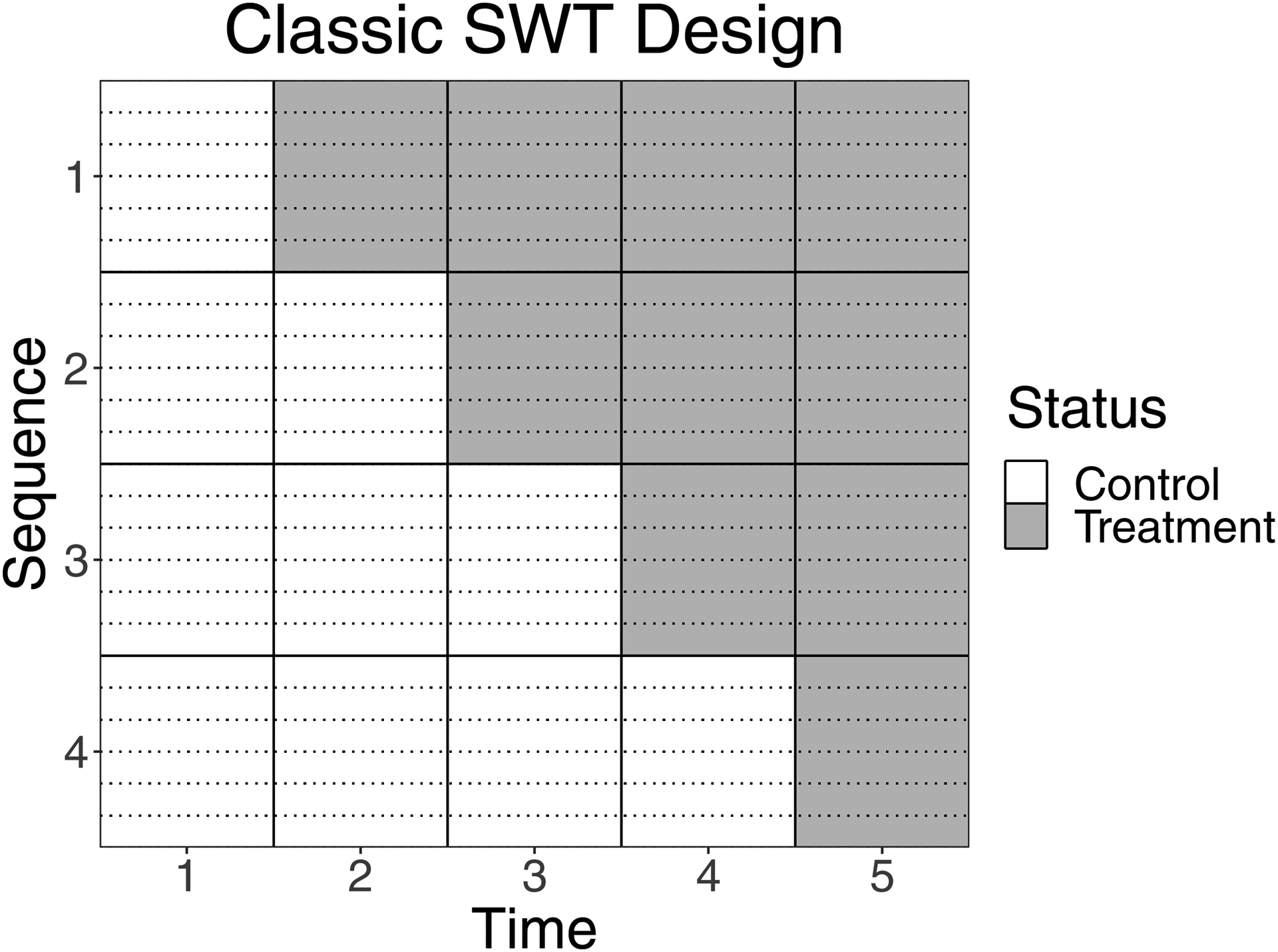
A classic SWT design with M=4 sequences and N=6 clusters per sequence. Dotted lines delineate clusters within sequences.
2.2. The model
Let Yijk denote the response recorded for individual k from cluster i at time j, where k = 1,…, K, j = 1,…, J, and i = 1,…, M * N. Also, let Xij have a value of one if cluster i is assigned to treatment at time j, and zero otherwise. Define the JK-by-1 vector of outcomes from cluster i as Yi = (Yi11, Yi12, …, YiJK)T. Then, for a Normal outcome and identity link, the mixed model can be written as
| (1) |
where Xi is the design matrix for the fixed effects, Φ is the vector of fixed effect coefficients, Zi is the design matrix for the random effects, ai is the vector of random effects, and ϵi is the residual variance. We assume the JK-by-1 vector ϵi has a MVN (0, σ2IJK) distribution, where IJK represents an identity matrix of dimension JK. Throughout, we assume that ϵi and ai are independent. We also assume that ai ~ MVN(0, G), where Zi, ai, and G all depend on which random effects model we select. See below for details.
Although some results hold regardless of the mean model specification, we will primarily be considering fixed effects for just treatment and time, and modeling time as linear. Thus, the fixed effect component for Yijk is μ + (j − 1) * β + θ * Xij, where μ is an intercept, β is the time slope, and θ is the treatment effect. Then we can write Φ = (μ, β, θ)T, and Xi is JK-by-3 with rows (1, j – 1, Xij).
Let α be the vector of all parameters in this model, including Φ, σ2, and any parameters contained in G.
2.2.1. The random time effect model
In the random time effect model, ai = (ui, wi1, …, wiJ)T, where ui is the random intercept effect and wij is the random time effect, treating time as categorical for maximum flexibility. Note that frequently both the fixed and random time effects are categorical, but using the simplified linear fixed time effects allows us to compare designs with different numbers of time points while holding fixed effects constant. The covariance matrix of the random effects is G = diag(τ2, γ2, …, γ2), a diagonal matrix with dimension J+1. Note that this forces the strong assumption that the random intercept and random time effects are all independent. This is sometimes called a nested exchangeable correlation structure. Allowing random time effects to be correlated may be more realistic in some scenarios, but we leave that extension for future work. Zi is a JK-by-(J+1) matrix arranged so that the random effects component of Yijk is ui + wij.
In cluster trials, the intra-cluster correlation (ICC) is frequently used to summarize the dependence between observations within the same cluster.10 Note that, in this model, the ICC is , which represents a ratio of the between-cluster and total variance.
2.2.2. The random treatment effect model
In the random treatment effect model, ai = (ui, vi)T, where ui is the random intercept effect and vi is the random treatment effect. The covariance matrix of the random effects is G = diag(τ2, η2), a diagonal matrix with dimension two. Note that this forces the strong assumption that the random intercept and random treatment effects are independent. Sometimes random intercept and treatment effects are allowed to be correlated,5 which involves an additional parameter. Although a correlation between random effects may be important in some studies, in this paper we make the simplifying assumption of independence for tractability and interpretability of results. Zi is a JK-by-2 matrix arranged so that the random effects component of Yijk is ui + Xijvi.
In this model, ICC is not well-defined because clusters have different correlations while on control and treatment. For convenience, we will define the average cluster correlation (ACC) as , which represents a ratio of the average of the between-cluster and total variances when Xij = 0 and Xij = 1, weighted by the proportion of cluster-time spent on treatment. For a classic design where there are an equal number of cluster-periods on and off treatment, the expression simplifies to . For convenience, we will use ACC to refer collectively to ACC in the random treatment effect model and ICC in the random time effect model. Note that in a random time effect model, since correlation is constant over all clusters and time points, calculating an ACC in an analogous way produces the ICC.
2.3. The misspecified models
We are considering two primary cases. In the first case, the researcher chooses the random time effect model, but the true model is actually the random treatment effect model. We call this the ‘time-fitted random treatment’ case. In the second case, the researcher chooses the random treatment effect model, but the true model is actually the random time effect model. We call this the ‘treatment-fitted random time’ case. Table 1 shows what parameters are fit in each model, and the true parameter values. Throughout, the ‘t’ subscript denotes a true parameter value.
Table 1:
Parameters used in the fitted and true (αt) models for the two cases.
| Model | Fixed effects | Random intercept variance | Random time variance | Random treatment variance | Residual variance |
|---|---|---|---|---|---|
| Fitted model | 0 | ||||
| True model | Φ t | 0 | |||
| Fitted model | 0 | ||||
| True model | Φ t | 0 |
3. Convergence of misspecified parameters
The maximum likelihood estimator of the parameters in the misspecified model (vector , where components depend on the case in question; see Table 1) converges to the value α* that satisfies
| (2) |
where αt represents the true values of the (correctly specified) parameters and pα (Yi|Xi) is the marginal (misspecified) likelihood for cluster i.11 Note that under the model described above, pα (Yi|Xi) is the same for every cluster within the same sequence, and we assumed that each sequence has the same number of clusters N, so using Ym to represent an arbitrary Yi from sequence m we can reduce this equation to:
| (3) |
Thus, the values the misspecified parameters converge to do not depend on the number of clusters per sequence. However, these values can be written as a function of the true parameters (αt) and elements of the SWT design (e.g. M, J, K). Unfortunately, this system is not restricted to a single, unique root. Finding the roots of this system of equations allows us to determine what the misspecified parameters may converge to, which enables us to assess the variance of the treatment effect estimate under a variety of scenarios when the number of clusters N is sufficiently large (see Section 4).
The roots for both misspecification cases are presented below; see supplemental materials for derivation of the system of equations. Because we are using a linear link and only the random effects are misspecified, the fixed effects are unbiased and consistent.6 Note that these roots are valid for any reasonable set of fixed effects, e.g. using categorical time adjustment in the mean model instead of linear. For solving the system of estimating equations, some steps were done using Mathematica, version 12.12
For the time-fitted random treatment case, closed-form solutions could be found for all the roots of Equation 3. We found four different roots which were real and non-negative (see Table 2). Note that these roots all have the same total variance (i.e. the denominator of the ACC), and each root is a linear combination of the true variance components. The total variance is an average between the total variance under control and the total variance under treatment, weighted by how many cluster-periods were on treatment vs control.
Table 2:
Roots of the system of equations in Equation 3. In the treatment-fitted random time case, cells marked ‘No closed form’ indicate values that do not have a simple closed form, but can be found via numerical methods (see supplemental files).
| Time-fitted random treatment | |||
|---|---|---|---|
| Root | σ2* | τ2* | γ2* |
| 1 | |||
| 2 | 0 | ||
| 3 | 0 | ||
| 4 | 0 | 0 | |
| Treatment-fitted random time | |||
| Root | σ2* | τ2* | η2* |
| 1 | No closed form | No closed form | No closed form |
| 2 | No closed form | 0 | No closed form |
| 3 | 0 | ||
| 4 | 0 | 0 | |
For the treatment-fitted random time case, two of the roots (Roots 3 and 4) are analogous to the roots from the time-fitted random treatment case and can be written in closed-form (see Table 2). However, we were not able to obtain closed-form solutions to the other roots (see supplemental files). From numerical solutions, it appears that there are two other roots, one with τ2* = 0 (Root 2) and one with all components non-zero (Root 1). The components of these two roots are more complicated than the ones from the time-fitted random treatment case. Although Roots 3 and 4 have the same total variance of , it is difficult to detect a pattern in the total variance or average total variance of the numerical solutions to Root 1.
In both cases, Root 1 is the most appealing because it does not reduce the desired fitted model and does not have boundary issues like the roots where some components are exactly zero. Roots 2 and 4 are associated with models most scientists would find unsatisfying for an SWT, since they exclude random intercept effects. Root 3 corresponds to a reduced model with only random intercept effects. Although this is a common model used for SWTs, we are considering a scenario where the scientist was originally interested in fitting the richer model so presumably Root 1 would be preferable over Root 3. Based on the abundance of sophisticated model fitting options, we hope that a researcher would rarely be forced to settle for Root 3. In fact, simulations (see Appendix A and Figure A1) show that Root 3 is relatively uncommon even when default fitting procedures are used, especially in scenarios where the study design is large enough to appeal to asymptotics; in those cases, Root 1 is by far the most common.
Because of the appeal and prevalence of Root 1, we will focus the rest of the discussion on this root and refer to it as the unreduced root since all components are nonzero. Researchers interested in other roots may modify the code provided (see supplemental files) to obtain results specific to their design and settings.
4. Impact on treatment effect variance
4.1. Calculating variance
For inference on the estimated treatment effect, we are interested in the variance of the estimated fixed effects . A simple and wide-spread practice is to use the model-based variance.6 However, the true variance of is given by the sandwich-based standard error form, which reduces to the model-based variance when the model is correct.13 Some researchers prefer to use sandwich-based standard errors when there is a sufficiently large number of clusters, since they are consistent regardless of whether the random effects are misspecified.14 In scenarios where use of a sandwich estimator is appropriate, large differences between the model-based and sandwich estimators can indicate model misspecification.15 Throughout, we assume that N is large so that we can rely on asymptotic results on parameter convergence.
For a model with fitted covariance matrices of Σ(α)i = cov(Yi) for clusters i = 1, …, MN, the model-based variance estimate is . Since we assumed every sequence has N clusters and clusters within a sequence all have the same Xi and Zi, we can rewrite this as a sum over sequences: . Note that this is only possible because the fixed effects in this model do not include any additional cluster-level covariates. That is, all clusters within a sequence have a common mean design matrix.
We will use to denote the model-based variance of the estimated treatment effect from the correctly specified model. That is, the covariance matrices are correctly specified and contain the true parameter values.
We will use for the model-based variance of the estimated treatment effect from the misspecified model. This involves the limit of the covariance matrices from the misspecified model, which are functions of the true parameter values. For example, in the treatment-fitted random time case, G will be a 2-by-2 diagonal matrix but instead of plugging in and , we will plug in the roots τ2* and η2*, which are functions of the true parameters , , and (see Table 2).
We will use to denote the true variance of the estimated treatment effect from the misspecified model (‘s’ for sandwich-form, as opposed to ‘m’ for model-based). In the misspecified model the true variance has a sandwich form , where (see above), and . Since the model is misspecified, we use the limit of the covariance matrices again for Σ(α)m, and the true covariance matrices for Σ(αt)m. Note that if the model is correctly specified, this expression simplifies and .
4.2. Ratios of variances
Note that in both the model-based and sandwich-form variance estimators, the only place N appears is as a multiplier of of the whole term, so the ratio of any two of these variances does not depend on N. That is, the multiplicative error of the misspecified model-based variance estimate is constant regardless of the number of clusters per sequence. Because it simplifies discussion of design choice, we will focus on multiplicative differences between variance estimates.
To examine the validity of misspecified model-based variances, we will use . If this ratio is greater than one, it means that using would result in conservative inference. If this ratio is less than one, using is anti-conservative.
To examine how much efficiency is lost by choosing the incorrect model, we will use . Values much smaller than one indicate large losses of efficiency. In situations where it is appropriate to apply the sandwich-form estimator, we would expect this ratio to never be above one.
4.3. Results
Plots and calculations were done with R, version 3.6.1.16
We focus on classic designs for simplicity, since they can be completely described by only M and K. Recall that the validity and efficiency ratios do not depend on N, so these results hold for any number of clusters per sequence.
In the time-fitted random treatment case, we found that the misspecified model-based variance was conservative for some designs, and anti-conservative for others (Figures 2, 3). The validity moved further from one as the number of observations per cluster-period (K) increased. For the time-fitted random treatment case, the trends in validity are dramatically different for a design with two sequences versus a design with more than two sequences, so we address these two scenarios separately.
Figure 2:
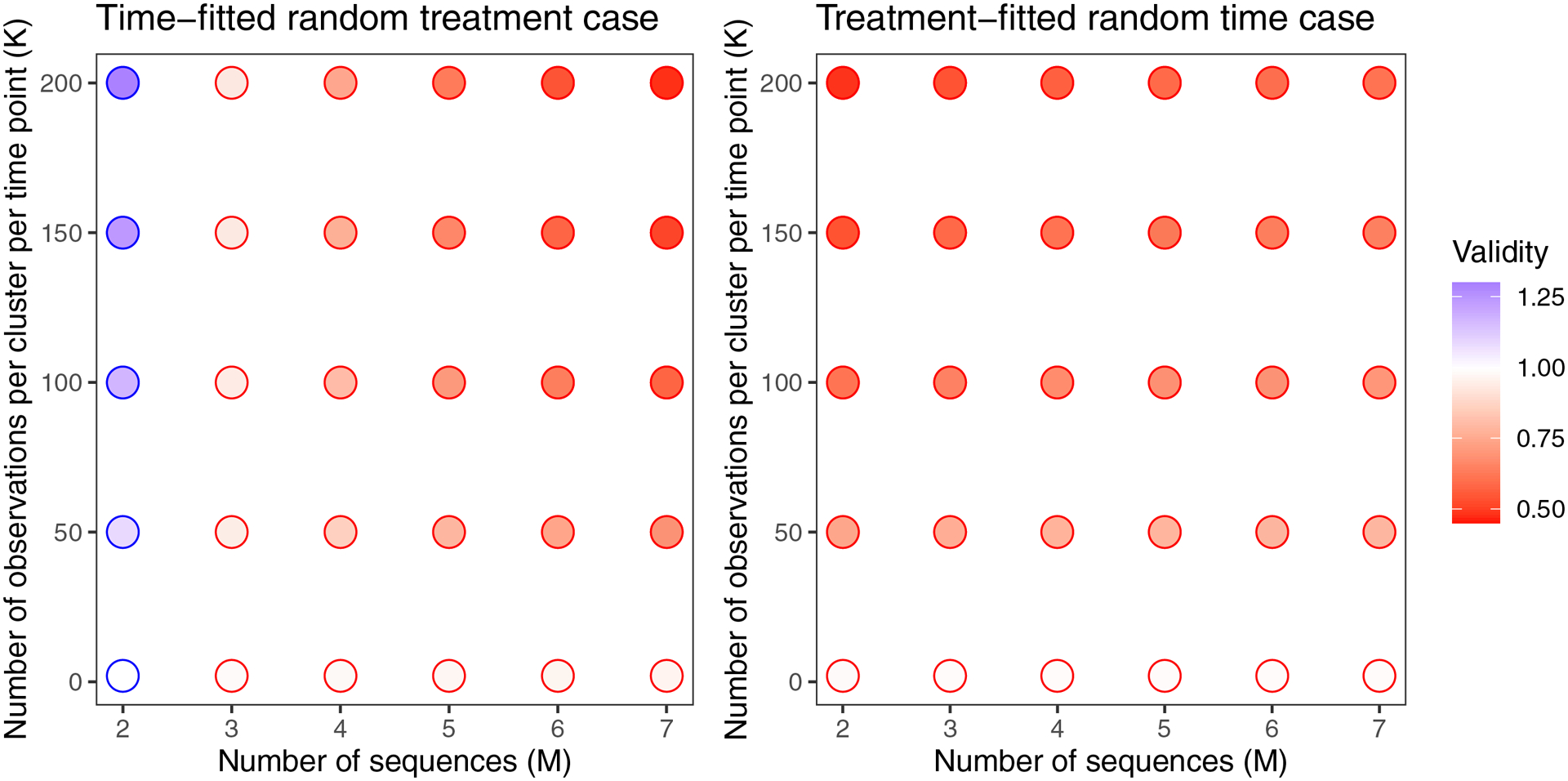
Validity of Root 1 for both cases, for a variety of classic designs. Ratios above 1 (indicated by blue outlines) correspond to conservative estimates. Ratios below 1 (indicated by red outlines) correspond to anti-conservative estimates. For each case, and . To keep the ACC consistent, we chose and for the time-fitted random treatment and treatment-fitted random time cases, respectively.
Figure 3:
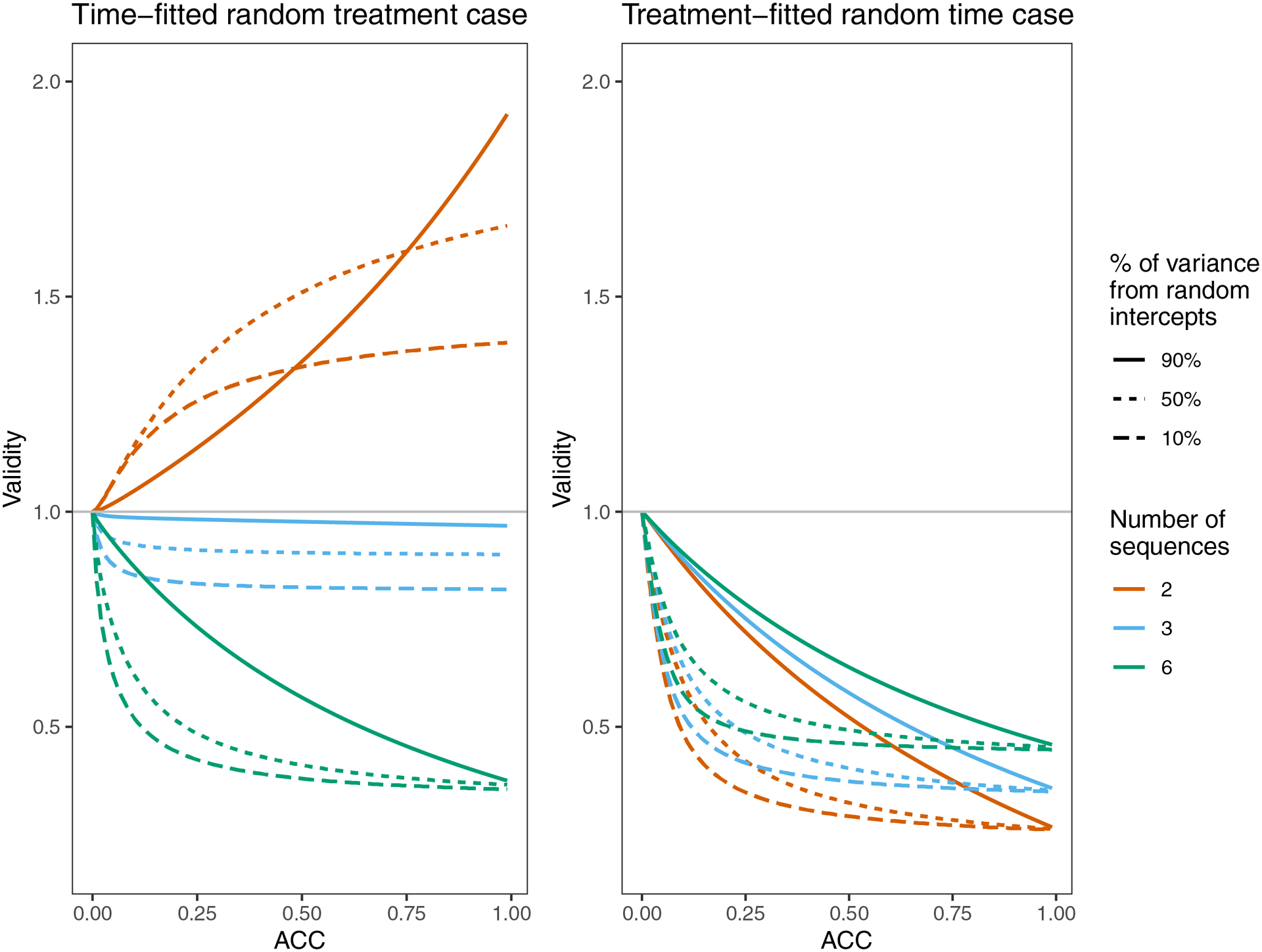
Validity of Root 1 for both cases, for three designs and a variety of true ACC’s. The three classic designs (M=2, M=3, and M=6 sequences) each have K=20 observations per cluster per time period. Throughout, . Each ACC is achieved in three different ways by adjusting the balance of and or . If or , 50% of the average between-cluster variance (the numerator of the ACC) comes from random intercepts. Similarly, if or , then 90% of the variance comes from random intercepts and if or , then 10% of the variance comes from random intercepts.
For a design with two sequences in the time-fitted random treatment case, was conservative for all the scenarios examined here. The validity was worse with high ACC, but trends related to the relative size of random intercept effects vs. treatment random effects were unintuitive and dependent on the ACC (Figure 3).
For designs with more than two sequences in the time-fitted random treatment case, was anti-conservative for all the scenarios examined here, and would therefore lead to inflated Type I error. In the scenarios we examined, was the worst for: larger number of sequences; higher ACC; and larger contribution of to the average between-cluster variance (Figures 2, 3).
For the treatment-fitted random time case, we found that the misspecified model under-estimated the variance of the treatment effect in all the scenarios we examined (Figures 2, 3). The validity moved further from one as the number of observations per cluster-period (K) increased. For the treatment-fitted random time case, validity of was worst for: smaller number of sequences; higher ACC; and larger contribution of to the average between-cluster variance.
In both cases, for the scenarios examined in Figure 2 (classic designs with 2 ≤ M ≤ 7, K ≤ 200, and , , or so ACC=0.03), the loss of efficiency from using the misspecified model with a robust variance was not more than 5% (Figure A2). Also, in both cases efficiency worsens as K increases. For an ACC of 0.03, loss of efficiency is not very significant; however, in some scenarios efficiency can be impacted dramatically (Figure 4). For the time-fitted random treatment case, efficiency is worse for higher ACC and larger when there were two or three sequences. For the six-sequence design, these trends only hold for some ranges of ACC and/or . For the treatment-fitted random time case, efficiency is worse for higher ACC and larger .
Figure 4:
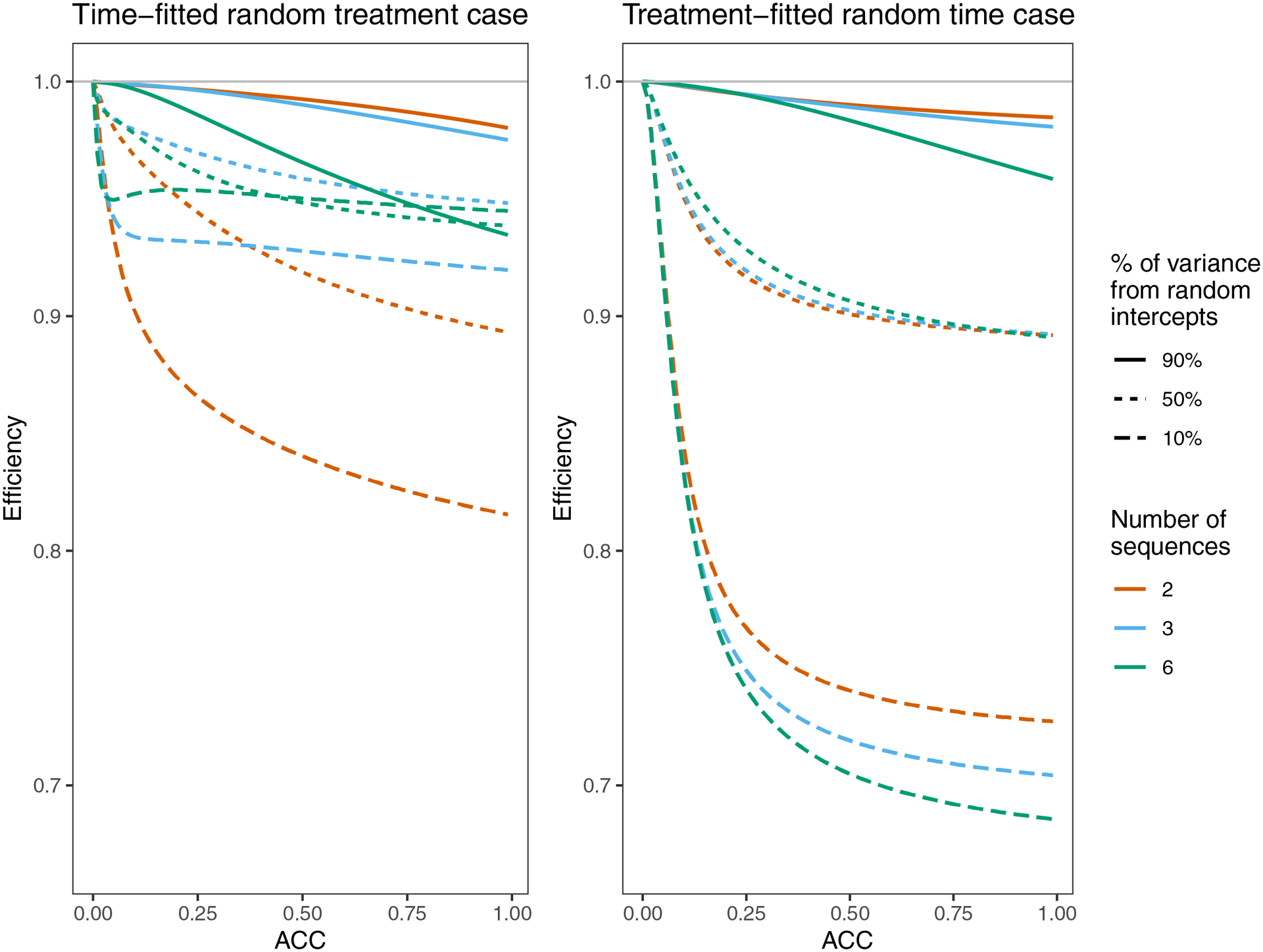
Efficiency of Root 1 for both cases, for three designs and a variety of true ACC’s. The three classic designs (M=2, M=3, and M=6 sequences) each have K=20 observations per cluster per time period. Throughout, . Each ACC is achieved in three different ways by adjusting the balance of and or . If or , 50% of the average between-cluster variance (the numerator of the ACC) comes from random intercepts. Similarly, if or , then 90% of the variance comes from random intercepts and if or , then 10% of the variance comes from random intercepts.
The relative loss of efficiency for the two cases depends on the study design and values of the true variance components. However, in the scenarios considered here the treatment-fitted random time case had the largest potential losses in efficiency (Figure 4).
For non-classic designs, it is very difficult to predict trends in validity, and even (for the time-fitted random treatment case) whether the misspecified model is conservative or anti-conservative (see Appendix B). For some non-classic designs, whether the misspecified model is conservative or anti-conservative even depends on the ACC (Figure A3). Researchers wondering about a specific design can use the roots in Table 2 (or system of equations in the supplemental files, for the treatment-fitted random time case Roots 1 and 2) to calculate validity and efficiency for their exact design. These roots hold for many non-classic designs but do rely on the assumption that the number of clusters per sequence and number of observations per cluster-period are constant.
These results have demonstrated some broad trends in validity and efficiency and have shown that the impact of misspecification can be very severe. Although we examined only classic designs here, it is clear that the precise design of a SWT plays a key role in how misspecification affects inference. For this reason, it is important for researchers to examine these effects for their specific SWT design. See supplemental files for R code which can be used to perform these calculations, which can be easily adapted for most SWT designs, alternative roots, and other ways of modeling time. Other fixed effects can also be included, although consideration must be given to the asymptotic nature of these results.
5. Example
We will use a study reported by Haines et al.9 as an example of how these results might be used. Researchers conducted a SWT in two metropolitan teaching hospitals in Australia. The study involved 14,834 patients clustered into 12 hospital wards. Researchers were interested in the effect of removing weekend allied health services from wards, which included physical therapy, social work, and other patient services. Researchers listed several outcomes of interest, but for the purposes of this example we will focus on log-transformed length of stay in days. Start times at the two hospitals were slightly different, but for simplicity we will disregard this so that we are considering a classic six-sequence SWT with two clusters in each sequence. We will also assume that there was no hospital-level clustering, although it would be straightforward to add hospital as a fixed effect.
Haines et al.9 used mixed-effects models, but focused on traditional nested mixed effects (i.e. hospital and ward effects). Suppose that we are conducting a post-hoc exploratory analysis which also considers random time and treatment effects. Using the data published by Haines et al.,9 we attempt to fit a full model with random intercept, time, and treatment effects in R (see supplemental files for code and complete output). Unfortunately, we find that the fitted random treatment variance is zero, and additional warning messages suggest that the fitted values may not be very accurate. For the purposes of this example, suppose we have followed the suggestions of Cheng et al.7 without success (see supplemental files for details), and that there is no previously reported study which can be used to inform the choice of random effects in this particular setting.
To improve model fit, we abandon the full model and fit two reduced models: a random time effect model, and a random treatment effect model. Both models produce similar estimates of the random intercept standard deviation (SD) τ (0.28) and residual SD σ (1.02 vs. 1.03 for the random time and random treatment models, respectively). In the random time model, the estimated random time SD γ is 0.12. In the random treatment model, the estimated random treatment SD η is 0.10. Unfortunately, these two models also produce different estimates of the treatment effect (0.13 vs. 0.10) and model-based treatment effect standard error (0.05 vs. 0.04). We might be inclined to use the random time model, since that was favored when fitting the full model. However, information on which model is more robust to misspecification might influence our decision. Quantifying the impact of potential misspecification may also affect our confidence in our results.
Figure 5 shows the impact on validity of the two models considered in this example. Using the results of the reduced models in which both random time and treatment SDs were around 0.1, it is clear that choosing the wrong model in this scenario could have a dramatic effect on the validity of our conclusions, underestimating the variance of the treatment effect by around 35% asymptotically. The impact of incorrectly excluding a random time effect is slightly more extreme than the impact of incorrectly excluding a random treatment effect. These results support the choice of the random time effect model. However, because the effect of misspecification may be large in this scenario, these results also suggest that scientific conclusions from the random time effect model should be made with caution. We did not examine trends in efficiency for this example, since calculating a sandwich variance based on only 12 clusters may not be advisable.14
Figure 5:
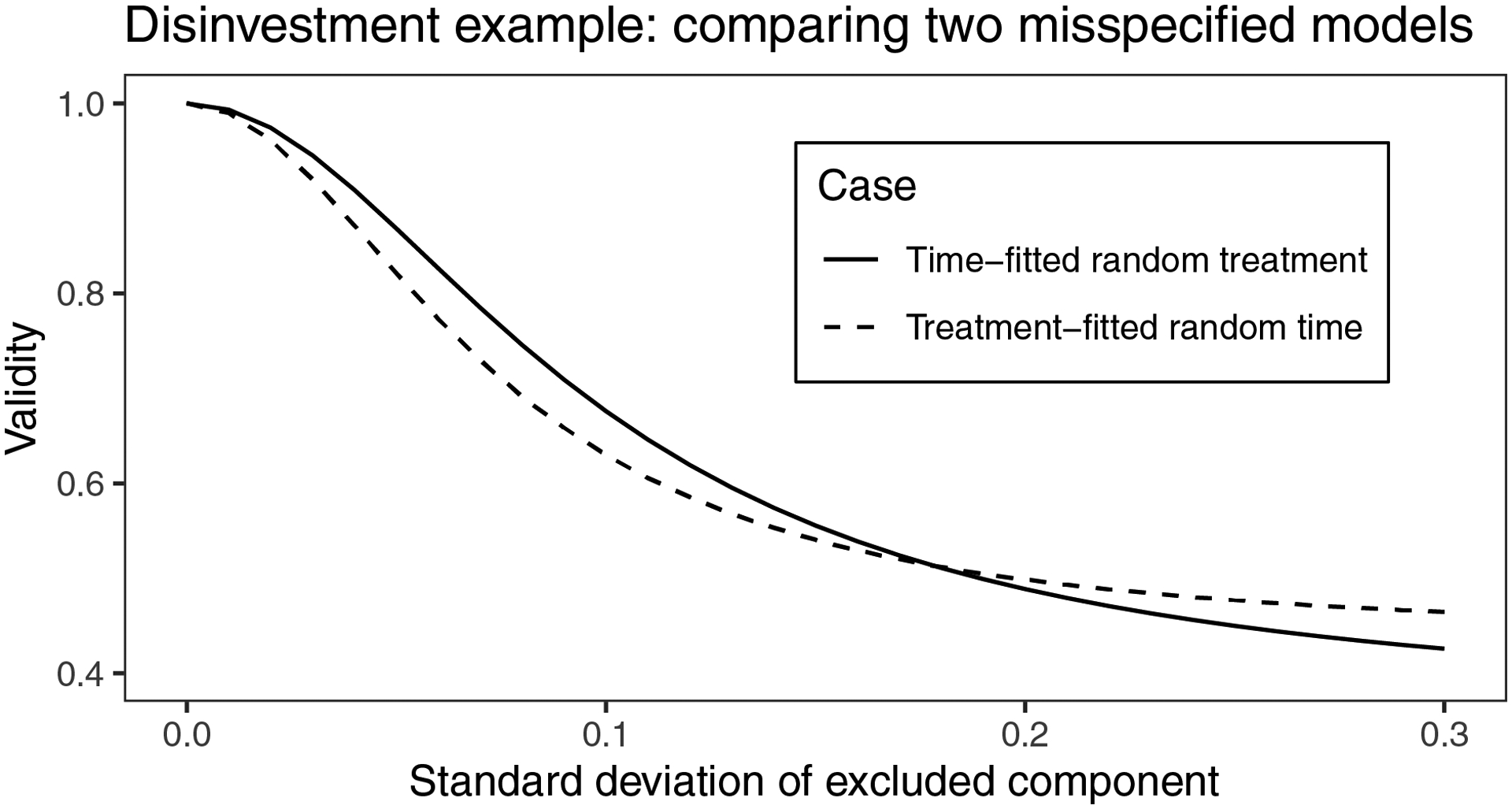
Validity of the two proposed models in the disinvestment example if they were both misspecified. Throughout, τt = 0.28 and σt = 1.03 were fixed, based on their average fitted values from the two models. We assumed there were K=177 observations per cluster per time period, which was the average K across the trial.
6. Discussion
In this paper, we have explored how choosing the wrong random effect in a SWT mixed model analysis can affect the estimated variance of the treatment effect. Since our method relies on analytical solutions instead of simulations, we were able to precisely study a vast landscape of study designs and settings. We focus here on the results for scenarios most relevant to a SWT: small ACC (<0.25) and the variance of the excluded random effect makes up a small portion of the average between-cluster variance. Some unsurprising trends hold across both cases. Validity and efficiency tended to be closer to 1.0 for smaller ACC and smaller variance of the excluded random effect. Other trends were more unexpected. Validity and efficiency both worsen as the number of observations per cluster-time period K increases. When the true model includes a random treatment effect but the researcher incorrectly fits a random time effect (time-fitted random treatment case), the number of sequences in a classic design has a dramatic impact on trends in both validity and efficiency. Our exploration of efficiency showed that in most cases, the cost of using the misspecified model with sandwich-based variance is relatively small. Although it was not the focus of this paper, researchers might consider using robust variance estimates when there are a sufficient number of clusters.
We used analytical solutions instead of simulations, which avoided some key issues. In addition to the obvious computational burden and variability of results, simulation studies in these types of settings can struggle significantly with the convergence of fitted models. This reduces efficiency and could bias results. Using analytical solutions also allowed us to gain more insight into the details of the model misspecification. For example, if we had used simulations we would not have detected the issue with multiple roots.
Through our motivating example, we have demonstrated how our methods may be used as a sensitivity analysis to assess robustness to misspecification without the use of simulations. Ideally, model selection including the choice of random effects would be informed primarily by scientific beliefs and analyses of similar data. However, when choosing random effects these may not be readily available, forcing researchers to rely more heavily on other considerations such as robustness to misspecification. For a large trial, if researchers have already committed to using robust standard errors then it may be helpful to focus on efficiency as a metric for model choice instead of validity.
In our motivating example, we used the data to inform assumptions about values of true variance parameters. To use this method for creating a pre-specified analysis, assumptions about true variance parameters would be based on pre-existing data17 and scientific beliefs instead of being estimated from the data of interest. This may sometimes be difficult, but we hope researchers can draw on their experience in estimating power for SWTs, since the methods of making assumptions about variance components before data collection should be similar. If some parameters are particularly difficult to estimate, it is easy to consider a range of potential values as we did in our example. In settings with abundant pre-existing data from similar studies, it may be possible to use that data to directly test for the existence of specific random effects.
The practical impact of the existence of multiple asymptotic solutions is unclear. Since these are asymptotic results and simulations suggest that the unreduced root (Root 1) becomes more common as the number of clusters increases, we believe that our focus on the unreduced root is appropriate for studies that are large enough to appeal to asymptotics. We informally examined some simulated datasets to determine whether multiple roots might exist for a single dataset. Although this was not an exhaustive analysis, we found no evidence of multiple roots within a dataset, so we hypothesize that this is a between-datasets issue rather than within-datasets. To see whether the issue of multiple roots is unique to misspecified models, we examined the behavior of a correctly specified model using the same methods described in this paper. In the few cases we checked, the correctly specified model equations also had four potential roots following the same pattern as the four roots identified in misspecified models, with only one root having all nonzero components. Although solutions on the boundary corresponding to roots 2, 3, and 4 occur in correctly specified models, consistency of the maximum likelihood estimator suggests that only Root 1 is asymptotically relevant when the model is correctly specified.
These results cannot be applied directly to simulations done by Thompson et al.4 since those simulations were for a cohort SWT with binary outcomes. However, our observations suggest that the specific SWT design can have a dramatic impact on results, and even the direction (conservative vs. anti-conservative) of validity in the time-fitted random treatment case. Thus, researchers concerned about misspecification in cohort SWTs with binary outcomes may want to conduct their own simulations similar to those done by Thompson et al.4 instead of relying on results that may not generalize to other SWT designs.
Some of the assumptions about the mixed models we considered here may be particularly restrictive. Because we focused on a Normal outcome with a linear link, our marginal and conditional fixed effects are equivalent and unbiased. With other link functions, marginal and conditional effects may differ, and the estimated treatment effect may be biased when random effects are misspecified. The assumption that all random effects are independent also has important implications. In particular, assuming that the random treatment effect is independent of the random intercept effect implies that variability of the outcome is higher in the treated time periods compared to control. Since these results about efficiency and validity are driven by nuanced differences in random effect structures, the exact correlation structure may be important. In addition to adding correlation between the random intercept and other effects, researchers might consider the many ways that random time effects could be related within a cluster. Popular choices include exchangeable and exponential decay models, but more complex alternatives are possible. Researchers could even consider a scenario where the true model is the full model, with correlations between random treatment and random time effects as well. Because of the complexity and diversity of these extensions, we have not addressed them in this paper. However, we have provided a Mathematica file that demonstrates how to obtain solutions for some of these extended cases. Alternatively, researchers could turn to simulations like Thompson et al.,4 who did allow for correlation between some random effects. Last, the fixed effects we considered were very minimal; in particular, we used a linear model for the fixed time effect, whereas it may often be important to use a more flexible model for time. If a model for time where the number of parameters depends on the study design (e.g. modeling time as categorical with J-1 indicator variables) is used, the trends relating validity or efficiency to the number of sequences may be different. Researchers familiar with R can modify the functions provided in the supplemental files in order to account for additional fixed effects or a more flexible time model.
We hope that scientists struggling to choose between random time effects and random treatment effects can use these results to understand how model choice might impact the validity and efficiency of inference on the treatment effect. Although there is no universal ‘correct’ choice, for some scenarios validity and efficiency are dramatically different between the time-fitted random treatment case and the treatment-fitted random time case. Particularly when supplementary data and pre-existing scientific beliefs are weak, the methods presented in this paper can be an important tool for developing statistical analysis plans and performing sensitivity analyses.
Supplementary Material
Acknowledgements
Research reported in this paper was supported in part by the National Institutes of Health under award number AI29168. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Appendix
Appendix A:
Relative frequencies of roots
To understand the practical importance of the roots of Equation 3, we use simulations to examine the relative frequencies of different roots under a variety of circumstances. We used the lme4 package18 (lmer command) in R (version 3.6.1)16 to fit mixed models, but these results may be different for other software. For example, one important characteristic of the lme4 package is that it allows fitted variance components to be exactly zero; other software packages that do not allow this may have a dramatically different distribution of roots. For these simulations, we used all the default settings in lme4, including fitting models using restricted maximum likelihoods (REML). In this paper, we present results from two designs: one minimal SWT design, and one large SWT design. The minimal design is a classic design with two sequences, six clusters per sequence, and two individuals per cluster per time point. The large design is a classic design with six sequences, ten clusters per sequence, and 100 individuals per cluster per time point. So the total number of clusters is 12 and 60 for the minimal and large designs, respectively; the total number of individual observations is 72 and 42,000. We also considered different true values of the variance components. Fixing , we allowed , , and to be either 0.001 or 0.125. For both cases, we examined all four combinations of large and small variance components. Throughout, we fit a model with a minimal number of fixed effects (see Section 2.2). For each setting, relative frequencies were calculated based on 1,000 replications.
The results of these simulations are presented in Figure A1. For both misspecification cases, prevalence of Root 1 increased as the total sample size MNK increased. In some scenarios with sufficiently large total sample size, Root 1 was the only root observed. For the time-fitted random treatment case when the random treatment effect was small, Root 3 was relatively common even when the total sample size was large. Roots 2 and 4 were only present when the total sample size was small. For the treatment-fitted random time case when the random time effect was small, Root 2 was relatively common even when the total sample size was large. Roots 3 and 4 were only present when the total sample size was small.
Through careful use of software settings and other strategies,7 it is possible to increase the prevalence of Root 1. Thus, these results are a ‘lower bound’ on how common Root 1 is. Additionally, we intentionally included settings which increase the presence of other roots (i.e. a very small minimal design, and a very small variance component lower bound). We would expect reasonable settings for most SWTs to be less extreme, and have a higher prevalence of Root 1. The results of these simulations support the decision to focus on Root 1 in this paper.
Appendix B:
Non-classic designs
For simplicity, we have focused primarily on classic designs. However, there are a wide variety of SWT designs that do not follow the standard crossover schedule that typifies a ‘classic’ SWT. For example, some SWTs may observe all sequences in the control condition for multiple time periods before beginning crossover. Figure A3 compares the validity and efficiency for some non-classic designs that have differing numbers of all-control periods as an example of how relatively simple design changes can impact inference. Because the design elements of a SWT are inexorably linked, it is difficult to isolate the effects of design choices. For example, in Figure A3, adding extra all-control periods also increases the total number of time points, increases the total number of observations, and changes how much of the total variation is attributed to the random treatment effect (by changing the proportion of cluster-periods that are assigned to treatment ). One plausible explanation for the association between worsening validity and adding extra control periods in Figure A3 is that when is close to zero, most cluster-periods have no additional variation beyond a random intercept, which causes the variance of a fitted random time effect to be close to zero. In contrast, in a classic design where , half of the cluster-periods have no additional variation and half have some additional variation from the random treatment effect, so we might expect a fitted random time effect to be a more balanced average between those states that has more flexibility to account for variation coming from the random treatment effect. Although it is difficult to identify universal trends in non-classic designs because of their complexity, the supplemental materials provide code that allows researchers to explore many non-classic designs. One important type of non-classic design which is not covered in the supplemental materials is a design in which the number of observations per cluster-period (K) varies. Simulations suggest that having a sample size that differs by sequence and/or time period can affect validity and efficiency, possibly by affecting the relative weights of cluster-periods on treatment and control.
Figure A1:
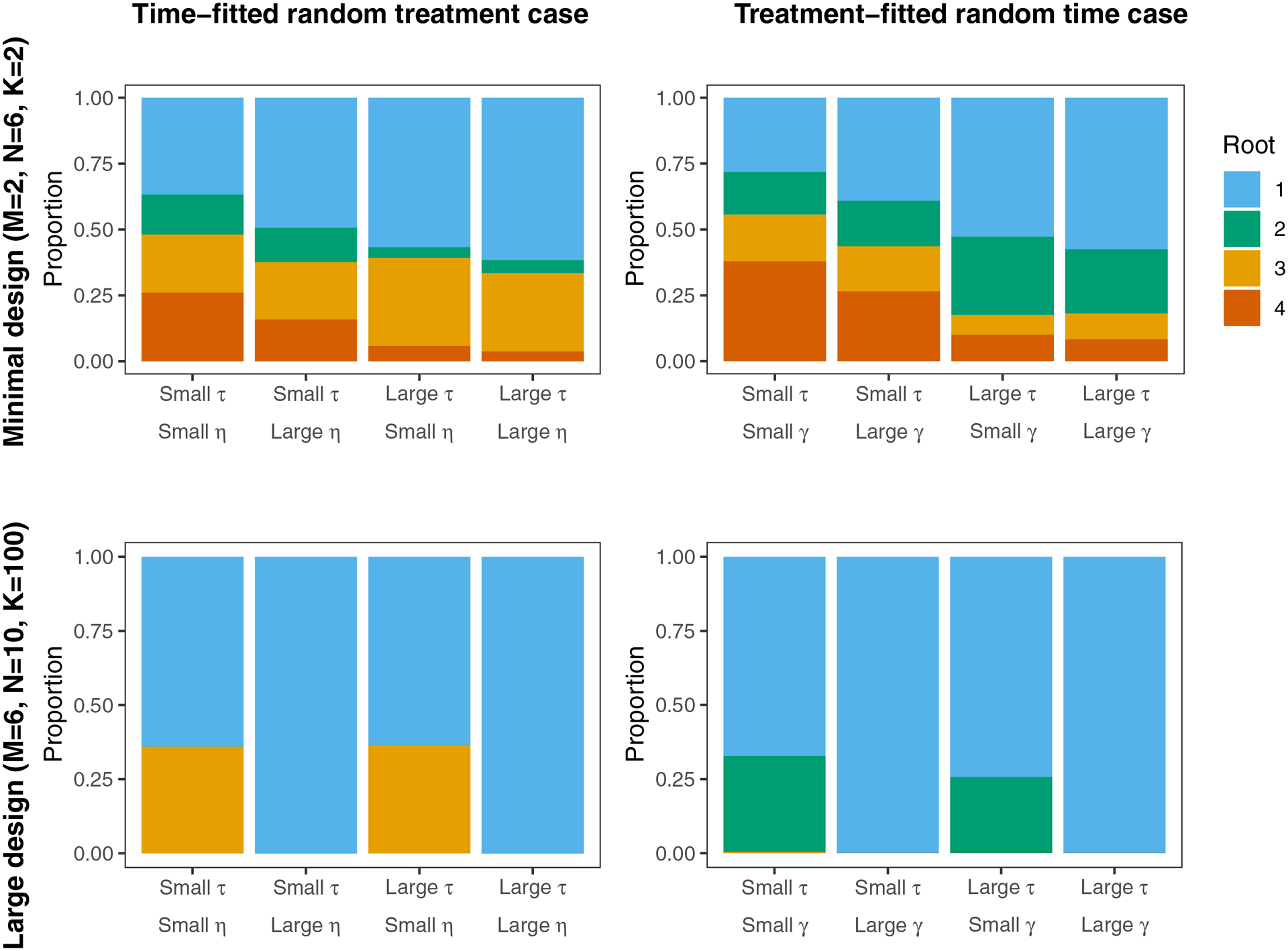
Frequency at which each root is observed in simulations using lme4’s default settings. Throughout, . For the ‘large’ values of , , and , we used 0.125. For the ‘small’ values, we used 0.001. Note that these correspond to ACCs ranging between 0.001 and 0.16 for the time-fitted random treatment case, and ranging between 0.002 and 0.20 for the treatment-fitted random time case.
Figure A2:
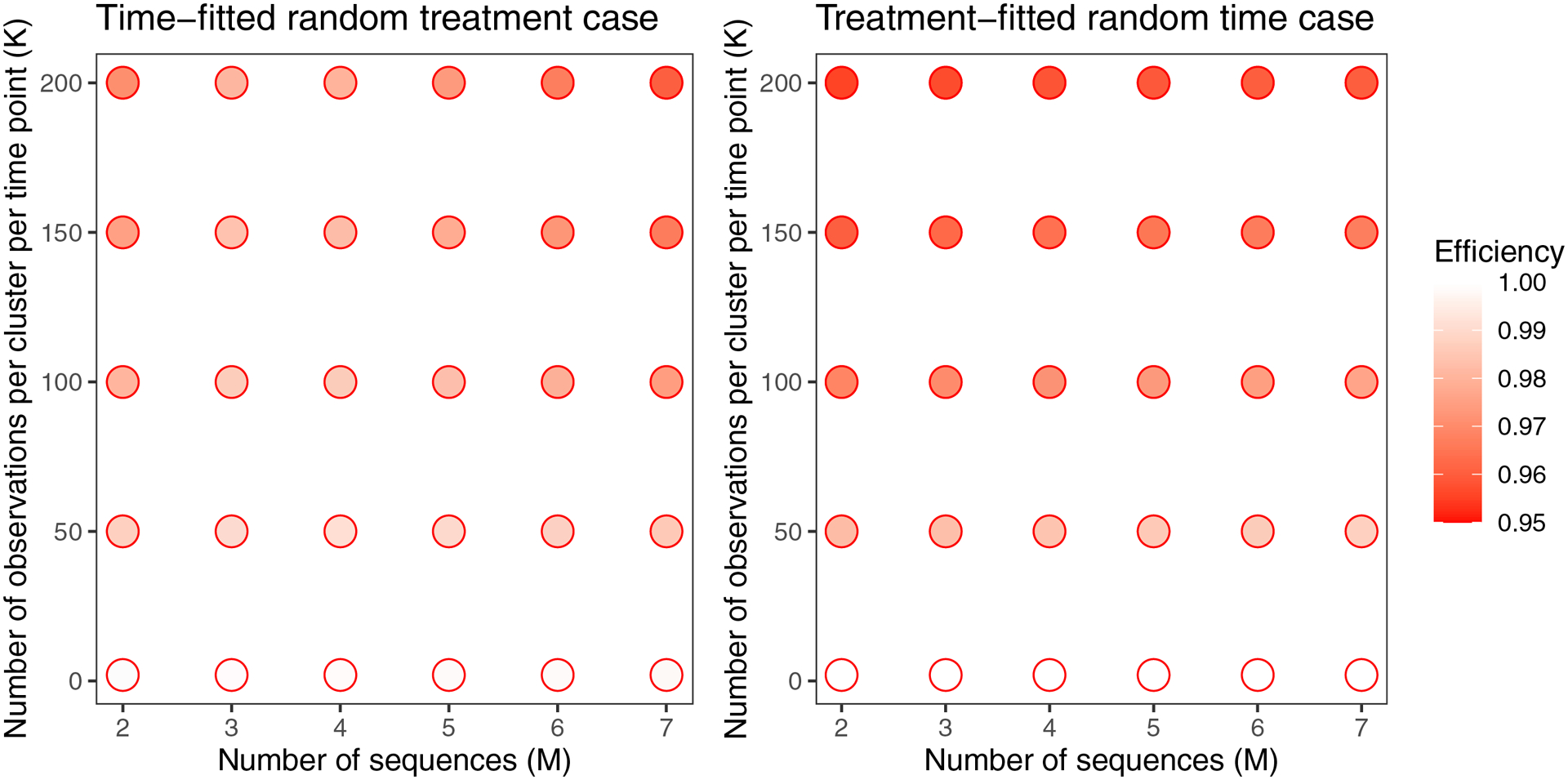
Efficiency of Root 1 for both cases, for a variety of classic designs. For each case, and . To keep the ACC consistent, we chose and for the time-fitted random treatment and treatment-fitted random time cases, respectively.
Figure A3:
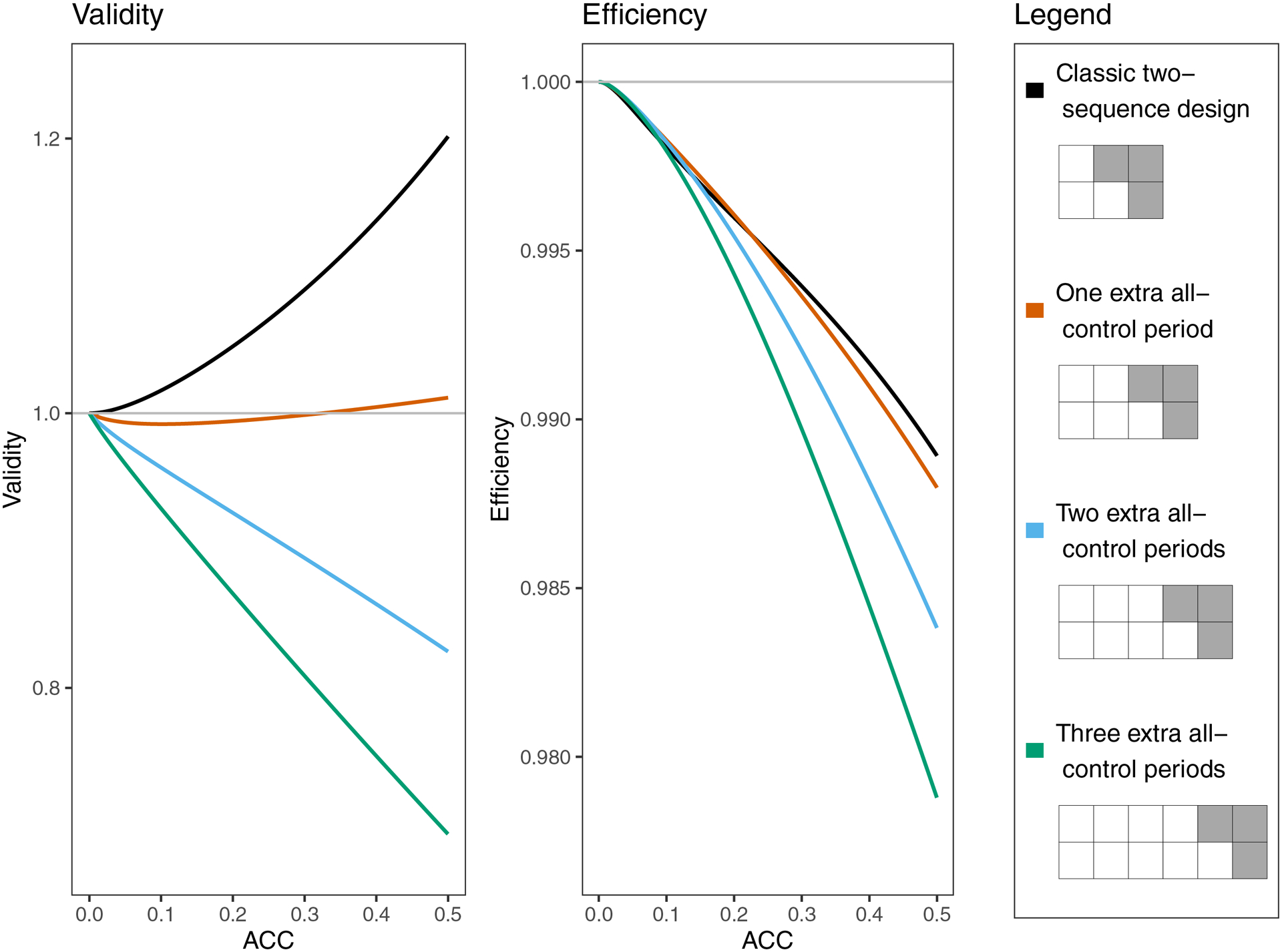
Validity and efficiency of Root 1 for the time-fitted random treatment case, for four different SWT designs and a variety of true ACC’s. The designs each have two sequences and K=5 observations per cluster per time period. Throughout, and the balance of and is fixed at .
Footnotes
Data accessibility
The code that supports the findings of this paper are available in the supplementary material of this article and at https://github.com/voldal/SWT_model_misspecification. The data from the disinvestment example are openly available at https://doi.org/10.1371/journal.pmed.1002412, reference number 9.
References
- 1.Barker D, McElduff P, D’Este C, Campbell MJ. Stepped wedge cluster randomised trials: a review of the statistical methodology used and available. BMC Med Res Methodol. 2016;16:69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hughes JP, Granston TS, Heagerty PJ. Current issues in the design and analysis of stepped wedge trials. Contemp Clin Trials. 2015;45:55–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hussey MA, Hughes JP. Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials. 2007;28(2):182–191. [DOI] [PubMed] [Google Scholar]
- 4.Thompson JA, Fielding KL, Davey C, Aiken AM, Hargreaves JR, Hayes RJ. Bias and inference from misspecified mixed-effect models in stepped wedge trial analysis. Stat Med. 2017;36(23):3670–3682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hemming K, Taljaard M, Forbes A. Modeling clustering and treatment effect heterogeneity in parallel and stepped-wedge cluster randomized trials. Stat Med. 2018;37(6):883–898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Verbeke G, Molenberghs G. Linear mixed models for longitudinal data. New York: Springer; 2000. [Google Scholar]
- 7.Cheng J, Edwards LJ, Maldonado-Molina MM, Komro KA, Muller KE. Real longitudinal data analysis for real people: building a good enough mixed model. Stat Med. 2010;29(4):504–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Moerbeek M The consequences of ignoring a level of nesting in multilevel analysis. Multivariate Behav Res. 2004;39(1):129–149. [DOI] [PubMed] [Google Scholar]
- 9.Haines TP, Bowles KA, Mitchell D, et al. Impact of disinvestment from weekend allied health services across acute medical and surgical wards: 2 stepped-wedge cluster randomised controlled trials. PLoS Med. 2017;14(10):e1002412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hooper R, Teerenstra S, de Hoop E, Eldridge S. Sample size calculation for stepped wedge and other longitudinal cluster randomised trials. Stat Med. 2016;35(26):4718–4728. [DOI] [PubMed] [Google Scholar]
- 11.Heagerty PJ, Kurland BF. Misspecified maximum likelihood estimates and generalised linear models. Biometrika. 2001;88(4):973–985. [Google Scholar]
- 12.Wolfram Research, Inc. Mathematica. Champaign, Illinois: Wolfram Research, Inc; 2020. [Google Scholar]
- 13.Huber PJ. The behavior of maximum likelihood estimates under non-standard conditions. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. 1967;5.1:221–233. [Google Scholar]
- 14.Thompson JA, Hemming K, Forbes A, Fielding K, Hayes R. Comparison of small-sample standard-error corrections for generalised estimating equations in stepped wedge cluster randomised trials with a binary outcome: A simulation study. Stat Methods Med Res. 2021;30(2):425–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chavance M, Escolano S. Misspecification of the covariance structure in generalized linear mixed models. Stat Methods Med Res. 2016;25(2):630–643. [DOI] [PubMed] [Google Scholar]
- 16.R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2019. [Google Scholar]
- 17.Korevaar E, Kasza J, Taljaard M, et al. Intra-cluster correlations from the CLustered OUtcome Dataset bank to inform the design of longitudinal cluster trials. Clin Trials. 2021;18(5):529–540. [DOI] [PubMed] [Google Scholar]
- 18.Bates D, Mächler M, Bolker B, Walker S. Fitting linear mixed-effects models using lme4. J Stat Softw. 2015;67(1):1–48. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


