fastISM: performant in silico saturation mutagenesis for convolutional neural networks

Abstract

Motivation

Deep-learning models, such as convolutional neural networks, are able to accurately map biological sequences to associated functional readouts and properties by learning predictive de novo representations. In silico saturation mutagenesis (ISM) is a popular feature attribution technique for inferring contributions of all characters in an input sequence to the model’s predicted output. The main drawback of ISM is its runtime, as it involves multiple forward propagations of all possible mutations of each character in the input sequence through the trained model to predict the effects on the output.

Results

We present fastISM, an algorithm that speeds up ISM by a factor of over 10× for commonly used convolutional neural network architectures. fastISM is based on the observations that the majority of computation in ISM is spent in convolutional layers, and a single mutation only disrupts a limited region of intermediate layers, rendering most computation redundant. fastISM reduces the gap between backpropagation-based feature attribution methods and ISM. It far surpasses the runtime of backpropagation-based methods on multi-output architectures, making it feasible to run ISM on a large number of sequences.

Availability and implementation

An easy-to-use Keras/TensorFlow 2 implementation of fastISM is available at https://github.com/kundajelab/fastISM. fastISM can be installed using pip install fastism. A hands-on tutorial can be found at https://colab.research.google.com/github/kundajelab/fastISM/blob/master/notebooks/colab/DeepSEA.ipynb.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

High-throughput experimental platforms have revolutionized the ability to profile diverse biochemical and functional properties of biological sequences, such as DNA, RNA and proteins. These datasets have powered highly performant deep-learning models of biological sequences that have achieved state-of-the art results for predicting protein-DNA binding, protein-RNA binding, chromatin state, splicing, gene expression, long-range chromatin contacts, protein structure and functional impact of genetic variation (Alipanahi et al., 2015; Avsec et al., 2021a; Eraslan et al., 2019; Fudenberg et al., 2020; Jaganathan et al., 2019; Kelley et al., 2016, 2018; Koo et al., 2018; Torrisi et al., 2020; Zhou et al., 2018; Zhou and Troyanskaya, 2015).

Convolutional neural networks (CNNs) are widely used for modeling regulatory DNA since they are well suited to capture known properties and invariances encoded in these sequences (Alipanahi et al., 2015; Kelley et al., 2016; Zhou and Troyanskaya, 2015). CNNs map raw sequence inputs to binary or continuous outputs by learning hierarchical layers of de-novo motif-like pattern detectors called convolutional filters coupled with non-linear activation functions. Recurrent neural networks (RNNs) (Hochreiter and Schmidhuber, 1997) are another class of sequential models that have been very effective for modeling protein sequences (Torrisi et al., 2020). However, RNNs and hybrid CNN-RNN architectures have only shown moderate performance improvements for modeling regulatory DNA (Hassanzadeh and Wang, 2016; Quang and Xie, 2016; Shen et al., 2018). Compared to recurrent architectures, CNNs also have the advantage of being more computationally efficient and easily interpretable. For example, convolutional filters are reminiscent of classical DNA motif representations known as position weight matrices (Trabelsi et al., 2019). Hence, CNNs continue to be the most popular class of architectures for modeling regulatory DNA sequences (Eraslan et al., 2019).

A primary use case for these deep-learning models of regulatory DNA is to decipher the de novo predictive sequence features and higher-order syntax learned by the models that might reveal novel insights into the regulatory code of the genome. Hence, several feature attribution methods have been developed and used to infer contribution scores (or importance scores) of individual characters in input sequences with respect to output predictions of neural network models, such as CNNs. A popular class of feature attribution methods use backpropagation to efficiently decompose the output prediction of a model, given an input sequence, into character-level attribution scores (Lundberg and Lee, 2017; Shrikumar et al., 2017; Simonyan et al., 2014; Sundararajan et al., 2017). The gradient of the output with respect to each observed input character—commonly referred to as a saliency map (Simonyan et al., 2014)—is one such method for attributing feature importance. Other related approaches, such as DeepLIFT (Shrikumar et al., 2017) and Integrated Gradients (Jha et al., 2020; Sundararajan et al., 2017), modify the backpropagated signal to account for saturation effects and improve sensitivity and specificity. These attribution scores can be used to infer predictive subsequences within individual input sequences, which can then be aggregated over multiple sequences to learn recurring predictive features, such as DNA motifs (Shrikumar et al., 2018).

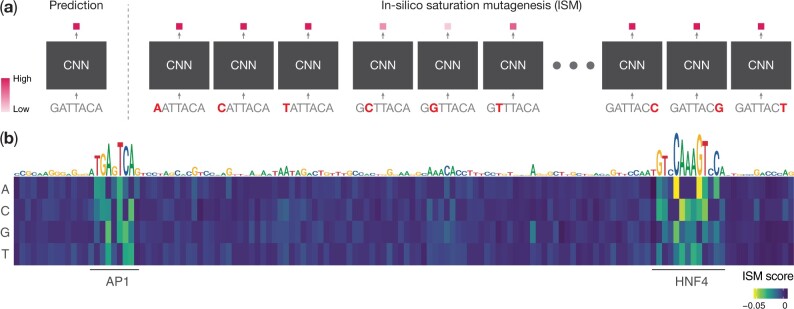
In silico Saturation Mutagenesis (ISM) is an alternate feature attribution approach that involves making systematic mutations to each character in an input sequence and computing the change in the model’s output due to each mutation (Fig. 1). ISM is the computational analog of saturation mutagenesis experiments (Patwardhan et al., 2009) that are commonly used to estimate the functional importance of each character in a sequence of interest based on its effect size of mutations at each position on some functional read out. ISM is the de-facto approach to predict the effects of genetic variants in DNA sequences (Kelley et al., 2016; Wesolowska-Andersen et al., 2020; Zhou and Troyanskaya, 2015).

Fig. 1.

ISM (a) given an input sequence, ISM proceeds by running the CNN forward propagation on all possible mutations of the input and recording the output. In practice, the mutated sequences are run through the model in a batched fashion; (b) an example of ISM using the DeepSEA Beluga model (Zhou et al., 2018) at hg38 chr3:138863109–138863254 for the small intestine DNase-seq output task. Differences from reference output are visualized in the matrix, while reference nucleotides are scaled by the L2-norm of the differences. The ISM scores highlight AP1 and HNF4 motifs at the locus

In the context of computing feature attributions with respect to a single scalar output of a model, ISM can be orders-of-magnitude more computationally expensive than backpropagation-based feature attribution methods, since it involves a forward propagation pass of the model for every mutation of every position in an input sequence (Eraslan et al., 2019). By contrast, backpropagation-based methods can compute attribution scores of all possible characters at all positions in an input sequence in one or a few backward propagations of the model. The inefficiency of ISM is particularly onerous when ISM is performed on a large number of sequences or for a large number of models. For example, to obtain robust variant effect prediction, Wesolowska-Andersen et al. (2020) recently trained 1000 CNNs to predict variants in chromatin regulatory features of pancreatic islets and averaged the ISM scores over the trained models to confer robustness against heterogeneity that stems from different random parameter instantiations of the same model at the beginning of the training process (Wesolowska-Andersen et al., 2020).

However, despite this gap in efficiency, ISM does offer some salient benefits over backpropagation-based methods. In comparison to most backpropagation-based methods that often use heuristic rules and approximations, ISM faithfully represents the model’s response to mutations at individual positions. This makes it the method of choice when evaluating the effect of genetic variants on the output (Wesolowska-Andersen et al., 2020; Zhou et al., 2018; Zhou and Troyanskaya, 2015), and it is also used as a benchmark reference when evaluating fidelity of other feature attribution methods (Koo and Ploenzke, 2021). Unlike ISM, backpropagation-based methods like DeepLIFT and Integrated Gradients rely on a predefined set of ‘neutral’ input sequences that are used as explicit references to estimate attribution scores. The choice of reference sequences can influence the scores and so far, the selection of reference sequences has been ad-hoc (Eraslan et al., 2019; Jha et al., 2020). ISM also has some benefits for models with a large number of scalar or vector outputs since each forward propagation performed during ISM reveals the impact of a single mutation on every output of the model. For example, massively multi-task models are quite popular for mapping regulatory DNA sequences to multiple molecular reads outs in large collections of biosamples (Alipanahi et al., 2015; Eraslan et al., 2019; Jaganathan et al., 2019; Zhou et al., 2018; Zhou and Troyanskaya, 2015). Further, a recent class of models called profile models have been developed to map regulatory DNA sequences to vector outputs corresponding to quantitative regulatory profiles (Avsec et al., 2021a; Kelley et al., 2018). These models output a vector of signal values often at base-resolution that can be as long as the input sequence. ISM can reveal how perturbing individual nucleotides in the input alters the signal across all positions in the output profile. By contrast, backpropagation-based importance scoring methods would need to perform a separate backpropagation for every output position in order to estimate comparable feature attributions, which would linearly increase the computational cost in the number of outputs. For these reasons, a computationally efficient implementation of ISM would be attractive.

We introduce fastISM, an algorithm that speeds up ISM for CNNs. fastISM is based on the observation that CNNs spend the majority of computation at prediction time in convolutional layers and that single point mutations in the input sequence affect a limited range of positions in intermediate convolutional layers. fastISM restricts the computation in intermediate layers to those positions that are affected by the mutation in the input sequence. fastISM cuts down the time spent in redundant computations in convolution layers at positions that are unaffected by mutations in the input, resulting in significant speedups.

We provide a fully functional and thoroughly tested package implementing the fastISM algorithm for Keras models in TensorFlow 2. We benchmark the speedup obtained by running fastISM on a variety of architectures and show that fastISM can achieve order-of-magnitude improvements over standard ISM implementations. fastISM reduces the gap between ISM and backpropagation-based methods in terms of runtime on single-output architectures, and far surpasses them on multi-output architectures.

2 Materials and methods

2.1 ISM for CNNs is bottlenecked by redundant computations in convolution layers

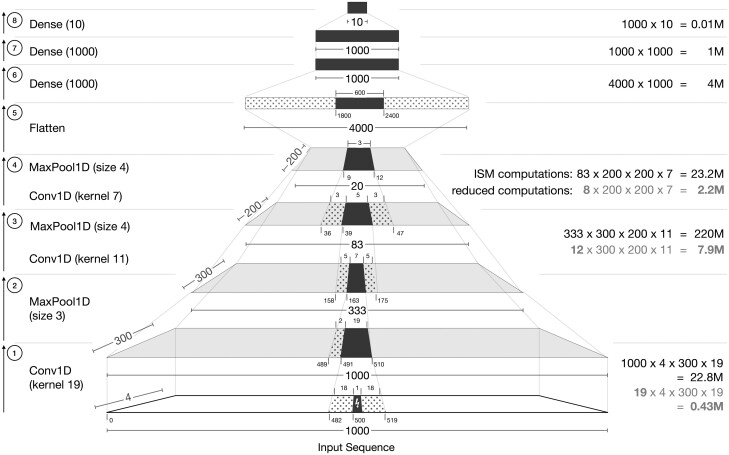
We motivate fastISM by using an example based on the multi-task Basset model (Kelley et al., 2016) that maps DNA sequences to binary labels of chromatin accessibility across 100 s of cell types and tissues (tasks). The Basset model consists of three convolution layers of kernel sizes 19, 11 and 7, which are followed by max pool layers of size 3, 4 and 4, respectively. The output after the third convolution and max pool is flattened. This is followed by two fully connected layers with 1000 hidden units, and a final fully connected layer that predicts the outputs. We consider a slight modification of the original architecture that operates on 1000 bp input sequence and has 10 binary scalar outputs. In addition, all convolution layers are assumed to be padded such that the length of the output sequence is the same as the input to the layer (Fig. 2).

Fig. 2.

Annotated diagram of a Basset-like architecture (Kelley et al., 2016) on an input DNA sequence of length 1000, with a 1 base-pair mutation at position 500 (0-indexed). Dark filled-in positions indicate the regions that are affected by the point mutation in the input. Dotted positions, flanking the dark filled-in positions, indicate unaffected regions that contribute to the output of the next layer. Ticks at the bottom of each layer correspond to position indices. Numbers on the right in indicate the approximate number of computations required at that layer for a standard implementation of ISM. For convolution layers, the numbers in gray indicate the minimal computations required. After the first Conv1D and MaxPool1D layers (Operations 1 and 2), the subsequent Conv1D and MaxPool1D layers are shown as a single operation (Operations 3 and 4). We omit layers, such as activations and batch normalization here for simplicity, as they do not change the affected regions

For a single forward propagation through the network, the majority of compute time is spent in the convolutional layers. For a given convolution layer, the number of computations is proportional to kernel size, input filters, output filters and output length. For a fully connected layer, it is proportional to input and output lengths. The numbers in black in Figure 2 show the approximate computations required at each convolution and fully connected layer for a single forward propagation. To simplify exposition, we ignore the computation spent in intermediate layers, such as activations, batch normalization and max pool, since they are dominated by the computational cost of convolutional and fully connected layers. The three convolutional layers require ∼23, 220 and 23 M computations, respectively, while the three fully connected layers require ∼4, 1 and 0.01 M computations, respectively. Thus, the computations required in the convolutional layers combined exceed that of the fully connected layers by a factor of 50×. In practice, we timed the convolutional layers and fully connected layers and observed that the factor is closer to 40× for the same architecture.

For a given reference input sequence, a simple implementation of ISM involves highly redundant computations. Typically, ISM is implemented by inserting mutations at each position in the input one at a time and making a forward pass through the entire model using the perturbed sequences as inputs. However, local perturbations in the input only affect local regions in intermediate convolutional layers, while regions farther away remain identical to their values for the reference (unperturbed) input sequence.

For each layer, the regions that are affected by the single base-pair mutation in the input, and the minimal regions required to compute the output of the next layer are shown in Figure 2. Consider a single base-pair mutation in the middle of the 1000 bp input sequence at position 500 (0-indexed). The first convolution (Layer 1) has a kernel size of 19 and the input sequence is padded with zeros at nine positions on both sides. The output sequence length is thus 1000. As the convolution filter scans across the input sequence, the mutation at position 500 will be involved in 19 contiguous output positions of the next layer from positions 491 to 510. None of the other 1000–19 outputs will be affected by the mutation and computing them is redundant. Total of 18 positional inputs on either side of the mutation will be involved in generating the 19 contiguous outputs of the next layer. The first max pool (Layer 2) has a size of three, and the output length is 333. The affected input region from 491 to 510 will only affect ⌊491/3⌋–⌊510/3⌋, i.e. 163–170 in the output of the max pool region. However, in order to compute the 163rd output, the max pool would also require the convolution output values at positions 489 and 490, which would be the same as the values for the reference (unperturbed) input sequence.

The above exercise can be extended to the next two convolution layers. For simplicity, the convolution and max pool layers are combined. The output of the first max pool affects positions 163–170. The next convolution has a kernel size of 11 and a padding of zeros at five positions on both sides. The output of the convolution followed by max pool (Layer 3) affects 5 out of 83 positions, and the output of Layer 4 affects 3 out of 20 positions. This output is then reshaped to a single vector, which is then fed through three fully connected layers. By design, a single mutation in the input sequence has the potential to affect every position in the fully connected layer; thus, the activations of all subsequent layers in the network must be recomputed for the mutated input, as is the case with standard ISM.

Given that the majority of computation occurs before the fully connected layer, the actual computations required to track the effect of a single base-pair mutation in the input are much smaller than the total computations in a standard forward propagation. The values on the right in gray in Figure 2 show the minimum number of computations required such that computations are only restricted to the regions affected by the mutation in the input. For saturation mutagenesis in which the above operations are repeated for perturbations at all positions, the amount of redundant calculations adds up and contributes to ISM’s unfavorable runtime.

Since the majority of activations prior to the fully connected layers remain unchanged by a single-base mutation, the activations of these layers on the unperturbed sequence can be computed once and reused when running ISM over the different positions in the input sequence. By restricting ISM computations to only positions affected by the input mutation at each layer, the number of computations can theoretically be reduced from ∼23 + 220 + 23 + 4 + 1 M = 271 M to 0.5 + 8 + 2 + 4 + 1 M = 15.5 M computations, down by a factor of 17. In practice, there may be overheads from other steps, such as concatenating the unperturbed flanking regions at each intermediate layer, that would dampen the realized speedup.

These observations suggest that it should be possible to define a custom model that performs only the required computations for a mutation at each input position. However, it would be cumbersome to write an architecture specifically for the purpose of ISM for each model, and compute the positions required at each intermediate layer for a specific input mutation. Hence, we developed fastISM, a method to speed up ISM by leveraging the above-mentioned redundancies without requiring any explicit re-specification of the model architecture by the user.

2.2 fastISM algorithm overview

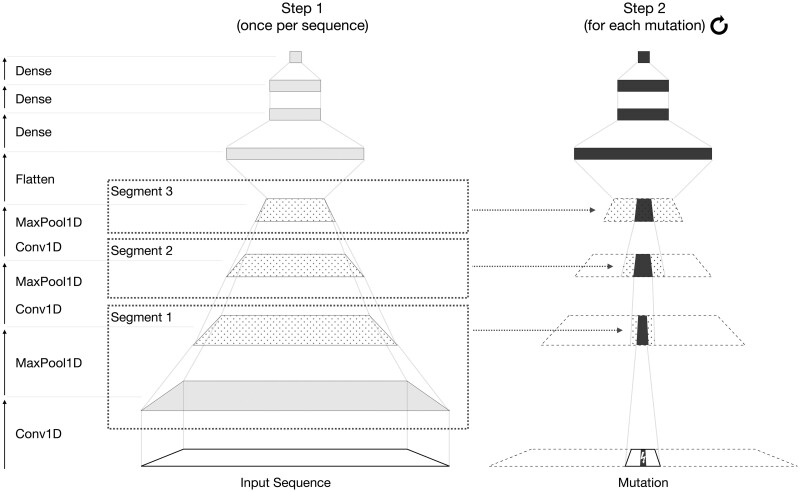
fastISM builds upon the observation that local perturbations in the input sequence tend to affect only local regions in the convolutional layers. These regions are narrower in the earlier convolutional layers and grow wider with increasing depth. Given a mutation at a fixed position in the input sequence, standard implementations recompute intermediate outputs from unperturbed regions farther away from the mutation that do not change after introducing the mutation. fastISM computes these intermediate outputs once for each reference unperturbed input sequence and caches them. For each different positional mutation in the input, appropriate windows around perturbed regions can be reused at each intermediate layer. fastISM restricts computation in convolutional layers to only the affected regions and unperturbed flanking regions around it, which typically depend on kernel width and dilation rate.

fastISM takes a Keras model as input. The main steps of fastISM are as follows (Fig. 3):

Fig. 3.

Overview of the fastISM algorithm for an input model similar to the Basset-like architecture in Figure 2. fastISM inspects the input model and partitions successive convolution and maxpooling layers into segments. For each input sequence, the input model is run once (Step 1) and returns the intermediate outputs of the final layer of each segment (dotted), which is cached. Note that after the first Conv1D and MaxPool1D layers, the subsequent Conv1D and MaxPool1D layers are shown as a single operation; similar to Segment 1, only the output of the maxpooling layer is cached. For each mutation of each sequence (Step 2), cached values are sliced appropriately, and recomputed values (dark filled-in) are overlaid at each layer. We omit layers, such as activations and batch normalization here for simplicity

• One-time initialization:

  • Obtain the computational graph from the model and chunk it into segments that can be run as a unit.

  • For each position, compute relevant minimal ranges for each intermediate output that are required to compute the output of the next layer.

• For each batch of input sequences:

  • Run the model on the (unperturbed) sequences and cache the intermediate outputs at the end of each segment (Step 1, Fig. 3).

  • For each positional mutation (Step 2 in Fig. 3):

    • Introduce the mutation in the input sequences.

    • At every layer, overlay the recomputed output from the previous layer with appropriate slices from the cached intermediate outputs.

    • Once a dense layer is reached, proceed as in the case of standard ISM.

Each of these steps is described in more detail in the Supplementary Methods.

3 Results

3.1 fastISM yields order-of-magnitude improvements in speed for different architectures

We benchmarked fastISM against a standard implementation of ISM. We choose three types of models that take DNA sequence as input—the Basset architecture (Kelley et al., 2016), the Factorized Basset architecture (Wnuk et al., 2019) and the BPNet architecture (Avsec et al., 2021a). The first two models output scalar values for each output task, whereas the BPNet model outputs a profile vector of length equal to the input sequence length, and a scalar count. ISM is performed by recording the outputs for all three alternate mutations at each position. We benchmark the three models for 1000 and 2000 bp length inputs.

We also compare fastISM to three backpropagation-based feature attribution methods—Gradient × Input (input masked gradient), Integrated Gradients (Sundararajan et al., 2017) and DeepSHAP (Lundberg and Lee, 2017). DeepSHAP is an extension of the DeepLIFT algorithm that is implemented by overriding tensorflow gradient operators; we used DeepSHAP because it has a more flexible implementation than the original DeepLIFT repository. We set the number of steps for Integrated Gradients to 50 and a single default reference of all zeros, and the number of dinucleotide reference sequences for DeepSHAP to 10. For models with a single scalar output, the backpropagation-based methods are run with respect to the scalar output. For BPNet, the methods are run with respect to each output in the profile vector as well as the scalar output. While ISM returns one value (change in output score) for each of the tree alternative nucleotides (with respect to the observed nucleotide) at each position; Integrated Gradients, DeepSHAP and Gradients return one value for each of the four possible nucleotides at each position.

The results are summarized in Table 1. For the Basset and Factorized Basset architectures, fastISM speeds up ISM by more than 10× when computing importance scores for a single-output task, and the speedup increases with increasing input sequence length. This is expected since, for a fixed architecture, the length of the affected regions in the convolutional layers is independent of input sequence length. Systematic analysis demonstrated that fastISM speedup improves on increasing input sequence length, number of convolution filters and number of convolution blocks, and on decreasing convolution kernel size for a simple architecture (Supplementary Fig. S1 and Methods).

Table 1.

Comparison of fastISM with standard ISM, Gradient × Input, Integrated Gradients and DeepSHAPfor three different models with 1000 and 2000 bp length inputs

Architecture	Layers	Input size	Outputs	fastISM	Standard ISM	Gradient × Input	Integrated Gradients	DeepSHAP
Basset	3 conv+3 max pool, 3 fully connected	1000	Single scalar	2.70	27.36	0.04	2.34	1.75
					(10.1)	(<1)	(0.8)	(0.7)
		2000		6.49	100.44	0.08	4.61	3.03
					(15.4)	(<1)	(0.7)	(0.4)
Factorized Basset	9 conv+3 max pool, 3 fully connected	1000	Single scalar	5.47	68.97	0.09	4.82	2.64
					(12.6)	(<1)	(0.9)	(0.5)
		2000		18.04	262.24	0.17	9.47	4.63
					(14.5)	(<1)	(0.5)	(0.25)
BPNet	2 conv, 9 dilated conv, skip connections	1000	Profile (length 1000 vector) + scalar	28.97	46.09	41.49*	4399*	1743*
					(1.6)	(1.4)	(151)	(60)
		2000	Profile (length 2000 vector) + scalar	81.52	173.96	126.41*	12 440*	6427*
					(2.1)	(1.5)	(152)	(78)

Note: All times in seconds per 100 input sequences. Integrated Gradients is computed with 50 steps and a single all-zeros reference. DeepSHAP is computed with 10 references. Time relative to fastISM in parentheses. For BPNet models, which output a profile vector as well as a count scalar, Gradient × Input, Integrated Gradients and DeepSHAP were computed in a loop with respect to each output of the profile and the count scalar (*).

fastISM runtimes, though slower than Gradient × Input, are competitive with runtimes of Integrated Gradients (within 2×) and DeepSHAP (within 4×) for single scalar output models. Also, fastISM and ISM provide importance scores with respect to every output task. In contrast, computing importance scores for multiple output tasks with backpropagation-based methods would multiply their runtime by the number of output tasks.

The speedup of fastISM for the BPNet architecture relative to standard ISM is more modest—1.6× for 1000 bp input and 2.1× for 2000 bp input. This can be attributed to dilated convolutions, which can have a larger effective kernel size. Since the BPNet architecture includes dilated convolutions with an exponentially increasing dilation rate, the receptive fields for the later dilated convolutions are very large. As a result, the regions affected by a single base-pair change in the input span a sizable fraction of intermediate layers, and the computations involved beyond those layers approach those of a standard implementation.

For the BPNet architecture, which outputs a profile vector, if one is interested in attributing the predicted value at each position in the output vector to the input nucleotides, one would need to run the backpropagation methods for every output position, which drastically slows them down. DeepSHAP and Integrated Gradients take over 50× time of the fastISM implementation. Thus, fastISM speeds up ISM by an order-of-magnitude and narrows the gap in compute time between backpropagation-based methods and ISM.

Since fastISM caches intermediate outputs at the beginning to efficiently calculate forward passes, it is expected to have a higher peak GPU memory footprint per input sequence compared to standard ISM. Indeed, we observed that the maximum number of sequences that could be packed into a GPU and processed simultaneously in a batched fashion was lower for fastISM compared to standard ISM (Supplementary Table S1). The size of the cached output is model architecture dependent, with the discrepancy being largest for BPNet models.

3.2 fastISM improves runtime of ISM for long-range models

Having shown that fastISM works well on small architectures, we next investigated the scalability of fastISM on larger architectures by benchmarking it on two recently published architectures—Akita (Fudenberg et al., 2020) and Enformer (Avsec et al., 2021b). Akita takes in a ∼1 Mb input sequence and outputs a Hi-C contact map at 2048 bp resolution in five cell types, and Enformer takes in a ∼200 kb input sequence and makes predictions for 5313 epigenomic and transcriptomic experiments at a bin size of 128 bp. Both these long-range models begin by employing multiple convolutions and pooling layers to exponentially reduce the length of the input, followed by transformers or dilated convolution layers that produce the final output. We anticipated that the primary determinant of fastISM speedup in such models would be the time spent in initial convolution layers with a smaller receptive field relative to time spent in layers with a full receptive field, e.g. the transformer layers.

Unfortunately, the large input size of these models made it time-intensive to perform ISM across the entire input. Instead, we performed ISM on the central 1 kb of input sequences (Table 2). We observed that fastISM achieves a speedup of 1.3× compared to standard ISM on Akita. Although this speedup is lower than the ones observed on the smaller models, further investigation revealed that fastISM is bottlenecked by layers outside the initial convolution-max pooling blocks, i.e. those with a large receptive field, in which Akita spends ∼60% of inference time. This means that an optimal method that would eliminate the time spent in initial layers to zero would only observe a ∼1.7× speedup.

Table 2.

Comparison of fastISM with standard ISM for large models

Architecture	Layers	Input size	Output size	fast ISM	Standard ISM
Akita	11 conv+max pool, 8 dilated conv block, 7 Conv2D blocks	1 048 576	99 681×5	6463	8700
					(1.3)
Enformer	14 conv, 7 attention pool, 11 transformer + feed-forward blocks, 2 conv	196 608	896×5313	1642*	3792*
					(2.3)
	Same as above with compressed output		896×20	10 086	31 980
					(3.2)
	Same as above except with 4 transformer		896×20	4878	26 694
					(5.5)

Note: All times in seconds per 100 input sequences for ISM of central 1000 bp windows, except the Enformer model with 896×5313 outputs for which central 100 bp windows were scored (*). Time relative to fastISM in parentheses.

For the Enformer model, fastISM yielded a speedup of 2.3× compared to standard ISM. Although less time is spent in layers with a full receptive field covering the entire input sequence (e.g. the transformer layers), we found that a significant portion of total time (∼15%) is spent in transferring the large output from GPU to CPU. When the outputs are compressed to 20 dimensions from 5313, as was done by the authors for distributing variant effect scores, the speedup improves to 3.2×. Noting that standard ISM would take nearly one GPU-year to score 100 000 1 kb bins, modest speedups of 2–3× can nonetheless translate to sizeable savings in compute and cost.

Taken together, our results indicate that relative gains of fastISM over ISM are strongly dependent on model architecture. fastISM reduces the time spent in convolution layers with limited receptive fields by orders-of-magnitude. Therefore, the key determinant of fastISM performance for a model is the inference time spent in initial convolution layers relative to layers with larger receptive fields. Consequently, upgrades to deep-learning software and hardware can also influence fastISM performance. For example, improved hardware that would speed up the execution speed of transformer layers, or GPU to CPU transfer, will have equal amounts from standard ISM and fastISM, and improve fastISM speedup. Empirically, we observed that fastISM speedup improved with increasing batch sizes, which is limited by GPU memory. Thus, larger GPUs can also potentially improve fastISM runtime.

If saturated mutagenesis is of paramount importance, model design decisions can be driven by ISM considerations. For example, the number of convolution filters can be increased and the number of transformer layers in the Enformer architecture can be minimized while keeping performance above a desired threshold. As an example, we reduced the number of transformer layers from 11 to 4 in the Enformer model and observed the speedup increase to 5.5× (Table 2). Similarly, one can choose a convolution-based architecture over a transformer-based architecture if both have comparable performance on a given task.

4 Discussion

ISM is an important post hoc feature attribution method that has gained applicability as a tool to interpret deep-learning models for genomics and to interrogate the effect of variants. ISM has largely been treated as a static method with unfavorable time complexity compared to more recent backpropagation-based model interpretability methods. We challenge this notion by introducing fastISM, a performant implementation of ISM for CNNs. fastISM leverages the simple observation that the majority of computations performed in a traditional implementation of ISM are redundant. fastISM improves runtime of ISM by over 10× for commonly used CNNs, and a factor of 2–3× for profile networks and long-range models. This brings down ISM’s runtime in the ballpark of backpropagation-based methods, such as Integrated Gradients and DeepSHAP for single-output models, and dramatically surpasses the runtime of backpropagation-based methods for multi-output methods, making it more feasible to run ISM genome-wide and on a large number of models.