Real-Time MRI Motion Estimation through an Unsupervised K-Space-Driven Deformable Registration Network (KS-RegNet)

Abstract

Purpose:

Real-time three-dimensional(3D) magnetic resonance(MR) imaging is challenging because of slow MR signal acquisition, leading to highly under-sampled k-space data. Here, we proposed a deep learning-based, k-space-driven deformable registration network(KS-RegNet) for real-time 3D MR imaging. By incorporating prior information, KS-RegNet performs a deformable image registration between a fully-sampled prior image and on-board images acquired from highly-under-sampled k-space data, to generate high-quality on-board images for real-time motion tracking.

Methods:

KS-RegNet is an end-to-end, unsupervised network consisting of an input data generation block, a subsequent U-Net core block, and following operations to compute data fidelity and regularization losses. The input data involved a fully-sampled, complex-valued prior image, and the k-space data of an on-board, real-time MR image(MRI). From the k-space data, under-sampled real-time MRI was reconstructed by the data generation block to input into the U-Net core. In addition, to train the U-Net core to learn the under-sampling artifacts, the k-space data of the prior image was intentionally under-sampled using the same readout trajectory as the real-time MRI, and reconstructed to serve an additional input. The U-Net core predicted a deformation vector field that deforms the prior MRI to on-board real-time MRI. To avoid adverse effects of quantifying image similarity on the artifacts-ridden images, the data fidelity loss of deformation was evaluated directly in k-space.

Results:

Compared with Elastix and other deep learning network architectures, KS-RegNet demonstrated better and more stable performance. The average(±s.d.) DICE coefficients of KS-RegNet on a cardiac dataset for the 5-, 9-, and 13-spoke k-space acquisitions were 0.884±0.025, 0.889±0.024, and 0.894±0.022, respectively; and the corresponding average(±s.d.) center-of-mass errors(COMEs) were 1.21±1.09, 1.29±1.22, and 1.01±0.86 mm, respectively. KS-RegNet also provided the best performance on an abdominal dataset.

Conclusion:

KS-RegNet allows real-time MRI generation with sub-second latency. It enables potential real-time MR-guided soft tissue tracking, tumor localization, and radiotherapy plan adaptation.

1. Introduction

Treatment efficacy of radiotherapy depends on the accuracy of delivering radiation doses to tumors and sparing surrounding normal tissues (Verellen et al. 2007). Precise tumor localization, together with the advances of conformal dose delivery, helps to pinpoint the radiation dose to tumors and improve the disease control probability (Tubiana and Eschwege 2000; Verellen et al. 2007). However, knowledge of tumor positions can be undermined by internal anatomical motion such as respiratory or cardiac motion, adding uncertainties to tumor localization. These uncertainties necessitate large treatment margins to be added beyond the tumor boundaries, which inevitably increases the radiation dose to normal tissues (Langen and Jones 2001). The introduction of image-guided radiotherapy allows frequent imaging before, during and after radiotherapy treatments for tumor localization, and enables margin reduction to improve the precision of radiotherapy (Xing et al. 2006; Jaffray 2012; Maund et al. 2014; Dhont et al. 2020). Among the available imaging modalities, magnetic resonance (MR) imaging is a non-invasive technique of high spatial resolution and superior soft tissue contrast (Foltz and Jaffray 2012; Liu et al. 2015; Liu et al. 2016). In comparison to computed tomography, MR imaging acquires anatomical and functional images without utilizing ionizing radiation, thus eliminating ionizing radiation damages to patients. In addition, the versatility of MR imaging acquisition protocols allows various contrast enhancement patterns, which helps to differentiate between healthy and tumorous tissues (Stemkens, Paulson, and Tijssen 2018). As a result, there are growing interests in MR-guided radiotherapy that combines a linear accelerator with a MR imaging scanner for tumor tracking and localization (Mutic and Dempsey 2014; Sawant et al. 2014; Kupelian and Sonke 2014; Menten, Wetscherek, and Fast 2017; Raaymakers et al. 2017; Stemkens, Paulson, and Tijssen 2018; Henke et al. 2018; Corradini et al. 2019; Gani et al. 2021). An ultimate goal of the MR-guided radiotherapy is to track tumors in real time and adaptively modify the treatment in an online fashion (Pollard et al. 2017). The real-time monitoring of three-dimensional (3D) anatomical motion requires low latency in MR acquisition, reconstruction and registration. However, a major drawback of MR imaging is its long acquisition time, as MR signals are sequentially measured in so-called k-space, which can take up to tens of minutes to achieve full sampling.

In order to reduce the acquisition time, k-space data may be under-sampled for a MR scan. However, under-sampling may violate the Nyquist-Shannon sampling theorem (Shannon 1984), leading to aliasing artifacts in reconstructed images. Conventional methods to accelerate MR imaging include parallel imaging and model-based compressed sensing, which can recover the missing data through reconstruction algorithms. Parallel imaging uses phased array coils to encode additional spatial information. Corresponding reconstruction algorithms can use this information to synthesize the missing k-space data or to remove the aliasing artifacts in reconstructed images (Pruessmann et al. 1999; Griswold et al. 2002; Lustig and Pauly 2010; Uecker et al. 2014). However, the maximal acceleration potential is limited by multiple factors, including the signal-to-noise ratio and the number of coils (Roemer et al. 1990; Hamilton, Franson, and Seiberlich 2017). Model-based compressed sensing enables significant imaging acceleration by exploiting the sparsity underlying MR images and incoherent measurements (Lustig, Donoho, and Pauly 2007; Ravishankar and Bresler 2011; Feng et al. 2017; Chen et al. 2019; Ravishankar, Ye, and Fessler 2020). However, the model-based compressed sensing usually needs a time-consuming nonlinear iterative reconstruction, and the reconstructed images can be overly smoothed for highly under-sampled k-space data (Jaspan, Fleysher, and Lipton 2015; Ravishankar, Ye, and Fessler 2020).

For real-time 3D MR imaging, more aggressive k-space under-sampling is required, which is often challenging for the conventional MR reconstruction algorithms. In order to further accelerate MR image acquisition, several methods have been investigated. Due to the success of deep learning (DL) in solving computer vision problems, the combination of DL and compressed sensing has been explored (Schlemper, Caballero, et al. 2018; Yang et al. 2018; Hammernik et al. 2018; Quan, Nguyen-Duc, and Jeong 2018; Qin et al. 2019; Zeng et al. 2019; Kustner et al. 2020; Yan et al. 2020; Zhang et al. 2020; Liu, Liu, et al. 2020; Sandino et al. 2021; Kofler et al. 2021; Ran et al. 2021). DL-based compressed sensing demonstrated dramatic reduction in the reconstruction time while still achieved high-quality images with more aggressive under-sampling factors. Schlmeper et al. developed a cascaded DL network to reconstruct dynamic 2D cardiac MR sequences, using DL for de-aliasing in the image domain (Schlemper, Caballero, et al. 2018). Similar to dictionary learning-based compressed sensing, convolutional neural networks were cascaded to perform de-aliasing of under-sampled MR images. To enforce k-space data fidelity, data consistency layers were interleaved between the cascaded convolutional neural networks. They demonstrated a 2D image can be reconstructed in about 23 milliseconds (ms) using 11-fold under-sampling. Yang et al. proposed a conditional generative adversarial network to solve the de-aliasing problem (Yang et al. 2018). Better reconstruction details were attained when the network training was driven by a loss function consisting of adversarial loss, image domain and k-space data fidelity loss, and perceptual losses. They achieved a 5 ms reconstruction for a 2D brain image. Exploiting the spatial-temporal redundancies in a sequence of dynamic images, Küstner et al. proposed a DL network for 3D cardiac cine MR image reconstruction (Kustner et al. 2020). The network alternates between data consistency layers and four-dimensional (4D) U-Nets performing complex-valued spatial and temporal convolutions. They demonstrated a scan time of less than 10 s and a reconstruction time of about 5 s for a single-breath-hold 3D cine of 16 cardiac phases. In addition to these image-domain-based DL methods, reconstructing MR images directly from raw k-space data using DL was also proposed. Zhang et al. designed an interpretable network based on the iterative process of primal dual hybrid gradient algorithm (Zhang et al. 2020). Their network architecture was based on a variant of total variation models in which the difference operator and total variation regularization terms were replaced by a learned linear operator and subnetwork, respectively. They showed a 64 ms test runtime on a 2D brain image. Sandino et al. proposed a cascaded DL network framework incorporating an ESPIRiT-based extended coil sensitivity model to improve the robustness to SENSE-related field-of-view limitations (Sandino et al. 2021). They showed better reconstruction of 2D cardiac cine images when compared to ESPIRiT.

While there has been tremendous progress in the DL-based compressed sensing, majority of the works were focused on 2D MR reconstruction. In image-guided radiotherapy, 3D volumetric MR imaging is more relevant, as 3D morphologies of tumors are needed for accurate treatment planning and beam delivery, and 3D motion information is desired for tumor tracking. In addition, these DL-based methods have only been tested for under-sampling factors ≲ 20, which may not meet the real-time 3D imaging requirement. Moreover, to apply these reconstruction algorithms in MR-guided radiotherapy, additional steps of image registration or segmentation are required to further localize tumor from the reconstructed images, adding additional latency in motion tracking. Compared to these image reconstruction-based algorithms, a new category of real-time imaging uses a deformation-driven approach to incorporate fully-sampled prior information to tackle the under-sampling issue (Asif et al. 2013; Zhao et al. 2019) and achieve simultaneous motion tracking. In particular, Huttinga et al. have developed methods to solve real-time MR images from deforming a prior fully-sampled MR image, based on limited k-space sampling (Huttinga et al. 2020; Huttinga et al. 2021). By these methods, B-spline-based motion models are developed to estimate non-rigid motion fields by k-space data matching. However, these methods were very computationally intensive, taking minutes to hours to generate a 3D image (Huttinga et al. 2021), which defeats the purpose of real-time imaging. DL-based methods have also been investigated to estimate motions for real-time MR imaging (Schlemper, Oktay, et al. 2018; Pham et al. 2019; Liang et al. 2020). Terpstra et al. reported a motion estimation algorithm by which two-dimensional (2D) MR images were first reconstructed from under-sampled k-space data, then followed by a motion estimation step using a multi-resolution DL network (Terpstra et al. 2020). They demonstrated high-quality deformation vector fields (DVFs) can be estimated in 60 ms at an under-sampling factor of 25. Based on their 2D model, Terpstra et al. developed a supervised multiresolution DL network that performs 3D motion estimation (Terpstra et al. 2021) from under-sampled MRIs. They reported a 200-ms latency including both MR acquisition and motion estimation with an error of < 2 mm. Like their 2D model, the 3D network was trained in a supervised manner that requires ‘gold-standard’ DVFs derived from high-quality, fully-sampled images. However, such DVFs are very difficult to obtain, especially for natural under-sampled images (not synthesized from retrospective under-sampling). Moreover, since the ‘gold-standard’ DVFs were solved by some other methods, the intrinsic biases presented in these methods to solve the DVFs may further propagate into the supervised deep learning model and bias its prediction. Stemkens et al. proposed a patient-specific, model-based method of 3D abdominal motion estimation (Stemkens et al. 2016). The motion estimation was based on a patient-specific motion model which was used in combination with fast 2D cine-MR images. The motion model was obtained from a principal component analysis of inter-volume DVFs derived from a pre-treatment 4D MRI. They reported a temporal resolution less than 500 ms with an average error of 1.45 mm. The motion estimation relies on the principal component analysis based motion model that may have difficulty in estimating unobserved motion, such as translation and rotation. Feng et al. proposed a method with a total latency about 300 ms (Feng, Tyagi, and Otazo 2020). Their method consists of an offline matching between motion-resolved 3D images and corresponding motion signatures, and an online matching system between an acquired motion signature and a corresponding image from the offline database. However, if there are inconsistencies between the offline learning and online matching signature signals, such as a baseline drift, the method can lead to inaccurate motion state estimation. The method cannot re-solve motion that is not contained in the offline database, either.

To address the above-mentioned challenges towards real-time imaging, we proposed an end-to-end, unsupervised DL-based framework to estimate motions from prior MR images, using highly under-sampled k-space data of real-time new images. The k-space-driven registration network is termed KS-RegNet. KS-RegNet used a deformation-driven approach (Huttinga et al. 2020; Terpstra et al. 2020; Huttinga et al. 2021; Zhang 2021), by generating real-time MR images from deforming a prior high-quality setup MR image taken before treatment starts. KS-RegNet is able to estimate 3D motion fields, in contrast to Refs. (Schlemper, Caballero, et al. 2018; Kofler et al. 2021). It enables efficient motion estimation (within 600 ms) from severely under-sampled data. In KS-RegNet, a U-Net-based architecture (Ronneberger, Fischer, and Brox 2015) was trained to predict the motion field between the prior image and highly under-sampled real-time images. We used the U-Net architecture, as it comprises multiple encoding and decoding layers to promote local and global feature extraction, and is able to make accurate predictions based on learned high-dimensional non-linear relations. The data fidelity loss of KS-RegNet is based on k-space data matching, which avoids computing similarity metrics directly on artifacts-ridden images. In order to enhance the registration accuracy and robustness, we also intentionally under-sampled the k-space data of the prior MR image, and fed the under-sampled prior image as an additional input into the KS-RegNet, such that the network was trained to perceive under-sampling artifacts.

We applied the proposed KS-RegNet on a multi-slice cardiac cine MR dataset and a liver 4D-MRI dataset to evaluate its performance on two types of motion (cardiac and respiratory). The heart shows complex contraction and relaxation motions during a cardiac cycle. On the other hand, liver or diaphragm motion due to breathing shows more extended, bulk movement along the superior-inferior direction. In addition, cardiac and abdominal MR images exhibit distinct features and qualities. Accordingly, the cardiac and abdominal images have different k-space data distributions and motion-induced modulations. We tested KS-RegNet on both datasets to evaluate its capability on accurately predicting various kinds of motion fields on different MR images. Ablative studies were performed to generate other variants of the DL network for comparisons. We also compared KS-RegNet against Elastix (Klein et al. 2010), an open-source deformable registration software package. Finally, we tested the robustness of KS-RegNet against under-sampling factor variations between training and testing, and against the image quality degradations of the fully-sampled prior images.

2. Materials and Methods

2.1. Problem formulation and assumptions

We considered the real-time motion estimation a deformable image registration problem between two 3D, complex-valued MR images (MRI) I_src and I_tar. For our purpose of real-time MR imaging, I_src represents a fully-sampled prior MR image (source) and I_tar denotes the real-time MR image to be estimated (target). The availability of the fully-sampled source MR images is guaranteed because, in MR-guided radiotherapy, they are always acquired for patient setup correction, inter-fractional anatomical verification, and plan adaptation (Raaymakers et al. 2017; Gani et al. 2021). Deformable image registration is to determine a geometric transformation that aligns the source I_src and the target I_tar images such that features in both images are associated based on an identical coordinate system (Brock et al. 2017). The transformation usually takes the form of a DVF, d(x). that deforms the source image as:

$${{\mathit{I}}^{\prime }}_{src}(\mathit{x})={\mathit{I}}_{src}(\mathit{x}+\mathit{d}(\mathit{x})),$$ (1)

where x denotes the coordinates of the deformed image voxels.

As the MR images were taken at two distinct time points, two assumptions were made regarding to the MR signal acquisition. We assumed that the steady-state condition was held for the transverse magnetization (Huttinga et al. 2020). The steady-state condition demands a sufficient short readout time, spatially slowly varying magnetic fields, and that the deformations do not alter the relaxation mechanism. This condition is valid under the field strength (1.5 T) of today’s clinical MR scanners (Huttinga et al. 2020). We also assumed that the spin density is minimally altered through deformation, which is a common assumption adapted in most deformable registration algorithms (Sotiras, Davatzikos, and Paragios 2013; Oh and Kim 2017; Balakrishnan et al. 2019). Thereby it is not necessary to correct for the MR signals strength changes resulting from the variation of the spin density. Under both conditions, the deformed source image will match the target image as:

$${\mathit{I}}_{tar}(\mathit{x})={{\mathit{I}}^{\prime }}_{src}(\mathit{x})={\mathit{I}}_{src}(\mathit{x}+\mathit{d}(\mathit{x})).$$ (2)

For real-time MR imaging, the k-space data of the target images, taken on-board, are highly undersampled. And the reconstructed target images are of degraded quality. Hence, direct registration between a fully-sampled source image and an under-sampled target image will be challenging for traditional deformable registration algorithms. Therefore, a DL-based deformable registration network (KS-RegNet) was employed. The DL network was trained to register between fully-sampled and highly under-sampled MR images to predict DVFs. The network training was driven by the optimization process:

$$\mathit{d}(\mathit{x})={\mathrm{argmin}}_{\theta }L\left({\mathit{I}}_{src},{\mathit{I}}_{tar}\right),$$ (3)

where $\theta$ denotes the network parameters, and L is the objective (loss) function quantifying the performance of the registration.

2.2. K-space-driven registration network (KS-RegNet)

2.2.1. Workflow overview

The general workflow of KS-RegNet is presented in Fig. 1. The workflow consists of an input data generation block, a subsequent U-Net core block for DVF prediction, and following layers with operations to compute data fidelity and regularization losses. The input raw data involve a source image obtained with fully-sampled k-space data, and the k-space data of a real-time target image along an undersampled readout trajectory. To pre-process the raw data for input into the U-Net core, we reconstructed the limited k-space data to an under-sampled target image by an inverse non-uniform fast-Fourier-transform (NUFFT) based reconstruction layer, to register with the fully-sampled source image. In addition, the k-space data of the fully-sampled source image was intentionally under-sampled using the same trajectory as the real-time target image, and reconstructed using the inverse NUFFT layer to serve as additional input channels to the U-Net. These three complex-valued images (fully-sampled source image, under-sampled target image, and intentionally under-sampled source image) were then combined as six parallel channels (each complex-valued image consists of two feature channels, representing the real and imaginary signals) and fed into the U-Net core. The channel separation is necessary for complex-valued data, as they are not well supported in current deep learning backends.

Figure 1.

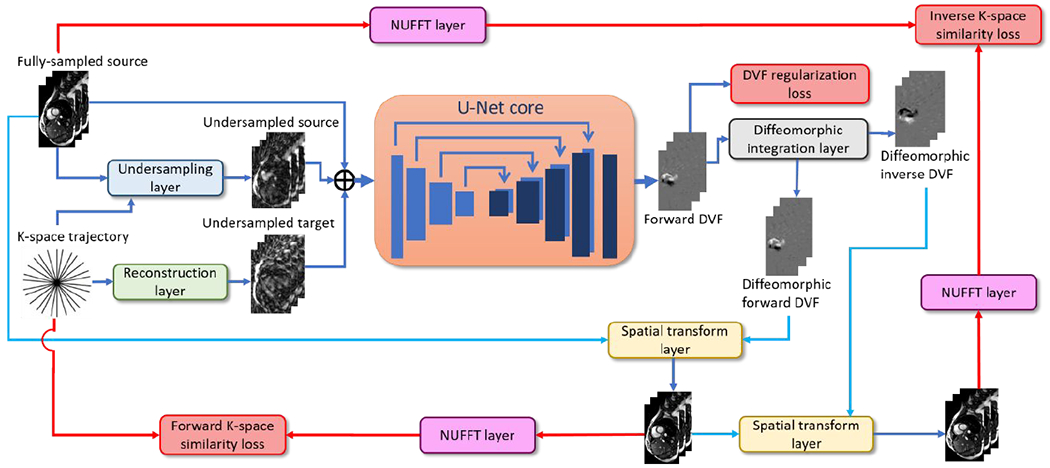
Workflow of the proposed k-space-driven registration network (KS-RegNet) that performs a deformable image registration between a fully-sampled source image and an on-board, highly under-sampled target image.

The U-Net core outputs a DVF composed of three Cartesian components, for the deformation fields along the x, y, and z directions, respectively. The DVF subsequently went through a diffeomorphic integration layer for fine-tuning as well as inverse DVF generation, to promote topology-preserving and inverse-consistent diffeomorphic registration (Balakrishnan et al. 2019; Dalca et al. 2019). During the training stage, the resulting forward and inverse DVFs went through two separate paths to quantify the registration accuracy. In the first path, the forward DVF deformed the source image to define a forward similarity loss. To avoid measuring image similarity on artifacts-ridden under-sampled images, we used a NUFFT layer to generate k-space data from the deformed source images. The re-projected k-space data of the deformed images were compared with the k-space data of the target images to assess their differences as the network loss. In the second path, the inverse DVF was applied to deform the deformed source image (by the forward DVF) back, to compare with the original source image in the k-space domain, since a fully-sampled target image was not available for direct inverse registration. The unsupervised training setup requires no gold-standard reference DVFs, which are difficult, if possible, to obtain. Details of the layers and operators used in the network are described in the following sections.

2.2.2. Details of network layers, operators and data

K-space data sampling trajectory

In this study, all the k-space data were sampled from 2D trajectories, and 3D images were stacks of these 2D images. In detail, the k-space readout trajectories were along radial directions with a golden-angle azimuthal spacing for each slice, and the same radial sampling was used along the stacked slices. Radial sampling was used because it usually permits fast scan time without sacrificing spatial resolution (Winkelmann et al. 2007), and is more robust to motion as the k-space center is traversed by each spoke (Stemkens, Paulson, and Tijssen 2018). Our framework can be readily generalized to other k-space sampling patterns, including 3D readout trajectories (e.g., stack-of-stars (Chandarana et al. 2011; Zhou et al. 2017) with Cartesian encoding in the slice-direction, or Koosh ball trajectories (Mendes Pereira et al. 2019)) without limitation.

Reconstruction (inverse NUFFT) and k-space data generation (NUFFT) layers

As the U-Net inputs used parallel channels of MR images, the target images need to be reconstructed from the on-board, under-sampled k-space data before feeding into the network. To introduce domain knowledge and to reduce the complexity and error bound of the network, we incorporated a preconfigured, non-trainable MR imaging reconstruction operator as the reconstruction layer, instead of training the reconstruction layer directly from raw k-space and reconstructed image data (Zhu et al. 2018). In detail, we adopted the inverse NUFFT operator used in the TorchKbNufft package (Muckley et al. 2020). The inverse NUFFT operator first interpolates off-grid radial k-space data to on-grid Cartesian locations using the Kaiser-Bessel kernel, and then applies density compensation on the re-gridded data to account for the fact that high-frequency components are less sampled in radial readout trajectories (Pipe and Menon 1999). In the end, FFT is applied to reconstruct MR images from the density-compensated and re-gridded k-space data.

Since the data fidelity losses of KS-RegNet were defined in k-space to assess the image registration accuracy, NUFFT layers were also implemented to transform the MR images into the k-space domain. The NUFFT layer is a reverse operation of the reconstruction layer. It applies the non-uniform Fourier transform to evaluate the k-space data at the frequencies specified by the radial readout trajectory. Note that the NUFFT layer takes complex-valued MR image data as input. Since each complex-valued MR image was separated into two channels (real and imaginary) before feeding into the U-Net, the correspondingly-deformed real and imaginary channels were re-combined into a complex-valued channel before being fed into each NUFFT layer.

Under-sampling layer

The k-space data of the fully-sampled source images were intentionally under-sampled with the same under-sampling trajectory as the target images, to form a third image input into the U-Net. The undersampling layer comprises a NUFFT and a reconstruction layer. By sharing the same under-sampling trajectory as the target image, the under-sampled source image provides additional information to inform the network of inherent under-sampling artifacts, to potentially reduce these artifacts’ impacts on image registration accuracy.

U-Net core architecture

We adopted the same U-Net core architecture as the Voxelmorph package (Balakrishnan et al. 2019; Dalca et al. 2019), which proves effective in solving both global and local deformation fields. The U-Net consists of a contraction and an expansion path with skip connections. The contraction path is composed of four blocks. Each block contains a convolution layer with a stride of 2 to down-sample the image volume, and a leaky rectified linear unit (ReLU) activation function with a negative slope of 0.2. The expansion path, symmetric to the contraction path, also contains four blocks. Each block involves a convolution layer with a stride of 1, a leaky ReLU activation function, and an up-sampling layer that doubles the image size. After up-sampling, the feature maps are concatenated with the counterparts in the contraction path through the skip connections to facilitate feature sharing and localization. The contraction and expansion paths are connected by a convolution layer with a stride of 1 and a leaky ReLU activation function. All convolution layers share the same kernel size of 3×3×3. The feature number of the first layer is 16, and 32 for the rest of the layers. Two additional convolution layers with a leaky ReLU activation function are added after the last block, and the feature number is reduced from 32 to 16. Lastly, a convolution layer is added as a conversion layer transforming the feature map to 3 channels, each channel representing the DVF along one Cardinal direction (x, y and z). The last convolution layer uses a padding of 1 to maintain the image size.

Diffeomorphic integration layer

A diffeomorphism is a geometric deformation which is one-to-one correspondence and, as well as its inverse, differentiable. Hence, constraining DVFs to diffeomorphisms preserves topological properties under the deformations, such as smoothness of surfaces or other features associated to anatomy (Beg et al. 2005). A diffeomorphic DVF can be obtained by integrating a stationary velocity field using the scaling and squaring algorithm (Arsigny et al. 2006). The diffeomorphic integration layer first scales the DVFs yielded from the U-Net core according to the number of integration steps. Then the scaled DVFs are treated as the starting velocity field and integrated iteratively using the spatial transform layer to obtain the diffeomorphic DVFs. The integration steps were empirically set to 7 in this study.

The inverse DVFs were obtained by reversing the forward DVFs (i.e., d⁻¹ (x) $\approx$ − d(x)), and then integrating the corresponding velocity fields to generate the diffeomorphic inverse DVFs. The diffeomorphic integration layers were adopted from the Voxelmorph package (Balakrishnan et al. 2019; Dalca et al. 2019).

Spatial transform layer

The spatial transform layer deforms an input image using the DVF, by trilinear interpolation (Jaderberg et al. 2015). KS-RegNet uses the spatial transform layer to deform the fully-sampled source image with a forward DVF [see Eq. (1)], and also to deform the target image with an inverse DVF d⁻¹ to promote inverse consistency (Yang et al. 2008). The inverse DVF deforms the target image to match with the source image. As mentioned, due to the lack of fully-sampled target images, we used the forwardly-deformed source images as the target images for inverse registration:

$${{\mathit{I}}^{″}}_{src}(\mathit{x})\approx {{\mathit{I}}^{\prime }}_{src}\left(\mathit{x}+{\mathit{d}}^{-1}(\mathit{x})\right),$$ (4)

where the double prime indicates the source image is first forwardly transformed by d, and then inversely deformed via d⁻¹.

2.3. Loss functions

To train the network, two loss functions were defined to measure the deformable registration data fidelity. The similarity metric was defined in k-space, as similarity in the image domain may not faithfully reflect the registration accuracy due to under-sampling aliasing and other artifacts. The first loss function measures the similarity between the input k-space data of the target image, and the k-space data of forwardly-deformed source image. In this study we used the mean absolute squared error between the two complex-valued k-space data as the similarity metric [Eq. (5)].

$$L_{kspace}\left({{\widehat{\mathit{I}}}^{\prime }}_{src},{\widehat{\mathit{I}}}_{tar}\right)=\frac{1}{N_{\mathit{k}}}\sum _{i=1}^{N_{\mathit{k}}}{\left|{{\widehat{\mathit{I}}}^{\prime }}_{src}\left({\mathit{k}}_i\right)-{\widehat{\mathit{I}}}_{tar}\left({\mathit{k}}_i\right)\right|}^2,$$ (5)

where $\widehat{\mathit{I}}(\mathit{k})$ denotes the Fourier transform of I(x), N_k is the number of sampling points in k-space, and k_i indicates the ith sampling frequency. Note that since the k-space data typically concentrate in the low-frequency region, the low-frequency error contributes most of the k-space loss. Although the motion signal is mostly low-frequency itself (Pipe 1999; Chen, Zhang, and Pang 2005; Liao et al. 1997), and may not be affected by the bias toward low-frequency k-space data, for some extreme cases the network may ignore some fine-detailed local deformations corresponding to high-frequency k-space data.

Since deformable image registration is an ill-posed problem, constrains are necessary to restrict the solution space to obtain a physically and physiologically plausible motion field. To enforce the inverse consistency, the second loss function is introduced to measure the similarity between inversely deformed target images and the source images.

$$L_{\mathit{\text{inversion}}}\left({{\widehat{\mathit{I}}}^{″}}_{src},{\widehat{\mathit{I}}}_{src}\right)=\frac{1}{N_{\mathit{k}}}\sum _{i=1}^{N_{\mathit{k}}}{\left|{{\widehat{\mathit{I}}}^{″}}_{src}\left({\mathit{k}}_i\right)-{\widehat{\mathit{I}}}_{src}\left({\mathit{k}}_i\right)\right|}^2.$$ (6)

The k-space sampling trajectory used in Eq. (6) is the under-sampled readout trajectory of the real-time MR image. In addition to the data fidelity losses, a third loss function is introduced to further regularize the smoothness of the DVFs. It calculates the mean deformation energy of the DVF via:

$$L_{\mathit{\text{smoothness}}}(\mathit{d})=\frac{1}{3}\sum _{l=x,y,z}\frac{1}{N}\sum _{i=1}^N\left({\left(\frac{\partial d_l\left({\mathit{x}}_i\right)}{\partial x}\right)}^2+{\left(\frac{\partial d_l\left({\mathit{x}}_i\right)}{\partial y}\right)}^2+{\left(\frac{\partial d_l\left({\mathit{x}}_i\right)}{\partial z}\right)}^2\right),$$ (7)

where d_l denotes a Cartesian component (x, y, z) of d, and N is the number of image voxels. The derivative is calculated using forward finite difference.

Finally, the total loss function is a weighted sum of the three loss functions:

$$L={\lambda }_{kspace}{L}_{kspace}+{\lambda }_{inversion}{L}_{inversion}+{\lambda }_{smoothness}{L}_{smoothness},$$ (8)

where λ are the weighting factors. In this work, λ_kspace= 1.0, λ_inversion= 4.0, and λ_smoothness= 0.04 were adopted for the cardiac dataset, and λ_kspace= 1.0, λ_inversion= 4.0, and λ_smoothness= 0.02 were used for the abdominal dataset by trial-and-error experiments.

2.4. Dataset curation

KS-RegNet was tested on a cardiac MRI dataset and an abdominal MRI dataset to evaluate its capability to accurately predict DVFs describing cardiac and respiratory motions, respectively. The following describes the details and pre-process steps of the cardiac and abdominal datasets.

2.4.1. Cardiac dataset

Multi-slice cardiac cine MR data from an open-access multi-coil k-space dataset (OCMR) were used in this study to train and evaluate the proposed KS-RegNet framework (Chen et al. 2020). The dataset included scans collected by three Siemens MAGNETON scanners: Prisma (3T), Avanto (1.5T), and Sola (1.5T) (Siemens AG, Munich, Germany). While the dataset includes both fully-sampled and undersampled 3D scans, only subjects of fully-sampled scans were used in this study as they can provide fully-sampled ‘gold-standard’ images for evaluation. The 3D multi-slice cine images of each subject were acquired in planar mode, and the slices were collected in the short-axis view covering from base to apex. The MR scans were acquired using the gradient-echo steady-state free precession pulse sequence, based on various acquisition parameters such as magnetic field strength, field-of-view, and resolution. Table 1 summarizes the imaging acquisition parameters of the subjects involved in our study. The cardiac cycles of the subjects were partitioned into different number of bins, and the cardiac bins started from the end of diastole for all subjects.

Table 1.

MR imaging acquisition parameters of the subjects in the cardiac dataset.

Subject	Field-of-view (x×y×z mm3)	Volume Size (x×y×z)	Resolution (mm3)	No. of Cardiac bins	Echo time (millisecond s, ms)	Repetition time (ms)	Flip angle (degrees)	Field strength (T)
1	760×285×80	384×144×10	1.98×1.98×8.0	25	1.53	36.60	33	3.0
2	720×309×112	384×156×14	1.88×1.98×8.0	22	1.49	35.64	70	1.5
3	720×270×80	320×120×10	2.25×2.25×8.0	30	1.43	28.50	70	1.5
4	760×285×96	384×144×12	1.98×1.98×8.0	19	1.49	35.64	70	1.5
5	760×285×96	384×144×12	1.98×1.98×8.0	25	1.49	35.64	70	1.5
6	760×285×96	384×144×12	1.98×1.98×8.0	21	1.49	35.64	70	1.5
7	600×233×66	288×112×11	2.08×2.08×6.0	18	1.41	39.34	40	3.0
8	760×285×96	384×144×12	1.98×1.98×8.0	25	1.49	35.64	70	1.5

In order to simulate under-sampled k-space data, we first reconstructed the complex-valued MR images from the fully-sampled k-space data provided by the OCMR dataset, using a reconstruction algorithm with adaptive coil sensitivity map estimation (Walsh, Gmitro, and Marcellin 2000). The reconstruction was performed slice by slice, and the volumetric MR images were a stack of the reconstructed 2D images. As the images were acquired in different sizes, the reconstructed images were then resampled to a uniform size of 256×256×32 using trilinear interpolation. In addition, voxel values of the resampled images were further normalized, such that the maximum absolute voxel value across the real and imaginary parts of a complex-valued image is one.

2.4.2. Abdominal dataset

The abdominal dataset contains 9 subjects with liver cancer. The dataset was shared from the Hong Kong Polytechnic University, with the study approved under an umbrella institutional review boards protocol. Unlike the OCMR dataset, the abdominal 4D-MRI data were post reconstruction (without access to the raw k-space data). The abdominal data were collected in planar mode and then retrospectively sorted into 4D-MRIs, all with a slice thickness of 5 mm (36-60 slices per 4D bin, dependent on subject). The image in-plane resolutions vary between 1.41×1.41 mm² to 1.88×1.88 mm² among different subjects, with inplane dimension all at 256×256. Except for one subject, all of them had 4D-MRIs with 10 respiratory-resolved bins. These 4D-MRIs are magnitude-only, so no phase information can be retrieved from the dataset. Table 2 summarizes the acquisition parameters of the subjects in the dataset.

Table 2.

MR imaging acquisition parameters of the subjects in the abdominal dataset.

Subject	Field-of-view (x×y×z mm3)	Volume Size (x×y×z)	Resolution (mm3)	No. of slices	No. of respiratory bins	Echo time (ms)	Repetition time (ms)	Flip angle (degrees)	Field strength (T)
1	480×480×180	256×256×36	1.88×1.88×5.0	36	6	1.13	3.01	50	1.5
2	480×480×200	256×256×40	1.88×1.88×5.0	40	10	1.13	3.01	50	1.5
3	480×480×200	256×256×40	1.88×1.88×5.0	40	10	1.13	3.01	50	1.5
4	480×480×215	256×256×43	1.88×1.88×5.0	43	10	1.13	3.01	50	1.5
5	360×360×200	256×256×40	1.41×1.41×5.0	40	10	1.13	3.01	50	1.5
6	480×480×300	256×256×60	1.88×1.88×5.0	60	10	1.13	3.01	50	1.5
7	420×420×240	256×256×48	1.64×1.64×5.0	48	10	1.13	3.01	50	1.5
8	360×360×210	256×256×42	1.41×1.41×5.0	42	10	1.13	3.01	50	1.5
9	480×480×200	256×256×40	1.88×1.88×5.0	40	10	1.13	3.01	50	1.5

The liver MRIs were resampled to a uniform size of 256×256×32 with the in-plane resolution intact. The slice thickness (5 mm) was also kept the same during re-sampling, and peripheral slices outside of liver were cut off. Since the MR images are magnitude-only, additional processing steps were added in the study to simulate complex-valued MR images, using phase simulation strategies similar to (Zhu et al. 2018; Terpstra et al. 2020). We first synthesized the phase map on the first respiratory bin of each 4D-MRI set, using sinusoidal functions, to simulate phase-modulated, complex-valued MR images. To propagate the phase map onto the remaining 4D MR bins, we registered the MR image at the first respiratory bin to the MR images at the other 4D bins using Elastix (Klein et al. 2010), and used the resulting DVFs for image and phase map propagation. After the DVF-based propagation, we simulated a set of complex-valued 4D MR images with phase-modulation. While these synthesized phase maps recapture some phase information lost in the post reconstruction, we acknowledge that there remains some information, such as tissue-dependent phase information, not simulated through the augmentation.

For each patient subject in the dataset, 20 sequences of phase maps were simulated for network training. The synthesized phase maps were assumed to take 3D sinusoidal forms with four combined spatial frequencies along each Cartesian dimension (Zhu et al. 2018; Terpstra et al. 2020). Along each Cartesian direction, the four spatial frequencies were randomly selected between 1.25×10⁻³ mm⁻¹ and 2.50×10⁻³ mm⁻¹ which correspond to wavelengths of 800 mm and 400 mm, respectively, with a random phase shift being added to each frequency. Because of the phase-map augmentation, the network performance can depend on the number of synthesized phase maps. Therefore, we examined the registration accuracy with different levels of phase-map augmentation to assess the robustness of the training process (See the supplementary material). In addition to the above case of 20 phase maps, we also trained KS-RegNet without the phase-map augmentation and with 40 sequences of phase maps. In addition to the synthesized phase maps, Gaussian noise was separately added to the real and imaginary parts of the complex-valued MR images at each respiratory bin, to augment network training and testing. We generated 40 noise maps with zero mean and standard deviation randomly selected between 3.0×10⁻³ and 5.0×10⁻³.

2.5. Network training and evaluation

2.5.1. Cross-validation and data augmentation

As only limited subjects were available in the cardiac and abdominal datasets, cross-validation was used to evaluate the performance of the proposed framework. For the cardiac dataset, the 8 subjects were equally partitioned into 4 subsets. For each round of the cross-validation, the model was trained on the subjects in 3 subsets, and tested on the subjects in the remaining subset (e.g., subject No. 3-8 for training and subject No. 1-2 for testing). For the abdominal dataset, the 9 subjects were equally divided into 3 subsets for a 3-fold cross-validation. For each fold, at each training step of KS-RegNet, we randomly selected a subject and two of its cardiac or respiratory bins from the training set, as the source and the target. While only 6 subjects were involved in each training set, there were 3,124 to 3,436 unique registration pairs of cardiac images (depending on cross-validation fold), and 536 to 600 registration pairs of abdominal images available for training, by using this randomization strategy. On top of this randomization strategy, in order to further avoid overfitting and to improve robustness, data augmentation was used on-the-fly during the training stage. For each pair of source and target images, we added random in-plane translations and reflections. The geometric augmentations (i.e., the translation and reflection) alter the k-space data. However, they do not affect the forward and inverse k-space similarity losses. For instance, translation of an object in the image domain corresponds to adding a linear phase in the frequency domain. Since the k-space losses were defined as the mean absolute square difference in Eqs. (5) and (6), the linear phase modulation has no effect on the calculated loss value. Therefore, this augmentation can improve the translational invariance of KS-RegNet, and the network is trained more robust.

In addition to these geometric transformations, the cardiac MR images were also rotated with a random phase angle (between real and imaginary channels) for additional data augmentation. The abdominal dataset, on the other hand, was augmented via randomizations using the 20 synthesized phase maps and the 40 noise maps (Sec. 2.4.2). For each training example, the phase and noise maps were randomly and independently chosen on-the-fly to enlarge the variation of the augmentation.

After the above mentioned randomizations and augmentations, we then used the complex-valued, fully-sampled source MRI as the source image, and the under-sampled k-space data of the target bin as the target k-space data, to feed into KS-RegNet for training. The k-space under-sampling was performed on the MRIs based on a radial sampling pattern, using the NUFFT operator from the TorchKbNufft package. For each slice, the sampling pattern was based on a radial readout trajectory with various numbers of spokes, with each spoke of 256 evenly distributed sampling points. The radial trajectory starts from some initial azimuthal angle, and the angle between two adjacent spokes is increased by the golden-ratio angle (111.25°). The initial azimuthal angle was randomly selected on-the-fly during the training stage. We simulated three readout trajectories of 13, 9, and 5 spokes, corresponding to under-sampling factors of around 31, 45, and 80, respectively (Terpstra et al. 2020). The under-sampling factor is defined as the ratio of the number of spokes required for a fully-sampled reconstruction to the number of spokes simulated for under-sampling.

The network was trained on a graphic processing unit card (NVIDIA Tesla V100). The framework was implemented in Python with the PyTorch 1.7.1 library (Paszke et al. 2019). The Adam optimizer was used for optimization, with an initial learning rate set to 0.0004. The learning rate was adaptively reduced by 20% if the loss stopped improving over 5 epochs. The network iterated 100 steps in an epoch, and each step had a batch size of 4. When the training loss stopped decreasing even with the adapted learning rate, the training was stopped and the model was used for testing. The numbers of training epochs used for 13-, 9-, and 5-spoke cases were 120, 70, and 60, respectively. It took about 90-120 hours to train a model with 13-spoke trajectories for the cardiac and abdominal datasets.

For testing, we used the first cardiac or respiratory bin as the prior (source) image, and used the trained KS-RegNet to predict DVFs between the first bin and all other remaining bins. The testing was repeated for the models trained using different under-sampling ratios (5-13 spokes).

2.5.2. Evaluation Metrics

The accuracy of KS-RegNet was evaluated by contour-based metrics including the 95th percentile Hausdorff distance (HD95), DICE coefficient, and center-of-mass error (COME). Let X and Y be the sets of the deformed and ‘gold-standard’ target contours, respectively. The HD95 (Taha and Hanbury 2015) between X and Y is defined by

$$d_H=\max \left\{P_{95\text{\%}}d(x,Y),P_{95\text{\%}}d(y,X)\right\},$$ (9)

where P_95% denotes the 95th percentile operation and

$$d(x,Y)=\underset{y\in Y}{\min }\parallel x-y\parallel .$$ (10)

Given two contours V₁ and V₂ as binary volumetric sets, the DICE coefficient is defined as

$$DICE=\frac{2\times \left|V_1\cap V_2\right|}{\left|V_1\right|+\left|V_2\right|},$$ (11)

where |V_j| denotes the cardinality of V_j, (j = 1, 2). It evaluates the degree of the overlap between the two contours. Higher value of the DICE coefficient represents a better overlap, with highest value 1 representing identical sets. In order to calculate the DICE coefficients for contour-based DVF evaluation, we manually segmented anatomical features in the MR images. For the cardiac dataset, we segmented the left ventricles for all subjects across all cardiac bins. Left ventricle was chosen because it displays well-defined boundary in the short-axis view and can be used to quantify the registration accuracy with a high confidence level. For the abdominal dataset, we manually segmented liver tumors in the images of the first respiratory bin and propagated the contours onto the other bins using the Elastix DVFs (which were used to simulate the complex-valued 4D-MRIs). After obtaining the ‘gold-standard’ contours for both datasets, the contours of the first bin were deformed to all other bins by applying the DVFs predicted from the network for comparison. Finally, the DICE coefficients were calculated between the deformed and ‘gold-standard’ contours. The COME, in addition, measures the center-of-mass distance between the deformed and ‘gold-standard’ contours.

2.5.3. Comparison with other methods

Comparison with conventional registration methods

Elastix was compared to KS-RegNet for the cardiac study (Klein et al. 2010). Since the abdominal MR images used in the network training were generated using Elastix (see Sec. 2.4.2), the comparison is biased in favor of the Elastix-based methods. Thus, only the cardiac dataset were used to compare with the Elastix methods. The Elastix deformable registration was evaluated under two settings. In the first setting, Elastix performed a registration between a fully-sampled source image and an under-sampled target image, to reflect the current standard practice of image registration. Because of disparate image qualities between the two images, the registration is expected to be challenging. In the second setting, the k-space of the source image was under-sampled to match that of the target image to reconstruct an intentionally under-sampled source image, and the registration was performed between the under-sampled source and target images. After the registration, the fully-sampled source image was deformed using the DVF estimated from the under-sampled pairs. For both settings, the registrations were performed on the images sampled by 5-, 9-, and 13-spoke trajectories. The performance of Elastix was similarly evaluated in terms of the HD95, DICE coefficient, and COME. Wilcoxon signed-rank test was performed to assess the statistical significance of the registration result differences between KS-RegNet and Elastix.

Ablative studies and robustness tests

To demonstrate the benefits of adding the intentionally under-sampled source image as the third set for KS-RegNet input, we performed an ablative study by removing this under-sampled image from the input, and trained a network to compare with KS-RegNet. This network is termed KS-RegNet-nup with nup indicating no under-sampled prior, to distinguish from KS-RegNet. In addition, to demonstrate the benefits of defining the data fidelity losses in k-space instead of the image domain, we performed another ablative study by defining the loss directly on the under-sampled image pairs (with the fully-sampled source image removed from the U-Net input). This network is termed RegNet. Another variant of RegNet that retains the fully-sampled source image is also tested to evaluate whether accessing the fully-sampled source image helps the motion estimation, even though it is not directly used to quantify the similarity losses. The results are presented in the supplementary materials (section 3) due to the length limitation.

Two robustness tests were performed to examine the sensitivity of KS-RegNet to various under-sampling factors, and to degradations of the prior image quality. In the first robustness test, a network trained with one under-sampling factor was also tested on k-space data featuring different under-sampling factors, without re-training. For example, the network trained on the k-space data sampled with 13-spoke trajectories was used to make a prediction of DVFs on the k-space data of 9- and 5-spoke trajectories. We performed this test on KS-RegNet and KS-RegNet-nup, to evaluate if the additional under-sampled source image input of KS-RegNet can help to enhance the robustness. Since KS-RegNet relies on high-quality prior images to register between the prior and under-sampled images, it is critical to understand the sensitivity of KS-RegNet to the quality of the prior images, considering that it may vary across MR scans. Therefore, in the second robustness test, the prior images were intentionally degraded before feeding into KS-RegNet for DVF prediction. To control and quantify the degradation, the k-space data of a fully-sampled prior image were firstly computed using a radial readout trajectory with a uniform angular spacing, and radial spokes were randomly removed from the readout trajectory according to the degradation factor. Finally, the degraded prior image was reconstructed from the degraded k-space data, and used as the prior image to feed into KS-RegNet. We used a radial trajectory of 403 spokes to compute the k-space data, and controlled the degradation by removing 10%-80% of the radial spokes.

3. Results

3.1. Qualitative comparison of cardiac MR images

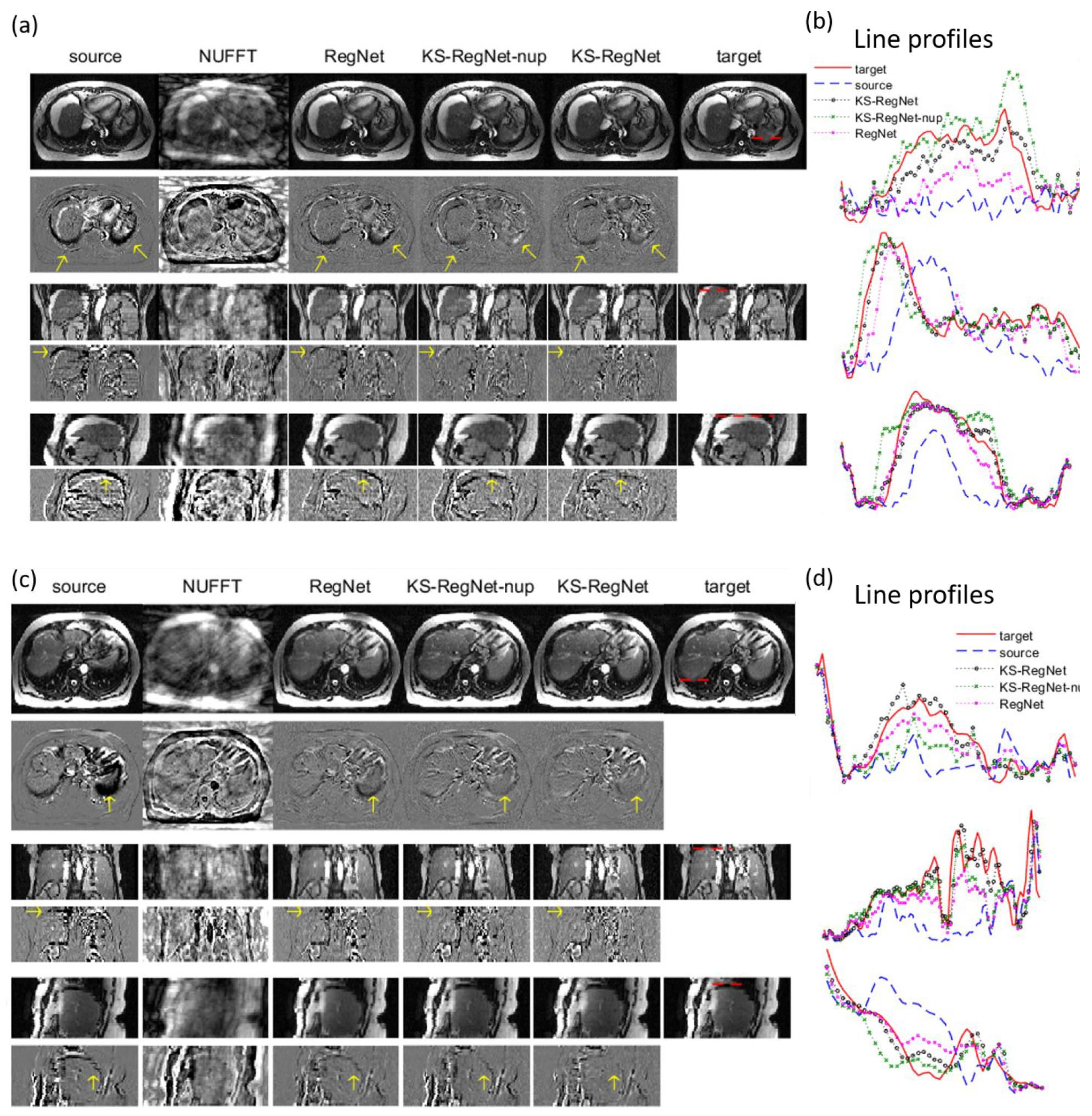
Figures 2(a) and 2(c) compare images by different methods for two study subjects. The k-space spoke number is 13, corresponding to an under-sampling factor of 31. The first and last columns show, respectively, the fully-sampled source image and the fully-sampled ‘gold-standard’ target image, in the short-axis view (first row) and the long-axis views (third and fifth rows). The source and target images correspond to the diastole and systole cardiac phases, respectively. The second column shows the under-sampled target image directly reconstructed by NUFFT. The third column shows the registered image, by registering between under-sampled (US) source and US target images using Elastix. The following three columns present the registered images from DL-based registrations: RegNet, KS-RegNet-nup, and KS-RegNet. The even rows show the differences between the corresponding images and the target image in the three views. The images of the Elastix registrations between the fully-sampled source and US target images are not presented because the registration errors were substantially larger than the other methods. Figures 2(b) and 2(d) compare line profiles located by the horizontal dashed lines in the target images of Figs. 2(a) and 2(c). It can be observed from the even rows that the deformed images by KS-RegNet had the smallest differences from the target images, which are corroborated by the line profiles.

Figure 2.

Comparison of cardiac MR images by different methods. Subfigures (a) and (c) present the images from different methods in three views (odd rows), and the differences between these images and the target images (even rows). The methods are indicated on top of each column. The spoke number used for k-space is 13. Figures (c) and (d) show the line profiles located by the horizontal dashed lines in the target images.

3.2. Qualitative comparison of abdominal MR images

Figure 3 presents a comparison of the DL-based methods (RegNet, KS-RegNet-nup, and KS-RegNet) for two subjects in the abdominal dataset. The respiratory bins of the source and target images are end-of-inhale and end-of-exhale phases, respectively. The first, third, and fifth rows are the MR images in the axial, coronal, and sagittal views, respectively. The k-space spoke number is 13. The results of Elastix are not presented because Elastix was used to generate the phase-modulated images, and thus the registration performance is biased in favor of the Elastix-based methods. Figures 3(b) and 3(d) compare line profiles located by the horizontal dashed lines in the target images of Figs. 3(a) and 3(c) in the three views.

Figure 3.

Comparison of abdominal MR images by different methods. Subfigures (a) and (c) present the images from different methods in the axial, coronal, and sagittal views (odd rows), and the differences between these images and the target images (even rows). The methods are indicated on top of each column. The spoke number used for k-space sampling is 13. Figures (c) and (d) show the line profiles located by the horizontal dashed lines in the target images.

From the difference images of the DL-based methods (columns 3-5), it can be observed that KS-RegNet provides the best registration accuracy, especially in the region near the liver boundary. Since the intensity and contrast of the liver is relatively low, the image differences within the liver are not as prominent as the cardiac cases. Nevertheless, from the line profiles it can be observed that KS-RegNet deforms the source images well to match with the target images.

3.3. Quantitative comparison of registration accuracy for the cardiac dataset

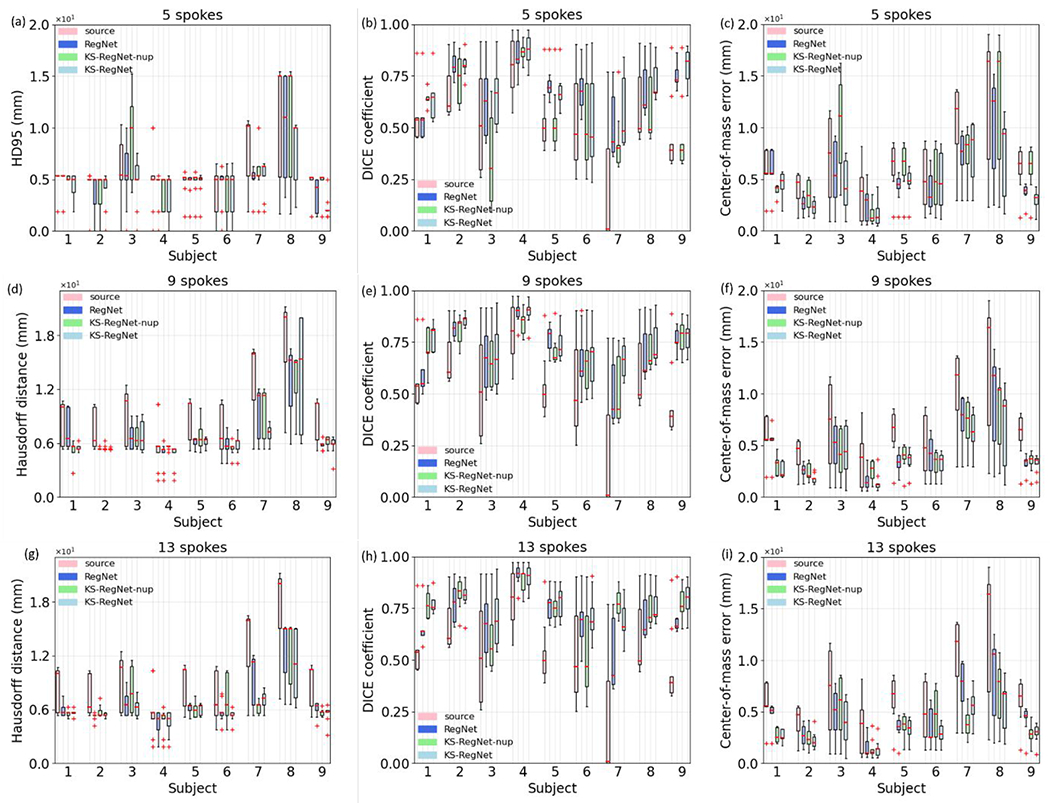
Figure 4 quantitatively compares the registration accuracy of different registration methods on the cardiac dataset using boxplots at three different under-sampling factors. For comparison, the HD95s, DICE coefficients, and COMEs between the fully-sampled (FS) source and target images are also presented as the first boxplot (i.e., source) of each subject.

Figure 4.

Boxplots of 95th percentile Hausdorff distances (HD95s), DICE coefficients, and center-of-mass errors (COMEs) of different methods for all subjects in the cardiac dataset, using different numbers of k-space spokes for motion estimation. For comparison, the first boxplot of each subject (i.e., source) presents the HD95, DICE coefficient, and COME between the fully-sampled source and target images. The COMEs for the FS-to-US Elastix method of the subject No. 3 are substantially worse than the others, and were not included in the corresponding boxplots.

KS-RegNet made an accurate DVF prediction for this subject, as compared to other methods. Of all the methods, the FS-to-US Elastix had the worst performance in terms of HD95 and DICE coefficient. For most of subjects in the 5- and 9-spoke cases, their DICE coefficients were even worse than those without deformation (i.e., source), which demonstrated the challenges of registering two images of unmatched image qualities.

The volume-based HD95, DICE coefficient, and COME show fluctuations as the under-sampling factor varies. The distributions of the DICE coefficient and COME of each subject can fluctuate, especially for the methods of US-to-US Elastix and KS-RegNet-nup [e.g., the COME of the US-to-US Elastix of the subject No. 4; the COME of the KS-RegNet-nup of the subject No. 8 in Figs. 4(c), 4(f), and 4(i)]. This fluctuation reflects the instability of these algorithms under highly under-sampled scenarios. In general, KS-RegNet performed better than the other methods for all under-sampling factors with demonstrated stability and consistency, demonstrating its robustness to various under-sampling patterns.

Table 3 presents the mean (±s.d.) of the HD95s, DICE coefficients, and COMEs for different methods, and the results of the Wilcoxon signed-rank tests between KS-RegNet and the other methods. The FS-to-US Elastix registrations were not included because of its low registration accuracy. The proposed KS-RegNet had the best registration accuracy for all under-sampling factors. Except for the statistical test between KS-RegNet and US-to-US Elastix of the 13- and 9-spoke cases, all statistical tests showed p-values < 0.05.

Table 3.

Mean (±s.d.) HD95s, DICE coefficients, COME, and Wilcoxon signed-rank test results of different methods. The Wilcoxon signed-rank tests are between the KS-RegNet and the other methods.

Number of spokes	Method	Mean (±s.d.)			p-value
		HD95 (mm)	DICE coefficient	COME (mm)	HD95	DICE coefficient	COME
5	KS-RegNet	4.97±2.78	0.884±0.025	1.21±1.09	--	--	--
	KS-RegNet-nup	6.45±1.80	0.807±0.064	2.22±1.96	< 10−3	< 10−3	< 10−3
	RegNet	6.24±1.88	0.797±0.051	1.82±1.85	< 10−3	< 10−3	< 10−3
	Elastix (US to US)	6.23±2.89	0.849±0.029	1.88±1.93	< 10−3	< 10−3	< 10−3
9	KS-RegNet	4.74±2.62	0.889±0.024	1.29±1.22	--	--	--
	KS-RegNet-nup	5.72±1.90	0.846±0.040	1.81±1.49	< 10−3	< 10−3	< 10−3
	RegNet	6.09±1.91	0.821±0.040	1.61±1.56	< 10−3	< 10−3	< 10−3
	Elastix (US to US)	6.33±3.32	0.863±0.038	1.59±1.70	< 10−3	0.007	0.107
13	KS-RegNet	4.51±2.82	0.894±0.022	1.01±0.86	--	--	--
	KS-RegNet-nup	4.99±2.21	0.868±0.024	1.36±0.92	< 10−3	< 10−3	< 10−3
	RegNet	5.93±1.97	0.835±0.042	1.49±1.40	< 10−3	< 10−3	< 10−3
	Elastix (US to US)	5.77±3.24	0.869±0.043	1.58±1.73	< 10−3	0.069	< 10−3

3.4. Quantitative comparison of registration accuracy for the abdominal dataset

Figure 5 shows the boxplots of HD95, DICE coefficient, and COME of the subjects in the abdominal dataset. The Elastix results (FS-to-US and US-to-US) are not included as Elastix was used to generate phase-modulated MR images and would bias the comparison. The mean (±s.d.) of the HD95s, DICE coefficients, and COMEs for different methods, and the results of the Wilcoxon signed-rank tests between KS-RegNet and the other methods are presented in Table 4.

Figure 5.

Boxplots of HD95s, DICE coefficients, and COMEs of different methods for all subjects in the abdominal dataset, using different numbers of k-space spokes for motion estimation. The spoke numbers are given in the subfigure title. For comparison, the first boxplot of each subject (i.e., source) presents the HD95, DICE coefficient, and COME between the fully-sampled source and target images.

Table 4.

Mean (±s.d.) HD95s, DICE coefficients, COME, and Wilcoxon signed-rank test results of different methods. The Wilcoxon signed-rank tests are between the KS-RegNet and the other methods.

Number of spokes	Method	Mean (±s.d.)			p-value
		HD95 (mm)	DICE coefficient	COME (mm)	HD95	DICE coefficient	COME
5	KS-RegNet	4.54±2.45	0.694±0.167	4.60±2.91	--	--	--
	KS-RegNet-nup	5.91±3.77	0.566±0.221	6.56±4.61	< 10−3	< 10−3	< 10−3
	RegNet	5.17±3.14	0.693±0.151	5.14±3.35	0.002	0.049	0.005
9	KS-RegNet	3.88±2.98	0.751±0.128	3.91±2.72	--	--	--
	KS-RegNet-nup	4.11±2.51	0.712±0.141	4.36±2.75	0.241	< 10−3	< 10−3
	RegNet	4.37±2.51	0.713±0.156	4.62±3.23	0.011	< 10−3	< 10−3
13	KS-RegNet	3.25±1.90	0.766±0.106	3.48±2.00	--	--	--
	KS-RegNet-nup	4.04±2.53	0.739±0.151	3.89±2.44	< 10−3	0.009	0.003
	RegNet	4.43±2.45	0.712±0.149	4.54±2.93	< 10−3	< 10−3	< 10−3

Comparing the DICE coefficients and COMEs among all subjects, KS-RegNet has the best performance for most of the subjects. While the variations for other methods gradually increase as the number of spoke decreases, KS-RegNet shows a relatively stable registration accuracy. Table 4 shows that KS-RegNet has the best performance across all three under-sampling factors with p-values < 0.05. Note that the relatively large COMEs are partially contributed by the large slice thickness of the 4D-MRI liver dataset (5 mm), thus the error is within the dimension of a single voxel.

3.5. Robustness tests

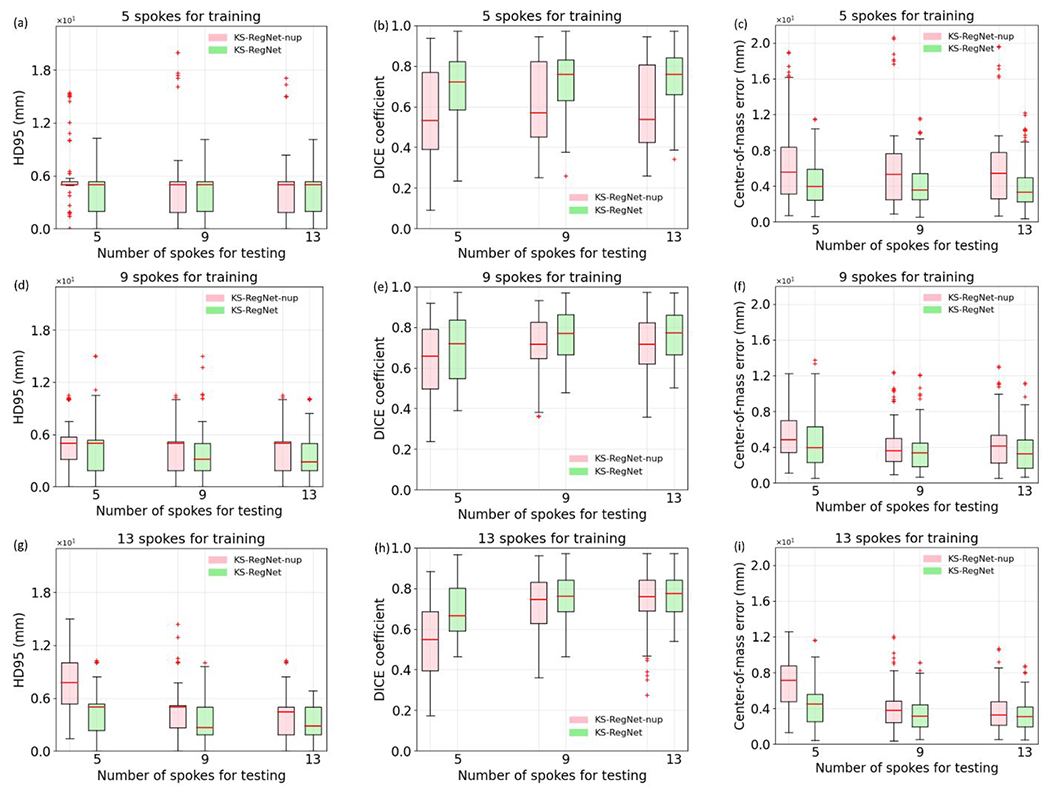
3.5.1. Robustness to under-sampling factor variations (between training and testing)

Figure 6 presents the results of the robustness test on the cardiac dataset. The spoke numbers specified in the subfigure titles are the numbers of spokes used to train the networks, and the spoke numbers given by the axis labels are the numbers of spokes used for testing. The performance of Elastix (US-to-US) is also given for each number of spokes as a benchmark, and the training spoke number denotation does not apply to Elastix.

Figure 6.

Robustness test of KS-RegNet and KS-RegNet-nup on the cardiac dataset. The networks were trained under the k-space spoke numbers indicated by the subfigure title, and tested for different under-sampling factors specified by the axis labels. For comparison, the results of Elastix registration between under-sampled (US) source and US target images are also given, and the training spoke number denotation does not apply to Elastix results.

The comparison shows that KS-RegNet was more robust, with its registration performance relatively stable under various degrees of under-sampling factors, even if the network was trained using data of a different under-sampling pattern. The KS-RegNet trained on the 13-spoke trajectories had only a mild decrease of its performance when it was tested on the 5- and 9-spoke trajectories [Figs. 6(g–h)]. On the other hand, KS-RegNet-nup had a more significant increases of the COME and decrease of DICE coefficient, especially for the cases where the network was trained with 9- and 13-spoke trajectories [Figs. 6(d–i)].

The results of the robustness test on the abdominal dataset are presented in Fig. 7. The results of Elastix are not shown because it is used to generate phase-modulated images for training and will bias the comparison. KS-RegNet has stable performance when the under-sampling patterns varies, especially for the 13-spoke training scenario. The narrow box of KS-RegNet-nup in Fig. 7(a) is due to the clustering of data at the 5-mm slice thickness. The comparisons in Figs. 6 and 7 demonstrate that adding the intentionally under-sampled source images into network input, as in KS-RegNet, helps to improves registration accuracy and enhances the robustness to the under-sampling factor variations between training and testing.

Figure 7.

Robustness test of KS-RegNet and KS-RegNet-nup on the abdominal dataset. The networks were trained under the k-space spoke numbers indicated by the subfigure title, and tested for different under-sampling factors specified by the axis labels.

3.5.2. Robustness to source image quality

Figures 8 presents the robustness test results to the prior image quality for the cardiac and abdominal studies. The quality of the prior image was intentionally degraded by removing 20%, 50%, and 80% of radial spokes from the fully-sampled readout trajectory. For comparison, we also present the metrics between the fully-sampled source and target images and the results of KS-RegNet using fully-sampled source images in the first and second boxplots, respectively. Based the degraded prior image, we did similar studies to predict DVFs between the prior image and under-sampled target image (based on 5-, 9- and 13- radial spokes per slice). Only results for the 13-spoke under-sampling patterns are presented here (see supplementary material for the 5- and 9-spoke results). However, we found consistent trends of the 5- and 9-spoke under-sampling patterns with the 13-spoke cases. It can be observed that there is no significant reduction in the registration accuracy when the source image quality was degraded during the tests.

Figure 8.

Robustness test results of KS-RegNet to the quality variations of source images. The quality of source images was controlled by under-sampling their k-space data by 20%, 50% and 80%, respectively. The first and second rows respectively present the results of the cardiac [Figs. 8(a–b)] and abdominal [Figs. 8(c–d)] datasets. For comparison, the first and second boxplots of each subject show the metrics between the source and target images, and the results of KS-RegNet using fully-sampled, non-degraded prior images, respectively.

The COMEs of subjects 3 and 5 in the abdominal dataset [Fig. 8(d)] exhibit a counterintuitive behavior that the COME decreases as the under-sampling factor increases. For subject 3, we found it has some unique anatomical features that are not shown in the training dataset. The fluctuations for subjects 3 and 5 are also likely due to the statistic fluctuation of the deep learning model, which is trained using a small dataset. The uncertainties from introducing under-sampling artifacts to high-quality prior images, and the relatively low resolution along the slice direction, may also play a role.

4. Discussion

In this study, we proposed a DL-based framework (KS-RegNet) for real-time motion estimation of on-board MR images. Due to the temporal resolution requirement of real-time MR imaging, on-board k-space data are highly under-sampled. The reconstructed images, therefore, suffer from severe under-sampling artifacts. The degraded image quality hinders accurate motion estimation and target localization. By incorporating high-quality prior information, KS-RegNet estimates motion by performing a deformable image registration between a fully-sampled, complex-valued MR image and the highly under-sampled, on-board k-space data. The network training was designed as un-supervised, thus eliminating the needs to generate gold-standard DVFs for network training, which proves a challenging task. In addition, instead of the image domain, KS-RegNet measures the accuracy of the deformable registration in the k-space domain, thus avoiding defining a similarity metric on images impacted by under-sampling aliasing and other artifacts. KS-RegNet also uses an intentionally under-sampled source MR image as an additional input, to train the network to perceive under-sampling artifacts and reduce their effects on registration accuracy.

Our results demonstrated the capabilities of KS-RegNet to predict DVFs associated with cardiac and respiratory motions on different anatomic sites. Compared with Elastix and other network architectures (i.e., RegNet and KS-RegNet-nup), KS-RegNet had the best registration accuracy and its performance was stable at various tested under-sampling factors (Figs. 2–7 and Tables 3–4). The qualitative comparisons in Figs. 2 and 3 show that even though the reconstructed target images by NUFFT suffer from under-sampling artifacts, our framework was able to accurate estimate the motion. Tables 3 and 4 show that KS-RegNet had the lowest mean HD95s and COMEs and highest mean DICE coefficients for the three under-sampling factors. The ablative studies and robustness tests supported the benefit of training the network to learn the under-sampling artifacts by introducing an intentionally under-sampled source image as input (Figs. 4–7). With the additional under-sampled source image as input to perceive the artifacts, KS-RegNet showed comparable accuracy under the three different under-sampling factors (Figs. 4–5) and remained accurate even if the under-sampling pattern changed between the training and testing (Figs. 6–7). Even KS-RegNet was trained with high-quality, fully-sampled prior images, it shows robustness to degradations of the quality of the prior images (Fig. 8).

4.1. Comparison with other works

To register large and complex deformations, multi-resolution pyramid scheme is usually employed to prevent the algorithm from being trapped in a local minimum during optimization. In such a scheme, the deformable registration is started at a low resolution, and the resolution is progressively increased at consecutive levels to fine-tune the registration. This scheme has been used in Elastix (Klein et al. 2010) and in DL-based methods (Terpstra et al. 2020; Jiang et al. 2020; Fu et al. 2020; Terpstra et al. 2021). We tested this scheme preliminarily on the cardiac dataset, but found it of limited benefits, which potentially could be due to the small training sample size. The multi-resolution scheme can be further evaluated when a larger sample size becomes available. Another way to further improve the performance of the proposed framework is to combine image registration with image reconstruction, by adding additional reconstruction blocks such as the cascaded DL networks (Schlemper, Caballero, et al. 2018; Kustner et al. 2020; Kofler et al. 2021), to further enhance the accuracy of the output real-time MR image.

Terpstra et al. recently reported a framework for real-time MR-guided radiotherapy (Terpstra et al. 2020). They divided their workflow into consecutive image reconstruction and motion estimation steps, and evaluated different method combinations in the two steps. When the framework was tested on 2D cine MR images under various under-sampling factors, the combination of NUFFT for reconstruction and SPyNET (Ranjan and Black 2017) for motion estimation performed the best for large under-sampling factors (> 30). However, ground-truth DVFs were needed to train SPyNET. As deformable registration is an ill-posed problem, it is difficult to obtain the ground-truth DVFs. Estimated ground-truth DVFs may contain inherent errors which will propagate into the network parameters to affect the registration accuracy. Instead, our DL network was trained in an unsupervised fashion and no ground-truth DVFs are required. Similar to our k-space-driven deformable registration strategy, Huttinga et al. have reconstructed motion fields directly from under-sampled k-space data, by developing a B-spline-based motion model that explicitly associates the k-space data of a deformed object to a reference image (Huttinga et al. 2020; Huttinga et al. 2021). While their iterative method had proved accurate for severely under-sampled data, it was very time-consuming, which may prohibit its application in real-time 3D MR imaging.

Küstner et al. (Kustner et al. 2021) proposed a deep-learning based approach to estimate motion directly from k-space data. Their network design was inspired by an extension of the local all-pass technique to k-space. The local all-pass technique considers a non-rigid deformation as local translational displacement and, together with the Fourier shift property, performs image-domain registration by finding an all-pass filter in k-space. Küstner extended this idea and implemented it with a deep learning network. The inputs of their network are the source and target k-space data, and their network was trained to predict DVFs in the image domain. They compared their method against traditional image-based registrations, and they found that their network outperformed the image-based methods. However, similar to Terpstra et al. (op. cit.), their network training was performed in a supervised manner which requires ‘gold-standard’ DVFs to be provided for training. On the other hand, our KS-RegNet is an unsupervised model that does not require ‘gold-standard’ DVFs for training. It gives our method a unique advantage, since true ‘gold-standard’ DVFs are very difficult, if possible, to obtain, especially for natural under-sampled images not generated from retrospective under-sampling. Our KS-RegNet uses k-space data to directly define the loss and drive the DVF solution, which can be more conveniently deployed. It also reduces potential biases of using ‘gold-standard’ DVFs solved by some other methods to train the model, since these methods may present their intrinsic biases in solving the DVFs, depending on what motion model is assumed.

4.2. Impacts of artifacts from the fully-sampled source MR images

KS-RegNet adopts the deformation-driven approach to solve the under-sampling issue in the real-time MR imaging, thus assuming the availability of high-quality, fully-sampled source MR images. Since the image quality may be inconsistent across MR scans, we performed a robustness test of KS-RegNet to the prior image quality with various degrees of degradation by under-sampling the k-space of the prior image (Sec. 3.5.2). However, besides the under-sampling artifacts, there may be other causes that can degrade the prior image quality, such as those caused by motion, Gibbs ringing, and inhomogeneous magnetic B₀ fields. In the following we discuss ramifications and implications of some common artifacts that may appear in the fully-sampled prior images and the potential solutions.

The fully-sampled prior information is used in two places in the workflow (Fig. 1), where (i) the prior images are fed as the input channels into the U-Net core, and (ii) the k-space data of the prior images/deformed prior images are re-projected to quantify the inverse/forward similarity loss during the network training. The artifacts both affect the k-space data and the reconstructed images, and may propagate into the registration. Physiological motion, such as blood flow, respiratory, or cardiac motion, is a principal cause of MR image artifacts. Motion artifacts cause spin signal dephasing and/or incorrect phase in the k-space data, and they manifest spurious features in the reconstructed images such as blurring and ghosting (i.e., misregistration). There are several approaches to minimize the consequence of motion artifacts: (i) one can use dynamic or four-dimensional (4D) imaging techniques to sort the MR signals into semi-static motion bins, such that images reconstructed out of each bin will present reduced motion artifacts (Feng et al. 2016). (ii). One can use pulse sequences with velocity compensating encoding gradients (Zaitsev, Maclaren, and Herbst 2015). (iii) Since the ghosting appears in the phase encoding direction, its effect can be reduced by golden-angle radial readout trajectories whose phase encoding direction varies during the signal acquisition (Zaitsev, Maclaren, and Herbst 2015). Thus, these misregistered image features are reduced due to incoherent k-space sampling. In addition, the central k-space data are sampled for each readout spoke. Since motion signals are concentrated in the central k-space, radial readout trajectories are more robust against inter-view motion (Stemkens, Paulson, and Tijssen 2018). (vi) The blurring and ghosting can be further reduced by a deep learning model that is trained to eliminate these artifacts (Liu, Kocak, et al. 2020). In our KS-RegNet model training and evaluation, we used a motion state of dynamic cardiac MRIs or 4D liver MRIs as the prior image, which effectively minimizes the motion-induced artifacts. Also, our algorithm is evaluated via gold-angle radial sampling, which also suppress the motion artifacts.

Gibbs ringing artifact results from an insufficient sampling of high-frequency k-space data and manifests intensity oscillations near sharp edges in the image domain. We expect mild Gibbs ringing artifact has minimal effects on the registration accuracy since the low-frequency k-space data are more important for motion estimation. The Gibbs ringing artifact can also be reduced with a deep learning model (Zhang et al. 2019). The artifacts from inhomogeneous magnetic B₀fields can be caused by multiple sources including hardware imperfection and air-tissue interfaces in body. The inhomogeneous field leads to incorrect phase, thus causing signal loss or image distortion. The inhomogeneity can be reduced by magnetic shimming (Belov et al. 1995).

In summary, we can use semi-static images extracted from motion-resolved dynamic MRIs or 4D MRIs as the prior and use radial sampling of k-space to effectively suppress the motion artifacts. Other artifacts like Gibbs ringing may have limited effects on motion estimation and can also be effectively suppressed through additional post-processing. For the clinical cardiac and abdominal images evaluated in this study, we did not observe obvious registration quality degradation from the above mentioned artifacts.

4.3. Generalization to 3D k-space readout trajectory

In our study, the volumetric MR images were formed by a series of separately-acquired 2D radial k-space trajectories (Sec. 2.2.2), to concur with the acquisition protocols of the evaluation datasets (Sec. 2.4). However, our framework can be readily generalized to 3D readout trajectories such as a stack-of-stars or Koosh-ball trajectories (Chandarana et al. 2011; Zhou et al. 2017; Mendes Pereira et al. 2019), as the reconstruction layer and the NUFFT operator in the framework accept both 2D and 3D readout trajectories. The 3D acquisition has several advantages over the 2D acquisition, which may be more favorable in real-time 3D MR imaging. As the signal-to-noise ratio is linearly proportional to the size of the excited volume, the slice thickness in a 2D acquisition is usually at least 3-4 mm (Stemkens, Paulson, and Tijssen 2018). Moreover, the relatively worse image resolution in the slice direction may not allow accurate image re-sampling in arbitrary directions (Kustner et al. 2020). Since 2D acquisition requires selective excitation at different slices, it may also suffer from slice crosstalk due to an imperfect slice excitation profile. Low resolution in the slice direction is also likely to hinder accurate motion estimation along this direction. On the other hand, 3D acquisition generates isotropic high-resolution images for accurate re-sampling. In addition, the entire volume is excited in a 3D acquisition, which leads to higher imaging signal-to-noise ratio for potentially higher motion estimation accuracy. Due to accessibility issues to MRIs acquired with 3D trajectories, evaluations of KS-RegNet with 3D trajectories were not performed in this study and remained to be investigated in future.

4.4. Prospect of real-time MR imaging

Realization of real-time MR-guided radiotherapy depends on an MR scan of low latency and fast adaptation of treatment plans. For the proposed framework, the latency for tumor localization in an MR scan can be broadly divided into MR signal acquisition and network-based DVF prediction. The MR acquisition comprises a measurement of the k-space data specified by a readout trajectory and data processing and transfer. Consider a pulse sequence with a repetition time of 2.8 ms (e.g., (Terpstra et al. 2020; Borman et al. 2018)) and a 5-spoke/slice radial trajectory, the MR acquisition latency is around 224 ms for a 3D image of 32 slices. The overall execution time for the proposed network can be divided into the image reconstruction latency (i.e., the reconstruction layer in Fig. 1) and inference time (i.e., the U-Net core). The inference time is between 140 ms and 150 ms, and the image reconstruction time is around 200 ms. Thus the overall execution time to make a DVF prediction from the acquired k-space data is around 300-400 ms. The computation time for the DVF prediction is based on a NVIDIA Tesla V100 graphic processing unit card, and it can vary among different configurations of hardware. There are additional latencies not included such as data transfer and image/contour deformation, though these latencies are much smaller than the latencies of the MR acquisition and DVF prediction. Therefore, the latency of tumor localization is about 600 ms for the provided scenario, which is at the borderline of 500 ms latency bound for the real-time purpose (Dietz, Fallone, and Wachowicz 2019). Note that the acquisition latency depends on the pulse sequence and under-sampling factor (i.e., the number of radial spokes) applied in a MR scan, and therefore the time can be further shortened if a 3D trajectory is used for MR acquisition. For example, for the 3D golden-mean radial Koosh-ball trajectory, it has been shown that an acquisition of a 146-slice 3D image takes only 132 ms using a steady-state spoiled gradient echo sequence (TR = 4.40 ms, TE = 1.80 ms) and a 30-spoke trajectory (Huttinga et al. 2021), which translates to image acquisition latency of 66 ms (Borman et al. 2018). For the image reconstruction latency, we performed a preliminary test, and the execution time for a 3D NUFFT to reconstruct an image size of 146×146×146 was around 250 ms for the 3D radial readout trajectory with a 30-spoke trajectory. Therefore, the total latency can be limited below 500 ms (66 ms + 250 ms + 150 ms = 466 ms). Moreover, algorithm optimization and dedicated hardware to improve the efficiency of NUFFT and DVF computations can further reduce the latency (Knoll et al. 2014; Shih et al. 2021).

4.5. Limitations and future directions

In order to test our framework, we simulated under-sampled k-space data from fully-sampled 4D MR images which were collected retrospectively. However, in practice on-board k-space data are acquired in real time to guide radiotherapy. Accordingly, there may exist features in the real-time k-space data that were not simulated by our method. For example, the signal-to-noise ratio of the real-time k-space data may differ from the fully-sampled data. Fast pulse sequences such as balanced steady-state free precession and k-space encoding schemes with significant jumps in k-space can be employed to reduce MR scan time. While for these pulses, pulsed magnetic field gradient can induce eddy currents leading to residual spin dephasing which, in turn, introduces spurious features in reconstructed images. While strategies have been developed to mitigate the effects of the eddy current (Bieri, Markl, and Scheffler 2005), future assessment of the robustness of the network to the noises and artifacts is warranted, with potential further developments to improve the utility of the framework in real-time MR imaging.

Recently, Shimron et al. raised a concern that using open-access databases without sufficient precaution may lead to biased, overly-optimistic results (Shimron et al. 2021). In particular, raw k-space data are frequently zero-padded in commercial MR scanners before the MR image reconstruction. As a result, when the reconstructed images are used to simulate on-board under-sampled k-space data using a variable-density readout trajectory such as a radial trajectory, the under-sampling ratio can be overestimated. For the cardiac dataset, we used the raw k-space data to reconstruct complex-valued MR images, and no zero-padding was used in the reconstruction. Thus for the cardiac data the under-sampling ratio is unlikely to be overestimated. For the abdominal dataset, however, the MR images were post-reconstruction. Therefore, this dataset is susceptible to potential overestimation of the under-sampling ratio since the pre/post-processing steps of these MRIs are not fully known. We would like to emphasize that although our evaluation is based on retrospectively under-sampled data from fully-sampled data (such that the fully-sampled target MRI can naturally serve as the ‘gold-standard’ reference to evaluate the accuracy of the deformed source image), retrospectively sampling is not a requirement to train our model. The KS-RegNet can be trained with native under-sampled k-space data and a high-quality prior image since the loss is defined in k-space. It does not need both fully-sampled source and target MRIs to provide ‘ground-truth’ DVFs for supervision, which is the case for the supervised methods as reported by Küstner et. al. (Kustner et al. 2021) and Terpstra et. al. (Terpstra et al. 2021).

In our framework, to tackle the under-sampling artifacts and distortions, we intentionally under-sampled the k-space data of prior images and fed the under-sampled prior images to the network, to improve the registration accuracy and the robustness of our model. In addition to the under-sampled prior images, the network training was driven by quantifying data fidelity directly on k-space data to avoid calculating the losses in the artifact-ridden MR images. To further regularize the predicted DVFs, inverse consistency and the energy of the DVFs were added to the loss function (Sec. 2.3). We found that using the above strategies provides adequate accuracy for our framework for under-sampling ratios up to 80 (i.e., 5-spoke radial trajectory) [Figs. 4(a–c) and Figs. 5(a–c)]. However, we acknowledge that our framework may fail under more aggressive under-sampling factors, and additional regularizations such as the spatial-temporal redundancy or contextual losses are required to complement the k-space data fidelity. Statistical dimension reduction techniques including principal component analysis can also be potentially grafted with the current network to further improve the motion estimation accuracy. However, exploiting these redundancies and additional regularizations are beyond the scope of the current work and remain to be incorporated into future studies.

The proposed framework was evaluated using small-scale cardiac and abdominal datasets of various MR acquisition parameters (Tables 1 and 2). A major hurdle to increase the dataset size is the limited availability of 4D MR dataset with raw, fully-sampled k-space data. As the datasets contain a small number of subjects due to limited data availability, we employed the randomization strategy in training to substantially increase the number of unique training samples (Sec. 2.5.1). Moreover, multiple data augmentation strategies were employed to avoid overfitting and improve the robustness of the trained network. Cross-validation was also used to evaluate the framework and assess its generalizability to independent datasets. With the above strategies, the issue of small sample size can be mitigated. However, we acknowledge that a larger cohort including both healthy subjects and patients will help to better support the proposed scheme. Moreover, with a large cohort, it is possible to comprehensively test on a wide variety of tumor geometries to better quantify, not only the effects of breathing, but also the accuracy of KS-RegNet to localize tumors in various shapes and sizes.

5. Conclusions

In conclusion, we have proposed and presented an end-to-end, unsupervised DL network that can estimate motion fields in real time from on-board k-space data. Our results show that KS-RegNet performs well for highly under-sampled cardiac and abdominal MR images and is robust to varying under-sampling factors. The same network can be readily adapted to different k-space sampling trajectories, and to different anatomic sites. Future studies enrolling more patients and MR acquisition protocols are warranted to further evaluate its accuracy and robustness.