Abstract
Summary
scFates provides an extensive toolset for the analysis of dynamic trajectories comprising tree learning, feature association testing, branch differential expression and with a focus on cell biasing and fate splits at the level of bifurcations. It is meant to be fully integrated into the scanpy ecosystem for seamless analysis of trajectories from single-cell data of various modalities (e.g. RNA and ATAC).
Availability and implementation
scFates is released as open-source software under the BSD 3-Clause ‘New’ License and is available from the Python Package Index at https://pypi.org/project/scFates/. The source code is available on GitHub at https://github.com/LouisFaure/scFates/. Code reproduction and tutorials on published datasets are available on GitHub at https://github.com/LouisFaure/scFates_notebooks.
Supplementary information
Supplementary data are available at Bioinformatics online.
Pseudotime analysis is a concept first introduced in the early days of single-cell analysis for microarray data (Magwene et al., 2003). Derived from the idea that the temporal structure of gene expression can be retrieved by looking at its geometry (Rifkin and Kim, 2002), pseudotime analysis consists in ordering cells in a single-dimensional value meant to recapitulate the underlying transcriptional transition. The advent of more sensitive scRNAseq methods was accompanied by the development of two main classes of high-resolution trajectory analysis tools. One relies on fate probability mapping of the cells, with tools such as Palantir (Setty et al., 2019), and CellRank (Lange et al., 2022). Such approaches have the advantages of being flexible and efficient in finding terminal states, with the possibility for manual selection of these. However, the results do not lead to an easily interpretable tree as each cell is given a probability value for each fate, without clearly defined branches or segments. The other class of tools relies on principal graph learning, with the most used tool being Monocle3 (Cao et al., 2019). Principal graph derives from the concept of principal manifold, which is defined as a group of surfaces or lines that goes across the ‘middle’ of the data (Hastie, 1984). Principal graph represents a skeleton of the data that aims to capture major geometric structures, usually involving nodes connected by edges, whose both positions are optimized within the reduced dimensions to approximate the underlying expression manifold based on the positions of cells within the same expression dimensions. Reconstructing a principal graph enables generating discrete segments and bifurcations, allowing easier interpretation. However, Monocle3 learns the principal graph on Uniform Manifold Approximation and Projection (UMAP) embedding, a low-dimensional representation highly sensitive to parameters and which can represent a highly distorted view of the data (Zhai, 2022). Among general pseudotime toolsets, both Monocle3 and STREAM (Chen et al., 2019) have functions for gene-pseudotime association testing, with STREAM going even further by providing branch differential expression (DE) related functions. However, no tool performs statistical analysis of the bifurcation point, including the discovery of early cell fate biasing factors (Bargaje et al., 2017).
Here, we introduce scFates, a python package to streamline the whole process of pseudotime analysis, with flexible tree learning options, advanced feature extraction tasks and specific functions focused on bifurcation analysis. scFates was initially based on crestree R package, developed for the analysis of cell fate dynamics in development (Faure et al., 2020; Krivanek et al., 2020; Soldatov et al., 2019). While the initial R version included a tree inference approach inspired by SimplePPT (Mao et al., 2015). scFates additionally implements ElPiGraph, another method for principal graph learning (Albergante et al., 2020), allowing investigators to impose topological constraints on trajectories to fit single curves or circular trajectories. scFates is fully compatible with the scanpy ecosystem (Wolf et al., 2018) by using the anndata format and provides Graphics Processing Unit (GPU) and multicore accelerated functions for faster and more scalable inference. scFates is divided into three main parts: (i) trajectory learning and graph operations, (ii) feature (transcript counts, ATAC peaks,…) significance over pseudotime testing and clustering and (iii) bifurcation analysis. All three parts implement publication-grade plotting capabilities to visualize the results.
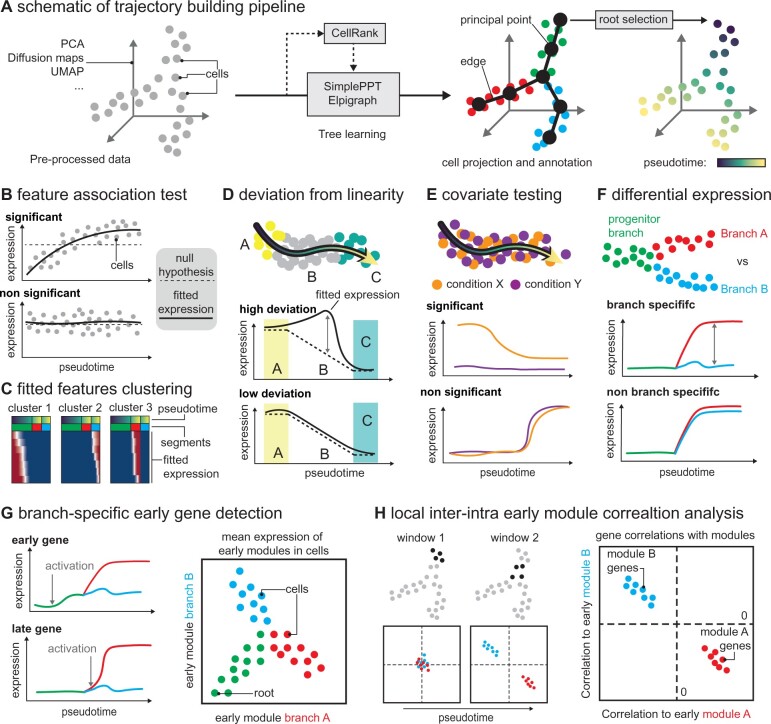
The trajectory learning can be performed on processed single-cell data at different stages of analysis, such as on normalized transcript count matrix, principal components or diffusion maps. The user has the choice of running either ElPiGraph or SimplePPT algorithms to learn a principal graph. ElPiGraph generates more robust structures by taking advantage of graph grammars and multiple topologies exploration at each iteration, at the cost of a lower scaling with the number of nodes (up to 50). When the transition is known to be non-bifurcating, simpler constrained curves can be learned instead. For example, a principal circle can be inferred for cell cycle analysis. While ElPiGraph can be used for higher number of nodes (up to 1000) by checking only one topology per iteration, we found that SimplePPT scales better with similar heuristics for trees with a higher number of nodes (up to 2000, Supplementary Fig. S1A), at the expense of the possibility of a less consistent tree output. To leverage the advantages of probabilistic mapping, scFates can also learn a principal graph on CellRank output by considering the combination of the absorption probabilities of each fate and calculated pseudotime as a manifold reduction, from which can be applied SimplePPT. The latter is relevant in cases where CellRank is more successful in capturing terminal fates than principal graph methods. The resulting trajectory, composed of connected principal points, can be projected onto any low-dimensional space, such as UMAP or ForceAtlas2. To orient a reconstructed trajectory, the user can choose one or two roots manually or according to the value of a feature, such as the level of expression of a known marker. Pseudotime positions of individual cells are then determined by projecting cells according to their position relative to the principal points (Fig. 1A). To account for uncertainty of a cell’s position along the trajectory, scFates leverages the soft assignment approach of SimplePPT. For that, each cell is assigned a probability to each principal point, which scFates can use to generate several pseudotime mappings to account for variability. In addition, scFates provides convenient functions for selecting specific portions of the tree, by selecting starting and endpoints, or by using pseudotime.
Fig. 1.
Schematic overview of scFates functionalities: (A) Dataset is first pre-processed via commonly used tools such as scanpy, to generate a reduced space where the tree will be learned using either ElPiGraph, SimplePPT or a combination of CellRank absorption probabilities and SimplePPT. After root selection, pseudotime and segment assignment is then calculated for each cell. (B) Features are tested for association with that pseudotime ordering using GAM models. (C) Fitted features can be clustered and visualized in different ways. (D) Transitions can be tested for deviation from linearity, to assess whether the bridge is likely to be an artifact and reveal transient features. (E) When two or more conditions are present, difference of amplitude or trends between conditions can be tested. (F) Branch-specific features (transcript count, ATAC-peak,…) are detected using GAM models. (G) A branch-specific feature (transcript count, ATAC-peak,…) is considered early if it displays activation dynamics prior to fork (left), early gene module mean expression can be used to detect co-activation of module prior to fork (right). (H) Early biasing analysis is done by calculating local gene-to-gene correlation of the detected early gene modules, before and around the fork. A separation of the two gene modules before the fork indicates repulsion of gene modules
We chose generalized additive models (GAM) as a framework for feature association testing, branch-DE and covariate analyses. Such models are well suited to capture non-linear gene trends in single-cell data and can provide amplitude measurement for prioritizing markers. Feature (e.g. gene expression and ATAC peaks) association testing is performed in a branch-specific manner for trees (Fig. 1B). We have performed benchmarks of the GAM model method for feature testing comparing to the alternative approaches implemented in STREAM and Monocle3. We found that while Monocle3’s Moran’s I does not yield amplitude measurements, that test can run faster as compared to GAM and agrees in terms of the detected features (Supplementary Fig. S1E and F). We have included wrappers for Monocle3’s approach to provide a choice to a user for feature testing. Associated features can be fitted and smoothed over pseudotime using the same GAM model. Smoothed features can be visualized and clustered using a distance metric of choice (Fig. 1C). In some cases, doublets can create transitions or bridges between two stationary populations. To detect such a situation, scFates incorporates a test based on deviations from linearity. Such a test consists of checking whether the expression dynamics observed in the bridge can be explained by a linear mixture of the flanking populations (Fig. 1D, Supplementary Fig. S2), such a test can be used to assure that the bridge is not an artifact, and uncover molecular transient features associated with these transitions (Kameneva et al., 2021). Additionally, a function specifically designed for covariate testing is proposed to test for differential gene expression between conditions on the same trajectory path. This test includes an amplitude difference part, as well as trend differences (Fig. 1E, Supplementary Fig. S3).
Finally, scFates implements a set of functions for detailed analysis of bifurcations. First, early and late gene modules separating within each branch are detected by testing for differential expression between branches, and determining the timing of their deviation relative to the bifurcation (Fig. 1F and G, Supplementary Fig. S5). scFates then priorities features of early modules that contribute to cell fate biasing prior to the bifurcation point through backtracking of their correlations in the progenitor branch (Fig. 1H, Supplementary Fig. S5).
In conclusion, scFates is a fast and versatile tool for in-depth tree learning, pseudotime analysis and characterization of bifurcation dynamics from single-cell data. It can be widely applied in developmental biology, disease trajectory or perturbation analysis. Moreover, scFates can work with any type of highly dimensional data, allowing it to use with modalities other than gene expression, such as single-neuron activity over time.
Supplementary Material
Contributor Information
Louis Faure, Department of Neuroimmunology, Center for Brain Research, Medical University Vienna, 1090 Vienna, Austria.
Ruslan Soldatov, Department of Biomedical Informatics, Harvard Medical School, Boston, MA 02115, USA.
Peter V Kharchenko, Department of Biomedical Informatics, Harvard Medical School, Boston, MA 02115, USA; Altos Labs, San Diego, CA 92121, USA.
Igor Adameyko, Department of Neuroimmunology, Center for Brain Research, Medical University Vienna, 1090 Vienna, Austria.
Funding
This work was supported by the Austrian Science Fund [DOC 33-B27], ERC Synergy [856529], Cancerfonden and Paradifference Foundation.
Conflict of Interest: All authors declare that they have no conflicts of interest.
References
- Albergante L. et al. (2020) Robust and scalable learning of complex intrinsic dataset geometry via ElPiGraph. Entropy, 22, 296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bargaje R. et al. (2017) Cell population structure prior to bifurcation predicts efficiency of directed differentiation in human induced pluripotent cells. Proc. Natl. Acad. Sci. USA, 114, 2271–2276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao J. et al. (2019) The single-cell transcriptional landscape of mammalian organogenesis. Nature, 566, 496–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H. et al. (2019) Single-cell trajectories reconstruction, exploration and mapping of omics data with stream. Nat. Commun., 10, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faure L. et al. (2020) Single cell RNA sequencing identifies early diversity of sensory neurons forming via bi-potential intermediates. Nat. Commun., 11, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T. (1984) Principal curves and surfaces. Technical report. Laboratory for Computational Statistics.
- Kameneva P. et al. (2021) Single-cell transcriptomics of human embryos identifies multiple sympathoblast lineages with potential implications for neuroblastoma origin. Nat. Genet., 53, 694–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krivanek J. et al. (2020) Dental cell type atlas reveals stem and differentiated cell types in mouse and human teeth. Nat. Commun., 11, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange M. et al. (2022) Cellrank for directed single-cell fate mapping. Nat. Methods, 19, 159–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magwene P.M. et al. (2003) Reconstructing the temporal ordering of biological samples using microarray data. Bioinformatics, 19, 842–850. [DOI] [PubMed] [Google Scholar]
- Mao Q. et al. (2015) SimplePPT: a simple principal tree algorithm. In: Proceedings of the 2015 SIAM International Conference on Data Mining, Vancouver, BC, Canada. pp. 792–800. SIAM.
- Rifkin S.A., Kim J. (2002) Geometry of gene expression dynamics. Bioinformatics, 18, 1176–1183. [DOI] [PubMed] [Google Scholar]
- Setty M. et al. (2019) Characterization of cell fate probabilities in single-cell data with Palantir. Nat. Biotechnol., 37, 451–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soldatov R. et al. (2019) Spatiotemporal structure of cell fate decisions in murine neural crest. Science, 364(6444). [DOI] [PubMed] [Google Scholar]
- Wolf F.A. et al. (2018) SCANPY: large-scale single-cell gene expression data analysis. Genome Biol., 19, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhai,Z. et al. (2022) Supervised capacity preserving mapping: A clustering guided visualization method for scrna-seq data. Bioinformatics, 38, 2496–2503. 10.1093/bioinformatics/btac131. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.