Abstract
Motivation
The post-transcriptional epigenetic modification on mRNA is an emerging field to study the gene regulatory mechanism and their association with diseases. Recently developed high-throughput sequencing technology named Methylated RNA Immunoprecipitation Sequencing (MeRIP-seq) enables one to profile mRNA epigenetic modification transcriptome wide. A few computational methods are available to identify transcriptome-wide mRNA modification, but they are either limited by over-simplified model ignoring the biological variance across replicates or suffer from low accuracy and efficiency.
Results
In this work, we develop a novel statistical method, based on an empirical Bayesian hierarchical model, to identify mRNA epigenetic modification regions from MeRIP-seq data. Our method accounts for various sources of variations in the data through rigorous modeling and applies shrinkage estimation by borrowing information from transcriptome-wide data to stabilize the parameter estimation. Simulation and real data analyses demonstrate that our method is more accurate, robust and efficient than the existing peak calling methods.
Availability and implementation
Our method TRES is implemented as an R package and is freely available on Github at https://github.com/ZhenxingGuo0015/TRES.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Epigenetics is the study of inheritable genomic modifications that do not involve alteration in DNA sequence. These modifications regulate gene activities and play important roles in many biological processes such as cell differentiation, development and aging, as well as a number of human diseases such as cancer (Bird, 2002; Feinberg, 2004; Greer and Shi, 2012; Portela and Esteller, 2010; Szulwach et al., 2011; Teschendorff et al., 2010). Traditional epigenetic studies mostly focus on different types of DNA methylation and histone modifications. Recently, a number of post-transcriptionally modified ribonucleosides have been identified in various types of RNA (Darnell et al., 2011; Dominissini et al., 2012; Meyer et al., 2012; Roundtree et al., 2017). These results suggest that post-transcriptional mRNA modifications are dynamically regulated and have functions beyond fine-tuning the structure and function of RNA. The study of RNA modifications represents an important new realm for gene regulation in the form of ‘RNA epigenetics’ or ‘epitranscriptomics’. There are multiple types of RNA modifications, including N6-methyladenosine (m6A), N3-methylcytosine (m3C) and N1-methyladenosine (m1A). Among them, m6A is the most common and abundant (occurring at roughly 1 in 3 adenosine residues in mammalian mRNA) modification on RNA molecules in eukaryotes (Dominissini et al., 2012). N6-Methyladenosine (m6A) refers to methylation of the adenosine base at the nitrogen-6 position. Studies have shown that m6A is associated with many human diseases such as cancer and neuronal disorders (Engel et al., 2018; Lan et al., 2019; Lin et al., 2019).
Recently developed high-throughput sequencing method named Methylated RNA Immunoprecipitation Sequencing (MeRIP-seq), enables one to profile transcriptome-wide m6A levels. MeRIP-seq can be technically seen as a combination of two well-known techniques: immunoprecipitation, widely used in chromatin immunoprecipitation sequencing (ChIP-seq) (Johnson et al., 2007), and RNA sequencing (RNA-seq) (Nagalakshmi et al., 2008). In MeRIP-seq, mRNA is first fragmented into approximately 100-nucleotide-long oligonucleotides, and then immunoprecipitated (IP) by an anti-m6A affinity purified antibody. In addition to the IP samples, libraries are also prepared for input control fragments to measure the corresponding reference mRNA abundance. This process is an RNA-seq experiment. After sequencing, the reads from both the IP and the input samples are aligned to the reference genome. Due to the enrichment from IP process, transcriptomic regions with m6A will have more reads clustered and have peak-like shapes when visualizing the read counts along the genome. Therefore, people often refer the m6A regions as ‘peaks’, which is a term usually used in ChIP-seq to represent the protein binding sites. Figure 1 shows some example peaks on the Fat2 gene from a dataset to study m6A dynamics during mouse brain development, where m6A in cerebellums from 2-week old mice are profiled with two biological replicates.
Fig. 1.
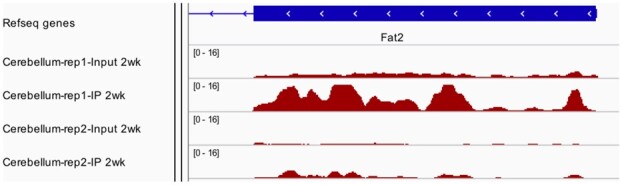
Peaks from MeRIP-seq in a mouse brain study
MeRIP-seq data resemble ChIP-seq data since both consist of paired IP and input samples. One of the main goals in MeRIP-seq is also similar to that in ChIP-seq: to identify transcriptomic regions with m6A methylation (‘peak calling’). Studies have reported that cells may coordinately modulate m6A modification levels for regulatory purposes (Dai et al., 2007). To explore the dynamics of m6A in response to physiological conditions, knowledge of the accurate locational distribution and the degree of methylation levels are important. It is tempting to directly apply ChIP-seq peak calling methods (Zhang et al., 2008). However, it is not appropriate for at least two reasons. First, the variation of the input from MeRIP-seq is much greater than that from ChIP-seq. The input of ChIP-seq consists of stable DNA fragments in which the variation is minimal. In contrast, the MeRIP-seq input measures the gene expression, which is known to vary greatly along the genome and across different subjects. This characteristic makes it undesirable to directly apply ChIP-seq methods on MeRIP-seq data because statistical tests developed for ChIP-seq data tend to call more peaks for highly expressed genes, since they have greater power in regions with more input reads (Chen et al., 2012). Second, due to cost constrains, the number of biological replicates in MeRIP-seq experiment is often small, making direct estimate of variance unstable. The small-sample problem is usually alleviated by ‘variance shrinkage’ procedures that are widely applied in RNA-seq but not included in ChIP-seq methods.
Compared to the large body of works for RNA- and ChIP-seq data analysis, method development for MeRIP-seq data is limited. To the best of our knowledge, there are two statistical methods for m6A peak calling: exomePeak (Meng et al., 2013) and MeTPeak (Cui et al., 2016) and two methods for differential peak calling: MeTDiff (Cui et al., 2018) and RADAR (Zhang et al., 2019). exomePeak performs a conditional test (C-test) (Przyborowski and Wilenski, 1940) to detect the enrichment of IP over input. Its main limitation is that it assumes the same enrichment level within a transcript and across biological replicates. In other words, it does not model the variation of methylation within a transcript and across biological replicates. MeTPeak models such biological variances with a hierarchical beta-binomial model. It builds a two-state (methylated and unmethylated) hidden Markov model (HMM) to account for the local dependency of nearby read counts. The HMM model can be problematic because the m6A levels are continuous, which cannot be modeled by two distinct states. Moreover, the HMM in MeTPeak runs on each gene independently, implying that the thresholds for calling m6A peaks can be different on different genes, which produces inconsistent results.
In this article, we develop a novel statistical method for MeRIP-seq peak calling. We name it TRES for Toolbox for mRNA Epigenetics Sequencing analysis. We adapt a Bayesian hierarchical negative binomial model to account for different sources of variation and address the small-sample problem in MeRIP-seq data. A variance shrinkage procedure is derived from the model to provide robust estimation for the biological variation of m6A levels cross replicates. Wald tests are then conducted to detect transcriptome-wide m6A modification regions. Extensive simulation studies and real data analyses demonstrate that TRES is more accurate, robust and efficient than existing peak calling methods.
2 Materials and methods
TRES conducts peak calling in two steps. In the first step, it quickly scans the whole transcriptome and loosely identifies m6A candidate regions using an ad hoc procedure. In the second step, more rigorous statistical modeling and hypothesis testing procedures are applied to detect and rank the peaks. The two-step approach avoids fitting complicated models on the whole transcriptome, thus greatly reduces the computational burden. In the meantime, the careful modeling on the candidate peaks in the second step delivers accurate and robust results. Reducing the hypothesis testing space also improves statistical power after multiple testing correction.
2.1 Obtaining the m6A candidate regions
For a MeRIP-seq dataset with multiple replicates, the first step (candidate region identification) is performed for each replicate separately. We first divide the whole genome into equal-sized bins (default bin size is 50 basepairs), and only keep the bins overlapped with exons (optionally keep intronic bins as well if explicitly specified). For bin b in replicate j, the bin-level counts from the input and the IP samples are denoted by xbj and ybj. We assume , where and are size factors corresponding to replicate j’s input and IP samples respectively, and the λ’s are Poisson rates. Here, the size factors are computed from the total read counts and used for normalizing the sequencing depth effects. Let , we have with . We then calculate a P-value for each bin from a binomial test with the null hypothesis of no methylation. Note that even if a region is unmethylated, we still have because of the background reads in the IP sample. We assume a constant methylation level for unmethylated regions. Then under the null, or . Benjamini–Hochberg method (Benjamini and Hochberg, 1995) is applied to estimate false discovery rate (FDR) for all bins. In addition, we also calculate the normalized log fold changes as , which are then smoothed using moving average to account for spatial correlation in the data. Here, is a constant acting as a pseudo-count to remove bins of very low counts. The choice of is the mean bin count from both the IP and the input of replicate j. Given FDR and smoothed log fold changes (LFC) of all bins, we adopt a bump finding algorithm (Jaffe et al., 2012) to combine bins with FDR (default 0.05) and LFC (default 0.7 for fold change of 2) to loosely identify candidate m6A regions. It is necessary to mention that, if there is only one replicate for both Input and IP samples, TRES will stop at this step. The final peaks are the list of bumps and the significance of each bump is determined by the aforementioned binomial test.
2.2 m6A peak calling
2.2.1. A hierarchical model for the counts in candidate regions
Given candidate regions from the first step, we obtain the region-level read counts based on the bin-level counts (note one region can contain multiple bins). For candidate region i and replicate j, denote the read counts from the input and the IP sample by xij and yij. Based on the property of Poisson distribution, we still have and , with and . To model the variation across biological replicates, we assume and . Here, αs and θ are shape and scale parameters in the specified Gamma distributions. Marginally, the read counts follow a negative binomial (Gamma-Poisson) distribution, which is widely used in modeling sequence count data (Love et al., 2014; Robinson et al., 2010; Wu et al., 2013).
To detect methylation regions, we are interested in the ratio of IP/input, i.e. . However, due to the technical artifact such as imperfect specificity of antibody, the ratio could be greater than 1 even for unmethylated regions. We define a new quantity that is monotonic to and naturally follows a beta distribution. We reparameterize the beta distribution by mean (μi) and dispersion (), with and . Then the α’s in the Gamma distribution can be represented by μi and : and . Similar to that in the RNA-seq DE problem, the dispersion parameter plays an important role in the peak calling. When the number of biological replicates is small, it is desirable to impose a prior on , which induces a ‘shrinkage’ effect and provides robust estimation. Here, we impose a log-normal prior on , which is based on the distribution of observed dispersion in MeRIP-seq data. Based on the above settings, our complete data model for counts in candidate regions is:
| (1) |
It is important to note that in our model, the quantity of interest is μi, which is related to the m6A methylation level. The dispersion is also related to the biological variation of methylation levels, and will be shrunk estimated.
2.2.2. Parameter estimation
The peak calling involves making statistical inferences on μi, for which one needs to obtain and the standard error of . For , we denote it as by the method of moment based on the marginal Gamma-Poisson distributions of xij and yij (more details in Supplementary Materials). For the variance of , we show that it can be approximated as: (details in Supplementary Materials). The variance estimator involves and θi, which need to be estimated first. For that, we use a maximum likelihood approach. Based on our model specification in (1), the joint posterior of and θi is proportional to the data likelihood. Then:
Maximizing the above likelihood provides estimates of and θi, denoted as and hereafter. Prior to the estimation of and θi in above data likelihood, we need to estimate hyperparameters and in the log-normal prior of . For that, we first estimate dispersion parameters with method of moment for all candidate regions. Then and are estimated based on the moment estimates for dispersion (more details in Supplementary Materials).
2.2.3. Calling and ranking the peaks
It is important to note that the IP sample will have sequence reads in background regions even with very low m6A methylation. Those are background reads brought by various biological or technical noises. The goal of peak calling is to identify regions with potentially higher level of m6A signals compared to the background. In our model, the parameter μi represents the m6A methylation signal in region i. Assuming that unmethylated regions have background signal of μ0, we perform the following one-sided hypothesis test for calling peaks:
The Wald test statistic for the hypothesis test is . The variance of is approximated as , where and are the posterior estimates from previous section. The background signal μ0 depends on the quality of the experiment, e.g. experiment with lower technical noises will have smaller μ0. We use a data-driven approach to estimate μ0. To be specific, we estimate μ0 as the ratios of normalized read counts between IP and input samples in all background regions (non-candidate regions). The Wald test statistics approximately follow normal distribution (shown in Section 3), and the P-values can be obtained accordingly. False discovery rate (FDR) can be estimated using established procedures (Benjamini and Hochberg, 1995).
Note that the P-values from the above hypothesis test represents the statistical significance, not the biological significance. A region with low methylation level could have very small P-value, due to small variance. Even though the P-values and FDRs provide a mean to call peaks, they are not necessarily the best metric to rank the candidate peaks. This is a prevalent problem in many high-throughput data analyses, and people have developed different ways to address the problem. For example in differential expression (DE) analysis, people use volcano plot to visualize the results and use a combination of FDRs and log fold changes to call DE genes. Here, we use the following score to rank the candidates: , where . This score prefers peaks whose methylation levels are significantly higher than the average of all candidates regions, which generates more robust and meaningful ranks than using the P-value.
2.3 Simulation setup
We conduct comprehensive simulations to evaluate the performance of TRES. Since our algorithm contains two steps: identification of candidate regions and calling peaks among the candidates, we constructed two types of simulations to validate the performances in different aspects. In the first type, termed as region-level simulation, we generate read counts at the region levels. The purpose is to validate the dispersion estimation and statistical inferences procedures in TRES. The simulation, however, cannot be used to validate other competing MeRIP-seq methods because those only work for counts from equal-sized bins. In order to fairly compare with other methods, we conducted another type of simulation, termed bin-level simulation, where we generate counts from smaller, equal-sized bins transcriptome wide. This simulation provide a basis for the comparison of overall peak calling performances from different methods. The methods compared to TRES in this simulation are MeTPeak and exomePeak, which are the popular choices in analyzing MeRIP-seq data.
In the region-level simulation, we simulate data for candidate regions based on our negative binomial model, where we assume that there are 5000 candidate regions, with 80% of them being positive (with m6A methylation). Details for the region-level simulation are provided in Supplementary Materials Section S2.1. In the bin-level simulation, we first apply TRES on a mouse dataset to obtain a list of peaks. Given these peaks and the raw data, we simulate bin-level counts for 50 bp bins transcriptome wide. The details for the bin-level simulation are provided in Supplementary Materials Section S2.2. Briefly, the input bin counts are directly obtained from the real data. The IP bin counts are generated from a Poisson model. The Poisson rates are related to the input counts and underlying methylation level, which is generated from a HMM. We carefully compare the characteristics of the simulated and real data, and demonstrate that the simulated data mimic the real data well in several aspects. Details for such comparison are provided in Supplementary Figure S4.
3 Results
3.1 Simulation
3.1.1. Accuracy of dispersion estimation
It has been shown that the estimation accuracy of dispersion parameter plays crucial roles in different types of sequencing data analysis (Feng et al., 2014; Love et al., 2014; Wu et al., 2013), with better dispersion estimation leading to improved statistical inference. Therefore, we first assess the dispersion estimation in region-level simulation studies by comparing the results from our proposed shrinkage estimator with the moment estimator. To assess the biases of the estimates, we use normalized mean squared errors (MSE) as criteria, which is defined as the MSE of divided by the true value of .
Figure 2(A) shows the normalized mean squared errors of shrinkage and moment estimates of when there are two or five replicates. As expected, more replicates lead to lower biases for both methods, but the proposed shrinkage estimates outperform the moment estimates in both cases. Furthermore, the variation in shrinkage estimates are also smaller than those in moment estimates, no matter when there are two or five replicates. As an example, the densities of for two-replicate scenario are shown in Figure 2(B). It shows that from the proposed shrinkage estimator, the extreme values are shrunk towards the population mean. These results demonstrate that our shrinkage dispersion estimator is more accurate and robust than the moment estimator.
Fig. 2.
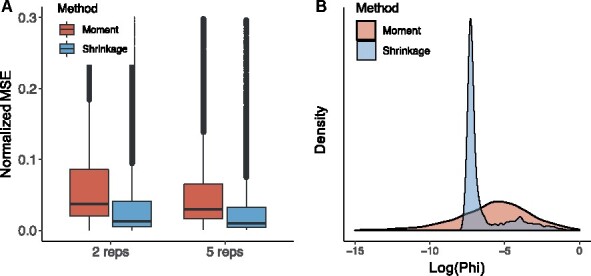
Evaluation of dispersion estimates from different methods under the scenario where and . (A) Comparison of normalized MSE (MSE divided by the true value of ) between moment and shrinkage estimates for dispersion parameters across 500 simulations, when there are two and five replicates respectively. (B) Density of moment and shrinkage dispersion estimates when there are two replicates
3.1.2. Accuracy of statistical inference
Next we evaluate the statistical inference from the region-level simulation. As we derive P-values based on the normal distribution of Wald-test statistics, we demonstrate the validity of this inference method by examining the distribution of Wald statistics. Histogram of Wald statistics and the normal quantile-quantile (QQ) plots in Supplementary Figure S2 suggests that the statistics follow a normal distribution very well in the middle, with the heavier tail to the right corresponding to methylated regions. Furthermore, we investigate the P-value distributions from the hypothesis test, for all regions and the background regions only. Under the null (background regions), P-values by TRES are roughly uniformly distributed (Supplementary Fig. S3), and provide accurate type I errors (Supplementary Table S1) and FDRs (Supplementary Table S2). These results support the validity of using normal P-values in TRES, and demonstrate that TRES provides accurate statistical inference.
3.1.3. Accuracy of peak calling
We next evaluate the overall peak calling accuracy from TRES through bin-level simulations. We compare TRES to exomePeak and MeTPeak, which are the popular choices in analyzing MeRIP-seq data. Because each method outputs its own ranked peak list, the total number of peaks and the length of each peak vary by different methods. We use two metrics in the comparison: (i) the proportions of called peaks overlapping the true peaks; and (ii) the percentage of base pairs within the called peak that are also in true peaks (referred to as %BP). We computed these metrics for different numbers of top ranked peaks from all methods. Higher values indicate better performance. To avoid potential biases brought by the peak lengths, all peaks are adjusted to length of 200 base pairs, i.e. we take the center of the called peaks and extend to both sides by 100 base pairs.
The comparison of the overlapping proportions is shown in Figure 3. In all cases, TRES outperforms MeTPeak and exomePeak. When the number of replicates increases (from left to right), TRES becomes better while MeTPeak and exomePeak do not. This is because TRES models the variation in biological replicates, which makes it better take advantage of large sample size. Although MeTPeak also models the biological variation in replicates, its two-state and gene-by-gene modeling of methylation may generate in-consistent inference results. These drawbacks could make it suffer from large sample. exomePeak neglects the biological variance, which may report more false positives when there are more than two biological replicates.
Fig. 3.
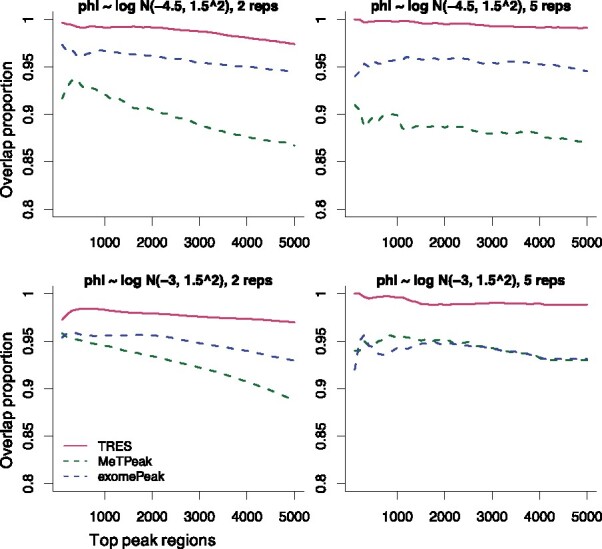
Comparison of overlap proportions among top 5000 peaks called by different methods. One panel presents results under one specific scenario. Panels from left to right in each row contain results with number of replicate 2 and 5. Panels from top to bottom in each column represent results with the mean of log-dispersion -4.5 and -3
To further assess the precision in peak position, we calculate the percentage of base pairs in a peak that are also covered by true peaks. As shown in Supplementary Figure S5, TRES still performs best in all scenarios compared to MeTPeak and exomePeak. Consistent with the results in Figure 3, TRES becomes better with larger sample size, while MeTPeak and exomePeak do not. In addition, the good results of TRES under conditions of large dispersion (bottom row) suggests the benefits of our shrinkage procedure for the dispersion of methylation levels. When the dispersion becomes large, more extreme values will appear, which could cause unstable inferences in peak calling. A shrinkage procedure of the dispersion helps to stabilize the dispersion estimate and generate robust inference.
3.2 Real data application
We apply TRES on three real m6A datasets to investigate its performance, and compare it to three existing peaking calling tools MeTPeak, exomePeak and MACS2. All methods take BAM file and generate a ranked list of m6A peaks. Since the biological truth are unknown in the real data, we evaluate the results based on some ‘silver standards’ from prior biological knowledge, including the motif content of the peaks, as well as the overlaps of peaks with important transcriptomic features.
3.2.1. Datasets
All data are obtained from the Gene Expression Omnibus (GEO) database. The first dataset (GEO accession number GSE113781) referred to as Stress mouse data hereafter, contains samples from mouse adult cortex under two conditions: treated with 15 min acute restraint stress (stress), and left in homecage and sacrificed 4 h after (basal). There are seven and six biological replicates in basal and stress mouse cortex sample respectively. The second dataset (GSE144032) referred to as Young mouse data hereafter, contains mouse brain samples from four brain regions: cerebellum, cortex, hippocampus and hypothalamus. Each sample contains two replicates. The third dataset (GSE46705) referred to as HeLa data, contains four samples from human HeLa cell line: one control sample and three treated samples. The treatments correspond to the knock-out of complex METTL3, METLL14 and WTAP respectively. Each sample contains two replicates. More details about these three datasets are in Supplementary Materials Section S3.1.
3.2.2. Motif content
It has been reported that motif DRACH (D = G/A/U, R = G/A, H = A/U/C) is the top binding motif of m6A reader YTHDC1 (Xu et al., 2014). Therefore, motif DRACH are expected to present in the vicinity of true methylation regions. We assess peaks called by different methods using the motif information as a silver standard, under the assumption that peaks with the DRACH motif are more likely to be true.
First, we explore the motif content in top 5000 peaks called by different methods. The motif content refers to the proportion of peaks whose genomic sequences contain DRACH motif. Because longer peaks tend to have higher motif content, we make the length of all top peaks similar to each other in order to avoid potential biases caused by length (Supplementary Fig. S6). Results in Figure 4(A) and Supplementary Figure S7(A) show that, peaks called from TRES consistently have the highest motif content across all datasets, followed by exomePeak, MACS2 and then MeTPeak. It is also important to note that the motif content curves are always downward from TRES. It shows that the higher ranked peaks have greater motif content, indicating good peak ranking. exomePeak reports a roughly similar trend but lower motif contents compared to TRES. In contrast, the motif content curves from both MACS2 and MeTPeak sometimes are upward. MeTPeak is particularly bad in this, since its top ranked peaks often have lower motif content than the lower ranked peaks. Overall, the motif content results suggest that TRES provides the best peak ranks compared to the other methods.
Fig. 4.
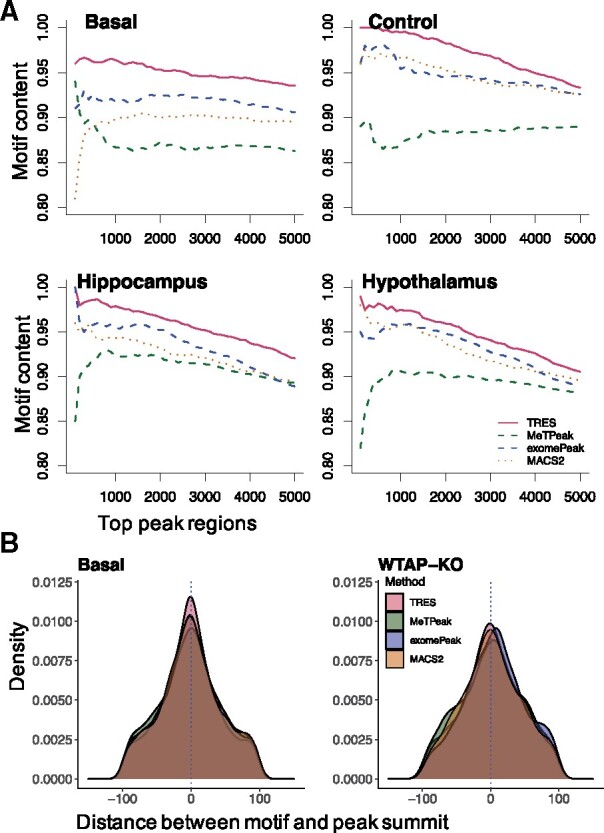
(A) Comparison of DRACH motif content among the top 5000 peak regions called by TRES, MeTPeak and MACS2 in basal sample from Stress mouse data, in control sample from HeLa data and two samples from Young mouse data. (B) Comparison of distances between DRACH motif to peak summits called by TRES, MeTPeak, exomePeak and MACS2, in the basal sample from Stress mouse data, the WTAP-knockout sample from HeLa data
In addition, we calculate the distance between DRACH motif to the summit of each peak. All peaks are adjusted to 200 base pair long centered around their summit. As shown in Figure 4(B) and Supplementary Figure S7(B), the distance densities in most samples peak around zero for TRES, MeTPeak and MACS2, with densities by TRES have the highest peak at 0. In contrast, the mode of density by exomePeak in WTAP-Knockout sample is relatively far from zero. Overall, these figures show that the peaks called by TRES have the highest peak at 0, indicating that our peak summits are closer to the motif than others’ peak summits.
To further assess the peaks, we conduct de novo motif search using HOMER (Heinz et al., 2010) for the top 5000 peak regions called by different methods. All peaks are adjusted to 400 base pair long centered around their summit. Supplementary Figure S8 shows example sequence logos of DRACH motif found in peak regions called by TRES for all samples in Stress mouse data, two samples in Young mouse data and two samples in HeLa data. Although DRACH motif also occurs in peaks called by the other methods for the same dataset, its rank and enrichment score varied. For example, among the 10 lists of peaks called by each method for all three datasets, DRACH is the most enriched motif in 10, 6, 9 and 7 lists of peaks called by TRES, MeTPeak, exomePeak and MACS2 respectively. In addition, more than half of the enrichment scores [-log10(P-value) with the P-values reported by HOMER for motif DRACH], are the highest in peaks called by TRES (Supplementary Fig. S9) compared to MeTPeak, exomePeak and MACS2. All of these results together demonstrate that peaks called by TRES are more accurate and better ranked compared to those from the other methods.
3.2.3. Consistency with other methods
It is important that peak lists by a newly developed tool show some consistency with existing tools of the same usage. Here, we investigate the consistency of TRES with other methods, by examining the overlapping pattern among top 5000 peaks identified by each method. Again, all peaks are adjusted to 400 base pair long centered around their summit to avoid potential bias from peak length. As shown in Supplementary Figure S10, overall, we found that the peaks called from different methods have moderate overlaps, while each method has non-trivial number of unique peaks. To further explore the overlaps, we calculate the proportion of peaks by each method that are also reported by at least two other methods (details are included in Supplementary Material Section S3.4). Since there is not gold standard for peaks, we think the peaks reported by at least two other methods can serve as ‘silver standard’, thus higher proportion indicates better performance. As shown in Supplementary Table S3, compared to the other methods, TRES has the largest proportion in most samples. These results indicate that, peaks by TRES are more consistent with others than peaks by MeTPeak, exomePeak and MACS2.
3.2.4. Robustness of the methods
Next, we evaluate the robustness of different peak calling methods. It is desirable that a method can produce consistent results when the number of biological replicates varies. We use the Stress mouse data to assess the consistency of peaks called with different number of replicates from the same method.
For each method, we first call peaks using all replicates (seven replicates for basal, and six for stress), and use these as benchmarks. We then randomly sample two replicates to call peaks, and calculate the overlapping proportions between the top 5000 peaks called with two replicates and with all replicates. A more robust method is expected to have higher overlapping proportions, since the results are not overly affected by the sample size. There are seven and six replicates for mouse basal and stress cortex samples respectively, then each of the three peak calling methods will output 21 and 15 overlapping proportions respectively. Results in Figure 5 show that, TRES consistently obtains the highest overlapping proportions between peaks called with two replicates and peaks called with all replicates. These results indicate that TRES is more robust than all compared methods. MACS is particularly sensitive to the data since it reports less than 60% overlaps. As the number of replicates are usually small due to cost constrains of sequencing experiments, TRES tends to be more stable and trustable than the other compared methods in such a situation.
Fig. 5.
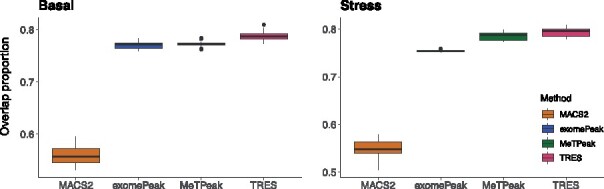
Comparison of overlapping proportions between top 5000 peaks called with two and all replicates in basal and stress mouse cortex samples respectively. In the calculation of overlapping proportions, each method is compared to itself
In addition to biological replicates, impact of sequencing depth is another important consideration for a peak calling method. Studies have shown that the performance of ChIP-seq peak calling algorithms suffer from low sequencing depth (Jung et al., 2014). Here, we investigate how much impacts the sequencing depth has on different methods. To create data with lower depth, we downsample raw BAM files at different rates, ranging from 0.3 to 0.7. As a criterion of comparison, for each method and each sample, we calculate the percentage of peaks called with raw data that are recaptured at different downsample rates. As shown in Supplementary Figure S11, TRES reports the highest percentage compared to MeTPeak, exomePeak and MACS2. Although there is an increasing trend in the percentage for all methods as sequencing depth increases, the increasing curve of TRES is more flat, meaning that TRES is more robust to lower sequencing depth than the other methods.
3.2.5. Location of the peaks over the transcriptome
Lastly, we examine the transcriptomic locations of called peaks from TRES. We focus on five important transcriptomic regions: transcription start site (TSS), 5′ untranslated region (UTR), coding sequence (CDS), stop codon and 3′UTR. Supplementary Figure S12 shows the results from two datasets: The cerebellum sample from the Young mouse data and the basal sample from the Stress mouse data. The pie charts of Supplementary Figure S12 show the proportions of peaks overlapping with these five regions, where the CDS and 3′UTR regions contain the most of peaks. Since the lengths of features are different, Supplementary Figure S12 also shows the density of peaks (peak counts rescaled by the feature lengths), computed using MetaPlotR (Olarerin-George and Jaffrey, 2017). The peaks from the Young mouse data cerebellum sample show very strong enrichment around stop codon, while the peaks from the Stress mouse data basal sample show strong enrichment at stop codon as well as 5′UTR. Both the overlapping proportion with CDS and 3′UTR regions and the enrichment at stop codon are consistent with previous reports (Dominissini et al., 2012), i.e. m6A is highly prevalent in coding regions and 3′UTRs, and is particularly abundant around stop codon. As the Stress mouse data was to study both m6A and m6Am, the relatively high enrichment of peaks around 5′UTR region was contributed by m6Am as reported in (Engel et al., 2018). Combining all information together, our peaks follow the unique transcriptomic-wide distribution patterns reported by previous studies.
3.2.6. Software and computational performance
TRES is implemented as an R package. It has excellent computational performance. To analyze a typical MeRIP-seq dataset with 2 replicates on a MacBook Pro laptop with i5 2.3 GHz CPU and 16 G RAM, it takes 19.7 min from TRES. However, if it does not consider intronic regions (note exomePeak and MeTPeak do not include introic regions), it only takes 3.43 min. With the same computing resource and same dataset, it takes 13.03 min from MACS2, 1.5 h from exomePeak and 3.19 h from MeTPeak. In other words, without intronic regions, our package is four times faster than MACS2, 30 times faster than exomePeak, 55 times faster than MeTPeak. Even it is slightly slower than MACS2 when intronic regions are included, it is still faster than exomePeak and MeTPeak. TRES, together with an example dataset and example code, is available on Github at https://github.com/ZhenxingGuo0015/TRES.
4 Discussion
RNA epigenetics, in particular m6A modification, is an emerging field to study gene expression regulation mechanism. MeRIP-seq is a recently developed sequencing method to provide transcriptome-wide m6A profile. Compared to the well-established study of DNA methylation where a number of data analysis tools have been developed, method to analyze MeRIP-seq data is still lacking. In this article, we develop a novel statistical model to detect transcriptome-wide m6A regions. It conducts peak calling in two steps. First, it scans the transcriptome to loosely identify candidate regions using an ad hoc procedure. Second, it detects and then ranks peaks through rigorous statistical modeling and inference. In particular, a Bayesian hierarchical negative binomial model is developed to model read counts of candidate regions, which accounts for all sources of variations and alleviates the problem caused by small sample size.
Extensive simulation and real data analyses demonstrate that TRES is more accurate, robust and efficient than existing peak calling methods such as MeTPeak, exomePeak and MACS2. In simulation, TRES provides more precise or less biased dispersion estimate than naive moment estimate evaluated by normalized MSE. Our shrinkage estimation procedure for dispersion of methylation level stabilizes the biological variance estimates in small-sample problem, and the proper modeling of dispersion makes it better take advantage of large sample size. In real data analyses, peaks called by TRES consistently have the best motif content compared to MeTPeak, exomePeak and MACS2 in all three datasets, which means peaks called by TRES are more likely to be true m6A regions. In addition, TRES is more robust to small number of replicates, and lower sequencing depth. Lastly, the consistency between transcriptome-wide distribution of peaks called by TRES and the distribution of m6A reported by previous studies further demonstrate the accuracy of TRES in m6A peak calling.
Given the precise locations of m6A modified regions under each condition, our future work will focus on developing methods to compare m6A methylation levels for samples under different biological and clinical conditions. The dynamics of m6A can shed light on gene regulation mechanisms in response to different conditions and potentially serve as biomarkers for diseases. In addition, since the sample profiles from the MeRIP-seq experiments are often mixtures of different cell types (e.g. brains or blood), it is desirable to identify cell type specific methylation and differential methylation. Similar works have been proposed for DNA methylation and gene expression data (Li et al., 2019; Li and Wu, 2019). To develop method for cell type specific m6A analysis is our research interest in the near future.
Funding
This project was partly supported by several grants from the National Institute of Health [GM122083, GM124061 and AG025688 to H.W., GM122083 and GM103645 to Z.W., NS111602, MH116441 and HG008935 to P.J.].
Conflict of Interest: none declared.
Data availability
The three MeRIP-seq datasets used in this manuscript are all publicly available. The Stress mouse data are available at the Gene Expression Omnibus (GEO) under accession code GSE113781. The Young mouse data are available at GEO under accession code GSE144032. The HeLa data are available at GEO under accession code GSE46705. The R package TRES is freely available on Github at https://github.com/ZhenxingGuo0015/TRES.
Supplementary Material
Contributor Information
Zhenxing Guo, Department of Biostatistics and Bioinformatics, Emory University, Atlanta, GA 30322, USA.
Andrew M Shafik, Department of Human Genetics, Emory University, Atlanta, GA 30322, USA.
Peng Jin, Department of Human Genetics, Emory University, Atlanta, GA 30322, USA.
Zhijin Wu, Department of Biostatistics, Brown University, Providence, RI 02806, USA.
Hao Wu, Department of Biostatistics and Bioinformatics, Emory University, Atlanta, GA 30322, USA.
References
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B (Methodological), 57, 289–300. [Google Scholar]
- Bird A. (2002) DNA methylation patterns and epigenetic memory. Genes Dev., 16, 6–21. [DOI] [PubMed] [Google Scholar]
- Chen Y. et al. (2012) Systematic evaluation of factors influencing chip-seq fidelity. Nat. Methods, 9, 609–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui X. et al. (2018) Metdiff: a novel differential RNA methylation analysis for merip-seq data. IEEE/ACM Trans. Comput. Biol. Bioinf., 15, 526–534. [DOI] [PubMed] [Google Scholar]
- Cui X. et al. (2016) A novel algorithm for calling mRNA m6A peaks by modeling biological variances in merip-seq data. Bioinformatics, 32, i378–i385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai Q. et al. (2007) Identification of recognition residues for ligation-based detection and quantitation of pseudouridine and n 6-methyladenosine. Nucleic Acids Res., 35, 6322–6329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darnell J.C. et al. (2011) FMRP stalls ribosomal translocation on mRNAs linked to synaptic function and autism. Cell, 146, 247–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dominissini D. et al. (2012) Topology of the human and mouse m6A RNA methylomes revealed by m6A-seq. Nature, 485, 201–206. [DOI] [PubMed] [Google Scholar]
- Engel M. et al. (2018) The role of m6a/m-RNA methylation in stress response regulation. Neuron, 99, 389–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg A.P. (2004) The epigenetics of cancer etiology. Semin. Cancer Biol., 14, 427–432. [DOI] [PubMed] [Google Scholar]
- Feng H. et al. (2014) A Bayesian hierarchical model to detect differentially methylated loci from single nucleotide resolution sequencing data. Nucleic Acids Res/, 42, e69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greer E.L., Shi Y. (2012) Histone methylation: a dynamic mark in health, disease and inheritance. Nat. Rev. Genet., 13, 343–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz S. et al. (2010) Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and b cell identities. Mol. Cell, 38, 576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe A.E. et al. (2012) Bump hunting to identify differentially methylated regions in epigenetic epidemiology studies. Int. J. Epidemiol., 41, 200–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson D.S. et al. (2007) Genome-wide mapping of in vivo protein–DNA interactions. Science, 316, 1497–1502. [DOI] [PubMed] [Google Scholar]
- Jung Y.L. et al. (2014) Impact of sequencing depth in chip-seq experiments. Nucleic Acids Res., 42, e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan Q. et al. (2019) The critical role of RNA m6a methylation in cancer. Cancer Res., 79, 1285–1292. [DOI] [PubMed] [Google Scholar]
- Li Z., Wu H. (2019) Toast: improving reference-free cell composition estimation by cross-cell type differentia l analysis. Genome Biol., 20, 190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z. et al. (2019) Dissecting differential signals in high-throughput data from complex tissues. Bioinformatics, 35, 3898–3905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X. et al. (2019) RNA m6A methylation regulates the epithelial mesenchymal transition of cancer cells and translation of snail. Nat. Commun., 10, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Love M.I. et al. (2014) Moderated estimation of fold change and dispersion for RNA-seq data with deseq2. Genome Biol., 15, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng J. et al. (2013) Exome-based analysis for RNA epigenome sequencing data. Bioinformatics, 29, 1565–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer K.D. et al. (2012) Comprehensive analysis of mRNA methylation reveals enrichment in 3′UTRs and near stop codons. Cell, 149, 1635–1646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagalakshmi U. et al. (2008) The transcriptional landscape of the yeast genome defined by RNA sequencing. Science, 320, 1344–1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olarerin-George A.O., Jaffrey S.R. (2017) Metaplotr: a perl/r pipeline for plotting metagenes of nucleotide modifications and other transcriptomic sites. Bioinformatics, 33, 1563–1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portela A., Esteller M. (2010) Epigenetic modifications and human disease. Nat. Biotechnol., 28, 1057–1068. [DOI] [PubMed] [Google Scholar]
- Przyborowski J., Wilenski H. (1940) Homogeneity of results in testing samples from Poisson series: with an application to testing clover seed for dodder. Biometrika, 31, 313–323. [Google Scholar]
- Robinson M.D. et al. (2010) EdgeR: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics, 26, 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roundtree I.A. et al. (2017) Dynamic RNA modifications in gene expression regulation. Cell, 169, 1187–1200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szulwach K.E. et al. (2011) 5-HMC-mediated epigenetic dynamics during postnatal neurodevelopment and aging. Nat. Neurosci., 14, 1607–1616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teschendorff A.E. et al. (2010) Age-dependent DNA methylation of genes that are suppressed in stem cells is a hallmark of cancer. Genome Res., 20, 440–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H. et al. (2013) A new shrinkage estimator for dispersion improves differential expression detection in RNA-seq data. Biostatistics, 14, 232–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C. et al. (2014) Structural basis for selective binding of m6A RNA by the YTHDC1 YTH domain. Nat. Chem. Biol., 10, 927–929. [DOI] [PubMed] [Google Scholar]
- Zhang Y. et al. (2008) Model-based analysis of chip-seq (macs). Genome Biol., 9, R137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z. et al. (2019) Radar: differential analysis of merip-seq data with a random effect model. Genome Biol., 20, 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The three MeRIP-seq datasets used in this manuscript are all publicly available. The Stress mouse data are available at the Gene Expression Omnibus (GEO) under accession code GSE113781. The Young mouse data are available at GEO under accession code GSE144032. The HeLa data are available at GEO under accession code GSE46705. The R package TRES is freely available on Github at https://github.com/ZhenxingGuo0015/TRES.


