Recombinatoric exploration of novel folded structures: A heteropolymer-based model of protein evolutionary landscapes

Abstract

The role of recombination in evolution is compared with that of point mutations (substitutions) in the context of a simple, polymer physics-based model mapping between sequence (genotype) and conformational (phenotype) spaces. Crossovers and point mutations of lattice chains with a hydrophobic polar code are investigated. Sequences encoding for a single ground-state conformation are considered viable and used as model proteins. Point mutations lead to diffusive walks on the evolutionary landscape, whereas crossovers can “tunnel” through barriers of diminished fitness. The degree to which crossovers allow for more efficient sequence and structural exploration depends on the relative rates of point mutations versus that of crossovers and the dispersion in fitness that characterizes the ruggedness of the evolutionary landscape. The probability that a crossover between a pair of viable sequences results in viable sequences is an order of magnitude higher than random, implying that a sequence's overall propensity to encode uniquely is embodied partially in local signals. Consistent with this observation, certain hydrophobicity patterns are significantly more favored than others among fragments (i.e., subsequences) of sequences that encode uniquely, and examples reminiscent of autonomous folding units in real proteins are found. The number of structures explored by both crossovers and point mutations is always substantially larger than that via point mutations alone, but the corresponding numbers of sequences explored can be comparable when the evolutionary landscape is rugged. Efficient structural exploration requires intermediate nonextreme ratios between point-mutation and crossover rates.

It is widely recognized that key events in evolution may involve large-scale genomic rearrangements (1–6). Experiments on plants suggest that dramatic restructuring of the genome in response to traumas may underlie formations of many new species (1). The presence of introns in the genes of higher organisms implies that even a single base change can result in the deletion or insertion of whole sequences in the protein product (2). It has been argued that cellular “natural genetic engineering” machineries have evolved to modulate genomic reorganization in lower organisms (3). Moreover, certain peculiarities in present-day genomes and cellular organizations may be explained best by “lateral” or “horizontal” transfers in the past (4, 5). Indeed, it is large-scale genomic rearrangements rather than the accumulation of point mutations that bear the main responsibility for the alarmingly quick emergence of bacterial antibiotic resistance.

Therefore, to capture evolutionary complexities better, theoretical perspectives that focus exclusively on point mutations should be augmented to include other types of sequence transformations. Such efforts would benefit the development of in vitro evolution for protein engineering (7–9) as well. In a recent insightful study, Bogarad and Deem (10) used a generalized (block) NK model, with terms in a potential function (interpreted to represent protein interactions and substrate binding affinities) assigned randomly to a large collection of sequences. Their model construction thus is formally very similar to Bryngelson and Wolynes' (11) seminal random energy model treatment of protein conformational space. Bogarad and Deem's simulation showed that nonhomologous recombination can lead to much more efficient searching of the fitness space than that achievable by point mutations alone (10).

Central to any model of evolution is a prescription for mapping sequences onto fitness. Most progress to date has been made by tractable but drastically simplified models. Prime examples are NK-type models, which have led to much insight (see e.g., refs. 7, 10, and 12), although they lack an explicit sequence-structure relationship. In certain applications, however, sequence-structure mappings based on polymer principles are useful in assessing how proposed ideas about evolutionary landscapes might depend on the underlying physical interactions, for the obvious reason that functions of biomolecules in most cases are intimately related to their folded structures. For example, the concept of “shape space covering” seems to hold for RNA secondary structure evolution (13) but not for proteins (14), presumably because their folding and compactification are governed by different potential functions (13, 14).

Modeling the Mortality Landscape

Here we apply the highly coarse-grained two-dimensional (2D) hydrophobic polar (HP) model (15–17) to recombination. Now, sequences are allowed to pair and crossover (recombine) in addition to undergoing point mutations (18). Similar HP and HP-like models (15, 18–22), other simplified chain constructs (23–26), and related statistical mechanics theories (27) have been used previously to study point mutations. Here, as in ref. 18, a favorable energy ε (<0) is assigned to each hydrophobic-hydrophobic (HH) contact in a chain conformation; other contacts are neutral. Results are presented for chain length n = 18. Unique sequences (model proteins) are those with a single ground-state (native) conformation. A conformation is encodable if it is the native state of at least one unique sequence (15–18).

The HP model is motivated by the prominence of hydrophobic interactions in protein folding. However, hydrophobic effects alone are insufficient to account for certain generic protein properties (28, 29), and simple lattice models with different alphabets can lead to significantly different folding codes (17, 30). Our premise here is that insofar as the 2D HP sequence to native structure mapping is concerned, it is competent in capturing the essential physics of the corresponding mapping for real proteins (31). This working assumption is consistent (31) with the “principle of minimal frustration” (11) or “consistency principle” (32) and is bolstered by at least two observations: (i) the hydrophobicity pattern in real proteins (33) has statistical properties similar to those of 2D HP model proteins (34), and (ii) results from recent mutagenesis experiments of Cordes et al. (35, 36) are highly suggestive of predicted features of the 2D HP model sequence-structure mapping (14, 18, 31).

We consider one-point crossovers, in which a single cut is made at the same position of a pair of sequences, followed by cross-splicing. For example, given two parent sequences HPPHHPHHPHPPHPPHHH and HPHPHPPHHPHPHHPHPH, cutting between the seventh and eighth monomers produces the offspring HPHPHPPHPHPPHPPHHH and HPPHHPHHHPHPHHPHPH, where underlined monomers are from the first parent sequence. Crossovers in which only one monomer is exchanged are not counted, because they are equivalent to point mutations at chain ends. It follows that each pair of n = 18 parent HP sequences may undergo (n − 3) = 15 crossover events to produce 2 × (n − 3) = 30 crossover offspring. Fitness or mortality measures (see details below) of a sequence are based on its native thermodynamic stability (18). Mutations or crossovers that lead to a nonunique sequence are considered lethal (i.e., infinitely unfit). These modeling choices merely serve to provide simple, biophysically motivated, structure-based fitness measures. They should not be construed as our view on how real proteins function, which of course are far more complex.

Native stability of a sequence is measured by the sticking parameter −ε₀ (in units of Boltzmann constant × absolute temperature) at its folding-denaturation midpoint (18). In other words, ε₀ (<0) is the favorable HH contact energy at which half the chain population adopts the native conformation. Because a weaker favorable HH energy (less negative ε₀, hence a smaller −ε₀ = |ε₀|) would be needed for a more stable sequence than that for a less stable sequence, lower values of −ε₀ imply higher native stabilities, which we correlate with higher fitness. The upward direction in our evolutionary landscapes denotes increasing “fitness deficiency” (e.g., as parameterized by −ε₀), not fitness itself. The resulting sequence-space representations may be called “inverse-fitness” or “mortality” landscapes. We choose to use these depictions instead of the conventional fitness landscape, because picturing a locally optimized sequence as a fitness peak (7, 37) does not quite convey its mutational stability (18, 38) in light of Earthings' experience with gravity. In contrast, on the mortality landscape such a sequence and the homologous sequences around it form a basin of attraction (18, 38) or superfunnel (18), which may be viewed as a sequence-space generalization of the conformational-space folding funnel on the energy landscape (39–42).

Effectiveness of Crossovers

The 6,349 viable model protein sequences (17) do not form a single network interconnected by point mutations. They split up into 700 networks (Table 1). A sequence can be transformed into any other sequence in the same network via viable (nonlethal) point mutations, but it cannot be so transformed to a sequence in a different network. Remarkably, there is a dominant network with 4,553 sequences, encompassing 71.7% of model protein sequences, and covering a majority (843, 57.2%) of the 1,475 encodable conformations (14, 18). The networks in Table 1 may be subdivided further into 1,706 neutral nets, each consisting of interconnected sequences encoding for the same conformation (14, 18). Irrespective of mutational connectivity, a conformation's neutral set is the collection of all sequences that encode for it. In the present HP model, an overwhelming majority (1,265 of 1,475, 85.8%) of neutral sets have only one single neutral net, but 193, 13, and 4 of them have 2, 3, and 4 neutral nets, respectively.

Table 1.

Distribution of n = 18 2D HP net sizes

Size*	1	2	3	4	5	6	7	8	9	10	11	12	13	15	16	17	21	37	4,553
No. of nets	337	182	42	49	19	22	4	11	11	4	4	4	2	3	1	1	1	2	1

^*The number of model protein sequences in a net. 

Altogether there are (6,349 × 6,348/2) × 15 = 302,275,890 one-point crossover events between (viable) model protein sequence pairs (Table 2). In the HP model, sequences in the same neutral set tend to share significant numbers of conserved monomers (14, 31). Therefore, we refer to crossovers between sequences in the same neutral set as homologous (14, 43) and to those between sequences in different neutral sets as nonhomologous. Our usage of “homologous” here is based entirely on empirical structure and sequence comparisons (as may be applied to real proteins), not on evolutionary ancestry, unlike some other works in which the term is rigorously reserved for sequences that are believed to be evolutionarily related. We find that 27.7% of crossover events between viable sequences lead to at least one viable offspring (11.5% have two viable offspring). Among the 604,551,780 offspring, a total of 118,426,082 (19.6%) are viable, but 60,916,664 (10.1%) are identical to one of the parent sequences. Of the remaining 543,635,116 offspring that differ from either parent, 57,509,418 (10.6%) are viable, 41,765,030 (7.68%) are viable and not in either parents' neutral nets, and 41,712,428 (7.67%) are viable and not in either parents' neutral sets.

Table 2.

Homologous and nonhomologous recombination

Crossover type	Structural innovation			No new structure		Total
	2/2	1/1	1/2	0/1	0/2
Homologous	18	1,753	1,458	108,714	313,520	469,020
	0.00384%	0.374%	0.311%	23.2%	66.8%	100%
	(0.00423%)	(0.412%)	(0.343%)	(25.6%)	(73.7%)	—
Nonhomologous	2,429,718	36,294,731	555,014	12,707,944	31,356,742	301,806,870
	0.805%	12.0%	0.184%	4.2%	10.4%	100%
	(2.92%)	(43.5%)	(0.666%)	(15.2%)	(37.6%)	—

Numbers of crossover events that result in at least one of the two offspring sequences being viable (third and sixth rows) are classified by a crossover event's number of viable offspring (denominator in each fraction) and the number of which that encode for structures different from either parents' (numerator). Percentages without parentheses are relative to the total number of all possible crossover events (last column). Percentages in parentheses are relative to the total number of homologous or nonhomologous crossover events that have at least one viable offspring. 

The difference in outcome between homologous and nonhomologous crossovers is dramatic. An overwhelming majority (90.7%) of homologous crossover events results in one or two viable sequences, with 78.9% of crossover offspring viable, but only 0.688% of the crossover events result in structural innovation, i.e., give rise to one or two sequences encoding for new structures different from either parent. These sequences account for only 0.346% of all homologous crossover offspring. On the other hand, the viability of nonhomologous crossover events is significantly lower. Only 27.6% have one or two viable offspring, with 19.5% of nonhomologous crossover offspring viable, yet their rate of structural innovation is at least an order of magnitude higher. Given that a nonhomologous crossover event produces at least one viable offspring, there is a 47.1% chance that one or both offspring sequences are innovative structurally, and 35.4% of all viable nonhomologous crossover offspring encode for new structures. Overall, 13.0% of all nonhomologous crossover events and 6.91% of all nonhomologous crossover offspring lead to new folds (Table 2).

We compare these new observations with the 18 × 6,349 point mutations on the same set of model proteins, 14.3% of which result in viable sequences (44). This viability rate is lower than that among all crossover events (27.7%) or crossover offspring (19.6%). Thus overall, crossovers are less lethal than point-mutation events in this model. However, among the crossover offspring that are different from either parent, only 10.6% are viable. This conditional viability rate is lower than that for point mutations, which necessarily produce offspring that are different from the original sequences. Most viable point mutations are neutral. Only 3,428 (3.0% of all point mutations) lead to new structures (44). This is significantly lower than the structural innovation rates of crossovers. Overall, 6.90% of all crossover offspring encode for new structures, corresponding to a structural innovation rate of 7.67% among crossover offspring that are different from either parent.

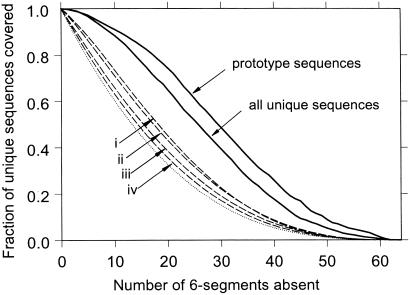
Because only 2.4% of all n = 18 HP sequences are viable (44), the high crossover viability rates (above) signify a high degree of nonrandomness in these processes, suggesting strongly that part of a sequence's signal for uniqueness is local. Fig. 1 confirms this idea. The sigmoidal solid curves say that certain local sequence patterns are preferred over others. In the absence of biases and sampling effects (see below), only (1/2)³ = 12.5% of the sequences would remain when one half of the 6-segments were disallowed (dotted curve). For the complete set of model proteins, however, 2,202 of 6,349 (34.7%) of the sequences remain. Segment popularity is not a function of H composition alone. For instance, HHPPPP has the same composition as the most popular 6-mer pattern but is much less frequent (0.35 vs. 3.7%). Segment bias is even more prominent among the subset of prototype sequences, which have relatively high mutational stabilities (14, 18). As much as 745 of 1,706 (43.7%) of them are covered by just one half of the 6-mer patterns. Although the small sizes of the two sets of model proteins in question and the biases in average H composition among the unique and prototype sequences contribute to this phenomenon, the large differences between the solid and dashed curves in Fig. 1 rule out the possibility that they are the primary causes of the significant segment preferences observed. We also divided the sequences in these sets into two or six segments each and enumerated the frequencies of the resulting 9- and 3-segments (fixed windows as in Fig. 1). Frequencies of segments extracted from the two sets by a sliding window of length ranging from 3 to 9 were determined as well. Significant nonrandomness is found in every case (data not shown), and the local preferences of unique and prototype sequences appear to be robust. For segments longer than 6 monomers, the most popular segment always contains the most popular PHPPHP as a subsequence. The most popular 4- or 5-mer patterns always contain the HPPH motif, and the most popular 3-mer pattern is PHP, both subsequences of the most popular 6-mer pattern. It is intriguing to note that these popular sequence patterns favor lattice helices and turns (45).

Figure 1.

Model proteins prefer certain local sequence patterns. Each 18-mer HP sequence is divided into three 6-segments (monomers 1–6, 7–12, and 13–18). For a given set of sequences, 6-segment frequencies among the 2⁶ = 64 HP patterns are sorted. Starting with the least frequent, 6-mer patterns are disallowed cumulatively until all 64 possibilities are disallowed when the most popular 6-segment is eliminated at the last step (horizontal scale). At each step, the fraction of full-length sequences that still can be assembled from the remaining 6-segments is determined (vertical scale). The solid curves are for all 6,349 unique sequences and the 1,706 prototype sequences (14, 18). In general, relative 6-segment frequencies are not identical for different sequence collections, but the sets of all unique and prototype sequences share much similarity in this regard; e.g., the all-P segment is least popular among both, accounting for 0.063 and 0.039% of their 3 × 6,349 and 3 × 1,706 6-segments, respectively. PHPPHP is most popular among all unique sequences (3.7%) and also the prototype sequences (5.1%). In fact, the five most popular (PHPPHP, HPPHPH, HPHPPH, HPPHHH, and HHHPPH) and the three least popular (PPPPPP, HPPPPP, and PPPPPH) of the two sets coincide. As controls, results from several random collections of sequences are included for comparison. Each dashed curve (i–iv) shown is an average over 10,000 samples. Each sample is calculated by the above sorting/disallowing procedure for: 6,349 (i) and 1,706 (ii) randomly selected sequences constrained to be all distinct and have an overall H-composition of 54.8 (i) and 53.6% (ii), respectively, equal to the average H compositions over the 6,349 unique sequences and the 1,706 prototype sequences; 1,706 (iii) and 6,349 (iv) unconstrained randomly selected sequences from all possible sequences. The lowest dotted curve is for all 2¹⁸ possible sequences. Further constraining the samples in i and ii to conform to their respective distribution of H composition results in plots that are practically indistinguishable from the dashed curves i and ii shown.

Tunneling and Autonomous Folding Units

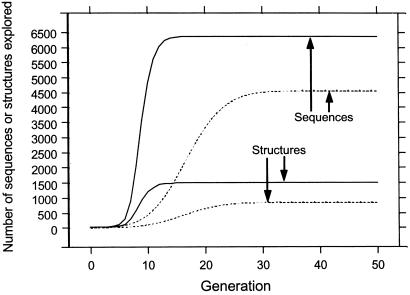
Evolutionary explorations by point mutations may be likened to diffusion. Their extent is limited on a fragmented mortality landscape, because sequences belonging to different networks (Table 1) are beyond reach. On the other hand, crossovers can “tunnel” through the infinitely high mortality barriers between networks. Fig. 2 shows that with point mutations alone, even if one starts in the largest network a substantial fraction of viable sequences and structures cannot be explored (dotted curves). In contrast, with both point mutations and crossovers, practically all viable sequences (6,347 of 6,349) can be reached from the dominant network (see Fig. 7, which is published as supporting information on the PNAS web site, www.pnas.org). Depending on the single starting sequence, the number of generations needed to explore all 4,553 sequences in the network by point mutations ranges from 25 to 42; the average over all possible starting sequences is 31.8 generations. Exploration of the same sequences is more efficient when crossovers are included (Fig. 2, solid curves), the corresponding average being only 12.8 generations.

Figure 2.

Sequence and structure exploration. As indicated, the curves show the average number of distinct unique sequences visited or the average number of distinct structures these sequences encode, over 4,553 explorations, each using one of the model protein sequences in the largest net (Table 1) as the starting point at generation 0. Exploration proceeds at any given generation to the next by including new unique sequences from (i) all possible single point mutations on all unique sequences visited thus far (dotted curves, point mutations only) or (ii) all possible crossovers between every pair of unique sequences visited thus far and those from (i) (solid curves, point mutations plus crossovers).

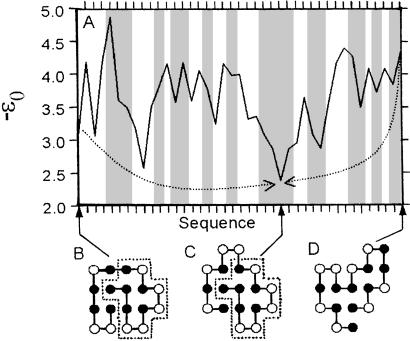
Fig. 3 compares an example crossover with point mutations. Here −ε₀ is the model mortality measure, playing a sequence-space role analogous to that of energy or “internal free energy” (40) in conformational space. A point mutation that results in a decrease in fitness, i.e., an increase in mortality, is represented by an upward step (a positive change in −ε₀) and vice versa. The two paths in Fig. 3 are optimized by Dijkstra's algorithm (44) such that (i) the total extent of upward climbs encountered (i.e., the sum of positive changes in −ε₀) along each of these paths is the minimum possible among, respectively, all paths from B to C and all paths from D to C, and (ii) each of these paths has the smallest number of steps if more than one path satisfies condition (i). We also obtained optimal point-mutation paths from each of the other 4,552 sequences in the dominant network to sequence C, which is one of the two global minima on the landscape (−ε₀ = 2.37). Barrier effects are significant. The average minimized sum of positive −ε₀ increments is 5.50 along these paths, which have 13.0 steps on average, indicating the point-mutational evolutionary landscape is rugged.

Figure 3.

Tunneling underneath a mortality landscape. (A) shows a 25- and a 15-step optimal point-mutation path that lead from sequences B and D to sequence C (shown in their unique native conformations), respectively. The graduations on the horizontal scale correspond to 41 different unique sequences that collectively encode 19 different structures (marked by vertical shadings, two of the regions encode for the same structure.) The −ε₀ vs. sequence profile is the mortality landscape along these point-mutation paths. The dotted arrows in A depict the “tunneling effect” of a crossover between sequences B and D that leads directly to sequence C. In this crossover, the 11-monomer segment (enclosed by dotted boxes) inherited by sequence C from parent sequence B acts similar to an “autonomous folding unit.”

Fig. 3 shows how crossovers make it possible to reach a structural target directly, bypassing tortuous point-mutation-only routes that often involve many intermediate structures. Of particular interest here is the 11-monomer segment that has the same fold in the native structures of sequences B and C (dotted boxes). This 11-mer is a 2D lattice analog of an autonomous folding unit (46) or a “least-frustrated foldon” (47), because as an independent sequence its unique native structure is identical to that in the dotted boxes of Fig. 3. This feature is not rare in the model: 821 (12.9%) and 285 (4.49%) of the n = 18 6,349 unique HP sequences contain, respectively, 11- and 12-mer autonomous folding units that act in a similar manner. Evolutionarily, the crossover in Fig. 3 has the important advantage of preserving the autonomous folding unit. In contrast, if the point-mutation-only route from B to C in Fig. 3 were taken, this unit would be dismantled first along the path before it could be reassembled.

Evolution in Time-Dependent Environments

Rapid exploration of a broad range of evolutionary possibilities is key to the survival of viruses and bacteria in an environment subjected to ever-changing attacks from the immune system and new drugs. To gain insight into such processes, we introduce a population dynamics model. The time dependence of the model is governed by the following nonlinear difference (master) equation relating the population P_i(q + 1) of any given viable sequence i at generation q + 1 to the populations of all viable sequences at generation q, namely

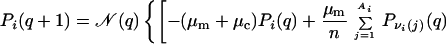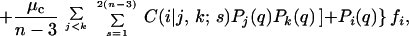1

where μ_m and μ_c are the point-mutation and crossover rates, respectively (μ_m is equivalent to μ/n in ref. 18), and ν_i(j) values label the A_i viable sequences that differ from i by a single point mutation. The matrix C(i|j,k;s) specifies crossover connectivities, where s labels the 2(n − 3) crossover offspring from any given pair of parent sequences j and k. For the n = 18 case studied here, the j < k summation is over all possible pairings among the 6,349 viable sequences. C(i|j,k;s) = 1 if the crossover offspring defined by {j,k;s} is identical to sequence i; otherwise C(i|j,k;s) = 0. The quantity enclosed by the square brackets in Eq. 1 represents the change in population of sequence i caused by point mutations and recombinations in a time step (generation). During the same time interval, part of the population of sequence i may be eliminated by the environment, and the remaining part can grow by faithful reproduction. The combined effect of death and faithful reproduction is accounted for by 𝒩(q) and f_i. For simplicity, here we constrain the total population to a constant by using 𝒩(q) as an overall normalization factor (independent of i) such that ∑_iP_i(q + 1) = 1 for all q ≥ 0. (This condition can be relaxed when necessary in future applications.) The likelihood of death and the efficiency of faithful reproduction affect the sequences' relative populations. These features are governed by the fitness factor f_i = R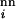 exp(αε₀), in which the fitness measure −ε₀ is exponentiated, with α ≥ 0; hence more stable sequences tend to be more efficient reproductively. But, native stability is not the only determinant of fitness in Eq. 1. To simulate a fluctuating environment, R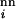, which takes the same value for all sequences in the neutral net containing a given sequence i, is assigned a new random number every GN generations in the range 0.1 < R < 10.0, and R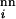 values of different neutral nets are uncorrelated. Here the role of α is similar to that of an inverse “temperature,” because disparities in survival rates increase with α. Thus it may be viewed as an average selection gradient as well as a measure of the ruggedness of the evolutionary landscape.

R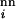 is the only nondeterministic factor in the present implementation of Eq. 1. Because population is treated as a continuous variable in our formulation, there is no explicit account of finite-population effects such as extinction (48). Instead, we use a population-threshold criterion for whether a structure has been explored to capture part of these effects (Figs. 4–6). (In contrast, Fig. 2 involves no nonzero population thresholds.) Because very low sequence populations are possible in this approximate treatment, the chances of trapping and extinction can be underestimated.

Figure 4.

Sequence and structure exploration in a changing environment. All results reported in Figs. 4–6 are computed by using Eq. 1, with the initial population at q = 0 equally divided between sequence C in Fig. 3 and its reverse sequence. Simulation results from one trajectory are reported for each given set of μ_m, μ_c, α, and GN. A model protein sequences that attained a normalized population threshold of P_i(q′) ≥ 10⁻⁶ at any q′ ≤ q is defined as already explored at generation q (A). Explored structures are those encoded by explored sequences (B). The exploration trajectories here are for GN = 20, 50, and 100 (as marked) with either point mutations plus crossovers (μ_m = 0.09, μ_c = 0.01; solid curves) or with point mutations alone (μ_m = 0.1, μ_c = 0; dashed curves).

Figure 6.

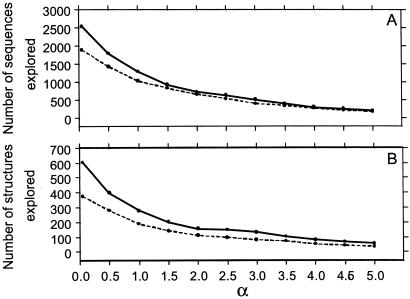
The number of sequences (A) and structures (B) explored after 5,000 generations (as defined in the Fig. 4 legend, GN = 100) with point mutations plus crossovers (μ_m = 0.09, μ_c = 0.01; solid curves) and with point mutations alone (μ_m = 0.1, μ_c = 0; dashed curves), both plotted as functions of α. The smallest α value considered is 0.05.

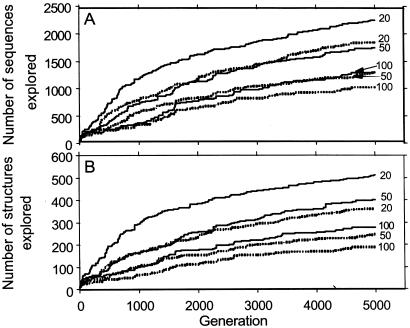
Fig. 4 shows that more rapidly changing environments (smaller GN) lead to faster and broader explorations of sequence and structure space. This is because a highly fluctuating environment means that there is a higher probability for any given sequence to be favorable for at least some time, during which it would enjoy some chance of being populated significantly. In all cases shown, the exploration is more effective with point mutations plus crossovers than with point mutations alone.

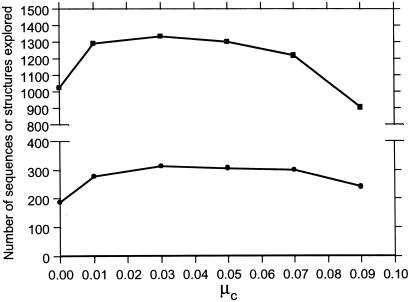
The power of recombination is in amplifying existing diversity (7), not in generating a high degree of diversity from a very small number of starting sequences. A case in point is that because the monomer types at eight of the positions along the starting sequences in Figs. 4–6 are identical, with this starting pair, crossovers alone can reach only 127/6,349 (2.0%) of all viable sequences and 58/1,475 (3.9%) of all encodable structures. This result underscores the importance of having a sizable rate of point mutation working in concert with crossovers. Fig. 5 suggests that optimal exploration in the present model requires approximately 0.1 < (μ_c/μ_m) ≤ 1, which is consistent with genetic algorithm studies (7).

Figure 5.

Number of sequences (squares) and structures (dots) explored after 5,000 generations at different crossover rates (as defined in the Fig. 4 legend) for GN = 100, α = 1, and μ_m + μ_c = 0.1 = constant. The lines between data points are merely visual guides.

Fig. 6 shows that exploration is more efficient when the evolutionary landscape is smooth (small α), but as ruggedness or the average selection gradient increases (larger α), exploration becomes sluggish. When α is large, populations are more concentrated in a relatively small number of low-mortality sequences. When the landscape is smooth, with the same total rate (0.1) of sequence transformation, point mutations plus crossovers visit more sequences and more structures than point mutations alone. When the landscape is rugged, the number of sequences explored by point mutations alone is comparable to that explored by point mutations plus crossovers. This is because point mutations are more effective in finding a low-mortality area from an already well populated spot nearby, whereas when the landscape is rugged many crossover offspring are likely to end up at high-mortality spots. Even so, Fig. 6B shows the remarkable result that structural innovation is still enhanced by crossovers at high α values. This result implies that when the average selection gradient is high, acting in concert with point mutations, crossovers can make more efficient use of their offspring sequences to achieve a higher structural diversity than a comparable number of sequences explored by point mutations alone.

Concluding Remarks

We have presented a simple structure-based study of evolution. Notwithstanding the present model's extreme simplicity, protein-like features such as autonomous folding units arise naturally from its minimalist construct. Segment analyses suggest that crossovers can be a much more effective means to explore new viable sequences than one might have hitherto posited, and nonhomologous recombination is seen as an efficient tool of structural innovation. These theoretical predictions may help elaborate the schema idea (7) of modular evolution (49) as well as the foldon concept (47) and are testable by experiments. The present results also bear on the evolution of sexual reproduction (50, 51). It is hoped that the insight gained from this effort would shed light not only on in vivo evolution but would facilitate the development of in vitro evolution technology as well (52, 53).

Abbreviations

2D

two-dimensional

H

hydrophobic

P

polar