How the folding rate constant of simple, single-domain proteins depends on the number of native contacts

Abstract

Experiments have shown that the folding rate constants of two dozen structurally unrelated, small, single-domain proteins can be expressed in terms of one quantity (the contact order) that depends exclusively on the topology of the folded state. Such dependence is unique in chemical kinetics. Here we investigate its physical origin and derive the approximate formula ln(k) = ln(N) + a + bN, were N is the number of contacts in the folded state, and a and b are constants whose physical meaning is understood. This formula fits well the experimentally determined folding rate constants of the 24 proteins, with single values for a and b.

Proteins spontaneously fold to a unique structure, more rapidly than would be possible were folding an exhaustive, random search of conformational space (1). This observation has led to numerous attempts to explain how naturally occurring proteins reach their native structures within a biologically relevant time-scale (reviewed in refs. 2–6).

Small, single-domain proteins often fold according to the first-order rate law

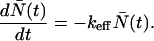1

Here, N̄(t) is the number of unfolded proteins at time t, and k_eff is an effective rate constant. The folding rates of these simple proteins satisfy the empirical relationship (7)

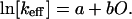2

Here, O is the contact order, a quantity calculated from the structure of the folded protein according to a well-defined recipe (7). The constants a and b have the same values for all the proteins in the data set. Their values were determined by fitting the experimental data. No physical significance was assigned to them. Since the publication of ref. 7, the folding rates of three dozen single-domain proteins have been measured (8, 9), all of which exhibit first-order kinetics with effective rate constants that satisfy Eq. 2.

This equation is rather intriguing. We know of no other example in chemical kinetics where the rate constants for dozens of distinct chemical compounds, involved in the same type of unimolecular reaction, depend only on the molecular structure of the products. This regularity is made more striking by the fact that the proteins in the data pool were selected on the basis of their structural dissimilarity (8). Despite the interest generated by this empirical result (10, 11), however, there has been only limited success in understanding its physical basis (12–16).

In this article, we present a kinetic model that leads to an expression for the rate constant that is similar in spirit to Eq. 2. In our analysis, we found it necessary to replace contact order with a different topological parameter: the number of native contacts (N). We say that two residues in the folded protein are in contact if the straight-line distance between their C_α atoms is less than d, and if there are more than C residues between them along the chain. Two residues separated by a distance (along the chain) smaller than the persistence length are not counted as being in contact. This excludes, for example, contacts occurring in α-helixes. Such contacts are not excluded by the counting method used to define the contact order.

Our main result is that the effective folding rate constant is given by

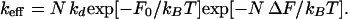3

Here, ΔF is the mean free energy gained when forming a contact, k_d is the mean rate constant for the “dissociation” of a contact, and F₀ = F[N] − NΔF, where F[N] is the free energy of formation of N contacts. These quantities will be given a more precise meaning later in this article.

If we assume that k_dexp[−F₀/k_BT] and ΔF have the same value for all proteins in the data set, then Eq. 3 fits well the known folding rate constants of the 24 proteins in our nonhomologous data set (8).

Like contact order, our model connects the folding rate constants to a quantity (the number of native contacts N) that depends only on the topology of the folded protein and two “universal constants.” Unlike the empirical contact order relationship, however, this relationship follows from a well-defined kinetic model and the constants have physical meaning.

The Model

We examine the structures of the folded proteins in our data set (7, 8) and generate a list of the residue pairs that are in contact, as defined in the introduction. We assume that folding proceeds through the following steps. The conformation of the unfolded polypeptide chain evolves in time because of the diffusional motion of the residues. Occasionally, the straight-line distance between two residues i and j, which form a contact in the native state, becomes smaller than d. When this happens, the native contact {i,j} is formed. After this, one of the two events can take place: a new contact is formed or the existing contact unravels. If, at a given time, the protein has managed to form m contacts, either one of them will break or one of the remaining N-m contacts will be formed. Folding is completed when all N native contacts are formed. This physical picture, where the protein performs diffusional motion until it finds itself in a configuration close enough to the native one, is somewhat similar to the topomer search model introduced by Debe and Goddard (14). Our model, however, is different from theirs in many respects. One result of the difference is that our model predicts well the folding rates of proteins having an α-helix, for which the topomer search model was found to be inadequate. Moreover, our model leads to a simple analytic expression that relates the folding rate and the number of native contacts.

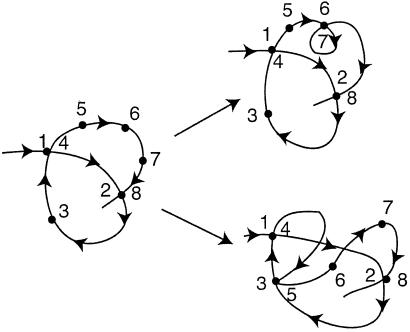
To explain the nomenclature and the simplifications contained in our model, we use as an example a protein that makes four native contacts when it is fully folded. The protein can have a large number of residues, but only the eight involved in the native contacts are of interest to us. We label them as 1, 2, … , 8, in the order in which they occur along the chain (they are not neighbors along the chain). The four native contacts in this example are {1,4}, {2,8}, {3,5}, and {6,7}.

We call a protein that has formed a specific set of m contacts an m-conformer. The 2-conformer {{1,4},{2,8}}, in which the contacts {1,4} and {2,8} are made, is shown in Fig. 1. There are six 2-conformers for this protein: {{1,4},{2,8}}, {{1,4},{3,5}}, {{1,4},{6,7}}, {{2,8},{3,5}}, {{2,8},{6,7}}, and {{3,5},{6,7}}. If we speak of a protein having m contacts and do not need (or want) to specify which contacts are formed, we call it an m-foldimer.

Figure 1.

A schematic representation of transitions from a 2-conformer to two different 3-conformers.

In our model, the progress of folding kinetics is described by the evolution of the number of native contacts in time and we will use this quantity as a “reaction coordinate.” Similar quantities have been used by others (e.g., refs. 3 and 17). When using this parameter, the evolution of the conformation of a single protein is a random walk in the number of contacts: we know only the probabilities that contact formation and breaking take place. Another folding experiment, with the same protein, under the same conditions, will reach the folding state by going through a different sequence of conformers. If the measurements are performed on an ensemble of molecules, the number of folded molecules evolves in time according to a deterministic kinetic equation. If this equation is of the form Eq. 1, then the probability π(t)dt that folding of a single molecule occurs between t and t + dt is given by a Poisson distribution π(t)dt = k_effexp[−k_efft]dt. This formula can be used to determine k_eff by performing a large number of single protein folding simulations with our model.

The rate R[{C₁, … , C_m−1} → {C₁, … , C_m−1, C_m}] of forming the m-conformer, {C₁, … , C_m−1, C_m}, by adding a specific contact C_m to a specific (m−1)-conformer, {C₁, … , C_m−1}, is

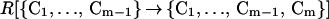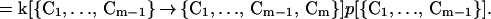4

Here C₁, C₂, … , C_m−1, are the pairs of residues that have already formed a native contact. The rate constant k[{C₁, … , C_m−1} → {C₁, … , C_m−1, C_m}] depends on which (m−1)-conformer we start with and which C_m contact is being made to obtain {C₁, … , C_m−1, C_m}. This is evident by looking at Fig. 1 where we show the processes {{1,4},{2,8}} → {{1,4},{2,8},{3,5}} and {{1,4},{2,8}} → {{1,4},{2,8},{6,7}}. The residues 6 and 7, which are closer to each other than 3 and 5, will form a contact faster (on average) than residues 3 and 5. For this reason, the rate constant k[{{1,4},{2,8}} → {{1,4},{2,8},{3,5}}] is smaller than k[{{1,4},{2,8}} → {{1,4},{2,8},{6,7}}].

A single protein will go through a variety of conformers on its way towards the folded state. The probability that the molecule forms a conformer {C₁, … , C_m−1} is given by

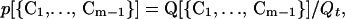5

where Q[{C₁, … , C_m−1}] is the partition function of the conformer {C₁, … , C_m−1} and Q_t is the total partition function of the chain (including all possible conformers and the unfolded chain).

Eq. 5 is supported by the following argument. We regard all conformers that have fewer than N native contacts as molecular configurations of the unfolded state. In a folding kinetics experiment, we start with an ensemble of unfolded molecules. Each molecule is in equilibrium (vibrational, translational, configurational) with its environment. The only variable that is out of equilibrium is the number of unfolded molecules. Because of this, the probability that an unfolded molecule reaches a given configuration (i.e., conformer) can be calculated by equilibrium statistical mechanics. Another way of looking at the same problem is to observe one molecule. As the time goes on, this will fold and unfold many times. At any time during this process, the protein is in equilibrium with the medium and the time it spends in each configuration (i.e., conformer) is given by the equilibrium statistical mechanics. Rigorous theory of the rate constant naturally incorporates this aspect of kinetics (18, 19).

The rate constants and the probabilities that the conformers are present are connected by the detailed balance equation

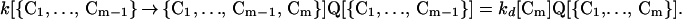6

Here, k_d[C_m] is the rate constant for breaking the contact C_m. We assume that its value depends mainly on which contact is broken, and not on what other contacts are present when breaking occurs. Using Eqs. 5 and 6 in 4 gives

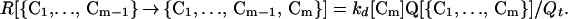7

If we assume a value for the rate constant k_d and use a Gaussian chain model, we can calculate the rates given by Eq. 7 for all conformers. By using these rates in a kinetic Monte Carlo program, we can simulate the random walk of the chain through the conformer space, determine the times when the protein folds, histogram them, and determine k_eff. The results of such simulations will be reported elsewhere (20). They are mentioned occasionally in this article, because they support some of the assumptions made to obtain Eq. 3.

We assume that the folding rate equals the rate of forming the N contacts present in the native state. Conformational changes taking place after these contacts are formed do not contribute to the rate constant. The state created when the Nth contact is formed is therefore a “transition state” for this model.

Next, we “coarsen” the description of the kinetic process by tracking the evolution of the foldimers instead of that of the conformers. The rate to form an m-foldimer from an (m−1)-foldimer is the sum of the rates of all possible transitions from an m−1-conformer to an m-conformer, each given by Eq. 7:

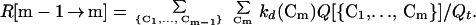8

The first sum is over all possible (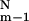) conformers with m−1 contacts, and the second is over all N − m + 1 contacts that can be formed for each specific (m−1)-conformer. “Coarsening” Eq. 8 means that we rewrite it as

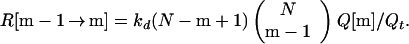9

Here, Q[m] is the mean partition function of an m-foldimer. This is the sum of the partition functions of all the m-conformers divided by the number (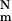) of such conformers. k_d is a mean rate constant for contact dissociation. Comparing Eqs. 8 and 9 gives a precise definition of Q[m] (this is useful if simulations are performed, but not for analytical work). The folding rate is obtained by setting m = N in this equation.

The effective rate constant k_eff is R[N−1 → N] divided by the probability P_r that the protein is in one of the conformations having less than N contacts. The latter quantity is given by

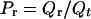10

with

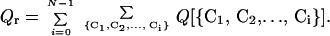11

The second sum is over all i-conformers. We can “coarsen” this expression by approximating it with

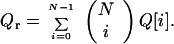12

To calculate the partition functions Q[k] we use the fact that all the foldimers are in equilibrium, with the equilibrium constant

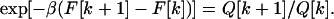13

Here, F[k] is the mean free energy of formation of k contacts and β = (k_BT)⁻¹, with k_B the Boltzmann constant and T the temperature in degrees Kelvin. By definition F[0] = 0. Using Eq. 13 as a recursion relation allows us to express the partition functions of all foldimers in terms of the partition function Q[0] of the protein with no contacts and the free energy F[m] to form an m-foldimer:

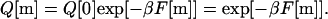14

The last equality follows from the fact that Q[0] = exp[−βF[0]] = exp[0] = 1. Introducing Q[m] given by Eq. 14 in Eq. 9 and taking m = N gives

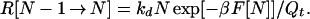15

Using Eq. 14 in Eq. 12 and then putting the result in Eq. 10 gives

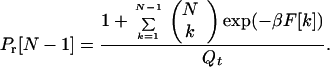16

Dividing Eq. 15 by this expression gives the effective rate constant

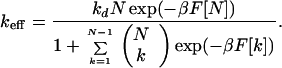17

Next, we assume that the free energy for the formation of m contacts is

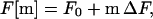18

where ΔF is the free energy change on the formation of a contact. We have replaced the energy of formation of a specific contact with an average value. For the Gaussian chain model, Jacobson and Stockmayer (21) have derived an expression for the change of free energy on formation of a contact. Contrary to the assumption made in Eq. 18, this is not a constant. However, Flory has shown (22) that in the mean-field approximation, the entropy associated with the formation of each new contact tends to a constant, as the number of contacts becomes large. Therefore, Eq. 18 is reasonable, for large values of m; the term F₀ in the equation reflects the fact that our assumption does not work for small m.

Simulations based on our kinetic model (20), supplemented with the assumption that the polymer is a Gaussian chain, support Eq. 18: the calculated values of F[m] are different for different m-conformers, but the deviations from the average value are small. Moreover, the average value of the free energy of formation is a linear function of m, when m is larger than 3.

Using Eq. 18 in Eq. 17 gives

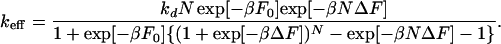19

If exp[−βΔF] ≪ 1 or exp[−βF₀] ≪ 1, this equation reduces to Eq. 3.

Comparison with Experiment

To test Eq. 3 we use the measured folding rate constants k_eff for a nonhomologous set of 24 small, simple, single-domain proteins (8). The number of contacts depends on the choice of the persistence-length cutoff C and the contact radius d; we use C = 12 residues and d = 6 Å. Knowing the folding rate constant k_eff and the number of native contacts N, for each protein in the set, we can test Eq. 3. A least-square fit of the data with this equation gives

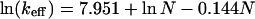20

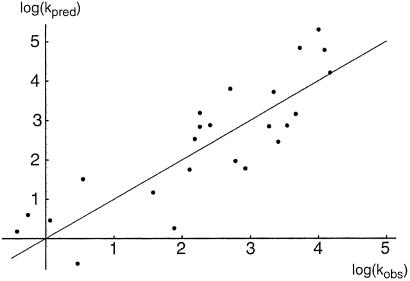
with a correlation coefficient of 0.887 (Fig. 2). Varying the cutoff C between 4 and 15 residues affects the two adjustable parameters in Eq. 3 but does not change the quality of the fit (the correlation coefficient remains greater than 0.85). Comparing Eqs. 3 and 20, we find that βΔF = 0.144 and k_dexp[−βF₀] = 3828 s⁻¹.

Figure 2.

The logarithm of the rate constant predicted by Eq. 21 vs. the logarithm of the measured rate constant. If the fit were perfect, all points would fall on the line. The rate constants are in s⁻¹.

By using the effective Gaussian chain model we can check whether the values of βΔF and k_dexp[−βF₀] generated by the fit are reasonable, and gain a better understanding of the results. Because this model provides a rather crude description of proteins, numerical values obtained from it (e.g., the binding energy of the contact, the rate of contact formation) are rough estimates. The aim of this analysis is to find out whether the numbers provided by the fit have an order of magnitude consistent with a Gaussian chain model.

The free energy of contact formation is (17, 21, 22) (for an effective Gaussian chain model)

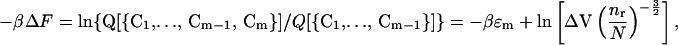21

where ɛ_m is the binding energy of the contact C_m and

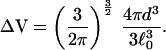22

Here, ℓ₀ = 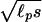, where ℓ_p is the persistence length and s is the distance between two C_α carbon atoms in the polypeptide chain (21). This formula is valid in the limit when many contacts are already formed, and this is why it does not depend on the mean distance between the specific residues forming the contact. For the ribosomal protein L9 (PDB ID code 1DIV), N = 24 and n_r = 55 residues. The persistence length of a protein is roughly 4s = 15.2 Å. With these numerical values and βΔF = 0.144, Eqs. 21 and 22 provide a connection between the contact radius d (the distance at which two residues are said to be in contact) and the energy of contact formation βɛ_m. Because we are using a coarse description of kinetics, the model contains only the mean contact energy, and the subscript m in ɛ_m is no longer necessary. For d = 4 Å, we obtain βɛ = −0.21. From ΔF = ɛ − T Δs, we calculate the entropy of contact formation Δs/k_B = −0.36. A negative value is reasonable: by making a contact we increase our ability to guess the position of all of the other residues in the protein, thus decreasing the entropy.

In this model, a protein must climb over a free energy barrier in order to fold. There is nothing unusual about this; most chemical reactions share this feature. A bit more unusual, as compared to other reactions, is that the entropy change needed to climb the “barrier” is relatively large.

The small value of the energy of contact formation βɛ is also reasonable. If the order in which the native contacts are formed matters, then it is important that the protein can easily break contacts made at the wrong time. The ability to break such contacts provides a mechanism of error correction. A higher contact energy will speed up folding but it is also likely to lead to erroneous folds.

We emphasize that because of the crudity of the effective Gaussian chain model, the values for βɛ obtained here are not accurate. By changing d it is possible to obtain βɛ = 0 from the equations above. In this case, one would argue that the barrier to folding is purely entropic.

For a Gaussian chain model, the rate of contact formation is (23)

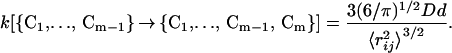23

Here, 〈r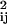〉 is the mean square distance between the residues i and j, forming the contact C_m, when the protein has already formed the contacts {C₁, … , C_m−1}. There is no simple analytical expression for this distance. We assume here that in the mean field limit 〈r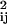〉 = n_rℓ_ps/N. The diffusion constant has been determined in several articles (24, 25) to be of order D = 4 × 10⁻⁷ cm²/s. This information allows us to calculate from Eq. 23 a mean rate constant of contact formation k = 4.36 × 10⁷ s⁻¹. Several experimental methods have been used recently (24, 26–29) to measure the rate of contact formation in unstructured polypeptides. The values obtained vary between 2.7 × 10⁷ s⁻¹ and 7.2 × 10⁶ s⁻¹, depending on the chain length. The order of magnitude agreement between the rate calculated here and the measurement is reassuring.

The detailed balance gives

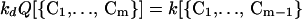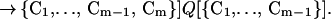24

For a Gaussian chain,

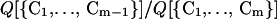25

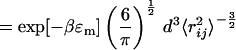and

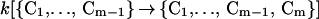26

Combining Eqs. 24–26 leads to

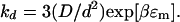27

Mercifully, the mean square distance between the residues making the dissociating contact has dropped out of this equation. This is in agreement with our intuition that the rate constant of contact breaking should be essentially independent of how many other contacts are present. Using βɛ = −0.214, d = 4 Å, and D = 4 × 10⁻⁷ cm²/s gives k_d = 6.15 × 10⁸ s⁻¹. The rate of breaking a contact is higher than the rate of forming it. This is in agreement with the fact that the free energy increases when a contact is formed.

We have performed Kinetic Monte Carlo simulations (20) with the rate constants provided by the effective Gaussian chain model, to simulate the process of conformer formation, until all the native contacts are formed. We find that (i) the folding rate calculated in this way satisfies first-order kinetics. (ii) The rate limiting step is almost always the formation of the Nth contact, which justifies the assumption m = N made in The Model. (iii) The rate obtained from Monte Carlo simulations is well described by Eq. 15. (iv) These simulations support the use of Eq. 18 as a mean value of free energy of formation of an m-foldimer.

Discussion

The model developed here assumes that the folding rate is controlled by the rate of forming all the native contacts observed in the folded protein. Once these contacts are formed, other forces (e.g., van der Waals interactions, hydrophobic interactions, electrostatic interactions) come into play and rapidly complete the folding process. In this model, the detailed chemical interactions that influence the folding of proteins are represented by two mean quantities (ΔF and k_d exp[−F₀/k_BT]). Surprisingly, these two parameters have roughly the same value for all proteins in our data set. It is common to most phenomenological models that the effects of various factors that influence the folding rate (e.g., presence of denaturants, changes in the amino acid sequence or in pH) are not treated explicitly. Their effect appears through modifications of the values of these two parameters and thus as scatter in Fig. 2.

Our model provides a generic picture of folding that explains a very striking observation: the relative folding rates of a large set of proteins are controlled by a parameter (the number of native contacts) that depends only on the topology of the folded configuration. Because N is simply related to the contact order (they are almost proportional), the model explains also the equation proposed by K.W.P. et al. (7).

Our central result, Eq. 3, is a consequence of two assumptions: (i) The rate-limiting step in folding is the formation of all (or nearly all) native contacts. This leads to Eq. 15. (ii) The free energy of a peptide with N native contacts formed, F[N], is linear with N. Other assumptions (such as the same value of the contact dissociation rate k_d) used in the derivation will affect only the prefactor in Eq. 3 and will not change the overall N dependence.

Note:

After the submission of this article, Gromiha and Selvaraj reported an empirical observation that the number of long-range contacts is strongly correlated with relative folding rates (30). The number of long-range contacts normalized by the length of the protein is correlated with folding rates more strongly still, but does not lend itself to a first-principles mechanistic explanation.