Accordion waves in Myxococcus xanthus

Abstract

Myxococcus xanthus are Gram-negative bacteria that glide on solid surfaces, periodically reversing their direction of movement. When starved, M. xanthus cells organize their movements into waves of cell density that sweep over the colony surface. These waves are unique: Although they appear to interpenetrate, they actually reflect off one another when they collide, so that each wave crest oscillates back and forth with no net displacement. Because the waves reflect the coordinated back and forth oscillations of the individual bacteria, we call them “accordion” waves. The spatial oscillations of individuals are a manifestation of an internal biochemical oscillator, probably involving the Frz chemosensory system. These internal “clocks,” each of which is quite variable, are synchronized by collisions between individual cells using a contact-mediated signal-transduction system. The result of collision signaling is that the collective spatial behavior is much less variable than the individual oscillators. In this work, we present experimental observations in which individual cells marked with GFP can be followed in groups of unlabeled cells in monolayer cultures. These data, together with an agent-based computational model demonstrate that the only properties required to explain the ripple patterns are an asymmetric biochemical limit cycle that controls direction reversals and asymmetric contact-induced signaling between cells: Head-to-head signaling is stronger than head-to-tail signaling. Together, the experimental and computational data provide new insights into how populations of interacting oscillators can synchronize and organize spatially to produce morphogenetic patterns that may have parallels in higher organisms.

Most cells exhibit periodic phenomena arising from internal biochemical and/or genetic circuits, and the literature on cellular oscillators is vast (1). Time scales for these oscillations span a range from <1 sec to circadian and even longer. Mathematical models for many of these oscillators have been published, with varying fidelity to experimental data (2). Recently, Strogatz and coworkers (3) have used modeling to show that, in bacteria, the collective periodicity of cellular oscillators can be more precise than the individual oscillators. In several microorganisms, individual periodic behavior is instrumental in generated spatial patterns, especially in the cellular slime molds (4, 5). In models of these spatiotemporal patterns, diffusion of extracellular substances plays a central role. Here, we present an experimental and theoretical analysis of a unique pattern-formation system that arises from an internal biochemical clock in the absence of such diffusion.

Myxococcus xanthus is a Gram-negative rod-shaped bacterium, abundant in soils and detritus. The bacteria do not contain flagella, but move by gliding on surfaces along slime trails, periodically reversing their direction of movement. There are two “motors” that drive gliding motion. At the leading pole, type IV pili extend, adhere to polysaccharides on the substratum or on the surface of a neighboring bacterium, and retract, pulling the cell forward. This type of motion is called S-motility and is similar to “twitching motility” observed in Pseudomonas aeruginosa and Vibrio cholerae (6, 7). The other type of locomotion is called A-motility. The mechanism underlying this motility is less well understood. In cyanobacteria, gliding speed is the same as slime extrusion from nozzle structures located at the cell poles (8). In myxobacteria, A-motility depends on slime extruded from pore structures at the trailing pole (9, 10). It has been shown theoretically that the swelling of the slime gel as it emerges from the nozzles generates sufficient force to propel the cell forward (11). All of these findings suggest that slime extrusion drives A-motility.

When nutrients are abundant, myxobacteria swarm out from the center of a colony, secreting exoenzymes that are used to digest macromolecules or prey bacteria. When nutrients are depleted, the bacteria aggregate into fruiting bodies where they convert into resistant myxospores. The process of fruiting-body formation is characterized by the expression of several developmental signals, the most studied of which is the C-signaling system that involves contact-mediated communication between cells (12). Contact signaling induces changes in gene expression and cell motility, leading to the formation of spatial patterns, including concentric and spiral waves and cellular streaming. This “ripple phase” (13, 14) is an especially interesting phenomenon from the viewpoint of pattern formation, because it can serve as a “readout” of the internal states of individual bacteria and of intercellular signaling between cells.

Elucidating the requirements for producing the various wave patterns can provide insights into the basic principles of the inter- and intracellular signaling systems. Indeed, the model we present here demonstrates that the only two requirements for ripple-pattern formation are an asymmetric internal biochemical limit cycle whose phase controls cellular reversals and polarized contact signaling, i.e., head-to-head contacts induce stronger resetting of the limit cycle phase than do head-to-tail contacts.

Experimental Results

To analyze rippling in greater detail, we developed a monolayer culture in which individual cells can be labeled and tracked in differential interference contrast movies. The monolayer culture is significantly different from the submerged culture developed by Welch and Kaiser (13), where the depth of the colony was more than one cell thick. Rippling occurs within a relatively narrow range of cell densities in both monolayer and multilayer cultures; however, in the latter, cells at different levels appear to move more or less independently. In the monolayer culture, individual cells can be counted along with interacting partners, allowing us to study how cells reorganize during and between collisions, because ripples span only three to four cell lengths.

M. xanthus colonies are multilayered, forming tiers of cells that move more or less independently. During fruiting-body formation, cells stream into large aggregates that later sporulate. However, ≈20% of the cells do not aggregate but remain as peripheral rods, a monolayer of cells behind and between the fruiting bodies (15). Ripples form in this monolayer ≈24 h after placing cells under starvation conditions and disappear at ≈72 h. During the ripple phase, cells almost never lose contact with their neighbors or with the underlying agar layer. The ripple waves are generally oriented toward nearby fruiting bodies (16) (see also supporting information, which is published on the PNAS web site). Fig. 1 shows two frames from a movie (that can be found in supporting information) of colliding waves.

Fig. 1.

Ripples in the monolayer culture. (a) Between collisions (differential interference contrast image). (b) At the moment of collision. Center lines of the waves are labeled with white lines and their directions of motion with arrows. (c) Fluorescence image corresponding to b. The figures are frames from movies of the waves that can be found in the supporting information.

At low resolution in both monolayer and multilayer cultures, two sets of parallel waves approach each other and then appear to interpenetrate, with the leading row of cells partially inter-digitating while still remaining in the monolayer. Presumably, this process is accompanied by deformation of the cell body or extracellular fibril material. Tracking of individual cells revealed that cells do not stay in one wave but reverse direction during each wave collision, exhibiting little net motion over many oscillation periods. Therefore, we refer to these waves as “accordion waves.” We are not aware of any similar phenomenon in biology, chemistry, or physics.

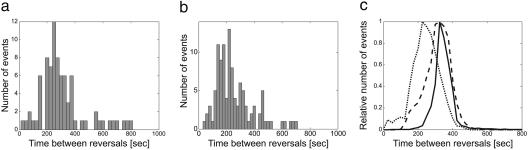
Fig. 2 gives a statistical profile of the behavior of cells participating in accordion waves versus those outside the ripple region. The distribution of times between reversals of individual cells in the monolayer culture shows a single-mode (Fig. 2a) in contrast to a bimodal distribution in the multilayer culture (13). Moreover, the monolayer culture showed only a small decrease in the width of the distribution in ripples compared with the cells in regions without ripples (see Fig. 2 a and b). Thus, differences in reversal times do not distinguish rippling from nonrippling cells.

Fig. 2.

Statistics of cells participating in waves. (a and b) Experiment. Distributions of the times between reversals for 24 cells tracked for 30 min. (a) Cells participating in ripples, 260 ± 144 sec. (b) Cells from an area of the same colony without ripples, 262 ± 137 sec. (c) Computations. Dotted line, the time between reversals (period) before ripples form; dashed line, the time between reversals in the ripple phase; solid line, the distribution of half-times between density maxima in formed waves measured at a single point in space as a function of time.

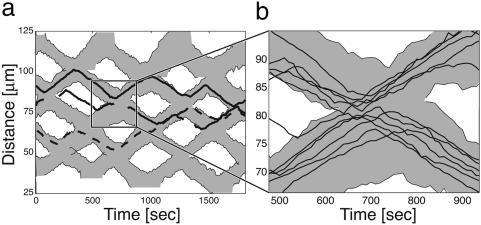
In the monolayer culture, one can track the positions of individual cells within a wave, as shown in Fig. 3 (compare with figure 3 in ref. 17). Between collisions, a wave is a monolayer stripe of cells ≈3-4 cell-lengths wide, with all of the cells moving synchronously in the same direction. When waves collide, the cells in the first row penetrate <1 cell length into the opposite wave before reversing. These reversed cells initiate a wave of reversals going back through the ripple, so that practically all of the cells reverse quickly after the first row reverses.

Fig. 3.

Space-time trajectories of cell centers (as they are visible in a microscope). (a) Space-time trajectories of three sample cell centers relative to the wave edge; each cell is ≈5-μm long. Most of the time, cells reverse at each collision; however, some cells occasionally switch waves (dashed line). (b) Detail of the collision region. Most cells stay with the wave they came from, rarely crossing the cell tracks of the oncoming wave.

This process is illustrated by a movie that can be found in supporting information on the PNAS web site. Because very few cells penetrate into the oncoming wave, most cells in the posterior rows never encounter the oncoming wave. The reversals happen very fast, as can be shown by a simple quantitative measure. From visual observation of recorded movies, one can count the number of collisions (i.e., the number of opposite-moving cells with which each cell comes in contact) between two successive reversals. Indeed, it appears that only three to four head-to-head encounters of a cell are sufficient to trigger a reversal.

Before a collision, the cells in a wave appear to be closely packed, covering the entire surface. However, as can be seen from Fig. 3, and the estimated distance between the centers of lateral neighbor cells in the Supporting Movies, the cell density in the middle of a collision is nearly double the initial density, even though cells do not detach from the monolayer, suggesting that the apparent diameter of cells is easily “compressed,” which could be a consequence of deformation of the cell body or the extracellular fibril material. Statistics on many trajectories such as those shown in Fig. 3 show that the gliding velocities of the cells is nearly constant; there are no pauses or obvious reduction in speed during collisions, even when a cell is surrounded by many cells moving in the opposite direction. This finding suggests that the A- and S-motility engines driving the cells are powerful enough to penetrate through the wall of opposite-moving cells, and that the decision to reverse is a signaling event unaffected by the mechanical impedance offered by other cells. The waves reflect from one another with no noticeable phase shift (Fig. 3); thus, without observing individual cells, the illusion that the waves pass through one another is nearly perfect.

The entire mass of rippling cells appears remarkably synchronous, so that the cell density on the plate changes from a surface-filling monolayer to zero with almost no transition region (Fig. 1). Occasionally, cells stray from their wave but are promptly absorbed by the next wave they encounter (Fig. 3). Between collisions, all of the cells in a wave move at the same velocity and, so, do not change their relative positions. Only during a collision are the cells reshuffled, and their new positions appear random. Thus the distance traversed by individuals varies significantly, despite how well the waves are synchronized (see Fig. 2 and the discussion below).

Modeling Myxobacteria Morphogenesis. We constructed a computational model to describe the behavior of the myxobacteria as a tool to explore the mechanisms underlying the ripple phase. The model is based on two assumptions, both supported by observations. First, isolated bacteria glide back and forth autonomously. This finding implies that there is an internal biochemical cycle that controls periodic reversals. This notion is strengthened considerably by the recent observation that FrzS, an essential protein for S-motility swarming, oscillates between the cell poles in synchrony with cell reversals (18). Second, a cell colliding “head-on” with an opposing cell alters the phase of its reversal cycle. This contact signaling provides the mechanism that coordinates the cells in the ripple phase.

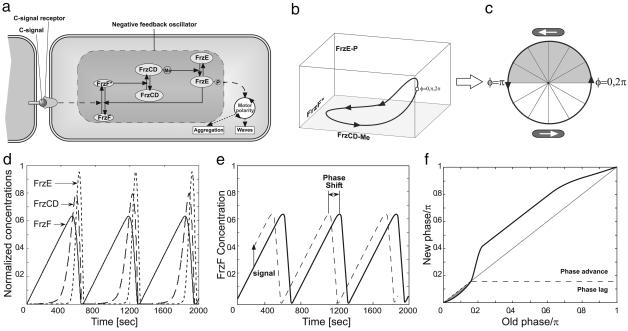
Based on these assumptions, we constructed an agent-based model of bacterial behavior consisting of two components. The first component models the external motion of cells and their interactions with neighboring cells. Each cell is located by its coordinates in the plane and its direction of motion. The propulsion force is opposed by frictional drag forces. Newton's laws of motion are used to compute the cell trajectories. The second component models the internal biochemical cycle that controls cell reversals and whose phase is altered by head-to-head cell collisions. Although the exact nature of this cellular clock is not critical, we used the Frizilator model proposed in ref. 19 (see Fig. 4). In the supporting information, we provide details of each of these components and show how they are integrated into a computational model that differs significantly from models proposed heretofore. In addition, we show several simplified versions of the biochemical clock to demonstrate which properties of the Frizilator model are required and which are not.

Fig. 4.

Frizillator model. (a) Schematic diagram, showing the proteins and pathways involved. (b and c) Limit cycle in concentration space for the Frizilator mapped onto the phase circle 0 ≤ φ ≤ 2π. (d) Dynamics of relative concentrations of active forms of all participating proteins, i.e., ratios of the concentrations of FrzF^*, FrzCD-CH₃, and FrzE-P to the inactive concentrations of these proteins. (e) Schematic representation of changing the phase clock by signaling used to build the resetting map of the Frizilator. Here, the time-dependence of relative FrzF^* concentrations is shown. A signal of the same amplitude was applied at different times, and, after a certain period, the position of the maximum of FrzF^* concentration relative to the unperturbed position was measured. Speed-up or delay was converted to phase shift by dividing the time change by the period and multiplying by π. (f) The resetting map of the Frizilator plotted with a signal amplitude of 0.15. This map was plotted with the origin at a point where the sensitivity crossed zero from positive to negative.

In the simulations, we used the parameters determined independently from experimental data, where possible. The values of those parameters not determined directly from the experiments were optimized to fit the properties of the waves. The exact parameter values are listed in the supporting information. If the simulations started with randomly oriented cells, the cells first aligned at an arbitrary angle before ripples formed. Therefore, we initiated most simulations with randomly located but prealigned cells. One of the principal conclusions of the model is that, to generate the ripple phase, intercellular signaling must be asymmetric: Head-to-head collisions deliver a stronger phase-resetting signal than do head-to-tail collisions; see further discussion below.

Computational Results: Spatial and Temporal Synchronization in the Ripple Phase. Fig. 5 shows a snapshot from a movie of the waves at the moment of collision computed from the model described above. The amount of phase advance per collision wasestimated from the experimentally observed number of collisions required to trigger a reversal. The reversal time distribution (i.e., the biochemical-clock speed) of individual bacteria is quite variable (20). Moreover, because of the small number of collisions, the variability in the time between reversals increases significantly (to the level shown in Fig. 2 a and b; see the discussion below for the role of different effects in contributing to variability). Thus, it is surprising that the waves that are organized by the collision-induced signaling are so well synchronized. The model provides an explanation for this puzzle.

Fig. 5.

Computed waves at the moment of wave collision. The simulations were performed by using the equations of motion described in the supporting information and the Frizilator model for the internal clock. Each line segment represents a cell characterized by its position and orientation, plus three concentrations of the active forms of the Frz proteins.

As mentioned above, experimental observations show that only three or four head-to-head collisions are required for a cell to reverse its direction, meaning that each collision leads to a significant change in the clock phase. However, the number of collisions varies dramatically from cell to cell, constituting a significant fraction of the randomness in the system. Thus, although the high variance for cells in the preripple phase is reduced by the synchronizing effect of wave collisions in the ripple phase, there still remains considerable variance in phase and space between cells in the ripple phase.

The statistical effects of the synchronization process are shown in Fig. 2c. Here, the clock speed for individuals in rippling and nonrippling phases is represented in the distributions of the time between reversals for both the experiments and the model. The average density of the cells is represented by the half-time between the local maxima of the right-(or left-) going cells at a single location. To plot the histogram, the data were collected at different points of the plane and at different times. The figure shows that the variance in clock speed does not change dramatically during the synchronization process. On the other hand, the average density synchronizes, even at very high noise levels (a detailed discussion of the role of noise in the model is given in supporting information). The resulting waves are very stable and uniform, even though the individuals are being actively reshuffled inside the waves. The wavelength is λ ≈ 2 〈v 〉 〈τ 〉, where 〈v 〉 is the mean cell speed, and 〈τ 〉 is the mean time between reversals (17, 21).

These observations on colliding waves show that discretization effects are important, making an agent-based approach more suitable for modeling this phenomenon. Mean-field models represent phase and spatial variance by adding noise terms to the equations of motion (17, 21-24), generally reflecting the cumulative effect of many collisions, each with a small effect on the phase. Another advantage of agent models is the possibility of incorporating a complex multivariable biochemical cycle, or a more complex phase clock, into each bacterium; this incorporation is very difficult with a mean-field model. At the other extreme, cellular automata models cannot simulate small directional changes and, so, crudely discretize both space and time (25-27). The advantage of these models is that they compute very quickly. The agent model we construct here treats spatial location and time as continuous, making it possible to reduce both time and space steps to arbitrarily small increments. We also constructed a mean-field model as a link between our agent-based model and previous mean-field models. The mean-field model can successfully reproduce some, but not all, of the collision process, as discussed in the supporting information.

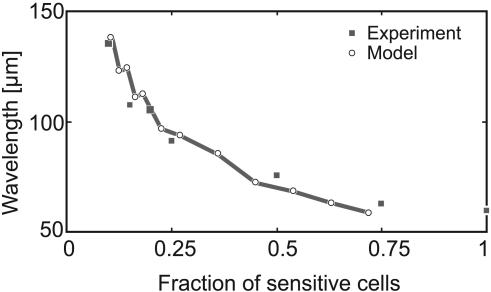
An experiment unrelated to the monolayer culture provides a quantitative test of the model. Wild-type cells were diluted with csgA^- mutants that can bind C-signal but are incapable of signaling themselves (28). Thus, the mutant cells act as a “sink” for C-signal, so adding them is equivalent to decreasing the cell density of wild-type (sensitive) cells. Fig. 6 shows that the ripple wavelength decreases roughly inversely to the fraction of wild-type cells, and the model presented here reproduces this trend closely. Simulation of this experiment requires that the phase-resetting map be asymmetric; i.e., the phase retardation or refractory period after a collision is smaller than the phase advance period after the collision (see Discussion and the supporting information for details).

Fig. 6.

Modeling the dilution experiment. Diluting wild-type bacteria with nonsignaling csgA^- mutants increases the wavelength as the fraction of wild-type (sensitive) cells decreases (data from ref. 14). Squares, data; circles, computed points.

To summarize, the model confirms what the experiments demonstrate: that the ripples are stabilized because of the following sequence of events. When the first rows of moving cells collide head-on, some cells penetrate a short way into the oncoming wave. Most of the cells in the first row reverse, and their head-on collisions with the next row trigger those cells to reverse, because they are close to their spontaneous phase anyway. This process repeats, so that a fast backward wave of reversals, coupled with some interdigitation, compacts the wave, canceling the spread accumulated during the forward motion; stragglers are absorbed into the reversed wave as well. The key ingredients are (i) asymmetric collision signaling, (ii) few collisions between reversals, and (iii) some overlap and/or compressibility of individual bacteria.

Discussion

In this paper, we studied both experimentally and computationally the accordion waves observed in M. xanthus during fruiting-body formation. These waves are unusual, in that they appear to interpenetrate when they collide but actually reflect off one another, so that each wave crest oscillates back and forth with no net displacement. To analyze the pattern of cell movement, we focused our studies on peripheral rods, a monolayer of cells behind and between the fruiting bodies, which form ripple waves from ≈24-72 h after starvation on an agar surface (note that these are not the only conditions for rippling). High-resolution differential interference contrast microcinematography of the monolayer culture made it possible to label and track the positions of individual cells within colliding waves, allowing us to track individual cells as they interacted with other cells. Using this approach, we made several observations on the coordinated cell movements observed in rippling waves: (i) Cells were observed to reshuffle within the wave, but they usually did not leave the wave; (ii) cell density did not change very much within a wave; (iii) only the leading row of cells in a wave penetrated into oncoming waves; thus, only cells at the wave front triggered the other cells in the wave to reverse; (iv) very few (three to four) head-to-head cell collisions were sufficient to trigger a cell reversal; and (v) the distributions of reversal times for rippling and nonrippling cells were not very different. These observations posed a puzzle: What distinguishes rippling from nonrippling cells?

The monolayer cultures described here differ from the multilayer cultures described in ref. 13. In both cultures, ripples arose in only a narrow range of cell densities. In the multilayer cultures, cells moved within the soft slime gel such that they appeared to remain at a certain focal depth, although the path of individual cells was difficult to follow. The monolayer culture permits one to easily distinguish individual cells and to follow the interactions of these cells with neighbor cells. Moreover, the ripple wavelength was reduced, making the interaction between waves a significant fraction of the entire process and reducing the dispersion that takes place between wave collisions.

A crucial ingredient for the model to produce waves is that collision signaling be asymmetric. That is, cells colliding head-to-head signal more strongly than do cells contacting head-to-tail. This asymmetry can be explained by the unequal status of the cell poles: The forward poles are grappling with type IV pili and, so, can draw one another into very close apposition, sometimes even contacting one another's outer membrane (29). The trailing pole, however, is secreting slime that may present a considerable barrier to direct contact, so that the strength of contact signaling is weaker. Another factor can be that the engines of two cells working in opposite directions are required to push through the fibril layer enveloping the cells. The necessity for asymmetric signaling is consistent with the known requirement that both A- and S-motility systems be operating to pass through the ripple phase (9, 12, 30).

Because the monolayer waves were observed only in isolated patches around incipient fruiting bodies, the periodic movements must be governed by an internal reversal clock that controls directional movements. This finding is in agreement with theoretical studies that demonstrate that such an internal cycle is both necessary and sufficient for wave formation (17, 21-24), raising two fundamental issues: What is the biochemical nature of the clock, and how are the clocks in neighboring cells synchronized to produce the ripple waves? In this work, using our experimental observations and mathematical modeling, we show that the wave patterns may arise because of the following three cellular properties.

1. Each cell contains a periodic biochemical cycle that controls when cells reverse their gliding direction. The cycle need have only the property that it has an asymmetric wave form, meaning that, in the absence of signaling, the wave form of the component affected by signaling (FrzF in the model used here) is asymmetric (the increase is slower than the decrease).

2. Cells signal by direct contact, and these contacts perturb the phase of the clock. The reversals induced by the clock are such that it is decelerated at earlier phases immediately after a collision signal and accelerated at later phases.

3. Intercell signaling is also asymmetric: Head-to-head collisions induce stronger signals than does head-to-tail contact. In other words, the effect a colliding cell produces on a test cell is strongest if the cells are moving in opposite directions.

In this study, we used the Frizilator model for the intracellular reversal clock, because it is based on the frz chemosensory system, which has been shown to control cell reversals (19, 31). This model is built on interactions and covalent modifications involving FrzF (a methyltransferase that may also be involved in signal input), FrzCD (a chemoreceptor which is subject to methylation and demethylation), and FrzE (a kinase/response regulator fusion protein). Oscillations would require a feedback loop, and several possibilities were suggested, although none have been verified experimentally (19). However, the model we constructed does not depend on the detailed biochemistry of the regulatory system; it is based only on the first property: that the clock is a limit cycle oscillation with an asymmetric wave form for the component receiving the contact signal (FrzF in the Frizilator model) (19). Cell contact has been shown to mediate intercell signaling and to effect the reversal cycle (9, 30, 31). The asymmetry of the clock wave form (property 1) is fulfilled by the Frizilator model. (Although simulations performed with a symmetric resetting map can produce waves under certain conditions, such a map cannot reproduce the dilution experiment; see Fig. 6.) The fact that the signaling retards the phase of the clock immediately after a reversal and advances it before the next reversal (property 2) is not a property of all limit cycle oscillators, but, without this property, there is no synchronization or waves in computations (data not shown). Additionally, the asymmetry in signal strength (property 3) is consistent with the observation that head-to-head collisions involve pili interdigitation that brings the outer membrane into direct apposition (29). Conversely, head-to-tail collisions entail penetrating the slime flow exuded by the posterior nozzles, which presents a considerable barrier to direct cell contact (11). Indeed, a model with symmetric collision signaling lacks a synchronization mechanism and does not produce ripples (see supporting information).

The agent model reproduces the major features of monolayer ripples and confirms the three requirements for rippling enumerated above. We also generalized the agent model to an approximate mean-field model to see whether the basic assumptions of the agent model could reproduce the ripple phenomena observed in the multilayer cultures (13) and explained by the previous mean-field model (21), as described in the supporting information, along with movies of the model and the experiments. The success of the mean-field approximation reinforces our confidence that we have identified the key components required for rippling in vivo.

Other models for the ripple phase have been developed to describe other aspects of the myxobacteria life cycle. Most have been cellular automata models (25-27, 32) or continuum models based on delayed-feedback mechanisms (33). The model developed here was tailored to our monolayer experimental system. However, several observations arising from the monolayer experiments, not documented here, greatly improve the prospects of generalizing the model to later stages of morphogenesis, including streaming aggregation and fruiting-body formation.

The experiments and the model touch on a broader theme of synchronization of cellular clocks. Coupled oscillators frequently lead to spatial pattern formation, as in Dictyostelium (34) and in somitogenesis (35). In many cases, synchronization occurs by means of diffusible signals whose secretion rate changes during the cycle (3, 36); by contrast, the oscillations in M. xanthus are synchronized by direct contact. Biological rhythms are generated by large populations of cellular oscillators, each of which contains variable periods. Nevertheless, the entire multicellular system can generate a clear and stable rhythm, with periods ranging from milliseconds for neural oscillators to ≈24 h for circadian rhythms. How can a population of noisy clocks collaborate to produce a synchronous coordinated clock? Strogatz and coworkers (3) revisited this puzzle theoretically for systems involving oscillators coupled by diffusion. The M. xanthus system synchronizes by a very different mechanism: Cellular communication occurs by signals resulting from direct cell contact, without exchange of phase information. Nevertheless, the precision of the waves exceeds the precision of the individual reversal clocks.

Finally, the pattern formation in M. xanthus is qualitatively different from wave phenomena observed in slime molds or in chemical systems. In the latter systems, patterns arise from a diffusion-driven spatial (Turing) instability, and colliding waves annihilate one another. By contrast, the myxobacteria waves are purely convective, and colliding density waves reflect off one another. When viewed from a distance, where only cell density can be perceived, the waves appear to pass through one another, analogous to soliton waves in various physical systems. However, this perception is an illusion, because the accordion waves are unlike any other in biology, chemistry, or physics.

Experimental Methods

The strain DK1622 (wild-type) (37) and DK10547, its derivative with GFP transcriptionally fused to the highly active pilA promoter (38), were used. The cells were grown in nutrient liquid media {CYE [1% Casitone (Difco/BD Biosciences), 0.5% yeast extract (EMD Biosciences, San Diego/Merck), and 8 mM MgSO₄ (EMD Biosciences) in 10 mM Mops buffer, pH 7.6 (Sigma)]} to midexponential phase (between Klett 50 and 100 or 2.8-5.6·10⁸ cells per ml). These bacteria were pelleted by centrifugation at 6,000 × g and resuspended in nutrient-deficient medium {CF [0.015% Casitone, 10 mM Tris (Sigma), 8 mM MgSO₄, 1 mM KPO₄ (EMD Biosciences)]} to 1,000 Klett density. The suspensions of DK1622 and DK10547 cells were then mixed in the proportion 19:1, respectively.

A 1-mm thick layer of 1.5% agar in CF medium was prepared on a glass slide by pouring hot liquid solution into the space between two washed and sterilized glass slides separated by a spacer. The glass slide with the gel layer on top was placed into a Petri dish with a 1.5% agar layer in it, so that the gel layer on the glass slide would not dry out. Cell solution (20 μl) was plated on the gel layer, placed back into the Petri dish, and incubated at 32°C for the indicated amount of time (see Experimental Results). Immediately before imaging, the glass slide was taken out of the incubator and covered with a #1 coverslip. All of the imaging was done at room temperature.

The images were taken by using an Applied Precision Delta-vision Spectris DV4 microscope. Pairs of fluorescence and differential interference contrast images were taken at 10-sec intervals for 30-40 min.

The images were postprocessed by image contrast enhancement and spatial band filtering. Individual cells were tracked semiautomatically by using home-made software, where manual tracking was required for tracking nonfluorescent cells or touching fluorescent cells. Cell positions were projected to the direction of the wave motion and their one-dimensional paths obtained in this way were high-frequency filtered before obtaining the reversals positions. For plotting cell positions relative to the wave fronts, only cells from a narrow strip along the direction of the wave motion were taken into account, and the wave-front position was obtained as cell-front positions averaged over the width of the stripe.