Effects of Disulfide Bonds on Folding Behavior and Mechanism of the β-Sheet Protein Tendamistat

Abstract

Tendamistat, a small disulfide-bonded β-sheet protein, and its three single/double-disulfide mutants are investigated by using a modified Gō-like model, aiming to understand the folding mechanism of disulfide-bonded protein as well as the effects of removal of disulfide bond on the folding process. Our simulations show that tendamistat and its two single-disulfide mutants are all two-state folders, consistent with the experimental observations. It is found that the disulfide bonds as well as three hydrogen bonds between the N-terminal loop-0 and strand-6 are of significant importance for the folding of tendamistat. Without these interactions, their two-state behaviors become unstable and the predictions of the model are inconsistent with experiments. In addition, the effect of disulfide bonds on the folding process are studied by comparing the wild-type tendamistat and its two mutants; it is found that the removal of either of the C11-C27 or C45-C73 disulfide bond leads to a large decrease in the thermodynamical stability and loss of structure in the unfolded state, and the effect of the former is stronger than that of the later. These simulation results are in good agreement with experiments and, thus, validate our model. Based on the same model, the detailed folding pathways of the wild-type tendamistat and two mutants are studied, and the effect of disulfide bonds on the folding kinetics are discussed. The obtained results provide a detailed folding picture of these proteins and complement experimental findings. Finally, the folding nuclei predicted to be existent in this protein tendamistat as well as its mutants are firstly identified in this work. The positions of the nucleus are consistent with those argued in experimental studies. Therefore, a nucleation/growth folding mechanism that can explain the two-state folding manner is clearly characterized. Moreover, the effect by the removal of each disulfide bond on the folding thermodynamics and dynamics can also be well interpreted from their influence on the folding nucleus. The implementation of this work indicates that the modified Gō-like model really describes the folding behavior of protein tendamistat and could be used to study the folding of other disulfide-bonded proteins.

INTRODUCTION

Protein folding, one of the most fundamental events in cells, is very complex and difficult to be characterized in detail. Although much progress, especially the energy landscape theory (1,2), has been made based on studies on some small and single domain proteins (3–5), this important problem has not been completely solved for more than 30 years. The folding processes of proteins involve a number of noncovalent weak interactions that result in contacts between the residues. However, many proteins, such as some membrane and secreted proteins in both bacteria and eukaryotes, fold into their native structures requiring the formation of disulfide bonds. Disulfide bonds are covalent interactions between residues, and are also vital for the stability and activities of the proteins (3–11). They can be formed in two kinds of compartments, namely the eukaryotic endoplasmic reticulum (ER) and the bacterial periplasm. When two sulfhydryl groups are close enough to each other in these two oxidative environmental compartments, oxidation of the thiol groups yields a disulfide bond. If the disulfide bond is of correct pairing, it can help to maintain the tertiary structure of the protein. Otherwise, incorrectly paired disulfide bonds can be recognized and broken up by certain special enzymes in ER or bacterial periplasm. This redox process involves the reaction between the thiol and the disulfide bond (namely thiol-disulfide bond exchange process) with the help of some special enzymes.

The folding process involving the formation of disulfide bonds is very complex. In the refolding experiment of the ribonuclease in vitro by Anfinsen and co-workers, different additive orders of oxidants and buffer lead to completely different final structures and activities (3). This indicates the delicate role of disulfide bonds in the folding process. Later, experiments showed that the folding process of some disulfide-contained proteins in vivo is much more complex because it requires not only the participation of oxidants but also the help of many special enzymes (12–14). For example, DsbA in bacterial periplasm can help to form disulfide bonds without ability of recognizing correct or incorrect pairing, and DsbC can recognize the incorrect pairing and cut it off by a thiol-disulfide exchange reaction.

Thus, it is difficult to explore such a complex folding process experimentally and theoretically. So far, people mostly focus on the refolding process without involving the rupture and reformation of disulfide bonds. If the denatured conformations of a protein are obtained by unfolding from native state in solvent without presence of reductant, the disulfide bonds remain intact. These denatured conformations act as the initial conformations of the following refolding process, and the disulfide bonds in these initial conformations are termed as preformed disulfide bonds. Thus the refolding only involves noncovalent interactions, and the formation process of disulfide bonds is avoided. The folding process becomes simple and could be clearly studied experimentally and theoretically. In fact, the folding of proteins with preformed disulfide bonds occurs in the unfolding-refolding experiments in the absence of reductant and oxidant. Such process is meaningful because it is shown experimentally that the formation of disulfide bonds is fast and the later folding process is mainly determined by the noncovalent interactions. As a matter of fact, in many previous works proteins with the preformed disulfide bonds were used, and many aspects related to the disulfide bonds have been obtained (15–21).

It has been shown in many experimental and theoretical studies that the preformed disulfide bonds can significantly increase the stability of the native structures of proteins. However, to the folding kinetics, there are two different opinions on the effects of the preformed disulfide bonds. One assumed that the preformed disulfide bonds can increase the folding rate because the number of possible conformations is decreased significantly (22,23), whereas the other argued that they can lead to kinetically trapped intermediates during the folding process and the folding becomes slow (24). Thus, which picture is more close to the reality is still an open question. Moreover, the folding processes of proteins with disulfide bonds mostly involve multiple pathways. The physical origins and biological behaviors of these pathways still need to be clarified.

To investigate the effects of disulfide bonds on the stability and the folding process of proteins, tendamistat, an α-amylase inhibitor from Streptomyces tenda, is a good model system. It is an all-β-sheet protein with 74 amino acids and has two disulfide bonds (25,26). It has been well studied in a number of experiments (16,17,19,20,27–30). It was found that protein tendamistat exhibits a two-state folding behavior that has not been found in any other disulfide-bonded proteins up to now. Interestingly, this two-state folding behavior cannot be eliminated by the removal of either disulfide bond (17). It is more intriguing that the removal of the C11–C27 disulfide bond that only circles 17 residues can lead to larger effects on the stability than the removal of the C45–C73 one that circles 29 residues (17,27). The transition state has also been studied. It is found that the first β-hairpin (the C11–C27 disulfide bond locating at its base) is formed in the transition state, and the regions of the outer strands near the C45–C73 disulfide bond are formed in the later folding process. Besides, the folding mechanism of protein tendamistat was investigated and a nucleation/growth mechanism was speculated by Kiefhaber et al. (17). Such a folding mechanism was also mentioned by Capaldi and co-workers (31). However, this mechanism has not been evidently proved yet. Although much insight has been obtained, there are still many questions to be answered. For example, i), why is protein tendamistat so special as to present a two-state folding behavior compared to other disulfide-bonded proteins? ii), How do we explain the specific effects of each disulfide bond on the thermodynamic stability and folding pathways? iii), Can the nucleation/growth mechanism describe the special folding process clearly as previously predicted?

Computer simulations, as a powerful theoretical method, can complement the experiments and provide detailed folding information related to the above-mentioned questions. The combination of experiments and computer simulations is essential for understanding the detailed folding mechanism and the roles played by disulfide bonds in the folding process. Computer simulations vary from simplified models to all atomic-level models. Although much detailed information of the folding process can be provided, the all atomic-level simulation is limited with timescale less than 1 μs, which is too short compared to the folding timescale (32,33). Only few studies concerning the effect of the disulfide bonds on the folding process are focused in the local fragments with preformed disulfide bond (34). Therefore, simplified models might be workable to simulate the folding of disulfide-bonded proteins for understanding the folding mechanism. Very recently, Cho and co-workers showed that a modified Gō-like model can be used to investigate the dimerization and aggregation with preformed disulfide bonds (35).

In this work, the detailed folding kinetics, pathway, and mechanism, as well as the effects of each disulfide bond on the thermodynamic stability and folding kinetics for the two-state folder tendamistat are studied using molecular dynamics simulations. A coarse-grained model with modified Gō-type interactions is used. The two-state folding behaviors of tendamistat and its two single-disulfide mutants are well studied. The folding transition of each mutant occurs at lower temperature than that of the wild type, corresponding to the decrease of the thermodynamic stability. The decrease in the thermodynamic stability of the C11A/C27S mutant is larger than that of the C45A/C73A mutant. This agrees well with the experimental observations (17,27). Furthermore, the detailed folding pathways of the wild-type tendamistat and its two mutants are found, which is consistent with the experimental findings. A nucleation/growth folding mechanism is clearly characterized, and the folding nuclei of the wild-type tendamistat and its two mutants are identified (36–38). This mechanism can well explain the two-state folding behavior. The effects of each disulfide bond on the thermodynamic stability and the folding processes are also interpreted from their influence on the folding nucleus.

The arrangement of this article is as follows. After the introduction, the model and methods employed in this article are described in “Models and Methods”. The two-state behaviors of the wild-type tendamistat and its two mutants, and the effects of the disulfide bonds are investigated in the following section. In “Folding Pathway and the Effects of the Disulfide Bonds”, the folding pathways of the wild type and its mutants are described in detail. The nucleation/growth mechanism is discussed in “The Folding Nucleus”. Finally, in “Conclusions”, the conclusions are given.

MODEL AND METHODS

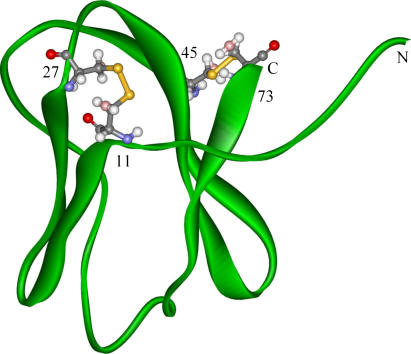
As shown in Fig. 1, a small all-β-sheet protein tendamistat is taken as the model protein in this work. It is an α-amylase inhibitor from S. tenda and consists of 74 amino acids (25,26). This small β-protein has two three-stranded antiparallel β-sheets named as S_I and S_II, respectively. The β-sheet S_I is composed of strand-1 (residues 12–17), strand-2 (residues 20–26), and strand-5 (residues 52–57), and S_II is composed of strand-3 (residues 30–37), strand-4 (residues 41–49), and strand-6 (residues 67–73). The N-terminal loop-0 (residues 5–8) interacts tightly with S_II by three hydrogen bonds. The notation of the first β-hairpin that is composed of strand-1 and strand-2 S_1–2 is S_1–2, as well as the second β-hairpin S_3–4 and other β-sheets. There are two disulfide bridges between Cys-11–Cys-27 and Cys-45–Cys-73. The Cys-11–Cys-27 disulfide bond locates at the base of the first β-hairpin, and the Cys-45–Cys-73 one connects two outer strand-4 and strand-6 of S_II. The three mutants of tendamistat are also studied in this work. These three mutants M₁ (C11A/C27S), M₂ (C45A/C73A), and M₃ (C11A/C27S and C45A/C73A) are obtained by substituting residue cysteine with residue alanine (A) or serine (S) as in the experiments. That is, in mutants M₁ and M₂, only one disulfide bond is kept, and in mutant M₃, both disulfide bonds are removed. In our theoretical study, the native structures of these three mutants are obtained by energy minimization based on the wild-type native structure; this takes into consideration in experiment that their native structures were observed to be similar to the wild type (28). The energy minimization is realized by using Amber software (version 7.0) (39) after the replacements of the related residues (17).

FIGURE 1.

The schematic representation (backbone model) of the structure of wild-type tendamistat. The cysteines are displayed with ball-and-stick model and the disulfide bonds are shown with yellow color. The first disulfide bond (Cys-11–Cys-27) is located at the base of the first β-hairpin (composed of strand-1 and strand-2). The second disulfide bond (C45– C73) connects the two outer strands-4 and strand-6.

The folding processes of protein tendamistat and its mutants are studied using the molecular dynamics (MD) simulations based on a Gō-like model, which was successfully applied in many works (40–50). However, in this work, the potential energy is modified as follows (48,49). Each residue in the model protein chain is represented as a single bead centered in its corresponding C^α position. The energy E_p of a certain conformation Γ (Γ₀ as its native state) is given by the expression:

(1)

In Eq. 1, r_i,i+1 denotes the distance between two consecutive residues, θ_i and φ_i represent the bond angle formed by three consecutive residues and dihedral angle formed by four consecutive residues at conformation Γ, respectively. The related quantities in the native state Γ₀ are represented as r₀, θ₀, and φ₀. Parameters K_r = 100ɛ, K_θ = 20ɛ, K₁ = ɛ, and K₂ = 0.5ɛ weigh the relative strength of each kind interaction. Here ɛ is the energy unit.

The term ξ₁ in Eq. 1 includes the native and nonnative contact interactions that take the form of Lennard-Jones potential as

(2)

Here, the native contact is defined when the distance between any pair of two heavy atoms from respective residues i and j is within 4.5 Å in the native structure of the protein. Thus, in any conformation, all contacts could be assigned as native or nonnative ones. For native contacts, we set ɛ₁(i, j) = ɛ and ɛ₂(i, j) = 0, and for nonnative contacts, ɛ₁(i, j) = 0 and ɛ₂(i, j) = ɛ. In Eq. 2, the parameter σ_ij is the distance between residues i and j at the native state for native interactions, while corresponds to the distance for nonnative repulsive interactions.

It is known that hydrogen bond is an important kind of interaction in proteins. Generally, in the Gō-like models, the hydrogen bonds are not taken into account explicitly but are implicitly included in the contact interactions that are approximately five times stronger than the van der Waals interactions. However, for many proteins, e.g., the protein tendamistat in this work, some hydrogen bonds are vital to the folding process and structural stability. Three specific hydrogen bonds (Ser-5–Arg-72, Leu-70–Ala-8, and Glu-6–Arg-72) existing between the N-terminal loop-0 and strand-6, are very important for the stability of protein tendamistat, especially when the C45–C73 disulfide bond is removed. It was clearly shown that strand-6 is held in place by the N-terminal arm and these hydrogen bonds keep the protein stable even after the C45–C73 disulfide bond is removed by residue replacement (27).

The roles of these three hydrogen bonds cannot be implemented by the contact interactions in the general Gō-like model because the strengths of contacts scaled by ɛ is only about one-fifth of the hydrogen bonds. Previous study indicated that the hydrogen bonds can also be described with the similar form of the van der Waals force but the interaction strength is ∼25 times stronger (51). Thus the interactions of hydrogen bonds can be characterized with the form of Eq. 2 when the parameter ɛ₁(i, j) and ɛ₂(i, j) are taken to be 5ɛ and 0, respectively. The interaction basin of a hydrogen bond is defined when the distance between each residue of the hydrogen-bond pair is <1.2 σ_ij. Out of this basin, the interaction of the hydrogen-bond pair is still considered the contact potential as discussed above. It is worthy of note that the folding behaviors of the mutants are distinctly different from the experimental results when the specific role of these three hydrogen bonds is not considered (see detailed discussion in the following section).

The covalent disulfide bond is formed between two thiol groups in each of the residue cysteines, and however, can be modeled as a virtual bond between the two beads of the related cysteines. Physically, such a form of disulfide bond must have more flexibilities than the two consecutive residues of the peptide bond. Because the formation and rupture of the disulfide bonds are not considered during our simulations for the folding and unfolding processes, a modification on the Gō-like model with disulfide bonds can be made. That is, the preformed disulfide bonds existed both in the initial state and the folding processes can be taken as a harmonic oscillation potential between a pair of cysteines. This form of disulfide bonds characterize well the strong interaction of each paired cysteines in nature as a term ξ₂ in Eq. 2

Here, the interaction strength K_s is taken to be 20ɛ, which can describe the flexibility of the related cysteines.

The Langevin dynamics is used to simulate the folding process (52–54). The motion equation includes terms of a damping with a proper friction coefficient γ, a random force F_r to balance the energy dissipation caused by friction, and the conformation force F_c = −∇_rE_P as follows

(4)

Here, and are the coordinate vector and the velocity, respectively. m is the mass (the mass of each residue is assumed to be same). F_r is obtained from the Gaussian distribution with a white noise spectrum and the standard variance related to temperature T as

(5)

where k_B is the Boltzmann constant, t denotes the time, and δ(t) is the Dirac δ-function. The equation of motion is numerically integrated using the velocity form of the Verlet algorithm (55,56). The integration time step is taken to be Δt = 0.005τ, where is a characteristic oscillatory time unit (a = 5 Å). The friction coefficient is taken to be γ = 0.2.

The specific heat is widely and successfully used to characterize the thermodynamic behaviors of the folding process (57–61). The curves of the specific heat versus temperature reflect the folding behaviors, i.e., a two-state folding corresponds to single transition peak and three-state folding to double transition peaks. In fact, the single transition peak is related to an overlapping of the collapse transition and the folding transition (58). The specific heat C_v and the free-energy F are calculated using the weighted histogram analysis method, which yields an optimal estimate of the density of states of the system and hence allows the calculation of relevant thermodynamic quantities (62,63). In details, the specific heat and the free energy are calculated based on 25 independent long-time runs at different temperatures (62,64).

TWO-STATE FOLDING BEHAVIORS AND THE EFFECTS OF DISULFIDE BONDS ON THERMODYNAMIC STABILITY

Previously, it has been shown that disulfide-bond contained proteins usually fold with multipathways. However, in a number of experiments, the folding and unfolding reactions of protein tendamistat (containing two disulfide bonds) were found to exhibit two-state behavior by Kiefhaber and co-workers (16,17,19–20). It was also shown that the removal of each disulfide bond has little effect on such behavior, but could lead to a large decrease in the thermodynamic stability. This decrease is larger for the removal of the C11–C27 disulfide bond than that for the C45–C73 one (17,27). In this section, some quantities (e.g., specific heat C_v, free-energy F, the structural similarity Q versus the time, unfolding time, and so on) based on the MD simulations are used to characterize the two-state folding and unfolding behaviors of the wild-type tendamistat and its mutants.

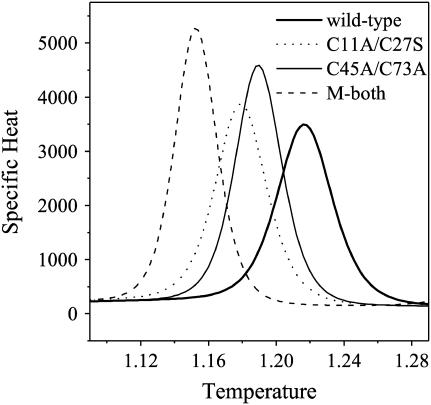
Fig. 2 shows the specific heat profile (C_v) as a function of temperature T for the wild-type tendamistat and its three mutants. There is only one main transition peak at temperature T = 1.217 for the wild-type tendamistat, at T_f = 1.179 for mutant M₁, and at T_f = 1.189 for mutant M₂, respectively, implying a two-state folding behavior as found in experiments (16). Here the temperature unit is ɛ/k_B and k_B is the Boltzmann constant. However, the peaks for the disulfide bond mutants shift obviously to the low-temperature range, which is well consistent with the experimental observations (17,27). These clearly elucidate that the removal of each disulfide bond has little effect on the two-state folding behavior, but considerably results in a large decreasing in the thermodynamic stability. Generally, this decreasing in the stability should be related to the removal of the disulfide bonds because their loop entropy, which is believed to be proportional to the loop size (65), is increased. Thus, for both mutants, the transition temperatures, i.e., T = 1.179 and T = 1.189, are smaller than that for the wild type. However, from the loop entropy, the transition temperature for M₂ should be lower than that of M₁ because the loop length is l = 17 for the later whereas it is l = 29 for the former. But this is not the case according to our simulations (Fig. 2) and the experiments. This cannot be explained simply by the loop entropy. From the detailed structure of M₂, it is known that the strand-6 in S_II is still held in place tightly by the N-terminal arm (loop-0, residues 5–8). Clearly, such a packing results from three hydrogen bonds between the loop-0 and strand-6, not from the C45–C73 disulfide bond that is removed for the M₂. Thus, the loss of stability due to the removal of the C45–C73 disulfide bond could be compensated and the region of S_II could still be kept intact, resulting in a transition temperature closer to that of the wild type.

FIGURE 2.

The specific heat C_v as a function of the temperature T. The transition temperatures of the wild-type tendamistat (thick solid line), the C11A/C27S mutant M₁ (dotted line), the C45A/C73A mutant M₂ (thin solid line), and the mutant M₃ removed both of the disulfide bonds (dashed line) are 1.217, 1.179, 1.189, and 1.152, respectively.

Differently, for M₁ the existence of these hydrogen bonds has no effect on the local structure S_I and the loss of the stability is mainly due to the removal of the C11–C27 disulfide bond. This disulfide bond (in the wild-type tendamistat) is located at the base of the first β-hairpin S_1–2, which acts as an important component for the folding nucleus. The removal of the C11–C27 disulfide bond changes the distribution of the nucleus (see the detailed discussion in the following section), which can decrease the barrier of the transition state and leads to the large loss of the thermodynamic stability. Thus, the folding transition of M₁ occurs at a much lower temperature than that of the wild-type tendamistat, so much as lower than that of the mutant M₂.

For the mutant M₃ in which both of the disulfide bonds are removed, the folding transition temperature shifts to a much lower value as T_f = 1.1526. Such a transition temperature is too low and beyond the foldable temperature region of the wild type. This means that the mutant M₃ cannot fold and yield native structure when it is settled at the temperatures in the foldable temperature region of the wild type. This agrees with the experimental observation that M₃ is unstable and no native structure can be found (17). It is worthy of note that in the temperature region lower than the folding temperature T_f = 1.1526 of the mutant M₃, the mutant is foldable and the folded structure is native-like, exhibiting obviously a two-state folding behavior from the simulations. However, such foldability for the mutant M₃ is artificial, and is only on the theoretical base and model related.

It is worth noting that when the above-mentioned hydrogen bonds are not considered, the folding processes of the wild-type tendamistat and its two single-disulfide mutants still exhibit two-state folding behaviors. However, the folding transition of the C45A/C73A mutant M₂ shifts to a temperature T_f = 1.171, which is lower than that of the C11A/C27S mutant M₁, i.e., T_f = 1.179 (here the transition temperature of M₁ shows no changes). Though this shift seems to accord with the theory of loop entropy, it is distinctly different from the experimental results and could not depict the structural specialty between loop-0 and S_II in reality. Therefore, these hydrogen bonds must be taken into account particularly due to their importance.

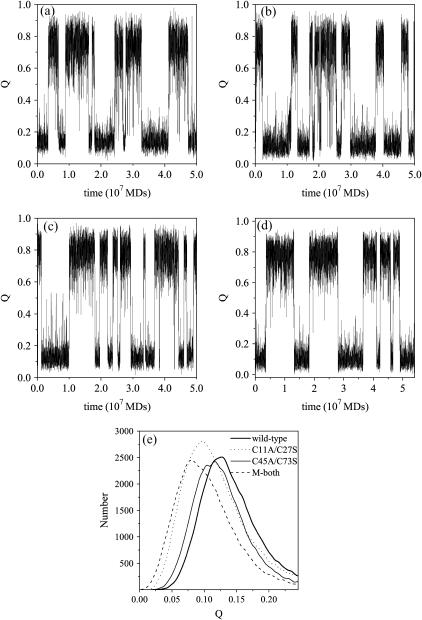
To display the two-state folding process clearly, we monitor the reaction coordinate Q, i.e., a fraction of native contacts, as a function of time (in unit of MD steps) near the folding temperature T_f. The two-state behaviors are shown obviously in Fig. 3, a–d, where the ensembles of unfolded state and the folded state are equally populated and no intermediates are observed. Removal of each or both disulfide bonds cannot have any effect on this two-state folding manner, but makes the structures of unfolded state more noncompact and dissimilar to the native state. Fig. 3 e shows the distribution of the structural similarity Q in the unfolded state for the wild-type tendamistat and its three mutants M₁, M₂, and M₃. The value of structural similarity at the peak of the distribution of unfolded state, namely Q_u, is used to characterize the structures in the unfolded state. The value of Q_u becomes small, implying that the structures in unfolded state are less native-like due to the removal of each disulfide bond. The difference of Q_u between the wild type and the mutant M₁ (or between the wild type and the mutant M₂, M₃) is ΔQ_u = 0.033 (ΔQ_u = 0.02, 0.048). This exhibits that the removal of the C11–C27 disulfide bond makes the structures in the unfolded state less native-like than those of the C45–C73 one. This is consistent with the increasing in Δm_eq = −0.55 for M₁ and Δm_eq = −0.42 for M₂ measured experimentally. Here reflects the changes in solvent-accessibility surface area that is proportional to m_eq upon unfolding processes. The increase of m_eq for mutants M₁ and M₂ indicates a loss of structure and a higher degree of solvent accessibility in the unfolded state (17). Lacking the two disulfide bonds, the unfolded state of the mutant M₃ becomes extraordinarily disordered and the value of Q at the center of the unfolded conformations is only 0.08.

FIGURE 3.

(a–d) The trajectories of the reaction coordinate Q as a function of time (in unit of 10⁷ molecular dynamics steps), which are obtained from the typical simulations around the respective folding temperature. Each of the model protein has equal probabilities to be found in the unfolded state and in the folded state, which exhibits the two-state folding behavior clearly; (a) for the wild-type tendamistat, (b) for the mutant M₁, (c) for the mutant M₂, and (d) for the mutant M₃. Fig. 3 e shows the distribution of the native contact in the unfolded states for the wild-type tendamistat (thick solid line), the mutant M₁ (dotted line), the mutant M₂ (thin solid line), and the mutant M₃ (dashed line). Q_u is the value of Q at each of the peak of the distribution.

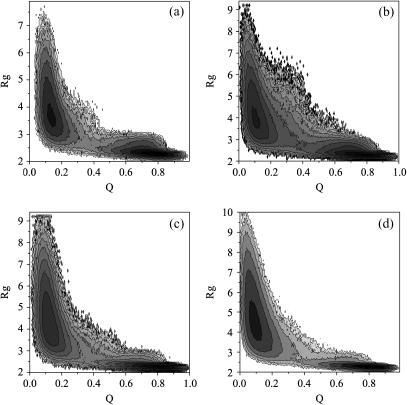
Furthermore, to obtain a better understanding of the two-state folding process and the effects caused by removal of single-disulfide bond, the free-energy landscapes are investigated in detail. Fig. 4, a–d, show the free-energy contours using the structural similarity Q and radius gyration R_g as reaction coordinates for the wild-type tendamistat and its three mutants at their folding temperatures. The free-energy landscape is smooth and funnel-like, indicating a very stable two-state folder sliding from the unfolded state into the folded state (16,66,67). The free-energy minimum of the unfolded state for the wild-type tendamistat is located around Q = 0.10 ∼ 0.17 and R_g = 3.1 ∼ 4.1, while the folded state is situated around Q = 0.64 ∼ 0.90 and R_g = 2.1 ∼ 2.5 (Fig. 4 a). The free-energy barrier, located between these two minima, is responsible for the thermodynamic stability. There is no kinetic intermediate in the folding process, which is extraordinarily particular for the disulfide-bonded proteins. Moreover, the experiments found that there is no obvious chain collapse in the folding process (16), which can also be validated in the free-energy landscape. For the three mutants M₁, M₂, and M₃, the free-energy landscapes also exhibit the obvious two-state folding features, respectively. The removal of each or both disulfide bonds cannot change such folding manner (consistent with the above discussion), but can change the structural characters of the two minima of the free energy, especially for the unfolded state. The removal of the C11–C27 disulfide bond makes the base of the first β-hairpin open, and increases the solvent accessibility of the ensemble of unfolded state. This can be shown from the position of center of the unfolded state in the free-energy plot, the values of the Q and R_g for unfolded state of the C11–C27 mutant change to Q = 0.1 and R_g = 4.1, comparable to Q = 0.15 and R_g = 3.5 for the wide-type (Fig. 4 b). For the case of the removal of the C45–C73 disulfide bond, the effects are less than that of the C11–C27 one (Fig. 4 c). When both of the disulfide bonds are mutated, the value of Q and R_g change to 0.08 and 4.8, respectively, which corresponds to the extraordinary disordered unfolded state (Fig. 4 d).

FIGURE 4.

Free-energy contour maps as the function of two reaction coordinates: the structural similarity Q and the radius gyration R_g near their respective folding temperatures. The two-state folding processes can be clearly exhibited in the free-energy landscapes of the wild-type tendamistat (a), the mutant M₁ (b), the mutant M₂ (c), and the mutant M₃ (d). The removal of each single-disulfide bond does not take any effects to the two-state folding behavior (refer to the text for more detailed discussion). The free-energy difference between adjacent contour lines is 1.0 k_BT.

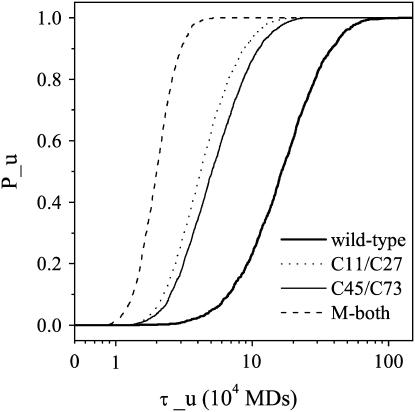
The profiles of the probability of the unfolded state P_u versus the unfolding time (τ_u) at high temperatures 1.2T_f are shown in Fig. 5 for the wild-type tendamistat and the two single-disulfide mutants, respectively. From these curves, it can obviously be seen that the unfolding process also follows the two-state model. Each removal of the disulfide bond can lead to large decrease of the stability, and increases the unfolding rate distinctly. This is consistent with the experimental results that the unfolding rate of the C11A/C27S mutant is faster than that of the C45A/C73A mutant and the mutant M₃ has no stable structure and unfolds completely in a very short time. The C11–C27 disulfide bond circling a loop of 17 residues leads to more effects on the stability than those by the C45–C73 disulfide bond circling a much longer loop of 29 residues.

FIGURE 5.

The probabilities of the unfolded state P_u as a function of the unfolding time τ_u (in unit of 10⁴ molecular dynamic steps) for the wild-type tendamistat (thick solid line), the mutant M₁ (dotted line), the mutant M₂ (thin solid line), and the mutant M₃ (dashed line). Each plot is obtained from the average on >5000 unfolding simulations.

FOLDING PATHWAY AND THE EFFECTS OF THE DISULFIDE BONDS

Experimentally, the folding behavior has been investigated intensively and many interesting features for the wild-type tendamistat and its mutants M₁ and M₂ have been shown (16,17,19,20,29). However, up to now, the detailed folding pathway and mechanism are still unclear and require theoretical interpretation. In this work, we calculate 〈Q_i〉 as a function of the structural similarity Q to show the detailed folding process. Here 〈Q_i〉 is an average formation probability of the i-th native contact over the set of all conformations with a given value Q collected in all the simulations performed at a certain temperature (68):

(6)

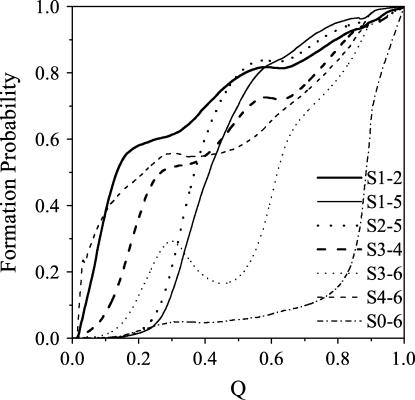
where each value is averaged over >500 different folding trajectories. Moreover, to simplify the notation, we indicate 〈Q_S1–2〉 to represent the formation probability of the total native contacts in the β-hairpin S_1–2, which is composed of strand-1 and strand-2. Other probabilities for S_3–4, S_1–5, S_2–5, S_3–6, S_4–6, and S_0–6 are similar to 〈Q_S1–2〉. The formation of each local region, clearly exhibited in the curves of these probabilities, is used to characterize the whole folding pathways in detail.

Fig. 6 shows the formation probabilities of different parts of the wild-type tendamistat. The first β-hairpin S_1–2 forms very fast and most of the native contacts (>60%) in S_1–2 have been formed in the very early folding process (Q < 0.1). The formation of the other β-hairpin S_3–4, which is mostly formed before the transition state is similar to that of the S_1–2. Here, the transition state corresponds to the minimal region with 0.4 ≤ Q ≤ 0.5 in the histogram of the distribution of Q values near the folding temperature. The formation processes of these two β-hairpins accord well with the experimental observation that the formation of β-hairpins occurs in the earlier folding process and completes in the transition state (16,69,70). Since the C11–C27 disulfide bond tightly encloses the base of S_1–2, the formation of S_1–2 is speeded up and is faster than that of S_3–4. It is noted that such early formation of β-hairpins also agrees with a general picture of the folding processes for the β-sheet proteins (31).

FIGURE 6.

The formation probability of different parts of the wild-type tendamistat as a function of the reaction coordinate Q. Different curves correspond to the formation trajectories of different parts: the first β-hairpin S1–2 (thick solid line), β-sheet S1–5 (thin solid line), β-sheet S2–5 (thick dotted line), the second β-hairpin S3–4 (thick dashed line), β-sheet S3–6 (thin dotted line), β-sheet S4–6 (thin dashed line), and the region S0–6 between the N-terminal loop0 and the strand-6 (thin dash-dotted line).

In Fig. 6, it is found that most of the contacts near the outer β-sheet S_4–6, which is connected by the C45–C73 disulfide bond, are formed very quickly in the early folding process. It is also found that the β-sheet S_3–6, an important component of S_II, undergoes a formation/rupture process before reaching its completely folded state. Due to the tight connection of S_4–6 and the earlier formed β-hairpin S_3–4, ∼30% native contacts of S_3–6 are formed in the unfolded state, which makes S_II more compact. However, these formed contacts in S_3–6 prevent the strand-5 from getting across S_3–6 to interact with S_1–2. The two β-sheets S_1–5 and S_2–5 can be formed quickly only when the formed contacts in S_3–6 break up gradually. (The unbroken contacts of S_3–6 in the transition state are found to be very important for the whole folding process (will be discussed later)). This process corresponds to the rate-limiting step, namely the transition state barrier for the whole folding process.

After the time-limiting step, the rest folding process is accomplished quickly without any large barrier. The contacts in S_0–6 between the N-terminal arm loop-0 and the strand-6, begin to form in the final stage of folding (Q > 0.8) when all of the other parts are almost completely formed. However, these last formed contacts play an essential role to the stability of the tendamistat because the N-terminal loop-0 situates like an arm on the outside of S_II and three hydrogen bonds interact strongly between each other as discussed above. The formation of this part also symbolizes the accomplishment of the total folding process.

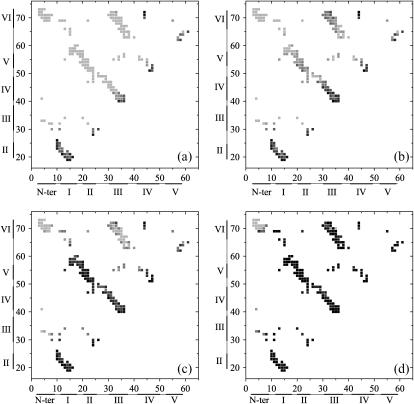
The detailed formation probabilities of each native contact at four typical moments in the folding process are shown in Fig. 7, a–d. Here four moments are: 1), the earlier folding stage at Q = 0.15; 2), near the beginning of the transition state at Q = 0.3; 3), right after the transition state at Q = 0.5; and 4), the late folding stage at Q = 0.8, respectively. The folding pathway of the wild-type tendamistat can be qualitatively observed from this evolution of contact maps. In Fig. 7 a, most of the native contacts of S_1–2 and S_4–6 are formed at Q = 0.15, while the other regions including the β-hairpin S_3–4 remain completely unstructured. The fast formation of S_1–2 is mainly due to the tight connection by the C11–C27 disulfide bond. Fig. 7 b shows that most of the native contacts of S_3–4 and some native contacts of S_3–6 are formed before the transition state, while other regions remain unstructured. Fig. 7 c illustrates that at the moment of the end of the transition state, the β-sheets S_1–5 and S_2–5 are completely formed, while most of the formed contacts of S_3–6 in Fig. 7 b are broken up. The wild-type tendamistat almost reaches its folded state except S_0–6 as clearly indicated in Fig. 7 d.

FIGURE 7.

The formation probability of each native contact of the wild-type tendamistat at the four typical moments in the folding process that the moment of Q = 0.15 (a), the moment of Q = 0.3 (b), the moment of Q = 0.5 (c), and the moment of Q = 0.8 (d). Different colors indicate different values from 0 to 1, as quantified by the color scale, i.e., the darker of the color corresponds to the bigger of the value of the formation probability.

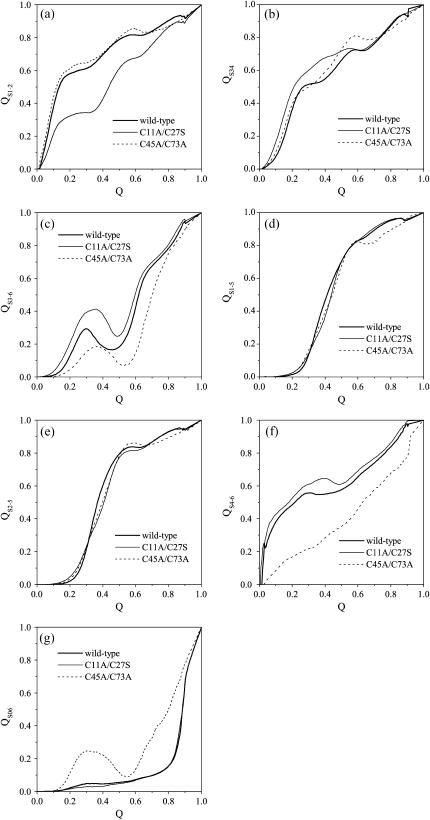
The formation probabilities of different parts versus the structural similarity Q for the wild-type tendamistat and its two single-disulfide mutants M₁ and M₂ are shown in Fig. 8, a–g. The removal of the C11–C27 disulfide bond leads to a large loss of the structure of S_1–2 in the unfolded state, and only ∼35% native contacts are formed in the early stage of folding at Q = 0.15 (see Fig. 8 a). Most of the contacts lost in the unfolded state due to the removal of the C11–C27 disulfide bond are found to be formed in the transition state. These contacts make S_1–2 solvent inaccessible in the transition state. This agrees well with the results obtained from experiments (17), and also with a study on the folding behavior of a single segment of the β-hairpin S_1–2 based on the all-atomic MD simulations (34). It is also shown in Fig. 8 a that the removal of the C45–C73 disulfide bond does not take any effects to the formation of this part.

FIGURE 8.

The formation probability of the different parts as a function of the structural similarity Q for the wild-type tendamistat (thick solid line), the mutant M₁ (thin solid line), and the mutant M₂ (dashed line). The different parts are presented, respectively, for S_1–2 (a), for S_3–4 (b), for S_3–6 (c), for S_1–5 (d), for S_2–5 (e), for S_4–6 (f), and for S_0–6 (g). These folding processes are simulated at the temperatures that are lower than their respective folding temperatures.

For the case of the second β-hairpin S_3–4 (Fig. 8 b), the removal of the C11–C27 disulfide bond enhances the formation probability thus 70% native contacts formed before the transition state. This probability is even larger than that of S_1–2, which is promoted by the loss of contacts in S_1–2. As a result, more than 40% native contacts of S_3–6 are formed before the transition state (Fig. 8 c). Thus, the rupture of these formed contacts in S_3–6, which is favorable for strand-5 getting across this broken part to interact tightly with S_1–2, becomes even more difficult. As shown in Fig. 8, d and e, the removal of the C11–C27 disulfide bond has a little effect on the formation rates of the β-sheets S_1–5 and S_2–5 compared to that of the wild type. This makes the formation of S_I even more time consuming and the folding of M₁ becomes slower (17). That is, the removal of the C11–C27 disulfide bond increases the formation time of these two β-sheets, which determines the folding rate of protein tendamistat. Such an observation quantitatively accords with the experimental result that a one-eighth folding rate for M₁ with respect to that of the wild type was found (17). Therefore, the first β-hairpin S_1–2 plays important roles not only in the thermodynamical stability but also in the folding rate.

On the contrary, there is no obvious influence of the removal of the C45–C73 disulfide bond on the early formation process of S_3–4 for the mutant M₂. However, strand-6 no longer interacts tightly with strand-4 in the unfolded state (Fig. 8 f), due to the removal of this disulfide bond. The released strand-6 can even form some contacts with the N-terminal arm loop-0 in the unfolded state (Fig. 8 g), which does not occur for the wild-type tendamistat and the mutant M₁. As a result, there are only ∼20% native contacts of S_3–6 formed before the transition state (Fig. 8 c), and these formed contacts can be broken up easily in the transition state. Thus, strand-5 can get across S_II easier than that in the case of wild type. Therefore, the formation of S_II becomes more difficult.

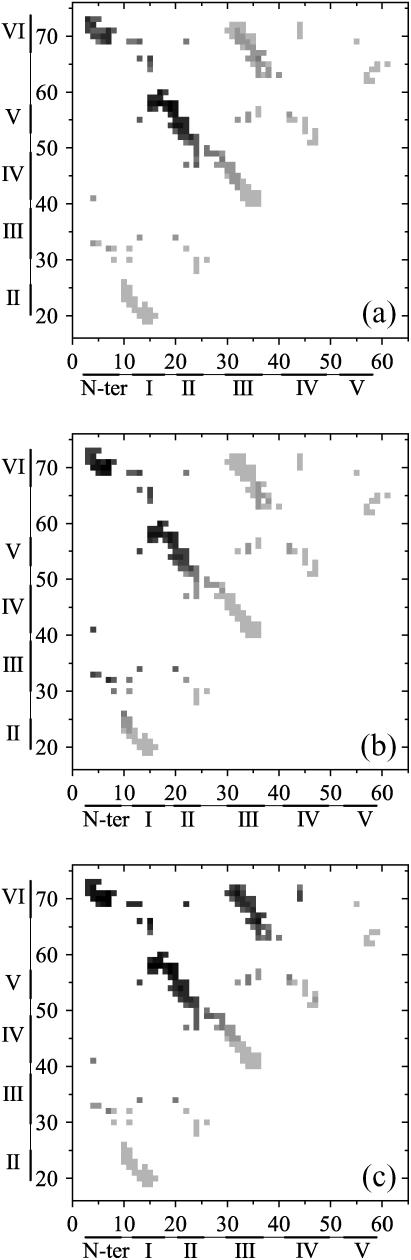
Folding rates of small proteins are strongly dependent on a factor termed as contact order (71). In addition, a good correlation between the separations of the contacts along the sequence and the average time of the first appearances of these contacts during the folding is found (72). The average time (τ_{i, j}) of the first appearance of contact between residues i and j can be used as a probe to study the folding pathways. In this work, such averaged times (τ_{i, j}) are shown in the contact maps to indicate the folding pathways for the wild-type tendamistat and the two mutants M₁ and M₂, respectively (Fig. 9, a–c). For each contact, τ_{i, j} is obtained by averaging >1000 different simulations. Fig. 9 a shows that the contacts of the β-hairpins S_1–2 and S_3–4 in the wild-type tendamistat, distributed in the diagonal of the contact map, are formed the earliest. This is consistent with the local contacts forming faster than the nonlocal contacts, and also with the results mentioned above. It is seen that the formation rate of S_1–2 is a little faster than that of S_3–4 due to the existence of the C11–C27 disulfide bond. S_3–6 seems to be formed faster than the β-sheets S_1–5 and S_2–5. However, this is not the case, because the time of the first appearance of contacts does not take into consideration the rupture and reformation of these contacts. The formation of contacts between S_1–2 and strand-5 is later than that of the hairpins. The largest sequence separations of the part S_0–6, located at the top left corner of the contact map, are the last formed part in our simulations. For the case of the mutant M₁ (Fig. 9 b), difference of (τ_{i, j}) between the two β-hairpins disappears due to the removal of the C11–C27 disulfide bond. As discussed above, this mutation increases the formation probability of S_3–6 before the transition state comparing to that of the wild type. This is obviously shown in Fig. 9 b. Moreover, the times of the first appearance of contacts in S_3–6 shown in Fig. 9 c also supports the result of the contact formation probability in Fig. 8 c because the removal of the C45–C73 disulfide bond makes the formation of the S3–6 more difficult before the transition state.

FIGURE 9.

The first appearance time τ_{i, j} of the i–j native contact averaged on 2000 simulations for the wild-type tendamistat (a), the mutant M₁ (b), and the mutant M₂ (c), respectively. The contact color from light gray to black represents the value of the first formation time changing from minimum to maximum gradually.

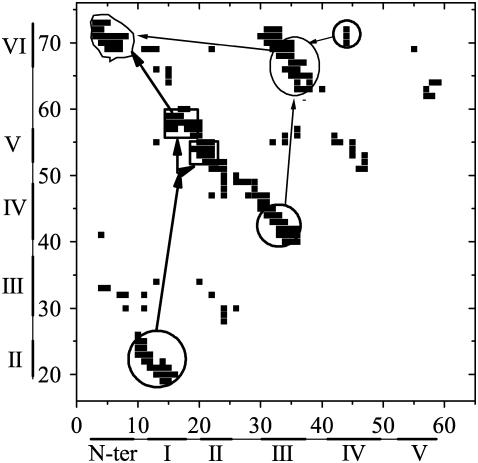
So far, from the various features mentioned above, we can obtain a detailed folding pathway as shown in Fig. 10. The two β-hairpins S_1–2 and S_3–4, situated in each of the three-stranded antiparallel β-sheets S_I and S_II, respectively, are formed in the earlier folding stage. S_1–2 folds faster than S_3–4, which is attributed to the tight connection of strand-1 and strand-2 by the C11–C27 disulfide bond. The interactions between S_1–2 and strand-5 are well established in the transition state, which occurs with most of the formed contacts in S_3–6 breaking up at the same time. Such an establishment corresponds to the rate-limiting step for the whole folding process, and this step can be considered as the nucleation process (will be discussed in the following section). Then, after the transition state, S_3–6 reaches its native conformation, indicating the formation of S_II. The last stage of the folding is the formation of the contacts between S_I and S_II with the N-terminal residues loop-0 covering tightly over the S_II like an arm. The folding process after the transition state occurs quickly without encountering any obvious energetic barriers.

FIGURE 10.

The simple description of the folding pathway for the wild-type tendamistat. The contacts inside the circle regions with thick lines are formed before the transition state; the ones inside the rectangular regions with thick line are formed in the TS; the ones inside the ellipse region with thin lines are formed in the later folding process except several key contacts are found to be formed in the TS; and the ones inside the irregular region with thin lines are formed in the last step of the whole folding process.

Comparing the two single-disulfide mutants with the wild-type tendamistat, all of the results exhibit that the mutation of each disulfide bond cannot change the overall folding mechanism. This is the reason that the single mutation of each disulfide bond cannot change the two-state folding behavior. However, for each mutant, there are some detailed changes in the folding pathway as discussed above and the removal of each disulfide bond can affect the main barrier caused by the formed contacts in S_3–6 in the unfolded state. That is, the removal of the C11–C27 disulfide bond increases the barrier, while the removal of the C45–C73 disulfide bond decreases the barrier. Thus, the related rate-limiting steps for M₁ and M₂ are changed to be dependent mainly on the formation of S_I and S_II, respectively.

THE FOLDING NUCLEUS

The folding behavior of a number of small two-state proteins follows a first-order transition between the unfolded state and folded state (73–76). Mostly, the dynamic process follows a nucleation/growth mechanism, with a slow rate-limiting step and then a rapid downhill folding to the native state (77,78–80). Previous studies showed that folding nucleus play an important role in the folding process. Proteins with similar structures but different sequences could have similar folding nucleus because the nucleus is found to be topologically dependent (37,74). Because protein tendamistat and SH3 domain are rich in β-strands and have similar secondary structures, Capaldi and co-workers predicted that protein tendamistat should also follow a nucleation/growth mechanism and the β-hairpins completely formed in the transition state may participate in the formation of the nucleus (31). Our results discussed in the above section actually imply that the folding pathways of the wild-type tendamistat and the two mutants M₁ and M₂ follow the nucleation/growth mechanism. Now, let us present a detailed argument.

It is well known that for the two-state proteins, the transition state is a rate-limiting region between the denatured and native states. During the folding, the extended protein chain in the denatured state collapses directly into the native state when several key interactions between residues are formed in the transition state. These residues, which are best formed in the transition state, are termed as folding nucleus (77,78). Nucleation and overall structural formation are thus coupled, and the folding process is highly cooperative (78). Generally, in experiment, the nucleus can be identified by the method of φ-value analysis (78,79). Theoretically, the local fluctuation method can also be employed as an useful tool to characterize the transition state and find the folding nucleus (36–38). Here, we use this method to find the folding nucleus for the wild-type tendamistat and the two mutants M₁ and M₂.

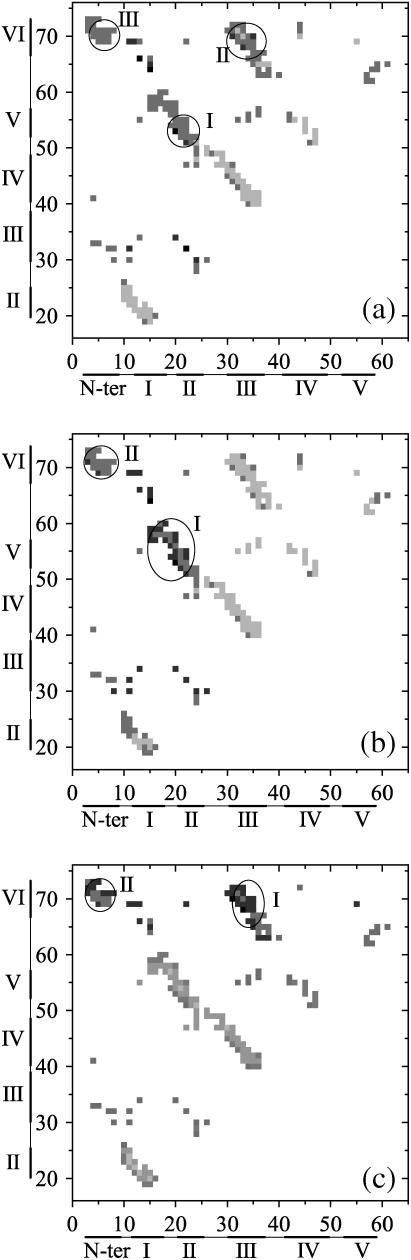
In details, the fluctuations around the folded state and around the unfolded state near the folding temperature T_f are analyzed to obtain the folding nucleus (36–38). The fluctuating events of folding ⇌ unfolding are divided into four types, namely FF, UU, UF, and FU types, respectively. Here, the four events are defined as: a), the FF event that originates in and returns to the folded region without descending to the unfolded region; b), the UU event that originates in and returns to the unfolded region without ascending to the folded region; c), the UF event that originates in the unfolded region and ascends to the folded region directly without returning to the original region; and d), the FU event that comes through an absolute unfolding process from the folded region to the unfolded region (37,38). The contacts in the nucleus are assumed to form preferably in the turning points of the FF events than in the turning points of the UU events. The probabilities of the native contacts in the turning point of the FF events (P_FF) and that in the UU events (P_UU) are obtained from tens of 10⁸ MD steps long-time simulations. The difference P_FF–UU between P_FF and the P_UU for each contact in the contact map is shown in Fig. 11, a–c. The folding nucleus correspond to those contacts that appear in the transition state and have positive values of P_FF–UU.

FIGURE 11.

The probability difference, P_FF–UU, between the P_FF and P_UU, for the native contacts are shown in the contact map. Where P_FF and P_UU represent the formation probability of native contact for the structures at the turning point of the FF and UU events, respectively (see the text for the detailed definition of these two events). (a) For the case of the wild-type tendamistat, most of the contacts within the circles I, II, and III have positive values, while others have negative values; (b) for the case of the mutant M₁ (C11A/C27S mutant), only most of the contacts within the circles I and II have positive values; and (c) for the case of the mutant M₂, only the contacts within the circles I and II have positive values.

Two clusters of contacts for the β-hairpins S_1–2 and S_3–4 have high probabilities both in the FF conformations (0.5–0.7) and in the UU conformations (0.7–0.9) (Fig. 11 a). This shows that these two β-hairpins are highly structured in the transition state, which agrees well with the previous experimental results (16,17) and theoretical prediction (31). However, all the related values of P_FF–UU for S_1–2 and S_3–4 have negative values, indicating obviously that the formation of these two parts do not correspond to the nucleation step. The contacts in S_0–6 (cluster-III) have quite low probabilities (<0.2) for both turning-point conformations although the values of P_FF–UU have positive values. Thus, these contacts are not formed in the transition state and are not included in the folding nucleus. The other two clusters (cluster-I and II) with positive values of P_FF–UU are also shown in Fig. 11 a.

Cluster-I corresponds to the region S_1–5, and cluster-II to the several key contacts in S_3–6. Clearly, there are two contacts in S_1–5 and three contacts in S_3–6. These contacts are close to each other in space and have higher probabilities in both the FF turning-point conformations (0.65–0.9) and the UU turning-point conformations (0.5–0.6). Thus, they are assumed to be the folding nucleus of the wild-type tendamistat. This is consistent with the discussion in the above section that the formation of the related parts acts as the rate-limiting step in the folding process. After this step, other parts are formed quickly without encountering any energetic barriers. The nucleation mechanism of protein tendamistat can be used to interpret the special two-state folding/unfolding behavior. Whether Tendamistat is located at the folded state or unfolded state mainly depends on the formation or rupture of its folding nucleus. As a result, the formation of folding nucleus and the whole folding process are highly cooperative.

For the case of the mutant M₁ shown in Fig. 11 b, only the region (cluster I) composed of S_1–2 and strand-5 has both positive values of P_FF–UU and high probabilities in the turning points of the FF ensemble and UU ensemble. This indicates that the residues of the nucleus are composed mainly of the residues in S_I due to the removal of the C11–C27 disulfide bond. This just validates the analysis as discussed above. The removal of the C11–C27 disulfide bond leads to a large loss of contacts in the unfolded state for S_1–2 and the formation is even slower than that of S_3–4. Thus, more contacts in S_3–6 are formed before the transition state and the adjustment of the positions of strands in S_3–6, which can favor the formation of contacts between strand-5 and S_1–2, becomes more difficult. Therefore, the formation of these important contacts in S_I (cluster-I) becomes even more important and rate-limited for the total folding process. However, the base of the first β-hairpin S_1–2 is opened by the removal of the C11–C27 disulfide bond, thus S_1–2 becomes less stable than that in the wild type. The loss of the stability of S_1–2 is tightly relative to the loss of the stability of the folding nucleus that determines the total stability of mutant M₁. This can clearly explain why the removal of the C11–C27 disulfide bond can lead to so large a loss of the thermodynamic stability.

In Fig. 11 c, only cluster-I (S_3–6) denotes the folding nucleus region for the mutant M₂. This also interprets the result that the rate-limiting step for the mutant M₂ changes to the formation of S_3–6 in S_II. As discussed above, the removal of the C45–C73 disulfide bond takes away the constraint between strand-6 and the β-hairpin S_3–4, which makes the contacts in S_3–6 decrease to a half-value before the transition state compared to that of the wild-type tendamistat. Thus, the three-stranded antiparallel β-sheet S_I can reach its native conformation easier for the mutant M₁ than for the wild type. However, the formation of the part S_3–6 in S_II becomes time-consuming for the whole folding. Due to the tight connections by the three hydrogen bonds, N-terminal loop-0 covers S_II like an arm, which can provide the required stability for the folding nucleus. Therefore, the mutant M₂ is more stable than the mutant M₁ although the related removal of the disulfide bond leads to a large loss in the thermodynamic stability.

CONCLUSION

This work is aimed to investigate the detailed folding mechanism of the disulfide-bonded protein tendamistat and the effects of the removal of each disulfide bond on the thermodynamic stability and the folding kinetics. The two-state folding behaviors for the wild-type tendamistat and its three mutants M₁, M₂, and M₃ are obviously exhibited in our simulations and agree well with the observations in experiments (16,17,19,21). Based on the modified Gō-type model, the folding pathways are also characterized in detail. Several processes, i.e., the formation of the first β-hairpin S_1–2, the formation of the rate-limiting step, and so on, are described. Here, the rate-limiting step corresponds to the formation of the nucleus, which is found by the local fluctuation method. The nucleation mechanism can well explain the two-state folding/unfolding behaviors for the wild-type tendamistat and the two mutants M₁ and M₂. Moreover, each removal of the disulfide bond leads to a large loss in the thermodynamic stability and the effect of the removal of the C11–C27 disulfide bond is larger than that of the C45–C73 one. This can also be clearly described by the influence on the folding nucleus. The disulfide bonds play an important role not only in the stability of the native structure but also in the kinetic process or the folding pathway.

The agreement with the experiments (16,17,19,21) indicates that our modified Gō-type model, especially, the introduction of the interactions of the disulfide bonds and the hydrogen bonds, really works. Since few theoretical studies on the folding behavior of disulfide-bonded proteins, e.g., protein tendamistat, are implemented, our work shows a successful example of study based on the coarse-grained models. The results obtained using this simplified model can provide useful insight into the folding mechanism of the disulfide-bonded proteins. In addition, this work on protein tendamistat can also help to understand the folding of β-sheet proteins, which appears to be different from that of helical and mixed α- and β-proteins (31).

For the limitation of the simplified model, we can only consider the fast folding pathway that follows a two-state process without populated intermediate states. However, for the case of the slow folding process, the rate-limiting step occurs mainly due to the cis to trans isomerization that cannot be investigated in our model. It is also noted that the formation process of the disulfide bonds is vital in the folding process, especially to the activities and functions of disulfide bonds. Although many results for the thiol-disulfide exchange process have been obtained in recent experiments, theoretically, a clear picture for the complicated formation process is still needed and more precise modeling study is required. Specifically, study based on the all-atomic model will be preferable.