Correlation Spectroscopy of Minor Fluorescent Species: Signal Purification and Distribution Analysis

Abstract

We are performing experiments that use fluorescence resonance energy transfer (FRET) and fluorescence correlation spectroscopy (FCS) to monitor the movement of an individual donor-labeled sliding clamp protein molecule along acceptor-labeled DNA. In addition to the FRET signal sought from the sliding clamp-DNA complexes, the detection channel for FRET contains undesirable signal from free sliding clamp and free DNA. When multiple fluorescent species contribute to a correlation signal, it is difficult or impossible to distinguish between contributions from individual species. As a remedy, we introduce “purified FCS”, which uses single molecule burst analysis to select a species of interest and extract the correlation signal for further analysis. We show that by expanding the correlation region around a burst, the correlated signal is retained and the functional forms of FCS fitting equations remain valid. We demonstrate the use of purified FCS in experiments with DNA sliding clamps. We also introduce “single-molecule FCS”, which obtains diffusion time estimates for each burst using expanded correlation regions. By monitoring the detachment of weakly-bound 30-mer DNA oligomers from a single-stranded DNA plasmid, we show that single-molecule FCS can distinguish between bursts from species that differ by a factor of 5 in diffusion constant.

INTRODUCTION

Fluorescence correlation spectroscopy (FCS) (1) probes dynamical processes in fluorescent species over the large range of timescales from nanoseconds to seconds. By introducing a sufficiently small confocal volume to FCS, single molecules can be detected (2), and the applications of FCS to analysis of biological processes have thereby multiplied (3). FCS has been proposed as a way to analyze rare species (4,5). Unfortunately, its usefulness can be limited in cases where multiple fluorescent species contribute to the same detection channel, contaminating the signal from a species of interest. If the dynamical processes of the contaminating species occur on similar timescales with the species of interest, it is very difficult and sometimes impossible to distinguish between contributions from different species. The correlation function for any minor species is obscured by contributions from other, more abundant species.

For example, we are performing solution-based single molecule experiments that monitor a DNA sliding clamp protein as it moves on DNA (β-clamp of Escherichia coli), by monitoring fluorescence energy transfer (FRET) between a donor (D) fluorophore on the β-clamp and an acceptor (A) at a specific location on a DNA plasmid. FRET is caused by the nonradiative transfer of excitations from D to A when they are in close proximity (within ∼5 nm). We perform these single-molecule FRET measurements of the dynamic complex of the β-clamp on DNA using alternating laser excitation (ALEX) (6) in the presence of free plasmids and free β-clamp proteins. With ALEX, three photon streams or channels are available: photons detected from donor fluorescence resulting from excitation by the donor excitation laser (hereafter, “donor channel”); acceptor-emitted photons detected in the acceptor channel that are the result of FRET excited by the donor excitation laser (“FRET channel”); and photons detected in the acceptor channel, that are the result of acceptor fluorescence, excited by the acceptor excitation laser (“acceptor channel”). In addition to signals from complexes undergoing FRET, the FRET channel contains contaminating signals caused by leakage of the donor emission into the acceptor channel and by direct excitation of the acceptor by the donor excitation laser (Fig. 1). Although both of these problems must be considered, the former is amplified in our experiments by aggregates of the β-clamp protein causing bright fluorescence bursts that leak into the acceptor channel. These bright bursts can appear indistinguishable from bursts caused by actual FRET. Autocorrelations performed on the FRET channel, therefore, have contributions from FRET and these contaminating sources, calling into question any conclusions drawn from correlation analysis, especially in the case where complexes are observed less frequently than the free components.

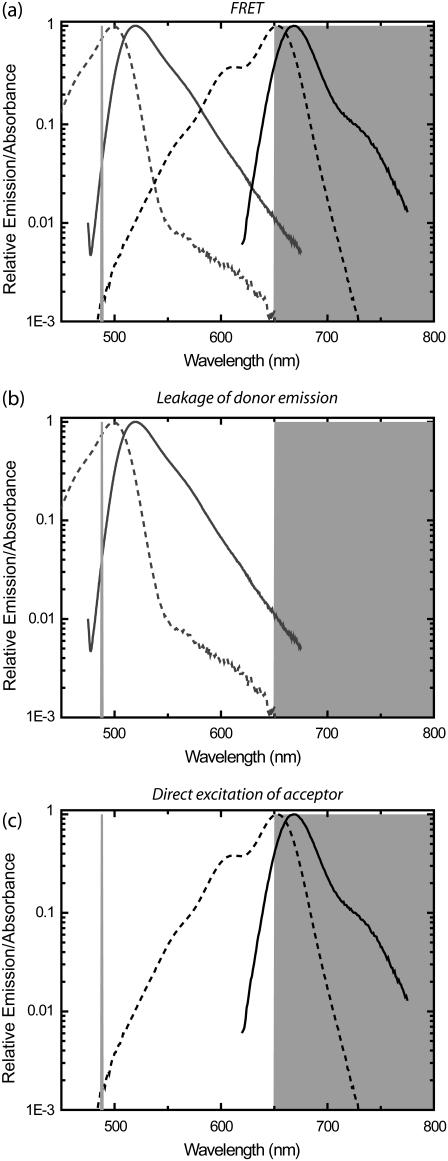
FIGURE 1.

Signals contributing to a detection channel monitoring fluorescence resonance energy transfer (FRET). (a) FRET is detected by exciting the donor fluorophore and monitoring emission of the acceptor fluorophore. Absorbance (dotted lines) and emission (continuous lines) are shown for Alexa 488 (Molecular Probes, shaded lines) as donor (D) and Alexa 647 (Molecular Probes, solid lines) as acceptor (A). The laser excitation of 488 nm is shown in open representation on the left as light shaded line, and the bandpass region for the emission filter (650LP, Omega Optical) is shown in shaded representation on the right. (b) Leakage of D signal into the A detection channel from the tail of the D emission curve (continuous line) causes detectable signals that contaminate the signal in the FRET channel. (c) Direct excitation of the A molecules by the D excitation laser (488 nm) also causes signals in the FRET channel.

The cross-correlation (7) between the FRET channel and the acceptor channel obtained from the acceptor laser excitation (8) eliminates contributions from the free protein and aggregates since those species are not excited by the acceptor excitation laser. However, fluctuations in FRET efficiency, which should reveal the protein-DNA intermolecular movement sought in these experiments, are unobservable by a cross-correlation between the FRET channel and acceptor channel. This is because the acceptor signal excited by the acceptor laser is only correlated with diffusion in and out of the detection volume, not fluctuations in the FRET efficiency. Hence, this cross-correlation reflects only the fluctuations caused by the translational diffusion of the complexes in and out of the detection volume.

Solution-based single-molecule fluorescence spectroscopy (SMFS) uses ratiometric variables and fluorescence lifetime measurements to allow for the identification and sorting of many species in complex mixtures (9–12). Signals from single molecules are detected by searching for “bursts” of photons with signal intensities above a preset threshold level, determined by the background levels and expected signal intensities. The recently introduced alternating laser excitation (ALEX) of single molecules allows sorting of species based on distance and association (6,13). Using ALEX, β-clamp-DNA complexes are easily distinguished from free components by searching for fluorescence bursts in the FRET channel. Only those bursts that have coincident bursts in the FRET channel and in the acceptor channel are due to complexes. Any burst with a coincident large burst in the donor channel is due to a β-clamp aggregate.

Although SMFS and FCS often use the same experimental setups and samples, techniques that take advantage of the power of SMFS to sort species while simultaneously using the ability of FCS to probe temporal dynamics remain underdeveloped. Selective fluorescence spectroscopy (10), which selects single molecule bursts for further correlation analysis, is the most advanced technique in this direction. The region over which the correlation is calculated is truncated at the beginning and end of the burst, allowing for analysis of fluctuations within the timescale of the bursts. To maximize the timescales monitored using the correlation analysis, only the brightest (>200 kHz) and longest single molecule bursts (>70 ms) are selected. These exceptional bursts correspond to fluorescent molecules that remain in the detection volume the longest. Nevertheless, the truncation used in the analysis prevents correlation analysis of fluctuations on the same timescale of the burst, including, for example, translational diffusion into and out of the optical detection volume.

The approach taken here also uses a selection of bursts, but it differs from selective fluorescence spectroscopy in two ways. First, the burst selection criteria are not as restrictive; we use much lower thresholds (5–15 kHz thresholds are typical), and allow much shorter bursts, only requiring sufficient signal over a 10 ms time bin. More importantly, the correlation calculations are not truncated at the burst edges. By expanding the region of the correlation around detected bursts, we introduce a way to use SMFS sorting to analyze temporal dynamics of specific species, including translational diffusion into and out of the optical detection volume, using standard FCS fitting equations (14,15). Truncation of the signal is moved to regions uncorrelated with the signal from the selected burst, allowing the functional forms of FCS fitting functions to remain unchanged except for a multiplicative factor.

Thus, by selecting only those bursts that are due to the species of interest and averaging the resulting correlations over all selected bursts, we can “purify” the signal of interest. This purification eliminates contributions both from leakage of the donor emission into the acceptor channel and direct excitation of the acceptor (Fig. 1). Due to the exclusion of contaminating signals, autocorrelations of the FRET channel calculated after signal purification may be used to study the fluctuations of an individual species. Signal purification may also be used for photon arrival-time interval distribution (PAID) functions (16) in the same way as for FCS. We call our method of purifying correlations signals by performing correlations over selected bursts “purified FCS”, or PFCS. We will refer to performing correlations only over the photons in the truncated single molecule bursts without correlation region expansion as “selective FCS”, or SFCS.

Here we demonstrate the use of PFCS using our β-clamp-DNA experiments. We also investigate how precisely a diffusion time can be extracted from the correlation calculated for a single burst. We call the method of analyzing FCS for single molecule bursts “single-molecule FCS”. Here, single-molecule FCS will be applied to experiments containing two species—one of free labeled DNA oligomers, the other of those oligomers hybridized to ssDNA plasmids. In this application of our method we show that many DNA oligomers weakly bound to plasmids during hybridization reactions with excess DNA oligomer are removed by gentle heating (at 37°C) of diluted solutions of the hybridized DNA.

THEORY

Purified FCS with correlation region expansion

We illustrate our new method through a simulation of an experiment of two interacting proteins, as shown in Fig. 2. In the simulated experiment, we monitor the fluctuations of the emission in the FRET channel from the intermolecular interaction between a protein labeled with a donor fluorophore D and a second protein labeled with an acceptor fluorophore A (Species 1 in Fig. 2). The emission in the FRET channel is contaminated by the presence of aggregates of the D-labeled species (Species 2 in Fig. 2). The D emission from Species 2 leaks into the FRET detection channel, leading to bursts that appear similar to those from Species 1 (the acceptor detection channel excited by the acceptor excitation laser is not simulated). Using values chosen to correspond roughly to the values found in our β-clamp experiments, Species 1 and 2 are both present with a molecular occupancy of c₁ = c₂ = 0.05 in the detection volume, and a molecular brightness of q_1,FRET = q_2,FRET = 35 kHz in the FRET channel. The molecular brightness is the number of photon counts per second received from a single fluorescent molecular species, averaged over the confocal detection volume. In the donor channel, Species 2 has a brightness of q_2,D = 141 kHz and Species 1 has a brightness of q_1,D = 0 kHz (the leakage of A into the donor channel is negligible, and will not be considered further). Due to translational diffusion through the optical detection volume, each molecular species is associated with a characteristic “diffusion time”, i.e., the average time a molecule remains in the detection volume. The diffusion times are τ_D,1 = 3 ms and τ_D,2 = 6 ms for Species 1 and 2, respectively. Species 2 is distinguished from Species 1 by the presence or absence of a coincident burst in the donor channel.

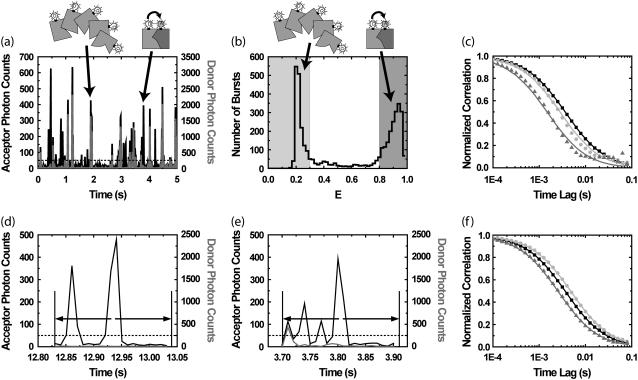
FIGURE 2.

Purified fluorescence correlation spectroscopy (PFCS) of individual species is performed by selection of single-molecule bursts. In this simulation, we separate the autocorrelation of the FRET channel for Species 1 undergoing FRET from donor D to acceptor A from that of the aggregated Species 2 with multiple copies of D (with leakage into the FRET channel). (a) Time trace of simulated emission from Species 1 and 2 in donor and FRET channels. Twenty-percent of the D emission (shaded) leaks in to the FRET detection channel (solid). (b) Histogram of uncorrected FRET efficiency ratio E (or proximity ratio) calculated for each detected burst. The peak near E = 1 (dark shading) is from Species 1, and the peak near E = 0.25 (light shading) is from Species 2. (c) Autocorrelations of the FRET channel calculated using selective FCS (using only photons within bursts). (Solid squares) Autocorrelation for the whole simulation without purification. In panels c and f, fits of data to Eq. 2 are shown as lines of same color as data points. (Dark shaded triangles) Selective FCS autocorrelation for bursts from Species 1. (Light shaded circles) Selective FCS autocorrelation for bursts from Species 2. (d) In PFCS, we expand the correlation region to include photons outside the bursts, in this case 100 ms on either side of each burst. If another burst is found within this region, the region is still included in the autocorrelation as long as the burst is from the same species. (e) A region is excluded if another burst from the wrong species is present. (f) By expanding the correlation region beyond the burst, we recover the correct autocorrelations for the individual species. Solid squares are the same as in panel c. (Dark shaded triangles) PFCS autocorrelation for bursts from Species 1. (Light shaded circles) PFCS autocorrelation for bursts from Species 2.

Bursts from Species 1 and 2 are distinguished using single molecule fluorescence analysis. Single-molecule fluorescence bursts are identified using the burst search method described in Kapanidis et al. (6), with the addition of a median-based background subtraction (Materials and Methods). A histogram of FRET efficiency ratio E (proximity ratio) for all bursts (17) clearly shows two subpopulations (Fig. 2 b).

Additional information may be gleaned from these bursts by calculating correlations on the photons contained in the bursts. The temporal cross-correlation function is defined as

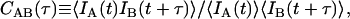(1)

where I_A(t) and I_B(t) are detected intensities for channels A and B, and t and τ are continuous time and time-lag variables. For a single fluorescent species diffusing within a Gaussian detection volume, the correlation function for FCS follows Aragon and Pecora (18),

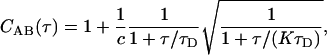(2)

where c is the average number of fluorescent species in the confocal detection volume, τ_D is the diffusion time of the species, and K is the square of the ratio between the ratio between the width of Gaussian detection volume along the optical axis and the width of the volume perpendicular to the optical axis (25 for our simulations). In experiments with relatively large pinholes, actual detection volumes are not Gaussian, and Eq. 2 generally works equally well without the square-root term (14). Additional terms can be added to Eq. 2 for additional species, but they must now account for differences in brightness for each species,

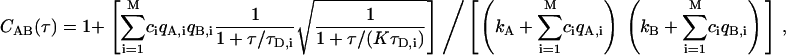(3)

where M is the number of species. For each species i, there is the molecular occupancy c_i, the brightness in channels A and B, q_A,i and q_B,i, and diffusion time τ_D,i. There are also background count rates in both channels, k_A and k_B. The relative contributions to the correlation function can be quantified by comparing the correlation amplitudes c_iq_A,iq_B,i from each species.

The data recorded for photon-timing SMFS/FCS experiments are series of photon time stamps with time-resolution Δt. The value t_i is the arrival time of the i^th photon from channel A, and u_j is the arrival time of the j^th photon from channel B. Assuming stationarity, the ensemble averages in the expression for C_AB(τ) are converted to averages over all time. Averaging over a finite experimental time T with N_A and N_B photons detected in the respective channels gives a correlogram 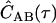, an estimate of the actual correlation function.

In terms of discrete photon time stamps t, I_A(t) is the number of photons i such that t = t_i; or I_A(t) = n({i|t_i = t})/Δt, where {i|t_i = t} is the set of all photons i such that t_i = t, and the operator n counts the number of elements in the set. Similarly, we have I_B(t) = n({j|u_j = t})/Δt. In this notation, using discrete time-lag τ, Eq. 1 becomes

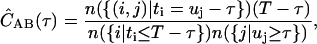(4)

where {(i,j)|t_i = u_j −τ} is the set of all photon pairs, (i,j), such that t_i = u_j −τ. The restrictions on the average intensities in the denominator are for symmetric normalization (19).

We use single-molecule ratiometric measurements to select a species of interest. If there are N bursts selected, then we average the correlations for all N bursts to obtain the accurate correlation for the species. For the k^th burst, we have the photons t_ki and u_kj in channels A and B, which occur over a burst duration T_k. The correlation functions are combined according to

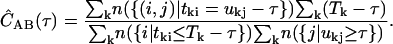(5)

If we combine correlations performed only on photons within bursts, the functional forms for the correlation do not match the FCS fitting equation in Eq. 2 on timescales near the burst width (Fig. 2 c). The autocorrelation of the FRET channel for the whole experiment fits well to the single-component FCS model in Eq. 2 with a diffusion time of 4.2 ± 0.1 ms (solid squares, simulation data; solid line, fit). FCS was not able to distinguish the two diffusing species present with a factor-of-2 difference in diffusion times. Using selective FCS (truncating correlations at burst edges) for all of the bursts from Species 1 or Species 2, we find a difference in the diffusion time between the two species (light shaded circles and dark shaded triangles in Fig. 2 c). The autocorrelation of the FRET channel for bursts from Species 1 (dark shaded region in Fig. 2 b) is fit by Eq. 2 with a diffusion time of 1.7 ± 0.1 ms (dark shaded triangles and curve in Fig. 2 c). The autocorrelation of the FRET channel for bursts from Species 2 (light shaded region in Fig. 2 b) is fit by Eq. 2 with a diffusion time of 3.3 ± 0.1 ms (light shaded circles and curve in Fig. 2 c). Unfortunately, both fits are poor, and the extracted values do not match the simulation values put in.

The primary problem encountered in Fig. 2 c is that burst searching routines select only those parts of the signal that are bright. The selected time regions have widths on the same timescale as the diffusion time, truncating a significant amount of correlated signal. To properly characterize the signal fluctuations, the timescale over which the correlation function is performed must be longer than the timescale of the fluctuations themselves. We introduce a simple way to do this: expand the region of the correlation function around the burst so that the region has a time-width much longer than the diffusion time (see Fig. 2 d). We expand it here by 10-fold (i.e., 100 ms) on either side of each burst. We expand enough to allow the correlation functions calculated to have the same functional form as the standard FCS fitting model in Eq. 2. We do not expand too much, so that we can exclude unwanted single molecule bursts from other species. We also want to exclude contributions from more persistent fluctuating signals, such as leakage from low-intensity, higher concentration signals. The correlations are calculated as in Eq. 5, except that now k is an index for expanded correlation regions rather than just the time of the bursts.

There is one change in the functional form in Eq. 2 for purified FCS due to the selection only of regions with bursts. FCS detects the molecular occupancy by comparing the variance and mean of the signal intensity. We are selecting regions that contain single molecule bursts, so the mean and variance of the signal intensity of the selected regions are different from the mean and variance for the entire experiment. Hence, the normalization as shown in Eq. 5 does not work properly. We use a multiplicative correction factor a as a parameter in all of our fits, accounting for this problem.

There are two uses for the expanded correlation regions for selected bursts. First, one may select only those correlation regions containing bursts of a specific species, excluding bursts from other species as well as leakage of higher concentration species into the channel of interest. The correlations for all regions can be averaged according to Eq. 5, obtaining the purified correlation function for a selected species. This methodology is an example of the use of single-molecule fluorescence to sort molecules for later subensemble analysis (13). Second, one may fit the correlations for individual regions to an FCS model, and the distribution of fitted diffusion times may be used to directly observe the distribution of diffusion times in the sample. This “single-molecule FCS” is described later.

There are two clear limitations to this method. First, PFCS is limited to cases where the methods of single molecule spectroscopy can distinguish the species involved; there must be some distinguishing parameter such as E that clearly reveals two or more subpopulations. Second, the concentration of fluorescent molecules monitored must be low so that bursts from multiple species are not included in the correlation region. In the correlation function example, handling cases where only one or two additional bursts are within the expanded correlation region is not difficult. In Fig. 2 d, the correlation region was expanded around the central burst from Species 1, and includes an additional, earlier burst. Since that burst is also from Species 1, that region is included in the analysis. However, in Fig. 2 e the expanded correlation region included a burst from Species 2, and that region is excluded from the analysis. Similar rules can be developed for a specific experimental situation.

Fig. 2 f shows that the purified correlations calculated for Species 1 and 2 match the correlations expected for those species if they were alone in solution. The correlation function for regions of interest containing bursts from Species 1 (dark shaded region in Fig. 2 b) is well fit by a single-component model with a diffusion time of 3.0 ± 0.1 ms (dark shaded triangles and curve in Fig. 2 f). The correlation function for regions of interest containing bursts from Species 2 (light shaded region in Fig. 2 b) is well fit by a single-component model with a diffusion time of 5.6 ± 0.1 ms (light shaded circles and curve in Fig. 2 f). The fitted values for the diffusion times are within 10% of the simulation input values.

Another situation in which PFCS may be used is the case in which Species 1 is again a complex undergoing FRET at single molecule concentrations, but Species 2′ is a nonaggregated donor-labeled protein present at higher concentrations. The donor emission from Species 2′ again leaks into the FRET channel, but now presents a low-intensity, fluctuating background that contributes to the FRET autocorrelation function. For PFCS to work in this situation, the species of interest must be significantly brighter than the fluctuating background. For these simulations, we used the same parameters for Species 1 as before, but with a lower molecular occupancy of c₁ = 0.02. We replace Species 2 with Species 2′, the molecular occupancy is c_2′ = 2.5, the brightness in the FRET Channel is q_1,FRET = 2.3 kHz (15-times smaller than for Species 1), and the diffusion time is τ_D,2′ = 600 μs. By selecting correlation regions around large fluorescence bursts in the FRET channel (as shown in Fig. 2), we effectively concentrate the signal of interest, excluding most of the experimental time where only the leakage signal from Species 2′ is present. The relative contribution of each species to the amplitude of the autocorrelation functions of the FRET channel can be calculated as 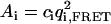, the contribution to the numerator in Eq. 3. For the autocorrelation of the FRET channel for the whole experiment, the amplitudes are A₁ = 24.5 kHz² and A′₂ = 13.6 kHz². After using PFCS, the amplitudes are A₁ = 183 kHz² and A′₂ = 13.6 kHz², increasing the contribution of Species 1 to the correlation amplitude from 64% to 93% of the total correlation amplitude. For the autocorrelation of the FRET channel over the entire simulated experiment, we obtain a diffusion time of 2.1 ± 0.1 ms with a poor fit to Eq. 2. Using PFCS to exclude most of the fluctuating background, we obtain a good fit to the autocorrelation of the FRET channel with a diffusion time of 2.9 ± 0.2 ms, matching the simulation value.

One important feature of PFCS is that the concentration of the species of interest does not affect the correlation obtained, except for the total experimental time it takes to obtain the correlation. The purity obtained (93%) for the correlation amplitude of Species 1 is lower than 100% since the contaminating, fluctuating background is always present. This upper limit on purity depends on the concentration and brightness of Species 2′ and on the brightness of Species 1, but not on the concentration of Species 1. As long as bursts can be identified, purified correlations may be obtained. For example, if we reduce the molecular occupancy of Species 1 from 0.02 to 0.005, the amplitude of the autocorrelation of the FRET channel decreases from A₁ = 24.5 kHz² to A₁ = 6.3 kHz². Under these conditions, only 20% of the correlation amplitude comes from Species 1, and the measured diffusion time is 1.1 ± 0.1 ms, close to the diffusion time of Species 2′. Using PFCS, the amplitude increases to A₁ = 172 kHz². Hence, Species 1 comprises 92% of the PFCS correlation amplitude (nearly identical to the 93% obtained above), and the diffusion time extracted is 2.8 ± 0.2 ms, close to the simulation value for Species 1.

We have demonstrated that PFCS can purify correlations for species present at single molecule concentrations with a distinguishing parameter. PFCS can also purify correlations when a low-intensity fluctuating background (caused by leakage of other fluorescence signals) is present. Unfortunately, there is currently no elegant, general theory for analyzing the effects of burst analysis on calculated correlations. This makes a quantitative theory of PFCS difficult to obtain. In place of such a general theory, we recreate experimental situations in simulations, and test for the accuracy of the PFCS methodology. For new experimental situations that differ significantly from the above simulations, it will be necessary to perform new simulations that match those conditions. One example is applying PFCS to species that are not as well separated by the E histogram, such as the folded and unfolded states of proteins (20).

Biases in fitted parameters using purified FCS

We now show that, for reasonable burst search thresholds, there are no large biases in the extracted fitting parameters. A previous work (21) describes how the detected diffusion time for a single burst depends on the threshold. High thresholds tend to increase the detected diffusion time, since bursts with larger numbers of photons tend to be those events that stayed in the detection volume longer. This implies that, for PFCS, there is a balance between selectivity from a higher threshold and lower bias obtained with a lower threshold. We investigate here the effects of the burst search threshold on PFCS. We also investigate the use of our expanded burst selection regions for the photon-arrival interval distribution (PAID) function (16), which adds an additional dimension of photon counts to the correlation function.

In Fig. 3, we illustrate the biasing effects of burst selection on fitted parameters. To quantitatively analyze bias, the simulation in this example contains only a single species. Ten simulations of 60 s each were performed with molecular occupancy c = 0.1, diffusion time τ_D = 3 ms, brightness q = 35 kHz, and background k_bkgd = 1 kHz. We plot the fitted parameters as a function of burst search threshold, ranging from 5 kHz to 45 kHz over 10 ms bins (Fig. 3, a–d). For fitted diffusion time τ_D and brightness q, an upward bias is seen as the threshold is raised, both in FCS and PAID fits (Fig. 3 b). However, this bias is small (within 5%) even for a significant threshold (up to 15 kHz). Hence, purified FCS and PAID do not introduce unreasonable bias in the fitted parameters as long as the burst search threshold is below the average burst intensity.

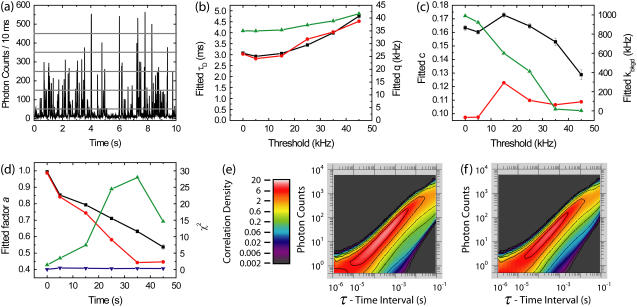
FIGURE 3.

Effects of burst search thresholds on fitted parameters obtained using purified FCS (PFCS) and purified PAID for simulations containing a single species. (a) Time trace of simulated fluorescence intensity with 10-ms time resolution. The burst search routine searched for consecutive time bins over a predetermined threshold. The five thresholds used are shown as horizontal shaded lines: 5, 15, 25, 35, and 45 kHz. In the following results, the points at the 0 kHz threshold are for the entire experiment. (b) Fitted τ_D using FCS (black), using PAID (red), and fitted q using PAID (green) as a function of burst search threshold. (c) Fitted c using FCS (black), using PAID (red), and fitted k_bkgd using PAID (green) as a function of burst search threshold. (d) Fitted values for the correction factor a using FCS (black) and PAID (red). χ² for FCS (blue) and PAID (green). (e) PAID histogram for entire experiment. (f) Purified PAID histogram for 15 kHz threshold.

In Fig. 3 c, we plot the fitted occupancy c from PFCS and purified PAID, and fitted background level k_bkgd from purified PAID. FCS values for c are higher since FCS cannot distinguish between increases in k_bkgd and increases in c. The fitted occupancy values are less consistent than the values for τ_D and q. This is not surprising, since the mean and variance of the signal intensities are affected by the correlation region selection process, and FCS detects the molecular occupancy by comparing the variance of the signal intensity with the signal mean. The fitted background from PAID drops off nearly linearly, vanishing at high thresholds. Since we are excluding regions that contain only background, this is not surprising. The fitted correction factor a decreases as the threshold is raised (Fig. 3 d). The χ² values for the fits are near 1 for all of the FCS fits. However, the χ² for PAID increases to high values for higher thresholds. The burst selection changes the shape of the PAID function (see Fig. 3, e and f). The largest change is a decrease in the correlation amplitude to the lower right of the main peak, accounting for the lower fitted value for k_bkgd. The main peak is largely unchanged, accounting for the slow change in q with threshold. The changes are due to the exclusion of regions with only background. Although Fig. 3 b shows that purified PAID may be used to extract accurate values of τ_D and brightness q for a single species, analysis of multiple subspecies with different q cannot be performed unless the PAID function model is changed to account for the burst selection.

Cross-correlations are often used in FCS to determine binding of two labeled, interacting molecules (7). In SMFS, ratios of fluorescence intensities from single bursts have also been used to determine the extent of binding (22). It is possible to use PFCS to select a species using ratios from SMFS, and to calculate cross-correlations of that species. We find that the selection of bursts with a specific ratio does not introduce spurious cross-correlations for timescales below the burst search timescale, allowing PFCS to distinguish bound molecules from random coincidence.

Fig. 4 shows the effects of burst selection on cross-correlation experiments. Two sets of 10 simulations of 60 s each with three species were performed. There are two detection channels A and B, with background levels k_A,bkgd = k_B,bkgd = 1 kHz . In both sets of simulations, Species 1 is present with molecular occupancy c₁ = 0.05, diffusion time τ_D,1 = 3 ms, brightness q_A,1 = 35 kHz in Channel 1, and q_B,1 = 0 kHz in Channel 2. For Species 2, c₂ = 0.05, q_A,2 = 0 kHz, q_B,2 = 35 kHz, and τ_D,2 = 3 ms. Species 3 simulates binding of Species 1 with Species 2, with q_A,3 = 35 kHz and q_B,3 = 35 kHz, and τ_D,3 = 3 ms. In the first set of simulations, c₃ = 0; in the second set, c₃ = 0.005. The burst search routine searched for consecutive 10-ms time bins where the sum of counts for both channels is above 5 kHz. In the first set of simulations, there are two species that emit only in one channel each, with no crosstalk. The ratio of the intensity in one channel over the sum of both channels, r = I_A/(I_A + I_B), is a bimodal distribution (shaded line, Fig. 4 b). The events with 0.3 < r < 0.7 are caused by random coincidence. In the second set of experiments, a third, minor species depicting bound molecules of Species 1 and 2 was added that emits in both channels equally (solid line, Fig. 4 b). A small peak in r near 0.5 is observed.

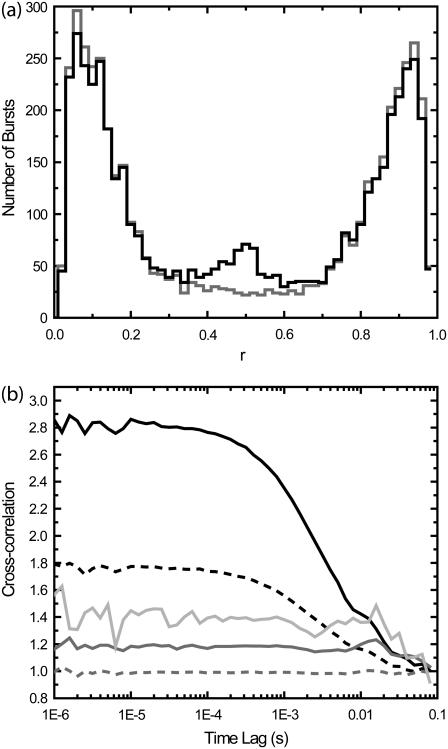
FIGURE 4.

Effects of PFCS burst selection on cross-correlations. In the first set of simulations, there are two species that emit only in channels A or B, with no crosstalk. In the second set of experiments, a third, minor species depicting bound molecules of Species 1 and 2 was added that emits in channels A and B equally. (a) Histograms of the ratio r = I_A/(I_A + I_B) calculated for each detected burst (similar to E histogram in Fig. 2), where I_A and I_B are detected intensities in channels 1 and 2. The first set of simulations without Species 3 is shown in shading, the second set with Species 3 is shown in solid representation. The peak near r = 1 is from Species 1, and the peak near r = 0 is from Species 2. The peak near r = 0.5 from the second set of simulations is from Species 3. (b) Cross-correlations obtained under various conditions. (Dotted shaded line) Standard cross-correlation for first set of simulations without Species 3. (Dark shaded line) PFCS on bursts with 0.3 < r < 0.7 are selected, and correlation regions are expanded by 100 ms. (Light shaded line) PFCS on bursts with 0.3 < r < 0.7 are selected, but correlation regions that also contain bursts with r < 0.3 or r > 0.7 are excluded. (Dotted dark line) Standard cross-correlation for second set of simulations with Species 3. (Solid line) PFCS on second set of simulations, bursts with 0.3 < r < 0.7 are selected.

A cross-correlation of the whole experiment produces a flat line for the first set of simulations (i.e., no cross-correlation, the dashed shaded line in Fig. 4 b), and a positive correlation for the second set of simulations (dashed solid line in Fig. 4 b). We first select only those bursts with 0.3 < r < 0.7, but do not further exclude any regions that contain other bursts outside this range in r. The first set of simulations produces a flat line (shaded line), and the second set of simulations produces a positive correlation (solid line). The shaded line is above 1.0 because of the modified normalization as discussed earlier. There is a drop in the cross-correlation at long timescales (>10 ms) that is introduced by the burst selection. Even if the coincidence of bursts in both channels is only due to random coincidence, the cross-correlation can detect this as revealed by the drop at long timescales (shaded line). Although this must be accounted for in any experiments, it is easily distinguished from an actual cross-correlation signal; a real cross-correlation caused by molecular binding also contains the correlation with the diffusion timescale (solid line). If we now selected the bursts with 0.3 < r < 0.7, and further exclude regions with other bursts with r > 0.7 or r < 0.3, we obtain the light shaded line. This line is further above 1.0 than the shaded line, and also shows a larger drop in the cross-correlation beyond 10 ms. However, in all cases, the cross-correlations of the first set of simulations are clearly distinguished from those of the second set of simulations. No spurious cross-correlations are introduced by purified analysis of cross-correlations at or below the diffusion time. However, the increase in the constant level as well as a drop in correlation at long times (beyond the burst width time) must be accounted for.

Although it is necessary to consider the biases in any use of this methodology, the results in this section indicate that these issues will not change the extracted results >10%, as long as the burst search threshold is below the average burst intensity.

Single-molecule FCS

Is it possible to get meaningful fits of correlation functions for regions containing only a single burst? It is not possible to get arbitrarily precise estimates of diffusion times for one single-molecule transit across the optical detection volume. Even arbitrarily strong signals will not help: FCS is a statistical method, and requires averaging over many such single-molecule transits to obtain a precise estimate of the diffusion time (21). However, as shown in Fig. 5, it is possible to obtain meaningful estimates of the diffusion by fitting correlation functions for single-molecule bursts when we expand the correlation region as described in Fig. 2.

FIGURE 5.

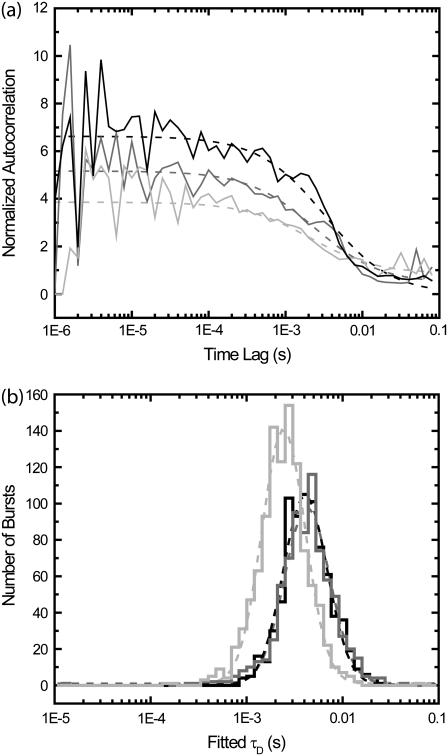
Extracting diffusion times found by fitting correlations of small regions around individual bursts (100 ms on either side). (a) Examples of correlations of individual burst correlation regions. Solid lines are correlations; dotted lines are fits. (b) Extracted diffusion times. The simulation is the same as used in Fig. 1. The x axis is the fitted diffusion time, and the y axis is the number of bursts. Three histograms are shown; fits to log-normal distributions are shown as dotted lines of same color. (Dark shading) Fits for autocorrelations of channel D of bursts from Species 2 in Fig. 1. (Medium shading) Fits for autocorrelations of channel A of bursts from Species 2 in Fig. 1. For Species 2, the brightness in channel A is five-times smaller than in channel D. (Light shading) Fits for autocorrelations of channel A of bursts from Species 1 in Fig. 1.

The means of the distributions match the diffusion times of the simulation parameters. Fitting the distributions with a log-normal distribution, the standard deviation of distributions is 0.52 ± 0.05 in units of ln(τ_D). The full-width half maximum values for the distributions are ∼0.5 in units of log₁₀(τ_D). For Species 1, the log-normal fit results in a central value of 3.2 ± 0.2 ms. For Species 2 in the donor channel, the log-normal fit results in a central value of 5.4 ± 0.3 ms. This is the same as for the FRET channel (fivefold dimer), where the log-normal fit results in a central value of 5.7 ± 0.3 ms. Hence, the width of the distribution is not limited by signal/noise, but by having only one transit through the detection volume.

Such single-molecule FCS analysis is useful for detecting subpopulations with large differences in diffusion time. Standard FCS analysis can do similar analysis using multicomponent fits, but it is often difficult to determine if the multiple timescales seen are really due to multiple species or are due to photophysical dynamics of a single species. The single-molecule FCS analysis introduced here allows these two cases to be distinguished.

The correlation function does not use the full information available in the photon stream. One way to improve on single-molecule FCS is to take advantage of more of this information. For example, analysis with a recursive Bayesian estimator would likely produce improved measurements of τ_D for a single molecule event (23).

MATERIALS AND METHODS

Simulations

The simulations are performed as described previously (16). A Gaussian detection volume was used in all cases, with transverse width of 0.35 μm, and longitudinal width of 1.75 μm. The three-dimensional simulation box is of size 3.5 × 3.5 × 17.5 μm³, with periodic boundary conditions (a molecule that leaves one side reappears at the opposite side with the same lateral position).

Single-molecule confocal fluorescence microscopy

Solution-based single molecule measurements are performed as in Kapanidis et al. (6). The alternating-laser excitation experiments were performed using the 488 nm line of an Argon ion laser (Innova 90C, Coherent, Santa Clara, CA) and the 633 nm line of a Helium-Neon laser (1163P, Uniphase, Milpitas, CA). The lasers are turned on and off using TTL timing pulses and an acousto-optic modulator (AOTF 48062 2.5–0.55, NEOS Technologies, West Melbourne, FL) rather than electro-optic modulators as used previously. The alternation period is set at 25 μs.

The excitation light is reflected using a custom dichroic mirror (488–633 DBDR, Omega Optical, Brattleboro, VT). A 1.4 NA oil-immersion objective (60 × 1.4 NA oil immersion Plan Apochromat, Nikon, Tokyo, Japan) mounted on a Nikon TE300 inverted confocal microscope is used for the excitation; a 100 μm pinhole is used on the emission detection path. The emission is split using a second dichroic mirror (580 DRLP, Omega Optical). The donor channel (for Alexa 488; Molecular Probes, Eugene, OR) is filtered using a bandpass filter (535DF45, Omega Optical), and the acceptor channel (for Alexa 647; Molecular Probes) is filtered using a long-pass filter (665AGLP, Omega Optical). The photodetectors, timing electronics, and software are as described previously (6). A neutral density filter (OD 1.2) is placed in front of the detector for the donor channel to reduce the signal intensity from the donor-labeled β-clamp. We time every photon, and without the neutral density filter our data acquisition was producing enormous files with uninteresting data produced by the donor channel. We still needed to monitor the donor channel to watch for β-clamp aggregates (see Fig. 6), but we did so with a much reduced count rate.

FIGURE 6.

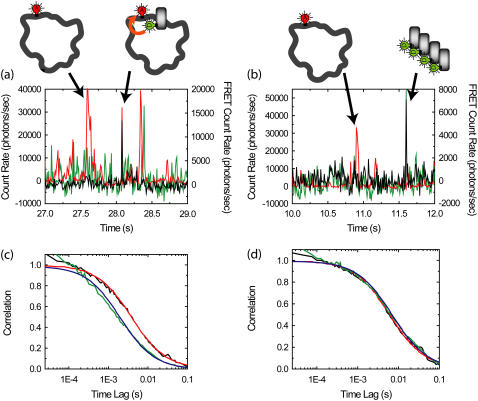
Purified FCS for autocorrelations of the FRET channel from complexes of D-labeled β-clamps and A-labeled DNA (concentration of β-clamp is larger than DNA). (a,b) Example time traces with 10-ms resolution for reaction mixtures. (Green) Donor emission; (red) acceptor emission excited by acceptor excitation laser; (black) FRET emission, or acceptor emission excited by donor excitation laser. The median count rate for the previous 100 bins is subtracted from each bin, leading to occasional negative count rates. Bursts in the red channel correspond to individual plasmids traversing the detection volume. Bursts in the green channel correspond to aggregates of β-clamp; individual β-clamps are not distinguished due to high concentrations. Bursts in the black channel correspond to complexes exhibiting FRET (a) or leakage from aggregates in the donor channel (b). We obtain the purified autocorrelation of the FRET channel by performing correlations only over regions within 100 ms of a burst-exhibiting FRET that does not have a corresponding burst in the donor channel. (c) The purified autocorrelation of the FRET channel (black line) and fit (red line) are shown. The autocorrelation of the FRET channel for the whole experiment (green line) and fit (blue line) are also shown. (d) The purified cross-correlation of the FRET channel and the acceptor channel (black line) and fit (red line) are shown. The cross-correlation of the FRET channel and the acceptor channel for the whole experiment (green line) and fit (blue line) are also shown.

Median-based background subtraction and burst searches

In processing the single-molecule signals and performing burst searches, we use a median-based background subtraction. A time trace with 10-ms time resolution is formed from the photon streams obtained from the single molecule microscope. At each time point, the background is determined by calculating the median of the previous 100 time bins. The median is used to avoid weighting the bursts in the signal too much in the calculation of the background. This background estimate is subtracted from each time point.

Obtaining error estimates using the bootstrap

We use a bootstrapping methodology to obtain error estimates for our fits of the purified correlation functions (16,24). In calculating the correlation, we average the correlation for all N_burst regions of interest surrounding selected bursts according to Eq. 5. For each correlation, we calculate 50 bootstrap instances of the correlations using the following procedure. We randomly select with replacement N_burst regions of interest from all N_burst regions of interest. Because we randomly select with replacement, a particular region of interest may be selected multiple times, or not at all. Using Eq. 5, we average the N_burst randomly selected regions of interest and obtain a bootstrap instance. Each bootstrap instance will have some regions missing, and some present twice or more. This allows the resulting bootstrap correlations to mimic additional experiments with similar noise characteristics. Using all 50 bootstrap instances, we calculate the variance for correlation time bin, and use this in weighting the fits for the correlation functions. Also, we fit each of the bootstrap instances to provide error bars for the fitted values.

DNA substrates

Analytical HPLC was performed on a HP1100 series instrument with 220 and 280 nm detection using a Vydac C18 column (5 μm, 4.6 × 150 mm; Grace Vydac, Hesperia, CA) at a flow rate of 1 mL/min. All runs used linear gradients of 0.1% aqueous trifluoroacetic acid (solvent A) versus 0.1% trifluoroacetic acid, 90% acetonitrile in H₂O (solvent B). Ultraviolet-visible spectroscopy was carried out on an Agilent 8453 diode array spectrophotometer (Agilent, Palo Alto, CA). Electrospray mass spectrometry (ES-MS) analysis was routinely applied to all compounds and components of reaction mixtures. ES-MS was performed on a Sciex API-150EX single-quadrupole electrospray mass spectrometer (MDS Sciex, Foster City, CA). Calculated masses were obtained by using ChemDraw 7.0.1 (CambridgeSoft, Cambridge, MA) or ProMac Ver. 1.5.3 (Sunil Vemuri and Terry Lee, City of Hope, Duarte, CA). Fluorescently labeled oligonucleotides were purchased from Invitrogen (Carlsbad, CA) or IDT (Skokie, IL) and purified by reverse phase HPLC. Fluorescent dyes were purchased from Invitrogen. Bio-Gel A-15m agarose was purchased from Bio-Rad (Hercules, CA). All other chemicals were obtained from Aldrich (Milwaukee, WI) unless otherwise indicated.

The M13mp18 phage was prepared by two consecutive bandings in cesium chloride, as described in Turner and O'Donnell (25). The ssDNA M13 plasmids with single hybridized DNA oligomers were prepared by annealing the synthetic DNA oligomers to purified single-stranded M13mp18 DNA, as described in Yao et al. (26). Briefly, 9 pmol of DNA oligomer(s) were added to 45 pmol of ssDNA template in buffer A (10 mM Tris-HCl, 300 mM NaCl, pH 8) and the final volume was adjusted to 500 ml. The reaction mixture was heated to 100°C for 5 min and slowly cooled to room temperature for 1 h. The reaction mixture was applied to a 5-ml column on Bio-Gel A-15m equilibrated in buffer B (20 mM Tris-HCl, 150 mM NaCl, pH 7.4). Fractions of 100 μl were collected and analyzed for UV absorption using the Agilent spectrophotometer. The molar concentration of M13 ssDNA with annealed DNA oligomer was calculated using known molar absorption coefficient.

DNA hybridization experiments

Single-molecule samples are prepared by diluting DNA oligomers hybridized to ssDNA plasmids to ∼100 pM concentration in a 20 mM 7.5 pH Tris buffer with 0.1 mM ethylene diamine tetraacetic acid (EDTA), 4% glycerol, 40 μg/ml bovine serum albumin, 8 mM MgCl₂, and 50 mM NaCl. A well is formed by using silicone well (Grace Biolabs, Bend, OR) on a coverslip. Ten microliters of sample is placed in the well, and a second coverslip is placed on top. The solutions are monitored using the single-molecule fluorescence microscope for 5 min with 70 μW excitation from the 633-nm laser.

In the experiments of Fig. 7 a, three sample solutions were prepared: one with ∼100 pM of labeled, DNA oligomer hybridized to ssDNA plasmid (excess plasmid); a second with ∼100 pM of labeled DNA oligomer without plasmid; and a third mixture sample prepared as a 1:1 mixture of the previous two samples. The samples were observed before and after heating at 37°C for 10 min. In the experiments of Fig. 7 c, the sample with ∼100 pM DNA oligomer hybridized to ssDNA plasmid (excess DNA oligomer) were observed before and after heating at 37°C for 10 min.

FIGURE 7.

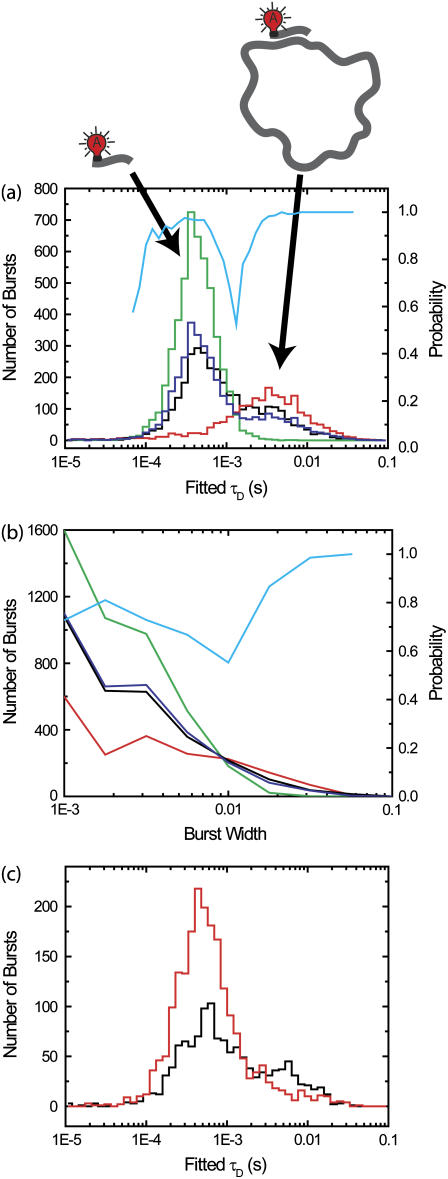
Species with a large difference between diffusion times may be distinguished by fitting diffusion times for single-molecule burst events. Single-molecule experiments were performed on solutions containing fluorescent-labeled 30-base DNA oligomers, both free and annealed to 7.2 kilobase ssDNA plasmids. (a) Annealed plasmids were prepared with a 5:1 excess of plasmid to ensure that only one DNA oligomer was annealed to each plasmid. Histograms of fitted diffusion times for single-molecule FCS with correlation regions within 100 ms of a single molecule burst are shown. (Green line) ∼50 pM solution of the DNA oligomers. (Red line) ∼100 pM solution of DNA oligomers annealed to the plasmids. (Black line) 1:1 mixture of the two previous solutions. (Blue line) Average of histogram of single component solutions (green and red lines), predicting the expected results for the 1:1 mixture. (Cyan) Probability that identification of burst is correct in mixture sample (black line), calculated using histograms of individual components (green and red lines). In panel b, we plot histograms of burst durations rather than fitted diffusion times. The colors refer to the same solutions (or averaged results) as in panel a. (Cyan) Probability that identification of burst is correct in mixture sample (black line). (c) The annealed plasmids were prepared with a 10:1 excess of DNA oligomer, allowing poorly bound DNA oligomers to remain attached to the plasmid during purification. The two measurements shown (performed at room temperature) are before (black line) and after (red line) heating the solution to 37°C.

Cloning and bacterial expression of β-clamp

The gene fragment encoding DNA β-clamp was amplified by polymerase chain reaction using E. coli K12 genomic DNA as template. The 5′-DNA primer (5′-GGT GGT CAT ATG AAA TTT ACC GTA GAA CGT GAG CAT TTA TTA AAA-3′) and the 3′-primer (5′-GGT GGT TGC TCT TCC GCA GCC CAG TCT CAT TGG CAT GAC AAC ATA-3′) introduced NdeI and SapI restriction sites, respectively. The polymerase chain reaction-amplified DNA was purified, digested simultaneously with NdeI and SapI and then ligated into a NdeI, SapI-treated pTXB1 plasmid (New England Biolabs, Ipswich, MA). The resulting pEY10 plasmid was shown to be free of mutations in the β-clamp-coding region by DNA sequencing.

Bacterial expression was carried out as follows. E. coli BL21 (DE3) pLysS cells (Novagen, Madison, WI) were transformed with pEY10. Cells were grown at 37°C to midlog phase (OD₆₀₀ ≈ 0.6) in Luria-Bertani medium and induced with 0.2 mM isopropyl β-D-thiogalactopyranoside at 30°C for 6 h. Cells were collected by centrifugation at 5000 rpm in a GS3 rotor for 10 min. The cell pellet from 1 L of bacterial culture was resuspended in 20 mL of lysis buffer (0.1 mM EDTA, 1 mM phenylmethanesulphonyl fluoride, 25 mM sodium phosphate, 150 mM NaCl buffer at pH 7.4 containing 10% glycerol) and lysed by sonication. The lysate was clarified by centrifugation at 14,000 rpm in a SS-34 rotor for 30 min. The clarified supernatant (∼20 mL) containing the β-clamp-Gyrase intein fusion protein was incubated with 5 mL of chitin beads (New England Biolabs) at 4°C for 1 h with gently shaking. The chitin beads were washed with 50 mL column buffer (0.1 mM EDTA, 50 mM sodium phosphate, 250 mM NaCl buffer at pH 7.2) containing 0.1% Triton X-100 then equilibrated with column buffer. The fusion protein adsorbed on the beads was subsequently cleaved with 100 mM NH₂OH in PBS at pH 7.0 (≈6 mL) overnight at 18°C to yield free β-clamp. The protein was further purified by fast protein liquid chromatography on a MonoQ 5/50 GL column (Pharmacia, Peapack, NJ) using a flow rate of 0.5 mL/min and a linear gradient from 0 to 500 mM NaCl in 50 mM Tris·HCl buffer at pH 8. The purified β-clamp was characterized as the desired product by ES-MS (Expected mass (average isotopic composition) = 40,642 Da; measured MW: 40,659 ± 15 Da). The isolated yield for purified β-clamp was at ∼20 mg/L.

Fluorescence labeling reaction

Fifteen microliters of Alexa488-maleimide in dimethylformamide (1 mg/100 μl) was added to 500 μl of 50 μM β-clamp in phosphate-buffered saline (50 mM phosphate, 150 mM NaCl, 2 mM Tris(2-carboxyethyl)phosphine hydrochloride, pH 7). The reaction was allowed to proceed for 2 h in the dark at room temperature. Excess glutathione was added to terminate the reaction and the reaction mixture was applied to a Sephadex G-25 gel filtration column ((Amersham Biosciences, Uppsala, Sweden)) and then eluted with buffer B to separate β-clamp from the small molecular weight reactant. The reaction resulted in ∼10% of fluorescently labeled β-clamp and, under this condition, no multiple labeling was observed.

Loading of β-clamp on DNA

The loading of the β-clamp is performed as in Yao et al. (27), but with a lower concentration of DNA and β-clamp. Briefly, a 100-μl reaction mixture was formed in a 20 mM 7.5 pH Tris buffer with 0.1 mM EDTA, 4% glycerol, 40 μg/ml bovine serum albumin, 8 mM MgCl₂, and 50 mM NaCl. Forty femtomoles of M13 plasmid with annealed DNA oligomer (described above) are added with 220 pmol of single-stranded binding protein. A quantity of 0.4 pmol of γ-clamp loading complex and 1 pmol of β-clamp (labeled monomer) are then added. Finally, adenosine triphosphate is added to a final concentration of 1 mM. Fifty microliters of this reaction mixture are placed in a well formed in a cell incubation chamber (WillCo-dish GWSt-3522, WillCo Wells, Amsterdam, The Netherlands) with a silicone gasket (Grace Biolabs). The solution is covered with a coverslip and is heated from room temperature to 35 ± 2°C over a period of 2 min using a microscope-based heater (Warner Instruments, Hamden, CT). ALEX-based single-molecule spectroscopy is then performed for 20 min at 35 ± 2°C.

RESULTS AND DISCUSSION

Purified FCS and the analysis of β-clamp-DNA complexes

We now apply purified FCS (PFCS) to the β-clamp-DNA interaction experiments mentioned in the Introduction. As seen in the time traces in Fig. 6, we use a relatively high concentration (10 nM) of donor-labeled β-clamp protein (from an even higher, 50 nM concentration of protein, 80% of which is unlabeled), and a low concentration (500 pM) of acceptor-labeled DNA oligomers hybridized to ssDNA plasmids. The β-clamp protein forms a dimer, so that we have 10 nM of donor labeled β-clamp dimer, implying that 40% of the dimers are labeled with at least one donor. There is a neutral density filter on the donor channel to reduce the signal intensity on the donor channel. Thus, there are four potential fluorescent species: labeled DNA oligomers free in solution; labeled DNA oligomers annealed/hybridized to ssDNA plasmids; labeled β-clamp free in solution (in dimeric form and occasional aggregates); and labeled β-clamp on DNA. Individual events are easily distinguished in time traces of the emission in the FRET (black) and acceptor (red) channels, but individual events corresponding to single β-clamp molecules are not identifiable since their concentration is too high. Bursts from complexes undergoing FRET (as in Fig. 6 a) are easily distinguished from β-clamp aggregate events leaking into the FRET channel (as in Fig. 6 b) by looking for coincident bursts in the donor channel (implies aggregates) or in the acceptor channel (implies complexes with FRET). Then, based on ratiometric expressions calculated using these signals, we select correlation regions containing only bursts from complexes undergoing FRET. For each selected burst, the correlation regions are expanded to include 100 ms before and after the burst. Correlations are calculated for each correlation region, and summed over all selected bursts.

The autocorrelation of the FRET channel (black line in Fig. 6 c) found using PFCS is significantly different from the autocorrelation of the FRET channel calculated for the entire experiment (green line in Fig. 6 c). The purified FCS FRET autocorrelation is well fit by Eq. 2 with a diffusion time of 4.0 ± 0.6 ms (red line). In contrast, the FRET autocorrelation for the whole experiment is poorly fit by Eq. 2 with a diffusion time of 2.0 ± 0.2 ms (blue line). The shorter diffusion time is due to contributions from leakage of the donor signal into the FRET channel (the β-clamp diffuses more quickly than the plasmid). Out of the 159 bursts in the FRET channel detected in this experiment, 21 were excluded because there was a coincident large burst in the D channel, indicating that the burst was likely a β-clamp aggregate. The measured diffusion time for the excluded bursts was 3 ± 1 ms. They were typically dimmer than the selected bursts, so these aggregates do not account for the difference in the above-measured diffusion times. It appears that the primary benefit of PFCS was to exclude the dimmer, but more consistent leakage signal from free, nonaggregated β-clamp, which accounts for a consistent, though fluctuating source of background photons collected in the FRET channel throughout the experiment.

Tables 1 and 2 show the effects of PFCS on the various auto- and cross-correlations calculated for this data set. Table 1 shows values for molecular occupancy, diffusion time, and brightness in three channels as extracted using photon arrival-time interval distribution (PAID) (16). Using PAID, we were able to extract diffusion times for each species, but the full autocorrelation was not able to be viewed independently from the other species. This ability, provided by PFCS, will be necessary for our application monitoring the movement of the DNA sliding clamp on DNA. Table 2 shows the contribution to the correlation amplitudes, or the numerator in Eq. 1, of each species in Table 1. First, the contributions are shown for the entire experiment. Second, the contributions are shown after PFCS is used to select for Species 4, the DNA sliding clamp-DNA complexes undergoing FRET. The contribution of these complexes to the autocorrelation of the FRET channel, which is of primary interest to us, is seen to increase from 60% to 91%.

TABLE 1.

Fluorescence parameters for data from Fig. 6

	Species	c	τD (ms)	qD (kHz)	qFRET (kHz)	qA (kHz)
1	Free β-clamp	2.4 ± 0.2	0.7 ± 0.1	710 ± 50	90 ± 50	0
2	β-clamp Agg.	0.005 ± 0.002	2 ± 1	3000 ± 400	600 ± 50	0
3	Free DNA	0.24 ± 0.02	8 ± 1	0	40 ± 10	1900 ± 100
4	Complexes	0.02 ± 0.01	4 ± 1	0	1200 ± 200	1900 ± 100

TABLE 2.

Effects of PFCS on contributions to correlations (factor of 7 in concentrating sample)

		FCS amplitude (kHz2) for entire experiment				FCS amplitude (kHz2) for complexes selected by PFCS
Correlation	Term	1	2	3	4	1	2	3	4
FRET autocorr.		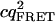1.9E4	1.8E3	380	2.9E4	1.9E4	0	380	2.0E5
Acceptor autocorr.		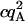0	0	8.7E5	7.2E4	0	0	8.7E5	5e5
Donor autocorr.		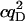1.2E6	4.5e4	0	0	1.2E6	4.5e4	0	0
FRET-acceptor cross.		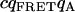0	0	1.8E4	4.6E4	0	0	1.8E4	3E5
FRET-donor cross.		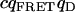1.5E5	9E3	0	0	1.5E5	9E3	0	0
Donor-acceptor cross.		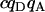0	0	0	0	0	0	0	0

Could the difference in diffusion times measured be an artifact of the burst selection? In addition to the simulation results above, several lines of reasoning indicate that it is not.

First, the diffusion of the β-clamp-DNA complexes is expected to be characterized by a single diffusion time, and the PFCS autocorrelation of the FRET channel fits better to a single-component FCS model of Eq. 2 than the autocorrelation of the FRET channel for the whole experiment.

Second, the PFCS cross-correlation is much more consistent with the total cross-correlations between the FRET channel and acceptor channel from the DNA oligomers hybridized to ssDNA plasmids (Fig. 6 d). The PFCS cross-correlation fits to Eq. 2 with a diffusion time of 6.4 ± 1.1 ms, and the cross-correlation for the whole file fits well to Eq. 2 with a diffusion time of 7.4 ± 0.4 ms, equivalent to within error. In this cross-correlation case (as mentioned in the Introduction), there are only two contributing signals: complexes undergoing FRET and direct excitation of lone DNA oligomers hybridized to ssDNA plasmids by the donor excitation laser. Both have similar diffusion timescales, and we expect cross-correlations for the whole experiment to match cross-correlations obtained with PFCS.

Third, the timescale for the PFCS autocorrelation of the FRET channel makes more sense compared to the diffusion time measured for the plasmid using the acceptor excitation laser (9.6 ± 0.4 ms). The detection volumes for the donor and acceptor excitation lasers are not the same, so we do not expect identical diffusion time values to be found in the two results. However, the diffusion times for the cross-correlation between FRET and acceptor channels should be halfway in-between the diffusion times for the autocorrelations of the FRET and acceptor channels (7). If we use the value of 9.6 ± 0.4 ms for the acceptor autocorrelation, and 7.4 ± 0.4 ms for the cross-correlation, we expect an autocorrelation diffusion time of 5.2 ± 0.6 ms. Within error, this matches the value of 4.0 ± 0.6 ms from the purified correlation analysis much better than the 2.0 ± 0.2 ms value extracted from the entire experiment.

As shown in this example, purified FCS with the correlation region expansion allows us to monitor the temporal dynamics of individual species even in the presence of other species. Using this methodology, we are studying the motion of the β-clamp protein on DNA (unpublished).

Single-molecule FCS and DNA hybridization

In our initial β-clamp experiments, we incubated the reaction mixture for 10 min at 37°C before spectroscopy (in later measurements the sample was heated on the microscope). In these first experiments, we noticed that the diffusion time measured in the acceptor channel decreased significantly after incubation. This was an apparent paradox since the signal in the acceptor channel should be exclusively from the labeled DNA oligomers annealed to ssDNA plasmids, which should not be affected by gentle heating or by loading of the β-clamp. A clue was that we found the change in diffusion time after heating occurred even without the β-clamp or clamp loading complex. FCS measurements (not shown) suggested two components, one with a long diffusion time (3.5 ms) and one with a short diffusion time (0.7 ms). The strength of the component with the shorter diffusion time increased after heating. By standard FCS, however, there is an ambiguity as to how much of the deviation from a one-component fit is due to a second diffusing species and how much is due to internal dynamics of the large DNA (28,29). Single-molecule FCS provides a way to show that there are indeed two diffusing components with different diffusion times.

Using single-molecule FCS, we found that the change in diffusion time was due to unbinding of labeled 30-mer DNA oligomers weakly bound to the ssDNA plasmid. We annealed the short DNA oligomers to the ssDNA plasmid using a 10:1 excess of DNA oligomers to be sure that each ssDNA plasmid was hybridized by a DNA oligomer. Depending on the sequence specificity of the short DNA oligomers, multiple DNA oligomers can be attached to a DNA plasmid at 40°C, as seen previously in FCS experiments under similar conditions (30). We hypothesize, therefore, that additional DNA oligomers are likely attached to the ssDNA plasmid at the lower temperature we used for purification, and then detach from the ssDNA plasmid upon heating of the DNA oligomer-plasmid complexes to 37°C.

In Fig. 7 a, we show that single-molecule FCS distinguishes between free 30-mer DNA oligomers and 30-mer DNA oligomers attached to ssDNA plasmids. The 30-mer is labeled with Alexa647 dye at the 5′ end. The green line in Fig. 7 a is the histogram for a solution with free 30-mer DNA oligomers. The red line is the histogram for DNA oligomers attached to plasmid, prepared using a 5:1 excess of plasmid to prevent attachment of weakly bound DNA oligomers. The black line is the histogram for a solution formed as a 1:1 mixture of the pure samples. The histogram for the mixture can be accurately predicted simply by averaging the results for the two pure samples (blue line). All of these histograms remain the same after heating to 37°C (not shown).

As can be seen by comparing results from Fig. 7, a and b, single-molecule FCS produces a better separation of species than can be obtained by using histograms of single-molecule burst widths. In comparing the histograms, one must keep in mind that the faster diffusing species produces more bursts than the slower diffusing species for the same concentrations. In Fig. 7 a, even though more bursts are detected from the faster diffusing species, the slower diffusing DNA oligomers attached to ssDNA plasmids are at a higher concentration. (Refer to Fig. S1 in the Supplementary Material to see histograms corrected for this effect.)

Since we measured the histograms produced by the free DNA oligomers alone and the DNA oligomers bound to the ssDNA plasmids alone, we can calculate the probability that the burst identification is correct in the 1:1 mixture sample. If, for the extracted diffusion time of a given burst, there were more bursts in the free DNA oligomer histogram, then most likely the burst was from that species. If there were more bursts in the histogram for DNA oligomers bound to the ssDNA plasmid, then most likely the burst was from that species. For a burst with a specific diffusion time, the probability that the species identification is correct is the ratio of the maximal number of bursts in one histogram with that diffusion time divided by the sum of the number of bursts in the histograms for both species with that diffusion time. This probability is plotted in Fig. 7 a as the cyan curve. A corresponding plot is shown in Fig. 7 b using burst widths. As can be seen, the probability of correct identification is significantly larger using single-molecule FCS than by using burst widths. Summing over all bursts, the probability of correct identification using single-molecule FCS is calculated to be 92%. For burst widths, the probability is 72%.

Now, suppose we did not use any of this information, and only used the total number of bursts in the individual species histograms. There were 2101 bursts in the histogram for DNA oligomers bound to ssDNA plasmids, and 4900 bursts in the histogram for free DNA oligomers. Using this, we could guess, based on no other information, that any burst has a 70% chance of coming from a free DNA oligomer. Hence, we see that the information gain in the case of burst widths is minimal, at only 2%. For longer burst widths, there is a >95% chance that the burst comes from the slower diffusing species, but there is only minimal discrimination for shorter burst widths. However, single-molecule FCS produces significant gains in information for both long and short bursts. There are single molecule diffusion times that provide a >95% chance of correct species identification both for the slower and faster diffusing species.

In Fig. 7 c, we show the results of experiments with a 10:1 excess of labeled DNA oligomer. In this case, there is a large increase in the amount of free DNA oligomer after the 10-min incubation at 37°C. There is some decrease in the number of long-diffusion time bursts, likely because these bursts are dimmer after losing weakly bound DNA oligomers. In these histograms, there are many more short diffusion-time bursts than long diffusion-time bursts. Here, there is approximately a factor-of-5 difference in the diffusion times of the labeled DNA oligomer and DNA oligomers hybridized to ssDNA plasmids, leading to a factor-of-5 more bursts from the labeled DNA oligomer even with the same concentration.

CONCLUSION

We have shown that purified FCS allows correlation analysis on individual subpopulations selected using single molecule measurements. We can use standard FCS models by expanding the region of interest around the detected bursts. This methodology will be useful in purifying correlations for species of interest. This will help improve our ability to apply FCS and single-molecule analysis to questions involving fast fluctuations in rare species.

Additionally, we have demonstrated single-molecule FCS analysis that may be used to distinguish between bursts from species with at least a fivefold difference in diffusion times. Here we showed that weakly bound DNA oligomers can fall off ssDNA plasmids even with gentle heating at 37°C. This methodology can be further used for measuring binding kinetics of large proteins/DNA with smaller proteins, DNA, or small molecules. These results indicate that, although the amount of information from single molecules bursts is finite (31), we have not yet taken full advantage of the information that is there.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.