What is the role of non-native intermediates of β-lactoglobulin in protein folding?

Abstract

The mechanism of α→β transition in folding of β-lactoglobulin is discussed based on free energy landscape analysis of a long lattice model. It is found that helical propensity of β-lactoglobulin is driven by conformational entropy and is intrinsically coded in its native structure. We propose a view on a role of folding intermediate, which is “on-pathway” but rich in non-native structures. The present results suggest that the native structure topology plays an important role in α→β transition.

Transitions from α-helix to β-sheet have been observed in folding processes of some mainly β-sheet proteins, such as β-lactoglobulin (βLG) (1) and plasminogen activator inhibitor type I (2). In these cases, α-rich structures appear as folding intermediates. Such folding processes via non-native intermediates are rather unusual and thus their mechanism has been attracting much attention. From the theoretical point of view, α→β transitions during the folding processes are of great interest because they seem not to be described by the funnel picture, although it successfully describes folding mechanism of some small proteins (3–10). To get more general insight into folding mechanism, it is important to understand the mechanism of the α→β transition.

In this paper, we discuss the folding mechanism of βLG as a prototype of the α→β transition. βLG has the following properties: (i) it has a predominantly β-sheet native structure [up-and-down β barrel (UDβ) topology] (11), and (ii) the refolding intermediate contains a significantly large amount of non-native α-helical structures. In other words, the folding process consists of two processes, namely, a fast process U→I(α) followed by a slow process I(α)→N, where U and N are the fully unfolded state and the native state, respectively, and I(α) is the highly helical intermediate (1), and (iii) accumulation of α-helical intermediate also is observed in the equilibrium unfolding experiment using guanidine hydrochloride (Gdn-HCl; ref. 13).

Why does the folding intermediate of βLG contain non-native highly α-helical structures? And what is their role? To understand the nature of α→β transition, we study a simple lattice protein model that has properties similar to those of βLG.

The Model

The model we study here is the modified HP model (13) in which a protein consists of a self-avoiding chain on a three-dimensional cubic lattice with two types of amino acids: H (hydrophobic) and P (polar). The energy (or solvent averaged free energy) E of a chain conformation is determined by the number of H−-H contact n_h and that of P−-P contact n_p as E = −ɛ(n_h + n_p), where ɛ > 0 is a constant (we measure the energy in the unit of ɛ hereafter). The chain length is 80 and the sequence is

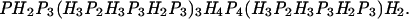1

This sequence was originally designed by O'Toole and Panagiotopoulos (13) so as to have a four-helix bundle-like native structure (shown in figure 4 of ref. 14), whose energy E is −94. But later, Bastolla et al. (14) found lower energy conformations (E = −98), which are doubly degenerate and only slightly different from one another. Interestingly, these conformations closely resemble the UDβ structure (15). In fact, they have nine β-strands and one α-helix as the real βLG does. The resemblance is manifested most clearly in the contact map (see figure 14 of ref. 14). Bastolla et al. have found four thermal phases for this sequence: (i) native phase (T ≤ 0.45), (ii) α-helix-dominated phase (0.45 ≤ T ≤ 0.62), (iii) unstructured globule phase (0.62 ≤ T ≤ 0.75), and (iv) unfolded phase (T ≥ 0.75).

In the following sections, we will show that this lattice model is indeed a good model of βLG for the purpose of qualitative discussions on α→β transition, through the calculation of the free energy landscape, and discuss the role of the helical intermediate in the folding process.

Results

Method.

We compute the free energy landscape and several physical quantities in thermal equilibrium by using a Monte Carlo scheme called multiself-overlap ensemble Monte Carlo method (MSOE) proposed recently by Iba, Chikenji, and Kikuchi (16, 17). This method is a highly powerful tool for ground state search and calculation of thermal equilibrium quantities of long chains, although it is not suitable for folding simulations because it is based on artificial dynamics. MSOE successfully reached the energy E = −98 and found no lower energy state than that. This result strongly suggests that it is indeed the ground state energy. Moreover, we also found the excited state at E = −97, which Bastolla et al. had failed to find.

Secondary Structure Participation.

Fig. 1 shows the temperature dependence of the percentage secondary structure participation. We follow the definition of the secondary structures of lattice polymers given in ref. 18, where α-helix means combined all helices of helix i ∼ iv in ref. 18. The antiparallel β-sheet content monotonically increases with decreasing temperature. On the other hand, the α-helix content significantly increases once it is up to T ∼ 0.6, and then decreases. Namely, there is a non-native α-helical phase between the native state and the unfolded state as was found by Bastolla et al. Although they called this phase the α-dominated phase based on analysis of the thermal averaged contact map, it actually contains almost equal amounts of α-helices and β-sheets as seen in Fig. 1. Note that if we regard the horizontal axis as the Gdn-HCl concentration rather than temperature, this behavior is similar to the equilibrium behavior of βLG (see also figure 4 of ref. 12).

Figure 1.

Temperature dependence of secondary structure participation of the modified HP model.

Free Energy Landscape.

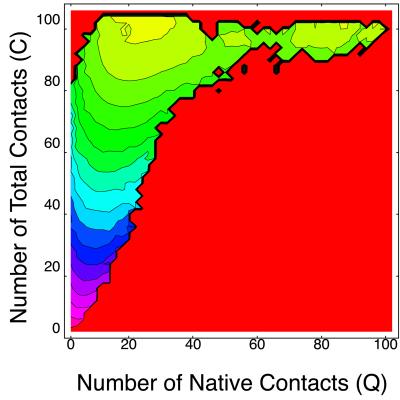
The free energy landscape is particularly informative for understanding folding mechanisms (19–22). Here, we compute free energy landscape on the two-dimensional plane of the number of native contacts Q and that of total contacts C. Fig. 2 shows the free energy landscape at T = 0.5% near the folding temperature, where the yellow region has lower free energy and red has a higher one. We can clearly see two free energy minima separated by a barrier. These minima correspond to the native state and the non-native compact state, respectively. [We take one of two native states (figure 13 of ref. 14) as a reference structure for calculating Q. The other native structure corresponds to Q = 91.] To see what are dominant structures of each free energy minima, next we compute the thermal average of percentage secondary structure participation 〈h(Q,C)〉_T on (Q,C) plane defined as

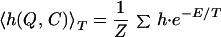2

at the same temperature, where h is the percentage of monomers that participate in the secondary structure (α-helix or antiparallel β-sheet), summation is taken only over the conformations with Q and C, and Z is the partition function.

Figure 2.

Free energy landscape on (Q,C) plane (T = 0.5) of the modified HP model. The interval between two contour lines is 3.0.

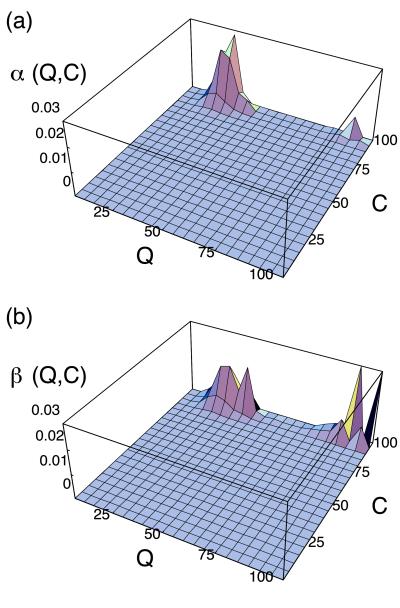
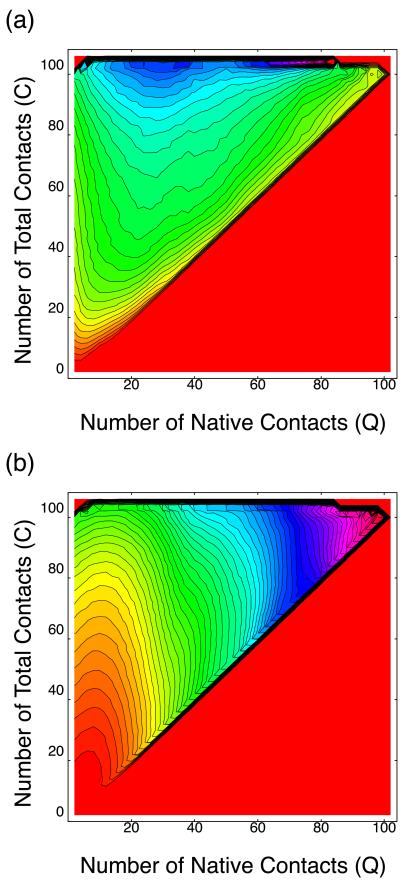
Fig. 3 shows 〈h(Q,C)〉_T of α-helices and antiparallel β-sheets, respectively. It is seen that dominant secondary structure near the native state is antiparallel β-sheets, whereas in the non-native compact state α-helices and antiparallel β-sheets are participated by almost equal amount of monomers. Thus we confirmed that the non-native α-helical phase found in Fig. 1 is separated from the native state by the free energy barrier, and we expect a two-state-like transition between them.

Figure 3.

Secondary structure distribution of the modified HP model on (Q,C) plane at T = 0.5. (a) α-Helix. (b) Antiparallel β-sheet.

Folding Route on (Q,C) Plane.

We now consider the folding route on (Q,C) plane from the unfolded state (Q ∼ 0, C ∼ 0) to the native one. Based on the free energy landscape, the folding process is expected as follows:

(i) At an early stage of refolding, a fast collapse to the intermediate accompanied by α-helix formations takes place. This process is expected to be fast, because there is no free energy barrier on the route. The folding speed also depends on diffusion constant on the free energy landscape. But generally, the helix formation is expected to be fast.

(ii) The late stage is a slow two-state transition from the α-helical intermediate to the native state. This entire picture of the folding process is fully consistent with the refolding experiment of βLG (1).

So far we have seen that both refolding and equilibrium unfolding behavior of βLG are well described by the present model. Thus we consider that the free energy landscape of βLG is mimicked by that shown in Fig. 2. One of the characteristic features of this free energy landscape is a strong tendency of forming non-native contacts at an early stage of folding. Why doesn't this model fold directly to the native state? In what follows, we will show by using a Gō model that the preference of non-native contacts is caused purely by the conformational entropy, which is determined by the native topology.

Gō Model.

In this model, the energy of each conformation is proportional simply to the number of native contacts (5). It is widely accepted that energy landscapes of the Gō model are in general funnel-like. We select the same UDβ-like topology as above for the native structure. Its thermodynamic quantities are computed by the multiself-overlap ensemble Monte Carlo method. We found that it exhibits a cooperative, two-state transition with a midpoint temperature T ∼ 0.8 from the unfolded phase with no persistent structure to the native phase.

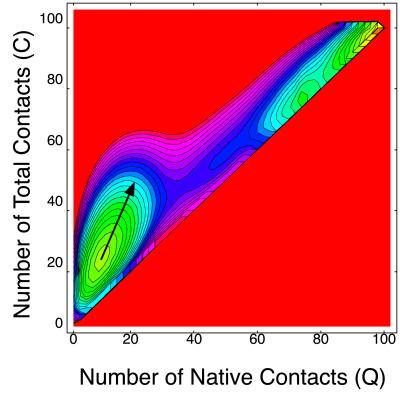
The free energy landscape of this Gō model on the (Q,C) plane at T = 0.8 is shown in Fig. 4. Two minima correspond to the unfolded phase, and the native phase are seen. No thermodynamically stable non-native compact state is found for this model. But interestingly, this UDβ Gō model also shows a tendency of having non-native contacts. Namely, the direction of the largest fluctuation near the unfolded state (indicated by an arrow in Fig. 4) heads for a non-native compact state rather than the native state. Because non-native contacts do not lower energy at all, this tendency is purely of an entropy effect.

Figure 4.

Free energy landscape on (Q,C) plane at T = 0.8 (UDβ Gō model). The direction of the largest fluctuation near the unfolded state is indicated by an arrow. The interval between two contour lines is 0.43.

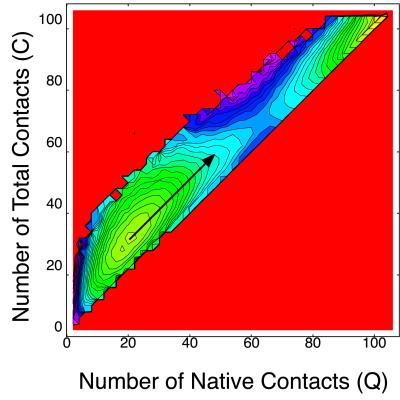
Note that such behavior is unusual for the Gō model. Typically a folding route of the Gō model connects directly the unfolded state and the native state and is roughly parallel to the diagonal line of the (Q,C) plane. In fact, the folding route of the Gō model, which has a four-helix bundle native structure, behaves so, as is suggested from the free energy landscape at T = 0.8 (Fig. 5). Hence, some types of native structures (including UDβ) have a tendency to form non-native contacts intrinsically because of entropy effect. Now, one interesting problem arises. Namely, do such non-native contacts tend to make α-helices? To address the question, next we consider how secondary structures are distributed on the (Q,C) plane when the native topology is UDβ. Fig. 6 shows the secondary structure participation 〈h(Q,C)〉_∞ of α-helix and antiparallel β-sheet, respectively. Note that 〈h(Q,C)〉_∞ is independent of energy parameter, but it depends only on the native topology. Fig. 6a shows that the non-native compact state with Q ∼ 30 has the largest α-helix content, and thus the direction of the largest fluctuation near the unfolded state of free energy landscape of UDβ Gō model in Fig. 4 heads for α-helical states. In the case of the Gō model, helical structures are not thermodynamically stable. Actually we observed only slight increase of α-helix content near the folding temperature for the UDβ Gō model, in contrast to Fig. 1. These results imply that all UDβ proteins would have a tendency to form α-helices in early stage of the folding. In other words, helical propensity of UDβ protein is intrinsically coded in its native structure.

Figure 5.

Free energy landscape on (Q,C) plane at T = 0.8 (four-helix bundle Gō model). The direction of the largest fluctuation near the unfolded state is indicated by an arrow. The interval between two contour lines is 0.43.

Figure 6.

Secondary structure distribution on (Q,C) plane for UDβ proteins. (a) α-Helix. (b) Antiparallel β-sheet. The interval between two contour lines is 0.0125.

Discussion

What Is the Role of the Helical Intermediate?

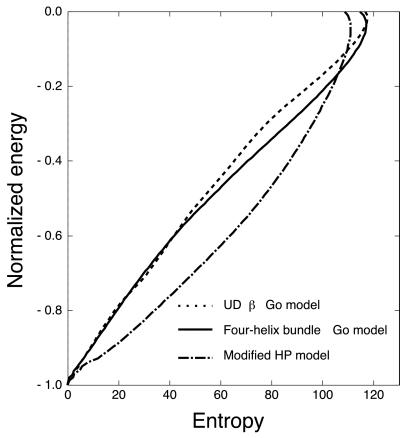
We show energy (normalized by absolute value of native energy) vs. entropy profile for three models we treated here in Fig. 7, which represent half of a well-known funnel cartoon. The entropy of the UDβ Gō model is considerably smaller than that of the four-helix bundle Gō model at intermediate energy. This implies that native contact formation near the unfolded state is entropically less favorable for UDβ native structure. On the other hand, shape of the funnel for the modified HP model is mostly downward convex. In other words, the entropy reduction is relaxed very much compared with two other models. On the contrary, the energy landscape would become more rugged.

Figure 7.

The entropy curves for UDβ, four-helix bundle Gō model, and modified HP model. Horizontal axis indicates entropy, and vertical axis indicates the normalized energy (E/|E_N|), where E_N is the native energy.

The folding process of the UDβ Gō model suffers from rapid entropy reduction. As a result, the large plateau appears in free energy landscape, as seen in Fig. 4. On the other hand, the free energy landscape of the modified HP model in Fig. 2 implies a direct two-state transition between the α-helical intermediate and the native state. It implies that the non-native intermediate acts so as to restrict the folding route and relax rapid entropy reduction as shown in Fig. 7. [We by no means insist that the modified HP model actually folds faster than the UDβ Gō model. Because they are totally different models, they should have different time scales.]

Based on above considerations, we may deduce a possible role of the helical intermediate of βLG. Presumably, the non-native intermediate is used as a sort of landmark, in the folding process. The role of the intermediate is not to act as an obstacle in this case, but to restrict the folding route. The reason it needs such a landmark is that otherwise the free energy landscape would become unfavorable for fast folding because of its UDβ native topology. We believe that the α-helical intermediate of βLG have acquired such a role as a result of Darwinian evolution.

The role of folding intermediates we propose is qualitatively different from those of previous theoretical studies. So far two types of folding intermediates have been discussed. One is “off-pathway” kinetic trap, which simply slows folding (23, 24). Another is partially folded “on-pathway” metastable state discussed by Pande et al. (25). This type of intermediate is characterized by having no non-native structure. On the other hand, the helical intermediate discussed in this paper is on-pathway but rich in non-native structures. It also has been proposed by some authors that initial collapse with few native contacts can help folding by restricting the space of conformation search (19, 26, 27). In these studies, however, no significant secondary structure changes were observed, and the role of the native topology was not discussed.

Guo and Brooks (29) also reported free energy landscape of a β-barrel protein model. They used a 46-mer off-lattice model with a three-letter code and designed the sequence so that the native structure is β-barrel consisting of four β-strands (see figure 2 of ref. 28), which is closely related to and much simpler than UDβ. They found that their model shows an L-shaped free energy landscape, which is similar to Fig. 2 of the present paper, on the plane of gyration radius and nativeness (29). Unfortunately, they did not discuss change of secondary structures nor the origin of the L shape in detail. Although it is plausible that the present scenario of α→β transition also is applicable to this simple β-barrel protein model, more detailed study is required to confirm that.

The α→β transition of lattice models also have been discussed by Abkebich et al. (30) in a different context. They showed that the conformation with the greater number of local contacts is kinetically more reachable than the other when a chain has two different native states. They called this phenomenon kinetic partitioning. Some aspects of the folding process of βLG may be described by the concept of the kinetic partitioning, although the intermediate state is a metastable state rather than the lowest energy state. But the specific feature of the native topology also should be stressed as we have shown in this paper for the folding mechanism to be fully understood.

A Possibility of the Presence of Other α→β Proteins.

There are many UDβ proteins in the so-called lipocalin family, such as retinol binding protein and biliverdin binding protein. As far as we know an α-helical folding intermediate has been observed only in βLG refolding experiments. But the present results suggest that any proteins whose native structure is UDβ have intrinsic helical propensity because of conformational entropy effect. Thus there is a strong possibility that some other lipocalin family proteins also have α-helical intermediates. This scenario may be applied to other types of native topology, which consists of mainly β-sheet structure, because such native structures will be difficult to access kinetically.

Abbreviations

βLG

β-lactoglobulin

UDβ

up-and-down β barrel

HP

hydrophobic-polar