Efficient supervised learning in networks with binary synapses

Abstract

Recent experimental studies indicate that synaptic changes induced by neuronal activity are discrete jumps between a small number of stable states. Learning in systems with discrete synapses is known to be a computationally hard problem. Here, we study a neurobiologically plausible on-line learning algorithm that derives from belief propagation algorithms. We show that it performs remarkably well in a model neuron with binary synapses, and a finite number of “hidden” states per synapse, that has to learn a random classification task. Such a system is able to learn a number of associations close to the theoretical limit in time that is sublinear in system size. This is to our knowledge the first on-line algorithm that is able to achieve efficiently a finite number of patterns learned per binary synapse. Furthermore, we show that performance is optimal for a finite number of hidden states that becomes very small for sparse coding. The algorithm is similar to the standard “perceptron” learning algorithm, with an additional rule for synaptic transitions that occur only if a currently presented pattern is “barely correct.” In this case, the synaptic changes are metaplastic only (change in hidden states and not in actual synaptic state), stabilizing the synapse in its current state. Finally, we show that a system with two visible states and K hidden states is much more robust to noise than a system with K visible states. We suggest that this rule is sufficiently simple to be easily implemented by neurobiological systems or in hardware.

Learning and memory are widely believed to occur through mechanisms of synaptic plasticity. Despite a huge amount of experimental data documenting various forms of plasticity, as e.g., long term potentiation and long term depression, the mechanisms by which a synapse changes its efficacy and those by which it can maintain these changes over time remain unclear. Recent experiments have suggested that single synapses could be similar to noisy binary switches (1, 2). Bistability could be in principle induced by positive feedback loops in protein interaction networks of the postsynaptic density (3–5). Binary synapses would have the advantage of robustness to noise and hence could preserve memory over long time scales, compared with analog systems which are typically much more sensitive to noise.

Many neural network models of memory use binary synapses to store information (6–12). In some of these network models, learning occurs in an unsupervised way. From the point of view of a single synapse, this means that transitions between the two synaptic states (a state of low or zero efficacy, and a state of high efficacy) are induced by pre- and postsynaptic activity alone. Tsodyks (13) and Amit and Fusi (9, 10) have shown that the performance of such systems (in terms of information stored per synapse) is very poor unless two conditions are met: (i) activity in the network is sparse (very low fraction of neurons active at a given time); and (ii) transitions are stochastic, with on average a balance between up (long term potentiation-like) and down (long term depression-like) transitions. This poor performance has motivated further studies (12) in which hidden states are added to the synapse to provide it with a multiplicity of time scales, allowing for both fast learning and slow forgetting.

In a supervised learning scenario, synaptic modifications are induced not only by the activity of pre- and postsynaptic neurons but also by an additional “teacher” or “error” signal that gates the synaptic modifications. The prototypical network in which this type of learning has been studied is the one-layer perceptron that has to perform a set of input–output associations; i.e., learn to classify correctly input patterns in two classes. In the case of analog synapses, algorithms are known to converge to synaptic weights that solve the task, provided that such weights exist (14, 15). On the other hand, no efficient algorithms are known to exist in a perceptron with binary (or more generally with a finite number of states) synapses, in the case where the number of patterns to be learned scales with the number of synapses. In fact, studies on the capacity of binary perceptrons (16, 17) used complete enumeration schemes to determine numerically the capacity. These studies found a capacity of ≈0.83 bits per synapse in the random input–output categorization task, very close to the theoretical upper bound of 1 bit per synapse. However, it is not even clear whether there exist efficient algorithms that can reach a finite capacity per synapse, in the limit of a large network size N. Indeed, learning in such systems is known to be an NP-complete task (18, 19).

Recently, “message passing” algorithms have been devised that solve efficiently nontrivial random instances of NP-complete optimization problems such as, e.g., K-satisfiability or graph coloring (20–23). One such algorithm, belief propagation (BP), has been applied to the binary perceptron problem and has been shown to be able to find efficiently synaptic weight vectors that solve the classification problem for a number of patterns close to the maximal capacity (>0.7 bits per synapse) (24). However, this algorithm has a number of biologically unrealistic features (e.g., memory stored in several analog variables). Here, we explore algorithms that are inspired from the BP algorithm but are modified to make them biologically realistic.

This article is organized as follows. First, we present the general scheme for the simplest setup of ±1 patterns and synapses as well as results with bounded and unbounded hidden variables. Then, we discuss the more realistic 0,1 case with results including the sparse coding limit. Implications of our results are discussed in the concluding section. Details are given in supporting information (SI) Text.

Binary ±1 Neurons and Synapses

The Model Neuron.

We consider a neuron with two states (“inactive” and “active”) together with its N presynaptic inputs that we take to be also binary. Depending on the time scale, these two states could correspond in a biological neuron either to emission of a single spike or not, or to elevated persistent activity or not. The strength of synaptic weights from presynaptic neuron i (i = 1, …, N) is denoted by w_i. Given an input pattern of activity {ξ_i,i = 1, …, N}, the total synaptic input received by the neuron is I = Σ_i^N = 1w_iξ_i. The neuron is active if this total input is larger than a threshold θ and is inactive otherwise. Such a model neuron is sometimes called a perceptron (14). In this article, we consider binary synaptic weights. In addition, each synapse is characterized by a discrete “hidden variable” that determines the value of the synaptic weight. In this section, we consider {−1,+1} neurons and synapses, and θ = 0; to simplify the notation, we will also assume N to be odd, so that the total synaptic input is never equal to 0. This assumption can be dropped when dealing with {0,1} model neurons.

The Classification Problem.

We assume that our model neuron has to classify a set of p = αN random input patterns {ξ_i^a,i = 1, …, N, a = 1, …, p} into two classes (active or inactive neuron, σ^a = ±1). The set of patterns which should be classified as +1 (−1) is denoted by Ξ₊ (Ξ₋), respectively. In each pattern, the activity of input neurons is set to 1 or −1 with probability 0.5, independently from neuron to neuron and pattern to pattern. The learning process consists in finding a vector of synaptic weights w such that all patterns in Ξ₊(resp. Ξ₋) are mapped onto output + (resp. −). Hence, the vector w has to satisfy the p equations

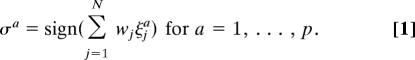We will call such a vector a perfect classifier for this problem.

In the case of ±1 synapses and inputs we are considering in this section, the problem is the same if we consider the set Ξ₋ to be empty, i.e., σ^a = +1 for all a = 1, …, p, as we can always redefine ξ_j^a → σ_j^aξ_j^a and require the output to be positive. This will no longer hold in the next section.

The Perceptron Learning Algorithm.

In the case of unbounded synaptic weights, there exists a standard learning algorithm that can find a perfect classifier, provided such a classifier exists, namely the perceptron algorithm (standard perceptron, SP) (14, 15). The algorithm consists in presenting sequentially the input patterns. When at time τ pattern ξ^τ is presented, one first computes the total input I = Σ_i^N = 1w_i^τξ_i^τ and then

• If I ≥ 0, do nothing.

• If I < 0, change the synaptic weights as follows: [w_i^τ+1 = w_i^τ + ξ_i^τ].

This algorithm has the nice feature that it is guaranteed to converge in a finite time if a solution to the classification problem exists. Furthermore, it has other appealing features that makes it a plausible candidate for a neurobiological system: the only information needed to update the synapse is an “error signal” (the synapse is modified only when the neuron gives an incorrect output) and the current activity of both presynaptic and postsynaptic neurons. However, the convergence proof exists for unbounded synaptic weights (14), or for sign-constrained synaptic weights (25), but not when synaptic weight can take only a finite number of states.

Requirements for Biologically Plausible Learning Algorithms with Binary Weights.

In this article, we explore learning algorithms for binary synaptic weights. Each synapse is endowed with an additional discrete “hidden” variable h_i. This hidden variable could correspond to the state of the protein interaction network of the postsynaptic density, which can in principle be multistable because of positive feedback loops in such networks (5, 4). Each synaptic weight w_j will depend solely on the sign of the corresponding hidden variable h_j; in the following, to avoid the ambiguous h_i = 0 state, we will always represent the hidden variables by odd integer numbers (this simplifies the notation but does not affect the performance). We first consider the (unrealistic) situation of an unbounded hidden variable and then investigate learning with bounded hidden variables. Similar to the perceptron algorithm, we seek “on-line” algorithms (i.e., modifications are made only on the basis of the currently presented pattern) that, at each time step τ, modify synapses based only on variables available to a synapse: (i) the current total synaptic input I^τ and hence the current postsynaptic activity; (ii) the current presynaptic activity ξ_i^τ; and (iii) an error signal indicating whether the output was correct or not. At each time step, the current input pattern is drawn randomly from the set of patterns, and the hidden variables h_j^τ → h_j^τ+1 and the synaptic weights w_j^τ → w_j^τ+1 are updated according to the algorithm.

Quantifying Performance of Various Algorithms.

The maximal number of patterns for which a weight vector can be found is α_max ≃ 0.83 for random unbiased patterns (16). Hence, the performance of an algorithm can be quantified by how close the maximal value of α at which it can find a solution is to α_max. In practice, one has to introduce a maximal number of iterations per pattern. For example, a complete enumeration algorithm (in which one checks sequentially the 2^N possible synaptic weight configurations) is guaranteed to find a solution for any α ≤ α_max, but it finds it in an implausibly long time (exponentially large in N). Here, we impose a maximal number of iterations (typically 10⁴ per pattern) and find the maximal value of α for which a given algorithm is able to find a solution.

BP-Inspired (BPI) Algorithms.

A modification of the BP algorithm was found by Braunstein and Zecchina (24) to perform remarkably well in the random binary perceptron problem. However, the BP algorithm has some features that make it implausible from the biological point of view. In SI Text, we show that with a number of simplifications, this algorithm can be transformed into a much simpler on-line algorithm that satisfies all of the requirements outlined above. The resulting algorithm is as follows:

• Compute I = ξ^τ·w^τ, where w_i^τ = sign (h_i^τ), then

• (R1) If I > 1, do nothing

• (R2) If I = 1 then

  1. If h_i^τξ_i^τ ≥ 1, then h_i^τ+1 = h_i^τ + 2ξ_i^τ
  2. Else do nothing

• (R3) If I ≤ −1 then h_i^τ+1 = h_i^τ + 2ξ_i^τ.

These rules can be interpreted as follows. (R1) As I > 1, the synaptic input is sufficiently above threshold, such that a single synaptic (or single neuron) flip would not affect the neuronal output; therefore, all variables are kept unchanged. (R2) As I = 1, the synaptic input is just above threshold (a single synaptic or single neuron flip could have potentially brought it below threshold), then some of the hidden variables need to be changed. The variables that are changed are those that were going in the right direction; i.e., those that contributed to having the synaptic input go above threshold. Finally, for (R3), I < 0 so the output is incorrect and then all hidden variables need to be changed. The factor of 2 included in rules R2 and R3 guarantees that the hidden variables will still be odd when updated if they are initialized to be so.

Note that this algorithm has two distinct features compared with the perceptron algorithm. (i) Hidden variables obey update rules that are similar to those of the SP algorithm, but the actual synaptic weight is binary. (ii) One of the update rules, rule R2 (corresponding to a synaptic input just above threshold), is new compared with SP.

To investigate the effect of rule R2 on performance, we also simulated a stochastic version of the BPI algorithm, in which such a rule is only applied with probability p_s for each presented pattern:

• As BPI, except rule R2 is replaced by

• (R2) If I = 1, then

  1. with probability p_s:

     1. If h_i^τξ_i^τ ≥ 1, then h_i^τ+1 = h_i^τ + 2ξ_i^τ
     2. Else do nothing
  2. with probability 1 − p_s, do nothing.

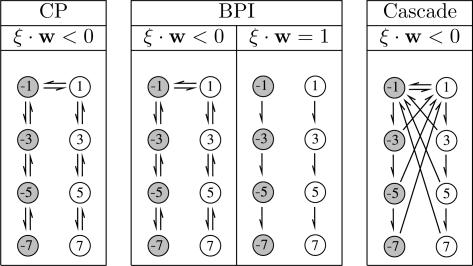
When the parameter p_s is set to 1, one recovers the deterministic BPI algorithm, whereas setting it to 0 (thus, in fact, removing rule R2) transforms it into a “clipped perceptron algorithm” (CP); i.e., a perceptron algorithm but with clipped synaptic weights. Both BPI and CP algorithms are sketched in Fig. 1.

Fig. 1.

Schematic representation of transitions between synaptic states in the CP algorithm and the BPI algorithm. The cascade model introduced by Fusi et al. (12) is shown for comparison. Circles represent the possible states of the internal synaptic variable h_i. Gray circles correspond to w_i = −1, and white circles correspond to w_i = 1. Clockwise transitions happen when ξ_i = 1, and counterclockwise transitions happen when ξ_i = −1. Horizontal transitions are plastic (change value of synaptic efficacy w_i), and vertical transitions are metaplastic (change internal state only). Downward transitions make the synapse less plastic, and upward transitions make the synapse more plastic. When the output of the neuron is erroneous, ξ · w < 0: transitions occur to the nearest-neighbor internal state. In the CP algorithm, when the output is correct, ξ · w > 0: no transitions occur. In the BPI algorithm, when the output is barely correct, ξ · w = 1 (a single synaptic flip could have caused an error): transitions are made toward less plastic states only. When the output is safely correct, ξ · w > 1: no transitions occur. In the cascade model, “down” transitions are toward nearest neighbors, whereas “up” transitions are toward the highest state with opposite sign. Transition probabilities decrease with increasing |h| (see ref. 12 for more details).

Performance with Unbounded Variables.

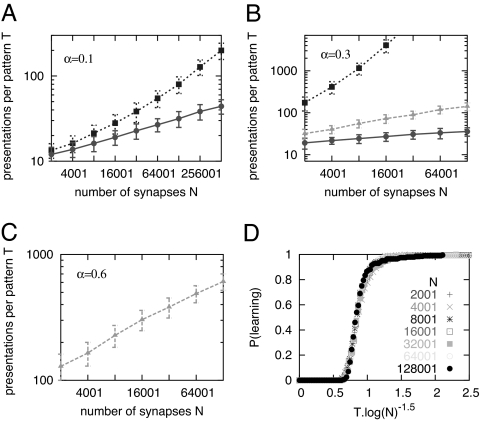
The performance of both deterministic and stochastic versions of the BPI algorithm was first investigated numerically with unbounded hidden variables, for different values of α, N, and p_s. It turns out that SBPI performs remarkably well, provided that the probability p_s is chosen appropriately—with p_s ≈ 0.3 the system can reach a capacity of order 0.65 with a convergence time that increases with N in a sublinear fashion (see Fig. 2). On the other hand, the deterministic BPI (p_s = 1) has a significantly lower capacity (α ≈ 0.3), but for those lower values of α it performs significantly faster than the SBPI algorithm—for α = 0.3 the time increases approximately as (log N)^1.5, as shown in Fig. 1D. As an example, the algorithm perfectly classifies 38,400 patterns with 128,001 synapses with ≈35 presentations of each pattern only. By eliminating completely rule R2 (i.e., CP), convergence time becomes exponential in N rather than logarithmic, for every tested value of α, as shown by the supralinearity of the blue curves in Fig. 2. Hence, the specificity of rule R2 with respect to synapses (only synapses that actually went in the right direction for the current pattern should be modified) is a crucial feature that makes the BPI algorithm qualitatively superior. Moreover, the convergence time increases only mildly with α, as shown in Fig. 2.

Fig. 2.

Performance of the BPI algorithm with unbounded hidden variables. (A–C) Convergence time vs. N for different values and α (indicated on each graph). Points correspond to the number of iterations per pattern until the algorithm converges averaged over 200 pattern sets; vertical bars are standard deviations. Dotted lines, CP; solid lines, BPI; dashed lines, SBPI with p_s = 0.3. The latter is the only one that can reach α = 0.6 but performs worse than BPI for α ≤ 0.3 (it is absent from A for clarity). (D) Probability that the BPI algorithm learns perfectly 0.3 · N patterns in less than T = x · log(N)^1.5 iterations per pattern vs. x for various values of N.

We also find that there is a tradeoff between convergence speed and capacity: for each value of α, there is an optimal value of p_s that minimizes average convergence time (shown in SI Fig. 6). This optimal value decreases with α; for α = 0.3, it is close to 1, and it decreases to 0.3 at α = 0.65. Hence, decreasing p_s enhances the capacity, at the cost of a slower convergence; nevertheless, Fig. 2C shows that for values of α ≤ 0.60, SBPI (p_s = 0.3) learns perfectly the set of input–output associations in a time that scales sublinearly with N. Above α ≥ 0.7, the algorithm fails to solve instances in a time shorter than the chosen cutoff time of 10⁴. Note that for p_s = 0.3, the convergence time depends in a more pronounced way on α than in the p_s = 1 case.

We have also investigated an algorithm in which p_s is itself a dynamical variable that depends on the fraction of errors averaged over a long time window—such an algorithm with an adaptive p_s is able to combine faster convergence at low values of α with high capacity associated with low values of p_s (not shown).

Performance with Bounded Hidden Variables.

We now turn to the situation when there is only a limited number of states K of the hidden variables h_i, since it is unrealistic to assume that a single synapse can maintain an arbitrarily large number of hidden states. Thus, we investigated the performance of an algorithm with symmetrical hard bounds on the values of the hidden states, |h_i| ≤ K − 1 for all i.

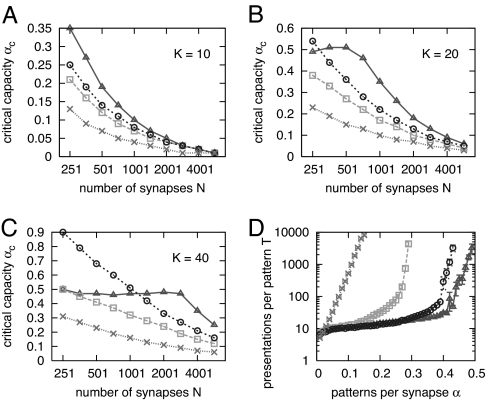
Fig. 3 shows what happens when the number of internal states is kept fixed while varying N. For the number of states we have considered (10 ≤ K ≤ 40), the optimal value of p_s is 1 since in general the stochastic version of the algorithm requires a larger number of states to be efficient. Here, we defined the capacity as the number of patterns for which there is 90% probability of perfect learning in 10⁴ iterations, and plotted in Fig. 3 the corresponding critical α against N for different values of the states number K, comparing BPI, CP, and the cascade model (defined as in Fig. 1). We also compared these algorithms that have only two “visible” synaptic states but K hidden states, with the SP algorithm with K visible states, w_i = h_i.

Fig. 3.

Performance of various algorithms with hard-bounded hidden variables. Triangles, BPI; squares, CP; circles, SP; crosses, cascade model. (A–C) Critical capacity vs. N, with fixed number of internal states K. (D) Convergence time vs. α at N = 1,415, K = 40, averaged over 100 samples. Figures for different number of states and synapses are qualitatively similar.

It turns out that BPI achieves a higher capacity than the SP algorithm with K visible states, when K is fixed and N is sufficiently large, even though the maximal capacity of the binary device is lower. Interestingly, adding an equivalent of rule R2 to the SP algorithm allows it to overcome BPI. This issue is further discussed in SI Text.

It is also interesting to note that at very low values of N, performance is better with 20 states than with an infinite number of states. Intuitively, this may be due to the fact that in the unbounded case some synapses are pushed too far and get stuck at high values of h_i, i.e., they lose all of their plasticity, while a solution to the learning problem would require them to come back to the opposite value of w_i.

Fig. 3D compares how convergence time changes with α for the same four algorithms, with the same number of synapses and same number of states per synapse: while the cascade model has a clear exponential behavior, the BPI and SP algorithms maintain nearly constant performance almost up to their critical point. The CP algorithm is somehow in between, its performance degrading rapidly with increasing α (note the logarithmic scale).

Following the observation that an appropriate number of internal states K can increase BPI capacity, we searched for the value of K that optimizes capacity and found that it scales roughly as $\sqrt{N}$ (see the corresponding section and SI Fig. 8); this is consistent with the observation that the distribution of hidden states scales as $\sqrt{N}$ (also discussed in SI Fig. 7). The fact that the capacity is optimal for a finite value of K makes the BPI algorithm qualitatively different from the other three, whose performances increase monotonically with K.

For a system with a number of states that optimizes capacity, the optimal value for p_s is 0.4, rather than 0.3 as in the unbounded case. With these settings it is possible to reach a capacity α_c of almost 0.7 bits per synapse, very close to the theoretical limit α_max ≃ 0.83. Convergence time at high values of α scales roughly linearly with N but with a very small prefactor (≈2 × 10⁻³).

Binary 0,1 Neurons and Synapses, Sparse Coding

The 0,1 Model Neuron.

±1 neurons with dense coding (equal probability of +1 or −1 inputs) have the biologically implausible feature of symmetry between the two states of activity.

A first step toward a more biologically plausible system is to consider the situation in which both the synaptic weights w_j and neurons are 0,1 binary variables, and the inputs are ξ_j^a = 1 with probability f, and 0 with probability (1 − f), where f ∈ [0,0.5] is the “coding level.” In this case, we need to take a nonzero threshold θ > 0. In the following, we choose the threshold to be ≈0.3N f (see SI Text for details). We consider each input pattern a to have a desired output σ^a = 1 with probability f and σ^a = 0 with probability (1 − f).

The new classification problem amounts at finding a vector w that satisfies the p equations:

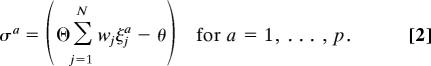The Optimized Algorithm.

The BP scheme can be straightforwardly applied to the 0,1 perceptron (see SI Text for details); the resulting BPI algorithm is very similar to the one presented above, with two major differences. (i) The quantity to be evaluated at each pattern presentation is not the total input I = Σ_jξ_j^τw_j^τ but rather the “stability parameter” Δ = (2σ^τ − 1)(I − θ), which is positive if the pattern is correctly classified and negative otherwise. (ii) Synaptic weights are now computed as $w_i^{\tau }=\frac{1}{2}(sign(h_i^{\tau })+1)$, making the synapse active (inactive) if the hidden variable is positive (negative), respectively. The 0,1 algorithm is then the same as the one for the ±1 case, in which Δ replaces I. The performance of this algorithm is qualitatively very similar to the one for the ±1 case, with a lower capacity; ≈0.25, to be compared with a theoretical limit of 0.59 (26). We have explored variants of the basic BPI algorithm. In particular, we have studied a stochastic version of the algorithm in which rule R2 is applied with probability p_s, but only for those patterns that require σ^a = 0. This SBPI01 algorithm consists in

• Compute I = ξ^τ·w^τ, where w_i^τ = ½ (sign (h_i^τ) + 1), and Δ = (2σ^τ − 1)(I − θ), then

• (R1) If Δ ≥ θ_m = 1, then do nothing

• (R2) If 0 ≤ Δ ≤ θ_m = 1, then

  1. If σ^τ = 0, with probability p_s, if w_j^τ = 0, then h_j^τ+1 = h_j^τ − 2ξ_j^τ;
  2. Else do nothing

• (R3) If Δ < 0, then h_i^τ+1 = h_i^τ + 2ξ_i^τ(2σ^τ − 1),

where we have introduced θ_m, the threshold for applying rule R2. Since rule R2 is only applied to patterns with zero output σ^τ, the metaplastic changes affect only silent synapses (for which w_j^τ = 0) involved in the pattern (those for which ξ_i^τ = 1). Note that using rule R2 only for patterns for which σ^a = 0 not only optimizes performance but also makes the algorithm simpler, since in this way there is only the need for one secondary threshold (θ − θ_m) instead of two (which would have been required if rule R2 had to be applied in all cases). The opposite choice, i.e., using rule R2 only for patterns for which σ^a = 1, can also be taken with similar results.

As in the preceding case, introducing boundaries for the hidden variables h_j can further improve performance, and the number of states K that maximizes capacity scales again roughly as $\sqrt{N}$ (shown in the SI Fig. 8). In the case of dense coding, f = 0.5, and using the optimal value p_s = 0.4, SBPI01 can reach a storage capacity α_c beyond 0.5 bits per synapse for sufficiently high N, very close to the maximum theoretical value α_max ≃ 0.59.

Heterogeneous Synapses and Sparse Coding.

One possible way to increase capacity with a very limited number of available states is to use “sparse” coding; i.e., a low value for f. In an unsupervised learning scenario, it has been shown that purely binary synapses (e.g., only two hidden states) can perform well if f is chosen to scale as log N/N (6, 10). Here, we chose an intermediate scaling $f=1/\sqrt{N}$. In addition, we also introduced heterogeneity in synaptic efficacies. Possible synaptic weights were no longer 0 and 1, but 0 and a_i, where a_i was drawn from a Gaussian distribution with mean 1 and standard deviation 0.1. Likewise, the threshold θ_m used for the implementation of rule R2 was drawn randomly at each pattern presentation from a Gaussian distribution centered in 1 with variance 0.1 The resulting algorithm SBPI-Het was shown to have very similar performance to SBPI01 in the f = 0.5 case.

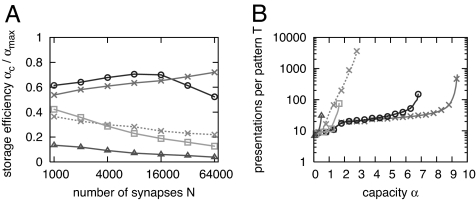
In Fig. 4A, we show the maximum capacity α_c (defined as for Fig. 3) reached in the sparse coding case divided by the maximum theoretical value α_max (which depends on f), with p_s = 1, N ranging from 1,000 to 64,000 and low number of internal states. The figure shows that a synapse with only two states (i.e., with no metaplasticity) has a capacity of only ≈10% of the maximal capacity in the whole range of N investigated. Adding hidden states up to K = 10 improves significantly the performance, which reaches ≈70% of the maximal capacity for sizes of N of order 10,000. In fact, for such values of N the capacity decreases when one further increases the number of states. The optimal number of states increases with N as in the dense coding case but with a milder dependence on N. In fact, simple arguments based on unsupervised application of rule R2 predicts in this case an optimal number of states scaling as $N^{1/4}/\sqrt{\text{log}N}$, which seems to be roughly consistent with our numerical findings. Fig. 4B shows convergence time versus α for N = 64,000. It demonstrates again the speed of convergence of the SBPI algorithm, whereas the cascade model is significantly slower.

Fig. 4.

Performance of SBPI-Het for different number of states K, with coding level f = N^−1/2. The number of samples ranges from 100 for N = 1,000 to 10 for N = 64,000. Triangles, K = 2; squares, K = 4; circles, K = 10; crosses, K = 20; dashed line, cascade model with K = 20. (A) Storage efficiency vs. N. (B) Convergence time vs. α for N = 64,000.

Robustness Against Noise.

Binary devices have the advantage of simplicity and robustness against noise. Here, we briefly address the issue of resistance against noise that might affect the multistable hidden states. Intuitively, the fact that the synaptic weights in the BPI algorithm only depend on the sign of the corresponding hidden variables suggests that a device implementing such a learning scheme would be more resistant against accidental changes in the internal states with respect to a device in which the multistable state is directly involved in the input summation. We verified this by comparing a perceptron with binary synapses and K hidden states implementing the SBPI algorithm with a perceptron with synapses with K visible states implementing the SP algorithm, both in the unbounded and in the bounded cases. The protocols used for testing robustness and the corresponding results are presented in SI Text.

In all of the situations we tested, we found a pronounced difference between the two devices, confirming the advantage of using binary synapses in noisy environments or in presence of unreliable elements.

Discussion

In this article, we have shown that simple on-line supervised algorithms lead to very fast learning of random input–output associations, up to close to the theoretical capacity, in a system with binary synapses and a finite number of hidden states. The performance of the algorithm depends crucially on a rule that leads to synaptic modifications only if the currently shown pattern is “barely learned”; that is, a single synaptic flip would lead to an error on that pattern. In this situation, the rule requires the synapse to have metaplastic changes only. Only synapses that contributed to the correct output need to change their hidden variable, in the direction of stabilizing the synapse in its current state. This rule originates directly from the BP algorithm. We have shown that this addition allows the BPI algorithm to learn a fraction of bits of information per synapse with at least roughly an order of magnitude fewer presentations per pattern than any other known learning protocol already at moderate system sizes and moderate values of α. Furthermore, for a neuron with ≈10⁴ to 10⁵ synapses, when α ∈ [0.3–0.6], the BPI algorithm finds a solution with a few tens of presentations per pattern, whereas the CP algorithm is unable to find such a solution in 10⁴ presentations per pattern. Finally, we showed that this algorithm renders a model with only two visible synaptic states and K hidden states much more robust to noise than a model with K visible states.

Other recent studies have considered the problem of learning in networks with binary synapses. Senn and Fusi (27) introduced a supervised algorithm that is guaranteed to converge for an arbitrary set of linearly separable patterns, provided there is a finite separation margin between the two classes. For sets of random patterns, this last requirement limits learning to a number of patterns that does not increase with N. Fusi et al. (12) introduced a model that bears similarity with the model we consider (binary synapses with a finite number of hidden states), with unsupervised transitions between hidden states. We have shown here that a supervised version of this algorithm performs significantly worse than the BPI algorithm.

Since the additional simple rule R2 has such a spectacular effect on performance, we speculate that neurobiological systems that learn in the presence of supervision must have found a way to implement such a rule. The prediction is that when a system learns in the presence of an “error” signal and synaptic changes occur in presence of that signal, then metaplastic changes should then occur in the absence of the error signal but when the inputs to the system are very close to threshold. After exposure to such an input, it should be more difficult to elicit a visible synaptic change, since the synaptic hidden variables take larger values. The fact that the algorithms developed here are digital during retrieval and that discrete (even noisy) hidden variables are only needed during learning could also have implications in large-scale electronic implementations, in which the overhead associated with managing and maintaining multistable elements in a reliable way may be of concern.

Abbreviations

BP

belief propagation

BPI

BP-inspired

CP

clipped perceptron

SBPI

stochastic BPI

SP

standard perceptron.