Abstract
The paper addresses a common problem in the analysis of high-dimensional high-throughput “omics” data, which is parameter estimation across multiple variables in a set of data where the number of variables is much larger than the sample size. Among the problems posed by this type of data are that variable-specific estimators of variances are not reliable and variable-wise tests statistics have low power, both due to a lack of degrees of freedom. In addition, it has been observed in this type of data that the variance increases as a function of the mean. We introduce a non-parametric adaptive regularization procedure that is innovative in that : (i) it employs a novel “similarity statistic”-based clustering technique to generate local-pooled or regularized shrinkage estimators of population parameters, (ii) the regularization is done jointly on population moments, benefiting from C. Stein's result on inadmissibility, which implies that usual sample variance estimator is improved by a shrinkage estimator using information contained in the sample mean. From these joint regularized shrinkage estimators, we derived regularized t-like statistics and show in simulation studies that they offer more statistical power in hypothesis testing than their standard sample counterparts, or regular common value-shrinkage estimators, or when the information contained in the sample mean is simply ignored. Finally, we show that these estimators feature interesting properties of variance stabilization and normalization that can be used for preprocessing high-dimensional multivariate data. The method is available as an R package, called ‘MVR’ (‘Mean-Variance Regularization’), downloadable from the CRAN website.
Keywords: Bioinformatics, Inadmissibility, Regularization, Shrinkage Estimators, Normalization, Variance Stabilization
1. Introduction: Estimation of Population Parameters
1.1. Scope - Motivation
We introduce a regularization and variance stabilization method for parameter estimation, normalization and inference of data with many variables. In a typical setting, this method applies to high-dimensional high-throughput ‘omics’-type data, where the number of variable measurements or input variables (gene, peptide, protein, etc . . . ) hugely dominates the number of samples (so called p ≫ n paradigm). The data may be any kind of continuous covariates.
It is common to deal in high-dimensional setting with the following issues:
A severe lack of degrees of freedom, generally due to tiny sample sizes (n ≪ 1), where usual variable-wise estimators lack of statistical power (Storey et al., 2004; Smyth, 2004; Tong and Wang, 2007; Wang et al., 2009) and lead to false positives (Efron et al., 2001; Tusher et al., 2001).
Spurious correlation and collinearity between a large number of variables (p ≫ 1) in part due to the nature of the data, but most of which due to an artifact of the dimensionality (see (Cai and Lv, 2007; Fan and Lv, 2008) for a detailed discussion). In addition, False Detection Rates (FDR) get high in part because of the regression-to-the-mean effect induced by correlated parameter estimates (Ishwaran and Rao, 2005).
Variables in high-dimensional data recurrently exhibit a complex mean- variance dependency with standard deviations severely increasing with the means (Rocke and Durbin, 2001; Huber et al., 2002; Durbin et al., 2002), while statistical procedures usually assume their independence.
In general, statistical inference procedures rely on a set of assumptions about the ideal form of the data such as normality of the measurements or errors, sample group homoscedasticity, and i.i.d variables. These issues make usual assumptions unrealistic, usual moment estimators unreliable (generally biased and inconsistent), and inferences inaccurate. The goal of this method is to get lower estimation errors of mean and variance population parameters and more accurate inferences in high-dimensional data.
1.2. Estimation in High-Dimensional Setting
A large majority of authors have used regularization techniques for estimating population parameters in high dimensional data. The premise is that because many variables are measured simultaneously, it is likely that most of them will behave similarly and share similar parameters. The idea is to take advantage of the parallel nature of the data by borrowing information (pooling) across similar variables to overcome the problem of lack of degrees of freedom.
Non-parametric regularization techniques for variance estimation have shown that shrinkage estimators can significantly improve the accuracy of inferences. Jain et al. (Jain et al., 2003), proposed a local-pooled error estimation procedure, which borrows strength from variables in local intensity regions to estimate variability. Shrinkage estimation was used by Wright & Simon (Wright and Simon, 2003), Cui et al. (Cui et al., 2005) and Ji & Wong (Ji and Wong, 2005). Similarly to Jain et al., Papana & Ishwaran (Papana and Ishwaran, 2006) proposed a strategy to generate an equal variance model. This is a form of variance stabilization that is achieved by quantile regularization of sample standard deviations by means of a recursive partitioning (CART-like) algorithm, which was initially used in Bayesian model selection (Ishwaran and Rao, 2005). Tong and Wang proposed a family of optimal shrinkage estimators for variances raised to a fixed power (Tong and Wang, 2007) by borrowing information across variables. The idea of borrowing strength across variables was also recently exploited by Efron in gene sets enrichment analyses (Efron and Tibshirani, 2007), and by Storey's Optimal Discovery Procedure (ODP) to control for compound error rates in multiple-hypothesis testing (Storey, 2007).
Shrinkage estimators have also been successfully combined with empirical Bayes approaches, where posterior estimators have been shown to follow distributions with augmented degrees of freedom, greater statistical power, and far more stable inferences in the presence of few samples (Lonnstedt and Speed, 2002; Smyth, 2004). Following this approach, Baldi & Long estimated population variances by a weighted mixture of the individual variable sample variance and an overall inflation factor selected using all variables (Baldi and Long, 2001). Lonnstedt & Speed (Lonnstedt and Speed, 2002) and later Smyth (Smyth, 2004) proposed an empirical Bayes approach that combines information across variables. Kendziorski et al. extended the empirical Bayes method using hierarchical gamma-gamma and log-normal-normal models (Kendziorski et al., 2003).
In a similar vein, shrinkage estimation was also used to generate (Bayesian-or not) “moderated” statistics. There, variable-specific variance estimators are inflated by using an overall offset. Efron et al. derived a t-test that estimates the offset by using a percentile of the distribution of sample standard deviations (Efron et al., 2001). Tusher et al. (Tusher et al., 2001) and Storey & Tibshirani (Storey and Tibshirani, 2003) added a small constant to the variable-specific variance estimators in their t-test to stabilize the small variances (SAM). Smyth and Cui et al. proposed regularized t-tests and F-tests by replacing the usual variance estimator with respectively a Bayesian-adjusted denominator (Smyth, 2004) or a James-Stein-based shrinkage estimator (Cui et al., 2005).
A Commonality to all previous method is that (i) they focus on variance estimation alone, (ii) they involve shrinkage of the sample variance towards a global value, which is used for all variables.
First, regularization of the variance is still a problem if the variance depends on the mean and this dependency is ignored. For instance, denoting by yi,j the individual response (expression level, signal, intensity, . . . ) of variable j ∈ {1, . . . , p} (gene, peptide, protein, . . . ) in sample i ∈ {1, . . . ,p}, and the usual population standard deviation estimates by , clearly the assumption that a variance estimator can be used in common to all variables (i.e., an equal variance model where for all j ∈ {1, . . . , p ) is unrealistic because of the mean-dependency issue, and because we still expect sampling variability at play even if an homoscedastic model was true. Exploiting the observation that the variance is an unknown function of the mean (Rocke and Durbin, 2001; Huber et al., 2002; Durbin et al., 2002) and Stein's inadmissibility result on variance estimators (Stein, 1964), it is clear that shrinkage variance estimates should improve if information contained in the sample mean is known or estimated. In line, Wang recently proposed to use a constant coefficient of variation model and a quadratic variance-mean model for variance estimation as a function of an unknown mean (Wang et al., 2009).
Second, a model that has a variable-specific variance estimator will lack power due to the aforementioned lack-of-degrees-of-freedom issue in high-dimensional data. Using for instance a variable-by-variable z-score transformation such as for j ∈ {1, . . . , p}, using regular sample mean and standard deviation estimates and of variable j, will generate corresponding variable- specific mean and standard deviation estimates , and , both of which use n as sample size. As the number of variables always dominates the number of samples in large high-dimensional datasets, empirical evidence about univariate modeling approaches suggest that the usual variable-wise estimators of variance recurrently lead to false positives (Efron et al., 2001; Tusher et al., 2001), and suffer of a lack of statistical power (Storey et al., 2004; Smyth, 2004; Tong and Wang, 2007; Wang et al., 2009).
In summary, in large datasets, when p ≫ n, inferences based on common- global-value shrinkage estimators or on variable-specific estimators are not reliable, mostly due to violation of assumptions, overfitting (Efron et al., 2001; Tusher et al., 2001; Ishwaran and Rao, 2003, 2005; Cui et al., 2005; Papana and Ishwaran, 2006), or lack of power (Storey et al., 2004; Smyth, 2004; Tong and Wang, 2007; Wang et al., 2009), and test statistics based on these estimators are as yet likely to give misleading inferences. Moreover, even though parametric models, such as additive and multiplicative error models and their derivations have emerged for scale normalization (Rocke and Durbin, 2001; Huber et al., 2002; Durbin et al., 2002), the variance structure of the data may be of a more complex nature than can be accommodated by a parametric model. We propose a new nonparametric approach that uses an alternative type of shrinkage, being more akin to joint adaptive shrinkage, using a joint and local regularization technique of the mean and variance parameters. By exploiting the ideas of simultaneously compensating for the parameter dependency, and for the lack of statistical power by local-pooling of information, we get joint regularized shrinkage estimates of population means and variances. We show that these estimators can not only stabilize the variance for each variable, but also allow novel regularized tests statistics (e.g. t-test) with greater statistical power and improved overall accuracy.
1.3. Organization of the Article
Section 2 lays out the principle and notations of regularization and joint estimation of population mean and variance in a single or multi-group situation. Section 3 introduces the so-called similarity statistic as the basis of our clustering algorithm. Section 4 shows how to derive regularized statistics from our approach, and how to use them in significance tests to make inferences. With the help of a synthetic example, Section 5 demonstrates the adequacy of our procedure and its performance in inferring significance and in improved variance stabilization in comparison to competitive estimators and other normalization/variance stabilization methods. Finally, in Section 6, we show how the procedure applies to a large proteomics dataset and we compare its performance in inferring differential expression. The method is available as an R package, called ‘MVR’ (‘Mean-Variance Regularization’), downloadable from the CRAN website (http://cran.r-project.org/) (Dazard et al., 2011c).
2. Joint Adaptive Regularization Via Clustering
2.1. Idea
If one clusters variables by their individual parameter estimates, it then becomes possible to get improved cluster-pooled parameter estimates and make inferences about each variable individually with higher accuracy. Essentially, this amounts to generating an adaptive or local-pooled shrinkage estimator, similarly to Jain et al. (Jain et al., 2003) and Papana & Ishwaran (Papana and Ishwaran, 2006). Our idea is to simultaneously (i) borrow information across (similar) variables, as well as (ii) use the information contained in the estimated population mean by performing a bi-dimensional clustering of the variables in the mean-variance parameter space.
By identifying those clusters, which tend to gather all variables j that have similar population mean μj along with similar population standard deviations σj, one can derive cluster-pooled versions of location and scale parameters estimates, which in turn can be used to standardize each variable individually within them. This is an important type of regularization of the mean and variance parameters that is done in a joint and local manner, which we coined Joint Adaptive Mean-Variance Regularization.
2.2. Single Group Situation
Suppose that variables assume a certain cluster configuration, denoted with C clusters. How this configuration is found is detailed in the next section 3. Let Cl denotes the lth cluster for l ∈ {1, . . . , C}. Let denote the cluster variable j belongs to, for j ∈ {1, . . . , p}, i.e. the cluster membership indicator of variable , for l ∈ {1, . . . , C} and j ∈ {1, . . . , p}, where I(.) denotes the indicator function throughout the paper.
Let and for cluster lj be the cluster mean of sample mean and cluster mean of sample variance respectively. In practice, the cluster mean of sample mean and the cluster mean of sample variance are given by:
| (1) |
where lj denotes the cluster membership indicator of variable j, is the usual sample mean for variable j, and is the usual unbiased sample variance for variable j defined as:
| (2) |
Then, use these within cluster shared estimates to standardize all response variables individually as follows: for j ∈ {1, . . . , p}.
2.3. Multiple Groups Situation
Let Gk denotes the kth sample group for k ∈ {1, . . . , G}. Let be the group sample i belongs to, for i ∈ {1 , . . . , n}, i.e. the group membership indicator of sample , for k ∈ {1, . . . , G} and i ∈ {1 , . . , n}. To deal with multiple groups of samples and the issue of variances differing across groups, one initially performs a separate bi-dimensional clustering of the variables within each group k ∈ {1, . . . , G} as in the case of a single group (G = 1). Next, get an optimal cluster configuration for each group k ∈ {1, . . . , G} and merge the cluster configurations from all groups k ∈ {1, . . . , G} into a single refined cluster configuration , usually containing more clusters (see e.g. Papana and Ishwaran, 2006). For instance, in the case of two groups (G = 2) the merging scheme is as follows:
If we let nk = |Gk|, nk ≠ 1 for k ∈ {1, . . . , G}, such that , derive similarly before (see 2.2) for the cluster membership indicator lj of variable j, the cluster mean of pooled sample mean and the cluster mean of pooled sample variance as:
| (3) |
where and are respectively the usual pooled sample mean and pooled sample variance across groups for each individual variable j:
| (4) |
and and are respectively the usual sample mean and the unbiased sample variance for each individual variable j in group k.
| (5) |
Finally, use these within cluster shared estimates to standardize to standardize all response variables individually as before: for j ∈ {1, . . . , p}. Note that this approach is required if an equal variance model cannot be assumed between groups. In practise, this situation arises very often.
3. Clustering by Similarity Statistic
3.1. Similarity Statistic
Suppose that variables assume a certain cluster configuration with clusters. Recall that the goal is to find these clusters (and their number) in the combined set of sample means and standard deviations. We need to perform a bi-dimensional clustering of the individual variables in the sample mean-variance space. Note that a cluster configuration is not unique due to the NP-hardness of the clustering problem (see subsection ‘Computational Complexity Considerations’ in (Dazard et al., 2011c)). Clustering in our method can be done using any algorithm. We chose here e.g. the K-Means agglomerative clustering algorithm with s replicated random start seedings.
Assuming a clustering algorithm, a major challenge in every cluster analysis is the estimation of the true number of clusters (or centroids) in the data. To estimate the true number Ĉ of clusters in the combined set , we designed a measure of significance, called Similarity Statistic, which is a modified version of the Gap Statistic introduced by Tibshirani (Tibshirani et al., 2001).
Let pl = |Cl| for l ∈ {1, . . . , C}, such that . Assume for a given cluster configuration that the data have been centered and standardized to have within-cluster means and standard deviations of 0 and 1 respectively. Let be the sum of pairwise distances (typically taken to be Euclidean distances) of all variables in cluster Cr for r ∈ {1, . . . , l}. Most methods for estimating the true number of cluster in a data set are based on the pooled within cluster dispersion defined as the pooled within cluster sum of squares around the cluster means: . An estimate of the true number of clusters is usually obtained by identifying a “kink” in the plot of Wp(l) as a function of l ∈ {1, . . . , C}. The gap statistic is a method for identifying this kink. The idea is to standardize the curve of log{Wp(l)} = g(l) by comparing it with its expectation under an appropriate null reference distribution (Tibshirani et al., 2001).
Our version of the Similarity Statistic compares the curves of log{Wp(l)} to its expectation under an appropriate null reference distribution with true i) mean- 0 and ii) standard deviation-1 (e.g. a standard Gaussian distribution ~N(0, 1)). Define a corresponding Similarity Statistic, denoted Simp(l) for each cluster configuration with l clusters, by the absolute distance between the two curves:
| (6) |
where and denote respectively the pooled within cluster dispersion as a function of l and sample size p, and its expectation under the reference distribution. Our objective criterion for determining the true number C of clusters of variables is by finding the largest value of l for which the (dis)similarity Simp(l) between the two distributions will be minimal:
| (7) |
The advantage of the Similarity Statistic is that it works well even if the true number of clusters is C = 1, where most other methods are usually undefined (Tibshirani et al., 2001). On the other hand, profiling the Similarity Statistic may be computationally intensive and may require usage of parallel computing (see subsection ‘Computational Complexity Considerations’ in (Dazard et al., 2011c)).
3.2. Estimation
Our estimate Ĉ of the true number of clusters of variables is done after assessing the sampling distribution of the Similarity Statistic. By sampling from the null distribution, we account for sampling variability even when the true parent distribution has the desired true moments. In practice, we estimate and the sampling distribution of Simp(l) by drawing B Monte-Carlo replicates from our standard Gaussian reference distribution. If we let the estimate expectation be , denoted by L̄, then the corresponding gap statistic estimate is:
| (8) |
The objective criterion to estimate the true number C of cluster is to take the largest value of l for which is minimal up to one standard deviation, i.e. by using the usual one-standard deviation rule Hastie et al. (2009):
| (9) |
where the estimated standard deviation as a function of l under a sample of size p is denoted
| (10) |
Notice in the Similarity Statistic profile of Figure 1 that the goodness of fit of the transformed data relative to the hypothesized underlying reference distribution degrades for smaller or larger cluster numbers than Ĉ. This over/under-regularization must be viewed as a form of over/under-fitting. A cluster configu-ration with a too small number of variable clusters Ĉ would lead to under-fitting (due to increased bias), while larger numbers would lead to over-fitting (due to increase variance). In other words, minimizing the (dis)similarity against an appropriate reference distribution is a way to optimize the bias-variance trade-off, i.e. to minimize the average Mean Squared Error (MSE) in the mean and variance estimates across variables. This automatic way of choosing an optimal number of variable clusters represents a significant advantage in parameter estimation.
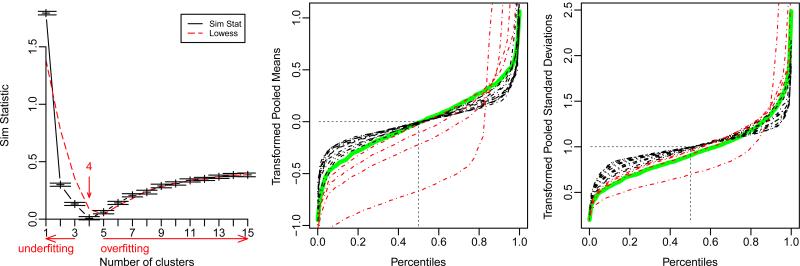
Figure 1.
Example with a single group design. Typical similarity statistic profile (left) showing the estimated number of clusters for the optimal clustering configuration. The vertical red arrow indicates the result of the stopping rule: i.e. the largest value of l for which is minimal up to one standard deviation. Directions of over/under-fitting are indicated. Red dashed line depicts the LOESS scatterplot smoother. Empirical quantile profiles of means (middle) and standard deviations (right) for each clustering configuration (dashed red and black lines) are shown to check how the distributions of first and second moments of the transformed data fit their respective theoretical null distributions under a given cluster configuration. The single cluster configuration, corresponding to no transformation, is the most vertical curve, while the largest cluster number configuration reaches horizontality. Notice how empirical quantiles of transformed pooled means and standard deviations converge (from red to black) to the theoretical null distributions (solid green lines) for the optimal configuration.
Empirically-determined factors at play in the Ĉ estimate are: (i) the dimensionality/sample size ratio p/n (larger p/n ⇒ larger Ĉ, (ii) the signal/noise ratio (lower ratio tends to create some over-regularization), and (iii) whether a pre-transformation has been applied (a pre-log transformation tends to create some under-regularization). In practise, the user input is required to specify how many clusters are to be explored in the search for the optimal cluster configuration. Specifically, what is the range l ∈ {1, . . . , Cmax} of number of clusters over which the Similarity Statistic is to be profiled to find its minimum and Ĉ estimate (see Figure 1). Empirically, we observed that a value of Cmax = 30 is sufficient in most cases.
The quantile diagnostic plots of Figure 1 uses empirical quantiles of the transformed means and standard deviations to check how closely they are approximated by theoretical quantiles derived from a standard normal equal-mean / homoscedastic model (solid green lines) under a given cluster configuration. To assess this goodness of fit of the transformed data, theoretical null distributions of the mean and variance are derived from a standard normal equal-mean / homoscedastic model with independence of the first two moments, i.e. assuming i.i.d. normality of the raw data. However, we do not require i.i.d. normality of the data in general: these theoretical null distributions are just used here as convenient ones to draw from. Note that under the assumptions that the raw data is i.i.d. standard normal (N(0, 1)) with independence of first two moments, the theoretical null distributions of means and standard deviations for each variable j are respectively: and (see Figure 1).
To address the above considerations, the user interface ‘Cluster Diagnostic’ in our R package ‘MVR’ helps determine (i) whether the minimum of the Similarity Statistic is observed (i.e. a large enough number of clusters has been accommodated), and (ii) whether the corresponding cluster configuration is a good fit (see (Dazard et al., 2011c)).
3.3. Algorithm
The overall algorithm of our procedure is as follows (1):
Algorithm 1.
Joint Adaptive Mean-Variance Regularization
| 1. for l = 1 to Cmax do |
| • Select a variable cluster configuration with l clusters. |
| • Standardize each variable individually using corresponding estimates where . |
| • Compute the corresponding Similarity Statistic estimates as in 8. |
| 2. Find the optimal cluster configuration with Ĉ clusters, where Ĉ is determined as in 9. |
| 3. Standardize all variables individually using this optimal cluster configuration . After which, all means and variances of the transformed data are assumed to follow sampling distributions with target first moments, i.e. (0, 1) respectively. |
4. Regularized Test Statistics Under Unequal Group Variance Model
4.1. Introduction
In high dimensional data, there are typically a very large number of variables and a relatively small number of samples, mostly due to the costly nature of assessing many variables simultaneously. Among the many challenges this situation poses to standard statistical methods, standard test statistics usually have low power and are unreliable (see for instance (Lonnstedt and Speed, 2002; Ge et al., 2003; Storey et al., 2004; Smyth, 2004; Cui et al., 2005)). A variety of methods have been proposed in the literature to overcome this problem of lack of degrees of freedom (Rocke and Durbin, 2001; Baldi and Long, 2001; Efron et al., 2001; Tusher et al., 2001; Chen et al., 2002; Broberg, 2003; Wright and Simon, 2003; Strimmer, 2003; Jain et al., 2003; Smyth, 2004; Cui et al., 2005; Ji and Wong, 2005; Tong and Wang, 2007). Recently, Wang et al. (Wang et al., 2009) explained that because the means are unknown and estimated with few degrees of freedom, naive methods that use the sample mean instead of a better estimate of the true mean are generally biased because of the errors-in-variables phenomenon. Also, recall that in the general case we are dealing with multi-group designs with, say G groups of samples (along with C clusters of variables), and a priori unequal sample group variances. Under this design, the standard or regularized t-test statistics will also suffer from the violation of the sample group homoscedasticity distribution assumption.
Ideally, one wants to address these issues simultaneously. We show in the next section that our Mean-Variance Regularized population estimators overcome the aforementioned bias and avoid the unrealistic assumption of sample group homoscedasticity. In addition, we show that they also avoid the unrealistic assumptions of variable homoscedasticity and independence. Finally, we show that they result in greater statistical power when used in test statistics.
4.2. Mean-Variance Regularized t-Test Statistic
Using previous notations with G groups of samples, and C clusters of variables, define the cluster mean of group sample mean and the cluster mean of group sample variance for variable j and group k:
| (11) |
where lk,j is the cluster membership indicator of variable j in the lth cluster and kth group, and where is the cluster mean of group sample mean, and is the unbiased cluster mean of group sample variance for variable j and for group k (2.3). Considering the case of a two-sample group problem (G = 2), define a Mean-Variance Regularized unequal group variance t-test statistic, further denoted t - MV R, as follows:
| (12) |
4.3. Inferring Significance
Statistical procedures often assume homoscedasticity or at least homogeneity of variances across sample groups in multiple group designs such as e.g. in ANOVA designs. The usual standard or regularized test-statistics (Subsection 4.1) usually make this assumption with the exception of Welch's t — test (which uses an approximation to the degrees of freedom) in order to use e.g.-the pooled sample variance (across groups) as a population variance estimate. However, one does not want to make this assumption in reality. In fact, regular estimates of group sample variance for variable j in group k are generally not equal/similar across groups (see e.g. raw intensities plots in simulated and real data situations in Supplementary_Figures 8 and 13). Further, variables are not necessarily identically distributed. Our unpaired two-sided test-statistic 12 does not need to make these assumptions. These are important relaxations.
For the computation of test-statistic p-values, when the total number of permutations cannot be practically enumerated, Monte Carlo (approximate) permutation tests are generally used. Given that the underlying exchangeability assumption does not hold anymore under a heteroscedastic model for the sample group variances, one has to resort to non-exact tests such as the bootstrap test, which entails less stringent assumptions (Good, 2002). The estimated p-values provided by bootstrap methods (with replacement) are less exact than p-values obtained from permutation tests (without replacement) (Dudoit et al., 2002), but can be used to test the null hypothesis of no differences between the means of two statistics (Efron and Tibshirani, 1993) without assuming that the distributions are otherwise equal (Bickel, 2002).
For all variables j ∈ {1, . . . , p}, approximate p-values of our unpaired two- sided t - MV R test-statistic are therefore computed as follows. For each variable j, 1, . . . , B′ bootstrap test-statistics of t - MV R are generated. Each of which is generated by sampling (with replacement) the sample group labels of the i ∈ {1, . . . , n} response values yi,j. Then, for each variable j, and for each bootstrap sample b ∈ {1, . . . , B′}, one computes the corresponding null test-statistic, denoted . Finally, the collection forms the approximate null bootstrap distribution of the jth test-statistic t - MV R. The jth p-value is finally estimated by the proportion , where I(.) denotes the indicator function.
5. Simulation Study
5.1. Setup
To explore and compare the performances of our regularization and variance stabilization procedure, we consider a simulation study where the data, referred to as synthetic dataset, simulates a typical real scenario situation where (i) a complex mean-variance dependency exists, and (ii) the variances are unequal across sample groups.
Most popular parametric models for the variance function in the high-throughput data analysis literature include the constant coefficient of variation model and the quadratic variance-mean model (reviewed in (Wang et al., 2009)). In the latter model, the variance is assumed to be a quadratic function of the mean to account for the commonly observed positive dependency of the variance as a function of the mean. In addition, to overcome the problem of low response values (e.g. low measured intensity signals) in comparison to the background, several authors such as Rocke and Durbin (Rocke and Durbin, 2001), Chen et al. (Chen et al., 2002) and Strimmer (Strimmer, 2003) have added a specific additive and multiplicative error component to this model.
Let's assume the response variable for any given j ∈ {1, . . . , p} follows some unknown continuous location-scale family distribution: , where . Under the latter model, and considering a multi-group experimental design, the response variable can be written for each variable j ∈ {1, . . . , p} and each group k {1, . . . ,G} as a random variable Yk,j with additive and multiplicative random error terms and respectively, which are assumed independent and identically distributed (e.g. as ~ N(0, 1)), and where for group k: μk,j is the true group mean, is the true group variance, αk represents the group mean background noise (i.e. the mean response value of unexpressed variables in expression experiments) and ρk and νk are some group specific error coefficients (Rocke and Durbin, 2001). Let yi,k,j denote the response for variable j ∈ {1, . . . , p} in sample i ∈ {1, . . . , n} and group k ∈ {1, . . . ,G}.
| (13) |
We considered a slight variation of the above model, where the mean background noise βk in group k is subject to the multiplicative error as well (14):
| (14) |
In each model, the independence and normality assumptions of the error terms are made for convenient reasons. As Rocke & Durbin pointed it out, these are reasonable assumptions in practise (Rocke and Durbin, 2001). It can be shown that either model ensures two things simultaneously:
□ the sample variance for a variable is proportional to the square of its mean: In fact, using the delta method, one can derive the expectation and variance of the response variable Yk,j under the current assumptions, wherefrom it follows that:
In fact, for small values of Hj the signal Yk,j is approximately normally distributed, while for large values of Hj the signal Yk,j is approximately log-normal distributed:
When Hj falls in between these two extremes, all terms in model (14) play a significant role (Rocke and Durbin, 2001). In this case, the signal Yk,j is approximately distributed as a linear combination of both distributions. What this means for the response is that (i) for small values of Hj its variance is approximately independent of its mean by property of the normal distribution (which is known to be the only distribution for which the standard deviation is independent its mean); (ii) while for large values of Hj its variance is approximately proportional to its squared mean.
□ sample variances for a variable across groups are unequal for k ≠ k′:
In this simulation, we consider a balanced two-group situation (G = 2) from e.g. model 14 with sample size n1 = n2 = 5 and of dimensionality p = 1000 of variables. Using a Bernoulli distribution with probability parameter ⅕, we selected 20% of the variables as significant as follows. Let be the p-indicator vector of significant variables, where d ~ Bernoulli(⅕) for j {1, . . . ,p}. With 80% probability (corresponding to non-significant variables) we set , while the other 20% of the time (corresponding to significant variables) and were independently sampled an exponential density with mean λ1 and λ2 respectively, where λ1 and λ2 were independently sampled from the uniform distribution , and with λ1 ~ U[1, 10] and λ2 ~ [1, 10]. For our simulation, we set β1 = β2 = 15, ρ = 0.1 and ρ2 = 0.2, ν1 = 1 and ν2 = 3. In this particular setting, even though we set a common mean background noise (β1 = β2), because ν1 ≠ ν2 and ρ1 ≠ ρ2, this represents a real scenario situation where variances are unequal across groups. The following subsections describe results for the second model only (14).
5.2. Standardization and Transformation Results
We compared our Joint Adaptive Mean-Variance Regularization procedure (hereafter referred to as MV R) to several normalization or variance stabilization transformations, using exploratory and diagnostic plots: (i) log transformation of the data, hereafter referred to as LOG; (ii) Papana & Ishwaran's CART Variance Stabilization Regularization (Papana and Ishwaran, 2006) (CVSR); (iii) the generalized log (glog2(exp(b) · x + a) + c, where ) as described in Wolfgang Huber et al. (Huber et al., 2002) and Durbin et al. (Durbin et al., 2002) (VSN); (iv) a robust locally weighted regression (Cleveland, 1979) (LOWESS); (v) a natural cubic smoothing splines transformation (Workman et al., 2002) (CSS); (vi) quantile normalization method (this latter normalization procedure is designed to combine the features of quantile normalization and supposedly to perform variance stabilization at the same time) (Bolstad et al., 2003) (QUANT ); and finally (vi) Khondoker et al.'s nonparametric smoothing normalization approach that uses a generalized additive model for location, scale and shape simultaneously (Khondoker et al., 2007) (GAMLSS).
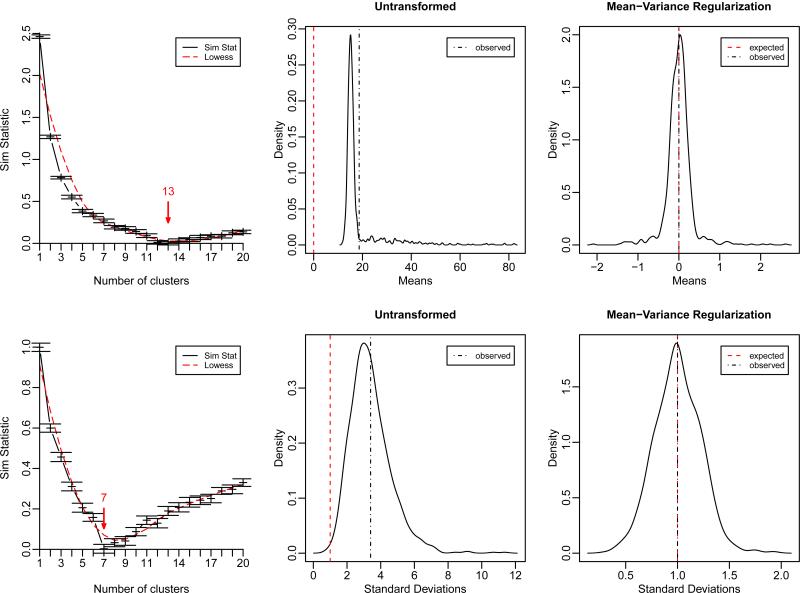
The similarity statistic profile of Figure 2 gives the estimated number of variable clusters by sample group. Using these estimates, we derived within cluster shared estimates of population means and variances and used them to standardize the variables according to our multi-group scheme 2.3. The result of MVR-transformation of the data in Figure 2 and Supplementary Figure 7 clearly shows that our algorithm is effective in terms of centering and scaling the data.
Figure 2.
First column: similarity statistic profiles giving the estimated number of variable clusters Ĉ1 = 13 andĈ2 = 10 for sample group G1 and G2 respectively. Red arrows indicate results of the stopping rule. Here, B = 128 Monte-Carlo replicates were drawn from a true mean-0, standard-deviation-1 model (N(0, 1)), and K-Means partitioning clustering algorithm was performed with s = 100 random start seedings. Middle and right columns: density distributions of pooled means and pooled standard deviations before (middle) and after (right) multi-group MV R-transformation. Notice how the sampling distributions of transformed means and standard deviations are centered about their target first moments (0, 1) respectively. Results are shown for the synthetic dataset from model 14.
Recall, however, that because the internal standardization is performed in a cluster-wise manner (i.e. not in an individual variable-wise manner), MV R does not intend to transform the data to achieve exact variable z-scores with individual mean-0, standard deviation-1. Instead, one expects to observe sampling distributions of transformed means and standard deviations centered about their target first moments (0, 1) respectively (Figure 2). In addition, after a successful MV R-transformation the variances are expected to be stabilized and approximately independent of the means (Figure 3).
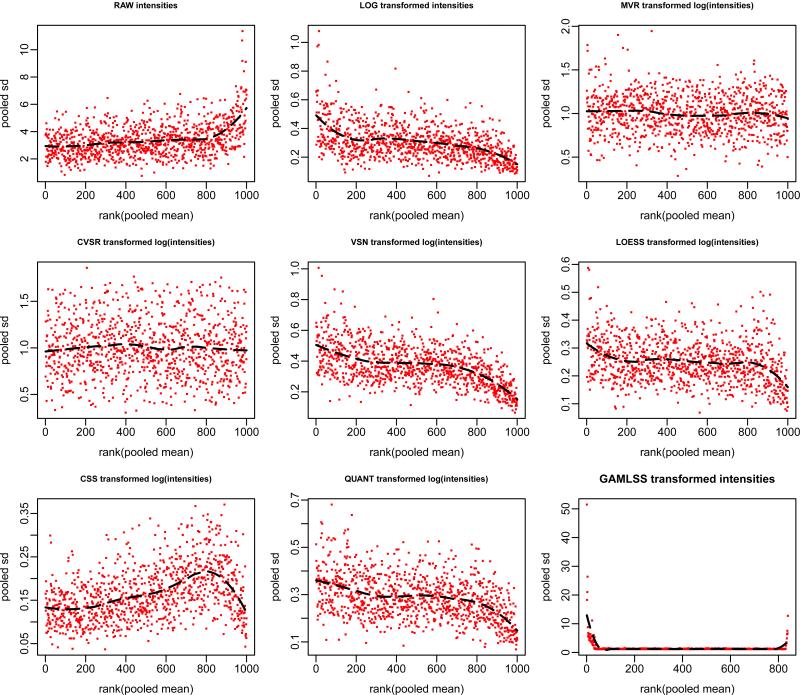
Figure 3.
Mean-SD scatter-plot for the synthetic dataset (model 14). This plot allows to visually verify the success of a variance stabilization, i.e. whether there is a dependence of the variance on the mean. Pooled sample variance across groups (pooled sd) are plotted are the against the ranks of pooled sample mean across groups (rank(pooled mean)) for each individual variable j under various transformations and variance stabilization procedures. The black dotted curve depicts the running median estimator (equal window-span of 0.5 for all procedures). In the absence of variance-mean dependence this curve is approximately linear horizontal. Notice how the variance increases as a function of the mean in the raw data (Figure 3), mimicking a real situation (see e.g. Supplementary Figure 11).
Figure 3 shows that only adaptive regularization techniques (CVSR and MVR) perform well in this respect. To quantify the fact that any normalization/variance stabilization procedure will not necessarily stabilize the variance across variables, we tested the null hypothesis for homogeneity of variances across variables: . Note that usually a standard Levene or Bartlett test would be used for that matter. However, because we do not have categorical variable to group the standard deviations, a trend test such as the Cox-Stuart trend test or the Mann-Kendall trend test is more appropriate (the latter is actually more a test for monotonic trend in a time series, based on the Kendall rank correlation). Table 1 reports the results of these tests for each procedure.
Table 1.
P-values of the one-sample two-sided Cox-Stuart (C-S) and Mann-Kendall (M-K) trend tests for the null hypothesis of no trend in the transformed standard deviations under several transformation or regularization methods. Results are shown for the synthetic dataset from model 14.
| RAW | LOG | MVR | CVSR | VSN | |
|---|---|---|---|---|---|
| C-S | 1.392 × 10–12 | 2.811 × 10–21 | 0.097 | 0.097 | 2.418 × 10–30 |
| M-K | 0 | 0 | 0.057 | 0.548 | 0 |
| LOESS | CSS | QUANT | GAMLSS | ||
|---|---|---|---|---|---|
| C-S | 4.954 × 10–7 | 1.131 × 10–23 | 2.665 × 10–12 | 8.785 × 10–2 | |
| M-K | 2.210 × 10–15 | 0 | 0 | 3.714 × 10–7 |
Notice the absence of trend of standard deviations in adaptive regularization techniques only such as CVSR and especially our method MVR, but not in any other procedures (Table 1). These results make amply clear the point that regular normalization and even variance stabilization procedures do not necessarily stabilize the variance, and may thereby be inappropriate for making inferences when homoscedasticity is assumed.
5.3. Regularized Test Statistics Results
Next, we used the previous simulated dataset from model 14 to assess the performance of our regularized variance estimator and its derived t-test statistic t - MVR vs. standard and various modified t-test statistics: (i) Welch's two- sample unequal variances t — REG t-statistic; (ii) Papana & Ishwaran's CART Variance Stabilized and Regularized t — CVSR t-statistic (Papana and Ishwaran, 2006); (iii) Baldi et al.'s Hierarchical Bayesian Regularized t — HBR t-statistic (Baldi and Long, 2001); (iv) Efron's Empirical Bayes Regularized t — EBR z-statistic (Efron et al., 2001); (v) Tusher et al.'s regularized SAM t — SR t-statistic (Tusher et al., 2001; Storey and Tibshirani, 2003); (vi) Smyth's Bayesian Regularized t — BR t-statistic (Smyth, 2004); and (vii) Cui et al.'s James-Stein shrinkage estimator-based Regularized t — JSR t-statistic (Cui et al., 2005). The new statistic is also compared to standard Welch's two-sample unequal variances t-test statistics, computed under previous common variance stabilization and/or normalization procedures (Subsection 5.2) and denoted t — LOESS, t — CSS, t — VSN, t — QUANT and t — GAMLSS. Here, the performance is assessed in terms of classification errors i.e. the statistical power to discriminate truly significant variables from the truly non-significant ones as measured by:
Because each test/procedure has a different cutoff value for identifying significant variables, statistics results had to be made comparable. Comparisons between tests/procedures were calibrated by selecting the top significant variables, ranked by absolute value of their t-test statistics. This avoids comparing the significant tests to the truth across the various test/procedure for a common arbitrary type-I error level or even an arbitrary FDR level to control for because there is no guarantee that the FDR level would be equal between tests/procedures (the number of significant tests as well as the number of within false positives, and therefore their ratio, may vary).
In this approach of fixing a percentile for the number of significant tests, notice that by taking a percentile (20%, i.e. variables with |tj| > t(1—0.2)) that is equal to the probability of success (⅕) that was used in our simulated data (see 5), we impose that the number of tests found significant be equal (up to sampling variability) to the number of true significant ones (i.e. the estimated model size equals the true model size). This translates into equating the number of False Positives to the number of False Negatives in a two-class situation (Table 2).
Table 2.
2 × 2 contingency table summarizing decisions versus truth in a two-class situation. Here and . The restriction that the number of tests found significant (V + S) be equal to the number of true significant ones (U + V) places a heavy restriction on the values of the table. In particular, we must have U + V = V + S and thus U = S, i.e. .
| Decision |
|||
|---|---|---|---|
| - | + | ||
| Truth | + | U | V |
| - | T | S | |
Table 3 reports Monte Carlo estimates of False Positives , False Negatives , and Total Misclassification . Overall, our Mean-Variance Regularized t-test statistic (t-MVR) outperforms other t-test statistics in terms of total misclassification errors (Table 3). Also, notice in Table 3 the loss of accuracy and power occurring: (i) in common normalization procedures that do not guarantee a stabilization of variance (t — REG, t — LOESS, t — CSS, t — QUANT or t — GAMLSS vs. e.g. t — VSN, t — MVR, t — CV SR), (ii) or in global variance stabilization procedures as compared to adaptive local regularization techniques (t — VSN vs. e.g. t — MVR, or vs. t — CVSR), (iii) or between regularization techniques themselves that use different population mean estimates (t — MVR vs. t — CVSR, t — HBR, t — EBR, t — SR, t — BR, t — JSR). Overall, this shows how sensitive these inferences are to a loss of accuracy and power, mostly due to small sample sizes and to violation of assumptions in dependency and heteroscedastic situations.
Table 3.
Number of False Positives , False Negatives and total Misclassifications estimates for each procedure (s.e), based on B = 512 Monte Carlo replicated synthetic datasets. With previous abbreviations (Subsection 5.2): LOG: log-transformed scale; RAW : untransformed scale. t – REG : regular two-sample unequal variances (Welch) t-test; t – MVR : Mean-Variance Regularized t-test; t – CVSR : CART-Variance-Stabilization Regularized t-test; t – HBR : Baldi's Hierarchical Bayesian Regularized t-test; t – EBR : Efron's Empirical Bayes Regularized z-test; t – SR : SAM Regularized t-test; t – BR : Smyth's Bayesian Regularized t-test; t – JSR : Cui et al.'s JamesStein Regularized t-test; t – VSN : VSN-transformed t-test; t – LOESS : LOESS-transformed t-test; t – CSS : CSS-transformed t-test; t – QUANT : QUANT-transformed t-test; t – GAMLSS : GAMLSS-transformed t-test. Results are shown on the RAW and LOG-scale for the synthetic dataset from model 14.
| t – REG | t – MVR | t – CVSR | t – HBR | t – EBR | ||
|---|---|---|---|---|---|---|
| LOG | 68.7 (0.8) | 62.8 (1.0) | 73.5 (0.8) | 61.1 (0.8) | 68.9 (0.8) | |
| 68.1 (0.8) | 62.2 (1.0) | 72.9 (0.8) | 60.5 (0.8) | 68.3 (0.8) | ||
| 136.7 (1.5) | 125.0 (1.9) | 146.5 (1.5) | 121.6 (1.5) | 137.1 (1.5) | ||
| RAW | 67.1 (0.8) | 57.6 (1.0) | 59.3 (0.8) | 62.5 (0.8) | 64.6 (0.8) | |
| 67.9 (0.8) | 58.5 (0.9) | 60.1 (0.8) | 63.4 (0.8) | 65.4 (0.8) | ||
| 135.0 (1.5) | 116.1 (1.8) | 119.4 (1.5) | 125.9 (1.5) | 130.0 (1.5) | ||
| t – SR | t – BR | t – JSR | t – VSN | t – LOESS | ||
|---|---|---|---|---|---|---|
| LOG | 73.8 (0.8) | 70.4 (0.8) | 70.4 (0.8) | 65.3 (0.8) | 70.4 (0.9) | |
| 73.2 (0.8) | 69.8 (0.8) | 69.9 (0.8) | 64.7 (0.8) | 69.8 (0.9) | ||
| 147.1 (1.5) | 140.2 (1.5) | 140.3 (1.5) | 130.0 (1.5) | 140.3 (1.7) | ||
| RAW | 63.0 (0.8) | 60.2 (0.8) | 60.1 (0.8) | 63.7 (0.8) | 69.5 (0.9) | |
| 63.8 (0.7) | 61.1 (0.8) | 60.9 (0.8) | 64.6 (0.8) | 70.3 (0.9) | ||
| 126.8 (1.4) | 4121.3 (1.5) | 121.0 (1.5) | 128.3 (1.5) | 139.8 (1.6) | ||
| t – CSS | t – QUANT | t – GAMLSS | ||||
|---|---|---|---|---|---|---|
| LOG | 69.7 (0.8) | 71.2 (0.8) | 68.7(0.8) | |||
| 69.1 (0.8) | 70.6 (0.8) | 68.1(0.8) | ||||
| 138.9 (1.5) | 141.8 (1.5) | 136.7(1.5) | ||||
| RAW | 69.3 (0.8) | 71.1 (0.8) | 67.1(0.8) | |||
| 70.1 (0.8) | 71.9 (0.8) | 67.9(0.8) | ||||
| 139.4 (1.5) | 143.0 (1.5) | 135.0(1.5) | ||||
5.4. Competitive Variance Stabilization & Regularization Methods
Normalization procedures that are commonly used in omics data preprocessing (Wolfgang Huber et al. and Durbin et al.'s variance stabilization procedure - Subsection 5.2) yield comparable classification errors compared to regularized test statistics (see t — VSN vs. t — MVR or t — CVSR test statistics in Table 3). Yet, surprisingly, VSN stabilizes poorly the variance in this simulation (Figure 3, Table 1), especially on the higher-hand means (Figure 3). In general, regularization procedures such as CVSR, HBR, EBR, SR, BR, and JSR, as well as MVR tend to be simultaneously the most efficient in stabilizing the variance (Figure 3, Table 1), and the most powerful in hypothesis testing (Table 3). Therefore, these regularization procedures turn out to be the only true competitors to each other.
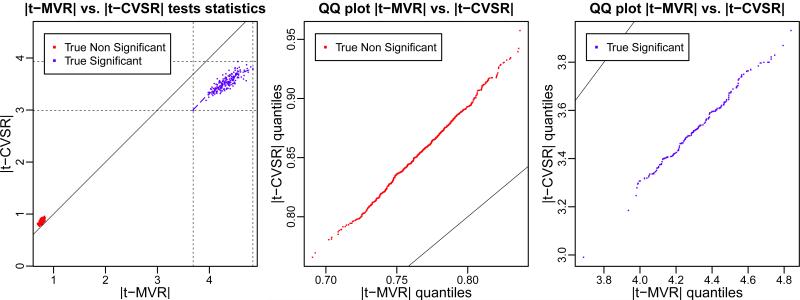
While CVSR and MVR regularization produce near perfect variance stabilization results (Figure 3 and Table 1), inferences from our regularized test statistic t — MVR outperform systematically t — CVSR (as well as all other regularization procedures: t — HBR, t — EBR, t — SR, t — BR, and t — JSR - Table 3). To elucidate what makes our MVR procedure more accurate than its counterpart CVSR, we compared Monte Carlo estimates of the regularized test-statistics t — MVR and e.g. t — CVSR, from B = 512 replicated synthetic datasets. A striking pattern arises when plotting the absolute value of the test-statistics |t — MVR| vs. |t — CVSR| and their quantiles against each other (Figure 4). What can be gathered from these plots is that the t — MVR test statistic is systematically larger in absolute value than t — CVSR for the variables that are truly significant (blue dots - Figure 4) and conversely for the variables that are truly non-significant (red dots - Figure 4). That is to say that a Joint Adaptive Mean-Variance Regularized shrinkage estimator systematically yields less false positive and more true positives than a variance-only shrinkage estimator in their corresponding test statistics t — MVR v.s. t — CVSR.
Figure 4.
Comparison of performance of our regularized test statistics t — MVR with its best competitor: t — CVSR for the synthetic dataset (model 14). Monte Carlo estimates of regularized test statistics are shown in absolute value: |t — MVR| and |t — CVSR|, based on B = 512 replicated synthetic datasets. Black solid line: identity line. Left: scatter-plot of |t — MVR| vs. |t — CVSR| tests statistics. Middle: Quantile-Quantile plot of |t — MVR| vs. |t — CVSR| for non-significant variables (red dots). Right: Quantile-Quantile plot of |t — MVR| vs. |t — CVSR| for significant variables (blue dots). Blue and red dashed lines are LOESS curves with a span of 0.3.
Population estimates used in t — MVR appeared to be less prone to estimation errors than those used in t — CVSR. This points to the recent work of Wang et al., who showed that when true means are unknown and estimated in high-dimensional settings with few degrees of freedom, naive methods that use the sample mean in place of a better estimate are generally biased (Wang et al., 2009). This implies that when the mean and variance are jointly included in the regularization procedure (as in ), both the numerator and the denominator of the t — MVR test-statistic tend to be better estimated, which ultimately translates into better inferences.
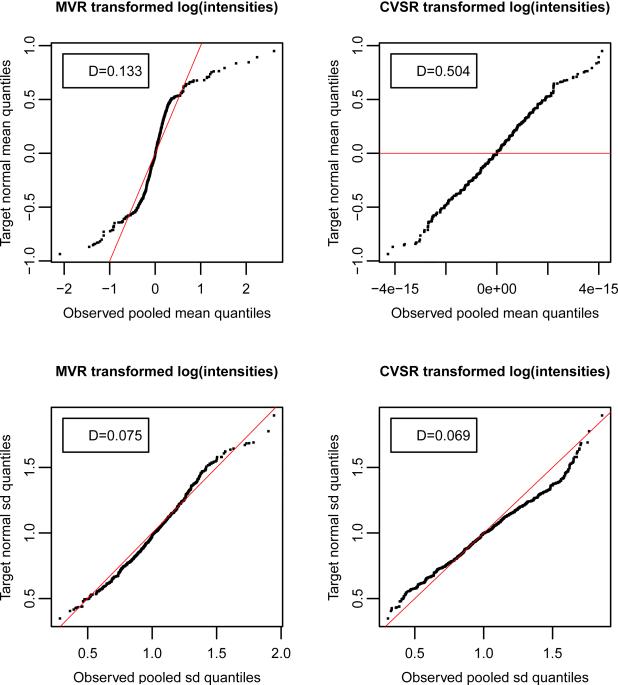
To further test this hypothesis, we first compared the local adaptive regularization procedures MVR vs. CVSR. We first followed a hypothesis framework and tested whether the empirical distributions of transformed means and standard deviations (for each variable j) after CVSR or MVR regularization follow their corresponding theoretical null distributions (i.e. under an arbitrary standard normal equal-mean/homoscedastic model). Using previous notations and assumptions, we tested the null hypotheses and respectively , or equivalently the following null hypothesis for j ∈ {1, . . . ,p}:
Notice immediately the greater lack of fit of transformed means by CVSR as compared to MVR (Table 4). This is precisely what we anticipated for the regularized means by CVSR and not by MVR.
Table 4.
One-sample two-sided Kolmogorov-Smirnov-test statistics Dn of the null hypothesis H01 for the regularized means, and H02 for the regularized standard deviations after either CVSR or MVR transformation. Note that Dn ∈ [0, 1], and that a larger value indicates more evidence to reject the null hypothesis.
| MVR | CVSR | |
|---|---|---|
| H 01 | 0.130 | 0.505 |
| H 02 | 0.127 | 0.104 |
We also plotted the observed empirical sample quantiles of transformed means and standard deviations for each variable j ∈ {1, . . . , p} after MVR or CVSR transformation versus those expected from their corresponding theoretical null distributions (i.e. under an arbitrary standard normal equal-mean/homoscedastic model). In general the variables are not necessarily normally distributed and not even independent and identically distributed before and/or after MVR or CVSR transformation. Therefore, the actual distributions of untransformed and/or transformed first and second target moments are usually unknown and differ from their respective theoretical null distributions, i.e., from for the means, and from for the standard deviations. This is reflected in the QQ plots, where observed quantiles do not necessarily perfectly align with theoretical values. However, notice especially the difference in lack of fit between transformed means by CVSR vs. MVR regularization procedures (Figure 5 - see also real data results in Supplementary Figure 12), and in the corresponding Table (Table 4).
Figure 5.
Comparative quantile-quantile plots to assess the goodness of fit or the lack thereof between observed target moments and those expected under an arbitrary equal-mean/homoscedastic data model. In case of good fit, estimated empirical sample quantiles from the observed data line up with those expected from the equal-mean/homoscedastic data model. Observed transformed means (top row) and standard deviations (bottom row) by MVR (left column) and CVSR (right column) regularization methods. Red line: inter-quartile line. One-sample two-sided Kolmogorov-Smirnov-test statistics are reported in boxes. Results are shown for the synthetic dataset from model 14.
These results clearly confirm that, when the sample size is relatively small, regular sample means are subject to bias, leading to increased average Mean Squared Error (MSE) of the means and variances estimates. In contrast, joint (local) shrinkage estimators of the mean and variance tend to be better estimates. Given the inherent bias-variance trade-off of any estimator, this seems to be achieved by minimizing the average MSE in both the mean and variance estimates across variables. Generally, under dependent parameters and especially under mean-variance dependency, a (local) shrinkage estimation procedure of population parameters is more likely to be accurate and to lead to better inferences when it is done jointly for all parameters.
6. Real Proteomics Dataset
6.1. Introduction
The regularization and variance stabilization procedure was tested on a real proteomics expression dataset. The dataset comes from a quantitative Liquid Chromatography/Mass Spectrometry (LC/MS) shotgun (bottom-up) proteomics experiment. It consists of n = 6 independent cell cultures of human of Myeloid Dendritic Cells (MDCs), prepared from normal subjects. Samples were split into a control (“M”) and a treated group (“S”), stimulated with either media alone or a Toll-Like receptor-3 Ligand respectively (G = 2 groups with 3 samples each).
The goal was to identify in vitro differentially expressed proteins between the two groups with top canonical biochemical pathways involved in the immune response of human MDCs upon TLR-3 Ligand binding, and eventually be able to monitor ex vivo the immune response of HIV patients in a future clinical study. To that end, we applied our Mean-Variance Regularization procedure (MVR) in order to stabilize the variance and get better population estimates in our regularized t — MVR test-statistic. The dataset is assumed to have been pre-processed for non-ignorable missing values, leaving a complete dataset with p = 9052 unique peptide sequences as predictor variables.
6.2. Normalization and Variance Stabilization of the Data
Using our multi-group regularization procedure in this real dataset, we estimated 11 peptide clusters for both sample groups “M” and “S” (Supplementary Figure 9). Standardization was then performed using our Mean-Variance Regularization and Variance Stabilization procedure (MVR) along with previous CART Variance Stabilization Regularization procedure (CVSR), simple log transformation, and other standard normalization/variance stabilization procedure (Subsection 5.2). We first verified that the transformed data is approximately standardized (Supplementary Figure 9) and normalized (Supplementary_Figure 10).
We also show the variance stabilization results for all these procedures in Supplementary Figure 11, and whether the transformed data fit or not an arbitrary equal-mean and homoscedastic model in Supplementary Figure 12. Clearly, MVR and CVSR perform the best in terms of removing the dependence of the variance on the mean (Supplementary_Figure 11) and in stabilizing the variance around a common value (Supplementary Figure_12).
6.3. Inferences - Differential Expression of Peptides
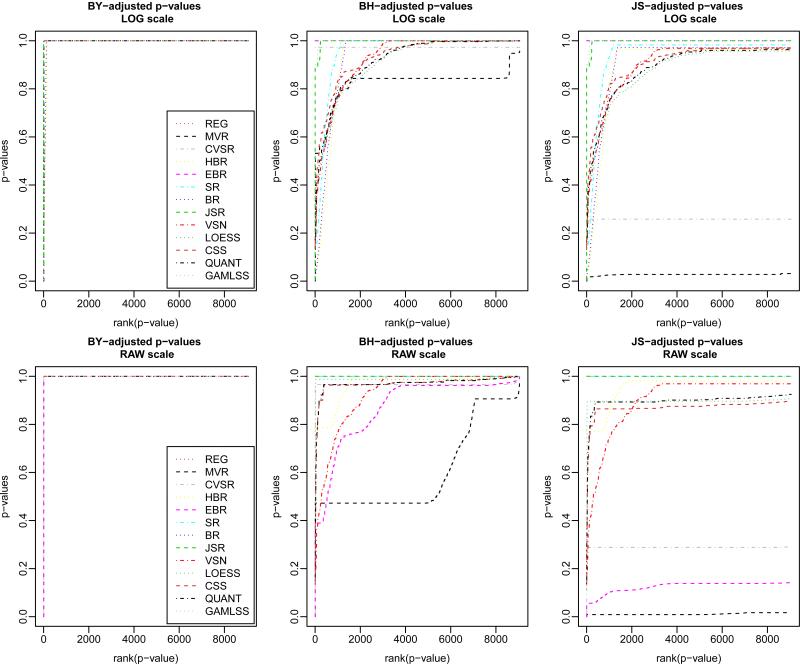
We compared the (FDR-controlled) number of significant peptides found differentially expressed in the “M” vs. “S” treatment contrast by our regularized unpaired two-sided t — MVR test-statistic vs. all the other tests statistics used in the previous section 5.3. Univariate FDR control procedures are known to be overly conservative when making inferences in high-dimensional settings (Genovese and Wasserman, 2002). In this example, this problem of large-scale inferences prompted us to report several FDR control procedures known for being more or less conservative. We report the numbers of significant adjusted p-values at fixed α levels of FDR ≤ α,α ∈ {0.01, 0.05} Yekutieli's FDR control procedure under variable dependency (BY) (Yekutieli and Benjamini, 2001), Benjamini-Hochberg's regular FDR control procedure (BH) (Benjamini and Hochberg, 1995), or John Storey's computation of the positive pFDR (JS) that was shown to be robust to a relaxation of the variable independence assumption (Storey et al., 2004). Results are reported in a two-way table, where test-statistics are crossed with RAW or LOG scales (Table 5).
Table 5.
Number of significant p-values (tests) found in the “M” vs. “S” treatment contrast of the real proteomics dataset as a function of test-statistics, FDR control procedure, and scale (RAW or LOG) at a fixed α level of False Discovery Rate (FDR ≤ α, α ∈ {0.01, 0.05}). Results are reported for each procedure with either Benjamini-Yekutieli's FDR control procedure under variable dependency (BY), Benjamini-Hochberg's regular FDR control procedure (BH), or John Storey's robust computation of the positive pFDR (JS). For the computation of the p-values, we followed the resampling scheme of Subsection 4.3 with B′ = 256 bootstrap samples.
|
t – REG |
t – MVR |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
BY |
BH |
JS |
|||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |
| LOG | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 11 | 11 | 11 | 11 | 9052 |
| RAW | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 7 | 7 | 7 | 5611 | 9052 |
|
t – CVSR |
t – HBR |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
BY |
BH |
JS |
|||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |
| LOG | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 17 | 23 | 75 | 23 | 78 |
| RAW | 6 | 6 | 6 | 6 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 |
|
t – EBR |
t – SR |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
BY |
BH |
JS |
|||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |
| LOG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| RAW | 3 | 3 | 3 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
|
t – BR |
t – JSR |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
BY |
BH |
JS |
|||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |
| LOG | 1 | 1 | 7 | 52 | 7 | 52 | 0 | 0 | 1 | 1 | 1 | 1 |
| RAW | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
t – VSN |
t – LOESS |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
BY |
BH |
JS |
|||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |
| LOG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| RAW | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
t – CSS |
t – QUANT |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
BY |
BH |
JS |
|||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |
| LOG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| RAW | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
t – GAMLSS |
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BY |
BH |
JS |
||||||||||
| 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | |||||||
| LOG | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| RAW | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
Overall, considering both RAW and LOG-scales, we observed that our regularized unpaired two-sided t — MVR test-statistic consistently yields larger numbers of significant peptides as compared to all other test-statistics for any given level of FDR and any given FDR control procedure (Table 5 and Figure 6). Thus, this result, combined with the fact the number of False Negatives in the synthetic dataset study was found less with our t — MVR test-statistic (Table 3), indicates that this is not simply a result of an increase in the number of False Positives , but rather a decrease in the number of False Negatives .
Figure 6.
Ranking of p-values found in the “M” vs. “S” treatment contrast of the real proteomics dataset as a function of test-statistics, FDR adjustment procedure, and scale (top row:LOG-scale - bottom row:RAW -scale). Results are reported for each procedure with either Benjamini-Yekutieli's FDR control procedure under variable dependency (BY), Benjamini-Hochberg's regular F DR control procedure (BH), or John Storey's robust computation of the positive pFDR (JS). For the computation of the p-values, we followed the resampling scheme as described in Subsection 4.3 with B′ = 256 bootstrap samples.
Also note that as our t — MVR test-statistic simultaneously takes advantage of regularization and stabilization of variance, the mean-variance dependency tends to be removed with our method from RAW to MVR-transformed data, and less violations of assumptions are made on (i) variables homoscedasticity (Supplementary_Figures 11, 12), and (ii) sample group homoscedasticity (Supplementary_Figures 8, 13).
7. Conclusion
To avoid unrealistic assumptions and pitfalls in inferences in high dimensional data, parameter estimation must be done carefully by taking into account the mean-variance dependency structure and the lack of degrees of freedom. Our non-parametric MVR regularization procedure performs well under a wide range of assumptions about variance heterogeneity among variables or sample groups in the multi-group design, and avoids by nature the problem of model mis-specification. In addition, it performs as well on either raw or log scales, which makes it altogether robust, versatile and promising. In practice, we recommend to use the MVR variance stabilization transformation for making inferences, and to use MVR test-statistics, applied on either RAW or possibly LOG-transformed data.
The improved performance of our joint regularized shrinkage estimators benefits from Stein's inadmissibility results (Stein, 1956, 1964), and Tong et al.'s recent extension (Tong and Wang, 2007). Essentially, when p 3 parameters are estimated simultaneously from a multivariate normal distribution with unknown mean vector, their combined estimator is more accurate than any estimator which handles the parameters separately, in that there exists alternative estimators, which always achieve lower risk under quadratic loss function (i.e. Mean Squared Error), even though the parameters and the measurements might be statistically independent (Stein, 1956). Later, Stein's showed that the ordinary decision rule for estimating a single variance of a normal distribution with unknown mean is also inadmissible (Stein, 1964). In addition, Tong and Wang recently showed that Stein's result for multiple means (Stein, 1956) extends to multiple variances as well (Tong and Wang, 2007). Our work benefits directly from the above combined inadmissibility results and shrinkage estimator in that the standard variance estimators are improved (i) when the information in the sample mean is known or estimated (Stein, 1964), and (ii) when regularization is used (Tong and Wang, 2007).
From these joint regularized shrinkage estimators, we showed that regularized t-like statistics offer significantly more statistical power in hypothesis testing than their standard sample counterparts, or regular common value-shrinkage estimators, or when the information contained in the sample mean is simply ignored. This result is a direct consequence of the strong mean-variance dependency and of the size/shape inherent to high-dimensional data. If one wants to jointly estimate the means and the variances in this type of data, the number of parameters to be simultaneously estimated can be as large as 2p. As Charles Stein states it, the possible improvement over the usual estimators can be quite substantial if p is large or p > n (Stein, 1964).
Supplementary Material
Acknowledgments
We thank Dr. Hemant Ishwaran for helpful discussion and for providing the R code of his CART Variance Stabilization and Regularization procedure (CVSR). This work was supported in part by the National Institutes of Health [P30-CA043703 to J-E.D., R01-GM085205 to J.S.R.]; and the National Science Foundation [DMS-0806076 to J.S.R.].
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplementary Materials
• Supplementary Figures 7, 8, 9, 10, 11, 12, 13.
• R package ‘MVR’, available from the CRAN website (Dazard et al., 2011c).
Conflict of Interest: None declared.
Contributor Information
Jean-Eudes Dazard, Division of Bioinformatics, Center for Proteomics and Bioinformatics, Case Western Reserve University. Cleveland, OH 44106, USA..
J. Sunil Rao, Division of Biostatistics, Dept. of Epidemiology and Public Health, The University of Miami. Miami, FL 33136, USA..
References
- Baldi P, Long AD. A bayesian framework for the analysis of microarray expression data: regularized t -test and statistical inferences of gene changes. Bioinformatics. 2001;17:509–19. doi: 10.1093/bioinformatics/17.6.509. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. (Series B).J R Statist Soc. 1995;57:289–300. [Google Scholar]
- Bickel D. Microarray gene expression analysis:data transformation and multiple comparison bootstrapping. 34th Symposium on the Interface, Computing Science and Statistics; Montreal, Quebec, Canada. 2002. pp. 383–400. [Google Scholar]
- Bolstad BM, Irizarry RA, Astrand M, Speed TP. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–93. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- Broberg P. Statistical methods for ranking differentially expressed genes. Genome Biol. 2003;4:R41. doi: 10.1186/gb-2003-4-6-r41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai T, Lv J. Discussion: The dantzig selector: Statistical estimation when p is much larger than n. The Annals of Statistics. 2007;35:23652369. [Google Scholar]
- Chen Y, Kamat V, Dougherty ER, Bittner ML, Meltzer PS, Trent JM. Ratio statistics of gene expression levels and applications to microarray data analysis. Bioinformatics. 2002;18:1207–15. doi: 10.1093/bioinformatics/18.9.1207. [DOI] [PubMed] [Google Scholar]
- Cleveland W. Robust locally weighted regression and smoothing scatter-plots. J Amer Stat Assoc. 1979;74:829–836. [Google Scholar]
- Cui X, Hwang JT, Qiu J, Blades NJ, Churchill GA. Improved statistical tests for differential gene expression by shrinking variance components estimates. Biostatistics. 2005;6:59–75. doi: 10.1093/biostatistics/kxh018. [DOI] [PubMed] [Google Scholar]
- Dazard JE, Xu H, Rao J. R package mvr for joint adaptive mean-variance regularization and variance stabilization. In: JSM Proceedings, editor. Section for Statistical Programmers and Analysts. American Statistical Association; Miami Beach, FL. USA.: 2011c. pp. 3849–3863. [PMC free article] [PubMed] [Google Scholar]
- Dudoit S, H. YY, Callow M, Speed TP. Statistical methods for identifying differentially expressed genes in replicated cdna microarray experiments. Statistica Sinica. 2002;12:111–139. [Google Scholar]
- Durbin BP, Hardin JS, Hawkins DM, Rocke DM. A variance-stabilizing transformation for gene-expression microarray data. Bioinformatics. 2002;18(Suppl 1):S105–10. doi: 10.1093/bioinformatics/18.suppl_1.s105. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. An Introduction to the Bootstrap. Chapman & Hall / CRC; London: 1993. [Google Scholar]
- Efron B, Tibshirani R. On testing the significance of sets of genes. The Annals of Applied Statistics. 2007;1:107–129. [Google Scholar]
- Efron B, Tibshirani R, Storey JD, Tusher V. Empirical bayes analysis of a microarray experiment. J Amer Stat Assoc. 2001;96:1151–1160. [Google Scholar]
- Fan J, Lv J. Sure independence screening for ultrahigh dimensional feature space. J R Statist Soc. 2008;70:849–911. doi: 10.1111/j.1467-9868.2008.00674.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge Y, Dudoit S, Speed TP. Resampling-based multiple testing for microarray data analysis. Test. 2003;12:1–77. [Google Scholar]
- Genovese C, Wasserman L. Operating characteristics and extensions of the false discovery rate procedure. J R Statist Soc. 2002;64:499–517. [Google Scholar]
- Good I. Extensions of the concept of exchangeability and their applications. J. Modern Appl. Statist. Methods. 2002;1:243–247. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Science; New York: 2009. [Google Scholar]
- Huber W, von Heydebreck A, Sultmann H, Poustka A, Vingron M. Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics. 2002;18(Suppl 1):S96–104. doi: 10.1093/bioinformatics/18.suppl_1.s96. [DOI] [PubMed] [Google Scholar]
- Ishwaran H, Rao JS. Detecting differentially expressed genes in microarrays using Bayesian model selection. J Amer Stat Assoc. 2003;98:438–455. [Google Scholar]
- Ishwaran H, Rao JS. Spike and slab gene selection for multigroup microarray data. J Amer Stat Assoc. 2005;100:764–780. [Google Scholar]
- Jain N, Thatte J, Braciale T, Ley K, O'Connell M, Lee JK. Local-pooled-error test for identifying differentially expressed genes with a small number of replicated microarrays. Bioinformatics. 2003;19:1945–51. doi: 10.1093/bioinformatics/btg264. [DOI] [PubMed] [Google Scholar]
- Ji H, Wong WH. Tilemap: create chromosomal map of tiling array hybridizations. Bioinformatics. 2005;21:3629–36. doi: 10.1093/bioinformatics/bti593. [DOI] [PubMed] [Google Scholar]
- Kendziorski CM, Newton MA, Lan H, Gould MN. On parametric empirical bayes methods for comparing multiple groups using replicated gene expression profiles. Stat Med. 2003;22:3899–914. doi: 10.1002/sim.1548. [DOI] [PubMed] [Google Scholar]
- Khondoker MR, Glasbey CA, Worton BJ. A comparison of parametric and nonparametric methods for normalising cdna microarray data. Biometrical journal. Biometrische Zeitschrift. 2007;49:815–23. doi: 10.1002/bimj.200610338. [DOI] [PubMed] [Google Scholar]
- Lonnstedt I, Speed TP. Replicated microarray data. Statistica Sinica. 2002;12:31–46. [Google Scholar]
- Papana A, Ishwaran H. Cart variance stabilization and regularization for high-throughput genomic data. Bioinformatics. 2006;22:2254–61. doi: 10.1093/bioinformatics/btl384. [DOI] [PubMed] [Google Scholar]
- Rocke DM, Durbin B. A model for measurement error for gene expression arrays. J Comput Biol. 2001;8:557–69. doi: 10.1089/106652701753307485. [DOI] [PubMed] [Google Scholar]
- Smyth GK. Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat Appl Genet Mol Biol. 2004;3:ARTICLE3. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- Stein C. Inadmissibility of the usual estimator for the mean of a multivariate distribution. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, University of California Press..1956. pp. 197–206. [Google Scholar]
- Stein C. Inadmissibility of the Usual Estimator for the Variance of a normal distribution with unknown mean. Vol. 16. Springer; Netherlands: 1964. [Google Scholar]
- Storey JD. The optimal discovery procedure: a new approach to simultaneous significance testing. J R Statist Soc. 2007;69(3):347368. [Google Scholar]
- Storey JD, E. TJ, D. S. Strong control, conservative point estimation, and simultaneous conservative consistency of false discovery rates: A unified approach. J R Statist Soc. 2004;66:187–205. [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genome wide studies. Proc Natl Acad Sci U S A. 2003;100:9440–5. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strimmer K. Modeling gene expression measurement error: a quasi-likelihood approach. BMC Bioinformatics. 2003;4:10. doi: 10.1186/1471-2105-4-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R, Walter G, Hastie T. Estimating the number of clusters in a data set via the gap statistic. (Series B).J R Statist Soc. 2001;63:411–423. [Google Scholar]
- Tong T, Wang Y. Optimal shrinkage estimation of variances with applications to microarray data analysis. J Amer Stat Assoc. 2007;102:113–122. [Google Scholar]
- Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci U S A. 2001;98:5116–21. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Ma Y, Carroll R. Variance estimation in the analysis of microarray data. J. R. Statist. Soc. B. 2009;71:425–445. doi: 10.1111/j.1467-9868.2008.00690.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Workman C, Jensen LJ, Jarmer H, Berka R, Gautier L, Nielser HB, Saxild HH, Nielsen C, Brunak S, Knudsen S. A new non-linear normalization method for reducing variability in dna microarray experiments. Genome Biol. 2002;3 doi: 10.1186/gb-2002-3-9-research0048. research0048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright GW, Simon RM. A random variance model for detection of differential gene expression in small microarray experiments. Bioinformatics. 2003;19:2448–55. doi: 10.1093/bioinformatics/btg345. [DOI] [PubMed] [Google Scholar]
- Yekutieli D, Benjamini Y. The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics. 2001;29:1165–1188. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.