Abstract
Internal friction, which reflects the “roughness” of the energy landscape, plays an important role for proteins by modulating the dynamics of their folding and other conformational changes. However, the experimental quantification of internal friction and its contribution to folding dynamics has remained challenging. Here we use the combination of single-molecule Förster resonance energy transfer, nanosecond fluorescence correlation spectroscopy, and microfluidic mixing to determine the reconfiguration times of unfolded proteins and investigate the mechanisms of internal friction contributing to their dynamics. Using concepts from polymer dynamics, we determine internal friction with three complementary, largely independent, and consistent approaches as an additive contribution to the reconfiguration time of the unfolded state. We find that the magnitude of internal friction correlates with the compactness of the unfolded protein: its contribution dominates the reconfiguration time of approximately 100 ns of the compact unfolded state of a small cold shock protein under native conditions, but decreases for more expanded chains, and approaches zero both at high denaturant concentrations and in intrinsically disordered proteins that are expanded due to intramolecular charge repulsion. Our results suggest that internal friction in the unfolded state will be particularly relevant for the kinetics of proteins that fold in the microsecond range or faster. The low internal friction in expanded intrinsically disordered proteins may have implications for the dynamics of their interactions with cellular binding partners.
Keywords: energetic roughness, Kramers theory, protein folding, Rouse model, single-molecule FRET
Conformational changes in proteins, including those involved in protein folding, are driven by thermal fluctuations. In the dense environment of an aqueous solution, these processes thus typically exhibit diffusive dynamics (1–4). A theoretical framework for describing such diffusive processes in the condensed phase is provided by Kramers-type theories, which have been successful in quantifying key properties of protein folding reactions (5–12). These theories predict the rate of folding to depend exponentially on the height of the folding free energy barrier, with a prefactor representing the “attempt frequency” of crossing the barrier. The latter is related to the inherent timescale at which the protein can diffusively explore its conformational space. As a result, the reaction rate is expected to depend on the friction (13). For simple reactions, only solvent friction may need to be taken into account, but in proteins, where the amino acid residues are only partially exposed to solvent, other dissipative, “internal friction” mechanisms are possible and result in a slowdown of the conformational dynamics. In particular, intrachain collisions, dihedral angle rotation, and other interactions within the polypeptide chain (1, 14, 15) lead to an increased “roughness” of the underlying energy landscape, thereby slowing conformational rearrangements within the molecule (16). Theory (5, 17), simulation (8, 12, 18–20), and recent experimental results (9, 11, 21–23) all indicate that changes in reconfiguration times due to changes in this internal friction can significantly modulate protein folding dynamics. In particular, the diffusive “speed limit” of the folding reaction (24), which is determined by the rate of reconfiguration of unfolded and nonnative conformations, should also be affected by internal friction.
Classic models of polymer dynamics, such as the Rouse and the Zimm models, present an opportunity to conceptualize the role of internal friction in unfolded proteins. These models provide estimates of the reconfiguration timescale of a polymer chain in a random-coil state given the average size of the coil and its translational diffusion coefficient (25). While in their original form they assume chain dynamics to be controlled only by the viscous drag from the solvent, internal friction can also be included. The analysis of experimental data with such models then allows a conceptually coherent quantification of internal friction. As pointed out above, internal friction effects may be due to a variety of mechanisms. Some of them would result in solvent-mediated (“wet”) friction, whose magnitude is proportional to the solvent viscosity (16). Others may lead to “dry” (or Cerf) friction, which is independent of the solvent viscosity (26). Differentiating between such mechanisms is essential for our understanding of the dynamics of the unfolded state, their role in folding, and the function of intrinsically disordered proteins (IDPs) (27, 28). Previous experiments have shown that changes in the dimensions of unfolded proteins or peptides (29–31) can be linked to changes in chain dynamics (21, 32, 33), and a role of internal friction at the transition state for folding has been demonstrated for several proteins (9, 15, 23, 34, 35). However, the contribution of internal friction to unfolded state dynamics has eluded experimental quantification (21, 36). Here we use single-molecule fluorescence experiments to quantify internal friction in unfolded proteins and IDPs.
Results
Dimensions and Dynamics from Single-Molecule FRET and Nanosecond FCS.
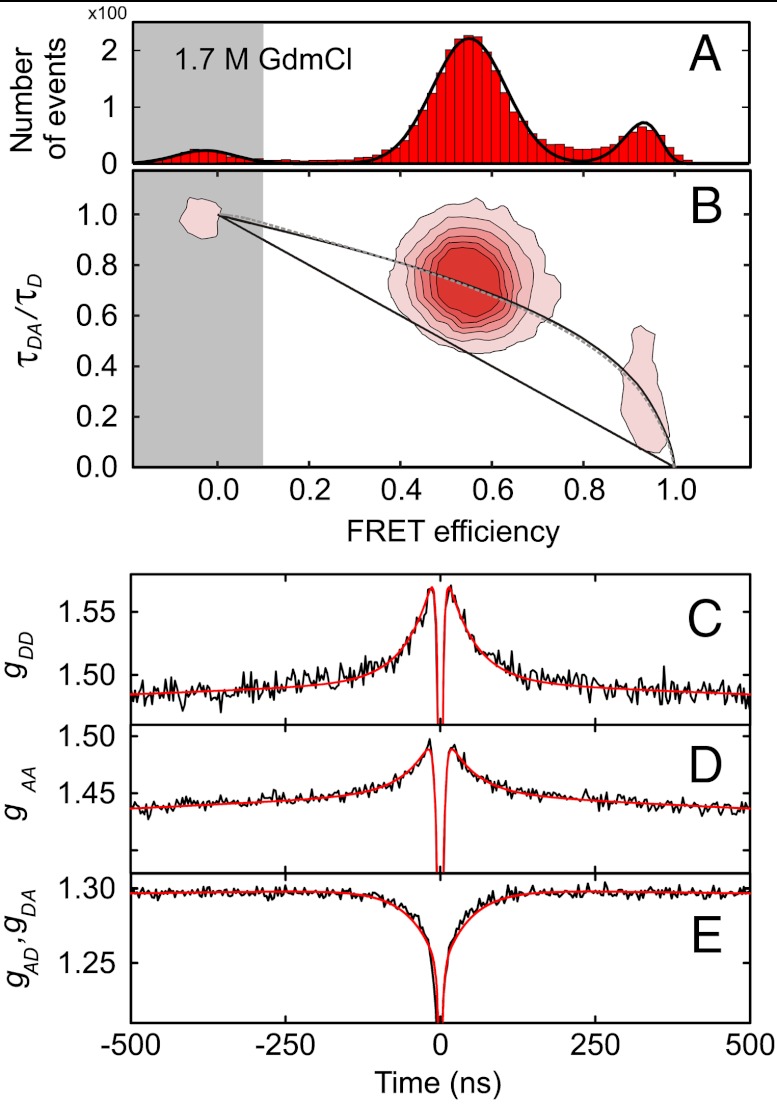
Quantifying unfolded state dynamics requires the accurate measurement of both distance distributions and reconfiguration kinetics. Fig. 1 shows a representative set of measurements on the unfolded state of the small cold shock protein from Thermotoga maritima (Csp) labeled at positions 2 and 68 with Alexa 488 and Alexa 594 as donor and acceptor, respectively, for Förster resonance energy transfer (FRET). From the FRET efficiency histogram (Fig. 1A), the mean transfer efficiency of the unfolded state can be determined and used to calculate the parameters of a suitable distance distribution (37). The good agreement of the observed donor fluorescence lifetimes with the dependence on the mean transfer efficiency E expected for a Gaussian or a wormlike chain (Fig. 1B, Supporting Information and Fig. S1) supports previous measurements that suggest that simple polymer models can provide a reasonable approximation for long-range distance distributions in the unfolded state (29–31, 37–41).
Fig. 1.
Unfolded state dimensions and dynamics from single-molecule FRET and nsFCS. (A) Example of a FRET efficiency histogram of terminally labeled Csp at 1.7 M GdmCl, with the unfolded subpopulation at E ≈ 0.55, the folded subpopulation at E ≈ 0.95, and the donor-only population at E ≈ 0 due to molecules with inactive acceptor dye (gray shading). (B) 2D histogram of relative donor fluorescence lifetime versus E. τDA is the donor lifetime in the presence of the acceptor, τD in the absence of acceptor. The straight line shows the dependence for a fixed distance, the curved lines the dependences for a Gaussian chain (solid) and a worm-like chain (dashed). (C–E) nsFCS measurements reporting on donor-acceptor distance dynamics in unfolded Csp at 1.7 M GdmCl. A global fit of donor-donor (C), acceptor-acceptor (D), and donor-acceptor correlations (E) is used to determine the reconfiguration time τr that characterizes the dynamics in the unfolded state (21, 42, 44). The autocorrelation functions (C, D) exhibit the correlated, and the crosscorrelation function (E) the anticorrelated behavior expected for distance dynamics (43) on the timescale of approximately 100 ns. The much faster anticorrelated signal in the range of a few nanoseconds (photon antibunching) is due to the intrinsic photophysical kinetics of the FRET process (21, 43).
The information on chain dynamics is obtained from nanosecond fluorescence correlation spectroscopy (nsFCS), which allows the fluctuations in distance between donor and acceptor to be monitored (21, 42). The decays of the fluorescence intensity correlation functions (Fig. 1 C–E) can be directly related to the reconfiguration time of the polypeptide chain (21, 43, 44), defined as the relaxation time of the distance correlation function (e.g., of the end-to-end distance, if the labels are located at the chain termini).* The resulting end-to-end distance reconfiguration times, τr, are in the range of 50 ns to 100 ns. This approach for determining τr is the basis for investigating the role of solvent friction and internal friction for chain dynamics.
Probing Internal Friction by Solvent Viscosity Variation.
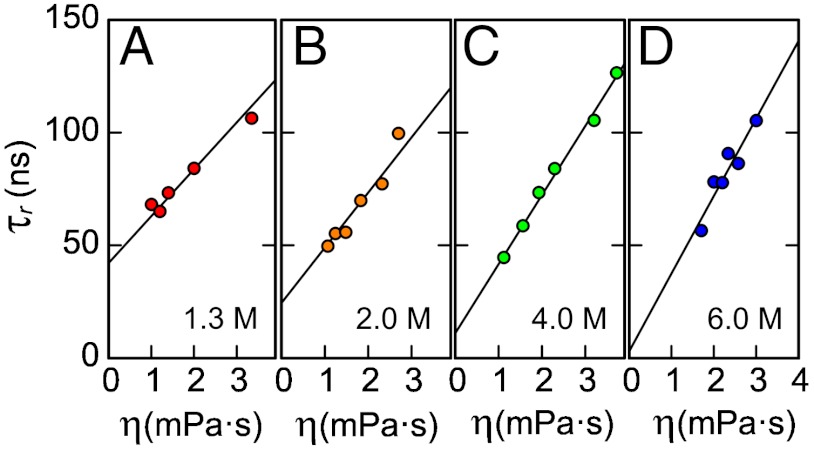
The most common and model-independent way of quantifying solvent-independent internal friction is a variation of solvent viscosity, η, and extrapolation to η = 0 (26). This approach has previously been used for investigating internal friction in native proteins (1) and at the transition state; i.e., for assessing the influence of internal friction on folding kinetics (9, 15, 23, 34, 35); here, we extend it to unfolded proteins. Fig. 2 shows the reconfiguration times τr of terminally labeled unfolded Csp at different guanidinium chloride (GdmCl) concentrations as a function of η, adjusted by varying the concentration of glycerol. Over the range of η used here, the glycerol concentration has no significant effect on the transfer efficiencies of the unfolded state subpopulations, which indicates that the equilibrium distributions and thus the energetics of the system are largely unaffected by the viscogen (Fig. S2). In all cases, the solvent viscosity dependences of τr are well described by linear relations. In the absence of solvent-independent internal friction, we expect τr to approach zero upon extrapolation to zero solvent viscosity, a behavior we indeed observe in 6 M GdmCl. In viscosity-dependent measurements at lower GdmCl concentrations, however, the values of τr extrapolated to η = 0 are greater than zero, suggesting a contribution from a solvent viscosity-independent timescale due to internal friction, τi, in addition to a solvent viscosity-dependent timescale equivalent to the reconfiguration time in the absence of internal friction, τs.
Fig. 2.
Solvent viscosity (η) dependences of chain reconfiguration times of terminally labeled Csp at different GdmCl concentrations (indicated in the lower right of each panel). Based on Eq. 2, data were fit with 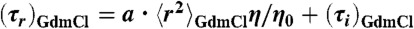 (solid lines, see Supporting Information), where the mean-squared end-to-end distances at a given GdmCl concentration,
(solid lines, see Supporting Information), where the mean-squared end-to-end distances at a given GdmCl concentration, 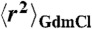 , are obtained from corresponding FRET efficiency histograms. a is a global fit parameter for all GdmCl concentrations, and the values of the internal friction time, (τi)GdmCl, correspond to the intercepts.
, are obtained from corresponding FRET efficiency histograms. a is a global fit parameter for all GdmCl concentrations, and the values of the internal friction time, (τi)GdmCl, correspond to the intercepts.
A framework for interpreting this result is provided by theories of polymer dynamics, where the additivity of τi and τs is well established (14, 26, 45, 46). Such additivity can be rigorously justified in an extension of the Rouse model known as the Rouse model with internal friction (RIF), which leads to an additional characteristic timescale,τi, associated with internal friction. The mathematical structure of the RIF model (see Supporting Information, Eq. S3 ff.) is such that the spatial dependences of the relaxation modes of the chain are identical to those of the Rouse modes while each corresponding relaxation time, τ(n), is increased by the same amount τi; i.e.,
| [1] |
Here, 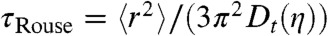 is the largest relaxation time of the Rouse chain (25);
is the largest relaxation time of the Rouse chain (25); 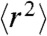 is the mean squared end-to-end distance of the chain; Dt(η) is the solvent viscosity-dependent translational diffusion coefficient of the chain with Dt ∼ η-1; and n is the mode number. The overall solvent-dependent relaxation time, τs, is the same as τRouse to within a numerical factor (47), leading to the same dependence on solvent viscosity, η, and chain dimension:
is the mean squared end-to-end distance of the chain; Dt(η) is the solvent viscosity-dependent translational diffusion coefficient of the chain with Dt ∼ η-1; and n is the mode number. The overall solvent-dependent relaxation time, τs, is the same as τRouse to within a numerical factor (47), leading to the same dependence on solvent viscosity, η, and chain dimension:
| [2] |
The common assumption that only the dynamics corresponding to τs depend on solvent viscosity, and τi does not (26), thus leads to the relation
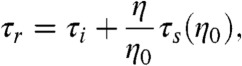 |
[3] |
where η0 is the viscosity of water.† τi thus corresponds to the extrapolated value of τr at η = 0 (Fig. 2). From a global fit of the datasets at all denaturant concentrations (Supporting Information), we find that τi increases with decreasing GdmCl concentration from a value indistinguishable from zero within experimental uncertainty at 6.0 M GdmCl (3±4 ns) to 19±2 ns, 28±2 ns, and 40±2 ns at 4.0 M, 2.0 M, and 1.3 M GdmCl, respectively. At the highest denaturant concentrations, the chains are thus sufficiently expanded that internal friction is negligible ‡, but at lower denaturant concentrations, where the chains are more compact (29, 37, 38), a large part of the reconfiguration time is due to internal friction. To exclude possible viscogen-specific effects or uncertainties in the type of function used for extrapolation (34), we combine our results with an independent approach.
Probing Internal Friction by Segment Length Variation.
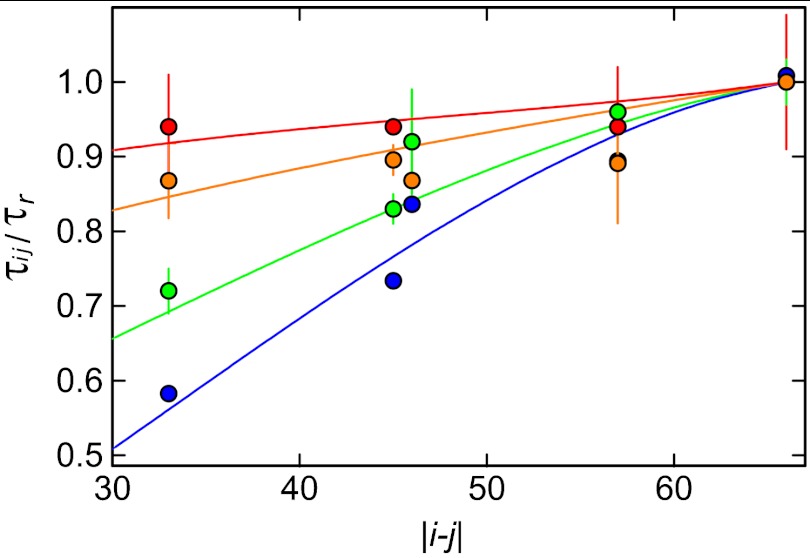
A complementary way of assessing the role of internal friction that does not rely on a change in solvent viscosity is the analysis of the reconfiguration times for different segments of the chain as probed by different labeling positions. Since a polymer exhibits a spectrum of fluctuation timescales or relaxation modes, each associated with a different length scale, segments of different lengths probe different parts of this spectrum (47, 48). As a result, the relative influence of internal friction on the reconfiguration dynamics will depend on the length of the segments (45). We thus prepared variants of Csp with the FRET labels in different positions (Table S1) and determined the reconfiguration times at different GdmCl concentrations (Fig. 3).§ Interestingly, at different GdmCl concentrations, the relative reconfiguration times (normalized by τr of the terminally labeled chain) exhibit very different dependences on the segment length. At 7 M GdmCl, the increase in τr from the shortest to the longest segment is pronounced, in agreement with both theory and simulations of polymers without internal friction (47). However, τr becomes less dependent on segment length with decreasing GdmCl concentration. Qualitatively, this is expected if internal friction dominates chain dynamics: in the limit where τi≫τRouse, Eq. 1 suggests that all modes will approach the same relaxation time τi, and τr will become independent of the segment length probed.
Fig. 3.
Dependence of chain dynamics on the length of the polypeptide segment probed (Table S1) in unfolded Csp at different GdmCl concentrations (1.3 M: red, 2.0 M: orange, 4.0 M: green, 7.0 M: blue). Error bars represent standard deviations estimated from independent measurements where available. The reconfiguration time, τij, for donor and acceptor in positions i and j normalized by the end-to-end reconfiguration time, τr, is shown as a function of the segment length, |i - j|. The fits with the modified RIF model (Supporting Information) used to determine the characteristic timescale associated with internal friction, τi, are shown as solid lines.
It was previously shown that a simple Rouse model agrees remarkably well with coarse-grained simulations of polypeptide dynamics that take into account both excluded volume and hydrodynamic interactions (47). We thus expect that the RIF model is similarly adequate when applied to situations where internal friction effects are important. To analyze our experimental results quantitatively, it was necessary to extend the RIF model (see Supporting Information). Specifically, the observed compaction of unfolded Csp with decreasing denaturant concentration (29, 37, 38) (Fig. S3) was mimicked by including a weak harmonic constraining potential adjusted to reproduce the experimentally determined value of 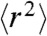 for the unfolded protein at the respective GdmCl concentrations (for comparison with coarse-grained simulations see Fig. S4). The effect of internal friction was included as an additional timescale τi that is independent of the chain segment probed (Eq. 1), but can vary with changes in
for the unfolded protein at the respective GdmCl concentrations (for comparison with coarse-grained simulations see Fig. S4). The effect of internal friction was included as an additional timescale τi that is independent of the chain segment probed (Eq. 1), but can vary with changes in 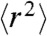 . Finally, the FRET dyes were taken into account explicitly and modeled as additional beads connected to the rest of the chain via harmonic springs ¶.
. Finally, the FRET dyes were taken into account explicitly and modeled as additional beads connected to the rest of the chain via harmonic springs ¶.
This model allows us to quantify the contribution of internal friction by adjusting τi for each GdmCl concentration such that the calculated reconfiguration times as a function of the segment length fit the experimental data (Supporting Information). Fig. 3 shows the good agreement of theory and experiment. The data measured in 7 M GdmCl are well fit by the Rouse model in the absence of internal friction. For 4 M, 2 M, and 1.3 M GdmCl, the resulting values for τi are 9±3 ns, 22±6 ns, and 30(+30,−20) ns, respectively, in good agreement with the results obtained from the solvent viscosity-dependent measurements (Fig. 2). This agreement suggests that a linear extrapolation of τr to η = 0 is a good approximation, and it lends additional support to the additivity of timescales as suggested in Eq. 3 ∥. However, these results are limited to GdmCl concentrations above approximately 0.8 M, where the population and thus the signal contribution of the unfolded state are large enough to allow measurements at equilibrium.
Probing Internal Friction by Denaturant Variation and Microfluidic Mixing.
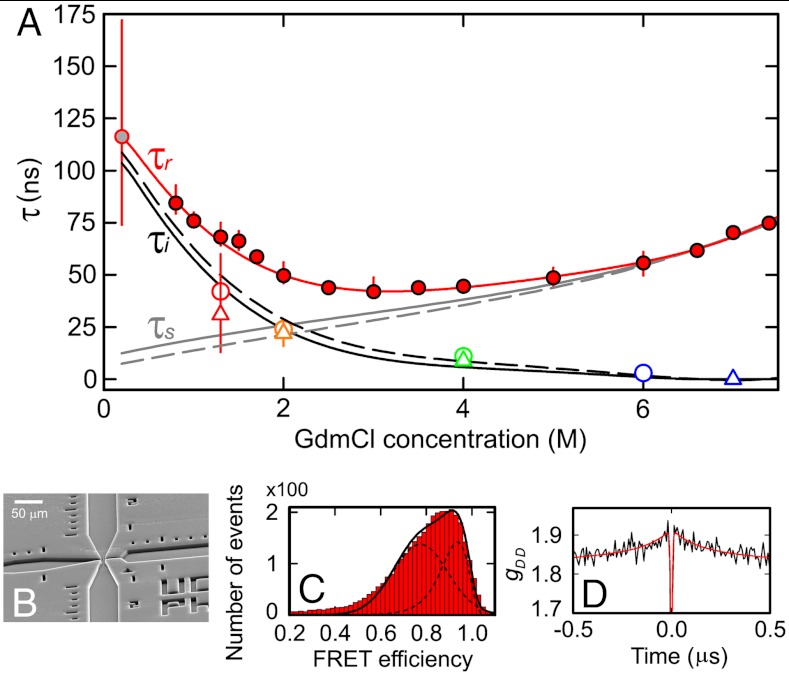
To enable a determination of τr in the virtual absence of denaturant, where the unfolded state is most compact (21, 29, 37) and where the effect of internal friction is expected to be most pronounced, we use a microfluidic mixing device that has recently been developed for investigating rapid protein folding reactions with single-molecule fluorescence (49, 50). By mixing protein unfolded in 1.5 M GdmCl entering from the middle inlet channel with denaturant-free buffer entering via the side channels (Fig. 4B) at a volume ratio of 1∶7, we can populate the unfolded state transiently with a dead time of approximately 5 ms (49). Under our experimental conditions, the folding time of Csp is in the range of 10 ms (38), which allows us to probe the dynamics of unfolded protein at 0.2 M GdmCl with nsFCS measurements in the early part of the observation channel, where the majority of the protein is still unfolded (Fig. 4C). We obtain a value for τr of 115 ns under these near-native conditions (Fig. 4).
Fig. 4.
Quantifying internal friction in unfolded Csp as a function of denaturant concentration. (A) The experimentally determined GdmCl dependence of the end-to-end reconfiguration time, τr, obtained in equilibrium measurements (filled red circles) and from microfluidic mixing (gray filled circle), with an empirical polynomial fit used for interpolation (red line). The solid (dashed) gray line shows the reconfiguration time expected for a Rouse (Zimm) chain in the absence of internal friction, τs (see main text). τi, the characteristic timescale associated with internal friction, calculated according to Eq. 3, is shown as a solid (dashed) black line for the Rouse (Zimm) model. The values of τi from Figs. 2 and 3 are shown as open circles and triangles, respectively, for comparison. (B) Electron micrograph of the microfluidic mixer used to determine τr in the absence of denaturant. FRET efficiency histogram (C) and donor-donor nsFCS curve (D) acquired (8 ± 2) ms after mixing. The uncertainties of τr were estimated by bootstrapping.
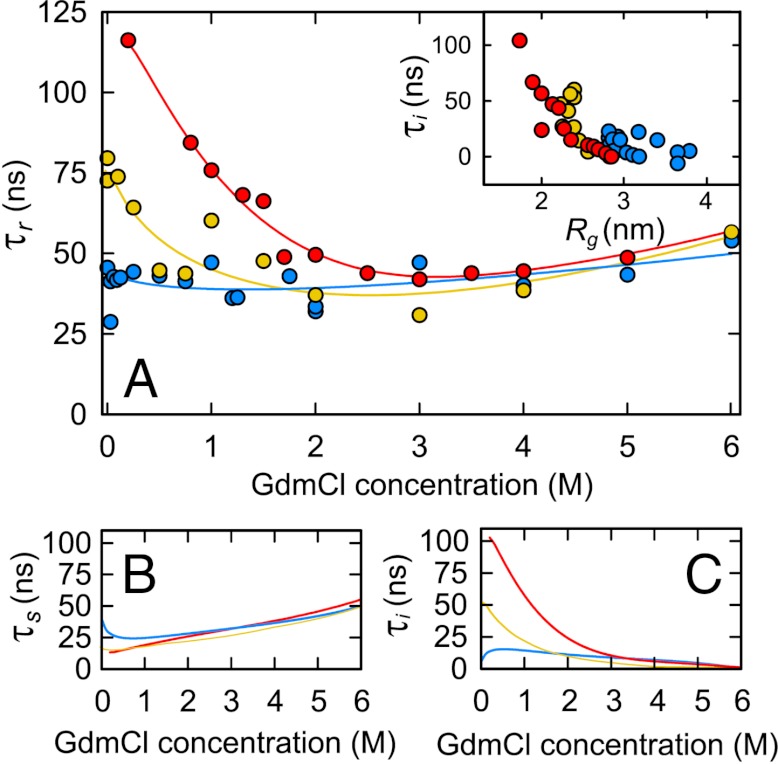
Fig. 4 shows the measured values of τr for unfolded Csp over the entire range of GdmCl concentrations accessible. A clear increase in τr with decreasing GdmCl concentrations is observed below approximately 2 M, indicating the onset of internal friction; at GdmCl concentrations above approximately 5 M, τr increases due to the increasing viscosity of the denaturant solution. Our results in Figs. 2 and 3 indicate that internal friction is absent above 6 M GdmCl. We can thus equate τr and τs under these conditions (Eq. 3) and use the scaling behavior expected from polymer dynamics (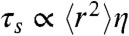 for the Rouse model, Eq. 2) to obtain τs at all GdmCl concentrations. With the values of
for the Rouse model, Eq. 2) to obtain τs at all GdmCl concentrations. With the values of 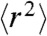 determined from the FRET efficiencies (Fig. S3) and the measured solvent viscosities, we can thus obtain the GdmCl concentration dependence of τs (Fig. 4, solid gray line). The differences between the observed values of τr and the calculated values of τs then yield the internal friction times τi (Eq. 3, Fig. 4A)**. Remarkably, the resulting dependence of τi on GdmCl concentration agrees well both with the values from the solvent viscosity-dependent measurements (Fig. 2) and the analysis based on the different segment lengths (Fig. 3). This agreement illustrates the consistency of the three different approaches we used to quantify internal friction, and it suggests that the result is robust and model-independent.
determined from the FRET efficiencies (Fig. S3) and the measured solvent viscosities, we can thus obtain the GdmCl concentration dependence of τs (Fig. 4, solid gray line). The differences between the observed values of τr and the calculated values of τs then yield the internal friction times τi (Eq. 3, Fig. 4A)**. Remarkably, the resulting dependence of τi on GdmCl concentration agrees well both with the values from the solvent viscosity-dependent measurements (Fig. 2) and the analysis based on the different segment lengths (Fig. 3). This agreement illustrates the consistency of the three different approaches we used to quantify internal friction, and it suggests that the result is robust and model-independent.
In summary, we can thus quantify the contribution of internal friction to the dynamics of unfolded Csp under solution conditions ranging from the virtual absence of denaturant to more than 7 M GdmCl. At the highest denaturant concentrations, the chains appear to be sufficiently expanded that internal friction becomes negligible, but in the absence of denaturant, where the chains are most compact, internal friction dominates the reconfiguration time, with a value of τi that is about an order of magnitude greater than τs.
Internal Friction in IDPs: Role of Sequence Composition.
To investigate how internal friction depends on amino acid composition, we studied the dynamics of two IDPs, the N-terminal domain of HIV integrase (IN), and the C-terminal segment of human prothymosin α (ProTα), which contain a larger fraction of charged and hydrophilic amino acids than Csp. The dimensions of IDPs have previously been shown to be modulated strongly by the interactions of charged residues within the chain (41, 51), and both IN and ProTα exhibit an expansion due to charge repulsion at low ionic strength (41) (Fig. S3). Here, IN was investigated in the absence of its ligand Zn2+, so both IDPs are disordered even in the absence of denaturant (41), and their unfolded state dynamics can be investigated at equilibrium over the entire range of GdmCl concentrations.
At high GdmCl concentrations, both the dimensions (Fig. S3) (41) and the reconfiguration times (Fig. 5) of IN, ProTα, and terminally labeled Csp converge, as expected for polypeptide segments of similar length under conditions where charge interactions are shielded by the ionic denaturant, and where proteins follow the length scaling expected for simple homopolymers (52). At lower GdmCl concentrations, however, the dynamics of the three proteins clearly diverge. Below 2 M GdmCl, IN shows an increase in τr, but to a lesser extent than Csp. Remarkably, τr of ProTα is almost independent of GdmCl concentration. With the procedure analogous to the one used for Csp (Fig. 4, Eq. 3) to separate τr into contributions of τs and τi, we find a similar dependence of τs for the three proteins, but very different contributions of internal friction (Fig. 5 B and C). The values of τs differ significantly only at the lowest GdmCl concentrations, where charge repulsion sets in (Fig. S3); especially ProTα shows a slight increase in τs concomitant with its expansion (41) (Fig. S3; Eq. 2).
Fig. 5.
Comparison of internal friction in Csp and IDPs. (A) Measured reconfiguration times of Csp (red circles), integrase (yellow circles), and ProTα (blue circles) as a function of GdmCl concentration. Polynomial fits used for interpolation are shown as solid lines. Reconfiguration time expected for a Rouse chain, τs, (B) and internal friction times, τi, (C) calculated from (A) as in Fig. 4. (Inset in A) Dependence of τi on the radius of gyration, Rg, for Csp (red), integrase (yellow), and ProTα (blue) for all conditions in (A).
The contribution of internal friction appears to be strongly dependent on the dimensions of the chain (Fig. 5C). IN exhibits a value of τi at 0 M GdmCl of about half the value of Csp, accompanied by a significantly less pronounced collapse (Fig. S3). Internal friction in ProTα remains low throughout and shows an additional drop below 1 M GdmCl, where the pronounced charge-mediated chain expansion sets in (41) (Fig. S3). The observation for ProTα that adding 1 M KCl in the absence of GdmCl also results in collapse (41) and an increase in τi (Fig. S5A) confirms that charge interactions (and not denaturant-specific interactions) are the dominant cause of this effect. The dependence of internal friction on chain dimensions is further illustrated by an inverse correlation of τi with Rg when all proteins and solution conditions are taken together (Fig. 5A, Inset). Internal friction in unfolded proteins thus decreases not only with increasing concentrations of denaturant, but also with increasing repulsive charge interactions in the chain, both of which lead to an expansion of the polypeptide.
Discussion
Timescale of Unfolded State Dynamics.
The results presented here, together with previous work (21, 32, 40, 42, 53), show that the relaxation dynamics of unfolded proteins in the absence of pronounced residual structure occur on timescales in the range expected for simple polymers based on theoretical concepts such as Rouse or Zimm theory (25). These diffusive dynamics put a limit on the timescale of forming long-range interactions within the chain, and are thus closely related to the effective diffusion coefficient on a free energy surface that can be used to describe the folding process in terms of Kramers-type theories (10, 21, 22) ††. Similar timescales have also been observed for unfolded state dynamics in molecular simulations (40, 58), and the same timescales are expected to govern the initial collapse of the chain from a more extended conformation (21). In the case of small cold shock proteins, previous experiments suggest that dynamics above the 100 ns range and below the millisecond timescale of folding are absent (42, 59). Such a separation of the timescales of unfolded state dynamics on the one hand and of barrier crossing on the other is a characteristic of systems well approximated by two-state kinetics (60). In contrast, for proteins folding in microseconds, the 100 ns timescale is sufficiently close to the barrier crossing times that changes in unfolded state dynamics need to be taken into account for a description of their rapid folding dynamics (22).
Mechanisms of Internal Friction.
Even though the concept that polymer chains are subject to internal friction has been well established in the field of polymer dynamics for more than half a century (14, 26, 45, 46), the molecular origin of internal friction has largely remained elusive. In terms of the kinetic description, at least two cases of internal friction can be distinguished. In one case, internal friction results in a change of the effective viscosity, ηeff, that will affect the dynamics in a purely multiplicative way; e.g., τ = τ0ηeff/η, with ηeff = η exp(ε/kBT)2, where τ is the observed relaxation time of the process (e.g. chain reconfiguration); τ0 is the relaxation time in the absence of internal friction; ε is the mean energetic roughness causing internal friction; kB is Boltzmann’s constant; and T is temperature (16). This type of behavior would entail that the relaxation time approaches zero upon extrapolation to η = 0; it would also imply full solvation of all parts of the macromolecule involved in internal friction processes (“wet” friction). In the other case, internal friction results in a constant timescale that is additive with the intrinsic dynamic timescale of the process in the absence of internal friction (14, 26, 45, 46). This behavior is suggestive of the exclusion of solvent from those parts of the polypeptide whose interactions cause internal friction (1), corresponding to “dry” friction. In our experiments, the extrapolation to zero solvent viscosity (Fig. 2), the position dependence of the reconfiguration times (Fig. 3), and the lack of a dependence of τi on solvent viscosity (Fig. 2 and consistency with Figs. 3 and 4) are unexpected for a multiplicative effect and clearly favor the additive contribution of an internal friction time (Eqs. 1, 3); i.e., “dry” friction.
A clue regarding the molecular contributions comes from the denaturant dependence of τr (Fig. 4): since dihedral angle rotations may not be expected to be accelerated by denaturant binding, but side chain or backbone interactions will be weakened, the latter may be the more probable cause of internal friction in our unfolded proteins, an inference that is supported by recent simulations (8). The similarity of the degree of unfolded state collapse for different chain segments (37) (Fig. S6) and the good agreement of the position dependence of the dynamics with a model that ignores specific sequence effects (Fig. 3) indicate that specific long-range interactions (e.g., clustering of hydrophobic residues distant in sequence) do not play a dominant role here. Furthermore, simulations show that specific interactions between two points along the chain cannot reproduce the position dependence of the dynamics we observe (Fig. S7), suggesting the predominance of nonspecific interactions evenly distributed along the chain. The prevalence of interactions that are short-range in sequence is also supported by the dynamics of a bisected variant of Csp, whose internal friction times are very similar to those of the full-length protein (Fig. S8).
A surprisingly large reconfiguration time of approximately 20 μs was recently suggested for compact unfolded protein L based on tryptophan triplet state quenching experiments (33). In spite of the large contribution of internal friction that would have to be invoked to explain this result, the contact formation rate extrapolated to η = 0 was indistinguishable from zero within experimental error. This observation would demand a dominant contribution of “wet” friction; i.e., complete solvation of the groups whose interactions cause internal friction, in contrast to our observations on the proteins investigated here. The uncertainty in the intercept of the solvent viscosity dependence of the contact rates of Waldauer et al. (33) does leave room for a possible contribution of “dry” friction in protein L, but this effect might be difficult to distinguish from a reaction-limited component of the quenching process. Contact formation experiments with a diffusion-limited quencher may help to address this question further. Results based on the almost diffusion-limited quenching of an oxazine dye by tryptophan in a 26 residue segment within the small binding domain BBL resulted in timescales of internal contact formation extrapolated to zero solvent viscosity of approximately 0.3 μs (61), comparable to the timescales due to internal friction observed here. A direct combination of FRET and contact quenching experiments may allow the identification of possible differences in internal friction between compact and expanded conformations within the ensemble of unfolded proteins.
Even though the detailed molecular origin of internal friction is still unclear, the approach to quantify internal friction developed here now opens the possibility of a more systematic investigation, aided, e.g., by a quantitative comparison with atomistic simulations or polymer models (14, 45, 47, 62). Approaches such as the molecular transfer model (31) may facilitate the inclusion of the effects of denaturants or other cosolvents.
Effect of Internal Friction on the Dynamics of Protein Folding and IDPs.
What do our results imply for the influence of internal friction on protein folding kinetics? For this question, it would be of interest to determine the effect of internal friction on chain dynamics for unstructured conformational ensembles that are as compact as the transition state. Based on the correlation of τi with Rg (Fig. 5), we can estimate the magnitude of τi in this compact regime. The transition state for folding of Csp exhibits native-like solvent accessibility (63), so we assume Rg of the native state (1.3 nm) as a lower bound on the dimensions of the transition state and estimate an extrapolated value of τi ≈ (0.3 ± 0.1) μs. A contribution of internal friction of this magnitude to the millisecond folding time of Csp is too small to be detectable experimentally (2, 15), but ultrafast-folding proteins exhibit contributions of internal friction ranging from approximately 0.7 μs to several microseconds (9, 15, 35). This observation suggests that for microsecond folders a contribution of τi in the range of 0.3 μs can have a significant effect on their folding rates (22), but the remaining discrepancy implies the existence of additional contributions or a change in mechanism of internal friction in the barrier region. The latter may not be entirely unexpected given the importance of the specific interactions in transition state ensembles. The mechanisms and the extent of internal friction at the transition state will depend on the relevant length scales and the possible role of collective modes that characterize the conformational transitions involved in the barrier crossing process (64). The importance of specific interactions for energetic roughness has recently been proposed for the folding of spectrin domains (23), which may allow a quantitative assessment of such effects.
The role of internal friction for the conformational dynamics of proteins is not limited to the folding reaction. With the realization that intrinsic disorder is an important property of a large number of proteins involved in intracellular interactions and regulatory processes (27, 28), the ability to quantify internal friction and to elucidate the underlying mechanisms will be crucial for understanding the properties of IDPs. Our observation that the contribution of internal friction depends on amino acid composition and charge repulsion (Fig. 5) may have important implications for the dynamics of intermolecular interactions involving IDPs. In a “flycasting” mechanism of the interactions of IDPs with a cellular target (65), both an increase in chain dimensions (41, 51) and higher reconfiguration rates of an IDP may contribute to an increase in the rate of binding.
Methods
Proteins were expressed, purified, and labeled with Alexa 488 and Alexa 594 essentially as reported previously (37, 41, 42). Single-molecule measurements were performed using a Micro Time 200 confocal microscope equipped with a HydraHarp 400 counting module (PicoQuant). For rapid mixing experiments, microfluidic mixers fabricated by replica molding in PDMS were used (49, 50). For details on experiments, theory, and simulations, see Supporting Information.
Supplementary Material
ACKNOWLEDGMENTS.
We thank Dr. J. Clark, I. König, and R. Wuttke for help in protein preparation, and Drs. A. Borgia, W. Eaton, H. Hofmann, L. Lapidus, R. Netz, and D. Thirumalai for helpful discussions. This work was supported by the Swiss National Science Foundation (to B.S.), the NCCR for Structural Biology (to B.S.), a Starting Investigator Grant of the European Research Council (to B.S.), the National Science Foundation (Grants CHE 0848571 and PHY05-51164, to D.E.M.), and the Robert A. Welch Foundation (grant F-1514, to D.E.M.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1117368109/-/DCSupplemental.
*We used here a variant of Csp devoid of Trp residues (see Supporting Information for details). A comparison to previous results (21, 37) shows that the collapse behavior and the dynamics of the chain are not affected significantly by this modification.
†Note that even though we are not aware of a model that accounts for internal friction within the Zimm framework, given the same linear dependence of the Zimm time on solvent viscosity (25), it is plausible to assume that the effect of internal friction is also additive and described by Eq. 3.
‡We note that residual structure in unfolded proteins detected by NMR has usually been observed in a range of urea concentrations that corresponds to up to approximately 4 M of the stronger denaturant GdmCl (28), where we still observe a significant contribution of internal friction. A direct comparison to such measurements may help to identify the molecular origin of internal friction.
§Note that we used here a variant of Csp devoid of Trp residues to eliminate the influence of static quenching on the correlation functions (see Supporting Information).
¶Note that all parameters in the extended RIF model are either well constrained by experimental observables or have insignificant effects on the overall results when varied within reasonable bounds (see Supporting Information), such that τi is the only free fit parameter.
∥A purely multiplicative effect of internal friction on reconfiguration times (16) would not affect the ratios of times plotted in Fig. 3 and would thus be not sufficient to explain the experimental results.
**The corresponding analysis with the Zimm model, where τs is scaled by 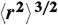 (25), yields very similar results (Fig. 4), indicating that the procedure is robust with respect to the polymer model used.
(25), yields very similar results (Fig. 4), indicating that the procedure is robust with respect to the polymer model used.
††Note that contact formation probed in quenching experiments (54, 55) for similar sequence separations is expected to occur on longer timescales than in FRET experiments (typically in the microsecond range) because of the low probability of populating sufficiently small intramolecular distances in the corresponding equilibrium distance distributions [see, e.g., (56, 57)].
References
- 1.Ansari A, Jones CM, Henry ER, Hofrichter J, Eaton WA. The role of solvent viscosity in the dynamics of protein conformational changes. Science. 1992;256:1796–1798. doi: 10.1126/science.1615323. [DOI] [PubMed] [Google Scholar]
- 2.Jacob M, Geeves M, Holtermann G, Schmid FX. Diffusional barrier crossing in a two-state protein folding reaction. Nat Struct Biol. 1999;6:923–926. doi: 10.1038/13289. [DOI] [PubMed] [Google Scholar]
- 3.Plaxco KW, Baker D. Limited internal friction in the rate-limiting step of a two-state protein folding reaction. Proc Natl Acad Sci USA. 1998;95:13591–13596. doi: 10.1073/pnas.95.23.13591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ladurner AG, Fersht AR. Upper limit of the time scale for diffusion and chain collapse in chymotrypsin inhibitor 2. Nat Struct Biol. 1999;6:28–31. doi: 10.1038/4899. [DOI] [PubMed] [Google Scholar]
- 5.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 6.Socci ND, Onuchic JN, Wolynes PG. Diffusive dynamics of the reaction coordinate for protein folding funnels. J Chem Phys. 1996;104:5860–5868. [Google Scholar]
- 7.Krivov SV, Karplus M. Diffusive reaction dynamics on invariant free energy profiles. Proc Natl Acad Sci USA. 2008;105:13841–13846. doi: 10.1073/pnas.0800228105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Best RB, Hummer G. Coordinate-dependent diffusion in protein folding. Proc Natl Acad Sci USA. 2010;107:1088–1093. doi: 10.1073/pnas.0910390107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cellmer T, Henry ER, Hofrichter J, Eaton WA. Measuring internal friction of an ultrafast-folding protein. Proc Natl Acad Sci USA. 2008;105:18320–18325. doi: 10.1073/pnas.0806154105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Best RB, Hummer G. Diffusion models of protein folding. Phys Chem Chem Phys. 2011;13:16902–16911. doi: 10.1039/c1cp21541h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu F, Nakaema M, Gruebele M. The transition state transit time of WW domain folding is controlled by energy landscape roughness. J Chem Phys. 2009;131:195101. doi: 10.1063/1.3262489. [DOI] [PubMed] [Google Scholar]
- 12.Chahine J, Oliveira RJ, Leite VBP, Wang J. Configuration-dependent diffusion can shift the kinetic transition state and barrier height of protein folding. Proc Natl Acad Sci USA. 2007;104:14646–14651. doi: 10.1073/pnas.0606506104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 14.Portman JJ, Takada S, Wolynes PG. Microscopic theory of protein folding rates. II. Local reaction coordinates and chain dynamics. J Chem Phys. 2001;114:5082–5096. [Google Scholar]
- 15.Hagen SJ. Solvent viscosity and friction in protein folding dynamics. Curr Protein Pept Sci. 2010;11:385–395. doi: 10.2174/138920310791330596. [DOI] [PubMed] [Google Scholar]
- 16.Zwanzig R. Diffusion in a rough potential. Proc Natl Acad Sci USA. 1988;85:2029–2030. doi: 10.1073/pnas.85.7.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hyeon CB, Thirumalai D. Can energy landscape roughness of proteins and RNA be measured by using mechanical unfolding experiments? Proc Natl Acad Sci USA. 2003;100:10249–10253. doi: 10.1073/pnas.1833310100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Whitford PC, et al. The origin of nonmonotonic complex behavior and the effects of nonnative interactions on the diffusive properties of protein folding. Biophys J. 2010;99:600–608. doi: 10.1016/j.bpj.2010.04.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alexander-Katz A, Wada H, Netz RR. Internal friction and nonequilibrium unfolding of polymeric globules. Phys Rev Lett. 2009;103:028102. doi: 10.1103/PhysRevLett.103.028102. [DOI] [PubMed] [Google Scholar]
- 20.Wang J, Oliveira RJ, Whitford PC, Chahine J, Leite VBP. Coordinate and time-dependent diffusion dynamics in protein folding. Methods. 2010;52:91–98. doi: 10.1016/j.ymeth.2010.04.016. [DOI] [PubMed] [Google Scholar]
- 21.Nettels D, Gopich IV, Hoffmann A, Schuler B. Ultrafast dynamics of protein collapse from single-molecule photon statistics. Proc Natl Acad Sci USA. 2007;104:2655–2660. doi: 10.1073/pnas.0611093104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cellmer T, Henry ER, Kubelka J, Hofrichter J, Eaton WA. Relaxation rate for an ultrafast folding protein is independent of chemical denaturant concentration. J Am Chem Soc. 2007;129:14564–14565. doi: 10.1021/ja0761939. [DOI] [PubMed] [Google Scholar]
- 23.Wensley BG, et al. Experimental evidence for a frustrated energy landscape in a three-helix-bundle protein family. Nature. 2010;463:685–U122. doi: 10.1038/nature08743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kubelka J, Hofrichter J, Eaton WA. The protein folding ‘speed limit’. Curr Opin Struct Biol. 2004;14:76–88. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 25.Doi M, Edwards SF. The Theory of Polymer Dynamics. USA New York: Oxford UniversityPress; 1988. [Google Scholar]
- 26.De Gennes PG. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell University Press; 1979. [Google Scholar]
- 27.Dunker AK, Silman I, Uversky VN, Sussman JL. Function and structure of inherently disordered proteins. Curr Opin Struct Biol. 2008;18:756–764. doi: 10.1016/j.sbi.2008.10.002. [DOI] [PubMed] [Google Scholar]
- 28.Dyson HJ, Wright PE. Unfolded proteins and protein folding studied by NMR. Chem Rev. 2004;104:3607–3622. doi: 10.1021/cr030403s. [DOI] [PubMed] [Google Scholar]
- 29.Schuler B, Eaton WA. Protein folding studied by single-molecule FRET. Curr Opin Struct Biol. 2008;18:16–26. doi: 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ziv G, Thirumalai D, Haran G. Collapse transition in proteins. Phys Chem Chem Phys. 2009;11:83–93. doi: 10.1039/b813961j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.O’Brien EP, Ziv G, Haran G, Brooks BR, Thirumalai D. Effects of denaturants and osmolytes on proteins are accurately predicted by the molecular transfer model. Proc Natl Acad Sci USA. 2008;105:13403–13408. doi: 10.1073/pnas.0802113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Möglich A, Joder K, Kiefhaber T. End-to-end distance distributions and intrachain diffusion constants in unfolded polypeptide chains indicate intramolecular hydrogen bond formation. Proc Natl Acad Sci USA. 2006;103:12394–12399. doi: 10.1073/pnas.0604748103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Waldauer SA, Bakajin O, Lapidus LJ. Extremely slow intramolecular diffusion in unfolded protein L. Proc Natl Acad Sci USA. 2010;107:13713–13717. doi: 10.1073/pnas.1005415107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jas GS, Eaton WA, Hofrichter J. Effect of viscosity on the kinetics of alpha-helix and beta- hairpin formation. J Phys Chem B. 2001;105:261–272. [Google Scholar]
- 35.Qiu LL, Hagen SJ. A limiting speed for protein folding at low solvent viscosity. J Am Chem Soc. 2004;126:3398–3399. doi: 10.1021/ja049966r. [DOI] [PubMed] [Google Scholar]
- 36.Sherman E, Haran G. Fluorescence correlation spectroscopy of fast chain dynamics within denatured protein L. Chemphyschem. 2011;12:696–703. doi: 10.1002/cphc.201000722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hoffmann A, et al. Mapping protein collapse with single-molecule fluorescence and kinetic synchrotron radiation circular dichroism spectroscopy. Proc Natl Acad Sci USA. 2007;104:105–110. doi: 10.1073/pnas.0604353104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Schuler B, Lipman EA, Eaton WA. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 2002;419:743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 39.Sherman E, Haran G. Coil-globule transition in the denatured state of a small protein. Proc Natl Acad Sci USA. 2006;103:11539–11543. doi: 10.1073/pnas.0601395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nettels D, et al. Single molecule spectroscopy of the temperature-induced collapse of unfolded proteins. Proc Natl Acad Sci USA. 2009;106:20740–20745. doi: 10.1073/pnas.0900622106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Müller-Späth S, et al. Charge interactions can dominate the dimensions of intrinsically disordered proteins. Proc Natl Acad Sci USA. 2010;107:14609–14614. doi: 10.1073/pnas.1001743107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nettels D, Hoffmann A, Schuler B. Unfolded protein and peptide dynamics investigated with single-molecule FRET and correlation spectroscopy from picoseconds to seconds. J Phys Chem B. 2008;112:6137–6146. doi: 10.1021/jp076971j. [DOI] [PubMed] [Google Scholar]
- 43.Wang ZS, Makarov DE. Nanosecond dynamics of single polypeptide molecules revealed by photoemission statistics of fluorescence resonance energy transfer: A theoretical study. J Phys Chem B. 2003;107:5617–5622. [Google Scholar]
- 44.Gopich IV, Nettels D, Schuler B, Szabo A. Protein dynamics from single-molecule fluorescence intensity correlation functions. J Chem Phys. 2009;131:095102. doi: 10.1063/1.3212597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Khatri BS, McLeish TCB. Rouse model with internal friction: A coarse grained framework for single biopolymer dynamics. Macromolecules. 2007;40:6770–6777. [Google Scholar]
- 46.Manke CW, Williams MC. Internal viscosity of polymers and the role of solvent resistance. Macromolecules. 1985;18:2045–2051. [Google Scholar]
- 47.Makarov DE. Spatiotemporal correlations in denatured proteins: The dependence of fluorescence resonance energy transfer (FRET)-derived protein reconfiguration times on the location of the FRET probes. J Chem Phys. 2010;132:035104. doi: 10.1063/1.3284509. [DOI] [PubMed] [Google Scholar]
- 48.Cheng RR, Uzawa T, Plaxco KW, Makarov DE. Universality in the timescales of internal loop formation in unfolded proteins and single-stranded oligonucleotides. Biophys J. 2010;99:3959–3968. doi: 10.1016/j.bpj.2010.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pfeil SH, Wickersham CE, Hoffmann A, Lipman EA. A microfluidic mixing system for single-molecule measurements. Rev Sci Instrum. 2009;80:055105. doi: 10.1063/1.3125643. [DOI] [PubMed] [Google Scholar]
- 50.Hofmann H, et al. Single-molecule spectroscopy of protein folding in a chaperonin cage. Proc Natl Acad Sci USA. 2010;107:11793–11798. doi: 10.1073/pnas.1002356107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mao AH, Crick SL, Vitalis A, Chicoine CL, Pappu RV. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc Natl Acad Sci USA. 2010;107:8183–8188. doi: 10.1073/pnas.0911107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kohn JE, et al. Random-coil behavior and the dimensions of chemically unfolded proteins. Proc Natl Acad Sci USA. 2004;101:12491–12496. doi: 10.1073/pnas.0403643101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hillger F, et al. Probing protein-chaperone interactions with single molecule fluorescence spectroscopy. Angew Chem Int Ed. 2008;47:6184–6188. doi: 10.1002/anie.200800298. [DOI] [PubMed] [Google Scholar]
- 54.Bieri O, et al. The speed limit for protein folding measured by triplet-triplet energy transfer. Proc Natl Acad Sci USA. 1999;96:9597–9601. doi: 10.1073/pnas.96.17.9597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lapidus LJ, Eaton WA, Hofrichter J. Measuring the rate of intramolecular contact formation in polypeptides. Proc Natl Acad Sci USA. 2000;97:7220–7225. doi: 10.1073/pnas.97.13.7220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Toan NM, Morrison G, Hyeon C, Thirumalai D. Kinetics of loop formation in polymer chains. J Phys Chem B. 2008;112:6094–6106. doi: 10.1021/jp076510y. [DOI] [PubMed] [Google Scholar]
- 57.Cheng RR, Uzawa T, Plaxco KW, Makarov DE. The rate of intramolecular loop formation in DNA and polypeptides: the absence of the diffusion-controlled limit and fractional power-law viscosity dependence. J Phys Chem B. 2009;113:14026–14034. doi: 10.1021/jp902291n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 59.Jacob M, et al. Microsecond folding of the cold shock protein measured by a pressure-jump technique. Biochemistry. 1999;38:2882–2891. doi: 10.1021/bi982487i. [DOI] [PubMed] [Google Scholar]
- 60.Zwanzig R. Two-state models of protein folding kinetics. Proc Natl Acad Sci USA. 1997;94:148–150. doi: 10.1073/pnas.94.1.148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Neuweiler H, Johnson CM, Fersht AR. Direct observation of ultrafast folding and denatured state dynamics in single protein molecules. Proc Natl Acad Sci USA. 2009;106:18569–18574. doi: 10.1073/pnas.0910860106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hyeon C, Morrison G, Thirumalai D. Force-dependent hopping rates of RNA hairpins can be estimated from accurate measurement of the folding landscapes. Proc Natl Acad Sci USA. 2008;105:9604–9609. doi: 10.1073/pnas.0802484105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Perl D, et al. Conservation of rapid two-state folding in mesophilic, thermophilic and hyperthermophilic cold shock proteins. Nat Struct Biol. 1998;5:229–235. doi: 10.1038/nsb0398-229. [DOI] [PubMed] [Google Scholar]
- 64.Straub JE, Sagnella DE, Thirumalai D. Time scales and pathways for kinetic energy relaxation in solvated proteins: Application to carbonmonoxy myoglobin. J Chem Phys. 2000;113:7702–7711. [Google Scholar]
- 65.Shoemaker BA, Portman JJ, Wolynes PG. Speeding molecular recognition by using the folding funnel: the fly-casting mechanism. Proc Natl Acad Sci USA. 2000;97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.