How amide hydrogens exchange in native proteins

Significance

Proteins tend to be compactly folded but occasionally undergo conformational fluctuations that expose even the most deeply buried parts of the polypeptide chain to external solvent. As a consequence, the backbone amide hydrogens can exchange with water hydrogens. Monitoring such hydrogen exchange is a well-established method for characterizing protein flexibility, even though the nature of the ‟open” exchange-competent state is unknown. We have used an ultralong computer simulation to identify the elusive open state as transient (100 ps), locally distorted conformations where the N–H group coordinates two water molecules.

Abstract

Amide hydrogen exchange (HX) is widely used in protein biophysics even though our ignorance about the HX mechanism makes data interpretation imprecise. Notably, the open exchange-competent conformational state has not been identified. Based on analysis of an ultralong molecular dynamics trajectory of the protein BPTI, we propose that the open (O) states for amides that exchange by subglobal fluctuations are locally distorted conformations with two water molecules directly coordinated to the N–H group. The HX protection factors computed from the relative O-state populations agree well with experiment. The O states of different amides show little or no temporal correlation, even if adjacent residues unfold cooperatively. The mean residence time of the O state is ∼100 ps for all examined amides, so the large variation in measured HX rate must be attributed to the opening frequency. A few amides gain solvent access via tunnels or pores penetrated by water chains including native internal water molecules, but most amides access solvent by more local structural distortions. In either case, we argue that an overcoordinated N–H group is necessary for efficient proton transfer by Grotthuss-type structural diffusion.

Before the tightly packed and densely H-bonded structure of globular proteins had been established, Hvidt and Linderstrøm-Lang (1) showed that all backbone amide hydrogens of insulin exchange with water hydrogens, implying that all parts of the polypeptide backbone are, at least transiently, exposed to solvent. In the following 60 y, hydrogen exchange (HX), usually monitored by NMR spectroscopy (2) or mass spectrometry (3), has been widely used to study protein folding and stability (4–10), structure (11, 12), flexibility and dynamics (13–15), and solvent accessibility and binding (16, 17), often with single-residue resolution. However, because the exchange mechanism is unclear, HX data from proteins can, at best, be interpreted qualitatively (18–25).

Under most conditions, amide HX is catalyzed by hydroxide ions (26, 27) at a rate that is influenced by inductive and steric effects from adjacent side chains (28). For unstructured peptides, HX is a slow process simply because the hydroxide concentration is low. For example, at 25$°$ C and pH 4, HX occurs on a time scale of minutes. Under similar conditions, amides buried in globular proteins exchange on a wide range of time scales, extending up to centuries. HX can only occur if the amide is exposed to solvent, so conformational fluctuations must be an integral part of the HX mechanism (18).

Under sufficiently destabilizing conditions HX occurs from the denatured-state ensemble, but under native conditions few amides exchange by such global unfolding (9, 29–31). For example, in bovine pancreatic trypsin inhibitor (BPTI), 8 amides in the core β-sheet exchange by global unfolding under native conditions (7, 32), whereas the remaining 45 amides require less extensive conformational fluctuations. Much of the debate in the protein HX field over the past half-century has concerned the nature of these subglobal fluctuations and their frequency, duration, amplitude, and cooperativity (18–25).

According to the standard HX model (18), each amide can exist in a closed (C) state, where exchange cannot occur, or in an open (O) state, where exchange proceeds at a rate $k_{\text{int}}$. The kinetic scheme for H exchange into D₂O then reads as

$${\left(\mathrm{N}-\mathrm{H}\right)}_{\mathrm{C}}\underset{k_{\mathrm{c}\mathrm{l}}}{\overset{k_{\mathrm{o}\mathrm{p}}}{\rightleftharpoons }}{\left(\mathrm{N}-\mathrm{H}\right)}_{\text{O}}\stackrel{k_{\mathrm{int}}}{\to }{\left(\mathrm{N}-\mathrm{D}\right)}_{\text{O}}$$

and the measured steady-state HX rate is $k_{\text{HX}}=k_{\text{op}}\hspace{0.17em}{k}_{\text{int}}/\left(k_{\text{op}}+k_{\text{cl}}+k_{\text{int}}\right)$. To make this phenomenological model practically useful, two auxiliary assumptions are needed to disentangle the conformational and intrinsic parts of the process: (i) The conformational fluctuations ($k_{\text{op}}$ and $k_{\text{cl}}$) are independent of pH, and (ii) HX from the O state proceeds at the same rate as in model peptides with the same neighboring side chains, so that $k_{\text{int}}=k_{\text{HX}}^0$.

Two HX regimes are distinguished with reference to the pH dependence of $k_{\text{HX}}$ (18). If $k_{\text{HX}}$ is constant in some pH range, it follows that $k_{\text{int}}\gg k_{\text{op}}+k_{\text{cl}}$ so that $k_{\text{HX}}=k_{\text{op}}$. In this so-called EX1 limit, the HX experiment measures the opening rate, or the mean residence time (MRT), of the C state, ${\tau }_{\text{C}}=1/k_{\text{op}}$. For BPTI, such pH invariance has only been observed for the eight core amides, and then only in a narrow pH interval (32).

More commonly, HX experiments are performed in the EX2 limit, where $k_{\text{int}}\ll k_{\text{op}}+k_{\text{cl}}$. Then $k_{\text{HX}}=k_{\text{int}}/\left(\kappa +1\right)$, where $\kappa \equiv k_{\text{cl}}/k_{\text{op}}={\tau }_{\text{C}}/{\tau }_{\text{O}}$ is the protection factor (PF). At equilibrium, the fractional populations, $f_{\text{C}}$ and $f_{\text{O}}$, and the rates are linked by detailed balance, $k_{\text{op}}\hspace{0.17em}{f}_{\text{C}}=k_{\text{cl}}\hspace{0.17em}{f}_{\text{O}}$, so the PF may also be expressed as $\kappa =f_{\text{C}}/f_{\text{O}}$. Clearly, $1/\left(\kappa +1\right)$ is the probability of finding the amide in the O state, $1/\kappa$ is the C $\rightleftarrows$ O equilibrium constant, and $\beta \hspace{0.17em}\mathrm{\Delta }G=\ln \kappa$ is the free energy difference between the O and C states in units of $k_{\text{B}}\hspace{0.17em}T\equiv 1/\beta$. The PF can thus be deduced from the HX rates measured (under EX2 conditions) for the amide in the protein and in a model peptide as $\kappa =k_{\text{HX}}^0/k_{\text{HX}}-1$.

The vast majority of the available protein HX data pertains to the EX2 regime and thus provides no information about the time scales, ${\tau }_{\text{C}}$ and ${\tau }_{\text{O}}$, of the conformational fluctuations, except for the EX2 bound: $1/{\tau }_{\text{C}}+1/{\tau }_{\text{O}}\gg k_{\text{int}}\approx k_{\text{HX}}^0$. In the typical case where $k_{\text{HX}}\ll k_{\text{HX}}^0$, so that ${\tau }_{\text{C}}\gg {\tau }_{\text{O}}$, we therefore only know that ${\tau }_{\text{O}}\ll 1/k_{\text{HX}}^0$, which is in the millisecond range at pH 9 (EX2 HX data are usually measured at lower pH, where $1/k_{\text{HX}}^0$ is even longer). Our analysis indicates that ${\tau }_{\text{O}}$ is seven orders of magnitude shorter than this upper bound estimate.

The HX experiment is unique in probing sparsely populated conformational states with single-residue resolution. However, the physical significance of the PF is obscured by our ignorance about the structure and dynamics of the O state. Several attempts have been made to correlate experimental PFs with physical attributes of the amides, such as solvent contact (33–37), burial depth (38), intramolecular H-bonds (35, 38–40), packing density (38, 41), or electric field (42). Where significant correlations have been found, they suggest that the chosen attribute can serve as a proxy for the propensity for C$\to$O fluctuations. However, whether based on crystal structures or molecular dynamics (MD) trajectories, these studies examined the time-averaged protein structure, which is dominated by the C state and therefore provides little or no information about the nature of the C$\to$O fluctuations.

In principle, the O state can be identified from molecular simulations, but this requires extensive conformational sampling because most C$\to$O transitions are exceedingly rare. To date, this approach has been tried only with coarse-grained and/or empirical protein models without explicit solvent (43–45), or for HX from the denatured-state ensemble (46). The recent availability of ultralong MD simulations with realistic force fields opens up new opportunities in the search for the elusive O state. We have thus analyzed the millisecond MD trajectory of fully solvated native BPTI performed by Shaw et al. (47). Fortunately, BPTI is also among the proteins that have been most thoroughly studied by HX experiments.

Results

Structure of the O State.

A classic MD simulation cannot reveal the O state directly because it does not describe the intrinsic HX step. Our strategy is therefore to postulate a generic (same for all amides) structural criterion that must be satisfied for proton transfer to take place (in the real protein). This criterion is then justified by mechanistic considerations and by its ability to reproduce experimental PFs. The O-state criterion adopted here is that the N–H hydrogen has at least two water oxygens within $R_{\text{HO}}=2.6$ Å. No angular constraint is imposed. This $R_{\text{HO}}$ cutoff distance closely matches the first minimum in the H – O_W pair correlation function computed from the MD trajectory (Fig. S1). The precise $R_{\text{HO}}$ value is not critical because the third water molecule, when present, is significantly more remote (Fig. S2).

With this criterion, 41 out of 53 amides sample the O state in the trajectory, with a mean water coordination within 2.6 Å of $N_{\text{W}}=2.001$ (Fig. 1A). For the 53 amides in the C state, $N_{\text{W}}=0.364\pm 0.393$, ranging from $\le 0.001$ (for the eight core amides and for amides 29, 35, 51, and 52) to $\ge 0.8$ (for the exposed surface amides 3, 11, 15, 19, 30, 32, 34, 39, 48, 57, and 58, and for amides 10, 38, and 41 that donate H-bonds to one of the four internal waters). For fully solvent-exposed model amides, such as N-methylacetamide, $N_{\text{W}}\approx 1$ (48). In the O state, the N–H group is thus overcoordinated.

Fig. 1.

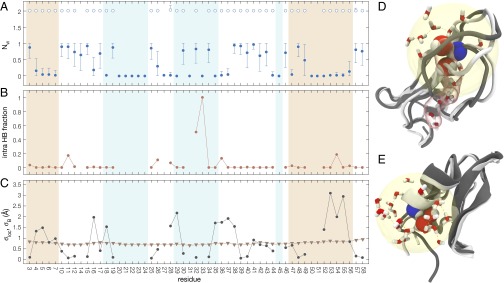
Structure of the O state for the amides in BPTI. (A) Primary water–oxygen coordination number, $N_{\text{W}}$, of amide hydrogen for amides in O (open symbols) and C (solid symbols) states. (B) Probability that an amide hydrogen with $N_{\text{W}}\ge 2$ has a polar protein atom from a nonneighbor residue within 2.6 Å. (C) O/C rmsd for atoms within 7 Å of amide N (circles) and crystallographic root-mean-square fluctuation for same set of atoms (triangles). In A–C, the background shading indicates helix (beige) and β-sheet (light blue) structure. Snapshots of O states for the amides of Gly36 (D) and Arg53 (E), with the N–H group and the two primary waters in space-filling and other waters within a 7-Å sphere (yellow) in stick representation. The backbone conformation is shown for the selected O-state frame (dark gray) and for the first C-state frame in the trajectory (light gray). Also shown for Gly36 is a five-water chain in a tunnel (translucent red) connecting one of the primary waters with the surface.

For nearly all of the examined amides, the requirement that $N_{\text{W}}\ge 2$ automatically guarantees that the intramolecular H-bond of the N–H group, which is present in the C state for more than 70% of the amides, is disrupted in the O state (Fig. 1B). (As discussed below, the converse is not true.) To eliminate the few remaining intramolecular H-bonds, we used a stronger O-state criterion requiring at least two water oxygens within 2.6 Å from the amide H as well as no protein N, O, or S atom within 2.6 Å of the amide H (except for backbone O or N atoms in the same or adjacent residues). The effect of this modification is significant only for Phe33 and Thr32 (Fig. 1B). The amide of Phe33 accesses the weak O state in only one frame, where the intramolecular H-bond partner (Arg20.O) and two water molecules are all just within the 2.6-Å cutoff. With the strong O-state criterion, this single frame is assigned to the C state, thereby excluding Phe33 from our quantitative comparison. The other outlier in Fig. 1B is Thr32, where the side-chain hydroxyl oxygen is just inside the 2.6-Å cutoff in half of the weak O-state frames.

To assess structural differences between the O and C states, we compute, for each amide that samples the O state, the local rmsd ${\sigma }_{\text{loc}}={\langle {\Vert {\langle \mathit{r}\rangle }_{\text{O}}-{\langle \mathit{r}\rangle }_{\text{C}}\Vert }^2\rangle }^{1/2}$, where ${\langle \mathit{r}\rangle }_{\text{O}}$ is the position of a particular atom averaged over all frames where the considered amide is in the O state, and the outer angular brackets denote an average over the $59\pm 14$ nonhydrogen atoms located within 7 Å of the amide nitrogen (in the first frame of the trajectory). Fig. 1C compares ${\sigma }_{\text{loc}}$ with the root-mean-square fluctuation ${\sigma }_B={\left[3\hspace{0.17em}\langle B\rangle /\left(8\hspace{0.17em}{\pi }^2\right)\right]}^{1/2}$, where $\langle B\rangle$ is the crystallographic B factor from the room-temperature BPTI structure 5PTI (49), averaged over the same set of atoms as for ${\sigma }_{\text{loc}}$. The systematic O/C structural difference measured by ${\sigma }_{\text{loc}}$ is not significantly correlated with the local flexibility ${\sigma }_B$ ($r^2=0.06$); the former shows much more variation along the backbone, from 0.05 to 3.1 Å. Moreover, ${\sigma }_{\text{loc}}$ does not correlate with secondary structure (or lack thereof) in the C state.

One expects that weakly protected amides require smaller structural adjustments to become exchange-competent. This is indeed the case; ${\sigma }_{\text{loc}}$ shows a significant correlation ($r^2=0.44$) with $\beta \hspace{0.17em}\mathrm{\Delta }{G}_{\text{exp}}=\ln {\kappa }_{\text{exp}}$ (Fig. S3). This correlation is virtually independent of the cutoff radius in the examined 5- to 8-Å range. In contrast to a previous suggestion (41), we do not find a significant correlation ($r^2=0.03$) between local rigidity, as measured by ${\sigma }_B^{-1}$, and $\mathrm{\Delta }{G}_{\text{exp}}$ (Fig. S3).

A more detailed view of the O state for two amides is provided by the snapshots in Fig. 1 D and E, to be discussed in the following. Additional (interactive) O-state structures can be found in Fig. S4.

Simulated Versus Experimental Protection Factors.

As a test of our O-state definition, we use it to compute PFs that can be compared with experiment. For each frame in the trajectory, we apply the structural criterion to assign each of the 53 backbone amides in BPTI to the O or C state. The PF is then computed as ${\kappa }_{\text{sim}}=N_{\text{FC}}/N_{\text{FO}}$, where $N_{\text{FO}}$ and $N_{\text{FC}}$ are the number of frames where the amide is in state O or C.

The HX rate, $k_{\text{HX}}$, for H exchange into D₂O has been measured by NMR for each of the 53 amides in BPTI (7, 50–53). For our analysis, we use experimental PFs (at 300 K) for a subset of 41 amides. The remaining 12 amides, all located at the protein surface, exhibit anomalous pH dependence (51) that renders unreliable any PFs derived with the aid of model peptide data (28). The 41 experimental PFs are listed in Table S1 and a detailed description of how they were deduced can be found in SI Materials and Methods.

In the simulation, 41 amides access the O state, whereas 12 amides remain in the C state throughout the trajectory. The former set of 41 amides includes 11 of the 12 surface amides for which we lack reliable experimental PFs. Consequently, 30 amides are available for a quantitative comparison between simulation and experiment. For all but three of these amides, the simulation-based prediction of the O/C free energy difference $\mathrm{\Delta }G$ agrees to better than 2.5 $k_{\text{B}}T$ with the corresponding experimental result (Fig. 2 A and B and Table S1). In terms of the deviation parameter $\mathrm{\Delta }\mathrm{\Delta }G\equiv \mathrm{\Delta }{G}_{\text{sim}}-\mathrm{\Delta }{G}_{\text{exp}}$, the overall agreement for these 30 amides can be expressed as the average absolute deviation, $\beta \langle \left|\mathrm{\Delta }\mathrm{\Delta }G\right|\rangle =1.57$, or the average signed deviation, $\beta \langle \mathrm{\Delta }\mathrm{\Delta }G\rangle =0.44$, showing that, on average, the simulation slightly overestimates the protection. The error bars in Fig. 2 A and B represent the statistical uncertainty in ${\kappa }_{\text{sim}}$ due to the finite length of the trajectory (SI Materials and Methods).

Fig. 2.

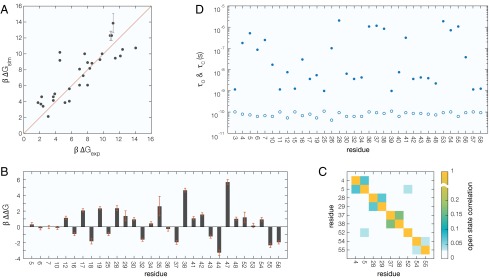
(A) Free energy difference between O and C states of 30 amides in BPTI, derived from simulation and experiment. (B) Simulation–experiment $\mathrm{\Delta }G$ mismatch for each amide in A. (C) Amides with significant temporal O-state correlation, $C\left(n,n^{\prime }\right)$. (D) Mean residence time for amides in O (open circles) and C (solid circles) states, corrected for the binning error (SI Materials and Methods). The statistical error is smaller than, or comparable to, the symbol size.

Our O-state definition is further supported by the complete absence in the trajectory of C$\to$ O transitions for the eight core amides (residues 20–24, 31, 33, and 45, with ${\kappa }_{\text{exp}}\gtrsim {10}^6$). Because these amides exchange by global unfolding (7, 32), they should not access the O state in the analyzed native-state trajectory. Assuming Poisson statistics, the probability of observing at least one C$\to$O transition in a trajectory of length T for an amide with PF κ and MRT ${\tau }_{\text{O}}$ in the O state is $P\left(T\right)=1-\exp \left[-T/\left(\kappa \hspace{0.17em}{\tau }_{\text{O}}\right)\right]$. Even if ${\tau }_{\text{O}}$ were as short as 1 µs for the globally unfolded protein, P would be merely $\sim {10}^{-4}$ for $T=0.26$ ms and $\kappa ={10}^6$. By the same token, the trajectory length required to observe at least one opening event with probability $P*=1-1/e\approx 0.63$ is $T^{*}={\tau }_{\text{C}}=\kappa \hspace{0.17em}{\tau }_{\text{O}}$. For amides exchanging by subglobal fluctuations with ${\tau }_{\text{O}}\approx 100$ ps (see below) and $\kappa ={10}^2$, ${10}^4$, and ${10}^6$, the required trajectory length is 10 ns, 1 μs, and 100 μs, respectively.

In summary, among the 41 available experimental PFs, 35 are fully consistent with the simulation, either quantitatively (27 amides) or qualitatively (8 amides). Two of the remaining six amides, in residues Cys14 and Cys38, are sensitive to the conformation of the 14–38 disulfide bond. If these two amides are allowed to access also the experimentally unresolved (54) minor disulfide conformations M2 and M3 in the O state, we obtain good agreement with experiment for both Cys14 ($\beta \hspace{0.17em}\mathrm{\Delta }\mathrm{\Delta }G=-0.78$) and Cys38 ($\beta \hspace{0.17em}\mathrm{\Delta }\mathrm{\Delta }G=1.43$). Apart from the eight amides in the slow-exchange core and the amide of Cys14, three more amides do not undergo any C$\to$O transitions: Ala27 (${\kappa }_{\text{exp}}={10}^{2.7}$) located in a turn, Asp50 (not included in the experimental data set) in the C-terminal α helix, and Cys51 (${\kappa }_{\text{exp}}={10}^{4.8}$) involved in a disulfide bond. The discrepancies for these three amides remain unaccounted for.

The PF comparison in Fig. 2 A and B is reassuring, considering the known sources of systematic error. Foremost among these is the assumption, used to extract the experimental PFs, that the intrinsic HX rate in the O state is the same as in model peptides (42). The PF comparison may also have been affected by differences in solvent conditions between simulation and experiment (stronger H-bonds and hydrophobicity in D₂O than in H₂O; about half of the five carboxyl groups protonated at pH* 3.5 but none at pH ∼7). As regards the simulation, the main concern is the quality of the empirical force field. However, the force field used in this simulation (47) has fared very well when benchmarked against NMR data related to conformational flexibility of native proteins (55–57). Moreover, the MD trajectory used here yields excellent agreement with the NMR-determined exchange times of the four internal water molecules in BPTI (58).

Cooperativity and Kinetics.

An important characteristic of subglobal $\text{C}\to \text{O}$ fluctuations is their degree of cooperativity. Are they truly local or do several nearby amides access the O state simultaneously? To address this question, we compute the O-state correlation matrix $C\left(n,n^{\prime }\right)$, which equals 0 if amides n and $n^{\prime }$ are uncorrelated and 1 if they are perfectly correlated (SI Materials and Methods). We find that the vast majority of the 41 amides that access the O state during the trajectory are uncorrelated. Only five amide pairs have $C\left(n,n^{\prime }\right)>0.03$ (Fig. 2C). The largest correlation, $C\left(\mathrm{37,38}\right)=0.17$, involves amides near the 14–38 disulfide bond. Other significantly correlated amide pairs are $C\left(\mathrm{4,5}\right)=0.07$ in the cooperatively unfolded N-terminal $3_{10}$ helix and $C\left(\mathrm{27,28}\right)=0.06$ in the turn between the two β-strands. The only significant correlation between residues that are far apart in the sequence is $C\left(\mathrm{5,52}\right)=0.04$ in polypeptide segments linked by the 5–55 disulfide bond.

To characterize the kinetics of $\text{C}\rightleftarrows \text{O}$ fluctuations, we compute the MRTs ${\tau }_{\text{O}}=1/k_{\text{cl}}$ and ${\tau }_{\text{C}}=1/k_{\text{op}}$ as the average number of consecutive frames in each state multiplied by the sampling resolution $\mathrm{\Delta }\tau =0.25$ ns. Most O-state visits are only a single frame and none lasts more than six frames (Table S2). Many visits must therefore be shorter than $\mathrm{\Delta }\tau$ and only a fraction of these will be recorded at the given sampling resolution. By modeling the $\text{C}\rightleftarrows \text{O}$ fluctuations as an alternating Poisson process, we can correct quantitatively for this systematic binning error. As shown in SI Materials and Methods, the corrected MRTs are given by ${\tau }_{\text{O}}=-\hspace{0.17em}\mathrm{\Delta }\tau /\ln \left(1-N_{\text{O}}/N_{\text{FO}}\right)$ and ${\tau }_{\text{C}}=N_{\text{FC}}\hspace{0.17em}\mathrm{\Delta }\tau /\left[1-N_{\text{FO}}\hspace{0.17em}\ln \left(1-N_{\text{O}}/N_{\text{FO}}\right)\right]$, where $N_{\text{FO}}$ and $N_{\text{FC}}$ were defined in connection with the PF and $N_{\text{O}}=N_{\text{C}}-1$ is the number of visits to the O state during the trajectory.

In this way we obtained the O-state and C-state MRTs for the 34 amides for which $N_{\text{FO}}>N_{\text{O}}$ (Fig. 2D). Whereas ${\tau }_{\text{C}}$ varies by three orders of magnitude (from 1 ns to 2 µs), ${\tau }_{\text{O}}$ varies by less than a factor of 3. The large variation in PF among the amides is therefore due almost entirely to variation in ${\tau }_{\text{C}}$ (or the opening rate, $k_{\text{op}}$). The mean and SD of ${\tau }_{\text{O}}$ for the 34 amides is $81\pm 18$ ps. For these amides, the O state is thus highly unstable, that is, the free energy barrier for the O$\to$C transition is small.

The remarkably short value of ${\tau }_{\text{O}}$ led us to examine the possibility that the amide water coordination fluctuates rapidly between 2 and 1 while the protein configuration remains open. O-state visits would then appear in clusters, rather than being randomly distributed along the trajectory. If this were the case, we would also observe a large number of short (one or a few frames) visits to the C state. However, this is not the case; the C-state residence time distributions for most of the 34 amides are close to exponential (Fig. S5), as expected for an alternating (C/O) Poisson process. We therefore conclude that the short ${\tau }_{\text{O}}$ is a robust property of the O-state definition introduced here, which also yields PFs in good agreement with experiment.

Discussion

Relation to Previous Work.

The simulation-based HX analysis presented here differs in two essential ways from previous computational HX studies. First, the MD trajectory used here is based on a realistic physical model with explicit water and state-of-the-art force field (47). An earlier study (45) with similar objectives used a coarse-grained implicit-solvent model and defined the O state as having no C_β atom within 6.5 Å of the reference C_β atom. This O-state definition is much more disruptive than ours (Fig. 1C); for example, the O state of Arg53 (Fig. 1E) has five other C_β atoms within 6.5 Å.

The second key feature of our analysis is the length of the MD trajectory, 262 µs. The longest atomistic MD trajectory previously used for HX analysis was three orders of magnitude shorter (90 ns) (36). Rather than attempting to identify the O state, that study correlated the trajectory-averaged (essentially C-state) amide solvent access with the number of exchanged hydrogens (detected by mass spectrometry) for a set of peptide fragments (36). However, the strong linear correlation thus obtained seems to be spurious, largely resulting from the trivial increase of both variables with peptide size.

Nature of the O State.

It is generally agreed that the two necessary conditions for exchange competence are direct access to external solvent and disruption of any intramolecular H-bond with the N–H group (18–25, 40). Our O-state definition incorporates these conditions by stipulating that the amide hydrogen has at least two water oxygens within 2.6 Å and that the amide hydrogen has no other polar protein atom (except in neighboring residues) within 2.6 Å. For all but a few amides (Fig. 1B), the second condition is automatically satisfied if the first one is obeyed.

We have explored several other O-state criteria, such as solvent-accessible surface area and intramolecular H-bonding, but the agreement with the experimental PFs is invariably worse than in Fig. 2 A and B. For example, if we retain the condition of disrupted intramolecular H-bond but require at least one (rather than two) waters within 2.6 Å of the amide hydrogen, then the O state is somewhat more long-lived (${\tau }_{\text{O}}=0.05-5$ ns) but the PF is severely underestimated ($\beta \hspace{0.17em}\mathrm{\Delta }\mathrm{\Delta }G=-4.85$). This more permissive O-state criterion may capture more of the water-penetrated conformations that are implicated in internal-water exchange (58).

According to our results, the O state is not only improbable ($f_{\text{O}}\ll 1$), it is also highly labile: ${\tau }_{\text{O}}=41-113$ ps for the examined amides (Fig. 2D). In the few cases where ${\tau }_{\text{O}}$ has been experimentally inferred for amides that exchange by subglobal fluctuations, values in the microsecond range have been reported (59). However, these inferences depend critically on the two auxiliary assumptions in the standard HX model, namely, that the relevant conformational fluctuations are pH-independent and that the intrinsic HX rate in the O state is the same as for model peptides. These assumptions are not likely to be quantitatively accurate for amides that exchange by subglobal fluctuations.

The ${\tau }_{\text{O}}$ values of order 100 ps inferred here are seven orders of magnitude shorter than the MRT of the globally unfolded protein, which is the O state for the eight core amides (32). At least for BPTI, few, if any, amides seem to have a ${\tau }_{\text{O}}$ value in the wide interval between these extremes. For an alternating Poisson process, there is a 90% probability that an amide with ${\tau }_{\text{C}}=\kappa {\tau }_{\text{O}}=T/\ln 10$ undergoes at least one opening event in a trajectory of length T (discussed above). Therefore, even if ${\tau }_{\text{O}}$ were as long as 1 µs, we would have observed the O state in the 0.26-ms trajectory for at least 10 of the 30 amides in Fig. 2A (i.e., those with $\kappa <100$).

The striking disparity in ${\tau }_{\text{O}}$ values of amides that exchange by subglobal versus global fluctuations is the result of a highly cooperative global unfolding. At least for a small single-domain protein such as BPTI (with three disulfide bonds), we do not observe a continuous spectrum of conformational fluctuations on all length and time scales. Instead, it seens that only highly localized and short-lived fluctuations can occur as long as the β-sheet core is intact.

Solvent Penetration Versus Local Unfolding.

Much of the debate about the HX mechanism in proteins has been framed as a dichotomy between “solvent penetration” and “local fluctuation” scenarios (18–25). These imprecisely defined scenarios are not necessarily mutually exclusive; to some extent they may be different sides of the same coin. Using the same MD trajectory, we have previously shown that the internal water molecules in BPTI exchange by way of H-bonded water chains that penetrate the protein through transient tunnels or pores (58). Such chains are not a general feature of the amide O state that we identify here, even though chains formed by some of the “native” internal waters are seen for a few amides, for example Gly36 (Fig. 1D) and Lys41, but not in all O-state configurations (Fig. S4). The open states for internal-water exchange are also short-lived (a few nanoseconds) (58), but the opening frequency is one to two orders of magnitude lower (60) than for the HX O states of the amides that H-bond to internal waters.

For most of the examined amides, the conformation of the O state is probably best described as locally distorted or “unfolded.” The almost complete lack of temporal correlation of C$\to$O transitions in different amides (Fig. 2C) does not exclude local unfolding cooperativity. Especially in the terminal helices, we do see that several adjacent residues are unfolded even if only one amide at a time is in the O state (Fig. 1E). This observation is consistent with the finding (Fig. 1B) that overcoordinated ($N_{\text{W}}\ge 2$) amides rarely have intramolecular H-bonds, whereas a disrupted intramolecular H-bond is not a sufficient O-state criterion (discussed above). In larger proteins, the O state may well be reached by cooperative unfolding of larger structural units (9). In any case, the intermittent nature of the C$\to$O fluctuations suggests that “coughing” may be a more accurate metaphor than “breathing.”

The modest extent of structural distortion in the O states identified here (Fig. 1C) is consistent with the small (less than an order of magnitude) effect of 8 M urea on $k_{\text{HX}}$ for the BPTI amides that exchange by subglobal fluctuations (29). Because urea has a similarly small effect on $k_{\text{int}}$ (61, 62), this observation indicates that the $\text{C}\rightleftarrows \text{O}$ equilibrium is much less sensitive to urea than the global $\text{N}\rightleftarrows \text{U}$ equilibrium, consistent with a modest increase of solvent exposure in the O state.

Among experimental probes, amide HX and internal-water exchange (60) are unique in their ability to monitor rare and transient conformational fluctuations. The $\text{C}\rightleftarrows \text{O}$ transitions discussed here are not observable by conventional NMR relaxation methods, whether relaxation is induced by anisotropic nuclear couplings ($f_{\text{O}}$ is too small) or by chemical shifts (the effective correlation time, $\sim {\tau }_{\text{O}}$, is too short).

Proton Transfer Mechanism.

Without “smoking gun” type of evidence, the exchange-competent state wherein the proton is transferred cannot be unambiguously established. Nevertheless, we believe that the O state identified here, with its overcoordinated amide hydrogen, is a plausible candidate also from a mechanistic standpoint.

The classic kinetic scheme for intermolecular proton transfer (PT) posits a diffusion-controlled formation of a H-bonded encounter complex, followed by a fast PT equilibrium within the complex (27). However, this phenomenological framework does not address the crucial participation of water molecules in the PT mechanism. In bulk aqueous solution, the hydroxide ion interacts strongly with three water molecules (63) during its picosecond lifetime (64). The excess negative charge migrates by structural diffusion, involving more or less concerted proton jumps through the H-bond network (65, 66). In keeping with these notions, we envision the following PT scenario in the overcoordinated O state (Fig. S6).

Upon approach of the hydroxide ion, the “first” water molecule, which accepts a H-bond from the N–H group, extracts the amide hydrogen, thereby converting the hydroxide ion into a water molecule, possibly via one or more intermediate H-bonded water molecules. Concomitantly, the “second” water molecule reorients to interact strongly (as H-bond donor) with the transient imidate ion, which now accepts H-bonds from both water molecules. Without the second water molecule, the incompletely solvated imidate ion would quickly revert to its original N–H form without having exchanged its proton. When two water molecules are present, there is at least a 50% chance (more if the process is concerted) for the amide to acquire a new proton (or deuteron) by extracting it from the second water molecule, which thereby regenerates the catalytic hydroxide ion. If the second water molecule is linked via H-bonds to additional water molecules, the regenerated hydroxide ion may appear at some distance from the N–H group. Indeed, either the entry or the exit of the excess charge might proceed along a water wire in a pore connecting the amide with bulk solvent. Although involvement of such water wires seems to be rare, Gly36 being the only case observed here (Fig. 1D), theoretical studies support this possibility (67).

If an overcoordinated N–H group is required for amide PT in the protein, then the PT mechanism must differ somewhat in model amides, where $N_{\text{W}}\approx 1$ (48). This would violate the assumption in the standard two-state model that the intrinsic HX rate, $k_{\text{int}}$, is the same in these two situations. At first sight, this assumption seems unlikely to be valid because the microsolvation of the N–H group must differ. However, the proton transfer process is diffusion-controlled (27) and is therefore not affected by the rate of equilibration within the encounter complex. Moreover, $k_{\text{int}}$ depends only linearly on the target size, which, in any case, is ill-defined owing to the “delocalization” of the hydroxide charge (65, 66). The imidate ion is likely to be coordinated by two water molecules also in the encounter complex of model peptides, but in that case a second water molecule is never far away and may move into position as the hydroxide ion approaches. In contrast, in the more confined O state of the protein, the N–H group must be “presolvated”’ with two water molecules. In conclusion, we believe that the evidence favors the overcoordinated N–H group as the salient feature of the O state for amides that exchange by subglobal fluctuations.

Materials and Methods

Our computational analysis is based on a previously reported all-atom MD simulation at 300 K of the protein BPTI, solvated by 4,215 water molecules (47). The protonation state of ionizable groups corresponds to neutral pH, with the net protein charge neutralized by six chloride ions. A subset of 1,048,349 frames with 0.25-ns spacing, corresponding to a 0.262-ms-long trajectory, was extracted by requiring that the 14–38 disulfide bond is in the experimentally dominant M1 conformation (54). Further details can be found in SI Materials and Methods.