Reconstruction of Genome Ancestry Blocks in Multiparental Populations

Abstract

We present a general hidden Markov model framework called reconstructing ancestry blocks bit by bit (RABBIT) for reconstructing genome ancestry blocks from single-nucleotide polymorphism (SNP) array data, a required step for quantitative trait locus (QTL) mapping. The framework can be applied to a wide range of mapping populations such as the Arabidopsis multiparent advanced generation intercross (MAGIC), the mouse Collaborative Cross (CC), and the diversity outcross (DO) for both autosomes and X chromosomes if they exist. The model underlying RABBIT accounts for the joint pattern of recombination breakpoints between two homologous chromosomes and missing data and allelic typing errors in the genotype data of both sampled individuals and founders. Studies on simulated data of the MAGIC and the CC and real data of the MAGIC, the DO, and the CC demonstrate that RABBIT is more robust and accurate in reconstructing recombination bin maps than some commonly used methods.

MANY synthetic animal and plant resources have been created for genetic mapping of quantitative trait loci (QTL). Examples include the mouse Collaborative Cross (CC) (Churchill et al. 2004), the heterogeneous stock (HS) (Mott et al. 2000), the diversity outcross (DO) (Svenson et al. 2012), the maize nested associated mapping (NAM) population (Buckler et al. 2009), the advanced intercross lines (AIL) (Darvasi and Soller 1995), the Arabidopsis multiparent recombinant inbred lines (RIL) (AMPRIL) (Huang et al. 2011), the Arabidopsis multiparent advanced generation intercross lines (MAGIC) (Kover et al. 2009), and the Drosophila synthetic population resource (DSPR) (King et al. 2012). The genome of an individual sampled from such a population is a random mosaic of ancestry blocks, each alternatively inherited from an inbred founder. The focus of this article is on reconstructing these ancestry blocks from single-nucleotide polymorphism (SNP) array data, a necessary step for downstream QTL mapping.

The pedigree-based approaches, such as MERLIN (Abecasis et al. 2002), are often used to solve ancestral inference in human genetics. However, in the fields of animal and plant breeding, these algorithms become computationally intensive because of the large size of breeding pedigrees, the absence of genotypic data in intermediate generations, and the dense marker data in the last generation. Recently, Liu et al. (2010) presented an efficient algorithm, GAIN, for simplifying the inbreeding structure of complex pedigrees. Specifically, the authors accounted for the symmetry of repeated sibling (brother–sister) mating in the CC, so that the four alleles in the beginning generation of inbreeding have equal probability $1/4$ of being passed down.

Nevertheless, the large breeding pedigrees (since the founder population) in advanced mapping populations such as the MAGIC and the DSPR are often unavailable or inaccurate. Moreover, inbreeding by selfing instead of sibling mating is usually adopted in plant population resources such as the MAGIC. The relatively simple hidden Markov model (HMM), implemented in HAPPY (Mott et al. 2000), is thus widely used, since it does not incorporate any pedigree information except the effective number of generations. HAPPY has implemented two extremes: the diploid mode where the ancestral origin processes between two homologous chromosomes are independent and the haploid mode for haploid genomes and for diploid lines where the processes are completely dependent.

The full range of the dependencies of the ancestral origin processes between two homologous chromosomes has been modeled by a continuous-time Markov chain (CTMC) for both autosomes (Zheng et al. 2014) and X chromosomes (Zheng 2015), where the optimal breeding design in terms of mapping resolution is of interest. In this article, we implement a Bayesian framework, denoted by reconstructing ancestry blocks bit by bit (RABBIT), in multiparental populations from SNP array data, where the previously developed CTMC is used as the prior of ancestral origin processes. RABBIT incorporates information on breeding designs through the hyperparameter Ω, a full set of parameters on which ancestral origin processes depend, describing the inbreeding level and the densities of junctions (recombination breakpoints) along two homologous chromosomes.

RABBIT is highly flexible, because a wide range of breeding designs and population types can be specified through the hyperparameter Ω. If the breeding design is stage-wise random mating, we may calculate Ω analytically according to our previous developed framework (Zheng et al. 2014; Zheng 2015), where the calculation is essentially an average over gene dropping on all the possible pedigrees conditional on the specified mating schemes. If the breeding pedigree is known but it cannot be regarded as stage-wise random mating, we may calculate Ω by simulating many replicates of gene dropping on the given pedigree. If both the breeding pedigree and the mating schemes are not known, we may estimate Ω from the marker data, an empirical Bayes method for setting the hyperparameter Ω.

In Materials and Methods, we describe three models for RABBIT, where the observation models are the same and the prior models of ancestral origin processes are similar to those used in GAIN and HAPPY; we describe in detail the calculations of the hyperparameter Ω by RABBIT in the Appendix. The observation model accounts for missing data and allelic typing errors in the genotype data of both sampled individuals and founders, which are not fully modeled in GAIN and HAPPY. We use simulated data from two example populations of the CC and the MAGIC to evaluate the three models of RABBIT and to compare among RABBIT, GAIN, and HAPPY. These methods are further evaluated by analyzing the real data of the MAGIC (Kover et al. 2009), the DO (Svenson et al. 2012), and the pre-CC (Durrant et al. 2011). Finally, the limitations of these methods and the possible extensions of RABBIT are discussed.

Materials and Methods

Data

We analyze independently each linkage group of each individual sampled from a mapping population. Each individual is genotyped at T biallelic SNPs of a linkage group, and the genetic distances $d_t$ $\left(t=1\mathrm{\dots }T-1\right)$ between consecutive marker locations t and $t+1$ are measured in morgans and known without errors. Let ${\left\{Y_t\right\}}_{t=1}^T$ denote the unphased genotype data along the two homologous chromosomes of a sampled individual, and H denote the founder haplotype, with matrix element $H_{ti}$ being the observed homozygous allele at locus $t=1\mathrm{\dots }T$ of inbred founder $i=1\mathrm{\dots }L$.

The genotype data are analyzed by an HMM model, where the process model describes the ancestral origin processes along two homologous chromosomes, and the observation model describes the probability of genotypes given latent ancestral origin states. In addition to the founder haplotypes and the sampled genotypes, we assume that there are no genetic data available in the intermediate generations.

The process model

Let ${\left\{O_t^{\mathrm{m}}\right\}}_{t=1}^T$ denote the ancestral origins along the maternally derived chromosome and ${\left\{O_t^{\mathrm{p}}\right\}}_{t=1}^T$ those along the paternally derived chromosome. Let $O_t=\left(O_t^{\mathrm{m}},O_t^{\mathrm{p}}\right)$ be the ordered ancestral origin state at locus t, and it is identical by descent (IBD) if $O_t^{\mathrm{m}}=O_t^{\mathrm{p}}$ and non-IBD otherwise. We label the ancestral origins by natural integers starting from 1. Let n denote the number of possible ancestral origins, and for simplicity set $n=L$, the number of inbred founders, throughout the article.

To study how the prior processes affect the reconstruction of ancestry blocks, we designate three models: jointModel, indepModel, and depModel, where the ancestral origin processes along two homologous chromosomes are modeled jointly, independently, and completely dependently, respectively. All three models have the same observation model described in the next section. The indepModel and the depModel apply to completely outbred and fully inbred genomes and correspond to the diploid and haploid modes of HAPPY, respectively. On the other hand, the jointModel applies to the full range of inbreeding levels and corresponds to the model of GAIN.

The introduction of the three models has multiple purposes. First, the indepModel and the depModel serve as two extreme baselines to show how much the jointModel can improve the reconstruction of genome ancestry blocks. Second, the comparison among the three models serves as a baseline to show whether the differences among RABBIT, HAPPY, and GAIN are due to the prior models of ancestral origin processes. Finally, the depModel is the only suitable model for haploid genomes such as the X chromosomes of males.

The three models are fitted into the framework of discrete time Markov chains, which can be described completely by the initial distribution at the first locus and the transition probability matrix from one locus to the next (Norris 1997). In the following, we focus on the two components of Markov chains and the hyperparameter Ω for each of the three models.

jointModel:

We model jointly the latent ancestral origin states ${\left\{O_t\right\}}_{t=1}^T$ along the two homologous chromosomes. Let $f=P\left(O^{\mathrm{m}}=O^{\mathrm{p}}\right)$ be the IBD probability at a locus, and the initial distribution is given by

$$P\left[O_1=\left(O_1^{\mathrm{m}},O_1^{\mathrm{p}}\right)\right]=\{\begin{array}{ll}\frac{f}{n}\hfill & \text{if }{O}_1^{\mathrm{m}}=O_1^{\mathrm{p}}\hfill \\ \frac{1-f}{n\left(n-1\right)}\hfill & \text{otherwise,}\hfill \end{array}$$

where n ancestral origins are assumed to be symmetric given the initial IBD state or non-IBD state. Denoting by Q the transition rate matrix of the CTMC with dimension $n^2\times n^2$, the transition probability matrix from $O_t$ to $O_{t+1}$ is given by

$$P\left[\left(O_{t+1}^{\mathrm{m}},O_{t+1}^{\mathrm{p}}\right)|\left(O_t^{\mathrm{m}},O_t^{\mathrm{p}}\right)\right]=e^{Q{d}_t}\approx I+Q{d}_t+\frac{1}{2}{Q}^2{d}_t^2$$

(Norris 1997) for $t=\mathrm{1...}T-1$, where I is an identity matrix, and the matrix exponential is approximated by its Taylor expansion up to the second order of $d_t$ under the assumption of small intermarker distances. We neglect the scenario with more than two crossovers between consecutive markers and assume that there are no genetic interferences. Higher-order Taylor expansion may be used for larger $d_t$, and more sophisticated methods for the calculation of the matrix exponential may be alternatively used (Moler and Van Loan 2003).

As described in detail in the previous method (Zheng et al. 2014; Zheng 2015), the rate matrix Q can be constructed from junction densities, under the assumption of exchangeable ancestral origins; see figure 1 of Zheng (2015) for an example of the four-way RIL by sibling mating. Let $J\left(abcd\right)$ denote the density (per morgan) of junctions of type $\left(abcd\right)$, where haplotype $ac\left(bd\right)$ is on the maternally (paternally) derived chromosome, the genotype $ab\left(cd\right)$ is on the left (right) side of the junction, and the same integer labels denote IBD. After accounting for the reversibility of chromosome directions, we need only to consider five junction types (see figure 2 of Zheng et al. 2014) and obtain for the jointModel

$$\Omega =\left\{f,J\left(1122\right),J\left(1211\right),J\left(1213\right),J\left(1222\right),J\left(1232\right)\right\},$$

where junction type $\left(1122\right)$ has two breakpoints shared on both chromosomes, junction types $\left(1211\right)$ and $\left(1213\right)$ have breakpoints only on the paternally derived chromosome, and junction types $\left(1222\right)$ and $\left(1232\right)$ have breakpoints only on the maternally derived chromosome. Junction type $\left(1122\right)$ has IBD states on both sides, junction types $\left(1213\right)$ and $\left(1232\right)$ have non-IBD states on both sides, and junction types $\left(1211\right)$ and $\left(1222\right)$ refer to the transitions from non-IBD to IBD.

indepModel:

Two homologous chromosomes have a priori completely independent ancestral origins. The initial distribution is given by

$$P\left[\left(O_1^{\mathrm{m}},O_1^{\mathrm{p}}\right)\right]=P\left(O_1^{\mathrm{m}}\right)P\left(O_1^{\mathrm{p}}\right)=\frac{1}{n^2},$$

and thus the prior IBD probability f is implicitly set to $1/n$. The transition probability matrix for the indepModel is given by

$$\begin{array}{l}P\left[\left(O_{t+1}^{\mathrm{m}},O_{t+1}^{\mathrm{p}}\right)|\left(O_t^{\mathrm{m}},O_t^{\mathrm{p}}\right)\right]=P\left(O_{t+1}^{\mathrm{m}}|O_t^{\mathrm{m}}\right)P\left(O_{t+1}^{\mathrm{p}}|O_t^{\mathrm{p}}\right),\\ P\left(O_{t+1}^x|O_t^x\right)=\delta \left(O_{t+1}^x=O_t^x\right)e^{-R^x{d}_t}+\delta \left(O_{t+1}^x\ne O_t^x\right)\\ \times \left(1-e^{-R^x{d}_t}\right)\frac{1}{n-1},x\in \left\{m,p\right\},\end{array}$$

where δ is an indicator function and it equals 1 if the argument is true and 0 otherwise, and $R^{\mathrm{m}}\left(R^{\mathrm{p}}\right)$ is the map expansion or the summed junction density on the maternally (paternally) derived chromosomes. Thus the hyperparameter $\Omega =\left\{R^{\mathrm{m}},R^{\mathrm{p}}\right\}$.

depModel:

Two homologous chromosomes have a priori identical ancestral origins. The initial distribution is given by

$$P\left[\left(O_1^{\mathrm{m}},O_1^{\mathrm{p}}\right)\right]=\frac{1}{n}\delta \left(O_1^{\mathrm{p}}=O_1^{\mathrm{m}}\right),$$

and thus the prior IBD probability f is implicitly set to 1. The transition probability matrix for the depModel is given by

$$\begin{array}{l}P\left[\left(O_{t+1}^{\mathrm{m}},O_{t+1}^{\mathrm{p}}\right)|\left(O_t^{\mathrm{m}},O_t^{\mathrm{p}}\right)\right]=P\left(O_{t+1}^{\mathrm{m}}|O_t^{\mathrm{m}}\right)\delta \left(O_{t+1}^{\mathrm{p}}=O_{t+1}^{\mathrm{m}}\right),\\ P\left(O_{t+1}^{\mathrm{m}}|O_t^{\mathrm{m}}\right)=\delta \left(O_{t+1}^{\mathrm{m}}=O_t^{\mathrm{m}}\right)e^{-\overline{R}{d}_t}\\ +\delta \left(O_{t+1}^{\mathrm{m}}\ne O_t^{\mathrm{m}}\right)\left(1-e^{-\overline{R}{d}_t}\right)\frac{1}{n-1},\end{array}$$

where $\overline{R}=\left(R^{\mathrm{m}}+R^{\mathrm{p}}\right)/2$ for autosomes or female XX chromosomes, and $\overline{R}=R^{\mathrm{m}}$ for the maternally derived X chromosome of a male. Thus the hyperparameter $\Omega =\left\{\overline{R}\right\}$.

Remarks:

Although the maternally and paternally derived X chromosomes are generally not symmetric because the latter did not experience any crossovers with Y chromosomes, the symmetry between the autosomes holds in many mapping populations with multistage random mating. Under this symmetry, it holds $J\left(1211\right)=J\left(1222\right)$ and $J\left(1213\right)=J\left(1232\right)$ so that the hyperparameter Ω for the jointModel can be simplified by removing two junction densities, and similarly it holds $R^{\mathrm{m}}=R^{\mathrm{p}}$ so that the hyperparameter Ω for the indepModel can be simplified to contain only one map expansion.

The general jointModel converges to the indepModel and the depModel at the two extreme inbreeding levels. Completely outbred genomes are possible only if the number of founder origins goes to be very large $\left(n\gg 3\right)$, so that the IBD probability $f=1/n$ goes to zero. Thus, the junction types $\left(1122\right)$, $\left(1211\right)$, and $\left(1222\right)$ become impossible, and the junction densities $J\left(1213\right)$ and $J\left(1232\right)$ converge to $R^{\mathrm{p}}$ and $R^{\mathrm{m}}$, respectively. For fully inbred genomes, so that the IBD probability $f=1$, there exists only the junction type $\left(1122\right)$ with density equal to the map expansion $R^{\mathrm{m}}$ or $R^{\mathrm{p}}$.

The observation model

In an HMM, the unphased genotypes ${\left\{Y_t\right\}}_{t=1}^T$ are conditionally independent given the latent ancestral origin states ${\left\{O_t\right\}}_{t=1}^T$. We thus focus on the likelihood at a locus and drop the locus subscript t. Let $D\left(H,O\right)=\left(H_{O^{\mathrm{m}}},H_{O^{\mathrm{p}}}\right)$ be the phased genotype derived from the founder haplotypes H and the ancestral origin state O at the locus. Denote by ϵ and ${\mathit{ϵ}}_{\mathrm{F}}$ the allelic typing error probabilities for sampled individuals and founders, respectively. The aim is to calculate the likelihood $l=P\left(Y|D\left(H,O\right),O,\mathit{ϵ},{\mathit{ϵ}}_{\mathrm{F}}\right)$ at the locus.

Let Z be the true phased genotype at the locus of the sampled individual. The likelihood l is calculated by integrating out the unknown true genotype Z, and it holds

$$l={\displaystyle \sum _{Z}P\left(Y|Z,\mathit{ϵ}\right)P\left(Z|D,O,{\mathit{ϵ}}_{\mathrm{F}}\right),}$$

where $P\left(Z|D,O,{\mathit{ϵ}}_{\mathrm{F}}\right)$ is the posterior probability given the derived genotype D and the ancestral origin state O. According to Bayes’ theorem, we have

$$P\left(Z|D,O,{\mathit{ϵ}}_{\mathrm{F}}\right)=\frac{P\left(D|Z,O,{\mathit{ϵ}}_{\mathrm{F}}\right)P\left(Z|O\right)}{P\left(D|O,{\mathit{ϵ}}_{\mathrm{F}}\right)},$$

where $P\left(Z|O\right)$ is the prior probability of the true genotype Z, and the marginal probability $P\left(D|O,{\mathit{ϵ}}_{\mathit{F}}\right)={\displaystyle \sum _{Z}P\left(D|Z,O,{\mathit{ϵ}}_{\mathit{F}}\right)P\left(Z|O\right)}$ according to the law of total probability. We assign a noninformative prior probability to $P\left(Z|O\right)$. Let 1 and 2 denote the two possible alleles of SNPs. Given non-IBD $\left(O^{\mathrm{m}}\ne O^{\mathrm{p}}\right)$ at the locus, the phased true genotypes $Z=\left(1,1\right)$, $\left(1,2\right)$, $\left(2,1\right)$, and $\left(2,2\right)$ have equal prior probability $1/4$. Given IBD $\left(O^{\mathrm{m}}=O^{\mathrm{p}}\right)$ at the locus, the true genotypes $\left(1,1\right)$ and $\left(2,2\right)$ have equal prior probability $1/2$.

The probabilities $P\left(Y|Z,\mathit{ϵ}\right)$ and $P\left(D|Z,O,{\mathit{ϵ}}_{\mathrm{F}}\right)$ are shown in detail in Supporting Information, Table S1 and Table S2, respectively. In the calculations of these probabilities, we account for missing alleles for sampled individuals and founders, conditional on the pattern of missing data. The typing errors are assumed to occur independently across observed alleles. Given that an error occurs, the observed allele is the alternative one. The probability $P\left(Y|Z,\mathit{ϵ}\right)$ in Table S1 is the same as the penetrance for a SNP described by Bauman et al. (2008) where the founder allelic errors are not modeled so that the true genotype Z is given by the derived genotype $D\left(H,O\right)$. For the X chromosome of a male, the probabilities $P\left(Y|Z,\mathit{ϵ}\right)$ and $P\left(D|Z,O,{\mathit{ϵ}}_{\mathrm{F}}\right)$ are very straightforward and shown in Table S3 and Table S4, where the genotypes refer to the haplotypes (alleles) at the locus.

Inference

We reconstruct ancestry blocks by independently sampling many times from the joint posterior distribution of ${\left\{O_t\right\}}_{t=1}^T$, conditional on the given hyperparameter Ω and allelic error probabilities ${\mathit{ϵ}}_{\mathrm{F}}$ and ϵ. For each posterior sample, calculate $\alpha \left(O_t\right)=P\left({\left\{Y_{\tau }\right\}}_{\tau =1}^t,O_t|\Omega ,\mathit{ϵ},{\mathit{ϵ}}_{\mathrm{F}}\right)$ iteratively for $t=1\mathrm{\dots }T$ by the forward algorithm (Rabiner 1989). Then sample $O_T$ according to the distribution $\alpha \left(O_T\right)$, and subsequently sample $O_t$ according to

$$P\left(O_t|{\left\{O_{\tau }\right\}}_{\tau =t+1}^T,{\left\{Y_{\tau }\right\}}_{\tau =1}^T,\Omega ,\mathit{ϵ},{\mathit{ϵ}}_{\mathrm{F}}\right)\propto \alpha \left(O_t\right)P\left(O_{t+1}|O_t,\Omega \right)$$

backwardly for $t=T-1,\dots ,1$, where the dependence of the transition probability matrix on hyperparameter Ω is explicitly shown.

The posterior samples contain complete information of the ancestry blocks along two homologous chromosomes. The marginal posterior probability of $P\left(O_t|{\left\{Y_{\tau }\right\}}_{\tau =1}^T,\Omega ,\mathit{ϵ},{\mathit{ϵ}}_{\mathrm{F}}\right)$ can be obtained by averaging over all the posterior samples or alternatively by the forward–backward algorithm (Rabiner 1989). The optimal sequence of the ancestry blocks can be obtained by selecting the posterior sample with the maximum marginal likelihood $P\left({\left\{Y_{\tau }\right\}}_{\tau =1}^t|\Omega ,\mathit{ϵ},{\mathit{ϵ}}_{\mathrm{F}}\right)={\displaystyle \sum _{O_T}\alpha \left(O_T\right)}$ or alternatively by dynamic programming such as the Viterbi algorithm (Rabiner 1989).

The marginal likelihood $P\left({\left\{Y_{\tau }\right\}}_{\tau =1}^T|\Omega ,\mathit{ϵ},{\mathit{ϵ}}_{\mathrm{F}}\right)$ is used as a Bayesian evidence for model comparisons. If the difference of the evidence in natural logarithm scale between two models is >5, the model with the higher evidence value is very strongly supported, according to the widely cited interpretation of Kass and Raftery (1995).

Simulation of mapping populations

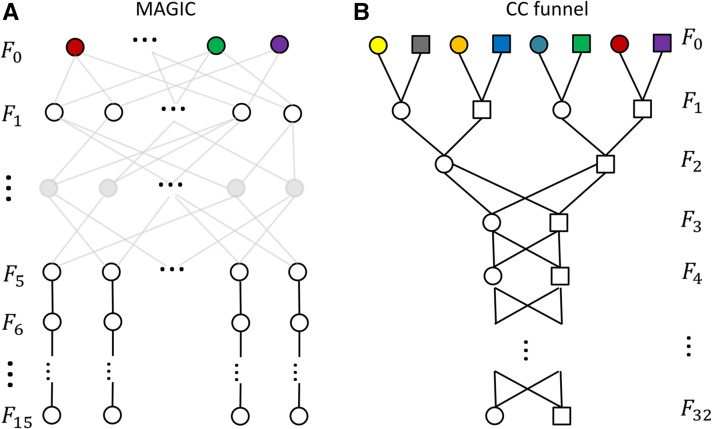
The models are evaluated by simulation studies in two example mapping populations: the Arabidopsis MAGIC and the mouse CC. The pedigrees of the MAGIC and the CC are first simulated according to the breeding design shown in Figure 1, where more generations of inbreeding are set to ensure complete inbreeding. In ancestral inferences, the mating schemes rather than the true pedigree of the MAGIC are assumed to be available. We simulate 100 funnels of the CC, the eight founders of each funnel being randomly permuted. A unique ancestral origin is assigned to each founder’s genome. Each descendant gamete is specified as a list of genome blocks determined by chromosomal crossovers between the two sets of parental chromosomes. The number of crossovers follows a Poisson distribution with mean being the chromosome length in morgans, and the positions of crossovers are randomly distributed on chromosomes.

Figure 1.

(A and B) Breeding schemes of the MAGIC (A) and the CC (B). Inbred founders are represented by different colors. (A) The $L=19$ founders are intercrossed by the full-diallel design, resulting in an F₁ population of size $L\left(L-1\right)$. Then the population is maintained at constant size by random-mating intercrossing for 4 generations. Each individual of the F₅ population is self-fertilized for 10 generations. (B) The $L=8$ founders are crossed by exclusively pairing for 2 generations, and then the two individuals in the F₂ population are inbred by sibling mating for 30 generations. The genders are alternatively female (circle) and male (rectangle) from left to right in each generation.

We use available real data as the true founder haplotypes. The SNP data for the 19 founder accessions of the Arabidopsis MAGIC are from Kover et al. (2009). There are 1260 SNPs distributed over 5 pairs of chromosomes of length 493 cM; there are no missing alleles. The SNP data for the 8 founder mouse strains of the CC are from Iraqi et al. (2012). The physical distances are transformed into genetic distance by setting the recombination rate 0.5 cM/Mbp. There are 7348 SNPs distributed on 19 pairs of autosomes of total length 1204 cM and 495 SNPs on X chromosomes of length 81 cM; $6\mathrm{\%}$ of alleles are missing.

We obtain the simulated founder haplotype by applying the same error model to the true founder data with error probability ${\mathit{ϵ}}_{\mathrm{F}}$. The true genotypes of each individual in each generation are derived by combining the true founder haplotypes and the realized distribution of ancestry blocks of the individual. The observed genotypes are obtained by applying the same error model to the true genotypes of the individual with error probability ϵ.

Software implementation

The RABBIT package is currently implemented in Mathematica 9.0 (Wolfram Research 2012), and it is freely available from the website https://github.com/chaozhi/RABBIT.git. For each of the three models, jointModel, indepModel, and depModel, RABBIT can output posterior marginal probabilities at all markers, optimal ancestral state paths, and multiple posterior samples of state paths by using the forward–backward algorithm, the Viterbi algorithm, and the forward-calculation backward sampling, respectively. The Appendix describes the running setups of RABBIT for various mapping populations and the setups for GAIN and HAPPY used in the comparisons with RABBIT.

Results

Comparisons among RABBIT models

We evaluate the jointModel, the indepModel, and the depModel of RABBIT by the forwardly simulated data, as described in Materials and Methods, with the allelic error probabilities ${\mathit{ϵ}}_{\mathrm{F}}=\mathit{ϵ}=\mathrm{0.005.}$ In each generation one individual from the MAGIC and one female from a single funnel of the CC are analyzed by the three models. Conditional on the true allelic error probabilities and the breeding design, genome-wide ancestry blocks were sampled independently 1000 times from their posterior distribution. For each sample, the mismatch fraction is calculated as the fraction of markers where the estimated ancestral origin states are different from the true values, the inbreeding coefficient is the fraction of markers where the two alleles are IBD, and the number of change points refers to the sampled ancestral state path along two homologous chromosomes at the resolution of marker locations. The change points shared between two chromosomes are counted only once, and one change point between consecutive markers may result from multiple change points at the continuous chromosome scale.

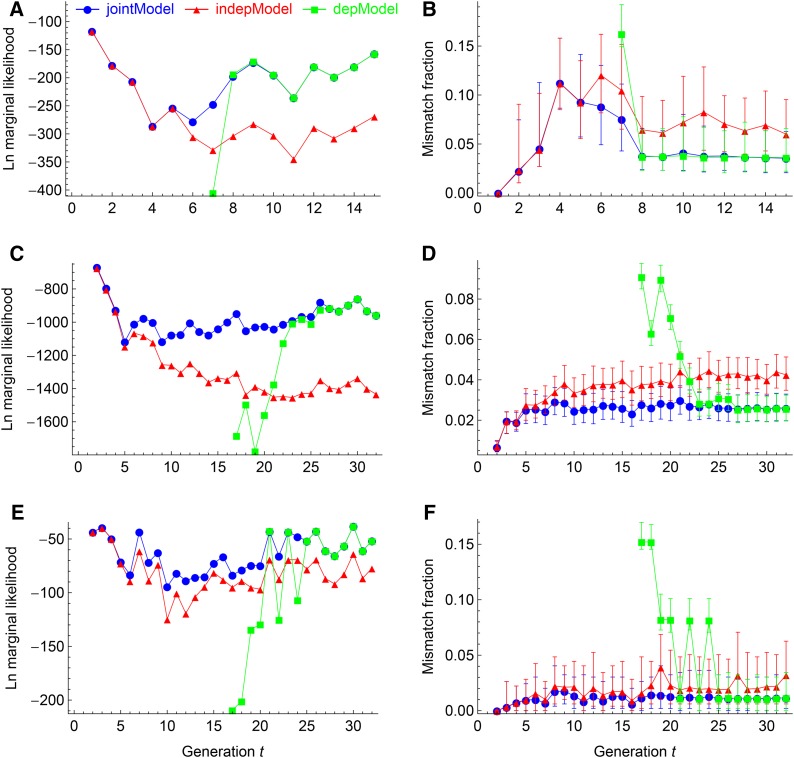
Figure 2 and Figure 3 show a consistent pattern of model evaluations by the four quantities: marginal likelihood, mismatch fraction, inbreeding coefficient, and number of change points. The jointModel converges to the indepModel in the early generations when the individual has little inbreeding and converges to the depModel in the late generations when the individual is almost fully inbred. In the intermediate generations, the jointModel outperforms the indepModel and the depModel. Specifically, the jointModel has larger Bayesian evidences, smaller mismatch fractions, and more accurate estimations of the inbreeding coefficient and the number of change points. As shown in Figure 2, left, the jointModel is statistically strongly supported (Kass and Raftery 1995) in the intermediate generations.

Figure 2.

Evaluations of the RABBIT models by the marginal likelihoods (A, C, and E) and the mismatch fractions (B, D, and F). A and B, C and D, and E and F show the results obtained from the MAGIC, the 19 pairs of autosomes of the CC, and the female XX chromosomes of the CC, respectively. The error bars refer to the 95% central posterior intervals. Results obtained from depModel in the early generations are not shown.

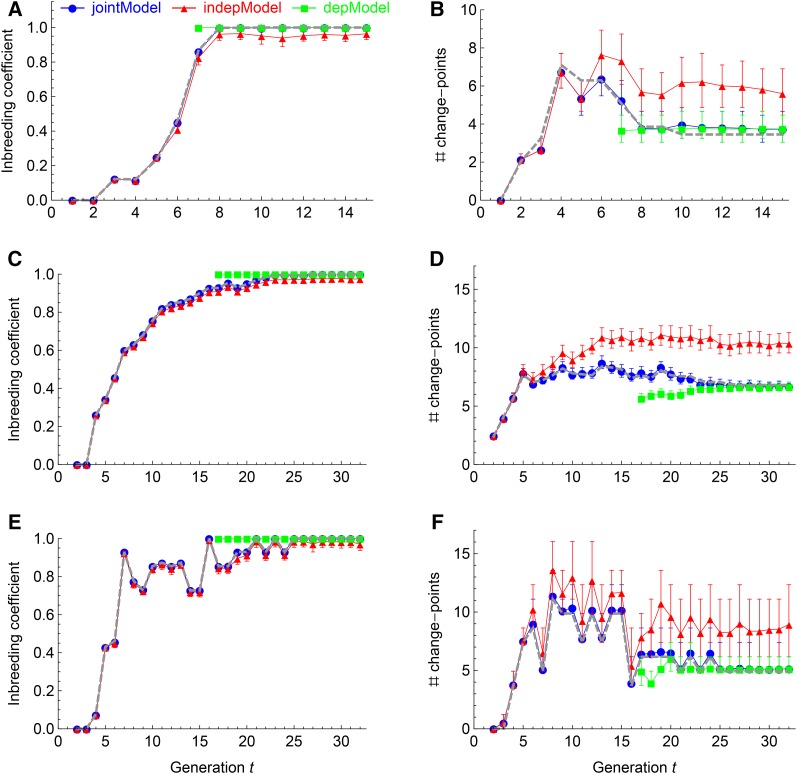
Figure 3.

Evaluations of the RABBIT models by the inbreeding coefficients (A, C, and E) and the numbers of change points (B, D, and F). The panels, the plot markers, and the error bars are the same as those in Figure 2. The additional gray dashed lines denote the true values, which largely overlap with the estimations from the jointModel (blue circles).

Figure 3 shows that the inbreeding coefficients obtained from jointModel fit the true values very well with tiny estimation uncertainties, even though the true values fluctuate across generations. In comparisons, the inbreeding coefficients obtained from the indepModel are underestimated and those from the depModel are always constrained to be 1. The true numbers of change points mostly fall within the $95\mathrm{\%}$ central posterior intervals obtained from the jointModel, whereas they are overestimated by the indepModel and underestimated by the depModel. The posterior intervals for the number of change points are larger than those for the inbreeding coefficient.

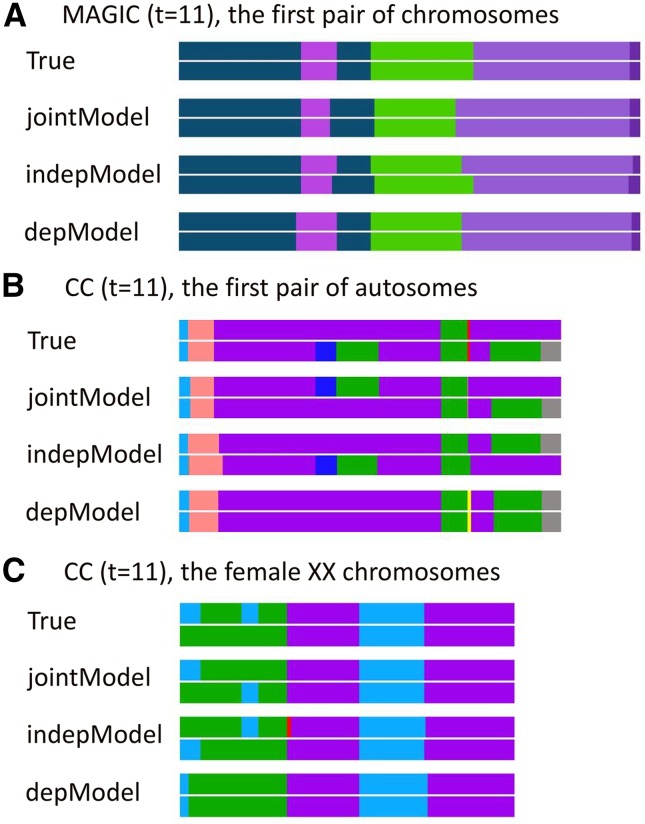
The results of Figure 3 can be further illustrated from the typical bin maps shown in Figure 4. The three models reconstruct the ancestry blocks very well in the regions between neighbor change points, and they differ mainly around the change points. This explains why the inbreeding coefficients can be well estimated since they are calculated as an average over all the marker locations and there are only a small fraction of markers around change points. Because of the independent-transition assumption in the indepModel, most of the true shared change points are resolved as nonshared, resulting in underestimated inbreeding coefficients and overestimated numbers of change points, whereas the assumption of completely dependent transitions forces all the non-IBD ancestry blocks into IBD blocks, resulting in complete inbreeding and underestimated numbers of change points.

Figure 4.

Evaluations of the RABBIT models by the bin maps obtained from a posterior sample of ancestral origins along a pair of homologous chromosomes. The ancestral origins are represented by different colors. (A) The first pair of chromosomes of a MAGIC line. (B) The first pair of autosomes of a pre-CC line. (C) The XX chromosomes of a female pre-CC line.

Comparisons with GAIN and HAPPY

We compare RABBIT with the two commonly used packages HAPPY and GAIN. We analyze six simulated data sets: MAGIC-F5, MAGIC-F11, CC-F11-AA, CC-F22-AA, CC-F11-XX, and CC-F22-XX, where the first part denotes the population type, the second part denotes the generation, and the third part denotes the pair of autosomes (AA) or X chromosomes (XX); only the first pair of autosomes is included in the analysis. Each MAGIC data set has 100 sampled individuals, and each CC data set has females from each of the 100 independent funnels. The data set MAGIC-F5 refers to the last generation of the intercrossing stage, and it represents advanced intercross populations such as the AIL. The data sets CC-F11-AA and CC-F11-XX represent heterogeneous pre-CC lines.

Since the founder allelic typing errors are not modeled in GAIN and HAPPY, the founder haplotypes without applying allelic errors $\left({\mathit{ϵ}}_{\mathrm{F}}=0\right)$ are dropped on the breeding pedigrees. We obtain the observed genotypes by applying the error model to the true genotypes with $\mathit{ϵ}=\mathrm{0.005.}$ GAIN uses genotype error probability and it is approximately given by $2\mathit{ϵ}$, and HAPPY accounts for allelic errors by adding $\mathit{ϵ}/L$ to each of the input allele frequencies among the founder marker data.

All three methods, RABBIT, GAIN, and HAPPY, output the marginal posterior probabilities at each marker for each of $L\left(L+1\right)/2$ unordered ancestral origin pairs, where $L=19$ for the MAGIC and $L=8$ for the CC. We evaluate the performance of each method by the following three quantities. The wrongly assigned probability is calculated as the sum of the posterior probabilities over the nontrue ancestral origin states, the wrongly called probability is the fraction of markers where the states corresponding to the maximum posterior probabilities are different from the true ancestral origin states, and the pedigree inconsistency is defined only for the CC as the sum of the posterior probabilities over the four mating pairs of founder strains since each pair cannot appear at a single locus in generation $t\ge 2$ (Liu et al. 2010). The three quantities are averaged over the 100 sampled individuals in each data set.

Table 1 shows the comparisons among the three methods in terms of the three probability quantities. We focus on the jointModel of RABBIT since it always performs better than the indepModel and the depModel. The wrongly called probabilities for GAIN are similar to those for RABBIT, but the wrongly assigned probabilities for GAIN are a bit larger than those for RABBIT, particularly for CC-F11-XX and CC-F22-XX since the scenarios of X chromosomes are roughly approximated in GAIN. GAIN has incorporated the pedigree information of the initial two generations of the CC, and thus the pedigree inconsistency is always 0. However, Table 1 shows that for RABBIT (jointModel) the contributions of the pedigree inconsistency to the wrongly assigned probability are only ∼2%, indicating that the pedigree provides little extra information relative to the dense marker data.

Table 1. Comparisons of ancestral inferences using RABBIT, GAIN, and HAPPY.

		RABBIT
Probability	Simulated data set	jointModel	indepModel	depModel	GAIN	HAPPY (diploid)	HAPPY (haploid)
Wrongly assigned	MAGIC-F5	0.143	0.143	0.935	NA	0.779	0.949
	MAGIC-F11	0.096	0.144	0.106	NA	0.446	0.323
	CC-F11-AA	0.027	0.036	0.209	0.037	0.196	0.243
	CC-F22-AA	0.024	0.038	0.046	0.032	0.123	0.090
	CC-F11-XX	0.013	0.017	0.185	0.032	0.160	0.208
	CC-F22-XX	0.011	0.019	0.029	0.027	0.078	0.058
Wrongly called	MAGIC-F5	0.105	0.105	0.934	NA	0.225	0.937
	MAGIC-F11	0.074	0.121	0.085	NA	0.200	0.129
	CC-F11-AA	0.020	0.028	0.205	0.020	0.050	0.214
	CC-F22-AA	0.018	0.030	0.040	0.016	0.051	0.050
	CC-F11-XX	0.008	0.012	0.182	0.014	0.031	0.188
	CC-F22-XX	0.008	0.014	0.026	0.011	0.027	0.032
Pedigree inconsistency	CC-F11-AA	0.00075	0.0040	0	0	0.026	0
	CC-F22-AA	0.00017	0.0039	0	0	0.015	0
	CC-F11-XX	0.00031	0.0014	0	0	0.020	0
	CC-F22-XX	0.00017	0.0017	0	0	0.009	0

As shown in Table 1, HAPPY performs worst for all the simulated data sets. The wrongly called probabilities for HAPPY are around twice as large as those for RABBIT and GAIN, and the differences are larger for the wrongly assigned probabilities. Figure S1 and Figure S2 show that the posterior probabilities for an example individual obtained from HAPPY are noisier than those from GAIN and RABBIT. Notably for the data set MAGIC-F5, the background noises distributed among the 190 states result in a very high wrongly assigned probability for HAPPY (diploid), although its wrongly called probability is only modestly larger than that for RABBIT and similarly for the data set MAGIC-F11 using HAPPY (haploid).

To remove the effects of the genotype error model, we analyzed the true genotype data without applying the error model so that ${\mathit{ϵ}}_{\mathrm{F}}=\mathit{ϵ}=0.$ As shown in Table 2, the overall performances for all three methods are improved due to the higher data qualities, but the relative performances are more or less the same, except that the outperformances of RABBIT are reduced a bit. According to the performances of the three models of RABBIT in Table 1 and Table 2, the poor performances of HAPPY are probably due to the differences in the data likelihood or the estimation details, but not due to the prior ancestral origin processes or the error model.

Table 2. Similar to Table 1, but without applying the error model to the simulated true genotypes of sampled individuals.

		RABBIT
Probability	Simulated data set	JointModel	indepModel	depModel	GAIN	HAPPY (diploid)	HAPPY (haploid)
Wrongly assigned	MAGIC-F5	0.132	0.132	0.935	NA	0.690	0.943
	MAGIC-F11	0.095	0.132	0.105	NA	0.324	0.239
	CC-F11-AA	0.024	0.031	0.209	0.030	0.139	0.225
	CC-F22-AA	0.023	0.033	0.045	0.028	0.079	0.068
	CC-F11-XX	0.012	0.015	0.185	0.018	0.105	0.194
	CC-F22-XX	0.011	0.015	0.028	0.016	0.043	0.041
Wrongly called	MAGIC-F5	0.098	0.098	0.934	NA	0.178	0.936
	MAGIC-F11	0.073	0.114	0.084	NA	0.151	0.097
	CC-F11-AA	0.017	0.024	0.205	0.017	0.039	0.210
	CC-F22-AA	0.017	0.027	0.040	0.016	0.040	0.045
	CC-F11-XX	0.008	0.011	0.182	0.008	0.023	0.186
	CC-F22-XX	0.007	0.012	0.026	0.007	0.020	0.029
Pedigree inconsistency	CC-F11-AA	0.00057	0.0034	0	0	0.020	0
	CC-F22-AA	0.00011	0.0032	0	0	0.009	0
	CC-F11-XX	0.00021	0.0012	0	0	0.015	0
	CC-F22-XX	0.000054	0.0014	0	0	0.005	0

Evaluations with real data

We evaluate RABBIT, GAIN, and HAPPY by the real data of the MAGIC lines (Kover et al. 2009), the DO individuals (Svenson et al. 2012), and the pre-CC lines (Durrant et al. 2011), and they were downloaded from the websites http://mus.well.ox.ac.uk/magic, http://cgd.jax.org/datasets/phenotype/SvensonDO.shtml, and http://mus.well.ox.ac.uk/CC, respectively. For comparisons, all the markers with missing data in the founder haplotypes are removed since GAIN and HAPPY cannot account for them, and the conditional probabilities over intermarker intervals obtained from HAPPY are transformed into marker-wise probabilities. The real marker densities are 2.6, 5.2, and 145 SNPs/cM for the MAGIC, the DO, and the pre-CC, respectively. The very high marker density of the real pre-CC lines makes it possible to reconstruct ancestry blocks very accurately and to study the effects of marker density by analyzing subsets of the markers. We assume that there are no allelic errors in the founder marker data $\left({\mathit{ϵ}}_{\mathrm{F}}=0\right)$ and conservatively set $\mathit{ϵ}=0.005$ for the sampled individuals.

Arabidopsis MAGIC:

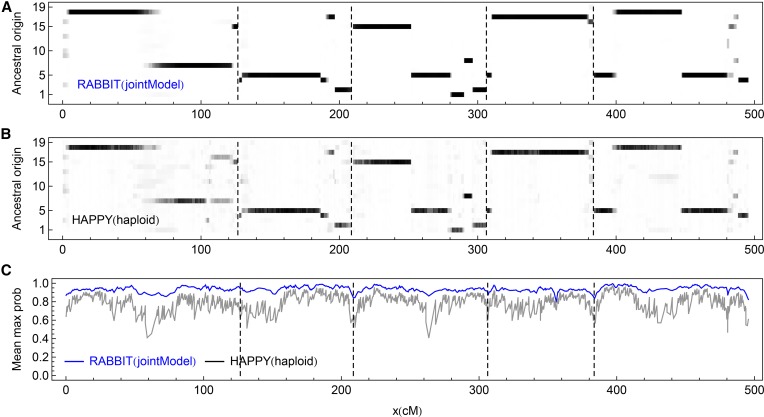
The real MAGIC lines were sampled in $t=11$, the sixth generation of selfing. Figure 5 shows the genome-wide marginal posterior probabilities of the 19 ancestral origins obtained from RABBIT (jointModel) and HAPPY (haploid); GAIN is not applicable. The HAPPY results are noisier especially around the probable recombination breakpoints and the chromosome ends (Figure 5B); the average maximum posterior probabilities from HAPPY are always smaller than those from RABBIT (Figure 5C).

Figure 5.

The posterior probabilities of the 19 ancestral origins for the real MAGIC lines. The dashed vertical lines indicate the chromosome boundaries. (A and B) The posterior probabilities for an example line (MAGIC.100) are represented by levels of gray shading, with white = 0 and black = 1. (C) The maximum posterior probabilities at each marker, averaged over all 703 MAGIC lines.

As shown in Figure 5, there are some unambiguous ancestry blocks detected by RABBIT but not by HAPPY, for example, ∼110 cM and at the right end of the fourth chromosome, although it is unknown whether those detected blocks are the true ones. We call ancestral origins for both methods by their maximum posterior probabilities. Among all the markers of the 703 MAGIC lines, $93.5\mathrm{\%}$ of the called ancestral origins are the same, and over these locations the average maximum posterior probabilities are 0.968 and 0.856 for RABBIT and HAPPY, respectively.

Mouse DO:

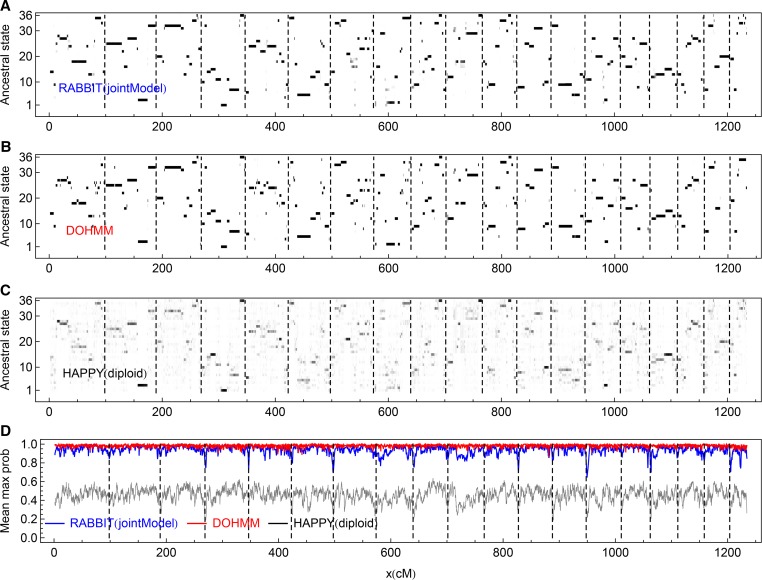
We use the 94 DO individuals sampled at the fourth generation (G₄), where the founder population consists of 144 pre-CC lines that were at various generations with frequencies in figure 1 of Svenson et al. (2012). We analyze marker data of the 19 pairs of autosomes by RABBIT and HAPPY and denote by DOHMM the haplotype reconstruction results by the DO-specific method where the probe intensity values rather than genotype calls were used (Svenson et al. 2012). Figure 6 shows the marginal posterior probabilities of the 36 ancestral origin states for the real DO individuals. Similarly, the HAPPY results are noisier and have on average lower maximum posterior probabilities.

Figure 6.

The posterior probabilities of the 36 ancestral origin states for the real DO individuals. The dashed vertical lines indicate the chromosome boundaries. (A–C) The posterior probabilities for a sampled individual (F01) are represented by levels of gray shading, with white = 0 and black = 1. (D) The maximum posterior probabilities at each marker, averaged over all 94 DO individuals.

We call ancestral origin states at the 6259 markers of the 94 DO individuals by their maximum posterior probabilities. Overall, $81.3\mathrm{\%}$ of markers have the same calls among the three methods, and $86.9\mathrm{\%}$ of markers have the same calls between RABBIT and DOHMM, $91.5\mathrm{\%}$ between RABBIT and HAPPY, and $82.6\mathrm{\%}$ between HAPPY and DOHMM. Thus, DOHMM has many calls inconsistent with those by RABBIT and HAPPY, although we do not know the true ancestral origin states. This is illustrated in Figure 6 for an example DO individual around 630 cM, where a large segment given by RABBIT and HAPPY is shown as many different small segments by DOHMM, probably because the transition probability parameters of DOHMM were selected so that evidence from approximately 4 sequential markers is necessary to change founder state (Svenson et al. 2012).

Mouse pre-CC:

For each pre-CC line, we estimate the funnel code, which is required by GAIN, based on the concept of pedigree inconsistency (Liu et al. 2010), conditional on the sampling generation t estimated by the maximum a posteriori with the prior being a discrete uniform distribution in the range of $8\le t\le 14$ (Durrant et al. 2011). We first obtain the optimal ancestral origin state path by the Viterbi algorithm of RABBIT (jointModel) for the 19 pairs of autosomes. Then we identify the founder pairs that never appear on the optimal state path, after removing $\sim 5\mathrm{\%}$ of small segments along the path. Finally, we set a funnel code for the pre-CC line compatible with those missed founder pairs. We are left with 103 pre-CC lines after deleting the 17 lines for which the above approach failed to estimate the funnel codes.

To study the effect of marker densities on ancestral inference, we analyze only the first pair of autosomes and thin the full data set by taking every second SNP marker and repeating the process to obtain nested subdata sets. The data fractions or the relative marker densities are given by ${\rho }_{\mathrm{M}}=1,2^{-1},\dots ,2^{-7}$. We set the pseudotrue ancestral origin states according to the marginal posterior probabilities obtained by RABBIT, GAIN, and HAPPY from the full data set. For each pre-CC line, the markers are called only if their best ancestral origin states are the same among the three methods. Overall $87.8\mathrm{\%}$ of markers are called to their best origin states.

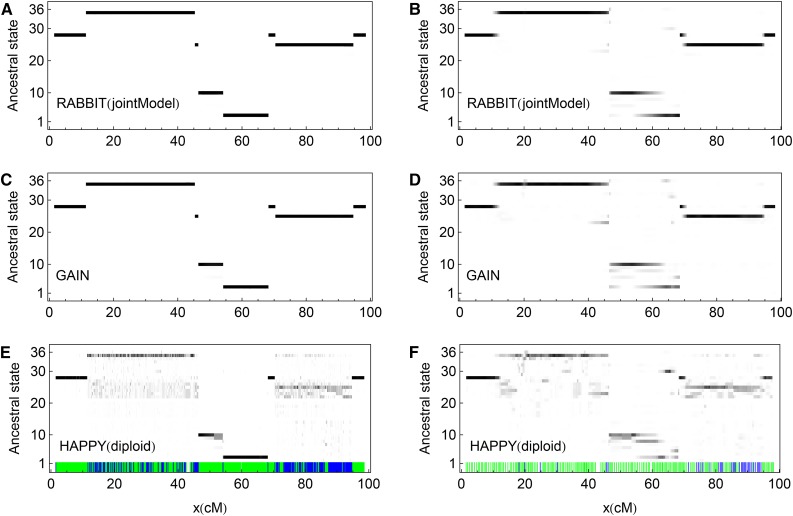
Figure 7 shows the posterior probabilities of the ancestral origin states for an example pre-CC line (IL-18) along the chromosomes obtained by the three methods. There are no visible differences between the results from RABBIT (jointModel) and GAIN for the full data set, although GAIN performs a little worse for the low SNP density $\left({\rho }_{\mathrm{M}}=2^{-6}\right)$. The results from HAPPY (diploid) are noisier than those from RABBIT and GAIN for both data sets, even for the two large non-IBD blocks ∼30 cM and 80 cM, respectively. The tiny non-IBD block ∼45 cM can be identified by RABBIT and GAIN from the full data set, but is almost nonidentifiable in other panels of Figure 7.

Figure 7.

The posterior probabilities of the 36 ancestral origin states for an example pre-CC line (IL-18) along the first pair of autosomes. A, C, and E are obtained from the full data set, and B, D, and F are from $1/64$ fraction of the full data set. The probabilities are represented by levels of gray shading, with white = 0 and black = 1. The green (blue) vertical bars in E and F denote the SNP markers with (without) pseudotrue origins, while all of them are used in the ancestral inferences.

Similar to Figure 7, Figure S3 shows the marginal posterior probabilities for each of the eight ancestral origins, where IBD blocks appear as a single black band and non-IBD blocks appear as two gray bands. As expected, Figure S3E apparently looks the same as figure 1 of Durrant et al. (2011) for the pre-CC line (IL-18), apart from some background noise.

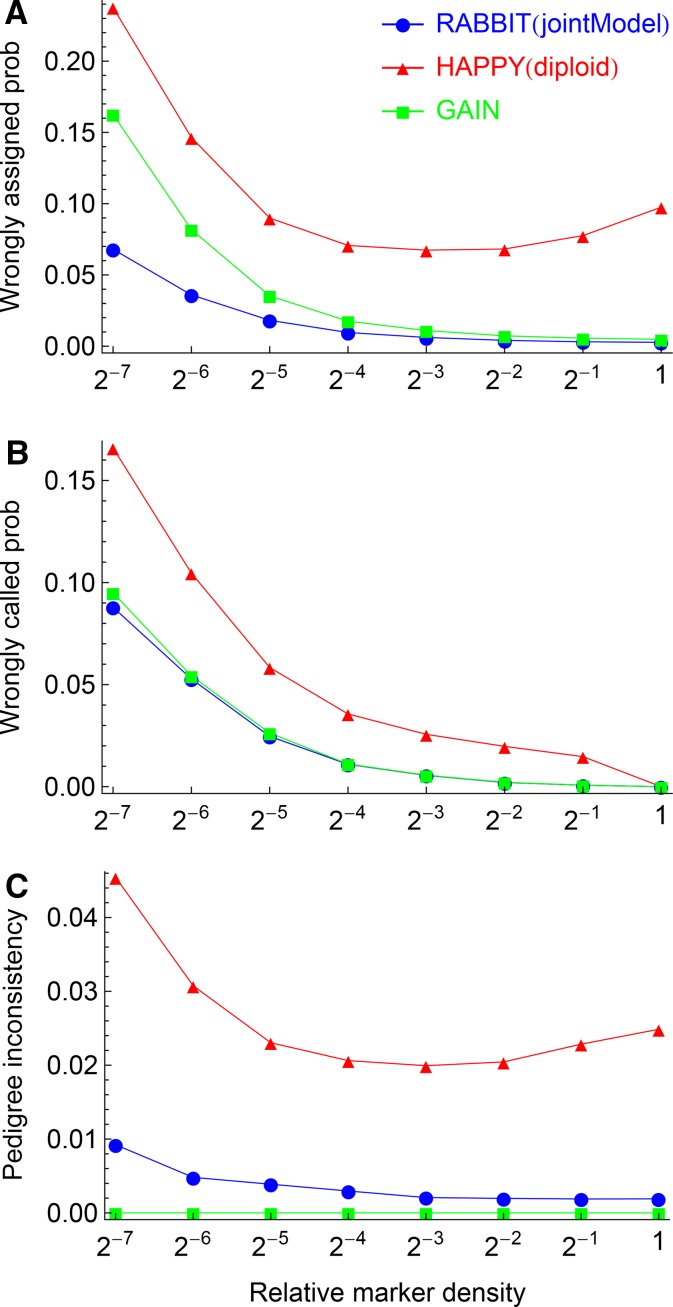
Figure 8 shows the effects of marker densities on the ancestral inferences from the nested data sets. The wrongly called probabilities converge to zero for the full data set due to the definition of the pseudotrue values. The three probabilities decrease with the increasing marker densities for RABBIT and GAIN as expected. However, they become almost flat for HAPPY when close to the full data set, and the reasons are not clear. The wrongly called probabilities for RABBIT are only a bit less than those for GAIN, but the wrongly assigned probabilities for RABBIT are about half those for GAIN, consistent with the simulation results (Tables1 and Table 2). The pedigree inconsistencies from RABBIT are very small, although they contribute $14\mathrm{\%}$ to the wrongly assigned probabilities at the lowest density.

Figure 8.

The effects of marker densities on the ancestral inferences from the first pair of autosomes of the 103 pre-CC lines. Panels (A-C) show the results for the wrongly assigned probability, the wrong called probability, and the pedigree inconsistency, respectively.

Discussion

We have implemented an HMM framework, RABBIT, for reconstructing genome ancestry blocks, where the general jointModel has been shown to be always the best choice. RABBIT can reconstruct genome-wide ancestry blocks including X chromosomes, whereas methods such as GAIN and HAPPY analyze X chromosomes roughly. The studies of the simulated data and the real data have shown that RABBIT (jointModel) is more robust and accurate than HAPPY and GAIN, although GAIN obtained similar results from a high density of marker data for the autosomes of the CC line.

In addition to the examples of the MAGIC, the DO, and the CC, RABBIT can be applied to RILs by sibling mating or selfing, the NAM, the AMPRIL, the AIL, the HS, the DSPR, and other mapping populations whether their breeding designs are available or not. By contrast, GAIN can be applied only to the CC (Liu et al. 2010), and HAPPY was developed for the outbred HS (Mott et al. 2000) and lately extended to the homozygous MAGIC lines (Kover et al. 2009). Durrant et al. (2011) have shown that the level of inbreeding was underestimated when applying HAPPY to pre-CC lines with residual heterozygosity. This is confirmed in Figure 3, where the indepModel of RABBIT underestimates the inbreeding coefficients and overestimates the numbers of change points.

There are two possible ways to fully incorporate pedigree information, if available, into RABBIT. First, as a generalization of GAIN, we may design a Lander–Green algorithm (Lander and Green 1987) where symmetric pedigree substructures are encoded into inheritance vectors. Second, we may incorporate the asymmetric information into the construction of HMMs, such as the impossible founder mating pairs of the CC. For the XX chromosomes of a female CC line, there are no contributions from two of the male founder strains, and we could set the number of possible ancestral origins $n=6$ rather than 8. However, our results indicate that it may not be worthwhile even in relatively low marker densities, for the example of the CC.

The sample individuals have been assumed to be independent, given the genotype data of founders. This is valid for CC lines if each of them is sampled from different funnels. The individuals from advanced intercross populations such the AIL and the HS are related to a certain extent based on the effective population size. RABBIT would underestimate the number of shared recombination breakpoints across sampled individuals. However, the similar results between jointModel and indepModel at the intercross stage of the MAGIC (Figure 2, A and B, Figure 3, A and B, and Figure 4A) demonstrate that the relationships between outbred sampled individuals may be well ignored, particularly for dense marker data to improve computational efficiency.

Since standard HMM algorithms (Rabiner 1989) are used in the methods of RABBIT, GAIN, and HAPPY, their time complexities remain similar, and running times depend critically on their implementation details. For the full real data set of the 103 pre-CC lines (14,076 markers), the running times on a standard desktop computer are ∼360, 182, and 28 sec for RABBIT, GAIN, and HAPPY, respectively. RABBIT is currently written in Mathematica (Wolfram Research 2012), and rewriting the core HMM algorithms in C++ may improve the speed, as GAIN and HAPPY did. HAPPY is much faster than GAIN, consistent with the previous comparisons (Liu et al. 2010).

There are a few other specially designed methods for ancestry block reconstruction in breeding populations. The R/qtl package (Broman et al. 2003) can be applied only to backcross and intercross data and possibly homozygous RIL data. King et al. (2012) have implemented an HMM for analyzing dense semicodominant restriction site-associated DNA (RAD) markers, where the prior model is parameterized for the DSPR. Zhou et al. (2012) have developed a penalized-likelihood imputation of ancestral origins, which is more competitive in computational efficiency and less preferred in accuracy than probabilistic HMM estimations.

Genotyping by sequencing (GBS) is becoming an attractive tool for linkage mapping in breeding populations (Stange et al. 2013), and HMMs for analyzing these data have been developed in biparental RILs (Xie et al. 2010; Andolfatto et al. 2011). It will be valuable to extend RABBIT to analyze GBS data in multiparental populations, while accounting for the large error rate in low-coverage sequencing.

Appendix: Running Setups for RABBIT, GAIN, and HAPPY

RABBIT

We describe briefly how to use RABBIT for reconstructing ancestral blocks in mapping populations; refer to the tutorial on the RABBIT website for details. The main function of RABBIT is magicReconstruct, and its usage is given by magicReconstruct[magicSNP, model, epsF, eps, pop, outfile], where magicSNP is the marker data or the input csv filename containing the marker data for both founders and sampled individuals; model must be “jointModel,” “indepModel,” or “depModel”; epsF and eps are the allelic error probabilities for founders and samples, respectively; pop specifies the information of population design; and outfile specifies the file names for RABBIT outputs.

In addition, we may use the option HMMMethod to specify the three possible methods of the HMM algorithms. By default, HMMMethod → “origPathSampling” and SampleSize → 1000 output 1000 posterior samples of state paths by using the forward-calculation backward-sampling algorithm. Alternatively, HMMMethod → “origPosteriorDecoding” outputs marginal posterior probabilities at all markers of all sampled individuals by using the forward–backward algorithm, or HMMMethod → “origViterbiDecoding” outputs optimal state paths of all sampled individuals by using the Viterbi algorithm. We overload the function magicReconstruct with various forms of pop, according to the availability of the breeding design of a mapping population.

Multistage random-mating populations

For a stage-wise random-mating population with discrete generations, pop = scheme where scheme is a list of random mating schemes. For example, schemes for the simulated data sets MAGIC-F5, MAGIC-F11, and CC-F11-AA are given by {“FullDiallel”, “RM1-E”,...,“RM1-E”}, {“FullDiallel”, “RM1-E”,...,“RM1-E”,“Selfing”,...,“Selfing”}, {“Pairing”, “Pairing”,“Sibling”,...,“Sibling”}, respectively, where RM1-E is repeated in total 4 times for the intercross stage, Selfing is repeated in total 6 times for the inbreeding stage, and Sibling is repeated in total 9 times for the inbreeding stage. For CC-F22-AA, Sibling is repeated in total 20 times. Scheme is the same for autosomes or XX chromosomes.

We may also set pop $=\mathrm{\Omega }$ and calculate Ω by using the function magicOrigPrior[nFounder, scheme] for autosomes and magicOrigPriorXY[nFounder, scheme] for sex chromosomes if they exist, where nFounder is the number of inbred founders. These functions are used internally if set pop = scheme.

The founder population of DO consists of pre-CC lines that were at different generations. Thus we set pop $=\mathrm{\Omega }$ and calculate the hyperparameter Ω analytically by using the function magicOrigPriorDO[nPower, preCCfreq, popSize, gCross, crossScheme], where nPower = 3 refers to the $2^3$-way RIL in producing the pre-CC lines; preCCfreq is the frequency distribution of the inbreeding generations when the pre-CC were sampled, and it is set to {{4, 0.148}, {5, 0.451}, {6, 0.169}, {7, 0.07}, {8, 0.035}, {9, 0.063}, {10, 0.021}, {11, 0.021}, {12, 0.021}} according to figure 1 of Svenson et al. (2012); the intercross population size popSize = 334; the number of intercross generations gCross = 4; and the intercross mating scheme crossScheme = RM1-E. As shown in Zheng et al. (2014) and Zheng (2015), the exact population size and the different random-mating scheme hardly affect the value of Ω. For X chromosomes use the function magicOrigPriorDOXY.

Fixed breeding pedigree

For a population with a fixed pedigree, the hyperparameter Ω can be calculated by simulations, using the function simOrigPrior[popPed, founderFGL, chrLength, interferStrength, isObligate, isOogamy, sampleSize], where popPed is the fixed pedigree, founderFGL is a list of founder genome labels, chrLength is a list of chromosome lengths in centimorgans and it has no effects if isObligate = False, interferStrength = 0 and isObligate = False so that there are no genetic interference and obligate crossovers, isOogamy = True if simulating sex chromosomes, and sampleSize is the number of simulation replicates of gene dropping on the pedigree popPed.

No information on breeding design

If we do not have any information on breeding design, the hyperparameter Ω can be estimated empirically from the marker data, by maximizing the log-marginal likelihood calOrigLogl[magicSNP, model, epsF, eps, pop], with respect to the parameter pop $=\mathrm{\Omega }\mathrm{.}$ The indepModel with one or two parameters in Ω is recommended if the sampled individuals are approximately completely outbred, and the depModel with one parameter in Ω is recommended if the sampled individuals are approximately fully inbred. The function calOrigLogl can also be used to estimate the mating schemes such as the number of inbreeding generations if set pop = scheme.

GAIN

GAIN can be applied only to the CC. The input of the genotype error probability is set to $2\mathit{ϵ}$, where ϵ is the allelic error rate used in RABBIT. The input of the total number of generations is set to 12, 23, 12, and 23 for the simulated data sets CC-F11-AA, CC-F22-AA, CC-F11-XX, and CC-F22-XX, respectively, where the options -f-x are used for the female XX chromosomes. Similarly for a pre-CC line, the total number of generations is given by one plus the sampling generation.

HAPPY

The main parameter input for HAPPY is the effective number of generations, which is set according to the map expansion of the population. The effective number of generations is set to 4, 6, 6, 7, 4, and 5 for the simulated data sets MAGIC-F5, MAGIC-F11, CC-F11-AA, CC-F22-AA, CC-F11-XX, and CC-F22-XX, respectively; it is set to 6, 9, and 6 for the real MAGIC lines, the DO individuals, and the pre-CC lines, respectively.