Synthetic biology and regulatory networks: where metabolic systems biology meets control engineering

Abstract

Metabolic pathways can be engineered to maximize the synthesis of various products of interest. With the advent of computational systems biology, this endeavour is usually carried out through in silico theoretical studies with the aim to guide and complement further in vitro and in vivo experimental efforts. Clearly, what counts is the result in vivo, not only in terms of maximal productivity but also robustness against environmental perturbations. Engineering an organism towards an increased production flux, however, often compromises that robustness. In this contribution, we review and investigate how various analytical approaches used in metabolic engineering and synthetic biology are related to concepts developed by systems and control engineering. While trade-offs between production optimality and cellular robustness have already been studied diagnostically and statically, the dynamics also matter. Integration of the dynamic design aspects of control engineering with the more diagnostic aspects of metabolic, hierarchical control and regulation analysis is leading to the new, conceptual and operational framework required for the design of robust and productive dynamic pathways.

1. Introduction

Metabolic engineering focuses on the design, construction and optimization of metabolic pathways and their regulatory processes with the aim of improving the production of chemicals, pharmaceuticals or bio-fuels [1]. It also increasingly relates to strategic approaches towards improved metabolic diagnosis and therapies (e.g. [2]). A central issue in metabolic engineering consists of identifying the components or processes that control and limit the production flux [3]. The dependency of steady-state fluxes and species concentrations on process activities such as enzyme-catalysed reactions can be quantified and understood by metabolic control analysis (MCA) [4,5]. Hierarchical control analysis (HCA), an extension of MCA, takes transcriptional regulation and signal transduction also into account [6]. Both MCA and HCA rely on the explicit account of the rate laws governing the biochemical transformations in the pathway. Alternatively to these approaches, linear optimization methods, such as flux balance analysis (FBA) [7], can be used to predict the flux distribution that supports the maximal formation rate of the product of interest using a purely stoichiometric description of the entire genome-scale metabolic network [8,9]. The actual implementation of the optimal flux distribution can then be achieved using pathway design approaches such as gene knockout and overexpression of native or heterologous genes [10,11], or modulation (e.g. partial inhibition) of gene expression. The ensemble of these approaches is named ‘systems metabolic engineering’ in recent literature [12].

Two important design schemes are often employed in metabolic engineering. One uses and modulates native pathways. The other constructs non-natural pathways through the import of heterologous genes, the synthesis of new DNAs and new enzymes [13], or the provocation of new interactions. The latter is part and parcel of synthetic biology. Synthetic biology uses a forward-engineering approach to create new biological parts or networks, modifying existing biological systems [14,15]. Early synthetic biology primarily designed and implemented individual genetic modules, such as genetic toggle switches, logic gates, oscillators, cascades and biosensors (as reviewed in [16–18]). Recently, a ‘second wave’ of synthetic biology created larger functional cellular systems, including signalling and metabolic networks [19]. The challenges include the need of new design principles that enable one to manage the complexity of biology, and a deeper understanding of biological network functions at a ‘systems level’. The former includes the ambition to make the synthetic circuits adaptive and robust even if precise information of the pathway is not available [20,21]; the latter requires the assistance of systems biology and advanced reverse engineering methods [22]. Synthetic biology can advance metabolic engineering significantly by producing new enzymes, novel enzymatic activities and creating new metabolic pathways [13]. Pioneering synthetic biology applications to metabolic-regulatory systems include a re-designing of the native regulatory gene circuits for the enhanced production of lycopene and a synthetic gene-metabolic oscillator with assistance from nonlinear dynamic analysis [23,24]. Reviews and perspectives of synthetic biology and metabolic engineering focusing on their applications, areas of synergism and overlaps can be found in recent literature [25–29].

Formulation of products by and inside living organisms offers the advantages of ready amplification of production capacity, self-repair of the production process and specificity. Thereby, when engineering microbial metabolism in order to maximize productivity, it is important to maintain the cells' functional stability (or a transition from one physiological state to another that does not compromise vitality) when they experience environmental perturbations or are subject to internal noise possibly including mutagenesis. Paradoxically, it can also be important for the cells to respond intensively to changes that are intentional in the production process such as a shift from a growth phase to a production phase. Such ‘agile robustness' is inherent in most living organisms but aimed at improving the organism's fitness rather than productivity. The metabolic pathways involved in productivity are typically subject to transcriptional, signal-transduction and metabolic regulation inclusive of feedback and feed-forward regulatory mechanisms (e.g. a repressor–inducer system) [9,30,31]. Some regulatory loops may serve homeostasis, whereas others may exhibit (nonlinear) dynamic behaviour such as that of bi-stable switches or stable oscillations (e.g. the collective yeast glycolytic oscillator [32] and the gene-metabolic oscillator [24]).

Functionalities such as oscillations and switching are often engineered into man-made mechanical or electronic control systems. Accordingly, the disciplines that help do this, i.e. systems and control engineering, might be able to help understand (i) how the regulatory mechanisms in natural systems promote the organism's fitness and (ii) whether the regulatory mechanisms that emanated from evolutionary ‘design’ are similar to, or better/worse than, what engineers would have designed. They may also help design new synthetic biological regulatory devices with properties that enhance the production process in the biological context [33,34], such as improving pathway robustness and stability. For example, three classical control mechanisms known in control engineering, i.e. proportional, integral and derivative control, have been identified in the regulation of energy metabolism in living organisms [35]. In addition, the closed-loop feedback control principle has been used to design both genetically encoded (RNA or protein) biosensors that help optimize and regulate heterologous pathways [36] and a sensor-regulator system that improves fatty acid-based biodiesel production [37]. When using engineering principles to construct a synthetic metabolic-regulatory system from isolated sub-parts or modules, several issues need to be taken into account. These include: (i) crosstalk and retroactivity effects when interconnecting biological sub-modules [38], (ii) stability and design constraints [39], (iii) response sensitivities and noise propagation [40], and (iv) interactions with their environment [41]. Almost all these issues can be analysed and interpreted using systems and feedback control theory, but have not fully been studied.

This work reviews and investigates how control and optimization approaches used in metabolic engineering as well as diagnostic, analytic and deductive approaches used in synthetic systems biology are related to approaches developed in control systems engineering. In §2, classical steady-state approaches employed in metabolic engineering, such as MCA, FBA, supply–demand theory and regulation analysis, are reviewed. Rather than exclusively discussing their roles in the design of pathways, which have been previously reviewed to some extent (e.g. [42,43]), the focus here is on their recent development for, and applications to, metabolic networks under both enzymatic and gene-expression regulation and the corresponding robustness analysis. In §3, the theoretical principles of control engineering are used to interpret the issues related with dynamic flux control and enzyme activation that have been analysed by a dynamic version of FBA. Metabolic and gene-expression regulation is related to both the proportional and the integral control of control engineering, and the MCA and HCA approaches of systems biology. In §4, synthetic biology-related design strategies, such as the re-engineering of gene circuits and allosteric proteins, together with issues such as modularity and crosstalk, design constraints and noise propagation, are discussed from a systems engineering perspective. A central issue in both the analysis and the engineering/design of a metabolic-regulatory network is a trade-off between optimality (e.g. maximum production, minimum transition time) and robustness (e.g. assurance of the system's stability). This issue is investigated throughout the review.

2. Steady-state control and regulation analysis

2.1. Regulatory motifs

To adapt to and maintain growth under various intracellular and extracellular conditions, both long- and short-term regulatory mechanisms are often present in the same metabolic network. Relatively long-term regulation is based on changing the expression level of genes or on the rewiring of the gene regulatory networks. Such ‘gene-expression regulation’ may be crucial for cell survival in circumstances requiring extensive and persistent cellular alterations. Short-term regulation is based on modification of enzymatic activities through (i) protein–protein interactions and covalent modification (e.g. phosphorylation) in signal transduction or (ii) substrate, product or allosteric regulation of metabolic reactions. Such ‘metabolic regulation’ provides a fast response to acute extracellular and intracellular perturbations and helps the cell to control the metabolic and Gibbs energy balance. The distribution of different types of regulation of the metabolism of organisms such as Escherichia coli [44,45] and yeast [46] over metabolic, signalling and gene expression has been studied intensively. A comprehensive review [47] outlined the regulation of important metabolic tasks at different levels, including nutrient uptake, energy and amino acid metabolism, and protein synthesis, and highlighted a set of metabolites that carry out specific regulatory functions. In pathways like glycolysis, nitrogen assimilation, the citric acid cycle and inorganic ion uptake, gene-expression regulation is important for long-term adaptation to the availability of nitrogen and carbon sources. Shorter term adaptation of these same pathways also seems important as it has given rise to the evolutionary emergence of sophisticated fast cascade control mechanisms [45]. In some amino acid biosynthesis pathways, such as those for glutamate, tyrosine, tryptophan, phenylalanine, arginine and proline, both gene expression and metabolic regulation have been identified. Such co-regulation ensures fine-tuning of metabolic activities and the rapid response to over-accumulation of end products.

The dynamics of a metabolic pathway under both metabolic and gene-expression regulation can be represented by the following generic model:

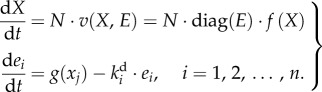2.1

Here N is the stoichiometry matrix indicating which reactions are involved in the metabolism of each metabolite x_i, E = [e₁, e₂, … , e_n]^T denotes the set of concentrations of the enzymes catalysing the various (n) reactions, diag(E) is a diagonal matrix with E along its diagonal, v is the vector of the reaction rates, and f(X) is a vector function of the concentrations of the metabolites X and kinetic parameters. Not all the enzymes are necessarily regulated through gene expression, although many are and their dynamics are modelled by the second equation. The gene-expression function g(·) is assumed to depend on metabolite concentrations, e.g. on the concentration of the (pen)ultimate metabolite in an end product pathway. is the degradation rate constant of the ith enzyme. In fast-growing organisms and for stable proteins, 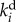mainly represents the dilution effect due to growth, but in other cases it will also depend on proteolysis.

In some metabolic networks, such as in a linear biosynthetic chain of reactions, two regulatory motifs are involved in controlling the flux. One is the end product feedback inhibition, typically acting on the first enzyme of the pathway; the other is the intermediate metabolite feed-forward activation of the downstream enzymes. The expression levels of enzymes may be controlled through transcription factors. These are themselves proteins whose functioning is inhibited or activated by the end product or an intermediate metabolite, and whose expression may also be regulated. According to the connectivity architectures of the gene networks alone, several transcription–regulation motifs have been identified [30,48]. These include the single-input module consisting of a set of operons controlled by a single transcription factor, the dense overlapping regulation motif and the feed-forward loop (see [48] for more discussions).

Feed-forward loops have been identified also in signal-transduction networks as inferred from observed protein–protein interactions. Signal-transduction networks are home to other motifs that are absent from transcription networks, such as the diamond pattern and multi-layer motifs. Mixed-feedback loop motifs have been observed in composite networks that consist of both transcription–regulation and protein–protein interactions [49]. When metabolic regulation is added explicitly, various structures are reinforced. It is not clear why and how the regulatory motifs occur at different ‘hierarchical levels', i.e. at the level of gene networks, signal-transduction networks and metabolic networks at the same time, although a recently developed ‘regulation analysis' has confirmed that such hierarchical regulation does occur in real metabolic pathways [46,50,51]. This will be further discussed in §2.3.3. Such hierarchical regulation calls for a critical analysis of existing interpretations of the functionality of gene regulatory networks that were based on the exclusive analysis of transcription regulation, but this resides beyond the scope of this review. In the following subsections, classical metabolic engineering approaches to the control of enzyme expression and network flux are reviewed and their recent attempts to take complex regulatory mechanisms into account are examined.

2.2. Flux balance analysis

FBA identifies flux patterns satisfying the steady-state condition imposed by setting equation (2.1) to zero, while maximizing a given objective function Z to obtain the corresponding v_optimal. In standard FBA, the objective function is a mathematical representation of a biological process, such as biomass or adenosine triphosphate (ATP) production, that the organism is assumed or required to perform optimally. Commonly Z takes the form of a linear combination of the flux variables v. Then the standard FBA can be formulated as a linear programming (LP) problem as follows:

2.2

where v^L and v^U are the lower and upper bounds, respectively, delimiting the range of possible values for the flux variables v, and c is the set of coefficients defining the objective function Z in terms of a linear combination of the fluxes v. The main advantage of FBA over other modelling approaches is that it only requires the stoichiometries of all the chemical reactions (without kinetic information f(X) in (2.1)), and these have become increasingly accessible with the generation of metabolic maps. In fact, it has become possible to generate genome-wide, hence essentially complete, versions of these maps thanks to the sequencing of the genomes of many organisms, the biochemical identification work done over many years, and intensive collaborations between laboratories (e.g. [9,52]). This makes FBA particularly suitable, and indeed widely used, in the study of the metabolic capabilities of an organism on a genome-wide scale. Genome-scale metabolic reconstructions of more than 45 organisms are already available [31], and FBA constitutes one important tool for extracting the knowledge encoded in such biochemical networks.

FBA is used to address different relevant biological questions in different ways:

• — Boolean perturbation analysis. In silico gene-deletion experiments can be performed by constraining the flux of the affected reactions to zero. FBA is then used to assess the criticality of these genes with respect to the criterion of optimality represented by the objective function Z. This kind of study is particularly useful for investigating synthetic genetic interactions [43], and for suggesting drug targets for drugs aimed at interfering with certain functionalities of the networks. Standard FBA cannot directly predict positive effects of gene knockouts on production or growth yield. However, one can infer that all steps with zero FBA flux may be knocked. Several more sophisticated, bi-level optimization algorithms [53–55] have been developed to predict gene knockouts that may improve product yield, and have been implemented to microbial strain design.

• — Optimization of medium composition. By changing the lower and upper bounds (v^L and v^U) of the so-called ‘exchange reactions' (i.e. those reactions involved in the transport of chemical species from the external environment to the cell and vice versa), it is possible to simulate different growth conditions. This application of FBA allows one to assess the relative suitability of different growth media with regard to a given biological process that the organism is supposed to carry out optimally [7]. This is relevant for industrial protein production.

• — Flux variability analysis (FVA). FVA consists of running FBA in an iterative manner so as to identify the widest range of values that each reaction flux can take without compromising the level of optimality of the network. In other words, FVA addresses the question which alternative flux patterns would lead to the same optimal performance. This procedure is closely related to a robustness analysis in which the effect on the objective function of varying a particular reaction flux can be analysed in terms of the number of potential escape mechanisms of the network [56]. FVA has also been used to find alternative optimal solutions, i.e. flux distributions that are equally optimal with regard to a given biological process [57].

The original FBA formulation has been extended and modified to encompass a wider range of possible studies on the genome-scale metabolic properties of an organism:

• — Regulatory FBA (rFBA). The standard FBA formulation is enriched with regulatory information by integrating Boolean logic operators [58,59]. Transcriptional regulatory events are incorporated in a reconstructed metabolic model to constrain the space of possible network functions further. This allows one to analyse and predict the effects of transcriptional regulation on cellular metabolism at a systemic level (see [43,60] for overview), provided the transcription regulation is essentially binary (on–off). Recently, a matrix formalism for representing transcriptional regulatory networks was proposed [61]. A pseudo-stoichiometric matrix R (similar to N in (2.2)) was introduced. Its rows represent extracellular metabolites, genes and gene products (i.e. proteins), and its columns describe the Boolean regulatory relationships. Boolean rules define which gene products are turned ‘ON’ and which ones remain ‘OFF’. This introduces additional constraints on the corresponding fluxes in (2.2).

• — Data-driven FBA. One of the main factors that affect the reliability of an FBA prediction is the choice of an appropriate objective function Z. The selection of Z is the subject of active research [62,63]. The reliance upon a specific cell function to be optimal may introduce a bias that prevents us from grasping the true physiological state of the organism [64]. Different reformulations of FBA have been proposed to predict flux patterns based on a set of measured quantities. Shlomi et al. [65] integrated tissue-specific gene and protein expression data with a genome-scale reconstruction of the human metabolic network to describe the tissue specificity of human metabolism. Different integer values were assigned to different gene-expression states, so as to distinguish among highly (1), hardly (−1) and moderately (0) expressed genes. The objective function was set to minimize the differences between the activity of each reaction in the predicted flux pattern and the integer representation of the corresponding experimental gene-expression level. By minimizing such an objective function, the authors retrieved flux patterns where the reaction rates were more strongly correlated with their corresponding expression state. In Lee et al. [66], absolute gene-expression data generated through RNA-Seq were used to provide a more precise indication of enzymatic activity than that generated through relative expression techniques such as in Shlomi et al. [65], although lack of correspondence between mRNA and protein levels may compromise this approach if protein levels are not also taken into account [67]. Data-driven FBA may also use the exometabolome, i.e. restrict the exchange flux pattern to what is observed experimentally. This has led to reasonable confinement of all possible flux patterns [64].

• — Dynamic FBA (DFBA). One strength of FBA is that it is computationally affordable, as it only relies on the reaction stoichiometry in the metabolic network. This makes FBA suitable to make predictions on a genome-wide scale. At the same time, however, this also represents a limitation as FBA can only describe or predict steady states [12]. There are studies extending FBA to include dynamic behaviour. Mahadevan et al. [68] introduced DFBA which incorporates rates of change of flux constraints. DFBA was used to predict the dynamics of diauxic growth of E. coli on glucose and acetate. DFBA also provides a suitable framework for multi-scale metabolic modelling, where the interplay of different cell types and tissues is taken into account [69]. More recently, DFBA has been extended to metabolic networks coupled with gene expression of the corresponding enzymes, where it incorporated constraints on resource allocation [70,71].

• — FBA and nonlinearity. In the standard formulation of FBA, it is implicit that the ATP cost of biomass is a constant, i.e. independent of the fluxes entertained by the network, although this is often not the case. Switching from fermentation to respiration implies the synthesis of more mitochondria, hence of a number of enzymes involved in the tricarboxylic acid (TCA) cycle and respiratory chain. Consequently, the Gibbs energy cost of such a respiratory regime is higher than that of fermentation. Simeonidis et al. [64] proposed an iterative approach where a modified formulation of FBA was used to take into account the different ATP requirements of different metabolic regimes. Although the approach was implemented in the form of a LP problem, their iterative algorithm allowed the authors to investigate a nonlinear property of the system, where the total consumption of ATP was made dependent on the mitochondrial flux. Thereby, they could predict a shift from respiratory to fermentative metabolism known as the Crabtree effect and related to the Warburg effect.

2.3. Metabolic, hierarchical control analysis and regulation analysis

2.3.1. Metabolic and hierarchical control analysis

In a biochemical network, the dependence of a system variable (e.g. the rate of metabolic reaction or phosphorylation, the concentration of a metabolite, the magnitude of a transmembrane electric potential) on the kinetic activity parameters (e.g. the activity of an enzyme) can be quantified by the control coefficients as introduced in MCA [4,72]. The control coefficients indicate the steady-state change in the concentration of a metabolite X or flux J in response to a modulation of an effector (e.g. inhibitor) p which acts directly on the activity of the reaction step i. The formal definition of concentration control coefficient (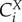) and flux control coefficient (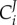) are given as follows:

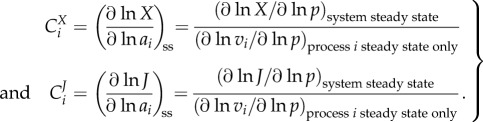2.3

The complexity of these definitions warrants elaboration, as it carries much of the essence of the complexity of systems with interacting processes, as opposed to individual processes in isolation [73]. The concentration control coefficient 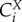is defined as the effect of a small modulation of the activity a_i of the process i on the steady-state concentration of X. 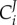measures the same for the control of flux J. The activity a_i is defined as any multiplier of the rate equation of process i that is fixed unless altered either virtually or experimentally; it does not depend on any of the concentrations of the metabolites or enzymes. In enzyme catalysed reactions, a_i may correspond to the catalytic rate constant k_cat, assuming the k_cat of the forward and the reverse reaction should be modulated proportionally in order to preclude violations of the second law of thermodynamics. In metabolic networks where gene expression is constant, the most concrete instantiation of a_i is the total concentration of the enzyme itself. This instantiation is valid when the reaction rate of the enzyme catalysed reaction is indeed proportional to the concentration of the enzyme-catalyst and when the total enzyme concentration is not altered by the internal regulation of the system. If the proportionality does not exist, such as in the case of metabolic channelling or enzyme dimerization, the meaning of a_i should regress to the multiplier mentioned above. Alternatively, one then should use the right-hand-side part of the definition, where a parameter p is used that specifically affects process i. Then the flux change between the two steady states (with and without parameter change) is compared to the effect of the parameter on the process rate v_i, had the latter been in isolation of the rest of the system but under the same nano-environmental conditions. When the parameter p is perturbed, the change in v_i in the denominator of (2.3) equals the change in the rate of reaction i only if all the other variables that affect that rate have been kept constant. This is referred to by the subscript ‘process i steady-state only’ and the fact that the derivative is partial: the process rates v_i are considered ‘local’ functions of the direct substrates, products and modifiers of the corresponding reactions i. By contrast, X and J are here considered as steady-state functions of all the parameters in the system but not of the metabolic variables.

The control coefficients describe the control exercised by a specific reaction or enzyme (‘process') on the overall system variables or fluxes, while ‘local’ regulatory properties of individual enzymes such as 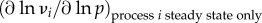are captured by the so-called elasticity coefficients. Such an elasticity coefficient corresponds to the local enzyme-only response of a reaction rate to one change in its immediate environment, for example, to a change in the concentration of metabolite X. The corresponding elasticity coefficient, 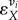, is defined as a partial log–log derivative of v_i with respect to X.

Two important types of law have been discovered by MCA (reviewed in [67]). The summation laws restrict the sums of control coefficients over all reaction steps in the network to simple integer values indicating that the control over network properties such as fluxes, concentrations, efficiency, yields, frequencies and transient times are conserved. One implication is that removal of a flux limitation in one step will always introduce more of a flux limitation elsewhere in the network. Connectivity laws relate the global network properties that are described by control coefficients to the local elasticities, i.e. they relate network function to the collective of molecular functions. For instance, using a summation and a connectivity law, the concentration control coefficients for a simple two-step pathway can be expressed into their elasticities,

2.4

reflecting not only that both the upstream and the downstream steps are important for the steady-state concentration of the intermediate, but also that they are precisely equally important, and that the importance of both decreases when either step is more elastic. Similar expressions for flux control coefficients exist [67], for instance, stipulating that the more rate limiting enzymes are the ones that are least responsive to their immediate metabolic environment, hence not necessarily the ones that catalyse irreversible reactions or are first in the pathway. Classical MCA studied the control in metabolic pathways. For ‘hierarchical’ regulatory networks with interactions at different levels, i.e. metabolic, signal transduction and gene expression, HCA [6] was developed as a generalization of MCA. It will be discussed in the next subsection.

2.3.2. Modular control analysis: hierarchical supply–demand theory

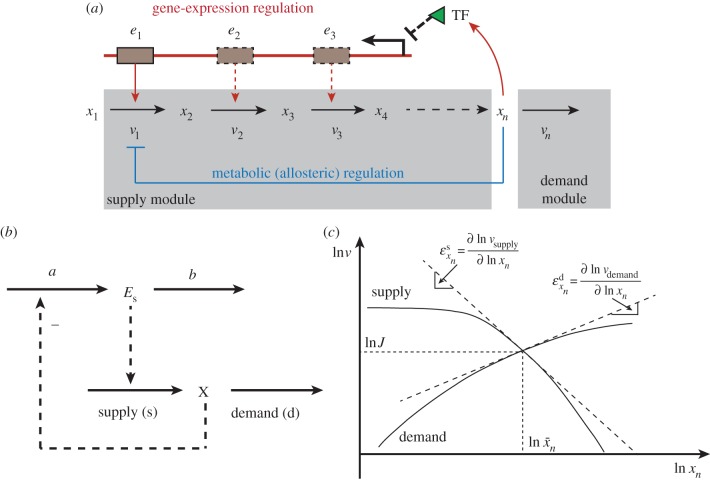
Engineering can benefit from the existence of supportive theories that are simpler to understand and are accompanied by precise theories such as MCA. To facilitate the control analysis and understanding of the functioning of large metabolic networks, modular MCA [74] has divided metabolic networks into modules with relatively autonomous activities connected through well-identified metabolites. Hofmeyr et al. [75,76] have developed a particular example of this, in their supply–demand theory. This theory serves to make the essence of the complex regulation of cell function understandable to the human. It may help design a new regulatory architecture which shifts control away from what evolved as best for the organism in its normal habitat to what is better for a metabolic engineering application. It achieves this by partitioning a pathway into supply and demand modules. More recently, supply–demand theory has been generalized from including exclusively metabolic regulation to both metabolic and gene-expression regulation, which is named the hierarchical supply–demand theory [77]. For example, an unbranched metabolic pathway under both allosteric inhibition and transcriptional regulation of the first enzyme by the end product (figure 1a) can be simplified into a hierarchical supply–demand system (figure 1b).

Figure 1.

An unbranched metabolic pathway under hierarchical regulation. (a) The first enzyme is regulated through both transcriptional repression and allosteric activity inhibition by the end product. Enzymes in other steps might also be regulated through gene expression (in dashed arrows), but this is not explicitly considered here. TF denotes transcription factor. (b) The hierarchical supply–demand representation of the pathway (a). The lower part represents the classical metabolic supply–demand system, in which only the metabolic regulation (in this case allosteric inhibition) is considered. The letter ‘X’ denotes the penultimate product x_n, still in pathway. The supply is catalysed by enzyme E_s (i.e. e₁ here or enzymes stemming from an entire operon). (c) Illustration of the steady-state properties of a supply–demand system in terms of changes in the flux, intermediate concentration and elasticity coefficients. (Online version in colour.)

In such a hierarchical supply–demand system, the steady-state dependence of a system function, e.g. the concentration of an intermediate metabolite X, on the ‘overall’ change in the reaction activity of a supply (or demand) module can be quantified by the hierarchical control coefficient employed in HCA:

2.5

Here, 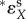is an ‘overall’ elasticity coefficient [72], including a classical ‘direct elasticity’ only related with metabolic responses and an ‘indirect elasticity’ due to gene-expression regulation, i.e. 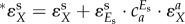. In HCA, the lower case c is used for metabolic control coefficients in a local network (i.e. metabolic or gene expression but not their combination). The control of gene expression 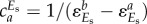. 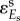is often equal to 1, i.e. when the rate of the reaction in isolation (e.g. supply module) is proportional to the concentration E_s of the enzyme catalysing it. As a result, the hierarchical concentration control coefficient (2.5) can be further expressed in terms of all the elasticity coefficients in the network:

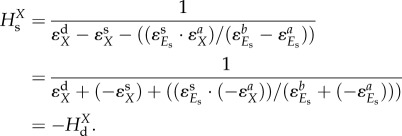2.6

The terms in parentheses are usually positive. The equation shows that the control by supply (i) decreases with the absolute magnitudes of the elasticities of the supply, demand and protein synthesis with respect to X, but (ii) increases for increasing elasticities of the protein synthesis and degradation reactions with respect to the concentration of the enzyme (E_s).

For the unbranched regulatory pathway given in figure 1a, only the first enzyme is regulated by the end product x_n through metabolic and transcriptional regulation. Hence, the ‘total elasticity’ in the supply module becomes 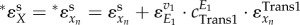, and the total elasticity through the metabolic regulation depends on the first and the (n − 1)th step as 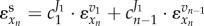. Because both metabolic and gene-expression regulation constitute negative feedbacks and x_n inhibits the activity of (n − 1)th step, the total elasticity in the supply 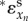is a monotonically decreasing function of x_n and becomes more negative with increasing x_n. 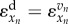is an increasing function of x_n but decreases asymptotically to zero with increasing x_n. The intersection of these two monotonic functions determines the steady-state properties of the pathway, i.e. the steady-state concentration of metabolite, the steady-state flux, the elasticities with respect to the supply and demand modules as shown in figure 1c, and thereby the distribution of control between supply and demand [75–77].

Some recent studies have extended standard MCA to take account of network uncertainties [78], to improve sampling of elasticity parameters using thermodynamic information [79] and to construct genome-scale MCA guided networks [80]. The appreciation that metabolic control does not reside in metabolism alone but also in transcription and translation, and in fact in all these, and other [81–83].

2.3.3. Regulation analysis: the diverse organism's response to perturbation

The magnitude of a flux or concentration ‘control’ coefficient employed in MCA or HCA represents a potential effect on the flux or metabolite concentration if the activity of a reaction step is modulated. This magnitude however does not indicate whether an enzyme or a kinase of a specific reaction step is actually activated by the network components (i.e. self-regulation) or modulated by an experimenter in a synthetic design [84], or not modulated at all.

To describe such regulatory information, Sauro [85] proposed a so-called ‘partitioned regulatory coefficient’ which describes how a perturbation in the rate of reaction i affects the enzyme activity of another reaction step j in terms of the change in the flux J_j and the altered concentrations of the metabolites that interact directly with that enzyme. This analysis only addressed regulation at the metabolic level such as allosteric or competitive effects. Ter Kuile & Westerhoff [86] generalized this and developed a hierarchical ‘regulation analysis' to accommodate regulation both by metabolic effects of chemical conversions and by ‘hierarchical’ effects of information transfer that includes signalling or gene expression. This approach has been successfully used to analyse the steady-state regulatory properties of several important metabolic pathways [46,50,86,87] typically showing that regulation tends to be distributed across all levels in the regulatory hierarchy.

More specifically, the rate v_i of an enzyme-catalysed reaction typically depends linearly on two functions which we here name h and f. The former is related to hierarchical effects where the changes in the rate of the enzyme are due to changes in enzyme concentration or covalent modification. The latter is related to metabolic effects where changes in rate are caused by changes in the concentrations of substrates, products and metabolic effectors. By denoting the rate v_i at steady state by the flux through the enzyme J (where v_i is the property of a single process i, while the flux J is a collective property and hence equal for a number of reactions in the same pathway, possibly including the process i), we realize that

2.7

Here e_i represents the concentration of the enzyme catalysing the process v_i. In the case of covalent modification, h(a_i) can be expressed as h(e_i, φ_a,i) = e_i · φ_a,i with φ_a,i denoting the fraction of the enzyme that is in the covalent modification state that is active catalytically (figure 2). As a result, the change in the logarithm of the steady-state flux J can be expressed as

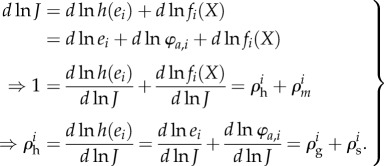2.8

Figure 2.

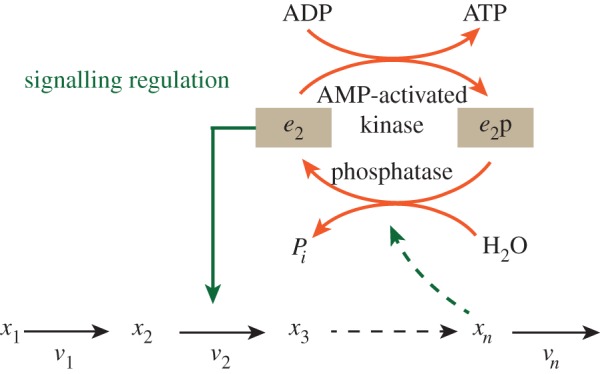
An illustration of signal-transduction regulation of a metabolic pathway. Signal-transduction regulation can be any post-translational (covalent) modification, such as phosphorylation or acetylation, of an enzyme or transcription factor that is an output of a signal-transduction pathway. In this example, the enzyme that catalyses the second reaction of a metabolic pathway is subject to covalent modification through phosphorylation by an adenosine monophosphate (AMP)-dependent protein kinase. e₂ denotes the fraction of the enzyme that is in the active state and e₂p denotes the fraction of enzyme that is phosphorylated and hence inactive. Another example is the covalent modification of glutamine synthase where AMP groups are covalently attached to the enzyme by an adenylyl transferase [88,89]. It may be noted that intermediates of central metabolism such as acetyl phosphate or the glycolytic intermediate 1,3-bisphosphoglycerate can directly cause covalent modifications of lysine residues of enzymes [90,91]. This then is metabolic regulation of metabolism through covalent modification, and constitutes yet another mechanism, which does not depend on signal transduction. (Online version in colour.)

Here d may seem to refer small changes or perturbations, but this is not a necessary limitation in regulation analysis to the extent that an enzyme rate is directly proportional to the enzyme concentration [69]. The hierarchical regulation coefficient 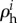comprises both gene-expression 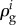, and signal-transduction regulation 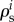. The sum of gene-expression, signal-transduction and metabolic regulation is always the same and equal to 1 [86]. This hierarchical regulation analysis has also been extended to time-dependent cases [92,93].

Importantly, the hierarchical regulation coefficient is typically not equal to the inverse of the flux control coefficient 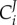defined in MCA (equation (2.3)). This is because commonly the living system changes the concentrations of many enzymes at the same time, and the flux can be affected by several reactions or enzymes [67]. We shall consider the example of a two-step pathway (catalysed by enzymes e₁ and e₂) with intermediate X in which the cell responds to an external challenge by changing the relative activities of the two genes encoding the two enzymes respectively (i.e. through dlng₁ and dlng₂). The gene-expression regulation of the first enzyme is

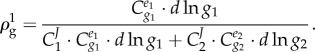2.9

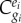denotes the control of gene i on the steady-state concentration of enzyme i. This equation indicates that the regulation coefficient is not simply the inverse of the corresponding flux control coefficient 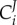, unless the corresponding enzyme has a flux control close to 1 (i.e. 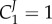and 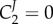), or the enzyme is the sole enzyme in the pathway that is regulated by gene expression (i.e. d ln g₂ = 0). It has been proved [94] that there exists a relationship between the metabolic control coefficients 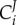and gene-expression regulation coefficients 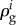in an unbranched pathway, and such a relationship can be generalized to hierarchical regulation coefficients 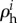by further including the effects stemming from signal-transduction regulation:

2.10

This law implies that (i) if there is only a single rate limiting step in an unbranched pathway and that step is being regulated, the hierarchical regulation coefficient of that enzyme is always 1, (ii) if flux control is distributed and only one reaction step is regulated hierarchically, its regulation coefficient equals the inverse of the control coefficient, i.e. there is a strong hierarchical regulation if the regulated step has little flux control, and (iii) if all regulation coefficients are equal they must equal 1.

Preliminary analyses show that the above law also applies to branched pathways, with a more complex interpretation however of the regulation coefficients. Indeed, there is nothing inherent in MCA, HCA or regulation analysis that limits these approaches to linear pathways, although most examples in the literature have been simple and thereby linear. A hierarchical control and regulation analysis of cyclic networks such as the TCA cycle should be of genuine interest. After early pioneering work by Wright and co-workers [95], this is now being taken up again [96]. A case in point is the TCA cycle where much of intermediary metabolism is controlled by and sometimes also regulated through the combined levels of all TCA-cycle intermediates.

2.3.4. Robustness and fragility

Organisms are often subject to changes in their internal and external environments. The robustness against such perturbations is a determinant of the fitness of living organisms. Because living systems depend fundamentally on non-equilibrium processes [72,84] there is no guarantee that they ultimately return to their original state. There are various aspects to robustness, which warrants multiple definitions. There is the maintenance of a specific functionality or variable of the system, where it is not required that all the variables of the system remain unchanged, i.e. homeostasis. This is known as disturbance rejection in control engineering. And, there is the transition to a new state after which the system is maintained in the new conditions. This is called robust tracking in the control engineering context. Finally, previous studies have investigated the effect of deleting one or multiple steps (e.g. knockout mutations or enzyme deficiencies) in metabolic pathways, which is termed ‘structural robustness' [97,98]. A physiologically more realistic scenario may be the adaptation of the network when a reaction step is only partially inhibited, which is known as ‘dynamic robustness' [99].

In a metabolic network, if the overall flux is robust to perturbations with respect to a specific step, this implies that this step is not the rate limiting step but on the contrary exerts little flux control. This suggests that there is a relationship between dynamic robustness and MCA. Quinton-Tulloch et al. [100] defined the robustness as the ratio between a 1% sustained perturbation in a process (i.e. perturbing the activity of an enzyme) and the corresponding percentage change in the steady-state biological function (e.g. flux). Mathematically, such a so-called MCA-based robustness coefficient equals the inverse of the corresponding control coefficient of that step. He et al. [77] studied the robustness of a metabolic network subjected to both metabolic and gene-expression regulation, and generalized the MCA-based analysis to HCA-based robustness analysis. The MCA (or HCA)-based robustness and fragility coefficient can be defined as follows:

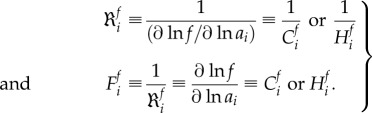2.11

Here f denotes the system function of interest, such as a particular flux J_j or a metabolite concentration x_j. Quinton-Tulloch et al. [100] calculated the flux robustness coefficients (FRCs) in realistic models of the glycolytic pathway of Trypanosoma brucei and of other in silico pathway models. They found that for the vast majority of the steps the individual FRCs were much larger than 1, reflecting small flux controls in those enzymatic steps. An increase in the robustness with respect to one step (e.g. glucose transporter) might come at the cost of a decrease in robustness with respect to other steps. However, the total robustness is not conserved under such operations, i.e. the sum of all the FRCs is not a constant. Unlike robustness, the MCA (or HCA)-based fragility is a conserved property because of the summation law (see §2.3.1).

Helping to understand the distribution of the control over the processes in a metabolic pathway, MCA has important applications for improving metabolite production through flux control [42] and for the identification of drug targets [101–103]. In addition, an elaborate example of using MCA and HCA to study hierarchical regulation and robustness has been reported [104]. A homeostatic control of DNA supercoiling in E. coli is conferred not just by enzyme activity (metabolic regulation) or just by enzyme expression (gene-expression regulation) but an unequal mixture of both. The former is responsible for 70% and the latter for 30% of the homeostasis. And even within gene-expression regulation there is a division between transcription and translation. Such control and regulatory information obtained from MCA or HCA can be crucial for engineering genetic circuits in a metabolic pathway by indicating not only which genes (or enzymes) should be engineered, but also at which level (e.g. transcription or translation) the gene circuits should be manipulated.

Although most MCA and much HCA have been developed in the context of pathways operating at steady state, it is not confined to steady states. Indeed, MCA has been extended [67,105–107] and applied to periodic phenomena such as glycolytic oscillations [108,109] and the cell cycle [110], to transient phenomena such as transient phosphorylation of signal-transduction proteins [111] and even to bistability [112]. It is especially interesting to consider such dynamic generalizations in a control systems context [113,114]. For a metabolic-regulatory network under both metabolic and transcriptional regulation, one can study the dynamic enzymatic control in terms of a control engineering framework and then ask how this then links in with MCA and HCA. These questions will be addressed in the next section.

3. Dynamic control and control-theoretic analysis

A central task in metabolic engineering is the optimization of pathway flux so as to maximize the metabolite or biomass production. The analytic approaches discussed in the previous section focused on establishing which molecular properties in a network determine the network's performance. Once this is known, up- or downregulations of genes that encode steps with much control may be used to improve steady-state pathway fluxes. One may overexpress enzymes that reside on the optimal paths calculated through FBA or overexpress the enzymes with the highest control coefficients over the requested flux or yield as computed by using MCA [115,116]. These strategies can maximize pathway fluxes but in the meantime they may also decrease cellular growth rate due to the reduced expression of enzymes with high control on that growth rate, e.g. through a protein burden effect [117]. ‘Dynamic metabolic engineering’ or ‘dynamic control’ strategies [118,119] have been proposed to control gene expression and enzyme activity dynamically such as to allow trade-offs between growth and production. Models that predict the impact of genetic modifications on growth rate were developed recently [120,121]. From a systems engineering viewpoint, this corresponds to a class of optimal control problems [122]. Here, time-dependent metabolite concentrations or enzyme activities cannot always be ignored. Dynamic metabolic control also relies on advances in synthetic biology to create genetic sensors and actuators, which will be further discussed in the sections that follow.

Apart from maximizing the metabolic production rate or yield, it is important to ensure pathway homeostasis and robust adaptation to perturbations especially for the effective implementation of a ‘dynamic control’ strategy. This is also true for engineering systems design where a trade-off between the optimal control performance and the robustness of the designed control system needs to be achieved. Robust perfect adaptation in a bacterial chemotaxis signalling system, in mammalian iron and calcium homeostasis, and in yeast osmoregulation have been interpreted as integral feedback control systems [123–125]. This suggests that engineering approaches may have some bearing on biological systems. One may therefore ask whether, for a genome-scale metabolic-regulatory system, robust adaptation at various hierarchical levels (i.e. metabolic and gene expression) such as observed in biology as a result of evolution, can be related to the different optimal control strategies designed in the discipline of control engineering. Does Nature beat human design? And, how could the application of control engineering to existing biological networks enhance those networks in the metabolic engineering or even the therapeutic sense? How could this lead to a better synthetic biology? Recent progress along these lines is discussed in this section.

3.1. Dynamic flux balance analysis and optimal control

FBA is mainly used to study the metabolic flux distribution at steady states; the dynamics of the pathway is rarely considered. However, the actual metabolite concentrations and enzymatic activities may be time-dependent and their temporal distribution could significantly affect the performance of the pathway. In addition, the ability to re-programme the optimized pathway and to reproduce features of the microbial growth process may be important for an engineering intervention that is minimally invasive.

DFBA (as reviewed in §2.2) extends standard FBA (2.2) by including the dynamics of the metabolic networks in the optimization process:

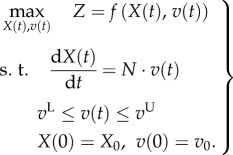3.1

This is very similar to an optimal control problem studied in control engineering. The metabolic concentrations X and process rates v can be interpreted as the state variables (state functions in thermodynamics) [72,86] and the process activities e_i (see (2.1)) as control variables or inputs. If the regulation of reaction rates is explicitly considered, for example, through allosteric control from metabolites, the optimization of the overall regulatory network corresponds to a state-feedback control problem. Under certain assumptions and when a quadratic objective function is employed, e.g. transitional responses in homeostasis, this DFBA can be formulated into a classical linear quadratic regulator (LQR) problem, i.e. DFBA–LQR [126], and solved efficiently using linear control theory. Interestingly, a connection between DFBA and MCA is identified here, where the flux control coefficients in MCA are shown to be correlated with the optimal gain computed from DFBA–LQR in a feedback regulatory network.

In the above paragraph, we used the word ‘control’ in the sense in which it is used in control engineering. This sense differs from the connotation of the same word in MCA that we used in earlier sections. The ‘control’ in MCA or HCA refers to the control exercised by a time-consuming [67] process on the system's performance. It is quantified as the sensitivity of that performance (e.g. a flux, a concentration or a cycle time) to changes in the process activity. It is called ‘control coefficient’ to distinguish it from the more general ‘sensitivity’, where the causative event that produces the change in the performance is a change in any parameter, such temperature or an equilibrium constant in the system. The ‘control’ in control engineering can be understood as a mechanism that could be or has been put in place by an engineer so as to improve the performance of the system. It corresponds to a strategy to alter the performance of a system. A feedback control loop in control engineering is analogous to a feedback regulatory mechanism (e.g. allosteric or transcriptional regulation) identified in a biological network and called regulatory strength in systems biology [88,127,128]. The usual aim of control engineering is to design a ‘controller’ that can improve the system's performance in tracking a signal or reject a disturbance to ensure robustness. Hence, the ‘control’ in control engineering is a strategy and in MCA it is a fact. One of the interests we have in the interface between MCA and control engineering is the use of MCA to determine which parameters are controlling most the properties of interest and to what extent, and then the use of control engineering to design extra networks and extra network properties so as to improve the robust behaviour of the biological system.

A sub-problem of DFBA is the dynamic optimal enzyme activation in biosynthetic pathways that has been studied by several authors. Klipp et al. [129] showed sequential enzyme (or gene expression) profiles that minimize the transition time needed to convert the substrate into the product and the sequence of which matched the enzyme order in the unbranched metabolic pathway. This ‘just-in-time’ activation profile was in agreement with experimental findings in the amino acid biosynthesis pathway of E. coli [130]. The analysis of a leucine biosynthesis pathway in yeast [131] indicated a more complex behaviour in which groups of enzymes are expressed either quickly at low amplitudes or slowly at high amplitudes. The influences of protein abundance and protein synthesis capacity on the optimal activation strategy have also been investigated [132]. A previously reported sequential activation strategy was only optimal if protein abundance relative to protein synthesis capacity was high; as protein abundance decreased, the strategy shifted to the simultaneous activation of all enzymes. These numerical approaches can be formulated into a more rigorous theoretical framework using optimal control theory [133,134] and by formulating the following optimization problem:

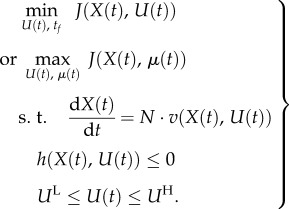3.2

The objective function represents either a minimization of the transition time to reach a given state of the system (or enzyme cost) or a maximization of biomass limited by for example the synthesis of the product of the pathway. U(t) is the vector of independent control variables representing enzyme concentrations E(t); μ(t) is the growth rate profile. The constraints are the system dynamics, the inequality path constraints h that restrict the synthesis capacity of individual enzymes and total amount of metabolites, and the lower and upper bounds for the control variables, i.e. the minimum and maximum amount of enzyme and the k_cat available for each reaction.

This optimal control problem can be solved using indirect methods such as Pontryagin's maximum principle or as a nonlinear programming problem. Recently, this optimal control formulation has been further generalized to multi-objective optimization, such as a trade-off between effectiveness (e.g. transition time) and economy (e.g. enzyme consumption), and for more realistic branched pathways [135]. Global optimization methods are required to solve such a more general problem.

3.2. Metabolic and gene-expression regulation: proportional and quasi-integral control

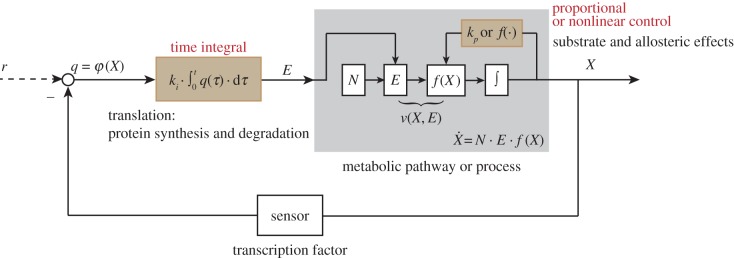
The optimization methods reviewed in the previous subsection are mainly used to obtain an optimal flux distribution or enzyme profile. They are less concerned with the underlying control mechanism even if applied to a feedback regulatory network. In reality, the control of the amount of enzymes through gene-expression (transcriptional) regulation and the control of enzymes' catalytic behaviour through metabolic (allosteric) regulation correspond to two types of feedback control mechanisms operating at different time scales, as shown in figure 3. This may ensure the robustness versus perturbations at various frequencies as widely considered in engineering system design.

Figure 3.

The closed-loop control structure of a metabolic network subject to metabolic and gene-expression regulation. The substrate or allosteric effects correspond to proportional or nonlinear controls that are often modelled together with the dynamics of the metabolic process. The gene-expression regulation can be described as a (quasi-) integral control, since protein synthesis requires time integration. The transcription process or the transcription factor can be regarded as a sensor of the control system. The metabolite concentration X is the output of the system and is the controlled dependent variable. Reaction rates v(X, E) are functions of both enzyme concentration E and metabolic process f(x). Here, the integral control input q is a function of the controlled dependent variable and a reference signal r. q compares the level of X with the level of r and differences between the two are time integrated and translated into alterations into altered enzyme levels, which then feed into the metabolic pathway. (Online version in colour.)

It has been shown [35,77,123] that metabolic regulation through allosteric or more direct substrate–product effects is related to a ‘proportional or nonlinear control’ action, because the catalytic activity of an enzyme can depend on a metabolite concentration in a proportional or nonlinear kinetic relationship. The metabolic regulation often acts as a fast actuator/controller that rapidly buffers against high-frequency perturbations but possibly with small amplitude or capability, such as adaptation to small fluctuations in the flux demand [86]. When such a fast actuator is saturated, indicating that the activity of that enzyme may be approaching its maximum capacity (V_max), the system has a second ‘actuator’ through gene expression which is slow but leads to increase (or decrease) in the concentration of that enzyme [86]. The gene-expression regulation is slow but may be able to accommodate very large and persistent perturbations and was identified to be related to a (quasi-) integral control action [77].

Recent analyses indicate that gene-expression regulation improves the robustness of a metabolic pathway significantly but that in practice such robustness may not be infinite, because perfect adaptation requires biochemically unrealistic features such as zero-order kinetics of protein degradation [77,136]. Such control engineering interpretations can also be linked with classical MCA and HCA. The relatively fast metabolic regulation (proportional control) is related to the ‘direct elasticities' of MCA, while the slow gene-expression regulation (integral control) corresponds to the ‘indirect elasticities' of HCA.

Let us take ATP energy metabolism as an example. This important intracellular process can be abstracted by a supply–demand system as illustrated in figure 4. The supply (s) process represents catabolism (e.g. glycolysis) that breaks down nutrients and produces ATP (from adenosine diphosphate (ADP) and phosphate). The demand (d) process represents anabolism that constructs macromolecules and consumes ATP. The concentration of ATP (i.e. [ATP]) equals C−[ADP], with the moiety conservation sum C a constant here because the catabolic/anabolic reactions only convert ATP into ADP or vice versa. The supply is catalysed by enzyme E that denotes enzymes of catabolic reactions which are here assumed to be encoded in a single operon or regulon. The gene expression of the enzyme(s) E is increased in proportion to the concentration of ADP. The metabolic regulation addresses the interplay between the supply and demand processes.

Figure 4.

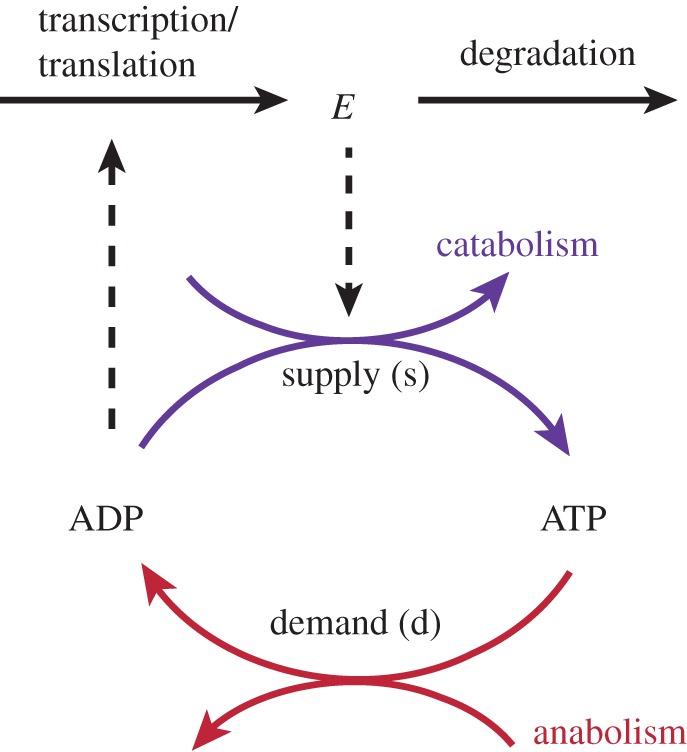
Illustration of ATP energy metabolism. This ATP supply–demand system is under both gene-expression and metabolic regulation. (Online version in colour.)

The dynamics of ADP and enzyme E will here be described by simple kinetics

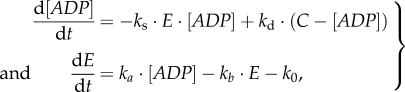3.3

where the degradation of E is assumed to be a mixture of the zero- and first-order processes. k₀ and k_b are the zero- and first-order protein degradation rate constants. k_a is the protein synthesis rate constant. k_s and k_d are the rate constants related to the supply and demand processes. The closed-loop control system structure of the pathway is shown in figure 5.

Figure 5.

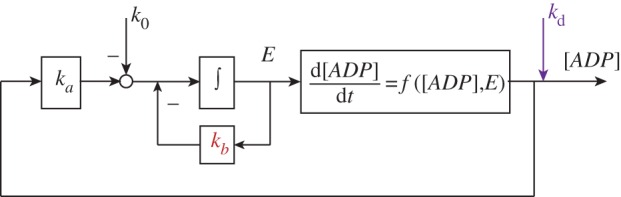
Control system structure of the ATP energy metabolism network of figure 3. k_a is the protein synthesis rate constant. k₀ and k_b are the zero- and first-order protein degradation rate constants. k_d is the perturbation. (Online version in colour.)

In this control system, the ADP concentration is a controlled (output) variable and the enzyme concentration E a manipulated (input) variable in the gene-expression feedback control loop. The zero-order degradation rate k₀ can be treated as a reference signal to the system. The metabolic regulation is included as part of the ADP kinetic process. By considering a perturbation of the demand process (i.e. δk_d) and reformulating the kinetics of ADP and E, one obtains

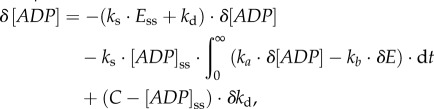3.4

where the subscript ss denotes the steady-state value and the left-hand side of the equation is a perturbation in the time dependence of the ADP concentration. On the right-hand side, the first term is a proportional response term, the second an integral response term and the third the perturbation term. The proportional response corresponds to the direct ‘elasticity’ of the supply and demand reactions with respect to ADP, which is a metabolic and instantaneous regulation. The integral response is related to the protein synthesis and degradation and thus to the gene-expression regulation. If k_b = 0, the second term corresponds to an ideal integral action. By further removing the time dependence of the change in ADP using the steady-state conditions [77], the hierarchical control coefficients, quantifying the control of the enzyme level and the flux by the demand reaction, are obtained:

3.5

Both the control of enzyme level and of demand flux are equal to 1 minus a hyperbolic function of k_b. For an ideal integral control scenario with k_b = 0, the enzyme concentration E perfectly tracks the activity of the pathway degrading ATP, and 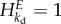. More importantly, the pathway flux perfectly tracks the perturbation in the demand flux and 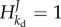. The control of k_d on ADP is zero and thereby this is the case of robust perfect adaptation. In practice, however, the dilution or the first-order proteolysis effect cannot be ignored and often k_b ≠ 0. In such cases, the adaptation of the pathway to the perturbation is not perfect. An MCA-based robustness coefficient has been proposed by Quinton-Tulloch et al. [100] and can be expressed in terms of the various parameters:

3.6

Only when k_b = 0 does the pathway exhibit infinite robustness (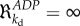) to the external or parametric perturbation. This example shows the consistency of control engineering and classical metabolic and HCA in understanding the adaptation of a metabolic pathway under both gene-expression and metabolic regulation. It also shows that a control engineering concept such as perfect adaptation can serve as inspiration for the understanding of the evolutionary design of the regulation of metabolic pathways.

4. Synthetic biology: design of metabolic-regulatory systems

To achieve optimal control of chemical production and to maintain pathway robustness in response to environmental changes, a number of elements in gene circuits can be designed and tuned at the transcription and translation stages. Post-translational control can be achieved via the modification of native allostery and the design of scaffold proteins. These synthetic biology-related design problems together with other issues related to the design, such as modularity, retroactivity, noise and stochastic effects, are reviewed in this section. Here, we focus on the more novel design of pathways at system level characteristic of synthetic biology, although most studies have considered the individual protein level, such as when modifying the protein sequence/function, activity or when designing new proteins in protein engineering [13].

4.1. Engineering gene expression and design constraints

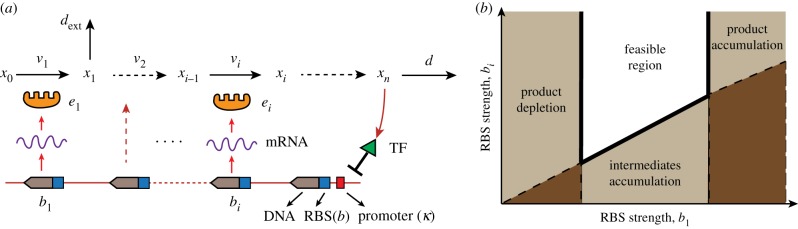
Several important elements (or parameters) in gene circuits, such as promoters for controlling transcription initiation rate, ribosome binding sites (RBS), riboswitches controlling translation levels, plasmid replicons controlling gene copy number, small inhibitory RNAs and long non-coding RNAs, can be tuned and manipulated with the aim of achieving a desired control over metabolism [16,137]. Pioneered implementations include a re-design of the native regulatory gene circuits for the enhanced production of lycopene and a synthetic gene-metabolic oscillator [23,24]. Since simple overexpression of flux-controlling enzymes can be toxic and can slow down cell growth in understandable ways [117], synthetic gene-metabolic feedback circuits have been built to control gene expression dynamically. Assuming all the enzymes of an unbranched pathway to be encoded in an operon under the control of a single promoter (figure 6a), the expression of catalytic enzymes can be expressed as

4.1

Figure 6.

Important tunable ‘design parameters' of synthetic gene circuits and design constraints of the RBS strength for a metabolic pathway with a branch consuming an intermediate. (a) The promoter characteristic (κ⁰,κ¹) and RBS strengths (b_i) can be re-engineered to modulate gene transcription and translation rates. (b) Design constraints with respect to RBS ratio b_i/b₁: the feasible RBS region prevents the accumulation of product and intermediates as well as avoids product depletion due to the weak control of flux through the branch. Adapted from [39]. (Online version in colour.)

Here i = 1, 2, … n. The functional σ(·) represents the metabolite–TF and TF–promoter feedback regulation. κ⁰ and κ¹ denote the promoter tightness and strength, and therewith describe the regulatory effect of TF on gene transcription. The translation rate of enzymes can be modified by choosing appropriate RBS strength b_i, while the protein degradation rate can be controlled by adding a degradation tag to the gene sequence or altering synonymous codons [138]. Recently, two engineered sensor-regulator systems were built to improve fatty acid-based biofuel production, where several heterologous genes and a flux-controlling enzyme acetyl-CoA carboxylase were controlled dynamically by key metabolites, acetyl-CoA and malonyl-CoA, respectively [37,139]. Additionally, a genetically encoded synthetic malonly-CoA switch was developed recently [140]. In such engineered feedback sensor-regulator systems, a transcription factor is often identified as a natural sensor that senses the biosynthetic intermediate. The naturally occurring cognate regulators or controllers (e.g. regulatory DNA elements) may need to be re-engineered for use with natural sensors.

Classical MCA has not yet been used much for the design of circuits in synthetic biology, but MCA and HCA can be used to analyse the effects on productivity of modifying parameters (e.g. promoter strengths or protein degradation tag) of both natural and synthetic gene circuits at the DNA, mRNA and protein levels. Hence, MCA/HCA can also assist in the design of more robust metabolic pathways because of their strength in quantifying network robustness as discussed in previous sections. HCA applies to any dynamic network, inclusive of those involved in transcriptional and translational regulation [117,141]. By viewing the level of mRNA as a resultant from a synthesis and a degradation process, HCA (or even MCA) predicts how promoter strength or degradation activity controls the level of the mRNA (e.g. [142]). This has been extended to the intricacies of transcriptional regulation in mammalian systems in the context of epigenetics and chromatin modification [143], although more work is needed here. Mathematically, the dynamics of a synthetic gene-metabolic pathway can be expressed by combining the expression of (2.1) and (4.1), and we can further break down the dynamics of the protein concentrations (4.1) into transcription (mRNA dynamics) and translation. As a result, this HCA can be used to track how the genetic parameters (such as the promoter strength κ¹) control the mRNA level or protein level E (or even flux) as

4.2

This is similar to the hierarchical control of enzyme level discussed for the ATP energy metabolism example (§3.2) and the concentration control coefficients used in MCA, although at a different biological network level.

Before implementing an engineered gene circuit, the design constraints with respect to design parameters need to be identified. Oyarzun & Stan [39] investigated the trade-offs and constraints in designing the gene-expression regulation circuits in unbranched pathways under the single operon assumption as expressed in (4.1). Constraints to tuneable design parameters, such as the promoter's dynamic characteristics and RBS strengths (figure 6a), must be satisfied to guarantee the existence of a stable steady state and to prevent the continued accumulation of intermediates (as shown in figure 6b). The local stability of the metabolic-regulatory system (i.e. combining (2.1) and (4.1)) under a perturbation, such as a change in cellular demand, was studied by applying a systems engineering approach in terms of the design elements in the gene circuits. In addition, it was concluded that the use of promoters with a broad dynamic range (e.g. increased tightness) can enlarge the feasible design region, whereas leakier promoters or higher substrate concentrations tighten the constraints. This is similar to the design of a mechanical or electronic control system. The stability of the closed-loop control system together with the actuator or output and state variable constraints need to be considered during the controller design process.

The design constraints of a synthetic metabolism at a pathway level were also studied [144] by combining FBA and Markov chain Monte Carlo sampling in a ‘global’ metabolic (genotype) network space. Specifically, this study investigated the quantitative relationships between different properties in a network, i.e. the number of alternative carbon sources it can use, the amount of biomass it can synthesize, the number of active reactions and the amount of waste the network produces, as well as how these metabolic network properties influence biosynthetic flux.

4.2. Synthetic allostery and protein–protein association

Apart from synthetic gene circuits for gene-expression regulation, post-translational control of the native allostery in metabolic regulation can also be re-engineered and optimized to provide a faster way for the control of metabolic pathways [145]. The allosteric network structure can be reconstructed to optimize a metabolic control, for example, eliminating allosteric enzyme inhibition so as to maximize product yield, or integrating allosteric inhibition into enzymes so as to increase product purity by eliminating by-product synthesis pathways [146]. The mechanism of allostery (i.e. structural and dynamic information related to the allosteric sites on the enzymes) can also be modified and fine-tuned to provide a more accurate and moderate regulation. Statistical coupling analysis and molecular dynamic simulation of proteins have been combined to re-engineer the allosteric regulation of aspartokinase, in E. coli and C. glutamicum, so that a reduced allosteric inhibition of the production of lysine and/or an enhanced inhibition of the formation of the by-product threonine was achieved [147] as shown in figure 7.

Figure 7.

Illustration of a simplified metabolic pathway and control of the by-product (threonine) synthesis for increased lysine production in bacteria. A non-natural allosteric regulation of homoserine dehydrogenase in response to lysine was constructed to reduce the flux to by-product threonine. (Online version in colour.)

Another attractive strategy for balancing pathway fluxes is to design scaffold protein [148] which then co-localizes cascade enzymes which results in synthetic protein–protein complex formation and substrate channelling. Substrate channelling has important potential applications in metabolic engineering, such as decreasing the effective free concentrations of unstable intermediates [149], preventing the accumulation of toxic metabolites, regulating fluxes by modulating enzyme–enzyme association and increasing sensitivity to regulatory signals [150]. Some examples have been reported, such as three non-endogenous mevalonate biosynthesis enzymes being scaffolded in E. coli using eukaryote protein–protein interaction domains [148]. Immobilized three-enzyme complexes (named synthetic metabolon), i.e. triosephosphate isomerase, aldolase and fructose 1,6-bisphosphatase in the glycolysis and gluconeogenesis pathways, have been constructed, which not only decreased protein purification labour and cost but also accelerated reaction rates by an order of magnitude when compared with non-complexed enzymes [151]. The flux control for a pathway with metabolic channelling at steady state was theoretically quantified under an MCA framework [152]. Quantitative analysis of substrate channelling and scaffold proteins on metabolic network dynamics, especially in a systems engineering context, and corresponding synthetic design constraints remain open research topics.

4.3. Modularity and retroactivity

A complex biochemical network is often decomposed into simpler components or into modules with common functions in order to facilitate the analysis and prediction of the overall system dynamic behaviour. On the other hand, the synthetic modular ‘circuits' composed of genes and proteins are also required to be placed into living cells (through the process of transformation or transfection). A fundamental systems engineering issue then arises when interconnecting several subsystems that is: whether and how the transmitting of a signal to a ‘downstream’ subsystem affects the dynamic behaviour of the ‘upstream’ subsystem. Recent studies on signalling and transcriptional network modules [38,153], such as the covalent modification cascades (e.g. MAPK cascades) and the machinery for protein synthesis (TF–protein interactions), reveal that modularity does not hold in general. Both an impedance-like effect that is well known in electrical systems and called ‘retroactivity’ [38], and unintended ‘crosstalk’ [154,155] have been identified and quantified in biochemical networks. They are at the very basis of the complexity of most biological networks that produces their circular causality, making an effect the cause of its cause [156]. Several approaches have been proposed to attenuate the effect of retroactivity or crosstalk, for example, inserting insulators between modules, layering methods, scaffolding [148], introducing negative feedback mechanisms (inspired by the design of amplifiers in electronics) through transcriptional activation or through phosphorylation of a protein that is in abundance [38], or using a classical loop-shaping control design [157] as an alternative to inserting insulators.

In a metabolic network, the metabolic supply and demand analysis (as discussed in §2.3) studies how the steady-state properties of a supply process can be controlled by the demand process that consumes the product. This is related to the retroactivity concept and analysis, and the latter concerns not only the steady-state behaviour but also transient situations. Similarly, modular MCA (or HCA) [74,128] may be used to quantify the retroactivity at the steady state that requires the measuring of the ‘overall’ control exerted by the processes catalysed by each module.

The retroactivity in gene transcriptional and signal-transduction networks has been formulated into a general control theoretic, i.e. disturbance rejection, problem [38,158]. It will be exciting to investigate the retroactivity problem of a metabolic network subject to both gene-expression and allosteric regulatory modules in terms of a generic control-theoretic problem and to study how it is related to MCA (and HCA) and supply–demand analysis.

4.4. Noise propagation and stochasticity

Gene expression is known to be noisy as transcription and translation may depend on infrequent events involving small numbers of molecules, as well as environmental fluctuations and genetic mutation [159]. There are many studies on the noise and stochastic effects in individual genes and gene regulatory circuits [160,161]. The retroactivity effects discussed in the previous subsection can also be practically inferred from the stochastic noise effect, because the ‘noise’ can be an information-rich ‘input’ signal designed to study the changes in the systems dynamic responses [162]. Stochastic effects in metabolic pathways were initially studied with respect to fluctuations in substrates and upstream metabolites [163]. Noise propagation from enzyme expression is typically neglected because of the assumptions on high metabolite counts and because stochasticity in enzyme expression occurs at much longer time scales. The above assumptions however may not hold for engineered metabolic pathways that can operate at low metabolite counts. Recently, simulation studies on noise propagation from enzyme expression to simple metabolic pathways [164,165] have been provided. How the extrinsic fluctuations (at the kinetic level) can affect the steady-state control of pathway fluxes and concentrations was investigated based on the stochastic generalizations of standard MCA [166,167]. Based on stochastic simulations, Oyarzun et al. [168] quantified the noise propagation in a simple synthetic metabolic pathway under transcriptional repression by the product and its dependency on the design parameters, such as promoter strength, promoter sensitivity and repression strength. It was concluded that attenuation of metabolic noise is a trade-off between the promoter strength and repression strength.

5. Conclusion and perspectives

Metabolic engineering has been applied to the analysis, design and optimization of metabolic pathways for more than three decades. Successful applications of synthetic biology on metabolic processes have been reported in the past decade, while the use of control engineering approaches to optimize, analyse and assist the synthetic biology design of metabolic networks has only begun to attract the attention in the last few years and may still be in its infancy. This review discussed important metabolic engineering approaches and synthetic biology-related design problems for metabolic-regulatory networks, and their connections with systems and control engineering.

Control theory can advance classical metabolic engineering techniques in pathway optimization, control and regulation analysis. To optimize the flux distribution and the production of a pathway while taking the network dynamics into account, the dynamic FBA can be formulated into an optimal control problem. As long as the objective function is linear or quadratic and the metabolic network is subject to only dynamic constraints, analytical solutions of such DFBA can be obtained from linear optimal control theory (e.g. the LQR approach mentioned in §3.1). When the objective function or system dynamics are nonlinear and the network is subject to certain constraints, such as in the dynamic enzyme activation problem, advanced nonlinear optimal control strategies need to be employed to solve such nonlinear optimization problems. One important future piece of work is to accommodate the stochastic effects and uncertainties in an FBA model, such as the uncertainties in the measured biomass composition or the flux capacities [169]. Robust control and optimal control theories are powerful tools that may be used to tackle this problem.

Apart from the optimization of flux distribution, the steady-state control of a network parameter (e.g. enzyme concentration or activity) on pathway fluxes or metabolite concentrations, or vice versa regulatory effects such as the inhibition of enzyme activities via allosteric regulation, are traditionally quantified by MCA and regulation analysis, respectively. Both control theory and HCA can generalize the MCA-based analysis to dynamic situations and take account of different regulation mechanisms at different hierarchical levels, such as the enzymatic and gene-expression regulation. These can be linked with the classical proportional and integral control mechanisms of control engineering. As a result, the enzymatic control, regulation and the cellular robust adaptation to environmental conditions can all be studied within the well-established control-theoretic framework both for steady state and for transient states.

Successful synthetic biology applications based on metabolic-regulatory networks have been reported in the past 10 years; the use of control engineering techniques to assist the synthetic design is more recent and less complete. It includes (i) the use of feedback control in the design and realization of synthetic gene-metabolic systems, including the implementation of biological sensors, controllers and actuators, (ii) the clarification of different metabolic or genetic regulatory mechanisms in terms of widely used control mechanisms [35,77], (iii) attenuation of the retroactivity, crosstalk and noise effects when interconnecting synthetic modules by introducing feedback loops around modules, and (iv) identification of the design constraints and of the existence of local stability in terms of design parameters such as promoter and ribosome characteristics.

It can be expected that systems and control engineering will now serve to advance existing metabolic engineering and synthetic biology techniques to improve metabolic product and network robustness. Challenges will be due to the nonlinear and complex nature of the metabolic networks and to the complicated regulatory mechanisms at different hierarchical levels. Important future work includes: (i) design and implementation of various new control strategies (i.e. a mixture of proportional, integral, derivate or nonlinear controllers) in a complex biosynthetic pathway with regulation at hierarchical (metabolic, gene expression and signal transduction) levels, (ii) design and implementation of bio-controllers that can accommodate network parametric uncertainties, which can be achieved either through quantifying the uncertainties in the design process by the use of robust control theory [170], or by engineering and inserting a non-natural bio-integrator into the metabolic-regulatory system, since an integral feedback control is known to achieve perfect robustness and adaptation, and (iii) rigorous analysis of the design constraints and network stability when adding a synthetic genetic or metabolic module to the overall network.

Much remains to be discovered and then engineered.

Authors' contributions

F.H. and H.V.W. generated the ideas for the manuscript, helped to draft and edit it. F.H. performed literature searches. E.M. contributed to the section on FBA. H.V.W. helped with the final editing done by F.H.

Competing interests

We declare we have no competing interests.

Funding

This work was supported various systems biology grants, including Synpol: EU-FP7 (KBBE.2012.3.4-02 no. 311815), Corbel: EU-H2020 (NFRADEV-4-2014-2015 no. 654248), Epipredict: EU-H2020 MSCA-ITN-2014-ETN: Marie Skłodowska-Curie Innovative Training Networks (ITN-ETN) no. 642691, BBSRC China: BB/J020060/1.