Abstract
A central goal of protein-folding theory is to predict the stochastic dynamics of transition paths — the rare trajectories that transit between the folded and unfolded ensembles — using only thermodynamic information, such as a low-dimensional equilibrium free-energy landscape. However, commonly used one-dimensional landscapes typically fall short of this aim, because an empirical coordinate-dependent diffusion coefficient has to be fit to transition-path trajectory data in order to reproduce the transitionpath dynamics. We show that an alternative, first-principles free-energy landscape predicts transition-path statistics that agree well with simulations and single-molecule experiments without requiring dynamical data as an input. This ‘topological configuration’ model assumes that distinct, native-like substructures assemble on a timescale that is slower than native-contact formation but faster than the folding of the entire protein. Using only equilibrium simulation data to determine the free energies of these coarse-grained intermediate states, we predict a broad distribution of transition-path transit times that agrees well with the transition-path durations observed in simulations. We further show that both the distribution of finite-time displacements on a one-dimensional order parameter and the ensemble of transition-path trajectories generated by the model are consistent with the simulated transition paths. These results indicate that a landscape based on transient folding intermediates, which are often hidden by one-dimensional projections, can form the basis of a predictive model of protein-folding transition-path dynamics.
Abstract Graphic
Introduction
In studies of complex molecular systems, free-energy landscapes provide a tractable and intuitive framework for predicting rare events. Free-energy landscapes are low-dimensional projections that describe the equilibrium distribution of molecular configurations with respect to a small number of collective variables. However, when appropriately defined, these landscapes can also be used to predict dynamical properties of equilibrium or near-equilibrium stochastic trajectories, such as the relative rates of transitions between macrostates. This feature, combined with the fact that a variety of computational techniques have been developed for efficiently calculating free energies without directly simulating rare events,1 makes freeenergy landscapes useful for rationalizing reaction and phase-transformation mechanisms in complex systems. Consequently, theories based on free-energy landscapes are widely applied to problems in classical2–4 and non-classical5,6 nucleation, phase separation,7,8 and protein folding.9–12
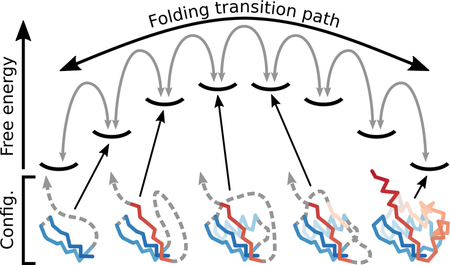
A particularly important problem in protein folding is the prediction of transition paths between the unfolded and folded ensembles.13–18 These trajectories are both rare and, at an atomistic level, extremely heterogeneous, making this problem ideal for landscape-based theories. One of the most widely adopted approaches is to model folding as a diffusion process on a smooth, one-dimensional free-energy landscape.19–25 Nevertheless, even when using a good reaction coordinate,1 one-dimensional landscapes typically have to be corrected empirically to reproduce the dynamical properties of the actual stochastic folding trajectories.25,26 This correction can be achieved by introducing a position-dependent diffusion coefficient,27 since the gradient of the free-energy landscape itself is not sufficient to predict the relative rates of molecular motions on the one-dimensional reaction coordinate. The key limitation of this approach is that the transition-path trajectories that we wish to predict are required as input, either to determine the coordinate-dependence of the diffusion coefficient26,28–30 or to find a projection for which the apparent diffusive behavior is coordinate-independent.31,32 It is also unclear whether a single optimized one-dimensional coordinate can always be found for large proteins, which may have more complicated or parallel folding pathways.33 Furthermore, recent single-molecule measurements of folding transition paths15,34 have provided experimental evidence of the shortcomings of one-dimensional landscapes, as the folding free-energy barrier inferred by applying a one-dimensional diffusion model to measured transit-time distributions is often inconsistent with the landscape determined directly in the sameexperiments.35,36
In contrast, an optimal free-energy landscape is one that is capable of predicting the statistical properties of stochastic transition paths without requiring additional, empirical kinetic information. To address this problem, we recently proposed an alternative, first-principles approach37 for constructing structure-based free-energy landscapes to describe protein-folding transition paths. Based on an analysis of a native-centric ‘Ising-like’ model,38–40 we postulated that the key events along transition paths coincide with the formation of native-like loops in the polymer backbone.41 We therefore devised a coarse-graining procedure in which microstates sharing the same set of native-like loops, but different sets of native contacts, are grouped into the same ‘topological configuration.’ Because the loss of entropy due to loop closure is not compensated until multiple stabilizing native contacts are formed, we further postulated that these topological configurations are, in general, separated by free-energy barriers, leading to a separation of timescales between the formation of individual native contacts and the assembly of topological configurations. Consistent with this prediction, we found that topological configurations interconvert on much slower timescales than individual native contacts in atomistic simulations and that these slower transitions follow roughly Markovian dynamics.37
In this paper, we show that the topological configuration model accurately describes the stochastic dynamics of transition-path trajectories. By estimating the free energies of the predicted topological configurations using equilibrium all-atom simulation snapshots,42 we apply this model to generate an ensemble of transition paths in terms of transitions between coarse-grained, partially folded states. First, we show that the distribution of transit times predicted by this approach is much closer to the distribution of simulated transit times than that predicted by a model of diffusion on a smooth one-dimensional landscape. Second, we demonstrate that the distribution of simulated finite-time displacements on a one-dimensional order parameter can be rationalized by the topological configuration model.
Lastly, we use a hidden Markov framework to show that the predicted separation of timescales generates an ensemble of transition paths that is consistent with the simulated folding trajectories. Overall, these results indicate that a free-energy landscape defined on the basis of transient, native-like intermediates can predict protein-folding transition paths without requiring post hoc corrections to the transition-path dynamics.
Theory
Definition of a topological configuration
The central principle of the topological configuration model 37 is a separation between three different timescales: a relatively fast timescale associated with native-contact formation, a slower timescale on which substantial portions of native structure assemble, and a slowest timescale on which the entire protein folds. The timescale separation for these processes has been well established experimentally, with measurements reporting single-contact formation on timescales of approximately 10 ns,43 native-like loop formation on timescales of 100 ns– 1 μs,44 and the folding of proteins with approximately 100 residues or more on timescales of 100 μs or longer.45 It is also well established that the entropy–enthalpy compensation of protein folding is imperfect, meaning that while a small number of native contacts is rarely sufficient to counter the associated loss of configurational entropy completely, the formation of subsequent native contacts tends to be more thermodynamically favorable.46,47 This general feature, which is responsible for the overall free-energy barrier that determines the slowest timescale of protein folding, also gives rise to many smaller barriers on folding transition paths. In particular, the entropic penalty associated with the closure of a single native-like loop typically results in a small yet significant free-energy barrier, which in turn leads to a dynamical timescale that is slower than the average rate of native-contact formation but faster than the rate at which the entire protein folds.
By identifying native loops and considering all permutations of the order in which they can form, we can construct a free-energy landscape that captures this key intermediate timescale. We previously demonstrated37 how this analysis could be applied to a structurebased, ‘Ising-like’ model based on the pioneering work of Eaton and colleagues.38,48,49 In that work, we calculated the free-energy barriers between configurations in the structure-based model to support the predicted separation of timescales. We also provided indirect evidence of intermediate barriers in an all-atom model by analyzing the dwell times associated with the predicted topological configurations in all-atom simulations.
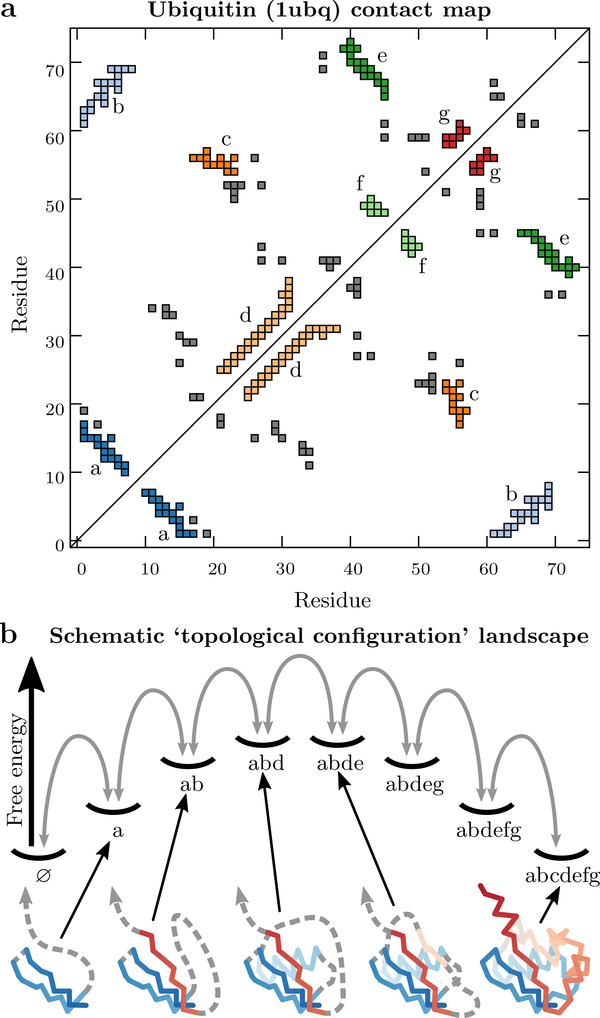
As in Ref. 37, we shall focus on the protein Ubiquitin in order to test the topological configuration model’s ability to predict transition-path dynamics. In the contact map shown in Figure 1a, individual ‘substructures’ comprise native contacts that are adjacent2 in the contact map. Topological configurations are defined as combinations of one or more substructures, including any additional native contacts between the residues that comprise these substructures. As shown in the schematic Figure 1b, we can then construct a free-energy landscape in the discrete space of topological configurations. Transitions are allowed between configurations that differ by a single substructure (and thus a single native-like loop closure). It is important to note that each topological configuration is not a rigid structure but rather an ensemble of microstates, in which different sets of native contacts are present but the same set of substructures (and, consequently, native-like loops) are represented. Furthermore, due to the predicted separation of timescales, the fluctuations in native-contact formation within a topological configuration are typically much faster than the transitions between configurations.
Figure 1:
Definition of topological configurations for the protein Ubiquitin. (a) A map of the residue–residue native contacts determined from a crystal structure (PDB ID: 1ubq). Substructures, comprising sets of at least six adjacent native contacts, are colored and labeled. Native contacts that are not part of any substructure are shown in gray. (b) A schematic topological configuration free-energy landscape showing a single pathway between the completely unfolded, ‘∅,’ and native, ‘abcdefg,’ configurations. These configurations are separated by free-energy barriers and thus interconvert on a slower timescale than the formation of individual native contacts. Selected configurations are illustrated below, where stretches of disordered residues are indicated by dashed lines.
Estimation of topological configuration free energies from Molecular Dynamics simulations
In this paper, our goal is to evaluate the predictions of a free-energy landscape constructed solely from thermodynamic data. For this purpose, we analyzed snapshots from all-atom Molecular Dynamics (MD) simulations,42 which were conducted under conditions where a total of ten unbiased, reversible folding and unfolding transition paths of Ubiquitin were observed. To calculate the free energy associated with each predicted topological configuration, we first classified all simulation snapshots, recorded at 1ns intervals, according to which substructures are present. In each snapshot, we found all native residue–residue contacts in which at least one pair of heavy atoms is less than 4.5 Å apart. We then considered a substructure to be formed if at least six of its native contacts were present in the largest structured region, i.e., the largest connected component of the graph of native residue–residue contacts in a simulation snapshot. As demonstrated in Ref.37, this definition prevents contacts with extremely brief lifetimes (on the order of 1ns) from influencing the identification of substructures. Free energy differences between pairs of configurations (i, j) were estimated according to the relative frequencies of the classified snapshots,
| (1) |
where Ni is the total number of snapshots assigned to configuration i, kB is the Boltzmann constant, and T is the absolute temperature. For comparison with theories based on one-dimensional free-energy landscapes, we also calculated the free-energy landscape as a function of the number of native heavy-atom contacts50 using a 4.5 Å cutoff distance,
| (2) |
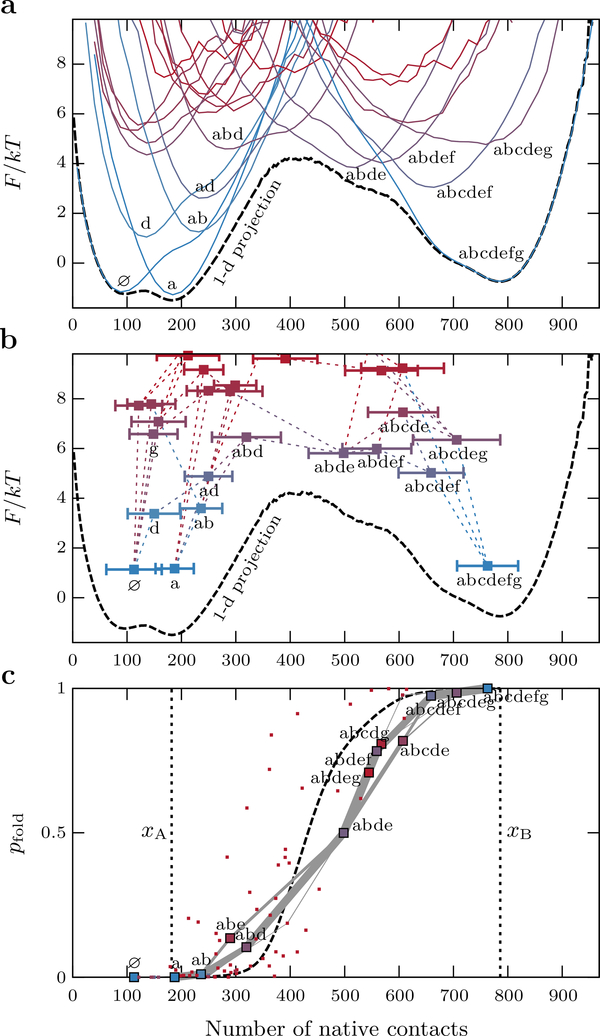
where N(x) is the total number of snapshots in which the number of native contacts falls in the range [x − Δx/2,x + Δx/2). This one-dimensional free-energy landscape is shown in Figure 2a, where the bin width Δx is taken to be 4 native contacts.
Figure 2:
Comparison of the topological configuration and one-dimensional (1-d) free-energy landscapes. (a) Projections of the free-energy surfaces onto the number of native contacts. Selected curves corresponding to distinct topological configurations (solid colored lines) are labeled; the 1-d projection F(x), with bin width Δx = 4 native contacts, is shown by the dashed black line. (b) The unimodal projections of the topological configurations onto the number of native contacts can be characterized by Gaussian distributions with the indicated means (squares) and standard deviations (error bars). The dotted lines indicate allowed transitions between configurations that differ by exactly one substructure. (c) The committors, pfold, associated with each configuration (squares), projected onto the number of native contacts. Selected configurations are labeled, and the predicted folding fluxes through the network of states are indicated by the widths of the gray lines; fluxes less than 5% have been omitted. For comparison, the dashed black line shows pfold(x) predicted by the 1-d landscape, where the vertical dotted lines indicate the boundaries of the transition-path region, xA and xB. In all panels, the configurations are colored according to their estimated free energies, Fi = −kBT logNi, with blue and red indicating low and high free energies, respectively.
The central object of the topological configuration model is the rate matrix T for transitions between topological configurations. Ideally, one should determine the transition rates either from the free-energy barriers or the mean first passage times between configurations, but accurate calculations of this type are not possible given the available simulation data. Instead, we simply assumed a symmetric form that enforces detailed balance for the forward and backward rates between configurations i and j,
| (3) |
for pairs of configurations (i, j) that differ by the addition or removal of a single substructure; the diagonal elements of the matrix are then . The prefactor k0 is the same for all transitions and is left as an adjustable parameter that scales all barrier heights between configurations equivalently. However, due to the assumed separation of timescales, we know that k0 should be slow compared to the average rate of native-contact formation. Then, given the matrix T, it is straightforward to calculate the overall folding rate, kfold; the committor associated with each configuration i, pfold,i; the probability of finding a trajectory in a specific configuration i on a transition path, ; and the folding fluxes between adjacent states i and j, , using transition-path theory.51 These quantities will be used throughout our analysis. We shall show that, despite not undertaking detailed calculations of the individual barrier heights, this model produces remarkably accurate transition-path statistics. Furthermore, alternative choices for the form of the rates given in Eq. (3), such as a Metropolis function,52 do not change the qualitative nature of our results. We also note that all timescales determined directly from the atomistic simulations are accelerated relative to experiments, in part due to the elevated temperature at which the simulations were conducted.42
General properties of topological configuration free-energy landscapes
In addition to a separation of timescales, our previous analysis37 of this model made two general predictions that hold up when comparing with simulation data. First, the Boltzmann-weighted ensemble of microstates associated with each topological configuration is predicted to be unimodal when projected onto a one-dimensional coordinate. For example, the free energy as a function of the number of native contacts is unimodal for all topological configurations, as shown by the labeled colored curves in Figure 2a, suggesting that there are no significant free-energy barriers between microstates within each configuration. Consequently, it is reasonable to approximate the projection of each configuration onto this order parameter using a Gaussian distribution with the estimated mean, ⟨x⟩i, and variance, , where the subscripts indicate averages over all snapshots classified as topological configuration i, as shown in Figure 2b. This approximation will be used in the discussion of hidden Markov modeling below.
Second, in the case of proteins such as Ubiquitin with little structural symmetry, the free energies of the various topological configurations are relatively heterogeneous, which results in a small number of high-probability transition paths through the network. By applying transition-path theory51 to the rate matrix T, we calculated pfold for each configuration and the folding flux between configurations on transition paths. Figure 2c shows that there is a nearly one-to-one correspondence between the predicted pfold and the number of native contacts when we consider only those configurations that are likely to be visited on transition paths, even though this order parameter played no role in the transition-path theory calculations. This observation is consistent with the fact that the number of native contacts is a good reaction coordinate for identifying the ensemble of transition states, where pfold = ½, from simulated Ubiquitin transition paths.50 However, knowing the location of the transition state on an order parameter is, in general, not sufficient to predict the transitionpath dynamics. In addition, any one-dimensional projection almost invariably hides some of the intermediate free-energy barriers on transition paths that play an important role in the transition-path dynamics.53,54
Statistical analyses
Distribution of transition-path transit times
As an initial test of the model, we examined the predicted distribution of transit times between the unfolded and folded ensembles. For two-state proteins, transit times are orders of magnitude smaller than the characteristic waiting time until a folding or unfolding event occurs.13,15,55,56 Nevertheless, recent advances in single-molecule experiments15,34 have made it possible to measure these brief trajectories. Although experimental measurements have confirmed that the distribution of transit times has an exponential tail as expected for stochastic barrier-crossing processes, the shape of the distribution generally disagrees with the predictions of one-dimensional landscape theories.34–36 In particular, the measured distributions are typically much broader than expected for a one-dimensional landscape with a harmonic barrier.
To compare the predictions of the one-dimensional (1-d) and topological configuration models, we used kinetic Monte Carlo (kMC) simulations57 to sample transition paths between absorbing states of a rate matrix, T. We first calculated the distribution of transit times for the 1-d native-contacts landscape shown in Figure 2a. To this end, we discretized this landscape between the unfolded and folded free-energy minima into 150 bins (such that Δx = 4 native contacts) and constructed a tri-diagonal transition matrix, T1-d. We assumed the symmetric form
| (4) |
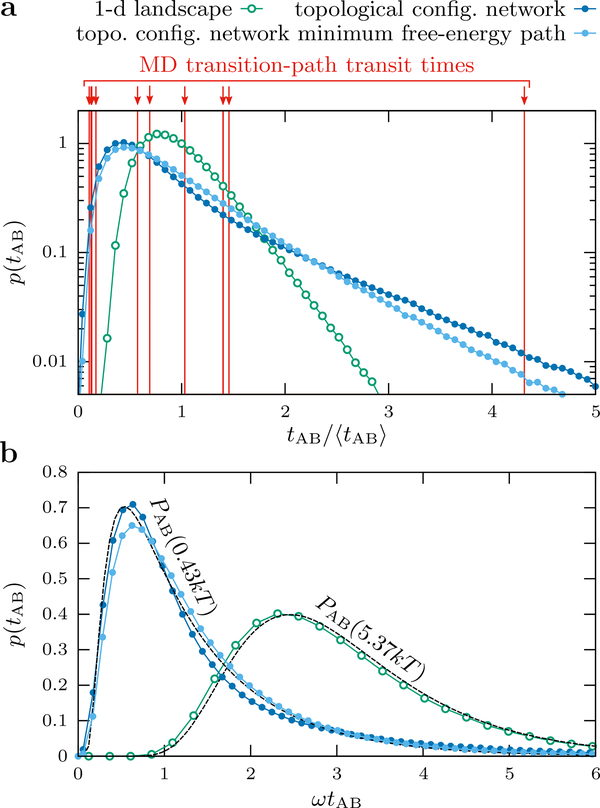
with . Because the transit times are inversely proportional to the transition-matrix prefactor k0, transit-time distributions for different models can be compared by scaling tAB according to the mean transit time, ⟨tAB⟩. In this way we can see that the predicted distribution of transit times, p(tAB), between the folded and unfolded free-energy minima xA and xB (Figure 2c) is relatively narrow, with a coefficient of variation of 0.39 and an exponential tail (Figure 3a). Alternatively, we can fit the decay constant of the exponential tail, 𝜔-1, in order to compare with the theoretical distribution for 1-d harmonic barrier crossings, ,58 where the shape parameter ΔF† is the height of the barrier (Figure 3b). The simulated distribution of 1-d transit times agrees well with this harmonic prediction using the barrier height ΔF† = 5.37kT determined directly from the empirical 1-d landscape (Figure 2a), despite the fact that this landscape is not perfectly harmonic.
Figure 3:
Distributions of transition-path transit times, p(tAB), for the models of Ubiquitin folding shown in Figure 2. (a) The distributions calculated via kinetic Monte Carlo simulations of the 1-d native contacts landscape model, the topological configuration model, and the quasi-one-dimensional minimum free-energy path through the topological configuration network. To compare the shapes of the distributions, all transit times are scaled according to the mean transit time, ⟨tAB⟩, for each model. Also shown are the ten transit times observed in all-atom MD simulations. (b) The same three distributions were fit to the theoretical distribution for a harmonic barrier, , in order to estimate the decay constant, 𝜔-1 of the exponential tail. The transit-time distribution calculated from the empirical 1-d landscape agrees well with the theoretical distribution using the empirical barrier height, 5.37kT, while the distribution calculated from the topological configuration model can only be fit by if we set the shape parameter ΔF† equal to a much lower barrier height of 0.43kT.
We then repeated these calculations using the topological configuration rate matrix defined in Eq. (3). The resulting distribution of transit times (Figure 3a) also has an exponential tail, but is substantially broader, with a coefficient of variation of 0.91. We find that the distribution of transit times obtained from the MD simulations, which has a coefficient of variation of 1.21 ± 0.45, is considerably closer to the distribution derived from the topological configuration model than the distribution derived from the 1-d model. (The maximum likelihood ratio for the two models given the ten MD transit times is 1019). When comparing the transit-time distribution predicted by the topological configuration model with the harmonic prediction , the best fit is obtained with a shape parameter ΔF† that corresponds to a one-dimensional landscape with a 0.43kT barrier (Figure 3b). Interestingly, this order-of-magnitude difference between the actual barrier height3 and that returned by a fit to the harmonic theory is reminiscent of the discrepancy found in experimental measurements.34
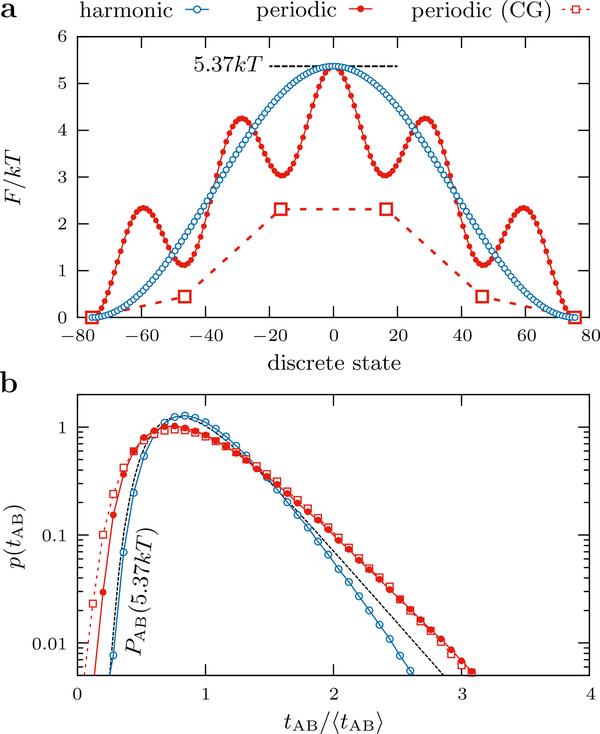
The striking difference between the shapes of these transit-time distributions is primarily a consequence of the intermediate barrier crossings, as opposed to the multidimensionality of the network model. For example, by simulating transition paths that only traverse the quasione-dimensional minimum free-energy path through the configuration network, we obtained a similar distribution of transit times (Figure 3). To explore this reasoning further, we constructed two toy 1-d landscapes with the same barrier height and number of bins as in the empirical 1-d landscape (Figure 4a). In the first landscape, the single barrier is, to a good approximation, harmonic, while in the second landscape, there are five intermediate barriers. We then computed T1-d using Eq. (4) and simulated the transition paths for these toy models via kMC. As expected, the presence of the intermediate barriers significantly broadens the transit-time distribution, resulting in a coefficient of variation of 0.47 for the intermediate-barrier landscape versus 0.36 for the single-barrier toy landscape (Figure 4b). It is also possible to coarse-grain the dynamics over the intermediate-barrier toy landscape by calculating the mean first passage times between the local free-energy minima (Figure 4a). Simulating the transition paths for this coarse-grained model results in a good agreement with the full intermediate-barrier toy landscape (Figure 4b). Although the difference between the transit-time distributions for these particular toy models is smaller than that shown in Figure 3, this comparison clearly demonstrates that the presence of intermediate barriers on the transition paths tends to broaden the distribution of transit times.
Figure 4:
Distributions of transition-path transit times for two one-dimensional toy landscapes. (a) The two toy free-energy landscapes, with a single harmonic barrier [blue empty circles; F(x) ∝ Acos(2πx/151)] and five intermediate barriers [red filled circles; F(x) ∝ Acos(2πx/151) + 2kT cos(10πx/151)], respectively. The maximum barrier height and number of discrete states were chosen to match the empirical 1-d landscape shown in Figure 2a for each toy landscape. Coarse-graining (CG) the intermediate-barrier landscape by calculating the mean first passage times between local free-energy minima results in the six-state model shown by red empty squares. (b) The transit-time distributions for the two toy landscapes, with all times scaled by the mean transit time, ⟨tAB⟩, for each model. The single-barrier landscape has a transit-time distribution that is narrower than the theoretical prediction, , for this barrier height (black dashed line), while the intermediate-barrier transit-time distribution and its coarse-grained approximation are significantly broader.
Distribution of finite-time displacements on a one-dimensional order parameter
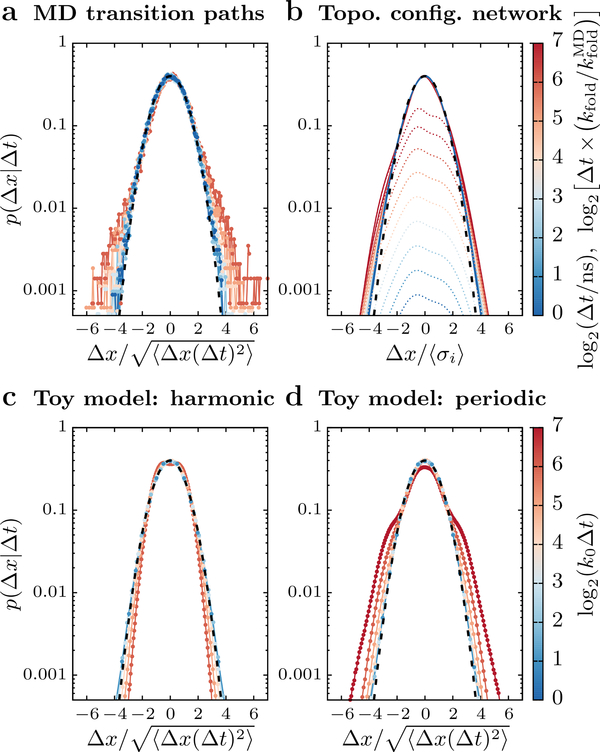
As a second statistical test, we examined distributions of finite-time displacements on a one-dimensional order parameter. Using the number of native contacts as the order parameter, we measured displacements, Δx, given a lag time Δt on all transition-path trajectories in the atomistic MD simulations. We considered lag times ranging from 1ns, which is longer than the typical time required for the formation of a single native contact, to ∼ 100ns, which is much shorter than the mean transit time, 2.43 μs, observed in the MD simulations. After verifying that Ubiquitin transition paths exhibit subdiffusive motion over this range of lag times,59 meaning that ⟨[Δx(Δt)]2⟩ ∝ (Δt)p with p < 1, we sought to determine whether, for a given lag time, the distribution of frequent, small displacements is predictive of larger jumps. By averaging over all MD transition-path trajectories and removing the net directional motion, (xB − xA)/tAB, we find that the vast majority of displacements, for which , are well described by Gaussian distributions over the entire range of lag times. However, larger displacements are much more frequent than predicted by the tails of the Gaussian distributions, regardless of the lag time. This ‘fat-tailed’ behavior is shown in Figure 5a, where the distribution for each lag time is scaled according to its root-meansquared displacement and compared to a unit Gaussian distribution indicated by the black dashed line.
Figure 5:
Distributions of finite-time displacements on the 1-d native contacts order parameter, averaged over the transition-path ensemble. (a) The distribution of displacements Δx after a lag time Δt observed in all-atom MD transition paths. The distributions are centered, such that ⟨Δx⟩ = 0, and scaled by the root-mean-squared displacement at each lag time. The frequent small displacements are well described by a Gaussian distribution with a unit standard deviation (black dashed line); however, larger displacements are much more frequent than predicted by the tails of this Gaussian distribution. Colors correspond to the lag time, in units of nanoseconds, as shown by the scale bar on the right. (b) The predicted distribution of displacements corresponding to transitions between configurations in the topological configuration model (dotted lines) is broader than a Gaussian distribution fit to the transition-path-ensemble-averaged fluctuations within individual configurations, leading to similar fat-tailed behavior. The lag times are scaled by the slowest timescale of the MD simulations, , for comparison with panel a. (c–d) Distributions calculated from kinetic Monte Carlo simulations of transition paths on the two toy landscapes shown in Figure 4a. Only the intermediate-barrier landscape (panel d) reproduces the fat-tailed behavior observed in the MD simulations.
This unusual feature is naturally predicted by the timescale separation in the topological configuration model, since the distribution of one-dimensional displacements is narrower for fluctuations within a configuration than for transitions from one configuration to another. To illustrate this idea, we compare the expected displacement associated with a step between configurations, , with the average size of a fluctuation within a configuration, , where the averages are taken over all configurations and weighted by , the probability of finding a transition-path trajectory in any configuration i (Figure 5b). The contribution from transitions between configurations, shown by colored dotted lines in Figure 5b, increases with the lag time, since the probability of moving from configuration i to j within a finite time Δt is given by the matrix exponential [exp(ΔtT)]ij. As a result of these larger displacements, the tails of the distribution are always outside of the unit Gaussian distribution, suggesting that the fat-tailed behavior observed in the MD simulation-derived distributions is also indicative of relatively rare intermediate barrier crossings.
To test this hypothesis, we analyzed the distributions of finite-time displacements obtained from simulated transition paths over the two toy landscapes shown in Figure 4a. By scaling the distributions according to their root-mean-squared displacements and compar-ing with a unit Gaussian distribution (Figure 5c,d), we find that only the landscape with intermediate barriers results in a qualitatively similar fat-tailed distribution. The singlebarrier toy landscape, by contrast, results in large displacements being less frequent than predicted by a Gaussian distribution. We therefore conclude that the relative enrichment of large displacements within lag times of a few tens of nanoseconds is a likely consequence of intermediate barrier crossings in the MD-simulated transition paths.
Likelihood comparison between predicted and simulated transitionpath trajectories
Finally, we tested whether the transition-path trajectories observed in the MD simulations, when projected onto a one-dimensional coordinate, are representative of the transition-path ensembles predicted by the topological configuration model. To do so, we treated this stochastic process as a hidden Markov model with a discrete state space of topological configurations. In this model, transition paths traverse the discrete state space in accordance with the rate matrix T, but we assume that we can only observe the instantaneous projection of each state s onto the 1-d coordinate x. With the exception of the transition-matrix prefactor k0, both the transition probabilities between states and the topological configuration-dependent probabilities of observing a given number of native contacts, p(x|s), are completely determined by quantities calculated from the equilibrium MD simulation data. We first removed all configurations in the topological configuration network that are not likely to be visited on transition paths (less than 1% of predicted folding flux) to guard against overfitting. We then used the standard Viterbi algorithm60,61 to determine the unique sequence of configurations, {sl}, that maximizes the log likelihood of the observed time series {xl} for each transition-path trajectory,
| (5) |
where the index l runs over all consecutive snapshots on each transition path, and we have normalized the log likelihood to remove the trivial dependence on the total trajectory length n.
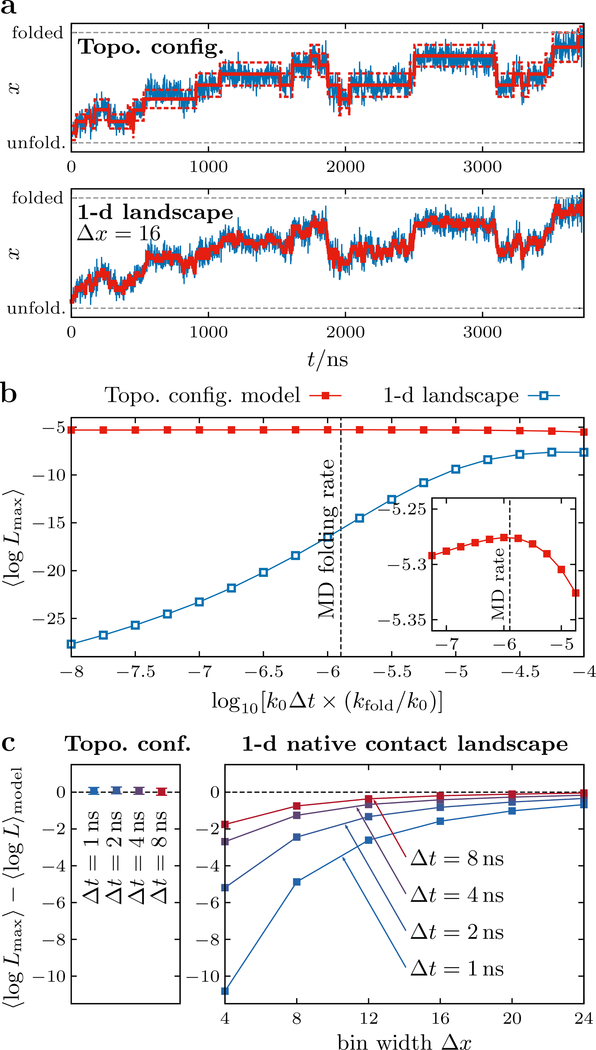
A representative maximum likelihood fit, using the fixed transition rates and emission probabilities defined in Eq. (3) and Figure 2b, respectively, is shown in Figure 6a, where the apparent separation of timescales between high-frequency oscillations and slower, step-like behavior can be easily discerned by eye. Furthermore, the log likelihood of most probable path, ⟨logLmax⟩, is only weakly dependent on the transition-matrix prefactor, k0. (Figure 6b). Analyzing one frame per nanosecond, the maximum of ⟨logLmax⟩ is found at a value of k0 that results in a predicted folding rate, kfold, of approximately 1 × 10-6 frames. Importantly, this folding rate agrees well with the empirical folding rate that we calculated directly from the mean in the full MD trajectories, (Figure 6b,inset).
Figure 6:
Comparison of transition-path trajectories from atomistic MD simulations and trajectories generated by theoretical models. (a) The maximum-likelihood transition paths (red solid lines) through the discrete states of the topological configuration and 1-d landscape models given a representative MD transition-path trajectory, projected onto the number of native contacts, x (blue lines). For the topological configuration model, the expected fluctuations (i.e., the standard deviations of the Gaussian approximations in Figure 2b) within the most probable states are shown by red dashed lines. (b) The dependence of the per-frame log likelihood of the most probable sequence of states on the transition-matrix prefactor, k0. This rate is scaled by the folding rate predicted by the model, kfold, for comparison with the estimated MD folding rate, (black dashed line). The maximum of ⟨logLmax⟩ for the topological configuration model coincides with the MD folding rate (inset). (c) Comparison between the log likelihood of the most probable sequence of states and the expected log likelihood for each model, ⟨logL⟩model (see text). When fitting to the 1-d model, the agreement between these quantities depends strongly on the spatial coarse-graining, Δx, of the landscape and temporal averaging of the MD transition-path trajectories over time windows of width Δt. Error bars indicate the standard error of the mean.
We then performed an analogous hidden Markov analysis for the 1-d landscape model with a constant diffusion coefficient. In this case, the discrete states {} are bins of width Δx, the rate matrix is given by Eq. (4), and the Gaussian emissions are assumed to have a standard deviation of Δx. For example, a representative maximum likelihood fit, assuming a bin width of Δx = 16 native contacts, is shown in Figure 6a. Unlike the topological configuration model, we find that the log likelihood of the most probable path in the 1-d model is strongly dependent on the transition-matrix prefactor, k0. Furthermore, the maximum with respect to k0 corresponds to a folding rate that is orders of magnitude greater than that determined from MD simulations. This means that, in order to generate a transition path with the observed high frequency fluctuations on the empirical 1-d landscape, k0 has to be tuned to a point where the predicted rates of folding and unfolding events are unrealistically fast. The topological configuration model does not suffer from this contradiction, since the separation of timescales between the fast motions within a topological configuration and slower transitions between configurations is an intrinsic feature of the model.
To ensure a fair comparison between these models, we calculated the expected values of the log likelihood for transition paths generated directly by both models,
| (6) |
where the expectation values for the emission and transition probabilities are and , respectively, in each state s. Fixing k0 to match the MD folding rate, Figure 6c shows that the log likelihood of the most probable path determined by fitting the MD data is consistent with the expected log likelihood for the ensemble of transition paths generated by the topological configuration model. This result is independent of temporal coarse-graining, i.e., down-sampling the trajectory x(t) by averaging over a moving window of width Δt. By contrast, temporal coarse-graining has a significant effect on the difference between the best-fit and expected log likelihoods for the 1-d landscape model when k0 is fixed according to the MD folding rate, since increasing Δt preferentially removes high frequency fluctuations. This difference is also sensitive to the landscape bin width Δx, since increasing Δx reduces the number of distinct states and consequently slows the rate of transitions between adjacent states. As a result, increasing the bin width results in an effective separation of timescales on the 1-d landscape, albeit without a first-principles justification. Only by introducing a separation of timescales through a post hoc combination of temporal coarse-graining of the trajectories and spatial coarse-graining of the 1-d landscape is it possible for the 1-d model to generate transition paths that are consistent with those observed in the MD simulations (Figure 6c).
In conclusion, this hidden Markov analysis highlights the importance of a separation of timescales for reproducing the transition-path trajectories observed in atomistic MD simulations. In particular, the co-occurrence of fast fluctuations in the number of native contacts and infrequent folding events is naturally captured by the topological configuration model, as seen by the agreement between the log likelihoods of the fitted and predicted transitionpath trajectory ensembles. One-dimensional landscape models that lack an intermediate timescale, by contrast, require that the trajectories observed in MD simulations be smoothed substantially in order to conform to the predicted transition-path dynamics.
Discussion
We have shown that a theoretical model of protein folding, which emphasizes an interme-diate timescale associated with transitions between distinct configurations of partial native structure, accurately predicts multiple statistical properties of the stochastic dynamics of folding transition paths. By using equilibrium simulation data to construct an approximate rate matrix for transitions between topological configurations, we demonstrated that the transition-path ensembles generated by this model have broad transit-time distributions that are consistent with both all-atom simulations and experimental observations. We then showed that the non-Gaussian distributions of finite-time displacements that are predicted by this model qualitatively match all-atom simulation results. Lastly, we demonstrated that this model can reconcile rapid local fluctuations on a one-dimensional order parameter with a slow overall rate of folding, two seemingly contradictory features that are simultaneously observed in simulated transition-path trajectories. Most importantly, all predictions of the topological configuration model were made without the use of any dynamical information.
The intermediate timescale in the topological configuration model is predicted to arise due to local free-energy barriers that separate transient states with distinct sets of native-like loops.37 In this work, we assumed that the rates of transitions between states could be approximated using a simple formula that satisfies detailed balance. However, a more accurate approach would involve the calculation of the rates between adjacent topological configurations in the all-atom model. Such an approach might benefit from recent advances in Markov state modeling,62,63 although, in this application, the definitions of the states would be as-sumed a priori on the basis of the native structure. Nevertheless, it is remarkable that we are able to obtain qualitatively accurate results for a variety of statistical tests using a highly simplified Markov model and the estimated free energies of the predicted topological configurations. This success indicates that the statistical analyses that we considered depend to a greater extent on the presence of intermediate barriers than on their precise heights, provided that these barriers are comparable to the thermal energy (≳ kBT) and are thus kinetically relevant. Generalizing beyond Ubiquitin, we anticipate that accounting for this intermediate timescale is likely to be especially important in the context of large proteins, which tend to have complicated native topologies. Transition-path analyses of small, ultrafast-folding proteins,64 by contrast, are less likely to benefit from the coarse-graining strategy described here, since these proteins typically contain only one or two native-state loops whose formation dominates the overall folding rate. The lower probability of encountering substantial free-energy barriers on folding transition paths, which are needed to assume approximately Markovian transitions between intermediate configurations, suggests that models of diffusion over a single harmonic barrier may be more appropriate in these particular cases.
To compare our approach with commonly used one-dimensional models, we assumed a projection onto the number of native contacts and a constant diffusion coefficient. The number of native contacts has been shown to be a good reaction coordinate in the sense that, for many small proteins, it can be used to locate the transition state from transition-path trajectories with high probability.50 The results presented here are not inconsistent with this notion of a good reaction coordinate when a single pathway through the network of topological configurations dominates, as shown by the similarity between the committors predicted by the two models. Furthermore, if one were to account for coordinate-dependent diffusion, it is likely that these two approaches would lead to similar predictions for the transition-path dynamics, since existing methods for fitting coordinate-dependent diffusion coefficients often reveal the existence of intermediate barriers that were hidden by the projection onto the original reaction coordinate.31 However, to carry out such an analysis, dynamical informa-tion is always required in some form,25 meaning that the underlying landscape is not, by itself, truly predictive.
The topological configuration model that we have examined here differs in a number of important ways from alternative models of folding intermediates that have been proposed previously. Unlike the early hierarchical model of Ptitsyn65 and the more recent ‘foldon’ hypothesis,66 the assembly of native-like intermediates need not lead to a more negative free energy at every step. At the same time, we have not assumed that the free energy decreases only upon incorporation of the final native-like substructure, as proposed in a recent ‘volcano’ model of folding.67 By contrast, the highest point on the minimum free-energy path through the network of topological configurations is determined by the free energies of the various configurations and the barriers between them, which depend, in turn, on the temperature and solvent conditions.37 The topological configuration model also suggests a natural definition of a folding pathway68 at the level of topological configurations while allowing for alternative, yet less probable, pathways.
Finally, this theoretical analysis has a number of implications for experimental investigations of protein-folding transition paths. The transit-time and finite-time displacement distributions that we have discussed can now be measured directly in single-molecule experiments. However, to distinguish between alternative theoretical models, it would be most useful to analyze high-resolution experimental transition-path measurements using hidden Markov models in order to detect and characterize transient folding intermediates. Using established non-parametric methods,69,70 it should be possible to assess both the number of distinct transient states and any separation of timescales objectively. Furthermore, by combining such analyses with structure-based models, like the type discussed here, it should be possible to extract more detailed information regarding the underlying free-energy landscape from these measurements. In this way, continued advances in single-molecule measurements can be used to improve predictive landscape-based models of protein-folding transition paths, in particular for large proteins with complex native-state topologies.
Conclusion
We have shown that the introduction of an intermediate timescale, which is faster than native-contact formation but slower than the typical time for folding an entire protein, can qualitatively alter the statistics of protein-folding transition paths. We proposed that this intermediate timescale is associated with the assembly of native-like loops, and we used this principle to build a coarse-grained free-energy landscape for Ubiquitin from equilibrium atomistic simulation data. Without relying on any dynamical information from simulations, we showed that this model predicts distributions of transit times and finite-time displacements that are consistent with simulated transition paths, but differ qualitatively from the predictions of a one-dimensional model of diffusion on an empirical free-energy landscape. We also used a hidden Markov analysis to demonstrate that this model generates transition paths that agree with both the dynamics and kinetics inferred from reversible folding simulations. Our results suggest that the analysis of single-molecule transition-path trajectories may be improved by accounting for intermediate free-energy barriers, which are a fundamental aspect of the complexity of folding large biomolecules.
Acknowledgement
The authors would like to thank D.E. Shaw Research for providing the all-atom Molecular Dynamics simulation data. In addition, the authors are grateful for many insightful discus-sions with Michael Manhart. This work was supported by NIH grants F32GM116231 and GM068670. All analysis and simulation code is available from the authors upon request.
Footnotes
In this context, a good reaction coordinate is one that not only distinguishes the unfolded and folded states, but also takes a single value for all configurations visited on transition paths that have an equal probability of reaching either of these macrostates.
Two contacts are adjacent if each residue in the first contact is an immediate neighbor of one of the residues in the second contact; for example (i, j) is adjacent to (i, j + 1) and (i + 1, j + 1).
Note that the barrier on the minimum free-energy path through the topological configuration network is also greater than 5kT.
References
- (1).Frenkel D; Smit B Understanding molecular simulation: From algorithms to applications; Academic Press, 2001. [Google Scholar]
- 2).Gibbs JW On the equilibrium of heterogeneous substances. Am. J. Sci 1878, 96, 441–458. [Google Scholar]
- 3).ten Wolde PR; Ruiz-Montero MJ; Frenkel D Numerical calculation of the rate of crystal nucleation in a Lennard–Jones system at moderate undercooling. J. Chem. Phys 1996, 104, 9932–9947. [Google Scholar]
- 4).De Yoreo JJ; Vekilov PG Principles of crystal nucleation and growth. Rev. Mineral. Geochem 2003, 54, 57–93. [Google Scholar]
- 5).ten Wolde PR; Frenkel D Enhancement of protein crystal nucleation by critical density fluctuations. Science 1997, 277, 1975–1978. [DOI] [PubMed] [Google Scholar]
- 6).Jacobs WM; Reinhardt A; Frenkel D Rational design of self-assembly pathways for complex multicomponent structures. Proc. Natl. Acad. Sci. U.S.A 2015, 112, 6313–6318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7).Frenkel D Entropy-driven phase transitions. Physica A: Stat. Mech 1999, 263, 26–38. [Google Scholar]
- 8).Poon W; Renth F; Evans R Kinetics from free-energy landscapes—How to turn phase diagrams into kinetic maps. J. Phys.: Condens. Matter 2000, 12, A269–A274. [Google Scholar]
- 9).Abkevich V; Gutin A; Shakhnovich E Free energy landscape for protein folding kinetics: Intermediates, traps, and multiple pathways in theory and lattice model simulations. J. Chem. Phys 1994, 101, 6052–6062. [Google Scholar]
- 10).Shakhnovich EI Protein folding thermodynamics and dynamics: Where physics, chemistry, and biology meet. Chem. Rev 2006, 106, 1559–1588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11).Gfeller D; De Los Rios P; Caflisch A; Rao F Complex network analysis of freeenergy landscapes. Proc. Natl. Acad. Sci. U.S.A 2007, 104, 1817–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12).Thirumalai D; O’Brien EP; Morrison G; Hyeon C Theoretical Perspectives on Protein Folding. Ann. Rev. Biophys 2010, 39, 159–183. [DOI] [PubMed] [Google Scholar]
- 13).Abkevich VI; Gutin AM; Shakhnovich EI Specific nucleus as the transition state for protein folding: Evidence from the lattice model. Biochemistry 1994, 33, 10026–10036. [DOI] [PubMed] [Google Scholar]
- 14).Shakhnovich EI Theoretical studies of protein-folding thermodynamics and kinetics. Curr. Opin. Struct. Biol 1997, 7, 29–40. [DOI] [PubMed] [Google Scholar]
- 15).Chung HS; McHale K; Louis JM; Eaton WA Single-molecule fluorescence experiments determine protein folding transition path times. Science 2012, 335, 981–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16).Chung HS; Eaton WA Single-molecule fluorescence probes dynamics of barrier crossing. Nature 2013, 502, 685–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17).Chung HS; Cellmer T; Louis JM; Eaton WA Measuring ultrafast protein folding rates from photon-by-photon analysis of single molecule fluorescence trajectories. Chem. Phys 2013, 422, 229–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18).Truex K; Chung HS; Louis JM; Eaton WA Testing landscape theory for biomolecular processes with single molecule fluorescence spectroscopy. Phys. Rev. Lett 2015, 115, 018101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19).Šali A; Shakhnovich EI; Karplus M How does a protein fold? Nature 1994, 369, 248–251. [DOI] [PubMed] [Google Scholar]
- 20).Bryngelson JD; Onuchic JN; Socci ND; Wolynes PG Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins: Struct., Func., and Bioinf 1995, 21, 167–195. [DOI] [PubMed] [Google Scholar]
- 21).Onuchic JN; Wolynes PG Theory of protein folding. Curr. Opin. Struct. Biol 2004, 14, 70–75. [DOI] [PubMed] [Google Scholar]
- 22).Berezhkovskii A; Szabo A One-dimensional reaction coordinates for diffusive activated rate processes in many dimensions. J. Chem. Phys 2005, 122, 014503. [DOI] [PubMed] [Google Scholar]
- 23).Best RB; Hummer G Diffusive model of protein folding dynamics with Kramers turnover in rate. Phys. Rev. Lett 2006, 96, 228104. [DOI] [PubMed] [Google Scholar]
- 24).Zhang BW; Jasnow D; Zuckerman DM Transition-event durations in onedimensional activated processes. J. Chem. Phys 2007, 126, 074504. [DOI] [PubMed] [Google Scholar]
- 25).Best RB; Hummer G Diffusion models of protein folding. Phys. Chem. Chem. Phys 2011, 13, 16902–16911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26).Hummer G Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New J. Phys 2005, 7, 34. [Google Scholar]
- 27).Berezhkovskii A; Szabo A Time scale separation leads to position-dependent diffusion along a slow coordinate. J. Chem. Phys 2011, 135, 074108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28).Best RB; Hummer G Reaction coordinates and rates from transition paths. Proc. Natl. Acad. Sci. U.S.A 2005, 102, 6732–6737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29).Hinczewski M; von Hansen Y; Dzubiella J; Netz RR How the diffusivity profile reduces the arbitrariness of protein folding free energies. J. Chem. Phys 2010, 132, 245103. [DOI] [PubMed] [Google Scholar]
- 30).Mugnai ML; Elber R Extracting the diffusion tensor from molecular dynamics simulation with Milestoning. J. Chem. Phys 2015, 142, 014105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31).Best RB; Hummer G Coordinate-dependent diffusion in protein folding. Proc. Natl. Acad. Sci. U.S.A 2010, 107, 1088–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32).Tiwary P; Berne B Predicting reaction coordinates in energy landscapes with diffusion anisotropy. J. Chem. Phys 2017, 147, 152701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33).Du R; Pande VS; Grosberg AY; Tanaka T; Shakhnovich EI On the transition coordinate for protein folding. J. Chem. Phys 1998, 108, 334–350. [Google Scholar]
- 34).Neupane K; Foster DAN; Dee DR; Yu H; Wang F; Woodside MT Direct observation of transition paths during the folding of proteins and nucleic acids. Science 2016, 352, 239–242. [DOI] [PubMed] [Google Scholar]
- 35).Makarov DE Reconciling transition path time and rate measurements in reactions with large entropic barriers. J. Chem. Phys 2017, 146, 071101. [DOI] [PubMed] [Google Scholar]
- 36).Satija R; Das A; Makarov DE Transition path times reveal memory effects and anomalous diffusion in the dynamics of protein folding. J. Chem. Phys 2017, 147, 152707. [DOI] [PubMed] [Google Scholar]
- 37).Jacobs WM; Shakhnovich EI Structure-based prediction of protein-folding transition paths. Biophys. J 2016, 111, 925–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38).Muñoz V; Eaton WA A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. U.S.A 1999, 96, 11311–11316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39).Alm E; Baker D Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc. Natl. Acad. Sci. U.S.A 1999, 96, 11305–11310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40).Galzitskaya OV; Finkelstein AV A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. U.S.A 1999, 96, 11299–11304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41).Frenkel D Folding proteins one loop at a time. Biophys. J 2016, 111, 893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42).Piana S; Lindorff-Larsen K; Shaw DE Atomic-level description of ubiquitin folding. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 5915–5920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43).Thompson PA; Eaton WA; Hofrichter J Laser temperature jump study of the helix–coil kinetics of an alanine peptide interpreted with a ‘kinetic zipper’ model. Biochemistry 1997, 36, 9200–9210. [DOI] [PubMed] [Google Scholar]
- 44).Lapidus LJ; Eaton WA; Hofrichter J Measuring the rate of intramolecular contact formation in polypeptides. Proc. Natl. Acad. Sci. U.S.A 2000, 97, 7220–7225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45).Garbuzynskiy SO; Ivankov DN; Bogatyreva NS; Finkelstein AV Golden triangle for folding rates of globular proteins. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 147–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46).Zimm BH; Bragg JK Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys 1959, 31, 526–535. [Google Scholar]
- 47).Dill KA; Fiebig KM; Chan HS Cooperativity in protein-folding kinetics. Proc. Natl. Acad. Sci. U.S.A 1993, 90, 1942–1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48).Kubelka J; Henry ER; Cellmer T; Hofrichter J; Eaton WA Chemical, physical, and theoretical kinetics of an ultrafast folding protein. Proc. Natl. Acad. Sci. U.S.A 2008, 105, 18655–18662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49).Henry ER; Best RB; Eaton WA Comparing a simple theoretical model for protein folding with all-atom molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 17880–17885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50).Best RB; Hummer G; Eaton WA Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 17874–17879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51).Metzner P; Schu¨tte C; Vanden-Eijnden E Transition path theory for Markov jump processes. Multiscale Model. Sim 2009, 7, 1192–1219. [Google Scholar]
- 52).Metropolis N; Rosenbluth AW; Rosenbluth MN; Teller AH; Teller E Equation of state calculations by fast computing machines. J. Chem. Phys 1953, 21, 1087–1092. [Google Scholar]
- 53).Krivov SV; Karplus M Hidden complexity of free energy surfaces for peptide (protein) folding. Proc. Natl. Acad. Sci. U.S.A 2004, 101, 14766–14770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54).Krivov SV; Karplus M One-dimensional free-energy profiles of complex systems: Progress variables that preserve the barriers. J. Phys. Chem. B 2006, 110, 12689–12698. [DOI] [PubMed] [Google Scholar]
- 55).Ding F; Dokholyan NV; Buldyrev SV; Stanley HE; Shakhnovich EI Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J 2002, 83, 3525–3532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56).Chung HS; Louis JM; Eaton WA Experimental determination of upper bound for transition path times in protein folding from single-molecule photon-by-photon trajectories. Proc. Natl. Acad. Sci. U.S.A 2009, 106, 11837–11844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57).Gillespie DT Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem 1977, 81, 2340–2361. [Google Scholar]
- 58).Chaudhury S; Makarov DE A harmonic transition state approximation for the duration of reactive events in complex molecular rearrangements. J. Chem. Phys 2010, 133, 034118. [DOI] [PubMed] [Google Scholar]
- 59).Krivov SV Is protein folding sub-diffusive? PLoS Comp. Biol 2010, 6, e1000921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60).Forney GD The Viterbi algorithm. Proc. IEEE 1973, 61, 268–278. [Google Scholar]
- 61).hmmlearn—hmmlearn 0.2.1 documentation. http://hmmlearn.readthedocs.io/en/latest/, Accessed: June 19, 2018.
- 62).Bowman GR; Pande VS; Noé F An introduction to Markov state models and their application to long timescale molecular simulation; Springer, 2014; pp 1–6. [Google Scholar]
- 63).Chodera JD; Noé F Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol 2014, 25, 135–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64).Lindorff-Larsen K; Piana S; Dror RO; Shaw DE How fast-folding proteins fold. Science 2011, 334, 517–520. [DOI] [PubMed] [Google Scholar]
- 65).Ptitsyn O Stages in the mechanism of self-organization of protein molecules. Doklady Akademii Nauk SSSR 1973, 210, 1213. [PubMed] [Google Scholar]
- 66).Maity H; Maity M; Krishna MM; Mayne L; Englander SW Protein folding: The stepwise assembly of foldon units. Proc. Natl. Acad. Sci. U.S.A 2005, 102, 4741–4746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67).Rollins GC; Dill KA General mechanism of two-state protein folding kinetics. J. Am. Chem. Soc 2014, 136, 11420–11427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68).Adhikari AN; Freed KF; Sosnick TR De novo prediction of protein folding pathways and structure using the principle of sequential stabilization. Proc. Natl. Acad. Sci. U.S.A 2012, 109, 17442–17447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69).Sgouralis I; Whitmore M; Lapidus L; Comstock MJ; Pressé S Single molecule force spectroscopy at high data acquisition: A Bayesian nonparametric analysis. J. Chem. Phys 2018, 148, 123320. [DOI] [PubMed] [Google Scholar]
- 70).Sgouralis I; Pressé S ICON: An adaptation of infinite HMMs for time traces with drift. Biophys. J 2017, 112, 2117–2126. [DOI] [PMC free article] [PubMed] [Google Scholar]