Summary
Social interactions occur between multiple individuals, but what is the detailed relationship between the neural dynamics across their brains? To address this question across timescales and levels of neural activity, we used wireless electrophysiology to simultaneously record from pairs of bats engaged in a wide range of natural social interactions. We found that neural activity was remarkably correlated between their brains over timescales from seconds to hours. The correlation depended on a shared social environment and was most prominent in high frequency local field potentials (>30 Hz) and local spiking activity. Furthermore, the degree of neural correlation covaried with the extent of social interactions, and an increase in correlation preceded their initiation. These results show that inter-brain neural correlation is an inherent feature of natural social interactions, reveal the domain of neural activity where it is most prominent, and provide a foundation for studying its functional role in social behaviors.
Graphical Abstract
Introduction
Every day, we engage in social interactions. The ease with which we do so belies the neural complexity underlying them. Unlike non-social behaviors, social interactions depend on the coordinated actions of at least two individuals, and hence require coordination between their brains. Because social interactions between two individuals are often asymmetric, the neural activity in the different brains is not expected to be the same. Therefore, to get a full picture of the neural activity underlying a complete social experience, it is important to record from the brains of the interacting individuals simultaneously. This approach, termed “hyperscanning,” was first proposed by Montague et al. (2002), and has led to the development of a significant field in human neuroscience (see the reviews of Babiloni and Astolfi, 2014; Dumas et al., 2011; Hasson et al., 2012; Hasson and Frith, 2016; Koike et al., 2015; Konvalinka and Roepstorff, 2012; Liu et al., 2018; Scholkmann et al., 2013; Schoot et al., 2016). In particular, it was discovered that some aspects of neural dynamics were significantly coupled across the brains of socially interacting individuals (e.g. Dikker et al., 2017; King-Casas et al., 2005; Stephens et al., 2010; Tomlin et al., 2006), a surprising finding considering that different brains are of course not physically connected.
Yet, tremendous gaps remain in our understanding of the relationship between the neural activity of different brains during social interactions, in three broad areas. First, hyperscanning experiments have been nearly exclusively restricted to humans, and the extent to which functional coupling across brains extends to, or can be studied in, other species during social interactions remains largely unknown. Second, as a result of the lack of animal models, research has primarily been restricted to non-invasive methodologies, such as functional magnetic resonance imaging (fMRI), electroencephalography (EEG), and functional near-infrared spectroscopy (fNIRS). While valuable, these methods lack the spatial and temporal resolutions needed to resolve local field potentials (LFP; especially in the high frequency range) and the spiking activity of individual neurons and local populations (Sejnowski et al., 2014). This represents a major gap in the field, as these neural signals are known to be strongly linked to social behaviors (Anderson, 2016; Bergan et al., 2014; Chang et al., 2013; Chang et al., 2015; Eliades and Miller, 2017; Falkner et al., 2014; Falkner et al., 2016; Haroush and Williams, 2015; Hong et al., 2014; Li et al., 2017; Liang et al., 2018; Miller et al., 2015; Nummela et al., 2017; Pearson et al., 2014; Remedios et al., 2017; Tremblay et al., 2017; Zhou et al., 2017), and combined, represent a major landscape of neural activity that has been unexplored in the context of hyperscanning during social interactions. Lastly, previous studies typically focused on artificial tasks involving instructed interactions between subjects (e.g. Dikker et al., 2014; Dumas et al., 2010; Kawasaki et al., 2013; Leong et al., 2017; Spiegelhalder et al., 2014; Tognoli et al., 2007), where a single social behavior was repeated over many short trials (e.g. Cui et al., 2012; Dumas et al., 2010; Kawasaki et al., 2013; Tognoli et al., 2007; Yun et al., 2012). While enabling a high degree of experimental control, these conditions differ from natural social interactions, which are often inherently variable and extend over a wide range of timescales.
Here, we took an entirely different experimental and analytical approach that bridges all these major gaps at once. In detail, we utilized a tractable mammalian model system for social neuroscience—the Egyptian fruit bat (Rousettus aegyptiacus), an ideal system due to its high level of sociality (Herzig-Straschil and Robinson, 1978; Harten et al., 2018; Prat et al., 2015, 2016, 2017; Omer et al., 2018; Cvikel et al., 2015; Egert-Berg et al., 2018; Kwiecinski and Griffiths, 1999). Using wireless electrophysiology, we conducted simultaneous extracellular recording of neural activity from multiple animals engaged in natural social interactions. Importantly, this allowed us to study signals across a wide range of neural regimes, from LFP to the activity of single neurons and local neuronal populations. We focused on the frontal cortex (Figure S1A–B), a region heavily implicated in social cognition across a wide range of mammalian species from rodents to primates (Adolphs, 2001; Amodio and Frith, 2006; Cao et al., 2018; Chang et al., 2013; Eliades and Miller, 2017; Forbes and Grafman, 2010; Liang et al., 2018; Miller et al., 2015; Nummela et al., 2017; Pearson et al., 2014; Rudebeck et al., 2008; Tremblay et al., 2017; Zhou et al., 2017). We hypothesized that studying neural activity under natural social conditions would facilitate robust detection of the neural dynamics that have evolved to subserve social behaviors. Thus, we recorded neural activity during natural, face-to-face social interactions, by simply allowing bats to freely behave and socially interact with one another as they see fit. Each recording session lasted ~100 minutes, which we analyzed as a single “trial,” allowing the study of neural activity at a wide range of timescales. In doing so, we were able to study the social interactions between the individuals and the underlying neural dynamics, as they unfolded in parallel.
With this combined approach, we were poised to ask the following questions. First, what is the relationship between the simultaneously recorded neural activity in two animals that share a social environment and engaged in natural social interactions? And second, how does this relationship compare across different timescales and domains of neural activity?
Results
Simultaneous neural recording from pairs of bats during natural social interactions
To study natural social interactions, we let pairs of male Egyptian fruit bats freely behave in chambers (Figure 1A) placed inside an electromagnetically and acoustically shielded room. The experiments took place in the dark, because in the wild, colonies of this species generally reside in dark caves, where much of their social interactions takes place (Kwiecinski and Griffiths, 1999; Herzig-Straschil and Robinson, 1978). In a subset of experimental sessions, we introduced a third bat into the chamber in the middle of the session, in order to explore a larger variety of behaviors and interactions than those exhibited by two male bats alone. We captured the behavior of the bats using high-speed infrared video cameras (100 frames/second) and ultrasonic microphones (STAR Methods). The unconstrained behavior of the bats in our experiments was highly complex; thus, we aimed to distill them into a form that is amenable to quantitative analysis, but that still lends itself to intuitive understanding. Taking an ethological approach, we clearly defined a set of discrete categories of behaviors, which encompassed the behavioral repertoire observed in our experiments (STAR Methods). These included both social behaviors that involved interactions between bats (such as fighting) and non-social behaviors (such as self-grooming). Unbiased observers, who were blind to the goals of the experiment, annotated the videos of the experimental sessions frame-by-frame, and manually classified the behavior of each bat at each frame according to our definitions (STAR Methods).
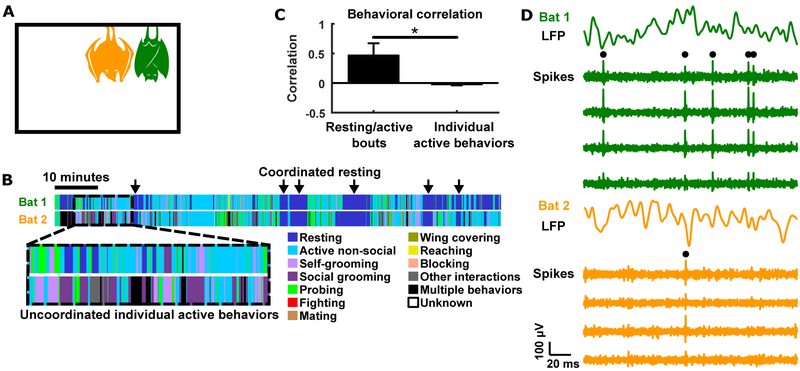
Figure 1. Experimental setup and behavior.
(A) Neural activity was wirelessly recorded simultaneously from pairs of bats that freely behaved and interacted in a chamber.
(B) Behavior of a pair of bats during one example session, as manually annotated frame-by-frame from the video recording. Resting tends to be coordinated between the bats (arrows), while individual active behaviors tend to be uncoordinated (dashed box).
(C) Quantification of behavioral correlation across bats (mean ± STD across sessions; see STAR Methods). Bouts of resting and active behaviors were correlated between bats, whereas individual active behaviors were not. *, p<0.05, Wilcoxon rank sum test.
(D) Example voltages traces intracranially recorded simultaneously on two tetrodes, each from a different bat. For each bat, the top trace is LFP, and the bottom traces show spiking activity from the four channels of a tetrode. Black dots highlight spikes for isolated single units.
We found that the bats engaged in a rich variety of behaviors in succession, including both social and non-social behaviors, rather than repeating the same behavior over and over (Figure 1B). If we examine the times when the bats were resting (the “resting” behavior was defined as hanging still), compared to the times when the bats engaged in various active behaviors, one prominent feature emerges: the bats were coordinated with each other, such that they often tended to rest at the same times, and be active at the same times. On the other hand, zooming in to periods when a pair of bats were both active, we observed that the bats did not generally engage in the same active behaviors at the same times (Figure 1B). A quantitative analysis, where behavioral time courses were represented as binary vectors, confirmed these observations (Figure 1C; STAR Methods).
During the sessions, we recorded neural activity simultaneously from the pairs of bats (no neural recording was done on the different “third” bats that were introduced on some of the sessions). We used a wireless electrophysiology system, which is miniaturized and light-weight enough to enable neural recording from freely flying bats (Yartsev and Ulanovsky, 2013; Finkelstein et al., 2014), and in the present study, allowed the bats to engage in unrestrained natural behaviors during recording (STAR Methods). This enabled us to study the neural activity of two naturally interacting animals simultaneously, at multiple levels that included LFP, local spiking activity, and the firing of single neurons (Figure 1D).
Dimensionality reduction of LFP
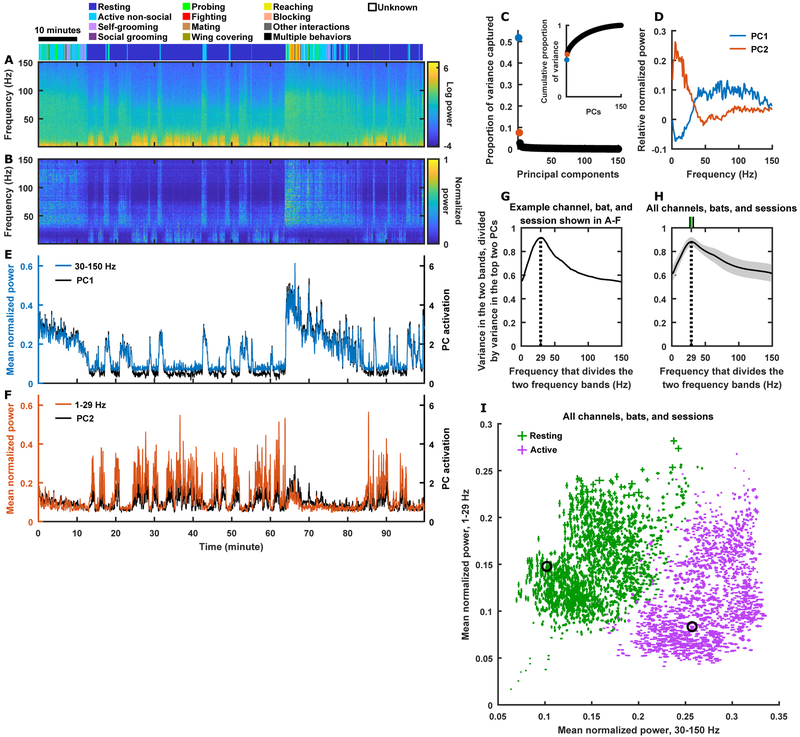
Frequently, to analyze LFP, one focuses on various frequency bands established in the literature (e.g. theta, gamma, etc.; Buzsáki and Draguhn, 2004). However, for the bat frontal cortex, there is no existing literature on the relevance of different frequency bands during social behaviors. Therefore, we instead took an unbiased, data-driven approach to identify the relevant signals in our LFP recording. Starting with a spectrogram of the LFP (Figure 2A), we separately peak-normalized the power at each frequency (Figure 2B), so that the different frequencies could be analyzed and visualized on equal footing. On typical normalized spectrograms, principal component analysis (PCA) consistently identified two dimensions that stood out from the noise (Figure 2C), one corresponding to the high frequencies being coactive and the other to the low frequencies being coactive (Figure 2D). This observation motivated us to reduce the dimensionality of the normalized spectrogram to two flat frequency bands corresponding to the high and low frequencies, which showed similar dynamics (Figure 2E–F) as the respective principal components (PCs). Their exact frequency ranges were defined to be 1–29 Hz and 30–150 Hz, because across all recording channels, bats, and sessions, these ranges robustly captured close to the maximal amount of variance that could be captured by two dimensions (Figure 2G–H). Consistent with previous literature (Rasch et al., 2008), we found that the 30–150 Hz band was linked to aggregate local spiking activity (Figure S1C–H).
Figure 2. Dimensionality reduction of LFP.
(A) Spectrogram of LFP from one recording channel from one bat on an example session. The bat’s behavior is indicated on top and aligned in time with the spectrogram.
(B) Normalized version of the spectrogram from (A), where power at each frequency was divided by the peak power at that frequency.
(C-D) PCA of the normalized spectrogram from (B), with frequencies as variables and time points as observations. (C) Proportion of variance captured by the PCs. Inset shows cumulative proportion of variance. (D) PC1 and PC2 approximately correspond to coordinated activation of high frequencies and low frequencies, respectively.
(E-F) Mean normalized power in the 30–150 Hz (E) and 1–29 Hz (F) bands as a function of time, compared to activation of the corresponding PCs.
(G-H) The combined variance of two frequency bands, divided by the combined variance of the top two PCs (which is the maximum amount of variance that can be captured by two dimensions), plotted as a function of the dividing frequency that defines the frequency ranges of the two bands (e.g. 29 Hz divides the 1–29 Hz band and the 30–150 Hz band).
(G) The optimal dividing frequency is 29 Hz for the example data from (A)-(F).
(H) Result averaged across all data. Shading indicates STD. The green tick on top indicates 29 Hz as the median optimal dividing frequency across all data, and the two black ticks indicate the first and third quartiles (27 Hz and 32 Hz). See STAR Methods.
(I) Mean normalized power in the two frequency bands, averaged across resting (green) and across active (purple) periods. Two points (one for resting and one for active) are plotted for each channel, bat, and session; error bars indicate SEM. Black circles indicate the example data from (A)-(F).
Modulation of neural activity in the bat frontal cortex during natural behaviors in a social context
Interestingly, even though the two frequency bands were not defined based on behavior, their power modulation nonetheless correlated tightly with behavior: the low frequency band had more power during resting than during active behaviors, whereas the high frequency band had more power during active behaviors than during resting (Figure 2E, F, I; Figure S2). Similarly, local spiking activity and single unit activity were overall higher during active behaviors than during resting (Figure S2). These results are consistent with the known effects of behavioral states on LFP power and spiking activity, which are readily observed in widespread brain regions (Gervasoni et al., 2004; McGinley et al., 2015).
In addition to examining the modulation of neural activity by the general states of resting and being active, we further characterized how neural activity in the brain of each bat was related to the specific active behaviors of that bat (Figure S2). We found that individual LFP channels and units showed a mosaic of behavioral modulation of neural activity (Figure S2A–L), and that all behaviors could be reliably decoded from neural activity with high accuracy (Figure S2M–P), consistent with the extensive literature showing the neural encoding of social signals in frontal cortex across species (Chang et al., 2013; Eliades and Miller, 2017; Liang et al., 2018; Miller et al., 2015; Nummela et al., 2017; Pearson et al., 2014; Tremblay et al., 2017; Zhou et al., 2017).
Yet, a social experience is more than the behaviors of the involved individuals considered in isolation. Thus, having considered how neural activity is related to behavior for each bat, we next turned to the central question of this study and asked how neural activity is related between the brains of the interacting bats during a social experience.
Highly correlated neural activity across the brains of bats sharing a social environment
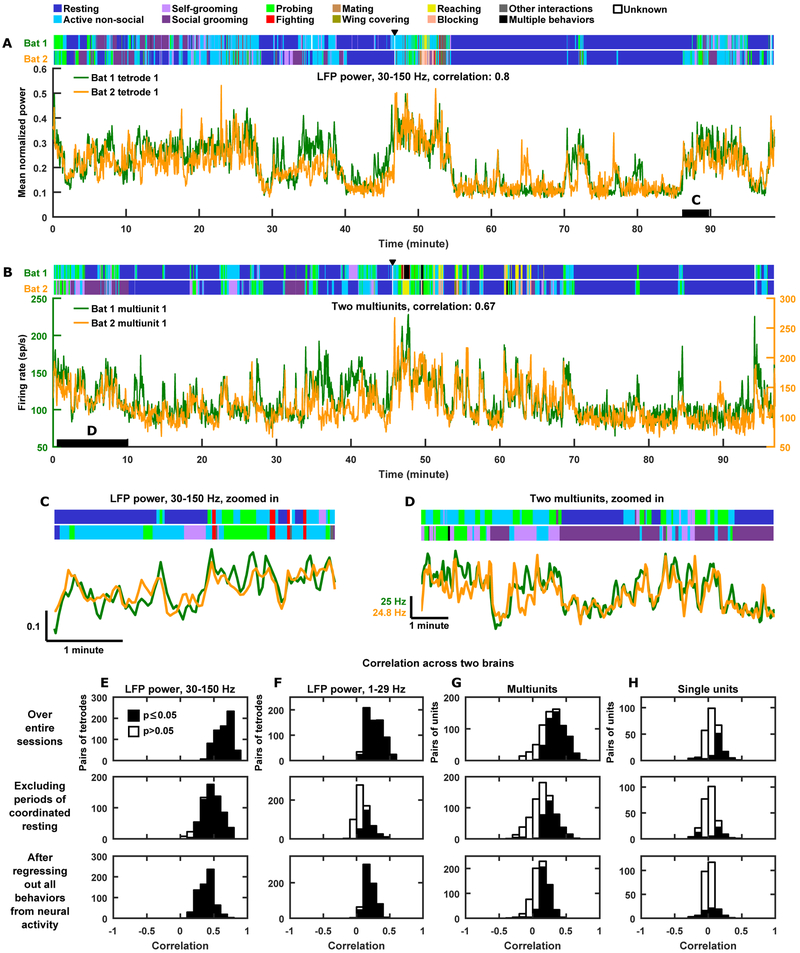
It was evident that the neural activity in the brain of a single bat was highly variable during the extended social experience of a recording session (e.g. see Figure 2E–F), as expected given that the bats engaged in completely unrestrained, highly variable, natural behaviors. Yet, we wondered whether the neural variability in the different brains might be related, given the social interactions between the bats. Hence, having examined the neural activity in single brains, we next turned to examine the relationship between neural activity from different brains. Figure 3A–B show neural activity at different levels (the high frequency LFP band and local spiking activity) simultaneously recorded from two brains over example experimental sessions lasting ~100 minutes, which we analyzed as single “trials”. It was immediately evident that there were very high levels of correlation (throughout this manuscript, “correlation” refers to the Pearson correlation coefficient, unless otherwise indicated) between neural activity in the two separate brains. In the case of the examples shown in Figure 3, the correlation was 0.8 for LFP power in the high frequency (30–150 Hz) band (Figure 3A) and 0.67 for local spiking activity (Figure 3B)—such high correlations are striking, especially considering they were calculated over 100-minutes-long single trials, across the brains of separate animals. Crucially, these are not cherry-picked examples—rather, they are representative of a highly reproducible phenomenon that was observed across experimental sessions, pairs of bats, recording channels, and levels of neural signals including both frequency bands of the LFP, local spiking activity, and single units (Figure 3E–H, top panels; Figure S3; see STAR Methods for estimated false discovery rates [FDR; Benjamini and Hochberg, 1995]). Indeed, on every single pair of tetrodes in every single experimental session, LFP power in the 30–150 Hz band was significantly correlated between the different brains (Figure 3E, top panel). The same result held true for LFP power in the 1–29 Hz band on nearly all pairs of tetrodes (98% of all pairs; Figure 3F top panel) and for the vast majority of pairs of multiunit sites (75% of all pairs; Figure 3G top panel). We note that, although correlations between single units from different brains were lower (Figure 3H top panel; 35% of all pairs were significantly correlated), they were nearly as high as the correlations between single units within the same brains (Figure S3C).
Figure 3. Highly correlated neural activity across brains.
(A) Mean normalized LFP power in the 30–150 Hz band during an example session, simultaneously recorded from two bats. Annotated behaviors are shown above. Black triangle indicates the time at which a third bat was introduced (neural activity was not recorded from it).
(B) Same as (A), but for the activity of two multiunit sites simultaneously recorded from two bats.
(C-D) The time periods spanned by the black bars in (A) and (B) are magnified in (C) and (D), respectively. Vertical scale bar in (C) indicates mean normalized power. Note the high levels of correlations, even when the behaviors of the bats were not correlated.
(E-H) Histograms of correlations across brains pooled across all sessions and all pairs of bats. Top row, correlations over entire sessions. Middle row, correlations after removing periods of coordinated resting. Bottom row, correlations after regressing out the behaviors of both bats from the neural activity of each bat (i.e. partial correlations). (E-F) LFP power in the high (E) and low (F) frequency bands. (G) Multiunit sites. (H) Single units. Statistical significance of correlations was assessed against null distributions of correlations between surrogate data whose autocorrelations were identical to those of the actual neural data (STAR Methods).
See also Figure S3.
Is this robust form of correlation merely a reflection of the behavioral correlation between the bats? As we have shown above, the neural activity of each bat was correlated with the resting/active state of that bat (Figure 2I and Figure S2), and that the resting and active bouts of the bats were themselves correlated (Figure 1C). Hence, we of course expected to find some level of co-fluctuations of neural activity in the two brains that mirrors the coordinated resting and active bouts of the bats; indeed, we observed such co-fluctuations (Figure 3A–B). On the other hand, we also showed that within active bouts, the individual active behaviors of the bats were not correlated (Figure 1C). Hence, we expected that within active bouts, neural activity would be uncorrelated across the brains as well. To our surprise, this was not what we found. Instead, neural activity remained highly correlated (Figure 3C–D). Indeed, even if we removed from each session all time periods when both bats were resting, so that co-fluctuations of neural activity reflecting coordinated resting and active bouts no longer contributed to the correlation, neural activity remained highly correlated across the different brains (Figure 3E–H middle panels). Similar results were obtained when we removed all time periods when at least one bat was resting, and calculated correlations for only the remaining active bouts (Figure S3H–K).
Furthermore, as we have shown above, neural activity was also modulated by specific active behaviors of the bats (Figure S2). Although overall, individual active behaviors were uncorrelated between bats (Figure 1C), one might still expect contributions to correlations across brains due to the bats occasionally engaging in the same active behaviors at the same times. Thus, we extended our analysis above to remove not only time periods of coordinated resting, but in addition, all time periods when the bats engaged in the same behaviors (Figure S3H–K). Again, high levels of correlation between the different brains persisted. To go one step further, we regressed out the behaviors of both bats from the neural activity of each bat and recalculated the neural correlation across brains (Figure 3E–H, bottom panels). Once more, high levels of correlation remained. These results together suggest that sharing the same social environment contributes to the correlation of neural activity across the brains of the animals, even when they are ostensibly engaged in different behaviors.
Shared sensory inputs and behavioral patterns cannot explain correlations across brains
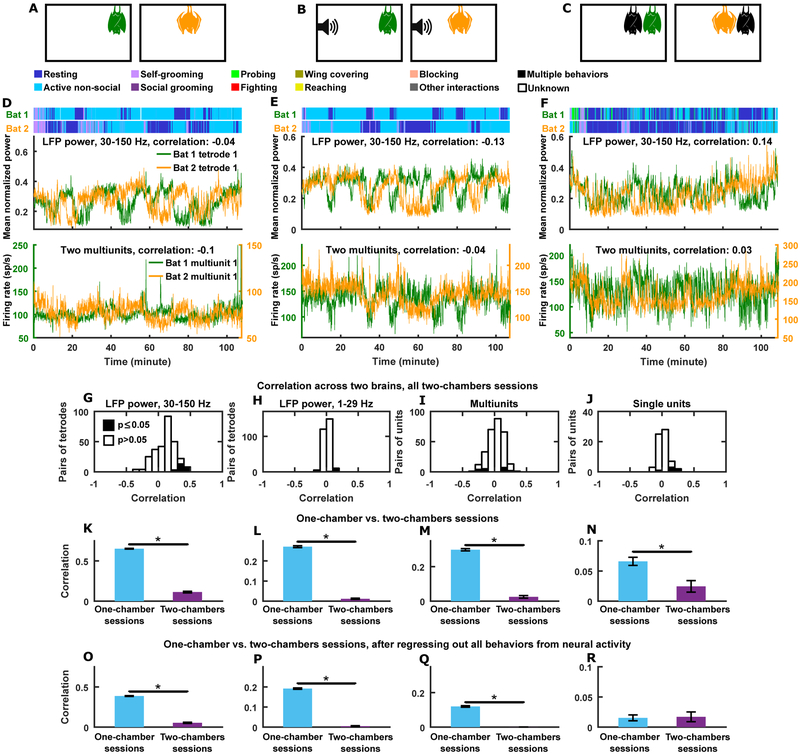
During the experiment described above, the bats shared a sensory environment, which might contribute to the correlation of their neural activity, independent of any interactions between them. Indeed, previous studies have reported coordinated neural activity across the brains of humans exposed to similar sensory inputs (Hasson et al., 2004; Nummenmaa et al., 2012; Schmälzle et al., 2015; Nguyen et al., 2019). Furthermore, as we showed above, the resting and active bouts of the bats were correlated (Figure 1C), which, while not fully accounting for the correlation of neural activity across brains (Figure 3E–H and Figure S3H–K), did contribute to it. It is possible that such behavioral correlations were not the result of social coordination, but rather coincidences resulting from each bat independently behaving according to similar stereotyped behavioral patterns. Thus, we next asked: to what extent do these non-social factors contribute to neural correlation? To answer this question, we performed an additional series of experiments. We recorded neural activity simultaneously from two bats placed in two separate chambers inside the same experimental room. The separate chambers were identical to each other as well as to the chamber used for the experiment described above. These two-chambers sessions and the one-chamber sessions described above used the same pairs of animals and both had durations of ~100 minutes, thus allowing direct comparison. The two-chambers experiments included three different conditions (Figure 4A–C), which we now proceed to describe.
Figure 4. Little to no correlation between neural activity across brains in two-chambers sessions.
(A-C) Experimental setup. (A) Simultaneous neural recording from two bats freely behaving in two separate, identical chambers. (B) Same as (A), but with bat social calls (identical for the two chambers) played throughout each session. (C) Same as (A), but each neural recording bat (green and orange) interacting with a different bat (black) in their respective chambers.
(D) Neural activity simultaneously recorded from two brains on an example session under the conditions illustrated in (A), plotted along with the behaviors of the two bats during the session. Top, mean normalized LFP power in the 30–150 Hz band; bottom, multiunit activity.
(E) Same as (D), but for an example session under the conditions illustrated in (B).
(F) Same as (D), but for an example session under the conditions illustrated in (C).
(G-J) Histograms of correlations across brains pooled across all two-chambers sessions and all pairs of bats. (G-H) LFP power in the high (G) and low (H) frequency bands. (I) Multiunit sites. (J) Single units. Note the near complete absence of significant correlations across brains in the two-chambers session. Statistical significance assessed in the same way as for Figure 3E–H.
(K-N) Mean correlation (± SEM) for one-chamber sessions (blue) and for two-chambers sessions (purple), for the LFP high frequency (K) and low frequency (L) band, multiunit sites (M), and single units (N).
(O-R) Same as (K-N), but calculated after regressing out the behaviors of both bats from the neural activity of each bat.
*, p<0.05, Wilcoxon rank sum test.
See also Figure S4.
In one type of two-chambers sessions, we let the two bats freely behave in their respective chambers (which have similar sensory environments) according to any behavioral patterns they had (Figure 4A). Figure 4D shows simultaneously recorded neural activity on such an example session, showing no correlation across brains. In a second type of two-chambers sessions, we additionally provided strong shared sensory inputs to the two bats, in the form of identical auditory stimuli played to the two bats throughout the session (Figure 4B). The stimuli played were social communication calls of this species. These are used by the bats exclusively during social interactions (Prat et al., 2016), contain extensive social information (Prat et al., 2016), and can induce stable, long-term changes to bat vocal dialects through their playback (Prat et al., 2017). Hence, these stimuli are ethologically relevant and highly salient for this species of bats. This experiment is analogous to previous studies that found correlated neural activity across the brains of humans watching the same movie (Hasson et al., 2004; Nummenmaa et al., 2012; Nguyen et al., 2019) or listening to the same speech (Schmälzle et al., 2015), leading us to expect that our highly salient sensory stimuli would similarly drive correlated neural activity across the brains of the bats. Yet this was far from being the case: under this condition, neural activity from different bats showed no correlation (Figure 4E). Finally, in a third type of two-chambers sessions, we mimicked the conditions of our one-chamber sessions, by simultaneously recording from two bats that each interacted with a different bat in their respective chambers (Figure 4C). Once again, we observed weak to no correlation across the brains (Figure 4F).
Overall, across all three types of two-chambers sessions, and across all levels of neural signals (both frequency bands of the LFP, local spiking activity, and single units), there was little to no correlation across brains (Figure 4G–J; Figure S4G–J; see STAR Methods for FDR), in stark contrast to the one-chamber sessions (Figure 4K–N). In fact, many of the two-chambers sessions happened immediately before or after a one-chamber session, without movement of the recording tetrodes, allowing correlations for the same neural signals at the same recording sites to be directly compared between the sessions. Such direct comparisons again showed that, neural correlations across brains fell apart when bats no longer shared a social environment, even as they continued to share similar sensory environments and behavioral contexts (Figure S4D–F).
It is important to note that resting and active bouts only showed weak correlation between bats in the two-chambers sessions (Figure S4C). Thus, the behavioral correlations seen in one-chamber sessions were the results of social coordination between the bats. Since behavioral correlation is not the only factor that contributes to neural correlation (Figure 3E–H; Figure S3H–K), we hypothesized that differences in neural correlation between the one-chamber and two-chambers sessions did not merely reflect behavior differences between the two types of sessions. To test this, we took two approaches. First, we regressed out the behaviors of both bats from the neural activity of each bat, then compared neural correlations on one-chamber and two-chambers sessions (Figure 4O–R). With the exception of single units, all neural signals showed significantly higher correlations on one-chamber sessions, indicating that differences in neural correlation between the two types of sessions indeed go beyond their behavioral differences. Second, we sought to compare inter-brain correlations between behaviorally matched time periods from one-chamber sessions and two-chambers sessions. For example, Figure 5A shows time periods from one-chamber and two-chambers sessions with matched behaviors: neural activity was much more correlated across brains in the example from the one-chamber session. Motivated by such observations, we next comprehensively compare behaviorally matched time periods.
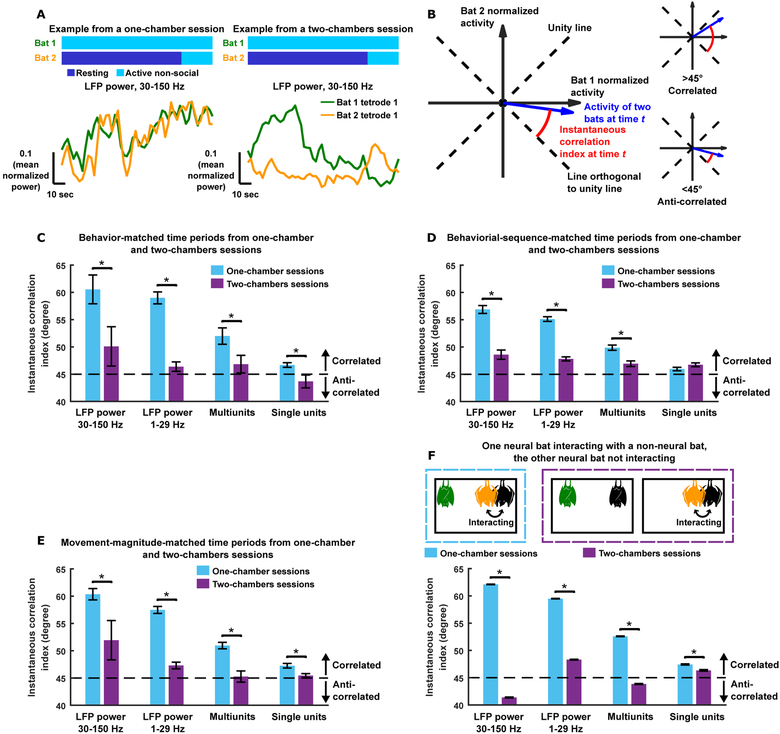
Figure 5. Correlation across brains is a signature that animals share a social environment.
(A) Mean normalized LFP power in the high frequency band simultaneously recorded from two bats, during two time periods with matched behaviors, one from a one-chamber session and the other from a two-chambers session. Note that neural activity was much more correlated on the one-chamber session, despite the matched behaviors.
(B) Schematic illustrating the instantaneous correlation index. Given two N-dimensional vectors X and Y representing neural activity at N time points from two bats, we subtract from each vector its mean, and then normalize each to unit length, resulting in two vectors of normalized activity x and y. At a given time point t, the normalized activity of the two bats, (xt, yt), is a vector in 2D space (blue vector). The instantaneous correlation index is defined as the smaller of the two angles between the blue vector (xt, yt) and the line orthogonal to the unity line. The instantaneous correlation index ranges from 0 degree to 90 degrees. If neural activity is correlated at a given time, i.e. activity is high in both bats or low in both bats, the blue vector is close to the unity line and the instantaneous correlation index is close to 90 degrees. If neural activity is anti-correlated at a given time, i.e. activity is high in one bat and low in the other bat, the blue vector is close to the line orthogonal to the unity line and the instantaneous correlation index is close to 0 degree. An instantaneous correlation index of 45 degrees indicates no correlation. See STAR Methods. (C-E) Instantaneous correlation index during behaviorally matched (C), behavioral-sequence-matched (D), and movement-magnitude-matched (E) time periods on one-chamber and two-chambers sessions (mean ± SEM; STAR Methods). Note that the matching in (C)-(D) included both interaction and non-interaction behaviors. Movement magnitude was estimated through deep-neural-network-based video analysis using DeepLabCut (Mathis et al., 2018; Figure S5). (F) Instantaneous correlation index (mean ± SEM across time points) under the conditions illustrated in the dotted boxes (see Results for details). Note that while the schematic only illustrates the case where the “orange bat” was the one interacting, for the actual analysis, any neural bat could be the one interacting.
Note that despite the matched behaviors or states of social interactions, in almost all cases the instantaneous correlation index was significantly higher when bats shared the same social environment, and when they did not share a social environment, their neural activity showed weak to no correlations (i.e. the purple bars are close to 45 degrees). *, p<0.05, one-tailed Wilcoxon signed rank test (C)-(E) or one-tailed Wilcoxon rank sum test (F).
See also Figures S5 and S7.
Specifically, at any given moment in time, a pair of bats display a pair of behaviors (e.g. “resting” by bat 1 and “self-grooming” by bat 2). For each possible pair of behaviors, we found all the time points when the bats showed this pair of behaviors in either the one-chamber sessions or the two-chambers sessions. This allowed us to directly compare the degree of neural correlation between those time points from one-chamber sessions and those from two-chambers sessions, which were matched with regard to the behaviors of the bats and differed only in whether the bats shared a social environment or not. For this analysis, we introduced a simple measure of instantaneous neural correlation (defined in Figure 5B and STAR Methods; see Figure S7A–I for results using Pearson correlation coefficient, which are similar) that allowed us to examine neural correlation at a fine time resolution (as opposed to correlation over an entire session). If neural correlation is simply dictated by the overt behaviors of the bats, one would expect the correlations to be the same during behaviorally matched time periods. Instead, we found that neural activity was more correlated across brains on one-chamber sessions than on two-chambers sessions even when the behaviors were matched (Figure 5C). Next, we extended this analysis to match not only behaviors at a single time point, but sequences of two behavioral episodes (longer sequences that were matched between the two types of sessions were rare; STAR Methods); again, neural activity was more correlated on one-chamber sessions (Figure 5D). Furthermore, using a video tracking algorithm based on deep neural networks (DeepLabCut; Mathis et al., 2018), we tracked the neural recording device on each bat’s head in the recorded videos, which provided an estimate of the moment-to-moment magnitude of movement by the bats, a surrogate for their behavioral activity levels (Figure S5). This in turn allowed us to compare time periods from one-chamber and two-chambers sessions that were matched for the movement magnitude of each bat. This behavioral matching approach, which is independent of human behavioral annotations, again showed that neural activity was more correlated on one-chamber sessions (Figure 5E). Combined, the above results suggest that the sharing of a social environment is strongly linked to neural correlations across brains. To examine this notion further, we next turned to consider the social experience of more than two individuals, where all share the same social environment, but not all are necessarily involved in each act of social interaction.
Our everyday experience tells us that for humans, sharing a social environment entails a group of people being engaged with one another, without necessarily requiring that all individuals in the group simultaneously interact with one another. For example, three friends having dinner together share a social environment and are all part of the same social experience, even if only two of them actively converse with one another at a particular moment in time. While bats are of course not humans and engage in group interactions differently, this intuition led us to further probe the importance of social environments, rather than active social interactions, on neural correlation. We did so by examining situations when only two out of a group of three bats were engaged in active interactions with each other. Such situations naturally occurred in the one-chamber sessions that included a third bat (“non-neural bat”) in addition to the two bats from which we recorded neural activity (“neural bats”). Specifically, in the three-bat one-chamber sessions, there were time periods when one neural bat was interacting with a non-neural bat, while the other neural bat was not actively engaged in the social interaction (analogous to the example above, where two individuals converse with each other while a third is not actively participating in the conversation). During these time periods, the two neural bats were often engaged in different behaviors (mean behavioral correlation for resting/active bouts: −0.006; for individual active behaviors: −0.01) and received different sensory inputs (e.g., one neural bat resting while the other neural bat fighting with the non-neural bat). Surprisingly, we found that neural activity was still highly correlated across their brains (Figure 5F). Furthermore, a particularly interesting comparison can be made between this condition and the analogous behavioral situation occurring in two-chambers sessions, where one of the neural bats was interacting with a non-neural bat in one chamber, and the second neural bat in the other chamber was not engaged in interactions. Even under these conditions where the states of social interactions were matched, we found that correlations were much higher in the one-chamber sessions compared to the two-chambers sessions (Figure 5F). Together, these results highlight the importance of a shared social environment for neural correlations across brains.
Neural correlation across brains at a wide range of timescales, above and beyond behavioral correlation
One link between social interactions and neural correlation, which we addressed above, is that the social coordination of resting and active bouts between bats is reflected in the co-fluctuation of their neural activity. But what happens to the neural activity when bats in the same chamber decide not to coordinate their resting and active bouts? Figure 6A shows such an example, where one bat was active, and the other was resting—neural activity was still very correlated across their brains at timescales that do not reflect the uncoordinated resting and active behaviors of the bats. This is another example of correlated neural activity across the brains of bats engaging in different overt behaviors but still sharing the same social environment. This example, as well as the fact that neural correlations persist even after removing coordinated resting or regressing out behaviors from neural activity (Figure 3E–H), suggests that the phenomenon of correlation between brains extended across multiple timescales, and did not merely reflect coordinated behaviors at those timescales. We thus asked the following questions: across what range of timescales are different brains correlated, and how do neural correlations compare to behavioral correlation at those timescales? We now address these points quantitatively, focusing on LFP power in the 30–150 Hz band, the signal showing the most robust link to behavior and exhibiting the strongest correlation across brains (Figure 3E–H; Figure 4K–N; Figure S2).
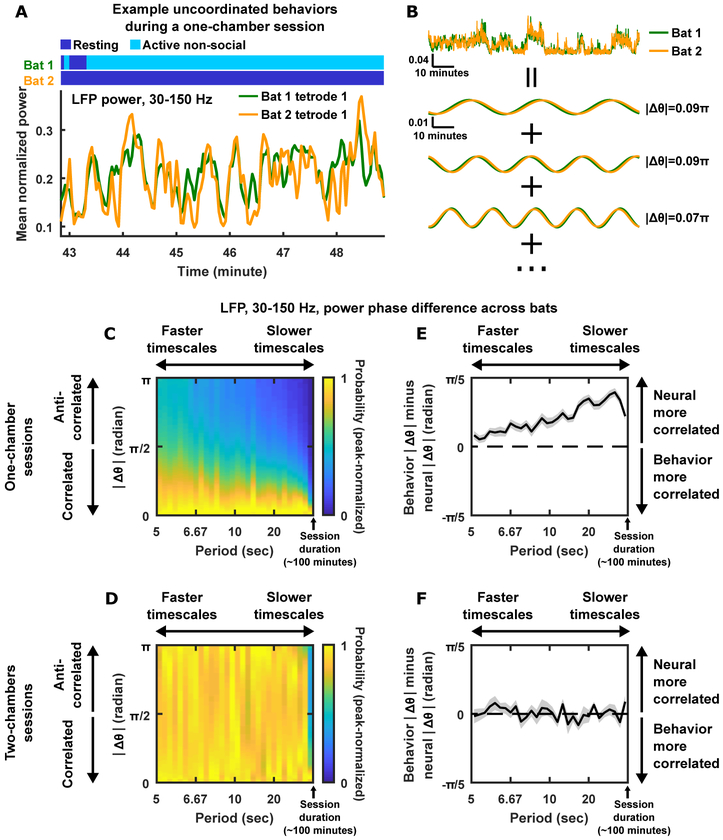
Figure 6. Neural correlation across brains over a wide range of timescales, above and beyond behavioral correlation.
(A) Mean normalized LFP power in the high frequency band simultaneously recorded from two bats when one of them was resting and the other was mostly active. Note the high degree of correlation between the two bats despite their very different behaviors.
(B) Analyzing phase difference. Example traces of mean normalized LFP power from two bats (top; scale bars denote mean normalized power and time) are decomposed into sums of sine waves at different timescales (bottom; scale bars are shared between the three pairs of sine waves). |Δθ|, the absolute value of the phase difference between a pair of sine waves, is indicated. The more correlated the LFP power traces are at a given timescale, the smaller |Δθ| is at that timescale.
(C) Distributions of |Δθ| as a function of timescale for one-chamber sessions (STAR Methods). The x-axis is the period of the sine waves into which the neural signals were decomposed (as shown in B); smaller periods correspond to faster timescales, with the maximum period being the session duration of ~100 minutes. Each vertical “slice” of the plot is a distribution of |Δθ| at a given timescale, computed over all pairs of channels, all pairs of bats, and all one-chamber sessions. Each distribution (i.e. each vertical slice) was individually peak-normalized for visualization, where the peak-normalized probability is indicated by color. Note that across the entire range of timescales, the distributions are peaked near a |Δθ| of 0, indicating that correlation across brains extended over the entire range of timescales, from seconds to hours.
(D) Same as (C) but for two-chambers sessions. Note that at most timescales, |Δθ| was randomly distributed, indicating the absence of correlation on two-chambers sessions.
(E-F) |Δθ| was calculated for binary time series of resting/active behaviors and compared with neural |Δθ| (STAR Methods). (E) Behavior |Δθ| minus neural |Δθ|, as a function of timescales, averaged across all one-chamber sessions. Shading indicates SEM. Note that the curve is positive throughout the entire range of timescales, indicating that neural correlation is above and beyond the behavioral correlation of resting/active bouts at these timescales. (F) Same as (E) but for two-chambers sessions. Note that for the two-chambers sessions, neural correlation was comparable to the behavioral correlation of resting/active bouts, suggesting that the neural correlations were largely a reflection of the behavioral correlation of resting/active bouts.
See also Figure S6.
Using the Fourier transform, a neural signal over time can be decomposed into a sum of sine waves at different frequencies that correspond to different timescales. Thus, at a given timescale, two signals from different brains are two sine waves, and the phase difference between them indicates how well they are aligned in time: the closer the phase difference is to zero, the more correlated the two signals are at that timescale (Figure 6B; STAR Methods). Calculations of the phase differences show that in one-chamber sessions, LFP power in the high frequency band was correlated across brains at timescales that extended from seconds to hours (Figure 6C). In contrast, the two-chambers sessions showed no correlation on most timescales (Figure 6D), consistent with our observations above.
Next, we sought to explicitly compare neural correlation with behavioral correlation at different timescales. To do so, for a given session, we represented the resting/active states of a pair of bats over time as a pair of binary vectors, and calculated their phase difference as a function of timescale, as above; these behavior phase differences can then be compared with the neural phase differences on the same session (STAR Methods). This analysis shows that, in one-chamber sessions, neural activity was more correlated across brains than behavior was correlated across bats, implying that neural correlation is not simply a reflection of behavioral correlation (Figure 6E). Moreover, the correlation of neural activity exceeded that of behavior across multiple timescales (note that the curve in Figure 6E is positive throughout the entire range of timescales). On the other hand, we found that in the two-chambers sessions, neural activity was not more correlated than behavior (Figure 6F). These results are consistent with our observation above, that comparing behavior-matched time periods from one-chamber and two-chambers sessions, neural activity was more correlated in one-chamber sessions (Figure 5C–E).
The same timescale analyses applied to LFP power in the low frequency band, local spiking activity, and single unit activity showed that, on one-chamber sessions, the correlations for these signals were weaker and extended over narrower ranges of timescales, compared to LFP power in the high frequency band (Figure S6). Similarly, on one-chamber sessions, neural correlation for these signals were more comparable to behavioral correlation, and only exceeded behavioral correlation over restricted ranges of timescales (Figure S6). On two-chambers sessions, at all levels of neural signals, neural correlation was weak or absent at all timescales and did not exceed behavioral correlation (Figure S6). Combined, these results demonstrate that the correlation of neural activity across brains extends over a broad range of timescales, from seconds to hours, and this phenomenon is strongest in the high frequency band of the LFP.
Relationship between neural correlation across brains and social interactions
What might be the utility of the robust correlations we observed between the brains of bats sharing a social environment? To probe this, we next turned to examine the relationship between neural correlation and social interactions. For this, we focus on the LFP high frequency band and local spiking activity, because the LFP low frequency band was inactive during most interactions, and the activity of single units were noisier than the other signals.
In our experiment, bats naturally engaged in a wide variety of behaviors (e.g. see Figure 1B), some of which involve interactions between bats (e.g. fighting), while others did not (e.g. self-grooming). Among one-chamber sessions, there was a large variability across sessions in the amount of interactions between the bats. Thus, we leveraged this natural variability to examine whether the amount of interactions co-varied with the degree of neural correlation. We found that on sessions where the bats interacted with each other more, the neural correlation across their brains was higher, and on sessions where the bats interacted less, the neural correlations were lower (Figure 7A–B). Moreover, using the measure of instantaneous correlation introduced above (Figure 5B), we examined correlation specifically during periods of interactions and periods without interaction. Consistent with our results above showing the effect of shared social environments on neural correlations, we found correlated neural activity across brains even when the bats were not explicitly interacting but were still part of the same social environment (Figure 7C–D). On the other hand, when the bats were explicitly interacting with each other, neural correlations were significantly higher (Figure 7C–D). Thus, neural correlation across brains is not an all-or-none phenomenon that exclusively reflects whether animals share a social environment; rather, it varies in degrees, reflecting the state of social interactions.
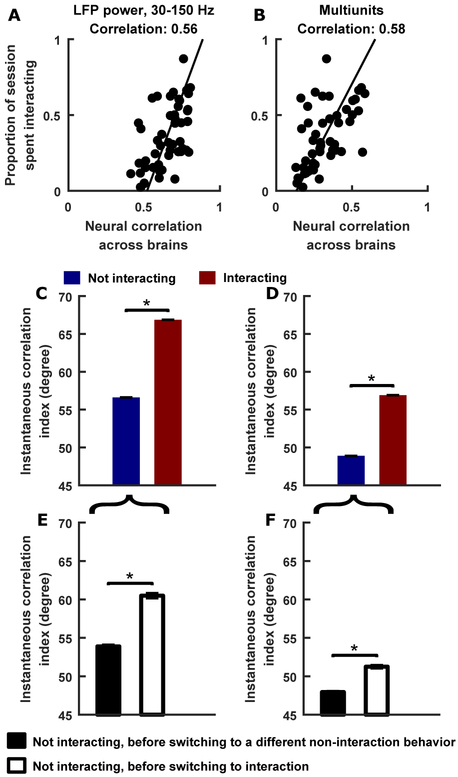
Figure 7. Relationship between neural correlation and social interactions.
(A-B) The proportion of time bats spent interacting with each other in each one-chamber session, as a function of the correlation across brains in that session, averaged across all pairs of tetrodes, for LFP power in the 30–150 Hz band (A), and for multiunit sites (B). Each point is a single session. Time spent interacting is defined as the amount of time when the behavior of at least one of the neural bats involved interaction with the other neural bat. Lines are total least squares regression lines.
(C-D) Instantaneous correlation index during non-interaction behaviors (blue bars) and during interactions (red bars), for LFP power in the 30–150 Hz band (C), and for multiunit sites (D), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions (mean ± SEM). Note that the blue bars are above 45 degrees, meaning neural activity was correlated across brains when the bats shared the same social environment without explicitly interacting with each other. Note also that the red bars are higher than the blue bars, indicating that correlations were higher when the bats were interacting compared to when they were not. (E-F) Instantaneous correlation index during non-interaction behaviors that preceded other non-interaction behaviors, and during non-interaction behaviors that preceded interactions, for LFP power in the 30–150 Hz band (E), and for multiunit sites (F), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions (mean ± SEM). Note that correlations were higher before transitions to social interactions, meaning that the initiation of interactions were preceded by an increase in correlation. *, p<0.05, one-tailed Wilcoxon rank sum test.
See also Figure S7.
Lastly, leveraging the detailed behavioral annotation of the bats’ social interactions in our experiment, we further asked whether the degree of correlation bears on social decision-making in the natural context. The natural behavior of bats in the one-chamber experiment can be viewed as a series of decisions. Over the course of any given episode of behavior, the bats decide as to what to do next. The space of behavioral decisions is large, but we can collapse it into a choice between interaction and non-interaction, and examine whether there is a relationship between this choice to interact and the degree of neural correlation. To do this, each behavioral episode that did not involve interactions was classified into one of two categories: episodes that were followed by a different behavioral episode that also didn’t involve interactions, and episodes that were followed by a social interaction. Comparing the instantaneous neural correlation between these two categories showed that neural correlations were significantly higher before bats transitioned from non-interaction to interaction (Figure 7E–F). In other words, an increase in neural correlation across brains preceded the initiation of social interactions, suggesting that the correlation reflects processes that facilitate social interactions. On the other hand, a decrease in neural correlation between the brains preceded the termination of social interactions (Figure S7J–K). Combined, these results show that correlation across brains is not a binary function of whether animals share a social environment or not. Instead, the correlation varies in degrees, reflecting both the current and future states of social interactions, in addition to the social environments where the interactions take place.
Discussion
The strongest and most robust inter-brain correlation we observed was for LFP power in the 30–150 Hz band, followed by multiunit spiking activity and LFP power in the 1–29 Hz band, with the weakest correlation observed for single unit activity. These signals have not been explored in previous human hyperscanning studies, due to the restrictive challenges of recording LFP and action potentials intracranially in humans, especially in multiple humans simultaneously. However, the fMRI blood oxygen level-dependent (BOLD) signal correlates with LFP power in the gamma band (Magri et al., 2012), which is contained in the 30–150 Hz band we identified here. Thus, our result highlighting the prominence of the 30–150 Hz LFP band in the phenomenon of inter-brain correlation provides a potential bridge between animal and human research on this phenomenon. Specifically, it suggests the possibility that BOLD signal correlations across the brains of interacting humans observed previously (e.g. Dikker et al., 2014; King-Casas et al., 2005; Silbert et al., 2014; Spiegelhalder et al., 2014; Stephens et al., 2010; Tomlin et al., 2006; Zadbood et al., 2017) might share a similar mechanistic origin as the correlations we report here in interacting bats, opening the door for a combined approach to the study of inter-brain correlations in animal models and humans.
What could be the utility and circuit mechanisms for two brains to co-modulate neural activity in the 30–150 Hz band during social interactions? The 30–150 Hz band contains the gamma band (Buzsáki and Draguhn, 2004; Ray and Maunsell, 2011) and overlaps with the high-gamma range (Ray and Maunsell, 2011). The gamma band, in particular, has been implicated in multiple cognitive functions and computations that likely play major roles in social interactions, such as sensory processing (Engel et al., 2001), attention (Fries et al., 2001; Jensen et al., 2007), social inference (Cohen et al., 2009), emotional processing (Headley and Paré, 2013), prediction (Engel et al., 2001), working memory (Jensen et al., 2007; Howard et al., 2003), and others. Furthermore, during social interactions between two individuals, the actions driven by each brain generate sensory inputs that are fed into the other, which in turn need to be perceived and interpreted to guide future actions. This necessarily requires the coordination of different brain areas, a process in which gamma band oscillations are believed to play a major role (Fries, 2009; Voytek and Knight, 2015; Bastos et al., 2015; Fries, 2015; van Kerkoerle et al., 2014; Besserve et al., 2015). Thus, it is possible that inter-areal coordination of neural activity in the 30–150 Hz range within each brain becomes correlated across the brains as the two form a closed sensory-motor loop during social interactions (Hasson et al., 2012).
The observation of inter-brain correlation in a non-human species opens the door for addressing the evolutionary origins and utility of this phenomenon from a comparative perspective. The utility of inter-brain correlation has been primarily attributed to its facilitation of the execution and coordination of complex social interactions (Hasson et al., 2012; Stephens et al., 2010; Nummenmaa et al., 2012; Leong et al., 2017). As different species exhibit different levels of social complexity (Dunbar and Shultz, 2007), one might predict the degree of inter-brain correlation to vary across species. Here, taking an ethological approach and using the Egyptian fruit bat—a social specialist (Herzig-Straschil and Robinson, 1978; Harten et al., 2018; Prat et al., 2015, 2016, 2017; Omer et al., 2018; Cvikel et al., 2015; Egert-Berg et al., 2018; Kwiecinski and Griffiths, 1999), we indeed observed a high level of inter-brain correlation. Future comparative studies in a variety of species, utilizing unsupervised learning algorithms to discover and define behaviors (e.g., Anderson and Perona, 2014; Klaus et al., 2017; Markowitz et al., 2018; Pereira et al., 2019; Wiltschko et al., 2015) that can be compared across species, will shed light on the relationship between sociality and inter-brain correlation across species.
Social interactions are some of the most complex behaviors exhibited by animals. Our results suggest that a reductionist approaches in social neuroscience can be fruitfully complemented by ethological approaches that embrace the natural complexity of social behaviors across species.
STAR Methods
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Michael M. Yartsev (myartsev@berkeley.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Neural activity was recorded from four adult male Egyptian fruit bats, Rousettus aegyptiacus (weight 162–186 g at implantation). 18 bats (11 males, 7 females) were used for behavioral experiments only (as the third bat that was introduced on some of the one-chamber sessions). All bats were caught from the wild; thus, their precise age could not be identified (this species of bats is very long-lived, with a maximum reported longevity of 25 years; Kwiecinski and Griffiths, 1999). Before the start of experiments, bats were housed in large communal rooms at the bat breeding colony of UC Berkeley. After the start of experiments, bats were single-housed in cages in a humidity- and temperature-controlled room. The bats were kept on a 12-hour reversed light-dark cycle, and all experiments were conducted during the dark cycle. All experimental procedures were approved by the Animal Care and Use Committee of UC Berkeley.
METHOD DETAILS
Unless otherwise specified, all data processing and analysis was performed using MATLAB (MathWorks).
Experimental setup and details
All experiments were conducted inside 40.6 × 33.7 × 52.1 cm (length × width × height) cages, which had netting on top that allowed bats to hang. Each cage was placed inside a 64.8 × 61 × 64.8 cm (length × width × height) chamber. Fans circulated air between the inside and outside of the chambers. The experiments were conducted in the dark. The only lights in the chambers were infrared lights to allow video recording. Video was recorded throughout the experimental sessions using one or two high-speed infrared cameras (Flea3, FLIR) at 100 frames/s. Ultrasonic microphones (USG Electret Ultrasound Microphone, Avisoft Bioacoustics; frequency range: 10–120 kHz) were used to record audio throughout the experimental sessions. Infrared light-emitting diodes (LEDs) on the wireless neural recording systems (see below) were flashed at intervals of ~20 minutes during recording sessions, which were captured by the video cameras and used to synchronize neural and video recordings. Transistor-transistor logic pulses were sent using UltraSoundGate Player 216H (Avisoft Bioacoustics) simultaneously to the wireless neural recording systems of both bats as well as to the audio recording system (UltraSoundGate 416H, Avisoft Bioacoustics), synchronizing neural recording from both bats and the audio recording. All experiments took place in an electromagnetically and acoustically shielded room (IAC Acoustics).
Before the first recording session, each bat used in the experiment was allowed to familiarize itself with the recording environment. This was done in ~5 familiarization sessions per bat, where a bat freely interacted with another bat for ~100 minutes per session. One to two of those ~5 familiarization sessions involved interaction between the same bats that were to be used in the upcoming simultaneous two-bat neural recording experiment.
In total, we recorded 52 one-chamber sessions and 18 two-chambers sessions. In all sessions, bats were allowed to freely behave without intervention or constraint from experimenters. Among the two-chambers sessions, there were 5 sessions of free behavior without playback or interaction partners (Figure 4A), 8 sessions of free behavior with playback of bat calls (Figure 4B), and 5 sessions of free behavior with non-implanted interaction partners (Figure 4C). Identical cages, chambers, and recording setups were used for all one-chamber and two-chambers sessions. Sessions lasted on average 105 ± 6 minutes (mean ± STD). On 31 of the one-chamber sessions, a non-implanted third bat was introduced in the middle of the session. The time of introduction was on average 44.1 ± 14.2 minutes (mean ± STD) from the beginning of the session. The bats that were introduced as the third bat included 11 males and 7 females.
On the two-chambers sessions with playback, bat social calls were played using ultrasound speakers (Vifa, Avisoft Bioacoustics; frequency range: 1–120 kHz). The contents of the playback were identical for the two chambers and were delivered simultaneously to both. On each playback session, a set of different calls were played. The number of different calls used for a given session ranged from 47 to 744. Calls were played for the entire duration of the sessions, with uniformly distributed inter-call intervals. The uniform distribution was from 1.5 to 3.5 s for five sessions, from 0.8 to 1.8 s for two sessions, and from 1 to 2 s for one session. At the end of each inter-call interval, a new call was randomly picked from the set of calls for that session (with replacement) and played. The playback was designed to provide an auditory experience that is similar to the near-constant chatter of bat calls in a bat cave in the wild or in our bat colony room, as was done previously (Prat et al., 2017). The calls used in playback sessions were recorded from the one-chamber sessions. On some of the playback sessions, the calls played to the bats were recorded from the same bats on one-chamber sessions; on other sessions, the calls played were recorded from different bats. Results from neural analyses were similar regardless of the range of inter-call intervals used and the set of calls played, and were thus combined together.
Behavior definitions and annotations
The behaviors of the bats in our experiments were manually annotated using a custom annotation program written in MATLAB (MathWorks). The annotations were done by experienced trained observers who did not know about the goals of the experiment, the analyses being performed, or the nature of the neural data, and were therefore unbiased. Annotations were done at a detailed level: the behaviors of each bat at each video frame were classified, according to a set of definitions, which we defined after extensive observation of bat behavior. Annotation was done for 65 of the 70 sessions (technical errors in the video recording prevented annotation for the other 5 sessions). It is important to note that due to the fine-grained annotation procedure and the length of the sessions (frame-by-frame annotation of videos recorded at 100 frames/s for sessions lasting ~100 minutes each), annotation for a single session typically takes between 1–2 months for a single person. Yet, considering that the fine-grained social behavior of this species of bats has not be characterized before, we chose to take this careful, ethological approach despite its time-consuming nature.
Here we detail the definitions of the different behaviors observed in our experiments. They represent the behavioral repertoire the bats exhibited in the experiments, and were defined based on extensive examination of the video recordings of the experiments.
Resting. A bat hanging by its feet, with its head and body still. Resting can be social resting or non-social resting. Social resting is when a bat rests while leaning its whole body against another bat. Otherwise, it is non-social resting.
Active non-social. A bat engaging in any kind of active behavior that doesn’t involve social interaction, including: the bat hanging by its feet or feet and thumbs, and moving its head or body; the bat climbing or crawling around; the bat shaking its body; the bat jumping or flying off from the roof of the cage.
Self-grooming. A bat either licking or scratching itself.
Social grooming. A bat either licking or scratching another bat.
Probing. A bat poking its snout at the head or body of another bat.
Fighting. A bat moving its wings or thumbs to quickly hit another bat, or biting another bat.
Mating. A male bat inserting or attempting to insert its penis into a female bat’s vagina.
Wing covering. A bat struggling with another bat in order to cover the other bat’s body with its opened wings.
Reaching. A bat attempting to reach over the body or wings of another bat with its head or thumbs.
Blocking. A bat using its wings to actively block another bat from accessing a location.
Other interactions. Any social interaction other than the ones already defined.
Of all these behaviors defined above, non-interaction behaviors include: non-social resting, active non-social, and self-grooming. All other behaviors are interaction behaviors.
Surgery
Anesthesia and surgical procedures generally followed those described previously in detail for Egyptian fruit bats (Yartsev and Ulanovsky, 2013). Surgeries were performed to implant a four-tetrode microdrive on each bat. Anesthesia was induced using an injectable cocktail of ketamine (22 mg/kgBW), dexamedetomidine (0.09 mg/kgBW) and midazolam (0.31 mg/kgBW). Subsequently, the bat was placed in a stereotaxic apparatus (Kopf) and anesthesia was maintained throughout surgery by repeated injections (roughly once per hour) of an anesthesia maintenance cocktail of dexamedetomidine (0.125 mg/kgBW), midazolam (2.5 mg/kgBW) and fentanyl (0.025 mg/kgBW). The depth of anesthesia was monitored by testing toe pinch reflexes and measuring the bat’s breathing rate. The body temperature of the bat was kept constant at approximately 35–36°C, using a closed-loop temperature controller (FHC) connected to a rectal temperature probe and a heating pad placed under the bat.
Each bat was implanted with a four-tetrode lightweight microdrive (Harlan 4 Drive, Neuralynx; weight 2.1 g). Tetrodes (~45 μm diameter) were constructed from four strands of platinum-iridium wire (17.8 μm diameter, HML-insulated), bound together by twisting and then melting their insulations. Each of the four tetrodes was loaded and glued separately into a telescoped assembly of polyimide tubes mounted into the microdrive. The tetrodes exited the microdrive through a guide cannula in an approximately rectangular arrangement with ~300 μm horizontal spacing between tetrodes. Each tetrode could be moved independently via a separate drive screw. On the day before surgery, the tip of each tetrode was cut flat using high-quality scissors (tungsten-carbide scissors with ceramic coating, CeramaCut; FST) and plated with Platinum Black (Neuralynx) to reduce the impedance of individual wires to 0.3–0.8 MΩ (at 1 kHz).
While the bat was under anesthesia, the skull was micro-scarred to improve subsequent adhesion, and a circular opening (craniotomy of 1.8 mm diameter) was made in the skull over the left hemisphere. The center of craniotomy was positioned over the frontal cortex of the bat at 1.7 mm lateral to the midline and 12.19 mm anterior to the transverse sinus that runs between the posterior part of the cortex and the cerebellum (N. Ulanovsky, M.P. Witter and R. Eilam, Stereotaxic Brain Atlas of the Egyptian Fruit Bat, in preparation). After removal of the dura, the microdrive was lowered and the tip of the microdrive’s guide tube was placed on the brain surface. The microdrive was placed vertically. The craniotomy was then filled with a biocompatible elastomer (Kwik-Sil, World Precision Instruments) to protect the brain. The exposed muscle tissue was then covered with a thin layer of biocompatible adhesive (Vetbond, World Precision Instruments) for protection. A bone screw (FST) with a soldered stainless-steel wire was fixed to the skull in the frontal plate, and served as a ground screw after its electrical connection to the dura was verified. An additional set of 3–5 bone screws were fixed to the skull and served as anchor screws for the mechanical stability of the implant. The bases of the screws were then covered with a thin layer of quick adhesive cement (C&B Metabond, Parkell) which held the screws firmly to the skull; dental acrylic was then added to secure the entire microdrive to the screws and to the skull. At the end of the surgery, bats were given the analgesic Metacam and the anti-inflammatory drug dexamethasone.
Electrophysiological recording
Electrophysiological recordings were conducted using a wireless neural data logging system (Neurolog-16, Deuteron Technologies), which amplifies the voltage signals from the 16 channels of the 4 tetrodes, performs analog-to-digital conversion at a sampling rate of 29.29 kHz, and stores the digitized data on an on-board SD card. The system has a bandwidth of 1 Hz - 7 kHz, records voltage with a fine resolution of 3.3 μv, and has a low level of noise generally close to the limit of Johnson noise from the impedance of a given source. The system also contains infrared LEDs that can be turned on and off during recording, whose on and off time stamps are recorded along with time stamps of neural data; these LEDs were used to synchronize video and neural recording (see above). Furthermore, the recording system is light-weight (9.9 g, including battery and plastic casing). The Egyptian fruit bats used in our experiment weighed more than 160 g and carried the recording system with ease, as expected from previous experiments using wireless recording systems with heavier or comparable weights during free flight for over an hour and covering multiple kilometers (Yartsev and Ulanovsky, 2013; Finkelstein et al., 2014).
After all recording sessions were concluded for the day, we connected the tetrodes to a wired recording system (Digital Lynx, Neuralynx) to monitor the neural signals and advance the tetrodes. Tetrodes were moved downward once every one to two days (mostly by 20–160 μm), in order to record single units, local spiking activity and LFP at new sites.
Preprocessing of electrophysiological data
All filtering described in this section were done twice, in the forward and reverse directions, to eliminate phase distortion.
To obtain LFP, we first low-pass filtered the raw voltage traces using a 10th-order Butterworth filter with a cut-off frequency of 200 Hz. The voltage traces were then downsampled by a factor of 59, resulting in a sampling frequency of 496.6 Hz. Power line noise was then filtered out using a 10th-order Butterworth band-stop filter with cut-off frequencies 59.5 Hz and 60.5 Hz, and another one with cut-off frequencies 119.5 Hz and 120.5 Hz.
We observed artifacts in our LFP recording, in the form of large amplitude, transient (~200 ms), irregular voltage fluctuations that are visually distinct from the normal LFP signal. To automatically detect these artifacts, we used the following algorithm. We note that this algorithm is only a heuristic method that worked well for our data; while it is convoluted, it performed better than a number of simpler methods we tried.
For a given LFP voltage trace (from one recording channel, spanning one recording session), we calculate its spectrogram over our frequency band of interest, 1–150 Hz. Specifically, modified periodograms are computed for short, overlapping segments (64 samples, or ~128.89 ms, with 50% overlap between consecutive segments) of the LFP trace, each windowed with a Hamming window. In the spectrogram, artifacts appear as spikes in power. To facilitate the detection of these power outliers at any frequency, we normalize the spectrogram as follows: for each frequency, we normalize the power at that frequency by the median absolute deviation of power at that frequency. This normalized spectrogram is a matrix (number of frequencies × number of time bins), which we denote by S. We average over the rows of S (i.e. averaging across frequencies) to obtain a vector M (1 × number of time bins), which is the average normalized power as a function of time. We set a threshold, Mthreshold, to be the median of M multiplied by a parameter Tm. Elements of M that are larger than Mthreshold are detected as potential artifacts. Tm was chosen separately for each recording channel on each session, based on manual inspection of the artifact detection results obtained using a range of Tm values. The median Tm across all recording channels, bats, and sessions (n = 1912) is 8, and the first and third quartiles are 5 and 12, respectively.
The detected potential artifacts could include normal large amplitude oscillations that occur during sleep. To detect these false positives, we used the following procedure. At each time bin that a potential artifact is detected, we take the corresponding column of S, and find the maximum in that column between 1 and 10 Hz, which we denote by Plow. Similarly, we find Pmid as the maximum between 10 and 20 Hz, and Phigh as the maximum between 45 and 120 Hz. Then, we classify a potential artifact as a false positive if all three of the following criteria are satisfied: (1) Pmid / Phigh > 6.5; (2) Pmid / Plow > 2; (3) the element of M at the given time bin is smaller than 1.5 Mthreshold.
Each element of M corresponds to 64 voltage samples. After rejecting the false positives, for each remaining element of M that is larger than Mthreshold, we define the corresponding 64 voltage samples as a single artifact. For consecutive elements of M that are larger than Mthreshold, their corresponding voltage samples are merged into a single artifact. Then, we define a voltage range within which normal LFP signal lies: the median ± 3 times the median absolute deviation of the entire voltage trace. For each artifact, if the first sample before it or the first sample after it is not within the normal voltage range, then we extend the artifact until both are within the normal range; this makes sure that the algorithm catches the “tails” of each artifact. Then, if the interval between any two artifacts is shorter than 210 ms, the two artifacts and the interval between them are merged into a single artifact.
When analyzing LFP, after we remove an artifact from an LFP trace, we close the resulting gap by joining the two ends of the trace. If the voltages at these two ends differ by a large amount, this effectively creates a new artifact, which we would like to avoid. Thus, before artifact detection, for a given voltage trace, we calculate the absolute value of the voltage difference between every pair of consecutive samples. We define the 90th percentile of all these absolute values as the largest acceptable voltage difference across the two ends of an artifact. If the voltage difference across the two ends of an artifact is larger than this threshold, we extend the artifact by up to 100 ms on each side, to bring the difference below the threshold, making sure to extend by the minimal length possible. If extensions by up to 100 ms on each side are not enough to bring the difference below threshold, we choose the lengths of extensions (still constrained to be below 100 ms on each side) to minimize the difference.
In total, artifacts amounted to a small proportion of our recordings. For each recording channel on each session, we calculated the total duration of artifacts, and the total duration of artifacts as a proportion of the total recording duration. For the total artifact duration, the median across all recording channels, bats, and sessions (n = 1912) was 36.7 s, and the first and third quartiles were 14.1 s and 126.7 s, respectively. For the total duration of artifacts as a proportion of the total recording duration, the median was 0.0058, and the first and third quartiles were 0.0023 and 0.020, respectively. For all the LFP analyses presented in this paper, artifacts were removed prior to analysis, as described in “Calculation of LFP spectrograms” below.
To detect spikes, we band-pass filtered the raw voltage traces using a 6th-order Butterworth filter with cut-off frequencies of 600 Hz and 6000 Hz. For each recording channel and each session, a voltage threshold was set as the following quantity: the difference between the 75th percentile and the median of the voltage trace, divided by the 75th percentile of the standard normal distribution, and multiplied by a factor of 3 (Quian Quiroga et al., 2004). Each time the voltage on one recording channel crossed its threshold, we found the sample having the peak voltage among the over-threshold samples, and extracted 32 samples (1.09 ms) from each channel of the tetrode around the time of the peak sample: from the 7th sample before the peak sample to the 24th sample after. These extracted samples were then used for spike sorting. We performed spike sorting automatically using SNAP Sorter (Neuralynx) with the default settings, then manually checked and cleaned up the results using SpikeSort3D (Neuralynx). For each tetrode on each session, after identifying spikes belonging to single units and after excluding artifacts based on waveform shape, all remaining spikes were grouped into a multiunit. All units with firing rate below 2 Hz were excluded from further analysis. Our dataset included a total of 326 single units and 530 multiunits (after excluding units with low firing rates).
Histology
Histology was done as described previously (Yartsev and Ulanovsky, 2013). Each batwas given a lethal overdose of sodium pentobarbital and, with tetrodes left in situ, was perfused transcardially using a flush of 50 ml phosphate-buffered saline followed by 200 ml of fixative (4% paraformaldehyde + 0.1 M phosphate-buffered saline). The brains were then removed and storedin fixative. Subsequently, a cryostat was used to cut 40 μm coronal sections of the brains. The sections were Nissl-stained with cresyl violet, and cover-slipped. A light microscope fitted with a digital camera was used to determine tetrode locations (Figure S1A–B).
Calculation of LFP spectrograms
For each LFP trace, we calculated its spectrogram (e.g. Figure 2A) as follows. Power spectra were calculated for 5 s sliding windows of the LFP trace, with 2.5 s overlap between consecutive windows. The window size of 5 s was chosen as the shortest window that resulted in tolerable levels of noise in the spectral estimates, as assessed by visual inspection of the power spectra. The power spectra were computed at integer frequencies from 1 to 150 Hz, using the multitaper method with a time half bandwidth product of 4. If a given window contained artifacts whose duration exceeded 3.5 s, we did not compute a power spectrum for that window, and instead interpolated its power spectrum from those of the neighboring windows. If a given window contained artifacts whose duration did not exceed 3.5 s, we computed its power spectrum after removing the artifacts. Thus, for all the LFP analyses presented in this paper, artifacts were removed prior to analysis. Furthermore, power at 60 Hz was interpolated from power at 59 and 61 Hz, and power at 120 Hz was interpolated from power at 119 and 121 Hz.
To analyze and visualize different frequencies on equal footing, for each LFP spectrogram, we separately peak-normalized the power at each frequency, i.e. power at each frequency was divided by the peak power at that frequency (e.g. see Figure 2B). Other methods of normalization and whitening (such as z-scoring the power at each frequency) gave similar results, so we opted for the simple method of peak-normalization.
Calculation of firing rates
For single units and multiunits, firing rate as a function of time was calculated in 5 s bins with 2.5 s overlap between consecutive bins. The bin size and overlap were chosen to be the same as for the computation of LFP spectrograms, so that the LFP and spiking results can be compared.
Dimensionality reduction of LFP
To reduce the dimensionality of the normalized LFP spectrograms, we performed PCA on them, with frequencies as variables and time bins as observations (e.g. see Figure 2C–F). We aimed to approximate the PCs with flat frequency bands, as they are easier to interpret. The flat frequency bands were chosen as follows. We can divide the range of 1–150 Hz into two frequency bands defined by a dividing frequency, e.g. a dividing frequency of 29 Hz divides the range of 1–150 Hz into the 1–29 Hz band and the 30–150 Hz band. For each normalized spectrogram (corresponding to one recording channel, bat, and session), we calculated the combined variance captured by two flat frequency bands, divided by the combined variance of the top two PCs (which is the maximum amount of variance that can be captured by two dimensions), as a function of the dividing frequency (e.g. Figure 2G). The dividing frequency at which this variance proportion is maximized is the optimal dividing frequency for this normalized spectrogram. To determine the optimal dividing frequency for all normalized spectrograms (i.e. all channels, bats, and sessions), we averaged the variance proportion curves across all normalized spectrograms (Figure 2H): the peak of the averaged curve occurred at 29 Hz. Consistent with this, the median across the optimal dividing frequencies of the different normalized spectrograms was also 29 Hz, and the first and third quartiles were 27 Hz and 32 Hz, respectively (Figure 2H, ticks on top). Thus, we chose to reduce the dimensionality of the normalized LFP spectrograms to the 1–29 Hz band and the 30–150 Hz band.
As a technical note, we detail here the normalization and mean-subtraction used for some of the analyses involving the flat frequency bands. In the 150-dimensional space of the 150 integer frequencies, a flat frequency band is the direction of the vector whose elements within the frequency band are 1 and whose elements outside are 0. To quantify the variance of a normalized spectrogram captured by a flat frequency band (Figure 2G–H), the band was represented as a unit vector pointing in its direction. For each frequency of the normalized spectrogram, we subtracted the mean of the normalized power values from them, centering the normalized spectrogram. Then, the variance captured by a frequency band is the variance of the projection of the centered, normalized spectrogram onto the unit vector in the direction of the frequency band. Thus calculated, the variance captured by the frequency bands can be directly compared with the variance captured by the PCs (Figure 2C). For all other analyses involving the activation of a flat frequency band (e.g. Figure 2E, F, and I; Figures 3–7), for ease of interpretation, we did not center the normalized spectrograms, and instead of using projection on a unit vector, we simply averaged the normalized power values within a frequency band. Since all these other analyses (such as computing the correlation coefficient) themselves involve mean-subtraction and normalization, using the mean normalized power gives the same results as projection of the centered, normalized spectrogram onto a unit vector.
Detection of social calls
We used the following procedure to automatically detect social calls from audio recordings of the experimental sessions. Given an audio signal (normalized to the range from −1 to 1, the range of the recording system), its envelope was calculated as the magnitude of its analytic representation (a complex function whose real part is the audio signal and whose imaginary part is the Hilbert transform of the audio signal). The envelope was low-pass filtered in both the forward and reverse directions using a 3rd-order Butterworth filter with a cut-off frequency of 750 Hz. Putative calls were detected as threshold-crossing by the filtered envelop at a threshold of 0.002. Putative calls with a root mean square below 0.01 or a duration shorter than 15 ms were discarded as false positives; all others were detected as calls. Consecutive calls whose inter-call interval was shorter than 20 ms were merged into a single call. The times of the detected calls were used for the analysis shown in Figure S3H–K bottom panels, where we removed periods of calls from the neural data before calculating correlation across brains. A subset of detected calls was further used for playback in the two-chambers playback sessions, as described above.
Video tracking and estimation of movement magnitude
We used DeepLabCut (Mathis et al., 2018) to track the neural recording device attached to the implant of each bat in the recorded videos. We trained DeepLabCut models using randomly selected frames on which the positions of the neural recording devices were manually labeled. The training was done with the default parameters, on a PC running a NVIDIA Quadro P4000 GPU.
On different sessions, the video cameras can be at different angles relative to the bats as well as different distances to them; therefore, for each session, the trajectory of each tracked neural recording device was normalized (z-scored separately for the x and y dimensions) prior to analysis. The normalized movement magnitude (e.g. Figure S5A) at each video frame was estimated as the distance between the positions of the neural recording device in that frame and the next frame.
QUANTIFICATION AND STATISTICAL ANALYSIS
Statistical tests
The statistical tests used are stated in the figure legends and described in detail below. A significance level of 0.05 was used for all tests. Tests were two-tailed unless otherwise indicated.
Quantification of behavioral correlation
For each behavior (e.g. resting, self-grooming, probing, etc.), each bat, and each session, we used a binary vector to represent the time course of the bat engaging in that behavior over the session: the elements of the vector correspond to time points (each time point is one video frame), and the values of the elements are “1” at time points when the bat was engaging in that behavior, and “0” when it was not. For a given behavior and a given session, the correlation between two such vectors (one for each of the bats) tells us how coordinated a given behavior is between the two bats. For example, for the “resting” behavior on a given session, the correlation between the two binary vectors representing the resting time courses of the two bats indicates how coordinated the resting behavior is between the two bats. Similarly, the correlation between different behaviors (e.g. the correlation between self-grooming by one bat and probing by the other bat) can be calculated between binary vectors representing those behaviors. As discussed in the Results section, resting was correlated between bats. This creates a problem when calculating the correlation of the other active behaviors. As an example, consider the “probing” behavior. When both bats were resting, the values of the binary vectors representing probing would be 0. This would contribute to a positive correlation for probing, but it actually reflects the coordination of resting, rather than the coordination of probing itself. Thus, when calculating the correlation of behaviors other than resting, we removed time points of coordinated resting from all binary behavior vectors to eliminate the contribution of coordinated resting.
Among all pairs of active behaviors where at least one of the behaviors had a total duration exceeding 1% of the total session duration on average, only two pairs of active behaviors showed a correlation higher than 0.05: probing-probing (average correlation across sessions: 0.22) and probing-mating (average correlation across sessions: 0.06). Not only are these correlations low, the probing and mating behaviors also only accounted for 3% and 0.06% of the total session duration on average, respectively. To summarize the correlations between all pairs of active behaviors, for each session, we first calculated the correlation between each pair of active behaviors, including correlation between the same behavior by the two bats (e.g. both bats probing), as well as correlation between different behaviors (e.g. probing by one bat and self-grooming by the other bat). For each session, we averaged the correlations between all possible pairs of active behaviors, where the correlation between each given pair of behaviors was weighted by the sum of the durations the two bats spent doing those behavior in that session. Then, mean and STD were calculated across the mean correlations from different sessions (Figure 1C). To summarize the correlation of resting/active bouts, we simply calculated the mean and STD across sessions of resting correlation (Figure 1C).
Correlation coefficient between time series of neural activity
When we calculated the correlation between two time series of neural activity (e.g. Figure 3E–H and Figure 4G–J), the statistical significance of the correlation was assessed as follows. Time series of LFP power and neuronal firing rate have autocorrelations both intrinsically and as a result of the overlapping windows we used to compute them. To assess the significance of correlations between neural time series, we need to consider their autocorrelations, rather than assume that samples from a neural time series are independent. Thus, given two time series of neural data, our null hypothesis is that the actual correlation between them is expected by chance between a pair of independent neural time series whose autocorrelations are identical to those of the actual neural time data. To test this, we first generated 1000 surrogate time series for each actual neural time series, as follows. We took the Fourier transform of the actual time series, kept the amplitude spectrum fixed, replaced the phase spectrum by independently drawing phases from the uniform distribution between 0 and 2π, then took the inverse Fourier transform to get a surrogate time series. Because the Fourier transform of the autocorrelation of a signal is proportional to the power spectrum of the signal, each surrogate time series shared the same autocorrelation with the actual time series, but was otherwise random. Then, the surrogate time series generated from the two actual time series were paired up into 1000 pairs, and the 1000 correlation coefficients calculated between the pairs formed the null distribution. The p value was computed as the proportion of the null distribution that was as extreme or more extreme than the correlation between the pair of actual neural time series. When we excluded some time periods from time series of neural activity before calculating correlations (Figure 3E–H, middle panels; Figure S3H–K), the surrogate time series were generated from the time series of neural activity after those time periods were excluded.
When we used histograms to summarize the correlation between LFP power across brains (e.g. Figure 3E–H and Figure 4G–J), each count of the histogram represented one pair of tetrodes from different brains on one session, not one pair of channels, because different channels of the same tetrode record essentially the same LFP signal. The correlation and p value for a pair of tetrodes were computed as follows. Each pair of tetrodes contained up to 16 pairs of channels (less than 16 when some channels were inactive), each having a correlation and p value. We took the median correlation and its corresponding p value to be the correlation and p value for the tetrode pair. When the median correlation was an average of two correlations (i.e. when there were an even number of channel pairs), we averaged the p values corresponding to the two correlations being averaged.
Correlation between neural activity after regressing out behavior
For Figure 3E–H, bottom panels, and Figure 4O–R, we calculated the partial correlations between neural activity from different brains controlling for the behaviors of the bats. In other words, we calculated correlations between neural activity after regressing behaviors out. For each session, we represented the time courses of all behaviors of both bats as binary vectors, as described in “Quantification of behavioral correlation” above. Then, for each channel or unit, we performed linear regression to predict the neural activity (mean normalized power in the 30–150 Hz or 1–29 Hz band, or firing rate of the single unit or multiunit) over time using the set of behavioral binary vectors as predictors. The linear regression fit was then subtracted from the actual neural activity, and the correlations between these residuals from different brains was calculated.
Estimation of the false discovery rate
Assessing the statistical significance of the correlations between pairs of neural signals entails multiple comparison. Thus, for each family of statistical tests (e.g. tests for all pairs of single units in one-chamber sessions, tests for all pairs of multiunit sites in two-chambers sessions, etc.), we estimated the FDR (Benjamini and Hochberg, 1995). Typically, FDR is used in the following way. A threshold of FDR is chosen, the α (the threshold for significance) corresponding to the chosen FDR is calculated for a given family of tests, and null hypotheses with p values less than or equal to α are rejected. Because the different families of tests in our study contained different numbers of tests, this procedure would result in different α’s for different families. This would mean that, for example, the threshold for significance would be different for single units on one-chamber sessions compared to two-chambers sessions, or the threshold for significance would be different for LFP power in the high frequency band on one-chamber sessions compared to single units on one-chamber sessions. Instead, we would like to have the same threshold for significance for all families, so as to fairly compare across types of neural signals and experimental conditions. Thus, we used FDR in the following way. A fixed α of 0.05 was used for all families of tests. For each family, we found the largest p value that was smaller or equal to 0.05 (i.e. the largest significant p value), and calculated the FDR for that family corresponding to this p value. This provides an estimation of the rate of false discoveries, while still allowing fair comparisons across neural signals and experimental conditions.
For Figure 3E–H, the FDRs are 0.0040, 0.050, 0.068, and 0.14 for the top panels, respectively; 0.051, 0.11, 0.10, and 0.21 for the middle panels, respectively; 0.034, 0.049, 0.084, and 0.18 for the bottom panels, respectively. Such low values suggest a low incidence of false positives.
For Figure 4G–J, the FDRs are 0.47, 1, 0.68, and 0.36, respectively. Such high values suggest that out of the small number of significant correlations, many are likely false discoveries.
For Figure S3C, the FDRs are: 0.14 (top) and 0.11 (bottom); for Figure S3D–G top panels: 0.004, 0.019, 0.064, and 0.12, respectively; for Figure S3D–G bottom panels: 0.001, 0.053, 0.072, and 0.22, respectively; for Figure S3H–K row (i): 0.056, 0.16, 0.13, and 0.22, respectively; for Figure S3H–K row (ii): 0.056, 0.090, 0.12, and 0.30, respectively; for Figure S3H–K row (iii): 0.003, 0.051, 0.073, and 0.14, respectively.
For Figure S4G–J top panels, the FDRs are: 0.32, 0.68, 0.43, and 0.14, respectively; middle panels: 0.76, 0.65, 0.54, and not applicable, respectively; bottom panels: 0.04, not applicable, 0.71, and 0.30, respectively (for panels without any significant correlation, the FDR is not applicable).
Linear regression analyses relating LFP power to firing rate
For Figure S1C and F, linear regression was used to predict the mean normalized LFP power in the 30–150 Hz and 1–29 Hz bands of each LFP channel on each session for each bat, using the firing rates of all multiunits and single units combined, all multiunits, or all single units recorded from the same bat and on the same session. Specifically, for each regression, firing rates over time of a given set of units are used to predict the power over time of one channel in one of the frequency bands.
The linear regression used for Figure S1D and G was similar to that described above, except that for each regression, the predictor was one multiunit or one single unit only. We estimated the distance between the recording sites from which the LFP and unit were recorded as follows. The vertical distance between two recording sites was estimated as the difference between the amounts by which the two tetrodes had been advanced downward. The horizontal distance between the two recording sites was estimated to be 300 μm, based on measurement of the microdrive. Figure S1D and G show the absolute distance calculated from the vertical and horizontal distances. Note that the actual travel of a tetrode through brain tissue is not entirely linear, and hence the distances should be considered as estimates only.
The linear regression used for Figure S1E and H was similar to those described above, with the following differences. For each regression, the predictor was the firing rates over time of one multiunit, shifted in time by a certain lag with respect to the LFP power to be predicted. The multiunit used as predictor was always the one recorded from the same tetrode as the LFP power to be predicted. For this analysis, LFP power and firing rates were calculated in 100 ms bins, and the time shifts used spanned the range from −3 seconds to 3 seconds, in 100 ms steps.
Decoding behavior from neural activity
For Figure 2M–P, we used each type of neural signal (30–150 Hz LFP power, 1–29 Hz LFP power, multiunit, or single unit) to classify one pair of behaviors at a time. We used a pseudo-simultaneous population decoding method based on previous approaches (Meyers et al., 2008; Rigotti et al., 2013; Saez et al., 2015). For this analysis, the activity of each unit/channel on each session was z-scored. Given a pair of behaviors A and B (e.g. probing and fighting), we found all the time points in each session when a given bat was engaged in these two behaviors. Then, for each unit/channel from each bat and on each session, we created a training set and a test set from its neural activity during behavior A, by splitting the time points of behavior A randomly: 80% for the training set and 20% for the test set. The same procedure was repeated for behavior B. All units/channels from all sessions and bats were subsequently combined to form a pseudo-simultaneous population. If a bat did not engage in either of the behaviors on a given session, then its units/channels on that session were not included in the population. To train a decoder, we used 1000 population activity vectors for behavior A and another 1000 for behavior B. Each population activity vector for behavior A was created by randomly and independently sampling the activity of each unit/channel from its training set for behavior A, and the same was done for behavior B. Similarly, 1000 population activity vectors were created from the test sets of each behavior. A linear support vector machine was trained on the 2000 training activity vectors and subsequently tested on the 2000 test activity vectors, yielding a classification accuracy. We repeated this procedure 1000 times (each time with new, random splits of training and test sets), and calculated the average accuracy across the 1000 iterations. Each element of each matrix in Figure S2M–P shows one such average accuracy.
Instantaneous correlation index
Given two vectors each representing neural activity over time from a bat, the Pearson correlation coefficient between them measures whether activity in the two bats covary: they positively covary if they tend to be both high at the same times and both low at the same times; they negatively covary if activity in one bat tends to be high at the time points when activity in the other bat is low. A related question is: at a given time point, are neural activity in two bats both high or both low, or is activity in one bat high and activity in the other bat low? The instantaneous correlation index was introduced to answer this question. It was defined in Figure 5B, and we elaborate on it with more details here.
Given two N-dimensional vectors X and Y representing neural activity at N time points from two bats, we first subtract from each vector its mean, and then normalize each to unit length, resulting in two vectors of normalized activity x and y. We note that this is the same normalization as in the definition of the Pearson correlation coefficient: the Pearson correlation coefficient between X and Y is the dot product between x and y. This normalization is needed because in order to meaningfully assess whether neural activity from a bat is high or low at a given time point, it needs to be compared to neural activity from the bat at other time points.
Then, at a given time point t, the normalized activity of the two bats, (xt, yt), is a vector in 2D space (blue vector in Figure 5B). If neural activity in the two bats are both high or both low at time t, then (xt, yt) points in a direction close to the direction of the unity line. If neural activity is high in one bat and low in the other bat at time t, then (xt, yt) points in a direction close to the direction orthogonal to the unity line. This motivates the definition of the instantaneous correlation index as the smaller of the two angles between (xt, yt) and the line orthogonal to the unity line (Figure 5B). Thus, the instantaneous correlation index ranges from 0 degree to 90 degrees. At a given time point, neural activity is correlated between bats when the instantaneous correlation index is above 45 degrees (the closer to 90 degrees, the more correlated), and neural activity is anti-correlated between bats when the instantaneous correlation index is below 45 degrees (the closer to 0 degree, the more anti-correlated).
Behavior-matching, behavioral-sequence-matching, movement-magnitude-matching, and interaction-state-matching analyses
For the behavior-matching analysis (Figure 5C), instantaneous correlation index was first averaged across all time points showing a behavior pair and all pairs of tetrodes (for LFP power) or multiunit sites or single units, separately for one-chamber and two-chamber sessions. Then, the mean instantaneous correlation indices for the different behavior pairs were averaged together; these averages across behaviors were plotted in Figure 5C. Only behavior pairs whose total duration of occurrence exceeded one minute in both one-chamber and two-chambers sessions were included in this analysis. Note that the behavior-matching here included both interaction and non-interaction behaviors.
For the behavioral-sequence-matching analysis (Figure 5D), we divided each session into a series of two-bat behavioral episodes. Each two-bat behavioral episode is a continuous period of time when the behaviors of both bats did not change. A two-bat behavioral episode is defined by its length and its behavioral content (what behaviors the two bats were engaged in). We first considered behavioral sequences consisting of two consecutive two-bat behavioral episodes. For two such behavioral sequences to match, the behavioral content and the length of the first episode must match between the two sequences, and the same must be true for the second episode. For example, Figure 5A illustrates two sequences that are matched (one from a one-chamber session, the other from a two-chambers session): each sequence contains two two-bat behavioral episodes, the first episode being “Bat 1, active non-social; Bat 2, resting”, the second episode being “Bat 1, active non-social; Bat 2, active non-social.” For each unique two-episode sequence found in our dataset, we found all occurrences of this sequence in both one-chamber and two-chambers sessions, and calculated the total duration of its occurrences in each type of sessions. If a sequence did not occur or occurred only rarely in one type of sessions, that means the sequence was not matched between the two types of sessions. Thus, we only analyzed sequences whose total duration of occurrence exceeded one minute in both one-chamber and two-chambers sessions. 0.09 of all unique two-episode sequences found in two-chambers sessions met this criterion. For longer sequences, very few met this criterion: for unique three-episode sequences found in two-chambers sessions, 0.007 of them met this criterion; for unique four-episode sequences, the proportion is 0.0005. Because of the low frequencies of matched sequences of three episodes or longer, we only analyzed two-episode sequences in the behavioral-sequence-matching analysis. For each matched behavioral sequence, the instantaneous correlation index was first averaged across all time points from all occurrences of this sequence and across all pairs of tetrodes (for LFP power) or multiunit sites or single units, separately for one-chamber and two-chambers sessions. Then, the mean instantaneous correlation indices for the different behavioral sequences were averaged together; these averages across behavioral sequences were plotted in Figure 5D. Note that the behavioral-sequence-matching here included both interaction and non-interaction behaviors.
For the movement-magnitude-matching analysis (Figure 5E), for each LFP power or firing rate time bin, we calculated the mean of the normalized movement magnitudes (see “Video tracking and estimation of movement magnitude” above) in the time bin for each of the bats, resulting in a 2D vector of movement magnitudes for each time bin. To match the 2D vectors from different time bins, we grouped the 2D vectors into 2D bins (as when making a 2D histogram). For each dimension of the 2D movement magnitude vectors, we used 10 equally-spaced bins of movement magnitude from 0 up to the 99.99th percentile of all the movement magnitude values from all sessions and bats (i.e. excluding 0.01% of large movement outliers), resulting in 100 2D bins. For each 2D bin, instantaneous correlation index was averaged across all time bins and all pairs of tetrodes (for LFP power) or multiunit sites or single units, separately for one-chamber and two-chamber sessions. Then, the mean instantaneous correlation indices for different 2D bins were averaged together; these averages across 2D bins were plotted in Figure 5E. Only 2D bins whose occupancy was at least one minute for both one-chamber and two-chambers sessions were included in this analysis.
For the interaction-state-matching analysis (Figure 5F), instantaneous correlation index was averaged across all time points that showed the interaction states depicted in Figure 5F (one neural bat interacting with a non-neural bat, the other neural bat not interacting), and also averaged across all pairs of tetrodes (for LFP power), multiunit sites or single units.
For variants of the above analyses that used Pearson correlation coefficient (Figure S7A–C), instead of averaging instantaneous correlation index across different time points, we averaged Pearson correlation coefficient across different two-bat behavioral episodes or behavioral sequences.
Interaction states and transitions analyses
For analyses of interaction states and transitions (Figure 7C–F and Figure S7J–K), we divided each session into a series of two-bat behavioral episodes, as described above. A two-bat behavioral episode is classified as an interaction if at least the behavior of one of the bats involves interaction with the other bat; otherwise the episode is classified as non-interaction. For example, if an episode consists of bat 1 grooming bat 2 and bat 2 grooming itself, it is classified as an interaction. Or, if an episode consists of the two bats grooming each other, it is classified as an interaction. For each type of two-bat behavioral episodes (e.g., interaction, non-interaction, non-interaction that was followed by non-interaction, etc.), Figure 7C–F and Figure S7J–K show the mean instantaneous correlation index and Figure S7D–I show the mean Pearson correlation coefficient.
Phase difference analyses
To examine correlation as a function of timescales, we analyzed the phases of neural activity vectors in the Fourier domain. Using the Fourier transform, a neural signal over time can be decomposed into a sum of sine waves at different frequencies that correspond to different timescales. At a given timescale, two signals from different brains are two sine waves, and the phase difference between them indicates how well they are aligned in time: the closer the phase difference is to zero, the more correlated the two signals are at that timescale (Figure 6B).
The relationship between correlation and phase differences can be seen more precisely as follows. As above, consider two N-dimensional vectors X and Y representing neural activity at N time points from two bats. We subtract from each vector its mean, and then normalize each to unit length, resulting in two vectors of normalized activity, which we call x and y. In the following, we use * to denote complex conjugate, [b]− to denote the largest integer that is strictly smaller than b, and to denote the Fourier transform of x at frequency k. We use ax,k and θx,k to denote the amplitude and phase of the Fourier transform of x at frequency k, respectively, so that . The Pearson correlation coefficient between X and Y is the dot product between x and y. Transforming this dot product to the Fourier domain and simplifying, we have:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
In the above, (4) results from the orthonormality of the Fourier basis; (6) is due to the N-periodicity of the Fourier transform and the fact that both x and y have a mean of zero; (8) is because the Fourier coefficients at k and −k have the same amplitude and opposite phases for real signals (x and y are real as they represent neural activity). Note that in Figure 6 and Figure S6, we dropped the subscript k from |Δθk| to avoid confusion, as k was not specifically mentioned in those figures.
Equation (11) shows that the correlation between two signals is equal to the sum of the cosine of their phase differences at different frequencies, weighted by the product of their amplitudes at those frequencies. Intuitively, the closer the phase differences are to zero, the more correlated the signals are; the larger the amplitudes of the signals are at a given frequency, the more that timescale influences correlation. This motivated us to use the phase difference to assess the correlation across brains as a function of timescale, and to use the amplitude product to weigh the observations of phase difference, as we detail next.
For two N-dimensional, mean-subtracted, and normalized vectors x and y representing neural signals from two brains (which could be normalized LFP power or firing rate over time), we computed their amplitude product (ax,k ay,k) and phase difference (|Δθk|; any |Δθk| outside the range between 0 and π was converted to within that range) at all frequencies from 1 to [N/2]−. Phase differences from different sessions, pairs of bats, and pairs of channels or units were pooled together, then grouped into 30 equal-sized frequency bins spanning the range from 0 to 0.2 Hz (the Nyquist frequency, given that LFP power and firing rate were calculated in windows spaced by 2.5 s). Then, at each frequency, we estimated the probability distribution of phase differences through kernel density estimation, using the MATLAB function ksdensity with a bandwidth of 0.35, with each observation of phase difference being weighed by its corresponding amplitude product (Figure 6C–D; Figure S6A–B, E–F, I–J, M–N). We note that noise in the data has random phase differences and small amplitudes, so this weighting helps to diminish the contribution of noise to the distributions. Without this weighting, results are qualitatively similar (data not shown), but all distributions are slightly flatter (i.e. closer to the uniform distribution), presumably due to the contribution of noise. We also note that when showing these phase difference distributions in the figures (Figure 6C–D; Figure S6A–B, E–F, I–J, M–N), instead of plotting frequency (i.e. k) on the x-axis, we plotted period, which is just 1/frequency. We did this to avoid confusing the frequency of the LFP power and firing rate over time (which is what this analysis concerns) with the frequency of the LFP itself.
To compare neural correlation with behavioral correlation as a function of timescale (Figure 6E–F; Figure S6C–D, G–H, K–L, O–P), we first represented behavioral time courses as binary vectors, as described in “Quantification of behavioral correlation” above. Each type of behavior was considered separately: “resting” in Figure 6E–F, and each behavior whose total duration exceeded 1% of the session duration on average (averaged across bats and across sessions, separately for one-chamber and two-chambers sessions) in Figure S6. For a given pair of binary vectors representing the time courses of a given type of behavior from two bats, phase differences and amplitude products were calculated as described above for neural activity. For each session and each type of behavior, the behavioral phase differences were grouped into the same 30 frequency bins, and the weighted average of the phase difference (weighted by the amplitude products) was calculated for each bin. Similarly, for each session and each frequency bin, a weighted average of the neural phase difference was calculated, which included all pairs of channels (for LFP power) or all pairs of multiunits or single units and all frequencies within the bin. Then, the resulting mean neural phase difference curve (as a function of frequency) was subtracted from the mean behavior phase difference curve. Thus, there is one “behavior phase difference minus neural phase difference” curve per session; these curves are then averaged across sessions, which was plotted in Figure 6E–F and Figure S6C–D, G–H, K–L, and O–P.
We note that the phase locking value and phase locking index (Lachaux et al., 1999; Sazonov et al., 2009), common measures that involve the phase difference, entail averaging across trials or time periods and are thus related to coherence, whereas our use of phase difference does not entail averaging across trials or time periods and are related to correlation rather than coherence, as shown above.
Sample sizes
In this section we list the sample sizes for all statistical tests presented in the manuscript.
Figure 1C: n = 50 sessions
Figure 4K–L: n = 675 tetrode pairs for one-chamber sessions, 284 tetrode pairs for two-chambers sessions
Figure 4M: n = 675 multiunit pairs for one-chamber sessions, 284 multiunit pairs for two-chambers sessions
Figure 4N: n = 256 single unit pairs for one-chamber sessions, 65 single unit pairs for two-chambers sessions
Figure 4O–P: n = 651 tetrode pairs for one-chamber sessions, 236 tetrode pairs for two-chambers sessions
Figure 4Q: n = 651 multiunit pairs for one-chamber sessions, 236 multiunit pairs for two-chambers sessions
Figure 4R: n = 250 single unit pairs for one-chamber sessions, 54 single unit pairs for two-chambers sessions
Figure 5C: n = 15 behavior pairs
Figure 5D: n = 259 behavioral sequence pairs for 30–150 Hz LFP, 1–29 Hz LFP, and multiunits, 159 behavioral sequence pairs for single units
Figure 5E: n = 10 two-bat movement magnitude bins
Figure 5F: for 30–150 Hz LFP, 1–29 Hz LFP, and multiunits, n = 181893 time points × tetrode/multiunit pairs on one-chamber sessions, n = 94304 time points × tetrode/multiunit pairs on two-chambers sessions; for single units, n = 63247 time points × single unit pairs on one-chamber sessions, n = 35118 time points × single unit pairs on two-chambers sessions
Figure 7C–D: n = 863354 time points × tetrode/multiunit pairs for non-interaction, n = 499134 time points × tetrode/multiunit pairs for interaction
Figure 7E–F: n = 637889 time points × tetrode/multiunit pairs for transitions to non-interaction, n = 225465 time points × tetrode/multiunit pairs for transitions to interaction
Figure S4C: n = 15 sessions
Figure S5B–C: n = 130 sessions × bats
Figure S7A: n = 15 behavior pairs
Figure S7B: n = 259 behavioral sequence pairs for 30–150 Hz LFP, 1–29 Hz LFP, and multiunits, and 159 behavioral sequence pairs for single units
Figure S7C: for 30–150 Hz LFP, 1–29 Hz LFP, and multiunits, n = 38552 episodes × tetrode/multiunit pairs on one-chamber sessions, n = 24112 episodes × tetrode/multiunit pairs on two-chambers sessions; for single units, n = 17745 episodes × single unit pairs on one-chamber sessions, n = 7260 episodes × single unit pairs on two-chambers sessions
Figure S7D–E: n = 127999 episodes × tetrode/multiunit pairs for non-interaction, n = 60829 episodes × tetrode/multiunit pairs for interaction
Figure S7F–G: n = 93083 episodes × tetrode/multiunit pairs for transitions to non-interaction, n = 34916 episodes × tetrode/multiunit pairs for transitions to interaction
Figure S7H–I: n = 34542 episodes × tetrode/multiunit pairs for transitions to non-interaction, n = 26287 episodes × tetrode/multiunit pairs for transitions to interaction
Figure S7J–K: n = 376652 time points × tetrode/multiunit pairs for transitions to non-interaction, n = 122482 time points × tetrode/multiunit pairs for transitions to interaction
Supplementary Material
Figure S1 Recording location and details on the recorded signal, related to Figures 1–2.
(A) Three-dimensional representation of an example Egyptian fruit bat brain reconstructed from block-face imaging. Red circle highlights the cortical recording location.
(B) Left: an example Nissl-stained coronal section, at the location of the red circle in (A), showing a tetrode track. Right: zoomed-in view showing the tetrode track (arrow).
(C) Linear regression was used to predict the mean normalized LFP power in the 30–150 Hz band of each LFP channel on each session for each bat, using the firing rates of all multiunits and single units combined (black), all multiunits (blue), or all single units (orange) recorded from the same bat and on the same session. Mean R2 (± STD) across recording channels, bats, and sessions are shown.
(D) Linear regression was used to predict the mean normalized LFP power in the 30–150 Hz band of each LFP channel on each session, using the firing rates of one multiunit (blue) or one single unit (orange) recorded from the same bat and on the same session. Plotted are mean R2 (± STD) across recording channels, bats, and sessions, as a function of estimated distance between the recording sites from which the LFP and unit were recorded. A distance of 0 denotes LFP and unit recorded from the same tetrode.
(E) Linear regression was used to predict the mean normalized LFP power in the 30–150 Hz band of each LFP channel on each session, using the time-lagged firing rate of the multiunit recorded from the same tetrode and on the same session. Firing rate preceding LFP is defined here as negative lag. Plotted are mean R2 (± STD) across recording channels, bats, and sessions, as a function of time lag.
(F-H) Same as (C-E) but for mean normalized LFP power in the 1–29 Hz band.
Note that LFP power in the 30–150 Hz band can be predicted from spiking activity to a large extent, while LFP power in the 1–29 Hz band cannot. See STAR Methods for details on the regression analyses.
Figure S2 Behavioral modulation of neural activity, related to Figure 2. (A-H) Example recording channels, multiunit sites, and single units showing varying degrees of behavioral modulation of neural activity. Each panel shows the mean and standard deviation of neural activity during a number of behaviors for a channel, multiunit site, or single unit. (A, E) Mean normalized LFP power in the 30–150 Hz band for two example channels. (B, F) Mean normalized LFP power in the 1–29 Hz band for two example channels. (C, G) Firing rate for two example multiunit sites. (D, H) Firing rate for two example single units. The examples in the first row (A-D) show stronger behavioral modulation, and the examples in the second row (E-H) show weaker behavioral modulation. Note that for each example, a number of behaviors are missing, because the bat from which the example was taken did not engage in those behaviors on the session from which the example was taken.
(I-L) Summaries of behavioral modulation across the entire dataset, for LFP power in the 30–150 Hz band (I), the 1–29 Hz band (J), local spiking activity (K), and single unit activity (L). Each panel shows a matrix which summarizes the fraction of channels, multiunit sites, or single units that showed activity that was significantly different between pairs of behaviors. Specifically, for a given matrix, the element at row a and column b indicates the fraction of LFP channels (I-J), multiunit sites (K), or single units (L) that showed significantly higher activity during the behavior indicated for row a than during the behavior indicated for column b. Note that across all levels of neural signals, neural activity reflects whether the animal was resting or active. Note also the widespread modulation of neural activity by different active behaviors. Significant difference between neural activity during two behaviors was determined using the Wilcoxon rank sum test at a threshold of α = 0.05.
(M-P) Linear decoders were used to classify each pair of behaviors based on pseudo-simultaneous population activity vectors of LFP power in the 30–150 Hz band (M), the 1–29 Hz band (N), local spiking activity (O), and single unit activity (P). Each panel shows, for each pair of behavior, the cross-validated classification accuracy averaged over 1000 iterations of training and testing. Note the overall high accuracies, indicating that all behaviors can be reliably decoded from neural activity. See STAR Methods.
No bat engaged in both “mating” and “reaching” during the same session, and therefore this pair of behaviors was not compared in (I)-(L) or classified in (M)-(P).
(Q) For each behavior, each bat, each session, and each recording channel from that bat, we averaged the normalized LFP power in the 30–150 Hz band across all time points when the bat engaged in that behavior. We did the same for normalized LFP power in the 1–29 Hz band. Thus, for a given type of behavior, we have one 2D data point of the average normalized LFP power for each channel, session, and bat (same as in Figure 2I). To visualize the ranges of the data points during different behaviors, a convex hull was plotted for each behavior, encompassing all data points corresponding to the behavior after excluding outliers having Mahalanobis distances greater than 2 (Golub et al., 2018). As shown in Figure 2I, resting (thick blue outline) exhibited relatively little overlap with active behaviors, while different active behaviors showed more overlap.
Figure S3 Details on correlations in one-chamber sessions, related to Figure 3. (A-B) Neural activity simultaneously recorded from two brains on example sessions, plotted along with the behaviors of the two bats during the sessions. (A) Mean normalized LFP power in the 1–29 Hz band. Same tetrodes and session as shown in Figure 3A. (B) Single unit activity. Correlations between the example neural activity traces are indicated above each plot. See Figure 3A–B for mean normalized LFP power in the 30–150 Hz band and multiunit activity.
(C) Histograms of correlations between single units, pooled across all one-chamber sessions and all pairs of bats. Top, correlations between single units from different brains; 35% of all pairs were significantly correlated. Bottom, correlations between single units within the same brains; 45% of all pairs were significantly correlated. Note that, in one-chamber sessions, correlations between single units from different brains were comparable to those between single units within the same brains.
(D-G) Histograms of correlations across brains pooled across one-chamber sessions. The top and bottom panels each shows data from one pair of bats. (D-E) Correlations across brains of LFP power in the high frequency band (D) and the low frequency band (E) for all pairs of tetrodes. (F-G) Correlations across brains of spiking activity for all pairs of multiunit sites (F) and single units (G).
(H-K) Histograms of correlations across brains pooled across all one-chamber sessions and all pairs of bats. Row (i): correlations after removing all periods when the two bats were engaged in the same behavior. Thus, correlations remain high after removing the influence of coordinated behaviors. Row (ii): correlations calculated only during periods when both bats were active. Thus, correlations remain high when considering only active bouts, during which the individual active behaviors of the bats were not correlated (Figure 1C). Row (iii): correlations after removing all time periods containing social calls from the bats, as well 10 seconds before and after each call. While social calls are an important aspect of bat social behavior, the correlations across brains did not simply stem from the moments of social calls. (H-I) Correlations across brains for LFP power in the high frequency band (H) and the low frequency band (I) for all pairs of tetrodes. (J-K) Correlations across brains of spiking activity for all pairs of multiunit sites (J) and single units (K). Statistical significance was assessed in the same way as for Figure 3E–H.
Figure S4 Details on correlations in the two-chambers sessions, related to Figure 4. (A-B) Neural activity simultaneously recorded from two brains on example sessions, plotted along with the behaviors of the two bats during the sessions. (A) Mean normalized LFP power in the 1–29 Hz band. Same tetrodes and session as shown in Figure 4D, top panel. (B) Single unit activity. Same session as shown in Figure 4E. Correlations between the example neural activity traces are indicated above each plot. See Figure 4D–F for mean normalized LFP power in the 30–150 Hz band and multiunit activity.
(C) Quantification of behavioral correlation across bats in two-chambers sessions (mean ± STD across sessions). Note that while the correlations of active behaviors remained as low as in the one-chamber sessions, the correlations of resting and active bouts were much lower (compare with Figure 1C). Thus, the behavioral correlations of the resting and active bouts seen in one-chamber sessions were the results of social coordination between bats, rather than by-products of any stereotyped behavioral patterns that bats might independently follow.
(D-F) Comparisons of correlations between one-chamber and two-chambers sessions for the same pairs of tetrodes (D, normalized LFP power in the 30–150 Hz band; E, in the 1–29 Hz band) or the same pairs of multiunit sites (F) from different brains. Each dot is one pair of tetrodes (D-E) or one pair of multiunit sites (F), comparing their correlations on a one-chamber session and a two-chambers session. Each pair of one-chamber and two-chambers sessions being compared happened on the same day, with one session immediately following the other without movement of the recording electrodes, thus allowing direct comparison for the same pairs of tetrodes and recording sites. Note that neural correlations across brains fell apart when bats no longer shared a social environment, even as they continued to share similar sensory environments and behavioral contexts.
(G-J) Histograms of correlations across brains pooled across two-chambers sessions and all pairs of bats. Each row of panels shows data from one type of two-chambers sessions (schematized on the left side, described in Figure 4A–C). (G-H) Correlations across brains of LFP power in the high frequency band (G) and the low frequency band (H) for all pairs of tetrodes. (I-J) Correlations across brains of spiking activity for all pairs of multiunit sites (I) and single units (J). Note that neural activity showed weak to no correlations across brains on all types of two-chambers sessions. Statistical significance was assessed in the same way as for Figure 3E–H.
Figure S5 Estimation of movement magnitude, related to Figure 5. (A) Normalized movement magnitude (the movement speed of the neural recording device estimated from video tracking) of one bat on an example session, shown along with the manually annotated behaviors of the bat (top). Note that movement magnitude was at a nearly constant, low level when the bat was resting, and it was high and more variable when the bat was active. The zoomed-in plot shows a 10-minute segment of the session that further illustrates the correspondence between movement magnitude and behavior.
(B-C) The mean (B) and variance (C) of normalized movement magnitude were calculated in 1-second windows, independently z-scored for each session and bat and averaged across all windows that corresponded to either resting or active behaviors. Plotted are mean ± STD across sessions and bats. *, p<0.05, Wilcoxon signed rank test. See STAR Methods for details.
Figure S6 Timescales of correlations across brains, and comparison of neural correlation with behavioral correlation, related to Figure 6. Results shown separately for LFP power in the 30–150 Hz band (A-D), the 1–29 Hz band (E-H), multiunit sites (I-L), and single units (M-P), on one-chamber sessions (A, C, E, G, I, K, M, O) and two-chambers sessions (B, D, F, H, J, L, N, P).
(A-B, E-F, I-J, M-N) The same analysis as in Figure 6C–D, showing distributions of |Δθ| as a function of timescale. In one-chamber sessions, correlations across brains were strongest and extended over the widest range of timescales for LFP power in the 30–150 Hz band (A), and were weaker and extended over narrower ranges of timescales for LFP power in the 1–29 Hz band (E) and multiunit sites (I). On the other hand, in two-chambers sessions, these signals show no correlations at most timescales (B, F, J). Results for single units for both one-chamber (M) and two-chambers sessions (N) show generally weak correlations that do not extend over wide range of timescales.
(C-D, G-H, K-L, O-P) The same analysis as in Figure 6E–F, showing behavior |Δθ| minus neural |Δθ|, as a function of timescales, averaged across sessions. Each plot shows a number of solid lines, each one showing the comparison of neural correlation with the correlation of one behavior. In one-chamber sessions, neural correlation is stronger than behavioral correlation for all behavior at multiple timescales for LFP power in the 30–150 Hz band (C). For LFP power in the 1–29 Hz band (G) and multiunit sites (K), neural correlation is stronger than behavioral correlation for a subset of behaviors, at a smaller range of timescales. For single units (O), neural correlation is weaker or comparable to behavioral correlation. In two-chambers sessions, neural correlation is comparable to behavioral correlation for all types of neural signals and all behaviors (D, H, L, P), suggesting that the neural correlations on two-chambers sessions were entirely a reflection of behavioral correlation. Only behaviors whose total duration exceeded 1% of the session duration on average (averaged across bats and across sessions, separately for one-chamber and two-chambers sessions) were considered for this analysis. The analysis of “resting” behavior here is equivalent to the analysis of resting/active bouts in Figure 6E–F.
Figure S7 Comparing correlations during matched behaviors and various interaction states, related to Figures 5 and 7. (A) Average correlation during behaviorally matched time periods on one-chamber and two-chambers sessions (mean ± SEM across behavior pairs).
(B) Average correlation during behavioral-sequence-matched time periods on one-chamber and two-chambers sessions (mean ± SEM across behavioral sequence pairs; STAR Methods).
(C) On one-chamber sessions that included a non-neural bat (black), sometimes one neural bat (orange in the illustration) was interacting with the non-neural bat, while the other neural bat (green in the illustration) was not engaged in any interaction (blue dotted box). The analogous situation in two-chambers sessions entails a neural bat interacting with a non-neural bat in one chamber, and the neural bat in the other chamber not interacting (purple dotted box). Bar plots show the average correlation under these two conditions (mean ± SEM across time points). Note that while the schematic only illustrates the case where the “orange bat” was the one interacting, for the actual analysis, any neural bat could be the one interacting.
Note that despite the matched behaviors or states of social interactions, in most cases correlation was significantly higher when bats shared the same social environment, and when they did not share a social environment, their neural activity showed weak to no correlations.
(D-E) Average correlation during non-interaction behaviors and during interactions (mean ± SEM), for LFP power in the 30–150 Hz band (D), and for multiunit sites (E), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions.
(F-G) Average correlation during non-interaction behaviors that preceded other non-interaction behaviors, and during non-interaction behaviors that preceded interactions, for LFP power in the 30–150 Hz band (F), and for multiunit sites (G), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions (mean ± SEM).
(A)-(G) are the same analyses as Figure 5C, D, F, Figure 7C, D, E, F, respectively, but using Pearson correlation coefficient instead of instantaneous correlation index; note that results using these two measures are consistent with each other. Note that the analysis in Figure 5E matches single time windows and therefore cannot be performed using Pearson correlation coefficient.
(H-I) Average correlation during interaction behaviors that preceded non-interaction behaviors, and during interaction behaviors that preceded other interaction behaviors (mean ± SEM), for LFP power in the 30–150 Hz band (H), and for multiunit sites (I), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions.
(J-K) Same as (H)-(I), but using instantaneous correlation index.
*, p<0.05, one-tailed Wilcoxon signed rank test (A)-(B) or one-tailed Wilcoxon rank sum test (C)-(K).
Highlights.
Simultaneous neural recording from pairs of bats during natural social interactions
LFP power and spiking activity highly correlated between socially interacting bats
Neural correlation between brains at timescales ranging from seconds to hours
Neural correlation between brains covaried with the extent of social interactions
Editor’s In Brief.
Social interactions involve complex animal behaviors. In socially interacting bats, there is inter-brain correlation of neural activity, reflecting current and future states of social behavior.
Draft In Brief.
Multiple levels of neural activity were highly correlated between the brains of socially interacting bats over timescales ranging from seconds to hours, and the correlation covaried with the extent of social interactions, reflecting the current and future states of social behaviors.
Acknowledgments
We thank E. S. Sevilla, A. Raha, J. Chau, K. Moi, N. Juthani, M. Zuercher, L. Kasraie, and C. Tran for behavioral annotation; S. A. Afjei for histology; N. Ulanovsky and Y. Yovel for animal collection; L. Jiang for machining; A. Halley and L. Krubitzer for providing the image of the 3D-reconstructed brain; T. Pereira and M. Murthy for help and advice on video tracking; W. Liberti for help with video tracking and comments on the manuscript; W. Hong, R. Knight, Y. Yovel, E. Azim, E. Rich, E. Lacey, K. Miller, D. Foster, and members of the Yartsev NeuroBat lab for helpful discussion and comments on the manuscript; C. Ferrecchia and G. Lawson for veterinary oversight; the staff of the Office of Laboratory Animal Care for support with animal husbandry and care. This research was supported by NIH (DP2-DC016163), the New York Stem Cell Foundation, the Alfred P. Sloan Foundation, the Brain Research Foundation, National Science Foundation (NSF-1550818), the Packard Fellowship, the Klingenstein-Simons Fellowship, the Pew Charitable Trust, and the Dana Foundation (M.M.Y).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DATA AND SOFTWARE AVAILABILITY
Data and custom software reported in this study will be made available upon reasonable request.
Declaration of Interests
The authors declare no competing interests.
References
- Adolphs R (2001). The neurobiology of social cognition. Curr. Opin. Neurobiol 11, 231–239. [DOI] [PubMed] [Google Scholar]
- Amodio DM, and Frith CD (2006). Meeting of minds: the medial frontal cortex and social cognition. Nat. Rev. Neurosci 7, 268–277. [DOI] [PubMed] [Google Scholar]
- Anderson DJ (2016). Circuit modules linking internal states and social behaviour in flies and mice. Nat. Rev. Neurosci 17, 692–704. [DOI] [PubMed] [Google Scholar]
- Anderson DJ, and Perona P (2014). Toward a science of computational ethology. Neuron 84, 18–31. [DOI] [PubMed] [Google Scholar]
- Babiloni F, and Astolfi L (2014). Social neuroscience and hyperscanning techniques: Past, present and future. Neurosci. Biobehav. Rev 44, 76–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos AM, Vezoli J, Bosman CA, Schoffelen J-M, Oostenveld R, Dowdall JR, De Weerd P, Kennedy H, and Fries P (2015). Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron 85, 390–401. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, and Hochberg Y (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B. Stat. Methodol 57, 289–300. [Google Scholar]
- Bergan JF, Ben-Shaul Y, and Dulac C (2014). Sex-specific processing of social cues in the medial amygdala. Elife 3, e02743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besserve M, Lowe SC, Logothetis NK, Schölkopf B, and Panzeri S (2015). Shifts of gamma phase across primary visual cortical sites reflect dynamic stimulus-modulated information transfer. PLoS Biol. 13, e1002257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, and Draguhn A (2004). Neuronal oscillations in cortical networks. Science 304, 1926–1929. [DOI] [PubMed] [Google Scholar]
- Cao W, Lin S, Xia Q, Du Y, Yang Q, Zhang M, Lu Y, Xu J, Duan S, Xia J, et al. (2018). Gamma oscillation dysfunction in mPFC leads to social deficits in Neuroligin 3 R451C knockin mice. Neuron 97, 1253–1260. [DOI] [PubMed] [Google Scholar]
- Chang SWC, Fagan NA, Toda K, Utevsky AV, Pearson JM, and Platt ML (2015). Neural mechanisms of social decision-making in the primate amygdala. Proc. Natl. Acad. Sci 112, 16012–16017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang SWC, Gariépy J-F, and Platt ML (2013). Neuronal reference frames for social decisions in primate frontal cortex. Nat. Neurosci 16, 243–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MX, David N, Vogeley K, and Elger CE (2009). Gamma-band activity in the human superior temporal sulcus during mentalizing from nonverbal social cues. Psychophysiology 46, 43–51. [DOI] [PubMed] [Google Scholar]
- Cui X, Bryant DM, and Reiss AL (2012). NIRS-based hyperscanning reveals increased interpersonal coherence in superior frontal cortex during cooperation. Neuroimage 59, 2430–2437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cvikel N, Egert Berg K, Levin E, Hurme E, Borissov I, Boonman A, Amichai E, and Yovel Y (2015). Bats aggregate to improve prey search but might be impaired when their density becomes too high. Curr. Biol 25, 206–211. [DOI] [PubMed] [Google Scholar]
- Dikker S, Silbert LJ, Hasson U, and Zevin JD (2014). On the same wavelength: predictable language enhances speaker-listener brain-to-brain synchrony in posterior superior temporal gyrus. J. Neurosci 34, 6267–6272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dikker S, Wan L, Davidesco I, Kaggen L, Oostrik M, McClintock J, Rowland J, Michalareas G, Van Bavel JJ, Ding M, et al. (2017). Brain-to-brain synchrony tracks real-world dynamic group interactions in the classroom. Curr. Biol 27, 1375–1380. [DOI] [PubMed] [Google Scholar]
- Dumas G, Nadel J, Soussignan R, Martinerie J, and Garnero L (2010). Inter-brain synchronization during social interaction. PLoS One 5, e12166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumas G, Lachat F, Martinerie J, Nadel J, and George N (2011). From social behaviour to brain synchronization: Review and perspectives in hyperscanning. IRBM 32, 48–53. [Google Scholar]
- Dunbar RIM, and Shultz S (2007). Evolution in the social brain. Science 317, 1344–1347. [DOI] [PubMed] [Google Scholar]
- Eliades SJ, and Miller CT (2017). Marmoset vocal communication: behavior and neurobiology. Dev. Neurobiol 77, 286–299. [DOI] [PubMed] [Google Scholar]
- Egert-Berg K, Hurme ER, Greif S, Goldstein A, Harten L, Herrera M, L.G., Flores-Martínez JJ, Valdés AT, Johnston DS, Eitan O, et al. (2018). Resource ephemerality drives social foraging in bats. Curr. Biol 28, 3667–3673.e5. [DOI] [PubMed] [Google Scholar]
- Engel AK, Fries P, and Singer W (2001). Dynamic predictions: oscillations and synchrony in top-down processing. Nat. Rev. Neurosci 2, 704–716. [DOI] [PubMed] [Google Scholar]
- Falkner AL, Dollar P, Perona P, Anderson DJ, and Lin D (2014). Decoding ventromedial hypothalamic neural activity during male mouse aggression. J. Neurosci 34, 5971–5984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falkner AL, Grosenick L, Davidson TJ, Deisseroth K, and Lin D (2016). Hypothalamic control of male aggression-seeking behavior. Nat. Neurosci 19, 596–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein A, Derdikman D, Rubin A, Foerster JN, Las L, and Ulanovsky N (2015). Three-dimensional head-direction coding in the bat brain. Nature 517, 159–164. [DOI] [PubMed] [Google Scholar]
- Forbes CE, and Grafman J (2010). The role of the human prefrontal cortex in social cognition and moral judgment. Annu. Rev. Neurosci 33, 299–324. [DOI] [PubMed] [Google Scholar]
- Fries P (2009). Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci 32, 209–224. [DOI] [PubMed] [Google Scholar]
- Fries P (2015). Rhythms for cognition: communication through coherence. Neuron 88, 220–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Reynolds JH, Rorie AE, and Desimone R (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563. [DOI] [PubMed] [Google Scholar]
- Gervasoni D, Lin S-C, Ribeiro S, Soares ES, Pantoja J, and Nicolelis MAL (2004). Global forebrain dynamics predict rat behavioral states and their transitions. J. Neurosci 24, 11137–11147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub MD, Sadtler PT, Oby ER, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Chase SM, and Yu BM (2018). Learning by neural reassociation. Nat. Neurosci 21, 607–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haroush K, and Williams ZM (2015). Neuronal prediction of opponent’s behavior during cooperative social interchange in primates. Cell 160, 1233–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harten L, Matalon Y, Galli N, Navon H, Dor R, and Yovel Y (2018). Persistent producer-scrounger relationships in bats. Sci. Adv 4, e1603293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson U, Nir Y, Levy I, Fuhrmann G, and Malach R (2004). Intersubject synchronization of cortical activity during natural vision. Science 303, 1634–1640. [DOI] [PubMed] [Google Scholar]
- Hasson U, Ghazanfar AA, Galantucci B, Garrod S, and Keysers C (2012). Brain-to-brain coupling: a mechanism for creating and sharing a social world. Trends Cogn. Sci 16, 114–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson U, and Frith CD (2016). Mirroring and beyond: coupled dynamics as a generalized framework for modelling social interactions. Philos. Trans. R. Soc. B Biol. Sci 371, 20150366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Headley DB, and Paré D (2013). In sync: gamma oscillations and emotional memory. Front. Behav. Neurosci 7, 170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herzig-Straschil B, and Robinson GA (1978). On the ecology of the fruit bat, Rousettus aegyptiacus leachi (A. Smith, 1829) in the Tsitsikama Coastal National Park. Koedoe 21, 101–110. [Google Scholar]
- Hong W, Kim D-W, and Anderson DJ (2014). Antagonistic control of social versus repetitive self-grooming behaviors by separable amygdala neuronal subsets. Cell 158, 1348–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MW, Rizzuto DS, Caplan JB, Madsen JR, Lisman J, Aschenbrenner-Scheibe R, Schulze-Bonhage A, and Kahana MJ (2003). Gamma oscillations correlate with working memory load in humans. Cereb. Cortex 13, 1369–1374. [DOI] [PubMed] [Google Scholar]
- Jensen O, Kaiser J, and Lachaux J-P (2007). Human gamma-frequency oscillations associated with attention and memory. Trends Neurosci. 30, 317–324. [DOI] [PubMed] [Google Scholar]
- Kawasaki M, Yamada Y, Ushiku Y, Miyauchi E, and Yamaguchi Y (2013). Inter-brain synchronization during coordination of speech rhythm in human-to-human social interaction. Sci. Rep 3, 1692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King-casas B, Tomlin D, Anen C, Camerer CF, Quartz SR, and Montague PR (2005). Getting to know you: reputation and trust in a two-person economic exchange. Science 308, 78–83. [DOI] [PubMed] [Google Scholar]
- Klaus A, Martins GJ, Paixao VB, Zhou P, Paninski L, and Costa RM (2017). The Spatiotemporal Organization of the Striatum Encodes Action Space. Neuron 95, 1171–1180.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koike T, Tanabe HC, and Sadato N (2015). Hyperscanning neuroimaging technique to reveal the “two-in-one” system in social interactions. Neurosci. Res 90, 25–32. [DOI] [PubMed] [Google Scholar]
- Konvalinka I, and Roepstorff A (2012). The two-brain approach: how can mutually interacting brains teach us something about social interaction? Front. Hum. Neurosci 6, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwiecinski GG, and Griffiths TA (1999). Rousettus egyptiacus. Mamm. Species 611, 1–9. [Google Scholar]
- Lachaux JP, Rodriguez E, Martinerie J, and Varela FJ (1999). Measuring phase synchrony in brain signals. Hum. Brain Mapp 8, 194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leong V, Byrne E, Clackson K, Georgieva S, Lam S, and Wass S (2017). Speaker gaze increases information coupling between infant and adult brains. Proc. Natl. Acad. Sci 114, 13290–13295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Mathis A, Grewe BF, Osterhout JA, Ahanonu B, Schnitzer MJ, Murthy VN, and Dulac C (2017). Neuronal Representation of Social Information in the Medial Amygdala of Awake Behaving Mice. Cell 171, 1176–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang B, Zhang L, Barbera G, Fang W, Zhang J, Chen X, Chen R, Li Y, and Lin D-T (2018). Distinct and dynamic ON and OFF neural ensembles in the prefrontal cortex code social exploration. Neuron 100, 700–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D, Liu S, Liu X, Zhang C, Li A, Jin C, Chen Y, Wang H, and Zhang X (2018). Interactive brain activity: review and progress on EEG-based hyperscanning in social interactions. Front. Psychol 9, 1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magri C, Schridde U, Murayama Y, Panzeri S, and Logothetis NK (2012). The amplitude and timing of the BOLD signal reflects the relationship between local field potential power at different frequencies. J. Neurosci 32, 1395–1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz JE, Gillis WF, Beron CC, Neufeld SQ, Robertson K, Bhagat ND, Peterson RE, Peterson E, Hyun M, Linderman SW, Sabatini BL, and Datta SR (2018). The striatum organizes 3D behavior via moment-to-moment action selection. Cell 174, 44–58.e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathis A, Mamidanna P, Cury KM, Abe T, Murthy VN, Mathis MW, and Bethge M (2018). DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci 21, 1281–1289. [DOI] [PubMed] [Google Scholar]
- McGinley MJ, Vinck M, Reimer J, Batista-Brito R, Zagha E, Cadwell CR, Tolias AS, Cardin JA, and McCormick DA (2015). Waking state: rapid variations modulate neural and behavioral responses. Neuron 87, 1143–1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyers EM, Freedman DJ, Kreiman G, Miller EK, and Poggio T (2019). Dynamic population coding of category information in inferior temporal and prefrontal cortex. J Neurophysiol 100, 1407–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller CT, Thomas AW, Nummela SU, and de la Mothe LA (2015). Responses of primate frontal cortex neurons during natural vocal communication. J. Neurophysiol 114, 1158–1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montague PR, Berns GS, Cohen JD, McClure SM, Pagnoni G, Dhamala M, Wiest MC, Karpov I, King RD, Apple N, et al. (2002). Hyperscanning: Simultaneous fMRI during linked social interactions. Neuroimage 16, 1159–1164. [DOI] [PubMed] [Google Scholar]
- Nguyen M, Vanderwal T, and Hasson U (2019). Shared understanding of narratives is correlated with shared neural responses. Neuroimage 184, 161–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nummela SU, Jovanovic V, de la Mothe L, and Miller CT (2017). Social context-dependent activity in marmoset frontal cortex populations during natural conversations. J. Neurosci 37, 7036–7047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nummenmaa L, Glerean E, Viinikainen M, Jaaskelainen IP, Hari R, and Sams M (2012). Emotions promote social interaction by synchronizing brain activity across individuals. Proc. Natl. Acad. Sci 109, 9599–9604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omer DB, Maimon SR, Las L, and Ulanovsky N (2018). Social place-cells in the bat hippocampus. Science 359, 218–224. [DOI] [PubMed] [Google Scholar]
- Pearson JM, Watson KK, and Platt ML (2014). Decision making: The neuroethological turn. Neuron 82, 950–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira TD, Aldarondo DE, Willmore L, Kislin M, Wang SS-H, Murthy M, and Shaevitz JW (2019). Fast animal pose estimation using deep neural networks. Nat. Methods 16, 117–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prat Y, Azoulay L, Dor R, and Yovel Y (2017). Crowd vocal learning induces vocal dialects in bats: Playback of conspecifics shapes fundamental frequency usage by pups. PLoS Biol. 15, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prat Y, Taub M, and Yovel Y (2015). Vocal learning in a social mammal: Demonstrated by isolation and playback experiments in bats. Sci. Adv 1, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prat Y, Taub M, and Yovel Y (2016). Everyday bat vocalizations contain information about emitter, addressee, context, and behavior. Sci. Rep 6, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quian Quiroga R, Nadasdy Z, and Ben-Shaul Y (2004). Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering. Neural Comput. 16, 1661–1687. [DOI] [PubMed] [Google Scholar]
- Rasch MJ, Gretton A, Murayama Y, Maass W, and Logothetis NK (2008). Inferring spike trains from local field potentials. J. Neurophysiol 99, 1461–1476. [DOI] [PubMed] [Google Scholar]
- Ray S, and Maunsell JHR (2011). Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol. 9, e1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remedios R, Kennedy A, Zelikowsky M, Grewe BF, Schnitzer MJ, and Anderson DJ (2017). Social behaviour shapes hypothalamic neural ensemble representations of conspecific sex. Nature 550, 388–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang X-J, Daw ND, Miller EK, and Fusi S (2013). The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudebeck PH, Bannerman DM, and Rushworth MFS (2008). The contribution of distinct subregions of the ventromedial frontal cortex to emotion, social behavior, and decision making. Cogn. Affect. Behav. Neurosci 8, 485–497. [DOI] [PubMed] [Google Scholar]
- Saez A, Rigotti M, Ostojic S, Fusi S, and Salzman CD (2015). Abstract context representations in primate amygdala and prefrontal cortex. Neuron 87, 869–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sazonov AV, Ho CK, Bergmans JWM, Arends JBAM, Griep PAM, Verbitskiy EA, Cluitmans PJM, and Boon PAJM (2009). An investigation of the phase locking index for measuring of interdependency of cortical source signals recorded in the EEG. Biol. Cybern 100, 129–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sejnowski TJ, Churchland PS, and Movshon JA (2014). Putting big data to good use in neuroscience. Nat. Neurosci 17, 1440–1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmälzle R, Häcker FEK, Honey CJ, and Hasson U (2014). Engaged listeners: shared neural processing of powerful political speeches. Soc. Cogn. Affect. Neurosci 10, 1137–1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholkmann F, Holper L, Wolf U, and Wolf M (2013). A new methodical approach in neuroscience: assessing inter-personal brain coupling using functional near-infrared imaging (fNIRI) hyperscanning. Front. Hum. Neurosci 7, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoot L, Hagoort P, and Segaert K (2016). What can we learn from a two-brain approach to verbal interaction? Neurosci. Biobehav. Rev 68, 454–459. [DOI] [PubMed] [Google Scholar]
- Silbert LJ, Honey CJ, Simony E, Poeppel D, and Hasson U (2014). Coupled neural systems underlie the production and comprehension of naturalistic narrative speech. Proc. Natl. Acad. Sci 111, E4687–E4696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalder K, Ohlendorf S, Regen W, Feige B, Tebartz van Elst L, Weiller C, Hennig J, Berger M, and Tüscher O (2014). Interindividual synchronization of brain activity during live verbal communication. Behav. Brain Res 258, 75–79. [DOI] [PubMed] [Google Scholar]
- Stephens GJ, Silbert LJ, and Hasson U (2010). Speaker-listener neural coupling underlies successful communication. Proc. Natl. Acad. Sci 107, 14425–14430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tognoli E, Lagarde J, DeGuzman GC, and Kelso JAS (2007). The phi complex as a neuromarker of human social coordination. Proc. Natl. Acad. Sci 104, 8190–8195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomlin D (2006). Agent-specific responses in the cingulate cortex during economic exchanges. Science 312, 1047–1050 [DOI] [PubMed] [Google Scholar]
- Tremblay S, Sharika KM, and Platt ML (2017). Social decision-making and the brain: a comparative perspective. Trends Cogn. Sci 21, 265–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tseng PH, Rajangam S, Lehew G, Lebedev MA, and Nicolelis MAL (2018). Interbrain cortical synchronization encodes multiple aspects of social interactions in monkey pairs. Sci. Rep 8, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kerkoerle T, Self MW, Dagnino B, Gariel-Mathis M-A, Poort J, van der Togt C, and Roelfsema PR (2014). Alpha and gamma oscillations characterize feedback and feedforward processing in monkey visual cortex. Proc. Natl. Acad. Sci. U. S. A 111, 14332–14341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voytek B, and Knight RT (2015). Dynamic network communication as a unifying neural basis for cognition, development, aging, and disease. Biol. Psychiatry 77, 1089–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiltschko AB, Johnson MJ, Iurilli G, Peterson RE, Katon JM, Pashkovski SL, Abraira VE, Adams RP, and Datta SR (2015). Mapping sub-second structure in mouse behavior. Neuron 88, 1121–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yartsev MM, and Ulanovsky N (2013). Representation of three-dimensional space in the hippocampus of flying bats. Science 340, 367–372. [DOI] [PubMed] [Google Scholar]
- Yun K, Watanabe K, and Shimojo S (2012). Interpersonal body and neural synchronization as a marker of implicit social interaction. Sci. Rep 2, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zadbood A, Chen J, Leong YC, Norman KA, and Hasson U (2017). How we transmit memories to other brains: constructing shared neural representations via communication. Cereb. Cortex 27, 4988–5000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Zhu H, Fan Z, Wang F, Chen Y, Liang H, Yang Z, Zhang L, Lin L, Zhan Y, et al. (2017). History of winning remodels thalamo-PFC circuit to reinforce social dominance. Science 357, 162–168. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 Recording location and details on the recorded signal, related to Figures 1–2.
(A) Three-dimensional representation of an example Egyptian fruit bat brain reconstructed from block-face imaging. Red circle highlights the cortical recording location.
(B) Left: an example Nissl-stained coronal section, at the location of the red circle in (A), showing a tetrode track. Right: zoomed-in view showing the tetrode track (arrow).
(C) Linear regression was used to predict the mean normalized LFP power in the 30–150 Hz band of each LFP channel on each session for each bat, using the firing rates of all multiunits and single units combined (black), all multiunits (blue), or all single units (orange) recorded from the same bat and on the same session. Mean R2 (± STD) across recording channels, bats, and sessions are shown.
(D) Linear regression was used to predict the mean normalized LFP power in the 30–150 Hz band of each LFP channel on each session, using the firing rates of one multiunit (blue) or one single unit (orange) recorded from the same bat and on the same session. Plotted are mean R2 (± STD) across recording channels, bats, and sessions, as a function of estimated distance between the recording sites from which the LFP and unit were recorded. A distance of 0 denotes LFP and unit recorded from the same tetrode.
(E) Linear regression was used to predict the mean normalized LFP power in the 30–150 Hz band of each LFP channel on each session, using the time-lagged firing rate of the multiunit recorded from the same tetrode and on the same session. Firing rate preceding LFP is defined here as negative lag. Plotted are mean R2 (± STD) across recording channels, bats, and sessions, as a function of time lag.
(F-H) Same as (C-E) but for mean normalized LFP power in the 1–29 Hz band.
Note that LFP power in the 30–150 Hz band can be predicted from spiking activity to a large extent, while LFP power in the 1–29 Hz band cannot. See STAR Methods for details on the regression analyses.
Figure S2 Behavioral modulation of neural activity, related to Figure 2. (A-H) Example recording channels, multiunit sites, and single units showing varying degrees of behavioral modulation of neural activity. Each panel shows the mean and standard deviation of neural activity during a number of behaviors for a channel, multiunit site, or single unit. (A, E) Mean normalized LFP power in the 30–150 Hz band for two example channels. (B, F) Mean normalized LFP power in the 1–29 Hz band for two example channels. (C, G) Firing rate for two example multiunit sites. (D, H) Firing rate for two example single units. The examples in the first row (A-D) show stronger behavioral modulation, and the examples in the second row (E-H) show weaker behavioral modulation. Note that for each example, a number of behaviors are missing, because the bat from which the example was taken did not engage in those behaviors on the session from which the example was taken.
(I-L) Summaries of behavioral modulation across the entire dataset, for LFP power in the 30–150 Hz band (I), the 1–29 Hz band (J), local spiking activity (K), and single unit activity (L). Each panel shows a matrix which summarizes the fraction of channels, multiunit sites, or single units that showed activity that was significantly different between pairs of behaviors. Specifically, for a given matrix, the element at row a and column b indicates the fraction of LFP channels (I-J), multiunit sites (K), or single units (L) that showed significantly higher activity during the behavior indicated for row a than during the behavior indicated for column b. Note that across all levels of neural signals, neural activity reflects whether the animal was resting or active. Note also the widespread modulation of neural activity by different active behaviors. Significant difference between neural activity during two behaviors was determined using the Wilcoxon rank sum test at a threshold of α = 0.05.
(M-P) Linear decoders were used to classify each pair of behaviors based on pseudo-simultaneous population activity vectors of LFP power in the 30–150 Hz band (M), the 1–29 Hz band (N), local spiking activity (O), and single unit activity (P). Each panel shows, for each pair of behavior, the cross-validated classification accuracy averaged over 1000 iterations of training and testing. Note the overall high accuracies, indicating that all behaviors can be reliably decoded from neural activity. See STAR Methods.
No bat engaged in both “mating” and “reaching” during the same session, and therefore this pair of behaviors was not compared in (I)-(L) or classified in (M)-(P).
(Q) For each behavior, each bat, each session, and each recording channel from that bat, we averaged the normalized LFP power in the 30–150 Hz band across all time points when the bat engaged in that behavior. We did the same for normalized LFP power in the 1–29 Hz band. Thus, for a given type of behavior, we have one 2D data point of the average normalized LFP power for each channel, session, and bat (same as in Figure 2I). To visualize the ranges of the data points during different behaviors, a convex hull was plotted for each behavior, encompassing all data points corresponding to the behavior after excluding outliers having Mahalanobis distances greater than 2 (Golub et al., 2018). As shown in Figure 2I, resting (thick blue outline) exhibited relatively little overlap with active behaviors, while different active behaviors showed more overlap.
Figure S3 Details on correlations in one-chamber sessions, related to Figure 3. (A-B) Neural activity simultaneously recorded from two brains on example sessions, plotted along with the behaviors of the two bats during the sessions. (A) Mean normalized LFP power in the 1–29 Hz band. Same tetrodes and session as shown in Figure 3A. (B) Single unit activity. Correlations between the example neural activity traces are indicated above each plot. See Figure 3A–B for mean normalized LFP power in the 30–150 Hz band and multiunit activity.
(C) Histograms of correlations between single units, pooled across all one-chamber sessions and all pairs of bats. Top, correlations between single units from different brains; 35% of all pairs were significantly correlated. Bottom, correlations between single units within the same brains; 45% of all pairs were significantly correlated. Note that, in one-chamber sessions, correlations between single units from different brains were comparable to those between single units within the same brains.
(D-G) Histograms of correlations across brains pooled across one-chamber sessions. The top and bottom panels each shows data from one pair of bats. (D-E) Correlations across brains of LFP power in the high frequency band (D) and the low frequency band (E) for all pairs of tetrodes. (F-G) Correlations across brains of spiking activity for all pairs of multiunit sites (F) and single units (G).
(H-K) Histograms of correlations across brains pooled across all one-chamber sessions and all pairs of bats. Row (i): correlations after removing all periods when the two bats were engaged in the same behavior. Thus, correlations remain high after removing the influence of coordinated behaviors. Row (ii): correlations calculated only during periods when both bats were active. Thus, correlations remain high when considering only active bouts, during which the individual active behaviors of the bats were not correlated (Figure 1C). Row (iii): correlations after removing all time periods containing social calls from the bats, as well 10 seconds before and after each call. While social calls are an important aspect of bat social behavior, the correlations across brains did not simply stem from the moments of social calls. (H-I) Correlations across brains for LFP power in the high frequency band (H) and the low frequency band (I) for all pairs of tetrodes. (J-K) Correlations across brains of spiking activity for all pairs of multiunit sites (J) and single units (K). Statistical significance was assessed in the same way as for Figure 3E–H.
Figure S4 Details on correlations in the two-chambers sessions, related to Figure 4. (A-B) Neural activity simultaneously recorded from two brains on example sessions, plotted along with the behaviors of the two bats during the sessions. (A) Mean normalized LFP power in the 1–29 Hz band. Same tetrodes and session as shown in Figure 4D, top panel. (B) Single unit activity. Same session as shown in Figure 4E. Correlations between the example neural activity traces are indicated above each plot. See Figure 4D–F for mean normalized LFP power in the 30–150 Hz band and multiunit activity.
(C) Quantification of behavioral correlation across bats in two-chambers sessions (mean ± STD across sessions). Note that while the correlations of active behaviors remained as low as in the one-chamber sessions, the correlations of resting and active bouts were much lower (compare with Figure 1C). Thus, the behavioral correlations of the resting and active bouts seen in one-chamber sessions were the results of social coordination between bats, rather than by-products of any stereotyped behavioral patterns that bats might independently follow.
(D-F) Comparisons of correlations between one-chamber and two-chambers sessions for the same pairs of tetrodes (D, normalized LFP power in the 30–150 Hz band; E, in the 1–29 Hz band) or the same pairs of multiunit sites (F) from different brains. Each dot is one pair of tetrodes (D-E) or one pair of multiunit sites (F), comparing their correlations on a one-chamber session and a two-chambers session. Each pair of one-chamber and two-chambers sessions being compared happened on the same day, with one session immediately following the other without movement of the recording electrodes, thus allowing direct comparison for the same pairs of tetrodes and recording sites. Note that neural correlations across brains fell apart when bats no longer shared a social environment, even as they continued to share similar sensory environments and behavioral contexts.
(G-J) Histograms of correlations across brains pooled across two-chambers sessions and all pairs of bats. Each row of panels shows data from one type of two-chambers sessions (schematized on the left side, described in Figure 4A–C). (G-H) Correlations across brains of LFP power in the high frequency band (G) and the low frequency band (H) for all pairs of tetrodes. (I-J) Correlations across brains of spiking activity for all pairs of multiunit sites (I) and single units (J). Note that neural activity showed weak to no correlations across brains on all types of two-chambers sessions. Statistical significance was assessed in the same way as for Figure 3E–H.
Figure S5 Estimation of movement magnitude, related to Figure 5. (A) Normalized movement magnitude (the movement speed of the neural recording device estimated from video tracking) of one bat on an example session, shown along with the manually annotated behaviors of the bat (top). Note that movement magnitude was at a nearly constant, low level when the bat was resting, and it was high and more variable when the bat was active. The zoomed-in plot shows a 10-minute segment of the session that further illustrates the correspondence between movement magnitude and behavior.
(B-C) The mean (B) and variance (C) of normalized movement magnitude were calculated in 1-second windows, independently z-scored for each session and bat and averaged across all windows that corresponded to either resting or active behaviors. Plotted are mean ± STD across sessions and bats. *, p<0.05, Wilcoxon signed rank test. See STAR Methods for details.
Figure S6 Timescales of correlations across brains, and comparison of neural correlation with behavioral correlation, related to Figure 6. Results shown separately for LFP power in the 30–150 Hz band (A-D), the 1–29 Hz band (E-H), multiunit sites (I-L), and single units (M-P), on one-chamber sessions (A, C, E, G, I, K, M, O) and two-chambers sessions (B, D, F, H, J, L, N, P).
(A-B, E-F, I-J, M-N) The same analysis as in Figure 6C–D, showing distributions of |Δθ| as a function of timescale. In one-chamber sessions, correlations across brains were strongest and extended over the widest range of timescales for LFP power in the 30–150 Hz band (A), and were weaker and extended over narrower ranges of timescales for LFP power in the 1–29 Hz band (E) and multiunit sites (I). On the other hand, in two-chambers sessions, these signals show no correlations at most timescales (B, F, J). Results for single units for both one-chamber (M) and two-chambers sessions (N) show generally weak correlations that do not extend over wide range of timescales.
(C-D, G-H, K-L, O-P) The same analysis as in Figure 6E–F, showing behavior |Δθ| minus neural |Δθ|, as a function of timescales, averaged across sessions. Each plot shows a number of solid lines, each one showing the comparison of neural correlation with the correlation of one behavior. In one-chamber sessions, neural correlation is stronger than behavioral correlation for all behavior at multiple timescales for LFP power in the 30–150 Hz band (C). For LFP power in the 1–29 Hz band (G) and multiunit sites (K), neural correlation is stronger than behavioral correlation for a subset of behaviors, at a smaller range of timescales. For single units (O), neural correlation is weaker or comparable to behavioral correlation. In two-chambers sessions, neural correlation is comparable to behavioral correlation for all types of neural signals and all behaviors (D, H, L, P), suggesting that the neural correlations on two-chambers sessions were entirely a reflection of behavioral correlation. Only behaviors whose total duration exceeded 1% of the session duration on average (averaged across bats and across sessions, separately for one-chamber and two-chambers sessions) were considered for this analysis. The analysis of “resting” behavior here is equivalent to the analysis of resting/active bouts in Figure 6E–F.
Figure S7 Comparing correlations during matched behaviors and various interaction states, related to Figures 5 and 7. (A) Average correlation during behaviorally matched time periods on one-chamber and two-chambers sessions (mean ± SEM across behavior pairs).
(B) Average correlation during behavioral-sequence-matched time periods on one-chamber and two-chambers sessions (mean ± SEM across behavioral sequence pairs; STAR Methods).
(C) On one-chamber sessions that included a non-neural bat (black), sometimes one neural bat (orange in the illustration) was interacting with the non-neural bat, while the other neural bat (green in the illustration) was not engaged in any interaction (blue dotted box). The analogous situation in two-chambers sessions entails a neural bat interacting with a non-neural bat in one chamber, and the neural bat in the other chamber not interacting (purple dotted box). Bar plots show the average correlation under these two conditions (mean ± SEM across time points). Note that while the schematic only illustrates the case where the “orange bat” was the one interacting, for the actual analysis, any neural bat could be the one interacting.
Note that despite the matched behaviors or states of social interactions, in most cases correlation was significantly higher when bats shared the same social environment, and when they did not share a social environment, their neural activity showed weak to no correlations.
(D-E) Average correlation during non-interaction behaviors and during interactions (mean ± SEM), for LFP power in the 30–150 Hz band (D), and for multiunit sites (E), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions.
(F-G) Average correlation during non-interaction behaviors that preceded other non-interaction behaviors, and during non-interaction behaviors that preceded interactions, for LFP power in the 30–150 Hz band (F), and for multiunit sites (G), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions (mean ± SEM).
(A)-(G) are the same analyses as Figure 5C, D, F, Figure 7C, D, E, F, respectively, but using Pearson correlation coefficient instead of instantaneous correlation index; note that results using these two measures are consistent with each other. Note that the analysis in Figure 5E matches single time windows and therefore cannot be performed using Pearson correlation coefficient.
(H-I) Average correlation during interaction behaviors that preceded non-interaction behaviors, and during interaction behaviors that preceded other interaction behaviors (mean ± SEM), for LFP power in the 30–150 Hz band (H), and for multiunit sites (I), averaged across all pairs of tetrodes, all pairs of bats, and all one-chamber sessions.
(J-K) Same as (H)-(I), but using instantaneous correlation index.
*, p<0.05, one-tailed Wilcoxon signed rank test (A)-(B) or one-tailed Wilcoxon rank sum test (C)-(K).