Concentration–QT Modeling Following Inhalation of the Novel Inhaled Phosphodiesterase‐4 Inhibitor CHF6001 in Healthy Volunteers Shows an Absence of QT Prolongation

Abstract

Concentration‐QTcF data obtained from two phase I studies in healthy volunteers treated with a novel phosphodiesterase‐4 inhibitor currently under development for the treatment of chronic obstructive pulmonary disease were analyzed by means of mixed‐effects modeling. A simple linear mixed‐effects model and a more complex model that included oscillatory functions were employed and compared. The slope of the concentration‐QTcF relationship was not significantly greater than 0 in both approaches, and the simulations showed that the upper limit of the 90% confidence interval around the mean ΔΔQTcF is not expected to exceed 10 ms within the range of clinically relevant concentrations. An additional simulation study confirmed the robustness of the simple linear mixed‐effects model for the analysis of concentration‐QT data and supported the modeling of data obtained from studies with different designs (parallel and crossover).

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

 The E14 International Conference on Harmonization guideline supports a model‐based analysis of concentration–QT data to exclude a significant QT prolonging effect. However, only a few real case examples have been published to illustrate the application.

• WHAT QUESTION DID THIS STUDY ADDRESS?

 Does the novel phosphodiesterase‐4 inhibitor CHF6001 prolong the QT interval at clinically relevant concentrations?

Is the pooling of QT data obtained from different studies with different designs (single‐ascending dose vs. multiple‐ascending dose) appropriate for model‐based QT analysis?

Is the application of a complex model with oscillatory functions providing any benefit when compared with a simple, linear mixed‐effect model?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

 CHF6001 is not expected to significantly increase the QT interval for clinically relevant concentrations.

An analysis of pooled data for concentration‐QT modeling is more powerful than separately analyzing the individual studies or study parts.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

 This analysis may encourage the concentration‐QT analysis of pooled phase I studies with a simple linear mixed‐effect model.

In 2015, the International Conference on Harmonization E14 guidance addressed the use of concentration–QTc (C‐QTc) modeling as the primary analysis for assessing proarrhythmic risks of new drugs in the early clinical phase as an alternative to performing a thorough QT (TQT) study.1 In a TQT study, the primary end point typically is the time‐matched mean difference in baseline‐adjusted QTc between the drug and placebo at each timepoint. A drug is deemed to exert negligible proarrhythmic risk (negative TQT study) if the upper limit of the one‐sided 95% confidence interval (CI; or two‐sided 90% CI) of the largest mean effect excludes 10 ms at all timepoints. This way of analyzing the data usually results in large, resource‐demanding, and expensive TQT studies in order to have sufficient power to exclude QT prolongation. C‐QTc modeling has the advantage of using data from all doses and timepoints allowing one to reduce the size of a TQT study or even replace it by collecting QT measurements in phase I trials. Single‐ascending dose (SAD) and multiple‐ascending dose (MAD) studies are well suited for collecting electrocardiogram (ECG) data because they often include supratherapeutic doses, thereby covering the wide concentration range requested by the guideline.1 Recently, Garnett et al.2 provided recommendations on how to plan and conduct a definitive QTc assessment of a drug using C‐QTc modeling in early‐phase clinical pharmacology and TQT studies. A critical recommendation is the use of a prespecified linear mixed‐effect (LME) model as the primary analysis to exclude a 10‐milliseconds QTc prolongation effect.

The potential for QT prolongation of CHF6001, a potent and selective phosphodiesterase‐4 (PDE‐4) inhibitor for the treatment of chronic obstructive pulmonary disease (COPD), was investigated using the C‐QTc approach. PDE‐4 is a family of enzymes that catalyze the degradation of adenosine 3′,5′‐monophosphate and cyclic guanosine monophosphate to their corresponding 5′‐nucleotide monophosphates. Therefore, PDE‐4 inhibitors act by increasing adenosine 3′,5′‐monophosphate, in turn leading to an anti‐inflammatory effect. Roflumilast, an oral PDE‐4 inhibitor, has been approved in many countries worldwide for use in patients with severe COPD associated with chronic bronchitis and a history of COPD exacerbation.3, 4, 5, 6 Unlike roflumilast, CHF6001 has been specifically designed and formulated to be delivered via inhalation, a route of administration that has the potential to avoid the gastrointestinal adverse effects that are characteristic of oral therapy in this class.7, 8

In this work, the C‐QT relationship of CHF6001 following administration to healthy volunteers was investigated using the LME model and an alternative model incorporating cosine functions to describe the circadian rhythm of the QT change during the day. In addition, a simulation study was performed to evaluate the operating characteristics of both models under various study designs.

Methods

Study design and treatment

Study CCD‐1006‐PR‐0048 (first in human (FIH)) and study CCD‐06001AA1‐08 (Extension) were randomized, double‐blind, placebo‐controlled studies in healthy participants to investigate the safety, tolerability, and pharmacokinetics of inhaled CHF6001. Both studies consisted of SAD and MAD parts, and the cohorts in the SAD and MAD parts were independent from each other. In the SAD parts of the two studies, single doses of CHF6001 ranging from 0.02 to 4.8 mg or placebo were administered via Aerolizer (Novartis AG. Kohlenstrasse 84, 4056 Basel, Switzerland) (FIH) or NEXThaler (Chiesi Farmaceutici S.p.A.. Via Palermo, 26 A, Parma, Italy) (Extension). Every participant received placebo as well as 2 to 3 different doses in multiple periods separated by at least 1 week of washout. In the MAD part of the FIH study, doses of 0.1, 0.3, 0.6, 1.2, or 1.6 mg or placebo were administered once daily in parallel cohorts, whereas in the Extension study 1.2, 2, or 2.4 mg or placebo were given twice daily.

Both studies were conducted in accordance with the Declaration of Helsinki and the principles of Good Clinical Practice. Study protocols and amendments were approved by independent ethics committees. All participants provided written informed consent prior to study enrollment.

ECG collection

ECG recording were performed using a 12‐lead digital Holter recorder (Mortara H12+, Mortara Inc, Welch Allyn 7865 N 86th St, Milwaukee, WI 53224, United States). The 12‐lead ECGs were extracted from the Holter ECG in triplicate. The extraction was performed at the following timepoints just before the blood sampling:

• FIH study SAD part: 0 (predose), 0.5, 1.5, 3, 8, 12, and 24 hours.

• FIH study MAD part (once daily), days 1 and 7: 0 (predose), 0.5, 1.5, 3, 8, 12, and 24 hours; days 2 to 6: predose.

• Extension study SAD part: 0 (predose), 0.5, 1, 2, 4, 8, 12, 24, and 48 hours.

• Extension study MAD part (twice daily), days 1, 8, 14: 0 (predose), 0.5, 1, 2, 4, 8, and 12 hours.

Note that the ECG measurements on day 8 in the Extension study were not included in the analysis because only a single pharmacokinetic (PK) sample (trough) was taken that day. Likewise, the 3‐hour measurement in the FIH study was excluded because at that timepoint no PK sample was taken.

The raw QT intervals were corrected for heart rate using Fridericia's method (QTcF). The arithmetic mean of triplicate QTcF measurements per timepoint was used in the data analysis.

C‐QT modeling

Two modeling approaches were employed.

First, we used the baseline‐adjusted QTcF (ΔQTcF) as the dependent variable analyzed with the recommended LME model recently reported according to the following equation (referred to as the LME model)2:

$$\begin{array}{cc}\hfill \mathrm{\Delta }\text{QTcF}=& (\text{INT}+{\mathrm{\eta }}_0)+\text{TRT}+(\text{SL}+{\mathrm{\eta }}_1)\times \mathit{Conc}+\text{TIME}\hfill \\ & +\text{BL.effect}\times ({\text{QTcF}}_0-\overline{{\text{QTcF}}_0})+\mathrm{ϵ}\hfill \end{array}$$

where INT is the intercept associated with a normally distributed random effect variable η₀, TRT is a parameter accounting for potential imbalance between placebo and active treatment groups (Θ_PLC if placebo, 0 for active treatment), SL is the slope of the concentration‐QT relationship associated with the random effect variable η₁, Conc is the observed plasma concentration of CHF6001, and TIME accounts for the natural time variation of QTcF throughout the day, treating scheduled time after dose as a categorical covariate. BL.effect adjusts for the deviation of the individual baseline measurement QTcF₀ from the overall mean baseline $\overline{{\text{QTc}}_0}$; ϵ is the additive residual error with a different magnitude (standard deviation) for each study.

Second, we used the observed QTcF measurements as dependent variable and an estimation of the diurnal change in QTcF with cosine function (referred to as the cosine model), similar to the model proposed by Grosjean and Urien.9 In contrast to the LME model, for the cosine model, stepwise techniques were employed to find the function that best described the data. One, two, and three cosine terms were tested during model building, guided by significant changes to the objective function (OFV). A linear slope, the maximal efficacy (Emax), and the sigmoidal E_max model were tested to describe the drug effect. The equation of the final model is shown in the Results section.

All analyses were performed with NONMEM 7.310 and Perl‐speaks‐NONMEM 4.4.811 using the first‐order conditional estimation with interaction method.

QT simulations

To assess if the upper limit of the two‐sided 90% CI around the predicted ΔQTcF and placebo‐adjusted QTcF (ΔΔQTcF) exceeds 10 ms at a clinically relevant concentration, simulations were performed using the final QT models from both approaches. Uncertainty and interindividual variability in the estimated model parameters were taken into account. A total of 1,000 replicates with 2,000 patients (1,000 placebo, 1,000 active) each were simulated, and the ΔΔQTcF was computed along the concentration axis.

In addition, a simulation study was conducted to investigate the influence of the following factors in QT modeling: the study design (SAD and MAD separately or jointly analyzed), the number of participants enrolled in the study design, the true QT slope, and the model used to analyze the QT data (cosine vs. LME model). The parameter estimates of the final models were used except for the slope parameter. For this, the following three different values of the slope were explored: no effect (zero slope), a slope resembling a high effect (0.00162 ms/pg/mL, corresponding to an average increase in QTcF of 10 ms at the peak plasma concentration (C_max) following twice‐daily dosing of 2.4 mg), and a slope representing an intermediate effect (0.00081 ms/pg/mL, half the high‐effect slope). In addition, because the final cosine model estimated on the study data did not include an interindividual variability component on the slope, this was incorporated in the simulations using the same interindividual variability that was estimated in the LME model.

In total, 33 scenarios were evaluated, as shown in Table  1 .

Table 1.

Overview of simulation scenarios

Study design	Doses	Number of participants	Slope	No. of scenarios
SAD (4 periods/participants)	0, 2.4, 4.0, 4.8 mg	12, 24, 36, 48	Zero, intermediate, high	12
MAD (parallel)	0, 1.2, 2.0, 2.4 mg twice daily	12, 24, 36, 48	Zero, intermediate, high	12
SAD/MAD	As above	12/36, 24/24, 36/12	Zero, intermediate, high	9

MAD, multiple‐ascending dose; SAD, single‐ascending dose.

Each scenario was simulated with the cosine model and analyzed with both models using NONMEM, leading to a total of 66 (33 × 2) combinations.

Plasma concentrations were simulated with a previously described population PK model.10 The simulation output was processed in R (version 3.2.513) to automatically create all of the NONMEM control stream files and the associated data sets. For the SAD study design, QT observations were simulated at times 0, 0.5, 1, 2, 4, 8, 12, 24, and 48 hours, i.e., a total of nine observations per patient and period. In the MAD study design, QT observations were collected at times 0, 0.5, 1, 2, 4, 8, 12, and 24 hours at day 1 and day 14, i.e., a total of 16 observations per patient. All simulations were performed using Simulo 7.1.0.14

Postprocessing

For each replicate, control stream files were run automatically using NONMEM. The parameter estimates of the NONMEM output file for each replicate were then imported in R to compute the 90% CI around the mean ΔΔQTcF at a concentration of 6189 pg/mL (typical C_max at day 14 for a dose of 2.4 mg twice daily as derived from the PK model). For each scenario, the rate of false positive (i.e., 90% CI of predicted ΔΔQTcF, including 10 ms when true effect was 0 or 5 ms) and false negative outcomes (i.e., upper limit of 90% CI ΔΔQTcF < 10 ms when true effect was 10 ms) was calculated. In addition, the mean error (bias) and imprecision (root mean squared error (RMSE)) for each scenario were derived as follows:

$$\%\text{bias}=100\times \frac{{\sum }_{k=1}^N({\text{slope}}_k-{\text{slope}}_{\mathrm{true}})}{N\times {\text{slope}}_{\mathrm{true}}}$$

$$\%\text{RMSE}=100\times \frac{\sqrt{\frac{\sum _{k=1}^N{({\text{slope}}_k-{\text{slope}}_{\mathrm{true}})}^2}{N}}}{{\text{slope}}_{\mathrm{true}}}$$

where slope_k is the slope estimate of the k ^th replicate, and N is the number of replicates per scenario (500).

Results

Analysis data

A total of 122 participants were available for data analysis in the two studies, 74 in the FIH study and 48 in the Extension study. As the MAD parts were executed in a parallel fashion, 22 participants (9 in Extension, 13 in FIH) did receive placebo only, whereas the remaining 100 participants did receive at least one dose of CHF6001 and plasma concentration measurements could be obtained. In total, 1808 QT measurements were subject to modeling. Demographics of the study population are shown in Table S1 .

LME modeling results

In this model, no stepwise model building was applied as this model is prespecified. As recommended by Garnett et al.,2 a study effect was included on the residual error to account for differences in the error magnitude. The interindividual variabilities in intercept and slope were evaluated using an unstructured covariance matrix.

The intercept and slope were estimated at −1.09 (90% CI, −2.14 to −0.0485) ms and −0.000576 (90% CI, −0.00112 to −0.0000316) ms per pg/ml, respectively. The visual predictive check in Figure  1 indicated that the model generally described the data well, apart from a slight underprediction of ΔQTcF in the SAD part of the Extension study. The overall goodness‐of‐fit and residual plots are provided in Figure S1 . The parameter estimates of the LME model are provided in Table S2 .

Figure 1.

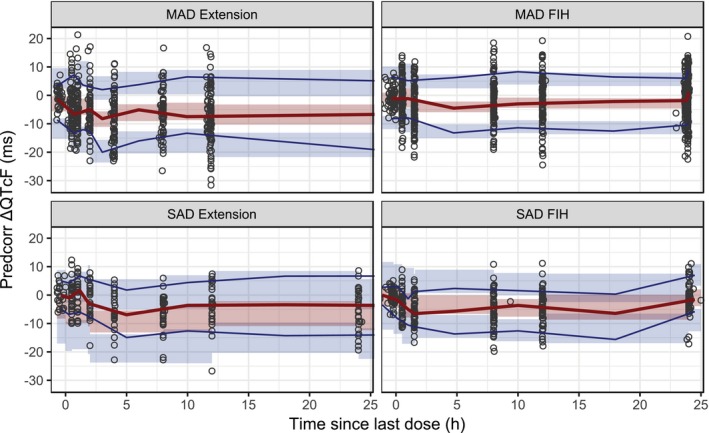
Visual predictive check of the linear mixed‐effect model. Solid lines are the 10th and 90th (blue) and 50th (red) percentiles of the observed data, and the shaded areas are the 95% confidence intervals around the corresponding percentiles of the predictions. Observed and simulated ∆QTcF data were prediction corrected (predcorr) before plotting. FIH, first in human; h, hour; MAD, multiple‐ascending dose; SAD, single‐ascending dose.

The simulations with the LME model showed that the upper limit of the 90% CI is not expected to exceed 10 ms in the concentration range of interest (Figure S2 ).

Cosine model results

Using only placebo data of the two studies, a baseline model for QTcF with three cosine functions was found to best describe the diurnal QTcF variation as it had a significantly lower OFV when compared with a model with only one or two cosine terms. The final baseline model is described by the following equation:

$$\begin{array}{c}\hfill \text{QTcFbase}=\\ \hfill \text{BASE}\times \left(1+\text{AMP}\times cos\left(\frac{2\pi \left(\text{TAD}-\text{PIK}\right)}{24}\right)+\text{AMP}2\times cos\left(\frac{2\pi \left(\text{TAD ‐ PIK2}\right)}{12}\right)+\text{AMP}3\times cos\left(\frac{2\pi \left(\text{TAD ‐ PIK}3\right)}{6}\right)\right)+ϵ\end{array}$$

where BASE is the overall 24‐hour average baseline; AMP, AMP2, AMP3 are the amplitudes of the cosine functions; and PIK, PIK2, and PIK3 are the time shift parameters relative to time after dose (TAD).

The parameter PIK was estimated to be close to zero and was therefore fixed to zero in the final baseline model. Interindividual variability was evaluated for all parameters and eventually retained on BASE, AMP, and AMP2.

None of the tested drug‐effect models did improve the model fit significantly. The linear model showed only a 2.5‐unit lower OFV when compared with the model without drug effect. Regardless, the slope parameter was kept in the model to make it comparable to the LME approach and allow simulations accounting for uncertainty in the slope estimate.

Higher baseline QTcF values in the Extension study when compared with the FIH study were observed (Table S1 ). This is plausible because in the FIH study, only male subjects participated, whereas in the Extension study, female participants were also allowed, and it is known that the QT interval is on average higher in females than in males.¹⁸ In fact, the inclusion of sex as a covariate on baseline did significantly improve the fit (ΔOFV: −9.5), estimating a 3.3% shorter baseline QT interval in males than in females.

In addition, the baseline value was higher in the SAD part than in the MAD part of the Extension study. This imbalance was incorporated in the model as a covariate on the baseline QTcF, estimating a 3.8% higher baseline QT interval in that study part when compared with the rest. The covariate relationships were included in a multiplicative fashion in the following model as shown:

$$\text{QTcF}=\text{QTcFbase}\times \left(1+{\mathrm{\Theta }}_{\mathrm{SEX}}\right)\times \left(1+{\mathrm{\Theta }}_{\mathrm{STUPART}}\right)+\text{SL}\times Conc$$

where Θ_SEX is the fractional change of QTcFbase for males, and Θ_STUPART the fractional change for patients in the SAD part of the Extension study.

Body weight and age were also tested as covariates, but they did not improve the model fit significantly.

A visual predictive check was performed for the final cosine model to investigate if model simulations correspond to the observed medians and ranges for the entire population (prediction corrected and split by study and study part) as shown in Figure  2 .

Figure 2.

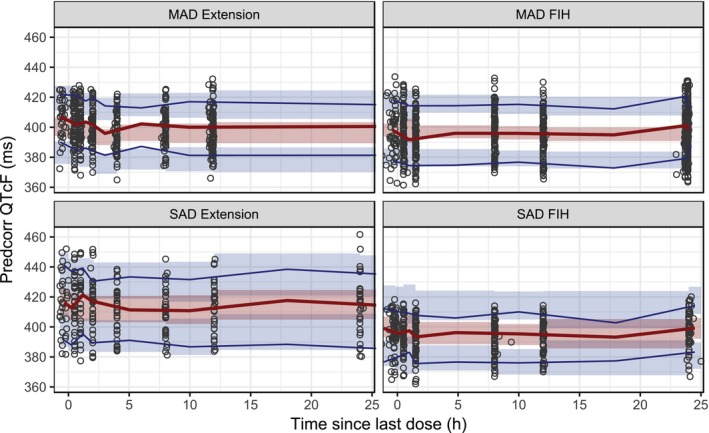
Visual predictive check of the cosine model. Solid lines are the 10th and 90th (blue) and 50th (red) percentiles of the observed data, and the shaded areas are the 95% confidence intervals around the corresponding percentiles of the predictions. Observed and simulated QTcF data were prediction corrected (predcorr) before plotting. FIH, first in human; h, hour; MAD, multiple‐ascending dose; SAD, single‐ascending dose.

Goodness‐of‐fit and residual plots also showed excellent agreement in the model predictions with the observed data (Figure S3 ). The parameter estimates of this model are shown in Table  2 .

Table 2.

Parameter estimates of the cosine model

Parameter	Estimate	SEa	90% CIb	Shr., %
Fixed effects parameters
BASE (ms)	409	3.28	404 to 415	–
AMP	0.00401	0.00106	0.00226 to 0.00575	–
PIK (h)	0 (fixed)	–	–	–
AMP2	0.0137	0.00591	0.00398 to 0.0234	–
PIK2 (h)	10.6	0.273	10.2 to 11.1	–
AMP3	0.00641	0.00588	−0.00327 to 0.0161	–
PIK3 (h)	21.3	0.0976	21.1 to 21.4	–
Slope (10−3 ms/pg/mL)	0.191	0.228	−0.184 to 0.567	–
% difference in BASE for males	−3.33	0.848	−4.73 to −1.94	–
% difference in BASE for SAD in Extension	3.83	1.12	1.98 to 5.68	–
Random effects parameters
IIV BASE (CV%)c	3.28	0.0019	2.95 to 3.58	0.453
IIV AMP (CV%)c	78.1	0.14	41.4 to 110	35.9
IIV AMP2 (CV%)c	20.3	0.113	0 to 34.9	68.9
Residual variability
Residual error, SD (ms)	5.65	0.149	5.4 to 5.9	4.8

BASE, baseline QTcF; AMP, AMP2, AMP3, amplitudes of the baseline QTcF; CI, confidence interval; h, hour; IIV, interindividual variability; PIK, PIK2, PIK3, time shift parameters of the cosine function; SAD, single‐ascending dose; SD, standard deviation; SE, standard error; CV, coefficient of variation; Shr., Shrinkage.

^aSE on SD scale for variability estimates. ^bAsymptotic confidence interval derived from NONMEM standard errors. ^cCoefficient of variation (CV) = 100*sqrt(exp(variance) − 1).

The concentration‐QT simulations with this model showed that the upper limit of the 90% CI around the predicted mean ΔΔQTcF did not exceed 10 ms for concentrations up to 17,500 pg/mL (Figure  3 ). It is worth noting that the highest observed concentration in the studies was 12,770 pg/mL, and the geometric mean C_max at day 14 following twice‐daily dosing of 2.4 mg was about 5,700 pg/mL.

Figure 3.

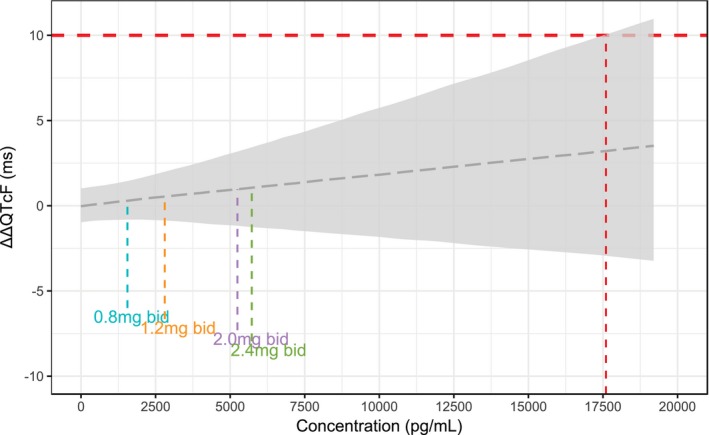
Simulation of the concentration–ΔΔQTcF relationship using the cosine model. The vertical lines indicate the geometric mean peak plasma concentration at steady state observed with twice‐daily (bid) dosing using the NEXThaler device in the Extension study. The gray area is the 90% confidence interval. The red vertical line marks the concentration at which the upper limit of the 90% confidence interval is predicted to cross the 10‐milliseconds limit.

Simulation study comparing the cosine and LME models

The simulation study indicated that the rate of false negative results is close to the nominal rate of 5% for the scenario with a true ΔΔQTcF of 10 ms at the C_max of a dose of 2.4 mg given twice daily. As can be seen in Figure S4 , the cosine model performed slightly better than the LME model as it produced fewer false negatives. However, it is worth noting that the data were simulated with the cosine model and therefore favoring to some extent this model when used also in the analysis step. The rate of false negatives does not appear to depend on the study design.

The rate of false positives (which is equivalent to 100% power to exclude a 10‐milliseconds change) is shown in Figure  4 . As expected, the rate of false positives decreases with an increasing number of participants. The cosine model appears more powerful to exclude a 10‐milliseconds change when compared with the LME model. If the true effect size is zero, it would require a study size of at least 24 individuals to achieve a false positive rate of <20%. When the true ΔΔQTcF is 5 ms, the rate of false positives is >35% for all design scenarios with the LME model, which is markedly higher when compared with the lowest rate obtained with the cosine model (~20%). The bias in the population estimate of the slope was between −2.5 and +4% in all scenarios for both models. On the other hand, the imprecision (i.e., RMSE) was clearly dependent on the true effect and the design, with a higher true slope and/or a higher number of participants leading to a more precise estimation of the slope (Figure S5 ). The cosine model tends to be more precise in the estimation of the slope, particularly in the SAD design. For a pooled analysis of data from the MAD and SAD studies (or study parts), the distribution of patients to either part does not appear to be important in the present case, as the three SAD/MAD scenarios with 48 participants in total results in similar bias/imprecision as the SAD 48 or MAD 48 scenarios. The combined SAD/MAD analyses outperform the scenarios with the corresponding number of patients analyzed separately. For example, a pooled analysis of 24 participants from a SAD study and 24 from a MAD study has a much lower false positive rate than analyzing the studies separately.

Figure 4.

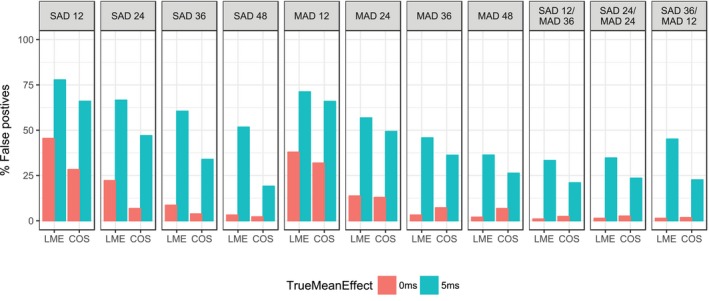
Rate of false positive study outcomes when simulated with the cosine (COS) model and a true slope of 0 or 0.00081 ms/pg/mL (corresponding to an average increase in QTcF of 5 ms at the peak plasma concentration following twice‐daily dosing of 2.4 mg). The labels on each panel indicate the design (single‐ascending dose (SAD) or multiple‐ascending dosing (MAD)) and the number of participants. LME, linear mixed effect.

Discussion

Two different mixed effects models were investigated to analyze C‐QT data of CHF6001. In both modeling approaches, the estimated slope was not significantly greater than zero. Consequently, simulations showed that the upper limit of the 90% CI around the predicted ΔΔQTcF did not exceed 10 ms in the concentration range studied. In fact, when extrapolating further for the purpose of illustration, the 10‐milliseconds limit is predicted to be reached at a concentration of ~18,000 pg/mL, much higher than the highest observed concentration (12,700 pg/mL) and the geometric mean C_max (~5,700 pg/mL) observed after multiple twice‐daily dosing of 2.4 mg.

Based on the current state of knowledge, it can be concluded that CHF6001 is unlikely to significantly prolong the QT interval at a clinically relevant dose.

The two methods resulted in slightly different estimates for the drug effect (slope), albeit with overlapping confidence intervals. The cosine modeling approach did not employ any baseline adjustment of the dependent variable but, rather, estimated baseline as a model parameter with an associated random effect. Dansirikul et al.¹⁶ showed that this way of handling baseline in model‐based analysis is superior in terms of bias and precision when compared with methods that use a baseline‐adjusted dependent variable. Random effect parameters, covariates, number of cosine terms and the shape of the drug effect were investigated using the traditional stepwise, model‐building technique, guided by the reduction of the OFV, plausibility of parameter estimates, and diagnostic plots. However, this approach has been challenged as being too subjective and prone to introduce (model) selection bias to be acceptable for the analysis of QT data with the purpose to exclude a significant QT prolongation.2 Instead, Garnett et al.2 proposed the application of a prespecified LME model, which is robust enough to be applicable “as is” in most situations, not requiring any model building. As the recommendations on C‐QT modeling using early‐phase clinical data are still relatively recent, comparing the different approaches is of value to gain confidence in the conclusions derived from the simple LME model. Huh and Hutmacher15 conducted a simulation study comparing the more biological oscillatory models to the LME model and showed that the LME model provided similar accuracy and precision as a model with one or two cosine terms.

Here we present a comparison with real data, where both approaches allowed the conclusion of absence of a significant QT‐prolonging effect of CHF6001. In addition, we also conducted a simulation experiment to investigate the effect of combining data from study parts with a different design: a crossover SAD (all participants received placebo) and a parallel MAD (only a group of the participants received placebo). Combining data from different studies with different design is the “bread and butter” of population (PK) pharmacodynamic modeling with nonlinear mixed effects modeling. However, the pooling of data across studies is not commonly done in the analysis of QT data. Our simulation results showed that the pooled analysis of SAD and MAD is more powerful than separately modeling data from small SAD or MAD studies (or study parts). This is of course not surprising as the total number of individuals is higher in the pooled analysis. Nevertheless, it illustrates the advantage of mixed effects modeling as a method to analyze data across multiple trials with one single model—appropriately accounting for the variability between and within participants and potential imbalances between studies. Of course, in the present case the quality of the ECG measurements in the two studies was comparable, which may not always be the case in practice. Moreover, in the present simulations the influence of differences in sampling schedule between pooled studies has not been systematically evaluated, and there might be situations where this is relevant.

The influence of the design is qualitatively similar for both analysis models, although the cosine model results in consistently better performance statistics. However, the simulations were performed using the cosine model that was subsequently used in the estimation step with the same initial estimates, which may favor to some extent the accuracy and precision of this model. Nevertheless, the LME model demonstrated its general applicability as a robust model for the analysis of QTc data obtained in regular SAD and MAD studies. It conserved the nominal type I error rate of 5% to a reasonable extent, which is an important aspect from a regulatory point of view, and also showed that a false negative conclusion in our analysis of CHF6001 is unlikely. As others have pointed out, the advantage of the LME model is that it can be prespecified and applied with minimal modifications to analyze the concentration‐QT relationship and assess the potential of a significant QT prolongation at a clinically relevant dose.2, 14 Besides the practical advantage of a faster analysis time compared with usually time‐consuming model development, the risk of model selection bias is reduced. The advantage of the alternative model‐building strategy, here resulting in the cosine model with oscillatory functions, is that these models will fit the data better and hence provide more precise estimates of the drug‐effect parameter. This, however, is less relevant for the purpose of excluding a significant QT prolongation with the model (i.e., zero or very small slope). On the other hand, if the LME model suggests a significant effect, it is recommended to continue with more thorough model development to obtain more precise parameter estimates. Such a model can then be used to optimize the design of a subsequent confirmatory study through simulations.

Conclusions

Based on concentration‐QT modeling, the novel‐inhaled PDE‐4 inhibitor CHF6001, developed for the treatment of COPD, is not expected to prolong the QT interval significantly at clinically relevant concentrations.

Additional simulations suggest that when the quality of the ECG measurement is comparable, pooling data from studies (and study parts) with different designs (parallel/crossover) and analyzing the data by means of LME modeling are more powerful than analyzing the study data separately.

Funding

This work was funded by Chiesi Farmaceutici.

Conflict of Interest

K.J., A.Ä., N.L., and A.L. were employed by SGS, a contract research organization that has received funding from Chiesi Farmaceutici. M.C., M‐A.N., and M.G. are employees of Chiesi Farmaceutici.

Author Contributions

K.J., M.C., and A.L. wrote the manuscript. K.J., M‐A.N., M.G., M.C., and A.L. designed the research. N.L., M‐A.N., M.G., M.C., and A.L. performed the research. K.J., A.Ä., N.L., and A.L. analyzed the data.

Supporting information

Figure S1. Goodness of fit and residual diagnostic plots for the LME model. DV is ΔQTcF, PRED, population predictions; IPRED, individual predictions; CWRES, conditional weighted residuals; IWRES, individual weighted residuals.

Figure S2. Simulation of the concentration‐ΔΔQTcF relationship using the LME model. The vertical dashed lines indicate the geometric mean C_max at steady state observed with twice‐daily dosing using the NEXThaler device in the Extension study. The gray area is the 90% confidence interval.

Figure S3. Goodness of fit and residual diagnostic plots for the cosine model. The clusters seen in the DV vs. PRED plots are the results of the covariates. DV is ΔQTcF, PRED, population predictions; IPRED, individual predictions; CWRES, conditional weighted residuals; IWRES, individual weighted residuals.

Figure S4. Rate of false negative outcomes, when the data were simulated with the cosine model (COS) and a true slope of 0.00162 ms/pg/mL, corresponding to an increase in QTcF of 10 milliseconds at the C_max following twice‐daily dosing of 2.4 mg. The labels on each panel indicate the design (single‐ascending dose (SAD) or multiple‐ascending dosing (MAD)) and the number of participants.

Figure S5. Bias (mean error) and imprecision (root mean squared error) when the data were simulated with the cosine model (COS) and a true slope corresponding to an increase in QTcF of 5 or 10 ms at the C_max following twice‐daily dosing of 2.4 mg. The labels on each panel indicate the design (single‐ascending dose (SAD) or multiple‐ascending dosing (MAD)) and the number of participants.

Table S1. Participant characteristics and baseline QTcF.

Table S2. Parameter estimates of the LME model.

Data S1. Excerpt of the concentration‐QTcF data used to build the LME and COS models.

Code S1. LME model file.

Code S2. COS model file.