Bayesian compositional regression with structured priors for microbiome feature selection

Summary:

The microbiome plays a critical role in human health and disease, and there is a strong scientific interest in linking specific features of the microbiome to clinical outcomes. There are key aspects of microbiome data, however, that limit the applicability of standard variable selection methods. In particular, the observed data are compositional, as the counts within each sample have a fixed-sum constraint. In addition, microbiome features, typically quantified as operational taxonomic units (OTUs), often reflect microorganisms that are similar in function, and may therefore have a similar influence on the response variable. To address the challenges posed by these aspects of the data structure, we propose a variable selection technique with the following novel features: a generalized transformation and z-prior to handle the compositional constraint, and an Ising prior that encourages the joint selection of microbiome features that are closely related in terms of their genetic sequence similarity. We demonstrate that our proposed method outperforms existing penalized approaches for microbiome variable selection in both simulation and the analysis of real data exploring the relationship of the gut microbiome to body mass index (BMI).

1. Introduction

The human microbiome consists of the trillions of microbial cells harbored by each person, primarily as bacteria in the gut (Turnbaugh et al., 2007). It has been estimated that there are more than 10 times as many microbial cells in the human body as our own somatic or germ cells, and that the gut microbiome may contain more than 100 times as many genes as the human genome (Bäckhed et al., 2005). Due to the emergence of next-generation sequencing techniques, which enable comprehensive profiling of the microbiome, there is growing recognition of its critical role in health and disease. In particular, there is increasing evidence showing that the composition of the gut microbiota may be associated with inflammation and metabolic disorders, which are common features of obesity and cancer (Cani and Jordan, 2018). The gut microbiome has also been linked to diabetes (Qin et al., 2012), cardiovascular disease (Jie et al., 2017), and response to immunotherapy (Gopalakrishnan et al., 2018).

The development of next-generation technologies has made it possible to directly quantify the composition of the microbiome using DNA sequencing. Although whole genome shotgun sequencing is increasing in popularity, due to its relative expense, most microbiome studies to date rely on sequencing of the 16S ribosomal RNA (rRNA) gene, a highly conserved region of the bacterial genome, which is the most commonly used molecular marker in microbial ecology (Case et al., 2007). Standard pipelines for analyzing 16S rRNA sequencing data include initial processing steps, such as demultiplexing and quality filtering (Nguyen et al., 2016). The processed sequences are then clustered based on sequence similarity into operational taxonomic units, or OTUs, which represent a group of closely related microorganisms (Ursell et al., 2012).

Analysis of microbiome data is challenging for several reasons. The number of sequencing reads observed in a single sample is an arbitrary total that may vary widely, and the observed counts assigned to a given OTU can only be interpreted relative to this fixed sum. The data are therefore compositional, and require specialized methods for analysis to avoid misleading results (Gloor et al., 2017). In particular, standard analytic methods such as regular linear regression are not applicable to microbiome data (Li, 2015). An additional challenge in the analysis of microbiome data is its high dimensionality. Sparse modeling approaches are therefore important to reduce noise in estimation and enable the identification of key features. The features identified can guide the future development of microbiome interventions. For example, understanding which bacteria increase cancer risk or drive response to therapy could inform recommendations on diet, probiotic use, or choice of antibiotics, as these factors play an important role in shaping the state of the microbiome.

Although the raw number of features for analysis may be large, many OTUs represent organisms that are phenotypically similar and have related function. This relatedness is captured by the phylogenetic tree structure, which reflects evolutionary relationships among the organisms surveyed based on their DNA sequence similarity. OTUs may also be mapped to existing taxonomic tree structures using bacterial 16S rRNA databases. Taxonomy refers to the grouping of microorganisms into the traditional Kingdom-Phylum-Class-Order-Genus-Species hierarchy, while phylogeny aims to capture the series of branching events during evolutionary history which separated the various bacterial species observed in the sample. Taxonomic classification is coarser than phylogenetic organization, but easier to compare across studies due to the standardized naming system. Although the relatedness among OTUs is a source of dependence, knowledge of the tree structure can be used to reduce dimension or improve power (Washburne et al., 2018). For example, microbiome data may be analyzed after aggregating the OTUs into a higher taxonomic level such as species, genus, or family.

In the current work, we propose a Bayesian sparse regression model for microbiome data which addresses the challenges outlined above, including the compositional nature of the data, the high dimension, and the relatedness among the features. To address the fixed-sum constraint, we propose a generalized transformation, which enables us to impose sparsity directly on the p regression coefficients. To take advantage of the phylogenetic tree information, we formulate a structured prior to link the selection of closely related organisms, which are likely to have a similar effect on the outcome.

The paper is organized as follows. Section 2 provides a brief review of existing methods for compositional data analysis and microbiome regression. In Section 3, we include a detailed description of the proposed modeling approach, including the generalized transformation and the prior formulation. We compare the performance of the proposed method with that of penalization-based approaches on simulated data in Section 4, and apply these methods to real data examining the association of the gut microbiome to body mass index (BMI) in Section 5. We conclude with a discussion in Section 6.

2. Background

We denote the compositional data by an n × p matrix of variables U = (u_ij), where each row of U is constrained to sum to 1 across the p variables. In the context of microbiome data, these values correspond to the relative abundances of the OTUs. Due to the unitsum constraint, the p components of each observation cannot be interpreted independently, as they are restricted to lie in a (p − 1)-dimensional simplex. In groundbreaking work on this issue, Aitchison (1982) proposed the additive log-ratio transformation. Since some of the observed counts may be 0s, a typical first step in these approaches is to add a small pseudo-count (typically 0.5), and then divide by the sum of the counts within each sample to obtain relative abundances that sum to 1. To link the compositional data with an n × 1 vector of continuous response values y, Aitchison and Bacon-Shone (1984) included the same transformation idea into linear regression and proposed the linear log-contrast model y = Xη_\p + ε, where X = {log(u_ij/u_ip)} is an n × (p − 1) matrix of the additive log-ratio transformed predictor values, taking the p-th predictor as the reference component, η_\p = (η₁, … , η_p−1)^T is the regression coefficient vector, and the noise vector ε has entries independently distributed as $\mathcal{N}(0,{\sigma }^2)$. An intercept term is not included in the model, since it can be eliminated by centering the response and predictor variables.

Several recently proposed methods have extended this framework to propose sparse regression models for microbiome data. In particular, Lin et al. (2014) reformulated the log-contrast model into a symmetric form with a linear constraint by letting ${\eta }_p=-{\sum }_{j=1}^{p-1}{\eta }_j$,

$$\mathit{y}=\mathit{Z}\eta +\epsilon ,\sum _{j=1}^p{\eta }_j=0,$$ (1)

where Z = (logu_ij) is an n × p matrix of log transformed predictor values, and η = (η₁, … , η_p)^T is the vector of regression coefficients. Lin et al. (2014) proposed applying an l₁ penalty to the coefficient vector to perform feature selection. Shi et al. (2016) extended this work by allowing the selection of subcompositions at a fixed taxonomic level. Finally, Lu et al. (2019) considered generalized linear regression analysis with linear constraints for microbiome compositional data.

The approaches developed by Aitchison (Aitchison, 1982; Aitchison and Bacon-Shone, 1984) rely on a transformation of the compositional variables. In the framework of Bayesian variable selection, we would like to instead focus on achieving sparsity of the regression coefficients. We therefore start from the symmetric form of a linear regression with constraints imposed on the parameters. In the remainder of this section, we create a general framework in which we shift the transformation from the compositional covariates to the linear coefficients, using the unified matrix operation T. This framework can accommodate the contrast transformation approach, as well as a generalized transformation that will be discussed in the next section.

Let T represent the contrast transformation matrix. By definition, T must be a p × (p − 1) matrix where each column sums to 0. Based on linear algebra, the p-vector η can be decomposed as η = Tθ + θ₀, where θ is a (p − 1)-vector with no constraints, and θ₀ is a solution to the linear equation 1θ₀ = 0, with the simplest choice being θ₀ = [0, 0, ⋯ , 0]^T. As above, we let U = (u_ij) represent the observed relative abundances, and Z = (log u_ij) represent their log-transformed values. Then the linear model in equation (1) can be expressed as

$$\mathit{y}=\mathit{Z}\mathit{T}\theta +\epsilon =\mathit{X}\theta +\epsilon ,$$ (2)

where X = ZT and θ = (θ₁, … , θ_p−1). In other words, the parameter space degenerates to p−1 dimensions after the contrast transformation T is performed on Z. The additive log-ratio (ALR) and centered log-ratio (CLR) transformations are widely used in microbiome analysis. Both belong to the category of contrast transformations, as they satisfy the constraint that each column sum to zero. We give their explicit matrix form in Supplementary Material Section S1. In the next section, we describe our proposed Bayesian modeling approach which allows the integration of either of these or a generalized transformation within a Bayesian variable selection framework.

3. Proposed model

We now describe our proposed sparse regression model, which has two key aspects designed to address the unique challenges of microbiome data: (1) a novel generalized transformation, which allows us to handle the compositionality of the data while still imposing sparsity directly on the p regression coefficients; and (2) a structured prior that encourages the joint selection of microbiome features based on their genetic sequence similarity. We provide a schematic illustration of our proposed model, which we discuss in detail in the remainder of this section, in Figure 1.

Figure 1:

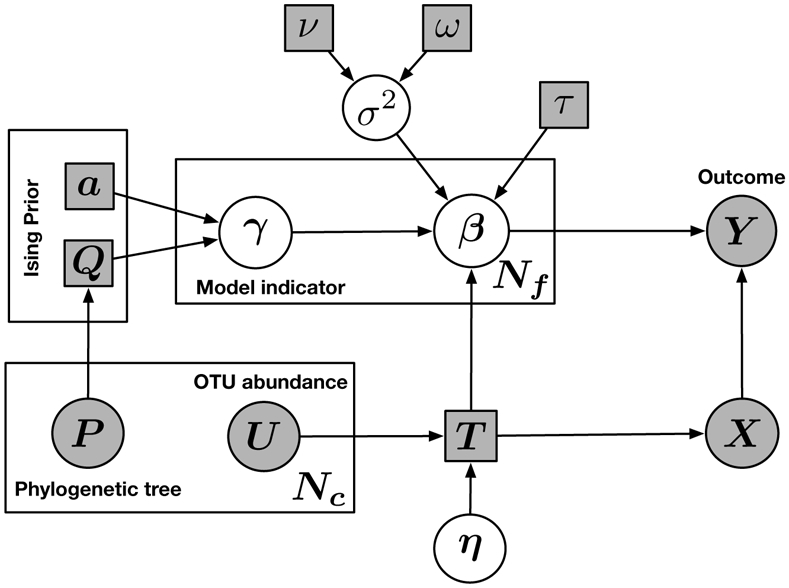
Schematic illustration of the proposed model. Squares indicate fixed parameters; circles indicate random variables. Filled-in squares indicate known values. Filled-in circles indicate observed data. T denotes the transformation matrix. η denotes constrained linear coefficients, while β denotes the unconstrained linear coefficients after transformation. X denotes the transformed covariates. The prior variance of each β is denoted by σ², which is assumed to follow an Inverse Gamma distribution with hyperparameters ν and ω. τ denotes the variance scale of β. N_c denotes the number of covariates. N_f denotes the number of unconstrained parameters. In the Ising prior, a denotes shrinkage parameter, and Q denotes the dependence structure.

3.1. Generalized transformation

One obvious drawback of the additive log-ratio and centered log-ratio transformations is that the transformed design matrix X depends on the choice of transformation and requires that one of the original variables be dropped. To address this limitation, we propose an generalized transformation, which allows us to avoid dropping variables and satisfy the permutation and selection invariance properties described in Lin et al. (2014). Our proposed approach allows us to maintain a parameter space of dimension p, corresponding to the number of observed variables. We write the linear model of equation (1) in the standard form

$$\mathit{y}=\mathit{X}\beta +\epsilon ,$$ (3)

where X = Z and β = η. Instead of conducting the contrast transformation on the linear coefficients in the regression model (2), we can perform a generalized transformation on the parameters and build the linear combination ${\sum }_{j=1}^p{\beta }_j$ into the Bayesian prior. We define the generalized transformation T as

$$\mathit{T}={\left[\begin{array}{c}\hfill {\mathit{I}}_p\hfill \\ \hfill c\times 1_p^{\prime }\hfill \end{array}\right]}_{(p+1)\times p},$$ (4)

where c is a constant and $1_p^{\prime }$ is a p dimensional row vector of 1s. Recalling the generalized lasso (Tibshirani et al., 2011), we can see that T plays a similar role as the penalty matrix in the generalized lasso formulation, which can be used to express structural or geometric constraints. We will provide details on the prior formulation in the next subsection. In addition to imposing shrinkage on the regression coefficients, we propose shrinkage of the linear sum term. This is controlled by the parameter c, where larger values of c induce more shrinkage on ${\sum }_{j=1}^p{\beta }_j$.

We now summarize the main differences between the contrast transformations (2) and the proposed generalized transformation (3) in terms of estimation of the regression coefficients. When using a contrast transformation, the linear regression has a parameter space of dimension p − 1. Within the Bayesian modeling framework, we can apply the ALR or CLR transform, and then estimate the parameter vector θ in the p−1 space. However, to obtain the estimated effect sizes for the originally measured variables, we then have to transform these estimates to the original p space via $\widehat{\eta }=\mathit{T}\widehat{\theta }$. When using the generalized transformation, we obtain estimates in the original p-dimensional space, which can be directly interpreted as the estimated coefficients.

3.2. Prior formulation

In our Bayesian variable selection approach, we rely on a latent indicator γ_i ∈ {0, 1} to represent the inclusion of the ith covariate in the model. We can therefore index the model space by the vector γ. Under model ${\mathcal{M}}_{\gamma }$, we assume that the n-dimensional response vector y follows a multivariate normal distribution

$$\mathit{y}\mid {\mathcal{M}}_{\gamma },{\beta }_{\gamma },{\sigma }^2\sim \mathcal{N}({\mathit{X}}_{\gamma }{\beta }_{\gamma },{\sigma }^2{\mathit{I}}_n),$$ (5)

where X_γ denotes a modified version of the X matrix including only those columns corresponding to nonzero entries in γ, and β_γ represents the corresponding linear coefficients for the selected covariates. The coefficient vector β_γ has length $p_{\gamma }={\sum }_i{\gamma }_i$.

From the frequentist perspective, the regression coefficients are fixed, but unknown, quantities. In this framework, linear algebra can be used to transform the constrained parameters to unconstrained parameters in a lower-dimensional space. These transformations need to satisfy the “contrast” property that each column of the transformation matrix sums to 0. From a Bayesian perspective, the regression coefficients are random. In this framework, we can assume a multivariate prior on the parameters, so that their random draws sum to zero. A natural idea inspired by the g-prior (Zellner, 1986) is the introduction of a specific structure into the Gaussian distribution. Suppose that the prior follows the form ${\beta }_{\gamma }\mid {\mathcal{M}}_{\gamma },{\sigma }^2,{\tau }^2\sim \mathcal{N}(0,{\tau }^2{\sigma }^2{\mathit{R}}_{\gamma })$. If the sum of all the elements of R_γ equals zero (which we refer to as the zero-constrained property), then the sum of the normal random variables Σ_γβ_γ will be zero because the variance of the sum becomes 0. We name the multivariate Gaussian prior that satisfies the zero-constrained property the z-prior. To give an explicit form for the z-prior, we use the generalized transformation T_γ to build the linear combination ${\sum }_{j=1}^p{\beta }_j$ into a multivariate Gaussian prior. We define the z-prior of β_γ conditional on ${\mathcal{M}}_{\gamma }$ as

$${\beta }_{\gamma }\mid {\mathcal{M}}_{\gamma },{\sigma }^2,{\tau }^2\sim \mathcal{N}(0,{\sigma }^2{\tau }^2({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma }{)}^{-1}),$$ (6)

where T_γ consists of the columns of the generalized transformation T defined in equation (4) corresponding to the selected variables, i.e., the non-zero entries of γ.

The term $({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma }{)}^{-1}$, which appears in the prior variance of equation (6) above, has the explicit form ${\mathit{I}}_{p_{\gamma }}-\frac{c^2}{1+c^2{p}_{\gamma }}{1}_{p_{\gamma }}^{\prime }{1}_{p_{\gamma }}$. Thus, the sum of the linear coefficients ${\sum }_{i\in \gamma }{\beta }_i$ follows a normal distribution with mean 0 and variance $\frac{p_{\gamma }}{1+c^2{p}_{\gamma }}{\sigma }^2{\tau }^2$. When c becomes large, the variance approaches 0, which implies that more shrinkage is imposed on ${\sum }_{i\in \gamma }{\beta }_i$. We can even let c be + ∞; then the term $({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma }{)}^{-1}$ converges to ${\mathit{I}}_{p_{\gamma }}-\frac{1}{p_{\gamma }}{1}_{p_{\gamma }}^{\prime }{1}_{p_{\gamma }}$ and $\text{var}({\sum }_{i\in \gamma }{\beta }_i)=0$. For more details, please see Section S3 of the Supplementary Material. This zero constraint on the sum of the coefficients is needed to handle compositionality, but is flexible enough to accommodate modifications, such as shrinkage on any individual β_i. Finally, the z-prior is analytically tractable, because the variance $\frac{p_{\gamma }}{1+c^2{p}_{\gamma }}{\sigma }^2{\tau }^2$ is less than $\frac{1}{c^2}{\sigma }^2{\tau }^2$, which does not depend on p_γ. For example, if we set c to be 100, then the variance will be sufficiently small. Thus, we successfully reframe the linear constraint on the coefficients in equation (3) to a joint Gaussian prior in the Bayesian framework.

We now discuss the link between our z-prior and the g-prior, which has a similar form. As described below, the z-prior addresses both the high dimensionality and compositionality of the data, and is therefore better suited to our applications than the g-prior. The g-prior (Zellner, 1986) has been widely adopted because of its simple form, which requires the specification of only a single parameter g, and because it has convenient analytical and computational properties. The g-prior and extensions are still quite popular in Bayesian inference (Liang et al., 2008; Bayarri et al., 2012). The variance of the g-prior is proportional to the inverse of the Fisher information matrix ${\sigma }^2({\mathit{X}}_{\gamma }^T{\mathit{X}}_{\gamma }{)}^{-1}$. However, in the context of high-dimensional data where p ⪢ n, such as microbiome data, ($({\mathit{X}}_{\gamma }^T{\mathit{X}}_{\gamma })$ is typically not invertible. Even if this matrix were invertible, a traditional g-prior is designed for Euclidean space rather than compositional space. In particular, the sum of all the elements in the matrix $({\mathit{X}}_{\gamma }^T{\mathit{X}}_{\gamma }{)}^{-1}$ is not equal to zero, so the traditional g-prior does not satisfy zero-constrained property. For more details, please see Section S2 of the Supplementary Material.

We introduce the Bayesian model and prior for the contrast transformation as follows. For the linear model of equation (2), which relies on a contrast transformation, the Bayesian likelihood is $y\mid {\mathcal{M}}_{\gamma },{\theta }_{\gamma },{\sigma }^2\sim \mathcal{N}({\mathit{X}}_{\gamma }{\theta }_{\gamma },{\sigma }^2{I}_n)$, where θ_γ = {θ_i∣i ∈ γ}. The coefficient θ_γ has p_γ − 1 degrees of freedom. We can impose a normal shrinkage prior on η_γ = T_γθ_γ to achieve sparsity in the original parameter space. So we define the normal shrinkage prior of θ_γ as ${\theta }_{\gamma }\mid {\mathcal{M}}_{\gamma },{\sigma }^2,{\tau }^2\sim \mathcal{N}(0,{\sigma }^2{\tau }^2({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma }{)}^{-1})$, where T_γ includes the columns of contrast transformation corresponding to the variables selected under γ.

We assume that σ² follows a conjugate inverse-gamma prior

$${\sigma }^2\mid \nu ,\omega \sim \text{InvGamma}(\frac{\nu }{2},\frac{\nu \omega }{2}).$$ (7)

For the prior on γ, the simplest choice is an independent Bernoulli prior P(γ_i = 1) = p. In the next section, we describe a more sophisticated alternative: a structured hyperprior which enables us to link the selection of closely related taxa.

3.3. Ising prior

To address the challenge of the relatedness among the observed taxa, a number of recent publications have attempted to incorporate information from the phylogenetic tree into statistical modeling. Wang et al. (2017) proposed a tree-guided regularization method to select subcompositions corresponding to sets of features grouped based on their position in the tree. This approach, however, has limited computational scalability. Xiao et al. (2018) developed a mixed modeling approach which incorporates the correlation among OTUs based on their evolutionary distance, but does not allow for feature selection. In the Bayesian framework, Li and Zhang (2010) proposed the use of an Ising prior, which captures known information about the structure among the covariates, for high-dimensional variable selection; this method is not designed for compositional data, however. Finally, Wadsworth et al. (2017) take the microbiome data as the response variable, and perform selection to identify environmental or clinical factors that affect the taxa abundances.

Since we are interested instead in treating the microbiome variables as predictors, we must incorporate the relatedness of with compositional covariates within the Bayesian variable selection framework. In our regression model, we would like to favor the inclusion of taxa which have similar genetic sequences to other taxa identified as relevant, as they are likely to play a similar functional role and have similar impact on clinical outcomes. To achieve this goal, we integrate prior information on the similarity of the taxa into an Ising prior on the variable inclusion indicators. Specifically, as shown in Figure 1, we rely on the phylogenetic tree P to capture the similarity between OTUs (U). We re-express this tree as a matrix Q, where large entries reflect close dependence, small entries reflect more distant relations, and 0s represent that no dependence is assumed. Let a = (a₁, … , a_p)^T be a vector and Q = (q_ij)_p×p be a symmetric matrix of real numbers, where q_ij = 0 for all features i and j whose selection is not linked under the prior. Then the Ising prior distribution for γ is defined as

$$P(\gamma )=e^{{\mathit{a}}^T\gamma +{\gamma }^T\mathit{Q}\gamma -\psi (\mathit{a},\mathit{Q})},$$ (8)

where ψ(a, Q) represents the normalizing constant. The shrinkage parameters a, which take negative values, control the sparsity of γ. The smaller a_i is, the more likely it is a priori that the ith covariate will not be included. The entries in the structural parameter Q control the strength of association between the selection of OTUs i and j. The larger q_ij is, the more likely it is that the ith and jth covariates will be jointly selected. Therefore, the Ising prior given in equation (8) acts to favor inclusion of OTUs that are close in genomic distance. When q_ij = 0 for all pairs (i, j), the Ising prior reduces to an independent Bernoulli prior.

3.4. Posterior inference

We now describe the Markov chain Monte Carlo (MCMC) method for generating samples from the posterior. We formulate an efficient Gibbs sampling approach by integrating out the parameters β and σ², so that we only need to update the inclusion indicators γ. Estimates of β and σ² can then be obtained post-MCMC conditional on the selected model. In the following, we assume that ν = ω = 0 in the inverse-gamma prior of equation (7). Given this choice of hyperparameters, the inverse-gamma reduces to a non-informative prior.

Marginal likelihood.

After integrating out β and σ², the marginal likelihood of y given model ${\mathcal{M}}_{\gamma }$ and the fixed hyperparameter τ² is

$$p(\mathit{y}\mid {\mathcal{M}}_{\gamma },{\tau }^2)=(\pi {)}^{-n∕2}\Gamma (\frac{n}{2})({\tau }^2{)}^{-p_{\gamma }∕2}\mid {\mathit{A}}_{\gamma }{\mid }^{-1∕2}\mid ({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma }){\mid }^{1∕2}[{\mathit{y}}^T\mathit{y}-{\mathit{y}}^T{\mathit{X}}_{\gamma }{\mathit{A}}_{\gamma }^{-1}{\mathit{X}}_{\gamma }^T\mathit{y}{]}^{-\frac{n}{2}},$$ (9)

where ${\mathit{A}}_{\gamma }={\mathit{X}}_{\gamma }^T{\mathit{X}}_{\gamma }+\frac{1}{{\tau }^2}({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma })$. More details on the derivations are given in Supplementary Material Section S4.

MCMC algorithm.

We now outline the construction of the Gibbs sampler on γ, which searches over the space of models {0, 1}^p. Let γ_(−i) = {γ_j : j ≠ i}, and I_(−i) be {γ_j = 1 : j ≠ i}, the set of indices for the selected variables other than i. τ is fixed at 1. The posterior distribution of γ given the data can be decomposed by Bayes formula as

$$P({\gamma }_i=1\mid {\gamma }_{(-i)},\mathit{y})=\frac{P({\gamma }_i=1\mid {\gamma }_{(-i)})}{P({\gamma }_i=1\mid {\gamma }_{(-i)})+F({\gamma }^{\prime }\mid \gamma {)}^{-1}\times P({\gamma }_i=0\mid {\gamma }_{(-i)})},$$ (10)

where F(γ′∣γ) is the Bayes factor for the indicator vectors γ′ and γ, and is defined as

$$F({\gamma }^{\prime }\mid \gamma )=\frac{\mid {\mathit{A}}_{\gamma }{\mid }^{1∕2}\mid ({\mathit{T}}_{{\gamma }^{\prime }}^{\prime }{\mathit{T}}_{{\gamma }^{\prime }}){\mid }^{1∕2}}{\mid {\mathit{A}}_{{\gamma }^{\prime }}{\mid }^{1∕2}\mid ({\mathit{T}}_{\gamma }^{\prime }{\mathit{T}}_{\gamma }){\mid }^{1∕2}}{\left(\frac{{\mathit{y}}^T\mathit{y}-{\mathit{y}}^T{\mathit{X}}_{\gamma }{\mathit{A}}_{\gamma }^{-1}{\mathit{X}}_{\gamma }^T\mathit{y}}{{\mathit{y}}^T\mathit{y}-{\mathit{y}}^T{\mathit{X}}_{{\gamma }^{\prime }}{\mathit{A}}_{{\gamma }^{\prime }}^{-1}{\mathit{X}}_{{\gamma }^{\prime }}^T\mathit{y}}\right)}^{\frac{n}{2}}.$$ (11)

From equation (8), the conditional distribution of γ_i under the prior is given by

$$P({\gamma }_i\mid {\gamma }_{(-i)})=\frac{e^{{\gamma }_i{a}_i+{\sum }_{j\in I_{(-i)}}{q}_{ij}{\gamma }_i{\gamma }_j}}{1+e^{a_i+{\sum }_{j\in I_{(-i)}}{q}_{ij}{\gamma }_j}}.$$

In each iteration, we select an index i at random, and then sample a Bernoulli random variable with probability P(γ_i = 1∣γ_(−i), y) following equation (10). Since we update only one index at a time, p_γ′ − p_γ will be 1 or −1, and γ′ and γ differ only in the ith position. If the proposed value equals the current γ_i, the model is unchanged; otherwise, we update γ accordingly. To accelerate the computationally intensive step of evaluating F(i∣γ_(−i)), we adopt the same procedure to calculate the matrix inverse and determinant as in Li and Zhang (2010).

Bayesian model selection approaches often use the scheme of calculating the posterior probability of a given model. However, this strategy is infeasible in high dimensions because any specific model is highly likely to be sampled only a small number of times in a workable length of MCMC. For our setting, it is therefore more appropriate to calculate the posterior marginal of each indicator p(γ_i = 1∣y), adopting an approach used by Ibrahim et al. (2002). We obtain posterior marginals by dividing the number of iterations where γ_i = 1 by the total number of iterations excluding the burn-in. To perform selection, we then threshold the posterior marginal probabilities following the median model approach of Barbieri et al. (2004), where covariates i with p(γ_i∣y) ⩾ 0.5 are positives, while those with posterior probabilities < 0.5 are negatives.

Conditional on the selected model ${\mathcal{M}}_{\gamma }$, the posterior density of the non-zero coefficients β_γ follows a multivariate t-distribution, with mean ${\widehat{\beta }}_{\gamma }={\mathit{A}}_{\gamma }^{-1}{\mathit{X}}_{\gamma }^T\mathit{y}$ and covariance $\frac{1}{n-2}{C}_{\gamma }{\mathit{A}}_{\gamma }^{-1}$, where $C_{\gamma }={\mathit{y}}^T\mathit{y}-{\mathit{y}}^T{\mathit{X}}_{\gamma }{\mathit{A}}_{\gamma }^{-1}{\mathit{X}}_{\gamma }^T\mathit{y}$. The posterior density of σ² follows an inverse-gamma distribution with the shape parameter $\frac{n}{2}$ and the scale parameter $\frac{1}{2}{C}_{\gamma }$. The mean is given by $\frac{C_{\gamma }}{n}$. For justification of the prior on σ², please refer to Supplementary Material Section S5.

4. Simulations

In this section, we compare our proposed Bayesian variable selection method using either the additive log ratio transformation (Bayesian ALR), centered log ratio transformation (Bayesian CLR), or the generalized transformation (Bayesian generalized) with the following existing approaches:

lasso ref: the lasso applied after dropping a reference variable, where the estimated coefficient of the reference variable is taken as −1 × the sum of the remaining coefficients

lasso std: a naïve application of the standard lasso, simply ignoring the sum constraint

lasso comp: the penalized approach proposed in Lin et al. (2014) which addresses the compositionality of the data

group lasso: the group lasso of Yuan and Lin (2006), which addresses structured dependence

Importantly, none of the first three lasso approaches take into account the phylogenetic relationship among the bacterial taxa, while the group lasso, which enables selection based on a pre-specified group structure, does not handle the compositional constraint. To compare the variable selection performance in settings with both independent and dependent compositional predictors, we design two simulation scenarios: one with independent covariates, and one with structured dependence among the covariates. We assume the following data-generating model,

$${\mathit{y}}_i=\sum _{j=1}^p{X}_{ij}{\beta }_j+{\epsilon }_i,\sum _{j=1}^p{\beta }_j=0,i=1,\dots ,n,$$ (12)

where ε_i is independent and identically distributed as $\mathcal{N}(0,{\sigma }^2)$.

4.1. Independent covariates

This simulation setup resembles the one included in Lin et al. (2014). We first generate an n × p data matrix O = (o_ij) from a multivariate normal distribution ${\mathcal{N}}_p(\theta ,\Sigma )$, and then obtain the OTU relative abundance matrix U = (u_ij) by the transformation $u_{ij}=e^{2o_{ij}}∕{\sum }_{k=1}^p{e}^{2o_{ik}}$. The variables generated using this approach follow a logistic normal distribution (Aitchison and Shen, 1980). Since the abundances of features in microbiome data often differ by orders of magnitude, we let θ_j = log(0.5p) for j = 1, … , 5 and θ_j = 0 otherwise. To assume that all the covariates are independent, we let Σ = I_p, where I_p is the identity matrix. We generate the responses y_i based on model (12) with β* = (1, −0.8, 0.6, 0, 0, −1.5, −0.5, 1.2, 0, …, 0)^T. We define the signal to noise ratio (SNR) as SNR = mean∣β_(γ=1))∣/σ. To generate settings with SNRs of 1, 5 and 10, we set σ as 0.933, 0.187 and 0.093. We set (n, p) = (100, 1000), and generated 100 simulated data sets for each setting.

For the lasso methods, penalty parameter selection was performed using cross validation. For the group lasso, the specified structure included two groups: one for the true variables, and one for the noise variables. We now describe the parameter choices used in applying the proposed Bayesian methods. For this simulation, which is focused on comparing the methods in a setting with independent predictors, we set the prior parameter Q to be a matrix consisting of 0s. The shrinkage parameter a is chosen to achieve a reasonable model size based on sensitivity analysis (shown in Supplementary Material Section S6). We set $a=-12\times 1_p^{\prime }$ to select approximately 6 covariates. The shrinkage constant c in equation (4) is set to be 10000, and the scaling parameter τ² in equation (6) is set to be 1.

We rely on four performance metrics for our comparison of methods. We compute the prediction error, defined as $\text{PE}=\frac{1}{n_{\text{test}}}({\mathit{y}}_{\text{test}}-{\mathit{X}}_{\text{test}}{\widehat{\beta }}_{\text{train}}{)}^T({\mathit{y}}_{\text{test}}-{\mathit{X}}_{\text{test}}{\widehat{\beta }}_{\text{train}})$, using an independent test sample of size n_test = n. The accuracy of the coefficient estimates is assessed by the l₂ loss $\Vert \widehat{\beta }-{\beta }^{\ast }{\Vert }_2$. To assess the accuracy of variable selection, we report the number of false positives and the number of false negatives, where positives and negatives refer to nonzero and zero coefficients, respectively. The means and standard errors of these performance measures across the 100 simulated data sets for the seven methods under consideration are reported in Table 1. For each simulated data set, we divide the data into ten folds, to enable model fitting on 90 samples, and evaluation on the held-out set of 10 samples; we repeat this procedure 100 times for each simulated data set. For simulation results with different values of n = 50 and p = 30, and with n =100 and p = 200, please refer to Supplementary Material Section S7.

Table 1:

Performance comparison on simulated data with sample size n = 100 and p = 1000 independent covariates

SNR	Method	PE	L2 loss	FP	FN
10	lasso ref	0.003 (0.0001)	0.005 (0.0003)	4.39 (0.26)	0 (0)
	lasso std	0.002 (0.0001)	0.004 (0.0002)	2.85 (0.28)	0 (0)
	lasso comp	0.002 (0.0001)	0.004 (0.0002)	2.28 (0.21)	0 (0)
	group lasso	0.021 (0.001)	0.05 (0.002)	0.29 (0.07)	0 (0)
	Bayesian ALR	0.02 (0.001)	0.04 (0)	0.01 (0.01)	0 (0)
	Bayesian CLR	0.01 (0.0003)	0.003 (0)	0 (0)	0 (0)
	Bayesian general	0.01 (0.0004)	0.003 (0)	0.01 (0.01)	0 (0)
5	lasso ref	0.01 (0.0006)	0.02 (0.001)	4.55 (0.28)	0 (0)
	lasso std	0.01 (0.0004)	0.01 (0.0007)	3.18 (0.28)	0 (0)
	lasso comp	0.01 (0.0005)	0.01 (0.0008)	2.37 (0.23)	0 (0)
	group lasso	0.024 (0.001)	0.05 (0.002)	0.70 (0.12)	0 (0)
	Bayesian ALR	0.04 (0.002)	0.04 (0)	0.02 (0.01)	0 (0)
	Bayesian CLR	0.03 (0.001)	0.005 (0)	0 (0)	0 (0)
	Bayesian general	0.04 (0.004)	0.005 (0)	0 (0)	0 (0)
1	lasso ref	0.27 (0.02)	0.49 (0.06)	4.34 (0.23)	0.10 (0.07)
	lasso std	0.23 (0.02)	0.40 (0.06)	2.92 (0.25)	0.08 (0.06)
	lasso comp	0.23 (0.02)	0.38 (0.06)	2.21 (0.18)	0.07 (0.06)
	group lasso	0.16 (0.008)	0.17 (0.007)	24.69 (0.87)	0 (0)
	Bayesian ALR	0.87 (0.04)	0.09 (0.005)	0.05 (0.02)	0.01 (0.01)
	Bayesian CLR	0.89 (0.03)	0.05 (0.001)	0.02 (0.01)	0 (0)
	Bayesian general	0.82 (0.31)	0.04 (0.001)	0.01 (0.01)	0 (0)

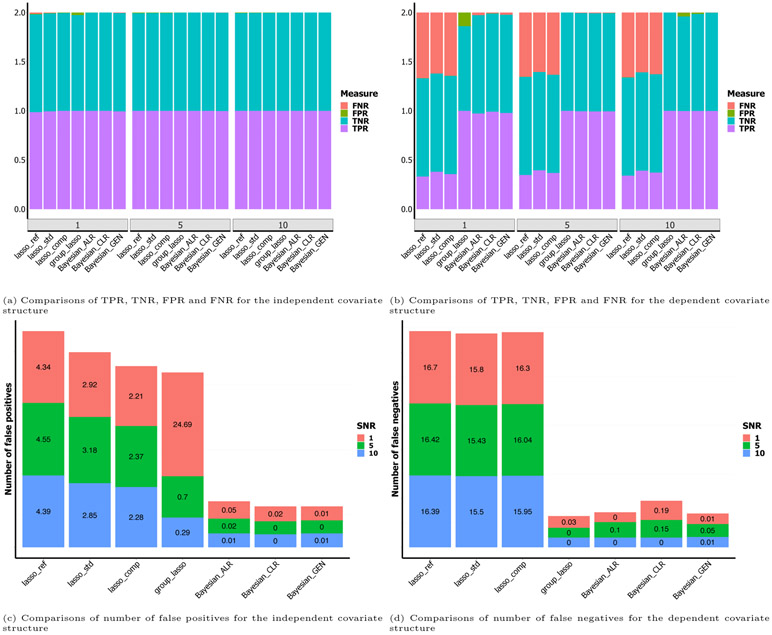
The proposed methods perform much better than existing penalization-based methods in terms of prediction and estimation with low to moderate dimensionality. Although all of the methods achieve similar TPR, TNR, FPR and FNR (Figure 2a), the proposed methods have fewer false positive selections (Figure 2c). As only 5 out of 1000 variables have truly non-zero effects, it is not surprising to observe that TPRs and TNRs of all the methods are approximately 1. This indicates that all methods perform well in this simple scenario. As shown in Table 1, the proposed methods achieve smaller estimation losses and similar numbers of false negatives. Among the penalized approaches, the group lasso identifies fewer false positives than the other lasso variants in settings with higher signal, but its false positive rate increases sharply in the low signal setting: since the group lasso jointly selects entire sets of variables, the false selection of a group results in a large number of false positive covariates. In addition, the standard and group lasso estimators violate the zero-sum constraint on the coefficients, which the proposed methods do not. The variable selection performance of the Bayesian generalized estimator is comparable to that of Bayesian ALR and CLR, but it does not require choosing a reference or dropping any of the observed variables. Moreover, our proposed methods perform better than the lasso methods when the compositional covariates are independent, demonstrating that our modeling approach has advantages even without the incorporation of the Ising prior.

Figure 2:

Bar plots of true positive rates (TPR), false positive rates (FPR), true negative rates (TNR), false negative rates (FNR), number of false positives and number of false negatives for predictions under different scenarios. The sample size n is 100, and the number of covariates p is 1000. The SNR is 1.

4.2. Dependent covariates

This simulation is designed to mimic real microbiome data, where the features have a complex dependence structure. Our simulation setup resembles that of Li and Zhang (2010). We first note that the expression $\{b_0+b_{1}l{\}}_{l=1}^L$ is used to represent the equally spaced sequence from (b₀ + b₁) to (b₀ + b₁ L) with spacing b₁. We let the sample size be n = 100 and number of variables be p = 1000. The true variables are those with γ_j set to be 1, where $j=\{160+20l{\}}_{l=1}^{12}\cup \{560+20l{\}}_{l=1}^{12}$. This corresponds to 24 nonzero coefficients, which are set to ${\beta }_j^{\ast }=[0.88,-1.41,-1.39,-1.15,1.04,0.51,1.21,-1.95,-1.86,1.93,-1.34,-0.85]$ for $j=\{160+20l{\}}_{l=1}^{12}$, and ${\beta }_j^{\ast }=[1.76,-1.66,-0.99,1.48,0.69,1.87,-0.54,0.72,1.35,0.67,-0.81,-0.16]$ for $j=\{560+20l{\}}_{l=1}^{12}$. We let θ_j = log(0.5p), when $j=\{160+20l{\}}_{l=1}^{12}\cup \{560+20l{\}}_{l=1}^{12}$. Among the true predictors, the covariance is assumed to be Σ_ij = 0.75 − 0.0015∣i − j∣, that is, the correlation between two covariates is negatively proportional to their distance (with a maximum of 0.75). To make the scenario more realistic and challenging, we let θ_j = log(0.25p) among the predictors $j=\{444+l{\}}_{l=1}^{16}\cup \{944+l{\}}_{l=1}^{16}$, which are not relevant to the response. The covariance between those predictors is assumed to be Σ_ij = 0.4−0.02∣i − j∣. The coefficients are set to be 0 for all the other covariates and the diagonals of Σ are set to be 1.

We now describe the parameter settings used in applying the Bayesian methods. In real microbiome data sets, the abundances of closely related OTUs are typically correlated, while more distantly related OTUs can be considered to be independent. To capture this structure, the prior parameter matrix Q should be sparse with blockwise nonzero elements, corresponding to compact neighborhoods in the phylogenetic tree P. We construct Q so that it has nonzero entries for the true variables and, to avoid giving advantage to the Bayesian methods, also for the false variables $j=\{44+l{\}}_{l=1}^{16}$, $\{444+l{\}}_{l=1}^{16}$, and $\{944+l{\}}_{l=1}^{16}$. The shrinkage parameter a is chosen to achieve a reasonable model size based on sensitivity analysis (shown in Supplementary Material Section S6) with a range from −30 to 0. We set $a=-11\times 1_p^{\prime }$ to select approximately 24 covariates. All the other parameters are fixed as before. In applying the group lasso, we mimicked the blocks within the Q matrix by specifying six groups, including two groups of correlated covariates with non-zero coefficients corresponding to the true signal, and four groups of noise covariates unrelated to the response.

The means and standard errors of these performance measures across the 100 simulated data sets for the seven methods under consideration are reported in Table 2. The proposed Bayesian methods generally outperform existing methods in terms of prediction and estimation. As shown in Figure 2b, the methods that account for the structure among the covariates, including the proposed methods and the group lasso, achieve smaller FNRs and bigger TPRs. As shown in Figure 2d, these methods also have fewer false negatives. As shown in Table 2, the proposed methods give much smaller estimation losses and prediction errors, and have a comparable number of false positives. As in the simulation with independent predictors, the group lasso has a high false positive rate in the low signal setting. The proposed Ising prior allows a more flexible approach to incorporate structural information, as it encourages, but does not force, joint selection of “nearby” covariates. Therefore, our proposed methods perform better than the lasso methods for data with a dependent covariate structure. Bayesian ALR and CLR have comparable performance to the Bayesian generalized method. The difference between the Bayesian ALR, CLR, and generalized methods is most obvious when the dimensionality is low to moderate and the signal is weak.

Table 2:

Performance comparison on simulated data with structured dependence, sample size n = 100, and p = 1000 covariates

SNR	Method	PE	L2 loss	FP	FN
10	lasso ref	5.18 (0.38)	27.89 (0.42)	1.29 (0.09)	16.39 (0.29)
	lasso std	4.52 (0.32)	26.57 (0.36)	0.20 (0.05)	15.50 (0.28)
	lasso comp	4.89 (0.34)	27.17 (0.40)	0.42 (0.08)	15.95 (0.30)
	group lasso	0.07 (0.003)	0.27 (0.008)	0 (0)	0 (0)
	Bayesian ALR	0.04 (0.005)	0.11 (0.0008)	1.49 (0.46)	0 (0)
	Bayesian CLR	0.03 (0.003)	0.11 (0.0002)	0.51 (0.27)	0 (0)
	Bayesian general	0.05 (0.008)	0.11 (0.002)	1.15 (0.47)	0.01 (0.01)
5	lasso ref	5.15 (0.36)	28.09 (0.42)	1.24 (0.09)	16.42 (0.29)
	lasso std	4.45 (0.31)	26.44 (0.34)	0.19 (0.05)	15.43 (0.27)
	lasso comp	5.02 (0.36)	27.29 (0.42)	0.40 (0.08)	16.04 (0.31)
	group lasso	0.08 (0.004)	0.28 (0.009)	0 (0)	0 (0)
	Bayesian ALR	0.50 (0.18)	0.27 (0.03)	0.70 (0.31)	0.10 (0.06)
	Bayesian CLR	0.33 (0.22)	0.18 (0.05)	0.67 (0.32)	0.15 (0.14)
	Bayesian general	0.30 (0.13)	0.16 (0.02)	0.68 (0.39)	0.05 (0.03)
1	lasso ref	5.47 (0.39)	28.49 (0.47)	1.29 (0.11)	16.70 (0.34)
	lasso std	4.81 (0.33)	27.00 (0.36)	0.13 (0.04)	15.80 (0.27)
	lasso comp	5.20 (0.37)	27.68 (0.43)	0.45 (0.10)	16.30 (0.32)
	group lasso	0.249 (0.013)	0.59 (0.023)	134.56 (31.57)	0 (0)
	Bayesian ALR	2.85 (0.17)	0.60 (0.02)	1.11(0.45)	0.03 (0.02)
	Bayesian CLR	2.71 (0.32)	0.58 (0.05)	1.14 (0.41)	0.19 (0.17)
	Bayesian general	2.08 (0.14)	0.49 (0.01)	1.03 (0.38)	0.01 (0.01)

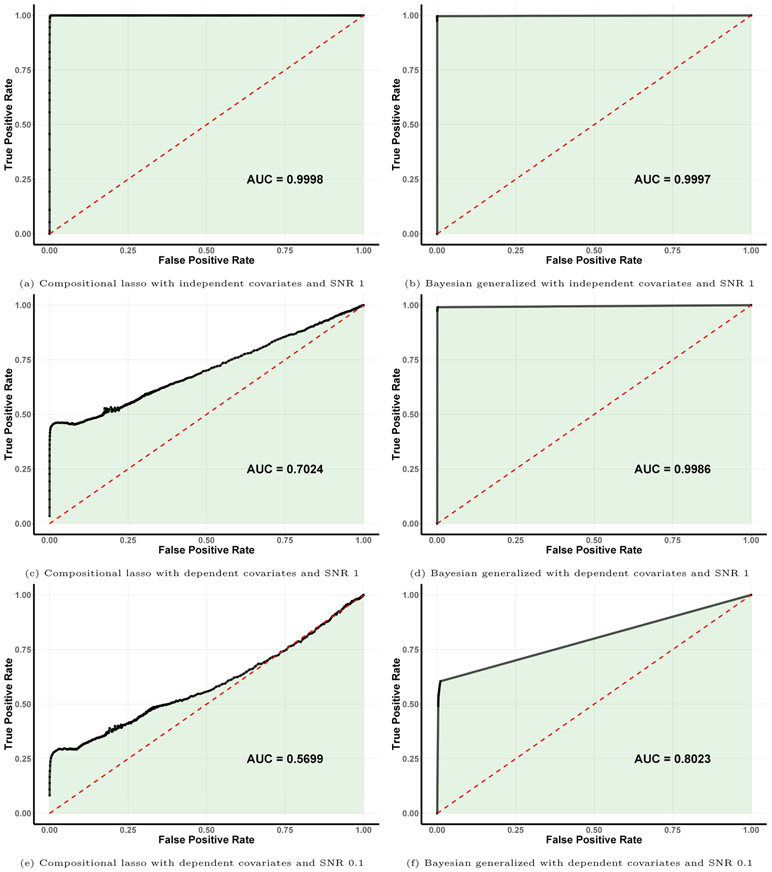
In addition, we compare the performance of the proposed Bayesian generalized method with the compositional lasso (Lin et al., 2014) in scenarios with different combinations of SNR and covariate dependence structure. To assess the accuracy of variable selection across a range of model sizes, we provide receiver operating in Figure 3 along with the area under the curve (AUC), which were obtained by varying the penalty term (for the compositional lasso method) or by changing the posterior threshold of inclusion (for the Bayesian approach). Our results demonstrate that the two methods both achieve almost perfect accuracy (AUC close to 1) for the setting with independent covariates and SNR 1, but that the Bayesian method enables improved selection for the more difficult scenarios with dependent covariates and lower SNR.

Figure 3:

Receiver operating characteristic (ROC) curves of variable selection results for the compositional lasso (left) and the Bayesian generalized method (right), along with the area under the curve (AUC), for progressively more difficult simulation settings: independent covariates (top), dependent covariates with SNR 1 (middle), and dependent covariates with SNR 0.1 (bottom).

The computational speed of the proposed method is quite fast, especially when the true model space is sparse. For all of the above simulations, each MCMC run has 20,000 iterations with the first 15,000 as burn-in. On average for data with the dependent covariate structure, it takes 80 seconds to run 20,000 iterations with an average posterior model size of 24 on an Intel Core(TM) i5-6500 with 3.2GHz CPU.

5. Application to gut microbiome data

The gut microbiome plays an important role in energy extraction and obesity. We illustrate the effectiveness of our proposed method by applying it to data from a study aimed at linking long-term diet with the composition of the gut microbiome (Wu et al., 2011, “COMBO” data), which was also analyzed by Lin et al. (2014). As a part of this study, 16S rRNA data was obtained via 454/Roche pyrosequencing from stool samples of 98 healthy subjects.

The OTU table, phylogenetic tree, and representative sequences were provided to us by the authors of Wu et al. (2011). We transformed the counts into relative abundances after adding a small constant of 0.5 to replace exact zero counts (Aitchison, 2003). We then used “mothur” (Schloss et al., 2009) to obtain taxonomic information on the 1763 OTUs based on the reference Silva Release 128, and obtained 112 genera.

5.1. Construction of prior parameter matrix Q

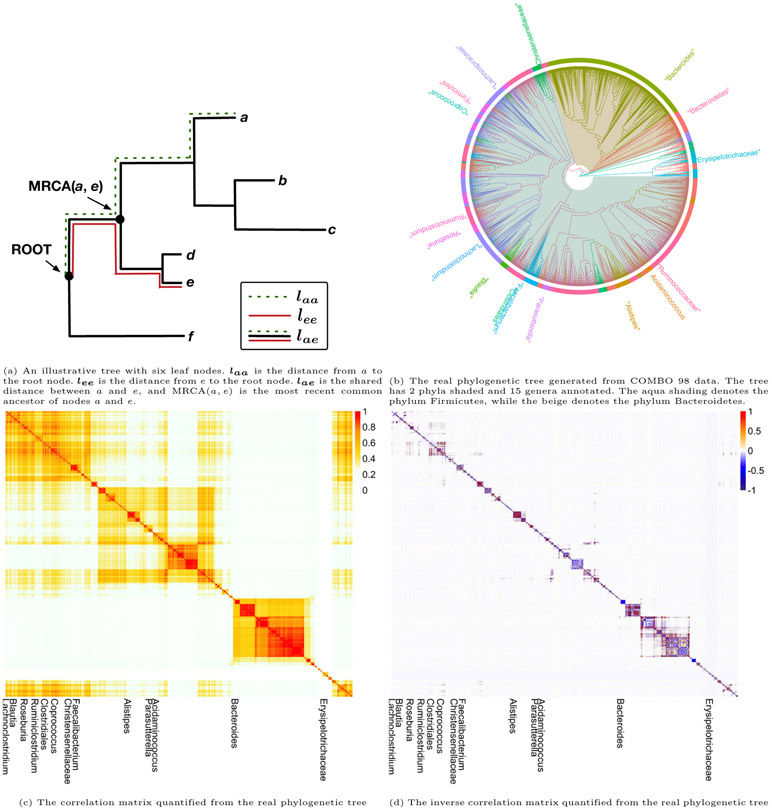
In order to apply our proposed Bayesian variable selection method, we need to determine the prior parameter Q which characterizes the similarity of OTUs based on their evolutionary history. Specifically, we define Q as the inverse of the phylogeny-induced correlation matrix, using either Euclidean correlation or an exponential correlation. Assume that we have p OTUs which belong to a phylogenetic tree P. We define the branch length from the leaf node k to the root node as l_kk, k = 1, … , p, and l_ij as the shared branch length between leaf nodes i and j. As shown in Figure 4a, the shared distance between a and e is l_ae, and the distances to the root node for a and e are l_aa and l_ee, respectively. A phylogenetic variance-covariance matrix V computes the shared distance between all pairs of leaf nodes within a phylogenetic tree, and is defined as V = (l_ij)_p×p. Following de Vienne et al. (2011), the Euclidean correlation matrix can be constructed as $\left(c_{ij}=\frac{l_{ij}}{\sqrt{l_{ii}}\sqrt{l_{jj}}}\right)$. This matrix can be calculated using published R packages (Paradis, 2011).

Figure 4:

Quantification procedures from phylogenetic tree to graphical structure to correlation/precision matrix.

The patristic distance between OTUs (i.e., the length of the shortest path linking OTU i and j in the tree) is denoted as d_ij. It can be computed as d_ij = l_ii + l_jj − 2l_ij. As seen from Figure 4a, the patristic distance between a and e can be calculated as d_ae = l_aa + l_ee − 2l_ae. Then the exponential correlation between OTUs i and j can be described using the evolutionary model C_ij(ρ) = e^−2pd_ij, i, j = 1, … , p (Martins and Hansen, 1997; Xiao et al., 2018). The Euclidean correlation can be considered as a special case of the exponential correlation (see Supplementary Material Section S7), because larger values of ρ (smaller c_ij) group OTUs into clusters at a lower phylogenetic depth (where a cluster is defined as a group of highly correlated OTUs). In this case study, we use the Euclidean correlation structure for analysis. We include other options in our code.

We plot the phylogenetic tree of the 1763 OTUs from the COMBO 98 data in Figure 4b. Most OTUs belong to two phyla: Firmicutes and Bacteroidetes. At the genus level, Bacteroides contains the largest number of OTUs. We plot the heatmap of the correlation and inverse correlation matrix between the OTUs in Figure 4c and 4d. Compared with the correlation matrix, its inverse (i.e., the structural prior parameter Q) is sparser and more focused on the highly correlated regions. The phylogenetic tree structure is consistent with the correlation, as the OTUs belonging to either Firmicutes or Bacteroidetes are clustered together. The shrinkage parameter a is set up as (−9, −9, … , −9) based on sensitivity analysis (Supplementary Material Section S6). All the other parameters are set the same as in the simulation studies.

5.2. Selection results

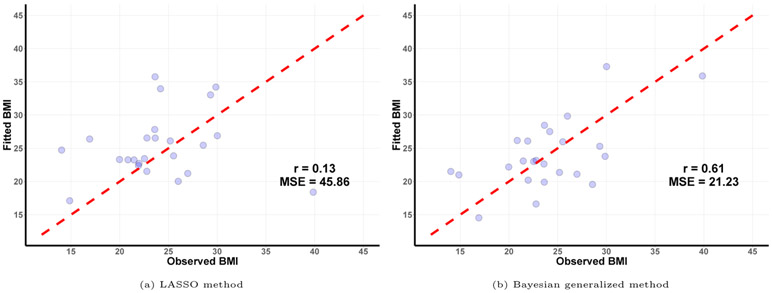
Since our simulations have demonstrated that the Bayesian contrast approaches perform similarly to the Bayesian generalized method, in the case study, we focus on a comparison of the Bayesian generalized method to the compositional lasso of Lin et al. (2014). We randomly divide the 98 samples into a training set of 74 samples and a test set of 24 samples, and use the fitted model chosen based on the training data to evaluate the prediction error on the test set. We repeat this procedure 100 times. For the compositional lasso method, the average prediction error is 45.86 with a standard error of 1.21. For the Bayesian generalized method, the average prediction error is 21.23 with a standard error of 2.67. As shown in the fitted versus observed plot (Figure 5), the predictions from the proposed Bayesian method are more tightly distributed around the diagonal line representing perfect accuracy. These results show that the proposed method can achieve improved predictive performance over the compositional lasso approach.

Figure 5:

Fitted versus observed values of BMI.

To gain insight into aspects of the microbiome associated with BMI, we examined the features selected by the two approaches on the training data: 27 OTUs were identified using the compositional lasso, and 55 OTUs were identified using the Bayesian generalized model. At the phylum level, both methods select Bacteroidetes and Firmicutes as being associated with BMI. Thus, our method is consistent with the previous findings by Lin et al. (2014). Furthermore, our selection results at the genus level indicate that obesity may be associated with the genera Alistipes, Allisonella, Bacteroides, Roseburia and Lachnoclostridium. These genera were identified by previous studies in this area (Van Hul and Cani, 2019; Andoh et al., 2016; Verdam et al., 2013).

6. Discussion

The proposed methodology makes two important advances to regression modeling of microbiome data: firstly, a novel approach to address the compositional constraint in estimation of the regression coefficients; and secondly, a structured prior that allows the phylogenetic relationships among the bacterial taxa to be taken into account. Our proposed method obviates the need to choose a specific reference variable and satisfies the selection invariance property. We have demonstrated that our proposed method outperforms existing penalized methods in both simulation and an application to human gut microbiome data. Finally, our highly efficient implementation allows model fitting within minutes in the p = 1000 setting, and therefore offers appropriate scaling for real data applications.

To analyze compositional data, the isometric log-ratio (ILR) transformation has been proposed as an alternative to the ALR and CLR transformations (Egozcue et al., 2003). Since the ILR has multiple references, analysis of ILR-transformed data is challenging, as the dependence among the transformed covariates will deviate from the original dependence structure. For this reason, in the current work, we only consider the ALR and CLR transformations, as we can use the original tree structure to define the prior associations.

In future work, we would like to further explore approaches for quantifying similarity among the predictors to further improve selection and accommodate such alternative transformations. We are also interested in extending the current model, which assumes a continuous response, to handle binary or survival outcomes.