Integrating Long-Range Regulatory Interactions to Predict Gene Expression Using Graph Convolutional Networks

Abstract

Long-range regulatory interactions among genomic regions are critical for controlling gene expression, and their disruption has been associated with a host of diseases. However, when modeling the effects of regulatory factors, most deep learning models either neglect long-range interactions or fail to capture the inherent 3D structure of the underlying genomic organization. To address these limitations, we present a Graph Convolutional Model for Epigenetic Regulation of Gene Expression (GC-MERGE). Using a graph-based framework, the model incorporates important information about long-range interactions via a natural encoding of genomic spatial interactions into the graph representation. It integrates measurements of both the global genomic organization and the local regulatory factors, specifically histone modifications, to not only predict the expression of a given gene of interest but also quantify the importance of its regulatory factors. We apply GC-MERGE to data sets for three cell lines—GM12878 (lymphoblastoid), K562 (myelogenous leukemia), and HUVEC (human umbilical vein endothelial)—and demonstrate its state-of-the-art predictive performance. Crucially, we show that our model is interpretable in terms of the observed biological regulatory factors, highlighting both the histone modifications and the interacting genomic regions contributing to a gene's predicted expression. We provide model explanations for multiple exemplar genes and validate them with evidence from the literature. Our model presents a novel setup for predicting gene expression by integrating multimodal data sets in a graph convolutional framework. More importantly, it enables interpretation of the biological mechanisms driving the model's predictions.

1. INTRODUCTION

Gene regulation determines the fate of every cell, and its disruption leads to diverse diseases ranging from cancer to neurodegeneration (Krijger and de Laat, 2016; Schoenfelder and Fraser, 2019). Although specialized cell types from neurons to cardiac cells exhibit different gene expression patterns, the information encoded by the linear DNA sequence remains virtually the same in all nonreproductive cells of the body. Therefore, the observed differences in cell type must be encoded by elements extrinsic to sequence, commonly referred to as epigenetic factors. Epigenetic factors found in the local neighborhood of a gene typically include histone marks (also known as histone modifications). These marks are naturally occurring chemical additions to histone proteins that control how tightly the DNA strands are wound around the proteins and the recruitment or occlusion of transcription factors.

Recently, the focus of attention in genomics has shifted increasingly to the study of long-range epigenetic regulatory interactions that result from the three-dimensional organization of the genome (Rowley and Corces, 2018). For example, one early study demonstrated that chromosomal rearrangements, some located as far as 125 kilo-base pairs (kbp) away, disrupted the region downstream of the PAX6 transcription unit causing aniridia (absence of the iris) and related eye anomalies (Kleinjan et al., 2001). Thus, chromosomal rearrangement can not only directly affect the expression of proximal genes but can also indirectly affect a gene located far away by perturbing its regulatory (e.g., enhancer/promoter) interactions.

This observation indicates that while local regulation of genes is informative, studying long-range gene regulation is critical to understanding cell development and disease. However, experimentally testing for all possible combinations of long-range and short-range regulatory factors for 20,000 genes is infeasible given the vast size of the search space. Therefore, computational and data-driven approaches are necessary to efficiently search this space and reduce the number of testable hypotheses.

In recent years, deep learning frameworks have been applied to predict gene expression from histone modifications, and their empirical performance has often exceeded the previous machine learning methods (Karlic et al., 2010; Cheng et al., 2011; Dong et al., 2012). Among their many advantages, deep neural networks perform automatic feature extraction by efficiently exploring feature space and then finding nonlinear transformations of the weighted averages of those features. This formulation is especially relevant to model complex biological systems since they are inherently nonlinear.

For instance, Singh et al. (2016) introduced DeepChrome, which used a convolutional neural network (CNN) to aggregate five types of histone mark ChIP-seq signals in a 10,000 bp region around the transcription start site (TSS) of each gene. Using a similar setup, they next introduced attention layers to their model (Singh et al., 2017), yielding a comparable performance but with the added ability to visualize feature importance within the local neighborhood of a gene. These methods framed the gene expression problem as a binary classification task in which the gene was either active or inactive.

Agarwal and Shendure (2020) introduced Xpresso, a CNN framework that operated on the promoter sequences of each gene and 8 other annotated features associated with mRNA decay to predict steady-state mRNA levels. This model focused primarily on the regression task, such that each prediction corresponded to the logarithm of a gene's expression. A recently published method by Avsec et al. (2021) used a self-attention neural network to derive predictions from sequence information, but it did not include epigenetic effects nor provide explanations of their importance to gene expression.

Furthermore, it should be noted that while all the studies previously surveyed accounted for some types of combinatorial interactions among features at the local level, none of them explicitly incorporated long-range regulatory interactions known to play a critical role in differentiation and disease (Krijger and de Laat, 2016; Schoenfelder and Fraser, 2019).

Modeling these long-range interactions is a challenging task due to two significant reasons. First, it is difficult to confidently pick an input size for the genomic regions as regulatory elements can control gene expression from various distances. Second, inputting a large region will introduce sparsity and noise into the data, making the learning task difficult. A potential solution to this problem is to incorporate information from long-range interaction networks captured from experimental techniques such as Hi-ChIP (Mumbach et al., 2016) and Hi-C (Van Berkum et al., 2010). These techniques use high-throughput sequencing to measure a 3D genomic structure, in which each read pair corresponds to an observed 3D contact between two genomic loci.

While Hi-C captures the global interactions of all genomic regions, Hi-ChIP focuses only on spatial interactions mediated by a specific protein. Recently, Zeng et al. (2019b) combined a CNN, encoding promoter sequences, with a fully connected network using Hi-ChIP data sets to predict gene expression values. The authors then evaluated the relative contributions of the promoter sequence and promoter/enhancer submodules to the model's overall performance. In addition, CNN models can only capture local topological patterns instead of modeling the underlying spatial structure of the data, thus limiting interpretation to local sequence features.

Another recent method by Karbalayghareh et al. (2021) also made use of H3K27ac Hi-ChIP data at 5 kb resolution using graph-based neural networks to recover fine-grained enhancer/promoter relationships. While both these methods incorporated long-range interaction information, their use of HiChIP experiments narrowed this information to spatial interactions facilitated by H3K27ac or YY1. Unlike high-quality Hi-ChIP experiments used in these studies, Hi-C experiments are easier to perform, the data sets are more broadly available, and the method is not limited to specific protein-mediated interactions.

To address these limitations outlined above, we developed a Graph Convolutional Model for Epigenetic Regulation of Gene Expression (GC-MERGE), a graph-based deep learning framework that integrates 3D genomic data with histone mark signals to predict gene expression. Figure 1 provides a schematic of our overall approach. Unlike previous methods, our model incorporates genome-wide interaction frequencies of the Hi-C data by encoding it via a graph convolutional network (GCN), thereby capturing the underlying genomic spatial structure.

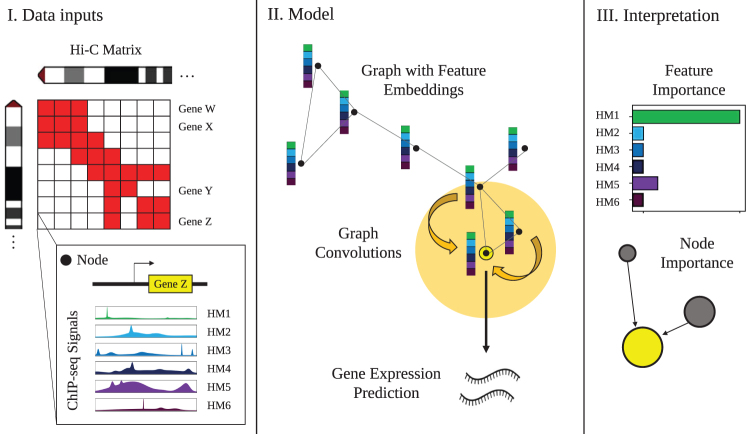
FIG. 1.

Overview of GC-MERGE. Our framework integrates local HM signals and long-range spatial interactions among genomic regions to predict and understand gene expression. (I) Inputs to the model include Hi-C maps for each chromosome, with the binned chromosomal regions corresponding to nodes in the graph, and the average ChIP-seq readings of six core histone marks in each region, which constitute the initial feature embedding of the nodes. (II) For nodes corresponding to regions containing a gene, the model performs repeated graph convolutions over the neighboring nodes to yield either a binarized class prediction of gene expression activity (either active or inactive) or a continuous, real-valued prediction of expression level. (III) Finally, explanations for the model's predictions for any gene-associated node can be obtained by calculating the importance scores for each of the features and the relative contributions of neighboring nodes. Therefore, the model provides biological insight into the pattern of histone marks and the genomic interactions that work together to predict gene expression. GC-MERGE, Graph Convolutional Model of Epigenetic Regulation of Gene Expression; HM, histone mark.

GCNs are particularly well-suited to representing spatial relationships, as a Hi-C map can be represented as an adjacency matrix of an undirected graph $G\in \left\{V,E\right\}$. Here, V nodes represent the genomic regions and E edges represent their interactions. Our formulation leverages information from both local and distal regulatory factors that control gene expression. While some methods use a variety of other features, such as promoter sequences or readings obtained from the Assay for Transposase Accessible Chromatin using sequencing (ATAC-seq) levels (Dong et al., 2012; Zeng et al., 2019b; Agarwal and Shendure, 2020), we focus our efforts solely on histone modifications and extract their relationship to the genes.

We show that our model provides state-of-the-art performance for the gene expression prediction tasks even with this simplified set of features for three difference cell lines—GM12878 (lymphoblastoid), K562 (myelogenous leukemia), and HUVEC (human umbilical vein endothelial).

A significant contribution of our work is to enable researchers to determine which regulatory interactions local or distal contribute toward the gene's expression prediction and which histone marks are involved in these interactions. This information can suggest promising hypotheses and guide new research directions by making the model's predictive drivers more transparent. To that effect, we adapt a recent model explanation approach specifically for GCNs known as GNNExplainer (Ying et al., 2019), which quantifies the relative importance of the nodes and edges in a graph that drive the output prediction.

We integrate this method within our modeling framework to highlight the important histone modifications (node features) and the important long-range interactions (edges) that contribute to a particular gene's predicted expression. To validate the model's explanations, we use two high-throughput experimental studies (Fulco et al., 2019; Jung et al., 2019) that identify significant regulatory interactions. While existing methods (Singh et al., 2016, 2017; Zeng et al., 2019b; Agarwal and Shendure, 2020) can provide feature-level interpretations (important histone modifications or sequences), the unique modeling of Hi-C data as a graph allows GC-MERGE to provide additional edge-level interpretations (important local and global interactions in the genome). Table 1 places the proposed framework among state-of-the-art deep learning models and lists each model's properties.

Table 1.

Comparison of the Properties of Previous Deep Learning Models Predicting Gene Expression with GC-MERGE

Computational study	Inputs			Interpretation
	Local histone marks	Additional features (e.g., promoter sequence)	Long-range interactions	Feature-level interpretation	Edge-level interpretation
DeepChrome	X			X
AttentiveChrome	X			X
Xpresso		X		X
DeepExpression		X	X	X
GC-MERGE	X		X	X	X

The proposed method integrates local and long-range regulatory interactions, capturing the underlying 3D genomic spatial structure as well as highlighting both the critical node-level (histone modifications) and edge-level (genomic interactions) features.

GC-MERGE, Graph Convolutional Model for Epigenetic Regulation of Gene Expression.

The code for our work is available at https://github.com/rsinghlab/GC-MERGE.

2. METHODS

2.1. Graph convolutional networks

GCNs are a generalization of CNNs to graph-based relational data that are not natively structured in Euclidean space (Liu and Zhou, 2020). Due to the expressive power of graphs, GCNs have been applied across a wide variety of domains, including recommender systems (Jin et al., 2020) and social networks (Qiu et al., 2018). The prevalence of graphs in biology has made these models a popular choice for tasks such as characterizing protein/protein interactions (Yang et al., 2020), predicting chromatin signature profiles (Lanchantin and Qi, 2020), and inferring the chemical reactivity of molecules for drug discovery (Sun et al., 2020). In the context of this work, we use graphs to encode genomic spatial interactions derived from Hi-C matrices.

We use the GraphSAGE formulation (Hamilton et al., 2017) as our GCN for its relative simplicity and its capacity to learn generalizable, inductive representations not limited to a specific graph. The input to the model is represented as a graph $G\in \left\{V,E\right\}$, with nodes V and edges E, and a corresponding adjacency matrix $A\in {ℛ}^{N\times N}$ (Liu and Zhou, 2020), where N is the number of nodes. For each node v, there is also an associated feature vector x_v. The goal of the network is to learn a state embedding $h_v^K\in {ℛ}^d$ for v, which is obtained by aggregating information over v's neighborhood K times, where d is the dimension of the embedding vector. This new state embedding is then fed through a fully connected network to produce an output ${ŷ}_v$, which can then be applied to downstream classification or regression tasks.

Within this modeling framework, the first step is to initialize each node with its input features. In our case, the feature vector $x_v\in {ℛ}^m$ is obtained from the ChIP-seq signals corresponding to the six ($m=6$) core histone marks (H3K4me1, H3K4me3, H3K9me3, H3K36me3, H3K27me3, and H3K27ac) in our data set:

$$h_v^0=x_v$$ (1)

Next, to transition from the (k − 1)th layer to the kth hidden layer in the network for node v, we apply an aggregation function to the neighborhood of each node. This aggregation function is analogous to a convolution operation over regularly structured Euclidean data such as images.

While standard convolution function operates over a grid and represents a pixel as a weighted aggregation of its neighboring pixels, in an analogous manner, a graph convolution performs this operation over the neighbors of a node in a graph. In our case, the aggregation function calculates the mean of the neighboring node features:

Here, $N\left(v\right)$ represents the adjacency set of node v. We update the node's embedding by concatenating the aggregation with the previous layer's representation to retain information from the original embedding. Next, just as done in a standard convolution operation, we take the matrix product of this concatenated representation with a learnable weight matrix to complete the weighted aggregation step.

Finally, we apply a nonlinear activation function, such as ReLU, to capture the higher order nonlinear interactions among the features:

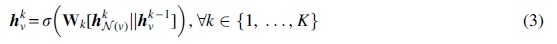
Here, $\left|\right|$ represents concatenation, $\sigma$ is a nonlinear activation function, and $W_k$ is a learnable weight parameter. After this step, each node is assigned a new embedding. After K iterations, the node embedding encodes information from the neighbors that are K-hops away from that node:

$$z_v=h_v^K$$ (4)

Here, z_v is the final node embedding after K iterations.

GC-MERGE is a flexible framework that can formulate gene expression prediction as both a classification task and a regression task. For the classification task, we feed the learned embedding z_v into a fully connected network and output a prediction ${ŷ}_v$ for each target node using a Softmax layer to compute probabilities for each class c and then take the argmax. Here, class $c\in \left\{0,1\right\}$ corresponds to whether the gene is either off/inactive ($c=0$) or on/active ($c=1$). We use the true binarized gene expression value $y_v\in \left\{0,1\right\}$ by thresholding the expression level relative to the median as the target predictions, consistent with other studies (Singh et al., 2016, 2017).

For the loss function, we minimize the negative log likelihood of the log of the Softmax probabilities. For the regression task, we feed z_v into a fully connected network and output a prediction ${ŷ}_v\in ℛ$, representing a real-valued expression level. We use the mean squared error as the loss function. For both tasks, the model architecture is summarized in Figure 2 and described in further detail in Supplementary Section S1.1.

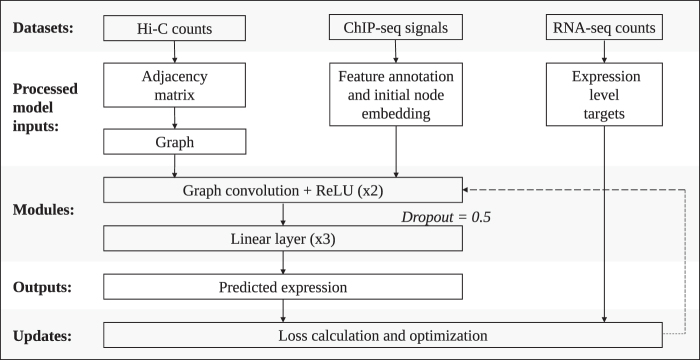
FIG. 2.

Overview of the GCN model architecture. The data sets used in our model are Hi-C maps, ChIP-seq signals, and RNA-seq counts. A binarized adjacency matrix ($A\in {ℛ}^{N\times N}$) is produced from the Hi-C maps by subsampling from the Hi-C matrix. The nodes v in the graph are annotated with features from the ChIP-seq data sets (x_v). Two graph convolutions, each followed by ReLU, are performed. The output from here is fed into a dropout layer (probability = 0.5), followed by a linear module that comprised three dense layers, in which ReLU follows the first two layers. For the classification model, the output is fed through a softmax layer, and then the argmax is taken to make the final prediction (y_v). For the regression model, the final output represents the base-10 logarithm of the expression level (with a pseudocount of 1).

2.2. Interpretation of GC-MERGE

Although a model's architecture is integral to its performance, just as important is the understanding how the model arrives at its predictions. Neural networks, in particular, have sometimes been criticized for being “black box” models, such that no insight is provided into how the model operates. Most graph-based interpretability approaches either approximate models with simpler models whose decisions can be used for explanations (Ribeiro et al., 2016) or use an attention mechanism to identify relevant features in the input that guide a particular prediction (Veličković et al., 2017). In general, these methods, along with gradient-based approaches (Simonyan et al., 2013; Sundararajan et al., 2017) or DeepLift (Shrikumar et al., 2017), focus on the explanation of important node features and do not incorporate the structural information of the graph. However, a recent method called Graph Neural Net Explainer (or GNNExplainer) (Ying et al., 2019), given a trained GCN, can identify a small subgraph as well as a small subset of features that are crucial for a particular prediction.

We adapt the GNNExplainer method and integrate it into our classifier framework. GNNExplainer maximizes the mutual information between the probability distribution of the model's class predictions over all nodes and the probability distribution of the class predictions for a particular node conditioned on some fractional masked subgraph of neighboring nodes and features. Subject to regularization constraints, it jointly optimizes the fractional node and feature masks, determining the extent to which each element informs the prediction for a particular node.

Specifically, given a node v, the goal is to learn a subgraph $G_s\subseteq G$ and a feature mask $X_s=\left\{x_j|v_j\in G_s\right\}$ that contribute the most toward driving the full model's prediction of ${ŷ}_v$. To achieve this objective, the algorithm learns a mask that maximizes the mutual information between the original model and the masked model. Mathematically, this objective function is as follows:

$${max}_{G_s}MI\left(Y,\left(G_s,X_s\right)\right)=H\left(Y\right)-H\left(Y|G_s,X_s\right)$$ (5)

where H is the entropy of a distribution. Since this is computationally intractable with an exponential number of graph masks, GNNExplainer optimizes the following quantity using gradient descent:

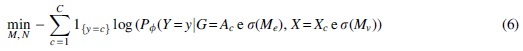
where c represents the class, A_c represents the adjacency matrix of the computation graph, M_e represents the subgraph mask on the edges, and M_v represents the node feature mask. The importance scores of the nodes and features are obtained by applying the sigmoid function to the subgraph edges and node feature masks, respectively. Finally, the element-wise entropies of the masks are calculated and added as regularization terms into the loss function. Therefore, in the context of our model, GNNExplainer learns which genomic interactions (via the subgraph edge mask) and which histone modifications (via the node feature mask) are most critical to driving the model's predictions.

3. EXPERIMENTAL SETUP

3.1. Overview of the data sets

GC-MERGE requires the following information: (1) Interactions between the genomic regions (Hi-C contact maps). (2) Histone mark signals representing the regulatory signals (ChIP-seq measurements). (3) Expression levels for each gene (RNA-seq measurements). Thus, for each gene in a particular region, the first two data sets are the inputs into our proposed model, whereas gene expression is the predicted target.

Being consistent with previous studies (Singh et al., 2016, 2017), we first formulate the prediction problem as a classification task. However, as researchers may be interested in predicting exact expression levels, we also extend the predictive capabilities of our model to the regression setting. For the classification task, we binarize the gene expression values as either 0 (low expression) or 1 (high expression) using the median as the threshold, as done in previous studies (Cheng et al., 2011; Singh et al., 2016, 2017; Zeng et al., 2019b). For the regression task, we take the base-10 logarithm of the gene expression values with a pseudocount of 1.

We focused our experiments on three human cell lines from Rao et al. (2014): (1) GM12878, a lymphoblastoid cell line with a normal karyotype, (2) K562, a myelogenous leukemia cell line, and (3) HUVEC, a human umbilical vein endothelial cell line. For each of these cell lines, we accessed RNA-seq expression and ChIP-Seq signal data sets for six uniformly profiled histone marks from the REMC repository (Roadmap Epigenomics Consortium, 2015).

These histone marks include (1) H3K4me1, associated with enhancer regions; (2) H3K4me3, associated with promoter regions; (3) H3K9me3, associated with heterochromatin; (4) H3K36me3, associated with actively transcribed regions; (5) H3K27me3, associated with polycomb repression; and (6) H3K27ac, also associated with enhancer regions. We chose these marks because of the wide availability of the relevant data sets as well as for ease of comparison with previous studies (Singh et al., 2016, 2017; Zeng et al., 2019b).

In addition, these six core histone marks are the same set of features used in the widely cited 18-state ChromHMM model (Ernst and Kellis, 2017), which associates histone mark signatures with chromatin states. See Supplementary Section S1.2 for further details regarding preprocessing of the data sets. Furthermore, it should be noted that the model is able to flexibly accommodate an arbitrary number of features for node annotation.

3.2. Graph construction and data integration

Our main innovation is formulating the graph-based prediction task to integrate two very different data modalities (histone mark signals and Hi-C interaction frequencies). We represented each genomic region with a node (v) and connected an edge (e) between it and the nodes corresponding to its neighbors (bins with nonzero entries in the adjacency matrix) to construct the graph ($G\in \left\{V,E\right\}$, with nodes V and edges E).

For chromosome capture data, we used previously published Hi-C maps at 10 kbp resolution for all 22 autosomal chromosomes (Rao et al., 2014). We obtained an $N\times N$ symmetric matrix, where each row or column represents a 10 kb chromosomal region. Therefore, each bin count corresponds to the interaction frequency between the two respective genomic regions. Next, we applied vanilla coverage (VC) normalization on the Hi-C maps. In addition, because chromosomal regions located closer together will contact each other more frequently than regions located farther away simply due to chance (rather than due to biologically significant effects), we made an additional adjustment for this background effect.

Following Sobhy et al. (2019), we determined the distance between the regions corresponding to each row and column. Then, for all pairs of interacting regions located the same distance away, we calculated the median of the bin counts along each diagonal of the N × N matrix and used this as a proxy for the background. Finally, for each bin, we subtracted the appropriate median and discarded any negative values. We converted all nonzero values to 1, thus obtaining the binary adjacency matrix for our model ($A\in {ℛ}^{N\times N}$).

Due to the large size of the Hi-C graph, we subsampled neighbors to form a subgraph for each node we fed into the model. While there are methods to perform subsampling on large graphs using a random node selection approach [e.g., Zeng et al. (2019a)], we used a simple strategy of selecting the top j neighbors with the highest Hi-C interaction frequency values. We empirically selected the value of $j=10$ for the number of neighbors. Increasing the size of the subsampled neighbor set (i.e., $j=20$) did not improve the performance further, as shown in Supplementary Figure S1.

To integrate the Hi-C data sets with the RNA-seq and ChIP-seq data sets, we obtained the average ChIP-seq signal for each of the six core histone marks over the 10 kbp chromosomal region corresponding to each node. In this way, we associated a feature vector of length six with each node ($x_v\in {ℛ}^6$). For assigning an output value to the node, we took each gene's TSS and assigned its expression value to the node corresponding to the chromosomal region with its TSS as output (y_v). If multiple genes were assigned to the same node, we took the median of the expression levels, that is, the median of all the values corresponding to the same node.

Given our framework, we could allot the output gene expression to only a subset of nodes that contained gene TSSs while aiming to use histone modification signals from all the nodes. Therefore, to enable training with such a unique setting, we applied a mask during the training phase so that the model made predictions only on nodes with assigned gene expression values. This was done by cross-referencing the gene coordinates in the RNA-seq data sets with the corresponding Hi-C regions and applying the mask such that the loss was calculated only on these gene-containing nodes. Note that the graph convolution operations still used information from related neighbor nodes, but loss calculations and predictions were computed only for the subset of gene-containing nodes.

The overall size of our data set consisted of 279,606 total nodes and 16,699 gene-associated nodes for GM12878, 279,601 total nodes and 16,690 gene-associated nodes for K562, and 279,598 total nodes and 16,681 gene-associated nodes for HUVEC. When running the model on each cell line, we assigned 70% of the gene-associated nodes to the training set, 15% to the validation set, and 15% to the testing set. Then, we performed hyperparameter tuning using the training and validation sets and reported performance on the independent test set. For the hyperparameter K corresponding to the number of graph convolutional layers, we determined the optimal number to be $K=2$ after testing over a range of 1–3 layers. Additional details of the hyperparameter tuning are provided in Supplementary Section S1.3 and Supplementary Table S1.

3.3. Baseline models

We compared GC-MERGE with the following deep learning baselines for gene expression prediction of both the classification and regression tasks:

• Multilayer perceptron (MLP): A neural network comprised three fully connected layers.

• Shuffled neighbor model: GC-MERGE applied to shuffled Hi-C matrices, such that the neighbors of each node are randomized. We include this baseline to see how the performance of the GCN is affected when the provided Hi-C information is random.

• CNN: A CNN based on DeepChrome (Singh et al., 2016). This model takes 10 kb regions corresponding to the genomic regions demarcated in the Hi-C data and subdivides each region into 100 bins. Each bin is associated with six channels, corresponding to the ChIP-seq signals of the six core histone marks used in the present study. A standard convolution is applied to the channels, followed by a fully connected network.

For the regression task, the range of the outputs is the set of continuous real numbers. For the classification task, a Softmax function is applied to the model's output to yield a binary prediction. None of the baseline methods incorporates long-range spatial information due to genomic interactions. Therefore, they only process histone modification information from the regions whose gene expression is being predicted. In contrast, GC-MERGE solves a more challenging task by processing information from the neighboring regions as well.

For the CNN baseline, genomic regions are subdivided into smaller 100-bp bins, consistent with Singh et al. (2016). However, GC-MERGE and the baselines other than the CNN average the histone modification signals over the entire 10 kb region. We also implemented GC-MERGE on higher resolution ChIP-seq data sets (1000-bp bins), which we fed through a linear embedding module to form features for the Hi-C nodes. We did not observe an improvement in the performance for the high-resolution input (Supplementary Fig. S2).

In addition, we compared our results to the published results of two other recent deep learning methods, Xpresso by Agarwal and Shendure (2020) and DeepExpression by Zeng et al. (2019b), when such comparisons were possible, although in some cases the experimental data sets were unavailable or the code provided did not run.

3.4. Evaluation metrics

For the classification task, we evaluated model performance by using two metrics: the area under the receiver operating characteristic curve (AUROC) and the area under the precision-recall curve (AUPR). For the regression task, we calculated the Pearson correlation coefficient (PCC), which quantifies the correlation between the true and predicted gene expression values in the test set.

4. RESULTS

4.1. GC-MERGE gives state-of-the-art performance for the gene expression prediction task

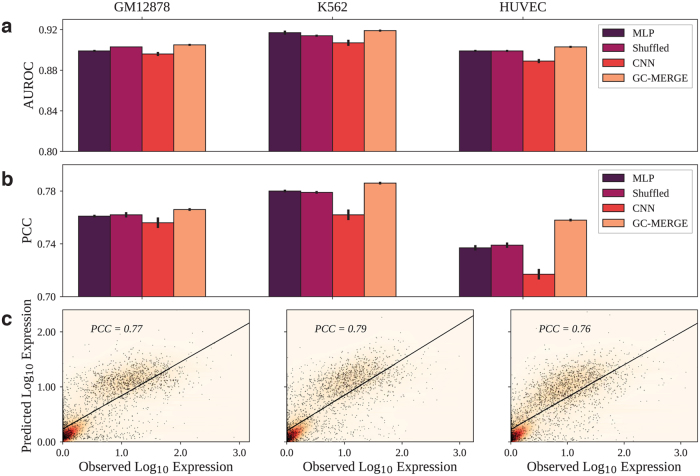
We evaluate GC-MERGE and the baseline models on both the classification and regression tasks for the cell lines, GM12878, K562, and HUVEC. As earlier studies formulated the problem as a classification task (Singh et al., 2016, 2017, Zeng et al., 2019b), we first apply GC-MERGE to make a binary prediction of whether each gene is active or inactive. In Figure 3a, we show that our model's performance is an improvement over all other alternatives, achieving 0.91, 0.92, and 0.90 AUROC scores. We also measure model performance using the AUPR score and achieve similar results (Supplementary Fig. S3).

FIG. 3.

Comparison of AUROC and PCC scores for all models. GC-MERGE gives state-of-the-art performance for both the classification and the regression tasks. For each reported metric, we take the average of 10 runs and denote the standard deviation by the error bars on the graph. (a) For the classification task, the AUROC metrics for GM12878, K562, and HUVEC were 0.91, 0.92, and 0.90, respectively. For each of these cell lines, GC-MERGE improves prediction performance over other baselines. (b) For the regression task, GC-MERGE obtains PCC scores of 0.77, 0.79, and 0.76 for GM12878, K562, and HUVEC, respectively. These scores are better than the respective baselines. (c) Scatter plots of the logarithm of the predicted expression values versus the true expression values are shown for all three cell lines. AUROC, area under the receiver operating characteristic curve; GM12878, lymphoblastoid; HUVEC, human umbilical vein endothelial cell; K562, myelogenous leukemia; PCC, Pearson correlation coefficient.

For the K562 cell line, we note that the performance of GC-MERGE (AUROC = 0.92) is similar to that reported for DeepExpression (AUROC = 0.91) by Zeng et al. (2019b), a CNN model that uses promoter sequence data as well as spatial information from H3K27ac and YY1 Hi-ChIP experiments. We could not compare with DeepExpression for the cell lines, GM12878 and HUVEC, as the experimental data sets were unavailable. For the Xpresso framework presented in Agarwal and Shendure (2020), a CNN model that uses promoter sequence and 8 features associated with mRNA decay to predict gene expression, the task is formulated as a regression problem, and so, no comparisons could be made for the classification setting.

With respect to the regression task, Figure 3b compares our model's performance with the baselines and Figure 3c shows the predicted versus true gene expression values for GC-MERGE. For GM12878, the PCC of GC-MERGE predictions (PCC = 0.77) is better than the other baselines. Furthermore, we note that our model performance also compares favorably with numbers reported for Xpresso (PCC $\approx$ 0.65) (Agarwal and Shendure, 2020). For K562, GC-MERGE again outperforms all alternative baseline models (PCC = 0.79).

In addition, GC-MERGE performance also exceeds that of Xpresso (PCC $\approx$ 0.71) (Agarwal and Shendure, 2020) as well as DeepExpression (PCC = 0.65) (Zeng et al., 2019b). Our model gives better performance (PCC = 0.76) relative to the baselines for HUVEC as well. Neither Xpresso nor DeepExpression studied this cell line. While the metrics presented for GC-MERGE are not directly comparable with the reported numbers for Xpresso and DeepExpression, it is encouraging to see that they are in the range of these state-of-the-art results.

A summary of the performance metrics for GC-MERGE, the deep learning baselines used for direct comparison, as well as traditional machine learning methods (random forest and logistic regression techniques) can be found in Supplementary Tables S4 and S5.

To determine in which cases incorporating information about long-range interactions make a substantive difference in predictive performance, we compare the performance of GC-MERGE (which includes the long-range chromatin interaction information) with the baseline MLP (which does not include long-range chromatin interaction information) as well as the shuffled model (which permutes the rows of the Hi-C matrix for each chromosome) on subgroups of genes stratified by their differential expression. Specifically, for each of the cell lines in our study, we take the log₂ fold-change (with a pseudocount of 1) of each gene expression relative to the mean expression for all 56 other cell lines in the REMC repository.

Then, we group the genes according to their log-fold change and compare the performance of GC-MERGE with the MLP and shuffled models, as seen in Supplementary Figure S4 and Supplementary Table S6. We find that GC-MERGE performance exceeds that of both the MLP and shuffled baselines under all conditions, but the improvement increases for genes with higher log fold-changes. For instance, for genes with a log-fold change of 0, the average improvement in the PCC performance metric of GC-MERGE over all cell lines is 0.086 and 0.049 for the MLP and shuffled baselines, respectively. However, for genes with a log-fold change of 3 or greater, the average performance increase of GC-MERGE is 0.213 and 0.122 relative to the MLP and shuffled baselines, respectively.

These results are plausible since genes with greater differential expression would be expected to be more cell-type specific and subject to greater control by long-range regulatory interactions. An interesting observation here is that the shuffled baseline has an intermediate performance between that of the MLP and GC-MERGE. We conjecture that the shuffled model learns to ignore the noise of the random neighbor interactions and focus primarily on the histone marks present in the genic region itself, and due to the greater complexity of the model, it is able to learn better than the MLP. However, for all expression levels, the shuffled model performance is still lower than that of GC-MERGE and particularly so for genes with a high differential expression.

Therefore, although GC-MERGE performs better than both the MLP and shuffled baselines for all expression levels, the utility of our model is most apparent for genes that are highly differentially expressed. Since the relative predictive advantage of GC-MERGE over both baselines increases at higher log-fold changes, this suggests that for genes with higher levels of differential expression, the significance of the contributions made by 3D genomic structure increases correspondingly.

Our model's state-of-the-art performance on this challenging prediction task indicates that it can leverage multimodal data sets to learn relevant connections. However, an important aim is to go beyond the prediction task and extract these learned relationships from the model. Thus, we present GC-MERGE as a hypothesis driving tool for understanding epigenetic regulation.

4.2. Interpretation of GC-MERGE highlights important histone modifications and relevant long-range interactions

To understand the underlying biological factors informing the model's predictions, we integrate the GNNExplainer method (Ying et al., 2019), designed for classification tasks, into our modeling framework. Once trained, we show that GC-MERGE can determine which genomic interactions and histone marks are most critical to the prediction of the expression level for a particular gene of interest. First, to demonstrate that the model is extracting relevant signals, we apply GNNExplainer to analyze model predictions across three subsets of genes: those that have high expression, intermediate expression, and low expression. We show that for each of these subsets, the model uses features that correspond to known chromatin signatures indicative of their respective expression levels.

Second, to show how our tool can be used to uncover possible biological drivers at the genic level, we validate our approach on exemplar genes using two experimental data sets that identify regulatory interactions. The first data set is drawn from an analytical study by Jung et al. (2019), which uses promoter capture Hi-C to identify candidate regulatory elements that interact with promoters of interest in conjunction with expression quantitative trait loci (eQTL) expression levels and other epigenetic signals. The second functional characterization study by Fulco et al. (2019) introduces a new experimental technique called CRISPRi-FlowFISH, in which candidate regulatory elements are perturbed, and the effects on the expression of specific genes of interest are measured.

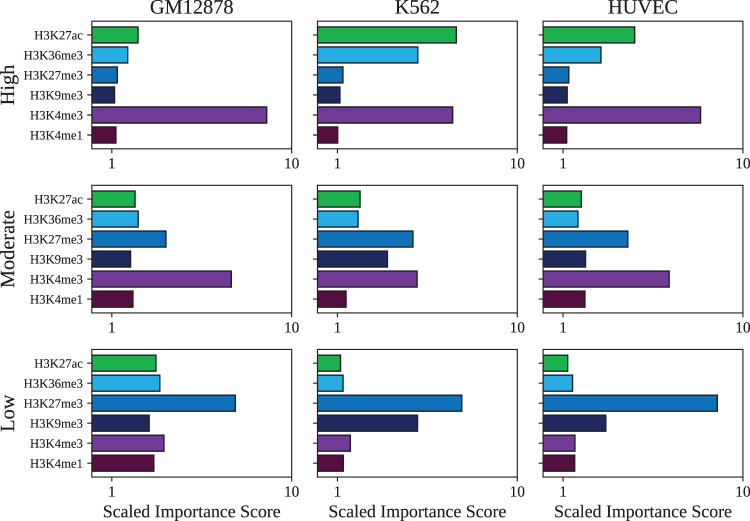
We apply GNNExplainer to each of the cell lines in this study to determine the most important features motivating GC-MERGE's predictions for three groups of genes with distinct expression levels. The three subsets of genes are defined as follows: genes with high expression (top 100 genes by expression), genes with moderate expression (100 genes with expression levels closest to the median), and genes with low expression (bottom 100 genes by expression). For each group, we run GNNExplainer on all the genes in the subset and calculate the mean value of the importance scores assigned to each of the six histone mark features, as displayed in Figure 4.

FIG. 4.

Histone mark profiles for subsets of genes expressed at high levels, intermediate levels, and low levels. (a) For GM12878, the average histone mark profile for the top 100 genes by expression level is dominated by H3K4me3 as would be expected for actively transcribed genes. The histone mark profile for genes at intermediate expression value is characterized by high importance scores for H3K4me3 and H3K27me3, which is correlated with a bivalent/poised TSS. Lastly, the histone mark profile for genes with low expression shows that the H3K27me3 signal is most important, which is associated with repression. Similar patterns can be observed for (b) K562 and (c) HUVEC. TSS, transcription start site.

Corroborating these model interpretations, all of the mean profiles are identifiable with the chromatin state signatures defined in the widely cited 18-state ChromHMM model by Ernst and Kellis (2017). For genes with high expression, H3K4me3 is the most important feature in determining predictions for the GM12878 cell line. For the cell lines, K562 and HUVEC, both H3K4me3 and H3K27ac have prominent importance scores. Each of these chromatin mark signatures correlates with active TSSs or sites flanking an active TSS. For moderately expressed genes, in all three cell lines, H3K4me3 has the highest importance score followed by H3K27me3. According to the ChromHMM taxonomy, this chromatin mark signature is characteristic of a bivalent/poised TSS, as would be expected. Lastly, for genes with low expression, H3K27me3 predominates, which corresponds to polycomb repression. We thus show that the model's predictions are biologically interpretable and based on relevant combinations of features that recapitulate well-characterized histone mark profiles.

To further demonstrate the utility of our model, we show that it can identify not only the histone mark signatures but also critical long-range genomic interactions that have been experimentally verified at the genic level. As mentioned previously, we use two complementary experimental sources: promoter capture Hi-C data from the study by Jung et al. (2019) and CRISPRi-FlowFISH data from the study by Fulco et al. (2019).

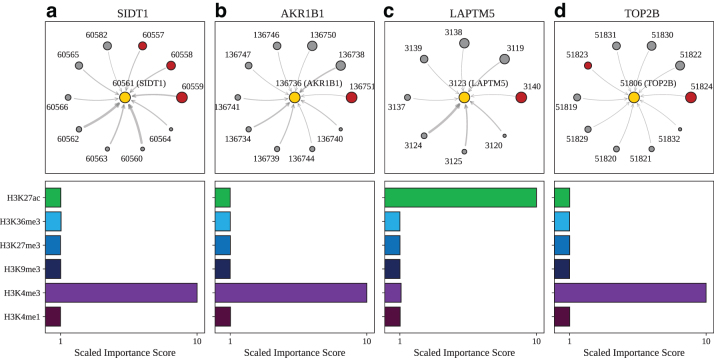
For the promoter capture Hi-C data (Jung et al., 2019), we examined GM12878, a lymphoblastoid cell line, and selected four exemplar genes that are among the most highly expressed in our data set: SIDT1, AKR1B1, LAPTM5, and TOP2B. Brief descriptions of the genes are included in Supplementary Section S2 and the chromosomal coordinates and corresponding node identifiers for each gene can be found in Supplementary Table S2. In Figure 5a, we show that for SIDT1, the nodes that are ranked as the top three by importance score (indicated by the size of the node) correspond to known regulatory regions.

FIG. 5.

Model explanations for exemplar genes validated by promoter capture Hi-C. Top: For (a) SIDT1, designated as node 60561 (yellow circle), the subgraph of neighbor nodes is displayed. The size of each neighbor node correlates with its predictive importance as determined by GNNExplainer. Nodes in red denote regions corresponding to known enhancer regions regulating SIDT1 (Jung et al., 2019) (note that multiple interacting fragments can be assigned to each node, see Supplementary Table S3). All other nodes are displayed in gray. The thickness of each edge is inversely correlated with the genomic distance between each neighbor node and the central node, such that thicker edges indicate neighbor nodes that are closer in sequence space to the gene of interest. Nodes with importance scores corresponding to outliers have been removed for clarity. Bottom: The scaled feature importance scores for each of the six core histone marks used in this study are shown in the bar graph. Results also presented for (b) AKR1B1, (c) LAPTM5, and (d) TOP2B.

In addition, we plot the importance scores assigned to the histone marks (node features) that are most consequential in determining the model's predictions. The bar graph shows that H3K4me3 is the most important feature in determining the model's prediction. This histone mark profile has been associated with regions flanking TSSs in highly expressed genes (Ernst and Kellis, 2017). We report similar results for AKR1B1 (Fig. 5b), where the node ranked as the most important corresponds to a confirmed regulatory region and TOP2B (Fig. 5d), where two of the most important nodes correspond to regulatory regions.

For LAPTM5, shown in Figure 5c, the top-ranked node corresponds to a validated regulatory region. For the histone importance score profile, the feature deemed most important is H3K27ac. This histone mark has been associated with the promoter regions of highly expressed genes as well as active enhancer regions (Ernst and Kellis, 2017).

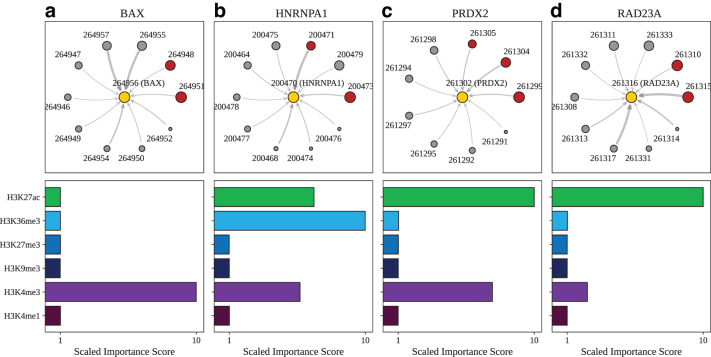
Unlike the promoter capture Hi-C study (Jung et al., 2019), the CRISPRi-FlowFISH study (Fulco et al., 2019) uses a functional definition of enhancers. Since the latter focuses primarily on a limited subset of 30 genes from the K562 cell line, we have select four highly expressed genes in our data set that also overlap with the genes examined in that study. These four exemplar genes are as follows: BAX, HNRNPA1, PRDX2, and RAD23A. Descriptions of each of these genes can be found in Supplementary Section S2, and the gene coordinates and corresponding node IDs can be found in Supplementary Table S2. For BAX, shown in Figure 6a, the two top-ranked nodes by importance score correspond to functional enhancer regions. The histone mark importance scores pinpoint the H3K4me3 mark as most critical to the model's predictions.

FIG. 6.

Model explanations for exemplar genes validated by CRISPRi-FlowFISH. Top: For (a) BAX, designated as node 264956 (yellow circle), the subgraph of neighbor nodes is displayed. The size of each neighbor node correlates with its predictive importance as determined by GNNExplainer. Nodes in red denote regions corresponding to known enhancer regions regulating BAX (Fulco et al., 2019) (note that multiple interacting fragments can be assigned to each node, see Supplementary Table S3). All other nodes are displayed in gray. The thickness of each edge is inversely correlated with the genomic distance between each neighbor node and the central node, such that thicker edges indicate neighbor nodes that are closer in sequence space to the gene of interest. Nodes with importance scores corresponding to outliers have been removed for clarity. Bottom: The scaled feature importance scores for each of the six core histone marks used in this study are shown in the bar graph. Results also presented for (b) HNRNPA1, (c) PRDX2, and (d) RAD23A.

For HNRNPA1 (Fig. 6b), two out of the three highest ranked nodes correspond to regulatory regions. The histone marks most important to the models predictions are H3K36me3, H3K27ac, and H3K4me3. This chromatin signature is indicative of genic enhancer regions (Ernst and Kellis, 2017). For PRXD2 (Fig. 6c), the top two nodes by importance correspond to functional enhancer regions, and the histone mark importance scores indicate that H3K27ac and H3K4me3 play crucial roles in driving the genes' predicted expression. For RAD23A (Fig. 6d), the top two nodes again correspond to experimentally validated regulatory regions. From the histone mark importance profile, it can be seen that H3K27ac plays an influential role.

Both H3K4me3 and H3K27ac are active cis-regulatory elements used to deduce the enhancer/promoter interactions (Salviato et al., 2021), and, interestingly, interpretation of GC-MERGE highlights these histone marks out of the six chosen for this study.

To confirm that the node importance scores obtained from GNNExplainer do not merely reflect the relative magnitudes of the Hi-C counts or the distances between the genomic regions, we investigate the relationships among the Hi-C counts, genomic distances, and scaled importance scores. We observe that the scaled importance scores do not correlate with the Hi-C counts or the pairwise genomic distances. For instance, for SIDT1 (Supplementary Fig. S5a and Supplementary Table S7), the three experimentally validated interacting nodes have importance scores ranking among the highest (10.0, 6.6, and 5.7).

However, they do not correspond to the nodes with the most Hi-C counts (413, 171, and 155 for each of the three known regulatory regions, while the highest count is 603). In addition, these nodes are located 20, 30, and 40 kbp away from the gene region—distances that are characteristic of distal enhancers (Dekker and Misteli, 2015)—while other nodes at the same or closer distances do not have promoter/enhancer interactions. For LAPTM5 (Supplementary Fig. S5c and Supplementary Table S7), the node with the highest importance score has an experimentally confirmed interaction and is located 170 kbp away from the gene region. We perform similar analysis for all of the other exemplar genes (Supplementary Fig. S5 and Supplementary Table S7).

Therefore, we show that by modeling the histone modifications and the spatial configuration of the genome, GC-MERGE infers connections that can serve as important hypothesis-driving observations for gene regulatory experiments.

5. DISCUSSION

We present GC-MERGE, a graph-based deep learning model, which integrates both local and long-range epigenetic data in a GCN framework to predict gene expression and explain its chief drivers. We demonstrate the model's state-of-the-art performance for the gene expression prediction task, outperforming the baselines on the cell lines, GM12878, K562, and HUVEC. We also determine the relative contributions of histone modifications and genomic interactions for multiple exemplar genes, showing that our model recapitulates known experimental results in a biologically interpretable manner.

For future work, we anticipate applying our model to additional cell lines as high-quality Hi-C data sets become available. Although our model is not currently optimized for model transfer and prediction across cell lines, we would like to pursue this direction by making comparisons between tissue types. Making these cross-comparisons will enable us to distinguish between regulatory mechanisms that are conserved and those that are tissue-specific. Another avenue of particular importance would be to develop more robust methods for interpreting GCNs.

For example, while the GNNExplainer model is a theoretically sound framework and yields an unbiased estimator for the importance scores of the subgraph nodes and features, there is variation in the interpretation scores generated over multiple runs. Furthermore, with larger GCNs, the optimization function utilized in GNNExplainer is challenging to minimize in practice. The importance scores converge with little differentiation for some iterations, and the method fails to arrive at a compact representation. This issue may be due to the relatively small penalties the method applies for constraining the optimal size of the mask and the entropy of the distribution. We plan to address this issue in the future by implementing more robust forms of regularization.

In addition, although much of the GCN literature has focused on node features, more recent work also incorporates edge weights. In the context of our problem, edge weights could be assigned by using the Hi-C counts in the adjacency matrix. Another natural extension to our model would be to include other types of experimental data as features, such as promoter sequence or ATAC-seq measurements. Lastly, the GCN framework is flexible and general enough to be applied to many other classes of biological problems that require integrating diverse, multimodal data sets relationally.

In summary, GC-MERGE demonstrates proof-of-principle for using GCNs to predict gene expression using both local epigenetic features and long-range spatial interactions. More importantly, interpretation of this model allows us to propose plausible biological explanations of the key regulatory factors driving gene expression and provide guidance regarding promising hypotheses and new research directions.

AUTHOR DISCLOSURE STATEMENT

The authors declare they have no conflicting financial interests.

FUNDING INFORMATION

Research reported in this publication was supported by an Institutional Development Award (IDeA) from the National Institute of General Medical Sciences of the National Institutes of Health under grant number P20GM109035.

SUPPLEMENTARY MATERIAL

Supplementary Material

Supplementary Figure S1

Supplementary Figure S2

Supplementary Figure S3

Supplementary Figure S4

Supplementary Figure S5

/doi/suppl/10.1089/cmb.2021.0316/suppl_file/Supp_FigS6.pdf

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3

Supplementary Table S4

Supplementary Table S5

Supplementary Table S6

Supplementary Table S7