Summary
Natural and induced somatic mutations that accumulate in the genome during development record the phylogenetic relationships of cells; whether these lineage barcodes capture the complex dynamics of progenitor states remains unclear. We introduce quantitative fate mapping, an approach to reconstruct the hierarchy, commitment times, population sizes, and commitment biases of intermediate progenitor states during development based on a time-scaled phylogeny of their descendants. To reconstruct time-scaled phylogenies from lineage barcodes, we introduce Phylotime, a scalable maximum likelihood clustering approach based on a general barcoding mutagenesis model. We validate these approaches using realistic in silico and in vitro barcoding experiments. We further establish criteria for the number of cells that must be analyzed for robust quantitative fate mapping and a progenitor state coverage statistic to assess the robustness. This work demonstrates how lineage barcodes, natural or synthetic, enable analyzing progenitor fate and dynamics long after embryonic development in any organism.
Keywords: lineage tracing, quantitative fate mapping (QFM), progenitor state dynamics, progenitor field, somatic mutations, Phylotime, ICE-FASE, coalescent theory, time-scaled cell phylogeny
Graphical Abstract
In Brief:
Estimating the temporal distance between cells using lineage barcodes enables reconstructing the hierarchy, commitment times, population sizes, and commitment biases of their progenitor states during development.
Introduction
Embryonic development is the genesis of complex body plans in the animal kingdom. It starts with the zygote, a single cell in a totipotent state, and ends with thousands of specialized terminal cell types organized in tissues. In between, dividing cells traverse a hierarchy of increasingly diverse but decreasingly potent intermediate progenitor states. Each progenitor state specifies the ensuing states that its descendant cells may assume, thus directing their fates. Collectively, progenitor states orchestrate the emergence of terminal cell types to form complex tissues. Therefore, delineating how progenitor states specify cell fate is critical for understanding normal and dysregulated development.
The recent advances in genome engineering and sequencing have inspired a new approach for interrogating cell fate: retrospective lineage analysis using synthetic or natural somatic DNA barcodes. These approaches rely on the accumulation of random mutations in the genome during development. Each mutation is inherited by the descendants of the cell in which it occurs; each descendant can add new mutations to the combination it inherited. This process marks each cell with a barcode—a combination of mutations—that encodes its phylogenetic relationship to the other cells1. Synthetic lineage barcoding, which relies on gene editing technologies to induce mutations, has been implemented in model organisms such as zebrafish2–4 and mouse5–7. Natural lineage barcoding, which relies on naturally-occurring somatic mutations, has been primarily used in humans8,9. These retrospective approaches hold a unique promise for mapping cell fate. Unlike prospective lineage tracing approaches10, they have the potential to resolve entire hierarchies of progenitor states, thereby facilitating the analysis of non-cell autonomous effects. Unlike single-cell molecular profiling approaches, they can bridge time gaps between terminal cells and their progenitors that existed far earlier in time. Moreover, they can be applied to humans and non-model organisms where analyzing somatic mutations from cadavers can be more practical and ethical than analyzing embryos.
Despite this compelling potential, the full scope of the information that lineage barcoding can provide about the fate of the intermediate progenitor states remains unclear for multiple reasons. First, cell phylogeny is a function of cell divisions and most cell divisions in higher organisms do not accompany fate decisions. In the roundworm C. elegans, a unique model organism in which almost all cell divisions give rise to daughters with different fates, the phylogeny of terminal cells is identical to the fate of their progenitors11. However, in more complex organisms, progenitor populations can undergo cell divisions that are not associated with fate decisions, leading to divergences between phylogeny and fate12,13. As a result, liver hepatocytes of an identical progenitor state history may have the maximum possible distance on the phylogenetic tree by being the descendants of different cells at the 2-cell stage. Second, while the progenitor states and their fate remain largely stereotyped within species, the phylogenetic histories of the cell populations that assume those progenitor states can vary greatly from embryo to embryo due to stochasticity in fate decisions14,15. As a result, phylogenies of different subsets of cells from different embryos cannot be combined to synthesize a full picture the same way they can be in C. elegans. Third, single-cell lineage barcodes can be obtained for only a small sample of cells as current technologies can only sequence thousands of single cells whereas most mammals have millions of cells in each tissue. Given the divergences between fate and phylogeny and the variable nature of the latter, it remains unclear how phylogenies derived from small samples can reliably inform organism-level fate maps. Complicating matters further, phylogenetic inference from lineage barcodes is inherently subject to error because a finite number of barcoding sites may not record every cell division16, and even with infinite barcodes, finding the optimal tree is still a computationally intractable (NP-hard) problem17. Collectively, these considerations raise critical questions about the value of measuring cell phylogeny through barcoding approaches in complex organisms: What features of progenitor states are reflected in the phylogeny of a limited sample of cells? How can these features be extracted from lineage barcodes?
To address these questions, we systematically studied the relationship between cell fate and cell phylogeny as derived using lineage barcodes. First, we established a method to generate cell phylogenies and developed the ICE-FASE algorithm to reconstruct quantitative fate maps—models that represent the hierarchy and dynamics of progenitor states—from time-scaled phylogenies. We found that quantitative fate mapping requires adequate representation of each progenitor state’s progeny among the sampled terminal cells. Second, we simulated synthetic lineage barcoding in mice and established Phylotime, a general and scalable method to infer time-scaled phylogenies from lineage barcodes. We found that Phylotime-inferred phylogenies enable robust quantitative fate map reconstruction when coupled with ICE-FASE. Overall, this work establishes quantitative fate mapping as a general framework for capturing the fate hierarchy and dynamics of progenitor populations using lineage barcodes of their descendants.
Results
Quantitative fate map: a model of progenitor field dynamics in development
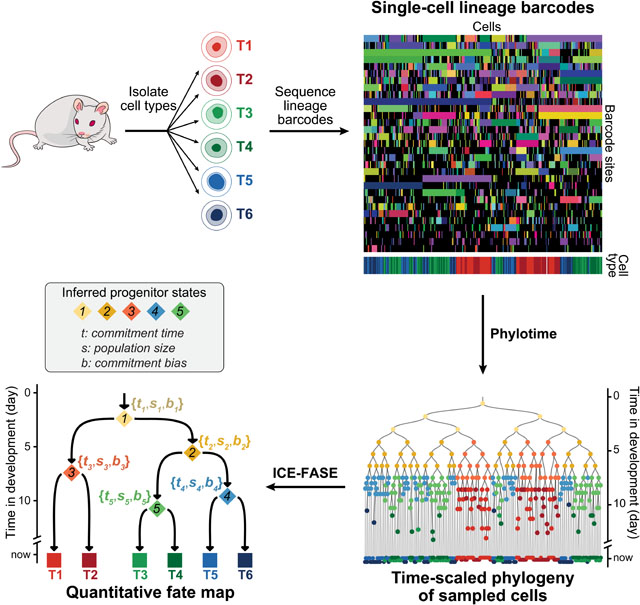
We began by establishing the quantitative fate map, a model of the progenitor state hierarchy that gives rise to a group of cell types (Figure 1A). Each progenitor state is defined by its potency, which is the set of cell types it can produce. It is also associated with a commitment event, when its cells transition to less potent downstream states. The commitment event confers each progenitor state three additional defining features: i) commitment time, which is the time when a progenitor state’s cells commit to its downstream states, ii) population size, which is its number of cells at commitment time, and iii) commitment bias, which is the proportions of its population committing to each downstream state (Figure 1B). Commitment times represent the order and pace of developmental events18, population sizes are important determinants of organ and tissue size19, and commitment biases reflect the epigenetic state of progenitors and the effect of non-cell autonomous cues20. The progenitor states are unobserved in barcoding experiments; only their descendants at the time of sample collection are observed. We refer to these observed descendants as terminal cell types. In summary, a quantitative fate map defines the fate dynamics of a progenitor field21—a collection of progenitor states that give rise to a set of observed cells.
Figure 1. Simulating time-scaled phylogenetic trees of sampled cells based on a panel of quantitative fate maps.
(A) Topology of a quantitative fate map. Arrows represent cell states, colored rectangles represent their commitment events. Triangles represent terminal types at the time of sampling.
(B) Quantitative fate map in A annotated with commitment time, population size, and commitment bias of its progenitor states. Pie charts show sampling fraction under fixed sampling at progenitor state commitment time or terminal type sampling; numbers on pies show corresponding true population sizes. The bottom two rows show the number of cells sampled from each terminal type under fixed and proportional sampling.
(C) The panel of 331 quantitative fate maps. The maps are in three sizes of 16, 32, and 64 terminal cell types. Three examples of each size are shown, including the most balanced (top) and the most unbalanced (bottom).
(D) Example time-scaled phylogeny of sampled cells generated by fixed sampling of 100 cells from each terminal type in the fate map shown in A. Node colors based on A.
See also Figures S1 and S2.
A diverse test panel of quantitative fate maps
We constructed 331 quantitative fate maps covering diverse developmental scenarios (Figures 1C and S1A, Methods). Representing increasing field sizes, the maps are in three categories of 16, 32 or 64 terminal cell types. We label progenitor states and terminal types with “P”s and “T”s followed by numerals, respectively. Within each category, the topologies of the maps range from perfectly balanced to highly unbalanced (Figures 1C and S1B,C) as measured by the Colless imbalance index22. In more unbalanced maps, progenitor states split into increasingly unequal diversities of terminal types (Figure 1C). In addition to size and topology, the parameters of progenitor states within each map vary (Figures S1D–J). Commitment times are between t = 2.5 and 10.9 days, which roughly correspond to the beginning of fate restrictions and the end of organogenesis in mouse development (Figures 1A–C and S1D). Commitment biases were drawn from a beta distribution and cover a wide range (Figures 1B and S1E, Methods). Cell division and death rates were drawn from uniform distributions, ranging from 0.6 to 0.35 days per doubling and 0.02 to 0.08 death probability per division, respectively (Figures S1F–H), broadly matching reported rates during mouse embryogenesis23,24. As all fate maps start with one founder cell at time t = 0, the division and death rates together with other fate map parameters dictate the progenitor population sizes at each point in time (Figures 1B and S1I,J). All fate maps end at t = 11.5 days when terminal cell types are sampled for observation based on either fixed or proportional sampling (Figure 1B). Under fixed sampling, the same number of cells are sampled from each terminal type, imitating experiments where target terminal cell types are purified using sorting or other methodology. Under proportional sampling, each terminal type is sampled based on its share of the total population, imitating experiments where cells are sampled without enrichment from whole tissues.
Modeling cell phylogeny based on a quantitative fate map
We next established a generative model to simulate cell phylogenies based on each quantitative fate map. Generating the entire tree of cell divisions for millions of cells (Figure 1B) is computationally impractical. To overcome this problem, we developed a model based on coalescent theory in population genetics25–27 to generate time-scaled phylogenies only for sampled terminal cells rather than for all terminal cells (Figure S2, Methods). In brief, after choosing the number of cells to be sampled from each terminal cell type of a fate map, the number of cells from each progenitor state ancestral to sampled terminal cells is generated at all prior time points going backward to the founder cell. These sampled terminal and progenitor cells compose the nodes of the phylogenetic tree. Edges are then assigned by randomly connecting nodes from each time point to their progenitor nodes in the earlier time point. This approach generates time-scaled phylogenies for sampled cells based on their progenitors’ fate map (Figure 1D) in a computationally efficient manner.
Using this model, we generated time-scaled phylogenies for all quantitative fate maps in our test panel, sampling an average of 100 cells per terminal type under both fixed and proportional sampling (Figure 1B). To capture the variable nature of phylogeny, we simulated five phylogenies for each condition, representing a different set of cells being sampled from the same set of terminal cell types in different individuals (Figure S2). Together, these results represent 3,310 experiments (331 maps × 2 sampling schemes × 5 repeats) wherein phylogeny is known for a small fraction of cells (average 0.07%) derived from a complex field of progenitors. We will use these phylogenies to benchmark fate mapping algorithms established below.
Reconstructing the hierarchy of progenitor states from cell phylogeny
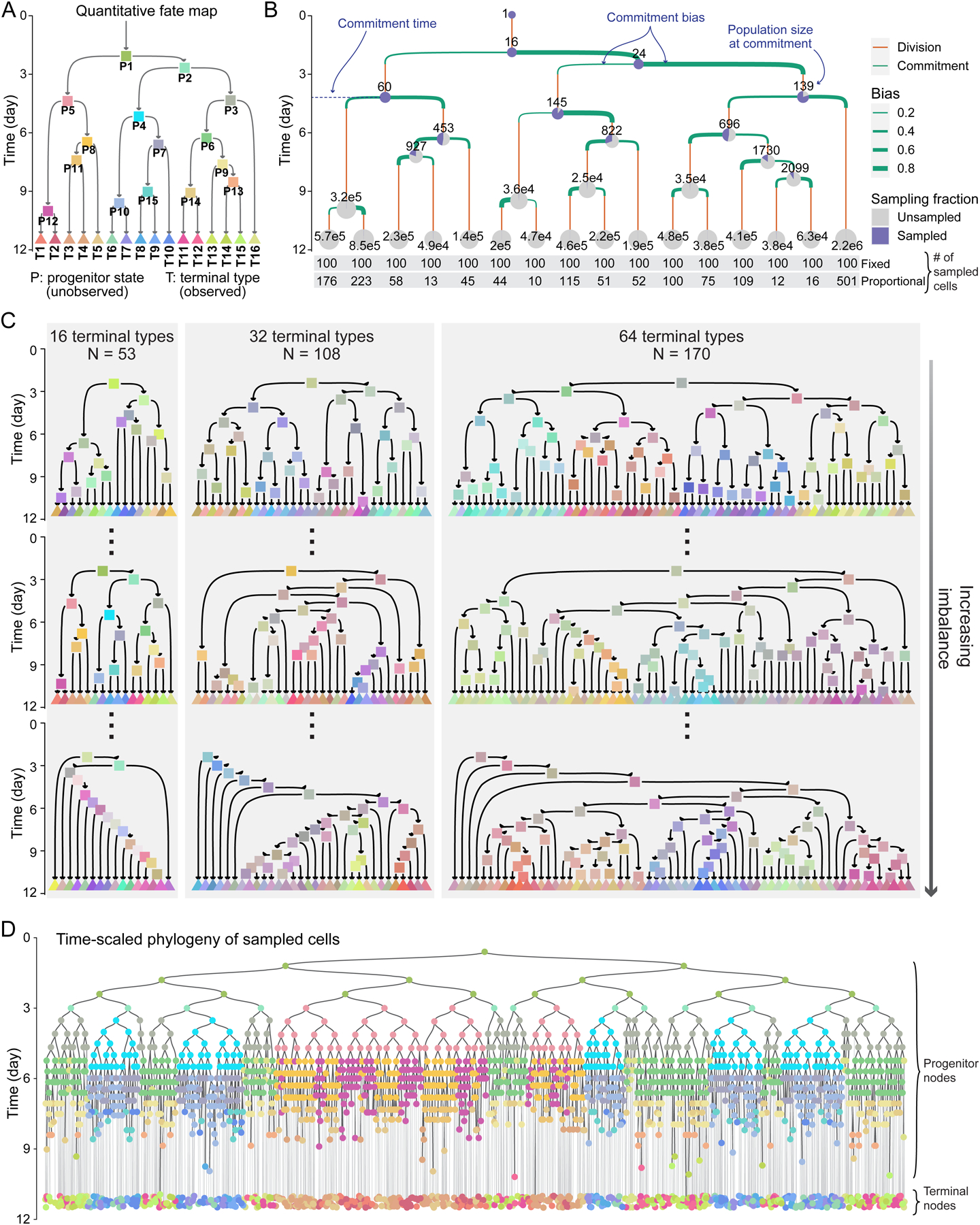
To derive fate map topology from time-scaled phylogenies, we used the timings of apparent fate separations between terminal cell types. First, we annotated each node in the phylogenetic tree with its observed fate—the types of its observed terminal descendants (Figure 2A). Next, we identified the nodes whose observed fates are more potent than that of both their daughter nodes (Figures 2A,B). For instance, if an internal node leads to terminal cell types {T3, T4, T5} but {T3, T4} are only seen in one of its branches and {T5} only in the other, this node constitutes a FAte SEparation (FASE) between T3 and T5 as well as between T4 and T5. The average time since FASEs between two terminal cell types (i.e., FASE distance) measures their developmental distance: long FASE distances indicate early separation in development and short FASE distances indicate more recent separation (Figures 2B,C). We can thus compile a matrix of FASE distances between all terminal cell types (Figure 2D) and apply a clustering method (UPGMA) to obtain fate map topology (Figure 2D, Methods). This fate map topology establishes a hierarchy of increasingly diverse but decreasingly potent “inferred” progenitor states (labeled with “iP”s followed by numerals) that give rise to the observed cell types (Figure 2E). To summarize, the FASE algorithm reconstructs a hierarchy of inferred progenitor states based on the patterns of potency restriction in the phylogeny.
Figure 2. Reconstructing fate map topology from time-scaled phylogeny of sampled cells.
(A) Example phylogenetic subtree. Each internal node is labeled with its observed fate. T4–T5 FASEs are colored orange.
(B) Phylogeny from Figure 1D showing T4–T5 (orange) and T15–T16 (blue) FASEs. T4, T5, T15, and T16 are colored according to the key on the bottom.
(C) Boxplots showing the temporal distribution of T4–T5 and T15–T16 FASEs in the tree in B.
(D) Heatmap showing the FASE distance matrix for all pairs of terminal types in the tree in B. Dendrogram shows hierarchical clustering result.
(E) The fate map topology reconstructed by clustering the FASE distance matrix in D. Triangles: observed terminal types; diamonds: inferred progenitor states (iPs).
(F) Scatter plots showing error of fate map topology reconstruction (KC0) using FASE algorithm (red) or SPS (blue) as a function of imbalance for all 3,310 simulated phylogenies faceted by fate map size (columns) and sampling strategy (rows). The gray points are based on random topology reconstructions. Solid trend lines are locally weighted smoothing (LOESS).
See also Figure S3.
We applied the FASE algorithm to reconstruct fate map topology for each simulated phylogeny in our panel of 3,310 (Figure S1K). For comparison, we also used the shared progenitor score (SPS) which estimates the distance between two terminal cell types based on the number of nodes in the phylogenetic tree that have those terminal types in their observed fate, weighted by how many other terminal types are among the observed fates6. We further generated random fate map topologies as negative control (Methods). In all cases, we compared the reconstructed topology to that of its corresponding true fate map using the Kendall-Colijn (KC) distance with its tuning parameter (λ) set to zero (KC0)28. The KC distance measures the difference between rooted trees. It compares the placement of the most recent common ancestor (MRCA) of all pairs of tips relative to the root based on either the number of edges (KC0) or path length (KC1). A KC0 distance of zero indicates that the reconstructed and true fate maps have identical topologies (a KC1 distance of zero, which we will use later, indicates identical topologies and branch lengths between two trees). The results show that FASE strategy consistently outperforms SPS (Figure 2F): It predicts perfectly accurate topologies when the fate map is small or has low imbalance; it predicts informative topologies even for large fate maps with extreme imbalances. Unbalanced maps have smaller intervals between commitment events (Figure S1L), making reconstruction of topology more challenging. We also observed that fixed sampling outperforms proportional sampling (Figure 2F), likely because it ensures better representation of rare terminal populations. These results establish the FASE algorithm as a robust and scalable method to reconstruct fate map topology from cell phylogeny.
To better understand the sources of topology reconstruction inaccuracies, we investigated FASE distance error, which is the difference between estimated FASE distance between two terminal cell types and the time since their last common progenitor state in the true fate map. We found a negative correlation between FASE distance error and the sampling fractions of progenitor states (Pearson’s R=−0.40, p < 2.2e–16) (Figure S3A) in the 3,310 simulated experiments. Sampling fraction is the proportion of the progenitor state population whose progeny are represented among sampled terminal cells and is known from simulations (Figure 1B). Later progenitor states tend to have larger population sizes and thus lower sampling fractions (Figure S3B). Undersampling the terminal descendants of a progenitor cell can bias its corresponding FASE distances (Figure S3C). To validate the effect of sampling fraction, we generated phylogenies for all our 16-terminal type fate maps, sampling an average of 25, 50, 100, and 200 cells per terminal type. We observed that increased sampling reduces topology reconstruction error (Figure S3D). For example, every doubling of the number of sampled cells, which increased the sampling fraction of progenitor states by 33% on average, increased the percent of perfectly reconstructed topologies by 18.9% on average. These results establish progenitor state sampling fraction as an important parameter for fate map topology reconstruction.
Estimating progenitor state commitment time from cell phylogeny
To characterize the dynamics of inferred progenitor states, we turned to the internal nodes of the time-scaled phylogenies. We assigned each internal node in the phylogenetic tree to the least potent inferred progenitor state or terminal type from the reconstructed fate map topology that contained the node’s observed fate (Figure 3A). For example, a node with an observed fate of {T2, T3, T4} can be assigned a more potent inferred state of iP2 capable of {T1 to T5} if the now-reconstructed fate map topology (Figure 2E) indicates that iP2 differentiates into fates {T1, T2} and {T3, T4, T5} (Figure 3B). To assess the fidelity of these assignments, we compared the inferred states of internal nodes in all 3,310 phylogenies to their true states which are known from simulations (Figure S3E). The only type of error was assigning an internal node to a progenitor state less potent than its true state, which occurred, on average, for 27.7% of the assignments in each phylogeny (Figures S3E,F). This type of error is also caused by undersampling (Figure S3G); hence, we will keep track of progenitor states’ sampling fractions going forward.
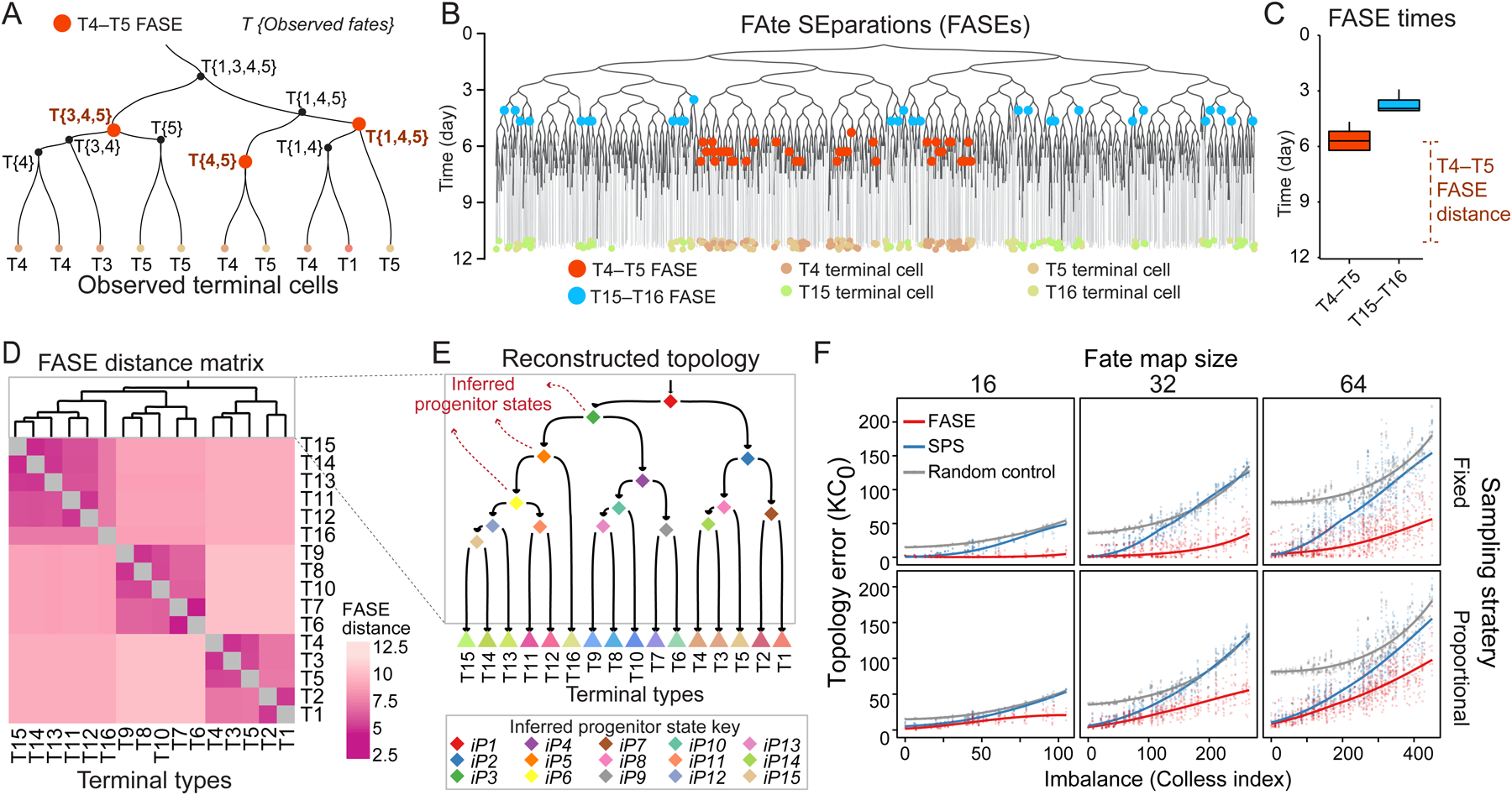
Figure 3. Obtaining progenitor state commitment times, population sizes, and commitment biases from time-scaled phylogeny of sampled cells.
(A) Phylogeny in Figure 2B with internal nodes colored according to their inferred progenitor state. Color key in Figure 2E.
(B) A subtree from A where each internal node is labeled by its inferred progenitor state or terminal type. Asterisks signify ICE nodes.
(C) The tree in A with nodes inferred as iP5 (orange) and iP8 (pink) labeled. Darker shades mark the nodes that are also ICEs.
(D) Boxplots showing the distribution of ICE times for all inferred progenitor states in the tree in A, representing their commitment times. The ICE times for iP5 and iP8 are boxed in red.
(E) Scatterplots showing the correlation between true commitment time of each progenitor state to the value estimated from the phylogenetic tree across all 3,310 simulated phylogenies broken down by sampling strategy. Dot colors represent progenitor states’ sampling fractions based on the key on the right. Blue line and value respectively show trendlines (LOESS) and Spearman’s ρ for progenitors with sampling fraction >= 25%. Those for progenitor states with sampling fraction < 25% are shown in red. Spearman’s ρ for all progenitor states is shown in black. Black lines are y=x.
(F) Scatter plot showing the error of inferred commitment time for progenitor states as a function of their sampling fraction (top) aligned to a histogram of sampling fraction for all progenitor states in the panel (bottom). Error is the absolute value of the difference between estimated and true commitment times. The vertical dashed line shows sampling fraction cutoff of 0.25. Trendline (LOESS) is in blue.
(G) The edges and the nodes relevant to population size and commitment bias of iP5 and iP8 are shown on the tree from A (left) aligned to the corresponding reconstructed fate map (right). Horizontal lines mark iP5 and iP8 commitment times. Edges in the phylogeny are classified and colored based on the commitment they represent, and nodes based on their inferred progenitor state or terminal type, with the fate map serving as the color key. Circular arrows on the fate map indicate divisions without commitment (self-renewal).
(H) Tally of edges and pre- and post-commitment nodes associated with iP5 (left) and iP8 (right) from the phylogeny in G, a part of which is magnified for added clarity. The number next to each edge indicates how many times the combination of incoming and outgoing progenitor state or terminal type was observed. Gray boxes on top indicate the nodes that were counted towards progenitor state population size, gray boxes on the bottom indicate post-commitment nodes counted for commitment bias. The number next to each gray box indicates the total count of nodes in that box. Arrows from G inset show in parenthesis counts being added to relevant tallies from the inset. Color key same as G.
(I) Barplots showing the estimated population size of each inferred progenitor state in A. Red boxes mark iP5 and iP8 estimates from H.
(J) Stacked barplots showing the estimated post-commitment population size of each inferred progenitor state in A, stacked and colored according to the downstream state they lead to. Red boxes mark estimates relevant to iP5 and iP8, colored according to Figure 2E.
(K,L) Scatter plots showing the correlation between true and estimated population size (K) and commitment bias (L) of inferred progenitor states in fixed (left) and proportional sampling (right) across all 3,310 simulated phylogenies. Other plot features identical to panel E.
See also Figure S3.
To derive the commitment time of each progenitor state, we defined Inferred Commitment Events (ICEs): An ICE is a node whose inferred state is more potent than that of both of its immediate descendants (Figures 3B,C). For example, in Figure 3B, when an internal node assigned to iP2 (capable of {T1 toT5}) splits into two nodes with assigned states of T2 and iP14 (capable of {T3, T4}) respectively, we count this node as an ICE for iP2. ICEs improve on FASEs by leveraging the now-reconstructed fate map topology to identify a more confident set of nodes that represent state transitions. We defined the commitment time for a progenitor state as the mean of its ICE times (Figure 3D). Across all progenitor states in our panel of 3,310, ICE times captured the relative timing of commitment events as indicated by a high rank correlation (Spearman’s ρ=0.90 for fixed sampling and 0.91 for proportional sampling) (Figure 3E). Like FASE distance error, the error of estimated commitment time for progenitor states showed a strong negative correlation with their sampling fraction (Pearson’s R = −0.97) (Figure 3F). In fact, when only considering progenitor states with a sampling fraction above 0.25 (Figure 3F), ICE times not only captured relative commitment times almost perfectly (Spearman’s ρ=1.00 for fixed and 0.99 for proportional sampling) but also captured the exact timing of commitments as indicated by a low root mean square error (RMSE=0.31 days for fixed and 0.27 days for proportional sampling) (Figure 3E). These results establish ICE times as estimates for the commitment times of the progenitor states from time-scaled phylogenies of sampled cells. They also demonstrate the central importance of progenitor state sampling fraction for obtaining reliable estimates.
Estimating progenitor state population size and commitment bias from cell phylogeny
We next leveraged both fate map topology and commitment times to estimate population sizes and commitment biases of progenitor states. To estimate population size for a progenitor state, we identified the subset of all edges in the phylogeny that (i) cross the progenitor state’s commitment time and (ii) connect nodes assigned as either the progenitor state itself or any of its upstream or downstream states in fate map topology (Figures 3G,H, Methods). These branches represent cells of the progenitor state that are present at its estimated commitment time. We thus counted the number of incoming nodes to these branches as the population size (Figures 3H,I). For commitment bias, we calculated the proportion of these branches that end in each of the downstream fates irrespective of their parental state (Figures 3H,J). Applying this algorithm to the 3,310 simulated time-scaled phylogenies, we found that the ability to estimate population size and commitment bias for a progenitor state depend heavily on its sampling fraction as well as the sampling method. For well-sampled progenitor states (sampling fraction > 0.25), population size estimates agree well with their true sizes (Spearman’s ρ=0.98 for fixed and ρ=0.90 for proportional sampling) (Figure 3K). For undersampled progenitor states, a progenitor population’s size estimate is capped at the number of its sampled terminal progeny, which is reasonably informative in proportional sampling (Spearman’s ρ=0.78) but uninformative in fixed sampling (Spearman’s ρ=0.06) (Figure 3K). For commitment bias, proportional sampling produced good estimates for the well-sampled progenitor states (Spearman’s ρ=0.83) and reasonable estimates for the undersampled ones (Spearman’s ρ=0.72). (Figure 3L). Fixed sampling produced good estimates only for well-sampled progenitor states (Spearman’s ρ=0.82) and was almost uninformative for undersampled ones (Spearman’s ρ=0.15) (Figure 3L). Consistent with these results, average population size and commitment bias estimate errors approach zero as sampling fraction approaches one (Figures S3H,I). The more effective estimation of population size and commitment bias with proportional sampling is due to the inherent correlation between the size of terminal populations, which proportional sampling captures, and that of their progenitors. Taken together, these results establish a strategy for estimating progenitor population size and commitment bias from a time-scaled phylogeny of cells.
Modeling realistic lineage barcoding results in development
So far, we have established a strategy—the ICE-FASE algorithm—to reconstruct quantitative fate maps which describe progenitor state hierarchy, commitment time, population size, and commitment bias from time-scaled phylogenies. The phylogenies that were used thus far represent the exact sequence and timing of cell divisions as simulated (i.e., true phylogeny). In actual experiments, phylogeny must be inferred from lineage barcodes and such inferences are inherently subject to error due to the limitations of both barcoding systems and computational techniques. Therefore, how close any inferred phylogeny is to the true phylogeny remains uncertain. To address whether quantitative fate maps can be obtained from inferred phylogenetic trees despite their uncertainty, we started by simulating realistic lineage barcoding outcomes. To do so, we established a mutagenesis model comprising independent barcoding sites that accumulate mutations according to a Poisson point process with a constant rate (Figures 4A,B). Each mutation converts an active copy of the site into one of many possible inactive mutated alleles, each with a distinct emergence probability. Next, we set the parameters of this model based on the MARC1 system5 wherein barcoding sites are homing guide RNA loci (hgRNAs)29. We estimated the mutation rates of MARC1 hgRNA from published embryonic time course measurements30 (Figure S4A, Table S1, Methods). We estimated emergence probabilities of mutant alleles for each hgRNA by modifying the inDelphi machine learning algorithm31, which predicts CRISPR-Cas9 mutations (Figure S4B, Methods). We validated the mutation model and its parameters by simulating barcoding in whole-mouse embryos and comparing the results to that of actual MARC1 barcoded embryos (Methods). The comparison showed a broad agreement between experimental and simulated barcoding with respect to the emergence probability of mutant alleles, total mutation levels over the course of embryogenesis, and the diversity and composition of mutant alleles within an embryo (Figures S4B–G). These results suggest that our strategy produces realistic barcoding results that are comparable to lineage barcoding in mouse embryos. We thus simulated mutagenesis in our panel of 3,310 phylogenies with 50 hgRNAs per cell (Methods). These simulations yielded in silico barcoding experiments wherein, similar to actual experiments, the barcodes and terminal types are known for sampled single cells (Figure 4C).
Figure 4. Modeling barcoding mutagenesis and inferring time-scaled phylogenies from lineage barcodes using Phylotime.
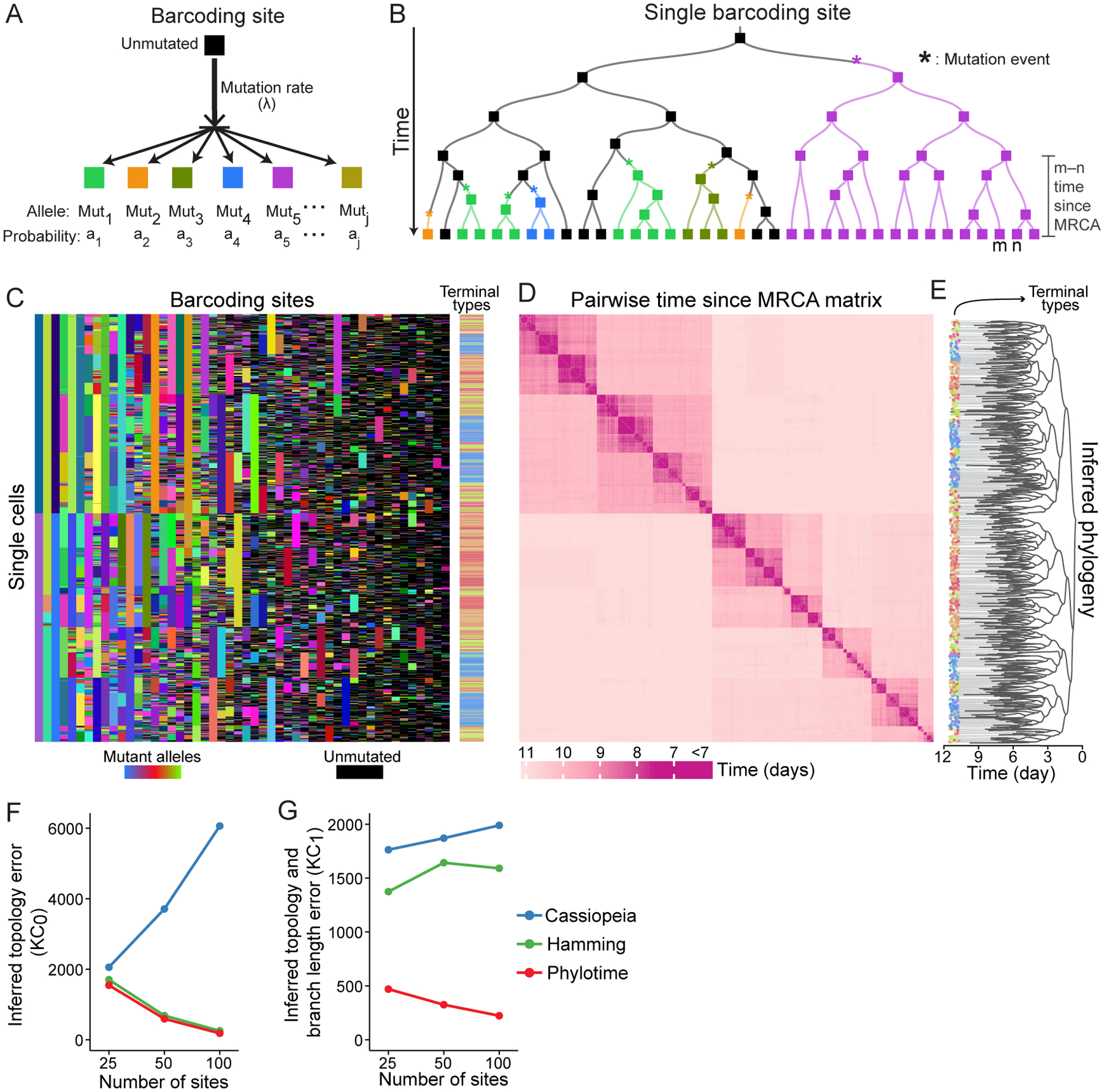
(A) Model of a barcoding site which mutates with a constant rate (λ) to convert to one of many possible mutant alleles (Mut1, …, Mutj), each with an emergence probability (a1, …, aj).
(B) Example time-scaled phylogeny showing the inheritance of a single barcoding site. Rectangles represent the site, their colors represent its allelic state according to A. Asterisks denote mutation events. Only the unmutated allele (black) can change, mutated alleles (colored) are inherited from a cell by all its descendants. The time since MRCA is shown for two terminal cells, m and n.
(C) Character matrix showing the output of a simulated barcoding experiment based on Figure 1A,B fate map with each barcoding site as a column and each cell as a row. Unmutated alleles are in black, mutant alleles in other colors. Color bar on the right shows cell types with Figure 1A as color key.
(D) Heatmap showing the estimated pairwise time since MRCA for all cells in C.
(E) Time-scaled phylogenetic tree inferred by applying Phylotime to D. Colors of terminal nodes signify cell type.
(F,G) Error of phylogenetic reconstruction using Phylotime (red), Hamming distance with UPGMA (green), and Cassiopeia (blue), with 25, 50, or 100 barcoding sites when considering only tree topology (F) or tree topology and branch length (G) across the panel of 530 simulated barcoding experiments with 16 terminal types (Mean ± SEM, N=530; SEM very small).
See also Figure S4.
Inferring time-scaled cell phylogenies from single-cell lineage barcodes using Phylotime
For quantitative fate mapping, the phylogenetic tree inferred from lineage barcodes must be time-scaled. However, many inference methods lack a mutagenesis model specific to lineage barcoding and thus their resulting phylogram branch lengths do not represent interdivision times. Those with a barcoding mutagenesis model32–34 require optimization techniques that do not scale to thousands of cells, as sampled here in each simulated experiment. Therefore, we developed a scalable method to infer time-scaled phylogenies from lineage barcodes. In this method, we first compute a maximum likelihood estimate of the time that separates a pair of cells from their most recent common ancestor (time since MRCA) for all pairs of terminal cells (Figures 4D and S4H, Methods). We then apply UPGMA hierarchical clustering to the pairwise time since MRCA matrix to obtain a time-scaled phylogenetic tree (Figure 4E). We call this approach, which scales in polynomial time, PHYlogeny inference using Likelihood Of TIME (Phylotime).
To evaluate Phylotime’s performance, we first compared estimated times since MRCA for all pairs of cells from a simulated barcoding experiment to those derived from the corresponding true phylogeny (Figure S4I) and found that the two were highly correlated (Pearson’s R = 0.93). We then simulated barcoding with 25, 50, and 100 hgRNAs in all 530 simulated phylogenies for the 16-terminal type fate maps and applied Phylotime to infer phylogeny from each. For comparison, we also inferred phylogenies using a Hamming distance-based clustering method as well as Cassiopeia35 which is a heuristic approach based on maximum parsimony (Methods). Other common methods do not scale well to this number of terminal cells (1,600) and barcoding sites (up to 100) in each experiment. We then evaluated the difference between inferred phylogenies and their corresponding true phylogenies using KC0 distance for topology and KC1 distance for combined topology and branch length (Figures 4F,G). KC0 results showed that Phylotime produced topologies that had on average 80% less error compared to Cassiopeia and 6% less error compared to Hamming (Figure 4F). KC1 results showed that Phylotime’s time-scaled phylogenies had on average 82% less error compared to Cassiopeia and 78% less error compared to Hamming (Figure 4G). Importantly, only Phylotime’s solutions converged to the true phylogeny with an increasing number of barcoding sites (Figure 4G). Together, these results show that Phylotime can accurately infer time-scaled phylogenies from lineage barcodes.
Reconstructing quantitative fate maps from lineage barcodes
With realistic barcoding simulation and a method to infer time-scaled phylogenies in hand, we finally assessed how well lineage barcodes can inform quantitative fate maps. We applied the ICE-FASE algorithm to all 3,310 Phylotime-inferred time-scaled phylogenies from experiments simulated with 50 hgRNAs to reconstruct quantitative fate maps and compared these fate maps to those obtained by applying ICE-FASE to the true phylogeny. Phylotime-inferred phylogenies performed almost as well as true phylogenies at reconstructing fate map topology, regardless of fate map size and imbalance or sampling strategy (Figure 5A), with 22% more error on average compared to the true phylogeny. Similarly, for commitment times, population sizes, and commitment biases of progenitor states, Phylotime-inferred phylogenies performed similarly to true phylogenies in all conditions, recovering on average 95%, 80%, and 76% of the correlation, respectively (Figure 5B). Taken together, these results show that quantitative fate maps can be faithfully reconstructed based on time-scaled phylogenies inferred using Phylotime despite errors inherent to phylogenetic inference.
Figure 5. Quantitative fate map reconstruction from lineage barcodes using Phylotime and ICE-FASE.
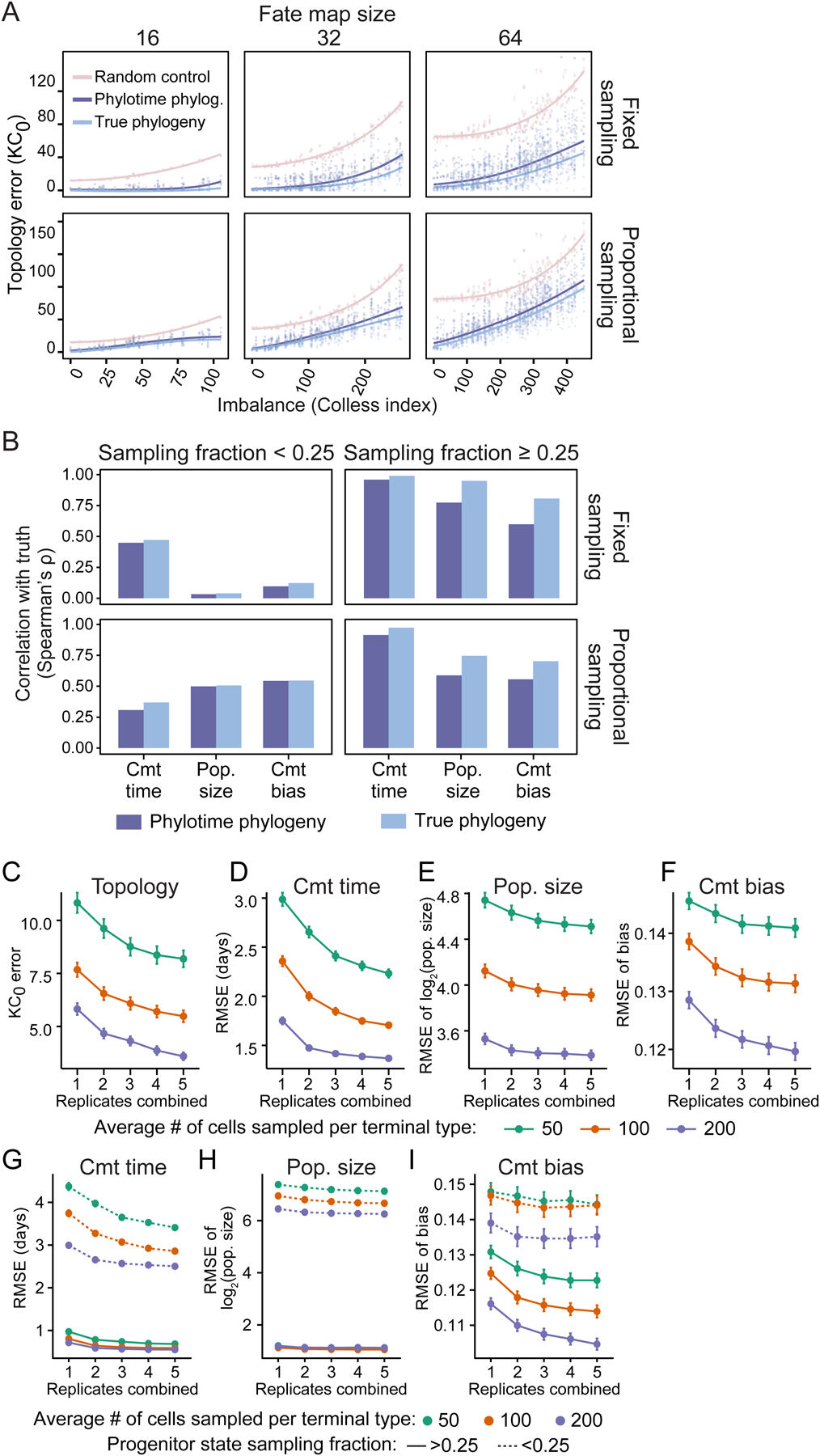
(A) Scatter plots showing error of fate map topology reconstruction (KC0) after applying ICE-FASE algorithm to true (light blue) or Phylotime-inferred (dark blue) phylogeny as a function of map imbalance for all 3,310 simulated barcoding experiments faceted by fate map size (columns) and sampling strategy (rows). The faded pink points establish baseline error based on random topology reconstruction. Trendlines (LOESS) are shown.
(B) Barplots of Spearman’s correlation between true and estimated commitment (cmt) time, population (pop.) size, cmt bias for all progenitor states in 3,310 simulated experiments, faceted by sampling fraction (columns) and sampling strategy (rows). Values from true phylogenies are shown in light blue and those from Phylotime-inferred in dark blue.
(C–F) Lineplots showing the performance of quantitative fate map reconstruction as a function of the number of replicates combined when sampling 50 (green), 100 (orange), or 200 (purple) cells on average from each terminal type in the panel of 16-terminal type fate maps, measured by the error of topology (C), cmt time (D), pop. size (E), and cmt bias (F) estimates (Mean±SEM; N=106).
(G–I) Same as D–F but estimates separated for well-sampled (solid lines) and undersampled (dotted lines) progenitor states.
See also Figures S4, S5, and S6.
Effect of barcoding site composition, experimental errors, and sampling time on quantitative fate mapping
We next analyzed how the number and the mutation rates of barcoding sites affect the ability to reconstruct quantitative fate maps from lineage barcodes. On the panel of 3,310 true phylogenies, we repeated barcoding simulation with 25, 50, or 100 hgRNAs per cell mutating at fast, intermediate, or slow rates, as observed in MARC1 hgRNAs (Figure S4A). We then applied Phylotime followed by ICE-FASE to these 29,790 simulated experiments to obtain quantitative fate maps. To assess these maps, we instituted a general evaluation strategy that will also be used in all later sections: we used KC0 error for topology; we used the RMSEs of progenitor state commitment times, log2(population sizes), and commitment biases irrespective of sampling fraction and based on the true topology (using imperfectly reconstructed topology would bias estimates in favor of easily resolvable progenitor states) (Methods). Note that RMSE measures absolute error; experiments with relatively high RMSEs often still have accurate relative ordering of progenitor state parameters. The analysis showed that very slow rates of mutations (~0.002 mutations per site per division) cannot resolve reliable quantitative fate maps under the conditions tested here (Figure S4J). Though increasing the number of slow-mutating sites increased reconstruction accuracy generally, indicating that the combined mutation rates of all sites ultimately dictate reconstruction efficiency (Figure S4J). Intermediate rates of mutation (~0.05 per site) performed better than fast mutation rates (~0.28 per site). As fast sites are more likely to record information only in the earlier days of development (Figures S4D–F) and before many of the progenitor states have come into existence (Figure S1D). Overall, these results show that for quantitative fate mapping, an adequate overall level of mutagenesis must take place during the development window of progenitor states.
We next considered two common modes of experimental error: allele dropout and allele switching. We carried out simulations with increasing levels of error in the resulting data and assessed the fidelity of quantitative fate map reconstruction (Methods). For missing alleles, before applying Phylotime, we imputed the missing alleles for each barcoding site sequentially by leveraging information from all other sites (Methods). The results, which are detailed in Figures S5A–D, suggest that while the accuracy of estimates declines with increasing experimental error, quantitative fate mapping algorithms can tolerate errors and behave stably in response.
We also simulated sampling of terminal types one to five days after the last commitment event. The results, which are detailed in Figures S5E–M, show that a progenitor field may be assessed by sampling its terminal cell types or the descendants of those terminal cell types at any time after its development.
Cell death, non-random sampling, and asymmetric divisions can empower quantitative fate mapping
Because cell death is a prevalent developmental control mechanism36, we carried out simulations with increasing rates of cell death in either all terminal types or all progenitor states. As detailed in Figures S5N–S, we found that cell death in progenitor states drastically improved estimates of commitment time, population size, and commitment bias by bottlenecking progenitor states to effectively increase their sampling fractions. These results in turn suggest that non-random sampling of terminal types can be employed to effectively bottleneck their progenitors and facilitate analyzing large progenitor states. Conversely, cell death in terminal states did not significantly alter reconstruction, suggesting that a progenitor state may be analyzed using a subset of its downstream states or types.
We also considered stereotyped cell fate commitment with asymmetric cell divisions, which are common in the development of the nervous system37. We simulated barcoding experiments on a pectinate 16 terminal type fate map (Figure 1C, bottom left) with commitments happening exclusively through asymmetric divisions. The results, which are detailed in Figures S5T–Z, indicate that asymmetric divisions facilitate quantitative fate mapping.
Consensus quantitative fate maps from multiple biological replicates
We expanded the ICE-FASE algorithm to take advantage of multiple biological replicates assuming they have a common underlying fate map. Briefly, to obtain consensus topology from replicates, their FASE distance matrices were averaged before applying the clustering algorithm (Figures 2D,E). To obtain consensus commitment times, the consensus topology was used to assign inferred progenitor states to each replicate’s phylogeny and ICE times of each progenitor state were pooled from different replicates (Figures 3A–D). To obtain consensus population sizes and commitment biases, the consensus commitment time for each progenitor state was used to estimate its population size and commitment bias in each phylogeny (Figures 3G–K) and these estimates were averaged to obtain respective consensuses.
We then assessed fate map reconstruction accuracy based on the number of replicates. For each of our 53 fate maps with 16 terminal types (Figure 1C), we simulated 10 replicates of barcoding experiments each for fixed and proportional sampling with an average of 50, 100, or 200 sampled cells per terminal cell type (53 maps × 2 sampling schemes × 3 sample sizes = 318 sets of 10 replicates). For each replicate, we applied Phylotime to obtain a time-scaled phylogeny. We then randomly combined 1, 2, 3, 4, or 5 of the 10 replicates to reconstruct consensus quantitative fate maps and compared their accuracies. The results show that additional replicates indeed reduce error of all quantitative fate map estimates (Figures 5C–F). However, the gains with additional replicates are diminishing and do not converge to zero error. This observation is best explained by undersampled progenitor states whose estimates in each replicate can be uninformative (Figure 5B). In fact, estimation error for the well-sampled progenitor states approached zero with additional replicates while it did not for the undersampled ones (Figures 5G–I).
Importantly, the gains achieved by sequencing more cells per replicate outweighed those achieved by combining more replicates. For example, quadrupling the number of replicates from one to four when sampling 50 cells decreased average error in topology, commitment time, population size, and commitment bias by 30%, 23%, 4%, and 3% respectively (Figures 5C–F). By contrast, a quadrupling of the number of cells sequenced in a single replicate from 50 to 200 decreased average error in topology, commitment time, population size, and commitment bias by 46%, 41%, 26%, and 12% respectively (Figures 5C–F). These results suggest that limited resources can be better spent on sequencing more cells per individual than a larger number of individuals.
Resolving multifurcations and prolonged commitments
Because some progenitor states undergo gradual commitment during development, we simulated a progenitor state committing over a 0.5-, 1.1-, or 1.7-day commitment window. The results, which are detailed in Figures S6A–E, indicate that the ICE-FASE algorithm can resolve progenitor states that gradually commit over a window of time.
Because progenitor states in development may simultaneously commit to more than two immediate downstream states or types, we simulated barcoding in a fate map where a progenitor state undergoes trifurcation. The results, which are detailed in Figures S6F–L, show that the ICE-FASE algorithm can resolve multifurcations in fate maps given adequate sampling.
Assessing robustness of quantitative fate map estimates from experimental data with PScov
Despite its central importance in evaluating the robustness of quantitative fate map reconstruction, progenitor state sampling fraction cannot be directly obtained from sampled terminal cells or their phylogeny. To address this gap, we introduce estimated progenitor state coverage (PScov), a proxy for sampling fraction that can be derived from sampled cells alone. PScov is defined as the number of observed terminal progeny for a progenitor state divided by its estimated population size (Figure 6A). Intuitively, this statistic indicates how many terminal descendants were sampled per inferred progenitor cell. We found that a high PScov is indeed predictive of a high sampling fraction (Figure 6B). For example, in our 3,310 simulated experiments, 69.8% of all progenitor states that are sampled more than 25% also have a PScov larger than 5, and more than 99.9% of progenitor states with PScov larger than 5 have sampling fractions larger than 25% (Figure 6C). Moreover, average commitment time, population size, and commitment bias errors approach zero with increasing PScov (Figures 6D–F). Therefore, PScov makes it possible to assess the robustness of quantitative fate map parameters for each progenitor state in actual experiments.
Figure 6. PScov measures robustness of reconstructed quantitative fate maps.
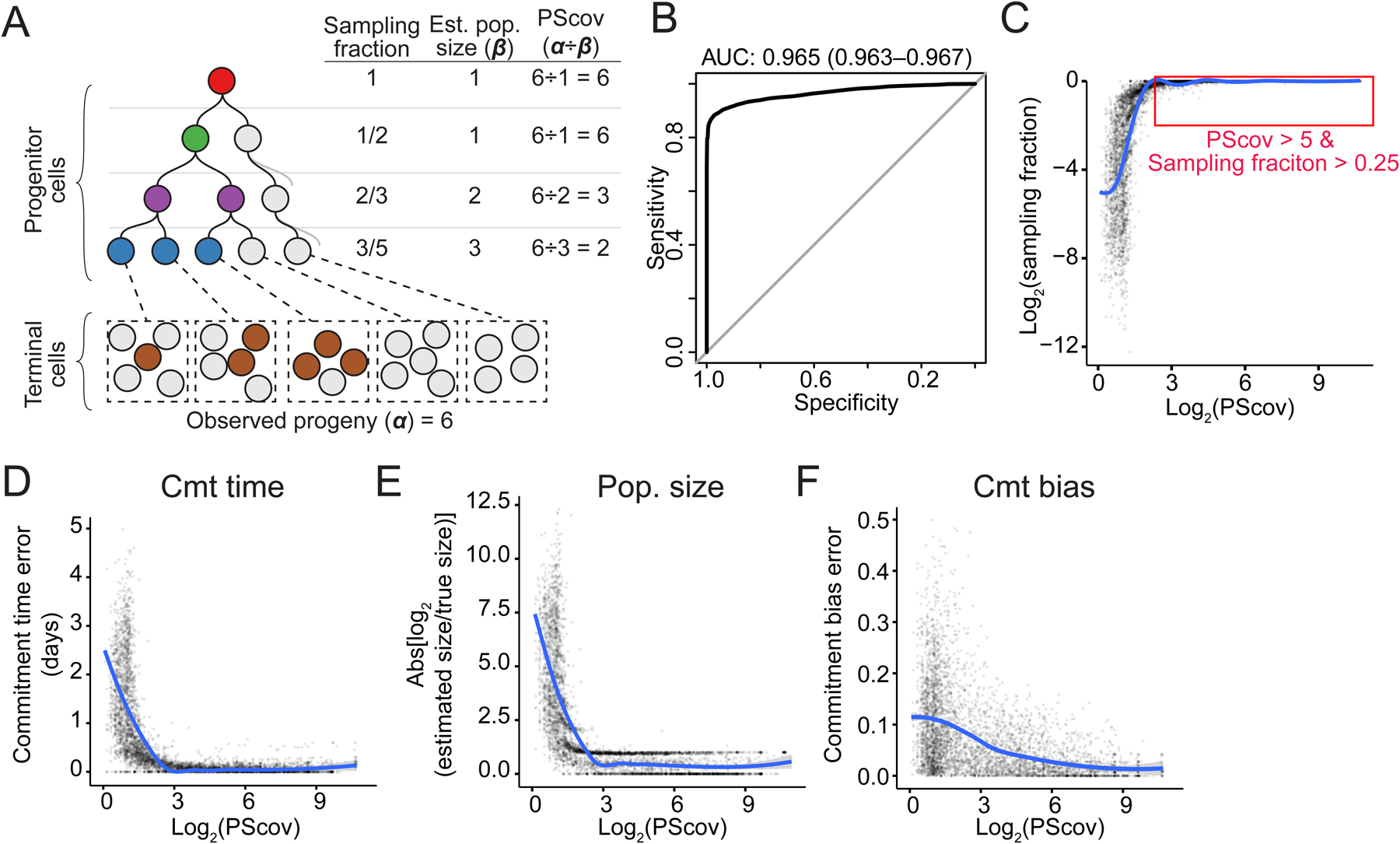
(A) Schematic showing how PScov is calculated. Each circle represents a cell, colors represent different progenitor states the cells have been assigned to, gray circles represent unsampled progenitor and terminal cells. Est: estimate; pop: population.
(B) Area Under the Receiver Operating Characteristics (auROC) curve for PScov shows a high sensitivity and specificity in detecting well-sampled progenitor states. CI: confidence interval.
(C) Scatter plot of progenitor state sampling fraction as a function of its PScov in 3,310 simulated experiments. Trendline (LOESS) shown in blue.
(D–E) Scatter plots showing the error of cmt time (D), pop. size (E), and cmt bias (F) estimates for progenitor states as a function of their PScov in our panel of 3,310 simulated experiments.
Trendline (LOESS) shown in blue.
Experimental validation of quantitative fate mapping
To test this quantitative fate mapping framework, we used an experimental system in which quantitative fate map parameters can be known. We established a human induced pluripotent stem cell (iPSC) line with 32 hgRNA barcoding sites (Table S2, Methods). The line also includes inducible Cas9 to activate barcoding. 24 of the 32 hgRNAs were determined to be active and accumulated random mutations upon Cas9 induction (Figure S7A). We then designed growing and splitting schemes in culture that mimic progenitor state hierarchies (Figure 7A). In two parallel experiments, starting from single cells, we initiated barcoding and passaged growing cells into subpopulations at known times, numbers, and split ratios (Figures 7B and S7B,C). The two experiments were similar except that in one (E1), progenitor state 3 (P3) was split two days before progenitor state 4 (P4), whereas in the other (E2), P4 was split two days before P3. In effect, the last populations of split cells in these experiments represent terminal cell types and their ancestral populations represent progenitor states. In the end, we sequenced barcodes from 192 single cells in each terminal population (Methods). After data processing, we obtained on average 158 cells per terminal population with a median of 26 hgRNAs detected per cell (Figures 7C and S7D,E). We also conducted simulations on the E1 and E2 reference fate maps (Figure S7B) with cell division rates derived from the actual progenitor population sizes at each split and hgRNA mutation rates (Figure S7C) and allele emergence probabilities respectively obtained from time-course measurements and inDelphi predictions (Figure S7F, Table S2). We applied Phylotime and ICE-FASE to both simulated and experimental data. The experimental data reconstructed the topology correctly for both E1 and E2 (Figure 7D), and so we refer to the inferred states by their true state names hereafter. In addition to the correct topology, the inferred fate maps recovered the correct orders of commitment in both experiments (Figure 7D), including the relative commitment times for P3 and P4 which were switched between E1 and E2. This result suggests that our strategy can identify quantitative fate map differences in different systems.
Figure 7. Validation of quantitative fate mapping using cell culture model system.
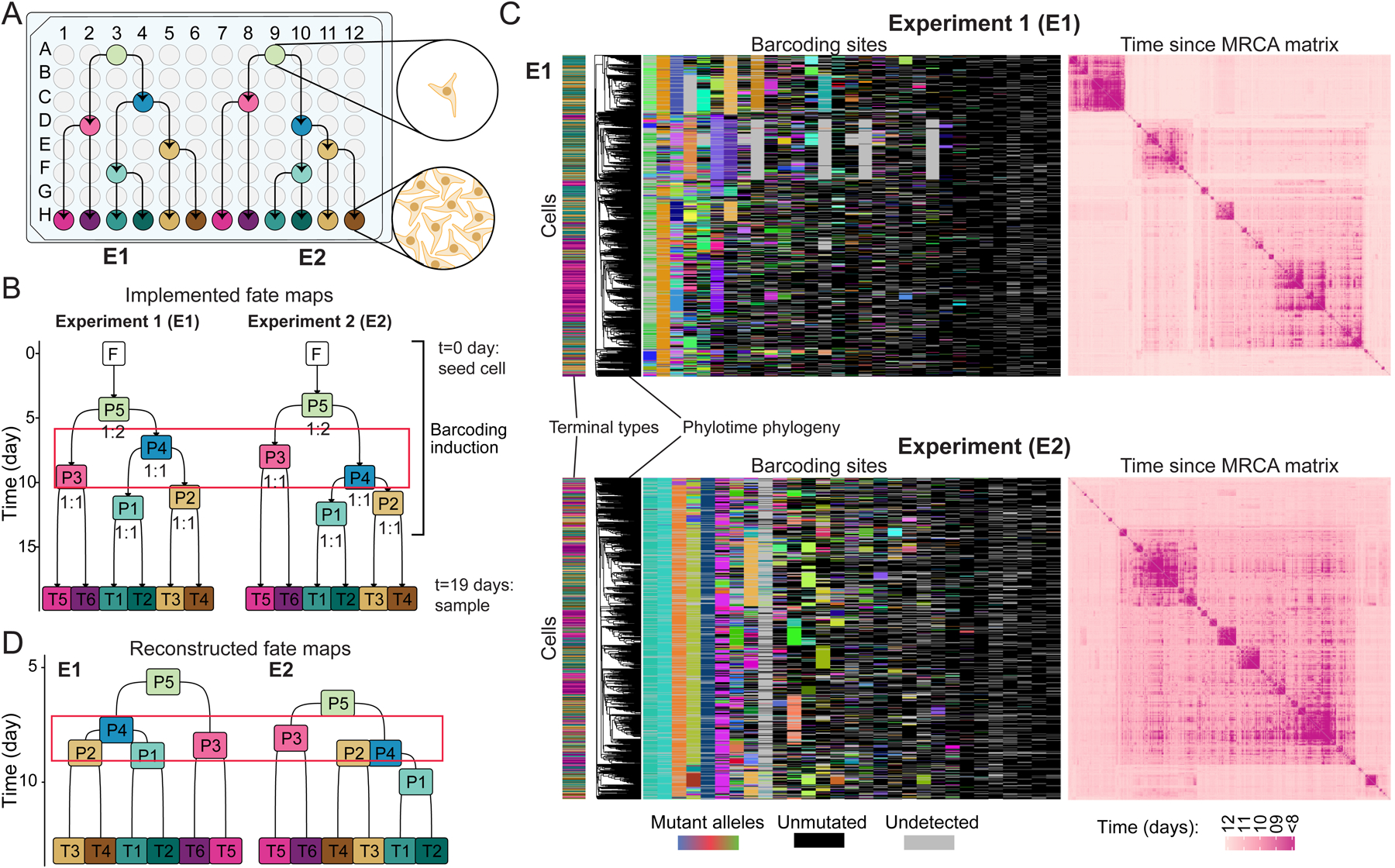
(A) Split–passage scheme in cultured iPSCs for E1 and E2 experiments. Arrows show passages.
(B) Quantitative fate maps implemented in E1 and E2 using scheme in A. Numbers under progenitor states mark split ratios (left:right); red box highlights the differences between progenitor state order. F: founder cell; P: progenitor states; T: terminal type.
(C) Character matrices of lineage barcodes (left) and heatmaps of pairwise time since MRCA matrix from hundreds of sequenced single cells in E1 (top) and E2 (bottom). Phylotime-inferred phylogeny is aligned to the matrix. Color bar on left marks the type of each cell according to B. Other plot features are the same as Figures 4C,D.
(D) Reconstructed quantitative fate maps for E1 (left) and E2 (right). The red box highlights the differences in progenitor state ordering. Labels same as B.
See also Figure S7.
PScov ranged from 1.68 to 2.36 in all progenitor states other than the founder (P5), indicating that they were highly undersampled. As such, we did not expect to recover the exact commitment times and population sizes of the passaged intermediate populations. Nevertheless, we evaluated if these estimates would approach the truth with increased sampling. We repeated quantitative fate map reconstruction 50 times each with varying numbers of terminal cells subsampled from the total sequenced population. In parallel, we carried out simulations with the same subsample sizes on reference fate maps. We then classified inferred fate maps based on their topology and correctness of relative ordering (Figure S7G) and found that the fraction of correct topology and relative order of commitment increased in a similar fashion with increasing sampling in both the simulated and experimental datasets. Additionally, commitment time and population size estimates for P3 and P4 approached their true values with increasing sampling in simulated and experimental sets alike (Figures S7H,I). Together, these observations validate our barcoding models used for simulation and suggest that our quantitative fate mapping strategy, ICE-FASE, and Phylotime are robust to natural variations in cellular behavior.
Discussion
In this study, we have established a robust and versatile approach, called quantitative fate mapping, to use cells’ lineage barcode and identity information to retrospectively characterize the progenitor field that gave rise to them. Quantitative fate mapping involves two stages. The first stage entails inferring a time-scaled phylogenetic tree from single-cell lineage barcodes. To do so, we have developed Phylotime, which scales to large trees with thousands of terminal branches. Moreover, its mutagenesis model can be adapted to other systems with multiple independent mutation sites such as natural somatic mutations. The second stage entails reconstructing the hierarchy of progenitor states that led to the observed cell types and estimating their commitment times, population sizes, and commitment biases. To do so, we have developed the ICE-FASE algorithm which uses nodes in the time-scaled phylogenetic tree that are associated with fate decisions as chronometers of progenitor population dynamics. While other studies have focused on reversible cell state transitions38, non-cumulative barcoding15,39, or single progenitor states34,40, our approach is unique in that it evaluates the dynamics of progenitor states using cumulative somatic mutations, scales to large and complex progenitor fields, and can tolerate the errors that are inherent to phylogenetic inference.
The choice of terminal cell types decides the progenitor states that are analyzed in a quantitative fate map. As a simplified example, taking ectoderm-derived neurons, mesoderm-derived myocytes, and endoderm-derived hepatocytes in adult mice as terminal cell types would analyze their common progenitor states prior to gastrulation. Therefore, quantitative fate mapping provides a unique approach to characterize development based on differentiated cells. This strategy complements those based on the direct analysis of progenitor cells (e.g., single-cell RNA sequencing)41 in multiple ways. Firstly, it provides information about the long-term fate of progenitors. Secondly, it enables analyzing progenitor states with respect to specific subsets of their progeny which may be of interest, for example due to relevance to a specific disorder. Finally, it can be applied to non-model species wherein accessing somatic mutations from cadavers is more practical than obtaining embryos.
Our results show that only when a progenitor state is sufficiently sampled can its potency and dynamics be meaningfully estimated in one individual and improved by combining biological replicates; estimates for severely undersampled progenitor populations are not meaningful irrespective of the number of replicates. In cases modeled here, adequate sampling often required more than 25% of the actual progenitor population to have descendants among sampled terminal cells (PScov > 5). To meet this sampling criterion in practice, the number of descendants that are analyzed should be, at least, in the same order as the actual progenitor population size. We propose this as a fundamental rule for retrospective lineage analysis. For prohibitively large progenitor populations, this sampling rule may be satisfied by bottlenecking the number of sampled progenitors using non-random sampling of terminal cells based on anatomical position or other criteria.
In summary, we have described quantitative fate mapping as a framework to characterize complex cell fate dynamics during development using retrospective lineage analysis at a later point in time. This framework is based on somatic mutations—synthetic or natural—that accumulate during development. Robust fate mapping requires good representation of each progenitor population among sampled cells as well as the ability to infer time-scaled phylogenetic trees. This framework facilitates the characterization of cell autonomous and non-cell autonomous genetic and environmental effects on development.
Limitations of the study
The parameters of our models were tailored to mouse embryogenesis. Hence, certain thresholds and cutoffs associated with specific conclusions may be different in later stages of development, other species, and other developmental systems such as organoids. In such cases, the simulation strategies described here can be employed to obtain system-specific values. Our models assume lineage-independent rates of mutagenesis. While this assumption is supported as a first-order approximation5,42, we expect our strategy to be robust to small lineage biases in mutation rates. We have not performed experimental validation of this framework in a model organism, which may reveal factors that were not considered here and require adjustments to ICE-FASE and Phylotime strategies.
STAR Methods
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Reza Kalhor (kalhor@jhu.edu).
Materials availability
The human induced pluripotent stem cell line generated in this study will be shared upon request.
Data and code availability
FASTQ files from sequencing single-cell hgRNA arrays have been deposited at SRA and are publicly available. Accession numbers are listed in the key resources table. All quantitative fate maps, simulated datasets, inDelphi predictions, and Phylotime-reconstructed phylogenies have been deposited on Zenodo. DOIs are listed in the key resources table.
R package for QFM and code to reproduce the results is publicly available at https://github.com/Kalhor-Lab/QFM/ as of the date of publication.
Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
| AAVS1-Neo-M2rtTA | DeKelver et al.50 | Addgene Cat#60843 |
| Chemicals, peptides, and recombinant proteins | ||
| Accutase™ | STEMCELL Technologies |
Cat#07920 |
| Antibiotic-Antimycotic (100X) | ThermoFisher | Cat#15240062 |
| Blasticidin S hydrochloride | MilliporeSigma | Cat#15205 |
| (−)-Blebbistatin | MilliporeSigma | Cat#B0560 |
| CloneR | STEMCELL Technologies |
Cat#05888 |
| Doxycycline hyclate | MilliporeSigma | Cat#D9891 |
| DreamTaq Hot Start PCR Master Mix | ThermoFisher | Cat#K9012 |
| Geneticin™ Selective Antibiotic (G418 Sulfate) | ThermoFisher | Cat#10131035 |
| KAPA HiFi HotStart ReadyMix | Roche | Cat#07958935001 |
| KAPA SYBR FAST qPCR Kits | Roche | Cat#07959389001 |
| Lipofectamine™ Stem Transfection Reagent | ThermoFisher | Cat#STEM00001 |
| Matrigel Growth Factor Reduced Basement Membrane Matrix | Corning | Cat#354230 |
| mTeSR™ Plus | STEMCELL Technologies |
Cat#100–0276 |
| Opti-MEM I Reduced Serum Media | ThermoFisher | Cat#31985062 |
| Pifithrin-α hydrobromide | Tocris Bioscience | Cat#1267 |
| Puromycin dihydrochloride | MilliporeSigma | Cat#P8833 |
| QuickExtract™ DNA Extraction Solution | Lucigen | Cat#QE09050 |
| SYBR Green I Nucleic Acid Gel Stain | ThermoFisher | Cat#S7563 |
| Critical commercial assays | ||
| DNA Clean & Concentrator-5 | Zymo Research | Cat#D4014 |
| MiSeq Reagent Micro Kit v2 (300-cycles) | Illumina | Cat#MS-103–1002 |
| MycoAlert® PLUS Mycoplasma Detection Kit | Lonza | Cat#LT07–701 |
| Qubit dsDNA HS Assay Kit | ThermoFisher | Cat#Q32851 |
| Deposited data | ||
| Single-cell hgRNA sequencing raw FASTQ files for E1 and E2 | This study | SRP386685 |
| MARC1 sequencing data for determining hgRNA mutation rates | Kalhor et al.5
Leeper et al.30 |
SRP155997 |
| All quantitative fate maps | This study | 10.5281/zenodo.7112097 |
| inDelphi predicted mutant allele probabilities for hgRNAs in MARC1 mice and iPSC line | This study | 10.5281/zenodo.7112097 |
| Simulated phylogenies, sets of MARC1 hgRNAs used, single cell lineage barcodes, Phylotime reconstructed phylogenies for all experiments | This study | 10.5281/zenodo.7112097 |
| Experimental models: Cell lines | ||
| iPSC line: EP1-Cas9-hgRNA | This study | N/A |
| Oligonucleotides | ||
| See Table S3 for oligonucleotides used in this study. | This study | N/A |
| Recombinant DNA | ||
| Modified pSpCas9(BB)-2A-Puro (PX459) V2.0 | Eldred et al.45 | N/A |
| Modified Puro-Cas9 donor | Eldred et al.45 | N/A |
| PB-U6insert hgRNA library | Kalhor et al.5 | Addgene Cat#104536 |
| PB-U6insert-EF1puro library | Kalhor et al.5 | Addgene Cat#104537 |
| Super piggyBac Transposase expression vector | System Biosciences | Cat#PB210PA-1 |
| Software and algorithms | ||
| Cassiopeia | Jones et al.35 | https://github.com/YosefLab/Cassiopeia |
| ICE-FASE | This study |
https://github.com/Kalhor-Lab/QFM/ DOI: 10.5281/zenodo.7114804 |
| ImageJ | Schneider et al.51 | https://github.com/imagej/ImageJ |
| InDelphi | Shen et al.31 | https://github.com/rnaxwshen/inDelphi-model |
| Phylotime | This study |
https://github.com/Kalhor-Lab/QFM/ DOI: 10.5281/zenodo.7114804 |
| MARC1 analysis pipeline | Leeper et al.30 | https://github.com/Kalhor-Lab/MARC1-Pipeline |
| Other | ||
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Cell culture
Human iPSCs were cultured in mTeSR Plus media (STEMCELL Technologies) on plates coated with Matrigel Growth Factor Reduced Basement Membrane Matrix (Corning). Cells were maintained at 37°C and 10% CO2/5% O2 conditions with daily media changes. When up to 80% confluent, cells were passaged by dissociation with Accutase (STEMCELL Technologies) and seeded in mTeSR Plus media supplemented with 5 μM blebbistatin (Millipore Sigma).
Lineage-tracing human induced pluripotent stem cell line
We established a clonal iPSC line with 32 hgRNA barcoding sites distributed in its genome as a non-tandem array. The line also includes doxycycline inducible Cas9 to activate barcoding. The EP1 human induced pluripotent stem cell (hIPSC) line was obtained from Bhise et al.52, originating from fetal lung fibroblasts obtained from a female donor. A clonal lineage-tracing inducible Cas9 cell line was generated by first transfecting the EP1 cells with plasmids to target and stably insert both a reverse tetracycline-controlled transactivator (rtTA) construct and a tetracycline-dependent Cas9 construct into each of the two copies of the AAVS1 safe harbor locus. The cells were then transfected with a hgRNA PiggyBac library and screened for high numbers of insertions. A KaryoStat™ Assay of the final engineered cell line confirmed that the sample originated from a female and had no chromosomal aberrations when comparing against the reference dataset. Cells were determined to be free of mycoplasma contamination based on MycoAlert® PLUS Mycoplasma Detection Kit (Lonza) test results.
METHOD DETAILS
Definition of quantitative fate map
A quantitative fate map (QFM) is characterized by a topology in the form of a bifurcating or multifurcating time-scaled tree. Each node in the tree is associated with a time, with the root node at time 0 and the terminal nodes at time of sampling. Each edge in the tree represents a progenitor state or terminal type, the starting and end time of the edge represent the duration for which the state existed. If an edge ends at the sampling time, it is a terminal type, otherwise a progenitor state. For progenitor states, the end node of the edge represents a commitment event. For terminal types, the end node of the edge represents the time at which the process is stopped for sample collection. For a bifurcating QFM with Z total terminal types, we denote the progenitor states as Pi, i = 1,2, …, (Z − 1) and the terminal types as Tj, j = 1,2, …, Z. Each progenitor state or terminal type has a set of parameters associated with it. We take a progenitor Pi as an example here. Along the edge representing Pi, cells undergo cell division and cell death at rates specific to the state. The doubling time for Pi is denoted dPi. When not committing, cells can be (i) dividing (ii) not dividing, or (iii) dying with probabilities cPi,D, cPi,N or cPi,L respectively. These probabilities are specific to the progenitor state. At the commitment time for Pi, denoted tPi, the cells commit to the downstream states. For a bifurcating commitment event, when cells of the Pi state commit to the downstream states, say Pj or Pk, it can do so via either via symmetric cell division or asymmetric cell division. For commitment via symmetric cell division, each cell of the Pi state gives rise to either two Pj cells or two Pk cells. For commitment via asymmetric cell division, each cell gives rise to two cells of different downstream states, that is, one cell Pj cell and one Pk cell. The corresponding commitment mode probabilities are denoted (pPjPj, pPkPk, pPjPk), where pPjPj and pPkPk are the probabilities of the symmetric modes that commits to Pj or Pk respectively and pPjPk is the probability of the asymmetric mode. The commitment bias is defined as the proportion of cells of each of the downstream states that are produced. In the above example, the commitment bias, denoted as bPi is (2pPjPj + pPjPk, 2pPkPk + pPjPk). In most fate maps simulated here, pPjPk = 0 as they did not include a specific asymmetric division mechanism. For the purpose of evaluation, for each bifurcating progenitor state, the proportion that commits to one of the two downstream states is chosen as a single value representing the progenitor state bias and is kept track of consistently throughout. The progenitor population size NPi is defined as the number of cells at the commitment time.
Definition of time-scaled phylogeny
A time-scaled phylogeny is defined as a rooted, ultrametric, bifurcating phylogenetic tree where branch lengths are in the unit of time and represent the time in between cell divisions. Terminal nodes, or tips, of the tree represent observed cells. Internal nodes in the time-scaled phylogeny represent cell divisions of unobserved progenitor cells. The root node represents the most recent common ancestor (MRCA) of all terminal cells. The length of the root edge is the time until the cell division of the root MRCA. Cophenetic distance is defined for each pair of terminal cells, which is the distance between the cells along the phylogenetic tree. The depth of a node in the phylogenetic tree is defined as the distance of a node to the root plus the length of the root edge. The ultrametric property requires that all tips are equidistant from the root, that is, have the same depth. The total time of a time-scaled phylogeny is defined as the depth of its tips.
Constructing a panel of quantitative fate maps
Generating each fate map in our panel involved several interrelated and iterative steps. These steps were designed to ensure that the fate maps in the panel explore a wide range of possibilities in terms of topology and progenitor state parameters while making sure: (i) the fate map generated resembles early mouse development (ii) the commitment events are placed within our prespecified time window ([2.4,10.9] days) (iii) two consecutive commitment events are at least one doubling time apart. For clarity, these steps are briefly listed here and detailed separately below. First, a candidate topology in the form of a bifurcating tree was generated from one of five categories of varying imbalance. Edges in the bifurcating tree represent progenitor states and terminal types; nodes in the tree represent their commitment events. Second, an ordering of the commitment events was generated. Third, doubling times of progenitor states were drawn, leading to a candidate fate map. Fourth, the timing of commitment events in the candidate fate map was checked against the minimum inter-commitment time and total span criteria. If the candidate fate map met these criteria, it was accepted and its commitment biases and death rates were drawn. Otherwise, a perturbation to the candidate topology was suggested, and steps one through four were repeated until a valid fate map emerged.
Generating candidate topologies:
To generate a panel of fate map topologies with varying levels of imbalance, tentative tree topologies were generated from five different categories: (i) ‘perfectly balanced’ (ii) ‘balanced-TBR’ (iii) ‘random’ (iv) ‘pectinate-TBR’ (v) ‘pectinate’. In the perfectly balanced topology, each bifurcation splits all terminal types into two equal halves. The balanced-TBR topologies are generated by applying one random TBR move to the perfectly balanced topology. The random topologies are generated by creating a sequence of bifurcations, each randomly splitting the set of terminal types into two sets; the ‘rtree’ function in the ‘ape’ R package53 was used to generate the random topologies. The random category tends to have topologies of medium balance. The pectinate topology is in the shape of a comb. In pectinate topology, each bifurcation always splits the terminal types such that one of the splits has exactly one terminal type (Figure 1C, bottom left). The pectinate topology is the maximally unbalanced topology for a fixed number of terminal types. The pectinate-TBR topology is generated by applying a number of TBR moves to the pectinate topology.
Generating event ordering:
In the second step, we generated an ordering of commitment events following a previously published method44. Briefly, to get an ordering of events in the entire topology, a ‘shuffling’ at each bifurcation was generated. A shuffling orders the events between two subtrees of a bifurcation without ordering within each subtree. For example, two shufflings of a given event are illustrated in Figure S8A. Events from the left subtree are shown as hollow circles and events from the right subtrees are shown as solid ones. The sequence of solid and hollow circles is defined as a shuffling at the bifurcation. A set of shufflings for every bifurcation (internal node) of a tree determines the exact ordering of its commitment events.
Generating doubling times and exact commitment times:
Given the event ordering, doubling times for each state/type are drawn. To have overall agreement with the mouse development but also allow variabilities across cell states/types, the following scheme was used. The root state has a doubling time of 0.6 days. All other progenitor states have the doubling time drawn from a uniform distribution whose center is determined by the time ranking of its commitment event. Specifically, for an event ranked i-th out of total I − 1 commitment events, the doubling time follows the uniform distribution below:
For example, for a 16-terminal type fate map, the earliest commitment non-root progenitor state has doubling time sampled from uniform(0.49, 0.59) and the latest committing progenitor state has doubling time sampled from uniform(0.35, 0.45). For all terminal types, the doubling time is sampled from uniform(0.35, 0.45) (Figures S1F,G). These doubling rates generally agree with rates reported in the literature23.
Next, we generated the duration between consecutive events in the commitment event ordering. In our model, consecutive commitment events were required to be at least one cell division (doubling time of the earlier state) apart. In addition, all of the commitment events need to fit in a predefined time window [l0, l1]. These requirements place constraints on the duration in between commitment events. Such a constraint can be formalized as follows:
Suppose there are I total events, where the duration between the (i − 1)-th and i-th event in the event ordering is yi. Let the doubling time of progenitor state i be di, then for an edge in the fate map topology that connects the earlier event j to the later event k, we have
There are I − 1 total such constraints, one for each edge that is not the root edge. Next, we used linear programming to find the vector of yi’s such that ∑i yi is minimized, the minimum value of ∑i yi is denoted ytotal. When generating the event timing, we tried to place the events within the given time window: [l0, l1] with its total length being ltotal = l1 − l0. For a valid placement of events to exist, one needs to have ytotal ≤ ltotal. At this stage, we checked if this condition is met. If it was not, the current value of ytotal was recorded and the candidate fate map topology is perturbed by applying one tree bisection and reconnection (TBR) move. TBR is a tree rearrangement that detaches a subtree from the main tree at an interior node and then reconnects to another random branch. After the TBR move, all the above steps were repeated and a new ytotal values was computed, denoted ytotal′. If ytotal′ < ytotal, then the newly perturbed topology was accepted as the tentative fate map topology. Otherwise, the newly generated perturbation was discarded, and another perturbation was generated. The process was repeated until a ytotal ≤ ltotal was found. With the new ltotal found, we tried to place events uniformly within the time window by distributing the remaining duration ztotal = ltotal − ytotal to each interval evenly, which was achieved by sampling from the following Dirichlet distribution:
Finally, the commitment time for the u-th event is (Figure S1D).
Generating commitment bias and death rate:
The raw commitment biases were drawn from Beta(5, 5), the raw values were later adjusted to actual values based on how many cells were split into each of the downstream fates. For example, when the progenitor population had 13 cells, and the raw commitment bias was (0.63,0.37) based on which [13 × 0.63] = 8 cells are committed to one downstream fate versus [13 × 0.37] = 5 cells to the other, with [.] being the rounding operation that rounds to the nearest integer. Then the actual commitment bias was adjusted to (8/13,5/13). We required that there are at least 4 cells committing to each downstream fate, this requirement resulted in the commitment bias to be closer to 0.5 for smaller progenitor populations (Figure S1E). The cell death rates were drawn from Uniform(0.02,0.08).
Generating the panel of fate maps:
The balance of a fate map topology can be measured by the Colless index. The Colless index of a bifurcating tree is defined as the sum of the balance values of its internal nodes, where the balance value of an internal node is defined as the absolute value of the difference between the number of descendant tips of its pair of daughter nodes22. To get a representative panel of fate maps topologies in terms of balance, we generated 1,000 fate maps based on topologies from the balanced-TBR, random and pectinate-TBR categories with either 16, 32 or 64 terminal types. After computing the Colless index for each topology, we classified the generated topologies into bins of different Colless index values by increments of 20. Next, within each bin, we randomly selected five (or fewer in bins with fewer than five in total) fate maps (Figure S1C). Finally, we add to this list the perfectly balanced topology and the pectinate topology. Note that because of the constraints of the minimum duration in between consecutive commitment events and the doubling times specified, the pectinate topology does not allow a valid placement of commitment events within the [2.4, 10.9] time window for the fate maps with 32 and 64 terminal types, so it was only added in the case of 16 terminal types. The above procedure produced 53 fate maps with 16 terminal types, 108 fate maps with 32 terminal types and 170 fate maps with 64 terminal types. To see if the steps used here generated topologies that show good variabilities, we embedded the tree topologies into the 2-dimensional space by applying multi-dimensional scaling to the pairwise KC0 distances. In the embedding, we observed that the first principle coordinate correlated well with the Colless index, and in addition, the second principle coordinate also had good variations, indicating that our topologies cover a range of possibilities (Figures S1A,B).
Generating a count graph for QFM
To carry out computation and generate time-scaled phylogenies from a QFM, an abstract count graph was constructed based on the QFM’s specifications, which is a detailed representation of the computations involved (Figure S2).
Each node in the count graph contains a group of cells. To distinguish the terms, we call a node in the count graph a ‘count node’. In addition to containing cells, each count node has other relevant attributes. It has a time window, which specifies the time during which its cells exist, it also has a state/type assignment, which specifies which progenitor state or terminal type its cells belong to. Generating a count graph for a QFM starts at its root (t = 0) with a single count node. The count nodes in the next time window are generated by applying four operations (which are indicated by bold font in text below) to the starting count node and its cells according to the QFM specifications to generate the count node(s) at the next time window. This process is then repeated on the nascent count nodes one round after the other until the entire count graph is created. The detailed implementation of each operation is given in the later section (Figure S2, Step 1).
During each time window, which is the length of a cell cycle, based on if the commitment time of the progenitor state has been reached in the QFM, each count node undergoes one of two processes before creating count node(s) in the next time window:
a proliferate-only process
a commit and proliferate process
Initially, the count node is in a “default” mode (labeled T), representing its total population of cells during the time window. If undergoing process 1 (proliferate-only), the count node is split into three sub-count nodes that represent cells that are (i) doubling (labeled D) (ii) not doubling (labeled N) or (iii) dying (labeled L). Specifically, cells (of cell state Pi) with N totals cells are split into three sub-count nodes of different proliferation modes, according to probabilities cD,Pi, cN,Pi and cL,Pi. Here, the split operation splits a count node into three sub-count nodes:
where ND, NN, NL are the counts of the sub-count nodes, cD,Pi, cN,Pi, cL,Pi are the doubling, non-doubling and dying probabilities, and mD, mN and mL are the minimum number of cells in each sub-count node after the split.
Then, the doubling sub-count node doubles in number and is merged with the non-doubling sub-count node to give rise to the default count node of the next time window, which starts one doubling time dPi later than the current time window. The dying sub-count node is lost in the process. The double operation doubles the count, and the merge operation adds up the counts of sub-count nodes.
If undergoing process 2 (commit and proliferate), cells in the default count node are first split into one of the commitment modes and subsequently double or asymmetric double depending on which commitment mode they are assigned to in the QFM. The asymmetric double operation originates from a sub-count node and gives rise to two sub-count nodes of the same size but are of two different downstream states/types. Suppose cells (of some progenitor state Pi) are committing during a time window to two downstream fates Pj and Pk, then the count node in default mode gets split into three sub-count nodes of different commitment modes. There are three different commitment modes when commitment is a bifurcation: two symmetric commitment modes Pi-PjPj and Pi-PkPk (one each for the two downstream fates) and one asymmetric commitment mode Pi-PjPk . Cells in one of the two symmetric commitment modes each gives rise to two cells of the same downstream types. Cells in the asymmetric commitment mode each gives rise to two cells of two different downstream types. Let the probabilities of the two symmetric commitment modes be pPjPj, pPkPk and the probabilities of the asymmetric commitment mode be pPjPk. Specifically, during a time window when cells are in process 2 (commit and proliferate), when there are N cells in the default count node, the cells are split into the commitment sub-count nodes via the split operations:
Where NPjPj, NPkPk, NPjPk are the counts of the sub-count nodes, pPjPj, pPkPk, pPjPk are the probabilities for the commitment modes, and mPjPj, mPjPk, mPkPk are the minimum number of cells in each sub-count node after the split. To ensure that there’s no progenitor population of very small size, we require that there be at least four cells in the symmetric modes in the main panel.
The commitment bias is defined as (2pPjPj + pPjPk, 2pPkPk + pPjPk), the two proportions sum to one and are interchangeable, we refer to one of the two sides as the commitment bias pPi of the Pi state, which is kept consistent throughout. In the main panel of experiments, all probabilities of the asymmetric commitment modes are set to zero. Subsequently, cells of the symmetric commitment modes double and then merge with the daughter cells of the asymmetric commitment modes for each of the downstream states. For Pj, N′Pj = 2NPjPj + NPjPk, and for similarly for Pk, N′Pk = 2NPkPk + NPjPk.
Backpropagation to generate progenitor population sample sizes
To generate a phylogeny for a set of sampled cells based on the quantitative fate map, the number of sampled cells was generated at each (sub-)count node in the count graph (Figure S2, Step 2). This process draws, for each (sub-)count node in the count graph, an additional quantity called its sample size. A progenitor cell is sampled if any of its progeny at the sampling time is sampled. The total number of sampled cells is defined as its sample size. The process was accomplished by propagating backwards in the count graph. During the backward propagation, each forward operation is replaced with a corresponding backward reverse operation. The detailed implementation of each operation is given in the later section, and the operations are again indicated with bold text. The sample size for the terminal population is set to the sample size of the experiment. For fixed sampling, the size is the same for all the terminal types. For proportional sampling, the total sample size is distributed to each terminal type according to their abundance, which is done using the stochastic split operation. The stochastic split operation is the reverse operation of merge. Given the sample size of the merged population, the reverse operation draws the number of cells sampled in each mode based on a multivariate hypergeometric distribution. In addition, the reverse operation for split is merge, which adds up the sample size of count nodes of different modes to the sample size of a count node with the default mode. The reverse operation for double is stochastic coalesce: given the number of sampled cells in a doubled population, the operation draws the number of cells that are sampled in the pre-doubling population. The reverse operation for asymmetric double is stochastic asymmetric coalesce: given the number of cells sampled in each of the populations after asymmetric doubling, the operation draws the number of cells sampled in the population pre-asymmetric double. In summary, the backpropagation process generates the sample size for each (sub-) count node in the count graph given the sample size of the terminal populations.
Generating phylogeny of sampled cells
Given sample size of each count node derived in the previous section, we moved to generate the phylogeny for a group of sampled cells. Before the individual cells were generated and connected to construct a cell phylogeny, the count graph was first reorganized (Figure S2, Step 3a). At this step, we are only concerned with the sample sizes of the count nodes, not the population sizes. During the reorganization, the three sub-count nodes during process 1 (proliferate only) were replaced with two new sub-count nodes, and the three sub-count nodes during process 2 (commit and proliferate) were replaced with five new sub-count nodes. The reorganization is done based on if a sampled cell in the current sub-count node either gives rise to one or two cells in the next (sub-)count node. Note that the sample size(s) for the next count node(s) determines exactly how many cells in the current count node give rise to one and how many give rise to two cells. For example, when there are 5 sampled cells in the current count node of the doubling sub-count node and there are 8 cells in the doubled sub-count node, then exactly 3 cells in the current count node give rise to two cells at the doubled sub-count node and 2 cells give rise to one. As another example, if the Pi-PjPk sub-count node have 5 cells sampled and the Pi doubled sub-count node has 3 cells sampled and the Pj doubled sub-count node has 4 cells sampled, then there are exactly 2 cells with both daughters sampled, 1 cell with one A daughter sampled and 2 cells with one B daughter sampled. We call progenitor cells with both daughters sampled ‘coalesced’, and progenitor cells with only one daughter sampled non-coalesced. Subsequently, the sub-count nodes are reorganized based on if cells are coalesced or non-coalesced as well as cells of which cell or state they give rise to.
For process 1, coalesced cells in the doubling sub-count node are organized into a new ‘coalesced’ sub-count node (labeled C) and non-coalesced cells in the doubling sub-count node sampled are combined with cells in the non-doubling sub-count node and organized into a new non-coalesced (labeled NC) sub-count node. Cells in the death sub-count node are lost. The original doubled sub-count node is replaced with the coalescing (labeled CI) sub-count node (Figure S2, Step 3a, top example).
For process 2, coalesced cells in each of the three original sub-count nodes (Pi-PjPj, Pi-PkPk and Pi-PjPk) that give rise to two cells in the next count nodes are organized into their respective new sub-count nodes (labeled the same name). Two new sub-count nodes were added that represent cells that give rise to only one cell (of either of the downstream types) in the next count node, (labeled Pi-Pj and Pi-Pk). Non-coalescent cells in the Pi-PjPj sub-count node are merged with non-coalesced cells that give rise to only one Pj cell in the Pi-PjPk sub-count node. Similarly, non-coalesced cells in the Pi-PkPk sub-count node are merged with cells that give rise to only one Pk cell in the Pi-PjPk sub-count node.
The reorganized count graph (Figure S2, Step 4a, right) specifies the number of sampled cells at each stage but does not distinguish between individual cells. To generate the sampled cell phylogeny, we next listed individual cells and specified which cells give rise to one or two sampled cells at the next time point without specifying which cells at the next stage they were connected to (Figure S2, Step 3b). Next, cells in an earlier time window were connected to cells in the later time window to make up the phylogeny (Figure S2, Step 4a). Finally, the phylogeny was further simplified by removing internal nodes that give rise to one cell only (Figure S2, Step 4b).
Definition of commitment time and progenitor population size
In our model, the fate commitment modes are assigned at the beginning of the process 2 time (commit and proliferate) window, before cells proliferate to become the downstream states or types. In fact, the fate decision could have been made any time during the previous cell cycle. Hence, the exact commitment time could be chosen as either at the beginning of the previous time window or at the end of the window. Similarly, the progenitor state population size may be defined as the number of cells at either time point. As detailed in Figure S8B, it can be observed that, for symmetric commitments, the time of fate separation (where daughter cells are exclusively one of the downstream states) on the phylogeny is, at the latest, at the beginning of the cell cycle (t1). On the contrary, for commitment by asymmetric cell division, fate separation is at the end of the cell cycle (t2). Therefore, we define the beginning of the window as the commitment time for progenitor states undergoing symmetric mode of commitment, and the end of the window as the asymmetric commitment time. The progenitor population sizes for symmetric and asymmetric commitment modes are defined as the number of cells N1 and N2 at the corresponding commitment times.
Definition of operations to generate count graph
The operations used in the count graph generation and backward propagation of sample sizes are formally defined here. Four deterministic operations are defined for generating the population counts in quantitative fate maps.
split: (N, (p1, p2, …, pI), (m1, m2, …, mI)) ↦ (N1, N2, …, NI)
The split operation splits some total count N into a vector of output counts N1, N2, …, NI based on the input probabilities p1, p2, …, pI and ensures the post-split counts: (i) add up to the total count, (ii) are larger than some minimum values m1, m2, …, mI and (iii) are all integers. First, let m be the smallest m such that pm ≥ pi, for i ∈ {1,2, …, I}. Then, the Ni = max([Npi], mi) for all i ≠ m, and Nm = N − ∑i≠m Ni, where [x] is the rounding operation that returns the integer that is closest to x.
merge: (N1, N2, …, NI) ↦ N
The merge operation takes a vector of input counts and them, i.e. N = ∑i Ni
double: N ↦ 2N
The double operation multiplies the input count by two.
asymm double: N ↦ (N, N)
The asymmetric double operation takes the input count and produces two input counts of the same size.
For each of the four forward operations, a reverse operation is defined for generating the sample sizes based on the population sizes.
stochastic split: (S, (N1, N2, …, NI)) ↦ (S1, S2, …, SI)
stochastic split is the reverse operation of merge. (S1, S2, …, SI) follows a multivariate hypergeometric distribution with the following probability mass function
merge is the reverse operation of split.
stochastic coal: (S, N) ↦ S′
stochastic coalesce is the reverse operation of double. When S cells are sampled from 2N cells that are direct descendants of N cells, S′ is the number of cells sampled in N cells. Here, the number of coalescences C = S − S′, follows the distribution with the below probability mass function:
After drawing C, S′ is computed with S′ = S − C.
stochastic asymm coal: ((S1, S2), N) ↦ S′
stochastic asymmetric coalesce is the reverse operation of asymmetric double. When N parent cells double, and each cell gives rise to two cells of two different downstream states/types, and S1 out of N cells of type A and S2 of N cells of type B are sampled. Then the number of cells sampled in the parent population is S′. Here, the number of coalescences C = S1 + S2 − S′ follows the distribution with the below probability mass function:
After drawing C, S′ is computed with S′ = S1 + S2 − C.
Fate map topology reconstruction with FASE
To determine if a node is a FAte SEparation (FASE), a list of unique terminal types is generated for all internal nodes of the phylogeny which constitutes its observed fate. A node is classified as a FASE (for at least one pair of terminal types) if either of its daughter nodes has an observed fate that is less potent. FASEs are identified across the entire phylogenetic tree. Next, for each FASE, all pairs of terminal types that the FASE separates are listed. A pair of terminal types is separated if one terminal type is seen in only one branch of the node and the other type only in the other. Then, for a pair of terminal types, the mean depth of the FASEs that separated the terminal fates were computed, referred to as the FASE time. If no FASE existed for a pair of terminal types, the FASE time was taken to be zero. Finally, the FASE distance between a pair of terminal types is equal to the difference between total time of the phylogenetic tree and their average FASE time. To reconstruct the topology from the full distance matrix, the upgma function from the “Phangorn” package54 was applied, which is a wrapper of hclust in base R.
Fate map topology reconstruction with SPS
Computation of shared progenitor scores was implemented as specified elsewhere6. The shared progenitor score or SPS was calculated between two terminal types as the number of internal nodes in the phylogeny that have both terminal types scaled by the number of total terminal types each internal node contributes to. The score was computed by going through all the internal nodes in the phylogeny. For each internal node, let T1, T2, …, TL be the list of terminal types it gives rise to, with L being the length of the list, then its contribution to all pairs of terminal types derived from the list is 1/(2L−1). For example, if an internal node is capable of {T1, T2, T3}, and let denote the shared progenitor score for the pair of terminal types Ti and Tj, then for we can compute the contribution of the internal node as 1/(23−1) = 1/4. Then
After iterating over all internal nodes, a matrix of shared progenitor scores MSPS was generated. The SPS matrix was converted to a similarity matrix by 1 − MSPS/max(MSPS). Finally, UPGMA clustering was applied to the similarity matrix to obtain the fate map topology.
Random topology generation
For providing a baseline of topology reconstruction errors, we generated a random topology for each experiment compared in Figures 2F and 5A using the same method as described in the fate map reconstruction section. Briefly, the ‘rtree’ function in the ‘ape’ R package53 was used. This method creates bifurcations by randomly assigning terminal types to each side of the bifurcation based on draws from a uniform distribution.
Mapping of inferred progenitor states to true progenitor states
Upon initial reconstruction of fate map topology, the correspondence between the inferred progenitor states and the true progenitor states in the original fate map is not known. For downstream evaluations, true and inferred progenitor states were matched based on their potency and commitment patterns. An inferred progenitor state was considered correctly resolved if there existed a true progenitor state that met the following conditions:
the true progenitor state had the exact same potency as the inferred progenitor state.
the immediate downstream states or types of the true progenitor state had the exact same potencies as the immediate downstream states/types of the inferred progenitor state.
Node state assignment in time-scaled phylogeny
One characteristic of a progenitor state is its potency: the set of terminal types it can lead to. Each node in the time-scaled phylogeny also had an observed potency determined by the set of states its progeny covers. The inferred progenitor state of a node of the phylogeny was assigned based on its potency: the node was assigned an inferred state that had the same potency as itself. If no such state existed in the fate map, then it was assigned the least potent state in the fate map that was more potent than the node but included all observed fates of the node in its potency.
Commitment time inference with ICEs
To infer commitment time of a progenitor state, a set of Inferred Commitment Events (ICEs) were identified. A node in the time-scaled phylogeny was considered an ICE if both daughters had a different assigned state than itself. Unlike FASEs, which are defined for each pair of terminal fates, ICEs are defined with respect to inferred progenitor states. If a node is an ICE, it is also a FASE for at least some pair of terminal states, but the opposite is not necessarily true. Each ICE was associated with a progenitor state. The depths of all ICEs associated with a state defined the ICE times. The mean of ICE times was used as an estimate for the commitment time. In the case where inferred commitment times of the downstream state was earlier than that of the upstream state, the commitment time of the downstream state was set to that of the upstream state. This situation is indicative of the lack of evidence supporting the relative ordering the two commitments in question.
Progenitor population size and commitment bias inference
To identify the population present at the commitment time of a progenitor state, first, a set of extended states was defined for each inferred progenitor state. The extended states included the state itself, its upstream states up to root and its downstream states down to the terminal types. Next, a state path was constructed on fate map topology for each branch that spanned the commitment time of the progenitor state: the state path included all the inferred progenitor states in the fate map topology between the state of the incoming node (closer to the root of the phylogeny) and the state of the outgoing node (closer to tips of the phylogeny) of the branch (Figure 3G). A branch was considered associated with the progenitor state if its state path was a subset of the extended states of the progenitor state. To estimate the progenitor population size, the collection of incoming nodes of the associated branches were counted (Figure 3H).
To quantify the bias of a progenitor state’s commitment, each associated branch was further classified as (i) committing to one of the downstream states, or (ii) uncommitted. The classification was made based on the state path; if the state path covered one of the immediate downstream states, it was classified accordingly. Otherwise, it was classified as uncommitted. For commitment bias, the proportion of committed branches committing to each downstream state of the inferred progenitor state was used.
Barcoding mutagenesis model
Let there be i = 1,2, …, I total barcoding sites. A barcoding site is unmutated at the beginning (i.e., t = 0) and once activated, starts to accumulate heritable mutations over time. Mutation events happen independently for each site according to a Poisson point process with a constant rate after activation (Figure 4A). Let the mutation rate of the Poisson process be λi for site i, then the probability of having a mutation event in a small time window [t, t + Δt] is λΔt. In our model, once a site has mutated, it can no longer mutate further. A mutant allele is inherited from a cell by all its descendants. The Poisson point process has the memoryless property, which means that if no mutation event has happened up until time t, then the probability of getting a mutation event in the time window [t, t + d] is 1 − e−λd, which does not depend on the value of t.
When a mutation event occurs, an unmutated active copy of the site is converted into one of many possible mutated inactive alleles, each with a distinct emergence probability (Figure 4A). Let be the set of possible alleles for site i, and be their corresponding probabilities, then a mutant allele Xi of site i created by a mutation event has P(Xi = Aij) = aij. To summarize, the parameters of the barcode mutagenesis model include the mutation rates {λi}i=1, …, I, and each site’s mutant allele emergence probabilities .
Parametrization of barcode mutagenesis model with MARC1 mouse data
To simulate lineage barcodes that mimic a realistic system, the mutagenesis model was parametrized based on the MARC1 (Mouse for Actively Recording Cells 1) system5 wherein extensive embryonic barcoding data are available30. In MARC1 mice, somatic mutations are induced in tens of independent homing guide RNA loci (hgRNAs)29. We estimated the mutation rates of MARC1 hgRNAs (i.e., rate of the Poisson process) using embryonic time course data (Figure S4A). We estimated emergence probabilities of mutant alleles for each hgRNA by adapting the inDelphi algorithm that predicts CRISPR-Cas9 mutations31. The details of this estimation can be found in the Quantification and Statistical Analysis section. We compared and verified inDelphi’s predictions against published MARC1 data (Figure S4B). To test how well the results resembled actual lineage barcoding data, we simulated barcoding in whole-mouse embryos for E3.5 to E16.5 in samples of 2,000 cells (or fewer when there were fewer than 2,000 cells in the organism) and compared the results to that of experiments. See Figures S4A–G and their legends for the results and their interpretation.
Parameters for simulating MARC1 lineage barcodes
Parameter estimates from the MARC1 data were used to simulate lineage barcodes from time-scaled phylogeny. The corresponding estimated mutation rates and inDelphi predicted allele emergence probabilities for each MARC1 hgRNA were used as parameters for the mutagenesis model. For reconstructing Phylotime phylogeny in Figure 5A,B, 50 hgRNAs of the ‘intermediate’ or ‘fast’ category were randomly sampled from the MARC1 pool of hgRNAs for each simulation.
Phylotime for reconstructing time-scaled phylogeny from lineage barcodes
Our approach to reconstructing time-scaled phylogenetic trees for thousands of cells was based on a maximum likelihood estimation of pairwise temporal distances between cells. Given a pair of terminal cells, with their MRCA being N1, the branch length parameter was estimated, which is the time since the MRCA of the two cells (Figure S4H).
For a barcoding site i with a mutation rate of λi, and probabilities of mutating into alleles , the likelihood of observing the given alleles and in a single barcoding site in two cells (c1, c2) is the sum of two terms:
| (Eq. 1) |
The first term, , is the probability that a mutation has occurred before the MRCA, leading to identical alleles in both cells. The second term is the probability of observing the allele in each terminal cell respectively ( and ) conditional on no mutation occurring before the MRCA (the probability of which is ).
For the first term, we first define the term for each mutant allele Aij, where if both C1 and C2 carry allele Aij for the site, and otherwise. Then the first is calculated as:
which is the sum over all probable mutations, where at most one term can be non-zero. For the second term, we have
and
where Mic denote the allele observed for c = C1, C2 and “0” denotes an unmutated allele, and Ind(.) is the indicator function.
Because barcoding sites in our model are assumed to be independent, the likelihood for the set of alleles observed in all barcoding sites is then the product of their individual likelihoods:
| (Eq. 2) |
To get estimates of pairwise distance, or equivalently, time since MRCA between two cells (), we first plugged in estimates of mutation rates and allele emergence probabilities. In the simulation experiments in this work, the true values of mutation rates and allele emergence probabilities were plugged in. In actual experiments, we suggest using naïve estimates for the mutation rate: , where Fi is the mutated fraction for site i and T is the total time from the start of the experiment to the sample collection. For mutant allele emergence probabilities, we suggest using estimates obtained from independent experiments or predictions such as inDelphi. If no such information is available, we suggest using a uniform prior, i.e. aj = 1/Jj = 1, …, J. To get the optimal value of , the following score equation was solved using the Newton-Raphson method:
| (Eq. 3) |
The distance between the two cells is . Once all pairwise distances were computed with the above method, we applied UPGMA hierarchical clustering to derive a phylogenetic tree wherein branch lengths represent actual time. We called this approach Phylotime.
Phylogenetic tree inference with Hamming distance and Cassiopeia
The Hamming distance between barcodes of two cells is defined as the number of sites for which the two cells do not share the same allele. To infer the phylogeny, UPGMA was applied to the pairwise Hamming distance matrix. For computing KC1 distance, the total length of the inferred tree is scaled to the sampling time. Phylogeny was also inferred with Cassiopeia, a phylogenetic reconstruction software package which was designed for barcode-based reconstruction35. Cassiopeia was run with default parameters with a single thread. The software uses a greedy top heuristic and an integer linear program bottom solver. We allowed Cassiopeia up to 24 hours to solve each tree. The Cassiopeia-reconstructed tree lacked branch lengths and also contained multifurcations that were not fully resolved. The multifurcations were resolved randomly using the ‘multi2di’ function from the ‘ape’ R package53, initial branch lengths were assigned to the tree using the Grafen option, and the ‘chronos’ function was applied to estimate the final branch length.
Simulations of experimental readout errors
To assess how quantitative fate mapping may be affected by readout errors, two common modes of experimental error were considered. These errors include allele dropout, when a fraction of barcoding sites is not detected in every single cell. This form of error is common in experiments where barcoding sites are directly amplified from a single cell’s genome or transcriptome8. To simulate allele dropouts, alleles were set to missing completely at random (MCAR), meaning that missing happens with the same probability for all cells and all sites. We also considered allele switching, an error that occurs when an allele from one cell is assigned to another. This form of error can emerge if template switching takes place during barcoding amplification, a possible outcome for synthetic barcoding loci that have a high degree of homology30. To simulate allele switching, we considered a single barcoding site where there are N total cells. For the site, the number of cells with different alleles were first counted: N1, …, NJ cells each with a different unique allele, the counts were then normalized to proportions fj = Nj/N. Given the probability of allele switching pswitch the number of cells with error was calculated as Nerror = ceiling(Npswitch). To set the error alleles, the Nerror cells were first drawn, and alleles for those cells were set randomly by a multinomial distribution where the probabilities were the f1, f2, …, fJ computed earlier. The process was repeated for each barcoding site.
In each case, we applied the error to 5, 10, 20, 30, 40, or 50% of the data from our panel of 3,310 simulated barcoding experiments then applied Phylotime followed by ICE-FASE to reconstruct quantitative fate maps. For allele dropout, we used a strategy to impute missing alleles before applying Phylotime. The strategy, detailed in the next section, predicts missing alleles for each barcoding site using a machine learning algorithm (XGBOOST)55 while leveraging information from all the other sites, and it does so sequentially from the site with the least amount of missing data to the site with the most.
Imputation of missing alleles with XGBoost
Given a character matrix that is the cell by site matrix where each element in the matrix is the allele observed, the missing percentages of all barcoding sites were computed first. Next, each site was imputed one by one going from the one missing in the fewest cells to the one missing in the most cells, using information from all other sites (Figure S8C).
Specifically, when imputing missing alleles of a single site, an ‘XGBoost’ model with multinomial ‘softmax’ objective was trained where all the cells whose alleles were observed for the site55 were used as the training examples, and all sites that is not the one to be imputed were used as training features, and treated as categorical variables, where each mutant allele is a category. The design matrix of the model was constructed by one-hot encoding each site, treating the missing in the other sites as unmutated, and subsequently column concatenating all one-hot matrices. The parameters ‘max_depth=4’ and ‘nrounds = 20’ were used for the XGBoost model.
Simulation of experiments with different sampling time
A progenitor field may be studied by obtaining its descendant cell types immediately after its development or at a later time point. For instance, development of the primary germ layers (mesoderm, ectoderm, endoderm) during gastrulation may be analyzed by obtaining these cell types immediately after gastrulation (~E7 in mouse) or in late gestation (~E15) by obtaining neuronal cells as ectoderm descendants, muscle cells as mesoderm descendants, and hepatocytes as endoderm descendants. To investigate the effect of sampling time, we simulated phylogeny and barcoding with 50 hgRNAs for all our 16-terminal type fate maps while sampling 100 cells from each terminal type at days 11.5, 12.5, 13.5, 14.5, or 15.5 days (Figure S5E), repeating each condition twice (53 fate maps × 2 sampling strategies × 2 repeats). We then applied Phylotime and ICE-FASE to obtain a quantitative fate map in each case and compared quantitative fate map reconstruction with terminal cell types sampled at various time points after the last commitment (Figures S5F–I). We also applied ICE-FASE to the true phylogeny for comparison (Figures S5J–M). For the results and detailed interpretation see Figures S5E–M and their legends.
Simulation of experiments with increased cell death
Because cell death is a prevalent developmental control mechanism36, we assessed how it affects quantitative fate mapping. In our fate maps with 16 terminal types, we set cell death per division to increasing levels for either all terminal types or all progenitor states with at least 500 cells at their times of commitment (Figure S5N). After simulating barcoding outcomes and applying Phylotime and ICE-FASE, we compared fate map reconstruction accuracy as a function of cell death rates. For the results and detailed interpretations, see Figures S5N–S and their legends.
Simulation of experiments with commitment via symmetric vs asymmetric divisions
Next, we considered stereotyped cell fate commitment involving asymmetric cell divisions, analogous to those seen in fruit flies eye development37. Asymmetric cell divisions are also common at later stages of development in mammals56. To investigate the effect of this mechanism of commitment on quantitative fate mapping, we simulated barcoding experiments on a pectinate 16 terminal type fate map (Figure 1C, bottom left) with commitments happening with either asymmetric divisions or symmetric division exclusively. The pectinate fate map with 16 terminal types was modified slightly for the comparison of commitment via symmetric and asymmetric cell division. All progenitor state biases were set to 0.5. To obtain a fate map whose terminal types have similar population sizes, the doubling time for the terminal state that was the i-th to emerge was set to 0.6 − 0.5/16i. Moreover, the cell death probabilities for the terminal population were set to 0.1 and a cell doubling probability per doubling time (cTj,L for terminal type Tj) of 0.4 was instituted. For the asymmetric mode, one daughter cell commits to the downstream terminal type and the other commits to the downstream progenitor state after commitment (Figure S5T). For the symmetric mode, each cell randomly commits to one of the downstream fates based on predefined probabilities and subsequently undergoes symmetric divisions (similar to all previous simulations) (Figures 1 and S5T). In each case, we simulated one hundred experiments with 50 hgRNAs and 50 cells sampled from each terminal type (Figures S5U,V). We then applied Phylotime and ICE-FASE to obtain quantitative fate maps and compared the results between the two commitment modes. For the results and detailed interpretation, see Figures S5T–Z and their legends.
ICE-FASE for multiple replicates
First, the FASE distance matrix was computed for each phylogeny separately. The distance matrices were then averaged, and a consensus topology was obtained by applying UPGMA clustering to the average FASE distance matrix. The set of inferred progenitor states were defined based on the consensus topology. For each replicate’s phylogeny, each of its nodes were assigned one of the progenitor states based on their potencies, based on which ICEs were identified. Next, ICEs identified from all replicates were pooled, and their average time was taken to be the consensus commitment time. Finally, edges associated with each inferred progenitor state were identified in each replicate’s phylogeny based on its consensus commitment time. The resulting population sizes of the progenitor states, and population sizes committing to each downstream states or types were averaged. The average population size was taken as the consensus population size and the proportion of average population size committing to each downstream state was taken as the consensus commitment bias.
Simulation of experiments with prolonged commitment
Commitment events modeled thus far involve all the progenitor population committing within one cell cycle. Because some progenitor states undergo gradual commitment during development, we expanded our models to allow progenitor states to commit over more extended time periods. We then created three fate maps with 16 terminal types that are identical in topology and other parameters, except that P11 commits to its downstream states (P1 and P9) between day 5.8 and 6.3 in the first map, between day 5.8 and 6.9 in the second map, and between 5.8 and 7.5 days in the third map (Figure S6A). The details of the modifications are given in the next section. We simulated phylogenies based on these fate maps with fixed sampling of 100 cells from each terminal type and repeated simulations one hundred times for each. After applying Phylotime followed by the ICE-FASE algorithm, we compared the accuracy of quantitative fate map reconstruction in each case. For the results and detailed interpretations, see Figures S6B–E and their legends.
Modified fate map with prolonged commitment
To illustrate the effect of progenitor cells committing over longer times, we modified an existing fate map with 16 terminal types from our panel. In the original fate map, the progenitor state P11 commits within a single cell cycle from 5.8 and 6.3 days. In a first modified version, the commitment happens within two cell cycles from 5.8 and 6.9 days. A random ⅓ of all the P11 population commits at the original time whereas the remaining population self-renews by going through an extra round of cell division. After the extra round of self-renewal, they commit to the downstream cell states of P9 and P1 according to the P11 commitment bias. Finally, in a second modified version, commitment happens over three cell cycles from 5.8 and 7.5 days. A random third of all the progenitor population again commit at the original commitment time. After one extra round of self-renewal, half of the remaining uncommitted population commit while the other half self-renew for yet another round, after which they also commit. To accommodate commitments happening over more than one cell cycle, the definition of commitment time and progenitor population size were modified accordingly. The progenitor population size was defined as the sum of the population size committing to downstream states during each cell cycle. The commitment time was defined as the start of the cell cycle during which commitment has happened weighted by the number of cells that have committed during the cell cycle. The ICE-FASE estimates of P11 for each fate map were compared to the respective definition of commitment time and progenitor population size.
Simulation of experiments with multifurcating fate commitments
Commitment events modeled thus far involved bifurcating progenitor states. However, some progenitor states in development may simultaneously commit to more than two immediate downstream states (e.g., trifurcate). To investigate this, our generative model was extended to simulate n-furcations in general. The details of the model extension are given in the next section. Next, we assessed whether the ICE-FASE algorithm can resolve trifurcations. First, a trifurcation in a 16 terminal type fate map was introduced by removing the progenitor state P8 from the fate map and making its downstream states (P5 and P6) directly emerge from the commitment event of its upstream state P11 (Figure S6F). We refer to this trifurcating progenitor state as P11*, compared to the original bifurcating P11 as they have identical potencies, commitment times, and population sizes. We then simulated phylogenies and barcoding with 50 hgRNAs based on both the original bifurcating and the new trifurcating fate maps with fixed sampling of 100 cells from each terminal type and repeated each simulation one hundred times. Finally, we applied Phylotime followed by the ICE-FASE algorithm to reconstruct a quantitative fate map based on each simulated experiment. For the results and detailed interpretation see Figures S6G–L and their legends.
Count graph for simulating progenitor state multifurcation
When the fate map involved a multifurcation, the model to generate cell phylogeny was extended. Only multifurcation via symmetric cell division was considered, where only minor adjustment to the methods described earlier needed to be made. Take a trifurcation of progenitor state Pi into Pj, Pk and Pl as an example. All computations with regard to process 1 (proliferate process) remained the same. During process 2 (commit and proliferate process) in the count graph generation step, the default count node was split into three sub-count nodes of commitment modes Pi-PjPj, Pi-PkPk and Pi-PlPl. The sample size generation step was carried out as usual. In the reorganization step, six different new sub-count nodes were created to replace the original three, including Pi-PjPj, Pi-PkPk, Pi-PlPl, Pi-Pj, Pi-Pk and Pi-Pl. During reorganization, non-coalesced cells in Pi-PjPj, Pi-PkPk, Pi-PlPl are moved to their respective non-coalesced sub-count nodes. The remaining steps were carried out as usual.
Generation of an inducible Cas9 barcoded stem cell line
Knock-in of an Inducible Cas9 Cassette:
EP1 iPSCs were modified to express Cas9 protein under doxycycline induction. CRISPR/Cas9 was used to target and insert both a reverse tetracycline-controlled transactivator (rtTA) construct and a tetracycline-dependent Cas9 construct into each of the two copies of the AAVS1 safe harbor locus. To stably introduce the cassette, cells were grown to 80% confluency and then dissociated with Accutase for 13 minutes to generate a single cell suspension. Dissociated cells were resuspended in mTeSR Plus media with 5 μM blebbistatin and counted- 50,000 cells were seeded into one well of a 24-well plate coated in Matrigel. The following day, 350 ng of plasmid expressing Cas9 and an AAVS1-targeted guide RNA (modified PX459, with T2A replaced by P2A) and 500 ng each of plasmids containing the Cas9 donor sequence (modified Addgene #58409 with blasticidin resistance)47 and rtTA donor sequence (Addgene #60843)50 were combined and added to 48 ul Opti-MEM (ThermoFisher). 2 ul of Lipofectamine Stem Transfection Reagent (ThermoFisher) were added to the transfection mix, which was then vortexed and incubated for ten minutes at room temperature. The entire transfection mix was added to one well of cells. Media was replaced the following day. 40 hours after transfection, cells were transiently selected for 24 hours with 0.95 ug/mL puromycin (MilliporeSigma), 5 ug/mL blasticidin (MilliporeSigma), and 200 ug/mL G418 sulfate (ThermoFisher).
Surviving cells were cultured to 30% confluency, and then dissociated to a single cell suspension for clonal expansion. 500–1000 cells were seeded in one well of a 6-well plate and cultured for 7–10 days before clonal colonies were picked and screened for the intended insertions. PCR was performed with a reverse primer complementary to the right homology arm of the targeted AAVS1 locus (GGAACGGGGCTCAGTCTGA) and a forward primer either targeting the Cas9 knockin (CACCTTGTACTCGTCGGTGA) or the rTTA constructs knockin (GCTGATTATGATCCTGCAAGC). Positive colonies were cultured and clonally expanded once more, with a second round of colony picking and PCR screening to ensure clonality of the final cell line.
Selected clones were then further screened for functionality of the inducible Cas9 cassette. Cells were treated with 2 ug/mL doxycycline (MilliporeSigma) for 5 days and cells were harvested for RNA extraction. RNA was converted into cDNA and qPCR was performed to confirm both Cas9 and rtTA mRNA expression when normalized against housekeeping genes GAPDH, CREBBP, and ACTB (Cas9 Fwd: CCGAAGAGGTCGTGAAGAAG; Cas9 Rev: GCCTTATCCAGTTCGCTCAG; rtTA Fwd: GCTAAAGTGCATCTCGGCAC; rtTA Rev: TGTTCCTCCAATACGCAGCC; GAPDH Fwd: TAGCCAAATTCGTTGTCATACC; GAPDH Rev: CTGACTTCAACAGCGACACC; CREBBP Fwd: GAGAGCAAGCAAACGGAGAG; CREBBP Rev: AAGGGAGGCAAACAGGACA; ACTB Fwd: GCGAGAAGATGACCCAGATC; ACTB Rev: CCAGTGGTACGGCCAGAGG).
Transfection with a homing guide RNA library:
50,000 cells from the doxycycline-inducible Cas9 line were seeded into one well of a 24-well plate. The following day, 300 ng of Super PiggyBac Transposase (SBI System Biosciences), 700 ng of PB-U6insert hgRNA library (Addgene #104536)5, and 50 ng of PB-U6insert-EF1puro library (Addgene #104537)5 were combined and added to 48 ul Opti-MEM (Gibco). 2 ul of Lipofectamine Stem Transfection Reagent (Thermo Fisher) were added to the transfection mix, which was then vortexed and incubated for ten minutes at room temperature. The entire transfection mix was added to one well of cells. Media was replaced the following day. Transfected cells were selected with 0.95 ug/mL puromycin for one week.
Selected cells were dissociated to single cell suspensions, and 500–1000 cells were seeded in one well of a 6-well plate and cultured for 7–10 days before clonal colonies were picked. Colonies were screened for relatively high numbers of hgRNA insertions using qPCR. Genomic DNA was extracted from each colony and the relative number of hgRNA insertions was measured by subtracting Cq values of genomic hgRNA amplification (Fwd: ATGGACTATCATATGCTTACCGT; Rev: TTCAAGTTGATAACGGACTAGC) from Cq values of genomic SOX11 amplification (Fwd: TGATGTTCGACCTGAGCTTG; Rev: TAGTCGGGGAACTCGAAGTG). Colonies with the largest cycle threshold value difference, indicating the highest number of hgRNA insertions, were cultured and clonally expanded once more. Colonies were picked one additional time to ensure clonality of the final EP1-Cas9-hgRNA iPS cell line.
Barcoding activity of cell line-integrated hgRNAs:
Cell line hgRNA identifiers and mutation activity levels were determined by performing a doxycycline time-course experiment- cells were treated with 1 ug/mL doxycycline daily for 11 days. Genomic DNA was extracted from cells after 0, 4, 8 and 11 days of doxycycline treatment and Cas9 induction. hgRNA sequencing libraries were prepared as follows: 5 ng of genomic DNA was amplified on a real-time PCR machine in 1X KAPA SYBR FAST (Roche) with 0.0625 uM hgRNA PCR1 forward primer (ACACTCTTTCCCTACACGACGCTCTTCCGATCTATGGACTATCATATGCTTACCGT), 0.1875 uM hgRNA PCR1 truncated forward primer (CTACACTCTTTCCCTACACGAC), 0.0625 uM hgRNA PCR1 reverse primer (TGACTGGAGTTCAGACGTGTGCTCTTCCGATCTGCCATACCAATGGGCCCGAA), and 0.1875 uM hgRNA PCR1 truncated reverse primer (GTGACTGGAGTTCAGACGTG). Reactions were denatured at 95°C for three minutes, and then cycled at 95°C for 20 seconds, 64°C for 20 seconds, and 72°C for ten seconds. The reactions were stopped when the real-time PCR curve reached early-to-mid-exponential phase. Reactions were then diluted 10–100 fold. 1 ul of diluted PCR was used as template for a subsequent PCR reaction in 1X KAPA HiFi HotStart ReadyMix (Roche) with 1X SYBR Green I Nucleic Acid Stain (ThermoFisher) and 0.25 uM each dual indexing primer pair for Illumina. Reactions were denatured at 98°C for thirty seconds, and then cycled at 98°C for 10 seconds, 64°C for 20 seconds, and 72°C for ten seconds. Reactions were stopped when the real-time PCR curve reached early-to-mid-exponential phase. Libraries were purified with DNA Clean & Concentrator-5 columns (Zymo), sequenced on an Illumina MiSeq instrument, and analyzed. hgRNA sequencing reads were analyzed using the published MARC1 data analysis pipeline30. The percent of reads for each hgRNA identifier sequence that were mutated was calculated at each time point (Figure S4), determining the relative activity for every hgRNA.
In vitro quantitative fate map experiments
Single cells from the EP1-Cas9-hgRNA iPSC cell line were FACS sorted into a 96-well plate coated with Matrigel and containing mTeSR plus medium supplemented with 5 μM blebbistatin, 10% CloneR (STEMCELL Technologies), 1 μM Pifithrin-α hydrobromide (Tocris Bioscience), 1X Antibiotic-Antimycotic (ThermoFisher), and 0.2 ug/uL doxycycline. Supplemented media was exchanged every other day. Three days after sorting, wells with surviving cells were identified and assigned to follow the quantitative fate map for either experiment one (E1) or experiment two (E2).
For E1, cells were grown in the sorted wells until there were approximately 32 cells, or 6 doublings, which was considered to be P5 of the QFM. P5 cells were then carefully dissociated and passaged- media was aspirated from wells and 30 ul of Accutase was added and incubated at 37°C for 8 minutes. The Accutase was then gently triturated to detach all cells from the plate, and 10 ul was directly added to a new well filled with supplemented media, corresponding to P3 of the QFM. The remaining 20 ul was directly added to a new well corresponding to P4, resulting in a 1:2 split of the cells. Passaged cells were incubated for 2 hours to allow cells to settle and attach to the Matrigel coating, after which a 50% media exchange was performed to decrease the total amount of Accutase remaining in the wells. Once the cells in P4 had gone through approximately two doublings, they were passed following the same protocol, this time splitting the cells evenly between progenitor states P1 and P2. After P3’s cells had gone through approximately 4 doublings since their passage they were split once again, evenly into terminal types T5 and T6. P2 cells were given four doublings before being split evenly into terminal types T3 and T4, and finally P1 was split evenly after five doublings into terminal types T1 and T2.
For E2, cells were propagated using the same techniques as E1, but following a slightly altered QFM. P3 cells were split into terminal types T5 and T6 after just two doublings, and P4 cells were split into P1 and P2 after four doublings, representing a switch in the order of commitment P3 and P4 commitment times between the E1 and E2 fate maps. After cells were passaged into their terminal wells, doxycycline treatment was ended so that barcode editing would discontinue. Cells were then passaged into 6-well plates and grown to confluency for terminal cell barcode extraction and analysis.
Sequencing single-cell lineage barcodes
Each terminal well from E1 and E2 were dissociated into single cell suspensions by incubating the cells in accutase for 14 minutes. Single cells were resuspended and diluted in PBS pH 7.4 for FACs sorting. Single cells from each terminal group were sorted into 192 wells of a 384-well plate (half a plate per terminal group), with each well containing 1 ul of QuickExtract DNA Extraction Buffer (Lucigen). Plates were vortexed and spun down directly after sorting to ensure cells were in the QuickExtract buffer. DNA was extracted from single cells by incubating the sorted plates for 10 minutes at 65°C followed by 5 minutes at 98°C to inactivate the QuickExtract.
Single-cell hgRNA sequencing libraries were generated using three serial PCR reactions as per the published protocol from Leeper et al.30, with each cell treated as an individual sample. Each well of single-cell DNA received 9 ul of PCR0 mix containing 1X DreamTaq Hot Start PCR Master Mix (ThermoFisher) and 0.5 uM each hgRNA pre-amplification forward and reverse primers (Fwd: AAGTAATAATTTCTTGGGTAGTTTGCAG; Rev: GAAAAAGCCATACCAATGGGC). Reactions were denatured at 95°C for three minutes, cycled five times for 95°C for 20 seconds, 55°C for 30 seconds, and 72°C for one minute, and then cycled 20 times for 95°C for 20 seconds, 60°C for 30 seconds, and 72°C for 30 seconds.
One microliter of each cell’s PCR0 reaction was used as template for the proceeding PCR1 reaction. Reactions for PCR1 and 2 were carried out as described above in the section “Determining profiles for integrated hgRNAs”, with each single cell continuing to be amplified and indexed as an individual sample. After PCR2, the reactions for each terminal cell type were normalized and purified together to create one combined sequencing library per terminal group. Libraries were quantified using the Qubit dsDNA HS Assay Kit (ThermoFisher) sequenced on a MiSeq System using Miseq Reagent Micro Kits (Illumina).
Determining actual progenitor population size from in vitro experiments
For each experiment, brightfield images were taken of P5, P4, and P3 wells just before passaging (Figure S6). To estimate the cell numbers at each progenitor state, images were analyzed in ImageJ. Outlines were drawn around 5 different cells within a colony and their average area was measured. All colonies within a well were then outlined and the total combined area of the colonies was measured and divided by the average cell area of a cell to estimate the total number of cells present in each well.
Processing of in vitro experimental data
Identifier and spacer sequence pairs were extracted for each sample using the initial step (BLAST search) detailed in the published pipeline30. For cells that were sequenced more than once, pair counts for unique “identifier+spacer” were first merged for each cell. The merged data were then provided as input to the remainder of the pipelines for sequencing error correction and filtering.
A total of 32 hgRNAs were identified from the filtered results, each observed in more than 921 cells. Sequencing errors among identifier sequences were first corrected. For each identifier sequence that was not one of the 32 hgRNAs observed in the unmutated sample, if the identifier sequence was within a hamming distance of 1 to any true identifiers, its spacer counts were merged with that of the known hgRNA’s. After the correction, no other identifiers other than the 32 known hgRNAs were observed in more than 3 cells.
Spacer sequencing errors were corrected next. First, the error reads within each cell and hgRNA combination were corrected. In one of our sequencing runs, one cycle of sequencing returned ‘N’ for all spacer sequences. These errors were computationally corrected: if there existed another spacer sequence for the same identifier and cell that was exactly the same except for the ‘N’ base pair, the count of the error spacer with the ‘N’ base was merged with the other spacer. Next, the spacer sequencing errors across different cells were corrected. Again, the error involving ‘N’ base pairs were further corrected across the cells using the same criteria as the within cell correction.
Each allele was labeled as unmutated or mutated by comparing the spacer sequences to that of the reference sequencing result, that is, if a spacer sequence was observed in the parent for the same identifier, it was labeled as unmutated. One identifier “GCCAAAAGCT” did not amplify in the parent data, and the sequence “GAAACACCGGTGGTCGCCGTGGAGAGTGGTGGGGTTAGAGCTAGAAATAG” was identified as the unmutated spacer based on alignments of its different observed alleles.
Noisy reads were further filtered for cell+hgRNA combinations that had more than one spacer observed. If the most abundant spacer was at least four times more abundant than all the other spacer reads observed, only the most abundant spacer was kept. All the spacer counts with fewer than five total reads were also excluded.
After processing, 1197 cell+hgRNA combinations out of the total 54,012 (2.2%) still had more than one spacer observed. If more than two spacers were observed for more than two hgRNAs in a single cell, the cell was likely a doublet. 33 such cells were identified and filtered. Each cell had a median 25 out of 32 hgRNAs detected. Each hgRNA was detected in a median of 83% of all cells (Figure S7D). Before reconstruction, non-informative cells and hgRNAs were filtered out. Any hgRNA with a diversity of one, that is, all cells in which an hgRNA was observed had the same allele, was considered non-informative and was excluded. An allele was considered informative if it was mutated and observed in more than one cell in each group, and cells with less than three informative alleles were filtered out. In all, 970 out of 1051 cells for 31 hgRNAs passed the filters for E1 and 943 out of 1032 cells for 29 hgRNAs passed filters for E2. For Phylotime reconstruction, naïve estimates for mutation rate and uniform prior for mutant allele emergence probabilities were used.
Simulation and ground truth fate map of in vitro experiment
To conduct simulations that best resembled the in vitro experiment, the effective cell division rates during the experiment were first determined. First, the division rate of P5 was chosen so that the population size at the first split is the most consistent with what was observed. Next, we assumed that cells were split in proportion to the volume of the suspension as P5 was split into P3 and P4. The division rate of P3 and P4 were set so that their respective population sizes at the split agreed with what was observed. The division rate for P1, P2 and all the terminal cells were set to once every 20 hours. The exact division rate chosen and the population size at each stage are detailed in Figure S7B. Notice that the commitment happens one cell division prior to the well split, so the ground truth commitment time is one cell division earlier than the spit time, and the progenitor field size is half of what was observed in the well at the split.
To simulate hgRNA barcodes from ground truth fate map, mutation rates were estimated from the time course data of bulk mutated fractions from the iPSC line. For mutant allele emergence probabilities, predictions from inDelphi were used.
QUANTIFICATION AND STATISTICAL ANALYSIS
Estimation of mutagenesis parameters in MARC1 mice
To get posterior estimates of mutation rates of MARC1 hgRNAs (i.e., λ, rate of the Poisson process), a grid search was conducted to match empirical distributions of mutated fractions among simulated and observed data across several embryonic time points. Previously reported hgRNAs formed three classes: the ‘slow’ class generated mutations on the order of 0.001 mutations/day, ‘intermediate’ class generated ~0.1 mutations/days, and fast class generated ~1.0 mutations/day during early mouse development. The ‘slow’ and ‘fast’ estimates expectedly had large uncertainties as most observed fractions are close to 0 or 100 percent mutated. Alternatively, a naïve estimate of mutation rate can also be used. If mutated fractions Fi were observed at time Ti in animal i for i = 1, …, N, then is a naïve estimate.
For mutant alleles of a barcoding site, estimating the probabilities of individual repair outcomes created by Cas9 DNA break-repair (mutant emergence probabilities) was challenging. Normally, the fraction of cells carrying a particular mutant allele among all cells with a mutated allele (within-animal estimates) is a good estimator of the allele emergence probabilities. However, when cells divide and mutate starting from a small field size, these fractions are largely affected by the time of the mutagenesis events, as early events result in larger clones carrying the same exact mutation. On the other hand, when hgRNA genotypes are observed for multiple animals, the fraction of animals that carry a particular genotype, once normalized, and when the probability is small, can be good estimates to the mutation probabilities (across-animal estimates) (Figures S4B,C). In this case, the estimation accuracy depends on the number of animals analyzed. From the MARC1 time course data, the within-animal estimates were calculated for each animal and averaged, and the across-animal estimates were calculated based on 173 embryos from 2 mouse lines. To get a more complete profile of possible mutant alleles and their occurrence probabilities for each hgRNA, we adapted the inDelphi machine learning algorithm to predict CRISPR-Cas9 mutation results31 for hgRNAs. We observed that the inDelphi-predicted probabilities agreed well with the across-animal estimates from MARC1, but poorly with within-animal estimates (Figure S4B). Further, the fact that the majority of the low probability mutations were not observed in any mouse suggests that the limited number of hgRNA mutation events during mouse development does not sufficiently cover a large portion of the mutational profiles. These conclusions were further validated by simulating multiple animal lineage barcode data based on inDelphi-predicted mutational profiles and comparing the within- and across-animal estimates from the simulated data of the true parameters (Figure S4C).
InDelphi predictions of hgRNA allele emergence probabilities
The emergence probabilities of hgRNA mutant alleles were computed by inDelphi. inDelphi is a machine learning algorithm to predict heterogeneous insertions and deletions resulting from CRISPR/Cas9 double-strand break31. In this study, inDelphi model trained with the mouse embryonic stem cell mutation dataset was used to predict the probabilities of hgRNA mutants from MARC1 mice. The original 64 hgRNA sequences in MARC1 mice were used as inputs. Since Cas9 nuclease cuts 3 bp upstream of the Protospacer Adjacent Motif (PAM, NGG sequence)1, the possible mutations from the cut site at −3 bp from the PAM sequence were computed. To take into account the repeated targeting of hgRNAs, inDelphi is first applied to predict a set of first-round mutations. Subsequently, the resulting first-round mutations were used as inputs to the next round of inDelphi predictions. Notably, only mutant sequences with >16 bp protospacer and PAM were subject to the second-round analysis as gRNA without >16 bp spacer sequence loses its activity57. Here, the probabilities of the next generation mutants were computed by multiplying the probabilities of the mutant in the current round by the probabilities of the mutant in the previous round. Repetitive application of inDelphi produces exponentially growing numbers of potential mutant alleles. Therefore, the analysis was limited to three cycles, resulting in first to third generations of mutants. The same mutation can be created in multiple rounds, in such cases, the probabilities from multiple rounds were summed. Finally, probabilities of all mutant alleles were normalized to have a sum of one. The inDelphi predictions for hgRNAs are provided on Zenodo (see Key Resources Table).
Assessing accuracy of progenitor state parameter estimates with RMSE
As a measurement of accuracy for the progenitor state parameter estimation, that is commitment time, progenitor population size and commitment bias, the root mean square error (RMSE) was used to quantify the amount of error in parameter estimation. The root mean square error is defined as
where the i index is over the number of progenitor states in the reconstructed fate map, xi is the true parameter and is its estimate. For progenitor population size, RMSE was computed for the log2 transformed population sizes. In cases where the reconstructed topology is used to assess parameter estimation accuracies, only the inferred progenitor states that could be correctly mapped to the truth were included. In cases where the true topology was used to assess parameter estimation accuracies, the RMSE is over all the progenitor states. Note that combining all progenitor states irrespective of sampling fraction inflates the RMSE values.
Supplementary Material
Figure S1. Topological diversity and distribution of various parameters in the quantitative fate map panel.
Related to Figure 1.
(A) Principal coordinate analysis of KC0 distances between all fate map pairs in each size category showing the fate maps occupy a broad space of topologies. Only the first two dimensions are plotted. Each dot corresponds to one fate map and its color indicates how the map topology was initially generated based on the key to the right and as described in STAR Methods. TBR: tree bisection and reconnection.
(B) Same as A, except each fate map’s dot is colored based on its Colless imbalance index according to the color key to its right. While Dimension 1 corresponds to imbalance, variation in Dimension 2 suggests that the fate map panel covers other unquantified aspects of topological diversity.
(C) Histograms showing the distribution of Colless index in fate maps of each size category. The histograms show that fate maps in the panel are well-distributed in a wide range of imbalance. For all panels, the 16, 32, and 64 terminal type categories are shown on the left, middle, and right respectively; ‘N’ indicates the number of fate maps in each category. Panels A–C show the topological diversity of the fate map panel. Distribution of various parameters in the quantitative fate map panel.
(D) Distribution of progenitor state commitment times for each fate map size category shown as rank ordered boxplots. For each boxplot, line marks the median and whiskers extend to the furthest data point within 1.5 times the interquartile range.
(E) Distribution of progenitor state commitment bias for all progenitor states in all fate maps shown as a histogram. Commitment biases were drawn from a beta distribution (α = 5, β = 5). However, a requirement was set for each progenitor state to be founded by at least four cells. The peak around 0.5 is a consequence of this requirement which forces small progenitor populations to assume biases closer to 0.5 (e.g., a committing progenitor population splits 4:4 if it has 8 cells in total, it will split 4:5 if it has 9 cells, it will split no more unequally than 4:6 if it has 10 cells in total, and so on).
(F) Plot showing cell doubling time distribution as a function of fate map time. Each black dot represents one progenitor state. Trendline (LOESS) is shown in blue. For a given embryonic time in fate maps, progenitor state doubling times are drawn from a uniform distribution; however, overall division rates become faster during embryogenesis43. Therefore, the underlying distribution for doubling times moves to shorter times as fate maps progress. All divisions before the first commitment, which occurs at day 2.4, proceed at a rate of 0.6 per day. Afterwards, division rates are drawn from uniform distributions as shown.
(G) Distribution of cell division rate for all progenitor states and terminal types in all fate maps shown as a histogram.
(H) Distribution of cell death rates per division for all progenitor states and terminal types in all fate maps shown as a histogram. Cell death probability was set to 0 until day 2.4 and then drawn from a uniform distribution between 0.02 and 0.08. These rates are based on rates reported during mouse embryogenesis24.
(I) Distribution of population size at the time of commitment for all progenitor states in all fate maps shown as a histogram.
(J) Distribution of total cell numbers for all fate maps as a function of time. The blue line signifies the average for all fate maps and the gray lines show each fate map and thus represent the range. Red dots represent the total number of cells in a mouse embryo43, showing general agreement in total number of cells between actual mouse embryogenesis and the fate maps simulated here.
(K) Histogram showing the average number of FASEs detected per pair of terminal types in our panel of 3,310 simulated phylogenies with 100 cells sampled from each terminal cell type. These phylogenies have an average of 4.4 FASEs per pair of terminal cell types.
(L) Scatter plots showing the average time between progenitor state commitment events as a function of imbalance (Colles index) broken down by fate map size, showing more imbalanced maps have commitments that are closer to each other. Blue line shows the fitted linear model.
Figure S2. Generative model of sampled cell phylogeny.
Related to Figure 1 and STAR Methods.
(Step 1) Generating a count graph using forward propagation. Part of the count graph where progenitor state Pi proliferates and commit to downstream states Pj and Pk is shown. Several instances of process 1 (proliferate-only process) and one instance of process 2 (commit and proliferate process) of the count graph are included. Horizontal lines represent time, in between horizontal lines are time windows during which the two processes take place. Different count nodes are listed. The black square node is the default count node. The rounded colored nodes are sub-count nodes. For process 1, the proliferation modes include: D: doubling, N: non-doubling, L: dying and DD: doubled. For process 2, Pi state cells commit to become downstream Pj and Pk state cells, sub-count nodes include Pi-PjPj, Pi-PjPk and Pi-PkPk. Four types of operations on the count nodes are listed in the box on the left labeled “Operations”; input is colored teal and output is colored brown, parameters to each operation are colored black.
(Step 2) Generating sampled terminal and progenitor cells counts using backward propagation. Given the counts of each (sub-)count node from Step 1, sample size for each count node was generated (lemon-colored number after comma in each node) using the four reverse operations shown in the box on the right.
(Step 3a) Reorganizing count graph. The count nodes at each time point were reorganized before phylogeny generation. Two examples of reorganizing process 1 and process 2 were given. Sub-count nodes after reorganization include: C: coalesced, NC: non-coalesced and CI: coalescing for process 1, and Pi-PjPj, Pi-PjPk, Pi-PkPk, Pi-Pj and Pi-Pk for process 2. The count graph after reorganization is given on the right.
(Step 3b) Listing tree nodes in the phylogeny. Sampled cells from different sub-count nodes are listed as ‘tree nodes’. One or two branches are attached to the tree nodes based on the number of cells they give rise to at the next time point. Fill of tree nodes indicate their cell state, and color of outline of tree nodes indicate which sub-count nodes they are from.
(Step 4a) Connecting tree nodes. Cells at each time point were connected randomly to open branches at the previous time point to generate the cell phylogeny.
(Step 4b) Simplifying tree phylogeny. The phylogeny is simplified by deleting nodes that do not give rise to two sampled cells at the next time point.
Figure S3. Accuracy and sources of error in estimating quantitative fate map parameters from time-scaled phylogeny.
(A) Line plot showing FASE distance error as a function of progenitor state sampling fraction for all pairs of terminal types in the panel of 3,310 simulated phylogenies (Mean±SD; N is variable). Dots in the background represent a random sampling of 500 individual values from each set to show the distribution.
(B) Boxplots showing the distribution of sampling fraction as a function of time in the panel of 3,310 simulated phylogenies.
(C) Example phylogenetic subtree, showing how undersampling can lead to FASEs appearing earlier in the tree (pink circles) than they really are (green circles). Gray circles: unsampled cells.
(D) Box plots of fate map topology reconstruction error (KC0) as a function of the average number of cells sampled per terminal type in fixed (left) and proportional (right) sampling schemes in our panel of 16 terminal type fate maps. P-values from Wilcoxon rank-sum test: ** p < 0.01, *** p < 0.001.
(E) Heatmap showing the agreement between inferred states and true states of all internal nodes in the phylogenetic tree shown in Figures 1D and 3A. Each rectangle represents the fraction of all nodes in the phylogenetic tree belonging to the true state shown on the left that were assigned the inferred state on the bottom. These results show that the only observed form of error is assigning a node to a state less potent than its true state.
(F) Histogram of the average accuracy of progenitor state node assignment to internal nodes of the phylogenetic tree across the panel of 3,310 phylogenetic trees showing that, on average, 72.3% of nodes were assigned to the correct progenitor state, the rest were assigned to states with lower potency.
(G) Schematic example of a phylogenetic tree, showing how undersampling can lead to a node being assigned a progenitor state with less potency than its true state.
(H) Scatter plot of population size estimate error for progenitor states as a function of their sampling fraction (top) aligned to a histograms of sampling fraction for all progenitor states in fixed or proportional sampling schemes (bottom). The vertical dashed line shows sampling fraction cutoff of 0.25 for separating well-sampled and undersampled progenitor states. Trendline (LOESS) for the correlation is shown in blue. The plot shows that population size is estimated more accurately for progenitor states that have higher sampling fraction.
(I) Scatter plot of commitment bias estimate error for progenitor states as a function of their sampling fraction (top) aligned to a histogram of sampling fraction for all progenitor states in our panel (bottom). Error is the absolute value of the difference between inferred and true commitment biases. The vertical dashed line shows sampling fraction cutoff of 0.25 for separating well-sampled and undersampled progenitor states. Trendline (LOESS) for the correlation is shown in blue. The plot shows that commitment bias estimate error approaches 0 as sampling fraction approaches 1.
Figure S4. Comparing barcoding outcomes between simulations and MARC1 mice, resolving time-scaled phylogenies, and assessing the effect of barcode site mutation rates.
(A) Heatmap showing the posterior probabilities of mutation rates for all MARC1 hgRNAs. Each row corresponds to one of the 64 active MARC1 hgRNAs and represents its estimated posterior mutation probability according to the color key on the bottom right. The axis and on top of the heatmap show the values of per-day mutation probabilities. The first sidebar to the right of the heatmap marks the initial characterization label of the hgRNA as either fast (green), intermediate (orange), or slow (slate blue)30. The second sidebar marks the origin of the hgRNA as either the PB3 founder (dark navy) or the PB7 founder (purple) mouse30. These values were estimated from published embryonic time course mutation analysis data30, as described in STAR Methods.
(B) Comparison of mutant allele emergence probability estimates of our modified inDelphi algorithm to those estimated from MARC1 mouse embryos by taking either abundance within the embryo when the allele is present (right) or fraction of embryos that present the allele (left). Blue dots represent predicted alleles that were observed in MARC1 embryos, gray ones were predicted by modified inDelphi but not observed in embryos. Alleles observed in embryos but not predicted by inDelphi, which were a small fraction, are not shown. Gray line has intercept 0, and slope 1. These results suggest that our modified inDelphi algorithm can recapitulate the actual distribution of MARC1 hgRNA allele emergence probabilities.
(C) Comparison of the true mutant allele emergence probabilities used for simulation (x-axis) with their average observed fraction in simulated mouse embryos (right) and fraction of simulated embryos that showed the allele (left). The true mutant allele emergence probabilities were obtained from our modified inDelphi algorithm (see STAR Methods). Blue dots represent alleles that were observed in simulated embryos, gray ones were possible in simulation by not observed in simulated embryos. Simulations were conducted 100 times for 9 time points. Gray line has intercept 0, and slope 1. Combined with B, these results show that our simulations of the barcoding process recapitulate the mutant allele emergence patterns in barcode mouse embryos. Together, B and C further show that estimations of allele emergence probability based on allele occurrences across multiple samples outperform average allele fraction in both simulation and MARC1 mouse data.
(D) Line-plots showing the mutated fraction of MARC1 barcoding sites over time in observed (left) and simulated (right) embryos for fast, mid, and slow categories of mutation rates. Means ± SEM are shown. Each barcoding site is colored according to its mutation rate using the color scale on the right. These plots show that the distribution of mutated fractions over the course of embryogenesis agrees between simulated and experimental results for hgRNAs with a range of mutation rates.
(E) Boxplots showing the number of mutant alleles for each MARC1 barcoding site over time in observed (left) and simulated (right) embryos for fast, mid, and slow categories of mutation rates. Each barcoding site is colored according to its mutation rate using the color scale shown in panel D. The boxplots for “observed” column look sparser because some hgRNAs had not segregated to any of the embryos analyzed at a given time point. These plots show that the total number of distinct mutant alleles (i.e. the mutant allele diversity) during embryogenesis were consistent between experiments and simulations.
(F) Line-plots showing the average mutant allele diversity as a function of barcoding site mutation rate for observed (blue) and simulated (purple) embryos. Means ± SEM are shown. These plots show that, similarly in both experimental and simulated results, the diversity of mutated hgRNA alleles increases as the hgRNA mutation rates increase because there are more mutagenesis events; however, at the fastest mutation rates, barcoding sites reach 100% mutated when there are fewer total cells, and the total diversities drop as a result.
(G) Line-plots showing the prevalence of a mutant allele among all mutant alleles as a function of its rank in observed (blue) and simulated (purple) embryos. A rank of one denotes the most abundant allele. Means ± SE are shown. These plots show that the compositions of mutant alleles within embryos agree between simulated and observed embryos because, after ranking all mutant alleles based on their frequencies, alleles of similar rank account for similar percentages of the mutated cells.
(H) The two-cell model. An Illustration of a phylogenetic model with two terminal cells used to estimate their distance since their most recent common ancestor (MRCA). N1 is the MRCA of the two cells. T is time from root to sampling. is the time from root to MRCA.
(I) Scatter plot showing the correlation between the Phylotime-inferred and the true cophenetic distances between all pairs of cells in Figure 4C, showing a high level of agreement between Phylotime-inferred and true cophenetic distances. Black line is y=x.
(J) Lineplots showing the performance of quantitative fate map reconstruction, measured by the error of topology, commitment (cmt) time, population size, and commitment (cmt) bias estimates, as a function of the number of hgRNA barcoding sites and their mutation rates (Mean±SEM; N=3,310; SEM very small). The table to the right shows the average and range of barcoding site mutation rates in each condition. Line colors signify the range and average of barcoding site mutation rates according to the table on the bottom. The mutation rate per cell division was calculated based on the average cell cycle length of 0.45 days (Figure S1F). T on X-axes: value using true phylogeny.
Figure S5. Effect of experimental errors, late sampling, cell death, and asymmetric divisions on quantitative fate mapping.
Related to Figure 5.
(A–D) Line graphs showing the performance of quantitative fate map reconstruction, measured by the error of topology (A), commitment (cmt) time (B), population (pop) size (C), and cmt bias (D) estimates, as a function of allele dropout (green) and allele switching (orange) error levels. Mean±SEM is shown, SEM too small to be seen. The gray dashed line in panel A marks the error of randomly generated fate map topologies. Allele dropout results in when a fraction of barcoding sites not to be detected in each single cell. This form of error is common in experiments where barcoding sites are directly amplified from a single cell’s genome or transcriptome8. Allele switching occurs when an allele from one cell is assigned to another. This form of error can emerge if template switching takes place during barcoding amplification, a possible outcome for synthetic barcoding loci that have a high degree of homology30. Both forms of error steadily degrade the accuracy of quantitative fate mapping; however, allele switching is more detrimental for quantitative fate map reconstruction. For example, panel A shows that 30% missing alleles produces fate map topologies that are, on average, as accurate as those produced with 20% allele switching. Additionally, panel B shows that the effect of allele switching on commitment times is the most drastic, with 10% allele switching producing, on average, as much error as 50% missing alleles. Overall, commitment times show the highest sensitivity to experimental error. For example, 5% allele dropout led to a 3%, 3%, and 7% error increase in average topology, population size, and commitment bias estimates respectively but a 21% error increase in average commitment time estimates. Similarly, 5% allele switching led to a 3%, 6%, and 16% error increase in average topology, population size, and commitment bias estimates respectively but a 53% error increase in average commitment time estimates. These observations suggest that missing alleles can bias branch lengths in the time-scaled phylogeny generated by Phylotime. These results further suggest that while the accuracy of estimates declines with increasing experimental error, quantitative fate mapping algorithms can tolerate errors and behave stably in response.
(E) An example quantitative fate map showing how the panel of 16-type quantitative fate maps were sampled at five points in time, representing scenarios wherein a progenitor field is studied by obtaining its descendant cell types immediately after its development or later. Phylogeny and barcoding with 50 hgRNAs were simulated for all 16-terminal type fate maps in the panel in Figure 1C while sampling 100 cells from each terminal type at day 11.5, 12.5, 13.5, 14.5, or 15.5 of development, repeating each condition twice (53 fate maps × 2 sampling strategies × 2 repeats). Phylotime and ICE-FASE were then applied to obtain a quantitative fate map in each case.
(F–I) Line graphs showing the performance of quantitative fate map reconstruction from lineage barcodes as a function of sampling time in our panel of 16-terminal type fate maps for proportional (green) and fixed (blue) sampling strategies, measured by the error of topology (F), commitment (cmt) time (G), population (pop) size (H), and cmt bias (I) estimates. Mean±SEM is shown. Panels F and H indicate that the accuracy of topology and progenitor state population size estimates remain unchanged in all sampling times. Panel I shows that the accuracy of commitment bias estimates remain independent of sampling time only under fixed sampling but deteriorated under proportional sampling. This degradation in proportional sampling is expected because this sampling strategy gains additional information about the commitment bias of undersampled progenitor states from their terminal population sizes (Figures 3L and 5B). However, with terminal types proliferating at different rates, this information decays over time, and unless the progenitor states are well-sampled, proportional sampling gradually loses its inherent advantage. Panel G shows that the accuracy of commitment time estimates deteriorated for both fixed and proportional sampling.
(J–M) Line graphs showing the performance of quantitative fate map reconstruction from true phylogeny as a function of sampling time in our panel of 16-terminal type fate maps for proportional (green) and fixed (blue) sampling strategies, measured by the error of topology (J), commitment (cmt) time (K), population (pop) size (L), and cmt bias (M) estimates. Mean±SEM is shown. When compared with panel G, panel K suggests that time estimate errors when using inferred phylogeny are due to the accumulation of mutations after final commitment as these estimates stay steady when using true phylogeny. Such mutations—that is those that occur after commitment—would not inform cell fate but can affect Phylotime’s estimates of branch length and thus alter time estimates derived from cell phylogeny, especially when barcode homoplasy is prevalent (i.e., same allele independently emerging in two cells). Therefore, the error observed when using inferred phylogeny is a barcoding artifact. Surprisingly however, while progenitor population size and commitment bias estimates depend on commitment time, they do not deteriorate in accuracy, as shown by panels H and I, even when this barcoding artifact results in a large error in commitment time estimates. This observation indicates that the barcoding artifact leads to isometric stretching or shrinking of the phylogenetic tree, biasing the absolute times of commitment but not the relative times of commitment. Taken together, panels F–M suggest that quantitative fate mapping is robust to sampling time. In other words, a progenitor field may be assessed by sampling its terminal cell types or the descendants of those terminal cell types at any point in time. However, with more elapsed time, barcoding artifacts can accumulate and reduce the accuracy of absolute commitment time estimates without affecting the relative commitment time estimates. Moreover, these results show that once the fate of a progenitor state is recorded in the mutations it accumulates, that information may be recovered at any later point in time.
(N) An example quantitative fate map highlighting the progenitor states (orange) and terminal types (blue) in which an increasing level of cell death was tested. Increased cell death probability was instituted for all fate maps with 16 terminal types. One experiment with 50 hgRNAs that collects 100 cells was conducted per fate map. Cell death probability per division was set between 0.1 to 0.4 with 0.05 increments for either all terminal types or all progenitor states with at least 500 cells at their times of commitment. Phylogenies and barcoding outcomes were then simulated and Phylotime and ICE-FASE were applied to reconstruct fate maps in each case.
(O–S) Line graphs showing the performance of quantitative fate map reconstruction as a function of cell death rate in progenitor state (orange) or terminal type (blue) in our panel of 16-terminal type fate maps, measured by the error of topology (O), commitment (cmt) time (P), population (pop) size (Q), and cmt bias (R) estimates. Mean±SEM is shown. The blue lines show that increasing rates of cell death in terminal types from 10% to 40% has a relatively small effect on reconstruction accuracy, leading to an increase in estimation error for topology (KC0 difference of 1.4) and commitment bias error (0.03 difference in RMSE) without any significant effect on commitment time and population size. This result suggests that a non-random subsample of a terminal type’s downstream populations may still be used to analyze its progenitor’s fate (e.g., progenitors of ectoderm, which leads to surface ectoderm and neuroectoderm, may be analyzed by sampling only surface ectoderm and assuming all neuroectoderm cells underwent death). The orange lines show that increasing cell death in progenitor states consistently reduce error of commitment time (45% when comparing 0.1 to 0.4 death probability; Wilcoxon p-value < 0.01), population size (150%; Wilcoxon p-value < 0.01), and commitment bias estimates (16%; Wilcoxon p-value < 0.01)
(S) Line graph showing the fraction of undersampled progenitor states (sampling fraction < 0.25) as a function of increasing cell death rate in progenitor states (orange) or terminal types (blue). Mean±SEM is shown. The graph shows that cell death in progenitor states, which reduces their population size, effectively increases their sampling fraction and reduces the prevalence of undersampled progenitor states. Panels O–S combined suggest that cell death in progenitor states allows the limited sampling power to be distributed among cell divisions with actual fate implications. By contrast, cell death in the terminal types distributes more sampling power to cell divisions after the last cell fate commitment which do not contain fate information. Cell death, as simulated here, is effectively a form of non-random sampling where progenitor cells that are dead can be thought of as having committed to lineages that are not subject to sampling. Therefore, these observations also suggest that designing sampling approaches that strategically bottleneck the effective progenitor population size (e.g., sampling only one side in a bilaterally symmetric system) can help overcome challenges associated with large progenitor populations and lead to more accurate estimates of fate.
(T) Topology of the quantitative fate map in which commitment via symmetric and asymmetric divisions were compared. Phylogeny and barcoding outcomes were simulated for this fate map with commitments happening with either asymmetric divisions or symmetric divisions exclusively. For the asymmetric mode, one daughter cell commits to the downstream terminal type and the other commits to the downstream progenitor state after commitment. For the symmetric mode, each cell randomly commits to one of the downstream fates based predefined probabilities and subsequently undergoes symmetric divisions. In each case, one hundred experiments with 50 hgRNAs and 50 cells sampled from each terminal type were simulated. Phylotime and ICE-FASE were then applied to obtain quantitative fate maps in each case.
(U,V) Example of simulated phylogenetic tree for 50 cells sampled from each terminal cell type in T when commitments take place exclusively with symmetric (U) or asymmetric (V) divisions. (W–Z) Boxplots comparing the performance of reconstruction for the quantitative fate map in T in 100 simulated experiments with either symmetric or asymmetric commitments, measured by the error of topology (W), commitment (cmt) time (X), population (pop) size (Y), and cmt bias (Z) estimates. Wilcoxon rank-sum p-values are shown: *** p < 0.001. The plots show that commitment via asymmetric division results in a significantly more accurate reconstruction of fate map topology as well as progenitor commitment time and population size. For example, topology is perfectly resolved 20% of times with asymmetric division commitments but only 5% of time with symmetric commitment. However, panel Z shows that asymmetric divisions lead to an increase in average commitment bias error from 0.15 to 0.21. The improvement in topology, commitment time, and population size estimates can be attributed to the fact that all commitments via asymmetric division result in FASEs in the phylogeny. In comparison, only a fraction of commitments via symmetric division by chance result in FASEs in the phylogeny. Overall, these results indicate that quantitative fate mapping is applicable to asymmetric cell divisions and that fate mapping is facilitated when more cell divisions are associated with fate decisions. Commitment bias estimate error, unlike all the others, is smaller for symmetric versus asymmetric division. This decline in the accuracy of commitment bias estimates is attributable to a reduction in sampling fraction when commitments take place via asymmetric divisions. The commitment bias estimate is affected by how many cells are sampled on each side of a bifurcation in the fate map topology, skewing the estimate towards the side with more cells sampled. In the case of fixed sampling on a pectinate topology, as simulated here, the imbalance of sampling is very large, particularly for earlier commitments. For example, in a 16-terminal type pectinate fate map, the first bifurcation has 15 times fewer cells sampled on the side committing to a terminal cell type compared to the other. When the sampling fraction is low, progenitor states are affected to a greater extent by such imbalances, and when cells are committing via asymmetric division, the sampling fraction is lower compared to committing via symmetric division due to the fact that the effective commitment time of asymmetric divisions is later than that of the symmetric counterpart (STAR Methods—Definition of commitment time). To validate this hypothesis, we defined a new parameter based on the true simulated phylogeny: sampled commitment bias, which is the proportion of sampled cells in a progenitor state that commit to each downstream fate. When we compared the estimated commitment bias to the sampled commitment bias instead of the progenitor state commitment bias, the simulated experiments with asymmetric divisions showed a better agreement. In fact, the RMSE of commitment bias compared to sampled commitment bias was smaller for the asymmetric division by 15% (Wilcoxon rank-sum test p-value = 2.3e–10). These observations indicate that specific structure of a pectinate topology, which leads to a large difference between true commitment bias and sampled commitment bias, combined with the lower effective progenitor state sampling fraction in asymmetrically committing progenitor states, underlies the smaller commitment bias estimate error for symmetric commitments compared to asymmetric commitments as observed in panel Z here.
Figure S6. Effect of commitment over an extended time period and progenitor trifurcation on quantitative fate map reconstruction.
Related to Figure 5.
(A) Graph showing the quantitative fate map in which commitment over a more extended time period was modeled for P11. Three fate maps with the topology displayed here and identical in all but one parameter were created. The only difference is that P11 (elongated green rectangle) commits to its downstream states (P1 and P9) between day 5.8 and 6.3 in the first map, between day 5.8 and 6.9 in the second map, and between 5.8 and 7.5 days in the third map. Phylogenies and barcoding with 50 hgRNAs were then simulated based on these fate maps with fixed sampling of 100 cells from each terminal with one hundred times for each. Phylotime followed by the ICE-FASE algorithm were then applied to reconstruct topology in each case.
(B) Line graph showing the performance of quantitative fate map topology reconstruction from lineage barcodes using ICE-FASE algorithm as a function of the length of P11’s commitment window in the fate map shown in A. This panels shows that reconstructing the topology of the fate map incurs a small but significant decline with the longest commitment window.
(C–E) Line graphs showing the error of commitment (cmt) time (C), population (pop) size (D), and cmt bias (E) estimates for progenitor states P1 (red), P9 (purple), P11 (green), and P13 (cyan) as a function of the length of P11’s commitment window in the fate map shown in A. P1, P9, and P13 are all the downstream and upstream progenitor states of P11 in the fate map. Mean±SEM is shown but SEM is too small to be visible for some data points. The error for estimating the quantitative parameters for P11 and its upstream and downstream states (P1, P9, and P13) remains generally consistent irrespective of the length of its commitment window. These results indicate that the ICE-FASE algorithm can resolve progenitor states that gradually commit over a window of time.
(F) A pair of quantitative fate maps that are identical except that in one (left) progenitor state P11 undergoes two bifurcations before generating T1, P5, and P6 and in the other (right) the equivalent progenitor state P11* undergoes a trifurcation before generating T1, P5, and P6. In each case, one hundred experiments with 50 hgRNAs and 100 cells sampled from each terminal type were simulated. All progenitor states in both maps are labeled, only terminal types relevant to the rest of the analysis are labeled (T1–T9).
(G) Example (2 out of 200) quantitative fate maps reconstructed using ICE-FASE from lineage barcodes that were simulated for each original quantitative fate map in panel F, one based on the original fully bifurcating map (left) and the other based on the original map with a trifurcation (right). The edge between inferred progenitor states iP11 and iP8 is labeled in magenta for the resolved bifurcation (left) and in green for the resolved trifurcation (right). Only the relevant terminal types are labeled. Similar to example shown on left, P11 and P8 were perfectly resolved in all 100 experiments with a bifurcating fate map, similar to the map on the left. For maps in experiments with trifurcation, because the standard ICE-FASE algorithm reconstructs topologies based on hierarchical clustering of pairwise FASE distances, it is expected to resolve the P11* trifurcation as two consecutive bifurcating inferred progenitor states in fate map topology. If correctly resolved, the first (i.e., more potent, and upstream) inferred progenitor state replacing P11* should have an observed fate of {T1, T2, T3, T4, T5}, and the second (i.e., less potent, and downstream) should have an observed fate of {T1, T2, T3}, {T2, T3, T4, T5}, or {T1, T4, T5}. Such a set of bifurcating progenitor states can be considered an equivalent encoding of the original trifurcation as two bifurcations. By these criteria, the ICE-FASE algorithm correctly resolved the trifurcation as two bifurcations in all 100 simulated experiments, similar to the example shown on the right. The two consecutive inferred progenitor states that ICE-FASE resolves in place of P11* are labeled as iP11 and iP8. Note that equivalents of iP11 and iP8 exist in the reconstructed fully bifurcating map, representing P11 and P8, respectively in panel F left. These results suggest that the ICE-FASE algorithm can resolve multifurcations in fate map topology as consecutive bifurcations.
(H) Boxplots showing the distribution of resolved iP8–iP11 edge lengths and all the other edge lengths in the 100 quantitative fate maps reconstructed from barcoding results simulated based on the fully bifurcating original map (left) or the map with P11* trifurcation (right). Dashed line signifies the 0.45 days cutoff applied for merging bifurcation in the ensuing steps. Boxplot features identical to Figure S1D. P-values from Wilcoxon rank-sum test: *** p <0.001. In actual trifurcations, state transitions into each of three downstream fates happen simultaneously. As a result, the consecutive candidate bifurcations that encode a trifurcation should have a very short edge length between them. These plots show that the edge lengths between iP11 and iP8 in reconstructed trifurcating maps are indeed significantly smaller than those in bifurcating ones. Moreover, they show that the edge lengths between iP11 and iP8 in reconstructed trifurcating maps were significantly smaller than all the other edge lengths in those same maps. These observations suggest that an edge length cutoff, defined as a minimum commitment time difference between two consecutive progenitor states, can be selected to merge close commitment events that are better considered as a single multifurcation than multiple bifurcations. Accordingly, a cutoff of 0.45 days was chosen here.
(I) Reconstructed quantitative fate maps in panel G after applying a 0.45 day cutoff for merging close edge lengths. For the 200 experiments simulated as described in panel F, a threshold of 0.45 days was applied to merge shorter bifurcations into multifurcations. In resulting reconstructed fate maps, a trifurcating inferred progenitor state (iP11*) matching P11* emerged in 87% of all the experiments simulated with a trifurcation, one of which is shown in this panel on the right. In comparison, only 1% of the iP11 became a trifurcation by these criteria in the bifurcating fate map (not shown). However, across all 200 experiments, 0.93 other trifurcations, on average, were created per experiment. These falsely identified trifurcations tend to involve progenitor states with close commitments or low sampling fractions. For example, the falsely identified trifurcations included inferred progenitor states with the same potency as P9, P14, or P12 respectively for 51%, 23%, or 9% of all simulated experiments, as shown in the map on the left. These progenitor states have larger uncertainties associated with them due to their transient nature or low sampling fraction. As such resolving them as trifurcations may represent a more conservative reconstruction of the fate map topology. These results suggest that the ICE-FASE algorithm can correctly resolve multifurcations in fate map topology given adequate sampling fraction and the selection of an appropriate cutoff. These results further show that progenitor state multifurcation can be resolved as multifurcations instead of an equivalent set of bifurcations.
(J,K) Histograms showing the distribution of iP11 or iP11* commitment time (J) and populations size (K) in the 100 experiments simulated based on a bifurcating P11 (top) and the 100 simulated based on a trifurcating P11* (bottom). Solid vertical line marks the true value from the original quantitative fate map in panel F; Dashed vertical line marks the mean of the values estimated from the 100 simulated experiments. ICE-FASE algorithm was expanded to handle multifurcations in fate map topology and applied to estimate iP11* from the 100 experiments simulated with the trifurcating P11* (STAR Methods). For comparison, ICE-FASE was also applied to obtain the same parameters for iP11 from the 100 experiments simulated with the bifurcating P11.
(L) Stacked bar plots showing the estimated fraction of each downstream state or type that P11 commits to in the 100 experiments simulated based on a bifurcating P11 (top) or P11* commits to in the 100 experiments simulated based on a trifurcating P11* (bottom). Bar colors match the downstream state as labeled to the right of each plot. Solid horizontal line marks the true value from the original quantitative fate map in panel F; Dashed horizontal line marks the mean of the values estimated from the 100 simulated experiments. Experimental details same as panels J and K. Together, panels J–L show that that the ICE algorithm can resolve the quantitative parameters of the trifurcating iP11* almost as well as the bifurcating iP11. The RMSE for commitment time, population size, and commitment bias of trifurcating iP11* were 0.18 days, 0.08, and 0.07 respectively, whereas they were 0.07 days, 0.04, and 0.07 respectively for the bifurcating version. These results show that the ICE-FASE algorithm can properly estimate progenitor state dynamics for multifurcating progenitor states. Combined together, the results in this section show that the ICE-FASE algorithm is robust to progenitor state multifurcations and can fully resolve them given adequate sampling fraction.
Figure S7. Features of the barcoding iPSC line and experiments with known barcoding parameters.
Related to Figure 7.
(A) Mutated fraction of each hgRNA over time in the iPSC line after induction of Cas9 expression with Doxycycline. Color of each line shows the estimated mutation rate of its corresponding hgRNA according to the key on bottom right. The list on the right shows the color of each hgRNA’s line on the plot.
(B) Cell division rates and progenitor population sizes in the ground truth fate maps for the E1 and E2 experiments. Numbers on the top right corner of each progenitor state show its total population size estimated from bright field images shown in C. Numbers on the bottom of each terminal type show its estimated population size from bright field images. The estimated doubling times, which represent cell division rates based on measured population sizes at different times are shown on the top right of each map.
(C) Bright field images showing the P3, P4, and P5 progenitor population size estimates (columns) for E1 and E2 (rows). Scale bars for P5 images are 200 microns. Scale bars for P4 and P3 images are 400 microns.
(D) Boxplots showing the number of hgRNAs detected (out of the total 32) from analyzed single cells from each terminal well of each experiment. Line marks the median and whiskers extend to the furthest data point within 1.5 times the interquartile range.
(E) Histogram of the fraction of cells in which each of the 32 hgRNAs was detected.
(F) Character matrices of lineage barcodes (left) and heatmaps of pairwise time since MRCA matrix from simulated single cells in E1 (top) and E2 (bottom) are shown. The simulation includes 140 cells for each terminal type. For each hgRNA, the same level of allele dropout as in the read data was applied to the simulated data. Only one of 100 simulation results is shows for each experiment. Phylotime-reconstructed phylogeny is shown aligned to the left. The type of each cell is marked on the bar to the left of the phylogram and the color code is according to panel B. Other plot features are the same as Figures 4C,D.
(G) Barplots showing the prevalence of different outcomes of topology and commitment order reconstruction from experimental data (left) and simulated data (right) for E1 (top) and E2 (bottom) as a function of number of cells sampled per terminal type. Color key on the bottom shows the reconstruction outcome. “Wrong topology” indicates a wrong tree shape (KC0 > 0 between implemented and reconstructed fate map); “wrong ordering” indicates correct topology (KC0 = 0 between implemented and reconstructed fate map) but the wrong order of commitment times excluding those involving wrong order for P1 and P2 as well as P3 and P4 which are included in the other four conditions in the color key.
(H,I) Boxplots comparing estimates of commitment time (H) and population size (I) in actual experiments (teal) and simulations (ruby) for P3 and P4 to the truth as a function of number of cells sampled per terminal type. Yellow lines or boxes mark the ground truth.
Figure S8. Using shuffling to generate random ordering of commitment events, defining commitment window, and imputing missing data using machine learning.
Related to STAR Methods.
(A) Illustration of two random shufflings at the root bifurcation of the tree. All solid circles are interchangeable and all hollow circles are interchangeable. A shuffling is a random ordering of solid and hollow circles. Reproduced with permission from Ford et al.44.
(B) Illustration comparing commitment by symmetric division to commitment by asymmetric division. For symmetric division, all cells at t2 randomly give rise to two red cells or two blue cells, with each color representing a downstream state. For asymmetric division, all cells give rise to one blue cell and one red cell. Green cells with red outlines are the observed FASEs.
(C) Schematic detailing imputation strategy for missing alleles. Barcoding sites are sorted from those missing in fewest cells (site #1 in this example) to those missing in most cells (site #5 in this example). Missing alleles (grey) are imputed from site #1 to site #5 (missing in most cells) sequentially. Imputation is illustrated for site #1 to the right where cells for which site #1 is observed are used to train the model.
Cumulative lineage barcodes record developmental dynamics
Phylotime infers time-scaled cell phylogenies from lineage barcodes
ICE-FASE reconstructs progenitor hierarchy and dynamics from time-scaled phylogenies
Progenitor State Coverage (PScov) measures the robustness of fate map inferences
Acknowledgments
The authors would like to acknowledge Kian Kalhor, Dr. Yuxin Zhu, Dr. Justus Kebschull, and Dr. Loyal Goff for comments on the manuscript. This work was supported by grants from the Simons Foundation (SFARI 606178, R.K.) and the National Institutes of Health (NIH) (U01HL156056, R.K.; R01HG012357, R.K.; R01HG009518, H.J.; R01HG010889, H.J.; P30EY001765, D.J.Z.; F31EY030769, C.M.B.) and the David & Lucile Packard Foundation (2020-71380, R.K.). Computation was carried out at the Advanced Research Computing at Hopkins (ARCH), supported by the National Science Foundation (NSF) (OAC1920103). D.J.Z. is supported by Research to Prevent Blindness and the Guerrieri Family Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing financial interests.
References
- 1.Stadler T, Pybus OG, and Stumpf MPH (2021). Phylodynamics for cell biologists. Science 371, eaah6266. 10.1126/science.aah6266. [DOI] [PubMed] [Google Scholar]
- 2.Alemany A, Florescu M, Baron CS, Peterson-Maduro J, and van Oudenaarden A (2018). Whole-organism clone tracing using single-cell sequencing. Nature 556, 108–112. 10.1038/nature25969. [DOI] [PubMed] [Google Scholar]
- 3.McKenna A, Findlay GM, Gagnon JA, Horwitz MS, Schier AF, and Shendure J (2016). Whole-organism lineage tracing by combinatorial and cumulative genome editing. Science 353, aaf7907. 10.1126/science.aaf7907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Spanjaard B, Hu B, Mitic N, Olivares-Chauvet P, Janjuha S, Ninov N, and Junker JP (2018). Simultaneous lineage tracing and cell-type identification using CRISPR-Cas9-induced genetic scars. Nat. Biotechnol 36, 469–473. 10.1038/nbt.4124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kalhor R, Kalhor K, Mejia L, Leeper K, Graveline A, Mali P, and Church GM (2018). Developmental barcoding of whole mouse via homing CRISPR. Science 361, 927–936. 10.1126/science.aat9804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chan MM, Smith ZD, Grosswendt S, Kretzmer H, Norman TM, Adamson B, Jost M, Quinn JJ, Yang D, Jones MG, et al. (2019). Molecular recording of mammalian embryogenesis. Nature 570, 77–82. 10.1038/s41586-019-1184-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bowling S, Sritharan D, Osorio FG, Nguyen M, Cheung P, Rodriguez-Fraticelli A, Patel S, Yuan W-C, Fujiwara Y, Li BE, et al. (2020). An Engineered CRISPR-Cas9 Mouse Line for Simultaneous Readout of Lineage Histories and Gene Expression Profiles in Single Cells. Cell 181, 1410–1422.e27. 10.1016/j.cell.2020.04.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bizzotto S, Dou Y, Ganz J, Doan RN, Kwon M, Bohrson CL, Kim SN, Bae T, Abyzov A, NIMH Brain Somatic Mosaicism Network, et al. (2021). Landmarks of human embryonic development inscribed in somatic mutations. Science 371, 1249–1253. 10.1126/science.abe1544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Spencer Chapman M, Ranzoni AM, Myers B, Williams N, Coorens THH, Mitchell E, Butler T, Dawson KJ, Hooks Y, Moore L, et al. (2021). Lineage tracing of human development through somatic mutations. Nature 595, 85–90. 10.1038/s41586-021-03548-6. [DOI] [PubMed] [Google Scholar]
- 10.Baron CS, and van Oudenaarden A (2019). Unravelling cellular relationships during development and regeneration using genetic lineage tracing. Nat. Rev. Mol. Cell Biol 20, 753–765. 10.1038/s41580-019-0186-3. [DOI] [PubMed] [Google Scholar]
- 11.Sulston JE, Schierenberg E, White JG, and Thomson JN (1983). The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev. Biol 100, 64–119. [DOI] [PubMed] [Google Scholar]
- 12.Salipante SJ, and Horwitz MS (2006). Phylogenetic fate mapping. Proc. Natl. Acad. Sci. U. S. A 103, 5448–5453. 10.1073/pnas.0601265103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wagner DE, and Klein AM (2020). Lineage tracing meets single-cell omics: opportunities and challenges. Nat. Rev. Genet 10.1038/s41576-020-0223-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Coorens THH, Moore L, Robinson PS, Sanghvi R, Christopher J, Hewinson J, Przybilla MJ, Lawson ARJ, Spencer Chapman M, Cagan A, et al. (2021). Extensive phylogenies of human development inferred from somatic mutations. Nature 597, 387–392. 10.1038/s41586-021-03790-y. [DOI] [PubMed] [Google Scholar]
- 15.Weinreb C, and Klein AM (2020). Lineage reconstruction from clonal correlations. Proc. Natl. Acad. Sci. U. S. A 117, 17041–17048. 10.1073/pnas.2000238117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Salvador-Martínez I, Grillo M, Averof M, and Telford MJ (2019). Is it possible to reconstruct an accurate cell lineage using CRISPR recorders? Elife 8. 10.7554/eLife.40292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chor B, and Tuller T (2005). Maximum likelihood of evolutionary trees: hardness and approximation. Bioinformatics 21 Suppl 1, i97–106. 10.1093/bioinformatics/bti1027. [DOI] [PubMed] [Google Scholar]
- 18.Ebisuya M, and Briscoe J (2018). What does time mean in development? Development 145. 10.1242/dev.164368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lui JH, Hansen DV, and Kriegstein AR (2011). Development and evolution of the human neocortex. Cell 146, 18–36. 10.1016/j.cell.2011.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leung CY, and Zernicka-Goetz M (2015). Mapping the journey from totipotency to lineage specification in the mouse embryo. Curr. Opin. Genet. Dev 34, 71–76. 10.1016/j.gde.2015.08.002. [DOI] [PubMed] [Google Scholar]
- 21.Davidson EH (1993). Later embryogenesis: regulatory circuitry in morphogenetic fields. Development 118, 665–690. 10.1242/dev.118.3.665. [DOI] [PubMed] [Google Scholar]
- 22.Shao K-T, and Sokal RR (1990). Tree Balance. Syst. Biol 39, 266–276. 10.2307/2992186. [DOI] [Google Scholar]
- 23.Ciemerych MA, and Sicinski P (2005). Cell cycle in mouse development. Oncogene 24, 2877–2898. 10.1038/sj.onc.1208608. [DOI] [PubMed] [Google Scholar]
- 24.Fabian D, Makarevich AV, Chrenek P, Bukovská A, and Koppel J (2007). Chronological appearance of spontaneous and induced apoptosis during preimplantation development of rabbit and mouse embryos. Theriogenology 68, 1271–1281. 10.1016/j.theriogenology.2007.08.025. [DOI] [PubMed] [Google Scholar]
- 25.Kingman JFC (1982). On the genealogy of large populations. J. Appl. Probab 19, 27–43. DOI: 10.2307/3213548. [DOI] [Google Scholar]
- 26.Kingman JFC (1982). The coalescent. Stoch. Process. their Appl 13, 235–248. 10.1016/0304-4149(82)90011-4. [DOI] [Google Scholar]
- 27.Yang Z (2014). Molecular Evolution: A Statistical Approach (Oxford University Press; ). [Google Scholar]
- 28.Kendall M, and Colijn C (2016). Mapping Phylogenetic Trees to Reveal Distinct Patterns of Evolution. Mol. Biol. Evol 33, 2735–2743. 10.1093/molbev/msw124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kalhor R, Mali P, and Church GM (2017). Rapidly evolving homing CRISPR barcodes. Nat. Methods 14, 195–200. 10.1038/nmeth.4108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Leeper K, Kalhor K, Vernet A, Graveline A, Church GM, Mali P, and Kalhor R (2021). Lineage barcoding in mice with homing CRISPR. Nat. Protoc 16, 2088–2108. 10.1038/s41596-020-00485-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shen MW, Arbab M, Hsu JY, Worstell D, Culbertson SJ, Krabbe O, Cassa CA, Liu DR, Gifford DK, and Sherwood RI (2018). Predictable and precise template-free CRISPR editing of pathogenic variants. Nature 563, 646–651. 10.1038/s41586-018-0686-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Feng J, Dewitt WS 3rd, McKenna A, Simon N, Willis AD, and Matsen FA 4th (2021). ESTIMATION OF CELL LINEAGE TREES BY MAXIMUM-LIKELIHOOD PHYLOGENETICS. Ann. Appl. Stat 15, 343–362. 10.1214/20-aoas1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gong W, Granados AA, Hu J, Jones MG, Raz O, Salvador-Martínez I, Zhang H, Chow K-HK, Kwak I-Y, Retkute R, et al. (2021). Benchmarked approaches for reconstruction of in vitro cell lineages and in silico models of C. elegans and M. musculus developmental trees. Cell Syst. 12, 810–826.e4. 10.1016/j.cels.2021.05.008. [DOI] [PubMed] [Google Scholar]
- 34.Seidel S, and Stadler T (2022). TiDeTree: A Bayesian phylogenetic framework to estimate single-cell trees and population dynamic parameters from genetic lineage tracing data. bioRxiv, 2022.02.14.480422 10.1101/2022.02.14.480422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jones MG, Khodaverdian A, Quinn JJ, Chan MM, Hussmann JA, Wang R, Xu C, Weissman JS, and Yosef N (2020). Inference of single-cell phylogenies from lineage tracing data using Cassiopeia. Genome Biol. 21, 92. 10.1186/s13059-020-02000-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Conradt B (2009). Genetic control of programmed cell death during animal development. Annu. Rev. Genet 43, 493–523. 10.1146/annurev.genet.42.110807.091533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Konstantinides N, Holguera I, Rossi AM, Escobar A, Dudragne L, Chen Y-C, Tran TN, Martínez Jaimes AM, Özel MN, Simon F, et al. (2022). A complete temporal transcription factor series in the fly visual system. Nature 604, 316–322. 10.1038/s41586-022-04564-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hormoz S, Singer ZS, Linton JM, Antebi YE, Shraiman BI, and Elowitz MB (2016). Inferring Cell-State Transition Dynamics from Lineage Trees and Endpoint Single-Cell Measurements. Cell Syst. 3, 419–433.e8. 10.1016/j.cels.2016.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Forrow A, and Schiebinger G (2021). LineageOT is a unified framework for lineage tracing and trajectory inference. Nat. Commun 12, 4940. 10.1038/s41467-021-25133-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yao Z, Liu K, Deng S, and He X (2021). An instantaneous coalescent method insensitive to population structure. J. Genet. Genomics 48, 219–224. 10.1016/j.jgg.2021.03.005. [DOI] [PubMed] [Google Scholar]
- 41.Mittnenzweig M, Mayshar Y, Cheng S, Ben-Yair R, Hadas R, Rais Y, Chomsky E, Reines N, Uzonyi A, Lumerman L, et al. (2021). A single-embryo, single-cell time-resolved model for mouse gastrulation. Cell 184, 2825–2842.e22. 10.1016/j.cell.2021.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cagan A, Baez-Ortega A, Brzozowska N, Abascal F, Coorens THH, Sanders MA, Lawson ARJ, Harvey LMR, Bhosle S, Jones D, et al. (2022). Somatic mutation rates scale with lifespan across mammals. Nature 604. 10.1038/s41586-022-04618-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kojima Y, Tam OH, and Tam PPL (2014). Timing of developmental events in the early mouse embryo. Semin. Cell Dev. Biol 34, 65–75. 10.1016/j.semcdb.2014.06.010. [DOI] [PubMed] [Google Scholar]
- 44.Ford D, Matsen FA, and Stadler T (2009). A method for investigating relative timing information on phylogenetic trees. Syst. Biol 58, 167–183. 10.1093/sysbio/syp018. [DOI] [PubMed] [Google Scholar]
- 45.Eldred KC, Hadyniak SE, Hussey KA, Brenerman B, Zhang P-W, Chamling X, Sluch VM, Welsbie DS, Hattar S, Taylor J, et al. (2018). Thyroid hormone signaling specifies cone subtypes in human retinal organoids. Science 362. 10.1126/science.aau6348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wahlin KJ, Maruotti JA, Sripathi SR, Ball J, Angueyra JM, Kim C, Grebe R, Li W, Jones BW, and Zack DJ (2017). Photoreceptor Outer Segment-like Structures in Long-Term 3D Retinas from Human Pluripotent Stem Cells. Sci. Rep 7, 766. 10.1038/s41598-017-00774-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.González F, Zhu Z, Shi Z-D, Lelli K, Verma N, Li QV, and Huangfu D (2014). An iCRISPR platform for rapid, multiplexable, and inducible genome editing in human pluripotent stem cells. Cell Stem Cell 15, 215–226. 10.1016/j.stem.2014.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Maruotti J, Wahlin K, Gorrell D, Bhutto I, Lutty G, and Zack DJ (2013). A simple and scalable process for the differentiation of retinal pigment epithelium from human pluripotent stem cells. Stem Cells Transl. Med 2, 341–354. 10.5966/sctm.2012-0106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Remeseiro S, Cuadrado A, Gómez-López G, Pisano DG, and Losada A (2012). A unique role of cohesin-SA1 in gene regulation and development. EMBO J. 31, 2090–2102. 10.1038/emboj.2012.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.DeKelver RC, Choi VM, Moehle EA, Paschon DE, Hockemeyer D, Meijsing SH, Sancak Y, Cui X, Steine EJ, Miller JC, et al. (2010). Functional genomics, proteomics, and regulatory DNA analysis in isogenic settings using zinc finger nuclease-driven transgenesis into a safe harbor locus in the human genome. Genome Res. 20, 1133–1142. 10.1101/gr.106773.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schneider CA, Rasband WS, and Eliceiri KW (2012). NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675. 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bhise NS, Wahlin KJ, Zack DJ, and Green JJ (2013). Evaluating the potential of poly(beta-amino ester) nanoparticles for reprogramming human fibroblasts to become induced pluripotent stem cells. Int. J. Nanomedicine 8, 4641–4658. 10.2147/IJN.S53830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Paradis E, and Schliep K (2019). ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35, 526–528. 10.1093/bioinformatics/bty633. [DOI] [PubMed] [Google Scholar]
- 54.Schliep KP (2011). phangorn: phylogenetic analysis in R. Bioinformatics 27, 592–593. 10.1093/bioinformatics/btq706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chen T, and Guestrin C (2016). XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining KDD ‘16. (Association for Computing Machinery; ), pp. 785–794. 10.1145/2939672.2939785. [DOI] [Google Scholar]
- 56.Huttner WB, and Kosodo Y (2005). Symmetric versus asymmetric cell division during neurogenesis in the developing vertebrate central nervous system. Curr. Opin. Cell Biol 17, 648–657. 10.1016/j.ceb.2005.10.005. [DOI] [PubMed] [Google Scholar]
- 57.Fu Y, Sander JD, Reyon D, Cascio VM, and Joung JK (2014). Improving CRISPR-Cas nuclease specificity using truncated guide RNAs. Nat. Biotechnol 32, 279–284. 10.1038/nbt.2808. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Topological diversity and distribution of various parameters in the quantitative fate map panel.
Related to Figure 1.
(A) Principal coordinate analysis of KC0 distances between all fate map pairs in each size category showing the fate maps occupy a broad space of topologies. Only the first two dimensions are plotted. Each dot corresponds to one fate map and its color indicates how the map topology was initially generated based on the key to the right and as described in STAR Methods. TBR: tree bisection and reconnection.
(B) Same as A, except each fate map’s dot is colored based on its Colless imbalance index according to the color key to its right. While Dimension 1 corresponds to imbalance, variation in Dimension 2 suggests that the fate map panel covers other unquantified aspects of topological diversity.
(C) Histograms showing the distribution of Colless index in fate maps of each size category. The histograms show that fate maps in the panel are well-distributed in a wide range of imbalance. For all panels, the 16, 32, and 64 terminal type categories are shown on the left, middle, and right respectively; ‘N’ indicates the number of fate maps in each category. Panels A–C show the topological diversity of the fate map panel. Distribution of various parameters in the quantitative fate map panel.
(D) Distribution of progenitor state commitment times for each fate map size category shown as rank ordered boxplots. For each boxplot, line marks the median and whiskers extend to the furthest data point within 1.5 times the interquartile range.
(E) Distribution of progenitor state commitment bias for all progenitor states in all fate maps shown as a histogram. Commitment biases were drawn from a beta distribution (α = 5, β = 5). However, a requirement was set for each progenitor state to be founded by at least four cells. The peak around 0.5 is a consequence of this requirement which forces small progenitor populations to assume biases closer to 0.5 (e.g., a committing progenitor population splits 4:4 if it has 8 cells in total, it will split 4:5 if it has 9 cells, it will split no more unequally than 4:6 if it has 10 cells in total, and so on).
(F) Plot showing cell doubling time distribution as a function of fate map time. Each black dot represents one progenitor state. Trendline (LOESS) is shown in blue. For a given embryonic time in fate maps, progenitor state doubling times are drawn from a uniform distribution; however, overall division rates become faster during embryogenesis43. Therefore, the underlying distribution for doubling times moves to shorter times as fate maps progress. All divisions before the first commitment, which occurs at day 2.4, proceed at a rate of 0.6 per day. Afterwards, division rates are drawn from uniform distributions as shown.
(G) Distribution of cell division rate for all progenitor states and terminal types in all fate maps shown as a histogram.
(H) Distribution of cell death rates per division for all progenitor states and terminal types in all fate maps shown as a histogram. Cell death probability was set to 0 until day 2.4 and then drawn from a uniform distribution between 0.02 and 0.08. These rates are based on rates reported during mouse embryogenesis24.
(I) Distribution of population size at the time of commitment for all progenitor states in all fate maps shown as a histogram.
(J) Distribution of total cell numbers for all fate maps as a function of time. The blue line signifies the average for all fate maps and the gray lines show each fate map and thus represent the range. Red dots represent the total number of cells in a mouse embryo43, showing general agreement in total number of cells between actual mouse embryogenesis and the fate maps simulated here.
(K) Histogram showing the average number of FASEs detected per pair of terminal types in our panel of 3,310 simulated phylogenies with 100 cells sampled from each terminal cell type. These phylogenies have an average of 4.4 FASEs per pair of terminal cell types.
(L) Scatter plots showing the average time between progenitor state commitment events as a function of imbalance (Colles index) broken down by fate map size, showing more imbalanced maps have commitments that are closer to each other. Blue line shows the fitted linear model.
Figure S2. Generative model of sampled cell phylogeny.
Related to Figure 1 and STAR Methods.
(Step 1) Generating a count graph using forward propagation. Part of the count graph where progenitor state Pi proliferates and commit to downstream states Pj and Pk is shown. Several instances of process 1 (proliferate-only process) and one instance of process 2 (commit and proliferate process) of the count graph are included. Horizontal lines represent time, in between horizontal lines are time windows during which the two processes take place. Different count nodes are listed. The black square node is the default count node. The rounded colored nodes are sub-count nodes. For process 1, the proliferation modes include: D: doubling, N: non-doubling, L: dying and DD: doubled. For process 2, Pi state cells commit to become downstream Pj and Pk state cells, sub-count nodes include Pi-PjPj, Pi-PjPk and Pi-PkPk. Four types of operations on the count nodes are listed in the box on the left labeled “Operations”; input is colored teal and output is colored brown, parameters to each operation are colored black.
(Step 2) Generating sampled terminal and progenitor cells counts using backward propagation. Given the counts of each (sub-)count node from Step 1, sample size for each count node was generated (lemon-colored number after comma in each node) using the four reverse operations shown in the box on the right.
(Step 3a) Reorganizing count graph. The count nodes at each time point were reorganized before phylogeny generation. Two examples of reorganizing process 1 and process 2 were given. Sub-count nodes after reorganization include: C: coalesced, NC: non-coalesced and CI: coalescing for process 1, and Pi-PjPj, Pi-PjPk, Pi-PkPk, Pi-Pj and Pi-Pk for process 2. The count graph after reorganization is given on the right.
(Step 3b) Listing tree nodes in the phylogeny. Sampled cells from different sub-count nodes are listed as ‘tree nodes’. One or two branches are attached to the tree nodes based on the number of cells they give rise to at the next time point. Fill of tree nodes indicate their cell state, and color of outline of tree nodes indicate which sub-count nodes they are from.
(Step 4a) Connecting tree nodes. Cells at each time point were connected randomly to open branches at the previous time point to generate the cell phylogeny.
(Step 4b) Simplifying tree phylogeny. The phylogeny is simplified by deleting nodes that do not give rise to two sampled cells at the next time point.
Figure S3. Accuracy and sources of error in estimating quantitative fate map parameters from time-scaled phylogeny.
(A) Line plot showing FASE distance error as a function of progenitor state sampling fraction for all pairs of terminal types in the panel of 3,310 simulated phylogenies (Mean±SD; N is variable). Dots in the background represent a random sampling of 500 individual values from each set to show the distribution.
(B) Boxplots showing the distribution of sampling fraction as a function of time in the panel of 3,310 simulated phylogenies.
(C) Example phylogenetic subtree, showing how undersampling can lead to FASEs appearing earlier in the tree (pink circles) than they really are (green circles). Gray circles: unsampled cells.
(D) Box plots of fate map topology reconstruction error (KC0) as a function of the average number of cells sampled per terminal type in fixed (left) and proportional (right) sampling schemes in our panel of 16 terminal type fate maps. P-values from Wilcoxon rank-sum test: ** p < 0.01, *** p < 0.001.
(E) Heatmap showing the agreement between inferred states and true states of all internal nodes in the phylogenetic tree shown in Figures 1D and 3A. Each rectangle represents the fraction of all nodes in the phylogenetic tree belonging to the true state shown on the left that were assigned the inferred state on the bottom. These results show that the only observed form of error is assigning a node to a state less potent than its true state.
(F) Histogram of the average accuracy of progenitor state node assignment to internal nodes of the phylogenetic tree across the panel of 3,310 phylogenetic trees showing that, on average, 72.3% of nodes were assigned to the correct progenitor state, the rest were assigned to states with lower potency.
(G) Schematic example of a phylogenetic tree, showing how undersampling can lead to a node being assigned a progenitor state with less potency than its true state.
(H) Scatter plot of population size estimate error for progenitor states as a function of their sampling fraction (top) aligned to a histograms of sampling fraction for all progenitor states in fixed or proportional sampling schemes (bottom). The vertical dashed line shows sampling fraction cutoff of 0.25 for separating well-sampled and undersampled progenitor states. Trendline (LOESS) for the correlation is shown in blue. The plot shows that population size is estimated more accurately for progenitor states that have higher sampling fraction.
(I) Scatter plot of commitment bias estimate error for progenitor states as a function of their sampling fraction (top) aligned to a histogram of sampling fraction for all progenitor states in our panel (bottom). Error is the absolute value of the difference between inferred and true commitment biases. The vertical dashed line shows sampling fraction cutoff of 0.25 for separating well-sampled and undersampled progenitor states. Trendline (LOESS) for the correlation is shown in blue. The plot shows that commitment bias estimate error approaches 0 as sampling fraction approaches 1.
Figure S4. Comparing barcoding outcomes between simulations and MARC1 mice, resolving time-scaled phylogenies, and assessing the effect of barcode site mutation rates.
(A) Heatmap showing the posterior probabilities of mutation rates for all MARC1 hgRNAs. Each row corresponds to one of the 64 active MARC1 hgRNAs and represents its estimated posterior mutation probability according to the color key on the bottom right. The axis and on top of the heatmap show the values of per-day mutation probabilities. The first sidebar to the right of the heatmap marks the initial characterization label of the hgRNA as either fast (green), intermediate (orange), or slow (slate blue)30. The second sidebar marks the origin of the hgRNA as either the PB3 founder (dark navy) or the PB7 founder (purple) mouse30. These values were estimated from published embryonic time course mutation analysis data30, as described in STAR Methods.
(B) Comparison of mutant allele emergence probability estimates of our modified inDelphi algorithm to those estimated from MARC1 mouse embryos by taking either abundance within the embryo when the allele is present (right) or fraction of embryos that present the allele (left). Blue dots represent predicted alleles that were observed in MARC1 embryos, gray ones were predicted by modified inDelphi but not observed in embryos. Alleles observed in embryos but not predicted by inDelphi, which were a small fraction, are not shown. Gray line has intercept 0, and slope 1. These results suggest that our modified inDelphi algorithm can recapitulate the actual distribution of MARC1 hgRNA allele emergence probabilities.
(C) Comparison of the true mutant allele emergence probabilities used for simulation (x-axis) with their average observed fraction in simulated mouse embryos (right) and fraction of simulated embryos that showed the allele (left). The true mutant allele emergence probabilities were obtained from our modified inDelphi algorithm (see STAR Methods). Blue dots represent alleles that were observed in simulated embryos, gray ones were possible in simulation by not observed in simulated embryos. Simulations were conducted 100 times for 9 time points. Gray line has intercept 0, and slope 1. Combined with B, these results show that our simulations of the barcoding process recapitulate the mutant allele emergence patterns in barcode mouse embryos. Together, B and C further show that estimations of allele emergence probability based on allele occurrences across multiple samples outperform average allele fraction in both simulation and MARC1 mouse data.
(D) Line-plots showing the mutated fraction of MARC1 barcoding sites over time in observed (left) and simulated (right) embryos for fast, mid, and slow categories of mutation rates. Means ± SEM are shown. Each barcoding site is colored according to its mutation rate using the color scale on the right. These plots show that the distribution of mutated fractions over the course of embryogenesis agrees between simulated and experimental results for hgRNAs with a range of mutation rates.
(E) Boxplots showing the number of mutant alleles for each MARC1 barcoding site over time in observed (left) and simulated (right) embryos for fast, mid, and slow categories of mutation rates. Each barcoding site is colored according to its mutation rate using the color scale shown in panel D. The boxplots for “observed” column look sparser because some hgRNAs had not segregated to any of the embryos analyzed at a given time point. These plots show that the total number of distinct mutant alleles (i.e. the mutant allele diversity) during embryogenesis were consistent between experiments and simulations.
(F) Line-plots showing the average mutant allele diversity as a function of barcoding site mutation rate for observed (blue) and simulated (purple) embryos. Means ± SEM are shown. These plots show that, similarly in both experimental and simulated results, the diversity of mutated hgRNA alleles increases as the hgRNA mutation rates increase because there are more mutagenesis events; however, at the fastest mutation rates, barcoding sites reach 100% mutated when there are fewer total cells, and the total diversities drop as a result.
(G) Line-plots showing the prevalence of a mutant allele among all mutant alleles as a function of its rank in observed (blue) and simulated (purple) embryos. A rank of one denotes the most abundant allele. Means ± SE are shown. These plots show that the compositions of mutant alleles within embryos agree between simulated and observed embryos because, after ranking all mutant alleles based on their frequencies, alleles of similar rank account for similar percentages of the mutated cells.
(H) The two-cell model. An Illustration of a phylogenetic model with two terminal cells used to estimate their distance since their most recent common ancestor (MRCA). N1 is the MRCA of the two cells. T is time from root to sampling. is the time from root to MRCA.
(I) Scatter plot showing the correlation between the Phylotime-inferred and the true cophenetic distances between all pairs of cells in Figure 4C, showing a high level of agreement between Phylotime-inferred and true cophenetic distances. Black line is y=x.
(J) Lineplots showing the performance of quantitative fate map reconstruction, measured by the error of topology, commitment (cmt) time, population size, and commitment (cmt) bias estimates, as a function of the number of hgRNA barcoding sites and their mutation rates (Mean±SEM; N=3,310; SEM very small). The table to the right shows the average and range of barcoding site mutation rates in each condition. Line colors signify the range and average of barcoding site mutation rates according to the table on the bottom. The mutation rate per cell division was calculated based on the average cell cycle length of 0.45 days (Figure S1F). T on X-axes: value using true phylogeny.
Figure S5. Effect of experimental errors, late sampling, cell death, and asymmetric divisions on quantitative fate mapping.
Related to Figure 5.
(A–D) Line graphs showing the performance of quantitative fate map reconstruction, measured by the error of topology (A), commitment (cmt) time (B), population (pop) size (C), and cmt bias (D) estimates, as a function of allele dropout (green) and allele switching (orange) error levels. Mean±SEM is shown, SEM too small to be seen. The gray dashed line in panel A marks the error of randomly generated fate map topologies. Allele dropout results in when a fraction of barcoding sites not to be detected in each single cell. This form of error is common in experiments where barcoding sites are directly amplified from a single cell’s genome or transcriptome8. Allele switching occurs when an allele from one cell is assigned to another. This form of error can emerge if template switching takes place during barcoding amplification, a possible outcome for synthetic barcoding loci that have a high degree of homology30. Both forms of error steadily degrade the accuracy of quantitative fate mapping; however, allele switching is more detrimental for quantitative fate map reconstruction. For example, panel A shows that 30% missing alleles produces fate map topologies that are, on average, as accurate as those produced with 20% allele switching. Additionally, panel B shows that the effect of allele switching on commitment times is the most drastic, with 10% allele switching producing, on average, as much error as 50% missing alleles. Overall, commitment times show the highest sensitivity to experimental error. For example, 5% allele dropout led to a 3%, 3%, and 7% error increase in average topology, population size, and commitment bias estimates respectively but a 21% error increase in average commitment time estimates. Similarly, 5% allele switching led to a 3%, 6%, and 16% error increase in average topology, population size, and commitment bias estimates respectively but a 53% error increase in average commitment time estimates. These observations suggest that missing alleles can bias branch lengths in the time-scaled phylogeny generated by Phylotime. These results further suggest that while the accuracy of estimates declines with increasing experimental error, quantitative fate mapping algorithms can tolerate errors and behave stably in response.
(E) An example quantitative fate map showing how the panel of 16-type quantitative fate maps were sampled at five points in time, representing scenarios wherein a progenitor field is studied by obtaining its descendant cell types immediately after its development or later. Phylogeny and barcoding with 50 hgRNAs were simulated for all 16-terminal type fate maps in the panel in Figure 1C while sampling 100 cells from each terminal type at day 11.5, 12.5, 13.5, 14.5, or 15.5 of development, repeating each condition twice (53 fate maps × 2 sampling strategies × 2 repeats). Phylotime and ICE-FASE were then applied to obtain a quantitative fate map in each case.
(F–I) Line graphs showing the performance of quantitative fate map reconstruction from lineage barcodes as a function of sampling time in our panel of 16-terminal type fate maps for proportional (green) and fixed (blue) sampling strategies, measured by the error of topology (F), commitment (cmt) time (G), population (pop) size (H), and cmt bias (I) estimates. Mean±SEM is shown. Panels F and H indicate that the accuracy of topology and progenitor state population size estimates remain unchanged in all sampling times. Panel I shows that the accuracy of commitment bias estimates remain independent of sampling time only under fixed sampling but deteriorated under proportional sampling. This degradation in proportional sampling is expected because this sampling strategy gains additional information about the commitment bias of undersampled progenitor states from their terminal population sizes (Figures 3L and 5B). However, with terminal types proliferating at different rates, this information decays over time, and unless the progenitor states are well-sampled, proportional sampling gradually loses its inherent advantage. Panel G shows that the accuracy of commitment time estimates deteriorated for both fixed and proportional sampling.
(J–M) Line graphs showing the performance of quantitative fate map reconstruction from true phylogeny as a function of sampling time in our panel of 16-terminal type fate maps for proportional (green) and fixed (blue) sampling strategies, measured by the error of topology (J), commitment (cmt) time (K), population (pop) size (L), and cmt bias (M) estimates. Mean±SEM is shown. When compared with panel G, panel K suggests that time estimate errors when using inferred phylogeny are due to the accumulation of mutations after final commitment as these estimates stay steady when using true phylogeny. Such mutations—that is those that occur after commitment—would not inform cell fate but can affect Phylotime’s estimates of branch length and thus alter time estimates derived from cell phylogeny, especially when barcode homoplasy is prevalent (i.e., same allele independently emerging in two cells). Therefore, the error observed when using inferred phylogeny is a barcoding artifact. Surprisingly however, while progenitor population size and commitment bias estimates depend on commitment time, they do not deteriorate in accuracy, as shown by panels H and I, even when this barcoding artifact results in a large error in commitment time estimates. This observation indicates that the barcoding artifact leads to isometric stretching or shrinking of the phylogenetic tree, biasing the absolute times of commitment but not the relative times of commitment. Taken together, panels F–M suggest that quantitative fate mapping is robust to sampling time. In other words, a progenitor field may be assessed by sampling its terminal cell types or the descendants of those terminal cell types at any point in time. However, with more elapsed time, barcoding artifacts can accumulate and reduce the accuracy of absolute commitment time estimates without affecting the relative commitment time estimates. Moreover, these results show that once the fate of a progenitor state is recorded in the mutations it accumulates, that information may be recovered at any later point in time.
(N) An example quantitative fate map highlighting the progenitor states (orange) and terminal types (blue) in which an increasing level of cell death was tested. Increased cell death probability was instituted for all fate maps with 16 terminal types. One experiment with 50 hgRNAs that collects 100 cells was conducted per fate map. Cell death probability per division was set between 0.1 to 0.4 with 0.05 increments for either all terminal types or all progenitor states with at least 500 cells at their times of commitment. Phylogenies and barcoding outcomes were then simulated and Phylotime and ICE-FASE were applied to reconstruct fate maps in each case.
(O–S) Line graphs showing the performance of quantitative fate map reconstruction as a function of cell death rate in progenitor state (orange) or terminal type (blue) in our panel of 16-terminal type fate maps, measured by the error of topology (O), commitment (cmt) time (P), population (pop) size (Q), and cmt bias (R) estimates. Mean±SEM is shown. The blue lines show that increasing rates of cell death in terminal types from 10% to 40% has a relatively small effect on reconstruction accuracy, leading to an increase in estimation error for topology (KC0 difference of 1.4) and commitment bias error (0.03 difference in RMSE) without any significant effect on commitment time and population size. This result suggests that a non-random subsample of a terminal type’s downstream populations may still be used to analyze its progenitor’s fate (e.g., progenitors of ectoderm, which leads to surface ectoderm and neuroectoderm, may be analyzed by sampling only surface ectoderm and assuming all neuroectoderm cells underwent death). The orange lines show that increasing cell death in progenitor states consistently reduce error of commitment time (45% when comparing 0.1 to 0.4 death probability; Wilcoxon p-value < 0.01), population size (150%; Wilcoxon p-value < 0.01), and commitment bias estimates (16%; Wilcoxon p-value < 0.01)
(S) Line graph showing the fraction of undersampled progenitor states (sampling fraction < 0.25) as a function of increasing cell death rate in progenitor states (orange) or terminal types (blue). Mean±SEM is shown. The graph shows that cell death in progenitor states, which reduces their population size, effectively increases their sampling fraction and reduces the prevalence of undersampled progenitor states. Panels O–S combined suggest that cell death in progenitor states allows the limited sampling power to be distributed among cell divisions with actual fate implications. By contrast, cell death in the terminal types distributes more sampling power to cell divisions after the last cell fate commitment which do not contain fate information. Cell death, as simulated here, is effectively a form of non-random sampling where progenitor cells that are dead can be thought of as having committed to lineages that are not subject to sampling. Therefore, these observations also suggest that designing sampling approaches that strategically bottleneck the effective progenitor population size (e.g., sampling only one side in a bilaterally symmetric system) can help overcome challenges associated with large progenitor populations and lead to more accurate estimates of fate.
(T) Topology of the quantitative fate map in which commitment via symmetric and asymmetric divisions were compared. Phylogeny and barcoding outcomes were simulated for this fate map with commitments happening with either asymmetric divisions or symmetric divisions exclusively. For the asymmetric mode, one daughter cell commits to the downstream terminal type and the other commits to the downstream progenitor state after commitment. For the symmetric mode, each cell randomly commits to one of the downstream fates based predefined probabilities and subsequently undergoes symmetric divisions. In each case, one hundred experiments with 50 hgRNAs and 50 cells sampled from each terminal type were simulated. Phylotime and ICE-FASE were then applied to obtain quantitative fate maps in each case.
(U,V) Example of simulated phylogenetic tree for 50 cells sampled from each terminal cell type in T when commitments take place exclusively with symmetric (U) or asymmetric (V) divisions. (W–Z) Boxplots comparing the performance of reconstruction for the quantitative fate map in T in 100 simulated experiments with either symmetric or asymmetric commitments, measured by the error of topology (W), commitment (cmt) time (X), population (pop) size (Y), and cmt bias (Z) estimates. Wilcoxon rank-sum p-values are shown: *** p < 0.001. The plots show that commitment via asymmetric division results in a significantly more accurate reconstruction of fate map topology as well as progenitor commitment time and population size. For example, topology is perfectly resolved 20% of times with asymmetric division commitments but only 5% of time with symmetric commitment. However, panel Z shows that asymmetric divisions lead to an increase in average commitment bias error from 0.15 to 0.21. The improvement in topology, commitment time, and population size estimates can be attributed to the fact that all commitments via asymmetric division result in FASEs in the phylogeny. In comparison, only a fraction of commitments via symmetric division by chance result in FASEs in the phylogeny. Overall, these results indicate that quantitative fate mapping is applicable to asymmetric cell divisions and that fate mapping is facilitated when more cell divisions are associated with fate decisions. Commitment bias estimate error, unlike all the others, is smaller for symmetric versus asymmetric division. This decline in the accuracy of commitment bias estimates is attributable to a reduction in sampling fraction when commitments take place via asymmetric divisions. The commitment bias estimate is affected by how many cells are sampled on each side of a bifurcation in the fate map topology, skewing the estimate towards the side with more cells sampled. In the case of fixed sampling on a pectinate topology, as simulated here, the imbalance of sampling is very large, particularly for earlier commitments. For example, in a 16-terminal type pectinate fate map, the first bifurcation has 15 times fewer cells sampled on the side committing to a terminal cell type compared to the other. When the sampling fraction is low, progenitor states are affected to a greater extent by such imbalances, and when cells are committing via asymmetric division, the sampling fraction is lower compared to committing via symmetric division due to the fact that the effective commitment time of asymmetric divisions is later than that of the symmetric counterpart (STAR Methods—Definition of commitment time). To validate this hypothesis, we defined a new parameter based on the true simulated phylogeny: sampled commitment bias, which is the proportion of sampled cells in a progenitor state that commit to each downstream fate. When we compared the estimated commitment bias to the sampled commitment bias instead of the progenitor state commitment bias, the simulated experiments with asymmetric divisions showed a better agreement. In fact, the RMSE of commitment bias compared to sampled commitment bias was smaller for the asymmetric division by 15% (Wilcoxon rank-sum test p-value = 2.3e–10). These observations indicate that specific structure of a pectinate topology, which leads to a large difference between true commitment bias and sampled commitment bias, combined with the lower effective progenitor state sampling fraction in asymmetrically committing progenitor states, underlies the smaller commitment bias estimate error for symmetric commitments compared to asymmetric commitments as observed in panel Z here.
Figure S6. Effect of commitment over an extended time period and progenitor trifurcation on quantitative fate map reconstruction.
Related to Figure 5.
(A) Graph showing the quantitative fate map in which commitment over a more extended time period was modeled for P11. Three fate maps with the topology displayed here and identical in all but one parameter were created. The only difference is that P11 (elongated green rectangle) commits to its downstream states (P1 and P9) between day 5.8 and 6.3 in the first map, between day 5.8 and 6.9 in the second map, and between 5.8 and 7.5 days in the third map. Phylogenies and barcoding with 50 hgRNAs were then simulated based on these fate maps with fixed sampling of 100 cells from each terminal with one hundred times for each. Phylotime followed by the ICE-FASE algorithm were then applied to reconstruct topology in each case.
(B) Line graph showing the performance of quantitative fate map topology reconstruction from lineage barcodes using ICE-FASE algorithm as a function of the length of P11’s commitment window in the fate map shown in A. This panels shows that reconstructing the topology of the fate map incurs a small but significant decline with the longest commitment window.
(C–E) Line graphs showing the error of commitment (cmt) time (C), population (pop) size (D), and cmt bias (E) estimates for progenitor states P1 (red), P9 (purple), P11 (green), and P13 (cyan) as a function of the length of P11’s commitment window in the fate map shown in A. P1, P9, and P13 are all the downstream and upstream progenitor states of P11 in the fate map. Mean±SEM is shown but SEM is too small to be visible for some data points. The error for estimating the quantitative parameters for P11 and its upstream and downstream states (P1, P9, and P13) remains generally consistent irrespective of the length of its commitment window. These results indicate that the ICE-FASE algorithm can resolve progenitor states that gradually commit over a window of time.
(F) A pair of quantitative fate maps that are identical except that in one (left) progenitor state P11 undergoes two bifurcations before generating T1, P5, and P6 and in the other (right) the equivalent progenitor state P11* undergoes a trifurcation before generating T1, P5, and P6. In each case, one hundred experiments with 50 hgRNAs and 100 cells sampled from each terminal type were simulated. All progenitor states in both maps are labeled, only terminal types relevant to the rest of the analysis are labeled (T1–T9).
(G) Example (2 out of 200) quantitative fate maps reconstructed using ICE-FASE from lineage barcodes that were simulated for each original quantitative fate map in panel F, one based on the original fully bifurcating map (left) and the other based on the original map with a trifurcation (right). The edge between inferred progenitor states iP11 and iP8 is labeled in magenta for the resolved bifurcation (left) and in green for the resolved trifurcation (right). Only the relevant terminal types are labeled. Similar to example shown on left, P11 and P8 were perfectly resolved in all 100 experiments with a bifurcating fate map, similar to the map on the left. For maps in experiments with trifurcation, because the standard ICE-FASE algorithm reconstructs topologies based on hierarchical clustering of pairwise FASE distances, it is expected to resolve the P11* trifurcation as two consecutive bifurcating inferred progenitor states in fate map topology. If correctly resolved, the first (i.e., more potent, and upstream) inferred progenitor state replacing P11* should have an observed fate of {T1, T2, T3, T4, T5}, and the second (i.e., less potent, and downstream) should have an observed fate of {T1, T2, T3}, {T2, T3, T4, T5}, or {T1, T4, T5}. Such a set of bifurcating progenitor states can be considered an equivalent encoding of the original trifurcation as two bifurcations. By these criteria, the ICE-FASE algorithm correctly resolved the trifurcation as two bifurcations in all 100 simulated experiments, similar to the example shown on the right. The two consecutive inferred progenitor states that ICE-FASE resolves in place of P11* are labeled as iP11 and iP8. Note that equivalents of iP11 and iP8 exist in the reconstructed fully bifurcating map, representing P11 and P8, respectively in panel F left. These results suggest that the ICE-FASE algorithm can resolve multifurcations in fate map topology as consecutive bifurcations.
(H) Boxplots showing the distribution of resolved iP8–iP11 edge lengths and all the other edge lengths in the 100 quantitative fate maps reconstructed from barcoding results simulated based on the fully bifurcating original map (left) or the map with P11* trifurcation (right). Dashed line signifies the 0.45 days cutoff applied for merging bifurcation in the ensuing steps. Boxplot features identical to Figure S1D. P-values from Wilcoxon rank-sum test: *** p <0.001. In actual trifurcations, state transitions into each of three downstream fates happen simultaneously. As a result, the consecutive candidate bifurcations that encode a trifurcation should have a very short edge length between them. These plots show that the edge lengths between iP11 and iP8 in reconstructed trifurcating maps are indeed significantly smaller than those in bifurcating ones. Moreover, they show that the edge lengths between iP11 and iP8 in reconstructed trifurcating maps were significantly smaller than all the other edge lengths in those same maps. These observations suggest that an edge length cutoff, defined as a minimum commitment time difference between two consecutive progenitor states, can be selected to merge close commitment events that are better considered as a single multifurcation than multiple bifurcations. Accordingly, a cutoff of 0.45 days was chosen here.
(I) Reconstructed quantitative fate maps in panel G after applying a 0.45 day cutoff for merging close edge lengths. For the 200 experiments simulated as described in panel F, a threshold of 0.45 days was applied to merge shorter bifurcations into multifurcations. In resulting reconstructed fate maps, a trifurcating inferred progenitor state (iP11*) matching P11* emerged in 87% of all the experiments simulated with a trifurcation, one of which is shown in this panel on the right. In comparison, only 1% of the iP11 became a trifurcation by these criteria in the bifurcating fate map (not shown). However, across all 200 experiments, 0.93 other trifurcations, on average, were created per experiment. These falsely identified trifurcations tend to involve progenitor states with close commitments or low sampling fractions. For example, the falsely identified trifurcations included inferred progenitor states with the same potency as P9, P14, or P12 respectively for 51%, 23%, or 9% of all simulated experiments, as shown in the map on the left. These progenitor states have larger uncertainties associated with them due to their transient nature or low sampling fraction. As such resolving them as trifurcations may represent a more conservative reconstruction of the fate map topology. These results suggest that the ICE-FASE algorithm can correctly resolve multifurcations in fate map topology given adequate sampling fraction and the selection of an appropriate cutoff. These results further show that progenitor state multifurcation can be resolved as multifurcations instead of an equivalent set of bifurcations.
(J,K) Histograms showing the distribution of iP11 or iP11* commitment time (J) and populations size (K) in the 100 experiments simulated based on a bifurcating P11 (top) and the 100 simulated based on a trifurcating P11* (bottom). Solid vertical line marks the true value from the original quantitative fate map in panel F; Dashed vertical line marks the mean of the values estimated from the 100 simulated experiments. ICE-FASE algorithm was expanded to handle multifurcations in fate map topology and applied to estimate iP11* from the 100 experiments simulated with the trifurcating P11* (STAR Methods). For comparison, ICE-FASE was also applied to obtain the same parameters for iP11 from the 100 experiments simulated with the bifurcating P11.
(L) Stacked bar plots showing the estimated fraction of each downstream state or type that P11 commits to in the 100 experiments simulated based on a bifurcating P11 (top) or P11* commits to in the 100 experiments simulated based on a trifurcating P11* (bottom). Bar colors match the downstream state as labeled to the right of each plot. Solid horizontal line marks the true value from the original quantitative fate map in panel F; Dashed horizontal line marks the mean of the values estimated from the 100 simulated experiments. Experimental details same as panels J and K. Together, panels J–L show that that the ICE algorithm can resolve the quantitative parameters of the trifurcating iP11* almost as well as the bifurcating iP11. The RMSE for commitment time, population size, and commitment bias of trifurcating iP11* were 0.18 days, 0.08, and 0.07 respectively, whereas they were 0.07 days, 0.04, and 0.07 respectively for the bifurcating version. These results show that the ICE-FASE algorithm can properly estimate progenitor state dynamics for multifurcating progenitor states. Combined together, the results in this section show that the ICE-FASE algorithm is robust to progenitor state multifurcations and can fully resolve them given adequate sampling fraction.
Figure S7. Features of the barcoding iPSC line and experiments with known barcoding parameters.
Related to Figure 7.
(A) Mutated fraction of each hgRNA over time in the iPSC line after induction of Cas9 expression with Doxycycline. Color of each line shows the estimated mutation rate of its corresponding hgRNA according to the key on bottom right. The list on the right shows the color of each hgRNA’s line on the plot.
(B) Cell division rates and progenitor population sizes in the ground truth fate maps for the E1 and E2 experiments. Numbers on the top right corner of each progenitor state show its total population size estimated from bright field images shown in C. Numbers on the bottom of each terminal type show its estimated population size from bright field images. The estimated doubling times, which represent cell division rates based on measured population sizes at different times are shown on the top right of each map.
(C) Bright field images showing the P3, P4, and P5 progenitor population size estimates (columns) for E1 and E2 (rows). Scale bars for P5 images are 200 microns. Scale bars for P4 and P3 images are 400 microns.
(D) Boxplots showing the number of hgRNAs detected (out of the total 32) from analyzed single cells from each terminal well of each experiment. Line marks the median and whiskers extend to the furthest data point within 1.5 times the interquartile range.
(E) Histogram of the fraction of cells in which each of the 32 hgRNAs was detected.
(F) Character matrices of lineage barcodes (left) and heatmaps of pairwise time since MRCA matrix from simulated single cells in E1 (top) and E2 (bottom) are shown. The simulation includes 140 cells for each terminal type. For each hgRNA, the same level of allele dropout as in the read data was applied to the simulated data. Only one of 100 simulation results is shows for each experiment. Phylotime-reconstructed phylogeny is shown aligned to the left. The type of each cell is marked on the bar to the left of the phylogram and the color code is according to panel B. Other plot features are the same as Figures 4C,D.
(G) Barplots showing the prevalence of different outcomes of topology and commitment order reconstruction from experimental data (left) and simulated data (right) for E1 (top) and E2 (bottom) as a function of number of cells sampled per terminal type. Color key on the bottom shows the reconstruction outcome. “Wrong topology” indicates a wrong tree shape (KC0 > 0 between implemented and reconstructed fate map); “wrong ordering” indicates correct topology (KC0 = 0 between implemented and reconstructed fate map) but the wrong order of commitment times excluding those involving wrong order for P1 and P2 as well as P3 and P4 which are included in the other four conditions in the color key.
(H,I) Boxplots comparing estimates of commitment time (H) and population size (I) in actual experiments (teal) and simulations (ruby) for P3 and P4 to the truth as a function of number of cells sampled per terminal type. Yellow lines or boxes mark the ground truth.
Figure S8. Using shuffling to generate random ordering of commitment events, defining commitment window, and imputing missing data using machine learning.
Related to STAR Methods.
(A) Illustration of two random shufflings at the root bifurcation of the tree. All solid circles are interchangeable and all hollow circles are interchangeable. A shuffling is a random ordering of solid and hollow circles. Reproduced with permission from Ford et al.44.
(B) Illustration comparing commitment by symmetric division to commitment by asymmetric division. For symmetric division, all cells at t2 randomly give rise to two red cells or two blue cells, with each color representing a downstream state. For asymmetric division, all cells give rise to one blue cell and one red cell. Green cells with red outlines are the observed FASEs.
(C) Schematic detailing imputation strategy for missing alleles. Barcoding sites are sorted from those missing in fewest cells (site #1 in this example) to those missing in most cells (site #5 in this example). Missing alleles (grey) are imputed from site #1 to site #5 (missing in most cells) sequentially. Imputation is illustrated for site #1 to the right where cells for which site #1 is observed are used to train the model.
Data Availability Statement
FASTQ files from sequencing single-cell hgRNA arrays have been deposited at SRA and are publicly available. Accession numbers are listed in the key resources table. All quantitative fate maps, simulated datasets, inDelphi predictions, and Phylotime-reconstructed phylogenies have been deposited on Zenodo. DOIs are listed in the key resources table.
R package for QFM and code to reproduce the results is publicly available at https://github.com/Kalhor-Lab/QFM/ as of the date of publication.
Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
| AAVS1-Neo-M2rtTA | DeKelver et al.50 | Addgene Cat#60843 |
| Chemicals, peptides, and recombinant proteins | ||
| Accutase™ | STEMCELL Technologies |
Cat#07920 |
| Antibiotic-Antimycotic (100X) | ThermoFisher | Cat#15240062 |
| Blasticidin S hydrochloride | MilliporeSigma | Cat#15205 |
| (−)-Blebbistatin | MilliporeSigma | Cat#B0560 |
| CloneR | STEMCELL Technologies |
Cat#05888 |
| Doxycycline hyclate | MilliporeSigma | Cat#D9891 |
| DreamTaq Hot Start PCR Master Mix | ThermoFisher | Cat#K9012 |
| Geneticin™ Selective Antibiotic (G418 Sulfate) | ThermoFisher | Cat#10131035 |
| KAPA HiFi HotStart ReadyMix | Roche | Cat#07958935001 |
| KAPA SYBR FAST qPCR Kits | Roche | Cat#07959389001 |
| Lipofectamine™ Stem Transfection Reagent | ThermoFisher | Cat#STEM00001 |
| Matrigel Growth Factor Reduced Basement Membrane Matrix | Corning | Cat#354230 |
| mTeSR™ Plus | STEMCELL Technologies |
Cat#100–0276 |
| Opti-MEM I Reduced Serum Media | ThermoFisher | Cat#31985062 |
| Pifithrin-α hydrobromide | Tocris Bioscience | Cat#1267 |
| Puromycin dihydrochloride | MilliporeSigma | Cat#P8833 |
| QuickExtract™ DNA Extraction Solution | Lucigen | Cat#QE09050 |
| SYBR Green I Nucleic Acid Gel Stain | ThermoFisher | Cat#S7563 |
| Critical commercial assays | ||
| DNA Clean & Concentrator-5 | Zymo Research | Cat#D4014 |
| MiSeq Reagent Micro Kit v2 (300-cycles) | Illumina | Cat#MS-103–1002 |
| MycoAlert® PLUS Mycoplasma Detection Kit | Lonza | Cat#LT07–701 |
| Qubit dsDNA HS Assay Kit | ThermoFisher | Cat#Q32851 |
| Deposited data | ||
| Single-cell hgRNA sequencing raw FASTQ files for E1 and E2 | This study | SRP386685 |
| MARC1 sequencing data for determining hgRNA mutation rates | Kalhor et al.5
Leeper et al.30 |
SRP155997 |
| All quantitative fate maps | This study | 10.5281/zenodo.7112097 |
| inDelphi predicted mutant allele probabilities for hgRNAs in MARC1 mice and iPSC line | This study | 10.5281/zenodo.7112097 |
| Simulated phylogenies, sets of MARC1 hgRNAs used, single cell lineage barcodes, Phylotime reconstructed phylogenies for all experiments | This study | 10.5281/zenodo.7112097 |
| Experimental models: Cell lines | ||
| iPSC line: EP1-Cas9-hgRNA | This study | N/A |
| Oligonucleotides | ||
| See Table S3 for oligonucleotides used in this study. | This study | N/A |
| Recombinant DNA | ||
| Modified pSpCas9(BB)-2A-Puro (PX459) V2.0 | Eldred et al.45 | N/A |
| Modified Puro-Cas9 donor | Eldred et al.45 | N/A |
| PB-U6insert hgRNA library | Kalhor et al.5 | Addgene Cat#104536 |
| PB-U6insert-EF1puro library | Kalhor et al.5 | Addgene Cat#104537 |
| Super piggyBac Transposase expression vector | System Biosciences | Cat#PB210PA-1 |
| Software and algorithms | ||
| Cassiopeia | Jones et al.35 | https://github.com/YosefLab/Cassiopeia |
| ICE-FASE | This study |
https://github.com/Kalhor-Lab/QFM/ DOI: 10.5281/zenodo.7114804 |
| ImageJ | Schneider et al.51 | https://github.com/imagej/ImageJ |
| InDelphi | Shen et al.31 | https://github.com/rnaxwshen/inDelphi-model |
| Phylotime | This study |
https://github.com/Kalhor-Lab/QFM/ DOI: 10.5281/zenodo.7114804 |
| MARC1 analysis pipeline | Leeper et al.30 | https://github.com/Kalhor-Lab/MARC1-Pipeline |
| Other | ||


