The Folding Energy Landscape and Free Energy Excitations of Cytochrome c

Abstract

The covalently bound heme cofactor plays a dominant role in the folding of cytochrome c. Due to the complicated inorganic chemistry of the heme, some might consider the folding of cytochrome c to be a special case that follows different principles than those used to describe folding of proteins without cofactors. Recent investigations, however, demonstrate that models which are commonly used to describe folding for many proteins work well for cytochrome c when heme is explicitly introduced and generally provide results that agree with experimental observations. We will first discuss results from simple native structure-based models. These models include attractive interactions between nonadjacent residues only if they are present in the crystal structure at pH 7. Since attractive nonnative contacts are not included in native structure-based models, their energy landscapes can be described as “perfectly funneled.” In other words, native structure-based models are energetically guided towards the native state and contain no energetic traps that would hinder folding. Energetic traps are sources of frustration which cause specific transient intermediates to be populated. Native structure-based models do include repulsion between residues due to excluded volume. Nonenergetic traps can therefore exist if the chain, which cannot cross over itself, must partially unfold in order for folding to proceed. The ability of native structure-based models to capture these type of motions is in part responsible for their successful predictions of folding pathways for many types of proteins. Models without frustration describe well the sequence of folding events for cytochrome c inferred from hydrogen exchange experiments thereby justifying their use as a starting point.

At low pH, the folding sequence of cytochrome c deviates from that at pH 7 and from those predicted from models with perfectly funneled energy landscapes. Alternate folding pathways are a result of “chemical frustration.” This frustration arises because some regions of the protein are destabilized more than others due to the heterogeneous distribution of titratable residues that are protonated at low pH. We construct more complex models that include chemical frustration, in addition to the native structure-based terms. These more complex models only modestly perturb the energy landscape which remains overall well funneled. These perturbed models can accurately describe how alternative folding pathways are used at low pH. At alkaline pH, cytochrome c populates distinctly different structural ensembles. For instance, lysine residues are deprotonated and compete for the heme ligation site. The same models that can describe folding at low pH also predict well the structures and relative stabilities of intermediates populated at alkaline pH.

The folding energy landscape of cytochrome c is particularly interesting because of the effects of its large, covalently bound heme cofactor.^1,2 In fact, the heme is one of the major reasons that cytochrome c has been studied for decades as a model system for protein folding and dynamics.^3–8 The heme molecule serves as a chromophore that is sensitive to conformational transitions of the protein and can therefore be a useful tool in many types of folding experiements. Cytochrome c was used in the first studies that established the notion of a “speed limit” for protein folding^9,10 and was used to jumpstart the “fast folding” field in many kinetic studies.^7,11,12 The heme also plays an important role during folding, not only due to the iron at the heme center which serves as a ligation site for some amino acid side chains, but also because of its large hydrophobic surface. As we will see, the preference of some heme ligands over others can be modulated by changing the experimental solvent conditions, allowing us to probe the system in many interesting ways. With the added complexity of the heme cofactor, some may think that the principles that determine its folding must be unique and different from typical single domain proteins. Cytochrome c folding is indeed more complex than the folding of many proteins without cofactors. Nevertheless, while the inorganic chemistry of ligation must be considered, the general theoretical framework used to explain many different folding phenomena is sufficient in this case.

The folding mechanism of cytochrome c, as first inferred by hydrogen exchange measurements,^13,14 involved the sequential stabilization of five submolecular folding units. Submolecular folding units, introduced as so-called “foldons”, have been described as quasi-independent folders.¹⁵ More recent hydrogen exchange experiments, however, have suggested that the relative stability of the folding units is sensitive to single mutations and solvent changes, which can allow alternate routes in the sequential folding pathway.¹⁶ What types of forces are necessary to describe the dynamics of cytochrome c that gives rise to these alternating sequential folding pathways? To answer this question we must be able to describe the protein’s energy landscape.

Energy landscape theory is a set of principles that determine a variety of protein folding mechanisms.¹⁷ For any given protein, there is a unique energy landscape dependent upon its sequence and structure. The theory states that, for proteins with a well defined native fold, the energy landscape must have an energy gap between closely related native structures and the unfolded, molten globule structures. This gap must be sufficiently larger than the energetic variance so that it is easy to overcome barriers needed for a protein to escape from one conformation and to sample a different conformation. The energy landscape of foldable proteins guides the random motions of the protein towards the native structure and therefore such landscapes are described as “funneled.” Funneled landscapes are said to be “minimally frustrated” because there are few alternate configurations that can act as traps in the landscape caused by attractive nonnative contacts.¹⁷ Theories based on funneled energy landscapes, through the use of free energy functionals, have successfully predicted folding routes for a variety of proteins.^18–21 Free energy functionals can be based on well defined analysis of the polymer statistical mechanics. Free energy functional calculations give precise numerical answers but are only approximate due to simplifying assumptions that go into such theories. Algorithms based on simple free energy functionals can miss alternative folding pathways. Variational methods, also based on analytical treatments, can be implemented to better account for chain entropy thus allowing a more complete survey of the multiple folding pathways that are accessible.²² Simulations use Newton’s equations of motion to model protein dynamics but often employ coarse-grained models. Software to run simulations is readily available so that such calculations are much more common than calculations based on analytical formalisms. Simulations based on native structure-based models are commonly used to predict folding routes and mechanisms.^23–27 These models only include interactions between residues if they are adjacent in the crystal structure. Because native structure-based models do not include attractive nonnative interactions, i.e. interactions not present in the averaged crystal structure, they are described by a perfectly funneled energy landscape. The success of native structure-based models in explaining many details of the folding kinetics in many proteins without cofactors strongly suggests that the funnel plays the dominant role in the folding of many proteins.

In this account, we will first discuss the results from a native structure-based model for the folding of cytochrome c. We will then review the consequences of adding frustration to the energy landscape through nonnative interactions. Particularly strong nonnative interactions can be induced experimentally by changing the solvent conditions, resulting in so called “chemical frustration”. For instance, at alkaline pH lysine residues are deprotonated. This deprotonation not only destabilizes the structure but also allows nonnative lysine misligation to the heme.^28–30 Changing the pH could thus result in a potentially enormous number of chemically distinct species considering that there are about 25 residues in cytochrome c that can deprotonate and a similar number that can misligate. The ensemble of structures nonetheless turns out to be dominated by only a few chemically distinct species. Due to the funneled nature of the energy landscape some conformations are favored and not others.

Folding on a Perfectly Funneled Energy Landscape

A perfectly funneled energy landscape is a zeroth order approximation that allows simple structure-based models, which are based on this concept, to correctly predict a broad range of folding mechanisms.^24–27 This implies that evolution has selected for sequences that fold robustly by ensuring that their energy landscapes contain only a small degree of ruggedness. While energetic frustration arising from nonnative contacts sometimes leads to the population of specific intermediates, structure-based models commonly demonstrate that a rather narrow set of folding routes should be observed and these are determined by fluctuations in the entropy cost of contacts and in the number of stabilizing contacts. One example of a structure-based model is the single memory associative memory Hamiltonian (AMH).^2,31 The AMH code, when more than one structure is used to parameterize the model, can be used for structure prediction.^32,33 The AMH code also includes the nonadditivity of forces caused by neglected degrees of freedom that are not modeled explicitly. Three and higher body interactions lead to cooperativity that arises from averaging over the solvent and from averaging over the side chain degrees of freedom. In both situations, when two residues come together there is a large entropic cost because the side chains and/or the surrounding solvent are no longer as free to move. The entropic cost is less however when a third group comes into contact with both residues because the entropic cost for freezing the side chains of the first two residues has already been taken into account. Therefore the AMH includes an additional free energy contribution that accounts for the decrease in entropic cost for adding the third residue. Consequently the energy is not a sum over pairs but is nonadditive. Including nonadditive interactions has been shown to increase the magnitude of folding free energy barriers^34,35 and to improve the accuracy of predicted folding rates and mechanisms.³⁶ Using reasonable amounts of nonadditivity in the model results in folding barriers that are commensurate with experimental values. To study heme proteins like cytochrome c the model includes an explicit, coarse grained heme with five pseudoatoms arranged in a square planar geometry. Results with this Hamiltonian show that heme has a dominant effect on the folding mechanism.

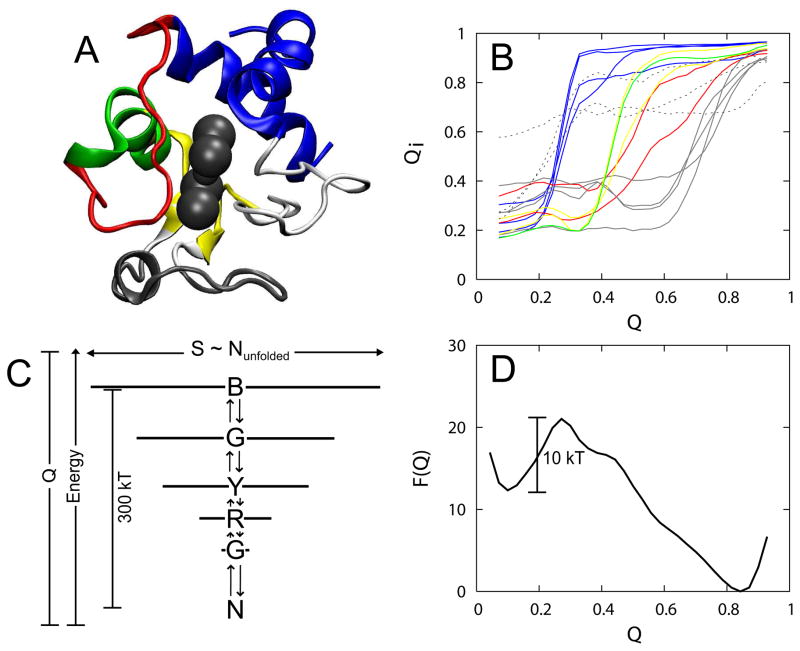
The single memory AMH, utilizing the crystal structure at pH 7, successfully predicts the sequential folding pathway of cytochrome c that has been inferred from hydrogen exchange experiments.² The hydrogen exchange experiments suggested that the folding pathway at pH 7 involves the sequential ordering of five pseudo-independent folding units.¹⁴ These same trends can be resolved in the AMH simulations by monitoring local structure formation as a function of the folding reaction coordinate Q (Figure 1A–B). Q is a distance similarity measure that quantifies the resemblance of the contact pattern of any conformation to that of the native crystal structure. In Figure 1A colors were attributed to the protein structure based on the value of Q corresponding to each individual residue’s folding transition. Folding of cytochrome c involves the sequential stabilization of five pseudo-cooperative substructures: terminal helices (blue), 60’s helix (green), β sheets (yellow), Met80 loop (red), and the 40’s loop (gray). The omega loop colored in white participates in a more ambiguous transition that is not clearly resolved along Q. In this case we can view the topology and chain connectivity as the only source of frustration, because folding is primarily impeded by the lack of secondary structure. The uncooperative folding of this omega loop togther with with nonnative interactions caused by histidine misligation (all of which are contained within the loop) gives rise to energetic frustration that decreases the experimental folding rate by several orders of magnitude.¹

Figure 1.

(A) The structure of cytochrome c colored by folding unit. The folding units are assigned by grouping residues that have a similar folding transition as a function of the folding reaction coordinate Q. (B) The ensemble average of the residue specific reaction coordinate Q_i as a function of the global folding coordinate Q for several residues. Corresponding to the structure in (A), the curves are colored by their assigned folding unit: blue (residues 95, 96, 98, and 99), green (residue 68), yellow (residues 60 and 64), red (residues 74 and 75), and grey (residues 43, 46, and 52). Shown with dashed lines are Q_i curves for several residues in the white omega loop (residues 16 to 33) that cannot be assigned to a folding unit because there is no clear single sigmoidal transition. (C) A representation of the folding funnel that depicts the sequential folding mechanism. Each level shown corresponds to the Q value at which each folding unit unfolds: (from top to bottom) blue, green, yellow, red, grey, and the native basin. The width of each line is proportional to the number of unfolded residues in the ensemble and is proportional to the configurational entropy. (D) Free energy profile as a function of the folding reaction coordinate Q calculated from a simulation of cytochrome c at 20°C.

The fact that a single folding reaction coordinate Q resolves the sequential ordering of cytochrome c demonstrates the importance of the funneled organization of the energy landscape. The global folding energy landscape maybe pictured as a diagram whose width is related to the configurational entropy and whose height corresponds to the energy. On a perfectly funneled energy landscape, such as that produced by a structure-based model, the energy and Q are strongly correlated since the energy from native contacts dominates the potential. Figure 1C shows a representation of the funnel in which discrete energy levels indicates the Q or energy pertaining to the folding transition of a given folding unit. The width of the funnel at each energy level in such a diagram is given by the number of unfolded residues. Since the number of accessible configurations for unfolded residues is much higher than that for folded residues, the width of the funnel in Figure 1C approximates the entropy.

The funnel depicted in Figure 1C shows the dominant sequential folding pathway calculated from an ensemble average of many protein folding trajectories. The same pathway is also observed in most single trajectories (Figure 2A). Prior to the folding transition, the structure of the folding units fluctuates and the units transiently sample native-like structure independently from the other units. Fluctuations in the unfolded ensemble sometimes cause the Q to approach the value expected for the folding transition state (0.3) but unfolding occurs because the folding nucleus has not been realized. Folding proceeds only once the most stable folding unit (N and C terminal helices, colored blue) becomes structured. The remaining structural units build onto the folding nucleus in a roughly sequential manner. Interestingly, even without energetic frustration due to nonnative contacts, misfolding can still occur due to topological problems. Figure 2B shows a single trajectory in which the protein encounters a topological trap that requires the Met80 loop (red) to unfold so that the green and yellow folding units can fold. The partial unfolding of a protein along its folding pathway to overcome topological frustration is called “backtracking”.³⁷ Using a native structure-based model, topological trapping occurs only very rarely for cytochrome c and are therefore completely averaged out in an ensemble averaged calculation.

Figure 2.

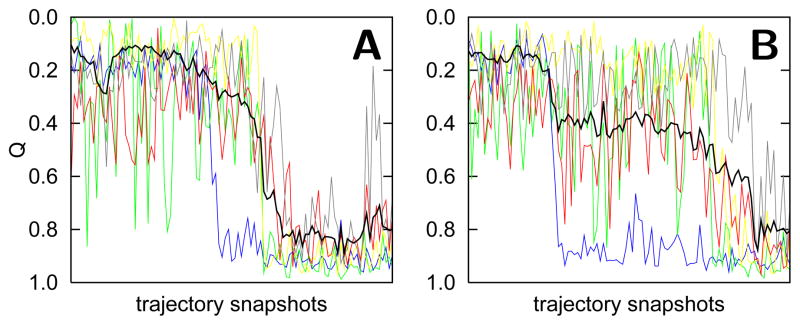
Two folding trajectories using a native structure-based model are shown in 100 snapshot windows. The Q of the entire protein is shown in black, while the Q of each folding unit is shown in blue, green, yellow, red, and grey. The folding trajectory in A shows the dominant type of transition, which occurs greater than 90% of the time. The folding trajectory in B rarely happens.

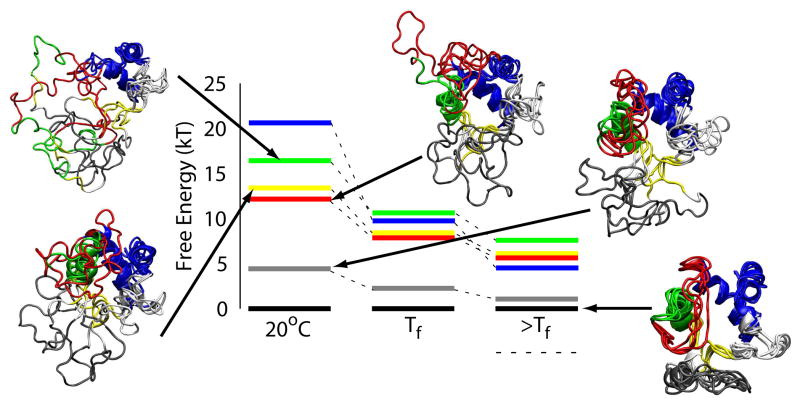
Using statistical mechanics, we can calculate the free energy using structures that represent the entire ensemble. The free energy, which is on the order of tens of kT, is related to the difference of the energy and entropy, each of which is on the order of hundreds of kT (Figure 1C–D). Well below the folding temperature, Q is well correlated with the free energy as well as the energy(Figure 1D). We can therefore simply relate the Q value corresponding to the midpoints for unfolding of local regions (Figure 1B) to the overall folding free energy corresponding to the same Q value. For instance, the stability of the terminal helices with a Q_i unfolding midpoint of 0.3 is about 20 kT. The result is a free energy spectrum (Figure 3) that shows the stability of all the folding units (colored lines) relative to the stability of the native state (black lines). The free energy levels can be directly compared to hydrogen exchange experiments.¹⁴ If the simulation temperature is raised to the folding temperature or higher, the correlation between Q and free energy breaks down and the folding units become degenerate in stability. Increasing temperature provides the same amount of destabilization energy to all the residues thereby destabilizing the structure as a whole. Local perturbations due to single point mutations or pH changes, however, can also give rise to degeneracy of the folding units’ stabilities.¹⁶

Figure 3.

Free energy levels of unfolding calculated from simulations based on a structure-based model at different temperatures. Overlayed structures are shown to represent a typical structural ensembles for each free energy level. Free energy levels are averages of the unfolding free energies for individual residues within a given folding unit. The unfolding free energy is calculated by matching the Q value of the unfolding transition midpoint of a specific residue (Figure 1B) to the Q value corresponding to the overall folding free energy (Figure 1D). The free energy levels and structures are colored to represent the folding units. Above the folding temperature, T_f , the free energy of the unfolded ensemble (horizontal dashed line) is less than that of the native state (black lines).

Folding with Chemical Frustration: pH Effects

Deviations from the sequential folding route of cytochrome c observed at pH 7 occur when the folding energy landscape has been greatly perturbed. Alternative folding routes for cytochrome c have been suggested based on hydrogen exchange experiments at pH 4.5.¹⁶ At acidic pH, some folding units are destabilized more than others thereby causing some degeneracy of the stability for the folding units. These alternative folding routes at acidic pH are caused by “chemical frustration” due to protonation at some amino acid side chains. This protonation disrupts stabilizing interactions that occur in the native structure. The native structural ensemble at pH 7 involves contacts that are optimized for the physiological solvent conditions and the electrostatic environment of titratable residues with their charge at that pH. The local perturbation of changing the charge of the titratable residues promotes structural heterogeneity in the vicinity of the perturbed residues. Models supplemented by nonnative electrostatic and hydrophobic interactions capture the effect of chemical frustration rather accurately. To account for pH effects, the strength of interactions involving protonated side chains is decreased and, in addition, nonnative electrostatic and hydrophobic forces can be included.^38,39 The comparison of the free energy levels between pH 7 and 4 shows that the folding units that are most destabilized also contain the most protonated residues upon decreasing pH (Figure 4). The blue, green, and yellow folding units contain four, two, and two protonated residues respectively. In contrast, the red folding unit, which is hardly destabilized, contains no protonated residues. A similar trend is observed in hydrogen exchange experiments.¹⁶ Long-range electrostatic effects, included in the model using a Coulomb potential, are also important to capture the destabilization of local regions due to protonation. For instance the least stable folding unit (grey) contains no residues that are protonated upon decreasing the pH to 4.5, but is destabilized due to like-charge repulsion of His26 and several protonated residues in the adjacent loop. The predicted magnitude of the destabilization of this least stable folding unit is smaller than what is observed in experiment. This discrepancy reflects the overestimation of the amount of funneled (native) interactions in generally unstable loops. The native structure-based model employs a single, consistent set of interactions to describe loops when in reality these loops are better described by a weaker and more heterogeneous set of contacts than other regions of the protein i.e. they are not minimally frustrated even under native conditions. Consequently the destabilizing electrostatic effects are not sufficiently large to compete with the perfectly funneled energetic terms in the original model.

Figure 4.

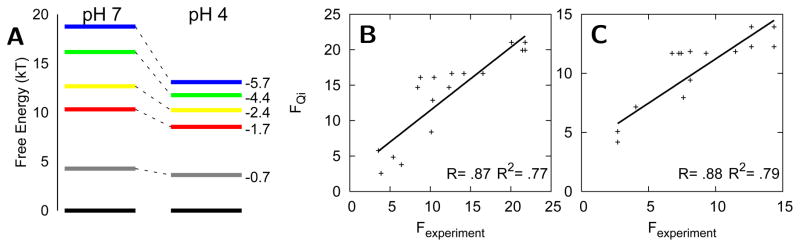
(A) Free energy levels calculated from simulations based on a model with a funneled landscape and nonnative electrostatic and hydrophobic forces. (B–C) Correlation of the unfolding free energies of individual residues determined from simulation (F_Qi), which are used to calculate the free energy levels in A, with the values obtained from hydrogen exchange experiments for pH 7 and pH 4 respectively.⁵¹

In the case of cytochrome c, the chemical frustration merely changes the sequence of folding events. In other cases, chemical frustration can drastically change the entire folding mechanism. For the protein BBL, different pH and salt concentrations will shift the populated ensemble of structures. These modest structural changes are only barely noticeable in the averaged NMR and crystal structures.^40–42 The structural and dynamical changes at different pH and salt concentrations seem sufficient to turn the folding mechanism for BBL from one well represented as two state folding to one resembling a barrierless, downhill folding scenario.²⁷

Folding with Chemical Frustration: Misligation Effects

Frustration on an energy landscape reflects the fact that nonnative interactions sometimes must be broken and assembled in a different way so that the protein can fold. These frustrated interactions slow folding and can give rise to stable intermediates. Small amounts of frustration, by allowing near degenerate configurations, enable conformational transitions between structures ordinarily thought of as being in the native basin of the energy landscape. Transitions related to such low free energy excited states are vital for a protein to function, for example, in catalysis or allosteric regulation.⁴³ In the case of cytochrome c, certain residues can compete for the heme ligation site giving rise to traps based on these specific nonnative interactions. The stability of these misligated intermediates depends strongly on the solvent conditions.

Some of the first evidence that there is at least some frustration on the folding landscapes of proteins was provided by kinetic experiments which showed that nonnative heme misligation slowed the folding of cytochrome c.⁷ These kinetic experiments, along with many others, employed optical absorbance spectroscopy of the heme to monitor structural changes that affect the heme’s electronic structure. Heme absorptions are useful because of their magnitude but can be difficult to interpret structurally. In an alternative approach, fluorescence from the single tryptophan of cytochrome c (Trp59) can be monitored which is quenched by the heme upon folding showing the proximity of the groups. Trp59 fluorescence has been measured in many kinetic studies of cytochrome c.^1,44–46 Simulations show that Trp59 fluorescence correlates with the protein’s radius of gyration. Trp59 fluorescence measurements, therefore, are sensitive to collapse of the protein chain but not necessarily to native-like folding. The Trp59 fluorescence decreases by 80% in the transition state ensemble (Q = 0.3) even though only 30% of the structure is well formed. The high sensitivity of Trp59 fluorescence to fluctuations between mostly unfolded structures explains the immediate decay of fluorescence intensity upon dilution of guanidinium chloride (GdmCl) in fast folding experiments.^1,45 A better probe for folding is the formation of the native bond between Met80 and the heme iron, which occurs only once the protein is mostly folded (Figure 5). The ligation of Met80 can be measured by the UV/vis absorbance of the 695 nm band.⁴⁷ In agreement with energy landscape ideas, experiments by Sosnick et al, which concurrently monitor collapse and folding, suggest that decreasing the roughness of the folding landscape increases the folding rate.¹ Frustration in the cytochrome c energy landscape can be reduced by lowering the pH to inhibit histidine misligation, which results in an increase of the folding rate as monitored by the UV/vis absorption at 695 nm. Misligation hardly affects the rate of collapse which suggests that misligated traps are present after the protein has crossed the transition state for collapse. At low pH, with histidine misligation inhibited, increasing the GdmCl concentration causes the rates of both collapse and folding to decrease.¹ The formation of native-like structure during the initial collapse and during folding is inhibited by the denaturant. At higher pH, where misligation occurs, increasing the GdmCl concentration also causes the rate of collapse to decrease. The rate of folding however actually increases, even though the rates are still slower than for folding without misligation at the same GdmCl concentration.¹ The results suggests that denaturant can easily destabilize misligated and misfolded structures by breaking weak, frustrated interactions that give rise to these transient intermediates. While frustration due to misligation can perturb the system by changing the folding rate, at more extreme pH, the protein can adopt completely different structures that are partially unfolded or even completely denatured.

Figure 5.

Normalized averages of the radius of gyration (×), Trp59 fluorescence (○), and Met80 ligation (□) as a function of the folding reaction coordinate Q. The Trp59 to heme fluorescence decay is calculated using the equation $k=(1+{(\frac{R_0}{r})}^6)$ in which r is the distance between the Trp59 C^α and the heme center and the Förster distance, R₀, is 35 A. ⁵² Met80 ligation is defined to occur when the distance between the Met80 C^α and the heme center is less than 8A.

Modeling the detailed effects of chemical frustration at first seems computationally prohibitive. Explicitly modeling all the chemistry for protonation changes and ligation events in a simulation involving folding and unfolding transitions is not currently practical. However such a treatment is not needed because although there are many possible chemically distinct species, only a few states are actually realized. Between pH 7 and 14, for instance, cytochrome c populates six states: III ⇌ 3.5 ⇌ (IV_a ⇌ IV_b) ⇌ V ⇌ U.^{28–30,48–50} State III is the native state at pH 7, U refers to the globally unfolded protein, and there are four partially unfolded intermediates. In order to incorporate detailed chemistry with energy landscape ideas that describe inter-residue forces which guide folding, we developed a grand canonical formalism.³⁸ The general strategy of this formalism is to run separate simulations corresponding to the most relevant chemical species, including all the relevant protonation and ligation changes (Figure 6). In the schematic representation of the grand canonical ensemble method (Figure 6), the middle funnel represents the perfectly funneled energy landscape at pH 7 without misligation. Chemical frustration due to pH change is accounted for by decreasing the contact energies involving deprotonated residues. In some cases, nonnative contacts are enforced by introducing explicit ligation between the heme and a misligating residue, giving rise to alternate states represented by M₁ and M₂ in Figure 6. Free energy profiles are then calculated from each of these discrete simulations, one for each chemical species, and are combined using a grand canonical partition function: Ξ (Q, pH) = Σ _s [e^−F_s(Q)/kT] [e^−μ_s/kT K_lig,s]. The summation runs over all relevant chemical species, s. The first part of the partition function (in brackets) describes the stability of each chemical species. This stability follows from the unique folding funnel for each species, all of which are quite similar. Discrete free energy profiles (F_s(Q)) calculated from each of these simulations are combined by relating to each other the free energies of completely unfolded ensembles (Q = 0.1), which are near-random coils in these models. The free energies of these unfolded ensembles, before accounting for the free energies of chemical events, are expected to be the roughly identical. Thus the free energy differences at Q = 0.1 reflect only the intrinsic chemical equilibrium constants which depend on the chemical potential for deprotonation of a free amino acid (μ_s) and the ligand dissociation constant (K_lig,s). The grand canonical partition function relates the free energies of an open system to the protein undergoing chemical equilibria between ligation and protonation states.

Figure 6.

A scheme for combining energy landscapes for folding individual chemical species with acid/base and coordination chemistry. In the above scheme, each chemical species, characterized by its protonation and ligation state, is represented by its own folding funnel of varying depths. The pH 7 folding funnel has an energy minima at the native state (N), but as the solvent conditions change, the energy landscape is perturbed giving rise to slightly different funnels with distinct minima such as misligated states M₁ or M₂.

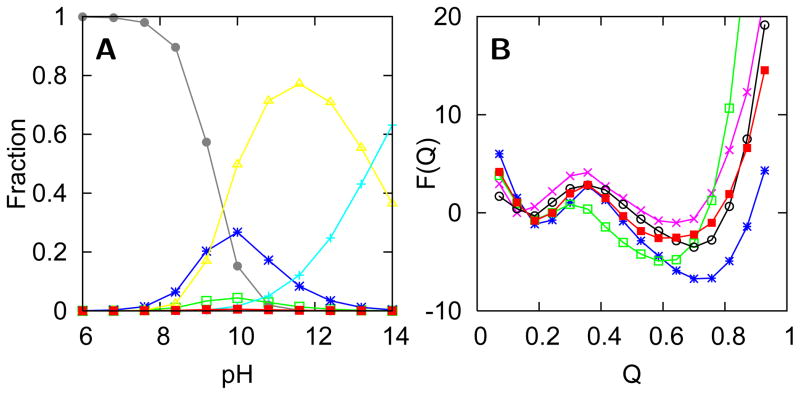
The grand canonical simulations predict, in agreement with experiment, that there are only a few species populated at alkaline pH. Figure 7A shows the population of different states as a function of pH. Using models based on funneled landscapes, only two of the 19 lysine residues are predicted to misligate, forming states IV_a and IV_b which are maximally populated at pH 10, in agreement with multiple experimental studies.^28–30 While only two lysine residues are predicted to misligate, Figure 7B shows that there are several other lysine misligates which are only slightly less stable. The funneled energy landscape favors stable structures that preserve native, stabilizing interactions, however other structures could be easily populated by perturbing the system. For instance, mutation of Lys73 or Lys79 may give rise to other misligated species. The structures of these predicted misligated species are also consistent with the information gathered from experiment. The Lys73 misligated structure, for instance, has been predicted with funneled energy landscape based on native cytochrome c and achieves an accuracy of 3.2 A as compared to the NMR structure of this somewhat misfolded species.³⁰ The structures of other intermediate ensembles (3.5 and V) are less precisely known from experiment. The grand canonical simulations yield predictions of these structures which are consistent with data from experiments.³⁰ Further details of these simulations can be tested with new experiments to generate further understanding of complex transitions such as the alkaline-induced unfolding of cytochrome c.

Figure 7.

(A) The fractional populations of the most stable species as a function of pH predicted using the grand canonical ensemble method: the native (●), fully unfolded (+), Lys79 misligated (*), Lys73 misligated (□), Lys72 misligated (■), and partially unfolded, hydroxide bound (△) states. (B) Free energy curves calculated from the simulation of the five most stable lysine misligated species. In addition to the three lysine misligated intermediates in A are the Lys53 (○) and Lys55 (×) misligated species.

The success of models based on funneled energy landscapes suggest that cytochrome c folding is primarily driven by native contacts. The folding transition state ensemble is well collapsed and involves the folding and binding of the terminal helices into a stable structure. The folding unit involving the terminal helices forms first since its density of contacts is higher than that for any other region in the protein. The remaining folding units take advantage of the more stable structured regions as an interface to nucleate folding. The sequential folding mechanism seems to be robust, even in the presence of misligation, unless specific folding units are destabilized by mutation or by a change of pH. The heme in cytochrome c seems to add chemical complexity to the process of folding but does not require modification of the general principles used to describe folding. More importantly perhaps, the heme has provided valuable methods to probe the folding energy landscape in greater detail than has been possible in many other cases.

Abbreviations

AMH

associative memory Hamiltonian

RMSD

root mean square deviation

GdmCl

guanidinium chloride

R_g

radius of gyration

Biographies

Patrick Weinkam achieved his Ph.D. at UCSD under the joint guidance of Peter G. Wolynes and Floyd E. Romesberg. He is currently a postdoc at UCSF with Andrej Sali.

Joerg Zimmermann received his Ph.D. in physics from Humboldt University Berlin in 2000. After a postdoctoral position with Prof. Graham Fleming at UC Berkeley he is currently a senior research associate at The Scripps Research Institute.

Floyd Romesberg received his Ph.D. in Chemistry from Cornell University. After completing postdoctoral research at UC Berkeley, he accepted a position at The Scripps Research Institute where he is currently an Associate Professor.

Peter Guy Wolynes holds the Francis Crick Chair in the Physical Sciences at the University of California, San Diego. Peter G. Wolynes received his Ph.D. in chemical physics from Harvard in 1976.