How native-state topology affects the folding of dihydrofolate reductase and interleukin-1β

Abstract

The overall structure of the transition-state and intermediate ensembles observed experimentally for dihydrofolate reductase and interleukin-1β can be obtained by using simplified models that have almost no energetic frustration. The predictive power of these models suggests that, even for these very large proteins with completely different folding mechanisms and functions, real protein sequences are sufficiently well designed, and much of the structural heterogeneity observed in the intermediates and the transition-state ensembles is determined by topological effects.

Explaining how proteins self assemble into well-defined structures is a long-standing challenge. Energy landscape theory and the funnel concept (1–7) have provided the theoretical framework necessary for improving our understanding of this problem: efficient folding sequences minimize frustration. Frustration may arise from the inability to satisfy all native interactions and from strong non-native contacts, which can create conformational traps. The difficulty of minimizing energetic frustration by sequence design, however, also depends on the choice of folding motif. Some folding motifs are easier to design than others (8, 9), suggesting the possibility that evolution not only selected sequences with sufficiently small energetic frustration but also selected more easily designable native structures. To address this difference in foldability, we have introduced the concept of “topological frustration” (10–13): even when sequences have been designed with minimal energetic frustration, variations in the degree of nativeness of contacts in the transition-state ensemble (TSE) are observed because of asymmetries imposed by the chosen final structure.

Recent theoretical and experimental evidence (14–18) suggests that proteins, especially small fast-folding (submillisecond) proteins, have sequences with a level of energetic frustration sufficiently reduced that the global characteristics of the observed heterogeneity observed in the TSE are strongly influenced by the native-state topology. We have shown (13) that the overall structure of the TSE for chymotrypsin inhibitor 2 and for the Src-Homology 3 (SH3) domain of the src tyrosine–protein kinase can be obtained with simplified models constructed by using sequences that have almost no energetic frustration (Gō-like potentials). These models drastically reduce the energetic frustration and energetic heterogeneity for native contacts, leaving the topology as the primary source of the residual frustration. Topological effects, however, go beyond affecting the structure of the TSE. The overall structure of the populated intermediate-state ensembles during the folding of proteins such as barnase, ribonuclease H, and CheY have also been determined successfully by using a similar model (13). It is interesting to note that, because they concern totally unfrustrated sequences, these models may not reproduce the precise energetics of the real proteins, such as the value of the barrier heights and the stability of the intermediates; nevertheless, they are able to determine the general structure of these ensembles. Therefore, the fact that these almost energetically unfrustrated models reproduce most of the major features of the TSE of these proteins indicates that real protein sequences are sufficiently well designed (i.e., with reduced energetic frustration) that much of the heterogeneity observed in the TSEs and intermediates has a strong topological dependence.

Do these conclusions hold to larger and slower folding proteins with a more complex folding kinetics than two-state folders such as chymotrypsin inhibitor 2 and SH3? The success obtained with barnase, ribonuclease H, and CheY intermediates already provides some encouragement: topology appears to be important in determining on-pathway folding intermediates. In this paper, this approach is extended to a pair of larger proteins: dihydrofolate reductase (DHFR) and interleukin-1β (IL-1β). The synoptic analysis of these two proteins is particularly interesting because they have a comparable size (slightly over 150 amino acids) but different native structures, folding mechanisms, and functions: DHFR is a two-domain α/β enzyme that maintains pools of tetrahydrofolate used in nucleotide metabolism, whereas IL-1β is a single-domain all-β cytokine with no catalytic activity of its own, but it elicits a biological response by binding to its receptor.

Numerical Procedures.

The energetically unfrustrated models of DHFR and IL-1β are constructed by using a Gō-like Hamiltonian (19, 20). A Gō-like potential takes into account only native interactions, and each of these interactions enters in the energy balance with the same weight. Residues in the proteins are represented as single beads centered in their C-α positions. Adjacent beads are strung together into a polymer chain by means of bond and angle interactions, whereas the geometry of the native state is encoded in the dihedral angle potential and a nonlocal bead–bead potential.

A detailed description of this energy function can be found elsewhere (13). The local (torsion) and nonlocal terms have been adjusted so that the stabilization energy residing in the tertiary contacts is approximately twice as large as the torsional contribution. This balance among the energy terms is optimal for the folding of our Gō-like protein models (4). Solvent mediation and side-chain effects are already included in these effective energy functions. Therefore, entropy changes are associated with the configurational entropy of the chain. The native contact map of a protein is derived with csu software (available at http://www.weizmann.ac.il/sgedg/csu/), based on the approach developed in ref. 21. Native contacts between pairs of residues (i, j) with j ≤ i + 4 are discarded from the native map, as any three and four subsequent residues are already interacting in the angle and dihedral terms. A contact between two residues (i, j) is considered formed if the distance between the C_αs is shorter than γ times their native distance σ_ij. It has been shown (11) that the results do not depend strongly on the choice made for the cutoff distance γ. In this work, we used γ = 1.2.

For both protein models (DHFR and IL-1β), folding and unfolding simulations have been performed at several temperatures around the folding temperature. The results from the different simulations have been combined by using the wham algorithm (22). Several very different initial unfolded structures for the folding simulations have been selected, and they have been obtained from high-temperature unfolding simulations. To have appropriate statistics, we made sure that for every transition-state ensemble or intermediate, we have sampled about 500 uncorrelated conformations (thermally weighted). For smaller proteins such as SH3 and chymotrypsin inhibitor 2 (which have about 1/3 of the tertiary contacts of DHFR and IL-1β), we have determined that about 200 uncorrelated conformations in the transition-state ensemble are necessary to have an error on the estimates of contact probabilities (or Φ values) of ±0.05 (13).

Comparing Simulations and Experiments for DHFR and IL-1β.

Not only do DHFR and IL-1β have dissimilar native folds, but also the nature of the intermediate states populated during the folding event is remarkably different. (The 162 residues of DHFR arrange themselves in 8 β-strands and 4 α-helices, grouped together in the folded state as detailed in Fig. 2d, whereas IL-1β is 153 residues, all β protein, composed of 12 β strands packed together as shown in Fig. 4 c and d.) To explore the connection between the protein topology and the nature of the intermediates, we used an energetically minimally frustrated Cα model for these two proteins, with a potential energy function defined by considering only the native local and nonlocal interactions as being attractive (see Numerical Procedures for details). This is a very simplified potential that retains only information about the native fold; energetic frustration is almost fully removed. Notice that, although the real amino acid sequence is not included in this model, the chosen potential is like a “perfect” sequence for the target structure, without the energetic frustration of real sequences (because this potential includes attractive native tertiary contacts, it implicitly incorporates hydrophobic interactions). Therefore, this model provides the perfect computational tool to investigate how much of the structural heterogeneity observed during the folding mechanism could be inferred from the knowledge of the native structure alone, without contributions from energetic frustration.

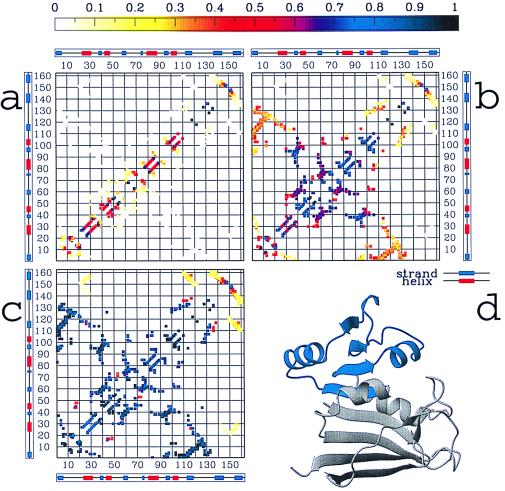
Figure 2.

The probability Q_ij(Q) of the native DHFR contacts being formed, resulting from the simulations at different stages of the folding process: (a) at an early stage (Q = 0.1 ± 0.05), (b) at the main intermediate, located in the interval Q = 0.4 ± 0.05 (see Fig. 1 a and c), and (c) at a late stage of the folding process (Q = 0.7 ± 0.05). In a topologically and energetically perfectly smooth funnel-like energy landscape, at any value Q during the folding, any contact (i, j) should have a probability Q_ij(Q) of being formed equal to Q (2). By computing Q_ij(Q) for each contact over different windows of the reaction coordinate Q, we can quantify the deviations from this smooth-funnel behavior and locate the early and late contacts along the folding process. It is worth noting that any deviation from “perfectly smooth” behavior is caused mainly by topological constraints, because energetic frustration has been mostly removed from the system. Different colors in the contact maps indicate different probability values from 0 to 1, as quantified by the color scale at the top. The preference for forming more local than nonlocal structure in the almost unfolded state (b) is because conformational entropy loss is smaller by forming local contacts than by pinching off longer loops (32). The most interesting result is that domain 1, identified by interactions among strands 2–5 and helices 2–3, is substantially formed at the intermediate I_HF (probabilities for individual contacts grater than 0.7), whereas the formation of domain 2 (i.e., interactions among strand 1, strands 6–8, helix 1, and helix 4) is highly unfolded (contact probabilities between 0 and 0.4). Helix 1 and helix 4 are largely formed, but their interactions with the remainder of the proteins are loose (probabilities less than 0.4). Overall, this description of the structure of the main intermediate I_HF—domain 1 almost formed and domain 2 largely unformed—is in agreement with the structure of I_HF experimentally observed. Moreover, the latest event in the folding process (c) appears to be the formation of interactions between strands 7–8 and the remainder of the protein. This again has been experimentally determined. d illustrates the regions of the native structure that both simulations and experiments agree to indicate as formed at the intermediate I_HF.

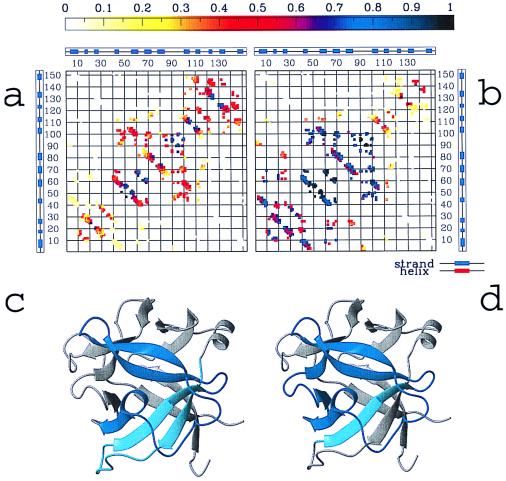
Figure 4.

Probability of contact formation for the native contacts, as obtained during a typical folding simulation of the IL-1β at different stages of the folding (data shown are obtained at T = 0.99T_f), (a) In a range of Q between 0.3 and 0.4 that corresponds to the early stage of folding leading to the formation of the intermediate ensemble; and (b) at the intermediate (Q between 0.45 and 0.55). At the intermediate, the interactions involving strands 4–8 are almost completely formed; interactions among strands 1–3 are likely formed, but interactions between them and the rest of the protein are loose. Contacts involving strands 9–12 appear weakened, and the interactions between the N (residues 1–40) and C termini (residues 110–153) are completely unformed. Experimental results confirm that strands 6–8 are well folded in the intermediate state and that strands 4–5 are partially formed. c and d show the regions of the IL-1β native structure formed at the intermediate as resulting from simulations (c) and experiments (d). The small difference between simulations and experiments (contact formation in the region between residues 110–125) may be caused by energetic considerations that are not taken into account in the model, as discussed in the text. In agreement with experimental results, the formation of contacts between the N and C termini is not accomplished until the late stage of folding; these contacts are still unformed for Q = (0.6 − 0.7) (data not shown).

Because early work suggests that proteins (at least small fast-folding proteins) have sufficiently reduced energetic frustration, they have a funnel-like energy landscape with a solvent-averaged potential strongly correlated with the degree of nativeness (but with some roughness because of the residual frustration). In this situation, the folding dynamics can be described as the diffusion of an ensemble of protein configurations over a low-dimensional free-energy surface, defined in terms of the reaction coordinate Q, where Q represents the fraction of the native contact formed in a conformation (Q = 0 at the fully unfolded state, and Q = 1 at the folded state) (10–13, 23). The ensemble of intermediates observed in this free-energy profile is expected to mimic the real kinetic intermediates.

Fig. 1 shows a comparison between the folding mechanism obtained from our simulations for the minimally frustrated analogue of DHFR (Fig. 1 a and c) and IL-1β (b and d). The different nature of the folding intermediates of the two proteins and their native ensembles emerging from these data is in substantial agreement with the experimental observations, with the adenine-binding domain of DHFR being folded in the main intermediate in the simulation and the central β strands of IL-1β being formed early in this single-domain protein. The absolute values of the free-energy barriers resulting from simulations may not necessarily agree with the experimental ones, because we are dealing with unfrustrated designed sequences. Thus, quantitative predictions that depend on barrier heights and stability of the intermediate ensembles (e.g., folding time, rate determining barriers, and lifetime of intermediates) are not possible for this kind of model. However, we show that topology is sufficient to detect correctly the positions of the transition and intermediate states. A more detailed description follows.

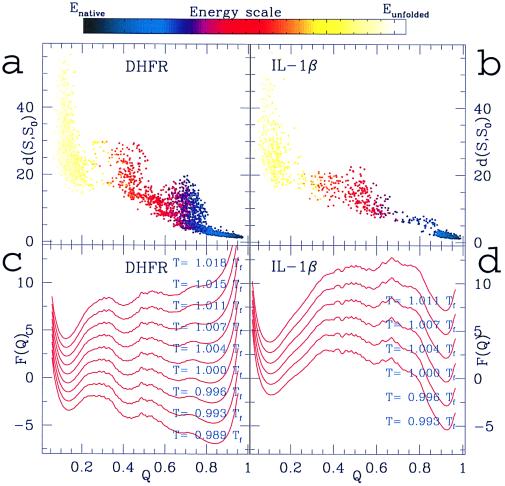
Figure 1.

(a) rms distances between the DHFR native structure and several computationally determined structures at different values of the reaction coordinate Q for an unfolding simulation at a temperature slightly above the folding temperature (T = 1.01T_f) and (c) free energy F(Q) of the DHFR Gō-like model as a function of Q around the folding temperature. The folding temperature T_f is estimated as the temperature where a sharp peak appears in the specific heat plotted as a function of the temperature (data not shown). Both temperatures and free energies are presented in units of T_f. Note that the thermal fluctuations around the lowest energy state (i.e., Q = 1, by construction of the model) account for motions around the free energy minimum. Therefore, the folded state ensemble has a minimum close to Q = 1, at Q ≈ 0.9, but not exactly at Q = 1. Indeed, at Q = 1, the structure would be frozen in the native configuration. A similar remark applies for the IL-1β free-energy profile shown in c. The energy of a configuration, as quantified by the color scale above the figure, is defined here as the bare value of the effective potential function in that configuration (i.e., no configurational entropy is accounted in the energy). Differences between energy and free energy (at finite temperature) are caused by the configurational entropy contribution to the free energy. In c, a main intermediate ensemble I_HF emerges in the folding process as a local minimum at Q around 0.4 after the overcoming of the first barrier. Indeed, this local minimum corresponds to a populated region in a (after the scarcely populated barrier around Q = 0.3) with energy significantly lower than in the unfolded state. This main intermediate then evolves toward a set of structures close to the native states (located between Q = 0.7 and Q = 0.8) that eventually interconvert into the fully folded state. A transient set of structures, close to the native state, is also apparent from Fig. 2b. The folding scheme resulting from these simulations is consistent with the sketch of Fig. 3d, proposed from the experimental data (24, 29). (b) rms distances between the native structure and several computationally determined structures at different values of the reaction coordinate Q for a folding simulation of the Gō-like model of IL-1β. The simulation is performed at a temperature near to the folding temperature (T = 0.99T_f). (d) Free energy F(Q) as a function of Q around to the folding temperature. The folding temperature is estimated from the sharp peak in the specific heat curve as a function of the temperature (data not shown). An intermediate ensemble is populated during the folding event, and it is identified by the broad local minimum in the free-energy profile (around Q = 0.55) and the corresponding populated region in b (with energy significantly lower than in the unfolded state). These results are consistent with the kinetic mechanism for the folding of IL-1β proposed by Heidary et al. (30). A set of structures close to the native conformation is transiently populated for Q between 0.75 and 0.8 [see b and the corresponding “flat” region in the free-energy panel (d)]. This fact could be interpreted as the presence of an additional intermediate state close to the native state. Experimentally, the possibility that another partially unfolded form could be populated during the folding process is currently under investigation. Several constant temperature simulations (both folding and unfolding) of the two protein models were made and combined to generate the free-energy plots.

DHFR.

The folding process emerging from the dynamics of the Gō-like analogue of DHFR (as summarized in Fig. 1 a and c) is interestingly peculiar and consistent with the experimentally proposed folding mechanism (24) (see Fig. 3d). Refolding initiates by a barrierless collapse to a quasistable species (Q = 0.2), which corresponds to the formation of a burst-phase intermediate, I_BP, with little stability but some protection from H-exchange across the central β sheet (25). This initial collapse is followed by production of the main intermediate I_HF (highly fluorescent), which is described in the mechanism of Fig. 3d as the collection of intermediates I₁−I₄. I₁−I₄ are structurally similar to each other but differentiated experimentally by the rate at which they proceed toward the native protein. Finally, after the overcoming of a second barrier, the protein visits an ensemble of native structures with different energies. The experimentally determined folding mechanism of DHFR shows transient kinetic control in the formation of native conformers (N₄ dominant). This is later overridden by thermodynamic considerations (N₂ dominant) at final equilibrium (24). This latter finding is consistent with the nature of the folding ensemble determined by the simulations. As shown in Fig. 3b, a set of structures close to the native state (Q around 0.7 − 0.8) is transiently populated beside the fully folded state (Q = 1). Because the main intermediate I_HF has been characterized recently by experimental studies (24, 29), we take our analysis a step further by comparing the average structure of the I_HF ensemble from our simulations to the one experimentally determined. For this purpose, we compute the formation probability Q_ij(Q) for each native DHFR contact involving residues (i, j) at different stages of the folding process by averaging the number of times the contact occurs over the set of structures existent in a selected range of Q. As detailed in Fig. 2, the central result from this analysis is that the main intermediate I_HF is characterized by a largely different degree of formation in different parts of the protein: domain 1 (i.e., interactions among strands 2–5 and helices 2–3) appears to be formed with probability greater than 0.7, whereas domain 2 (i.e., interactions among strands 6–8, helix 1 and helix 4) is almost nonexistent.

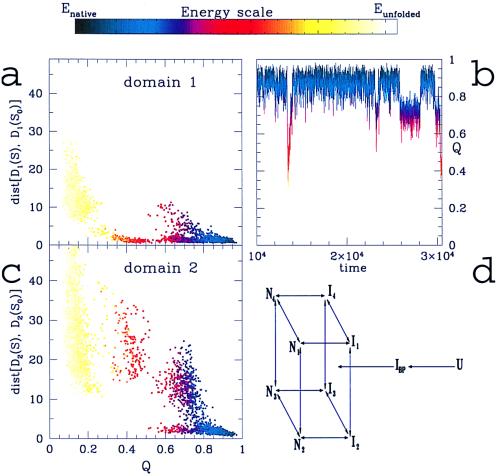
Figure 3.

The rms distances between the regions of the DHFR structure identified as (a) domain 1 and (c) domain 2 and their corresponding native configurations are plotted vs. the reaction coordinate Q. Domain 1 collapses to a structure close to its native conformation (rms distance less than 5 Å) in the early stages of folding, leading to the formation of the main intermediate I_HF (located at Q around 0.4), whereas domain 2 remains largely unfolded (rms distance larger than 15 Å). In the interval of Q from 0.6 to 0.8, there are several possible structures. Consistent with the multichannel folding model proposed from experimental evidence (24), from a and c one can propound several possible ways to proceed from I_HF to the folded state. In b, the fraction of native contacts formed, Q, is plotted vs. the simulation time for a region of our simulations where the transition from folded to unfolded state is observed (at a simulation temperature slightly higher than the folding temperature, T = 1.01T_f). A set of structures close to the native state (Q around 0.7) is transiently populated. Different colors represent different energies of a configuration (quantified by the energy scale above the figure), as well as for a and c. (d) The kinetics mechanism for the folding of DHFR, proposed on the basis of experimental results (24, 29). Experimentally, a first step of folding is detected as a very rapid collapse of the unfolded form to the burst-phase intermediate (I_BP), which has a significant content of secondary structure. The folding state is reached through four different channels, involving the formations of the main intermediate I_HF. I_HF is represented as a set of structures I₁−I₄ structurally similar to each other but proceeding toward the native state with a different rate. These intermediate structures evolve to the native forms N₁−N₄ via slow-folding reactions.

The formation of domain 1 and domain 2 during the folding event is more closely understood from Fig. 3 a and c, where the rms distance of the parts of the protein constituting each domain from the corresponding native structures is shown for a typical folding simulation. Indeed, the two domains fold in a noticeably different way: in the stable intermediate I_HF, domain 1 is closer than 5 Å (rms) to that found in the native structure, whereas domain 2 is highly variable (rms distance greater than 15 Å from its native structure). Still, in agreement with hydrogen exchange studies (25), some protection is expected across domains from our simulations, and complete protection from exchange is expected only after the formation of the fully folded protein. A combination of fluorescence, CD mutagenic, and new drug-binding studies on DHFR indeed demonstrates that domain 1 is largely folded with specific tertiary contacts formed and that this collection of intermediates is obligatory in the folding route (29).

IL-1β.

Supported by some recent experiments, Heidary et al. (30) have proposed a kinetic mechanism for the folding of IL-1β that requires the presence of a well-defined on-pathway intermediate species. The structural details of these species were determined from NMR and hydrogen exchange techniques (30, 31). We have compared these experimental data with our simulations for the IL-1β Gō-like analogue (Fig. 1 b and d). The folding picture emerging from these numerical studies differs substantially from that observed for DHFR (see Fig. 1 a and c). An intermediate state is populated for Q around 0.55, followed by a rate-limiting barrier (around Q = 0.7), after which the system proceeds to the well-defined native state.

Is the theoretical intermediate similar to the one observed experimentally? By using the same procedure as for DHFR, a comparison between the average structure of the IL-1β intermediate ensemble and the one emerging from experimental studies is shown in Fig. 4. These results indicate that in the calculated intermediate, residues 40–105 (strands 4–8) are folded into a native-like topology, but interactions between strands 5 and 8 are not fully completed. Experimental results confirm that strands 6–8 are well folded in the intermediate state and that strands 4–5 are partially formed. However, results of experiments and theory differ in the region between residues 110–125, where hydrogen exchange shows early protection, and theory predicts late contact formation. This region contains four aromatic groups, Phe-112, Phe-117, Tyr-120, and Trp-121, which may be sequestered from solvent because of clustering of these residues and removal from unfavorable solvent interactions. This effect would not be fully accounted for from our model, where all native interactions are considered as energetically equivalent, and large stabilizing interactions are not differentiated. Thus, energetics may favor early formation of the structure corresponding to residues 105–125, whereas topology considerations favor the formation of strands 4–8.

Conclusions

Theoretical and experimental studies of protein folding at times appear to be at odds. Theoretical analysis of simple model systems oftentimes predicts a large number of routes to the native protein, whereas experimental work on larger systems indicates that folding proceeds through a limited number of intermediate species. Although in the eyes of some people these two descriptions are inconsistent, this is clearly not true. The large number of routes may or may not lead to the production of on-route kinetic intermediate ensembles, depending on the result of the competition between configurational entropy and the effective folding energy. In this study, we show that productive intermediate species are produced by using simplified protein models with funnel-like landscapes based on purely topological considerations, and the results are in good agreement with the available experimental data. The fact that these simplified minimally frustrated models for DHFR and IL-1β can predict the overall features of the folding intermediates and transition states experimentally measured for these two proteins, with completely different folding mechanisms and functions, supports our general picture that real proteins have a substantially reduced level of energetic frustration, and a large component of the observed heterogeneity during the folding event is determined topologically. Such observations lead us to propose that the success in designing sequences that fold to a particular shape is constrained by topological effects (32). What is more challenging are the consequences of this conclusion: do these topological constraints have to be tolerated only during the folding event, or are they actually used by biology to help function? Here we speculate only in the context of these two examples, but this question should be addressed more generally in the future.

Abbreviations

TSE

transition-state ensemble

DHFR

dihydrofolate reductase