A kinetically significant intermediate in the folding of barnase

Abstract

A series of studies on the small protein barnase in the 1990s established it as a paradigm for protein folding in which there is a kinetically important intermediate. But, a recent study in PNAS claims that there are no stable intermediates on the folding pathway. I summarize the evidence that proves that the folding kinetics of barnase is inconsistent with the absence of a folding intermediate. I reinterpret the major evidence presented against the intermediate (an inflection in the unfolding limb of a chevron plot) and show that the inflection is precisely what is predicted from the energy diagram for a three-state reaction with a kinetically significant on-pathway intermediate. The inflection is indicative of a change of rate determining step from the formation to breakdown of an intermediate on unfolding. Other evidence presented against the intermediate is, in fact, consistent with a kinetically important intermediate. I show how the complexities in the kinetics provide a means for measuring otherwise unobtainable rate constants and provide a strategy for mapping the structure of the early transition state in folding. Rather than refute multistate kinetics, the presence of the inflection in the unfolding plot constitutes a novel type of evidence for on-pathway folding intermediates.

One fundamental question about the pathway of protein folding is whether or not there are folding intermediates; that is, whether a pathway is two-state or multistate. The next question is whether intermediates are on-pathway, that is, on the route between the denatured state, D, and the native state, N. Unequivocal proof of mechanism by kinetics is often neither simple nor straightforward because much of kinetic evidence is by its very nature indirect and hence ambiguous. But the kineticist has two powerful tools for defining mechanisms. The first is the principle of microscopic reversibility. It is a necessary consequence of two-state kinetics that the ratio of forward and reverse rate constants is identical to the independently measured equilibrium constant. A corollary is that a two-state reaction must have the same transition state in its forward and reverse reactions. These tests apply both to true reversible first-order reactions and to pseudofirst order reactions that have high-energy intermediates. The second is direct observation of intermediates. In general, kinetics is at its most powerful in disproving particular mechanisms because it can show that only a restricted set of mechanisms is consistent with observed data. For example, the kineticist can formulate the simplest reaction scheme consistent with the kinetics. But, it is nearly always possible to fit to the data more complex mechanisms that have additional intermediates. Thus, reactions that are apparently two state always have the possibility of containing high-energy intermediates that are not amenable to direct detection and are kinetically silent. Conversely, it is possible to demonstrate unequivocally by using the consequences of microscopic reversibility that a reaction scheme has to have a minimum number of intermediates and hence eliminate all mechanisms with a smaller number of steps. It is more difficult to prove whether the intermediates are on-pathway or are side-reactions that are nonproductive.

My laboratory has over the period of a decade developed the 110-residue protein barnase as a paradigm for analyzing the stability of proteins and the pathway of folding via an intermediate (1–3). We have demonstrated that an intermediate occurs during the folding of barnase by rigorously applying all three tests (1, 4, 5). Parallel studies with chymotrypsin inhibitor 2 (CI2) have shown that it folds cleanly by two-state kinetics (6), and those experiments act as controls for those on barnase. Despite the apparently incontrovertible evidence and other data that are inconsistent with a two-state folding pathway for barnase, Bai and coworkers claimed first (7) that the only evidence supporting the intermediate came from curvature in the folding limb of a chevron plot. They now claim in PNAS (8) to have shown from simple direct experiments the “absence of stable intermediates on the folding pathway of barnase.”† First, I review the most substantial evidence in support of an intermediate accumulating in the energy landscape of the folding of barnase and show that it proves beyond reasonable doubt that there is a folding intermediate. I then reanalyze their key experiment and show that, rather than refute the existence of a folding intermediate, it does the opposite: it provides additional evidence for an intermediate and additional information on the free energy profile for folding. Further, it provides the best evidence to date that the intermediate is on-pathway.

Microscopic Reversibility Test 1

Landmark findings from Tanford and his colleagues established two general equations for the denaturation of proteins by chemicals (9, 10). The free energy of denaturation of proteins, ΔG_D-N, follows the law

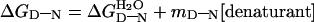1

where 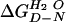is the value in water, m_D-N a constant of proportionality, and the denaturant being urea or guanidinium chloride (GdmCl). Similarly, the activation energy of unfolding, ΔG_‡-N, follows the analogous law:

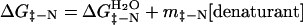2

Detailed kinetic studies on more than 200 mutants of two very simple proteins, barnase and the 64-residue CI2, have shown that these linear relationships are still very useful. But we found that there are deviations from linearity and more precise analyses require a quadratic equation to fit the data in solutions of urea for barnase (11–13). Smooth, but pronounced, curvature is seen in the kinetics of unfolding in the presence of urea and possibly results from a movement of the transition state because of the Hammond effect. [For barnase, the movement is small, and the plots of activation energies for unfolding of wild-type and mutants against urea all fit to a smooth curve of low and constant curvature (13, 14)]. The most precise data for the equilibria and kinetics of folding of barnase are listed by Dalby et al. (5), who measured the dependence of the folding and unfolding of wild-type and selected mutants of barnase as a function of urea concentration and temperature. Values of the rate constant for folding were determined from 0 to >2.5 M urea and values for unfolding from >1.7 M urea. Data were fitted to nonlinear equations (second-order polynomials):

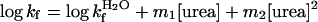3

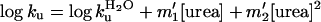4

where log k_f is the rate constant for folding in urea and log 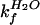 for that in the absence of urea, etc. The free energies of denaturation of the proteins were also measured independently by differential scanning calorimetry (DSC). These data also fit a second-order polynomial from 0–5 M urea:

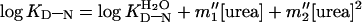5

where K_D-N is the equilibrium constant at any concentration of urea and 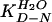is the value in water, etc. (15). The curvature in equilibrium denaturation curves is small and usually much less than found for the unfolding kinetics (C. M. Johnson and A.R.F., unpublished data). These equations give two criteria for establishing whether or not the reaction is two state (6). First, the observed value of 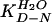must be equal to the ratio of 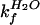/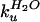. Secondly, the sum of initial dependence of the logarithms of the rate constants on urea concentration (or the free energies of activation) must equal the value for the equilibrium data. The data in Dalby et al. (5), and illustrated in Fig. 1, show that both these criteria are violated. For the cases indicated (and some 100 others not shown), the free energies calculated from the ratios of rate constants underestimate the free energy of denaturation by 2–4 kcal⋅mol⁻¹. Further, the sums of the initial slopes (m-values) are too low by a factor of 2 for two-state kinetics. In contrast, the correct behavior is observed for the folding of the two-state protein CI2 (6, 16). The data for barnase thus eliminate a two-state energy landscape in which no intermediate accumulates. There has to be at least one additional folding state, I, such as in (6)

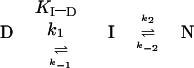6

There may even be further intermediates, indicated by stopped-flow kinetics (17, 18) and molecular dynamics (19) and other simulation (20) and equilibrium measurements (5). For simplicity, all of the intermediates before I, the late intermediate, are lumped together as a “preequilibrium.” The free energy of state I relative to D (ΔΔG_I-D), including all of the other states, was calculated from the discrepancy between the free energies derived from kinetics and equilibria (5). Plots of ΔΔG_I-D vs. temperature show that the intermediate melts at high temperatures and becomes a high-energy state for most mutants. The preequilibrium melts with urea concentration and disappears above about 1–2 M. But the overall process is effectively cooperative: its unfolding fits to Eq. 1 with an m-value of 1.2. The intermediate also becomes high energy with increasing pH because of the deprotonation of His-18, the protonated form of which interacts with Trp-94 and stabilizes both the native and intermediate states (21, 22).

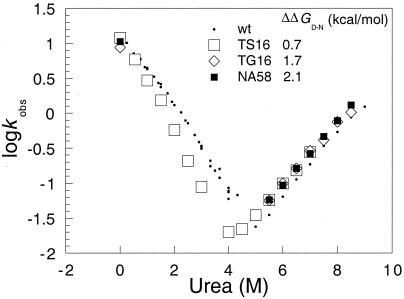
Figure 1.

Log k_obs vs. [urea] plots for the folding and unfolding of wild-type barnase and the mutants TS16, TG16, and NA58. k_obs is the unfolding rate constant at high urea concentration and the refolding at low urea concentration. Note how the unfolding data closely parallel each other and the refolding rate constants are nearly identical in 0 M urea. Yet, there are differences in stability of up to 2.1 kcal⋅mol⁻¹ (Inset). NA58 is one of the few mutants of barnase for which the ratio of folding and extrapolated unfolding rate constants in water is close to the independently measured value.

Oliveberg et al. (23) measured the temperature dependence of the folding rate constant and showed that there is a change of rate determining step with temperature, consistent with the melting of the intermediate and inconsistent with simple two-state kinetics. Conversely, the kinetics of folding of CI2 shows no change of rate determining step (23).

Microscopic Reversibility Test 2: Φ-Value Analysis

The discrepancies between the ratios of rate constants and equilibrium constants are highlighted further by measurements on mutant proteins. For example, the unfolding rate constants of the mutants TS16, TG16, and NA58 (Fig. 1) are very similar and parallel those of wild-type barnase as a function of urea concentration, and they have very similar refolding rate constants at 0 M urea. Yet, their stabilities vary by up to 2.1 kcal⋅mol⁻¹. This analysis can be formalized as follows. The fine structure of transition states and intermediates can be derived from Φ-value analysis (24–26). Suppose, mutation of a residue changes the free energy of denaturation by ΔΔG_D-N and alters the rate constant for folding from k_f(wt) to k_f(mut). The activation energy for the reaction changes by ΔΔG_‡-D, which equals RTln(k_f(mut)/k_f(wt)). Similarly, the activation energy for unfolding changes by ΔΔG_‡-N = RTln(k_u(mut)/k_u(wt)). Φ_F is defined by ΔΔG_‡-D/ΔΔG_N-D, and Φ_U = ΔΔG_‡-N/ΔΔG_D-N. Φ_F is a measure of formation of structure in the transition state, relative to that in the denatured state. Conversely, Φ_U is a measure of the breaking of structure in the transition state, relative to the native structure. Importantly, for a two-state reaction, ΔΔG_‡-N − ΔΔG_‡-D = ΔΔG_D-N and so Φ_F = 1 − Φ_U. A reaction following two-state kinetics without a stable intermediate in the energy landscape has the same transition state for forward and reverse reactions. Its detailed structure should, therefore, appear the same when analyzed by the kinetics of either the forward or the reverse reactions.

Thus, the use of mutants provides an essential criterion that has to be satisfied for a reaction to be a two-state reaction: Φ_F = 1 − Φ_U, which is a consequence of thermodynamics. Further, the Φ-values provide a description of the transition state that has to be chemically reasonable. These criteria are satisfied for the two-state folding and unfolding of CI2 (6, 16). Φ-value analysis affords the equivalent of the principle of microscopic reversibility for the analysis of protein folding transition states. For barnase, however, the mutants conspicuously fail the Φ-value test and clearly, in general, Φ_F ≠ 1 − Φ_U (5, 18).

Direct Observation of the Accumulation of the Intermediate at Equilibrium

Sanz and Fersht used the data from Φ-values to design multiply substituted mutants in which the intermediate is stabilized with respect to the denatured state (4). The intermediate was directly detected at equilibrium by the non-coincidence of melting curves monitored by fluorescence, CD, and hydrodynamic volumes. The intermediate aggregates, especially at low pH and high concentration (27).

H/²H-Exchange in Mutants Rules Out Two-State Folding

Most of the evidence used by Bai et al. concerns H/²H-exchange measurements. Deeply buried backbone residues in many proteins, including a set in barnase (28), cannot exchange with those from solvent until the protein completely unfolds. The process is defined by three rate constants: an “opening” rate constant k_o; a “closing rate” constant k_c; and a specific rate constant for exchange of each backbone peptide group, k_int (Eq. 7).

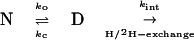7

If barnase unfolds by the two-state equation (7), where k_f = k_c and k_u = k_o, then the kinetics is simple. The observed rate constant for exchange is given by k_ex = k_uk_int/(k_int + k_f). At high [GdmCl], k_int >> k_f, and the equation reduces to k_ex = k_u, a condition that is known as the EX1 limit (29, 30). When k_int << k_f, the equation reduces to k_ex = k_uk_int/k_f, the EX2 limit. The transition between the two mechanisms occurs when k_int ∼ k_f.

Perrett et al. (31) examined the switch between EX1 and EX2 kinetics for a barnase and mutants of higher or lower stability. The mechanistic transition does not correlate with the value of k_f but more with the stability of the mutant. For example, some destabilized mutants exchange by EX1 at 33°C and pH 7.8 whereas wild-type and stabilized mutants retain EX2. At pH 7.9 and 37°C, wild type, which has an observed rate constant for folding of 17 s⁻¹, moves to an EX1 mechanism whereas the more stable mutant C43-C80 remains EX2, despite its having a significantly lower value of k_f of 7 s⁻¹. The lack of correlation between the observed folding rate constant and exchange mechanism proves that the two-state exchange mechanism does not hold for barnase and k_f is not necessarily the closing rate constant.

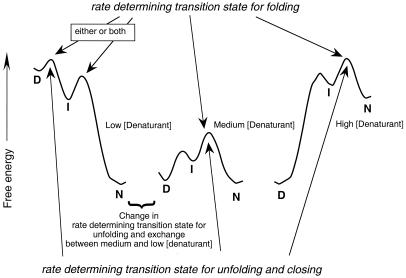
The reason for the lack of correlation is illustrated in Fig. 2. Whenever the intermediate, I, is at high energy relative to D and N, the transition states for folding and closing are the same. But, if, as on the left of the figure, the transition state between I and N is lower than that between D and I, folding and closing may have different rate determining transition states. When I is protected and the energy barrier between D and I is lower than that between I and N, the closing step is k₁ but the observed folding step is k₂. The Perrett et al. observation of k_f not correlating with k_c is key evidence. It also shows that, for some mutants and under some conditions, the formation of the intermediate is rate determining and for others the interconversion of I to N is rate determining in folding. But the evidence does not show whether the intermediate is on- or off-pathway (5) or whether there are further intermediates.

Figure 2.

Free energy diagram for folding and unfolding, and H/²H-exchange for a three-state reaction where the intermediate is protected from exchange. At medium to high concentrations of denaturant, the intermediate is at high energy and there is a common rate determining transition state for all three processes. At very low denaturant, the intermediate is at lower energy than the denatured state, and the rate determining step for unfolding may change. The rate determining state for closing is formation of I, but the rate determining step for folding may be either D to I or I to N. In either case, I is at lower energy than D. [Modified from figure 18.5 of Fersht (34) and figure 1 of Serrano et al. (42).]

Analysis of Unfolding Data at Low Denaturant Concentration

In their case against an intermediate, Bai et al. (8) do not cite or address any of the above evidence, except for one point, the value of the unfolding rate constant of barnase in the absence of denaturant. They claim that the linear extrapolation of data from urea-denaturation underestimates the unfolding rate constant by a factor of ten compared with that from GdmCl. In fact, since 1993, we have fitted all kinetic data on the unfolding of barnase to second-order polynomials, and there is excellent agreement between extrapolation of unfolding experiments from urea and GdmCl solutions (11, 12).

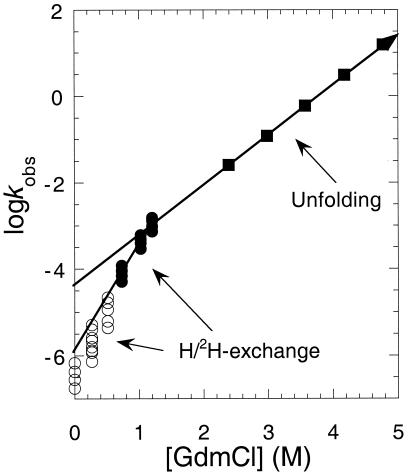
Bai et al. presented a plot of log k_u vs. [GdmCl] over a very wide range of concentration by using data from H/²H-exchange from our laboratory at very low [GdmCl] and stopped-flow data of their own at higher concentrations (Fig. 3). They analyzed the data according to a two-state mechanism, despite the Perrett et al. demonstration that this mechanism is inconsistent with H/²H-exchange results on mutants (31). The data in Fig. 3 are somewhat complicated because there is a transition from the EX1 to the EX2 limit below 0.5 M GdmCl. The plot is sharply kinked at low concentrations of GdmCl. Bai et al. claim that the true value of 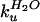is obtained from the linear slope below the kink (8). The observed intercept, 10⁻⁶ s⁻¹, when divided by the observed value of k_f (14.7 s⁻¹) is close to the true equilibrium constant for denaturation. They suggest the sudden change in slope is probably caused by a movement of the transition state by the Hammond effect.

Figure 3.

Plots of log k_ex and log k_unfolding vs. [GdmCl] [Modified from Bai et al. (8)].

Sharp kinks in plots of rate constants against smooth changes in reaction conditions are not consistent with a smooth movement of a transition state. Instead, kinks signal that there is a change in rate determining step or change in mechanism. This behavior is precisely what is predicted from the energy diagrams in Fig. 2. At high concentrations of denaturant, the rate determining transition state for unfolding is between N and I. But, at very low concentrations, the free energy of D is greater than that of I, and the transition state lies between them. Thus, at moderate to high concentrations of denaturant, the observed rate constant for unfolding is k₋₁. But, at very low concentrations, it decreases to k₋₁k₋₂/(k₋₁ + k₂), where k₋₁ can be neglected when it is <<k₂. Thus, rather than refute the presence of intermediates, the experiment of Bai et al. (8) flags up the presence of a kinetically significant intermediate.

The presence of parallel pathways that differ in degree of exposure of the transition state could also lead to kinks in plots of rate constant vs. concentration of denaturant. But crossover of parallel pathways would lead to an upward curvature in the plot in Fig. 2 because the pathway with the more exposed transition state and higher m-value would dominate at high concentrations of denaturant, and vice versa.

Presence of an Inflection as a Test for On-Pathway Intermediate

An alternative scheme to Eq. 7 is the sequence I ↔ D ↔ N; i.e., the exchange-protected intermediate is off-pathway. This pathway would still account for the anomalies in the switchover between EX1 and EX2 kinetics (5). In order for an off-pathway intermediate to be significant in conventional refolding kinetics, D would have to partition preferentially to I when diluted from denaturing into fully renaturing conditions. The highest barrier on the pathway at low denaturant would then have to be the transition state for the formation of D from N. Therefore, the rate determining transition state for opening would be always between D and N, and so there would not be an inflection in the unfolding kinetics curve with denaturant concentration. Thus, the presence of the inflection is a novel test for an on-pathway intermediate in folding.

Analysis of Barnase Folding Kinetics from Combining H/²H-Exchange and Other Kinetic Data

The solution of Eq. 7 when k_c ∼ k_int is complicated because the general solution involves a quadratic equation with two roots (29, 32). But, adequate equations can be obtained for exchange at equilibrium by using Cleland's method of net rate constants (33) and the procedure of summing transit times (ref. 34, pp. 122–126). Each rate step is reduced to a net rate constant (k′) and the transit times (1/k′) summed. These give for two-state folding

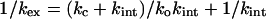8

This equation is the same as that from the original Hvidt and Nielsen treatment (29). Further, the complex quadratic equation from the presteady state analysis reduces to Eq. 8 when k_o << k_c and k_int, which is the situation at low concentrations of denaturant. Eq. 8 may be transformed into a linear form,

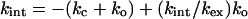9

At low GdmCl, Eq. 9 reduces to

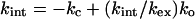10

since k_c ≫ k_o.

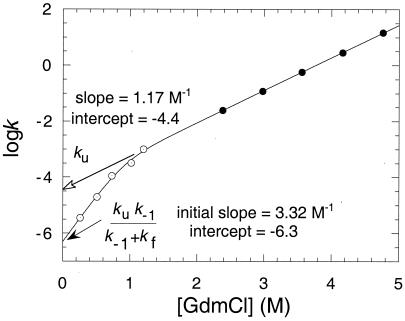
This equation, or statistically superior variants, may be applied to the series of different backbone NH groups that exchange by global unfolding in proteins. Application to the data for k_ex in Fig. 3 allows the estimation of k_c at 0.51 and 0.73 M GdmCl, and of k_o from 0.26 to 1.2 M (Fig. 4). The standard tables for k_int (35) give values of k_c that are nearly three times smaller than the observed values of k_f for the two most accurate data points at 0.51 and 0.73 M GdmCl. It is impossible for the closing rate constant to be less than the observed rate constant for folding. Perhaps the listed values are some two to three times too low under the reaction conditions. The values of k_o that are derived from Eq. 8 are insensitive to the value of k_int because it occurs on both sides of the equation.

Figure 4.

Plots of log k_o and log k_u vs. [urea].

The simple net rate constant method is readily applied to more complicated schemes, such as Eq. 6 for three-state folding. We can use the values of k_c and k_o in the three-state kinetic equations to obtain rate constants for the reaction. The analytical method applied to Eq. 6 for three-state folding where exchange takes place only from D and not I gives

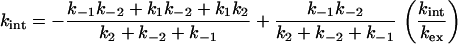11

At low [GdmCl], k₋₂ can be ignored to give

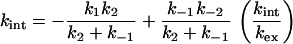12

This is analogous to Eq. 10, where k_c = k₁k₂/(k₂ + k₋₁), and k_o = k₋₁k₋₂/(k₂ + k₋₁). Note that the ratio of k_o/k_c = k₋₁k₋₂/k₁k₂ is always the value of the equilibrium constant for denaturation.

Rate Constants for Three-State Folding of Barnase

The data from Bai et al. (8) and us fit well to the three-state model of Eq. 7 and the kinetics of Eq. 12. The unfolding kinetics can be divided into two phases. At high [GdmCl], k_o = k₋₂, and there is the usual linear relationship of log k_unfolding vs. [GdmCl].

But, as [GdmCl] decreases, k_o = k₋₁k₋₂/(k₂ + k₋₁) and then tends to k₋₁k₋₂/k₂. The logarithm of each of k₂, k₋₁, and k₋₂ was assumed to vary linearly with [GdmCl] (Eq. 1), and the data for k_o from H/²H-exchange and k₋₂ were fitted to the equation k_o = k₋₁k₋₂/(k₂ + k₋₁) (Fig. 4). At high [GdmCl], log k₋₂ = −4.40 + 1.17[GdmCl]. As [GdmCl] tends to zero, log(k₋₁k₋₂/(k₂ + k₋₁)) = −6.3, and the initial slope tends to 3.32 M⁻¹.

From those two relationships, we can calculate the value of k₋₁/(k₂ + k₋₁) at 0 M GdmCl to be log(k₋₁/(k₂ + k₋₁)) = −6.3 + 4.4. That is, k₋₁/k₂ = 10^−1.9, because k₋₁ << k₂. The quantity k₋₁/k₂ is the partitioning ratio of the intermediate because it measures the ratio of the rate constants for its breakdown in the reverse and forward directions. Further, because the initial slope of log(k₋₁k₋₂/(k₂ + k₋₁)) vs. [GdmCl] is 3.32 as k₋₁ tends to zero, we can combine this with the equation for log k₋₁ at high [GdmCl] to give log(k₋₁/k₂) = −1.9 + 2.2[GdmCl].

The intermediate partitions equally in each direction at about 0.86 M GdmCl. The value of k₁ can be calculated from the equilibrium constant for denaturation, which equals k₋₁k₋₂/k₁k₂, and the value of k₋₁k₋₂/k₂, which was found from the intercept in Fig. 4. The free energy of denaturation is calculated from the exchange kinetics to be 10.6 kcal⋅mol⁻¹, using the higher values of k_int that seem more consistent, or 10.1 kcal⋅mol⁻¹ using the standard values, compared with the value of 10.4 kcal⋅mol⁻¹, measured by differential scanning calorimetry under the reaction conditions (unpublished data). This gives k₁ = 10^7.6–6.3 = 20 s⁻¹, within a factor of about 2.

The dependence of k₁ on [GdmCl] may be calculated from the initial slope of log(k₋₁k₋₂/k₂) and that of log(k₋₁k₋₂/k₁k₂). The latter was calculated by dividing the free energy of unfolding by the concentration of GdmCl at the midpoint of denaturation in the chevron plot (1.95 M) and RT to be 3.92. Thus, log k₁ = 1.3 − 0.6[GdmCl].

By substituting observed rate constants for folding and unfolding as a function of GdmCl concentration, it will be possible to determine the magnitude of all of the rate constants in the three-state scheme and their dependence on denaturant.

Inflection in β_T vs. GdmCl Concentration Shows Change of Rate Determining Step

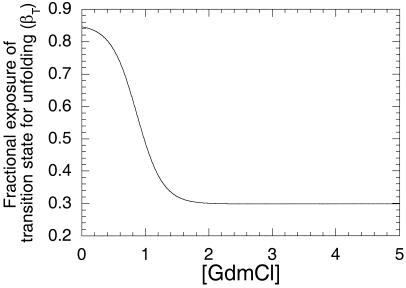
A very useful parameter in analyzing the nature of protein folding transition state is the Tanford β-value for unfolding, which equals (∂log k_u/∂[denaturant])/(∂log K_D-N/∂[denaturant]) (9, 14, 36). This is a measure of the relative degree of exposure of the transition state for unfolding relative to the denatured and native states. ∂log k_u/∂[denaturant] was calculated from 0 to 5 M GdmCl from the derivative of the analytical equation for the curve in Fig. 4. ∂log K_D-N/∂[denaturant] was calculated by dividing the free energy of unfolding (10.6 kcal⋅mol⁻¹) by the concentration of GdmCl at the midpoint of denaturation in the chevron plot and RT as described above. The value of β_T, plotted in Fig. 5, changes from 30% exposure at high GdmCl to 85% at low, the switchover being at 0.85 M, when k₋₁ = k₂. Such a rapid and large change is a consequence of the change in rate determining step. It is too large and the transition region is too narrow for the Hammond effect.

Figure 5.

Tanford β-value for the unfolding of barnase as a function of [GdmCl].

The β-value for the step k₁ implies a 15% surface area compaction on formation of the transition state for formation of the intermediate. The transition state for k₂ has 70% compaction.

Pre-Steady State Amplitudes in Refolding Kinetics

k₁ is similar to the observed rate constant for folding (14.7 s⁻¹). It is difficult experimentally to establish whether k₁ is fully rate determining or whether both k₁ and k₂ contribute to the rate-determining step. Although in theory there should be a lag in the kinetics for two consecutive processes of similar rate constant s, there are serious complications from the spectroscopic properties of barnase. The near UV fluorescence spectrum of the native state overlaps with that of the denatured state. The two spectra are of similar intensities and are shifted in wavelength maxima. The spectroscopic properties of the intermediate are also unknown. If the intermediate has a fluorescence spectrum between that of the denatured and native states, then its amplitude will mask a lag in the appearance of the fluorescence of N. The circular dichroism spectrum of barnase is also uncharacteristic and does not have high signals associated with formation of secondary structure (37).

The spectral properties and k₁ contributing to the rate determining step explain why the other tests applied by Bai et al. failed. The first test concerns amplitudes of phases in presteady kinetics. Bai et al. (8) followed the folding of barnase by using the CD signal at 230 nm, which they attribute to the formation of secondary structure. But we have shown that this signal is attributable mainly to a tertiary interaction of Trp-94 with His-18 (37). Given the spectral difficulties associated with barnase and k₁ ∼ k₂, it is not expected that there should be well-resolved amplitudes associated with the rapid formation of an intermediate monitored either by CD or fluorescence.

Bai et al. also suggest that, if any intermediate is formed in the folding of barnase, then it would just be a conformational readjustment of the denatured state as suggested for a “burst” phase in the folding of cytochrome c. Recent work from Roder and colleagues (38), using fast mixing, and from Eaton and colleagues, using laser T-jump (39), has shown that the “burst” is a submillisecond exponential transition between two distinct thermodynamic states, an expanded and a compact denatured state (an ensemble of partly folded states), as indicated by radius of gyration measurements using time-resolved low-angle scattering (40).

Failure to Trap the Intermediate Using H/²H-Exchange

Bai et al. (8) do not find evidence for a protected folding intermediate from competition experiments between refolding of deuterated barnase in H₂O and H/²H-exchange. They assumed that a protected intermediate is formed rapidly compared with the values of k_int (in the 5–20 s⁻¹ region). But the degree of hydrogen exchange they find, ≈50%, is in the range expected for the rate constant for formation of the intermediate being on the same time scale as for exchange (≈8–20 s⁻¹) because the fraction exchanging during folding is expected to be k_int/(k₁ + k_int).

Bai et al. did not find evidence for a protected folding intermediate from quenched-flow measurements of hydrogen-exchange (7). We once thought we had direct evidence for an intermediate that is formed at about 12–30 s⁻¹ compared with overall folding at 5 s⁻¹ (17). But we have now found that the intermediate is unstable during the labeling pulse (41). This instability is a recurrent problem in such trapping experiments, and so the failure to trap partly folded states does not prove they are absent. Our quenched-flow experiments of 11 yr ago were performed with very high concentrations of protein because of the low sensitivity of the ¹H NMR detection then available. Under such conditions, the folding intermediate may have been stabilized by transient aggregation (27), and so fortuitously we may have detected an intermediate that should otherwise have been unstable.

Conclusions

Either the formation or breakdown of the intermediate can be rate determining for folding of barnase and its mutants, depending on reaction conditions and nature of mutation, as implied by the studies of Perrett et al. (31). One can, therefore, choose suitable mutants for detecting different steps of the reaction. Conversely, just examining wild-type protein may lead to the missing of important steps. One of the strengths of studying many mutants is that they can illuminate different aspects of the kinetics and also act as a series of control experiments. This laboratory has espoused the combining of H/²H-exchange experiments and protein engineering for analyzing protein folding (28, 31). We first used exchange on mutants of barnase to detect which backbone protons required global unfolding for exchange (28). The analysis in this paper extends the evidence for a kinetically important intermediate in the folding of barnase, using these assignments. The latest development provides evidence for the intermediate being on-pathway, rather than off-pathway, a test that may be applicable to other systems. The methods of kinetics analysis described here can now be applied to mutants of barnase, as well as other proteins, to obtain previously inaccessible rate constants. Further, we should be able to obtain extensive measurements on k₁ and perform a Φ-value analysis for the formation of the transition state for the formation of the folding intermediate.

Abbreviations

CI2

chymotrypsin inhibitor 2

I

late intermediate state

N

native state

D

denatured state