Likelihood-based complex trait association testing for arbitrary depth sequencing data

Abstract

Summary: In next generation sequencing (NGS)-based genetic studies, researchers typically perform genotype calling first and then apply standard genotype-based methods for association testing. However, such a two-step approach ignores genotype calling uncertainty in the association testing step and may incur power loss and/or inflated type-I error. In the recent literature, a few robust and efficient likelihood based methods including both likelihood ratio test (LRT) and score test have been proposed to carry out association testing without intermediate genotype calling. These methods take genotype calling uncertainty into account by directly incorporating genotype likelihood function (GLF) of NGS data into association analysis. However, existing LRT methods are computationally demanding or do not allow covariate adjustment; while existing score tests are not applicable to markers with low minor allele frequency (MAF). We provide an LRT allowing flexible covariate adjustment, develop a statistically more powerful score test and propose a combination strategy (UNC combo) to leverage the advantages of both tests. We have carried out extensive simulations to evaluate the performance of our proposed LRT and score test. Simulations and real data analysis demonstrate the advantages of our proposed combination strategy: it offers a satisfactory trade-off in terms of computational efficiency, applicability (accommodating both common variants and variants with low MAF) and statistical power, particularly for the analysis of quantitative trait where the power gain can be up to ∼60% when the causal variant is of low frequency (MAF < 0.01).

Availability and implementation: UNC combo and the associated R files, including documentation, examples, are available at http://www.unc.edu/∼yunmli/UNCcombo/

Contact: yunli@med.unc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Next generation sequencing (NGS) technologies have transformed genomic studies since their appearance in 2005. In the past few years, NGS technologies have extended genome-wide association studies (GWAS) from common variants (minor allele frequency [MAF] > 0.05) to low frequency variants (MAF < 0.05) and provided a powerful tool to identify less common genetic variants associated with both Mendelian and complex traits (Auer et al., 2012; Bamshad et al., 2011; Goldstein et al., 2013; Haack et al., 2010; Kiezun et al., 2012; Lange et al., 2014; Torgerson et al., 2012). Most association testing methods are designed for genotypes, which are not directly available from NGS data. Thus, to perform association testing on NGS data, researchers typically perform genotype calling first (Chen et al., 2012; Li et al., 2009, 2011; McKenna et al., 2010; Mechanic et al., 2012; Wang et al., 2013). There are multiple sources of non-negligible error in NGS data, such as base-calling error and assembly or alignment error (Lee and Zhao, 2013; Li et al., 2012; Nielsen et al., 2011), each of which can cause considerable uncertainty in genotype calling. To take these various sources of error into account, many existing genotype calling algorithms adopt a probabilistic framework and generate genotype likelihood functions (GLF). Currently, accurate genotype calling can be achieved from GLF data either with high depth sequencing, or with low depth sequencing if a large number of individuals are sequenced (Kang et al., 2013; Li et al., 2009, 2010, 2011, 2012; Nielsen et al., 2011; Pasaniuc et al., 2012; Yan et al., 2014; Zhi et al., 2012; Zollner, 2012). However, genotype calling can incur a number of problems, particularly when served as an intermediate step for association testing or inference in population genetics. First, uncertainty in genotype calls is ultimately lost in subsequent inference, leading to possible power loss. Second, for low coverage sequencing data, multi-sample lineage disequilibrium (LD) aware methods can be rather computationally intensive. Third, the dependence of genotype calling on LD pattern may lead to potential bias in population genetics inference (Li, 2011). Lastly, both uncertainty (particularly differential uncertainty across varying values of phenotypic traits) and inconsistencies in called genotypes may result in inflated type-I error in association testing (Hong et al., 2012), particularly when combined from multiple datasets of varying sequencing depths.

In the literature, as an attractive alternative to the two-step testing approach (i.e. genotype calling in the first step and association testing based on called genotypes in the second step), computationally efficient one-step methods have been proposed for association analysis that directly model sequencing data for association testing without the intermediate genotype calling step. These one-step methods test association by incorporating GLF into the association testing likelihood function and carrying out likelihood based association inference (focusing primarily on testing) without explicitly calling genotypes (Derkach et al., 2014; Kim et al., 2010, 2011; Li, 2011; Satten, 2013; Skotte et al., 2012). Among them, Kim et al. (2010, 2011) and Li (2011) test allele frequency difference between cases and controls via likelihood ratio test (LRT). However, LRT requires numerical optimization under both the null and the alternative hypothesis and is therefore computationally demanding for large-scale datasets. Furthermore, existing LRT methods are designed only for binary traits and do not allow covariates adjustment. Skotte et al. (2012) adopt a generalized linear model (GLM) framework to accommodate both quantitative and binary traits and to allow covariates with a motivation conceptually similar to the one proposed for haplotype association testing (Schaid et al., 2002). Skotte et al. (2012) sketch the possibility of an LRT, where they envision a two-step approach that first estimates MAF based on a partial likelihood without phenotype information and then plugs the estimated MAF into the likelihood function to carry out association testing. However, the maximum likelihood estimator (MLE) of MAF in the two-step approach is not the oracle estimator (details to follow) and thus may incur power loss in subsequent association testing. Skotte et al. (2012) develop a computationally efficient score test (abbreviated as SKA score test hereafter) within the GLM framework; however, the information matrix used for the construction of the SKA score test ignores the correlation between the MAF estimator and estimators for the regression parameters, likely causing the SKA score test statistically underpowered. Moreover, the score test is generally not applicable when MAF is low (Satten, 2013; Skotte et al., 2012) because the minimal degree of variation in log-likelihood function required for numerical stability of score test statistic cannot be reached. Type-I error inflation was reported in the original work for MAF under 0.01 (Skotte et al., 2012). For the same reason, a variation of the SKA score test developed particularly for accommodating publicly available control groups (Derkach et al., 2014) also adopts 0.01 as MAF threshold.

In this paper, we first provide an LRT for association analysis of NGS data (UNC LRT), which allows covariate adjustment and handles both quantitative and binary phenotypic traits. In our LRT, the statistically efficient MLE of MAF is obtained in one unified framework that simultaneously estimates MAF and association parameters. Second, we improve upon the work of Skotte et al. (2012) by considering the correlation between MAF estimator and regression parameter estimators in the information matrix and develop a statistically more powerful score test (UNC score test). Third, although LRT and score test are asymptomatically equivalent, it is well known that their performance can differ considerably in practice. We evaluate the performance of our proposed LRT and score test by simulations and propose a combination strategy to take advantage of both tests (hereafter, referred to as UNC Combo). Extensive simulations and real data based analysis are carried out to examine the robustness, computational efficiency and statistical power of SKA score test, UNC score test, UNC LRT and UNC Combo. Our results suggest advantages of UNC combo in practice when genetic architecture (in particular, MAF of associated or causal genetic variant(s)) is unknown, particularly for quantitative traits. In our simulations, we observe gains in power up to 60% with losses of less than 8% across a wide range of scenarios considered, when using UNC Combo. In our real data based simulations, UNC Combo is able to identify all causal SNPs while other methods miss at least one.

2 Methods

2.1 Joint likelihood function

Suppose that a total of $n$ individuals are sequenced and $m$ SNPs are discovered. Further assume that all $m$ SNPs are biallelic and autosomal. For the $i\text{th}$ individual, let $D_i$ be the observed sequencing data and $Y_i$ the quantitative or binary phenotypic trait of interest, $X_i=\{X_{ij},j=1,\dots ,d\}$ the vector of $d$ covariates and $G_{ik}$ the unobserved true genotype at the $k\text{th}$ SNP. Our goal is to test whether the $k\text{th}$ SNP is associated with the trait of interest by performing single marker association testing without explicit genotype calling.

Let $p_k$ denote MAF of the $k\text{th}$SNP. By Hardy-Weinberg equilibrium (HWE), $f(G_{ik}|p_k)$, the probability of $G_{ik}$, follows a binomial distribution Binom$(2,p_k)$. For a quantitative or binary trait $Y_i$, we capture the dependence of $Y_i$ on $G_{ik}$ and $X_i$ through a GLM in the same way as in Skotte et al. (2012). Specifically, the probability density function of $Y_i$ takes the following form:

$$f(Y_i|X_i,G_{ik};{\alpha }_0,{\alpha }_1,\beta ,\varphi )=\exp \left(\frac{Y_i{\eta }_i-b({\eta }_i)}{a(\varphi )}+c(Y_i,\varphi )\right)$$ (1)

where $a(·), b(·)\text{ and }c(·)$ are known functions; $a(·)\text{, }c(·)$ depend on the distribution of $Y_i$ and $b(·)$ corresponds to a particular link function. ${\eta }_i$ is the linear predictor with ${\eta }_i={\eta }_{\alpha ,\beta }(X_i,G_{ik})={\alpha }_0+{\alpha }_1^T{X}_i+\beta G_{ik}$. Here, ${\alpha }_0$ is the intercept, ${\alpha }_1^{}$ the vector of coefficients for covariates, $\beta$ the effect of the unobserved true genotype $G_{ik}$ and $\varphi$ the parameter in $a(·), c(·)$. For example if $Y_i$ is quantitative and follows a normal distribution given $G_{ik}$ and $X_i,$ then $\varphi ={\sigma }^2,$ $a(\varphi )=\varphi ,$ $b(\eta )={\eta }^2\text{/2}$ $\text{and }c(Y_i,\varphi )=-Y_i^2/(2\varphi )-\log (2\pi \varphi )/2.$

The joint log-likelihood function of the parameters $\{\alpha =({\alpha }_0,{\alpha }_1),\beta ,\varphi ,p_k\}$ given $O=\{Y_i,D_i,X_i,i=1,\dots ,n\}$ can be written as:

$$\begin{array}{l}l(\alpha ,\beta ,\varphi ,p_k|O)=\\ {\displaystyle \sum _{i=1}^n\log \left[{\displaystyle \sum _{G_{ik}\in (0,1,2)}\left\{f(Y_i|X_i,G_{ik};\alpha ,\beta ,\varphi )f(D_i|G_{ik})f(G_{ik};p_k)\right\}}\right]}\end{array}$$ (2)

where $f(D_i|G_{ik})$ is the GLF from NGS data. To test whether the $k\text{th}$ SNP is associated with phenotypic trait of interest, the null hypothesis is $H_0:\beta =0$. This can be done using likelihood based testing methods such as an LRT or score test.

2.2 A powerful LRT statistic

Skotte et al. (2012) sketch the possibility of a two-step LRT approach to test the $H_0$ above: (step 1) $p_k$ is estimated by maximizing a partial log-likelihood function ${\displaystyle \sum _{i=1}^n\log \left[{\displaystyle \sum _{G_{ik}\in (0,1,2)}\left\{f(D_i|G_{ik})f(G_{ik};p_k)\right\}}\right]}$ without taking any phenotype information into account; (step 2) estimator of $p_k$ from step 1, ${\widehat{p}}_k$, is plugged into Equation (2) where an LRT can be carried out. However, step 1 ignores the correlation between $Y_i$ and $D_i$ and thus ${\widehat{p}}_k$ obtained in step 1 is not the oracle estimator of $p_k$ under the alternative hypothesis, which can consequently render the LRT in step 2 underpowered.

Here, we propose a statistically more powerful LRT (hereafter referred to as UNC LRT) to test $H_0:\beta =0$ by maximizing the log-likelihood function $l(\alpha ,\beta ,\varphi ,p_k|O)$ in Equation (2) in one single step. Specifically, UNC LRT statistic is

$$T_{\text{UNC LRT}}=-2\left[l(\stackrel{\sim }{\alpha },\beta =0,\stackrel{\sim }{\varphi },{{\displaystyle \stackrel{\sim }{p}}}_k|O)-l(\widehat{\alpha },\widehat{\beta },\widehat{\varphi },{\widehat{p}}_k|O)\right]$$ (3)

where $\{{\displaystyle \stackrel{\sim }{\alpha }},{\displaystyle \stackrel{\sim }{\varphi }},{{\displaystyle \stackrel{\sim }{p}}}_k\}$ (MLEs of $\{\alpha ,\varphi ,p_k\}$ under the null) are obtained by maximizing $l(\alpha ,\beta =0,\varphi ,p_k|O)$ and $\{\widehat{\alpha },\widehat{\beta },\widehat{\varphi },{\widehat{p}}_k\}$ (MLEs of $\{\alpha ,\beta ,\varphi ,p_k\}$ under the alternative) by maximizing $l(\alpha ,\beta ,\varphi ,p_k|O)$. Existing optimization functionalities such as optim() function in R can be used to maximize the log-likelihood functions above. The $T_{UNC LRT}$ statistic asymptotically follows a ${\chi }^2$ distribution with 1 degree of freedom.

2.3 Improved score test statistic (UNC score test)

The score test is appealing because parameters only need to be estimated under $H_0$. Under $H_0:\beta =0$,

$$\begin{array}{c}l(\alpha ,\beta =0,\varphi ,p_k|O)\\ ={\displaystyle \sum _{i=1}^n\log }\left[{\displaystyle \sum _{G_{ik}\in (0,1,2)}\left\{f(Y_i|X_i,G_{ik};\alpha ,\beta =0,\varphi )f(D_i|G_{ik})f(G_{ik};p_k)\right\}}\right]\\ ={\displaystyle \sum _{i=1}^n\log f(Y_i|X_i;\alpha ,\beta =0,\varphi )}\text{+}{\displaystyle \sum _{i=1}^n\log \left[{\displaystyle \sum _{G_{ik}\in (0,1,2)}\left\{f(D_i|G_{ik})f(G_{ik};p_k)\right\}}\right]}\end{array}$$ (4)

Consequently, $\{\alpha ,\varphi ,p_k\}$ can be estimated separately: ${{\displaystyle \stackrel{\sim }{p}}}_k$ (MLE of $p_k$ under $H_0$) can be estimated by only optimizing the second part of the Equation (4); $\{{\displaystyle \stackrel{\sim }{\alpha }},{\displaystyle \stackrel{\sim }{\varphi }}\}$ (MLEs of $\{\alpha ,\varphi \}$) can thus be easily obtained by applying starndard GLM algorithms on the first part of Equation (4). The time-consuming numerical optimization over the entire parameter space is thus avoided. Our score test statistic (hereafter referred to as UNC score test) takes the following form:

$$T_{UNC\text{ score}}=S^T(\stackrel{\sim }{\alpha },\beta =0,\stackrel{\sim }{\varphi },{{\displaystyle \stackrel{\sim }{p}}}_k)I^{-1}(\stackrel{\sim }{\alpha },\beta =0,\stackrel{\sim }{\varphi },{{\displaystyle \stackrel{\sim }{p}}}_k)S(\stackrel{\sim }{\alpha },\beta =0,\stackrel{\sim }{\varphi },{{\displaystyle \stackrel{\sim }{p}}}_k)$$ (5)

where $S(\alpha ,\beta ,\varphi ,p_k)$ is the score function (the first-order derivative of the log-likelihood function) and $S({\displaystyle \stackrel{\sim }{\alpha }},\beta =0,{\displaystyle \stackrel{\sim }{\varphi }},{{\displaystyle \stackrel{\sim }{p}}}_k)$ is its value evaluated at $\{{\displaystyle \stackrel{\sim }{\alpha }},\beta =0,{\displaystyle \stackrel{\sim }{\varphi }},{{\displaystyle \stackrel{\sim }{p}}}_k\}$ (MLE under $H_0:\beta =0$). $I(\alpha ,\beta ,\varphi ,p_k)$ is the observed information matrix (the second derivative of the log-likelihood function, mulitplied by –1) and $I({\displaystyle \stackrel{\sim }{\alpha }},\beta =0,{\displaystyle \stackrel{\sim }{\varphi }},{{\displaystyle \stackrel{\sim }{p}}}_k)$ is its value evaluated at $\{{\displaystyle \stackrel{\sim }{\alpha }},\beta =0,{\displaystyle \stackrel{\sim }{\varphi }},{{\displaystyle \stackrel{\sim }{p}}}_k\}$. Skotte et al. (2012) ignor the correlation between ${\displaystyle \stackrel{\sim }{\alpha }},{\displaystyle \stackrel{\sim }{\beta }},{\displaystyle \stackrel{\sim }{\varphi }}$ and ${{\displaystyle \stackrel{\sim }{p}}}_k$ and SKA score test statistic is:

$$T_{SKA\text{score}}=S^T({\displaystyle \stackrel{\sim }{\alpha }},\beta =0,\stackrel{\sim }{\varphi })I^{-1}(\stackrel{\sim }{\alpha },\beta =0,\stackrel{\sim }{\varphi })S(\stackrel{\sim }{\alpha },\beta =0,\stackrel{\sim }{\varphi })$$ (6)

The information matrix in Equation (6) contains only the second derivative with respect to $\alpha ,\beta ,\varphi$. It can be verified that

$$T_{UNC\text{score}}\ge T_{\text{SKA score}}.$$ (7)

Thus SKA score test is therefore theoretically less powerful than UNC score test. Details for the UNC score statistic and the proof of inequality (7) can be found in supplementary materials.

As manifested in Equations (5) and (6), both the UNC and SKA score test statistics involve the inverse of the information matrix $I^{-1}(·)$. In practical settings, a very small $p_k$ would lead to little variation in the log-likelihood function, which may cause $I(·)$ to be ill-conditioned. Consequently, $I^{-1}(·)$ may become numerically unstable which could result in inflated type-I error (Skotte et al., 2012). The practical implication is that these score test statistics cannot be blindly applied without MAF threshold (Derkach et al., 2014; Skotte et al., 2012).

2.4 Combination strategy (UNC combo)

We propose a practical combination strategy (UNC combo) which combines the strengths of the two UNC tests to achieve a good balance between computational efficiency, applicability (over the entire MAF spectrum) and statistical power. Denote the MAF of a SNP by $p$. UNC combo performs UNC score test when $p>p_{threshold}$ and UNC LRT when $p\le p_{threshold}$. UNC combo enjoys the advantages of UNC score test and UNC LRT in that: (i) it carries out UNC LRT only for SNPs with $p\le p_{threshold}$ and is thus computationally more efficient than UNC LRT; and (ii) unlike UNC score test, which fails to control type-I error for low frequency SNPs (details to follow), we can apply UNC combo over the entire MAF spectrum. In practice, $p$ can be estimated by optimizing the second part of Equation (4) before UNC combo is applied.

3 Simulations

We perform extensive simulation studies under a range of settings to evaluate the performance of SKA score test, UNC score test, UNC LRT and UNC combo. We use COSI’s bestfit model to generate a 100-kb region that mimics LD pattern, local recombination rate and population history of Europeans through a coalescent model (Schaffner et al., 2005). Within the region, 45 000 chromosomes are generated. We consider two baseline covariates: a binary covariate $X_1$ sampled from Bernoulli distribution with a success probability of 0.5 and a continuous covariate $X_2$ sampled from standard normal distribution. Quantitative trait values are generated via a simple linear regression model:

$$Y={\alpha }_0+{\alpha }_1{X}_1+{\alpha }_2{X}_2+\beta G_k+\epsilon$$

where ${\alpha }_0=1, {\alpha }_1=1, {\alpha }_2=1$ and $\epsilon$ follows a standard normal distribution. Binary trait values are generated via a logistic regression model:

$$\log \text{it}(\text{Prob}(Y=1))={\alpha }_0+{\alpha }_1{X}_1+{\alpha }_2{X}_2+\beta G_k$$

where ${\alpha }_0=-3.65\text{ (trait with 2.5\% prevalence),}$ ${\alpha }_1=1$and ${\alpha }_2=1$. Under the null hypothesis, 10 000 replicates are generated to evaluate Type-I errors. We evaluate type-I errors for three sample sizes: 500, 1000 and 2000. Under the alternative hypothesis, we assume one causal SNP and specify three MAFs for the causal SNP: 0.006, 0.011 (so that it is slightly above the MAF threshold) and 0.02. For each MAF, 1000 replicates each with sample size 1000 are generated. Sequencing data are simulated using ShotGun (Kang et al., 2013) with a per base pair error rate of 0.5%. Average sequencing depths ($d$) are chosen to be 2X, 4X, 10X and 30X to cover a wide range of depth scenarios.

3.1 Simulation results

We conduct our first series of simulation studies to evaluate SKA score test, UNC score test and UNC LRT when only one SNP is tested. Type-I errors across all scenarios of sample sizes and sequencing depths are displayed in Tables 1, 2 and in Supplementary Tables S1–S4 with significant threshold 1e−4. Intuitively, MAF threshold to achieve controlled Type-I error may vary with sample size and/or sequencing depth. Our simulations show that MAF threshold of $20/2n$ would be conservative enough to control type-I errors across a wide spectrum of scenarios. For example in Tables 1 and 2, type-I errors of the two score tests are well controlled for all sequencing depths if $\widehat{p}>p_{threshold}=0.01$ ($\widehat{p}\text{ is the MAF estimate}$). The severity of type-I error inflation varies by sequencing depth $d$ and $p_{threshold}$: the lower $d$ and $p_{threshold}$ are, the greater the inflation of type-I error is. That is because a lower sequencing depth and a smaller $p$ cause the information matrix to be more ill-conditioned and result in a more numerically unstable score test statistic (more details in the Section 5). The calculation of UNC LRT statistic involves only the subtraction of two log-likelihoods and is fairly stable even when variation in log-likelihoods is small. As can be seen, the type-I errors of the UNC LRT are all controlled, even when all SNPs are included ($p_{threshold}=0$).

Table 1.

Type-I errors of single SNP testing for quantitative trait

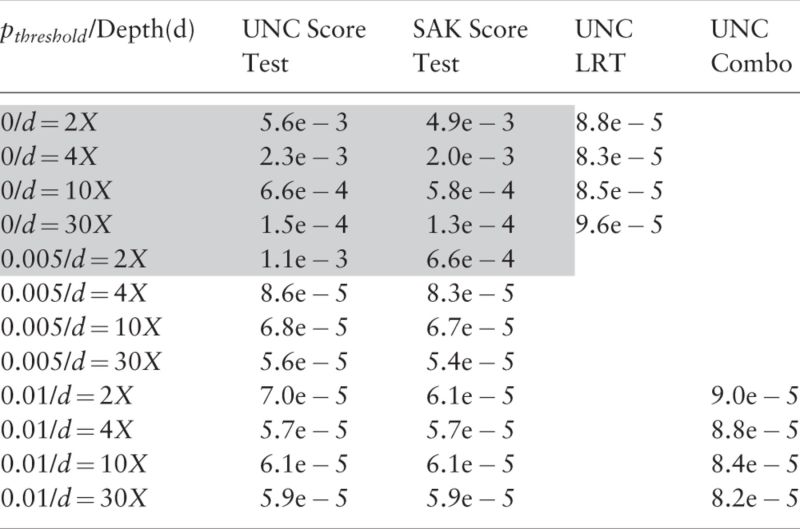Note: Significant threshold is 1e − 4. Sample size $n=1000$.

Grey marks inflated type-I errors.

Table 2.

Type-I errors of single SNP testing for binary trait

Note: Significant threshold is 1e − 4. Sample size $n=1000$.

Grey marks inflated type-I errors.

Supplementary Figures S1–S6 present the power results of single SNP testing for quantitative and binary trait, with MAF of the causal SNP taking three values: $0.006, 0.011\text{ and 0.02}$. MAF thresholds for score tests are chosen based on Tables 1 and 2 to assure control of type-I errors ($p_{threshold}=0.01$). Powers of association tests based on dosage after multi-sample LD aware calling are also provided for comparison. For a quantitative trait, UNC LRT outperforms the two score tests by a large margin (up to ∼95%) when $p\le p_{threshold}$ or $p\approx p_{threshold}$, which is expected since the causal SNP(s) would be filtered out by a score test if $\widehat{p}<p_{threshold}$. For a binary trait, the powers of the score tests are maintained even if $p\le p_{threshold}$. This is because the causal allele is enriched among cases, making $\widehat{p}>p_{threshold}$. Overall, the performance of UNC score test is always slightly better than or at least comparable to that of SKA score test under various scenarios.

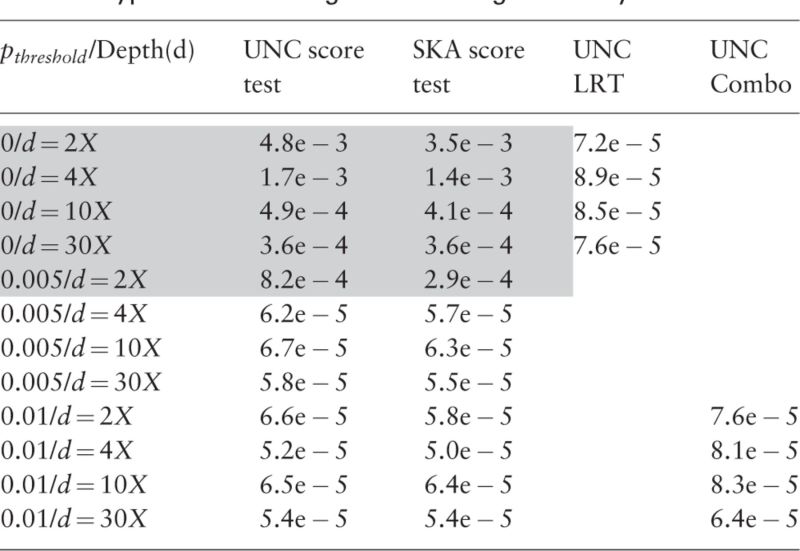
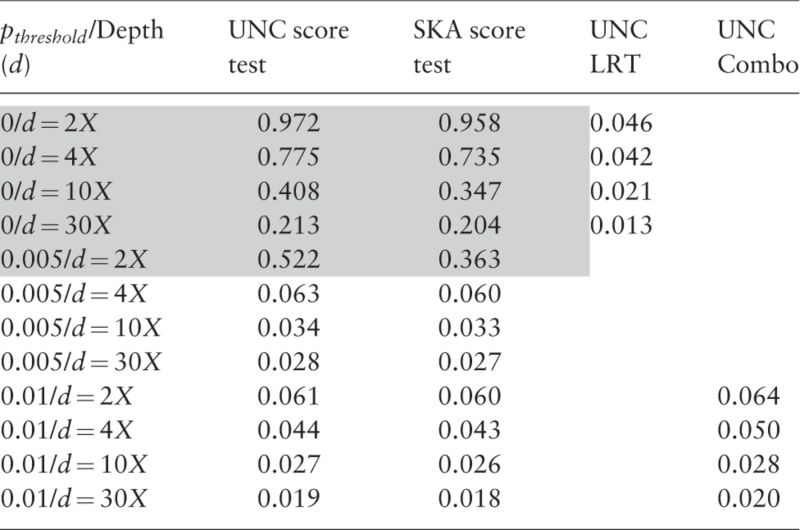
In practice, causal SNPs are unknown and we need to test all SNPs in the genetic region(s) of interest. The second series of simulation studies are therefore devoted to investigating the performance of SKA score test, UNC score test and UNC LRT when multiple SNPs are tested. The two score tests are carried out only for SNPs satisfying $\widehat{p}>p_{threshold}$. Meanwhile, UNC LRT is applied on all SNPs. The type-I errors of these methods across all scenarios are displayed in Tables 3, 4 and in Supplementary Tables S5–S8 for quantitative and binary traits, respectively. We use a Bonferroni correction to control type-I errors. As can be seen, type-I errors of UNC LRT are well controlled across the entire spectrum of sequencing depths and sample sizes without MAF filtering. Therefore, UNC LRT is generally more robust than the two score tests and more appropriate for the entire MAF spectrum. Similar to the single SNP testing series, the two score tests have controlled type-I errors when $\widehat{p}>p_{threshold}=0.02$ for $n=500$, $\widehat{p}>p_{threshold}=0.01$ for $n=1000$ and $\widehat{p}>p_{threshold}=0.005$ for $n=2000$.

Table 3.

Type-I errors of multiple testing (multiple SNPs are separately tested within each genomic region of interest) for quantitative trait

Note: Significant threshold of is 0.05/(# of SNPs) in the targeted region.

Grey marks inflated type-I errors.

Table 4.

Type-I errors of multiple testing (multiple SNPs are separately tested within each genomic region of interest) for binary trait

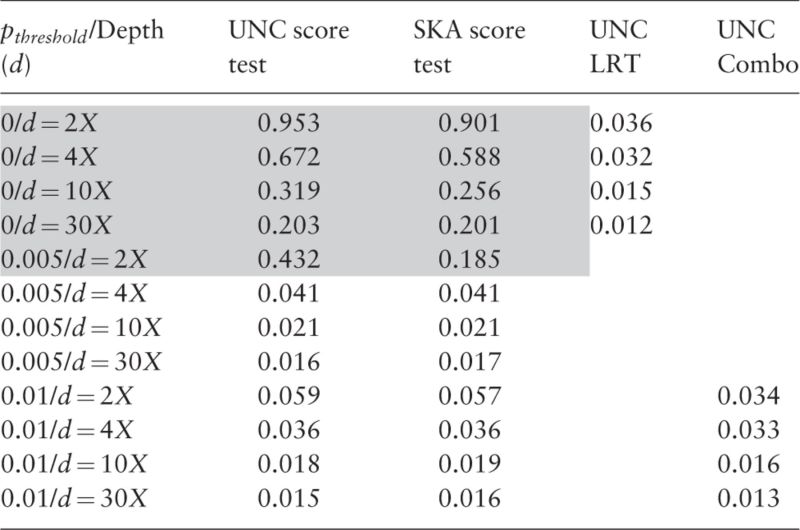Note: Significant threshold of is 0.05/(# of SNPs) in the targeted region.

Grey marks inflated type-I errors.

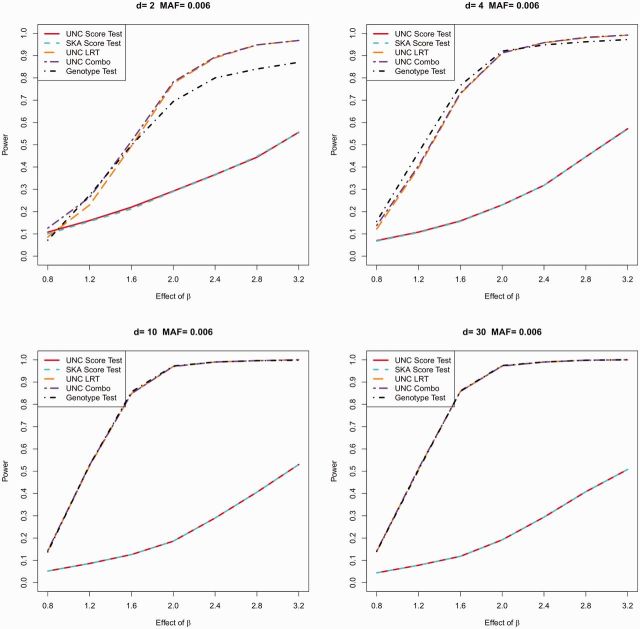
Figure 1 and Supplementary Figures S7–S11 present the statistical power in this second series of simulations. Similar to the single SNP testing series: if $p_{threshold}>p_{causal}$ (e.g. $p_{causal}=0.006$) for a quantitative trait, UNC LRT is much more powerful than UNC score test; when the trait is binary, the powers of the two UNC tests are comparable. If $p_{threshold}<p_{causal}$, UNC score test is more powerful than UNC LRT under most scenarios for both quantitative and binary traits. Finally, the power of UNC score test is usually slightly better than or at least comparable to that of the SKA score test under all scenarios (e.g. $p_{causal}=0.006, d=2\text{X}$ for a binary trait). The extent to which UNC score test improves over SKA score test depends on the nature of the underlying association. In Appendix F, we demonstrate a scenario in which the UNC score test outperforms SKA score test by up to ∼15% by letting the effect of causal SNP depend on covariates.

Fig. 1.

Powers of multiple testing for quantitative trait with $p_{\text{threshold}}=0.01$ . MAF = 0.006 and n = 1000

Now, we focus on the performance of UNC Combo in both series of simulations described above. As demonstrated in Tables 1–4 and Supplementary Tables S1–S8, type-I errors of UNC combo are all well controlled with $p_{threshold}$($20/2n$). Statistical power results of UNC combo are also presented in Figure 1 and Supplementary Figures S1–S11. Note that UNC combo is most effective for quantitative traits: it outperforms at least one of the two other UNC tests under all scenarios. By using UNC combo instead of the UNC score test, power gain can be as high as ∼90% ($d=30\text{ and MAF}=0.006$ in single SNP testing series [Supplementary Fig. S1]) and ∼70% ($d=30\text{ and MAF}=0.006$ in multiple testing series [Fig. 1]) with minimal loss (∼8%) ($d=4\text{ and MAF}=0.02$ in the multiple testing series [Supplementary Fig. S8]). For binary trait simulations, UNC combo is uniformly the least powerful test, even when the causal MAF is small. In fact, as aforementioned, case-control design makes $\widehat{p}$ much larger than $p$ and thus causal SNPs with small $p$ are less likely to be filtered out and missed by score tests (discussions regarding using controls only to estimate MAF can be found in the Section 5). Therefore, the ability of UNC combo to include all SNPs becomes less necessary for binary traits and the added noise becomes the dominating consequence. In summary, we recommend UNC combo with $p_{threshold}$ ($20/2n$) for quantitative traits and UNC score test with $p_{threshold}$ ($20/2n$) for binary traits.

Table 5 presents the comparison of computational costs of SKA score test, the three UNC methods and dosage-based test when sequencing depth $d=4\text{X}$. As displayed in Table 5, 33%$-$41% of computation cost can be saved by adopting UNC combo instead of UNC LRT. In practice, we usually have little prior knowledge regarding the MAFs of the causal SNPs and thus UNC combo can achieve a reasonable trade-off between power and computational burden for quantitative traits.

Table 5.

Comparison of computational costs (time in seconds)

Depth (d)	Trait	SKA score test	UNC score test	UNC LRT	UNC Combo	Dosage
d = 4X	quanti	32.1	32.5	365.6	214.1	13317.2
d = 4X	binary	57.2	57.6	231.2	153.0	13315.6

The average number of SNPs in one simulated genetic region is ∼762 when d = 4X. “quanti” is abbreviation for quantitative.

4 Real data analysis

We apply our proposed methods to a targeted sequencing dataset from the CoLaus study, where 1956 CoLaus subjects from Lausanne (Switzerland) are sequenced at relatively high depth (medium depth ∼27X) in the exons of 202 genes (Firmann et al., 2008; Nelson et al., 2012). 7 genes on chromosome X are excluded from drug related analysis. A total of 22 992 SNPs are discovered across the 195 autosomal genes among the 1956 subjects. Three SNPs ($G_1,G_2\text{and}{G}_3$) on chromosomes 1, 6 and 8 are chosen to be casual with $p_{causal}=0.004,\text{ 0.01 and 0}.15$, respectively. Quantitative trait is generated by

$$Y={\alpha }_0+{\alpha }_1{X}_1+{\alpha }_2{X}_2+{\beta }_1{G}_1+{\beta }_2{G}_2+{\beta }_3{G}_3+\epsilon$$

where $X_1,X_2\text{and}\epsilon$ are generated in the same way as in the simulation study. ${\alpha }_0={\alpha }_1={\alpha }_2=1, {\beta }_1=1.8, {\beta }_2=1\text{ and }{\beta }_3=0.16$. Moreover, data of two different sequencing depths are simulated by (i) choosing 1 out of every 5 short reads (“Divided by 5” where 6574 SNPs are detected); (ii) choosing 1 out of every 10 short reads (“Divided by 10” where 4255 SNPs are detected). As in the simulation study, we pick $p_{threshold}=0.005$ for score tests and UNC combo when trait is quantitative. Bonferroni correction is adopted to control type-I error.

Manhattan plots of association test statistics based on SKA score test, UNC score test, UNC LRT and UNC combo are displayed in Supplementary Figure S12. As shown in Supplementary Figure S12, the two score tests perform similarly and both outperform UNC LRT when $p_{causal}>p_{threshold}$. On the other hand, UNC LRT can identify causal SNPs with $p_{causal}\text{ < }{p}_{threshold}$. As expected, UNC combo combines the advantages of UNC score test and UNC LRT and is more powerful than both under the realistic setting where MAFs of the causal SNPs are unknown. Take “Divided by 5” as an example: first, none of the methods result in any false positives; second, UNC score test identifies $G_2$ ($p_{causal}>p_{threshold}$) while UNC LRT fails to; on the other hand, UNC LRT successfully identified $G_1$ ($p_{causal}\text{ < }{p}_{threshold}$); third, UNC combo successfully detects both $G_1\text{and}{G}_2$; finally, “Divided by 5” is more powerful than “Divided by 10”, which is expected as statistical power for association testing decreases with sequencing depth.

5 Discussion

Association testing using NGS data without genotype calling is an appealing approach. This approach not only avoids the potentially computationally intensive genotype calling step but also carries all of the information from sequencing into association, in contrast to at least some information loss with an intermediate genotype calling step. Population structure and other potential confounding factors are almost inevitable in GWAS studies and need to be adjusted for. In this article, we develop UNC score test and UNC LRT to allow covariate adjustment in association testing based on GLFs. Both UNC score test and UNC LRT directly incorporate the uncertainty of the observed sequencing data into analysis by constructing likelihood function based on GLFs and do not require explicit genotype calling. Instead of a two step approach (Skotte et al., 2012), UNC LRT produces MLE of MAF together with MLEs of regression parameters in one step and thus is theoretically more powerful. The UNC score test improves upon the previous work of Skotte et al. (2012) by taking into account the correlation between regression parameter estimators and MAF estimator.

Using simulations, we have demonstrated that UNC score test is generally statistically more powerful than, or at least comparable to, SKA score test. UNC score test is computationally faster than UNC LRT because score test only involves the model under the null hypothesis and does not require time-consuming optimization. On the other hand, in practice, UNC LRT can be applied to SNPs over the entire MAF spectrum while UNC score test can only be applied to SNPs with MAFs greater than certain threshold ($p_{threshold}$) because type-I errors of score tests are inflated without MAF filtering. We therefore propose a combination strategy (UNC combo) to take advantage of the strengths of our two tests. As shown in simulation results for quantitative trait, UNC combo improves upon the two UNC tests in three aspects: (i) it can be applied to all SNPs across the entire MAF spectrum, a desirable feature inherited from UNC LRT; (ii) it is computationally more efficient than UNC LRT, because LRT is calculated only for SNPs with MAF below $p_{threshold}$; (iii) it manifests higher statistical power than at least one of the two UNC tests. In the real data analysis, UNC combo outperforms both UNC LRT and UNC score test for simulated quantitative traits. For the reasons above, we recommend UNC combo when the trait(s) of interest is/are quantitative. For binary traits, UNC score test outperforms other methods and is thus recommended.

MAF and variation in log-likelihood function are two factors potentially correlated with the inflation of type-I error of the score test. We fit regression models to investigate the relationship among them. We use the determinant of the information matrix as a measure of variation in the log-likelihood function. A linear regression analysis shows that UNC score test statistic is negatively associated with the determinant of information matrix (P-value < 2e−16). Moreover, another linear regression indicates that the determinant of the information matrix is positively associated with MAF (P-value < 2e−16). Consequently, the lower the MAF of a SNP, the more ill-conditioned the information matrix becomes and the more likely to result in inflated type-I error.

For a simulated binary trait, we also evaluate an alternative approach to filter out SNPs for the score tests: namely, estimating MAFs using only controls and filtering SNPs based on control MAF estimation. Simulation results show that this approach may lead to inflated type-I error (e.g. type-I error is 0.265 for UNC score test and 0.132 for SKA score test with $p_{threshold}=0.01$, $d=2$ and $n=1000$). This is because MAFs of rare variants tent to be over-estimated when only controls are used in estimation (Li and Leal, 2009; Liu and Leal, 2012; Yan and Li, 2014). For example, the MAF estimate of ascertained singletons in controls would be double of its true value (assuming equal numbers of cases and controls) if only controls were used to estimate the MAF. These unwarrantedly retained rare variants consequently lead to numerical instability and eventually to inflated type-I errors.

In Appendix F, we introduce correlation between MAF estimator and association parameter estimators by letting the effect of the causal SNP depend on covariates. In real data, this can be observed due to gene environment interactions. Under the scenario, UNC score test outperforms SKA score test by up to ∼15%. In practice, non-negligible correlation between MAF and association parameters estimators can arise in various and unknown ways. It is thus desirable to have a theoretically more powerful score test (UNC score test) to guard against such scenarios where correlation among MAF and regression parameters is non-negligible.

The optimal MAF threshold depends on the genetic architecture (number, MAFs and effect sizes of the causal SNPs), which is generally unknown. This threshold also depends on the sample size ($n$) and sequencing depth. To err on the conservative side, we choose $p_{threshold}=20/2n$ as adopted in the literature (Derkach et al., 2014; Skotte et al., 2012) and as supported by our own simulation results. In the future, an optimal threshold might be derived by taking sequencing depth into account. Moreover, differential sequencing depths between cases and controls introduce additional biases, leading to inflated type-I error of SKA as shown in Derkach et al. (2014). Future work is desired to study the impact of differential sequencing depths on our proposed UNC tests. Lastly, while the current work focuses on single variant association, extension to rare variant association testing is highly warranted given the higher level of uncertainty in genotype calling for rarer variants.

Funding

This research is supported byNIH grants R01-HG006292 and R01-HG006703.

Conflict of Interest: none declared.