Abstract
Ultrasound neuromodulation holds promise as a non-invasive technique for neuromodulation of the central nervous system. However, much remains to be determined about how the technique can be transformed into a useful technology, including the effect of ultrasound frequency. Previous studies have demonstrated neuromodulation in vivo using frequencies less than 1 MHz, with a trend towards improved efficacy with lower frequency. However, using higher frequencies could offer improved ultrasound spatial resolution. We investigate the ultrasound neuromodulation effects in mice at various frequencies both below and above 1 MHz and find that frequencies up to 2.9 MHz can still be effective for generating motor responses, but also confirm that as frequency increases, sonications require significantly more intensity to achieve equivalent efficacy. We argue that our results provide evidence that favors either a particle displacement or a cavitation-based mechanism for the phenomenon of ultrasound neuromodulation.
Keywords: ultrasound neuromodulation, ultrasound neurostimulation, brain stimulation, cavitation, radiation force, particle displacement, electromyography
Introduction
As a technique for non-invasive stimulation of the brain, ultrasound neuromodulation has received rapidly increasing interest in recent years for two main reasons: first, encouraging developments in the use of ultrasound neuromodulation in vivo have raised the possibility of using the technique more extensively in a wide variety of research and perhaps even therapeutic applications; second, alternative neuromodulation technologies face significant technical limitations. Electrical stimulation using implanted electrodes are precise and effective but require invasive procedures for placement. Transcranial direct current stimulation and transcranial magnetic stimulation are both noninvasive techniques but suffer from low spatial resolution and are unable to reach deep targets (Wagner et al. 2007). Optogenetic techniques have high spatial resolution and precise cell-type specificity, but rely on methods of genetic vector delivery that have yet to be approved for widespread human use (Fenno et al. 2011).
In contrast, ultrasound has been shown to be a noninvasive, safe, and spatially specific method for neuromodulation in various animal models. Ultrasound neuromodulation has been successfully performed transcranially in various animal species, including mice (King et al. 2013; King et al. 2014; Mehić et al. 2014; Tufail et al. 2010), rats (Kim et al. 2012; Kim et al. 2014; Kim et al. 2015; Min et al. 2011; Younan et al. 2013), sheep (Lee et al. 2016), monkeys (Deffieux et al. 2013), and even humans (Lee et al. 2015; Legon et al. 2014). Histological techniques have confirmed that it is possible to deliver sonications powerful enough to elicit ultrasound neuromodulation without causing damage to tissues (Tufail et al. 2010; Yoo et al. 2011). At higher intensities, focused ultrasound is already used to reach deep, subcortical targets for ablation applications (Fry et al. 1954; Wang et al. 2015), and several studies have demonstrated non-destructive spatially specific ultrasound neuromodulation (Fry et al. 1958; King et al. 2014; Mehić et al. 2014; Yoo et al. 2011).
The vast majority of published transcranial in vivo neuromodulation studies have been performed using relatively low ultrasound frequencies of less than 1 MHz. The use of such frequencies has generally been necessary because attenuation in tissues and the skull increases with frequency. Excessive attenuation is undesirable because it can both lead to potentially harmful heating effects in the attenuating tissues and reduce the ability to reach deeper structures. In addition, within the window of frequencies below 1 MHz, at least three in vivo studies have observed decreasing neuromodulation efficacy at the upper end of the frequency range tested that could not be attributed to heating effects. Tufail et al. 2010 observed decreasing normalized EMG amplitudes of ultrasound-evoked contractions with increased frequency (250 kHz to 500 kHz), while King et al. 2013 reported that increased intensities were required at higher frequencies to obtain the same success rate (250 kHz to 600 kHz). More recently, Kim et al. (2014) observed a 30%–40% lower threshold for inducing motor responses at 350 kHz than at 650 kHz. These trends have also been observed in the peripheral nervous system over a more extensive frequency range that goes beyond 1 MHz; Gavrilov et al. 1976 demonstrated that sonicating at higher frequencies up to 2.67 MHz required higher intensity to produce threshold sensations in human fingers.
From a practical point of view, these trends appear to be unfortunate because sonicating at higher frequency has the potential for achieving more spatially specific effects, given the shorter wavelengths involved and the ability to resolve smaller focal spot sizes. The eventual hope is to demonstrate targeted neuromodulation-based therapies and techniques that focus tightly on specific regions of the brain. One striking example is offered by Menz et al. 2013b, who used a 43 MHz ultrasound transducer to achieve a focal spot size of 87 microns in salamander retina in vitro, a scale perhaps necessary for achieving the high spatial resolution required for a retinal prosthesis.
However, the use of pure-tone, high frequencies far above 1 MHz has yet to be found effective in vivo for transcranial applications, and even at intermediate frequencies, both the scale and the cause of reduced efficacy associated with increasing frequency remains undetermined. One possibility is that as frequency rises, the focal spot size typically tightens, inevitably changing the amount of stimulated brain tissue. If it were possible to factor out the effect of focal spot size, any frequency dependence could cast light on what remains the most vexing problem in understanding ultrasound neuromodulation: there is still no accepted theory of how it works. Nevertheless, several of the proposed candidate mechanisms for ultrasound neuromodulation, including cavitation and radiation force, are inherently frequency dependent but in distinguishably different ways, so at least one of these could play a role in explaining the observed frequency effects. In addition, the notion of particle displacement, in which neurocellular components are buffeted by ultrasound waves, has been proposed as another potential mechanism that could underlie ultrasound neuromodulation (Gavrilov et al. 1976). It is thus of potentially great importance to explore the effects of higher ultrasound frequencies in vivo as these could not only be relevant for optimizing clinical and research applications, but could also help to clarify how ultrasound elicits its neuromodulatory effects.
Our goal in this study was to achieve a better understanding of the frequency response of in vivo ultrasound neuromodulation. We first sought to quantify the intensities required to achieve effective transcranial neuromodulation for several ultrasound frequencies both above and below 1 MHz. We then aimed to explain differences observed across ultrasound frequencies by examining the contributions of focal spot size, as well as different hypothesized frequency-dependent mechanisms underlying ultrasound neuromodulation.
Materials and Methods
Experimental design
Five sets of experiments were performed to examine the effects of ultrasound frequencies ranging from 0.3 to 2.9 MHz (Table 1). Experiment A was designed to determine how much of the previously reported frequency dependence at low frequencies (i.e., below 1 MHz) was due to changing sonication duration. King et al. 2013 varied the ultrasound frequency while simultaneously varying the ultrasound pulse duration; thus, whether the effects observed were due to ultrasound frequency, to sonication duration, or some combination of the two, was left ambiguous. In order to overcome this ambiguity, we tested the response of mice to continuous wave sonications at four low frequencies (0.3, 0.4, 0.5, and 0.6 MHz) using a constant number of ultrasound cycles (40,000 cycles, as in King et al. 2013) and, in addition, using pulses of constant duration (80 ms). Employing a 0.5 MHz planar transducer with a waveguide similar to King et al. 2013, we sonicated five mice according to a semi-randomized schedule consisting of blocks of sonications (Figure 1). Within each block, while frequency and duration of each sonication were held constant, four sonications of different intensities and one sham sonication (where the output of the function generator responsible for generating the ultrasound was off) were performed in random order. The blocks themselves were randomly ordered within sets, each chosen to include all combinations of frequency and duration. For each mouse, at least 10 sets were performed resulting in at least 10 trials for each sonication type (i.e. unique combination of intensity, frequency, and duration).
Table 1.
Experiment parameters. Larger cone images can be found in Supplemental Figure 9.
| Experiment | Center frequency (MHz) | Diameter (in.) | Focusing | Cone | US parameters | N mice |
|---|---|---|---|---|---|---|
| A | 0.5 | 1 | planar |

|
Frequency: 0.3, 0.4, 0.5, and 0.6 MHz Duration: 80 ms CW and 40,000 cycles Intensities: 4 intensities plus sham for each frequency, within a range from 0.1 to 3.5 W/cm2 sppa after attenuation |
5 |
| B | 1.0 | 0.75 | 1.90″ PTF |

|
Frequency: 0.6, 1.0, and 1.4 MHz Duration: 80 ms CW Intensities: 5 intensities plus sham for each frequency, within a range from 0.02 to 9.4 W/cm2 sppa after attenuation |
5 |
| C | 2.25 | 0.75 | 1″ PTF |

|
Frequency: 1.4, 1.9, 2.4, and 2.9 MHz Duration: 80 ms CW Intensities: 4 intensities plus sham for each frequency, within a range from 1.1 to 127 W/cm2 sppa after attenuation |
5 |
| D | 0.5 | 1 | 1.25″ PTF |

|
Frequency: 0.3, 0.4, 0.5, and 0.6 MHz Duration: 80 ms CW Intensities: 4 intensities plus sham for each frequency, within a range from 0.04 to 3.1 W/cm2 sppa after attenuation |
5 |
| E | 2.25 | 0.75 | 1″ PTF |

|
Frequency: 1.4 and 2.9 MHz Duration: 80 ms CW Intensities: at 1.4 MHz, 56.9 W/cm2 sppa after attenuation plus sham; at 2.9 MHz, 90.7 W/cm2 sppa after attenuation plus sham |
6 |
CW = continuous wave; PTF = point target focus; SPPA = spatial peak pulsed average; US = ultrasound.
Figure 1.

Experimental protocol. The sets labeled in this example are for Experiment A including sonications with constant number of cycles and constant duration. US = ultrasound.
We designed Experiments B and C to extend our knowledge of the neuromodulatory efficacy of ultrasound in vivo to pure-tone frequencies beyond 1 MHz, a regime that as far as we know has not been previously explored in vivo. For Experiment B, we sonicated five mice at three frequencies (0.6, 1.0, and 1.4 MHz) and at five intensities for each frequency. For Experiment C, a different set of five mice was sonicated at four higher frequencies (1.4, 1.9, 2.4, and 2.9 MHz) and at four intensities. All sonications were kept at constant pulse duration of 80 ms. Similar to Experiment A, mice were sonicated in random block order where in this case each block was defined by the sonication frequency. By combining this data with the constant duration sonications from Experiment A, our results span the frequency range from 0.3 to 2.9 MHz.
One confound while investigating the frequency dependence was focal spot size, which typically changes such that higher frequencies generally result in smaller focal spot sizes. To gain further insight into the effect of focal spot size, we performed Experiment D, which tested the same frequencies as Experiment A using 80 ms pulse durations while using a focused transducer instead of planar to change the focal spot size. All beam plots can be found in the Supplemental Figures S1–8.
A possible complication associated with a changing focal spot size is that sonications with smaller focal spot sizes may be less likely to modulate the specific cortical areas required for eliciting a muscle contraction. To test this hypothesis, we performed Experiment E, in which we sonicated at multiple different points across an area of the mouse brain using two different frequencies in order to determine whether a tighter focal spot might activate a sensitive region better than a more diffuse spot. We sonicated six mice across the brain in random order in 1 mm increments, alternating between 1.4 and 2.9 MHz sonications at the highest intensity used in Experiment C. Focal spot sizes were 1.20 mm and 0.65 mm full width half max intensity, respectively (Supplemental Figure S7). Each location was sonicated at least 5 times and at most 10 times for each frequency.
Ultrasound transducers
Four ultrasound transducers (Olympus, Waltham, MA) were used, one for each set of experiments, to cover a range of frequencies from 0.3 MHz to 2.9 MHz (Table 1). A plastic waveguide filled with degassed water was attached to the end of each transducer to reduce the surface area coupled to the mouse head. Dimensions of all transducers and waveguides can be found in Table 1 and Supplemental Figure S9 respectively.
Animal experiments
Mice were used in this study because the neurostimulatory effects of ultrasound have been well-established in this animal model (King et al. 2013; King et al. 2014; Mehić et al. 2014; Tufail et al. 2010), and because of their relatively thin skulls, which allow for efficient ultrasound transmission even at higher frequencies.
All animal procedures were approved by the Stanford Administrative Panel on Laboratory Animal Care. Adult female C57BL/6 mice (Charles Rivers, Wilmington, MA) were housed in a facility with 12-hour light/12-hour dark cycle, and had free access to water and food. Anesthesia was induced in a clean induction chamber using 2% isoflurane at 1 LPM O2, after which anesthesia was delivered through a glove-covered nose cone with a crossed slit opening. An evacuation hose was placed near the mouse to prevent buildup of isoflurane fumes. During preparation, mice were kept warm on a heating blanket, and rectal temperature was periodically monitored. The eyes were covered with ophthalmic ointment to prevent drying and irritation. The mouse head was shaved first using clippers and then depilatory cream (Nair, Church & Dwight, Ewing, NJ). The mouse was then placed in a clean plastic half-cylinder with four holes cutout for limbs (Figure 2). 22-gauge catheters (Nipro, Osaka, Japan) were inserted into the triceps muscles of both forelimbs, through which two copper hooks were placed at each site to record the electromyogram (EMG) signal. Each hook consisted of 32-gauge enamel-coated copper wire for which the distal 4–5 mm of coating was stripped. A ground lead was attached to copper tape wrapped around the tail base. After attachment of all leads, the mouse in the half-cylinder was then suspended to allow for free movement of the limbs. The transducer with the attached waveguide was placed above the mouse head based on external anatomical markers (Figure 3), with the waveguide in contact with the scalp of the mouse, thus ensuring consistent placement of the transducer relative to the mouse brain. Ultrasound gel was used to couple the waveguide on the transducer with the head of the mouse. A heat lamp was used to keep the animal warm while elevated from the table.
Figure 2.
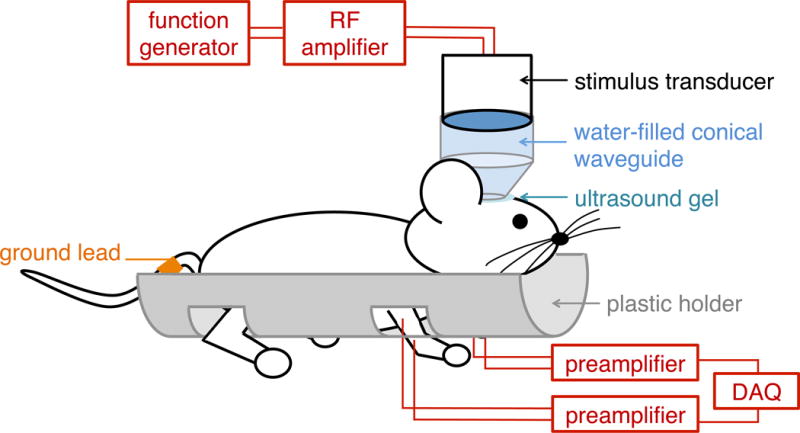
Diagram of animal setup. DAQ = data acquisition; RF = radiofrequency.
Figure 3.
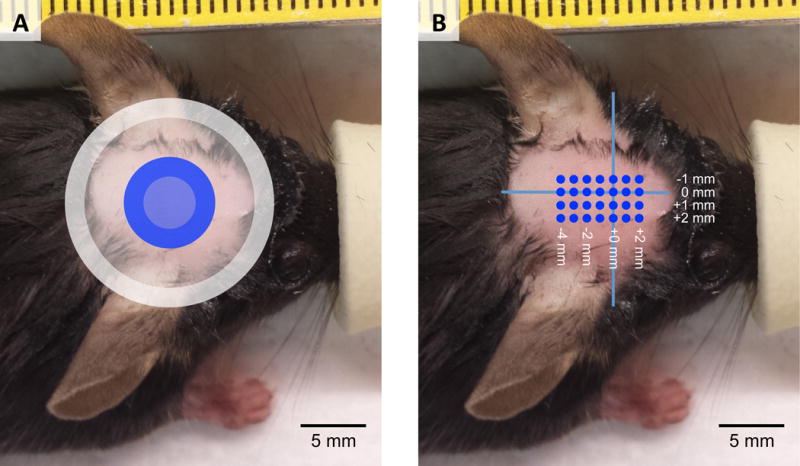
Placement of transducer waveguide relative to the head of the mouse for Experiments A–D (Figure 3A) and Experiment E (Figure 3B). The gray ring marks the placement of the waveguide for Experiments A and D, and the blue ring indicates the location of the waveguide for Experiments B and C. The width of the ring indicates the width of the plastic at the tip of the waveguide. Both are centered in the left-right direction. For Experiment E, we sonicated across the mouse brain with high frequency ultrasound. Locations of sonications are marked in blue dots at 1 mm spacing, with the origin (0,0) defined as midline in the right-left direction and the rostral tip of the ears in the rostral-caudal direction.
To minimize experimental variation resulting from anesthesia while allowing time for completion of the aforementioned procedures, the isoflurane level was reduced to 0.5% in all mice thirty-four minutes after the start of anesthesia, using a vaporizer calibrated at low levels of isoflurane. This was done to bring the mouse down to a less anesthetized state required in order to elicit muscle contractions. Typically within five minutes, sub-contraction EMG activity was observed, and the anesthesia was then set to and maintained at 0.6%. Setting a sufficiently low level of anesthesia was necessary in order to observe motor responses, while keeping the anesthesia high enough to prevent the mouse from crawling out of the experimental setup. Preliminary experiments showed that a change in isoflurane level of 0.2% could change motor responses. Five minutes after the increase to 0.6% isoflurane, sonications were started. Rectal temperature was measured for 30 seconds immediately after the last sonication; the final temperature was within 2 degrees Celsius of the beginning of the experiment for all experimented mice. After each mouse experiment, the EMG leads were removed, and the mouse was allowed to recover and then returned to its home cage.
Data acquisition, post processing, and analysis
Following King et al. 2013, we used EMG recordings to measure ultrasound neurostimulation efficacy in order to obtain quantifiable contraction amplitude and contraction latency data with high temporal resolution. While we recorded from both forelimbs in all experiments, typically we used only the signal from the right forelimb for analysis unless it was too noisy, in which case we used the left forelimb signal. In Experiment E, where lateralization might have come into play, all signals used in the analysis were recorded from the right forelimb. EMG signals were amplified with a gain of 1000× and bandpass filtered between 300 Hz and 3 kHz using a preamplifier (World Precision Instruments, Sarasota, FL) for each channel. Data was acquired at 1 kHz sampling rate (LabJack U3, LabJack, Lakewood, CO).
The timing and parameters for the sonications were controlled by a computer running software written in MATLAB (Mathworks, Natick, MA). This was achieved by using an externally controlled function generator (Model 33250, Agilent, Santa Clara, CA) to trigger sonications of prescribed amplitudes and durations. In order to reduce interference from spontaneous contractions (contractions that occur when no ultrasound is delivered), sonications were triggered when the EMG signal, averaged over the last 200 ms, dropped below a set threshold. After a sonication, there was a delay of at least two seconds before the next sonication ensued. The set of parameters (e.g. frequency, intensities, and duration) for each block was manually entered prior to each set of sonications, and each block was manually initiated via the software’s graphical user interface. The signal generated from the function generator was amplified by an RF amplifier (Model 150A100B, Amplifier Research, Souderton, PA), which in turn powered the ultrasound transducer.
Signal post-processing was performed using additional software written in MATLAB. For each trial, we removed the DC component from the recorded signal (Figure 4A) by subtracting the mean of the signal obtained during the quiet period. The subtracted signal was then full-wave rectified (Figure 4B). The rectified signal was then smoothed (Figure 4C) with a bilaterally truncated Gaussian filter of width 40 ms and standard deviation 10 ms. A noncausal filter was used to avoid artificial delays in signal timings associated with causal filters. Because of the filtering, the calculated temporal latency was defined as the raw latency plus 19 ms (see Supplemental Figure S10). Sonications were programmatically classified as causing a successful contraction if the smoothed EMG signal fulfilled the following criteria:
Exceeded a contraction threshold, defined as 3 standard deviations of the signal during the quiet period (between 251 and 19 ms prior to sonication), plus the mean of the signal during the quiet period.
Exceeded the contraction threshold within a calculated temporal latency less than 225 ms (see Supplemental Figure S11)
Remained above the contraction threshold for at least 100 ms (see Supplemental Figure S12)
Figure 4.
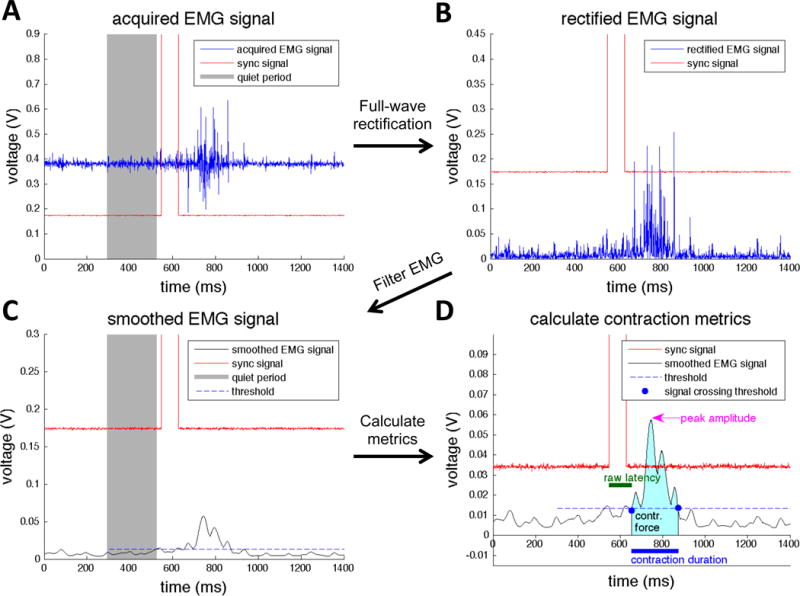
EMG post-processing methods. Acquired EMG signals (A) are first full-wave rectified (B), and then Gaussian filtered (C). A threshold is calculated based on the standard deviation and the mean of the smoothed EMG signal during quiet period, which is used to determine the beginning and end of the contraction. Then, several contraction metrics are calculated (D) including raw latency, peak amplitude, contraction duration, and contraction force. contr. = contraction; EMG = electromyography.
Results classified using these criteria were compared with results that were manually classified by two co-authors (PY and JB). The criteria proved to exhibit good sensitivity and specificity (Supplemental Table S1). The success rate was then calculated for each unique set of ultrasound parameters by dividing the number of successful contractions by the total number of sonications. If a set of trials had zero successful sonications across all frequencies, those sonications were excluded from the success rate analysis (see Supplemental Table S2 for the number of excluded trials for Experiments A–D). Experiments were excluded if the mouse escaped prior to the completion of 10 sets, if there was excessive noise on EMG signal, if the average success rate was too low, or if there was a lack of response to increased intensity. A total of five experiments were excluded for Experiment B, one experiment for Experiment C, and five experiments for Experiment D.
In addition to success rate, several parameters including contraction latency, contraction duration, peak amplitude, and contraction strength were calculated for successful sonications from the post-processed signal (Figure 4D).
Hydrophone scans
Each transducer with its respective waveguide was characterized in a degassed water tank using hydrophone scans (HNR-0500, Onda, Sunnyvale, CA). The waveguide was submerged about 1–2 mm into the water, and pressures were measured in a transverse plane approximately 2 mm from the tip of the waveguide in order to determine the pressure at the approximate location of the mouse cortex. Pressure measurements in the axial plane were also performed.
Using the pressures measured by the hydrophone, spatial peak pulsed average intensity Isppa [W/m2] was calculated as follows:
| (1) |
where T is the duration of an integer number of periods of the pressure waveform [s], P is the pressure [Pa], ρ is 1040 kg/m3, the density of brain tissue, and c is 1560 m/s, the speed of sound in brain tissue (International Commission on Radiation Units and Measurements 1998).
The effect of the mouse skull was quantified using hydrophone measurements based on three mouse skulls. Mice were humanely euthanized using carbon dioxide, and the roof of the mouse skull was removed from the head. Ultrasound pressure was measured over a 4 mm2 area about 4–5 mm away from the waveguide, as close as possible without damaging the hydrophone, both with and without the roof of the mouse skull between the transducer and the hydrophone. Insertion loss was calculated by dividing the spatial peak pressures of each scan. Insertion losses were then applied to the intensity calculations to estimate the amount of pressure that reaches the cortex. Insertion losses as a function of frequency can be found in Supplemental Figure S13. The location of the spatial peak pressure varied less than one millimeter with the insertion of the skull (Supplemental Figure S14).
Calculation of physical metrics
To examine the possible underlying causes of the ultrasound frequency dependence, we compared neurostimulation with several types of physical metrics: particle displacement, two types of cavitation indices including the mechanical index, a metric for cavitation, radiation force, and radiation-force-based strain. We correlated success rates from Experiments A–D with these quantities in order to see how relevant these physical mechanisms are in explaining the effects we observed.
1. Particle displacement
The amplitude of particle displacement in an oscillating pressure field is directly proportional to the amplitude of particle velocity.
| (2) |
where u is amplitude of particle displacement [m], v is the amplitude of particle velocity [m/s], and ω is the ultrasound carrier angular frequency [rad/s].
The amplitude of particle velocity, and thus the amplitude of particle displacement, can be related to intensity as follows:
| (3) |
| (4) |
| (5) |
where I is the pulse averaged intensity [W/m2], ρ is the density [kg/m3], and c is the speed of sound [m/s].
2. Mechanical index and cavitation index
Mechanical index [MPa/MHz1/2] is defined as follows:
| (6) |
defined as the peak negative pressure (PNP) [MPa] divided by the square root of center frequency f [MHz] (Apfel and Holland 1991).
Because mechanical index was intended to calculate the risk of inertial cavitation due to short-pulse, low duty cycle, diagnostic ultrasound, we also calculated a corresponding cavitation index for stable cavitation associated with longer ultrasound pulses. Derived from thresholds for subharmonic emissions from optimally sized free bubbles (Bader and Holland 2013), the cavitation index is potentially relevant because the intensities of the ultrasound pulses we used may induce bubble formation and thus lead to stable cavitation (ter Haar and Daniels 1981).
| (7) |
where PNP is the peak negative pressure [MPa] and f is the center frequency [MHz].
3. Radiation force and radiation-force-induced strain
Another mechanism that has been proposed to explain ultrasound neuromodulation is radiation force. Ultrasound induces radiation force in tissue proportional to intensity and absorption, and the spatial difference in intensity could result in strain within the tissue. To test whether this hypothesis would be consistent with our results, we calculated the correlation between success rate and radiation force and radiation-force-induced strain. Radiation force is defined as follows:
| (8) |
where F [N/m3] is the radiation force, α [Np/m] is the absorption coefficient, I [W/m2] is the spatially varying pulse average intensity after accounting for skull attenuation, and c [m/s] is the speed of sound in brain (Doherty et al. 2013; Vyas et al. 2014). We assumed a speed of sound of 1560 m/s for brain tissue (International Commission on Radiation Units and Measurements 1998). The absorption coefficient is a function of frequency of the form:
| (9) |
where a and b are tissue-specific constants, α [Np/m] is the absorption coefficient, and f is the frequency [MHz] (Duck 1990). We assumed the values for cat brain, where a is 0.024 Np/cm/MHz−b and b is 1.18 (Goss et al. 1979).
After calculating radiation force, we assume that the tissue behaves elastically, given small strains, such that the radiation-force-induced displacement d is directly proportional to radiation force with some constant k.
| (10) |
| (11) |
If we consider the brain as a lattice of many small, equally sized, cubic volumes of tissue, we can calculate the normal strain (or axial strain) at the depth of the motor cortex, which is defined as the ratio of the change in length of each cube in the direction of ultrasound propagation divided by its original length l0.
| (12) |
| (13) |
| (14) |
It is plausible that the spatial derivative of tissue displacement in the transverse plane, which is related to shear strain, could also play a role. Intuitively, a sharper focal spot could induce more of a shear stretching effect than a broader focal spot with the same spatial peak intensity. We calculated the spatial derivative as follows:
| (15) |
| (16) |
| (17) |
4. Heating effects
The amount of ultrasound-induced heating in tissues is also frequency dependent and has often been cited as another possible mechanism for ultrasound neuromodulation. To estimate the thermal effect due to sonications, we begin with the Pennes Bioheat Transfer Equation (Pennes 1948).
| (18) |
where ρ is density [kg/m3], C is specific heat [kJ/kg/C], T is temperature [degrees Celsius], t is time, K is thermal conductivity, hm is rate of heat deposition in tissue [kJ/s/m3 ], and hb is rate of heat transfer due to perfusion. The right hand side of the equation represents conduction, heat deposition, and perfusion factors, respectively.
For the maximal possible increase in temperature, we ignore cooling factors such conduction and perfusion. For the radiation term, the expression for the rate of heat production in tissue with ultrasound is given by Nyborg 1981.
| (19) |
| (20)(Duck 1990) |
where a is the absorption coefficient and I is spatial peak pulse average intensity. We use accepted values for C = 3640 J/kg/K and ρ = 1040 kg/m3 from ICRU Report 61 (International Commission on Radiation Units and Measurements 1998), and absorption values from cat brain: a = 0.024 Np/cm/MHz−b and b = 1.18 (Goss et al. 1979). Using ∂t = 0.080 seconds to be the length of the sonication, we can calculate a maximum temperature rise.
Key differences with King et al. 2013
Many of these methods were very similar to those used in King et al. 2013; however, we felt compelled to make a few significant changes. One decision was to better maintain the mouse’s body temperature to prevent hypothermia. First, we decreased the flow rate of cold oxygen from 2 liters per minutes to 1 liters per minute. Second, we covered the nose cone with a latex membrane which was cut open with a crossed slit, instead of leaving the nose cone uncovered. These two changes greatly reduced the exposure of the mouse to cold oxygen from the compressed gas tank. In addition, we modified the method of keeping the mouse warm while suspended in the holder: instead of using tail warming pads, we deployed a heating lamp indirectly aimed towards the mouse. The heat lamp provided more consistent warmth compared to the tail pads, which gradually produce less heat over time and need to be replaced with fresh heating pads during the experiment. With these changes, a higher percentage of isoflurane was required compared with previous studies to compensate for the decreased flow rate.
Another difference was with regard to our hydrophone measurements. Our hydrophone sensitivities were calibrated from 0.25–1 MHz, and we applied the respective sensitivities to our measurements instead of assuming the same 1 MHz calibration sensitivity for all frequencies less than 1 MHz. Using these adjusted sensitivities resulted in a decrease in measured intensity ranging from 3% at 0.3 MHz to 38% at 0.6 MHz compared to the previously used 1 MHz sensitivity. The hydrophone calibration was performed by Onda.
Results
Increasing ultrasound frequency continues to reduce success rate efficacy at higher frequencies
We compared the neuromodulatory effects of ultrasound frequencies from 0.3 to 2.9 MHz by compiling the results from Experiments A (constant sonication duration data only), B, C, and D (Figure 5A–D). In agreement with previous studies, increased intensities generally resulted in higher success rates. In order to compare the frequency dependence across the full range of frequencies, we fitted the success rate curves of individual frequencies from Figure 5A–D using logistic regression, and then from these fits we plotted the intensities required to achieve a given success rate against frequency (Figure 5E and F). These threshold intensities generally increased as frequency increased (p < 0.001 for all three success rates, Spearman’s rank correlation), ranging from about 1 W/cm2 for frequencies less than 1 MHz to more than 100 W/cm2 at the higher frequencies. There was a smaller variation in threshold intensities for frequencies below 1 MHz compared with frequencies above 1 MHz in terms of absolute intensity units, although the threshold intensities covered a greater range for lower frequencies when viewed on a logarithmic scale.
Figure 5.
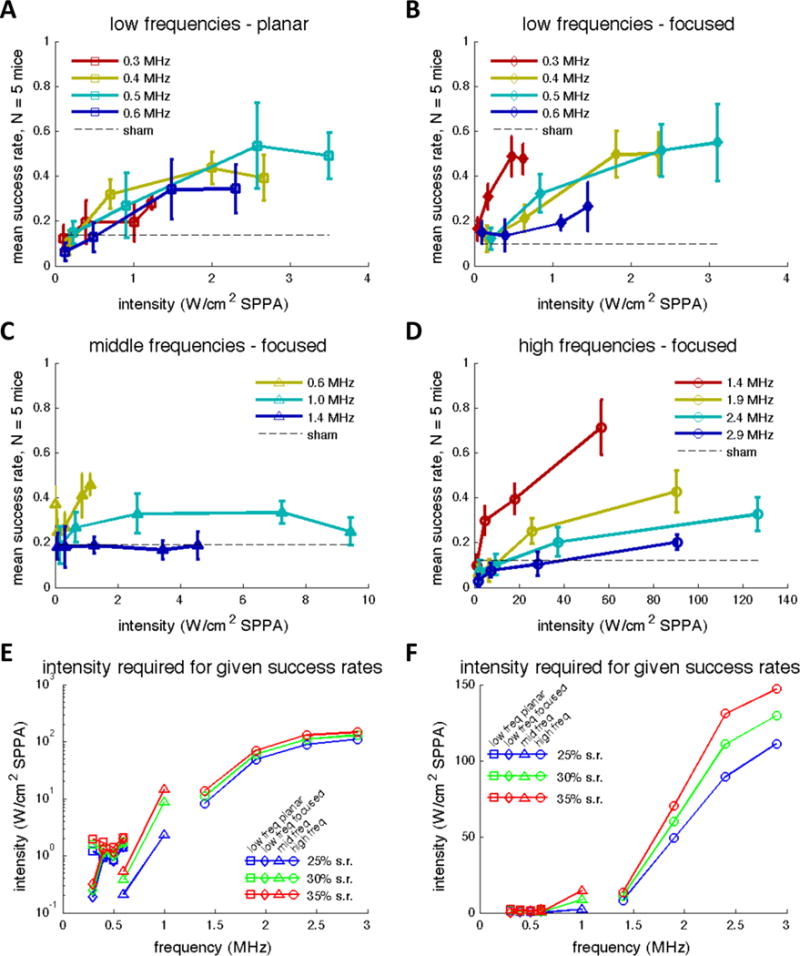
Mean success rates as a function of spatial peak intensity after accounting for skull attenuation at low, middle, and high frequencies from Experiments A–D (Figure 5A–D respectively). Error bars reflect standard error of the mean. Figure 5E and F represent the intensities required to achieve 25%, 30%, and 35% success rates plotted as a function of frequency combining all data collected from Experiments A–D. Intensity values were calculated by fitting the mean success rates in Figure 5A–D with logistic regression. Data marker shape indicates from which experiment the data was interpolated. freq = frequency; SPPA = spatial peak pulsed average; s.r. = success rate.
We also examined the effect of intensity and frequency on EMG peak amplitude by calculating least-squares best-fit equations. While we observed that increased intensity generally resulted in greater EMG peak amplitude, there was no consistent trend across different frequencies. Furthermore, no consistent trend was observed in muscle contraction latency with changing frequency or intensity.
Sonication duration confound has little effect on frequency dependence
The success rates from Experiment A are plotted in Figure 6. Success rates generally increased with sonication intensity. However, in comparing sonications chosen to represent constant durations across the three frequencies and ones chosen to represent a constant number of cycles as reported by King et al. 2013, our results showed no significant differences in success rates at any of the frequencies whether averaged across intensity or examined one by one.
Figure 6.
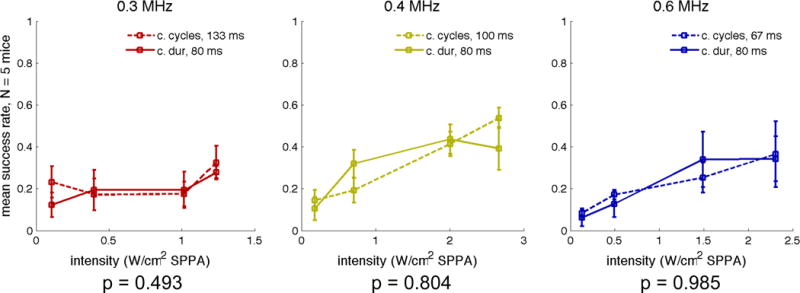
Success rate as a function of spatial peak intensity with different duration pulses at three different frequencies: 0.3 MHz (left), 0.4 MHz (center), and 0.6 MHz (right). Error bars indicate the standard error of the mean across mice. P-values were calculated within mice using a two-tailed paired t-test. Plotted intensities account for attenuation due to the mouse skull. dur = duration; SPPA = spatial peak pulsed average.
Success rate correlates well with particle displacement, mechanical index, and cavitation index, but not with radiation-force or radiation-force-induced strain
Mean success rate was not well correlated with spatial peak pulse average intensity (Figure 7A, R2 = 0.03) but was strongly correlated with particle displacement (Figure 7B, R2 = 0.50), mechanical index (Figure 7C, R2 = 0.18) as well as cavitation index (Figure 7D, R2 = 0.50). On the other hand, mean success rate showed virtually no correlation with radiation force (Figure 7E, R2 = 0.00) or radiation-force-induced normal and shear strain (Figure 7F, R2 = 0.00 and Figure 7G, R2 = 0.01).
Figure 7.
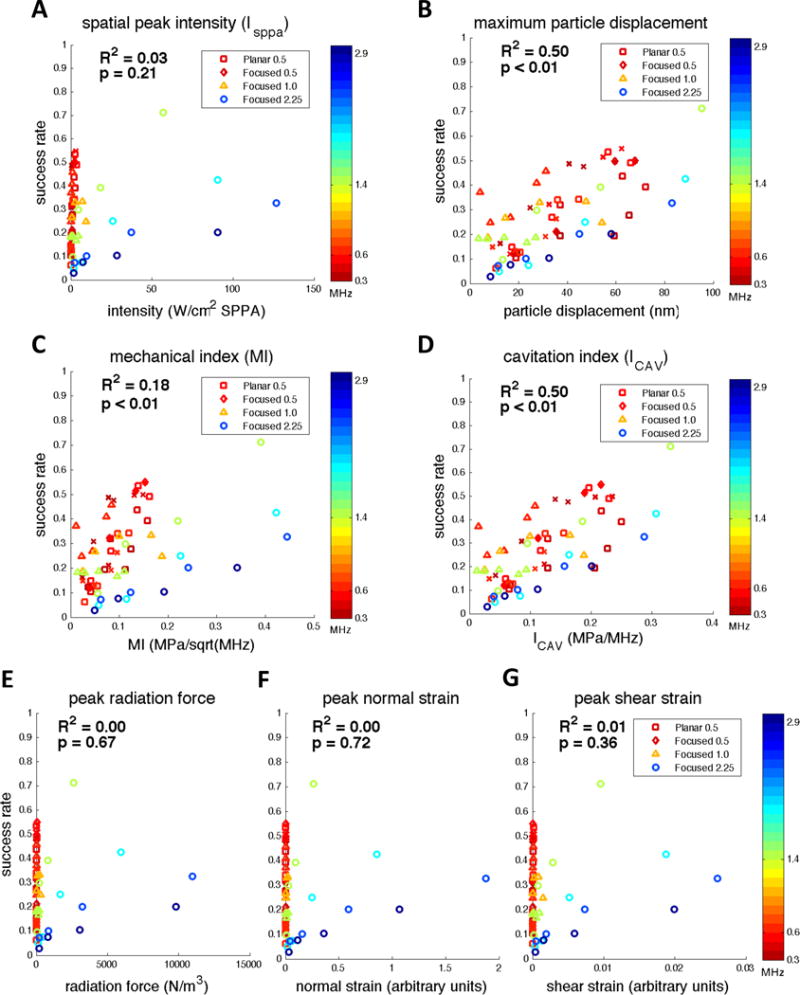
Mean success rates from Experiments A–D as a function of spatial peak intensity (A), maximum particle displacement (B), spatial peak mechanical index (C), spatial peak cavitation index (D), spatial peak radiation force (E), peak normal strain (F), and peak shear strain (G). Skull attenuation was taken into account when calculating each physical metric. All spatial peaks were calculated for intensities estimated to be located at a plane represented by the motor cortex. SPPA = spatial peak pulsed average.
Cavitation index-based model describes threshold intensity and frequency relationship well
Because particle displacement and cavitation index showed the greatest correlation with success rate, we examined how well these two parameters describe the frequency dependence. Based on the hypothesis that a threshold value of either particle displacement or cavitation index is required to achieve a certain success rate, the threshold intensities for a given success rate should be proportional to the square of frequency. Therefore, we fitted our threshold intensity and frequency data from Figure 5F using a quadratic Ith = k*f2 model (Figure 8). The model fits the data in this range of frequencies remarkably well overall, with R2-values greater than 0.96 for all three sets of success rate threshold intensities.
Figure 8.
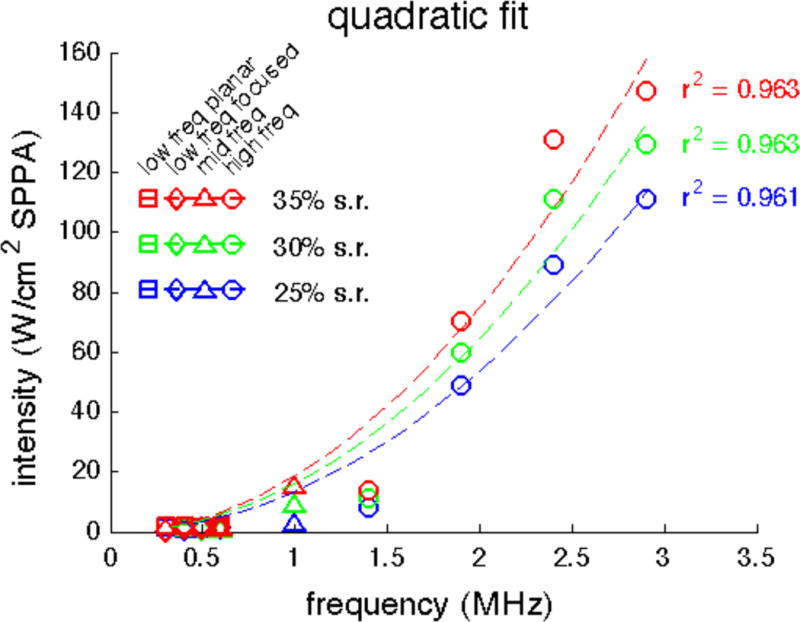
Quadratic fit of threshold intensities for three success rates as a function of frequency (data from Figure 5F). Fits were calculated using a least-squares approach with corresponding R2 coefficient of determination values. freq = frequency; SPPA = spatial peak pulsed average; s.r. = success rate.
Area of focal spot does not account for much frequency dependence
In addition to frequency-dependent physical mechanisms, another possible source of frequency dependence is the changing focal spot size, which generally decreases in size as the ultrasound frequency increases (Figure 9A and B). To test whether focal spot size was in fact the primary cause for the observed frequency dependence, we compared the fraction of explained variance due to frequency alone, focal spot area alone, and both variables combined. First, we performed a least-squares fit of the threshold intensity as a function of focal spot area, as measured by the area greater than the half maximum pressure, using an inverse quadratic function which fits the data reasonably well (Figure 9C). Then, we calculated the coefficients and R2 values for this fit and another fit including both a quadratic frequency term and an inverse quadratic area term (Table 2, Models A and B). For both models, the coefficients were positive, indicating that decreased area and increased frequency result in increased threshold intensity. However, frequency proved to explain more variance in the observed threshold intensity than focal spot area. We then created a model that combined the terms from Models A and B, and we found that including both terms did not improve the explained variance significantly compared to a frequency-only model (Table 2, Model C). Looking more specifically at the residual error resulting from the quadratic frequency fit, there is no apparent trend with focal spot area (Figure 9D).
Figure 9.
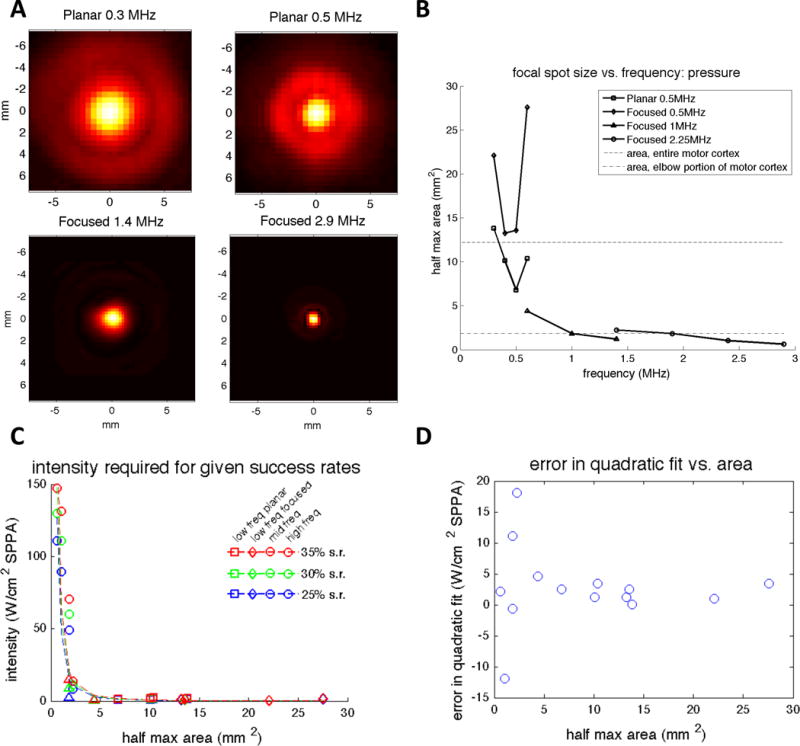
Effect of focal spot size. (A) Transverse normalized pressure beam profiles at four total frequencies using the Planar 500 kHz transducer (top), the Focused 1 MHz transducer (bottom left), and the Focused 2.25 MHz transducer (bottom right). All beam profiles can be found in Supplemental Figures 1–8. (B) Focal spot size as measured by the area above the half maximum of the pressure profile. The area of the entire motor cortex and the area represented by the elbow portion of both forelimbs, as reported by Tennant et al. 2011, are plotted for reference. The elbow portion of the forelimb was most relevant based on the placement of the EMG leads. (C) Threshold intensity as a function of focal spot area. An inverse quadratic fit appears to fit the data well. (D) Residual error in quadratic frequency fit as a function of focal spot area. freq = frequency; SPPA = spatial peak pulsed average; s.r. = success rate.
Table 2.
R2 coefficient of determination values for fitting threshold intensities
| success rate | Model A frequency alone Ith = β * f2 |
Model B area alone Ith = β * area−2 |
Model C both frequency and area Ith = β1 * f2 + β2 * area−2 |
|---|---|---|---|
| 25% | β: 13.45 R2: 0.963 |
β: 51.11 R2: 0.807 |
β1: 13.84 β2: −1.667 R2: 0.963 |
| 30% | β: 16.17 R2: 0.963 |
β: 60.89 R2: 0.785 |
β1: 17.72 β2: −6.691 R2: 0.965 |
| 35% | β: 18.72 R2: 0.961 |
β: 70.07 R2: 0.767 |
β1: 21.36 β2: −11.41 R2: 0.964 |
To further disentangle the effects caused by changing frequency and focal spot area, we also measured the effect of focal spot area independently from the effects of frequency by sonicating with different transducers but at the same frequencies. We observed that at 0.3 MHz, the larger focal spot size was more effective, but at 0.6 MHz, a smaller focal spot size proved more effective (Figure 10A and D). At 0.4 and 0.5 MHz, the success rates were similar despite differences in focal spot size (Figure 10B and C). These results suggest that, at least at low frequencies, focal spot size does not have a consistent effect on neuromodulation efficacy.
Figure 10.
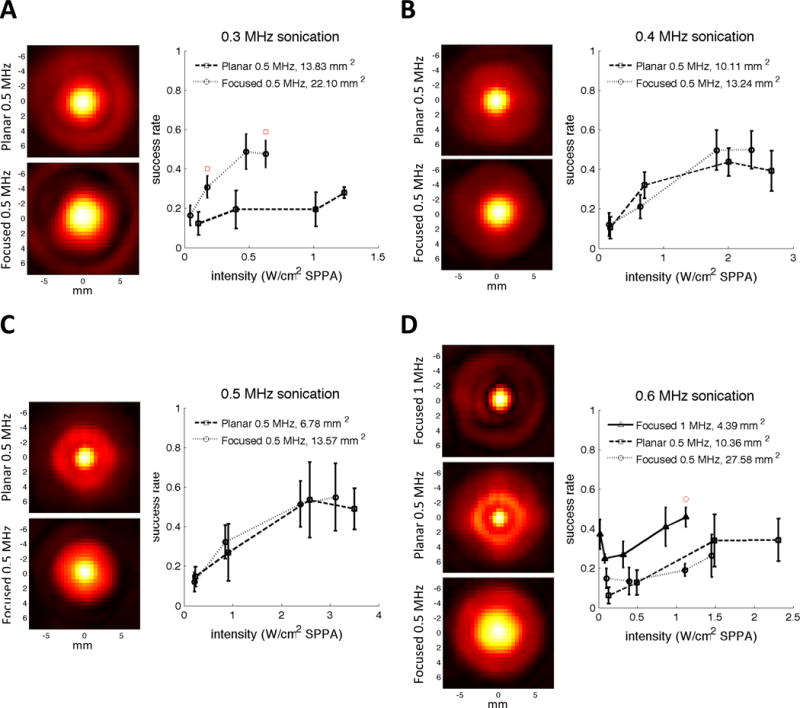
Sonicating with different focal spot sizes at the same frequencies. (A) Transverse pressure profiles for two different transducers at 0.3 MHz (left) and the resulting success rates as a function of spatial peak intensity after accounting for skull attenuation (right). Red squares indicate when the success rate achieved using the planar transducer was significantly greater than the success rate achieved using the focused transducer at the closest tested intensity (p<0.05, 2-tailed unpaired t-test). (B) Transverse pressure profiles for two different transducers at 0.4 MHz (left) and the resulting success rates as a function of spatial peak intensity after accounting for skull attenuation (right). (C) Transverse pressure profiles for two different transducers at 0.5 MHz (left) and the resulting success rates as a function of spatial peak intensity after accounting for skull attenuation (right). (D) Transverse pressure profiles for three different transducers at 0.6 MHz (left) and the resulting success rates as a function of spatial peak intensity after accounting for skull attenuation (right). The red circle indicates the intensity for which the success rate achieved using the Focused 1 MHz transducer was significantly greater than the success rate achieved using Focused 0.5 MHz transducer at the closest tested intensity (p<0.05, 2-tailed unpaired t-test). SPPA = spatial peak pulsed average.
Higher frequency sonication is not less effective because it misses the sensitive cortical area
We performed Experiment E to test the hypothesis that smaller focal spot sizes account for the lower efficacy of higher frequencies, perhaps because the tighter spot size failed to modulate the most sensitive cortical area for eliciting a muscle contraction. The success rates for 1.4 MHz and 2.9 MHz sonications applied at different locations across the mouse brain are shown in Figure 11A and B. 1.4 MHz remained globally more effective than 2.9 MHz (35% compared to 16%), which is a similar ratio as observed in Figure 5C, yet the spatial peak mouse-average success rate at 1.4 MHz remained higher than that at 2.9 MHz (70% vs. 40%).
Figure 11.

Mouse-average success rates for right forelimb muscle contraction across the mouse brain at 1.4 MHz (Figure 11A) and 2.9 MHz (Figure 11B). The global spatial average success rate was 35% and 16% at 1.4 and 2.9 MHz respectively. The average success rate for sham sonications was 4%. Gray regions were not sonicated. The success rates for individual mice can be found in Supplemental Figure S15.
Success rate does not correlate well with estimated heating
Using the Pennes Bioheat Transfer equation, we estimated the greatest heating effects to be up to 0.36 degrees Celsius at the high frequencies, but less than 0.02 degrees Celsius was predicted at the low frequencies. However, the heating effect showed no correlation with mean success rate (Figure 12, R2 = 0.00).
Figure 12.
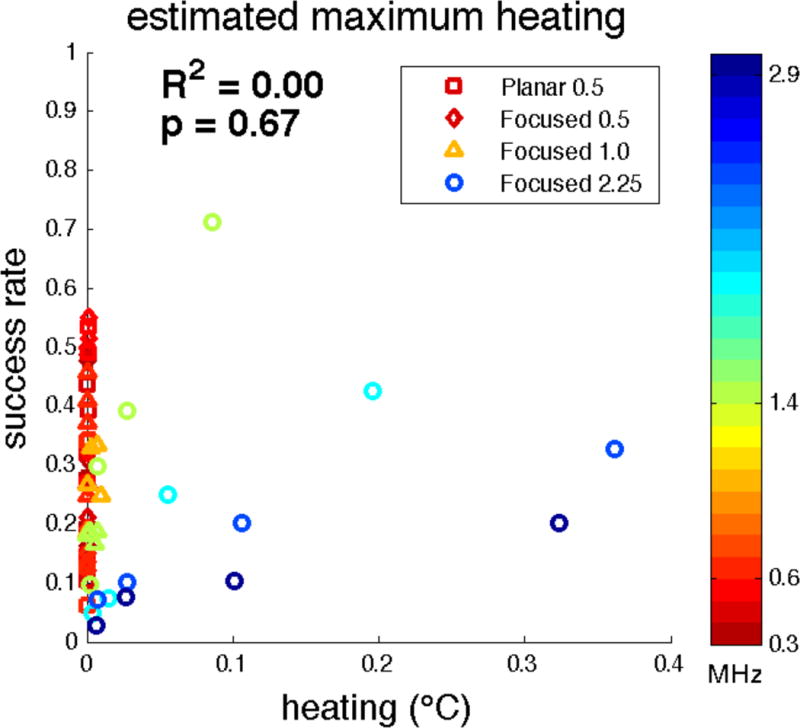
Mean success rates from Experiments A–D as a function of estimated spatial peak heating within the brain.
Discussion
In this study, we systematically quantified the efficacy of ultrasound neurostimulation using a larger and higher range of ultrasound frequencies in the in vivo mouse model than has previously been explored. In testing an extended range of frequencies, we observed changes in efficacy that clearly confirmed a previously suspected trend whereby higher frequency yields less efficacy. To account for the observed frequency dependence, we examined several potential contributing factors including sonication duration, focal spot size, particle displacement, mechanical index, cavitation index, radiation force, radiation-force-induced strain, and heating.
We first examined lower sonication frequencies, comparable to ones used in previous studies that have suggested higher frequencies are less effective for neuromodulation (King et al. 2013; Tufail et al. 2010). By using sonications of both constant and variable duration, we addressed a potential confound of the King et al. 2013 study, where sonication duration changed as the frequency changed. Our results comparing constant and variable duration sonications at the same frequency suggest that the different sonication durations that were used in King et al. 2013 did not impact the success rate significantly, most likely because the durations that were used were already sufficiently long to result in similar success rates. However, somewhat surprisingly, our results also show that there was little variation in success rate at different low ultrasound frequencies regardless of whether sonication durations were variable (as in King et al.) or held constant. We were thus unable to reproduce the frequency response reported by King et al. at these low frequencies even when using the same variable duration sonications they had employed. We should note that our overall success rates using the same sonication parameters were lower than theirs. This difference may have arisen from changes in experimental setup, particularly the changes that affected anesthesia. Lower overall success rates could have made it more difficult to distinguish success rate differences with small changes in sonication duration or changes in frequency.
Nevertheless, in examining the extended frequency response up to 2.9 MHz that went far beyond the lower frequencies used by King et al. 2013, we did find a clear trend of reduced efficacy as the frequency increased, showing that increased spatial peak intensities were required to achieve the same success rates compared to lower frequencies. This effect was strongest at the highest frequencies. As far as we know, no other in vivo experiments have reported sonicating cortex at frequencies above 0.65 MHz. However, similar results have been reported in the peripheral nervous system by Gavrilov et al. 1976 who observed increasing threshold intensities to elicit sensations in human finger at higher frequencies. We can also compare the trend we observed with the predictions made by Plaksin et al. 2014, who reported results from a cellular-scale simulation of ultrasound neuromodulation based on intramembrane cavitation. Given the relatively small amount of frequency dependence at low frequencies, we were unable to confirm their claim that the frequency dependence found by King et al. 2013 was “primarily a result of different pulse durations.” However, our observations over the full frequency range from 0.3 MHz to 2.9 MHz (Figure 5E) qualitatively agree with their predicted frequency response: both our results and their model show a nearly flat response at lower frequencies but one that changes increasingly rapidly at higher frequencies. Of course, there are limitations with this comparison of our in vivo data with their in silico simulation, especially given that they simulated the behavior of single neurons, and these neurons were only of a single cell type.
Another possibility in explaining the frequency dependence arises from the concomitant variation in the focal spot size. As frequency increases, the focal spot size general decreases, though the exact relationship depends on the transducer used (Figure 9B). Assuming the overall general trend, it could be argued that higher frequencies are less effective simply because less brain tissue is stimulated given a smaller spot size and the same spatial peak intensity. Experimentally, the issue is difficult to answer decisively because while frequency can be varied on demand, focal spot size is not so easily kept constant or varied as an independent parameter using single-element transducers. Nevertheless, we collected some data in which frequency was kept constant and the focal spot size was varied by using different transducers. In Figure 10, we see that at 0.3 MHz, a larger spot size yielded higher success rates, a trend we might expect if the key to success were simply the amount of brain stimulated. However, at 0.6 MHz, we observed the opposite effect: a larger spot size yielded a lower success rate. This trend did not prove to be consistent for the other low frequencies we tested, nor did a combined frequency and area-dependent term explain much more variance in our fitted model (Table 2).
The possibility that a larger focal spot size with the same spatial peak intensity can be less effective, while counterintuitive, has some precedent. Mihran et al. 1990 demonstrated in an in vitro study on frog sciatic nerves that sonications at 2, 4, and 7 MHz had very similar modulatory effect when acoustic spot sizes were kept the same, but, surprisingly, at 2 MHz a smaller focal spot size was more effective at modulating neural activity. Of course, given that they were using single nerves rather than brain tissue, studying suppression rather than stimulation, and working in vitro, it is difficult to know how applicable their result would be to our experiments, but their finding was at least indicative of the possibility of an unexpected effect of spot size.
There are many reasons why the effect of spot size might not be straightforward to predict. It is very unlikely that all parts of the sonicated regions of the brain are equally sensitive or receptive to ultrasound nor is it likely that they would all contribute equally to the behavioral response we were measuring. Indeed, the relevant parameter to study is less likely to be the raw focal spot size but, rather, some function of the overlap between the spot area and the area of brain responsible for eliciting forearm muscle contractions. Furthermore, a scalar value for focal spot area does not capture the sharpness of the focal spot nor does it account for the depth to which the ultrasound may reach. Increasing the focal spot size could also differentially boost the number of inhibitory neurons affected by ultrasound rather than simply stimulating more excitatory neurons.
Nevertheless, putting aside all of these complications, in order to get some idea of the independent contributions of frequency and spot size, we used a linear regression analysis to examine how much variance in the success rates each factor could explain. The results (Table 2) show that frequency explains more of the observed variance in threshold intensity than focal spot area when each factor is considered alone, and that the focal spot area explains little additional variance when combined with frequency.
As an additional test, we examined whether success rates were reduced at higher frequencies simply because of a failure to stimulate the area of the brain that is both ultrasound-sensitive and required to induce muscle contractions. By sequentially sonicating the mouse brain at multiple sites across a grid-like pattern using two different frequencies, effectively creating a sensitivity map for the motor cortex, we observed that the higher frequency never reached the same success rate as the lower frequency, suggesting that we were not “missing” the sensitive brain region using the higher frequency (Figure 11). Also despite the decrease in focal spot size, we did not observe consistently improved spatial selectively in motor outputs using the higher frequency, such as lateralization of muscle responses or differences in muscle contraction latency. This could be because the sonications were sufficiently intense to stimulate bilateral pathways in the motor cortex.
This apparent lack of improved spatial selectivity and reduction in efficacy at higher frequencies could represent an obstacle to making this technique useful. Further work will be necessary to refine the optimal parameters for mapping brain function and to determine the extent of spatial selectivity that can be achieved with ultrasound neuromodulation. Simulation of ultrasound beam propagation within the skull could provide more accurate representations of ultrasound in the brain as well as capture spatiotemporal effects such as standing waves (Younan et al. 2013). Future experiments using phased array transducers to generate larger focal spot areas while maintaining the same frequency could potentially help further disentangle the effects of the focal spot beam profile from frequency.
Given the lack of evidence for a direct causal role of spot size in explaining the observed frequency response, we are obliged to consider other possibilities. Adopting an approach similar to that of Gavrilov et al. 1976, we correlated our results against several well-described ultrasound physical bioeffects. From this, we observed, like Gavrilov et al., that our mean success rates correlate well with the amplitude of particle displacement (Figure 7B). While the amplitude of particle displacement will be relatively small compared to the wavelength of the ultrasound, the displacements could still be sufficient to perturb subcellular neural structures (Jolesz and Hynynen 2008). Specifically, these mechanisms could involve deforming the lipid bilayer (Prieto et al. 2013), acting on the mechanisms for synaptic vesicle release (Tyler 2011), and/or activating stretch-sensitive ion channels (Bystritsky et al. 2011; Heureaux et al. 2014; Tyler 2011). In fact, several mechanosensitive ion channels have been found in the transcriptome of mouse cortical neurons, including TREK-1, TREK-2, TRAAK, and members of the TRP channel family (Zhang et al. 2014). The exact bioeffects caused by particle displacement have not been well described in the literature, presumably because of the high speed and high magnification that would be required for imaging studies.
The fact that success rate also correlated strongly with mechanical index and cavitation index compared to raw spatial peak intensity (Figure 7A, C, and D) points to an alternative explanation for the frequency dependence: the phenomenon of cavitation. Mechanical index is a commonly used metric to quantify the risk of onset of inertial cavitation using short-pulse, low-duty cycle diagnostic ultrasound in tissue (Apfel and Holland 1991). Even though we observed a strong correlation between success rate and inertial cavitation, we believe that inertial cavitation is unlikely at the sonication intensities used, given that the corresponding spatial peak and average mechanical indices in our experiments are below the safety threshold of 1.9 MPa/MHz0.5 set by the FDA. Furthermore, it is not the most accurate index for describing the effects of our long-pulse sonications.
Therefore, we also examined the cavitation index to quantify stable cavitation, as any inherent bubbles will oscillate in a non-zero acoustic pressure (Bader and Holland 2013). It should be noted that stable cavitation has been observed to occur without externally injected microbubbles with at least 80 mW/cm2 intensity at 0.75 MHz continuous wave sonications in in vivo guinea pig leg (ter Haar and Daniels 1981), although this result has yet to be independently verified (Hynynen 1991; Jolesz and Hynynen 2008). We observed a strong correlation between success rate and the cavitation index, and in addition, a quadratic model as described by the cavitation index fits the relationship between threshold intensities and frequency well (Figure 8), suggesting that stable cavitation could be a contributing factor, if not the main mechanism underlying the neurostimulation effects we observed. There is experimental evidence for stable cavitation as a mechanism: a recent in vitro study has shown increased subharmonic and harmonic emissions that accompany the generation of compound action potentials in crab peripheral neurons using ultrasound (Wright et al. 2015). Similar to particle displacement, a stable cavitation-based mechanism could cause neuromodulation by generating mechanical bioeffects around the neuron, via bubble oscillations and cavitation microstreaming (Elder 1959).
Because both particle displacement and stable cavitation mechanisms exhibit similar frequency responses, our correlation-based analysis cannot differentiate between them as possible explanations. Thus, further work will be required to measure indicators of stable cavitation in order to confirm or disprove that at least one potential mechanism underlying ultrasound neuromodulation is cavitation-related.
Radiation force, the next leading alternative mechanism that has been proposed (Menz et al. 2013b; Mihran et al. 1990; Wahab et al. 2012) to explain the phenomenon of ultrasound neuromodulation, is not well supported by our data, as we found that radiation force and radiation-force-induced strain were poorly correlated with success rate (Figure 7E and F). Indeed, as radiation force is proportional to frequency, we would expect ultrasound neuromodulation to become more effective at higher frequencies, which is the opposite of what we saw, if radiation force was truly the mechanism at play. Our analysis is correlation-based, as we did not directly measure radiation force or radiation-force-induced strain in this study, but using techniques such as acoustic radiation force imaging could better quantify those physical parameters (McDannold and Maier 2008). While radiation force may not account for the ultrasound neuromodulation we saw in our experiments, it could still play a key role in other experimental paradigms. For example, Menz et al. 2013b stimulated salamander retina in vitro using 10–30 W/cm2 ultrasound at 43 MHz, a frequency more than an order of magnitude higher than the highest frequency we tested. Menz et al. 2013a also presented video evidence of retinal tissue displacement due to ultrasound. Extrapolating to 43 MHz from our observed frequency trends, we would expect ultrasound at such a high frequency to be completely ineffective for mouse in vivo neurostimulation. If so, we believe the primary mechanisms involved in our study and Menz et al. are quite likely to be different. These differences in mechanism could also be partially explained by the fundamental differences between our setups. We were sonicating intact whole brain in vivo while Menz et al. were sonicating isolated tissue in vitro. Nevertheless, the gap between the frequencies we studied and that of Menz et al. remains unexplored. More experimental data on these intermediate frequencies could lead to further insight regarding the frequency response at different frequency regimes.
While we were able to successfully demonstrate ultrasound neuromodulation using frequencies over 1 MHz in mice, the use of such higher frequencies may present additional obstacles in people due to the thickness of the human skull. The maximum advisable intensity for human transcranial ultrasound applications is limited by the attenuation of the skull and the corresponding generation of heat due to absorption within bone. Such attenuation and absorption is greater at higher frequencies, reducing the amount of ultrasound that would arrive at intended targets within the brain while increasing the amount of heating. The human skull may therefore exacerbate the problems created by the frequency response of ultrasound neuromodulation.
Conclusion
We found that ultrasound neurostimulation varies in efficacy at a variety of frequencies ranging from 0.3 to 2.9 MHz in the mouse model, with higher frequencies requiring increased spatial peak intensity to maintain equal efficacy compared to lower frequencies. By fitting threshold intensities with both frequency and focal spot size, we found that area does not explain the observed variance nearly as well as frequency does. In addition, our results suggest that stable cavitation and particle displacement are plausible mechanisms to explain our frequency-dependent success rates in achieving neuromodulation, whereas heating, radiation force, and radiation force-induced strain are not. Altogether, our study offers important insights into some of the tradeoffs that will need to be assessed in choosing the optimal frequencies for ultrasound neuromodulation as this exciting technique gains currency in research and clinical use.
Supplementary Material
Acknowledgments
The authors would like to acknowledge the following groups and individuals. The ultrasound neuromodulation group at Stanford provided helpful research advice. Randy King trained Patrick Ye to perform mouse experiments. Wendy Baumgardner, Yamil Saenz, and Aurea Pascal-Tenorio provided valuable expertise handling animals and suggestions for the animal experimental setup. This research was funded by NIH R01 EB019005, GE Healthcare and Stanford Bio-X Neuroventures. Patrick Ye has been supported by the Bruce E. and Doris A. Nelson Bioengineering Fellowship and the Bruce and Elizabeth Dunlevie Fellowship (Stanford Interdisciplinary Graduate Fellowship/Bio-X Graduate Fellowship).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Apfel RE, Holland CK. Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound. Ultrasound Med Biol. 1991;17:179–185. doi: 10.1016/0301-5629(91)90125-g. [DOI] [PubMed] [Google Scholar]
- Bader KB, Holland CK. Gauging the likelihood of stable cavitation from ultrasound contrast agents. Phys Med Biol. 2013;58:127–44. doi: 10.1088/0031-9155/58/1/127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bystritsky A, Korb AS, Douglas PK, Cohen MS, Melega WP, Mulgaonkar AP, Desalles A, Min BK, Yoo SS. A review of low-intensity focused ultrasound pulsation. Brain Stimul Elsevier Inc. 2011;4:125–136. doi: 10.1016/j.brs.2011.03.007. [DOI] [PubMed] [Google Scholar]
- Deffieux T, Younan Y, Wattiez N, Tanter M, Pouget P, Aubry J-F. Low-intensity focused ultrasound modulates monkey visuomotor behavior. Curr Biol. 2013;23:2430–3. doi: 10.1016/j.cub.2013.10.029. [DOI] [PubMed] [Google Scholar]
- Doherty J, Trahey G, Nightingale K, Palmeri M. Acoustic radiation force elasticity imaging in diagnostic ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control. 2013;60:685–701. doi: 10.1109/TUFFC.2013.2617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duck Fa. Acoustic Properties of Tissue at Ultrasonic Frequencies. Phys Prop Tissues Elsevier. 1990:73–135. [Google Scholar]
- Elder SA. Cavitation Microstreaming. J Acoust Soc Am. 1959;31:54. [Google Scholar]
- Fenno L, Yizhar O, Deisseroth K. The development and application of optogenetics. Annu Rev Neurosci. 2011;34:389–412. doi: 10.1146/annurev-neuro-061010-113817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fry FJ, Ades HW, Fry WJ. Production of reversible changes in the central nervous system by ultrasound. Science. 1958 doi: 10.1126/science.127.3289.83. [DOI] [PubMed] [Google Scholar]
- Fry WJ, Mosberg WH, Barnard JW, Fry FJ. Production of focal destructive lesions in the central nervous system with ultrasound. J Neurosurg. 1954;11:471–478. doi: 10.3171/jns.1954.11.5.0471. [DOI] [PubMed] [Google Scholar]
- Gavrilov LR, Gersuni GV, Ilyinsky OB, Sirotyuk MG, Tsirulnikov EM, Shchekanov EE. The effect of focused ultrasound on the skin and deep nerve structures of man and animal. Prog Brain Res. 1976;43:279–92. doi: 10.1016/S0079-6123(08)64360-5. [DOI] [PubMed] [Google Scholar]
- Goss SA, Frizzell LA, Dunn F. Ultrasonic absorption and attenuation in mammalian tissues. Ultrasound Med Biol. 1979;5:181–6. doi: 10.1016/0301-5629(79)90086-3. [DOI] [PubMed] [Google Scholar]
- Heureaux J, Chen D, Murray VL, Deng CX, Liu AP. Activation of a Bacterial Mechanosensitive Channel in Mammalian Cells by Cytoskeletal Stress. Cell Mol Bioeng. 2014;7:307–319. doi: 10.1007/s12195-014-0337-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hynynen K. The threshold for thermally significant cavitation in dog’s thigh muscle in vivo. Ultrasound Med Biol. 1991;17:157–169. doi: 10.1016/0301-5629(91)90123-e. [DOI] [PubMed] [Google Scholar]
- International Commission on Radiation Units and Measurements. Tissue Substitutes, Phantoms and Computation Modelling in Medical Ultrasound. Bethesda, MD: 1998. [Google Scholar]
- Jolesz Fa, Hynynen KH. In: MRI-Guided Focused Ultrasound Surgery. Jolesz Fa, Hynynen KH., editors. Boca Raton, FL: CRC Press; 2008. [Google Scholar]
- Kim H, Chiu A, Lee SD, Fischer K, Yoo S-S. Brain Stimul. Vol. 7. Elsevier Ltd; 2014. Focused ultrasound-mediated non-invasive brain stimulation: examination of sonication parameters; pp. 748–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, Park MY, Lee SD, Lee W, Chiu A, Yoo S-S. Suppression of EEG visual-evoked potentials in rats through neuromodulatory focused ultrasound. Neuroreport. 2015;26:211–215. doi: 10.1097/WNR.0000000000000330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, Taghados SJ, Fischer K, Maeng L-S, Park S, Yoo S-S. Noninvasive transcranial stimulation of rat abducens nerve by focused ultrasound. Ultrasound Med Biol. 2012;38:1568–75. doi: 10.1016/j.ultrasmedbio.2012.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King RL, Brown JR, Newsome WT, Pauly KB. Effective parameters for ultrasound-induced in vivo neurostimulation. Ultrasound Med Biol. 2013;39:312–31. doi: 10.1016/j.ultrasmedbio.2012.09.009. [DOI] [PubMed] [Google Scholar]
- King RL, Brown JR, Pauly KB. Localization of Ultrasound-Induced In Vivo Neurostimulation in the Mouse Model. Ultrasound Med Biol. 2014;40:1–11. doi: 10.1016/j.ultrasmedbio.2014.01.020. [DOI] [PubMed] [Google Scholar]
- Lee W, Kim H, Jung Y, Song I-U, Chung YA, Yoo S-S. Image-guided transcranial focused ultrasound stimulates human primary somatosensory cortex. Sci Rep. 2015a;5:8743. doi: 10.1038/srep08743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee W, Lee SD, Park MY, Foley L, Purcell-Estabrook E, Kim H, Fischer K, Maeng L-S, Yoo SS. Image-guided focused ultrasound-mediated regional brain stimulation in sheep. Ultrasound Med Biol. 2016;42:459–470. doi: 10.1016/j.ultrasmedbio.2015.10.001. [DOI] [PubMed] [Google Scholar]
- Legon W, Sato TF, Opitz A, Mueller J, Barbour A, Williams A, Tyler WJ. Transcranial focused ultrasound modulates the activity of primary somatosensory cortex in humans. Nat Neurosci. 2014;17:322–9. doi: 10.1038/nn.3620. [DOI] [PubMed] [Google Scholar]
- McDannold N, Maier SE. Magnetic resonance acoustic radiation force imaging. Med Phys. 2008;35:3748–3758. doi: 10.1118/1.2956712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehić E, Xu JM, Caler CJ, Coulson NK, Moritz CT, Mourad PD. Increased Anatomical Specificity of Neuromodulation via Modulated Focused Ultrasound. PLoS One. 2014;9:e86939. doi: 10.1371/journal.pone.0086939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menz M, Nikoozadeh A, Khuri-Yakub P, Baccus S. 2013 Neurosci Meet Plan. San Diego, CA: Society for Neuroscience; Origins of ultrasound neural stimulation in the retina; p. 2013a.p. 218.p. 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menz MD, Oralkan O, Khuri-Yakub PT, Baccus Sa. Precise neural stimulation in the retina using focused ultrasound. J Neurosci. 2013b;33:4550–60. doi: 10.1523/JNEUROSCI.3521-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihran RT, Barnes FS, Wachtel H. Temporally-specific modification of myelinated axon excitability in vitro following a single ultrasound pulse. Ultrasound Med Biol. 1990;16:297–309. doi: 10.1016/0301-5629(90)90008-z. [DOI] [PubMed] [Google Scholar]
- Min B-K, Bystritsky A, Jung K-I, Fischer K, Zhang Y, Maeng L-S, Park SI, Chung Y-A, Jolesz Fa, Yoo S-S. Focused ultrasound-mediated suppression of chemically-induced acute epileptic EEG activity. BMC Neurosci BioMed Central Ltd. 2011;(12):23. doi: 10.1186/1471-2202-12-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyborg WL. Heat generation by ultrasound in a relaxing medium. J Acoust Soc Am. 1981:310. [Google Scholar]
- Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol. 1948;1:93–122. doi: 10.1152/jappl.1948.1.2.93. [DOI] [PubMed] [Google Scholar]
- Plaksin M, Shoham S, Kimmel E. Intramembrane cavitation as a predictive bio-piezoelectric mechanism for ultrasonic brain stimulation. Phys Rev X. 2014;4:1–10. [Google Scholar]
- Prieto ML, Oralkan Ö, Khuri-Yakub BT, Maduke MC. Dynamic Response of Model Lipid Membranes to Ultrasonic Radiation Force. In: Phillips W, editor. PLoS One. Vol. 8. 2013. p. e77115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tennant Ka, Adkins DL, Donlan Na, Asay AL, Thomas N, Kleim Ja, Jones Ta. The organization of the forelimb representation of the C57BL/6 mouse motor cortex as defined by intracortical microstimulation and cytoarchitecture. Cereb Cortex. 2011;21:865–76. doi: 10.1093/cercor/bhq159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ter Haar GR, Daniels S. Evidence for ultrasonically induced cavitation in vivo. Phys Med Biol. 1981;26:1145–9. doi: 10.1088/0031-9155/26/6/013. [DOI] [PubMed] [Google Scholar]
- Tufail Y, Matyushov A, Baldwin N, Tauchmann ML, Georges J, Yoshihiro A, Tillery SIH, Tyler WJ. Neuron. Vol. 66. Elsevier Ltd; 2010. Transcranial pulsed ultrasound stimulates intact brain circuits; pp. 681–94. [DOI] [PubMed] [Google Scholar]
- Tyler WJ. Noninvasive neuromodulation with ultrasound? A continuum mechanics hypothesis. Neuroscientist. 2011;17:25–36. doi: 10.1177/1073858409348066. [DOI] [PubMed] [Google Scholar]
- Vyas U, Kaye E, Pauly KB. Transcranial phase aberration correction using beam simulations and MR-ARFI. Med Phys. 2014;41:032901. doi: 10.1118/1.4865778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner T, Valero-Cabre A, Pascual-Leone A. Noninvasive human brain stimulation. Annu Rev Biomed Eng. 2007;9:527–565. doi: 10.1146/annurev.bioeng.9.061206.133100. [DOI] [PubMed] [Google Scholar]
- Wahab RA, Choi M, Liu Y, Krauthamer V, Zderic V, Myers MR. Mechanical bioeffects of pulsed high intensity focused ultrasound on a simple neural model. Med Phys. 2012;39:4274–83. doi: 10.1118/1.4729712. [DOI] [PubMed] [Google Scholar]
- Wang TR, Dallapiazza R, Elias WJ. Neurological applications of transcranial high intensity focused ultrasound. Int J Hyperthermia. 2015;00:1–7. doi: 10.3109/02656736.2015.1007398. [DOI] [PubMed] [Google Scholar]
- Wright CJ, Rothwell J, Saffari N. Ultrasonic stimulation of peripheral nervous tissue: a study of mechanisms. 15th Int Symp Ther Ultrasound. 2015 [Google Scholar]
- Yoo S-S, Bystritsky A, Lee J-H, Zhang Y, Fischer K, Min B-K, McDannold NJ, Pascual-Leone A, Jolesz Fa. Neuroimage. Vol. 56. Elsevier Inc; 2011. Focused ultrasound modulates region-specific brain activity; pp. 1267–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Younan Y, Deffieux T, Larrat B, Fink M, Tanter M, Aubry J-F. Influence of the pressure field distribution in transcranial ultrasonic neurostimulation. Med Phys. 2013;40:082902. doi: 10.1118/1.4812423. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Chen K, Sloan Sa, Bennett ML, Scholze AR, O’Keeffe S, Phatnani HP, Guarnieri P, Caneda C, Ruderisch N, Deng S, Liddelow Sa, Zhang C, Daneman R, Maniatis T, Barres Ba, Wu JQ. An RNA-sequencing transcriptome and splicing database of glia, neurons, and vascular cells of the cerebral cortex. J Neurosci. 2014;34:11929–47. doi: 10.1523/JNEUROSCI.1860-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


