Abstract
We propose a general theory to describe the distribution of protein-folding transition paths. We show that transition paths follow a predictable sequence of high-free-energy transient states that are separated by free-energy barriers. Each transient state corresponds to the assembly of one or more discrete, cooperative units, which are determined directly from the native structure. We show that the transition state on a folding pathway is reached when a small number of critical contacts are formed between a specific set of substructures, after which folding proceeds downhill in free energy. This approach suggests a natural resolution for distinguishing parallel folding pathways and provides a simple means to predict the rate-limiting step in a folding reaction. Our theory identifies a common folding mechanism for proteins with diverse native structures and establishes general principles for the self-assembly of polymers with specific interactions.
Introduction
Protein folding has been described as both exceedingly complex and remarkably simple (1, 2, 3, 4, 5, 6). Although kinetic measurements are often consistent with simple two-state folding behavior (7), experiments probing folding at higher resolution have provided evidence of considerable additional complexity (8, 9). Direct observations of folding transition paths in both simulation (10, 11) and experiment (12, 13, 14), including demonstrations that folding pathways can be redirected under various conditions (15, 16, 17), can provide insight into these crucial yet fleeting events. However, the factors that determine the distribution of folding transition paths and the detailed kinetics along these pathways remain poorly understood.
To address this question, we propose a general theory to predict the folding transition paths of globular proteins. We adopt a simplified representation of a protein based on native contacts that are derived from a crystal structure (18). Discrete Ising-like models (19, 20, 21) have had great success in reproducing a wide variety of experimental measurements (22, 23) without computationally expensive simulations. However, due to the inherent combinatorial complexity of such models, previous studies have relied on the simplifying assumption that regions of native structure can only grow in one or two contiguous sequences. This assumption is justified for very small proteins on the basis of helix-coil theory, but it limits the applicability of Ising-like models to proteins with relatively simple native-state topologies. Here we take an alternative approach that enforces the intrinsic kinetic connectivity of the microstates and allows for a much larger space of physically realistic combinations of native contacts. As a result, we are able to show that proteins fold by assembling discrete substructures via a small number of well-defined pathways. In contrast to previous studies, our assumptions do not impose a specific mechanism of folding and are thus applicable to proteins with complex native-state topologies.
Our central finding is that folding can be described as a predictable sequence of transitions between discrete transient states. First, we explain how kinetically distinct transient states can be predicted on the basis of a protein’s native-state topology by developing a principle of substructure cooperativity. We then show that the resulting network of transient states leads to a mechanistic description of protein-folding transition paths. Consequently, we are able to distinguish the small set of native contacts that are made precisely at the rate-limiting step from the many contacts that are formed earlier on a folding transition path. As an example, we apply our theory to ubiquitin, a 76-residue α/β protein, for which detailed atomistic folding simulations and experimental characterizations are available. We then show that our predictions are consistent with kinetic measurements on a large number of proteins. Our results have implications both for understanding the folding transition paths of naturally occurring proteins at a detailed level and, more generally, for manipulating the self-assembly pathways of designed polymers with specific interactions.
Materials and Methods
Theory
For a protein to fold to a thermodynamically stable structure, the native state must be stabilized by a large energy gap relative to the many alternative configurations (1, 2, 3, 4). Analysis of atomistic folding simulations provides strong evidence that the native contacts also play a central role in determining protein-folding transition paths (24). Here we develop a nativecentric, coarse-grained polymer model, where the pairwise contacts that define the completely folded state are associated with energetically favorable bonds. We define native residue–residue interactions according to a fixed cutoff distance (4 Å) between heavy atoms in a crystallographically determined native structure (Fig. 1, a and b). We further restrict these interactions to residues that are more than one Kuhn length, taken here to be two residues, apart in the protein sequence. This excludes native contacts that are typically not independent due to their close proximity and are likely to be present in the unfolded state.
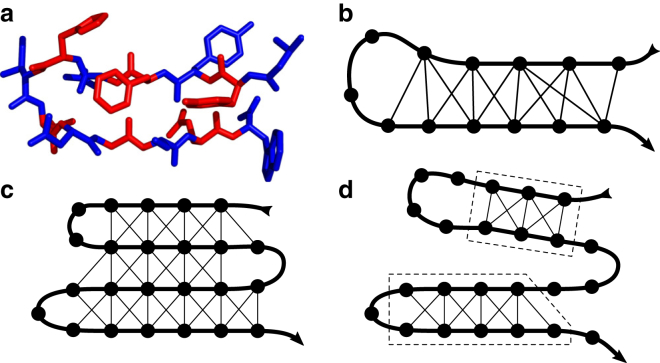
Figure 1.
Construction of the contact-graph model. (a) A portion of a β-hairpin, with sequential residues indicated by alternating colors. We assume that the residues are segmented at the N–Cα bond. (b) An abstract graph representation of this structure, where vertices correspond to residues and edges to residue–residue contacts. The polymer backbone is indicated by the thick line. (c) A schematic contact graph and (d) an allowed microstate, with independent structured regions indicated by dashes. Within each structured region, all possible native contacts are formed. To see this figure in color, go online.
The essential advantage of our theory is the identification of kinetically distinct transient states. This aspect is crucial because it allows us to define a free-energy landscape that preserves the kinetic connectivity of microstates in the full combinatorial model. Moreover, this reduction of complexity to a smaller number of coarse-grained configurations allows us to obtain a mechanistic description of protein-folding transition paths. In the following sections, we outline the steps required for this approach. First, we describe the statistical mechanics of the model and the choices of adjustable energetic parameters. We then explain the physical justification for decomposing a protein into discrete, cooperative substructures, which contribute to the kinetically distinct states. (Free-energy calculations and evidence from atomistic molecular dynamics simulations in support of our approach are presented in the Results.) Lastly, we show how these coarse-grained states can be incorporated into a master-equation framework for predicting protein-folding transition paths.
Contact-graph model
Microstates in this discrete model refer to coarse-grained representations of the polymer: each microstate comprises an ensemble of microscopic polymer configurations in which the residues make a specific combination of native contacts. The microstate in which all specific contacts are formed corresponds to the completely folded configuration, while microstates with a subset of specific contacts are associated with partially folded configurations. However, not all combinations of contacts correspond to physical configurations, because the conformational space of the polymer is restricted by steric constraints (the residues occupy finite volumes that cannot overlap) and the chain connectivity (sequential residues are covalently linked). We therefore limit the set of allowed microstates to physically realistic configurations by imposing two rules. First, we note that every microstate with a specific set of contacts can be decomposed into disconnected structured regions (Fig. 1 c). Within each structured region, it is reasonable to assume that the native contacts between interacting residues are geometrically correlated due to their close spatial proximity. We therefore require that all possible native contacts be formed within each structured region (Fig. 1 d). Second, to define a self-consistent configurational entropy, we do not allow microstates with disordered loops of contact-forming residues (i.e., residues that make contacts in the native state) that are shorter than one Kuhn length (see the Supporting Material).
Because the microstates correspond to ensembles of constrained polymer configurations, each microstate g is associated with a free energy, ,
| (1) |
where is the number of residues in each structured region , T is the absolute temperature, and is the Boltzmann constant. Within each structured region, we account for the loss of configurational entropy per ordered residue, , and the energetic contributions, , of all native contacts. (The notation indicates unity if a native contact is present between residues u and v in structured region c, and zero otherwise.) The remaining entropic penalty, , accounts for closed loops of noninteracting residues. Assuming Gaussian polymer statistics (25) for sequences longer than one Kuhn length b, we sum the entropic penalties for all loops,
| (2) |
where the sum runs over every loop in the microstate g, , is the number of noninteracting residues in the loop, is the distance between the fixed ends of the loop, and is the spatial dimension (see the Supporting Material).
To apply Eqs. 1 and 2, we must choose the parameters μ and . On the basis of atomistic simulations (26), we have chosen ; values between 1.5 and 2.5 kBT give very similar results. The energy of each bond is estimated from the crystal structure by counting the number of heavy-atom contacts among residues u and v and , and by determining whether a main-chain hydrogen bond exists; the hydrogen-bond contribution is times that of a single heavy-atom contact. Because native-centric models are known to overstabilize helices (27, 28), we weaken all energies associated with helical contacts by a factor . The bond energy formula is thus , where indicates the presence of a hydrogen bond and indicates a helical contact. The constants and were chosen empirically to maximize the agreement with experiments on protein G (see Fig. S2 and Table S1 in the Supporting Material). The inverse temperature is then tuned to achieve a fixed free-energy difference between the unfolded and folded ensembles (see the Supporting Material).
Identification of cooperative substructures and transient states
We now seek to identify kinetically separated folding intermediates by examining the factors that give rise to free-energy barriers between microstates. In the contact-graph model, all free-energy barriers are purely entropic, because the native contacts are assumed to be energetically favorable. The most significant free-energy barriers arise from the formation of loops, which entail an entropic penalty of at least that is not immediately compensated by energetically favorable native contacts. Once an initial loop has been formed, the recruitment of residues that are adjacent in the protein sequence may result in a net decrease in the free energy. As a result, the model naturally gives rise to cooperative substructures, i.e., sets of contacts that require the formation of a single loop and thus share a common free-energy barrier. As in the helix-coil (29) and kinetic-zipper (30) models of peptide assembly, the sets of contacts comprising an individual substructure are typically bistable: either none of the contacts are made in the high-entropy state, or else many contacts are required to compensate for the loss of conformational entropy in the low-energy state.
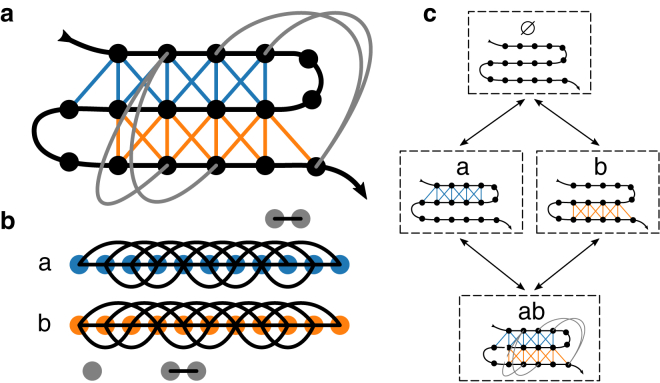
We identify groups of contacts that constitute the distinct substructures of a contact graph using the following algorithm. First, we find all pairs of contacts where the interacting residues are either identical or are adjacent on the polymer backbone; that is, two contacts and are linked if and . These pairs of contacts define a backbone-dual graph in which the vertices represent native interactions and the edges indicate adjacency along the polymer backbone (Fig. 2, a and b). We then decompose this graph into connected components, retaining only those components with at least six contacts to counter the minimum entropic cost of forming a Kuhn-length loop. The role of contacts that are not assigned to substructures is discussed below. While the substructures identified by this algorithm often align with elements of secondary structure, this does not have to be the case, because the substructures are defined purely on the basis of the three-dimensional native structure.
Figure 2.
Identification of substructures and topological configurations. (a) An example contact graph, with contacts colored by substructure. Each substructure requires the formation of one loop in the polymer backbone. Unassigned contacts are shown in gray. (b) The backbone-dual graph, in which the vertices represent native contacts (see text). (c) A substructure is part of this topological configuration if one or more of its contacts are formed in the largest structured region. The unassigned contacts contribute to the stability of configuration ab. Arrows indicate allowed transitions between topological configurations that differ by the addition or removal of one substructure. To see this figure in color, go online.
Advancing toward the folded state requires building up successive substructures, each of which is associated with a free-energy barrier. A transition path must cross each of these barriers one at a time, regardless of the precise order in which the contacts are formed. These intermediate states can be described by a discrete set of topological configurations that indicate the assembly of one or more substructures (Fig. 2 c). In the remainder of this work, we simplify our analysis by tracking only the largest native-like cluster of residues. As a result, each topological configuration refers to the assembly of a specific set of substructures within a single structured region. The validity of this assumption is discussed in the Results.
Native contacts that are not assigned to substructures contribute to the stability of topological configurations that consist of multiple substructures in a single structured region. For example, in Fig. 2, the unassigned contacts shown in gray contribute to topological configuration ab but not to configuration a or b. In cases where some residues do not participate in any of the identified substructures, we define a separate native configuration that contains all substructures plus the additional contacts involving these residues. Because such residues do not contribute to any of the intermediate topological configurations, they do not affect the folding transition paths predicted by our theory; the contacts formed by these residues serve only to stabilize the native state.
Because of the significant free-energy barriers associated with loop formation, cooperative substructures are predicted to have long lifetimes compared to individual native contacts. Furthermore, the free-energy barriers between topological configurations are expected to give rise to metastability: microstates that share the same set of loops can interconvert rapidly, while transitions between topological configurations that differ by the addition or removal of one substructure occur on a much slower timescale. These topological configurations therefore serve as an appropriate set of coarse-grained, transient states for analyzing the dynamics of protein-folding transition paths.
Prediction of folding transition paths
Having established a structural definition of a transient state, we can now construct a rate matrix to describe stochastic transitions between the coarse-grained configurations. First, we calculate the free-energy of each configuration, , by summing over all microstates that conform to the topological configuration i: . The compatible microstates are those that have a single structured region and contain one or more contacts from each substructure comprising configuration i. This sum can be calculated efficiently via Monte Carlo integration using the technique described in Jacobs et al. (31) (and see text in the Supporting Material). This calculation also yields the equilibrium probability of contact formation within each topological configuration, . As we shall demonstrate, the most probable microstates within a topological configuration may not form all possible contacts.
We then calculate the free-energy barriers, , between topological configurations i and j that differ by the addition or removal of one substructure. We consider two mechanisms of substructure addition: either the formation of a new loop via a single contact or the consolidation of a preformed substructure with the existing structured region. The former mechanism is applicable when the added substructure shares residues with substructures in the existing structured region. In contrast, the latter mechanism is applicable when the added substructure and the existing structured region have no residues in common but nevertheless form contacts in the native structure. In both cases, we calculate the mean-field probability of forming an initial contact with one or more residues of the new substructure, assuming that the existing structured region is in local equilibrium. The details of these calculations, which take into account fluctuations within each topological configuration, are provided in the Supporting Material.
Finally, we construct a rate matrix to describe transitions between topological configurations. The dimensionless rates obey detailed balance and are assumed to follow from the Metropolis criterion,
| (3) |
From this rate matrix, it is straightforward to obtain ensemble-averaged properties of transition paths between the unfolded and folded ensembles using transition-path theory (32). Of particular interest are the commitment probabilities, (33), and the folding fluxes, , between adjacent configurations. In addition, we can predict folding intermediates by calculating the average time spent in each configuration within the transition-path ensemble. Details are provided in the Supporting Material.
Results
Proteins fold via a sequence of transient states
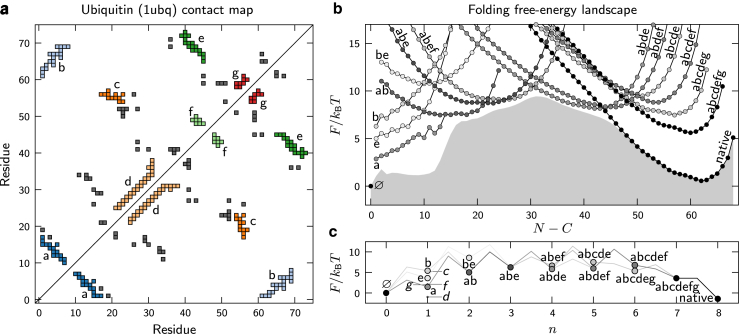
Free-energy calculations support the interpretation of the substructures identified in the Materials and Methods as the minimal cooperative units on a folding transition path. As an example, we present calculations for ubiquitin in Fig. 3; its seven substructures are indicated on the contact map in Fig. 3 a. When plotted as a function of the total number of interacting residues, N, we find that every topological configuration is associated with a single local free-energy minimum (Fig. 3 b). Single-substructure configurations are typically unstable, as the free energy increases with the number of interacting residues. In contrast, the energetically favorable native contacts in multiple-substructure configurations more than compensate for the loss of conformational entropy due to loop formation. However, at the local minimum in each of these configurations, the polymer is unlikely to form all possible native contacts for entropic reasons: there are many more partially assembled microstates, and some residues make too few native contacts to offset the entropic cost of ordering completely. As a result, the free-energy minimum typically occurs at a value of N that is less than the maximum number of residues in each configuration. Because of this competition between stabilizing native contacts and various entropic contributions, the locations of these free-energy minima are temperature-dependent.
Figure 3.
Predicted folding free-energy landscapes for ubiquitin. (a) The contact map obtained from the crystal structure of ubiquitin (PDB: 1UBQ) indicating the discrete substructures a–g described in the Materials and Methods. (b) The free energy of each topological configuration as a function of the total number of interacting residues, N. The number of structured regions, C, is 1 for all configurations except the unfolded state, Ø, where C = 0. The shaded region shows the one-dimensional free-energy profile. (c) The free energy of each topological configuration as a function of the number of assembled substructures, n. All free energies are calculated relative to the state Ø, and the inverse temperature is tuned to achieve equal stabilities of the native and unfolded ensembles. The shading indicates the fraction of the net folding flux through each configuration. Only configurations with at least 10% of the net folding flux are shown, except in (c), n = 1, where all substructures are labeled. To see this figure in color, go online.
Plotting the free-energy landscape as a function of the number of assembled substructures more clearly shows the free-energy barriers between adjacent topological configurations (Fig. 3 c). Microstates belonging to different topological configurations are kinetically separated by at least one entropic barrier and cannot interconvert rapidly. The existence of significant free-energy barriers between unimodal free-energy basins supports the assertion that the topological configurations constitute transient states on the transition paths between the completely unfolded and native states. Alternate pathways may be traversed, depending on the order in which the free-energy barriers between configurations are crossed. Yet in general, we find that only a small number of parallel pathways contain the vast majority of the reactive flux between the unfolded and native states. In Fig. 3, b and c, the shading of each topological configuration indicates the fraction of the net folding flux, , passing through that configuration on folding transition paths; the many other configurations with negligible net folding flux are not shown.
Free-energy landscapes predict a common folding mechanism
These multimodal free-energy landscapes point to a common folding mechanism. As expected on the basis of Eq. 1, our free-energy calculations indicate that there are no significant barriers separating microstates within individual topological configurations. Instead, the relevant barriers are found between topological configurations. These landscapes thus predict that folding proceeds by the stepwise consolidation of cooperative structures within a single structured region. The transition state on a folding pathway is reached upon the formation of a specific set of substructures, after which all subsequent barriers on the pathway are lower in free energy and folding can proceed downhill to the native state.
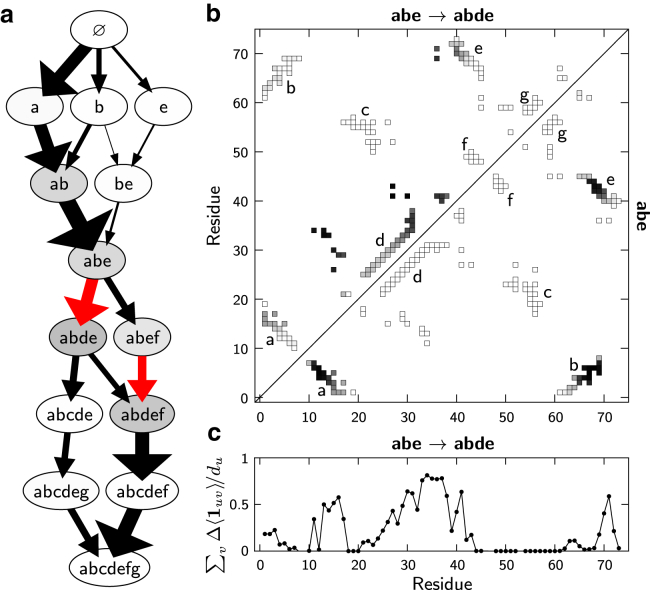
To preserve the kinetic connectivity of the transient states, the folding free-energy landscape is best represented by a network of the discrete topological configurations. In Fig. 4 a, we show all configurations containing at least 10% of the net folding flux. Arrows indicate the net folding flux between configurations, while the shading indicates the fraction of the total transition-path time spent in each configuration. The transitions that pass through the rate-limiting step, from which the protein has an equal probability of folding or unfolding, are highlighted. This kinetic network shows that substructures tend to assemble in a remarkably well-ordered sequence, despite the stochastic nature of the transitions between transient states. It is important to note that this ordering is not dictated simply by the stability of the isolated structures: the sequence of events on folding transition paths does not match the ranking of the substructure free energies (n = 1) in Fig. 3 c. Instead, the most likely pathway depends on the stability of the intermediate configurations and the barriers between them, which in turn depend on the contacts between substructures.
Figure 4.
Specific contacts are formed at the rate-limiting step on the folding transition paths of ubiquitin. (a) The folding network of ubiquitin, showing the topological configurations containing at least 10% of the net folding flux (see text). (b) Below the diagonal, the equilibrium distribution of native contacts in topological configuration abe. Above the diagonal, the difference between the equilibrium contact distributions of configurations abe and abde. Black indicates a probability of 1, while white indicates 0. (c) The difference in equilibrium contact formation, , between configurations abe and abde, averaged over each residue. The total number of native contacts made by residue u is . A small number of essential long-distance contacts, primarily involving residues 13–17, 27–41, and 69–71, are formed at the transition between these configurations. To see this figure in color, go online.
Although many proteins are commonly described by two-state kinetics, our analysis indicates that folding transition paths may have greater kinetic complexity due to the presence of transient, high-free-energy folding intermediates. For comparison, a one-dimensional profile showing the free energy as a function of the number of interacting residues is shown in Fig. 3 b. In contrast to our approach, this representation of the folding landscape does not distinguish among microstates in directions orthogonal to the order parameter and consequently hides the barriers that prevent microstates with similar numbers of interacting residues from interconverting rapidly. Decomposing the landscape into topological configurations provides more detailed insights into the folding free-energy barrier and the tradeoff between native-contact formation and the loss of conformational entropy. In particular, our analysis shows that a specific set of loops in the polymer backbone must be formed for subsequent native contacts to lower the free energy as folding progresses toward the native state.
Specific contacts are formed at the rate-limiting transition
Fig. 4 a shows that the assembly of topological configuration abde or abdef is required for ubiquitin to reach the folded ensemble. Common to both of the highlighted transitions is the consolidation of the helix (substructure d) with a partially formed β-sheet (substructures a, b, and e); the final hairpin of the β-sheet (substructure f) is optional and thus largely irrelevant. This analysis provides a clear mechanistic description of the essential rate-limiting event on a folding transition path. In addition, our analysis predicts that the majority of the transition-path time is spent in the metastable configurations just before and after the transition, configurations ab–abdef.
Importantly, this approach allows us to distinguish between the native contacts that are prerequisite for reaching the transition state and those that are formed precisely at the rate-limiting step. As illustrated in Fig. 4 b, a relatively small number of native contacts are involved in the rate-limiting step on ubiquitin’s folding pathway. Shown below the diagonal in this plot is the contact distribution in the pretransition configuration abe, assuming local equilibrium in this metastable state. Not all contacts within the three contributing substructures are equally probable; in particular, residues near the extremities of the β-sheet are more likely to be disordered. To determine the contacts that are formed upon the incorporation of the helix into the largest structured region, we subtract the union of the contact distributions of configuration abe and the isolated substructure d from the post-transition configuration abde. We find that a specific set of ∼15 long-range contacts between the helix and partial β-sheet is essential for the rate-limiting transition. The residue-averaged contact differences (Fig. 4 c) indicate that these specific contacts primarily involve residues 13–17, 27–41, and 69–71. As we shall show below, this distribution of rate-limiting contacts is significantly different from the complete set of contacts present at the transition state.
Comparison with atomistic molecular dynamics simulations
The accuracy of these predictions can be tested by comparison with atomistic molecular dynamics simulations. For this purpose, we obtained unbiased simulation trajectories of the reversible folding and unfolding of wild-type ubiquitin from Piana et al. (34). We shall focus our attention on the native contacts formed during the ∼1–10 μs-long transition paths (two folding and eight unfolding) that were captured from six independent simulations. The details of our analysis are provided in the Supporting Material; the molecular dynamics simulations are described in Lindorff-Larsen et al. (11) and Piana et al. (34).
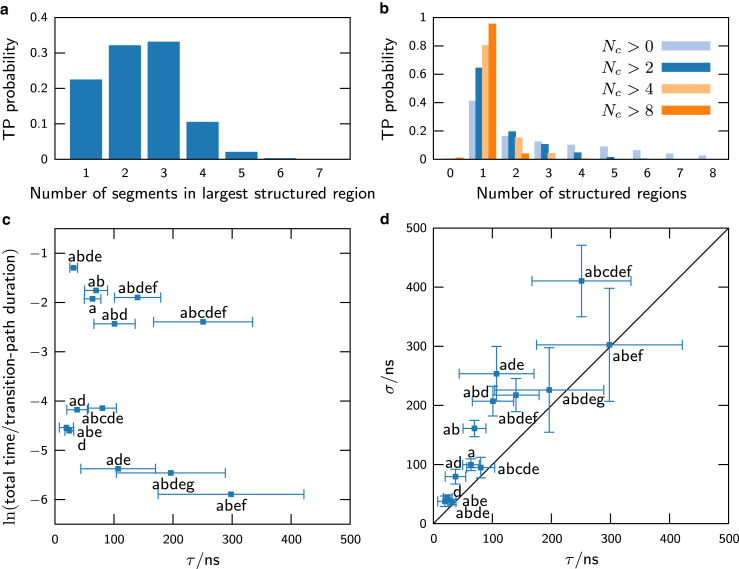
We first tested the underlying assumptions of our theoretical approach. Fig. 5 a shows a histogram of the number of segments within the largest structured region in the ensemble of transition-path structures. The segments here are defined as stretches of sequential residues forming native contacts, with the additional constraint that each segment is separated by at least b noninteracting residues. This histogram clearly shows that a single or double-sequence approximation, i.e., assuming one or two native-like segments, is inadequate. In contrast, we verified that modeling only the largest structured region is sufficient to describe most of the transition-path ensemble. In Fig. 5 b, we plot the probability of finding one or more structured regions, each containing a minimum number of residues on a transition path. If we ignore all native-like clusters containing eight or fewer residues, then we find that the assumption of a single structured region is valid for >95% of the (un)folding trajectories.
Figure 5.
Verification of the assumptions and predictions of the theory using atomistic simulations (see Piana et al. (34)). (a) For ∼50% of the transition-path (TP) duration, more than two native-like segments are formed in the largest structured region. (b) Histograms of the number of distinct structured regions with a minimum number of residues in the transition-path ensemble. (c) The fraction of the total transition-path time spent in each topological configuration. (d) The mean, τ, versus standard deviation, σ, of the topological-configuration lifetimes. The line σ = τ is indicative of an exponential waiting-time distribution. To see this figure in color, go online.
Next, we calculated the lifetimes of the predicted transient states on the observed transition paths. As in our theoretical approach, we identified the topological configuration in the simulation trajectories by determining which substructures are at least partially formed within the largest structured region. We then calculated the mean, τ, and standard deviation, σ, of the distribution of lifetimes for all visits to each topological configuration. In Fig. 5 c, we plot the fraction of the total transition-path time spent in each configuration versus its mean lifetime. We find that the three most populated configurations (abde, ab, and abdef) agree with the predictions shown in Fig. 4 a. Meanwhile, the average lifetimes of all visited transient states range from 20 to 300 ns, considerably longer than the timescale for native-contact formation. Finally, Fig. 5 d shows that the coefficient of variation of the lifetimes, σ/τ, is close to unity for most configurations. This is indicative of an exponential distribution of waiting times, which supports our prediction that the barrier-separated configurations constitute metastable states.
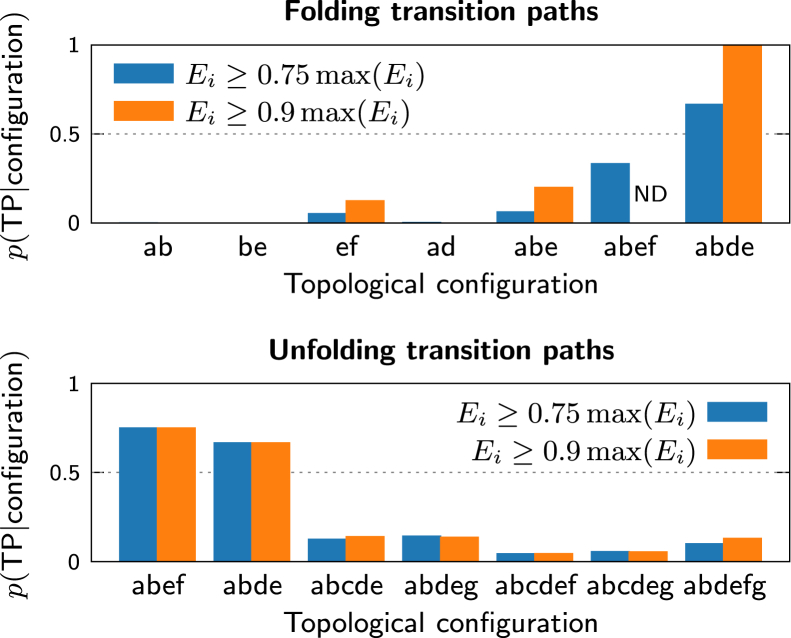
Having verified our fundamental assumptions and the most general predictions of our theory, we then assessed the accuracy of our predictions regarding the rate-limiting step of the folding reaction. We identified all excursions away from the free-energy minima of the unfolded and folded ensembles in the simulation trajectories and counted the number of excursions that reached each topological configuration starting from either the unfolded, U, or folded, F, ensemble. Transitions were only counted if a minimum fraction of the total number of contacts, , are formed in configuration i. We then calculated the commitment probability for each configuration, i.e., the probability of being on a transition path given that a specific topological configuration is reached, using the Bayesian formula
| (4) |
where is the number of folding or unfolding transition paths, is the probability of reaching configuration i on a folding or unfolding transition path, and is the total number of excursions that reached configuration i. The results of this analysis are presented in Fig. 6.
Figure 6.
Commitment probabilities for transient states in atomistic simulations. The probability of being on a transition path given that an excursion from the unfolded (bottom) or native (top) ensemble either reaches or disrupts the indicated topological configuration, respectively. Only excursions that achieve a minimum fraction of the total number of contacts in a topological configuration, , are counted. No data is available in the case of configuration abef for the stricter condition , because no qualifying events were observed in the available simulation trajectories. To see this figure in color, go online.
As predicted, the probability of folding surpasses 50% once configuration abde is reached from the unfolded ensemble; with the stricter criterion , this probability increases to 100%. The necessary precursors to this transition, including the assembly of substructures a, b, and e, have considerably smaller commitment probabilities. We also find that disrupting configuration abde increases the probability of unfolding above 50% for excursions starting from the folded ensemble. Despite the limited statistics from the available simulation trajectories, these results lend strong support to our predictive theory. This agreement is crucial because it demonstrates that our description in terms of transient states can provide mechanistic insights into the rate-limiting events on the transition paths of topologically complex proteins.
Comparison with kinetic measurements
Experimentally, the folding transition-state ensemble can be probed indirectly by perturbing interactions between residues. The most commonly used techniques are ϕ-value analysis (35), which compares changes in the rate of folding to changes in the equilibrium constant due to single-residue point mutations, and ψ-value analysis (36), which applies an analogous strategy to pairwise contacts between solvent-exposed residues. While ϕ- and ψ-values do not test our theory directly—for instance, they cannot distinguish the rate-limiting contacts from prerequisite contacts at the transition state, nor can they provide detailed information on transition-path dynamics—they remain the only experimental techniques for which consistent data exist for a large number of proteins.
To compare our model with experimental measurements, we calculate ϕ- and ψ-values due to energetic perturbations in the small-perturbation limit,
| (5) |
| (6) |
where is the folding rate calculated from transition-path theory; indicates the change due to a perturbation in the contact energy ; and is the number of contacts made by residue u in the native state. In ϕ-value comparisons, we consider only mutations to alanine or glycine; in cases where data for both mutations are available, we choose the substitution that is chemically most similar to the wild-type residue at that position. We also leave ϕ-values that are negative or significantly greater than unity out of the comparison (see the Supporting Material).
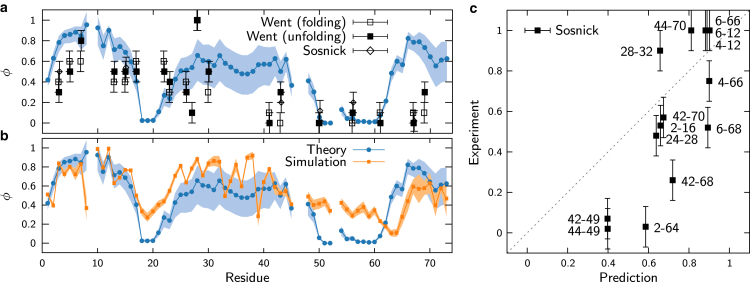
In Fig. 7, we show the agreement between the predicted ϕ- and ψ-values and three experimental measurements for ubiquitin. Calculating the ϕ-value predictions under conditions of equal folded and unfolded populations (see the Supporting Material), we obtain a correlation coefficient R = 0.43 and p-value p = 0.063 with the unfolding data of Went and Jackson (37). To get an idea of the variability in our predictions due to changes in the native-state stability, we also plot the predicted range of ϕ-values due to stabilizing or destabilizing the native state by 2 kBT. This agreement is reasonable considering that many mutations perturb the energy of the transition state by several kBT. The correlation between the predicted and experimental ψ-values is considerably stronger, with R = 0.80 and p = 0.00061. There is less ambiguity in the latter comparison, because the experimental perturbations are intended to affect only a single native contact and are reported in the small-perturbation limit. We also compare our predictions with ϕ-values calculated from the atomistic simulations following the transition-path ensemble method of Best and Hummer (38) and the native-contact definition used in Figs. 5 and 6. Here we find that the theory-simulation and simulation-experiment correlations for ϕ-values are similar (R = 0.60, p = 4.5 × 10−8 and R = 0.51, p = 0.024, respectively); however, the agreement between simulation and experiment is weaker for ψ-values (R = 0.48, p = 0.080). Notably, both the theoretical predictions and the simulation results indicate a more pronounced role for the C-terminus in the transition-state ensemble than is apparent from the experimental ϕ-values (Fig. 7, a and b).
Figure 7.
Comparison of ϕ- and ψ-values for ubiquitin. (a) Comparison of predicted ϕ-values in the small-perturbation limit with three sets of experimental measurements: folding and unfolding, Went et al. (37), and Sosnick et al. (52). Circles indicate predictions assuming ; the light-blue region indicates the range of predictions from (upper limit) to −2 kBT (lower limit). Predictions are not shown for residues that do not form native contacts. (b) Comparison with ϕ-values calculated from atomistic simulations. The light-orange range reports an estimate of the variability across individual transition paths (see the Supporting Material). (c) Comparison of predicted and experimental ψ-values from Sosnick et al. (52). To see this figure in color, go online.
To examine the generality of our predictions, we have also calculated ϕ- and ψ-values for comparison with experiments on an additional 14 proteins. Overall, we find good agreement, indicating that our native-centric model captures the essential physics of folding across a wide variety of proteins with 50 or more amino acids (Table 1). Detailed case studies for protein G (Protein Data Bank (PDB): 1IGD), protein L (PDB: 1K53), chymotrypsin inhibitor 2 (PDB: 2CI2), cold-shock protein (PDB: 1CSP), and an SH3 domain (PDB: 1SHG) are provided in the Supporting Material; complete details of all mutations tested are provided there as well. We find that the agreement between our predictions and experiments is generally better for ψ-values than ϕ-values and is worst for small helix bundles, such as the engrailed homeodomain proteins (PDB: 1ENH), which are known to have heterogeneous folding pathways that are highly sensitive to the force field used in computer simulations (38, 39). In fact, the greatest source of uncertainty in making these comparisons is the sensitivity of the predicted ϕ- and ψ-values to the native-contact energies, and, consequently, the relative stabilities of the substructures. We caution that the calculated correlation coefficients and p-values are affected by correlations in the ϕ- and ψ-values of neighboring residues and the choice of mutations for experimental characterization. Nevertheless, these results indicate that the predictions of our theory are compatible with the available experimental data on a diverse set of proteins.
Table 1.
Comparison of Predicted and Experimental ϕ- and ψ-Values for a Diverse Set of Proteins
| PDB entry number | n | R | p |
|---|---|---|---|
| ϕ-values | |||
| 1ENH | 11 | 0.14 | 0.69 |
| 1IGD | 20 | 0.80 | 0.000023 |
| 1SHG | 10 | 0.70 | 0.024 |
| 1K53 | 37 | 0.36 | 0.031 |
| 2CI2 | 32 | 0.42 | 0.018 |
| 1CSP | 16 | 0.71 | 0.0041 |
| 1UBQ | 19 | 0.43 | 0.063 |
| 1IMP | 14 | 0.73 | 0.003 |
| 1TIU | 22 | 0.48 | 0.024 |
| 1BTB | 21 | 0.44 | 0.045 |
| 1FKB | 21 | 0.65 | 0.0015 |
| 1RNB | 12 | 0.60 | 0.038 |
| 3CHY | 7 | 0.91 | 0.0044 |
| 2VIL | 17 | 0.43 | 0.088 |
| ψ-values | |||
| 1IGD | 8 | 0.69 | 0.059 |
| 1K53 | 7 | 0.93 | 0.022 |
| 1UBQ | 14 | 0.80 | 0.00061 |
| 2ACY | 8 | 0.71 | 0.048 |
For each protein, identified by its Protein Data Bank (PDB) entry, we list the number of data points, n; the Pearson correlation coefficient, R; and the associated p-value, p. Note that the PDB: 1IGDϕ-values were used in the parameterization of the empirical two-parameter potential (see Materials and Methods). Complete details and accompanying figures are provided in the Supporting Material (see Tables S1–S3 and Figs. S7–S9).
Discussion
We have introduced a theory to predict the detailed kinetics and intermediate states on protein-folding transition paths. We have shown that the folding of topologically complex proteins follows a predictable sequence of transitions between transient states, which can be identified directly from the native structure. While our approach has been developed using a discrete, native-centric model of globular proteins, our conclusions are broadly applicable to the self-assembly of polymers with specific interactions, such as non-coding RNA (40) and DNA origami (41).
Physical explanation for the emergence of “foldons”
Our analysis shows that there is a natural level of resolution for describing transition-path dynamics. Although all macromolecular transition paths are heterogeneous when examined in sufficient detail, modeling the assembly and disassembly of discrete substructures fully captures the long-timescale motions and metastable states on folding pathways. In addition, this ability to predict transient states on the basis of a protein’s native structure alleviates the need for contiguous-sequence approximations that are not justified for proteins with complex native topologies.
Many lines of evidence, including hydrogen-exchange (8), metal-binding kinetics at bi-histidine sites (42), and single-molecule pulling experiments (15), support the existence of transient, high-free-energy folding intermediates composed of cooperative units that are often referred to as “foldons” (9, 43). In fact, sequential folding through a series of intermediates was proposed in some of the earliest models of protein-folding (44, 45). Our theory predicts that these transient states emerge directly from the topology of the native state. We have further shown that the cooperativity among these groups of native contacts is a consequence of the central role of loop formation in protein folding, which gives rise to entropic barriers between transient states. While these cooperative units are most easily identified in the context of a native-centric model, the appearance of structurally defined metastable states in atomistic simulations supports the generality of this finding.
Ordered pathways are determined by the native-state structure
Although protein-folding is a stochastic process, the most probable transition paths tend to follow a small number of distinct pathways. Calculations for a structurally diverse set of examples (see Figs. S2–S6) show that the dominant folding pathways are highly predictable when analyzed at the level of discrete substructures. However, the order in which the substructures assemble is not determined by their stabilities in isolation. Instead, the lowest-free-energy path through the folding landscape depends on both the stabilities of composite assemblies of multiple substructures and the barriers between these intermediate states.
This description in terms of transient states provides a detailed explanation for the origin of the folding free-energy barrier. In the unfolded ensemble, the individual substructures tend to be unstable because the native contacts do not completely compensate for the loss of configurational entropy. The lowest-free-energy folding pathway requires the assembly of a specific set of native-like loops in the polymer backbone, which then allows for the formation of stabilizing native contacts. In particular, long-distance contacts (46, 47) that connect the discrete substructures are most likely to form during a transition between topological configurations. Because the ensemble of transition paths passes through a network of intermediates (48, 49), a folding reaction may be poorly described by a single order parameter. In contrast to one-dimensional free-energy projections, coarse-graining on the basis of the topology of the polymer backbone preserves the kinetic connectivity of the complete folding landscape.
Mechanistic description of a folding reaction
Our theory provides a mechanistic description of protein-folding transition paths by identifying the crucial event that must occur for a protein to fold to its native state. The ability to predict the contacts that are formed at each step along the folding pathway is a key insight that is difficult to discern from kinetic measurements alone. Whereas ϕ- and ψ-values can, in principle, report the set of contacts that are formed at the transition state, our approach is able to distinguish which contacts are responsible for commitment to the folded ensemble. In fact, many of the residues that form such crucial contacts, and are thus essential to the mechanism of folding, are found to have low to moderate ϕ-values. This is largely a consequence of averaging over all native contacts involving the residue of interest, only some of which may be formed at the transition state. Core-facing residues that form a large number of stabilizing contacts in the native state are particularly likely to have low ϕ-values for this reason (50, 51). Other authors have noted that misleadingly low ϕ-values from destabilizing mutations can result from structural relaxation in the transition state (52) or redirection of the transition-path ensemble through parallel pathways (38).
It is important to note that our predictions and the agreement with kinetic measurements are affected by the native-contact energies. While the two-parameter empirical potential that we have used here is insufficient to capture all aspects of the interatomic interactions, we nevertheless achieve similar or greater accuracy in ϕ- and ψ-value predictions to that of atomistic simulations (see, e.g., Best and Hummer (38)). This aspect of our theoretical predictions could be improved by increasing the complexity of the empirical potential and tuning the parameters by comparison with detailed simulation data. Nevertheless, we expect that the general features of the predicted transition paths, including the metastability of structurally defined transient states, will remain unchanged.
Conclusions
In summary, we have developed an approach to predict protein-folding transition paths and high-free-energy intermediate states using a discrete native-centric model. Our theory yields detailed, mechanistic insights into protein folding without the use of computationally expensive simulations. Fundamentally, this advance relies on the physically realistic restrictions placed on the polymer configurations in our model, a crucial aspect that differs significantly from earlier efforts (19, 20, 21).
Beyond proteins, our theory can be applied more generally to polymers with specific interactions, such as noncoding RNA and DNA origami, where the ability to distinguish among kinetically separated pathways is essential for describing complex folding reactions. The model that we have presented here is transferable to a variety of such systems due to the similar underlying physics of self-assembling structures that are built around polymer backbones and stabilized by native contacts. We anticipate that this work will open up new avenues for addressing poorly understood aspects of protein-folding kinetics, including the molecular mechanisms of cotranslational and chaperone-assisted folding.
Author Contributions
W.M.J. and E.I.S. conceived the project; W.M.J. performed the calculations; and W.M.J. and E.I.S. analyzed the results and wrote the article.
Acknowledgments
The authors acknowledge Adrian Serohijos, Michael Manhart, and David de Sancho for many insightful discussions and William Eaton for helpful comments on the article. We are grateful to DE Shaw Research for providing access to the atomistic simulation trajectories.
This work was supported by National Institutes of Health grants No. R01GM068670 and No. F32GM116231.
Editor: Amedeo Caflisch.
Footnotes
Supporting Materials and Methods, nine figures, and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30477-5.
Supporting Citations
References (53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71) appear in the Supporting Material.
Supporting Material
References
- 1.Šali A., Shakhnovich E., Karplus M. How does a protein fold? Nature. 1994;369:248–251. doi: 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
- 2.Shakhnovich E.I. Proteins with selected sequences fold into unique native conformation. Phys. Rev. Lett. 1994;72:3907–3910. doi: 10.1103/PhysRevLett.72.3907. [DOI] [PubMed] [Google Scholar]
- 3.Onuchic J.N., Wolynes P.G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 4.Shakhnovich E. Protein folding thermodynamics and dynamics: where physics, chemistry, and biology meet. Chem. Rev. 2006;106:1559–1588. doi: 10.1021/cr040425u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Daggett V., Fersht A. The present view of the mechanism of protein folding. Nat. Rev. Mol. Cell Biol. 2003;4:497–502. doi: 10.1038/nrm1126. [DOI] [PubMed] [Google Scholar]
- 6.Thirumalai D., O’Brien E.P., Hyeon C. Theoretical perspectives on protein folding. Annu. Rev. Biophys. 2010;39:159–183. doi: 10.1146/annurev-biophys-051309-103835. [DOI] [PubMed] [Google Scholar]
- 7.Jackson S.E., Fersht A.R. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry. 1991;30:10428–10435. doi: 10.1021/bi00107a010. [DOI] [PubMed] [Google Scholar]
- 8.Maity H., Maity M., Englander S.W. Protein folding: the stepwise assembly of foldon units. Proc. Natl. Acad. Sci. USA. 2005;102:4741–4746. doi: 10.1073/pnas.0501043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Englander S.W., Mayne L. The nature of protein folding pathways. Proc. Natl. Acad. Sci. USA. 2014;111:15873–15880. doi: 10.1073/pnas.1411798111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shaw D.E., Maragakis P., Wriggers W. Atomic-level characterization of the structural dynamics of proteins. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- 11.Lindorff-Larsen K., Piana S., Shaw D.E. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 12.Chung H.S., McHale K., Eaton W.A. Single-molecule fluorescence experiments determine protein folding transition path times. Science. 2012;335:981–984. doi: 10.1126/science.1215768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hu W., Walters B.T., Englander S.W. Stepwise protein folding at near amino acid resolution by hydrogen exchange and mass spectrometry. Proc. Natl. Acad. Sci. USA. 2013;110:7684–7689. doi: 10.1073/pnas.1305887110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Neupane K., Foster D.A.N., Woodside M.T. Direct observation of transition paths during the folding of proteins and nucleic acids. Science. 2016;352:239–242. doi: 10.1126/science.aad0637. [DOI] [PubMed] [Google Scholar]
- 15.Mickler M., Dima R.I., Rief M. Revealing the bifurcation in the unfolding pathways of GFP by using single-molecule experiments and simulations. Proc. Natl. Acad. Sci. USA. 2007;104:20268–20273. doi: 10.1073/pnas.0705458104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jagannathan B., Elms P.J., Marqusee S. Direct observation of a force-induced switch in the anisotropic mechanical unfolding pathway of a protein. Proc. Natl. Acad. Sci. USA. 2012;109:17820–17825. doi: 10.1073/pnas.1201800109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guinn E.J., Jagannathan B., Marqusee S. Single-molecule chemo-mechanical unfolding reveals multiple transition state barriers in a small single-domain protein. Nat. Comm. 2015;6 doi: 10.1038/ncomms7861. 6861–6689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Taketomi H., Ueda Y., Gō N. Studies on protein folding, unfolding and fluctuations by computer simulation. I. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int. J. Pept. Protein Res. 1975;7:445–459. [PubMed] [Google Scholar]
- 19.Muñoz V., Eaton W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alm E., Baker D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc. Natl. Acad. Sci. USA. 1999;96:11305–11310. doi: 10.1073/pnas.96.20.11305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Galzitskaya O.V., Finkelstein A.V. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. USA. 1999;96:11299–11304. doi: 10.1073/pnas.96.20.11299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kubelka J., Henry E.R., Eaton W.A. Chemical, physical, and theoretical kinetics of an ultrafast folding protein. Proc. Natl. Acad. Sci. USA. 2008;105:18655–18662. doi: 10.1073/pnas.0808600105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Henry E.R., Best R.B., Eaton W.A. Comparing a simple theoretical model for protein folding with all-atom molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 2013;110:17880–17885. doi: 10.1073/pnas.1317105110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Best R.B., Hummer G., Eaton W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA. 2013;110:17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vanderzande C. Cambridge University Press; Cambridge, UK: 1998. Lattice Models of Polymers; p. 11. [Google Scholar]
- 26.Baxa M.C., Haddadian E.J., Sosnick T.R. Loss of conformational entropy in protein folding calculated using realistic ensembles and its implications for NMR-based calculations. Proc. Natl. Acad. Sci. USA. 2014;111:15396–15401. doi: 10.1073/pnas.1407768111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shimada J., Shakhnovich E.I. The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation. Proc. Natl. Acad. Sci. USA. 2002;99:11175–11180. doi: 10.1073/pnas.162268099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hubner I.A., Deeds E.J., Shakhnovich E.I. Understanding ensemble protein folding at atomic detail. Proc. Natl. Acad. Sci. USA. 2006;103:17747–17752. doi: 10.1073/pnas.0605580103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zimm B.H., Bragg J.K. Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 1959;31:526–535. [Google Scholar]
- 30.Dill K.A., Fiebig K.M., Chan H.S. Cooperativity in protein-folding kinetics. Proc. Natl. Acad. Sci. USA. 1993;90:1942–1946. doi: 10.1073/pnas.90.5.1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jacobs W.M., Reinhardt A., Frenkel D. Communication: theoretical prediction of free-energy landscapes for complex self-assembly. J. Chem. Phys. 2015;142:021101. doi: 10.1063/1.4905670. [DOI] [PubMed] [Google Scholar]
- 32.Metzner P., Schütte C., Vanden-Eijnden E. Transition path theory for Markov jump processes. Multiscale Model. Simul. 2009;7:1192–1219. [Google Scholar]
- 33.Du R., Pande V.S., Shakhnovich E.I. On the transition coordinate for protein folding. J. Chem. Phys. 1998;108:334–350. [Google Scholar]
- 34.Piana S., Lindorff-Larsen K., Shaw D.E. Atomic-level description of ubiquitin folding. Proc. Natl. Acad. Sci. USA. 2013;110:5915–5920. doi: 10.1073/pnas.1218321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fersht A.R., Matouschek A., Serrano L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 1992;224:771–782. doi: 10.1016/0022-2836(92)90561-w. [DOI] [PubMed] [Google Scholar]
- 36.Krantz B.A., Dothager R.S., Sosnick T.R. Discerning the structure and energy of multiple transition states in protein folding using ψ-analysis. J. Mol. Biol. 2004;337:463–475. doi: 10.1016/j.jmb.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 37.Went H.M., Jackson S.E. Ubiquitin folds through a highly polarized transition state. Protein Eng. Des. Sel. 2005;18:229–237. doi: 10.1093/protein/gzi025. [DOI] [PubMed] [Google Scholar]
- 38.Best R.B., Hummer G. Microscopic interpretation of folding ϕ-values using the transition path ensemble. Proc. Natl. Acad. Sci. USA. 2016;113:3263–3268. doi: 10.1073/pnas.1520864113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Piana S., Lindorff-Larsen K., Shaw D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011;100:L47–L49. doi: 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Eddy S.R. Non-coding RNA genes and the modern RNA world. Nat. Rev. Genet. 2001;2:919–929. doi: 10.1038/35103511. [DOI] [PubMed] [Google Scholar]
- 41.Rothemund P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature. 2006;440:297–302. doi: 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
- 42.Bosco G.L., Baxa M., Sosnick T.R. Metal binding kinetics of bi-histidine sites used in ψ analysis: evidence of high-energy protein folding intermediates. Biochemistry. 2009;48:2950–2959. doi: 10.1021/bi802072u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lindberg M.O., Oliveberg M. Malleability of protein folding pathways: a simple reason for complex behaviour. Curr. Opin. Struct. Biol. 2007;17:21–29. doi: 10.1016/j.sbi.2007.01.008. [DOI] [PubMed] [Google Scholar]
- 44.Ptitsyn O., Rashin A. Stagewise mechanism of protein folding. Dokl. Akad. Nauk SSSR. 1973;213:473–475. [PubMed] [Google Scholar]
- 45.Karplus M., Weaver D.L. Protein-folding dynamics. Nature. 1976;260:404–406. doi: 10.1038/260404a0. [DOI] [PubMed] [Google Scholar]
- 46.Vendruscolo M., Dokholyan N.V., Karplus M. Small-world view of the amino acids that play a key role in protein folding. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:061910. doi: 10.1103/PhysRevE.65.061910. [DOI] [PubMed] [Google Scholar]
- 47.Dokholyan N.V., Li L., Shakhnovich E.I. Topological determinants of protein folding. Proc. Natl. Acad. Sci. USA. 2002;99:8637–8641. doi: 10.1073/pnas.122076099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rao F., Caflisch A. The protein folding network. J. Mol. Biol. 2004;342:299–306. doi: 10.1016/j.jmb.2004.06.063. [DOI] [PubMed] [Google Scholar]
- 49.Gfeller D., De Los Rios P., Rao F. Complex network analysis of free-energy landscapes. Proc. Natl. Acad. Sci. USA. 2007;104:1817–1822. doi: 10.1073/pnas.0608099104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Shakhnovich E.I. Theoretical studies of protein-folding thermodynamics and kinetics. Curr. Opin. Struct. Biol. 1997;7:29–40. doi: 10.1016/s0959-440x(97)80005-x. [DOI] [PubMed] [Google Scholar]
- 51.Hubner I.A., Shimada J., Shakhnovich E.I. Commitment and nucleation in the protein G transition state. J. Mol. Biol. 2004;336:745–761. doi: 10.1016/j.jmb.2003.12.032. [DOI] [PubMed] [Google Scholar]
- 52.Sosnick T.R., Dothager R.S., Krantz B.A. Differences in the folding transition state of ubiquitin indicated by φ and ψ analyses. Proc. Natl. Acad. Sci. USA. 2004;101:17377–17382. doi: 10.1073/pnas.0407683101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang F., Landau D.P. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001;86:2050–2053. doi: 10.1103/PhysRevLett.86.2050. [DOI] [PubMed] [Google Scholar]
- 54.Frenkel D., Smit B. Academic Press; Cambridge, MA: 2001. Understanding Molecular Simulation: From Algorithms to Applications. [Google Scholar]
- 55.Belardinelli R.E., Pereyra V.D. Wang-Landau algorithm: a theoretical analysis of the saturation of the error. J. Chem. Phys. 2007;127:184105. doi: 10.1063/1.2803061. [DOI] [PubMed] [Google Scholar]
- 56.McCallister E.L., Alm E., Baker D. Critical role of β-hairpin formation in protein G folding. Nat. Struct. Biol. 2000;7:669–673. doi: 10.1038/77971. [DOI] [PubMed] [Google Scholar]
- 57.Kim D.E., Fisher C., Baker D. A breakdown of symmetry in the folding transition state of protein L. J. Mol. Biol. 2000;298:971–984. doi: 10.1006/jmbi.2000.3701. [DOI] [PubMed] [Google Scholar]
- 58.Itzhaki L.S., Otzen D.E., Fersht A.R. The structure of the transition state for folding of chymotrypsin inhibitor 2 analysed by protein engineering methods: evidence for a nucleation-condensation mechanism for protein folding. J. Mol. Biol. 1995;254:260–288. doi: 10.1006/jmbi.1995.0616. [DOI] [PubMed] [Google Scholar]
- 59.Martínez J.C., Serrano L. The folding transition state between SH3 domains is conformationally restricted and evolutionarily conserved. Nat. Struct. Biol. 1999;6:1010–1016. doi: 10.1038/14896. [DOI] [PubMed] [Google Scholar]
- 60.Garcia-Mira M.M., Boehringer D., Schmid F.X. The folding transition state of the cold shock protein is strongly polarized. J. Mol. Biol. 2004;339:555–569. doi: 10.1016/j.jmb.2004.04.011. [DOI] [PubMed] [Google Scholar]
- 61.Gianni S., Guydosh N.R., Fersht A.R. Unifying features in protein-folding mechanisms. Proc. Natl. Acad. Sci. USA. 2003;100:13286–13291. doi: 10.1073/pnas.1835776100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Friel C.T., Capaldi A.P., Radford S.E. Structural analysis of the rate-limiting transition states in the folding of Im7 and Im9: similarities and differences in the folding of homologous proteins. J. Mol. Biol. 2003;326:293–305. doi: 10.1016/s0022-2836(02)01249-4. [DOI] [PubMed] [Google Scholar]
- 63.Fowler S.B., Clarke J. Mapping the folding pathway of an immunoglobulin domain: structural detail from ϕ-value analysis and movement of the transition state. Structure. 2001;9:355–366. doi: 10.1016/s0969-2126(01)00596-2. [DOI] [PubMed] [Google Scholar]
- 64.Nölting B., Golbik R., Fersht A.R. The folding pathway of a protein at high resolution from microseconds to seconds. Proc. Natl. Acad. Sci. USA. 1997;94:826–830. doi: 10.1073/pnas.94.3.826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Fulton K.F., Main E.R., Jackson S.E. Mapping the interactions present in the transition state for unfolding/folding of FKBP12. J. Mol. Biol. 1999;291:445–461. doi: 10.1006/jmbi.1999.2942. [DOI] [PubMed] [Google Scholar]
- 66.Serrano L., Matouschek A., Fersht A.R. The folding of an enzyme. III. Structure of the transition state for unfolding of barnase analysed by a protein engineering procedure. J. Mol. Biol. 1992;224:805–818. doi: 10.1016/0022-2836(92)90563-y. [DOI] [PubMed] [Google Scholar]
- 67.López-Hernández E., Serrano L. Structure of the transition state for folding of the 129-aa protein CheY resembles that of a smaller protein, CI-2. Fold. Des. 1996;1:43–55. [PubMed] [Google Scholar]
- 68.Choe S.E., Li L., Shakhnovich E.I. Differential stabilization of two hydrophobic cores in the transition state of the villin 14T folding reaction. J. Mol. Biol. 2000;304:99–115. doi: 10.1006/jmbi.2000.4190. [DOI] [PubMed] [Google Scholar]
- 69.Baxa M.C., Yu W., Sosnick T.R. Even with nonnative interactions, the updated folding transition states of the homologs proteins G & L are extensive and similar. Proc. Natl. Acad. Sci. USA. 2015;112:8302–8307. doi: 10.1073/pnas.1503613112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yoo T.Y., Adhikari A., Sosnick T.R. The folding transition state of protein L is extensive with nonnative interactions (and not small and polarized) J. Mol. Biol. 2012;420:220–234. doi: 10.1016/j.jmb.2012.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Pandit A.D., Jha A., Sosnick T.R. Small proteins fold through transition states with native-like topologies. J. Mol. Biol. 2006;361:755–770. doi: 10.1016/j.jmb.2006.06.041. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.