Pattern formation in Escherichia coli: A model for the pole-to-pole oscillations of Min proteins and the localization of the division site

Abstract

Proper cell division requires an accurate definition of the division plane. In bacteria, this plane is determined by a polymeric ring of the FtsZ protein. The site of Z ring assembly in turn is controlled by the Min system, which suppresses FtsZ polymerization at noncentral membrane sites. The Min proteins in Escherichia coli undergo a highly dynamic localization cycle, during which they oscillate between the membrane of both cell halves. By using computer simulations we show that Min protein dynamics can be described accurately by using the following assumptions: (i) the MinD ATPase self-assembles on the membrane and recruits both MinC, an inhibitor of Z ring formation, and MinE, a protein required for MinC/MinD oscillation, (ii) a local accumulation of MinE is generated by a pattern formation reaction that is based on local self-enhancement and a long range antagonistic effect, and (iii) it displaces MinD from the membrane causing its own local destabilization and shift toward higher MinD concentrations. This local destabilization results in a wave of high MinE concentration traveling from the cell center to a pole, where it disappears. MinD reassembles on the membrane of the other cell half and attracts a new accumulation of MinE, causing a wave-like disassembly of MinD again. The result is a pole-to-pole oscillation of MinC/D. On time average, MinC concentration is highest at the poles, forcing FtsZ assembly to the center. The mechanism is self-organizing and does not require any other hypothetical topological determinant.

How a bacterium finds its center to localize the division machinery is a long standing question (1, 2). The preparation for division starts with the assembly of a polymeric ring of the tubulin-like GTPase FtsZ just underneath the cytoplasmic membrane (Z ring). Recruitment of other division factors to this structure culminates in the septal ring organelle, which mediates cell wall invagination in the exact plane of the initial Z ring (3, 4). Placement of the Z ring is regulated negatively by two autonomous but partially redundant systems (5). The best understood is the Min system, which directs Z-ring assembly toward midcell by blocking the process at noncentral membrane sites. The other is called “nucleoid occlusion,” which refers to the observation that nucleoids somehow interfere with FtsZ assembly in their direct vicinity (6, 7). The mechanism of nucleoid occlusion is obscure, and the phenomenon is not considered in detail here.

In Escherichia coli, the Min center-finding system is based on highly dynamic behavior of the MinC, D, and E proteins in vivo. MinC inhibits FtsZ polymerization (8), and its activity is regulated by MinD and MinE through modulation of its cellular location. In wild-type cells virtually all of MinC and MinD and a fraction of MinE assemble on the membrane in the shape of a test tube covering the membrane from one pole up to approximately midcell. In contrast, the majority of MinE accumulates at the rim of this tube in the shape of a ring (the E ring). The rim of the MinC/D tube and associated E ring move from a central position to the cell pole until both the tube and ring vanish. Meanwhile, a new MinC/D tube and associated E ring form in the opposite cell half and the process repeats, resulting in a pole-to-pole oscillation cycle of the division inhibitor. A full cycle takes ≈50 s (9–16).

MinC binds to and colocalizes with MinD but is itself not involved in the oscillation mechanism (11, 12, 17). Oscillation requires both MinD and MinE, however. These two proteins also interact and modulate each other's behavior (10, 13–16, 18).

MinD is an ATPase that accumulates on the cytoplasmic side of the membrane to where it recruits both MinC and MinE (9–12, 19). In the absence of MinD, both MinC and MinE remain in the cytoplasm. A lack of MinC at the membrane results in a MinC⁻ phenotype where cells frequently produce minicells because of inappropriate assembly of Z rings near cell poles. In the absence of MinE, MinD (and hence MinC) is distributed evenly over the entire membrane. As a result, Z-ring assembly is blocked at any site, and cells form long nonseptate filaments (Sep⁻).

In this paper we develop a theory addressing two outstanding questions raised by the oscillatory behavior of the Min proteins in E. coli. What is the purpose of an oscillating division inhibition system, and how might such oscillation be accomplished? We suggested previously that oscillation of a division inhibitor might function as a center-finding tool, because on time average the concentration of the inhibitor would be expected to be lowest at the cell center (10, 11, 15). Here we show that pole-to-pole oscillation can be explained by assuming that MinD and MinE undergo coupled pattern-forming reactions based on local self-enhancement and long range antagonistic effects. The minimum molecular machinery for such oscillation, the localization of a signal to the cell center, and the actual implementation in E. coli are worked out. As demonstrated by computer simulations, the system is self-organizing, does not require any prelocalized determinants, and returns to its normal mode after separation into two daughter cells. The model accurately describes the known behavior of the Min proteins under various conditions and suggests particular functions for the known components.

Molecular Interactions That Enable the Formation of Stable Patterns: Short Range Self-Enhancement and Long Range Inhibition

The possibility of generating patterns by the interaction of two substances with different diffusion rates was discovered by Turing (20). However, a different spread of two interacting substances does not guarantee pattern-forming capabilities. In fact, only a very restricted class of interactions allows pattern formation, specifically those in which a local self-enhancing reaction is coupled with an antagonistic reaction of longer range (21–25). For example, assume that a single molecular species called the “activator” accomplishes a self-enhancing reaction. The antagonistic reaction can result from the production or the release of a rapidly diffusing “inhibitor” that is controlled by the activator and which in turn suppresses the self-enhancing reaction in a more extended region. Alternatively, the antagonistic effect results from the depletion of a substrate or cofactor that is required for the autocatalysis. Because none of the known Min components has the expected properties of the inhibitor type required for the first mode, the following discussion is restricted to patterns formed by an activator/depleted-substrate mechanism.

In a field larger than the range of the activator, a uniform distribution of the activator and its antagonist is unstable (the range of a molecule is the mean distance it can travel during the interval it is available to participate in the reaction).

The resulting pattern depends on the size of the area in which the reaction takes place. When the field size is of the order of the activator range, only a polar pattern can be generated. High and low activator concentrations emerge at the maximum distance from each other, i.e., at opposite sides of the field. Random fluctuations are sufficient to initiate pattern formation. Therefore, there is no need to assume any prelocalized factors to accomplish an asymmetric accumulation of the activator at one pole. When this field size is about twice that of the activator range, symmetrical patterns are favored. Either a high concentration forms at each pole and a minimum in the center or a single maximum forms in the center and both poles are nonactivated. At even larger sizes, several maxima can form at more or less regular distances (refs. 20–23; see also supporting information, which is published on the PNAS web site, www.pnas.org).

A polar pattern generated as described above can be forced to oscillate if, in addition, the activator controls the production or activity of a local-acting inhibitor. This inhibitor has to have a longer time constant than the activator. Its local accumulation causes a breakdown of the activator production after a certain time. This interruption of the self-enhancing process also terminates the consumption of the substrate. Provided the substrate redistributes rapidly, this reduced substrate consumption leads to a fast rise of its concentration in the whole cell. If a certain level is attained, a new activation is triggered at the opposite pole, because this is the region with the lowest concentration of the poisonous and long lasting inhibitor. The newly formed maximum similarly will break down, after which the original site becomes activated again, and so on. High concentrations emerge at the poles in an alternating fashion (see supporting information, which is published on the PNAS web site). Models of patterns in space that oscillate out of phase were developed previously to describe the generation of pigment patterns on the shells of tropical mollusks (22, 34).

A Model for Min Protein Dynamics and FtsZ Localization Based on Pattern-Forming Reactions

The minimal mechanism described above generates an oscillating polar pattern in a reliable way. However, the known properties of the MinD and MinE proteins in E. coli suggest that a somewhat more complex model is required to describe their dynamic behavior. In the model, several assumptions are made. (i) FtsZ, MinD, and MinE molecules are produced at a constant rate and can diffuse rapidly in the cytoplasm. (ii) All three species associate with the membrane by a self-enhancing process, i.e., the association is faster next to molecules of the same type already bound to the membrane. Of course, membrane association depletes the pool of cytoplasmic molecules. This depletion of freely diffusing molecules constitutes a rapidly spreading and rapidly acting antagonistic reaction to the self-enhancing membrane association, satisfying the crucial condition for pattern formation mentioned above. There is good evidence that Z rings form by localized polymerization of the FtsZ protein, of which only a limited amount is available (26, 27). Whether the associations of MinD and MinE with the membrane occur in a self-enhancing fashion is not known currently but is predicted by the model. (iii) MinE displaces MinD from the membrane.

To illustrate the mechanism envisioned, Fig. 1 shows simulations in which FtsZ, MinD, and MinE are introduced consecutively. The parameters are chosen such that the behavior of each subsystem corresponds to that reported in the literature.

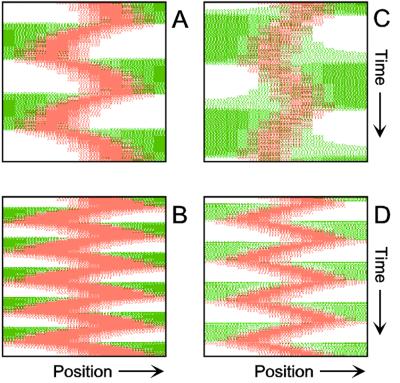
Figure 1.

Components of the center-finding system in E. coli. MinC/D, MinE, and FtsZ are assumed to be pattern-forming systems that assemble in a self-enhancing way on the membrane. In this simulation, the elements are introduced one at a time to show the interplay of the subsystems. Shown is a one-dimensional simulation of patterning at the membrane along the long axis of the cell. Local concentrations are plotted as function of time; concentrations are indicated by the densities of pixels. (A) FtsZ (blue) alone can make a pattern, but the location of the maximum need not be central (σ_d = 0; σ_e = 0; μ_DE = 0). (B) MinD precursor production switched on (σ_d = 0.0035). MinD (green) on its own does not make a pattern but suppresses FtsZ patterning. (C) MinE precursor production switched on (σ_e = 0.002). MinE (red) on its own would make a stable pattern. (D) However, because MinE removes MinD from the membrane (μ_DE = 0.0004) and MinE association depends on MinD, the MinE maximum destabilizes itself and shifts toward a region of higher MinD concentration. Shortly before the MinE wave reaches the pole, MinD and MinE concentrations collapse. On its way, the MinE wave removes MinD from the membrane. Meanwhile, a new plateau of membrane-bound MinD is rising in the other part of the cell. A new high MinE concentration is triggered at its flank, causing this peak to disappear also, leading to a polar MinD oscillation in counter phase. Because of the low MinC/D level at the center, the FtsZ signal for septum formation appears there. (E) FtsZ remains in place there even after switching off of MinD (σ_d = 0). MinE disappears from the membrane, although the precursor is still produced. Eight hundred iterations are calculated between each pixel row; 80,000 time steps (iterations) are required for one full cycle. The total region has been subdivided into 15 spatial units. Assuming a length of E. coli of 3 μm and a full cycle of 50 s, the spatial unit size equals ≈0.15 μm, and one iteration corresponds to 0.6 ms.

Step 1.

Pattern formation by FtsZ (Fig. 1, blue) results in membrane-associated maxima (Z rings) with extensions of only a fraction of the cell length. As is true for Z rings (7), the location of maxima in the model is close to random in the absence of an additional positioning system (Fig. 1A).

Step 2.

In the absence of MinE, MinD accumulates evenly at the membrane of the entire cell (10, 13). In the model, such homogeneous accumulation occurs if the diffusion rate of nonattached MinD is too low to allow pattern formation. Because of the colocalization of MinC with MinD (11, 12, 17), formation of FtsZ maxima is prevented all over the membrane (Fig. 1B).

Step 3.

MinE patterning requires its recruitment to the membrane by MinD (9, 13, 15). By itself, this would lead to stable MinE maxima (Fig. 1C). However, because it is assumed that MinE displaces MinD from the membrane, a MinD depression appears at the position of a MinE maximum. Because MinE can remain attached only in the presence of MinD, a MinE maximum causes its own local destabilization. It shifts from a region of local MinD depression into a neighboring region richer in MinD where it removes the latter as well, and so on. The result is a wave of MinE maximum that “peels” MinD off the membrane (Fig. 1D). This wave comes to rest shortly before it reaches the pole because of a fading amount of membrane-bound MinD, a shortage of freely diffusible MinE in the remaining portion next to the pole, and possibly by the trigger of a new MinD activation at the opposite pole that also consumes MinD precursor molecules. A new MinD assembly in the opposite half of the cell attracts the assembly of a new E-maximum that travels to the pole of this cell half as well, etc. MinE has the highest affinity for sites at the flank of a MinD accumulation (14, 15). This preference for the flank will occur if MinE binding requires both MinD and unoccupied sites on the membrane.

Step 4.

Lowering the MinD concentration allows the Z ring to form. Because on time average the MinD concentration is lowest in the center, the FtsZ pattern becomes localized correctly (Fig. 1D).

Fig. 1E demonstrates that the system satisfies the observation that MinE fails to accumulate in any pattern when MinD is removed (9, 14). Note that the disappearance of MinD has no effect on the pre-established FtsZ pattern (Fig. 1 D and E).

Equations Used and Details of the Computer Simulations

It is assumed that the three major components, MinD, MinE, and FtsZ are synthesized as diffusible molecules in the cytoplasm. All three components can associate under appropriate conditions with the membrane. In the following equations the concentrations of the membrane-bound form are denoted with D, E, and F and those of the free form are denoted with d, e, and f. In all cases, binding to the membrane is assumed to be a self-enhancing process. The increase of D, E, and F is at the expense of d, e, and f. The concentration changes are given in the form of partial differential equations. Numerical constants are given in Greek letters: ρ, catalytic production rates; σ, constant production rates; μ, decay rates; κ, saturations and mutual interferences; 𝒟, diffusion. The index denotes the corresponding substance(s). These reactions correspond to the activator/depleted-substrate scheme (21), a reaction that has similarities with the Brussellator reaction (28). For the change of FtsZ per time unit the following interaction has been assumed:

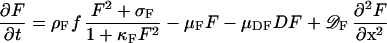1

The first term describes the accretion of new molecules to the membrane. This accretion depends on the concentration of the precursor molecules f and in a nonlinear way on already bound F molecules (F²). The factor ρ_F determines the arbitrary absolute level. A small baseline production σ_F is necessary to maintain a low level of F from which the self-enhancing reaction starts at low F concentrations. The term 1 + κ_FF² in the denominator leads to the saturation of the autocatalysis at high F concentrations and is required for an activation to remain as a ring on a cylinder wall (see Fig. 5). The second term describes the removal. It is, of course, proportional to the number of existing F molecules. The third term describes the removal of FtsZ molecules from the membrane by MinD. This removal is proportional to the local FtsZ and MinD concentrations (−μ_DFDF). The last term describes the exchange with neighboring space elements by diffusion; 𝒟_F is the diffusion constant.

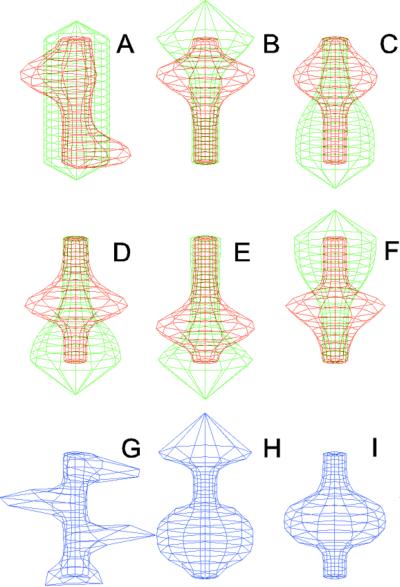
Figure 5.

Simulation on a cylinder and the problem of ring formation. (A) Assuming a more realistic cylindrical geometry for the bacterium, a simple activator-depletion mechanism can lead to unpredictable patterns. Several maxima may emerge, preferentially at opposite positions of the cylinder. The simulation corresponds to the static MinE pattern formation as shown in Fig. 1C. (B–F) In the mechanism proposed, the diffusion of MinE leads to a synchronization of the wave and to ring-shaped bands. Shown are the MinD (green) and MinE (red) distributions in one full MinD cycle. (G–I) Patterning of the FtsZ ring. (G) The FtsZ ring also would decay into individual patches. (H) By a saturation of the F autocatalysis (κ_F = 0.2), this decay can be avoided. Nevertheless, the position of the ring(s) would be unpredictable. (I) The elaborate mechanism proposed is able to generate one central band as required. Simulations are made of the surface of a cylinder; the diffusion within the cylinder is not considered (cell length = 19 space elements, circumference = 9 space elements). Except for a diffusion term generalized for two dimensions, the same equations and parameters as in Figs. 1–4 are used. For animated simulations, see the supporting information.

The formation of the FtsZ ring, i.e., the association of F molecules to the membrane, goes on expense of the freely diffusible molecules f:

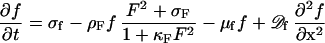2

where σ_f is the constant and space-independent production rate. The removal rate of f caused by accretion at the membrane is identical to the rate at which new F molecules appear. The independent decay rate −μ_ff is small in comparison with the removal rate by the accretion to the membrane. If nonzero, this restricts the maximum precursor concentration outside the maximum. In this way, these regions become less attractive. Such a term delays a split of a maximum at increasing field sizes.

The assumed change of MinD is given by an analogous equation:

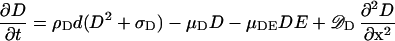3

The term −μ_DEDE describes the removal of bound MinD by MinE, a process assumed to be proportional to the local MinD and MinE levels.

The nonattached, highly diffusible MinD molecules d are produced at a constant rate σ_d. Because this rate is assumed to be larger than the decay rate of D (μ_D, see below), MinD does not oscillate on its own but only because of the action of MinE. d disappears at the same rate at which new D molecules become attached; μ_d is zero or small

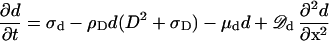4

Analogously, the membrane association of MinE is given by the following equation:

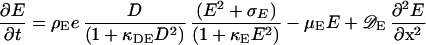5

Thus, MinD is required for the association of MinE to the membrane, but at high concentrations this positive influence decreases back to zero (D/(1 + κ_DED²). This decrease is important for initiation of MinE maxima at the flank and not at the peak of MinD maxima, which is in agreement with experimental observations. At the flank more precursor molecules are available that are diffusing in from the nonactivated region in which they are not consumed. This leads to an activation at the flank as long as the activation at the MinD peak is not favored strongly. In the absence of this condition, MinE waves would start at one pole, move to the other, and start again at the first. Molecularly, MinE might require both MinD molecules and free sites to attach to the membrane, rendering the flank the favorable place. κ_E limits the maximum density MinE can obtain.

Likewise, the association of MinE is at the expense of diffusible MinE:

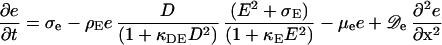6

For the computer simulations, the “bacterium” has been subdivided into several space elements i, i = 1… n, for instance n = 15 in Fig. 1. Numerical solutions have been obtained by using the equations above in the form of difference equations. To give an example, the new concentration F′ after one time unit in the space element i is calculated according to Eq. 1 from the given concentration F:

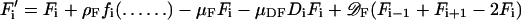7

Repetition of such iterations allows calculation of the total time course. Boundaries are assumed to be impermeable. The initial conditions are not crucial. In Figs. 1–5, all initial concentrations have been set to zero.

Because the absolute concentrations are arbitrary, the production rates ρ were set equal to the corresponding decay rates μ. This leads to numerical concentrations of the nonpatterned steady states around one. Small random fluctuations (<1%) are superimposed. This is necessary to allow the initial patterning of MinE and FtsZ when starting from homogeneous initial situations. These fluctuations remain unchanged during a set of iterations. The following numerical constants have been used:

For Eqs. 1 and 2: μ_F = ρ_F = 0.004; κ_F = 0 (Figs. 1–4) or = 0.2 as indicated in Fig. 5; σ_F = 0.1; μ_DF = 0.002; 𝒟_F= 0.002; σ_f = 0.006; μ_f = 0.002; and 𝒟_f = 0.2. For Eqs. 3 and 4: ρ_D = μ_D = 0.002; σ_D= 0.05; μ_DE = 0.0004; 𝒟_D = 0.02; σ_d = 0.0035; μ_d = 0; and 𝒟_d = 0.2. For Eqs. 5 and 6: ρ_E = μ_E = 0.0005; σ_E = 0.1; κ_DE = 0.5; κ_E = 0.02; 𝒟_E = 0.0004; σ_e = 0.002; μ_e = 0.0002; and 𝒟_e = 0.2.

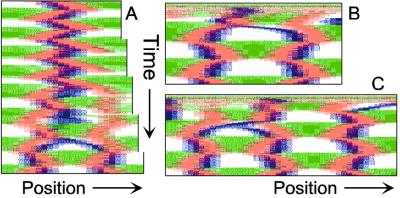
Figure 4.

Inverse relationship of the MinD and MinE concentrations on oscillation frequency. (A) “Normal” pattern. (B) An increase of the MinE precursor production (σ_e from 0.002 to 0.004) leads to a higher oscillation frequency, because less time is required to remove MinD. (C) Conversely, a decrease (σ_e = 0.001) leads to a lower frequency (note that the MinE wave does not have to reach a pole before MinD can trigger at the opposite pole). (D) The lowering of MinD precursor synthesis (σ_d from 0.0035 to 0.002) leads to more rapid oscillations, because less MinD has to be removed from the membrane. All simulations start with identical initial situations.

Many of the assumed rate constants are unknown. The observed oscillation frequency and the real extension of E. coli (3 μm) allow some estimations. Using a subdivision into 20 space units leads to a unit length of 0.15 μm. With 80,000 iterations for one full cycle of the MinD oscillation (50 s), one iteration corresponds to 0.6⋅10⁻³ s. A numerical diffusion rate of 0.2 therefore corresponds to 7.3 μm²/s. This rate corresponds well with measured rates between 2.5 and 7.7 μm²/s of average-sized proteins in E. coli cytoplasm (29). The surprising aspect of this estimation is that the half-life of the bound molecules is of the order of a second, i.e., much faster than the MinD oscillation. It is not clear yet whether this high turnover is real.

Because the absolute concentrations are arbitrary, in Figs. 1–4 the concentrations are not plotted as curves but as densities of pixels. This should facilitate comparisons with the existing microscopy data. After the given number of iterations, a line is added to the plot. The densities of colored pixels correspond to the local concentrations of the substances. Thus, these plots show membrane-associated molecules along the long axis of the cell as a function of time. Further computational details for pattern-forming reactions in general and corresponding PC software are given elsewhere (22). Animated simulations are available at www.eb.tuebingen.mpg.de/abt.4/meinhardt/theory.html.

Behavior During Growth and Division and in Long Filaments

Because the bacterium increases in length during growth, the center-finding mechanism must work even if the field size increases at least 2-fold. Moreover, after the separation of a mother cell into two daughter cells, the centers of the latter must be detected quickly. As shown in the simulations of Fig. 2, the model has these properties.

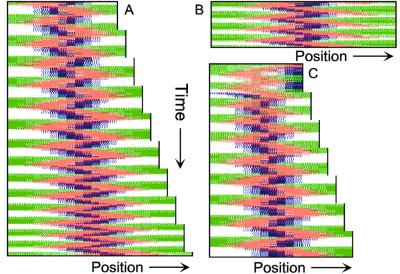
Figure 2.

Center finding during growth and division. (A) Only to demonstrate the correct center detection, a unilateral enlargement of the field is assumed. For that, the rightmost spatial element is doubled (after each 100,000 iterations = 50 pixel lines). Both daughter elements initially have identical concentrations. The FtsZ signal remains at the actual central position. (B) After separation of the large field into two parts, traveling MinE waves and the pole-to-pole oscillation of MinD are re-established quickly (shown is the left half). (C) The FtsZ ring becomes relocalized rapidly to the new center. For animated simulations, see the supporting information.

When cell division is blocked, E. coli grows into long filamentous cells. Such filaments show multiple dynamic MinD accumulations flanked by E rings, and the number of these increases with cell length (9–11, 14, 15). The model provides a straightforward explanation for this phenomenon. Fig. 3 shows in a growing cell the transition from a single to a double MinE wave and the formation of two FtsZ rings. With growth, the region in which MinE substrate is produced enlarges, whereas the region of consumption, the E ring, remains approximately constant. With increasing size, therefore, the concentration of unbound MinE molecules outside of the MinE-maximum increases, which leads eventually to the formation of an additional one. Wave duplication can happen in two ways: (i) the concentration of MinE substrate molecules at the flank of the ring becomes so high that the self-enhancement rate there exceeds that at the MinE maximum itself, causing the latter to split into two, or (ii) at a distance from the existing MinE maximum, some remnant membrane-bound MinE develops into a second maximum. In either case, the two rings together remove substrate sufficiently fast until the cell attains a certain larger size at which an additional MinE maximum is generated again. In these larger fields, MinE waves that flank a polar MinD accumulation travel toward the pole like single waves in smaller fields, but pairs of MinE waves that flank an internal MinD maximum move from both sides toward the center of this maximum until both activities disappear at near collision. During this process, new MinD maxima appear in the regions cleared by the waves. As a result, MinD maxima oscillate in counterphase over time (Fig. 3 B and C). These properties of the model are in striking agreement with the observations of live filaments (10, 11, 14, 15).

Figure 3.

Oscillation in counterphase in long extended filaments. (A) In a cell surpassing the critical size (≈23 space units with the parameters chosen), a transition occurs from one to two zones in which MinE sweeps back and forth. Localization of the FtsZ ring follows the corresponding change in MinD distribution. (B and C) In longer filaments, several sites of MinE “sweeping,” and thus several potential division sites emerge. MinD oscillates in counter phase. Each pixel row corresponds to the distribution after 800 iterations; 32 (B) and 42 (C) space units are used. For animated simulations, see the supporting information.

Inverse Relationship of the MinD and MinE Concentrations on Oscillation Frequency

An observation that provides a crucial test for any model is that the MinD oscillation frequency is inversely related to the MinD/MinE ratio in the cell. An increase in the cellular concentration of MinD leads to slower oscillation, whereas an increase in the level of MinE leads to acceleration (10, 15). This behavior also is described readily by the model (Fig. 4), and is a straightforward consequence of the assumed interactions. Because MinE removes MinD from the membrane, an increase in the MinE level leads to accelerated removal of the MinD “tube” and thus to a more rapid movement of the E ring toward the pole. Conversely, if more MinD is produced, more molecules accumulate in the tube. It takes longer to remove the surplus of molecules from the membrane, leading to a decrease in the oscillation frequency, which is in full agreement with the observation.

Patterning the Two-Dimensional Cell Surface

The simulations shown in Figs. 1–4 consider only an extension along the axes, i.e., a one-dimensional arrangement of spatial elements. However, the E. coli cell resembles a cylinder with hemispherical caps, and its circumference relative to its length is certainly not negligible. A static pattern-forming system could lead to several activator maxima at unpredictable positions on a cylinder wall (Fig. 5A). Therefore, the ability to generate a central hot spot on a linear extended field is not sufficient. Rather, the system must be able to define the site for Z-ring formation by generating an activated ring on the cylindrical cell wall that does not disintegrate into spots around the circumference. In the model, the diffusion of the MinE molecules leads to a synchronization of the MinE waves around the cylinder. For FtsZ, a saturation of the autocatalysis allows the generation of activated regions that have a stripe-like geometry with a long extension in one dimension and a short extension in the other (30). In this way a decay of FtsZ in individual maxima can be avoided. Together, the proposed mechanism accounts for the generation of coherently moving bands on the cell wall (Fig. 5 B–F) and for the correct positioning of an FtsZ band (Fig. 5I).

Discussion

Pattern formation theory was applied to model the dynamic properties of the Min proteins in E. coli. A pattern-forming reaction of MinE is used to keep a region free of the division inhibitor. Because this pattern destabilizes itself by removing MinD as a necessary component, a pole-to-pole movement occurs that explores the size of the cell. Because both poles play a symmetrical role, on time average the pattern is necessarily symmetric. Similar to the windshield wiper of a car, MinE keeps the center free of MinC/D, enabling the proper initiation of division.

The modeling shows that reliable patterning is possible without the need for any prelocalized determinants. An independence of prelocalized determinants is an important property of the model, because a requirement for such factors would immediately raise the question of how they themselves would become localized. Starting with homogenous initial conditions, random fluctuations are sufficient to allow the formation of a MinE maximum and the subsequent movement of the wave to one or the other pole (Fig. 1). Obviously, our work does not preclude the existence of prelocalized determinants but demonstrates that they are not necessary. The equations given are certainly only examples, and, for instance, higher nonlinearities or saturations terms caused by membrane occupation are conceivable.

Reproduced in the simulation thus far is only the MinE ring but not yet the “tube,” i.e., the elevated MinE concentration at the MinD plateau. Although the MinD/MinE mechanism is robust, there are of course limits. Parameters can be changed only as long as the general character of the subsystems is maintained (Fig. 1). If pattern formation has to start from homogeneous initial conditions, a situation that is certainly rare in E. coli, the removal of MinD by MinE should not be too fast, or otherwise a homogeneous MinD/MinE oscillation will occur: MinD builds up and triggers MinE, which causes the removal of MinD and therewith MinE before a local MinE maximum can build up. Such homogeneous oscillations are expected in the range of seconds. Once a pattern is formed, the chance of homogeneous oscillation occurring is much lower. Therefore, the actual pattern also depends on the history of the system, a typical feature of nonlinear reactions. Less robust is the localization of the FtsZ ring in the center. In the simulation, trails of the MinD plateau can reach the center of the cell. In the simulations, this inhibitory influence on the FtsZ activation can lead to some back-and-forth movement of the latter. This effect is stronger in large cells, because more time is available for MinD to recover at the center (Fig. 2). This spillover of MinD occurs in a flash-like manner when a new MinD activation is triggered. If the proper FtsZ inhibitor, MinC, would need some time to associate with MinD, this short central MinD activation would loose its irritating influence. In addition, the position of the division apparatus in actual cells is sharpened further by nucleoid occlusion and becomes fixed already at moderate cell length (3–5)

The question may arise as to why bacteria use such complex systems to find their center. As mentioned, a simple self-activation/substrate-depletion system can generate a pattern with a single central maximum. However, a pattern with a maximum at each of the poles is equally likely. The model proposed is able to repress the second mode reliably. This feature is maintained if the two-dimensional nature of the cell wall is considered.

It is proposed that the formation of MinE waves (E rings) depends on the depletion of two substances: membrane-bound MinD and diffusible MinE subunits not yet bound to the membrane. The question may arise as to whether one can simplify the mechanism by using a single depleted substance only. This is not the case, however, because the two substances fulfill different purposes and have to satisfy different requirements. The depletion of diffusible MinE in the cytoplasm is required as a long ranging antagonist to generate local MinE maxima at the membrane. In contrast, the removal of MinD from the membrane by MinE must be a local process to accomplish the displacement of MinE into adjacent positions.

The traveling MinE wave around the center is not the only possible mechanism to detect the center of a cell. In fact, center-finding in Bacillus subtilis is accomplished without MinE waves (31–33). A corresponding alternative mechanism could use the property of activator-inhibitor interactions that, under certain conditions, generate a stable symmetric pattern with a maximum at each pole (21–25; see supporting information). If these maxima suppress septum formation, the latter can only be initiated at the center and only if a certain size is surpassed. Although the activation at the poles can have a more or less patch-like extension, the center-detecting system has to satisfy again the condition for stripe formation to generate an activation all around the circumference of the cell (see Fig. 5).

The general class of reactions that generates dynamic patterns has been deduced from the pigment patterns on some tropical sea shells (22, 34). A mollusk enlarges its shell only at the growing edge. Most shell patterns reserve time records of one-dimensional reactions that took place along the growing edge. A chessboard-like pattern, as occurring on some shells, results from an out-of-phase oscillating in the pigment production in adjacent groups of cells. This pattern is analogous to the counterphase oscillations of MinC/MinD in long filaments (Fig. 3 B and C). Likewise, for leaf initiation, signals are required in the narrow ring-shaped zone next to the dome-shaped apical meristem. The actual arrangement of leaves is a time record of the signaling in this leaf-forming zone. For instance, the formation of leaves at alternating opposite positions results from the formation of temporary signals displaced by 180°, very similar to the pole-to-pole oscillation in E. coli. Because the leaf-forming zone has the form of a ring (not a rod as in E. coli), the displacement need not to be 180°. A displacement by 137.5°, the golden angle, is an especially stable pattern in the model, corresponding to a well known pattern in phyllotaxis (35).

Also, the orientation of chemotactic sensitive cells can be accounted for under the assumption that by a pattern-forming reaction signals are generated on the cell surface to form protrusions. Their local destabilization enforces the formation of new signals, preferentially at positions indicated by the external cue (36). In this way, the system obtains an extraordinary sensitivity against external signals. Even in the absence of the latter, e.g., in tissue culture, these cells maintain this dynamic patterning. Thus, local destabilization of a pattern combined with the generation of new signals seems to be a widely used strategy in biology for very different purposes in single cells as well as in multicellular systems.