Abstract
Φ values are experimental measures of how the kinetics of protein folding is changed by single-site mutations. Φ values measure energetic quantities, but they are often interpreted in terms of the structures of the transition-state ensemble. Here, we describe a simple analytical model of the folding kinetics in terms of the formation of protein substructures. The model shows that Φ values have both structural and energetic components. It also provides a natural and general interpretation of “nonclassical” Φ values (i.e., <0or >1). The model reproduces the Φ values for 20 single-residue mutations in the α-helix of the protein CI2, including several nonclassical Φ values, in good agreement with experiments.
Keywords: transition-state ensemble, mutational analysis, statistical mechanics
The folding kinetics of small single-domain proteins has been widely studied by single-site mutagenesis (1-16). The central quantity in these studies, the Φ value, is defined as (17, 18)
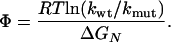 |
[1] |
Here, kwt and kmut are the folding rates of the wild type and mutant protein, and ΔGN is the change of the protein stability upon mutation. The stability GN of a protein is the free-energy difference between the native (N) and the denatured (D) state.
There are several theoretical studies of Φ values and transition states. The thermal unfolding kinetics of CI2 has been extensively studied in molecular dynamics simulations (19-24). Here, the transition state is defined as a “small ensemble of structures populated immediately prior to the onset of a large structural change” (20) in the unfolding trajectories. Other groups have considered statistical mechanical or Go-type models (25-36). In some of these models, transition states are identified as free-energy maxima along a folding reaction coordinate or as free-energy saddle points if two or more degrees of freedom are used for the reaction coordinate. More recent approaches define the transition state ensemble (TSE) from experimental Φ values by using these Φ values as restraints in simulations (37-39). Each of these definitions of transition state, although plausible, is nevertheless based on one or more ad hoc premises.
In classical transition-state theory, the folding rate is proportional to exp[-GT/RT], where GT = Gtransition state - Gdenatured state is the free-energy difference between the TSE and the denatured state. Possible changes in the prefactor of this proportionality relation upon mutation are usually neglected. Thus, Φ=ΔGT/ΔGN. In this way, Φ values measure the energetic consequences of mutations on the TSE relative to the native state.
A central question is whether Φ values also give structural information about the TSE (18, 40, 41). In the traditional interpretation, Φ = 1 is taken to indicate that the mutated residue has native-like structure in its TSE, whereas Φ = 0 is taken to indicate that the mutated residue is not structured in the TSE. Typically, experiments give Φ values that are fractional, with values between 0 and 1, apparently indicating partial native-like structural character of the residue in the TSE.
However, there are three problems with this traditional structural interpretation. First, Φ values are sometimes “nonclassical”; they can be <0 or >1. In the traditional view, such values are impossible, implying a transition state that is more denatured than D or more native than N; hence, there is some controversy about how such Φ values should be interpreted. Second, a given sequence position can have very different Φ values, depending on which amino acid is substituted there, leading to the question of whether such energetic changes always have a simple structural interpretation.
Third, there is a problem of continuity: two residues that are neighbors in the chain are sometimes observed to have very different Φ values. A structural interpretation of this observation would be that there can be sharp boundaries between native-like and non-native-like structure in the TSE, which seems implausible. For example, the protein CI2 consists of an α-helix packed against a four-stranded β-sheet (see Fig. 1). In the α-helix of CI2, 20 single residue mutations have been studied, giving Φ values ranging over the full spectrum from -0.35 to 1.25. Although helix formation is usually regarded as fast and cooperative, these results would seem to imply that this helix does not form as a single cooperative unit: parts are folded, and parts are not in the TSE. It is not clear whether these are problems of experimental errors or problems in the traditional model that is used to interpret Φ values.
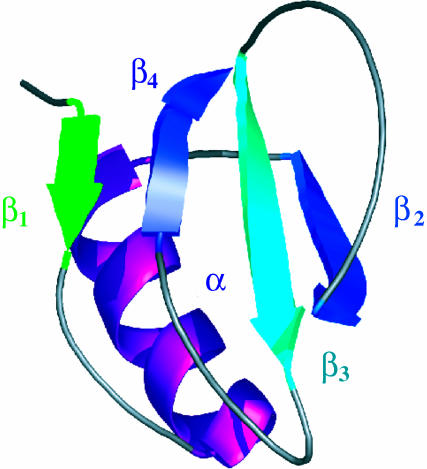
Fig. 1.
The native structure of CI2 consists of a four-stranded β-sheet packed against an α-helix (Protein Data Bank ID code 1COA).
Is there a more physical way to interpret the formation of protein substructures that comprise the TSE of protein folding? Here, we develop a model. First, we consider the simplest subdivision of the protein: into one α-helical substructure and one β-sheet substructure. Because of its simplicity, the model can be solved analytically and exactly. Then, we generalize this model to apply to CI2. Despite its simplicity, this model reproduces the experimental Φ values in the α-helix of CI2 with a correlation coefficient of 0.85, including some of the nonclassical Φ values. A key conclusion is that it is not sufficient to interpret Φ values solely in terms of structures. However, a Φ value can be decomposed into structural and energetic components.
Model and Methods
The Dynamics. Our approach has the following two aspects, (i) the model, which expresses the relative free energies of the various substructures of the protein as it folds, and (ii) the dynamics of the model. We first describe our treatment of the dynamics. To simplify the notation, we define here the free-energy Gn of each partially folded state n = 1, 2, 3,..., and the dimensionless free-energy gn ≡ Gn/RT, with respect to the fully denatured state in which none of the substructures is formed. Thus, the denatured state is the reference, defined as having zero free energy. The transition rate from any state m to state n is given by the following expression:
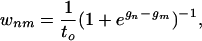 |
[2] |
provided the states n and m are connected by a single step in which only one substructure folds or unfolds (36). For other transitions, the transition rates are zero. Here, to is a reference time scale.§
The folding kinetics is described by the following master equation:
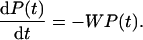 |
[3] |
The elements of the vector P(t) are the probabilities Pn(t) that the protein is in state n at time t, and the matrix elements of W are given by Wnm = -wnm for n ≠ m and Wnn = ∑m≠nwmn. The general solution of the master equation has the form
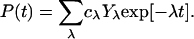 |
[4] |
Here, λ are the eigenvalues and Yλ are the eigenvectors of the matrix W. The prefactors cλ depend on the initial conditions at time t = 0. The eigenvalues represent relaxation rates. It can be shown that one eigenvalue is zero, corresponding to the equilibrium distribution, whereas all other eigenvalues are positive (42). For t → ∞, the probability vector P(t) tends to coYo, where Yo is the eigenvector with eigenvalue 0.
The Model: Two Substructures. The dynamics described above is applicable to any model of the protein, its substructures, and their relative free energies. Here, we first apply the dynamics to the simplest possible model of the substructures of CI2. The model has the following four states: (i) the denatured state, D, in which neither the helix nor the sheet is formed; (ii) a partially folded state, α, in which only the helix is formed; (iii) a partially folded state, β, in which only the β-sheet is formed; and (iv) the native state, N, in which both the helix and sheet are formed and packed against each other.
In this simple four-state model, the energy landscape is characterized by the dimensionless free-energy differences gα, gβ, and gN of the states α, β, and N, each taken with respect to the denatured state D, which is defined as having zero free energy.
The folding kinetics of this model can be solved exactly by determining the eigenvalues λ and eigenvectors Yλ of the matrix W. Because this model has four states, W is a 4 × 4 matrix. In units of 1/to, the eigenvalues are given by λ = 0, 1 - q, 1 + q, and 2, where
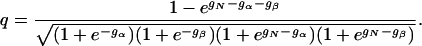 |
[5] |
Because we have -1 < q < 1, the three nonzero eigenvalues are positive and describe the relaxation to the equilibrium state of the model (see Eq. 4). The equilibrium state simply is coYo, where Yo is the eigenvector with eigenvalue 0.
This model exhibits two-state folding kinetics under two conditions. First, the native state must be stable; the free-energy gN of the native state must be significantly smaller than the free energies of the other three states. Under such folding conditions, the equilibrium native state will be more populated than the other three states. Second, the intermediate states α and β must have positive free energies, relative to D, so that the system will have a kinetic barrier, which is required to achieve single-exponential dynamics.
Under these two conditions, the three Boltzmann weights egN-gα-gβ, egN-gα, and egN-gβ in Eq. 5 are much less than 1 and also much less than e-gα and e-gβ. Therefore, these three Boltzmann weights can be neglected. We set them equal to zero. The factor q in Eq. 5 then simplifies to the following expression:
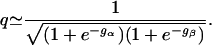 |
[6] |
For large barrier energies gα and gβ, we have e-gα ≪ 1 and e-gβ ≪ 1 and, therefore, (1 + e-gα)(1 + e-gβ) ≅ (1 + e-gα + e-gβ). If we next use the expansion (1 + x)-½ ≅ 1 - x/2 with x = e-gα + e-gβ ≪ 1, the smallest nonzero relaxation rate, or folding rate, k ≡ 1 - q is given by
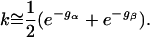 |
[7] |
The folding rate k is much smaller than the other two relaxation rates 1 + q and 2. In that case, these two fast relaxations constitute an initial “burst phase,” and the model otherwise gives two-state single-exponential folding behavior with the slowest rate k (see Eq. 4). The folding rate k simply is the sum of the rates for the two possible folding routes: one folding route in which α forms first and the other in which β forms first. The factor 1/2 in the equation above arises because a molecule, after reaching one of the barrier states α or β, either falls back to D or falls forward to N, with almost equal probability.
By using this model, we next explore the effects of mutations. Consider a mutation within the α-helix. The free energy of the helix will change from gα → gα +Δgα, and the free energy of the native state will change from gN → gN + ΔgN. In contrast, gβ is not affected by the mutation. The folding rate of the mutant will be kmut = k(gα+Δgα, gβ), with k given by Eq. 7. For small perturbations Δgα, we have ln kwt - ln kmut ≅ - (∂ ln k/∂ gα)Δgα. For mutations in the α-helix, the Φ value defined in Eq. 1 has the following general form:
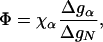 |
[8] |
with
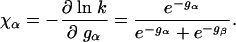 |
[9] |
Hence, the Φ value is a product of the two following terms: a structural factor χα and an energetic factor Δgα/ΔgN. The term χα describes the fractional structure formation of the α-helix within the TSE. In this example, the TSE consists of the two barrier states α and β on the two parallel folding routes. χα ranges between 0 and 1. We have χα = 1 for gα ≪ gβ when the state α dominates the TSE, and χα = 0 when β dominates the TSE.
Whereas χα gives structural information, the second term, Δgα/ΔgN, can take on either negative or positive values. Thus, this term accounts for nonclassical Φ values <0 or >1. In the simplest case, ΔgN = Δgα + Δgαβ. Here, Δgαβ is the free-energy change for a tertiary contact between the α-helix and the β-sheet, for example. In that case, negative Φ values arise when Δgαβ is larger in magnitude and opposite in sign to that of Δgα. That is, a negative Φ value is predicted when a helical mutation also has a counteracting and larger effect on a tertiary contact. Correspondingly, Φ > 1 occurs when the following two conditions are met: (i) Δgαβ is opposite in sign but smaller in magnitude than Δgα, and (ii) χα is sufficiently large. This explanation of nonclassical Φ values may also rationalize why more Φ values are <0 than >1 (42). If gα and gαβ have a similar magnitude, it should be more difficult to satisfy the latter two conditions than the former condition.
However, our model is rather general and captures also that nonclassical Φ values can arise from shifts in the free energy of the denatured state. For example, if a mutation only lowers the free energy of the denatured state, we have Δgα > 0 and ΔgN < 0, which gives a negative Φ value according to Eq. 8. In contrast, the traditional structural interpretation of Φ values fails if mutations shift the free energy of the denatured state (48).
In this simple example, a mutation in the α-helix affects only a single structural element formed in the TSE: the α-helix. In general, mutations may affect several structural elements of the TSE. A generalization of Eq. 8 is then Φ = (∑iχi Δgi)/ΔgN with χi = -(∂ ln k)/(∂ gi), provided that the free energies gi of the structural elements are additive.
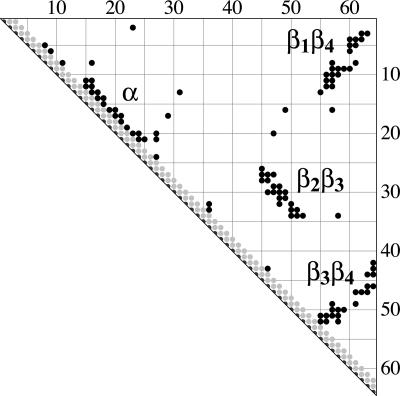
Mutations in the α-Helix of CI2. To model the folding kinetics of CI2, we must consider at least four substructural units: the α-helix and the three strand pairings β2β3, β3β4, and β1β4. These substructures correspond to contact clusters on the native contact map of CI2 (see Fig. 2). Therefore, the model energy landscape of CI2 is more complex than the landscape of the simple four-state model given above. However, under two assumptions, Eq. 3 also holds for the helix of CI2. These assumptions are as follows: (i) the helix is either fully formed or not formed in each of the states of the TSE, and (ii) the helix does not form tertiary contacts in the TSE. Under these assumptions, the free-energy contribution of the helix to a state of the TSE (in which the helix is formed) simply is gα, and then χα has the same interpretation as described above.¶
Fig. 2.
Contact matrix of CI2. Each black dot represents a contact between two amino acids in the native structure, with a distance of <6 Å between the Cα or Cβ atoms of the amino acids. The four large clusters of contacts correspond to the main structural elements of CI2: the α-helix and the β-strand pairings β2β3, β3β4, and β1β4. The few “isolated” contacts represent either turns or tertiary interactions of α-helix and β-sheet.
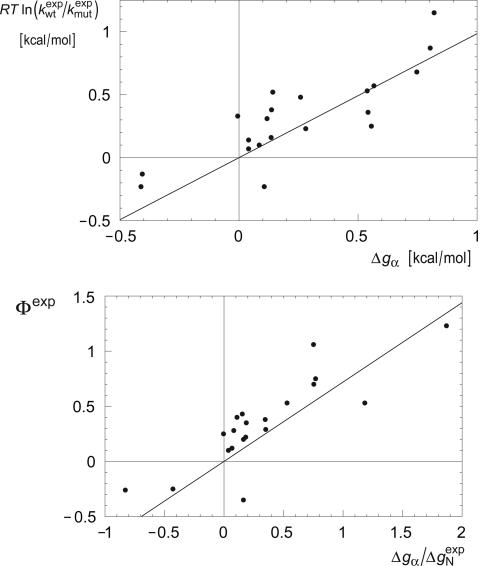
To test Eq. 8, we consider the 20 single-residue mutations in the CI2 helix (2). We estimate the change in intrinsic helix stability Δgα from helicities predicted by the program agadir (44-46) (see Table 1). The experimentally measured change in folding rate for these mutations, 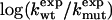 , correlates with Δgα with a coefficient r = 0.83, and the experimentally determined Φ values correlate with
, correlates with Δgα with a coefficient r = 0.83, and the experimentally determined Φ values correlate with 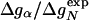 with r = 0.85 (see Fig. 3). According to Eq. 8, the change in log k is proportional to Δgα, and the Φ values are proportional to
with r = 0.85 (see Fig. 3). According to Eq. 8, the change in log k is proportional to Δgα, and the Φ values are proportional to 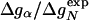 , both with proportionality constant χα. From the two linear fits shown in Fig. 3, we obtain the estimate χα = 0.88 ± 0.12. We have estimated the errors for χα by using a jackknife method in which up to two data points are deleted randomly from the data set (see legend to Fig. 3). This estimate for χα indicates that the helix is almost fully formed in the TSE. In agreement with this interpretation, molecular dynamics unfolding simulations indicate that a fraction of 0.91 ± 0.14 of the helical residues are structured in the TSE (21).
, both with proportionality constant χα. From the two linear fits shown in Fig. 3, we obtain the estimate χα = 0.88 ± 0.12. We have estimated the errors for χα by using a jackknife method in which up to two data points are deleted randomly from the data set (see legend to Fig. 3). This estimate for χα indicates that the helix is almost fully formed in the TSE. In agreement with this interpretation, molecular dynamics unfolding simulations indicate that a fraction of 0.91 ± 0.14 of the helical residues are structured in the TSE (21).
Table 1. Data for single-residue mutations in the α-helix of CI2.
| Mutation | 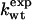 |
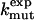 |
Φexp | Δgα | 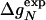 |
|---|---|---|---|---|---|
| S12G | 0.23 | 0.8 | 0.29 | 0.28 | 0.35 |
| S12A | 0.38 | 0.89 | 0.43 | 0.14 | 0.16 |
| E14Q | 0.36 | 0.29 | 1.23 | 0.54 | 1.86 |
| E14D | 0.10 | 0.52 | 0.2 | 0.08 | 0.15 |
| E14N | 0.53 | 0.7 | 0.75 | 0.54 | 0.77 |
| E15Q | 0.25 | 0.47 | 0.53 | 0.56 | 1.19 |
| E15D | 0.16 | 0.74 | 0.22 | 0.13 | 0.18 |
| E15N | 0.57 | 1.07 | 0.53 | 0.57 | 0.53 |
| A16G | 1.15 | 1.09 | 1.06 | 0.82 | 0.75 |
| K17A | 0.14 | 0.49 | 0.28 | 0.04 | 0.08 |
| K17G | 0.87 | 2.32 | 0.38 | 0.80 | 0.34 |
| K18G | 0.68 | 0.99 | 0.7 | 0.75 | 0.76 |
| V19A | −0.13 | 0.49 | −0.26 | −0.41 | −0.84 |
| 120V | 0.52 | 1.3 | 0.4 | 0.14 | 0.11 |
| L21A | 0.33 | 1.33 | 0.25 | −0.01 | −0.01 |
| L21G | 0.48 | 1.38 | 0.35 | 0.26 | 0.19 |
| Q22G | 0.07 | 0.6 | 0.12 | 0.04 | 0.07 |
| D23A | −0.23 | 0.96 | −0.25 | −0.41 | −0.43 |
| K24A | −0.23 | 0.65 | −0.35 | 0.11 | 0.17 |
| K24G | 0.31 | 3.19 | 0.1 | 0.12 | 0.04 |
Experimental data for folding rates 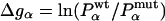 and
and 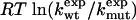 of wild type and mutants, stability changes
of wild type and mutants, stability changes 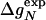 , and Φ values are from Itzhaki et al. (2). The change
, and Φ values are from Itzhaki et al. (2). The change 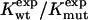 in the “intrinsic helix stability” gα is estimated from helicities Pα predicted by agadir (44-46). The wild-type sequence of the 13-residue helix is SVEEAKKVILQDK. Helicities have been calculated at the experimental temperature 298 K, pH 6.25, and ionic strength 0.03 mol, with acetylated N terminus and amidated C terminus of the peptide to avoid terminal charges. The energetic quantities RT
in the “intrinsic helix stability” gα is estimated from helicities Pα predicted by agadir (44-46). The wild-type sequence of the 13-residue helix is SVEEAKKVILQDK. Helicities have been calculated at the experimental temperature 298 K, pH 6.25, and ionic strength 0.03 mol, with acetylated N terminus and amidated C terminus of the peptide to avoid terminal charges. The energetic quantities RT 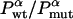 ,
, 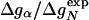 , and Δgα are given in kcal/mol.
, and Δgα are given in kcal/mol.
Fig. 3.
Correlation analysis for mutations in the CI2 helix. (Upper) ln(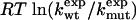 ) versus Δg = ln (
) versus Δg = ln (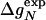 ) estimated from helicities Pα predicted by agadir (see Table 1). The correlation coefficient r is 0.83, and the slope of the fitted line through the origin is 0.98. The slope of this line is an estimate for the parameter χα of Eq. 8. For subsets of the data generated by deleting up to two data points, the correlation coefficient r varies from 0.77 to 0.93, and the linear slope varies from 0.87 to 1.07. (Lower) Φexp versus
) estimated from helicities Pα predicted by agadir (see Table 1). The correlation coefficient r is 0.83, and the slope of the fitted line through the origin is 0.98. The slope of this line is an estimate for the parameter χα of Eq. 8. For subsets of the data generated by deleting up to two data points, the correlation coefficient r varies from 0.77 to 0.93, and the linear slope varies from 0.87 to 1.07. (Lower) Φexp versus 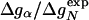 . The correlation coefficient r is 0.85, and the slope of the fitted line through the origin is 0.71. For data subsets generated by deleting up to two data points, r varies from 0.79 to 0.90, and the slope varies from 0.64 to 0.90.
. The correlation coefficient r is 0.85, and the slope of the fitted line through the origin is 0.71. For data subsets generated by deleting up to two data points, r varies from 0.79 to 0.90, and the slope varies from 0.64 to 0.90.
Discussion
Our model gives a physical explanation for nonclassical Φ values, but an alternative explanation is in terms of experimental errors. Sánchez and Kiefhaber (47) have observed that mutations with nonclassical Φ values often have relatively small changes ΔgN in stability. Because ΔgN appears in the denominator of the expression for Φ, it means that nonclassical Φ values can arise when a mutation has little effect on the protein stability. Sánchez and Kiefhaber argue that unavoidable experimental errors may be responsible for the nonclassical Φ values, and that Φ values for mutations with ΔgN < 1.7 kcal/mol are unreliable. Others have argued that this error threshold should be considerably smaller, ≈0.6 kcal/mol (16, 48). The analysis of Sánchez and Kiefhaber is based on the assumption that different mutations at a given residue position should lead to the same “true” Φ value for this residue position. Our model gives a different interpretation. In our model, different mutations at a given position can affect the energy landscape in different ways. For example, we believe E14Q in the CI2 helix may affect the helicity significantly, whereas E14D does not (see Table 1).
Our model can explain isolated nonclassical Φ values, such as the four in the α-helix of CI2 (see Table 1). They are “isolated” insofar as they are interspersed among classical Φ values within a local region of the protein. There are other cases in which nonclassical Φ values are clustered together within a given region of the protein. In the second α-helix of ACBP for example, seven Φ values are clearly negative, whereas the other six Φ values are close to 0. Previously, clustered nonclassical Φ values have been explained in terms of parallel flow processes on slightly more complex energy landscapes than we have considered here (49). That is, mutations that destabilize a particular substructure can cause a back flow on the energy landscape into faster flow channels, leading to an increase in the folding rate and negative Φ values.
Here, we considered the α-helix of CI2 to illustrate our structural interpretation of Φ values. One reason is that the helix is very well characterized (i.e., a large number of Φ values is available). Another reason is that these Φ values cover a wide range of possible values, from -0.35 to 1.23. Two other well characterized helices are the α-helices of protein L (9) and G (10). There are 15 single-residue mutations that have been considered in the protein L helix. One of the Φ values is -0.39, whereas the others span a rather narrow range from -0.05 to 0.28 (9). Similarly, one of nine Φ values for the helix of protein G is -0.81, whereas the others range from 0.05 to 0.55. In both cases, our model reproduces the clearly negative, nonclassical Φ value, which leads to relatively high correlation coefficients of 0.58 and 0.81 between the experimental and theoretical Φ value distributions. But because the other Φ values lie in a rather narrow range, the statistical uncertainties from experimental and modeling errors are high, and χα cannot be determined reliably.
Summary
The Φ values give information about the routes of protein folding. The central question is: What information do they give? Previous modeling has been limited in certain ways. First, some models treat only topological aspects of folding and, therefore, cannot explain how single-site mutations can have the large effects on folding rates that are often observed. Second, current models usually make some plausible, but ad hoc, assumption about folding routes, transition states, and reaction coordinates. Protein folding is sufficiently different from simpler reactions that some of these assumptions are not likely to be valid. In particular, Φ values are often assumed to reflect only structural information about transition states. Here, we present a more rigorous approach for interpreting Φ values, and we show that Φ values have both structural and energetic components. We show that our approach gives a consistent interpretation of mutational experiments on the CI2 helix.
Abbreviation: TSE, transition-state ensemble.
Footnotes
The transition rates obey detailed balance 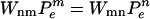 , where
, where 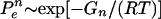 is the equilibrium weight for the state n. Detailed balance ensures that the system ultimately reaches thermal equilibrium.
is the equilibrium weight for the state n. Detailed balance ensures that the system ultimately reaches thermal equilibrium.
These two assumptions are clearly simplifying. Based on unfolding simulations, Daggett et al. (21) argue for a crucial tertiary interaction between the residues Ala-16 of the α-helix and Ile-49 of the β-sheet in the TSE of CI2. In contrast, Lazaridis and Karplus (23) found that “the number of contacts made by the Ala side chain [in the TSE]... depend[s] primarily on the presence of the helix and not on interactions with β-strands.”
References
- 1.Otzen, D. E., Itzhaki, L. S., elMasry, N. F., Jackson, S. E. & Fersht, A. R. (1994) Proc. Natl. Acad. Sci. USA 91, 10422-10425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Itzhaki, L. S., Otzen, D. E. & Fersht, A. R. (1995) J. Mol. Biol. 254, 260-288. [DOI] [PubMed] [Google Scholar]
- 3.Villegas, V., Martinez, J. C., Aviles, F. X. & Serrano, L. (1998) J. Mol. Biol. 283, 1027-1036. [DOI] [PubMed] [Google Scholar]
- 4.Chiti, F., Taddei, N., White, P. M., Bucciantini, M., Magherini, F., Stefani, M. & Dobson, C. M. (1999) Nat. Struct. Biol. 6, 1005-1009. [DOI] [PubMed] [Google Scholar]
- 5.Martinez, J. C. & Serrano, L. (1999) Nat. Struct. Biol. 6, 1010-1016. [DOI] [PubMed] [Google Scholar]
- 6.Riddle, D. S., Grantcharova, V. P., Santiago, J. V., Alm, E., Ruczinski, I. & Baker, D. (1999) Nat. Struct. Biol. 6, 1016-1024. [DOI] [PubMed] [Google Scholar]
- 7.Ternström, T., Mayor, U., Akke, M. & Oliveberg, M. (1999) Proc. Natl. Acad. Sci. USA 96, 14854-14859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kragelund, B. B., Osmark, P., Neergaard, T. B., Schiodt, J., Kristiansen, K., Knudsen, J. & Poulsen, F. M. (1999) Nat. Struct. Biol. 9, 594-601. [DOI] [PubMed] [Google Scholar]
- 9.Kim, D. E., Fisher, C. & Baker, D. (2000) J. Mol. Biol. 298, 971-984. [DOI] [PubMed] [Google Scholar]
- 10.McCallister, E. L., Alm, E. & Baker, D. (2000) Nat. Struct. Biol. 7, 669-673. [DOI] [PubMed] [Google Scholar]
- 11.Hamill, S. J., Steward, A. & Clarke, J. (2000) J. Mol. Biol. 297, 165-178. [DOI] [PubMed] [Google Scholar]
- 12.Fowler, S. B. & Clarke, J. (2001) Structure (London) 9, 355-366. [DOI] [PubMed] [Google Scholar]
- 13.Jäger, M., Nguyen, H., Crane, J. C., Kelly, J. W. & Gruebele, M. (2001) J. Mol. Biol. 311, 373-393. [DOI] [PubMed] [Google Scholar]
- 14.Otzen, D. E. & Oliveberg, M. (2002) J. Mol. Biol. 317, 613-627. [DOI] [PubMed] [Google Scholar]
- 15.Northey, J. G. B., Di Nardo, A. A. & Davidson, A. R. (2002) Nat. Struct. Biol. 9, 126-130. [DOI] [PubMed] [Google Scholar]
- 16.Garcia-Mira, M. M., Böhringer, D. & Schmid, F. X. (2004) J. Mol. Biol. 339, 555-569. [DOI] [PubMed] [Google Scholar]
- 17.Matouschek, A., Kellis, J. T., Serrano, L. & Fersht, A. R. (1989) Nature 340, 122-126. [DOI] [PubMed] [Google Scholar]
- 18.Fersht, A. R. (1999) Structure and Mechanism in Protein Science (Freeman, New York).
- 19.Li, A. & Daggett, V. (1994) Proc. Natl. Acad. Sci. USA 91, 10430-10434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li, A. & Daggett, V. (1996) J. Mol. Biol. 257, 412-429. [DOI] [PubMed] [Google Scholar]
- 21.Daggett, V., Li, A., Itzhaki, L. S., Otzen, D. E. & Fersht, A. R. (1996) J. Mol. Biol. 257, 430-440. [DOI] [PubMed] [Google Scholar]
- 22.Ladurner, A. G., Itzhaki, L. S., Daggett, V. & Fersht, A. R. (1998) Proc. Natl. Acad. Sci. USA 95, 8473-8478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lazaridis, T. & Karplus, M. (1997) Science 278, 1928-1931. [DOI] [PubMed] [Google Scholar]
- 24.Kazmirski, S. L., Wong, K.-B., Freund, S. M. V., Tan, Y.-J., Fersht, A. R. & Daggett, V. (2001) Proc. Natl. Acad. Sci. USA 98, 4349-4354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Alm, E. & Baker, D. (1999) Proc. Natl. Acad. Sci. USA 96, 11305-11310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Munoz, V. & Eaton, W. A. (1999) Proc. Natl. Acad. Sci. USA 96, 11311-11316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Galzitskaya, O. V. & Finkelstein, A. V. (1999) Proc. Natl. Acad. Sci. USA 96, 11299-11304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Portman, J. J., Takada, S. & Wolynes, P. G. (2001) J. Chem. Phys. 114, 5069-5081. [Google Scholar]
- 29.Alm, E., Morozov, A. V., Kortemme, T. & Baker, D. (2002) J. Mol. Biol. 322, 463-476. [DOI] [PubMed] [Google Scholar]
- 30.Kameda, T. (2003) Proteins 53, 616-628. [DOI] [PubMed] [Google Scholar]
- 31.Clementi, C., Nymeyer, H. & Onuchic, J. N. (2000) J. Mol. Biol. 298, 937-953. [DOI] [PubMed] [Google Scholar]
- 32.Hoang, T. X. & Cieplak, M. (2000) J. Chem. Phys. 113, 8319-8328. [Google Scholar]
- 33.Li, L. & Shakhnovich, E. I. (2001) Proc. Natl. Acad. Sci. USA 98, 13014-13018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Karanicolas, J. & Brooks, C. L. (2002) Protein Sci. 11, 2351-2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kaya, H. & Chan, H. S. (2003) J. Mol. Biol. 326, 911-931. [DOI] [PubMed] [Google Scholar]
- 36.Weikl, T. R., Palassini, M. & Dill, K. A. (2004) Protein Sci. 13, 822-829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vendruscolo, M., Paci, E., Dobson, C. M. & Karplus, M. (2001) Nature 409, 641-645. [DOI] [PubMed] [Google Scholar]
- 38.Lindorff-Larsen, K., Paci, E., Serrano, L, Dobson, C. M. & Vendruscolo, M. (2003) Biophys. J. 85, 1207-1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lindorff-Larsen, K., Vendruscolo, M., Paci, E. & Dobson, C. M. (2004) Nat. Struct. Mol. Biol. 11, 443-449. [DOI] [PubMed] [Google Scholar]
- 40.Hammond, G. S. (1955) J. Am. Chem. Soc. 77, 334-338. [Google Scholar]
- 41.Matthews, C. R. (1993) Annu. Rev. Biochem. 62, 653-683. [DOI] [PubMed] [Google Scholar]
- 42.van Kampen, N. G. (1992) Stochastic Processes in Physics and Chemistry, (Elsevier, Amsterdam)
- 43.Goldenberg, D. P. (1999) Nat. Struct. Biol. 6, 987-990. [DOI] [PubMed] [Google Scholar]
- 44.Muñoz, V. & Serrano, L. (1994) J. Mol. Biol. 245, 275-296. [DOI] [PubMed] [Google Scholar]
- 45.Muñoz, V. & Serrano, L. (1994) J. Mol. Biol. 245, 297-308. [DOI] [PubMed] [Google Scholar]
- 46.Lacroix, E., Viguera, A. R. & Serrano, L. (1998) J. Mol. Biol. 284, 173-191. [DOI] [PubMed] [Google Scholar]
- 47.Sánchez, I. E. & Kiefhaber, T. (2003) J. Mol. Biol. 334, 1077-1085. [DOI] [PubMed] [Google Scholar]
- 48.Fersht, A. R. & Sato, S. (2004) Proc. Natl. Acad. Sci. USA 91, 10422-10425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ozkan, S. B., Bahar, I. & Dill, K. A. (2001) Nat. Struct. Biol. 8, 765-769. [DOI] [PubMed] [Google Scholar]