Abstract
Recent observations show that the single-cell response of p53 to ionizing radiation (IR) is “digital” in that it is the number of oscillations rather than the amplitude of p53 that shows dependence on the radiation dose. We present a model of this phenomenon. In our model, double-strand break (DSB) sites induced by IR interact with a limiting pool of DNA repair proteins, forming DSB–protein complexes at DNA damage foci. The persisting complexes are sensed by ataxia telangiectasia mutated (ATM), a protein kinase that activates p53 once it is phosphorylated by DNA damage. The ATM-sensing module switches on or off the downstream p53 oscillator, consisting of a feedback loop formed by p53 and its negative regulator, Mdm2. In agreement with experiments, our simulations show that by assuming stochasticity in the initial number of DSBs and the DNA repair process, p53 and Mdm2 exhibit a coordinated oscillatory dynamics upon IR stimulation in single cells, with a stochastic number of oscillations whose mean increases with IR dose. The damped oscillations previously observed in cell populations can be explained as the aggregate behavior of single cells.
Keywords: DNA damage response, mathematical model of p53, p53 regulation, p53 pathway
Cells under stresses such as DNA damage, hypoxia, and aberrant oncogene signals trigger their internal self-defense machinery. One critical response is the activation of the tumor suppressor protein p53, which transcribes genes that induce cell cycle arrest, DNA repair, and apoptosis (1–4). A central node in the p53 network is the Mdm2 protein, the product of one of the p53 target genes and a negative regulator of p53. The negative feedback loop formed by p53 and Mdm2 can produce oscillatory dynamics. Indeed, damped oscillations of p53 and Mdm2 protein level have been observed upon ionizing radiation (IR)-induced DNA damage in cell populations (5). Intriguingly, recent in vivo fluorescence measurements in individual cells revealed that in response to IR, these two proteins exhibit a “digital” response that produces discrete pulses of p53 and Mdm2. The average height and duration of these pulses are fixed, whereas the mean number increases with the strength of DNA damage (6).
Several models have been proposed (5, 7, 8) to explain the damped oscillations of p53 in cell populations. However, these modeling efforts did not explore sustained pulses as found in single-cell responses and did not attempt to characterize the signaling between DNA damage and the activation of the p53 oscillatory response.
In this study, we present a model for the digital, undamped oscillatory p53 activity elicited by IR at the single-cell level consisting of three subsystems: a DNA damage repair module, an ataxia telangiectasia mutated (ATM) switch, and the p53–Mdm2 oscillator. We investigate the controlling role of ATM to set a threshold level of DNA damage during the radiation response, as suggested by growing biochemical evidence (9–12). Finally, by adding stochasticity to selected model parameters, we replicate the variable number of p53 pulses in individual cells as well as the cell population dynamics.
Methods
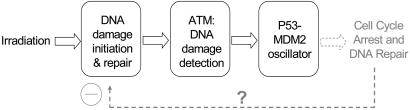
Model Description. Overview. The basic three-module structure of the model is shown in Fig. 1. In the first module, a random number of double-strand breaks (DSBs) is formed based on the initial radiation level, after which DNA damage repair complexes are assumed to form around the DSBs. The repair process proceeds in a stochastic fashion in which repair complexes take a variable time to fix the DSB at each site. In the second module, the repair complexes are assumed to be the signal that induces activation of ATM. ATM activation is assumed to be autocatalytic (11), with positive feedback rapidly activating the pool of ATM with only a small number of DSBs. The third module consists of the well known p53 and Mdm2 negative feedback loop. Mathematical analysis has shown that there is a wide range of parameters for which the oscillations persist (13). The dashed arrow in Fig. 1 represents the induction of DNA repair proteins and important cell cycle players triggered by the p53 response to IR. However, the paucity of data for this process prevents us from including this mechanism in our model. These three modules are described in more detail below.
Fig. 1.
The p53 signaling model is composed of three modules: a DNA damage repair module, an ATM activation module, and the p53–Mdm2 oscillator. The input IR causes DNA DSBs. While getting repaired, the signal of the remaining DSB is detected by ATM and further stimulates the p53–Mdm2 oscillator. The dashed arrow represents a potential negative feedback of p53 induction of DNA repair genes, not included in the model.
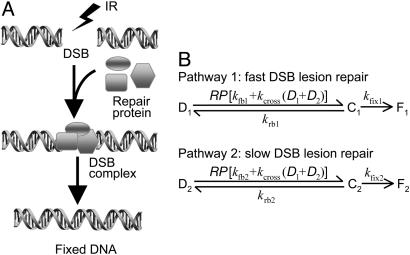
DNA damage initiation and repair. DSBs are the primary DNA lesions caused by IR (14, 15). In eukaryotic cells, the repair proteins Mre11, Rad50, and NBS1 (which form the MRN complex) are reported to bind to DSB, forming complexes that activate ATM (16). These repair mechanisms can be represented as the set of reactions shown in Fig. 2A. Quantification of remaining DSBs in cells after IR showed that the typical DSB repair process exhibits biphasic dynamics consisting of a fast initial component and a decreasing rate at longer repair intervals (17, 18). To account for such dynamics, our model of DNA repair contains two parallel repair pathways with distinct reaction rates corresponding to fast and slow repair (Fig. 2B). The fast and slow kinetics refer to repair of simple and complex DSBs, respectively, as described in refs. 19 and 20. Both processes are described by a reversible binding of repair proteins and DSB lesions into a DSB–protein complex followed by an irreversible repair process from the complex to repaired DSBs. Both the fast and slow kinetics contain a first-order and a second-order repair rate. DSB repair is a first-order process if break ends associated with the same DSB are rejoined, and it is a second-order process if the break ends associated with two different DSBs are involved in the repair event (19, 20).
Fig. 2.
Schematic representation of the repairing process of DSBs. (A) A pool of activated repair proteins binds to DSBs, forming lesion–enzyme complexes, which initiate damage repair. (B) Reactions in the DNA repair module with a fast binding-repair pathway and a slow one. D, DSB; C, DSBC; F, fixed DSB; RP, repair protein.
Given the small number of DSBs present at low and moderate IR doses, we simulate DNA repair at the single-cell level as a stochastic process. We assume that the initial number of DSBs obeys a Poisson distribution whose average is proportional to the radiation dose (10, 21) and compute the repair dynamics by using Monte Carlo methods. The model implementation details, parameter values, and further discussion can be found in the supporting information, which is published on the PNAS web site.
ATM-mediated DSB signal transduction. The role of ATM as DSB detector is well documented (11, 22–25). In unstressed cells, ATM exists as a dimer whose kinase activity is impeded by its partner ATM molecule. After IR, intermolecular autophosphorylation occurs, causing the dimer to dissociate rapidly into active monomers, which can then phosphorylate p53. The kinase activity of ATM is augmented after IR doses as low as 0.2 Gy and is saturated at doses of ≈0.5 Gy. Such a low IR dose only induces a few DSBs in the cell, suggesting that ATM is extremely sensitive as a DNA damage detector. Here, we assume that the DSB repair–protein complex activates ATM directly (26, 27), although other intermediate components may be involved.
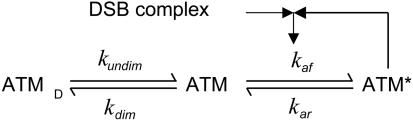
Based on previous experiments, we propose an ATM activation module of three components: ATM dimer, inactive ATM monomer, and active ATM (ATM*) monomer, which are interconnected by a dimerization process and a DSB-induced phosphorylation reaction coupled with positive feedback (Fig. 3). We assume that kdim >> kundim, so that inactive ATM dimers predominate in resting cells. After IR, phosphorylation of inactive ATM monomers is promoted first by the DSB complex-induced activation and then rapidly by means of the positive feedback from ATM*, accounting for intermolecular autophosphorylation (11). More precisely, the rate of ATM activation is assumed to be a function of the amount of DSB complex and ATM* monomer (see the supporting information). The total concentration of ATM is assumed to be a constant. The mathematics and parameters of this module can be found in the supporting information. We elaborate on the limitations of this module in Discussion.
Fig. 3.
The ATM activation module. The dimerization between two inactive ATM monomers occurs significantly faster than the undimerization reaction (kdim >> kundim), producing predominantly ATM dimers (ATMD) in unstressed cells. Upon IR stimulation, ATM monomers are activated by ATM* (a positive feedback loop) and a DSB–protein complex.
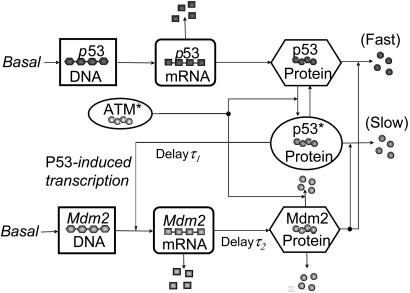
The p53–Mdm2 oscillator. The core regulatory circuitry of p53 is a loop formed by p53 and its principal antagonist, Mdm2, a p53-specific ubiquitin ligase that is transactivated by p53 (28, 29). We model this well studied negative feedback loop (30–32) according to the scheme displayed in Fig. 4, which includes transcriptional (τ1) and translational/translocation (τ2) time delays to account for transcriptional elongation times and to describe only nuclear concentrations, respectively (see the supporting information for equations and parameters). This circuit alone can produce stable oscillations of p53 and Mdm2 in response to a sufficiently strong ATM activation (13).
Fig. 4.
Diagram of the p53–Mdm2 oscillator. p53 is translated from p53 mRNA and is inactive for induction of its targets. Phosphorylated by ATM*, p53 becomes active (p53*) and able to transcribe (after a time delay) Mdm2, which also has a basal transcription rate. Mdm2 protein promotes a fast degradation of p53 and a slow degradation of p53*. In addition to a basal self-degradation, Mdm2 is degraded by a mechanism stimulated by ATM*.
Our model contains some features not considered in earlier mathematical models of this system. We include ATM* phosphorylation of p53, which elevates the transcriptional activity of p53 after IR (33, 34). We model this mechanism by the ATM*-induced reaction of p53 from the inactive state to the active state (p53*). We further assume that inactive p53 is degraded rapidly by Mdm2 but that p53* is degraded with a slower rate to account for a decreased binding affinity between these two proteins and decreased polyubiquitination efficacy (35). This inefficient degradation of p53* and the assumption that only p53* can induce target genes cause an overall effect of increased transcriptional activity and decreased degradation of the total p53, as observed. To account for the accelerated autodegradation of Mdm2 induced by stress-activated kinases [including ATM (36)], which makes the Mdm2 half-time as short as 5 min, we assume that ATM* promotes Mdm2 destabilization through a Hill mechanism. Based on our measurement that shows that the p53 concentration lies in the range of 0.06–0.5 μM (see the supporting information), the oscillator parameters are calibrated such that the basal p53 concentration is 0.35 μM.
Results
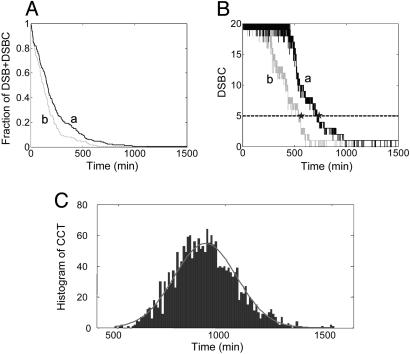
DNA Damage Repair Dynamics. In our simulations, an acute IR dose of x Gy is first applied. The number of resulting DSBs obeys a Poisson distribution with a mean of 35x, consistent with the measured 30–40 DSBs per Gy per cell (37–39). Because there may be many repair proteins nucleated around each DSB (for example, Mre11–Rad50–NBS1 complexes form foci that may arise from the creation of multiple binding sites near DSBs), we assume that we have 20 repair proteins per cell, representing the maximum number of DSBs that can be repaired simultaneously. The important assumption here is that the relatively small number of repair proteins is initially rate-limiting in DSB repair. The small number of breaks and the assumption of a small number of repair proteins make it necessary to simulate the process by using stochastic techniques. Simulation details can be found in the supporting information. Fig. 5A shows a time plot of the fraction of DSBs remaining, consisting of both unrepaired DSBs and DSBs in complex with repair proteins (DSBCs) in response to 5-Gy IR for two independent runs. The traces show a decaying process with discontinuous jumps due to the assumption that the final step of DSB repair is irreversible. In contrast, the time plot of DSBCs in Fig. 5B shows an initial plateau value of 20 because, initially, all of the repair proteins are in complexes.
Fig. 5.
Temporal response of the DNA repair module to an IR dose of 5 Gy. (A) The remaining fraction of unrepaired DSBs and DSBCs. Curves a and b represent two different runs. (B) DSBC (solid lines) and threshold values for the activation of the downstream DNA damage sensor (dashed line). The last time point (star) where the two traces intersect the threshold is defined as the CCT. (C) Histogram of the CCT after 2,000 individual runs of the DNA repair module. The fit (gray curve) is a Gaussian distribution with a mean of 904 min and a SD of 146 min.
We argue below that ATM activation drives downstream events with a threshold behavior and that the crossing of this threshold is responsible in part for the stochastic nature of the number of p53–Mdm2 oscillations. To illustrate this point, we define here the critical crossing time (CCT) as the last time when the DSBC trace intersects the threshold (Fig. 5B). We chose five DSBCs as a plausible threshold value based on the experimental quantification that at IR doses of 0.1–0.2 Gy, a measurable amount of ATM* appears (11) and on the calibration of ≈35 DSBs per Gy per cell. Fig. 5C shows a histogram of the CCT distribution for 2,000 runs of the DNA repair module. The CCT values range from ≈500 to ≈1,500 min, with a mean of 904 min. Clearly, the duration of events downstream from the DNA repair module will reflect the intrinsic stochasticity in the damage repair processes.
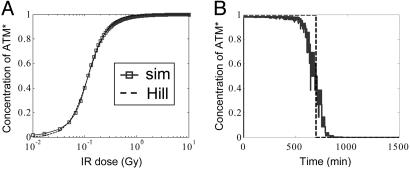
Activation of ATM. Here, we address how ATM shows a switch-like behavior and relays the DNA damage signal. ATM* responds to DSBCs in our model as described in the supporting information. We have seen above that DSBCs reach a maximal value because of limited repair resources soon after irradiation. Because DSBCs change on a time scale of hours but ATM equilibrates in minutes because of fast phosphorylation, ATM* follows the time course of DBSCs adiabatically. In Fig. 6A, we plot steady-state ATM* versus IR dose between 10-2 and 10 Gy. This relation is well fitted by a Hill function with a Hill coefficient of 2 and a half-saturation threshold corresponding to IR ≈ 0.14 Gy (about five DSBCs). Immunoblot studies by Bakkenist and Kastan (11) show a rather abrupt onset of activated ATM that starts at 0.1–0.2 Gy and reaches saturation at ≈0.4 Gy (see figure 5d in ref. 11). Our model qualitatively resembles the actual data reported in ref. 11 except that it has not yet saturated at 0.4 Gy (see the supporting information). In other words, a Hill coefficient of 2, although sufficiently high to account for the digital behavior as shown below, appears less cooperative than the actual data. The cooperativity in our model arises from a reasonable kinetic mechanism of ATM activation (see the supporting information) whose details might need to be modified as more experimental information becomes available.
Fig. 6.
Switch-like behavior of the ATM module. (A) Input–output relation between IR dose and the concentration of ATM* normalized by total ATM at steady state. The solid line represents simulation results of the three-component ATM activation module, and the dashed line is a fit using a Hill function with a Hill coefficient of 2. (B) A time course of ATM* normalized by total ATM (solid line) in response to the DSBC signal stimulated by 5-Gy IR as shown in Fig. 5B. The step function (dashed line) represents a perfect switch.
In Fig. 6B, we plot the time course of ATM* stimulated by the input signal labeled “a” in Fig. 5B. At time 0, all of the ATM is activated very rapidly in response to the saturating DSBCs, and ATM* remains maximal over the first 500 min. Once DSBCs fall below threshold, the ATM* level decays to zero much faster than DSBCs because of the cooperativity in ATM activation. The sharp, step-like shape of the trace in Fig. 6B suggests that the ATM module with a Hill coefficient of 2 can produce an on–off switching signal to the downstream oscillator.
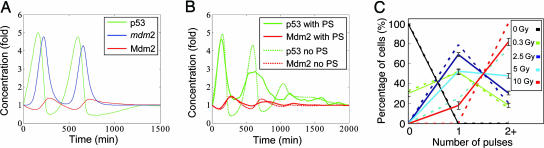
IR-Induced Oscillations of p53. In response to the on–off input, the p53–Mdm2 module generates one or more oscillations for IR doses over ≈0.2 Gy. Fig. 7A shows the response of p53, Mdm2 mRNA, and Mdm2 protein after an acute application of 5-Gy IR at time 0; the upstream DSB and ATM signals are displayed in Figs. 5 and 6, respectively. Upon activation by ATM* and decreased degradation by Mdm2, the total amount of p53 protein increases quickly. The initial drop of Mdm2 is due to the accelerated ATM*-stimulated self-degradation. Mdm2 then rises because of the p53-dependent induction of Mdm2 transcription, albeit with a delay. The increase in Mdm2 protein is sufficiently large to lower the p53 level, which in turn reduces Mdm2 production and Mdm2 protein. This sequence describes one oscillation. The oscillation pulses in Fig. 7 have a period of 420 min (≈7 h), and the phase difference between p53 and Mdm2 is ≈115 min, both of which are consistent with experimental observations (6). Note that, consistent with the average trend observed in ref. 6, the first pulse is slightly higher than the second, probably due to the transition between basal equilibrium and the limit cycle as well as repaired DNA damage.
Fig. 7.
Whole-model simulations results. (A) Responses of p53 (green), mdm2 mRNA (blue), and Mdm2 (red) stimulated by 5-Gy IR with two pulses. (B) Cell population response to 5-Gy IR with (solid lines) or without (dotted lines) PS. The data are the average of 100 individual responses. (C) Fraction of cells with zero, one, two, or more pulses as a function of IR dose with (solid lines) or without (dotted lines) PS. The data show mean ± SEM.
The stochasticity of DNA repair displayed in Fig. 5C is propagated to the oscillator. For example, at an IR dose of 5 Gy, one, two, or three pulses of p53 could be produced. Fig. 7A shows the case with two pulses. (See the supporting information for instances with one or three pulses.) This result resembles the behavior observed in single-cell measurements, showing that at the same IR dose, different cells from the same clone may display different numbers of p53 pulses (6). We further quantified the relation between the IR dose and the elicited p53 pulse number as in Lahav et al. (figure 3a in ref. 6). For each IR dose, we ran 10 experiments of 100 simulation runs representing 100 cells (from the same clone) and computed the average fraction of cells with zero, one, and two or more p53 pulses at different doses (Fig. 7C, dashed lines). Our simulation reproduces to a great degree the results reported in ref. 6: The more severe the damage, the greater the number of p53 pulses, on average. The distribution of pulse numbers mimics the experimental trend at all IR doses, except that at 10 Gy, our model predicts uniform (100%) oscillations with two or more pulses, whereas Lahav et al. (6) observed a large fraction (40%) of the cells exhibiting only one pulse. This discrepancy will be addressed later.
It was shown in ref. 6 that the average of single-cell p53 data were damped oscillations with a second peak smaller and broader than the first peak. To compare with experimental behavior, we computed the average of p53 and Mdm2 from 100 simulations representing 100 individual cells (Fig. 7B, dotted lines). The response does show decreasing amplitudes of p53 pulses, but the second peak is not as small and wide as experimentally observed (6). Taken together with the data above, our results indicate that the stochasticity in the DNA damage signaling process alone is not enough to account for the variability between the cells sampled in the experiments. Likely sources of experimental variability not considered in our model include different stages of the cell cycle, uneven extracellular disturbance, cells undergoing apoptosis, and noisy gene expression (40, 41). As a result, different individual cells may have different internal parameters. For our model, we allow parameter stochasticity (PS) in four parameters: the transcriptional time delay τ1, the translational/transport time delay τ2, the total number of DNA repair proteins, and the total amount of ATM. They are assumed to be uniformly distributed in a range [0.5λ, 1.5λ], where λ represents their respective nominal value. We then recomputed the distribution of pulse numbers (Fig. 7C, solid lines) and the cell population response (Fig. 7B, solid lines) under PS. PS effectively adds more variability to the dynamics in that now ≈20% of individual cells oscillate with one pulse at 10 Gy rather than uniformly showing two or more pulses. In addition, the error bars of p53 pulse-number distribution under PS are considerably larger than without PS (data not shown). The cell population time courses under PS also exhibit a smaller and broader second pulse, better mimicking experiments. In contrast to the variability in the number of pulses, the mean amplitude and the period of the pulses were relatively constant with respect to changes in IR dose (see the supporting information), as was also found in ref. 6. Taken together, these results show that our model of p53 response to IR yields roughly equal-sized pulses with a mean number that increases with IR strength.
Finally, we stress the dynamical importance of the ATM*-dependent degradation of Mdm2 (see the supporting information). As discussed earlier, the p53–Mdm2 module includes explicit time delays τ1 and τ2. Interestingly, if we remove the ATM*-dependent degradation of Mdm2, keeping the rest of the parameters at their nominal values, then there are no sustained oscillations regardless of how high the time delay and the DNA damage is (see the supporting information). In the present model, which includes ATM*-stimulated Mdm2 degradation, sustained oscillations occur if the total time delay is more than the ≈16-min threshold (see the supporting information). Thus, the mechanism of ATM*-dependent degradation of Mdm2 confers the system with additional oscillatory robustness.
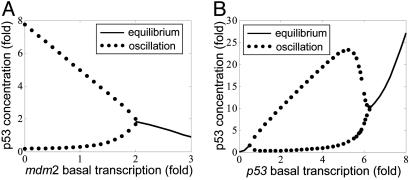
Model Predictions. We can derive quantitative predictions on how perturbations of different parameters of the system affect p53 oscillations under DNA damage. A first prediction is that a 2-fold or larger increase of the basal transcription rate for Mdm2 will disable oscillations (Fig. 8A). If oscillations are of importance for an apoptotic response, this prediction implies that cells with abnormally high Mdm2 basal transcription rates should be associated with enhanced tumorigenesis. Indeed, this conjecture seems to be consistent with the recent study of SNP309 (42), a SNP in the basal Mdm2 promoter that is associated with accelerated tumor formation. Preliminary experiments have indeed shown that homozygous cell lines on this SNP with 2-fold higher basal Mdm2 transcription do not oscillate in response to IR (data not shown). A second prediction is that a 2-fold decrease or 6-fold increase of the basal p53 transcription rate will disable oscillations (Fig. 8B). The latter effect is counterintuitive, and it would be interesting to test whether enhancing p53 transcription (by using p53 gene-transfected cell lines, for instance) could destroy IR-induced oscillations.
Fig. 8.
One-dimensional bifurcation diagrams of steady-state p53 versus single-parameter variation of Mdm2 basal transcription rate (A) or p53 basal transcription rate (B). The stable equilibrium is represented by a solid line. The lower and upper bounds of stable oscillation are represented by paired dotted lines.
The consequences of perturbations in the concentration of key signaling components can also be predicted. For example, we predict that knocking down DNA damage repair proteins (such as the Mre11–Rad50–NBS1 complex) will lead to a longer repairing time and an enhanced variability in the number of oscillations at a given IR dose. The model also predicts that, while the onset of oscillation requires a sufficient amount of ATM (13), an excessive total amount of ATM (≈20-fold) annihilates p53 oscillation. This large ATM excursion is clearly difficult to realize experimentally.
Discussion
Mechanism of Threshold Sensing. Our model exhibits strong sensitivity to the number of DSBs, which may be necessary to arrest the cell cycle in response to a small number of DSBs. When studying the p53–Mdm2 module in isolation (13), we observed that increasing the ATM* level produces an abrupt onset of oscillations, technically called a Hopf bifurcation. A possible role of a Hopf bifurcation as a threshold sensor has been suggested recently by Tyson and coworkers (43, 44). We also modeled IR ATM* response with a Hill function, leaving the Hill coefficient nH as a free parameter to study the effect of a higher cooperativity of the ATM module on the response of the p53–Mdm2 oscillator (see the supporting information). A steeper cooperative activation function of ATM* can produce an even sharper transition to oscillations as the steepness of the ATM response is compounded with the steepness of the Hopf bifurcation. As a result, the whole-model behavior of ATM* and the p53–Mdm2 oscillator closely resembles an on–off switch with an abrupt onset that quickly saturates as the apparent cooperativity of ATM activation increases (see the supporting information). Hence, once the IR dose is sufficiently large to produce oscillations, the amplitude of the oscillations is essentially fixed.
Model Limitations. The three-component formulation of the ATM module is reasonable but speculative. For example, the choice of the DSB complex as input to the ATM-sensing module explains part but not all possible means of ATM activation; ref. 11 also suggest that changes in chromatin structure are sufficient to activate ATM even in the absence of DSBs. We chose a rather simplistic representation for the activation of ATM that provides a fairly minimal representation for events that may be more complex, like the role of ATM dimerization or possibly higher multimerization in the autophosphorylation process. Although the work in ref. 11 indicated the presence of dimers of inactive ATM, the researchers also pointed out that higher-order multimers could not be ruled out, which could potentially increase the cooperativity in the ATM system as shown in the classic literature on allosteric enzyme reactions, such as the Monod–Wyman–Changeaux model (45).
Despite the fact that, in a stressed cell, there exists a variety of modified p53 protein states (46, 47), we assume that p53 has only an inactive state and an active state for transactivation to emphasize that, as a transcription factor, p53 is latent in unstressed cells and transcriptionally active in irradiated cells. Reality is more complex, and other p53 states may be important.
According to initial reports that suggest that after binding in the nucleus, the p53–Mdm2 complex shuttles to the cytoplasm for p53 degradation, our model should differentiate between nuclear and cytosolic pools of p53 and Mdm2 with appropriate translocation rates. However, recent reports suggest that Mdm2-mediated degradation occurs in the nucleus at a high rate (32, 48, 49), although the exact roles and ratios of degradation rates in the two compartments are not known. For this initial model, we have considered only nuclear components, although a multicompartment model could be a necessary extension as more data become available.
We have omitted many known players in the p53 circuit, such as Wip1 and cyclin G, two other negative regulators of p53 (50, 51). Although their contribution to the oscillatory dynamics after IR may be important, at this stage, we are more confident including only Mdm2 as the primary negative regulator of p53. Other genes that are part of the p53 circuit, such as YY1 (52) (which negatively regulates p53) and ARF (53) [a negative regulator of Mdm2 activated by oncogenes such as Myc, E2F-1, Ras, and DMP1 (54)] do not seem to have a dynamic role in the response of p53 to IR and therefore have not been included in our model.
Biological Speculation. Why do single cells show digital behavior? We propose that the oscillations of p53 act as a timer for downstream events such as cell cycle arrest and apoptosis. We speculate that genes inducing growth arrest (e.g., p21) are rapidly expressed during the first oscillation of p53, whereas proapoptotic p53 target genes such as Noxa, Puma, or Bax are gradually integrated over multiple cycles of p53 pulses, ratcheting up at each pulse until they reach a certain threshold value that activates apoptosis. Selective activation of genes via different temporal induction profiles has been seen in other cellular pathways (55).
Conclusions
Our model provides a framework for the theoretical analysis of the mechanisms underlying the digital response of p53 to IR. Although some aspects of the biology involved in this process, such as the role of cellular compartments and the inclusion of other feedback loops present in the system, were not fully addressed, model building requires successive iterations to capture the ever growing and sometimes confusing body of experimental facts. Efforts such as the one presented here will play important roles in the synthesis of existing data, the elucidation of what is dynamically relevant in this system, and the generation of hypotheses for further experimentation.
Supplementary Material
Acknowledgments
We thank Gyan Bhanot and Yuhai Tu for many fruitful discussions.
Author contributions: L.M., J.W., J.J.R., W.H., A.J.L., and G.A.S. designed research; L.M., J.W., J.J.R., W.H., A.J.L., and G.A.S. performed research; L.M., J.W., J.J.R., and G.A.S. analyzed data; and L.M., J.W., J.J.R., and G.A.S. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: IR, ionizing radiation; DSB, double-strand break; DSBC, DSB in complex with repair proteins; ATM, ataxia telangectasia mutated; ATM*, active ATM; PS, parameter stochasticity; p53*, active p53; CCT, critical crossing time.
References
- 1.Clarke, A. R., Purdie, C. A., Harrison, D. J., Morris, R. G., Bird, C. C., Hooper, M. L. & Wyllie, A. H. (1993) Nature 362, 849-852. [DOI] [PubMed] [Google Scholar]
- 2.Wahl, G. M., Linke, S. P., Paulson, T. G. & Huang, L. C. (1997) Cancer Surv. 29, 183-219. [PubMed] [Google Scholar]
- 3.el-Deiry, W. S. (1998) Semin. Cancer Biol. 8, 345-357. [DOI] [PubMed] [Google Scholar]
- 4.Lane, D. P. (1992) Nature 358, 15-16. [DOI] [PubMed] [Google Scholar]
- 5.Lev Bar-Or, R., Maya, R., Segel, L. A., Alon, U., Levine, A. J. & Oren, M. (2000) Proc. Natl. Acad. Sci. USA 97, 11250-11255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lahav, G., Rosenfeld, N., Sigal, A., Geva-Zatorsky, N., Levine, A. J., Elowitz, M. B. & Alon, U. (2004) Nat. Genet. 36, 147-150. [DOI] [PubMed] [Google Scholar]
- 7.Mihalas, G. I., Simon, Z., Balea, G. & Popa, E. (2000) J. Biol. Syst. 8, 21-29. [Google Scholar]
- 8.Monk, N. A. (2003) Curr. Biol. 13, 1409-1413. [DOI] [PubMed] [Google Scholar]
- 9.Marples, B., Wouters, B. G., Collis, S. J., Chalmers, A. J. & Joiner, M. C. (2004) Radiat. Res. 161, 247-255. [DOI] [PubMed] [Google Scholar]
- 10.Bonner, W. M. (2003) Proc. Natl. Acad. Sci. USA 100, 4973-4975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bakkenist, C. J. & Kastan, M. B. (2003) Nature 421, 499-506. [DOI] [PubMed] [Google Scholar]
- 12.Canman, C. E. & Lim, D. S. (1998) Oncogene 17, 3301-3308. [DOI] [PubMed] [Google Scholar]
- 13.Wagner, J., Ma, L., Rice, J. J., Hu, W., Levine, A. J. & Stolovitzky, G. (2005) J. Syst. Biol., in press. [DOI] [PubMed]
- 14.Ward, J. F. (1990) Int. J. Radiat. Biol. 57, 1141-1150. [DOI] [PubMed] [Google Scholar]
- 15.Haber, J. E. (1999) Trends Biochem. Sci. 24, 271-275. [DOI] [PubMed] [Google Scholar]
- 16.Yamaguchi-Iwai, Y., Sonoda, E., Sasaki, M. S., Morrison, C., Haraguchi, T., Hiraoka, Y., Yamashita, Y. M., Yagi, T., Takata, M., Price, C., et al. (1999) EMBO J. 18, 6619-6629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Frankenberg-Schwager, M. (1989) Radiother. Oncol. 14, 307-320. [DOI] [PubMed] [Google Scholar]
- 18.Nunez, M. I., Villalobos, M., Olea, N., Valenzuela, M. T., Pedraza, V., McMillan, T. J. & Ruiz de Almodovar, J. M. (1995) Br. J. Cancer 71, 311-316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stewart, R. D. (2001) Radiat. Res. 156, 365-378. [DOI] [PubMed] [Google Scholar]
- 20.Guerrero, M., Stewart, R. D., Wang, J. Z. & Li, X. A. (2002) Phys. Med. Biol. 47, 3197-3209. [DOI] [PubMed] [Google Scholar]
- 21.Rief, N. & Lobrich, M. (2002) J. Biol. Chem. 277, 20572-20582. [DOI] [PubMed] [Google Scholar]
- 22.Pandita, T. K., Lieberman, H. B., Lim, D. S., Dhar, S., Zheng, W., Taya, Y. & Kastan, M. B. (2000) Oncogene 19, 1386-1391. [DOI] [PubMed] [Google Scholar]
- 23.Andegeko, Y., Moyal, L., Mittelman, L., Tsarfaty, I., Shiloh, Y. & Rotman, G. (2001) J. Biol. Chem. 276, 38224-38230. [DOI] [PubMed] [Google Scholar]
- 24.Rouse, J. & Jackson, S. P. (2002) Science 297, 547-551. [DOI] [PubMed] [Google Scholar]
- 25.Bakkenist, C. J. & Kastan, M. B. (2004) Cell 118, 9-17. [DOI] [PubMed] [Google Scholar]
- 26.Uziel, T., Lerenthal, Y., Moyal, L., Andegeko, Y., Mittelman, L. & Shiloh, Y. (2003) EMBO J. 22, 5612-5621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mochan, T. A., Venere, M., DiTullio, R. A., Jr., & Halazonetis, T. D. (2003) Cancer Res. 63, 8586-8591. [PubMed] [Google Scholar]
- 28.Momand, J., Zambetti, G. P., Olson, D. C., George, D. & Levine, A. J. (1992) Cell 69, 1237-1245. [DOI] [PubMed] [Google Scholar]
- 29.Chen, J., Wu, X., Lin, J. & Levine, A. J. (1996) Mol. Cell. Biol. 16, 2445-2452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Prives, C. (1998) Cell 95, 5-8. [DOI] [PubMed] [Google Scholar]
- 31.Freedman, D. A. & Levine, A. J. (1999) Cancer Res. 59, 1-7. [PubMed] [Google Scholar]
- 32.Moll, U. M. & Petrenko, O. (2003) Mol. Cancer Res. 1, 1001-1008. [PubMed] [Google Scholar]
- 33.Banin, S., Moyal, L., Shieh, S., Taya, Y., Anderson, C. W., Chessa, L., Smorodinsky, N. I., Prives, C., Reiss, Y., Shiloh, Y. & Ziv, Y. (1998) Science 281, 1674-1677. [DOI] [PubMed] [Google Scholar]
- 34.Canman, C. E., Lim, D. S., Cimprich, K. A., Taya, Y., Tamai, K., Sakaguchi, K., Appella, E., Kastan, M. B. & Siliciano, J. D. (1998) Science 281, 1677-1679. [DOI] [PubMed] [Google Scholar]
- 35.Li, M., Brooks, C. L., Wu-Baer, F., Chen, D., Baer, R. & Gu, W. (2003) Science 302, 1972-1975. [DOI] [PubMed] [Google Scholar]
- 36.Stommel, J. M. & Wahl, G. M. (2004) EMBO J. 23, 1547-1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lobrich, M., Ikpeme, S. & Kiefer, J. (1994) Radiat. Res. 138, 186-192. [PubMed] [Google Scholar]
- 38.Lobrich, M., Rydberg, B. & Cooper, P. K. (1995) Proc. Natl. Acad. Sci. USA 92, 12050-12054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rothkamm, K. & Lobrich, M. (2003) Proc. Natl. Acad. Sci. USA 100, 5057-5062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Raser, J. M. & O'Shea, E. K. (2004) Science 304, 1811-1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Blake, W. J., Kaern, M., Cantor, C. R. & Collins, J. J. (2003) Nature 422, 633-637. [DOI] [PubMed] [Google Scholar]
- 42.Bond, G. L., Hu, W., Bond, E. E., Robins, H., Lutzker, S. G., Arva, N. C., Bargonetti, J., Bartel, F., Taubert, H., Wuerl, P., et al. (2004) Cell 119, 591-602. [DOI] [PubMed] [Google Scholar]
- 43.Tyson, J. J. (2004) Nat. Genet. 36, 113-114. [DOI] [PubMed] [Google Scholar]
- 44.Ciliberto, A., Novak, B. & Tyson, J. J. (2005) Cell Cycle 4, 488-493. [DOI] [PubMed] [Google Scholar]
- 45.Monod, J., Wyman, J. & Changeaux, J.-P. (1965) J. Mol. Biol. 12, 88-118. [DOI] [PubMed] [Google Scholar]
- 46.Vogelstein, B., Lane, D. & Levine, A. J. (2000) Nature 408, 307-310. [DOI] [PubMed] [Google Scholar]
- 47.Prives, C. & Hall, P. A. (1999) J. Pathol. 187, 112-126. [DOI] [PubMed] [Google Scholar]
- 48.Shirangi, T. R., Zaika, A. & Moll, U. M. (2002) FASEB J. 16, 420-422. [DOI] [PubMed] [Google Scholar]
- 49.Joseph, T. W., Zaika, A. & Moll, U. M. (2003) FASEB J. 17, 1622-1630. [DOI] [PubMed] [Google Scholar]
- 50.Fiscella, M., Zhang, H., Fan, S., Sakaguchi, K., Shen, S., Mercer, W. E., Vande Woude, G. F., O'Connor, P. M. & Appella, E. (1997) Proc. Natl. Acad. Sci. USA 94, 6048-6053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ohtsuka, T., Jensen, M. R., Kim, H. G., Kim, K. T. & Lee, S. W. (2004) Oncogene 23, 5405-5408. [DOI] [PubMed] [Google Scholar]
- 52.Sui, G., Affar el, B., Shi, Y., Brignone, C., Wall, N. R., Yin, P., Donohoe, M., Luke, M. P., Calvo, D., Grossman, S. R. & Shi, Y. (2004) Cell 117, 859-872. [DOI] [PubMed] [Google Scholar]
- 53.Honda, R. & Yasuda, H. (1999) EMBO J. 18, 22-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jin, S. & Levine, A. J. (2001) J. Cell Sci. 114, 4139-4140. [DOI] [PubMed] [Google Scholar]
- 55.Hoffmann, A., Levchenko, A., Scott, M. L. & Baltimore, D. (2002) Science 298, 1241-1245. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.