Abstract
The folding mechanisms of proteins are increasingly being probed through single-molecule experiments in which the protein is immobilized on a surface. Nevertheless, a clear understanding of how the surface might affect folding, and whether or not it changes folding from its bulk behavior, is lacking. In this work, we use molecular dynamics simulations of a model β-barrel protein tethered to a surface to systematically investigate how the surface impacts folding. In the bulk, this protein folds in a three-state manner through a compact intermediate state, and its transition state (TS) has a well formed hydrophobic core. Upon tethering, we find that folding rates and stability are impacted differently by the surface, with dependencies on both the length and location of the tether. Significant changes in folding times are observed for tether points that do not alter the folding temperature. Tethering also locally enhances the formation of structure for residues proximal to the tether point. We find that neither the folding mechanism nor the TS of this protein are altered if the tether is in a fully structured or completely unstructured region of the TS. By contrast, tethering in a partially structured region of the TS leads to dramatic changes. For one such tether point, the intermediate present in bulk folding is eliminated, leading to a two-state folding process with a heterogeneous, highly unstructured TS ensemble. These results have implications for both the design of single-molecule experiments and biotechnological applications of tethered proteins.
Keywords: molecular dynamics simulations, protein–surface interactions, single-molecule spectroscopy
Single-molecule spectroscopy has recently emerged as a powerful technique for watching individual proteins fold (1–3). By attaching donor and acceptor dyes to key residues of a protein, fluorescence resonance energy transfer (FRET), already successful in ensemble folding experiments (4), can be used as a distance probe to monitor individual folding pathways. There are several different experimental techniques for doing FRET-based single-molecule experiments on proteins, each with distinct advantages and challenges. Bulk experiments use a focusing laser beam that monitors folding as proteins diffuse freely through the area illuminated by the laser (5, 6). Although this approach is advantageous in that the protein is allowed to fold in a relatively nondisrupted manner, solution experiments are diffusion limited and cannot examine slower (≳10 ms) phenomena (2). Proteins enclosed in surface-tethered vesicles allow observations on a more spatially localized scale than the bulk but do not allow for the rapid exchange of buffer conditions or the use of extreme denaturing environments (7). By immobilizing them directly on a surface (8), proteins can be observed in both a spatially localized region and over longer time scales than those accessible in diffusion-limited experiments. Despite these advantages, the folding behavior of surface-tethered proteins also may be influenced by the surface itself, leading to behavior that differs from the bulk. It seems that an optimal experimental situation would allow for surface-tethered proteins whose folding is unchanged by the surface; however, there are several practical considerations to realizing this situation.
In surface-tethered folding studies, the surfaces in question must be chemically inert so that nonspecific protein adsorption is reduced. Additionally, they must have a negligible impact on the dynamics of the attached proteins. Nienhaus and coworkers (9, 10) have developed and analyzed several types of surfaces, deemed minimally interacting, for the explicit purpose of performing experiments on individually tethered biomolecules. In particular, they have designed a star-shaped polyethylene glycol (PEG) surface that allows for the reversible folding and unfolding of attached proteins (10, 11). Other groups have performed single-molecule experiments of biomolecules on a variety of surfaces, including BSA (12–14). In addition to the composition of the surface, another key point of consideration is how the protein is attached to the surface. To date, there are several different means for immobilizing proteins on surfaces. These methods include biotin–streptavidin linkers (10), nonspecific electrostatic interactions (8), immobilization via a hexahistidine tag (15), and nonspecific adsorption (16). Each of these attachment schemes leaves the immobilized biomolecule at a different height above the surface.
In the development of the chemically inert surfaces detailed above, researchers have taken care to ascertain that the stability and function of attached proteins are retained (10, 12). However, it is not obvious that retaining protein function guarantees that folding is unchanged by tethering. Tethering also may affect rates and mechanisms of folding, but there have been no systematic studies of these effects. Additionally, an understanding of how linker length or tether location (N vs. C terminus, for example) might influence folding is lacking.
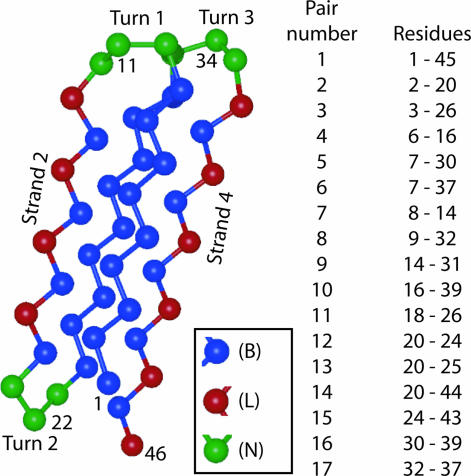
Molecular dynamics simulations of proteins are ideally suited for a detailed investigation of how surfaces impact the folding behavior of immobilized peptides. Although there has been a great deal of theoretical and computational work on the subject of protein–surface interactions and nonspecific adsorption in particular (17–21), there has been significantly less attention devoted to understanding precisely how surfaces impact immobilized peptides (22, 23). In this work, we use molecular dynamics simulations to investigate how tethering impacts the folding of a model protein. Our protein model is a small, 46-monomer Gō-type variant of the Honeycutt Thirumalai β-barrel protein model, depicted in Fig. 1. We emulate tethering by fixing one residue of the protein at a tethering height (ht) above a purely repulsive surface. By tethering the protein to the surface at five different residues (labeled in Fig. 1), we are able to systematically investigate the way in which tethering impacts the kinetics and folding mechanism of this model protein.
Fig. 1.
Protein model. (Left) A cartoon of the four-stranded β-barrel model used in this study. Each amino acid is represented by a single bead of diameter σ. The tether points, residues 1, 11, 22, 34, and 46, are on the outside of the native structure of the protein and are labeled, along with strands 2 and 4. (Right) A list of the representative contact pairs used to examine the folding mechanism through Pform. A list of native contacts for this protein is given in Table 2, which is published as supporting information on the PNAS web site.
Results
Tethering Alters Thermodynamic Stability and Protein Folding Rates.
It has been established (24) that the variant of the β-barrel protein used in this study has distinct collapse (Tc) and folding (Tf) temperatures. This finding indicates that folding proceeds in a non-two-state manner: first, the protein collapses to a compact but nonnative structure and subsequently rearranges to find its native state. In Table 1, the collapse and folding temperatures for each tether point, in addition to the bulk transition temperatures, are listed. For every tether point at ht = σ, with the exception of residue 34, Tf and Tc remain distinct, indicating that folding continues to proceed through an intermediate upon surface tethering. Conversely, the fact that Tf = Tc for tether point 34 is indicative of a two-state folding process and is a first indication that tethering has altered the folding mechanism.
Table 1.
Average folding times and thermodynamic transition temperatures
| Tether point | Height | Tc | Tf | τave |
|
|---|---|---|---|---|---|
| T = Tf | T = 0.480 | ||||
| Bulk | N/A | 0.600 | 0.523 | 3,383 ± 127 | 2,729 ± 93 |
| 1 | σ | 0.583 | 0.488 | 9,536 ± 309 | 9,022 ± 209 |
| 11 | σ | 0.600 | 0.557 | 3,768 ± 152 | 2,657 ± 101 |
| 22 | σ | 0.625 | 0.514 | 3,227 ± 130 | 2,829 ± 110 |
| 34 | σ | 0.591 | 0.591 | 6,154 ± 289 | 3,232 ± 146 |
| 46 | σ | 0.600 | 0.523 | 5,562 ± 214 | 5,313 ± 209 |
Average folding times and transition temperatures for the bulk protein and for tether points 1, 11, 22, 34, and 46. τave = (1/M) τ1i, and τ1i is the first passage time to the native state (χ ≥ 0.9) for the ith folding trajectory. All times are reported in units of τ, and all temperatures are given in units of εh/kB. Error estimates are given by σ/ (25), where σ2 = 〈τ2〉 − 〈τ〉2 and N = 400, the total number of folding times.
Further evidence of two-state folding vs. folding with an intermediate can be obtained by looking at a plot of a protein’s unfolded population [Pv(t)] as a function of time (26). A protein that folds in a two-state manner will have an exponential Pv(t) curve, indicating a single rate constant for folding. Proteins that fold via an intermediate have distinctly nonexponential Pv(t) curves. Here, the bulk β-barrel protein and tether points 1, 11, 22, and 46 at ht = σ have Pv(t) curves that are nonexponential, whereas tether point 34 at ht = σ has an exponential Pv(t) curve. Representative Pv(t) curves are shown in Fig. 5, which is published as supporting information on the PNAS web site.
In Table 1, we list the average folding times (τave) for each tether point, as well as the average bulk folding time. Like the thermodynamic transition temperatures, average folding times are highly dependent on where the protein is tethered. At a tethering height of σ and at their respective folding temperatures, residues 11 and 22 have similar average folding times to the bulk, whereas residues 1, 34, and 46 take significantly longer to fold. At a fixed temperature T that is lower than all values of Tf, we find that stability and folding times are not correlated. Tethering at residues 1 and 22 destabilizes the native state, but only tether point 1 leads to an increase in folding times. Additionally, tethering at residue 46 does not change either Tc or Tf, but the protein’s average folding time is significantly increased.
Tethering Changes the Folding Mechanism.
To examine the folding mechanism of this β-barrel protein and how it is affected by tethering, we consider the probability of contact formation as a function of time (designated Pform and defined in Model and Methods). We begin with the bulk case, which will give us a reference point for better understanding tethering effects. All of the discussion below is based on the plots shown in Fig. 2, which were generated at the respective folding temperatures for the bulk and tethered proteins at ht = σ. Similar conclusions were reached for T < Tf.
Fig. 2.
Probability of contact formation (Pform) for the β-barrel protein in the absence of a surface and for all tether points at ht = σ. The numbers on the x-axes correspond to the contact pair numbers listed in the first column of the table in Fig. 1. Normalized folding times are shown on the y-axes. The turns are labeled on the bulk folding map, and the contact pair closest to the tether point is labeled in each of the other maps. Tether points 1 and 46 are both closest to pair 1, which is between residues 1 and 45. In every map except for the one corresponding to tether point 34, the order of contact formation is the same for the bulk, whereas tethering at residue 34 significantly alters the folding mechanism.
The bulk Pform map indicates that folding proceeds in several steps. After the formation of turn 2, there is a quick hydrophobic collapse where the protein reaches a state with strands 1 and 3 in native or near-native position. The formation of turn 1 and native contacts between strand 2 and strands 1 and 3 occurs shortly thereafter. During most of the folding process, strand 4 remains away from the main body of the protein structure. The β-barrel remains in this intermediate state (3 strands in near native formation with the 4th strand out) until turn 3 commits to folding, at which point the 4th strand folds in, and the protein finds its native state.
To understand how tethering impacts the folding mechanism, we begin by examining tether points 1 and 46, the protein’s termini. The Pform plots shown in Fig. 2 indicate that tethering at either terminus results in contact formation that happens in the same order as the bulk, but certain pairs of contacts (for example, around turn 2) form earlier and are more stable sooner in the folding process. This result is particularly interesting in light of the fact that τave > τavebulk for both tether points at Tf and T < Tf. Although it takes longer for the protein to fold, many contact pairs are stable earlier in the folding process. This finding implies that early contact formation and stabilization of the protein’s core, combined with the restriction of tethering, prevents the mobility needed for the correct contacts to form later in the folding process, thus resulting in longer folding times. In essence, the protein becomes “trapped,” an effect that results from the tether.
We now focus our attention on the turn regions of the protein: tether points 11, 22, and 34. For tether points 11 and 22, contact formation again proceeds in the same order as the bulk, and we also observe stabilization and early formation of contact pairs around the tether point. Although tethering at residue 11 causes most contacts to form slightly later in the folding process than they would in the bulk, the formation of contact pair 7 (in the region of the tether) happens slightly earlier than in the bulk, indicating an increase in stability relative to other contacts. For tether point 22, the contacts around turn 2 form almost immediately in the folding process, which subsequently accelerates the formation of other contact pairs. Folding times for these two tether points are very close to τavebulk, implying that the protein does not get trapped as it does for tethering at the termini. This result indicates that there is an interplay between early contact formation and the location of the tether that determines folding times.
Finally, we look at tether point 34. Unlike the other tether points examined, contact formation does not happen in the same order as it does in bulk folding. Additionally, most contact formation does not occur until very late in folding, with the exception of turns 2 and 3. Although both turns have reasonably low values of Pform until the late stages of folding, the value of Pform for turn 3 is higher for most of the folding process than all of the other contact pairs with the exception of turn 2. Again, we see evidence that tethering stabilizes and accelerates contact formation in the vicinity of the tether.
Pfold Analysis: Tethering Alters the Transition State (TS) of Folding.
Identifying a protein’s TS can provide crucial insight into its folding mechanism. The TS ensemble (TSE) is difficult to determine both experimentally and computationally (27, 28). Experimentally, φ-value analysis is used to infer the structure of the TSE (29). With respect to computation, there are many methods (30–35) for identifying protein folding TS. In this work, we identified putative TS structures based on free energy surfaces for this protein and subsequently used probability of folding (Pfold) analysis to refine our choice of TS structures (36). The Pfold value for a given structure measures whether or not it will fold before unfolding.
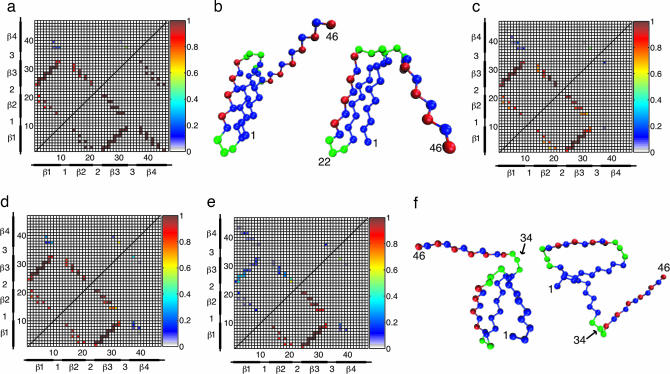
Native contact maps for the TSE of both the bulk and tethered proteins are shown in Fig. 3. The native contact map for the TSE of the bulk β-barrel protein is shown in the upper quadrant of Fig. 3a. For comparison, the native contact map of the protein’s native state is shown is the lower quadrant of Fig. 3a. This protein has a highly structured TS; because it undergoes a distinct collapse before folding, folding proceeds at Tf from a compact state with residual structure rather than a fully extended one. In the bulk TS, all of the native contacts between strands 1 and 3 have an extremely high probability of formation (Pform), indicating a well formed hydrophobic core. The contacts between strands 1 and 2 and strands 2 and 3 are also well formed, including the native contacts around turn 1. By contrast, turn 3 has only a 50% chance of formation in the TS, resulting in unformed contact pairs between strand 4 and strands 1, 2, and 3. In conjunction with the bulk Pform plot in Fig. 3, these results indicate that the TS for folding of this β-barrel protein occurs near the end of the folding process. An example bulk TS structure is shown in Fig. 3b Left.
Fig. 3.
TS native contact maps and representative structures. (a) Native contact map for the bulk TS (upper quadrant). The native contact map for the native state is shown in the lower quadrant for comparison. (b) Representative TS structures for the bulk (Left) and tether point 22 (Right). The structures are very similar, with well formed hydrophobic cores. (c and d) TS native contact maps for tether points 1 (c, upper quadrant), 11 (c, lower quadrant), 22 (d, upper quadrant), and 46 (d, lower quadrant). The native contact maps for these tether points are qualitatively similar to each other and the bulk TS. In this respect, the structures shown in b are representative TS structures for all tether points except 34. (e) TS native contact map for tether point 34 (upper quadrant) with the bulk TS map (lower quadrant) shown for comparison. (f) Two representative TS structures for this tether point. In contrast to the other tether points and the bulk, tether point 34 has a highly unstructured TS. Moreover, whereas the TS structures for the bulk and other tether points are relatively homogeneous, the TS for tether point 34 has a significant amount of structural diversity, as evidenced in part by the example structures shown in f.
The native contact maps for tether points 1, 11, 22, and 46, shown in Fig. 3 c and d, are similar to the bulk contact map. The TS for all of these tether points includes a well formed hydrophobic core, with the probability of contact formation between strands 1 and 3 as high as for the bulk protein. Well formed contacts (probabilities ≥ 0.6) also exist between strands 1 and 2 and strands 2 and 3. There are other minor differences present between these contact maps and the map for the bulk TS, but in general, the TSE for tether points 1, 11, 22, and 46 is similar to that of the bulk, with only slight local distortions due to the presence of the tether. A representative TS structure for tether point 22 is shown in Fig. 3b Right.
Unlike all of the other tether points considered, tether point 34 has a TSE that is significantly different from that of the bulk. The native contact map shown in Fig. 3e indicates a highly unstructured TSE. Native contacts in the hydrophobic core, a region well formed in the bulk TSE, have a low Pform (0.1–0.4) for tethering at residue 34. Of those contacts, the ones with the highest Pform are in the vicinity of turn 2, which forms first in the folding process. Two representative TS for tether point 34 are shown in Fig. 3f. These structures are markedly different from the examples shown in Fig. 3b. In addition to being relatively unstructured, the two conformations shown are significantly different from each other, indicating a structural diversity in the TS that is not present in the bulk. This heterogeneous, unstructured TS is a further reflection of the mechanism change induced by tethering at residue 34, and a schematic of this change is presented in Fig. 4.
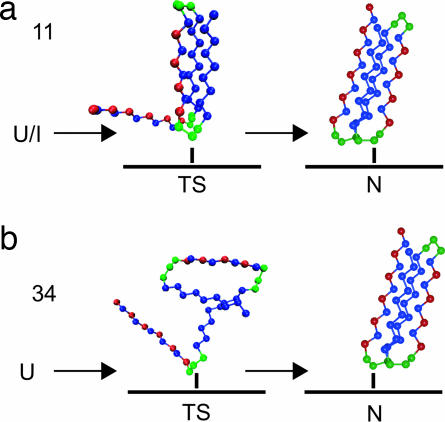
Fig. 4.
A cartoon of the folding process for tether points 11 (a) and 34 (b) at their respective folding temperatures. For tether point 11, U/I is designated as a starting point for the folding process to indicate that at Tf, the protein proceeds to its native state from a compact intermediate state. In contrast, when tethered at residue 34, the protein does not fold through an intermediate. The difference in the TS for these two tether points is also illustrated. Although tether point 11 has a compact, bulk-like TS with a well formed core, tether point 34 folds through a highly unstructured TS that is significantly different from that of the bulk.
Increasing ht Shifts Folding Back Toward Bulk-Like Behavior.
Our discussion of tethering has heretofore focused on tethering at a single height, ht = σ, above the surface. A pertinent question is how the behavior of the protein changes with increasing ht, which is analogous to increasing the length of the linker in an experimental situation. To examine this scenario, we performed simulations with tether points 1, 22, and 34 at ht = 2σ and 5σ. A table of thermodynamic transition temperatures and folding times, as well as Pform plots for these simulations, can be found in Table 3 and Fig. 6, which are published as supporting information on the PNAS web site.
For each of these three tether points, as ht is increased, folding tends toward its bulk behavior; however, the extent to which behavior is altered depends on the location of the tether. For tether point 1 at both ht = 2σ and 5σ, Pform is virtually indistinguishable from the bulk, and at ht = 5σ, Tf = TfB, the bulk folding temperature. Nevertheless, at both of these values of ht the protein still takes significantly longer to fold than in the bulk. Conversely, for tether point 22, stabilization of certain contacts persists at ht = 2σ and 5σ, with little to no impact on either the average folding time or Tf. These results further indicate that even if a tethered protein has thermodynamic stability that is equivalent to the bulk, the surface can still impact the protein’s behavior, either through increased folding times or local contact stabilization.
For tether point 34, the folding mechanism at ht = 2σ is similar to the mechanism at σ, with most contacts forming late in the folding process. Nevertheless, turn 3 is less stabilized than when the protein is tethered at a height of σ, so the overall order of contact formation shifts back toward that of the bulk. Additionally, the collapse and folding temperatures are no longer concurrent for higher values of ht. We performed a Pfold analysis for tether point 34 at ht = 2σ and found TS structures very similar to the ones shown in Fig. 3b. Evidently, only a small increase in linker length is enough to allow folding to proceed in a much more bulk-like fashion, indicating the critical importance of linker length in folding behavior.
Discussion and Conclusions
Surface-immobilized proteins are increasingly being used for the performance of single-molecule experiments. There are several different methods used to immobilize proteins on surfaces, with different types of linkers leaving the protein at varying heights above the surface. Nevertheless, a clear understanding of how a surface might impact the folding behavior of immobilized proteins is lacking. In this work, we used molecular dynamics simulations of a minimalist β-barrel protein to systematically explore how varying the location of the attachment point impacts folding.
One of the most significant results of this work is that tethering can profoundly alter a protein’s folding mechanism and TS. By tethering the protein at residue 34 at ht = σ, its folding mechanism shifts from three-state to a two-state, and its TSE becomes heterogeneous and highly unstructured. In general, we observe that tethering locally enhances contact formation. With respect to the TSE, this effect will result in more significant changes in regions of the protein that are only partially formed. Residue 34 is in a partially structured region of the protein’s bulk TS; as such, tethering there dramatically alters the mechanism of folding. By contrast, if one tethers in a fully structured region of the TS (residues 1, 11, 22) or an area that is completely unstructured (residue 46), small, local changes to folding will occur (along with changes in folding times and temperature), but the overall order of contact formation, and thus the folding mechanism, is not expected to change.
A second conclusion of our work is that tethering in similar structural regions of a protein, turn regions for example, does not necessarily result in the same behavior. In the β-barrel model studied here, tethering in each of the three turn regions (residues 11, 22, and 34) results in distinct behavior, with tether point 34 experiencing a particularly drastic shift away from bulk folding. Nevertheless, attachment at all of these points stabilizes the contacts proximal to them, indicating that tethering can be used as a means to expedite local contact formation in key structural regions of a protein. Although the specific response to tethering observed for each of these attachment points is unique to the model studied, the lack of parity observed among similar structural motifs has the potential to occur for many different proteins.
In addition to demonstrating that choosing tether locations carefully is critical, we have shown that recovering thermodynamic stability is not sufficient to conclude that a surface has an entirely negligible impact on folding. For example, when residue 46 is tethered at ht = σ, thermodynamic transition temperatures are identical to the bulk, and the overall folding mechanism remains unchanged. Nevertheless, τave > τavebulk, illustrating that thermodynamics and kinetics respond to tethering in an uncorrelated fashion.
Although most of our analysis focused on a relatively short linker (ht = σ), we found that by increasing ht, protein behavior was universally shifted in the direction of the bulk, regardless of tether location. In particular, the dramatic shift in behavior that occurs for tether point 34 is absent for a linker length of 5σ. This evidence can be used to inform the location of the tether in experimental situations. With a long enough linker, any residue on the outside of the folded structure may be used as a tether point, and the bulk folding mechanism will be recovered. Another way to minimize the impact of the surface is to make use of φ-value analysis to select the location of the tether, because our simulations suggest that tethering in a fully structured region of the TS will minimally impact folding, even with a short linker. Conversely, by using a short linker or tethering in a partially structured region of a protein’s TSE, although not appropriate for single-molecule studies, can be used to intentionally alter protein folding mechanisms. Hence, tethering can potentially be used as a powerful tool in the development of bioengineering applications, such as biosensors and related microarray technologies (17, 37).
Model and Methods
The model protein used in this study is a Gō variant (38, 39) of the Honeycutt Thirumalai β-barrel protein model. In this 46-monomer protein, each amino acid is modeled as a single bead that is hydrophobic (B), hydrophilic (L), or neutral (N). Its sequence is B9N3(LB)4N3B9N3(LB)5L, and details of its Hamiltonian can be found elsewhere (24, 30, 40–45). Although there are several Gō-type variants of this model (24, 30, 43, 44), we used the one explicitly described in ref. 24. A cartoon of this protein is shown in Fig. 1.
The surface used in this study is a purely repulsive, short-ranged, minimally interacting surface located in the x-y plane. The total protein–surface interaction potential is given by Vsurface = Σi[(4πεh)/5](σ/zi)10. Here zi is the z coordinate of the ith residue; εh is an energetic parameter equivalent to the value of εh in the Lennard–Jones potential that models the attractive interactions between BB residues; and σ is the diameter of each monomer in the protein as well as the equilibrium length of the bonds between each monomer. To emulate tethering, we fixed one residue (1, 22, 22, 34, or 46) at a tethering height (ht) of σ, 2σ, or 5σ above the surface. Different values of ht correspond to different linker lengths. Further details about our simulation methods can be found in Supporting Text, which is published as supporting information on the PNAS web site. To examine the protein’s folding mechanism, we constructed the probability of contact formation Pform for various key pairs of residues. The set of representative contacts chosen for the calculation of Pform is listed in Fig. 1. The pairs are distributed throughout the protein, and with the exception of pairs 10 and 14, all contact pairs are native contacts. To compute the Pform for a given contact pair at any point during the folding process, we used a procedure that is similar in nature to analysis done by Klimov and Thirumalai (46). For each contact pair ij, the cutoff distance for formation was set to rij0 + ε. ε is a parameter defined in the calculation of χ, the reaction coordinate used in this study. (χ is explicitly defined in Supporting Text.)
To average over 400 simulations (the total number performed for each tether point at a given temperature), each having a different value of τ1i, we first normalized each trajectory by its value of τ1i. After doing this, folding for each trajectory started at time 0 and ends at time 1. We then found Pform for each contact pair listed in Fig. 1 by averaging over all 400 structures at 100 different times δ, where 0 ≤ δ≤ 1. Thus, although the actual time step corresponding to a particular value of δ is different for each trajectory, it happens at the same relative time in the folding process.
To locate structures in the TSE, we performed Pfold analysis as described in Supporting Text. Once TS structures were selected in this way, we calculated the probability of native contact formation in the TSE for each tether point and for bulk folding. For a given TS structure, the distance between each native contact pair was calculated, and if |rij − rij0| < ε, then the contact was designated as formed for that particular structure. These are the same cutoff criteria used in our Pform analysis. Distances between all pairs in all structures for a given TSE were calculated and averaged over.
Supplementary Material
Acknowledgments
We thank Gilad Haran and Guy Ziv for helpful discussions. This work was supported by National Science Foundation (NSF) CAREER Award 0133504 (to J.-E.S.), a NSF Graduate Research Fellowship (to M.F.), the A. P. Sloan Research Foundation, the David and Lucille Packard Foundation, and U.S. Army Research Office Institute for Collaborative Biotechnologies Grant DAAD19-03-D-0004. Simulations were performed in part by using the computational resources of the California Nanosystems Institute (supported by NSF Grant CHE-0321368).
Abbreviations
- TS
transition state
- TSE
TS ensemble
- Pform
probability of formation
- Pfold
probability of folding.
Footnotes
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office. J.R.W. is a guest editor invited by the Editorial Board.
References
- 1.Schuler B. ChemPhysChem. 2005;6:1206–1220. doi: 10.1002/cphc.200400609. [DOI] [PubMed] [Google Scholar]
- 2.Rasnik I., McKinney S. A., Ha T. Acc. Chem. Res. 2005;38:542–548. doi: 10.1021/ar040138c. [DOI] [PubMed] [Google Scholar]
- 3.Leite V. B. P., Onuchic J. N., Stell G., Wang J. Biophys. J. 2004;87:3633–3641. doi: 10.1529/biophysj.104.046243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pletneva E. V., Gray H. B., Winkler J. R. Proc. Natl. Acad. Sci. USA. 2005;102:18397–18402. doi: 10.1073/pnas.0509076102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Deniz A. A., Laurence T. A., Beligere G. S., Dahan M., Martin A. B., Chemla D. S., Dawson P. E., Schultz P. G., Weiss S. Proc. Natl. Acad. Sci. USA. 2000;97:5179–5184. doi: 10.1073/pnas.090104997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schuler B., Lipman E. A., Eaton W. A. Nature. 2002;419:743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 7.Rhoades E., Gussakovsky E., Haran G. Proc. Natl. Acad. Sci. USA. 2003;100:3197–3202. doi: 10.1073/pnas.2628068100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Talaga D. S., Lau W. L., Roder H., Tang J., Jia Y., DeGrado W. F., Hochstrasser R. M. Proc. Natl. Acad. Sci. USA. 2000;97:13021–13026. doi: 10.1073/pnas.97.24.13021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Groll J., Amirgoulova E. V., Ameringer T., Heyes C. D., Röcker C., Nienhaus G. U., Möller M. J. Am. Chem. Soc. 2004;126:4234–4239. doi: 10.1021/ja0318028. [DOI] [PubMed] [Google Scholar]
- 10.Amirgoulova E. V., Groll J., Heyes C. D., Ameringer T., Röcker C., Möller M., Nienhaus G. U. ChemPhysChem. 2004;5:552–555. doi: 10.1002/cphc.200400024. [DOI] [PubMed] [Google Scholar]
- 11.Kuzmenkina E. V., Heyes C. D., Nienhaus G. U. Proc. Natl. Acad. Sci. USA. 2005;102:15471–15476. doi: 10.1073/pnas.0507728102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhuang X., Bartley L. E., Babcock H. P., Russell R., Ha T., Herschlag D., Chu S. Science. 2000;288:2048–2051. doi: 10.1126/science.288.5473.2048. [DOI] [PubMed] [Google Scholar]
- 13.Forkey J. N., Quinlan M. E., Shaw M. A., Corrie J. E. T., Goldman Y. E. Nature. 2003;422:399–404. doi: 10.1038/nature01529. [DOI] [PubMed] [Google Scholar]
- 14.Rasnik I., Myong S., Cheng W., Lohman T. M., Ha T. J. Mol. Biol. 2004;336:395–408. doi: 10.1016/j.jmb.2003.12.031. [DOI] [PubMed] [Google Scholar]
- 15.Ha T., Ting A. Y., Liang J., Caldwell W. B., Deniz A. A., Chemla D. S., Schultz P. G., Weiss S. Proc. Natl. Acad. Sci. USA. 1999;96:893–898. doi: 10.1073/pnas.96.3.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wazawa T., Ishii Y., Funatsu T., Yanagida T. Biophys. J. 2000;78:1561–1569. doi: 10.1016/S0006-3495(00)76708-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gray J. J. Curr. Opin. Struct. Biol. 2004;14:110–115. doi: 10.1016/j.sbi.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 18.Carignano M. A., Szleifer I. Mol. Phys. 2002;18:2993–3003. [Google Scholar]
- 19.Tie Y., Calonder C., Van Tassel P. R. J. Colloid Interface Sci. 2003;268:1–11. doi: 10.1016/s0021-9797(03)00516-2. [DOI] [PubMed] [Google Scholar]
- 20.Raffaini G., Ganazzoli F. Langmuir. 2004;20:3371–3378. doi: 10.1021/la0357716. [DOI] [PubMed] [Google Scholar]
- 21.Zhou J., Tsao H.-K., Sheng Y.-J., Jiang S. J. Chem. Phys. 2004;121:1050–1057. doi: 10.1063/1.1757434. [DOI] [PubMed] [Google Scholar]
- 22.Knotts T. A., IV, Rathmore N., de Pablo J. J. Proteins Struct. Funct. Bioinform. 2005;61:385–397. doi: 10.1002/prot.20581. [DOI] [PubMed] [Google Scholar]
- 23.Shang J., Geva E. J. Phys. Chem. B. 2005;109:16340–16349. doi: 10.1021/jp052275c. [DOI] [PubMed] [Google Scholar]
- 24.Friedel M., Sheeler D. J., Shea J.-E. J. Chem. Phys. 2003;118:8106–8113. [Google Scholar]
- 25.Allen M. P., Tildesley D. J. Computer Simulation of Liquids. Oxford: Oxford Univ. Press; 1989. [Google Scholar]
- 26.Zhou Y., Zhang C., Stell G., Wang J. J. Am. Chem. Soc. 2003;125:6300–6305. doi: 10.1021/ja029855x. [DOI] [PubMed] [Google Scholar]
- 27.Oliveberg M. Curr. Opin. Struct. Biol. 2001;11:94–100. doi: 10.1016/s0959-440x(00)00171-8. [DOI] [PubMed] [Google Scholar]
- 28.Nymeyer H., Socci N. D., Onuchic J. N. Proc. Natl. Acad. Sci. USA. 2000;97:634–639. doi: 10.1073/pnas.97.2.634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fersht A. R., Matouscheck A., Serrano L. J. Mol. Biol. 1992;224:771–782. doi: 10.1016/0022-2836(92)90561-w. [DOI] [PubMed] [Google Scholar]
- 30.Shea J.-E., Onuchic J. N., Brooks C. L., III J. Chem. Phys. 2000;113:7663–7671. [Google Scholar]
- 31.Vendruscolo M., Paci E., Dobson C. M., Karplus M. Nature. 2001;409:641–645. doi: 10.1038/35054591. [DOI] [PubMed] [Google Scholar]
- 32.Hummer G. J. Chem. Phys. 2004;120:516–523. doi: 10.1063/1.1630572. [DOI] [PubMed] [Google Scholar]
- 33.Ding F., Guo W., Dokholyan N. V., Shakhnovich E. I., Shea J.-E. J. Mol. Biol. 2005;350:1035–1050. doi: 10.1016/j.jmb.2005.05.017. [DOI] [PubMed] [Google Scholar]
- 34.Cho S. S., Levy Y., Wolynes P. G. Proc. Natl. Acad. Sci. USA. 2006;103:586–591. doi: 10.1073/pnas.0509768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shea J.-E., Friedel M. R., Baumketner A. In: Reviews in Computational Chemistry. Lipkowitz K. B., Cundari T. R., Gillet V. J., editors. New York: Wiley–VCH; 2006. [Google Scholar]
- 36.Du R., Pande V. S., Grosberg A. Y., Tanaka T., Shakhnovich E. I. J. Chem. Phys. 1998;108:334–350. [Google Scholar]
- 37.Zhu H., Snyder M. Curr. Opin. Chem. Biol. 2003;7:55–63. doi: 10.1016/s1367-5931(02)00005-4. [DOI] [PubMed] [Google Scholar]
- 38.Gō N. Annu. Rev. Biophys. Bioeng. 1983;12:183–210. doi: 10.1146/annurev.bb.12.060183.001151. [DOI] [PubMed] [Google Scholar]
- 39.Kaya H., Liu Z., Chan H. S. Biophys. J. 2005;89:520–535. doi: 10.1529/biophysj.104.057471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Honeycutt J., Thirumalai D. Proc. Natl. Acad. Sci. USA. 1990;87:3526–3529. doi: 10.1073/pnas.87.9.3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Guo Z., Thirumalai D. Biopolymers. 1995;36:83–102. [Google Scholar]
- 42.Guo Z., Brooks C. L., III Biopolymers. 1997;42:745–757. doi: 10.1002/(sici)1097-0282(199712)42:7<745::aid-bip1>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 43.Nymeyer H., Garćia A. E., Onuchic J. N. Proc. Natl. Acad. Sci. USA. 1998;95:5921–5928. doi: 10.1073/pnas.95.11.5921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shea J.-E., Nochomovitz Y. D., Guo Z., Brooks C. L., III J. Chem. Phys. 1998;109:2895–2903. [Google Scholar]
- 45.Berry R. S., Elmaci N., Rose J. P., Vekhter B. Proc. Natl. Acad. Sci. USA. 1997;94:9520–9524. doi: 10.1073/pnas.94.18.9520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Klimov D. K., Thirumalai D. Proteins Struct. Funct. Genet. 2001;43:465–475. doi: 10.1002/prot.1058. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.