Protein Unfolding Behavior Studied by Elastic Network Model

Abstract

Experimental and theoretical studies have showed that the native-state topology conceals a wealth of information about protein folding/unfolding. In this study, a method based on the Gaussian network model (GNM) is developed to study some properties of protein unfolding and explore the role of topology in protein unfolding process. The GNM has been successful in predicting atomic fluctuations around an energy minimum. However, in the GNM, the normal mode description is linear and cannot be accurate in studying protein folding/unfolding, which has many local minima in the energy landscape. To describe the nonlinearity of the conformational changes during protein unfolding, a method based on the iterative use of normal mode calculation is proposed. The protein unfolding process is mimicked through breaking the native contacts between the residues one by one according to the fluctuations of the distance between them. With this approach, the unfolding processes of two proteins, CI2 and barnase, are simulated. It is found that the sequence of protein unfolding events revealed by this method is consistent with that obtained from thermal unfolding by molecular dynamics and Monte Carlo simulations. The results indicate that this method is effective in studying protein unfolding. In this method, only the native contacts are considered, which implies that the native topology may play an important role in the protein unfolding process. The simulation results also show that the unfolding pathway is robust against the introduction of some noise, or stochastic characters. Furthermore, several conformations selected from the unfolding process are studied to show that the denatured state does not behave as a random coil, but seems to have highly cooperative motions, which may help and promote the polypeptide chain to fold into the native state correctly and speedily.

INTRODUCTION

One of the open fundamental questions in molecular biology is how the protein folds into a three-dimensional structure from its one-dimensional sequence. Understanding the process of protein folding has been the subject of many theoretical and experimental studies (1–3). To date, monitoring the details of the protein folding process is beyond computational capabilities, since the timescale of protein folding is several orders-of-magnitude larger than that attainable by computer simulation. Many works focus on unfolding events at high temperature. It has been shown that the increase in temperature accelerates protein unfolding without changing the unfolding pathway (4). Furthermore, several works have demonstrated that the pathways of folding and unfolding are similar (5), thereby justifying the use of unfolding simulations to obtain useful information about protein folding.

Experimental and theoretical studies have showed that the native-state topology conceals a wealth of information about protein folding/unfolding. Protein-folding rates and mechanism are found to be largely determined by the native structure (6), and the naturally occurring proteins with similar folds but very different sequences are generally of similar folding rates (7). Protein folding free-energy landscapes can be mapped-out based on the native-state structures and have been used to predict the protein-folding mechanism (8). The process of protein unfolding can be simulated through breaking the hydrogen bonds and salt bridges one by one within the native structure according to their relative energy (9). Recently the folding process and elastic properties of proteins were studied with the topology-based approaches independent of the sequence specificity (10,11). A graph-based method has been used to identify the rigid and flexible regions in proteins, and to study the changing of flexibility during protein unfolding (9,12). Taken together, these results suggest that the native-state topology is a key point of protein folding/unfolding mechanisms.

In this study, we used a simple topology-based model called the Gaussian network model (GNM) to study the process of protein unfolding. GNM is a schematic, coarse-grained model which is topology-based and independent of sequence specificity (13,14). This model can provide the dynamic properties of proteins near an equilibrium state (usually native state). In this model, each residue is represented by its C_α atom, and the detailed interactions between residues to be in contact in the native state are replaced with springs. Several studies have indicated that such a simple treatment of the interactions in the native protein is sufficient to account for many experimental facts; for example, x-ray crystallographic B-factors (15,16), H/D exchange protection factors, or free energies of exchange (17), order parameters obtained from ¹⁵N-NMR relaxation (18), and so on. The GNM can provide information on conformational transition of proteins from the crystal structures and does not require the high computational cost of molecular dynamics (MD). This method has been proved in numerous application studies to be a simple yet useful tool for investigating the large-scale conformational motions, domain motions, and collective dynamics of the biomolecular systems (19–26). The GNM has also been used to find kinetically hot residues and folding cores of proteins (27,28). A method that combines MD and harmonic modes has been developed to study the protein unfolding and large-scale domain motions (29). Several previous studies proved that the results obtained with the GNM are in agreement with the MD simulation data (30,31).

Gaussian network model has been successful in predicting atomic fluctuations and in investigating large-scale conformational motions, but this model describes only the excitations around a single minimum. Clearly, this linear normal mode description cannot be completely accurate because of the considerable anharmonicity in protein dynamics. The limited adequacy of a normal mode description becomes even more apparent in studying protein folding/unfolding, which has many local minima in the energy landscape. A method to overcome this disadvantage is to update the modes of motions frequently based on new conformations during the folding/unfolding simulation, as adopted by Zhang et al. (29,32). In the work of Miyashita et al. (33), the nonlinearity of the protein conformational changes is described through an iterative use of normal mode calculation and they used this method to study functional transitions in proteins. In our work, a similar method is adopted. The nonlinearity of residues motions during protein unfolding is considered by iterative use of the GNM.

In this article, the process of protein unfolding was simulated through breaking the native contacts between the residues one by one according to the fluctuation of the distance between them. At first, the mean-square fluctuations of the distance in all residue pairs were calculated with the GNM based on the native structure topology. Next, the residue pair with the largest fluctuation was chosen and the contact between them was broken. The breaking of the contact will result in the change of the protein topology. Then the mean-square fluctuation of the distance between all residue pairs were recalculated with the GNM based on the new topology, and the contact of the residue pair with the largest fluctuation was broken. These above steps were repeated until all the noncovalent contacts were broken. This process is similar to the way in which these native contacts break in response to slowly increasing temperature. As the temperature is gradually increased, the fluctuations between residues will also increase. The larger the fluctuation is, the easier the breaking of the contact between them. The native contacts are expected to break in a fluctuation-dependent manner. In this method, the unfolding process is considered to be composed of a series of quasi-equilibrium processes corresponding to slowly increasing temperature. This method is similar to that adopted by Rader and co-workers (9).

With this approach, using two well-characterized proteins, CI2 and barnase, we have showed that this method can reproduce the order of protein unfolding events. It is implied that the unfolding process is largely determined by the topology of the protein. It is also showed that the unfolding pathway is robust against the introduction of some noise into the order in which the noncovalent contacts are broken. Then, several denatured states are selected from the unfolding process and the changes of the mechanical characters of the denatured state are studied as the native contacts are lost during unfolding.

METHODS

The Gaussian network model

The Gaussian network model describes a three-dimensional protein structure as an elastic network of C_α atoms connected by harmonic springs within a certain cutoff distance (7.0 Å is adopted in this work). In this work, we separate residue interactions into the covalent and noncovalent ones. Unlike the conventional GNM, the force constant is not identical for the springs of covalent and noncovalent pairs. The spring constants between all pairs of nonbonded residues that are within the cutoff distance are taken as γ. The strengths of the interactions between all covalently bonded pairs along the chain backbone are chosen as cγ. The values of c and γ are determined by fitting predicted fluctuations against the crystallographic B-factors, as described in the next section. Considering all contacting residues, the internal Hamiltonian of the system can be written as (26)

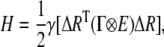(1)

where {ΔR} represents the 3N-dimensional column vectors of fluctuations ΔR₁, ΔR₂,…ΔR_N of the C_α atoms, where N is the number of residues; the superscript T denotes the transpose; E is the third-order identity matrix; ⊗ is the direct product; and Γ is the N×N symmetric matrix in which the elements are written as (34)

(2)

where R_ij is the separation between the i^th and j^th C_α atoms and r_c is the cutoff distance.

The mean-square fluctuation of each atom and the cross-correlation fluctuations between different atoms are in proportion to the diagonal and off-diagonal elements of the pseudo-inverse of the Γ matrix. The inverse of the matrix can be decomposed as

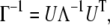(3)

where U is an orthogonal matrix whose columns u_i (1 < i ≤ N) are the eigenvectors of Γ, and Λ is a diagonal matrix of eigenvalues λ_i of Γ. The cross-correlation fluctuations between the i^th and j^th residues are given by

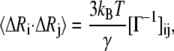(4)

where k_B is Boltzmann constant, T is absolute temperature, and the meanings of γ and Γ are the same as Eq. 1. When i = j, the mean-square fluctuation of the i^th residue can be obtained. The Debye-Waller or B-factor, which is related to the mean-square fluctuation, can be calculated with the expression

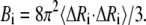(5)

The mean-square fluctuation of the i^th residue associating with the k^th mode is given by

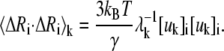(6)

The mean-square fluctuation in the distance vector R_ij between the residues i and j can be written as (35)

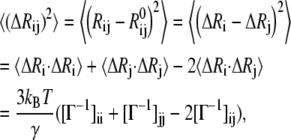(7)

where R_ij and 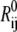are the instantaneous and equilibrium separation vectors between residues i and j. In the GNM, the cross-correlation is normalized as

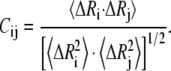(8)

As the temperature of a protein is gradually increased, the native contacts between residues are expected to break in a fluctuation-dependent manner. The fluctuations in the distance between all residues are calculated based on the GNM. The nonlinear elasticity during protein unfolding is considered through iterative normal mode calculations. We mimic the protein unfolding process by using the following procedure:

1. The mean-square fluctuations of the distance in all residue pairs are calculated based on the native structure topology with Eq. 7.

2. The contact in the residue pair with the largest distance fluctuation is broken. Then, a new matrix Γ is obtained, which represents a new topology during protein unfolding.

3. The mean-square fluctuations of the distance in all residue pairs are recalculated based on the new matrix Γ using Eq. 7.

4. The above two steps are repeated until all the noncovalent contacts are broken.

5. All the topologies of different conformation during protein unfolding are obtained and the unfolding pathway can be derived from the above obtained data.

Protein systems

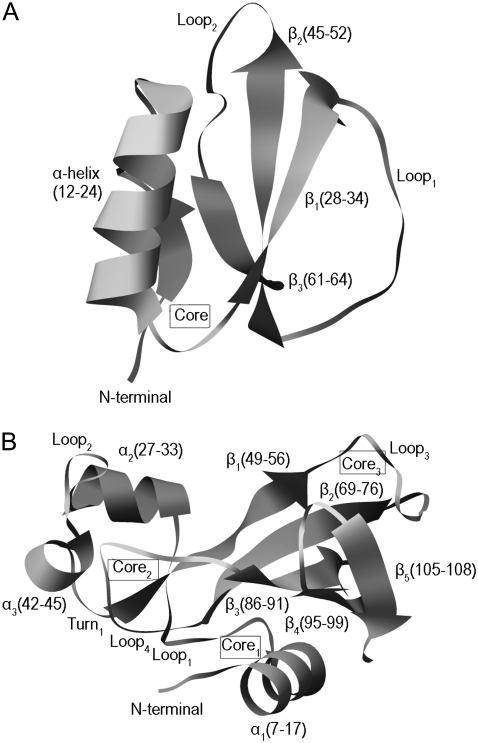
Two well-characterized proteins, CI2 and barnase, are used to show how topology of protein conformation determines the unfolding process. CI2 is a 64-residue protein (PDB code 2ci2) (36) that consists of an α-helix and a three-strand β-sheet. The main hydrophobic core is formed by the packing of the α-helix against the β-sheet (Fig. 1 A). The folding kinetics of CI2 has been investigated theoretically both with the atomistic (37–44) and the simplified statistical-mechanical models (45–49). Daggett and co-workers have used MD unfolding simulations of CI2 to characterize the transition-state ensemble (39,40,42,43). Lazaridis and Karplus (38), Ferrara et al. (44), and Ozkan et al. (49) have extracted characteristic sequences of events from average unfolding times of contacts in MD and Monte Carlo (MC) simulations.

FIGURE 1.

(A) Ribbon representation of the main-chain fold of CI2. The diagram is based on the crystal structure with PDB code 2CI2 determined to 2 Å resolution. The boundaries of the secondary structure elements are given in parentheses and the location of the hydrophobic core is indicated. The structure of the first 19 residues is not resolved. The residues of CI2 are renumbered to begin with 1 instead of 20 for ease of comparison with previous studies. (B) Ribbon representation of the main-chain fold of the crystal structure of barnase (PDB code 1A2P). The residues forming the secondary structure elements are showed in parentheses and the locations of the hydrophobic cores are indicated.

Barnase is a small, 110-residue ribonuclease (PDB code 1A2P) from Bacillus amyloliquefaciens. It is a α + β protein with three α-helices and a five-stranded β-sheet. There are three hydrophobic cores. The first (core₁) is formed by the packing of the major helix (α₁) against on the side of the β-sheet. The second (core₂) consists of hydrophobic residues from loop₁, loop₂, α₂, α₃, and β₁. The third core (core₃) is formed by the packing of loop₃ and loop₅ against the other side of the β-sheet (Fig. 1 B). Because the first two residues are missing in the crystal structure, the indexes of the residues are changed by subtracting 2 in the following text. The folding/unfolding pathway of barnase has been studied extensively using the protein engineering method (50–55) and MD simulations (56–60).

RESULTS AND DISCUSSION

Force constants for the covalent and noncovalent interactions

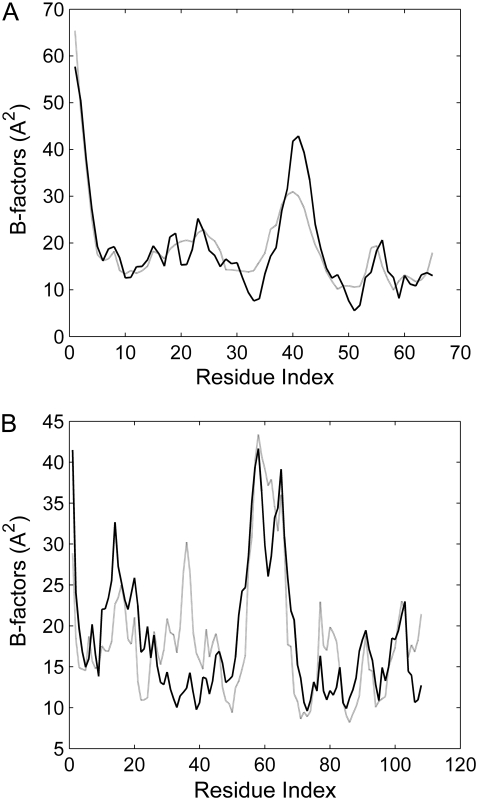
The values of the force constants cγ for the covalent interactions and γ for the noncovalent interactions are determined by comparing the theoretical B-factor with the x-ray experimental data. The theoretical B-factor is calculated using Eq. 5. Because the absolute value of γ does not affect the distribution (or relative size) of residue fluctuations, it has no influence on the correlation between the computed and experimental B-factors. So, the value of γ was set to 1 at first and the value of c was determined through maximizing the correlation between the computed and experimental B-factors. Then, the value of parameter γ was determined by normalizing the computed fluctuation with the experimental B-factors. Based on this method, the values of c and γ are obtained to be c = 9.3 and γ = 0.493 k_BT/Ų for CI2; c = 2.3 and γ = 0.945 k_BT /Ų for Barnase. Fig. 2 shows the correlation between the theoretical B-factor and the experimental one. The correlation coefficients are 0.912 and 0.730 for CI2 and barnase, respectively. These results imply that the GNM can give a good estimation for the fluctuations of the residues in proteins. It should be noted that we introduce different interaction parameters for the covalent and noncovalent residual contacts. It is found that by separating residue interactions into covalent and noncovalent, the correlation between the calculated residual fluctuation and the experimental B-factor is improved. The correlation coefficient is increased from 0.826 to 0.912 for CI2, and from 0.725 to 0.730 for barnase.

FIGURE 2.

Experimental (solid line) and calculated (shaded line) B-factors of CI2 (A) and barnase (B).

However, it should be noted that in most crystal structures, many factors are taken into account in experimentally determining B-factors, such as static disorder, wrong scaling of measurements, absorption, and incorrect atomic scattering curves. Hence, the force constants determined by B-factor may not be precise and should only be taken as a rough approximation (61). Therefore, it is important to study the influence of the force constants on the protein unfolding process. Noting that the absolute value of γ does not affect the distribution (or relative size) of residue fluctuations, it has no influence on the protein unfolding process in our model. But the value of c, which represents the relative intensity between the bonded and nonbonded interactions, will affect the distribution of residue fluctuations. It is found that when increasing the value of c, the secondary structure in proteins become stable during unfolding. On the contrary, when the value of c is decreased, the secondary structure will be easily disrupted in the early stage of protein unfolding. But the results showed that in a wide range of c-value, there is little influence on the main process of protein unfolding.

Sequences of unfolding events of CI2 and barnase revealed by this method

Using the method described above, the unfolding processes of CI2 and barnase are obtained. This method is coarse-grained, topology-based, and independent of amino-acid sequence. Based on this simple model, the results show that the order of the unfolding events are consistent with that of the thermal unfolding of proteins obtained with full atom MD simulation and experiments, which indicates that it is an effectual method to explore the protein unfolding process. It is also implied that the topology may play an important role in the protein unfolding process.

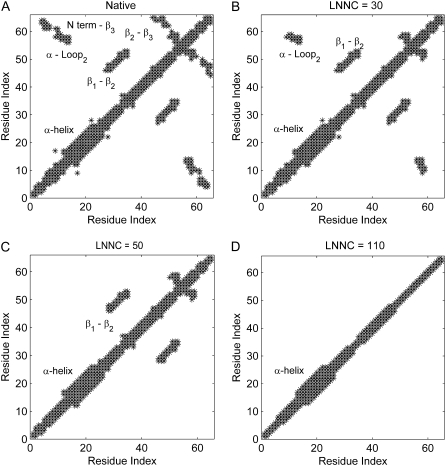
To elaborate the loss of the native contacts in the course of unfolding simulations, the contact maps of the conformation in different snapshots are constructed. Fig. 3 presents the contact maps of the native structure (A), of the conformations with the loss-number-of-native-contact (LNNC) to be 30 (B), 50 (C), and 110 (D) for CI2, respectively. The result reveals that there is a preferred process that shows a sequence of events for the unfolding of CI2. The first unfolding event is the disappearance of the native contact between the N-terminal and β₃, as shown in Fig. 3. Then the native contacts between the α-helix and the loop₂ are lost, which implies that the helix moves away from the loop between the β-strands 2 and 3. This causes the exposure of the hydrophobic core. During the exposure of the hydrophobic core, the contacts between the residues in β₂ and β₃ (β₂ − β₃) are lost. The previous MD simulations also have showed that after early displacement of the N-terminal, a key event is disruption of the hydrophobic core formed by α-helix, loop₂, and β₃, and the disappearance of the core occurred simultaneously with the destruction of the β₂ − β₃ sheet (38). Then the loss of contacts between residues in β₁ and β₂ (β₁ − β₂) is followed. The most persistent contacts are mainly between the residues within the α-helix and between the residues in the α-helix and β₁ loop, which disappeared at a later stage of the simulation. The sequence of unfolding events of CI2 obtained by this method is consistent with the thermal unfolding by MD and MC simulations (37–44,49).

FIGURE 3.

The contact maps of the native conformation (A), of the conformations with the LNNC to be 30 (B), 50 (C), and 110 (D) for CI2, respectively. Each native contact is marked by the symbol * in the map.

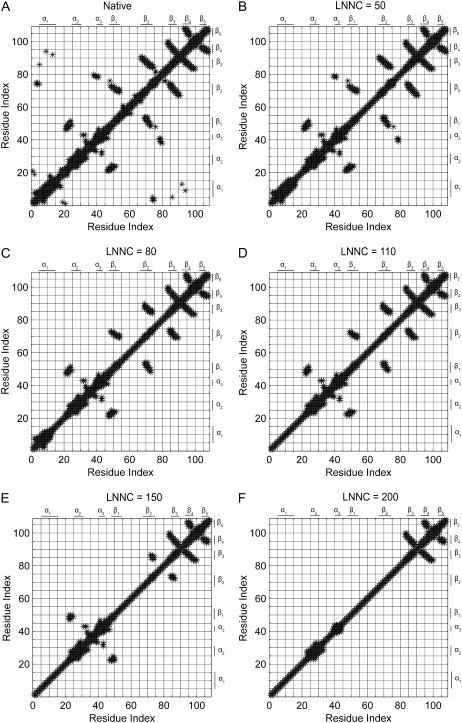
The contact maps of the conformation in different snapshots during unfolding for barnase are shown in Fig. 4. This figure presents the contact maps of the native structure (Fig. 4 A), the conformations with the LNNC to be 50 (Fig. 4 B), 80 (Fig. 4 C), 110 (Fig. 4 D), 150 (Fig. 4 E), and 200 (Fig. 4 F) for barnase, respectively. The unfolding process of barnase can be obtained from the change of the contact map. At the initial stage of unfolding, the N-terminus and α-helix₁ (α₁) move apart from the β-sheets, which results in the exposure of the hydrophobic core₁. During the exposure of core₁, loop₁, loop₃, and loop₄ are unwound. Then the native contacts between α₃ and loop₄ are gone. At the same time, α₁ is distorted. The more persistent contacts are between β₁ and β₂, between β₂ and β₃, between loop₂, α₃ and β₁, and between β₃, β₄, and β₅. The most stable structures are β₃, β₄, and β₅. The native contacts between them disappear at the latest stage of the unfolding simulation. The previous MD simulation, NMR, and other experimental techniques also have revealed that the central β-strands, β₃ and β₄, are stable in the denatured state and they act as a nucleation site in folding (53,59). The MD simulations have showed that the contacts between α₁ and the β-sheets are lost early in unfolding process. And the native contacts within three modules are relatively well sustained compared to the intermodule contacts. One module includes α₂, α₃, and loop₂; another includes β₁ and β₂; the last module includes β₃ and β₄ (58). These results are consistent with those obtained with our method. It should be noted that α₁ is stable in MD simulations, but it unfolds early in our method. The reason may be that the force constant c is small for barnase. If we increase the value of c, α₁ becomes stable without changing other unfolding events.

FIGURE 4.

The contact maps of (A) the native conformation, (B) the conformations with the LNNC to be 50, (C) 80, (D) 110, (E)150, and (F) 200 for barnase, respectively. Each *-mark in the map represents a native contact.

In the model adopted here, the detailed interactions among amino acids are replaced by springs, so the topology is the determinant for the results. Besides that, the effect of the water is not taken into account. But the sequence of the unfolding events is consistent with that obtained by MD simulations in water solution. Therefore, the results imply that the topology is an important factor in the protein unfolding process.

In this method, the protein unfolding process is simulated through breaking the native contact. Because of the simplicity of the model, the explicit conformational change during protein unfolding cannot be obtained. But the main events in protein unfolding can be identified from this method. It can reproduce the approximate order of events of protein unfolding. Based on the results, we can distinguish which region is more mobile, and which region more stable, in the thermal unfolding of the protein. It may help us in understanding the protein unfolding mechanism and the role of topology in the unfolding process.

A basic assumption in this method is that the native contacts alone can describe the overall shape of the funnel energy landscape and the interactions of any nonnative contacts are neglected. Many experimental and theoretical evidences have suggested that proteins, especially small fast-folding proteins, have selected sequences with minimal energetic frustration under evolutionary pressure, leaving the topology as the main source of the frustration in protein folding/unfolding. For these proteins, the main folding routes in the energy landscape are strongly shaped by their native topologies (8,62–64). In our work, the results also imply that the topology may play a main role in the protein unfolding process and the nonnative contacts may have little influence on the unfolding process for CI2 and barnase.

The robustness of unfolding process against noise

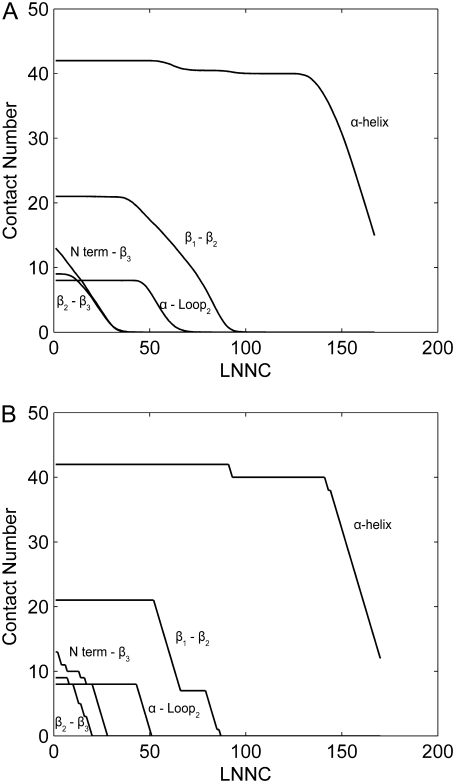
To introduce some noise into the method, reflecting the stochastic nature of thermal denaturation, similar to the method adopted by Rader et al. (9), the native contact to be removed is randomly selected from contacts with the first three largest fluctuations. Fig. 5 shows the losing process of the native contacts during the unfolding for CI2. The unfolding process with some noise is simulated 500 times and the average result is shown in Fig. 5 A. As contrast, the unfolding process without noise is represented in Fig. 5 B. It can be seen that the two figures are very similar. The native contacts between N-terminal and β₃ are lost early, simultaneously with the destruction of the β₂ − β₃ sheet. Then the loss of contacts between α-helix and the loop₂ (α-loop₂) occurs. After that, the contacts between residues in β₁ and β₂(β₁ − β₂₎ are broken. The contacts within the α-helix are gone, by the end. This process is consistent with that obtained from contact maps (see Fig. 3). Comparing Fig. 5 A with Fig. 5 B, it is founded that introducing some randomness into the thermal denaturation has little effect on the unfolding process. A similar result is obtained for barnase (data not shown).

FIGURE 5.

The process of losing of native contacts during unfolding of CI2. The unfolding process with some noise is simulated 500 times and the average result is showed in panel A. As contrast, the unfolding process without noise is represented in panel B. The x axis of the maps is the LNNC during unfolding, which represents the unfolding process. The y axis is the native contact number between those secondary structures mentioned above.

Change of fluctuations in the fast modes during protein unfolding

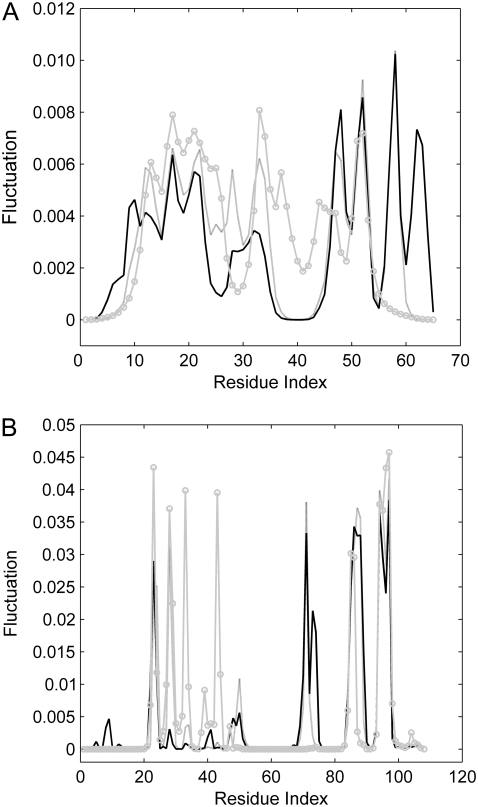
The fast modes correspond to geometric irregularity in the local structure and residues acting in the fast modes are thought of as kinetically hot residues. They are critically important for the stability of the tertiary fold (14,19,27). Several conformations are selected from the unfolding process and the fluctuations of all the residues in these conformations are calculated with Eq. 6. Fig. 6 A shows the fluctuations of the residues in the fastest eight modes for several conformations during the unfolding of CI2, in which the peaks of the fluctuations are mainly located in the hydrophobic core. This is considered to be the folding core of CI2. The similar results of barnase are represented in Fig. 6 B. It is also found that the residues with largest fluctuations are mainly located in the three hydrophobic cores. It should be noted that the peaks of the fluctuations are similar for these conformations selected from different stages in unfolding process. It implies that these residues appear to maintain a relatively high total number of contacts throughout the unfolding process, yet the tertiary structure is gradually disrupted during unfolding. This is consistent with the results obtained by MC simulation and GNM (49).

FIGURE 6.

The fluctuations of the residues in the fastest eight modes by GNM analysis of the several conformations visited during the unfolding of CI2 (A) and barnase (B). The solid, shaded, and shaded circled lines represent the native conformation, the conformation with LNNC = 50, and the conformation with LNNC = 80 for CI2, respectively. For barnase, they represent the native conformation, the conformation with LNNC = 80, and the conformation with LNNC = 150, respectively.

Change of correlation between the fluctuations of residues during protein unfolding

Similar to the analysis of Ozkan et al. (49), we explore the change of correlation between the fluctuations of residues during protein unfolding. The cross-correlations between the fluctuations of residues are calculated with Eq. 8. Fig. 7 depicts the cross-correlation maps of the fluctuations of residues, including all modes of motion, for several conformations selected from the unfolding process of CI2. The cross-correlation value ranges from −1 to 1, in which the positive values represent the residue motion in the same direction, and the negative values represent that they move in the opposite direction. The higher the absolute cross-correlation value is, the more the two residues are correlated (or anti-correlated). On the other hand, uncorrelated fluctuations yield C_ij = 0.

FIGURE 7.

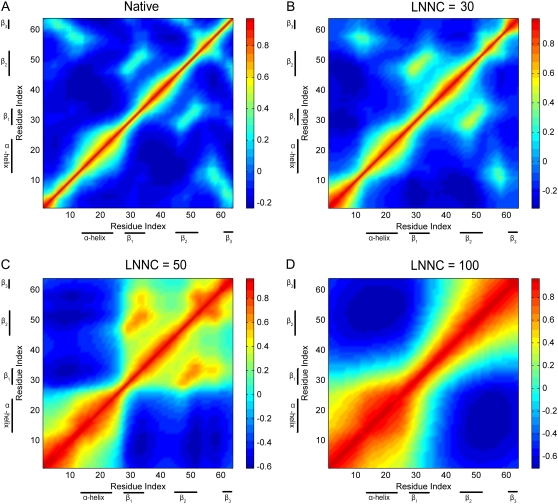
The cross-correlation maps calculated using all modes for native conformation (A) and several conformations with LNNC to be 30 (B), 50 (C), and100 (D) during the unfolding process of CI2. As shown in the color bar on the right, the blue regions in the figure indicate negative correlation and the green-yellow-red regions present positive correlation. Both the x and y axes of the maps are residue indices.

Fig. 7 A presents the correlation of the fluctuations in the native state of CI2. Along the diagonal of the map, there are several red blocks with positive correlations, which correspond to the secondary structures of α-helix and β-sheets. The figure also shows positive correlations between the strands β₁ and β₂, between β₂ and β₃, and between N-terminal and β₃, agreeing with the contact maps. With the loss of the native contacts during unfolding, the structure becomes flexible. As shown in Fig. 7 B, the positive correlations of the residue fluctuations along the diagonal are increasing. When the native contacts between N-terminal and β₃ (N term −β₃) and between α-helix and β₃ are gone, the N-terminal and helix will move apart from the β-strands to expose the hydrophobic core. As shown in Fig. 7 C, the negative correlations appear between them. At that time, the structure of the protein seems to be divided into two parts that fluctuate in the opposite directions. The positive correlation between β₁ and β₂ is persistent during the unfolding process. This consists with the contact maps (see Fig. 4). Overall, Fig. 7 shows that the denatured state does not behave as a random coil, and that long-range correlations exist in the denatured state.

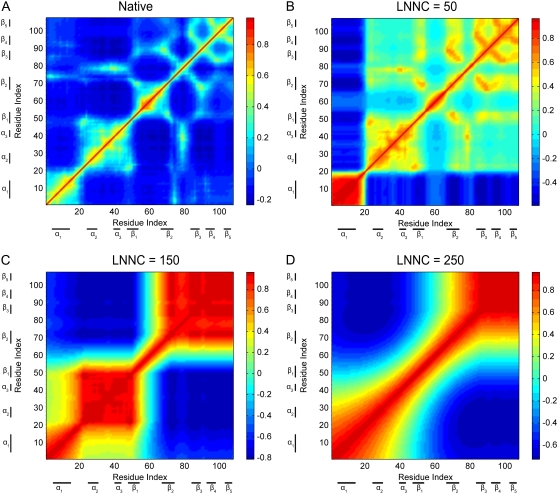
The cross-correlation maps of the fluctuations in the conformations visited during the unfolding process of barnase are also shown in Fig. 8. It is easy to identify the secondary structures and native contacts with positive correlations from the correlation map of the native structure shown in Fig. 8 A. The correlation map has a sudden change when the native contacts between N-terminal and β-strands and between α-helix1 (α₁) and β-strands disappear. The negative correlations between them appear as shown in Fig. 8 B, which implies that the N-terminus and α₁ move apart from the β-strands. In Fig. 8 C, when the native contacts between β₁ and β₂ are disrupted, the protein seems to be divided into two parts and they fluctuate around β₁ and β₂ in the opposite directions. The α₂, α₃ and the β₃, β₄, and β₅ are stable during barnase unfolding, which have positive correlations. A general view in these maps is that the positive correlations of the residue fluctuations along the diagonal become more pronounced during protein unfolding.

FIGURE 8.

The cross-correlation maps calculated with all modes for native conformation (A) and several conformations with LNNC to be 50 (B), 150 (C), and 250 (D) during the unfolding of barnase. The blue regions in the figure indicate negative correlation and the green-yellow-red regions represent positive correlation, as shown in the color bar on the right. Both the x and y axes of the maps are residue indices.

All the results suggest that long-range correlations exist in the denatured state. The highly cooperative structural dynamics is important for protein folding/unfolding to reduce the population searched in the conformation space.

CONCLUSIONS

A method based on the iterative use of the GNM is proposed to study protein unfolding, and the unfolding processes of CI2 and barnase are simulated with this method. As is well known, the GNM is a coarse-grained and topology-based model that is independent of amino-acid sequence. The detailed interactions among amino acids and the effect of water are not taken into account in this model. But the obtained results with this method are consistent with that of thermal unfolding studied by MD and MC simulations in solution. Our method can reproduce the approximate order of events of protein unfolding and can identify the flexible and rigid regions in the thermal unfolding of proteins. It is implied that our method is effective in studying protein unfolding. The results also imply that the unfolding processes of CI2 and barnase are largely determined by their topology. It is also shown that the unfolding process is robust against the introduction of some noise or stochastic characteristics.

Several conformations selected from unfolding process are studied to show how the fluctuations of residues and their correlations change as the native contacts are lost during unfolding. The results indicate that the residues acting in the fast modes are good candidates to be the key residues for folding. These residues maintain a relatively high total number of contacts during unfolding. The results also show that the denatured state does not behave as a random coil, but seems to have highly cooperative motions. It may help and promote the polypeptide chain to fold into the native state correctly and speedily.